基于 Transformers 的编码器-解码器模型

本文也提供英文版本 English。

基于 Transformers 的编码器-解码器模型

!pip install transformers==4.2.1
!pip install sentencepiece==0.1.95

Vaswani 等人在其名作 Attention is all you need 中首创了 基于 transformer 的编码器-解码器模型，如今已成为自然语言处理 (natural language processing，NLP) 领域编码器-解码器架构的 事实标准 。

最近基于 transformer 的编码器-解码器模型训练这一方向涌现出了大量关于 预训练目标函数 的研究，例如 T5、Bart、Pegasus、ProphetNet、Marge 等，但它们所使用的网络结构并没有改变。

本文的目的是 详细 解释如何用基于 transformer 的编码器-解码器架构来对 序列到序列 (sequence-to-sequence) 问题进行建模。我们将重点关注有关这一架构的数学知识以及如何对该架构的模型进行推理。在此过程中，我们还将介绍 NLP 中序列到序列模型的一些背景知识，并将 基于 transformer 的编码器-解码器架构分解为 编码器 和 解码器 这两个部分分别讨论。我们提供了许多图例，并把 基于 transformer 的编码器-解码器模型的理论与其在 🤗 transformers 推理场景中的实际应用二者联系起来。请注意，这篇博文 不 解释如何训练这些模型 —— 我们会在后续博文中涵盖这一方面的内容。

基于 transformer 的编码器-解码器模型是 表征学习 和 模型架构 这两个领域多年研究成果的结晶。本文简要介绍了神经编码器-解码器模型的历史，更多背景知识，建议读者阅读由 Sebastion Ruder 撰写的这篇精彩 博文。此外，建议读者对 _自注意力 (self-attention) 架构_有一个基本了解，可以阅读 Jay Alammar 的 这篇博文 复习一下原始 transformer 模型。

截至本文撰写时，🤗 transformers 库已经支持的编码器-解码器模型有: T5 、Bart 、MarianMT 以及 Pegasus ，你可以从 这儿 获取相关信息。

本文分 4 个部分:

• 背景 - 简要回顾了神经编码器-解码器模型的历史，重点关注基于 RNN 的模型。
• 编码器-解码器 - 阐述基于 transformer 的编码器-解码器模型，并阐述如何使用该模型进行推理。
• 编码器 - 阐述模型的编码器部分。
• 解码器 - 阐述模型的解码器部分。

每个部分都建立在前一部分的基础上，但也可以单独阅读。

背景

自然语言生成 (natural language generation，NLG) 是 NLP 的一个子领域，其任务一般可被建模为序列到序列问题。这类任务可以定义为寻找一个模型，该模型将输入词序列映射为目标词序列，典型的例子有 摘要 和 翻译 。在下文中，我们假设每个单词都被编码为一个向量表征。因此，$n$ 个输入词可以表示为 $n$ 个输入向量组成的序列:

$$\mathbf{X}_{1:n} = {\mathbf{x}_1, \ldots, \mathbf{x}_n}$$

因此，序列到序列问题可以表示为找到一个映射 $f$，其输入为 $n$ 个向量的序列，输出为 $m$ 个向量的目标序列 $\mathbf{Y}_{1:m}$。这里，目标向量数 $m$ 是先验未知的，其值取决于输入序列:

$$f: \mathbf{X}_{1:n} \to \mathbf{Y}_{1:m}$$

Sutskever 等 (2014) 的工作指出，深度神经网络 (deep neural networks，DNN)“_尽管灵活且强大，但只能用于拟合输入和输出维度均固定的映射。_” ${}^1$

因此，要用使用 DNN 模型 ${}^2$ 解决序列到序列问题就意味着目标向量数 $m$ 必须是先验已知的，且必须独立于输入 $\mathbf{X}{1:n}$。这样设定肯定不是最优的。因为对 NLG 任务而言，目标词的数量通常取决于输入内容 $\mathbf{X}{1:n}$，而不仅仅是输入长度 $n$。 例如 ，一篇 1000 字的文章，根据内容的不同，有可能可以概括为 200 字，也有可能可以概括为 100 字。

2014 年，Cho 等人 和 Sutskever 等人 提出使用完全基于递归神经网络 (recurrent neural networks，RNN) 的编码器-解码器模型来解决 _序列到序列_任务。与 DNN 相比，RNN 支持输出可变数量的目标向量。下面，我们深入了解一下基于 RNN 的编码器-解码器模型的功能。

在推理过程中，RNN 编码器通过连续更新其 隐含状态 ${}^3$ 对输入序列 $\mathbf{X}_{1:n}$ 进行编码。我们定义处理完最后一个输入向量 $\mathbf{x}_n$ 后的编码器隐含状态为 $\mathbf{c}$。因此，编码器主要完成如下映射:

$$f_{\theta_{enc}}: \mathbf{X}_{1:n} \to \mathbf{c}$$

然后，我们用 $\mathbf{c}$ 来初始化解码器的隐含状态，再用解码器 RNN 自回归地生成目标序列。

下面，我们进一步解释一下。从数学角度讲，解码器定义了给定隐含状态 $\mathbf{c}$ 下目标序列 $\mathbf{Y}_{1:m}$ 的概率分布:

$$p_{\theta_{dec}}(\mathbf{Y}_{1:m} |\mathbf{c})$$

根据贝叶斯法则，上述分布可以分解为每个目标向量的条件分布的积，如下所示:

$$p_{\theta_{dec}}(\mathbf{Y}_{1:m} |\mathbf{c}) = \prod_{i=1}^{m} p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c})$$

因此，如果模型架构可以在给定所有前驱目标向量的条件下对下一个目标向量的条件分布进行建模的话:

$$p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c}), \forall i \in \{1, \ldots, m\}$$

那它就可以通过简单地将所有条件概率相乘来模拟给定隐藏状态 $\mathbf{c}$ 下任意目标向量序列的分布。

那么基于 RNN 的解码器架构如何建模

$p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c})$ 呢?

从计算角度讲，模型按序将前一时刻的内部隐含状态 $\mathbf{c}{i-1}$ 和前一时刻的目标向量 $\mathbf{y}{i-1}$ 映射到当前内部隐含状态 $\mathbf{c}_i$ 和一个 logit 向量 $\mathbf{l}_i$ (下图中以深红色表示):

$$f_{\theta_{\text{dec}}}(\mathbf{y}_{i-1}, \mathbf{c}_{i-1}) \to \mathbf{l}_i, \mathbf{c}_i$$

此处，$\mathbf{c}_0$ 为 RNN 编码器的输出。随后，对 logit 向量 $\mathbf{l}_i$ 进行 softmax 操作，将其变换为下一个目标向量的条件概率分布:

$$p(\mathbf{y}_i | \mathbf{l}_i) = \textbf{Softmax}(\mathbf{l}_i), \text{ 其中 } \mathbf{l}_i = f_{\theta_{\text{dec}}}(\mathbf{y}_{i-1}, \mathbf{c}_{\text{prev}})$$

更多有关 logit 向量及其生成的概率分布的详细信息，请参阅脚注 ${}^4$。从上式可以看出，目标向量 $\mathbf{y}i$ 的分布是其前一时刻的目标向量 $\mathbf{y}{i-1}$ 及前一时刻的隐含状态 $\mathbf{c}{i-1}$ 的条件分布。而我们知道前一时刻的隐含状态 $\mathbf{c}{i-1}$ 依赖于之前所有的目标向量 $\mathbf{y}0, \ldots, \mathbf{y}{i- 2}$，因此我们可以说 RNN 解码器 隐式 (或间接) 地建模了条件分布 $p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c})$。

目标向量序列 $\mathbf{Y}{1:m}$ 的概率空间非常大，因此在推理时，必须借助解码方法对 = ${}^5$ 对 $p{\theta_{dec}}(\mathbf{Y}_{1:m} |\mathbf{c})$ 进行采样才能高效地生成最终的目标向量序列。

给定某解码方法，在推理时，我们首先从分布 $p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c})$ 中采样出下一个输出向量; 接着，将其添加至解码器输入序列末尾，让解码器 RNN 继续从 $p_{\theta_{\text{dec}}}(\mathbf{y}{i+1} | \mathbf{Y}{0: i}, \mathbf{c})$ 中采样出下一个输出向量 $\mathbf{y}_{i+1}$，如此往复，整个模型就以 _自回归_的方式生成了最终的输出序列。

基于 RNN 的编码器-解码器模型的一个重要特征是需要定义一些 特殊 向量，如 $\text{EOS}$ (终止符) 和 $\text{BOS}$ (起始符) 向量。 $\text{EOS}$ 向量通常意味着 $\mathbf{x}_n$ 中止，出现这个即“提示”编码器输入序列已结束; 如果它出现在目标序列中意味着输出结束，一旦从 logit 向量中采样到 $\text{EOS}$，生成就完成了。$\text{BOS}$ 向量用于表示在第一步解码时馈送到解码器 RNN 的输入向量 $\mathbf{y}_0$。为了输出第一个 logit $\mathbf{l}_1$，需要一个输入，而由于在其之前还没有生成任何输入，所以我们馈送了一个特殊的 $\text{BOS}$ 输入向量到解码器 RNN。好，有点绕了！我们用一个例子说明一下。

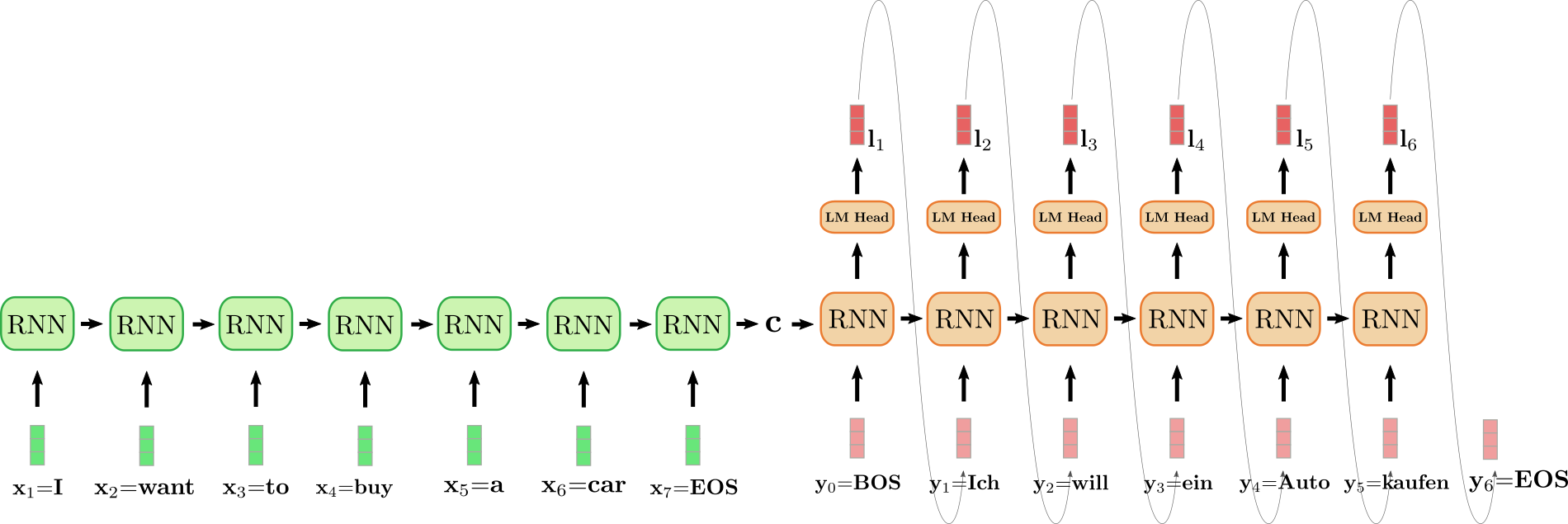
上图中，我们将编码器 RNN 编码器展开，并用绿色表示; 同时，将解码器 RNN 展开，并用红色表示。

英文句子 I want to buy a car，表示为 $(\mathbf{x}_1 = \text{I}$，$\mathbf{x}_2 = \text{want}$，$\mathbf{x}_3 = \text{to}$，$\mathbf{x}_4 = \text{buy}$，$\mathbf{x}_5 = \text{a}$，$\mathbf{x}_6 = \text{car}$，$\mathbf{x}_7 = \text{EOS}$)。将其翻译成德语: “Ich will ein Auto kaufen"，表示为 $(\mathbf{y}_0 = \text{BOS}$，$\mathbf{y}_1 = \text{Ich}$，$\mathbf{y}_2 = \text{will}$，$\mathbf{y}_3 = \text {ein}$，$\mathbf{y}_4 = \text{Auto}$，$\mathbf{y}_5 = \text{kaufen}$，$\mathbf{y}_6=\text{EOS}$)。首先，编码器 RNN 处理输入向量 $\mathbf{x}_1 = \text{I}$ 并更新其隐含状态。请注意，对编码器而言，因为我们只对其最终隐含状态 $\mathbf{c}$ 感兴趣，所以我们可以忽略它的目标向量。然后，编码器 RNN 以相同的方式依次处理输入句子的其余部分: $\text{want}$、$\text{to}$、$\text{buy}$、$\text{a}$、$\text{car}$、$\text{EOS}$，并且每一步都更新其隐含状态，直到遇到向量 $\mathbf{x}_7={EOS}$ ${}^6$。在上图中，连接展开的编码器 RNN 的水平箭头表示按序更新隐含状态。编码器 RNN 的最终隐含状态，由 $\mathbf{c}$ 表示，其完全定义了输入序列的 编码 ，并可用作解码器 RNN 的初始隐含状态。可以认为，解码器 RNN 以编码器 RNN 的最终隐含状态为条件。

为了生成第一个目标向量，将 $\text{BOS}$ 向量输入给解码器，即上图中的 $\mathbf{y}_0$。然后通过 语言模型头 (LM Head) 前馈层将 RNN 的目标向量进一步映射到 logit 向量 $\mathbf{l}_1$，此时，可得第一个目标向量的条件分布:

$$p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \mathbf{c})$$

最终采样出第一个目标词 $\text{Ich}$ (如图中连接 $\mathbf{l}_1$ 和 $\mathbf{y}_1$ 的灰色箭头所示)。接着，继续采样出第二个目标向量:

$$\text{will} \sim p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \text{Ich}, \mathbf{c})$$

依此类推，一直到第 6 步，此时从 $\mathbf{l}6$ 中采样出 $\text{EOS}$，解码完成。输出目标序列为 $\mathbf{Y}{1:6} = {\mathbf{y}_1, \ldots, \mathbf{y}_6}$, 即上文中的 “Ich will ein Auto kaufen”。

综上所述，我们通过将分布 $p(\mathbf{Y}{1:m} | \mathbf{X}{1:n})$ 分解为 $f_{\theta_{\text{enc}}}$ 和 $p_{\theta_{\text{dec}}}$ 的表示来建模基于 RNN 的 encoder-decoder 模型:

$$p_{\theta_{\text{enc}}, \theta_{\text{dec}}}(\mathbf{Y}_{1:m} | \mathbf{X}_{1:n}) = \prod_{i=1}^{m} p_{\theta_{\text{enc}}, \theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{X}_{1:n}) = \prod_{i=1}^{m} p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c}), \text{ 其中 } \mathbf{c}=f_{\theta_{enc}}(X)$$

在推理过程中，利用高效的解码方法可以自回归地生成目标序列 $\mathbf{Y}_{1:m}$。

基于 RNN 的编码器-解码器模型席卷了 NLG 社区。2016 年，谷歌宣布用基于 RNN 的编码器-解码器单一模型完全取代其原先使用的的含有大量特征工程的翻译服务 (参见 此处)。

然而，基于 RNN 的编码器-解码器模型存在两个主要缺陷。首先，RNN 存在梯度消失问题，因此很难捕获长程依赖性， 参见 Hochreiter 等 (2001) 的工作。其次，RNN 固有的循环架构使得在编码时无法进行有效的并行化， 参见 Vaswani 等 (2017) 的工作。

---

${}^1$ 论文的原话是“_尽管 DNN 具有灵活性和强大的功能，但它们只能应用于输入和目标可以用固定维度的向量进行合理编码的问题_”，用在本文时稍作调整。

${}^2$ 这同样适用于卷积神经网络 (CNN)。虽然可以将可变长度的输入序列输入 CNN，但目标的维度要么取决于输入维数要么需要固定为特定值。

${}^3$ 在第一步时，隐含状态被初始化为零向量，并与第一个输入向量 $\mathbf{x}_1$ 一起馈送给 RNN。

${}^4$ 神经网络可以将所有单词的概率分布定义为 $p(\mathbf{y} | \mathbf{c}, \mathbf{Y}{0 : i-1})$。首先，其将输入 $\mathbf{c}, \mathbf{Y}{0: i-1}$ 转换为嵌入向量 $\mathbf{y'}$，该向量对应于 RNN 模型的目标向量。随后将 $\mathbf{y'}$ 送给“语言模型头”，即将其乘以 词嵌入矩阵 (即$\mathbf{Y}^{\text{vocab}}$)，得到 $\mathbf{y'}$ 和词表 $\mathbf{Y}^{\text{vocab}}$ 中的每个向量 $\mathbf{y}$ 的相似度得分，生成的向量称为 logit 向量 $\mathbf{l} = \mathbf{Y}^{\text{vocab}} \mathbf{y'}$，最后再通过 softmax 操作归一化成所有单词的概率分布: $p(\mathbf{y} | \mathbf{c}) = \text{Softmax}(\mathbf{Y}^{\text{vocab}} \mathbf{y'}) = \text {Softmax}(\mathbf{l})$。

${}^5$ 波束搜索 (beam search) 是其中一种解码方法。本文不会对不同的解码方法进行介绍，如对此感兴趣，建议读者参考 此文。

${}^6$ Sutskever 等 (2014) 的工作对输入顺序进行了逆序，对上面的例子而言，输入向量变成了 ($\mathbf{x}_1 = \text{car}$，$\mathbf{x}_2 = \text{a}$，$\mathbf{x}_3 = \text{buy}$，$\mathbf{x}_4 = \text{to}$，$\mathbf{x}_5 = \text{want}$，$\mathbf{x}_6 = \text{I}$，$\mathbf{x}_7 = \text{EOS}$)。其动机是让对应词对之间的连接更短，如可以使得 $\mathbf{x}_6 = \text{I}$ 和 $\mathbf{y}_1 = \text{Ich}$ 之间的连接更短。该研究小组强调，将输入序列进行逆序是他们的模型在机器翻译上的性能提高的一个关键原因。

编码器-解码器

2017 年，Vaswani 等人引入了 transformer 架构，从而催生了 基于 transformer 的编码器-解码器模型。

与基于 RNN 的编码器-解码器模型类似，基于 transformer 的编码器-解码器模型由一个编码器和一个解码器组成，且其编码器和解码器均由 残差注意力模块 (residual attention blocks) 堆叠而成。基于 transformer 的编码器-解码器模型的关键创新在于: 残差注意力模块无需使用循环结构即可处理长度 $n$ 可变的输入序列 $\mathbf{X}_{1:n}$。不依赖循环结构使得基于 transformer 的编码器-解码器可以高度并行化，这使得模型在现代硬件上的计算效率比基于 RNN 的编码器-解码器模型高出几个数量级。

回忆一下，要解决 序列到序列 问题，我们需要找到输入序列 $\mathbf{X}{1:n}$ 到变长输出序列 $\mathbf{Y}{1:m}$ 的映射。我们看看如何使用基于 transformer 的编码器-解码器模型来找到这样的映射。

与基于 RNN 的编码器-解码器模型类似，基于 transformer 的编码器-解码器模型定义了在给定输入序列 $\mathbf{X}{1:n}$ 条件下目标序列 $\mathbf{Y}{1:m}$ 的条件分布:

$$p_{\theta_{\text{enc}}, \theta_{\text{dec}}}(\mathbf{Y}_{1:m} | \mathbf{X}_{1:n})$$

基于 transformer 的编码器部分将输入序列 $\mathbf{X}{1:n}$ 编码为 隐含状态序列 $\mathbf{\overline{X}}{1:n}$，即:

$$f_{\theta_{\text{enc}}}: \mathbf{X}_{1:n} \to \mathbf{\overline{X}}_{1:n}$$

然后，基于 transformer 的解码器负责建模在给定隐含状态序列 $\mathbf{\overline{X}}{1:n}$ 的条件下目标向量序列 $\mathbf{Y}{1:m}$ 的概率分布:

$$p_{\theta_{dec}}(\mathbf{Y}_{1:m} | \mathbf{\overline{X}}_{1:n})$$

根据贝叶斯法则，该序列分布可被分解为每个目标向量 $\mathbf{y}i$ 在给定隐含状态 $\mathbf{\overline{X} }{1:n}$ 和其所有前驱目标向量 $\mathbf{Y}_{0:i-1}$ 时的条件概率之积:

$$p_{\theta_{dec}}(\mathbf{Y}_{1:m} | \mathbf{\overline{X}}_{1:n}) = \prod_{i=1}^{m} p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n})$$

因此，在生成 $\mathbf{y}i$ 时，基于 transformer 的解码器将隐含状态序列 $\mathbf{\overline{X}}{1:n}$ 及其所有前驱目标向量 $\mathbf{Y}{0 :i-1}$ 映射到 logit 向量 $\mathbf{l}i$。 然后经由 softmax 运算对 logit 向量 $\mathbf{l}i$ 进行处理，从而生成条件分布 $p{\theta{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}{1:n})$。这个流程跟基于 RNN 的解码器是一样的。然而，与基于 RNN 的解码器不同的是，在这里，目标向量 $\mathbf{y}i$ 的分布是 显式(或直接) 地以其所有前驱目标向量 $\mathbf{y}0, \ldots, \mathbf{y}{i-1}$ 为条件的，稍后我们将详细介绍。此处第 0 个目标向量 $\mathbf{y}0$ 仍表示为 $\text{BOS}$ 向量。有了条件分布 $p{\theta{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X} }{1:n})$，我们就可以 自回归_生成输出了。至此，我们定义了可用于推理的从输入序列 $\mathbf{X}{1:n}$ 到输出序列 $\mathbf{Y}{1:m}$ 的映射。

我们可视化一下使用 基于 transformer 的编码器-解码器模型 _自回归_地生成序列的完整过程。

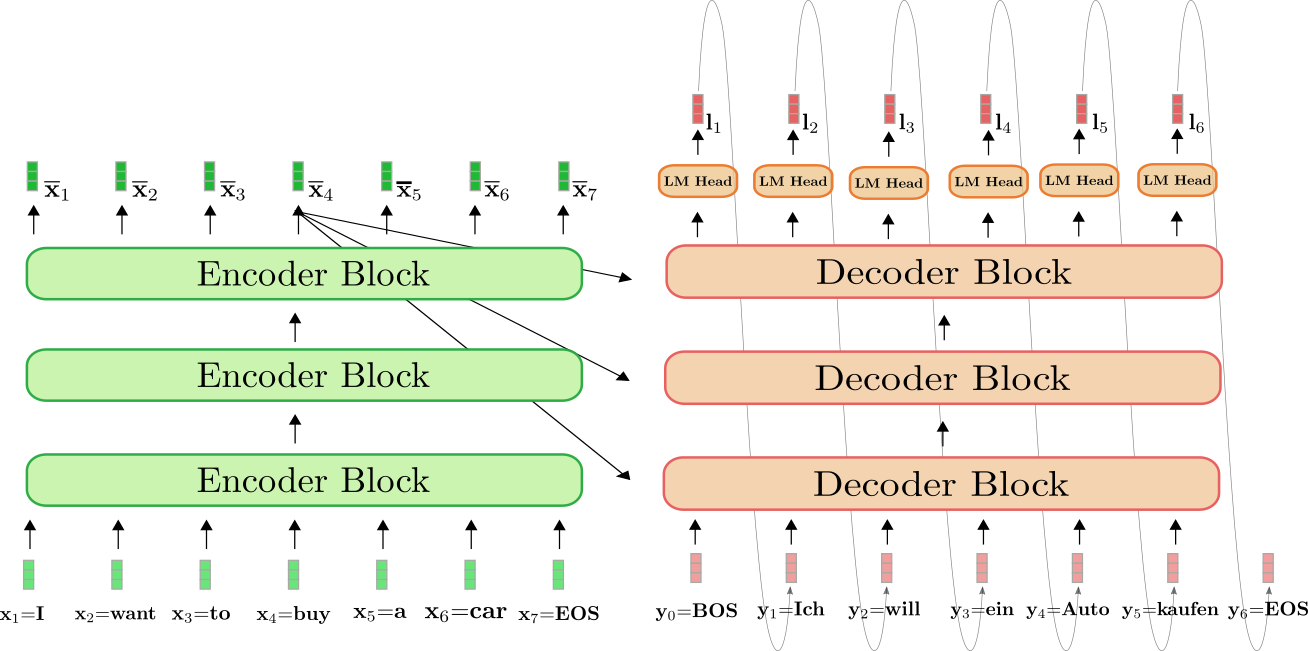
上图中，绿色为基于 transformer 的编码器，红色为基于 transformer 的解码器。与上一节一样，我们展示了如何将表示为 $(\mathbf{x}_1 = \text{I}，\mathbf{ x}_2 = \text{want}，\mathbf{x}_3 = \text{to}，\mathbf{x}_4 = \text{buy}，\mathbf{x}_5 = \text{a}，\mathbf{x}_6 = \text{car}，\mathbf{x}_7 = \text{EOS})$ 的英语句子 “I want to buy a car” 翻译成表示为 $(\mathbf{y}_0 = \text{BOS}，\mathbf{y }_1 = \text{Ich}，\mathbf{y}_2 = \text{will}，\mathbf{y}_3 = \text{ein}，\mathbf{y}_4 = \text{Auto}，\mathbf{y}_5 = \text{kaufen}，\mathbf{y}_6=\text{EOS})$ 的德语句子 “Ich will ein Auto kaufen”。

首先，编码器将完整的输入序列 $\mathbf{X}{1:7}$ = “I want to buy a car” (由浅绿色向量表示) 处理为上下文相关的编码序列 $\mathbf{\overline{X}}{1:7}$。这里上下文相关的意思是， 举个例子 ，$\mathbf{\overline{x}}_4$ 的编码不仅取决于输入 $\mathbf{x}_4$ = “buy”，还与所有其他词 “I”、“want”、“to”、“a”、“car” 及 “EOS” 相关，这些词即该词的 上下文 。

接下来，输入编码 $\mathbf{\overline{X}}_{1:7}$ 与 BOS 向量 ( 即 $\mathbf{y}0$) 被一起馈送到解码器。解码器将输入 $\mathbf{\overline{X}}{1:7}$ 和 $\mathbf{y}_0$ 变换为第一个 logit $\mathbf{l }_1$ (图中以深红色显示)，从而得到第一个目标向量 $\mathbf{y}_1$ 的条件分布:

$$p_{\theta_{enc, dec}}(\mathbf{y} | \mathbf{y}_0, \mathbf{X}_{1:7}) = p_{\theta_{enc, dec}}(\mathbf{y} | \text{BOS}, \text{I want to buy a car EOS}) = p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \mathbf{\overline{X}}_{1:7})$$

然后，从该分布中采样出第一个目标向量 $\mathbf{y}_1$ = $\text{Ich}$ (由灰色箭头表示)，得到第一个输出后，我们会并将其继续馈送到解码器。现在，解码器开始以 $\mathbf{y}_0$ = “BOS” 和 $\mathbf{y}_1$ = “Ich” 为条件来定义第二个目标向量的条件分布 $\mathbf{y}_2$:

$$p_{\theta_{dec}}(\mathbf{y} | \text{BOS Ich}, \mathbf{\overline{X}}_{1:7})$$

再采样一次，生成目标向量 $\mathbf{y}_2$ = “will”。重复该自回归过程，直到第 6 步从条件分布中采样到 EOS:

$$\text{EOS} \sim p_{\theta_{dec}}(\mathbf{y} | \text{BOS Ich will ein Auto kaufen}, \mathbf{\overline{X}}_{1:7})$$

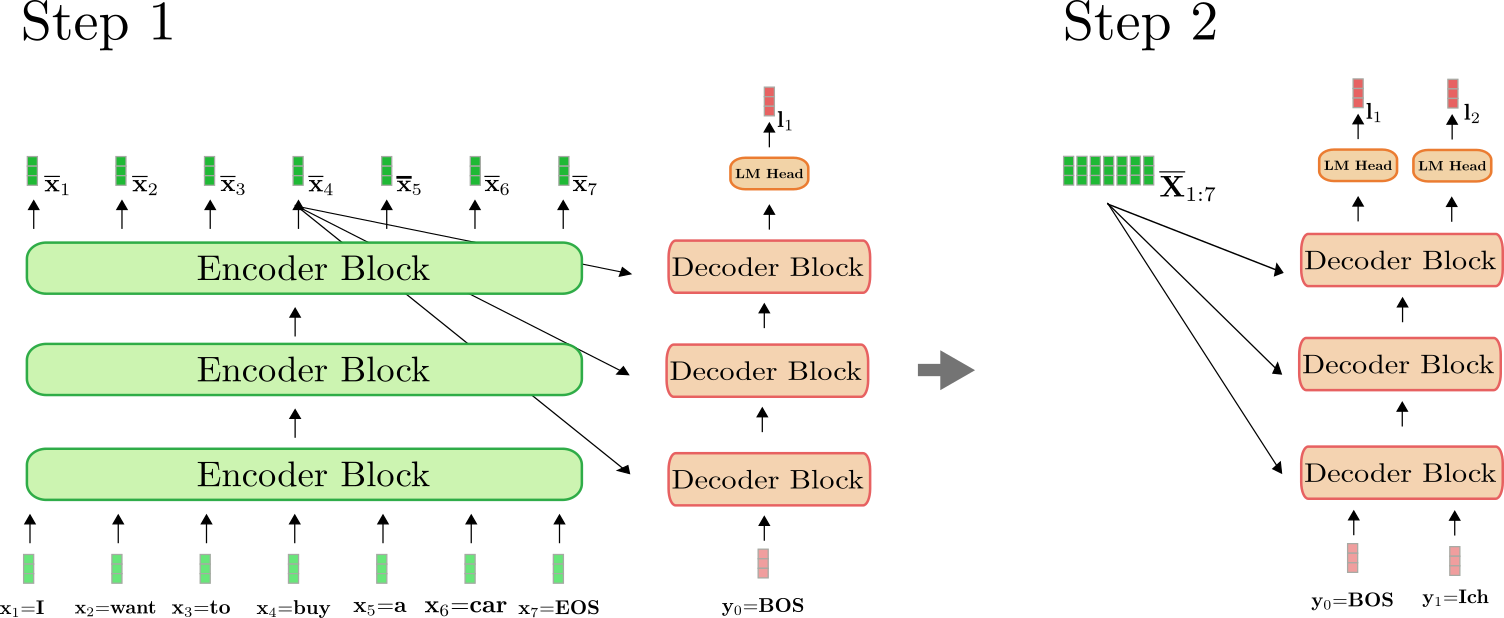
这里有一点比较重要，我们仅在第一次前向传播时用编码器将 $\mathbf{X}{1:n}$ 映射到 $\mathbf{\overline{X}}{ 1:n}$。从第二次前向传播开始，解码器可以直接使用之前算得的编码 $\mathbf{\overline{X}}_{1:n}$。为清楚起见，下图画出了上例中第一次和第二次前向传播所需要做的操作。

可以看出，仅在步骤 $i=1$ 时，我们才需要将 “I want to buy a car EOS” 编码为 $\mathbf{\overline{X}}_{1:7}$。从 $i=2$ 开始，解码器只是简单地复用了已生成的编码。

在 🤗 transformers 库中，这一自回归生成过程是在调用 .generate() 方法时在后台完成的。我们用一个翻译模型来实际体验一下。

from transformers import MarianMTModel, MarianTokenizer

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")

# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# translate example
output_ids = model.generate(input_ids)[0]

# decode and print
print(tokenizer.decode(output_ids))

输出:

    <pad> Ich will ein Auto kaufen

.generate() 接口做了很多事情。首先，它将 input_ids 传递给编码器。然后，它将一个预定义的标记连同已编码的 input_ids一起传递给解码器 (在使用 MarianMTModel 的情况下，该预定义标记为 $\text{}$)。接着，它使用波束搜索解码机制根据最新的解码器输出的概率分布${}^1$自回归地采样下一个输出词。更多有关波束搜索解码工作原理的详细信息，建议阅读 这篇博文。

我们在附录中加入了一个代码片段，展示了如何“从头开始”实现一个简单的生成方法。如果你想要完全了解 _自回归_生成的幕后工作原理，强烈建议阅读附录。

总结一下:

• 基于 transformer 的编码器实现了从输入序列 $\mathbf{X}{1:n}$ 到上下文相关的编码序列 $\mathbf{\overline{X}}{1 :n}$ 之间的映射。
• 基于 transformer 的解码器定义了条件分布 $p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{ \overline{X}}_{1:n})$。
• 给定适当的解码机制，可以自回归地从 $p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}{1:n}), \forall i \in {1, \ldots, m}$ 中采样出输出序列 $\mathbf{Y}{1:m}$。

太好了，现在我们已经大致了解了 基于 transformer 的_编码器-解码器模型的工作原理。下面的部分，我们将更深入地研究模型的编码器和解码器部分。更具体地说，我们将确切地看到编码器如何利用自注意力层来产生一系列上下文相关的向量编码，以及自注意力层如何实现高效并行化。然后，我们将详细解释自注意力层在解码器模型中的工作原理，以及解码器如何通过 交叉注意力 层以编码器输出为条件来定义分布 $p{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}_{1:n})$。在此过程中，基于 transformer 的编码器-解码器模型如何解决基于 RNN 的编码器-解码器模型的长程依赖问题的答案将变得显而易见。

---

${}^1$ 可以从 此处 获取 "Helsinki-NLP/opus-mt-en-de" 的解码参数。可以看到，其使用了 num_beams=6 的波束搜索。

编码器

如前一节所述， 基于 transformer 的编码器将输入序列映射到上下文相关的编码序列:

$$f_{\theta_{\text{enc}}}: \mathbf{X}_{1:n} \to \mathbf{\overline{X}}_{1:n}$$

仔细观察架构，基于 transformer 的编码器由许多 _残差注意力模块_堆叠而成。每个编码器模块都包含一个 双向自注意力层，其后跟着两个前馈层。这里，为简单起见，我们忽略归一化层 (normalization layer)。此外，我们不会深入讨论两个前馈层的作用，仅将其视为每个编码器模块 ${}^1$ 的输出映射层。双向自注意层将每个输入向量 $\mathbf{x'}_j, \forall j \in {1, \ldots, n}$ 与全部输入向量 $\mathbf{x'}_1, \ldots, \mathbf{x'}_n$ 相关联并通过该机制将每个输入向量 $\mathbf{x'}_j$ 提炼为与其自身上下文相关的表征: $\mathbf{x''}j$。因此，第一个编码器块将输入序列 $\mathbf{X}{1:n}$ (如下图浅绿色所示) 中的每个输入向量从 上下文无关 的向量表征转换为 上下文相关_的向量表征，后面每一个编码器模块都会进一步细化这个上下文表征，直到最后一个编码器模块输出最终的上下文相关编码 $\mathbf{\overline{X}}{1:n}$ (如下图深绿色所示)。

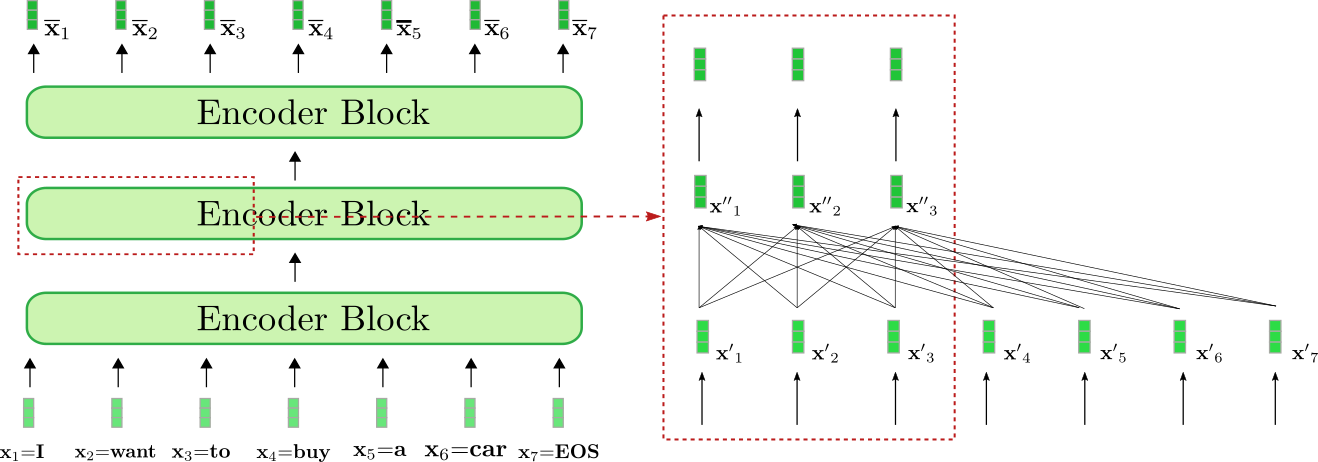
我们对 编码器如何将输入序列 "I want to buy a car EOS" 变换为上下文编码序列这一过程进行一下可视化。与基于 RNN 的编码器类似，基于 transformer 的编码器也在输入序列最后添加了一个 EOS，以提示模型输入向量序列已结束 ${}^2$。

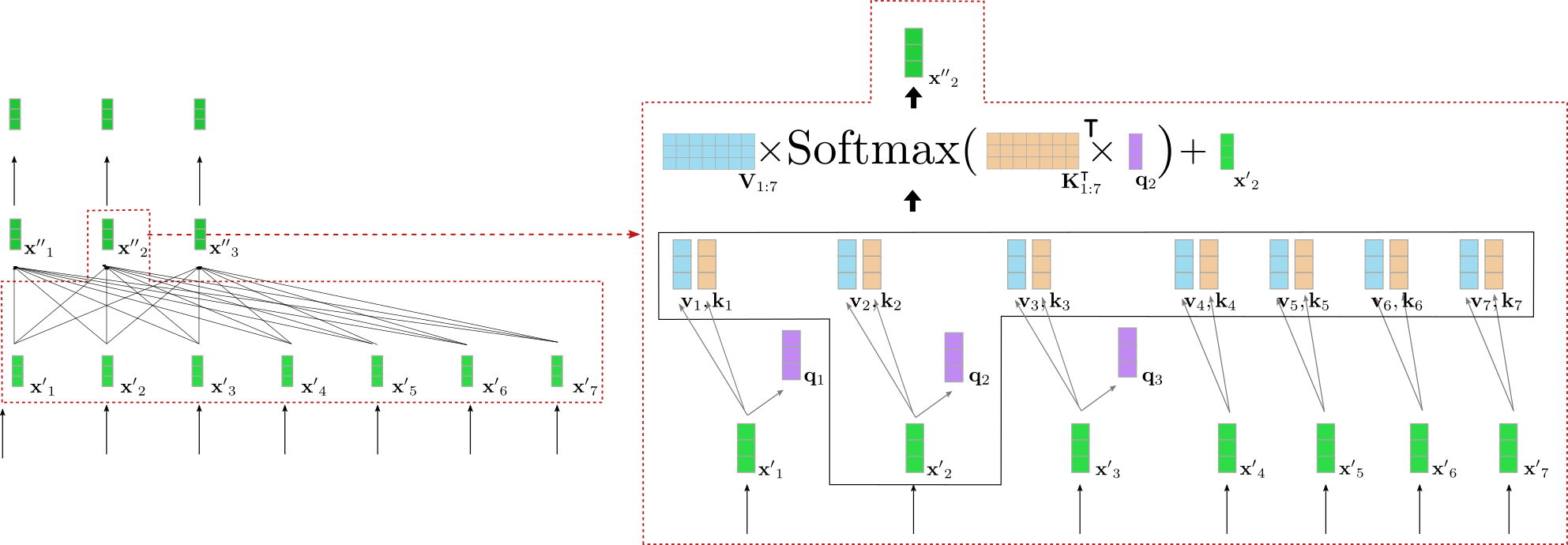
上图中的 基于 transformer 的编码器由三个编码器模块组成。我们在右侧的红框中详细列出了第二个编码器模块的前三个输入向量: $\mathbf{x}_1$，$\mathbf {x}_2$ 及 $\mathbf{x}_3$。红框下部的全连接图描述了双向自注意力机制，上面是两个前馈层。如前所述，我们主要关注双向自注意力机制。

可以看出，自注意力层的每个输出向量 $\mathbf{x''}_i, \forall i \in {1, \ldots, 7}$ 都 直接 依赖于 所有 输入向量 $\mathbf{x'}_1, \ldots, \mathbf{x'}_7$。这意味着，单词 “want” 的输入向量表示 $\mathbf{x'}_2$ 与单词 “buy” (即 $\mathbf{x'}_4$) 和单词 “I” (即 $\mathbf{x'}1$) 直接相关。 因此，“want” 的输出向量表征，_即 $\mathbf{x''}_2$，是一个融合了其上下文信息的更精细的表征。

我们更深入了解一下双向自注意力的工作原理。编码器模块的输入序列 $\mathbf{X'}_{1:n}$ 中的每个输入向量 $\mathbf{x'}_i$ 通过三个可训练的权重矩阵 $\mathbf{W}_q$，$\mathbf{W}_v$，$\mathbf{W}_k$ 分别投影至 key 向量 $\mathbf{k}_i$、value 向量 $\mathbf{v}_i$ 和 query 向量 $\mathbf{q}_i$ (下图分别以橙色、蓝色和紫色表示):

$$\mathbf{q}_i = \mathbf{W}_q \mathbf{x'}_i,$$ $$\mathbf{v}_i = \mathbf{W}_v \mathbf{x'}_i,$$ $$\mathbf{k}_i = \mathbf{W}_k \mathbf{x'}_i,$$ $$\forall i \in {1, \ldots n }$$

请注意，对每个输入向量 $\mathbf{x}_i (\forall i \in {i, \ldots, n}$) 而言，其所使用的权重矩阵都是 相同的。将每个输入向量 $\mathbf{x}_i$ 投影到 query 、 key 和 value 向量后，将每个 query 向量 $\mathbf{q}_j (\forall j \in {1, \ldots, n}$) 与所有 key 向量 $\mathbf{k}_1, \ldots, \mathbf{k}_n$ 进行比较。哪个 key 向量与 query 向量 $\mathbf{q}_j$ 越相似，其对应的 value 向量 $\mathbf{v}_j$ 对输出向量 $\mathbf{x''}_j$ 的影响就越重要。更具体地说，输出向量 $\mathbf{x''}_j$ 被定义为所有 value 向量的加权和 $\mathbf{v}_1, \ldots, \mathbf{v}_n$ 加上输入向量 $\mathbf{x'}_j$。而各 value 向量的权重与 $\mathbf{q}_j$ 和各个 key 向量 $\mathbf{k}_1, \ldots, \mathbf{k}n$ 之间的余弦相似度成正比，其数学公式为 $\textbf{Softmax}(\mathbf{K}{1:n}^\intercal \mathbf{q}_j)$，如下文的公式所示。关于自注意力层的完整描述，建议读者阅读 这篇 博文或 原始论文。

好吧，又复杂起来了。我们以上例中的一个 query 向量为例图解一下双向自注意层。为简单起见，本例中假设我们的 基于 transformer 的解码器只有一个注意力头 config.num_heads = 1 并且没有归一化层。

图左显示了上个例子中的第二个编码器模块，右边详细可视化了第二个输入向量 $\mathbf{x'}_2$ 的双向自注意机制，其对应输入词为 “want”。首先将所有输入向量 $\mathbf{x'}_1, \ldots, \mathbf{x'}_7$ 投影到它们各自的 query 向量 $\mathbf{q}_1, \ldots, \mathbf{q}_7$ (上图中仅以紫色显示前三个 query 向量)， value 向量 $\mathbf{v}_1, \ldots, \mathbf{v}_7$ (蓝色) 和 key 向量 $\mathbf{k}_1, \ldots, \mathbf{k}_7$ (橙色)。然后，将 query 向量 $\mathbf{q}2$ 与所有 key 向量的转置 ( 即 $\mathbf{K}{1:7}^{\intercal}$) 相乘，随后进行 softmax 操作以产生 自注意力权重 。 自注意力权重最终与各自的 value 向量相乘，并加上输入向量 $\mathbf{x'}_2$，最终输出单词 “want” 的上下文相关表征， 即 $\mathbf{x''}2$ (图右深绿色表示)。整个等式显示在图右框的上部。 $\mathbf{K}{1:7}^{\intercal}$ 和 $\mathbf{q}_2$ 的相乘使得将 “want” 的向量表征与所有其他输入 (“I”，“to”，“buy”，“a”，“car”，“EOS”) 的向量表征相比较成为可能，因此自注意力权重反映出每个输入向量 $\mathbf{x'}_j$ 对 “want” 一词的最终表征 $\mathbf{x''}_2$ 的重要程度。

为了进一步理解双向自注意力层的含义，我们假设以下句子: “ 房子很漂亮且位于市中心，因此那儿公共交通很方便_”。 “那儿”这个词指的是“房子”，这两个词相隔 12 个字。在基于 transformer 的编码器中，双向自注意力层运算一次，即可将“房子”的输入向量与“那儿”的输入向量相关联。相比之下，在基于 RNN 的编码器中，相距 12 个字的词将需要至少 12 个时间步的运算，这意味着在基于 RNN 的编码器中所需数学运算与距离呈线性关系。这使得基于 RNN 的编码器更难对长程上下文表征进行建模。此外，很明显，基于 transformer 的编码器比基于 RNN 的编码器-解码器模型更不容易丢失重要信息，因为编码的序列长度相对输入序列长度保持不变， 即 $\textbf{len }(\mathbf{X}{1:n}) = \textbf{len}(\mathbf{\overline{X}}{1:n}) = n$，而 RNN 则会将 $\textbf{len}((\mathbf{X}{1:n}) = n$ 压缩到 $\textbf{len}(\mathbf{c}) = 1$，这使得 RNN 很难有效地对输入词之间的长程依赖关系进行编码。

除了更容易学到长程依赖外，我们还可以看到 transformer 架构能够并行处理文本。从数学上讲，这是通过将自注意力机制表示为 query 、 key 和 value 的矩阵乘来完成的:

$$\mathbf{X''}_{1:n} = \mathbf{V}_{1:n} \text{Softmax}(\mathbf{Q}_{1:n}^\intercal \mathbf{K}_{1:n}) + \mathbf{X'}_{1:n}$$

输出 $\mathbf{X''}_{1:n} = \mathbf{x''}_1, \ldots, \mathbf{x''}_n$ 是由一系列矩阵乘计算和 softmax 操作算得，因此可以有效地并行化。请注意，在基于 RNN 的编码器模型中，隐含状态 $\mathbf{c}$ 的计算必须按顺序进行: 先计算第一个输入向量的隐含状态 $\mathbf{x}_1$; 然后计算第二个输入向量的隐含状态，其取决于第一个隐含向量的状态，依此类推。RNN 的顺序性阻碍了有效的并行化，并使其在现代 GPU 硬件上比基于 transformer 的编码器模型的效率低得多。

太好了，现在我们应该对 a) 基于 transformer 的编码器模型如何有效地建模长程上下文表征，以及 b) 它们如何有效地处理长序列向量输入这两个方面有了比较好的理解了。

现在，我们写一个 MarianMT 编码器-解码器模型的编码器部分的小例子，以验证这些理论在实践中行不行得通。

---

${}^1$ 关于前馈层在基于 transformer 的模型中所扮演的角色的详细解释超出了本文的范畴。Yun 等人 (2017) 的工作认为前馈层对于将每个上下文向量 $\mathbf{x'}_i$ 映射到目标输出空间至关重要，而单靠 自注意力 层无法达成这一目的。这里请注意，每个输出词元 $\mathbf{x'}$ 都经由相同的前馈层处理。更多详细信息，建议读者阅读论文。

${}^2$ 我们无须将 EOS 附加到输入序列，虽然有工作表明，在很多情况下加入它可以提高性能。相反地，基于 transformer 的解码器必须把 $\text{BOS}$ 作为第 0 个目标向量，并以之为条件预测第 1 个目标向量。

from transformers import MarianMTModel, MarianTokenizer
import torch

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")

embeddings = model.get_input_embeddings()

# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# pass input_ids to encoder
encoder_hidden_states = model.base_model.encoder(input_ids, return_dict=True).last_hidden_state

# change the input slightly and pass to encoder
input_ids_perturbed = tokenizer("I want to buy a house", return_tensors="pt").input_ids
encoder_hidden_states_perturbed = model.base_model.encoder(input_ids_perturbed, return_dict=True).last_hidden_state

# compare shape and encoding of first vector
print(f"Length of input embeddings {embeddings(input_ids).shape[1]}. Length of encoder_hidden_states {encoder_hidden_states.shape[1]}")

# compare values of word embedding of "I" for input_ids and perturbed input_ids
print("Is encoding for `I` equal to its perturbed version?: ", torch.allclose(encoder_hidden_states[0, 0], encoder_hidden_states_perturbed[0, 0], atol=1e-3))

输出:

    Length of input embeddings 7. Length of encoder_hidden_states 7
    Is encoding for `I` equal to its perturbed version?: False

我们比较一下输入词嵌入的序列长度 ( 即 embeddings(input_ids)，对应于 $\mathbf{X}{1:n}$) 和 encoder_hidden_​​states 的长度 (对应于$\mathbf{\overline{X}}{1:n}$)。同时，我们让编码器对单词序列 “I want to buy a car” 及其轻微改动版 “I want to buy a house” 分别执行前向操作，以检查第一个词 “I” 的输出编码在更改输入序列的最后一个单词后是否会有所不同。

不出意外，输入词嵌入和编码器输出编码的长度， 即 $\textbf{len}(\mathbf{X}{1:n})$ 和 $\textbf{len }(\mathbf{\overline{X}}{1:n})$，是相等的。同时，可以注意到当最后一个单词从 “car” 改成 “house” 后，$\mathbf{\overline{x}}_1 = \text{“I”}$ 的编码输出向量的值也改变了。因为我们现在已经理解了双向自注意力机制，这就不足为奇了。

顺带一提， 自编码 模型 (如 BERT) 的架构与 基于 transformer 的编码器模型是完全一样的。 _自编码_模型利用这种架构对开放域文本数据进行大规模自监督预训练，以便它们可以将任何单词序列映射到深度双向表征。在 Devlin 等 (2018) 的工作中，作者展示了一个预训练 BERT 模型，其顶部有一个任务相关的分类层，可以在 11 个 NLP 任务上获得 SOTA 结果。你可以从 此处 找到 🤗 transformers 支持的所有 自编码 模型。

解码器

如 编码器-解码器 部分所述， 基于 transformer 的解码器定义了给定上下文编码序列条件下目标序列的条件概率分布:

$$p_{\theta_{dec}}(\mathbf{Y}_{1: m} | \mathbf{\overline{X}}_{1:n})$$

根据贝叶斯法则，在给定上下文编码序列和每个目标变量的所有前驱目标向量的条件下，可将上述分布分解为每个目标向量的条件分布的乘积:

$$p_{\theta_{dec}}(\mathbf{Y}_{1:m} | \mathbf{\overline{X}}_{1:n}) = \prod_{i=1}^{m} p_{\theta_{dec}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n})$$

我们首先了解一下基于 transformer 的解码器如何定义概率分布。基于 transformer 的解码器由很多 解码器模块_堆叠而成，最后再加一个线性层 (即 “LM 头”)。这些解码器模块的堆叠将上下文相关的编码序列 $\mathbf{\overline{X}}{1:n}$ 和每个目标向量的前驱输入 $\mathbf{Y}{0:i-1}$ (这里 $\mathbf{y}0$ 为 BOS) 映射为目标向量的编码序列 $\mathbf{\overline{Y} }{0:i-1}$。然后，“LM 头”将目标向量的编码序列 $\mathbf{\overline{Y}}{0:i-1}$ 映射到 logit 向量序列 $\mathbf {L}_{1:n} = \mathbf{l}_1, \ldots, \mathbf{l}_n$, 而每个 logit 向量$\mathbf{l}_i$ 的维度即为词表的词汇量。这样，对于每个 $i \in {1, \ldots, n}$，其在整个词汇表上的概率分布可以通过对 $\mathbf{l}_i$ 取 softmax 获得。公式如下:

$$p_{\theta_{dec}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n}), \forall i \in {1, \ldots, n}$$

“LM 头” 即为词嵌入矩阵的转置， 即 $\mathbf{W}_{\text{emb}}^{\intercal} = \left[\mathbf{ y}^1, \ldots, \mathbf{y}^{\text{vocab}}\right]^{​​T}$ ${}^1$。直观上来讲，这意味着对于所有 $i \in {0, \ldots, n - 1}$ “LM 头” 层会将 $\mathbf{\overline{y }}i$ 与词汇表 $\mathbf{y}^1, \ldots, \mathbf{y}^{\text{vocab}}$ 中的所有词嵌入一一比较，输出的 logit 向量 $\mathbf{l}{i+1}$ 即表示 $\mathbf{\overline{y }}_i$ 与每个词嵌入之间的相似度。Softmax 操作只是将相似度转换为概率分布。对于每个 $i \in {1, \ldots, n}$，以下等式成立:

$$p_{\theta_{dec}}(\mathbf{y} | \mathbf{\overline{X}}_{1:n}, \mathbf{Y}_{0:i-1})$$ $$= \text{Softmax}(f_{\theta_{\text{dec}}}(\mathbf{\overline{X}}_{1:n}, \mathbf{Y}_{0:i-1}))$$ $$= \text{Softmax}(\mathbf{W}_{\text{emb}}^{\intercal} \mathbf{\overline{y}}_{i-1})$$ $$= \text{Softmax}(\mathbf{l}_i)$$

总结一下，为了对目标向量序列 $\mathbf{Y}{1: m}$ 的条件分布建模，先在目标向量 $\mathbf{Y}{1: m-1}$ 前面加上特殊的 $\text{BOS}$ 向量 ( 即 $\mathbf{y}0$)，并将其与上下文相关的编码序列 $\mathbf{\overline{X}}{1:n}$ 一起映射到 logit 向量序列 $\mathbf{L}_{1:m}$。然后，使用 softmax 操作将每个 logit 目标向量 $\mathbf{l}_i$ 转换为目标向量 $\mathbf{y}_i$ 的条件概率分布。最后，将所有目标向量的条件概率 $\mathbf{y}_1, \ldots, \mathbf{y}_m$ 相乘得到完整目标向量序列的条件概率:

$$p_{\theta_{dec}}(\mathbf{Y}_{1:m} | \mathbf{\overline{X}}_{1:n}) = \prod_{i=1}^{m} p_{\theta_{dec}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n}).$$

与基于 transformer 的编码器不同，在基于 transformer 的解码器中，其输出向量 $\mathbf{\overline{y}}{i-1}$ 应该能很好地表征 下一个_目标向量 (即 $\mathbf{y}i$)，而不是输入向量本身 (即 $\mathbf{y}{i-1}$)。此外，输出向量 $\mathbf{\overline{y}}{i-1}$ 应基于编码器的整个输出序列 $\mathbf{\overline{X}}{1:n}$。为了满足这些要求，每个解码器块都包含一个 单向自注意层，紧接着是一个 交叉注意层，最后是两个前馈层${}^2$。单向自注意层将其每个输入向量 $\mathbf{y'}_j$ 仅与其前驱输入向量 $\mathbf{y'}_i$ (其中 $i \le j$，且 $j \in {1, \ldots, n}$) 相关联，来模拟下一个目标向量的概率分布。交叉注意层将其每个输入向量 $\mathbf{y''}j$ 与编码器输出的所有向量 $\mathbf{\overline{X}}{1:n}$ 相关联，来根据编码器输入预测下一个目标向量的概率分布。

好，我们仍以英语到德语翻译为例可视化一下 基于 transformer 的解码器。

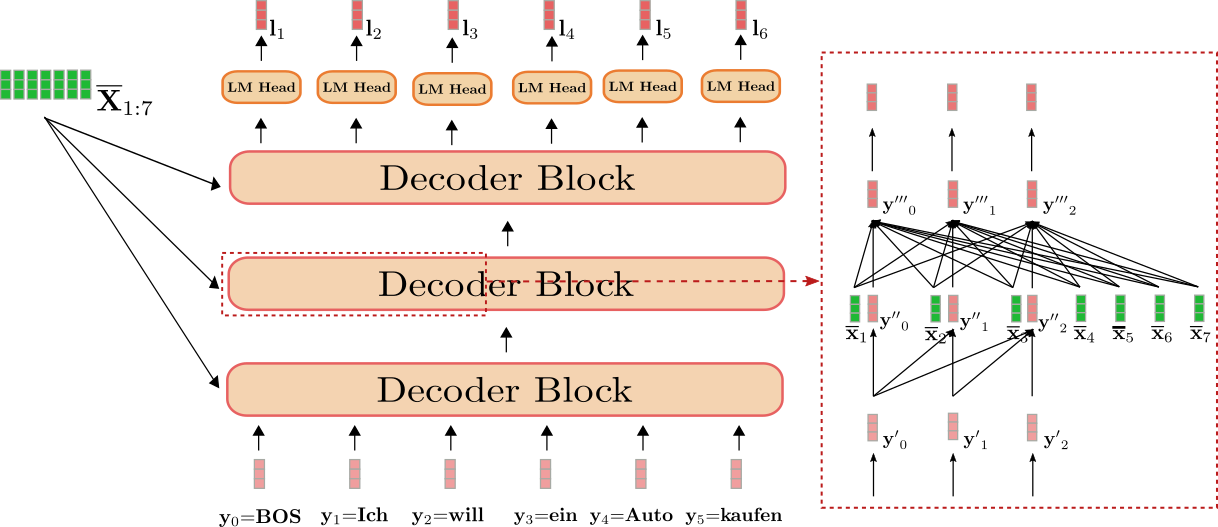
我们可以看到解码器将 $\mathbf{Y}{0:5}$: “BOS”、“Ich”、“will”、“ein”、“Auto”、“kaufen” (图中以浅红色显示) 和 “I”、“want”、“to”、“buy”、“a”、“car”、“EOS” ( 即 $\mathbf{\overline{X}}{1:7}$ (图中以深绿色显示)) 映射到 logit 向量 $\mathbf{L}_{1:6}$ (图中以深红色显示)。

因此，对每个 $\mathbf{l}_1、\mathbf{l}_2、\ldots、\mathbf{l}_6$ 使用 softmax 操作可以定义下列条件概率分布:

$$p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \mathbf{\overline{X}}_{1:7}),$$

$$ p_{\theta_{dec}}(\mathbf{y} | \text{BOS Ich}, \mathbf{\overline{X}}{1:7}), $$ $$ \ldots, $$ $$ p{\theta_{dec}}(\mathbf{y} | \text{BOS Ich will ein Auto kaufen}, \mathbf{\overline{X}}_{1:7}) $$

总条件概率如下:

$$p_{\theta_{dec}}(\text{Ich will ein Auto kaufen EOS} | \mathbf{\overline{X}}_{1:n})$$

其可表示为以下乘积形式:

$$p_{\theta_{dec}}(\text{Ich} | \text{BOS}, \mathbf{\overline{X}}_{1:7}) \times \ldots \times p_{\theta_{dec}}(\text{EOS} | \text{BOS Ich will ein Auto kaufen}, \mathbf{\overline{X}}_{1:7})$$

图右侧的红框显示了前三个目标向量 $\mathbf{y}_0$、$\mathbf{y}_1$、 $\mathbf{y}_2$ 在一个解码器模块中的行为。下半部分说明了单向自注意机制，中间说明了交叉注意机制。我们首先关注单向自注意力。

与双向自注意一样，在单向自注意中， query 向量 $\mathbf{q}0, \ldots, \mathbf{q}{m-1}$ (如下图紫色所示)， key 向量 $\mathbf{k}0, \ldots, \mathbf{k}{m-1}$ (如下图橙色所示)，和 value 向量 $\mathbf{v }0, \ldots, \mathbf{v}{m-1}$ (如下图蓝色所示) 均由输入向量 $\mathbf{y'}0, \ldots, \mathbf{ y'}{m-1}$ (如下图浅红色所示) 映射而来。然而，在单向自注意力中，每个 query 向量 $\mathbf{q}_i$ 仅 与当前及之前的 key 向量进行比较 (即 $\mathbf{k}_0 , \ldots, \mathbf{k}_i$) 并生成各自的 注意力权重 。这可以防止输出向量 $\mathbf{y''}_j$ (如下图深红色所示) 包含未来向量 ($\mathbf{y}_i$，其中 $i > j$ 且 $j \in {0, \ldots, m - 1 }$) 的任何信息 。与双向自注意力的情况一样，得到的注意力权重会乘以它们各自的 value 向量并加权求和。

我们将单向自注意力总结如下:

$$\mathbf{y''}_i = \mathbf{V}_{0: i} \textbf{Softmax}(\mathbf{K}_{0: i}^\intercal \mathbf{q}_i) + \mathbf{y'}_i$$

请注意， key 和 value 向量的索引范围都是 $0:i$ 而不是 $0: m-1$，$0: m-1$ 是双向自注意力中 key 向量的索引范围。

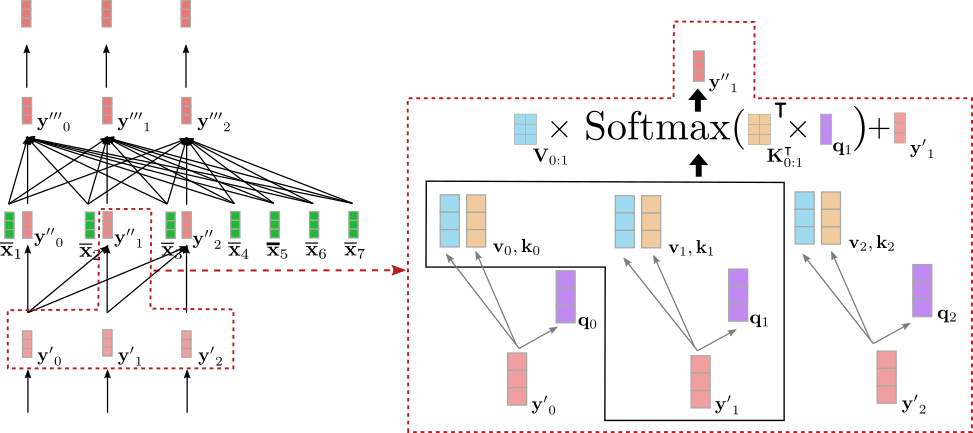
下图显示了上例中输入向量 $\mathbf{y'}_1$ 的单向自注意力。

可以看出 $\mathbf{y''}_1$ 只依赖于 $\mathbf{y'}_0$ 和 $\mathbf{y'}_1$。因此，单词 “Ich” 的向量表征 ( 即 $\mathbf{y'}_1$) 仅与其自身及 “BOS” 目标向量 ( 即 $\mathbf{y'}_0$) 相关联，而 不 与 “will” 的向量表征 ( 即 $\mathbf{y'}_2$) 相关联。

那么，为什么解码器使用单向自注意力而不是双向自注意力这件事很重要呢？如前所述，基于 transformer 的解码器定义了从输入向量序列 $\mathbf{Y}{0: m-1}$ 到其 下一个 解码器输入的 logit 向量的映射，即 $\mathbf{L}{1:m}$。举个例子，输入向量 $\mathbf{y}_1$ = “Ich” 会映射到 logit 向量 $\mathbf{l}_2$，并用于预测下一个输入向量 $\mathbf{y}_2$。因此，如果 $\mathbf{y'}1$ 可以获取后续输入向量 $\mathbf{Y'}{2:5}$的信息，解码器将会简单地复制向量 “will” 的向量表征 ( 即 $\mathbf{y'}_2$) 作为其输出 $\mathbf{y''}_1$，并就这样一直传播到最后一层，所以最终的输出向量 $\mathbf{\overline{y}}_1$ 基本上就只对应于 $\mathbf{y}_2$ 的向量表征，并没有起到预测的作用。

这显然是不对的，因为这样的话，基于 transformer 的解码器永远不会学到在给定所有前驱词的情况下预测下一个词，而只是对所有 $i \in {1, \ldots, m }$，通过网络将目标向量 $\mathbf{y}i$ 复制到 $\mathbf {\overline{y}}{i-1}$。以下一个目标变量本身为条件去定义下一个目标向量，即从 $p(\mathbf{y} | \mathbf{Y}_{0:i}, \mathbf{\overline{ X}})$ 中预测 $\mathbf{y}_i$， 显然是不对的。因此，单向自注意力架构允许我们定义一个 _因果的_概率分布，这对有效建模下一个目标向量的条件分布而言是必要的。

太棒了！现在我们可以转到连接编码器和解码器的层 - _交叉注意力_机制！

交叉注意层将两个向量序列作为输入: 单向自注意层的输出 $\mathbf{Y''}{0: m-1}$ 和编码器的输出 $\mathbf{\overline{X}}{1:n}$。与自注意力层一样， query 向量 $\mathbf{q}0, \ldots, \mathbf{q}{m-1}$ 是上一层输出向量 $\mathbf{Y''}{0: m-1}$ 的投影。而 key 和 value 向量 $\mathbf{k}0, \ldots, \mathbf{k}{n-1}$、$\mathbf{v}0, \ldots, \mathbf {v}{n-1}$ 是编码器输出向量 $\mathbf{\overline{X}}{1:n}$ 的投影。定义完 key 、value 和 query 向量后，将 query 向量 $\mathbf{q}_i$ 与 所有 key 向量进行比较，并用各自的得分对相应的 value 向量进行加权求和。这个过程与 _双向_自注意力对所有 $i \in {0, \ldots, m-1}$ 求 $\mathbf{y'''}_i$ 是一样的。交叉注意力可以概括如下:

$$\mathbf{y'''}_i = \mathbf{V}_{1:n} \textbf{Softmax}(\mathbf{K}_{1: n}^\intercal \mathbf{q}_i) + \mathbf{y''}_i$$

注意，key 和 value 向量的索引范围是 $1:n$，对应于编码器输入向量的数目。

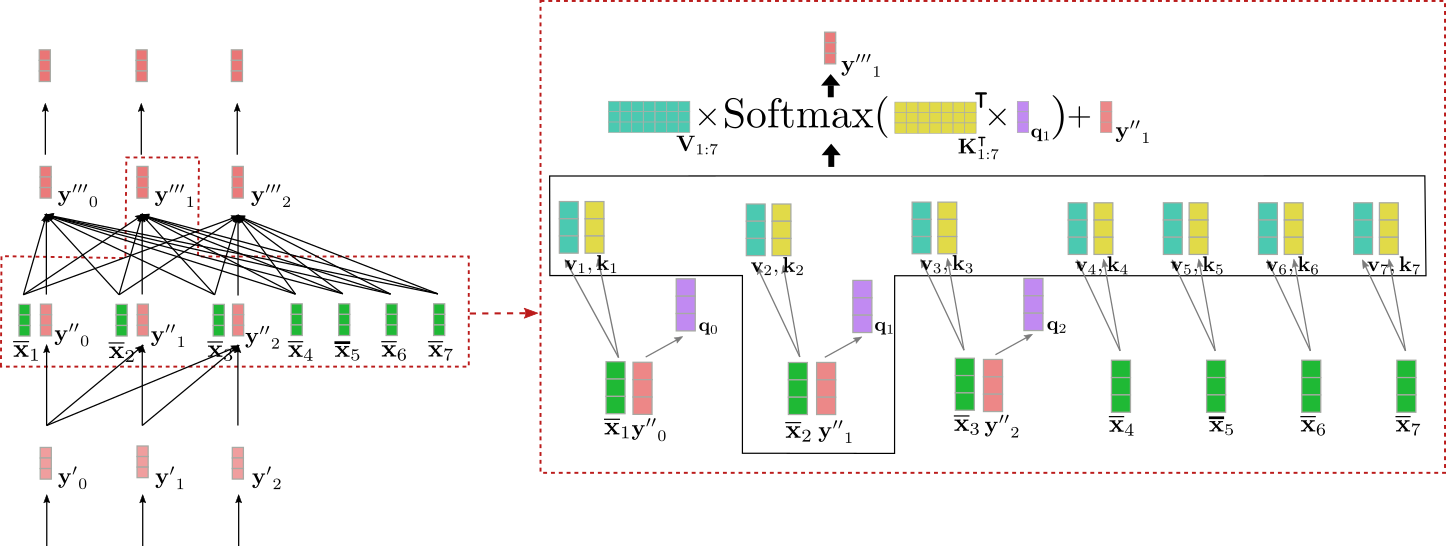
我们用上例中输入向量 $\mathbf{y''}_1$ 来图解一下交叉注意力机制。

我们可以看到 query 向量 $\mathbf{q}_1$（紫色）源自 $\mathbf{y''}_1$（红色），因此其依赖于单词 "Ich" 的向量表征。然后将 query 向量 $\mathbf{q}_1$ 与对应的 key 向量 $\mathbf{k}_1, \ldots, \mathbf{k}7$（黄色）进行比较，这里的 key 向量对应于编码器对其输入 $\mathbf{X}{1:n}$ = "I want to buy a car EOS" 的上下文相关向量表征。这将 "Ich" 的向量表征与所有编码器输入向量直接关联起来。最后，将注意力权重乘以 value 向量 $\mathbf{v}_1, \ldots, \mathbf{v}_7$（青绿色）并加上输入向量 $\mathbf{y''}_1$ 最终得到输出向量 $\mathbf{y'''}_1$（深红色）。

所以，直观而言，到底发生了什么？每个输出向量 $\mathbf{y'''}i$ 是由所有从编码器来的 value 向量（$\mathbf{v}{1}, \ldots, \mathbf{v }_7$ ）的加权和与输入向量本身 $\mathbf{y''}i$ 相加而得（参见上图所示的公式）。其关键思想是：_来自解码器的 $\mathbf{q}_i$ 的 query 投影与 _来自编码器的 $\mathbf{k}j$ 越相关，其对应的 $\mathbf{v}_j$ 对输出的影响越大。

酷！现在我们可以看到这种架构的每个输出向量 $\mathbf{y'''}i$ 取决于其来自编码器的输入向量 $\mathbf{\overline{X}}{1 :n}$ 及其自身的输入向量 $\mathbf{y''}_i$。这里有一个重要的点，在该架构中，虽然输出向量 $\mathbf{y'''}i$ 依赖来自编码器的输入向量 $\mathbf{\overline{X}}{1:n}$，但其完全独立于该向量的数量 $n$。所有生成 key 向量 $\mathbf{k}_1, \ldots, \mathbf{k}_n$ 和 value 向量 $\mathbf{v}1, \ldots, \mathbf{v}n $ 的投影矩阵 $\mathbf{W}^{\text{cross}}{k}$ 和 $\mathbf{W}^{\text{cross}}{v}$ 都是与 $n$ 无关的，所有 $n$ 共享同一个投影矩阵。且对每个 $\mathbf{y'''}_i$，所有 value 向量 $\mathbf{v}_1, \ldots, \mathbf{v}_n$ 被加权求和至一个向量。至此，关于为什么基于 transformer 的解码器没有远程依赖问题而基于 RNN 的解码器有这一问题的答案已经很显然了。因为每个解码器 logit 向量 直接 依赖于每个编码后的输出向量，因此比较第一个编码输出向量和最后一个解码器 logit 向量只需一次操作，而不像 RNN 需要很多次。

总而言之，单向自注意力层负责基于当前及之前的所有解码器输入向量建模每个输出向量，而交叉注意力层则负责进一步基于编码器的所有输入向量建模每个输出向量。

为了验证我们对该理论的理解，我们继续上面编码器部分的代码，完成解码器部分。

---

${}^1$ 词嵌入矩阵 $\mathbf{W}_{\text{emb}}$ 为每个输入词提供唯一的 _上下文无关_向量表示。这个矩阵通常也被用作 “LM 头”，此时 “LM 头”可以很好地完成“编码向量到 logit” 的映射。

${}^2$ 与编码器部分一样，本文不会详细解释前馈层在基于 transformer 的模型中的作用。Yun 等 (2017) 的工作认为前馈层对于将每个上下文相关向量 $\mathbf{x'}_i$ 映射到所需的输出空间至关重要，仅靠自注意力层无法完成。这里应该注意，每个输出词元 $\mathbf{x'}$ 对应的前馈层是相同的。有关更多详细信息，建议读者阅读论文。

from transformers import MarianMTModel, MarianTokenizer
import torch

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")
embeddings = model.get_input_embeddings()

# create token ids for encoder input
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# pass input token ids to encoder
encoder_output_vectors = model.base_model.encoder(input_ids, return_dict=True).last_hidden_state

# create token ids for decoder input
decoder_input_ids = tokenizer("<pad> Ich will ein", return_tensors="pt", add_special_tokens=False).input_ids

# pass decoder input ids and encoded input vectors to decoder
decoder_output_vectors = model.base_model.decoder(decoder_input_ids, encoder_hidden_states=encoder_output_vectors).last_hidden_state

# derive embeddings by multiplying decoder outputs with embedding weights
lm_logits = torch.nn.functional.linear(decoder_output_vectors, embeddings.weight, bias=model.final_logits_bias)

# change the decoder input slightly
decoder_input_ids_perturbed = tokenizer("<pad> Ich will das", return_tensors="pt", add_special_tokens=False).input_ids
decoder_output_vectors_perturbed = model.base_model.decoder(decoder_input_ids_perturbed, encoder_hidden_states=encoder_output_vectors).last_hidden_state
lm_logits_perturbed = torch.nn.functional.linear(decoder_output_vectors_perturbed, embeddings.weight, bias=model.final_logits_bias)

# compare shape and encoding of first vector
print(f"Shape of decoder input vectors {embeddings(decoder_input_ids).shape}. Shape of decoder logits {lm_logits.shape}")

# compare values of word embedding of "I" for input_ids and perturbed input_ids
print("Is encoding for `Ich` equal to its perturbed version?: ", torch.allclose(lm_logits[0, 0], lm_logits_perturbed[0, 0], atol=1e-3))

输出:

    Shape of decoder input vectors torch.Size([1, 5, 512]). Shape of decoder logits torch.Size([1, 5, 58101])
    Is encoding for `Ich` equal to its perturbed version?: True

我们首先比较解码器词嵌入层的输出维度 embeddings(decoder_input_ids) (对应于 $\mathbf{Y}{0: 4}$，这里 <pad> 对应于 BOS 且 "Ich will das" 被分为 4 个词) 和 lm_logits (对应于 $\mathbf{L}{1:5}$) 的维度。此外，我们还通过解码器将单词序列 “<pad> Ich will ein” 和其轻微改编版 “<pad> Ich will das” 与 encoder_output_vectors 一起传递给解码器，以检查对应于 “Ich” 的第二个 lm_logit 在仅改变输入序列中的最后一个单词 (“ein” -> “das”) 时是否会有所不同。

正如预期的那样，解码器输入词嵌入和 lm_logits 的输出， 即 $\mathbf{Y}{0: 4}$ 和 $\mathbf{L}{ 1:5}$ 的最后一个维度不同。虽然序列长度相同 (=5)，但解码器输入词嵌入的维度对应于 model.config.hidden_​​size，而 lm_logit 的维数对应于词汇表大小 model.config.vocab_size。其次，可以注意到，当将最后一个单词从 “ein” 变为 “das”，$\mathbf{l}_1 = \text{“Ich”}$ 的输出向量的值不变。鉴于我们已经理解了单向自注意力，这就不足为奇了。

最后一点， _自回归_模型，如 GPT2，与删除了交叉注意力层的 基于 transformer 的解码器模型架构是相同的，因为纯自回归模型不依赖任何编码器的输出。因此，自回归模型本质上与 _自编码_模型相同，只是用单向注意力代替了双向注意力。这些模型还可以在大量开放域文本数据上进行预训练，以在自然语言生成 (NLG) 任务中表现出令人印象深刻的性能。在 Radford 等 (2019) 的工作中，作者表明预训练的 GPT2 模型无需太多微调即可在多种 NLG 任务上取得达到 SOTA 或接近 SOTA 的结果。你可以在 此处 获取所有 🤗 transformers 支持的 _自回归_模型的信息。

好了！至此，你应该已经很好地理解了 基于 transforemr 的编码器-解码器模型以及如何在 🤗 transformers 库中使用它们。

非常感谢 Victor Sanh、Sasha Rush、Sam Shleifer、Oliver Åstrand、Ted Moskovitz 和 Kristian Kyvik 提供的宝贵反馈。

附录

如上所述，以下代码片段展示了如何为 基于 transformer 的编码器-解码器模型编写一个简单的生成方法。在这里，我们使用 torch.argmax 实现了一个简单的 _贪心_解码法来对目标向量进行采样。

from transformers import MarianMTModel, MarianTokenizer
import torch

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")

# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# create BOS token
decoder_input_ids = tokenizer("<pad>", add_special_tokens=False, return_tensors="pt").input_ids

assert decoder_input_ids[0, 0].item() == model.config.decoder_start_token_id, "`decoder_input_ids` should correspond to `model.config.decoder_start_token_id`"

# STEP 1

# pass input_ids to encoder and to decoder and pass BOS token to decoder to retrieve first logit
outputs = model(input_ids, decoder_input_ids=decoder_input_ids, return_dict=True)

# get encoded sequence
encoded_sequence = (outputs.encoder_last_hidden_state,)
# get logits
lm_logits = outputs.logits

# sample last token with highest prob
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)

# concat
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)

# STEP 2

# reuse encoded_inputs and pass BOS + "Ich" to decoder to second logit
lm_logits = model(None, encoder_outputs=encoded_sequence, decoder_input_ids=decoder_input_ids, return_dict=True).logits

# sample last token with highest prob again
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)

# concat again
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)

# STEP 3
lm_logits = model(None, encoder_outputs=encoded_sequence, decoder_input_ids=decoder_input_ids, return_dict=True).logits
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)

# let's see what we have generated so far!
print(f"Generated so far: {tokenizer.decode(decoder_input_ids[0], skip_special_tokens=True)}")

# This can be written in a loop as well.

输出:

    Generated so far: Ich will ein

在这个示例代码中，我们准确地展示了正文中描述的内容。我们在输入 “I want to buy a car” 前面加上 $\text{BOS}$ ，然后一起传给编码器-解码器模型，并对第一个 logit $\mathbf{l}_1 $ (对应代码中第一次出现 lm_logits 的部分) 进行采样。这里，我们的采样策略很简单: 贪心地选择概率最高的词作为下一个解码器输入向量。然后，我们以自回归方式将采样得的解码器输入向量与先前的输入一起传递给编码器-解码器模型并再次采样。重复 3 次后，该模型生成了 “Ich will ein”。结果没问题，开了个好头。

在实践中，我们会使用更复杂的解码方法来采样 lm_logits。你可以参考 这篇博文 了解更多的解码方法。