Goedel-LM/Goedel-Prover-SFT

---

Evaluation Results | Model Download | Setup Environment | Quick Start | Questions and Bugs | License | Citation | Contact

Paper Link👁️

Goedel-Prover: A New Frontier in Automated Theorem Proving

1. Introduction

Large language models (LLMs) have shown impressive reasoning capabilities, especially in tackling mathematical problems. There are two main approaches: informal reasoning, which employs natural language but lacks verifiability, and formal reasoning, which utilizes proof assistants like Lean to produce machine-verifiable proofs. While state-of-the-art LLMs, such as OpenAI's o1 and DeepSeek's R1, excel in informal problem-solving, they face challenges in formal theorem proving.

A significant challenge in training LLMs for formal reasoning is the scarcity of data. To overcome this, we synthesize a large and diverse dataset by auto-formalizing a substantial corpus of informal mathematical problems. Our approach transforms natural language statements into various formal styles in Lean 4, resulting in 1.78 million syntactically correct and content-accurate statements. We then iteratively train a prover, alternating between generating verified proofs and training the model using these proofs. Our model, Goedel-Prover, achieves state-of-the-art performance across multiple benchmarks for whole-proof generation, which generates the entire proof without interacting with Lean. On the miniF2F benchmark (Pass@32), it attains a 57.6% success rate, surpassing the previous best open-source model by 7.6%. On PutnamBench, Goedel-Prover successfully solves 7 problems (Pass@512), securing the top position on the leaderboard. Furthermore, it generates 29.7K formal proofs for Lean-workbook problems, nearly doubling the 15.7K produced by earlier works.

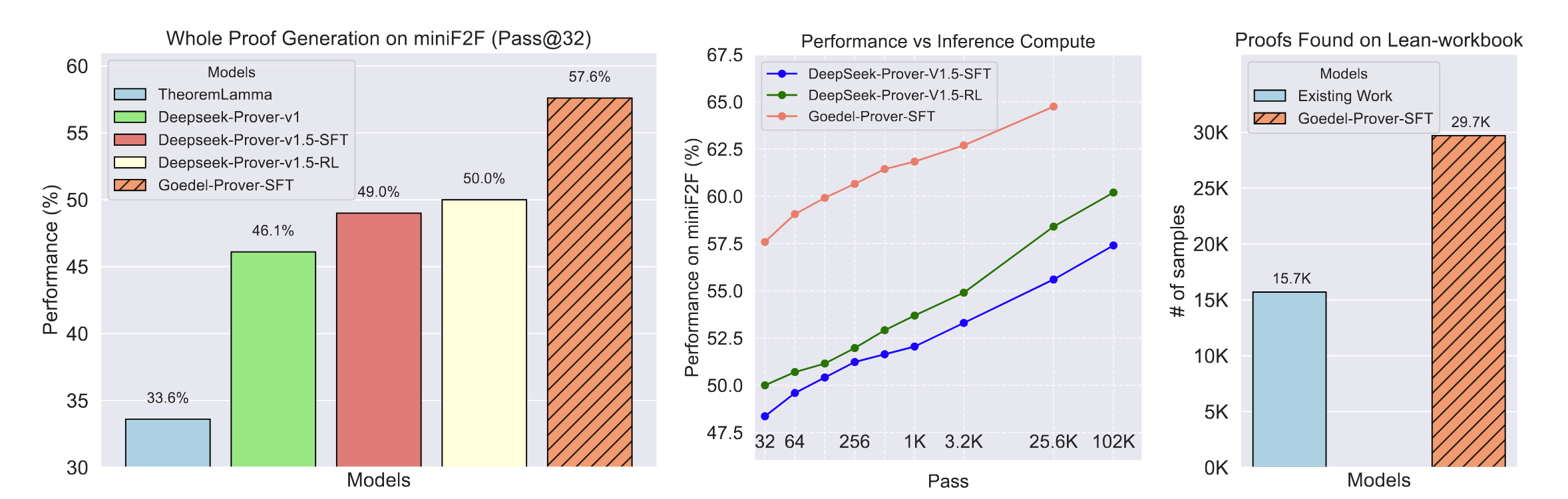
Caption: The Pass@N metric indicates that we generate N proofs for a single problem; if any one of these N proofs successfully solves the problem, it is considered solved. (Left): The performance of Pass@32 for full proof generation on miniF2F. Due to limited compute, we compare with DeepSeek-Prover-v1.5 on the Pass@32 metric. (Middle): This sub-figure presents a comparison of Goedel-Prover-SFT and Deepseek-Prover-v1.5 in terms of miniF2F performance across different inference budgets, ranging from Pass@32, 64, 128, ..., 4 * 6400, to 16 * 6400. The performance numbers of Deepseek-Prover-v1.5 are directly taken from Table 1 of Xin et al. (2024b). Due to computational resource constraints, we tested Goedel-Prover-SFT only up to Pass@4 × 6400. Notably, Goedel-Prover-SFT's Pass@256 already exceeds the Pass@16 * 6400 performance of Deepseek-Prover-v1.5-RL (without inference time tree search). (Right): The number of problems solved in Lean-workbook by Goedel-Prover-SFT compared to prior works. InternLM2.5-Step-Prover and InternLM-Math-Plus collectively solve and open-source 15.7K samples, while we solve and open-source 29.7K samples.

2. Evaluation Results

Model	Compute (Pass)	miniF2F-test
TheoremLamma	128	33.6%
DeepSeek-Prover-V1	32	46.1%
DeepSeek-Prover-V1.5-SFT	32	48.2%
DeepSeek-Prover-V1.5-RL	32	50.0%
Goedel-Prover-SFT	32	57.6%
------------------------	------------------	------------------
DeepSeek-Prover-V1.5-SFT	3200	53.3%
DeepSeek-Prover-V1.5-RL	3200	54.9%
Goedel-Prover-SFT	3200	62.7%
------------------------	------------------	------------------
DeepSeek-Prover-V1.5-SFT	25600	55.8%
DeepSeek-Prover-V1.5-RL	25600	58.5%
Goedel-Prover-SFT	25600	64.7%

Caption: Comparison of Goedel-Prover-SFT with existing methods for whole proof generation on miniF2F, assessing performance across various inference time computations.

MultiDataset

	miniF2F	ProofNet	FormalNumina	Lean-workbook
Deepseek-Prover-v1.5-RL	50.0%	16.0%	54.0%	14.7%
Goedel-Prover-SFT	57.6%	15.2%	61.2%	21.2%

Caption: Comparison of Goedel-Prover-SFT with Deepseek-Prover-v1.5-RL for whole proof generation on miniF2F, ProofNet,FormalNumina,Lean-workbook. We report the Pass@32 performance for miniF2F, ProofNet, and FormalNumina datasets. For the Lean-workbook, we evaluate performance using Pass@16 due to the large number of problems (140K) it contains, allowing us to save on computational costs. FormalNumina is a private test set created by formalizing a randomly sampled collection of 250 problems from Numina.

Putnam

Ranking	Model	Type	Num-solved	Compute
1	Goedel-Prover-SFT 🟩	Whole Proof Generation	7	512
1	ABEL	Tree Search Method	7	596
3	Goedel-Prover-SFT 🟩	Whole Proof Generation	6	32
3	InternLM2.5-StepProver 🟩	Tree Search Method	6	2×32×600
5	InternLM 7B	Whole Proof Generation	4	4096
6	GPT-4o	Whole Proof Generation	1	10
7	COPRA (GPT-4o) 🟩	Whole Proof Generation	1	1
8	ReProver w/ retrieval 🟩	Whole Proof Generation	0	1
9	ReProver w/o retrieval 🟩	Whole Proof Generation	0	1

Caption: Our model rank the 1st on Putnam Leaderboard. The performance numbers for existing works are taken from the leaderboard. 🟩 indicates open sourced models.

3. Dataset Downloads

We are also releasing 29,7K proofs of the problems in Lean-workbook found by our Goedel-Prover-SFT.

Datasets	Download
Lean-workbook-proofs	🤗 HuggingFace

4. Citation

@article{lin2024Goedelprover,
      title={Goedel-Prover: A New Frontier in Automated Theorem Proving}, 
      author={Yong Lin and Shange Tang and Bohan Lyu and Jiayun Wu and Hongzhou Lin and Kaiyu Yang and Jia Li and Mengzhou Xia and Danqi Chen and Sanjeev Arora and Chi Jin},
}