Add data for India National MO
#23
by
LxYxvv
- opened
This view is limited to 50 files because it contains too many changes.
See the raw diff here.
- INMO/download_script/download.py +75 -0
- INMO/md/en-2000.md +206 -0
- INMO/md/en-2001.md +211 -0
- INMO/md/en-2002.md +196 -0
- INMO/md/en-2003.md +194 -0
- INMO/md/en-2004.md +233 -0
- INMO/md/en-2005.md +354 -0
- INMO/md/en-2006.md +359 -0
- INMO/md/en-2007.md +349 -0
- INMO/md/en-2008.md +227 -0
- INMO/md/en-2009.md +411 -0
- INMO/md/en-2010.md +270 -0
- INMO/md/en-2011.md +306 -0
- INMO/md/en-2012.md +307 -0
- INMO/md/en-2023.md +428 -0
- INMO/md/en-INMO_2021_solutions.md +370 -0
- INMO/md/en-INMO_2024_final_solutions.md +284 -0
- INMO/md/en-Inmo-2019-Solutions.md +225 -0
- INMO/md/en-inmo-2014.md +51 -0
- INMO/md/en-inmo2013-solutions.md +94 -0
- INMO/md/en-inmosol-15.md +261 -0
- INMO/md/en-sol-inmo-20.md +218 -0
- INMO/md/en-sol-inmo16.md +505 -0
- INMO/md/en-sol-inmo_17.md +418 -0
- INMO/raw/en-2000.pdf +3 -0
- INMO/raw/en-2001.pdf +3 -0
- INMO/raw/en-2002.pdf +3 -0
- INMO/raw/en-2003.pdf +3 -0
- INMO/raw/en-2004.pdf +3 -0
- INMO/raw/en-2005.pdf +3 -0
- INMO/raw/en-2006.pdf +3 -0
- INMO/raw/en-2007.pdf +3 -0
- INMO/raw/en-2008.pdf +3 -0
- INMO/raw/en-2009.pdf +3 -0
- INMO/raw/en-2010.pdf +3 -0
- INMO/raw/en-2011.pdf +3 -0
- INMO/raw/en-2012.pdf +3 -0
- INMO/raw/en-2023.pdf +3 -0
- INMO/raw/en-INMO_2021_solutions.pdf +3 -0
- INMO/raw/en-INMO_2024_final_solutions.pdf +3 -0
- INMO/raw/en-Inmo-2019-Solutions.pdf +3 -0
- INMO/raw/en-inmo-2014.pdf +3 -0
- INMO/raw/en-inmo2013-solutions.pdf +3 -0
- INMO/raw/en-inmosol-15.pdf +3 -0
- INMO/raw/en-sol-inmo-20.pdf +3 -0
- INMO/raw/en-sol-inmo16.pdf +3 -0
- INMO/raw/en-sol-inmo_17.pdf +3 -0
- INMO/segment_script/segment.py +127 -0
- INMO/segmented/en-2000.jsonl +6 -0
- INMO/segmented/en-2001.jsonl +6 -0
INMO/download_script/download.py
ADDED
|
@@ -0,0 +1,75 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# -----------------------------------------------------------------------------
|
| 2 |
+
# Author: Jiawei Liu
|
| 3 |
+
# Date: 2024-12-24
|
| 4 |
+
# -----------------------------------------------------------------------------
|
| 5 |
+
'''
|
| 6 |
+
Download script for Nordic MO
|
| 7 |
+
To run:
|
| 8 |
+
`python INMo/download_script/download.py`
|
| 9 |
+
'''
|
| 10 |
+
|
| 11 |
+
import requests
|
| 12 |
+
from bs4 import BeautifulSoup
|
| 13 |
+
from tqdm import tqdm
|
| 14 |
+
from pathlib import Path
|
| 15 |
+
from requests.adapters import HTTPAdapter
|
| 16 |
+
from urllib3.util.retry import Retry
|
| 17 |
+
from urllib.parse import urljoin, unquote
|
| 18 |
+
|
| 19 |
+
|
| 20 |
+
def build_session(
|
| 21 |
+
max_retries: int = 3,
|
| 22 |
+
backoff_factor: int = 2,
|
| 23 |
+
session: requests.Session = None
|
| 24 |
+
) -> requests.Session:
|
| 25 |
+
"""
|
| 26 |
+
Build a requests session with retries
|
| 27 |
+
|
| 28 |
+
Args:
|
| 29 |
+
max_retries (int, optional): Number of retries. Defaults to 3.
|
| 30 |
+
backoff_factor (int, optional): Backoff factor. Defaults to 2.
|
| 31 |
+
session (requests.Session, optional): Session object. Defaults to None.
|
| 32 |
+
"""
|
| 33 |
+
session = session or requests.Session()
|
| 34 |
+
adapter = HTTPAdapter(max_retries=Retry(total=max_retries, backoff_factor=backoff_factor))
|
| 35 |
+
session.mount("http://", adapter)
|
| 36 |
+
session.mount("https://", adapter)
|
| 37 |
+
session.headers.update({
|
| 38 |
+
"User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/58.0.3029.110 Safari/537.3"
|
| 39 |
+
})
|
| 40 |
+
|
| 41 |
+
return session
|
| 42 |
+
|
| 43 |
+
|
| 44 |
+
def main():
|
| 45 |
+
base_url = "https://olympiads.hbcse.tifr.res.in/how-to-prepare/past-papers/"
|
| 46 |
+
req_session = build_session()
|
| 47 |
+
|
| 48 |
+
output_dir = Path(__file__).parent.parent / "raw"
|
| 49 |
+
output_dir.mkdir(parents=True, exist_ok=True)
|
| 50 |
+
|
| 51 |
+
resp = req_session.get(base_url)
|
| 52 |
+
soup = BeautifulSoup(resp.text, 'html.parser')
|
| 53 |
+
|
| 54 |
+
link_eles = soup.find_all('a', href=lambda x: x.endswith(".pdf") and "inmo" in x.lower())
|
| 55 |
+
|
| 56 |
+
links = [ele["href"] for ele in link_eles]
|
| 57 |
+
|
| 58 |
+
for url in tqdm(links):
|
| 59 |
+
output_file = output_dir / f"en-{unquote(Path(url).name)}"
|
| 60 |
+
|
| 61 |
+
# Check if the file already exists
|
| 62 |
+
if output_file.exists():
|
| 63 |
+
continue
|
| 64 |
+
|
| 65 |
+
pdf_resp = req_session.get(urljoin(base_url, url))
|
| 66 |
+
|
| 67 |
+
if pdf_resp.status_code != 200:
|
| 68 |
+
print(f"Failed to download {url}")
|
| 69 |
+
continue
|
| 70 |
+
|
| 71 |
+
output_file.write_bytes(pdf_resp.content)
|
| 72 |
+
|
| 73 |
+
|
| 74 |
+
if __name__ == "__main__":
|
| 75 |
+
main()
|
INMO/md/en-2000.md
ADDED
|
@@ -0,0 +1,206 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# INMO-2000 <br> Problems and Solutions
|
| 2 |
+
|
| 3 |
+
1. The in-circle of triangle $A B C$ touches the sides $B C, C A$ and $A B$ in $K, L$ and $M$ respectively. The line through $A$ and parallel to $L K$ meets $M K$ in $P$ and the line through $A$ and parallel to $M K$ meets $L K$ in $Q$. Show that the line $P Q$ bisects the sides $A B$ and $A C$ of triangle $A B C$.
|
| 4 |
+
|
| 5 |
+
Solution. : Let $A P, A Q$ produced meet $B C$ in $D, E$ respectively.
|
| 6 |
+
|
| 7 |
+
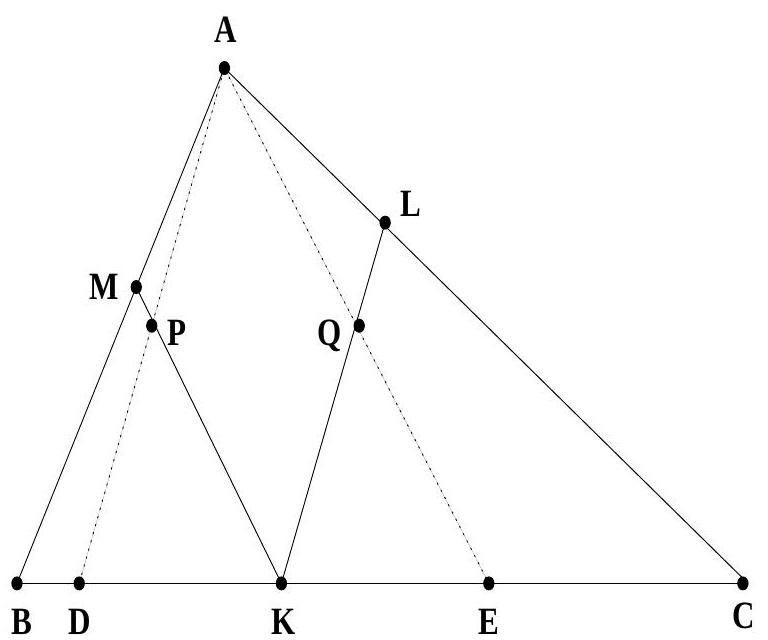
|
| 8 |
+
|
| 9 |
+
Since $M K$ is parallel to $A E$, we have $\angle A E K=\angle M K B$. Since $B K=B M$, both being tangents to the circle from $B, \angle M K B=\angle B M K$. This with the fact that $M K$ is parallel to $A E$ gives us $\angle A E K=\angle M A E$. This shows that $M A E K$ is an isosceles trapezoid. We conclude that $M A=K E$. Similarly, we can prove that $A L=D K$. But $A M=A L$. We get that $D K=K E$. Since $K P$ is parallel to $A E$, we get $D P=P A$ and similarly $E Q=Q A$. This implies that $P Q$ is parallel to $D E$ and hence bisects $A B, A C$ when produced.
|
| 10 |
+
|
| 11 |
+
[The same argument holds even if one or both of $P$ and $Q$ lie outside triangle $A B C$.]
|
| 12 |
+
|
| 13 |
+
2. Solve for integers $x, y, z$ :
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
x+y=1-z, \quad x^{3}+y^{3}=1-z^{2}
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
Sol. : Eliminating $z$ from the given set of equations, we get
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
x^{3}+y^{3}+\{1-(x+y)\}^{2}=1
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
This factors to
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
(x+y)\left(x^{2}-x y+y^{2}+x+y-2\right)=0
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
Case 1. Suppose $x+y=0$. Then $z=1$ and $(x, y, z)=(m,-m, 1)$, where $m$ is an integer give one family of solutions.
|
| 32 |
+
|
| 33 |
+
Case 2. Suppose $x+y \neq 0$. Then we must have
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
x^{2}-x y+y^{2}+x+y-2=0 \text {. }
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
This can be written in the form
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
(2 x-y+1)^{2}+3(y+1)^{2}=12
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
Here there are two possibilities:
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
2 x-y+1=0, y+1= \pm 2 ; \quad 2 x-y+1= \pm 3, y+1= \pm 1
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
Analysing all these cases we get
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
(x, y, z)=(0,1,0),(-2,-3,6),(1,0,0),(0,-2,3),(-2,0,3),(-3,-2,6) .
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
3. If $a, b, c, x$ are real numbers such that $a b c \neq 0$ and
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
\frac{x b+(1-x) c}{a}=\frac{x c+(1-x) a}{b}=\frac{x a+(1-x) b}{c}
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
then prove that either $a+b+c=0$ or $a=b=c$.
|
| 64 |
+
|
| 65 |
+
Sol. : Suppose $a+b+c \neq 0$ and let the common value be $\lambda$. Then
|
| 66 |
+
|
| 67 |
+
$$
|
| 68 |
+
\lambda=\frac{x b+(1-x) c+x c+(1-x) a+x a+(1-x) b}{a+b+c}=1
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
We get two equations:
|
| 72 |
+
|
| 73 |
+
$$
|
| 74 |
+
-a+x b+(1-x) c=0, \quad(1-x) a-b+x c=0
|
| 75 |
+
$$
|
| 76 |
+
|
| 77 |
+
(The other equation is a linear combination of these two.) Using these two equations, we get the relations
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
\frac{a}{1-x+x^{2}}=\frac{b}{x^{2}-x+1}=\frac{c}{(1-x)^{2}+x}
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
Since $1-x+x^{2} \neq 0$, we get $a=b=c$.
|
| 84 |
+
|
| 85 |
+
4. In a convex quadrilateral $P Q R S, P Q=R S,(\sqrt{3}+1) Q R=S P$ and $\angle R S P-\angle S P Q=$ $30^{\circ}$. Prove that
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
\angle P Q R-\angle Q R S=90^{\circ}
|
| 89 |
+
$$
|
| 90 |
+
|
| 91 |
+
Sol. : Let $[$ Fig $]$ denote the area of Fig. We have
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
[P Q R S]=[P Q R]+[R S P]=[Q R S]+[S P Q]
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
Let us write $P Q=p, Q R=q, R S=r, S P=s$. The above relations reduce to
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
p q \sin \angle P Q R+r s \sin \angle R S P=q r \sin \angle Q R S+s p \sin \angle S P Q
|
| 101 |
+
$$
|
| 102 |
+
|
| 103 |
+
Using $p=r$ and $(\sqrt{3}+1) q=s$ and dividing by $p q$, we get
|
| 104 |
+
|
| 105 |
+
$$
|
| 106 |
+
\sin \angle P Q R+(\sqrt{3}+1) \sin \angle R S P=\sin \angle Q R S+(\sqrt{3}+1) \sin \angle S P Q
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
Therefore, $\sin \angle P Q R-\sin \angle Q R S=(\sqrt{3}+1)(\sin \angle S P Q-\sin \angle R S P)$.
|
| 110 |
+
|
| 111 |
+
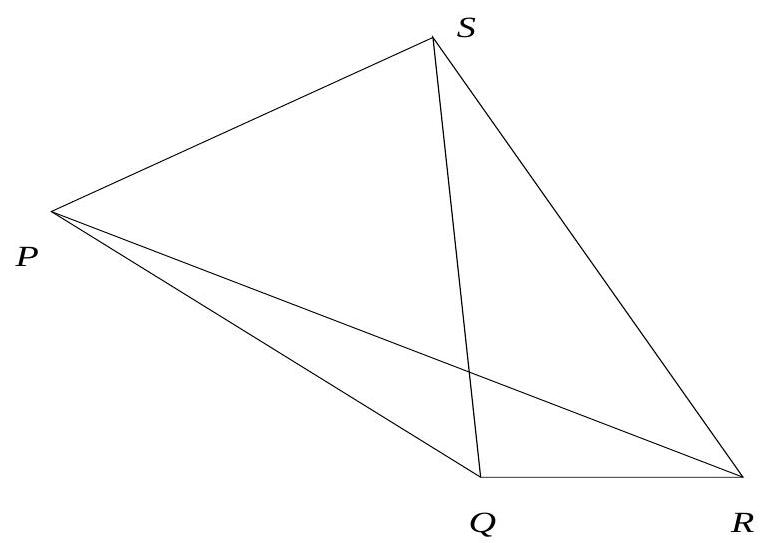
|
| 112 |
+
|
| 113 |
+
Fig. 2.
|
| 114 |
+
|
| 115 |
+
This can be written in the form
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
\begin{aligned}
|
| 119 |
+
2 \sin & \frac{\angle P Q R-\angle Q R S}{2} \cos \frac{\angle P Q R+\angle Q R S}{2} \\
|
| 120 |
+
& =(\sqrt{3}+1) 2 \sin \frac{\angle S P Q-\angle R S P}{2} \cos \frac{\angle S P Q+\angle R S P}{2}
|
| 121 |
+
\end{aligned}
|
| 122 |
+
$$
|
| 123 |
+
|
| 124 |
+
Using the relations
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
\cos \frac{\angle P Q R+\angle Q R S}{2}=-\cos \frac{\angle S P Q+\angle R S P}{2}
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
and
|
| 131 |
+
|
| 132 |
+
$$
|
| 133 |
+
\sin \frac{\angle S P Q-\angle R S P}{2}=-\sin 15^{\circ}=-\frac{(\sqrt{3}-1)}{2 \sqrt{2}}
|
| 134 |
+
$$
|
| 135 |
+
|
| 136 |
+
we obtain
|
| 137 |
+
|
| 138 |
+
$$
|
| 139 |
+
\sin \frac{\angle P Q R-\angle Q R S}{2}=(\sqrt{3}+1)\left[-\frac{(\sqrt{3}-1)}{2 \sqrt{2}}\right]=\frac{1}{\sqrt{2}}
|
| 140 |
+
$$
|
| 141 |
+
|
| 142 |
+
This shows that
|
| 143 |
+
|
| 144 |
+
$$
|
| 145 |
+
\frac{\angle P Q R-\angle Q R S}{2}=\frac{\pi}{4} \quad \text { or } \quad \frac{3 \pi}{4}
|
| 146 |
+
$$
|
| 147 |
+
|
| 148 |
+
Using the convexity of $P Q R S$, we can rule out the latter alternative. We obtain
|
| 149 |
+
|
| 150 |
+
$$
|
| 151 |
+
\angle P Q R-\angle Q R S=\frac{\pi}{2}
|
| 152 |
+
$$
|
| 153 |
+
|
| 154 |
+
5. Let $a, b, c$ be three real numbers such that $1 \geq a \geq b \geq c \geq 0$. Prove that if $\lambda$ is a root of the cubic equation $x^{3}+a x^{2}+b x+c=0$ (real or complex), then $|\lambda| \leq 1$.
|
| 155 |
+
|
| 156 |
+
Sol. : Since $\lambda$ is a root of the equation $x^{3}+a x^{2}+b x+c=0$, we have
|
| 157 |
+
|
| 158 |
+
$$
|
| 159 |
+
\lambda^{3}=-a \lambda^{2}-b \lambda-c
|
| 160 |
+
$$
|
| 161 |
+
|
| 162 |
+
This implies that
|
| 163 |
+
|
| 164 |
+
$$
|
| 165 |
+
\begin{aligned}
|
| 166 |
+
\lambda^{4} & =-a \lambda^{3}-b \lambda^{2}-c \lambda \\
|
| 167 |
+
& =(1-a) \lambda^{3}+(a-b) \lambda^{2}+(b-c) \lambda+c
|
| 168 |
+
\end{aligned}
|
| 169 |
+
$$
|
| 170 |
+
|
| 171 |
+
where we have used again
|
| 172 |
+
|
| 173 |
+
$$
|
| 174 |
+
-\lambda^{3}-a \lambda^{2}-b \lambda-c=0
|
| 175 |
+
$$
|
| 176 |
+
|
| 177 |
+
Suppose $|\lambda| \geq 1$. Then we obtain
|
| 178 |
+
|
| 179 |
+
$$
|
| 180 |
+
\begin{aligned}
|
| 181 |
+
|\lambda|^{4} & \leq(1-a)|\lambda|^{3}+(a-b)|\lambda|^{2}+(b-c)|\lambda|+c \\
|
| 182 |
+
& \leq(1-a)|\lambda|^{3}+(a-b)|\lambda|^{3}+(b-c)|\lambda|^{3}+c|\lambda|^{3} \\
|
| 183 |
+
& \leq|\lambda|^{3}
|
| 184 |
+
\end{aligned}
|
| 185 |
+
$$
|
| 186 |
+
|
| 187 |
+
This shows that $|\lambda| \leq 1$. Hence the only possibility in this case is $|\lambda|=1$. We conclude that $|\lambda| \leq 1$ is always true.
|
| 188 |
+
|
| 189 |
+
6. For any natural number $n,(n \geq 3)$, let $f(n)$ denote the number of non-congruent integer-sided triangles with perimeter $n$ (e.g., $f(3)=1, f(4)=0, f(7)=2$ ). Show that
|
| 190 |
+
|
| 191 |
+
(a) $f(1999)>f(1996)$
|
| 192 |
+
|
| 193 |
+
(b) $f(2000)=f(1997)$.
|
| 194 |
+
|
| 195 |
+
Sol. :
|
| 196 |
+
|
| 197 |
+
(a) Let $a, b, c$ be the sides of a triangle with $a+b+c=1996$, and each being a positive integer. Then $a+1, b+1, c+1$ are also sides of a triangle with perimeter 1999 because
|
| 198 |
+
|
| 199 |
+
$$
|
| 200 |
+
a<b+c \quad \Longrightarrow \quad a+1<(b+1)+(c+1)
|
| 201 |
+
$$
|
| 202 |
+
|
| 203 |
+
and so on. Moreover $(999,999,1)$ form the sides of a triangle with perimeter 1999, which is not obtainable in the form $(a+1, b+1, c+1)$ where $a, b, c$ are the integers and the sides of a triangle with $a+b+c=1996$. We conclude that $f(1999)>f(1996)$.
|
| 204 |
+
|
| 205 |
+
(b) As in the case (a) we conclude that $f(2000) \geq f(1997)$. On the other hand, if $x, y, z$ are the integer sides of a triangle with $x+y+z=2000$, and say $x \geq y \geq z \geq 1$, then we cannot have $z=1$; for otherwise we would get $x+y=1999$ forcing $x, y$ to have opposite parity so that $x-y \geq 1=z$ violating triangle inequality for $x, y, z$. Hence $x \geq y \geq z>1$. This implies that $x-1 \geq y-1 \geq z-1>0$. We already have $x<y+z$. If $x \geq y+z-1$, then we see that $y+z-1 \leq x<y+z$, showing that $y+z-1=x$. Hence we obtain $2000=x+y+z=2 x+1$ which is impossible. We conclude that $x<y+z-1$. This shows that $x-1<(y-1)+(z-1)$ and hence $x-1, y-1, z-1$ are the sides of a triangle with perimeter 1997. This gives $f(2000) \leq f(1997)$. Thus we obtain the desired result.
|
| 206 |
+
|
INMO/md/en-2001.md
ADDED
|
@@ -0,0 +1,211 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# INMO-2001 <br> Problems and Solutions
|
| 2 |
+
|
| 3 |
+
1. Let $A B C$ be a triangle in which no angle is $90^{\circ}$. For any point $P$ in the plane of the triangle, let $A_{1}, B_{1}, C_{1}$ denote the reflections of $P$ in the sides $B C, C A, A B$ respectively. Prove the following statements:
|
| 4 |
+
|
| 5 |
+
(a) If $P$ is the incentre or an excentre of $A B C$, then $P$ is the circumcentre of $A_{1} B_{1} C_{1}$;
|
| 6 |
+
|
| 7 |
+
(b) If $P$ is the circumcentre of $A B C$, then $P$ is the orthocentre of $A_{1} B_{1} C_{1}$;
|
| 8 |
+
|
| 9 |
+
(c) If $P$ is the orthocentre of $A B C$, then $P$ is either the incentre or an excentre of $A_{1} B_{1} C_{1}$.
|
| 10 |
+
|
| 11 |
+
## Solution:
|
| 12 |
+
|
| 13 |
+
(a)
|
| 14 |
+
|
| 15 |
+
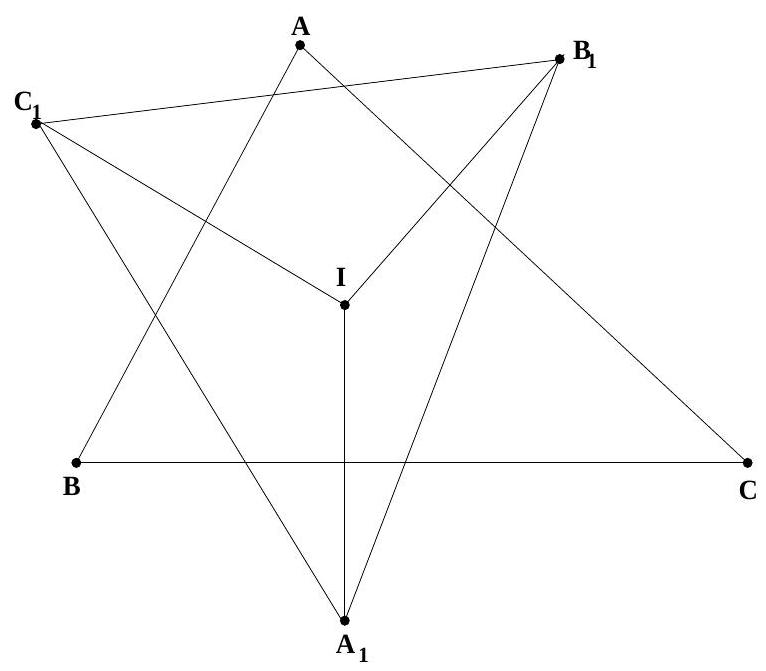
|
| 16 |
+
|
| 17 |
+
If $P=I$ is the incentre of triangle $A B C$, and $r$ its inradius, then it is clear that $A_{1} I=B_{1} I=C_{1} I=2 r$. It follows that $I$ is the circumcentre of $A_{1} B_{1} C_{1}$. On the otherhand if $P=I_{1}$ is the excentre of $A B C$ opposite $A$ and $r_{1}$ the corresponding exradius, then again we see that $A_{1} I_{1}=B_{1} I_{1}=C_{1} I_{1}=2 r_{1}$. Thus $I_{1}$ is the circumcentre of $A_{1} B_{1} C_{1}$.
|
| 18 |
+
|
| 19 |
+
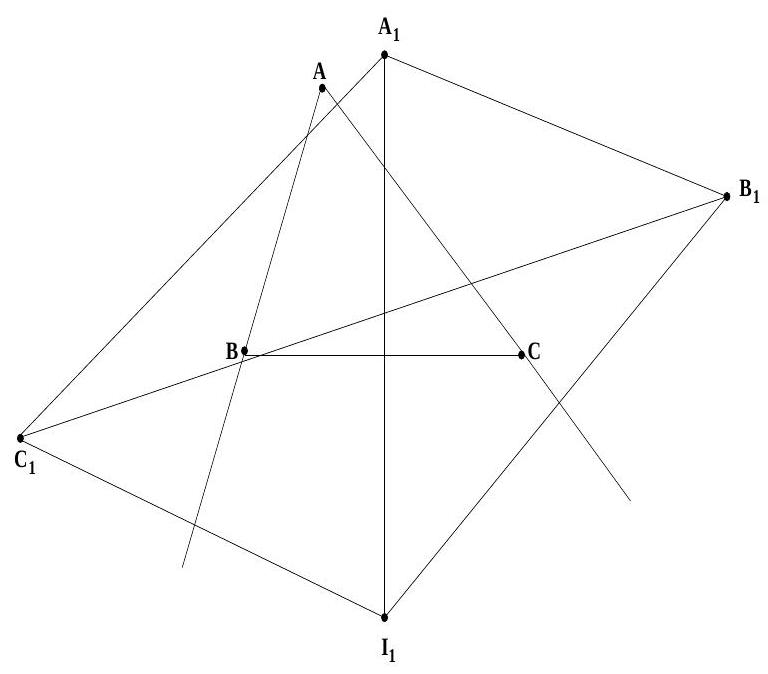
|
| 20 |
+
|
| 21 |
+
(b)
|
| 22 |
+
|
| 23 |
+
Let $P=O$ be the circumcentre of $A B C$. By definition, it follows that $O A_{1}$ bisects and is bisected by $B C$ and so on. Let $D, E, F$ be the mid-points of $B C, C A, A B$ respectively. Then $F E$ is parallel to $B C$. But $E, F$ are also mid-points of $O B_{1}, O C_{1}$ and hence $F E$ is parallel to $B_{1} C_{1}$ as well. We conclude that $B C$ is parallel to $B_{1} C_{1}$. Since $O A_{1}$ is perpendicular to $B C$, it follows that $O A_{1}$ is perpendicular to $B_{1} C_{1}$. Similarly $O B_{1}$ is perpendicular to $C_{1} A_{1}$ and $O C_{1}$ is perpendicular to $A_{1} B_{1}$. These imply that $O$ is the orthocentre of $A_{1} B_{1} C_{1}$. (This applies whether $O$ is inside or outside $A B C$.)
|
| 24 |
+
|
| 25 |
+
(c)
|
| 26 |
+
|
| 27 |
+
let $P=H$, the orthocentre of $A B C$. We consider two possibilities; $H$ falls inside $A B C$ and $H$ falls outside $A B C$.
|
| 28 |
+
|
| 29 |
+
Suppose $H$ is inside $A B C$; this happens if $A B C$ is an acute triangle. It is known that $A_{1}, B_{1}, C_{1}$ lie on the circumcircle of $A B C$. Thus $\angle C_{1} A_{1} A=\angle C_{1} C A=90^{\circ}-A$. Similarly $\angle B_{1} A_{1} A=\angle B_{1} B A=90^{\circ}-A$. These show that $\angle C_{1} A_{1} A=\angle B_{1} A_{1} A$. Thus $A_{1} A$ is an internal bisector of $\angle C_{1} A_{1} B_{1}$. Similarly we can show that $B_{1}$ bisects $\angle A_{1} B_{1} C_{1}$ and $C_{1} C$ bisects $\angle B_{1} C_{1} A_{1}$. Since $A_{1} A, B_{1} B, C_{1} C$ concur at $H$, we conclude that $H$ is the incentre of $A_{1} B_{1} C_{1}$.
|
| 30 |
+
|
| 31 |
+
OR If $D, E, F$ are the feet of perpendiculars of $A, B, C$ to the sides $B C, C A, A B$ respectively, then we see that $E F, F D, D E$ are respectively parallel to $B_{1} C_{1}, C_{1} A_{1}$, $A_{1} B_{1}$. This implies that $\angle C_{1} A_{1} H=\angle F D H=\angle A B E=90^{\circ}-A$, as $B D H F$ is a cyclic quadrilateral. Similarly, we can show that $\angle B_{1} A_{1} H=90^{\circ}-A$. It follows that $A_{1} H$ is the internal bisector of $\angle C_{1} A_{1} B_{1}$. We can proceed as in the earlier case.
|
| 32 |
+
|
| 33 |
+
If $H$ is outside $A B C$, the same proofs go through again, except that two of $A_{1} H$, $B_{1} H, C_{1} H$ are external angle bisectors and one of these is an internal angle bisector. Thus $H$ becomes an excentre of triangle $A_{1} B_{1} C_{1}$.
|
| 34 |
+
|
| 35 |
+
2. Show that the equation
|
| 36 |
+
|
| 37 |
+
$$
|
| 38 |
+
x^{2}+y^{2}+z^{2}=(x-y)(y-z)(z-x)
|
| 39 |
+
$$
|
| 40 |
+
|
| 41 |
+
has infinitely many solutions in integers $x, y, z$.
|
| 42 |
+
|
| 43 |
+
Solution: We seek solutions $(x, y, z)$ which are in arithmetic progression. Let us put $y-x=z-y=d>0$ so that the equation reduces to the form
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
3 y^{2}+2 d^{2}=2 d^{3}
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
Thus we get $3 y^{2}=2(d-1) d^{2}$. We conclude that $2(d-1)$ is 3 times a square. This is satisfied if $d-1=6 n^{2}$ for some $n$. Thus $d=6 n^{2}+1$ and $3 y^{2}=d^{2} \cdot 2\left(6 n^{2}\right)$ giving us $y^{2}=4 d^{2} n^{2}$. Thus we can take $y=2 d n=2 n\left(6 n^{2}+1\right)$. From this we obtain $x=y-d=(2 n-1)\left(6 n^{2}+1\right), z=y+d=(2 n+1)\left(6 n^{2}+1\right)$. It is easily verified that
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
(x, y, z)=\left((2 n-1)\left(6 n^{2}+1\right), 2 n\left(6 n^{2}+1\right),(2 n+1)\left(6 n^{2}+1\right)\right)
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
is indeed a solution for a fixed $n$ and this gives an infinite set of solutions as $n$ varies over natural numbers.
|
| 56 |
+
|
| 57 |
+
3. If $a, b, c$ are positive real numbers such that $a b c=1$, prove that
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
a^{b+c} b^{c+a} c^{a+b} \leq 1
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
Solution: Note that the inequality is symmetric in $a, b, c$ so that we may assume that $a \geq b \geq c$. Since $a b c=1$, it follows that $a \geq 1$ and $c \leq 1$. Using $b=1 / a c$, we get
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
a^{b+c} b^{c+a} c^{a+b}=\frac{a^{b+c} c^{a+b}}{a^{c+a} c^{c+a}}=\frac{c^{b-c}}{a^{a-b}} \leq 1
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
because $c \leq 1, b \geq c, a \geq 1$ and $a \geq b$.
|
| 70 |
+
|
| 71 |
+
4. Given any nine integers show that it is possible to choose, from among them, four integers $a, b, c, d$ such that $a+b-c-d$ is divisible by 20 . Further show that such a selection is not possible if we start with eight integers instead of nine.
|
| 72 |
+
|
| 73 |
+
## Solution:
|
| 74 |
+
|
| 75 |
+
Suppose there are four numbers $a, b, c, d$ among the given nine numbers which leave the same remainder modulo 20 . Then $a+b \equiv c+d(\bmod 20)$ and we are done.
|
| 76 |
+
|
| 77 |
+
If not, there are two possibilities:
|
| 78 |
+
|
| 79 |
+
(1) We may have two disjoint pairs $\{a, c\}$ and $\{b, d\}$ obtained from the given nine numbers such that $a \equiv c(\bmod 20)$ and $b \equiv d(\bmod 20)$. In this case we get $a+b \equiv c+d$ $(\bmod 20)$.
|
| 80 |
+
|
| 81 |
+
(2) Or else there are at most three numbers having the same remainder modulo 20 and the remaining six numbers leave distinct remainders which are also different from the first remainder (i.e., the remainder of the three numbers). Thus there are at least 7 disinct remainders modulo 20 that can be obtained from the given set of nine numbers. These 7 remainders give rise to $\binom{7}{2}=21$ pairs of numbers. By pigeonhole principle, there must be two pairs $\left(r_{1}, r_{2}\right),\left(r_{3}, r_{4}\right)$ such that $r_{1}+r_{2} \equiv r_{3}+r_{4}(\bmod 20)$. Going back we get four numbers $a, b, c, d$ such that $a+b \equiv c+d(\bmod 20)$.
|
| 82 |
+
|
| 83 |
+
If we take the numbers $0,0,0,1,2,4,7,12$, we check that the result is not true for these eight numbers.
|
| 84 |
+
|
| 85 |
+
5. Let $A B C$ be a triangle and $D$ be the mid-point of side $B C$. Suppose $\angle D A B=\angle B C A$ and $\angle D A C=15^{\circ}$. Show that $\angle A D C$ is obtuse. Further, if $O$ is the circumcentre of $A D C$, prove that triangle $A O D$ is equilateral.
|
| 86 |
+
|
| 87 |
+
## Solution:
|
| 88 |
+
|
| 89 |
+
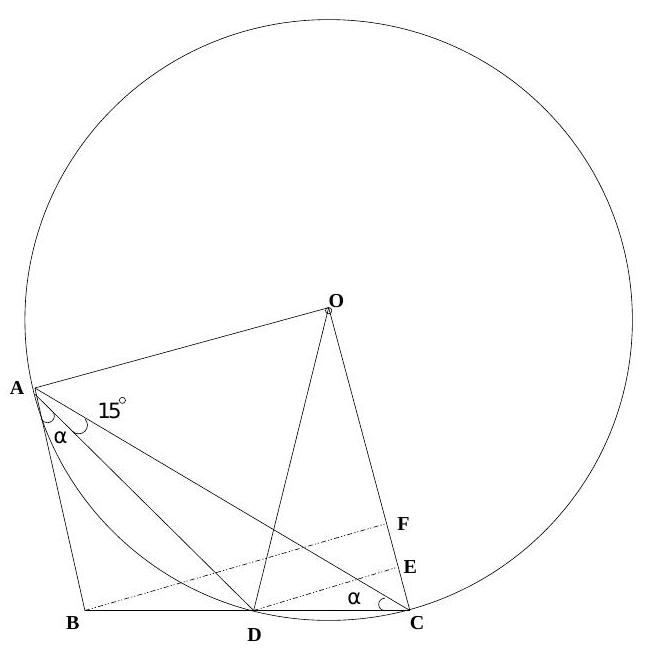
|
| 90 |
+
|
| 91 |
+
Let $\alpha$ denote the equal angles $\angle B A D=\angle D C A$. Using sine rule in triangles $D A B$ and $D A C$, we get
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
\frac{A D}{\sin B}=\frac{B D}{\sin \alpha}, \quad \frac{C D}{\sin 15^{\circ}}=\frac{A D}{\sin \alpha}
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
Eliminating $\alpha$ (using $B D=D C$ and $2 \alpha+B+15^{\circ}=\pi$ ), we obtain $1+\cos \left(B+15^{\circ}\right)=$ $2 \sin B \sin 15^{\circ}$. But we know that $2 \sin B \sin 15^{\circ}=\cos \left(B-15^{\circ}\right)-\cos \left(B+15^{\circ}\right)$. Putting $\beta=B-15^{\circ}$, we get a relation $1+2 \cos (\beta+30)=\cos \beta$. We write this in the form
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
(1-\sqrt{3}) \cos \beta+\sin \beta=1
|
| 101 |
+
$$
|
| 102 |
+
|
| 103 |
+
Since $\sin \beta \leq 1$, it follows that $(1-\sqrt{3}) \cos \beta \geq 0$. We conclude that $\cos \beta \leq 0$ and hence that $\beta$ is obtuse. So is angle $B$ and hence $\angle A D C$.
|
| 104 |
+
|
| 105 |
+
We have the relation $(1-\sqrt{3}) \cos \beta+\sin \beta=1$. If we set $x=\tan (\beta / 2)$, then we get, using $\cos \beta=\left(1-x^{2}\right) /\left(1+x^{2}\right), \sin \beta=2 x /\left(1+x^{2}\right)$,
|
| 106 |
+
|
| 107 |
+
$$
|
| 108 |
+
(\sqrt{3}-2) x^{2}+2 x-\sqrt{3}=0
|
| 109 |
+
$$
|
| 110 |
+
|
| 111 |
+
Solving for $x$, we obtain $x=1$ or $x=\sqrt{3}(2+\sqrt{3})$. If $x=\sqrt{3}(2+\sqrt{3})$, then $\tan (\beta / 2)>2+\sqrt{3}=\tan 75^{\circ}$ giving us $\beta>150^{\circ}$. This forces that $B>165^{\circ}$ and hence $B+A>165^{\circ}+15^{\circ}=180^{\circ}$, a contradiction. thus $x=1$ giving us $\beta=\pi / 2$. This gives $B=105^{\circ}$ and hence $\alpha=30^{\circ}$. Thus $\angle D A O=60^{\circ}$. Since $O A=O D$, the result follows.
|
| 112 |
+
|
| 113 |
+
## OR
|
| 114 |
+
|
| 115 |
+
Let $m_{a}$ denote the median $A D$. Then we can compute
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
\cos \alpha=\frac{c^{2}+m_{a}^{2}-\left(a^{2} / 4\right)}{2 c m_{a}}, \quad \sin \alpha=\frac{2 \Delta}{c m_{a}}
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
where $\Delta$ denotes the area of triangle $A B C$. These two expressions give
|
| 122 |
+
|
| 123 |
+
$$
|
| 124 |
+
\cot \alpha=\frac{c^{2}+m_{a}^{2}-\left(a^{2} / 4\right)}{4 \Delta}
|
| 125 |
+
$$
|
| 126 |
+
|
| 127 |
+
Similarly, we obtain
|
| 128 |
+
|
| 129 |
+
$$
|
| 130 |
+
\cot \angle C A D=\frac{b^{2}+m_{a}^{2}-\left(a^{2} / 4\right)}{4 \Delta}
|
| 131 |
+
$$
|
| 132 |
+
|
| 133 |
+
Thus we get
|
| 134 |
+
|
| 135 |
+
$$
|
| 136 |
+
\cot \alpha-\cot 15^{\circ}=\frac{c^{2}-a^{2}}{4 \Delta}
|
| 137 |
+
$$
|
| 138 |
+
|
| 139 |
+
Similarly we can also obtain
|
| 140 |
+
|
| 141 |
+
$$
|
| 142 |
+
\cot B-\cot \alpha=\frac{c^{2}-a^{2}}{4 \Delta}
|
| 143 |
+
$$
|
| 144 |
+
|
| 145 |
+
giving us the relation
|
| 146 |
+
|
| 147 |
+
$$
|
| 148 |
+
\cot B=2 \cot \alpha-\cot 15^{\circ}
|
| 149 |
+
$$
|
| 150 |
+
|
| 151 |
+
If $B$ is acute then $2 \cot \alpha>\cot 15^{\circ}=2+\sqrt{3}>2 \sqrt{3}$. It follows that $\cot \alpha>\sqrt{3}$. This implies that $\alpha<30^{\circ}$ and hence
|
| 152 |
+
|
| 153 |
+
$$
|
| 154 |
+
B=180^{\circ}-2 \alpha-15^{\circ}>105^{\circ}
|
| 155 |
+
$$
|
| 156 |
+
|
| 157 |
+
This contradiction forces that angle $B$ is obtuse and consequently $\angle A D C$ is obtuse.
|
| 158 |
+
|
| 159 |
+
Since $\angle B A D=\alpha=\angle A C D$, the line $A B$ is tangent to the circumcircle $\Gamma$ of $A D C$ at $A$. Hence $O A$ is perpendicular to $A B$. Draw $D E$ and $B F$ perpendicular to $A C$, and join $O D$. Since $\angle D A C=15^{\circ}$, we see that $\angle D O C=30^{\circ}$ and hence $D E=O D / 2$. But $D E$ is parallel to $B F$ and $B D=D C$ shows that $B F=2 D E$. We conclude that
|
| 160 |
+
$B F=D O$. But $D O=A O$, both being radii of $\Gamma$. Thus $B F=A O$. Using right triangles $B F O$ and $B A O$, we infer that $A B=O F$. We conclude that $A B F O$ is a rectangle. In particular $\angle A O F=90^{\circ}$. It follows that
|
| 161 |
+
|
| 162 |
+
$$
|
| 163 |
+
\angle A O D=90^{\circ}-\angle D O C=90^{\circ}-30^{\circ}=60^{\circ}
|
| 164 |
+
$$
|
| 165 |
+
|
| 166 |
+
Since $O A=O D$, we conclude that $A O D$ is equilateral.
|
| 167 |
+
|
| 168 |
+
OR
|
| 169 |
+
|
| 170 |
+
Note that triangles $A B D$ and $C B A$ are similar. Thus we have the ratios
|
| 171 |
+
|
| 172 |
+
$$
|
| 173 |
+
\frac{A B}{B D}=\frac{C B}{B A}
|
| 174 |
+
$$
|
| 175 |
+
|
| 176 |
+
This reduces to $a^{2}=2 c^{2}$ giving us $a=\sqrt{2} c$. This is equivalent to $\sin ^{2}\left(\alpha+15^{\circ}\right)=$ $2 \sin ^{2} \alpha$. We write this in the form
|
| 177 |
+
|
| 178 |
+
$$
|
| 179 |
+
\cos 15^{\circ}+\cot \alpha \sin 15^{\circ}=\sqrt{2}
|
| 180 |
+
$$
|
| 181 |
+
|
| 182 |
+
Solving for $\cot \alpha$, we get $\cot \alpha=\sqrt{3}$. We conclude that $\alpha=30^{\circ}$, and the result follows.
|
| 183 |
+
|
| 184 |
+
6. Let $\mathbf{R}$ denote the set of all real numbers. Find all functions $f: \mathbf{R} \rightarrow \mathbf{R}$ satisfying the condition
|
| 185 |
+
|
| 186 |
+
$$
|
| 187 |
+
f(x+y)=f(x) f(y) f(x y)
|
| 188 |
+
$$
|
| 189 |
+
|
| 190 |
+
for all $x, y$ in $\mathbf{R}$.
|
| 191 |
+
|
| 192 |
+
Solution: Putting $x=0, y=0$, we get $f(0)=f(0)^{3}$ so that $f(0)=0,1$ or -1 . If $f(0)=0$, then taking $y=0$ in the given equation, we obtain $f(x)=f(x) f(0)^{2}=0$ for all $x$.
|
| 193 |
+
|
| 194 |
+
Suppose $f(0)=1$. Taking $y=-x$, we obtain
|
| 195 |
+
|
| 196 |
+
$$
|
| 197 |
+
1=f(0)=f(x-x)=f(x) f(-x) f\left(-x^{2}\right)
|
| 198 |
+
$$
|
| 199 |
+
|
| 200 |
+
This shows that $f(x) \neq 0$ for any $x \in \mathbf{R}$. Taking $x=1, y=x-1$, we obtain
|
| 201 |
+
|
| 202 |
+
$$
|
| 203 |
+
f(x)=f(1) f(x-1)^{2}=f(1)[f(x) f(-x) f(-x)]^{2}
|
| 204 |
+
$$
|
| 205 |
+
|
| 206 |
+
Using $f(x) \neq 0$, we conclude that $1=k f(x)(f(-x))^{2}$, where $k=$
|
| 207 |
+
|
| 208 |
+
$f(1)(f(-1))^{2}$. Changing $x$ to $-x$ here, we also infer that $1=k f(-x)(f(x))^{2}$. Comparing these expressions we see that $f(-x)=f(x)$. It follows that $1=k f(x)^{3}$. Thus $f(x)$ is constant for all $x$. Since $f(0)=1$, we conclude that $f(x)=1$ for all real $x$.
|
| 209 |
+
|
| 210 |
+
If $f(0)=-1$, a similar analysis shows that $f(x)=-1$ for all $x \in \mathbf{R}$. We can verify that each of these functions satisfies the given functional equation. Thus there are three solutions, all of them being constant functions.
|
| 211 |
+
|
INMO/md/en-2002.md
ADDED
|
@@ -0,0 +1,196 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Solution to INMO-2002 Problems
|
| 2 |
+
|
| 3 |
+
1. For a convex hexagon $A B C D E F$ in which each pair of opposite sides is unequal, consider the following six statements:
|
| 4 |
+
|
| 5 |
+
$$
|
| 6 |
+
\begin{array}{ll}
|
| 7 |
+
\text { (a } \left.\mathrm{a}_{1}\right) A B \text { is parallel to } D E ; & \left(\mathrm{a}_{2}\right) A E=B D \\
|
| 8 |
+
\left(\mathrm{~b}_{1}\right) B C \text { is parallel to } E F ; & \left(\mathrm{b}_{2}\right) B F=C E \\
|
| 9 |
+
\text { (c } \left.\mathrm{c}_{1}\right) C D \text { is parallel to } F A ; & \left(\mathrm{c}_{2}\right) C A=D F
|
| 10 |
+
\end{array}
|
| 11 |
+
$$
|
| 12 |
+
|
| 13 |
+
(a) Show that if all the six statements are true, then the hexagon is cyclic(i.e., it can be inscribed in a circle).
|
| 14 |
+
|
| 15 |
+
(b) Prove that, in fact, any five of these six statements also imply that the hexagon is cyclic.
|
| 16 |
+
|
| 17 |
+
## Solution:
|
| 18 |
+
|
| 19 |
+
(a) Suppose all the six statements are true. Then $A B D E, B C E F, C D F A$ are isosceles trapeziums; if $K, L, M, P, Q, R$ are the mid-points of $A B, B C$, $C D, D E, E F, F A$ respectively, then we see that $K P \perp A B, E D ; L Q \perp$ $B C, E F$ and $M R \perp C D, F A$.
|
| 20 |
+
|
| 21 |
+
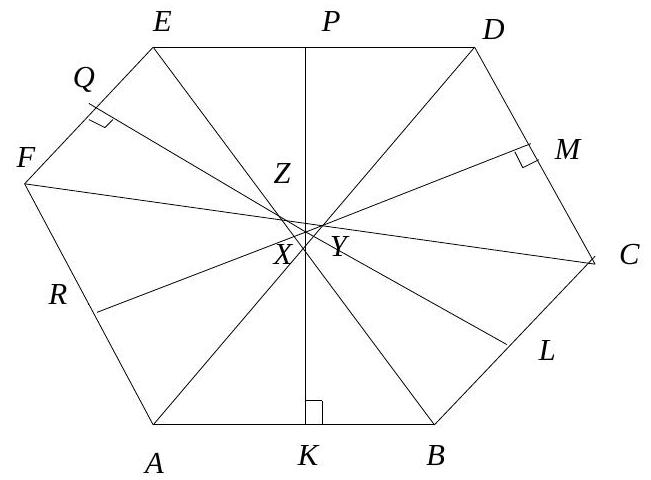
|
| 22 |
+
|
| 23 |
+
If $A D, B E, C F$ themselves concur at a point $O$, then $O A=O B=O C=$ $O D=O E=O F$. ( $O$ is on the perpendicular bisector of each of the sides.) Hence $A, B, C, D, E, F$ are concyclic and lie on a circle with centre $O$. Otherwise these lines $A D, B E, C F$ form a triangle, say $X Y Z$. (See Fig.) Then $K X, M Y, Q Z$, when extended, become the internal angle bisectors of the triangle $X Y Z$ and hence concur at the incentre $O^{\prime}$ of $X Y Z$. As earlier $O^{\prime}$ lies on the perpendicular bisector of each of the sides. Hence $O^{\prime} A=O^{\prime} B$ $=O^{\prime} C=O^{\prime} D=O^{\prime} E=O^{\prime} F$, giving the concyclicity of $A, B, C, D, E, F$.
|
| 24 |
+
(b) Suppose $\left(\mathrm{a}_{1}\right),\left(\mathrm{a}_{2}\right),\left(\mathrm{b}_{1}\right),\left(\mathrm{b}_{2}\right)$ are true. Then we see that $A D=B E=$ $C F$. Assume that ( $\mathrm{c}_{1}$ ) is true. Then $C D$ is parallel to $A F$. It follows that triangles $Y C D$ and $Y F A$ are similar. This gives
|
| 25 |
+
|
| 26 |
+
$$
|
| 27 |
+
\frac{F Y}{A Y}=\frac{Y C}{Y D}=\frac{F Y+Y C}{A Y+Y D}=\frac{F C}{A D}=1
|
| 28 |
+
$$
|
| 29 |
+
|
| 30 |
+
We obtain $F Y=A Y$ and $Y C=Y D$. This forces that triangles $C Y A$ and $D Y F$ are congruent. In particular $A C=D F$ so that ( $\mathrm{c}_{2}$ ) is true. The conclusion follows from (a). Now assume that ( $\mathrm{c}_{2}$ ) is true; i.e., $A C=F D$. We have seen that $A D=B E=C F$. It follows that triangles $F D C$ and $A C D$ are congruent. In particular $\angle A D C=\angle F C D$. Similarly, we can show that $\angle C F A=\angle D A F$. We conclude that $C D$ is parallel to $A F$ giving $\left(\mathrm{c}_{1}\right.$ ).
|
| 31 |
+
|
| 32 |
+
2. Determine the least positive value taken by the expression $a^{3}+b^{3}+c^{3}-3 a b c$ as $a, b, c$ vary over all positive integers. Find also all triples $(a, b, c)$ for which this least value is attained.
|
| 33 |
+
|
| 34 |
+
Solution: We observe that
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
\left.Q=a^{3}+b^{3}+c^{3}-3 a b c=\frac{1}{2}(a+b+c)\right)\left((a-b)^{2}+(b-c)^{2}+(c-a)^{2}\right)
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
Since we are looking for the least positive value taken by $Q$, it follows that $a, b, c$ are not all equal. Thus $a+b+c \geq 1+1+2=4$ and $(a-b)^{2}+(b-$ $c)^{2}+(c-a)^{2} \geq 1+1+0=2$. Thus we see that $Q \geq 4$. Taking $a=1$, $b=1$ and $c=2$, we get $Q=4$. Therefore the least value of $Q$ is 4 and this is achieved only by $a+b+c=4$ and $(a-b)^{2}+(b-c)^{2}+(c-a)^{2}=2$. The triples for which $Q=4$ are therefore given by
|
| 41 |
+
|
| 42 |
+
$$
|
| 43 |
+
(a, b, c)=(1,1,2),(1,2,1),(2,1,1)
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
3. Let $x, y$ be positive reals such that $x+y=2$. Prove that
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
x^{3} y^{3}\left(x^{3}+y^{3}\right) \leq 2
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
Solution: We have from the AM-GM inequality, that
|
| 53 |
+
|
| 54 |
+
$$
|
| 55 |
+
x y \leq\left(\frac{x+y}{2}\right)^{2}=1
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
Thus we obtain $0<x y \leq 1$. We write
|
| 59 |
+
|
| 60 |
+
$$
|
| 61 |
+
\begin{aligned}
|
| 62 |
+
x^{3} y^{3}\left(x^{3}+y^{3}\right) & =(x y)^{3}(x+y)\left(x^{2}-x y+y^{2}\right) \\
|
| 63 |
+
& =2(x y)^{3}\left((x+y)^{2}-3 x y\right) \\
|
| 64 |
+
& =2(x y)^{3}(4-3 x y)
|
| 65 |
+
\end{aligned}
|
| 66 |
+
$$
|
| 67 |
+
|
| 68 |
+
Thus we need to prove that
|
| 69 |
+
|
| 70 |
+
$$
|
| 71 |
+
(x y)^{3}(4-3 x y) \leq 1
|
| 72 |
+
$$
|
| 73 |
+
|
| 74 |
+
Putting $z=x y$, this inequality reduces to
|
| 75 |
+
|
| 76 |
+
$$
|
| 77 |
+
z^{3}(4-3 z) \leq 1
|
| 78 |
+
$$
|
| 79 |
+
|
| 80 |
+
for $0<z \leq 1$. We can prove this in different ways. We can put the inequality in the form
|
| 81 |
+
|
| 82 |
+
$$
|
| 83 |
+
3 z^{4}-4 z^{3}+1 \geq 0
|
| 84 |
+
$$
|
| 85 |
+
|
| 86 |
+
Here the expression in the LHS factors to $(z-1)^{2}\left(3 z^{2}+2 z+1\right)$ and $\left(3 z^{2}+2 z+1\right)$ is positive since its discriminant $D=-8<0$. Or applying the AM-GM inequality to the positive reals $4-3 z, z, z, z$, we obtain
|
| 87 |
+
|
| 88 |
+
$$
|
| 89 |
+
z^{3}(4-3 z) \leq\left(\frac{4-3 z+3 z}{4}\right)^{4} \leq 1
|
| 90 |
+
$$
|
| 91 |
+
|
| 92 |
+
4. Do there exist 100 lines in the plane, no three of them concurrent, such that they intersect exactly in 2002 points?
|
| 93 |
+
|
| 94 |
+
Solution: Any set of 100 lines in the plane can be partitioned into a finite number of disjoint sets, say $A_{1}, A_{2}, A_{3}, \ldots, A_{k}$, such that
|
| 95 |
+
|
| 96 |
+
(i) Any two lines in each $A_{j}$ are parallel to each other, for $1 \leq j \leq k$ (provided, of course, $\left|A_{j}\right| \geq 2$ );
|
| 97 |
+
|
| 98 |
+
(ii) for $j \neq l$, the lines in $A_{j}$ and $A_{l}$ are not parallel.
|
| 99 |
+
|
| 100 |
+
If $\left|A_{j}\right|=m_{j}, 1 \leq j \leq k$, then the total number of points of intersection is given by $\sum_{1 \leq j \leq l \leq k} m_{j} m_{l}$, as no three lines are concurrent. Thus we have to find positive integers $m_{1}, m_{2}, \ldots, m_{k}$ such that
|
| 101 |
+
|
| 102 |
+
$$
|
| 103 |
+
\sum_{j=1}^{k} m_{j}=100, \quad \sum m_{j} m_{l}=2002
|
| 104 |
+
$$
|
| 105 |
+
|
| 106 |
+
for an affirmative answer to the given question.
|
| 107 |
+
|
| 108 |
+
We observe that
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
\begin{aligned}
|
| 112 |
+
\sum_{j=1}^{k} m_{j}^{2} & =\left(\sum_{j=1}^{k} m_{j}\right)^{2}-2\left(\sum m_{j} m_{l}\right) \\
|
| 113 |
+
& =100^{2}-2(2002)=5996
|
| 114 |
+
\end{aligned}
|
| 115 |
+
$$
|
| 116 |
+
|
| 117 |
+
Thus we have to choose $m_{1}, m_{2}, \ldots, m_{k}$ such that
|
| 118 |
+
|
| 119 |
+
$$
|
| 120 |
+
\sum_{j=1}^{k} m_{j}=100, \quad \sum_{j=1}^{k} m_{j}^{2}=5996
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
We observe that $[\sqrt{5996}]=77$. So we may take $m_{1}=77$, so that
|
| 124 |
+
|
| 125 |
+
$$
|
| 126 |
+
\sum_{j=2}^{k} m_{j}=23, \quad \sum j=2^{k} m_{j}^{2}=67
|
| 127 |
+
$$
|
| 128 |
+
|
| 129 |
+
Now we may choose $m_{2}=5, m_{3}=m_{4}=4, m_{5}=m_{6}=\cdots=m_{14}=1$. Finally, we can take
|
| 130 |
+
|
| 131 |
+
$$
|
| 132 |
+
k=14, \quad\left(m_{1}, m_{2}, \ldots, m_{14}\right)=(77,5,4,4,1,1,1,1,1,1,1,1,1,1)
|
| 133 |
+
$$
|
| 134 |
+
|
| 135 |
+
proving the existence of 100 lines with exactly 2002 points of intersection.
|
| 136 |
+
|
| 137 |
+
5. Do there exist three distinct positive real numbers $a, b, c$ such that the numbers $a, b, c, b+c-a, c+a-b, a+b-c$ and $a+b+c$ form a 7-term arithmetic progression in some order?
|
| 138 |
+
|
| 139 |
+
Solution: We show that the answer is NO. Suppose, if possible, let $a, b, c$ be three distinct positive real numbers such that $a, b, c, b+c-a, c+a-b$, $a+b-c$ and $a+b+c$ form a 7-term arithmetic progression in some order. We may assume that $a<b<c$. Then there are only two cases we need to check: (I) $a+b-c<a<c+a-b<b<c<b+c-a<a+b+c$ and (II) $a+b-c<a<b<c+a-b<c<b+c-a<a+b+c$.
|
| 140 |
+
|
| 141 |
+
Case I. Suppose the chain of inequalities $a+b-c<a<c+a-b<b<$ $c<b+c-a<a+b+c$ holds good. let $d$ be the common difference. Thus we see that
|
| 142 |
+
|
| 143 |
+
$$
|
| 144 |
+
c=a+b+c-2 d, b=a+b+c-3 d, a=a+b+c-5 d
|
| 145 |
+
$$
|
| 146 |
+
|
| 147 |
+
Adding these, we see that $a+b+c=5 d$. But then $a=0$ contradicting the positivity of $a$.
|
| 148 |
+
|
| 149 |
+
Case II. Suppose the inequalities $a+b-c<a<b<c+a-b<c<$ $b+c-a<a+b+c$ are true. Again we see that
|
| 150 |
+
|
| 151 |
+
$$
|
| 152 |
+
c=a+b+c-2 d, b=a+b+c-4 d, a=a+b+c-5 d
|
| 153 |
+
$$
|
| 154 |
+
|
| 155 |
+
We thus obtain $a+b+c=(11 / 2) d$. This gives
|
| 156 |
+
|
| 157 |
+
$$
|
| 158 |
+
a=\frac{1}{2} d, b=\frac{3}{2} d, c=\frac{7}{2} d
|
| 159 |
+
$$
|
| 160 |
+
|
| 161 |
+
Note that $a+b-c=a+b+c-6 d=-(1 / 2) d$. However we also get $a+b-c=[(1 / 2)+(3 / 2)-(7 / 2)] d=-(3 / 2) d$. It follows that $3 e=e$ giving $d=0$. But this is impossible.
|
| 162 |
+
|
| 163 |
+
Thus there are no three distinct positive real numbers $a, b, c$ such that $a$, $b, c, b+c-a, c+a-b, a+b-c$ and $a+b+c$ form a 7-term arithmetic progression in some order.
|
| 164 |
+
|
| 165 |
+
6. Suppose the $n^{2}$ numbers $1,2,3, \ldots, n^{2}$ are arranged to form an $n$ by $n$ array consisting of $n$ rows and $n$ columns such that the numbers in each row(from left to right) and each column(from top to bottom) are in increasing order. Denote by $a_{j k}$ the number in $j$-th row and $k$-th column. Suppose $b_{j}$ is the maximum possible number of entries that can occur as $a_{j j}, 1 \leq j \leq n$. Prove that
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
b_{1}+b_{2}+b_{3}+\cdots b_{n} \leq \frac{n}{3}\left(n^{2}-3 n+5\right)
|
| 169 |
+
$$
|
| 170 |
+
|
| 171 |
+
(Example: In the case $n=3$, the only numbers which can occur as $a_{22}$ are 4,5 or 6 so that $b_{2}=3$.)
|
| 172 |
+
|
| 173 |
+
Solution: Since $a_{j j}$ has to exceed all the numbers in the top left $j \times j$ submatrix (excluding itself), and since there are $j^{2}-1$ entries, we must have $a_{j j} \geq j^{2}$. Similarly, $a_{j j}$ must not exceed eac of the numbers in the bottom right $(n-j+1) \times(n-j+1)$ submatrix (other than itself) and there are $(n-j+1)^{2}-1$ such entries giving $a_{j j} \leq n^{2}-(n-j+1)^{2}+1$. Thus we see that
|
| 174 |
+
|
| 175 |
+
$$
|
| 176 |
+
a_{j j} \in\left\{j^{2}, j^{2}+1, j^{2}+2, \ldots, n^{2}-(n-j+1)^{2}+1\right\}
|
| 177 |
+
$$
|
| 178 |
+
|
| 179 |
+
The number of elements in this set is $n^{2}-(n-j+1)^{2}-j^{2}+2$. This implies that
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
b_{j} \leq n^{2}-(n-j+1)^{2}-j^{2}+2=(2 n+2) j-2 j^{2}-(2 n-1)
|
| 183 |
+
$$
|
| 184 |
+
|
| 185 |
+
It follows that
|
| 186 |
+
|
| 187 |
+
$$
|
| 188 |
+
\begin{aligned}
|
| 189 |
+
\sum_{j=1}^{n} b_{j} & \leq(2 n+2) \sum_{j=1}^{n} j-2 \sum_{j=1}^{n} j^{2}-n(2 n-1) \\
|
| 190 |
+
& =(2 n+2)\left(\frac{n(n+1)}{2}\right)-2\left(\frac{n(n+1)(2 n+1)}{6}\right)-n(2 n-1) \\
|
| 191 |
+
& =\frac{n}{3}\left(n^{2}-3 n+5\right)
|
| 192 |
+
\end{aligned}
|
| 193 |
+
$$
|
| 194 |
+
|
| 195 |
+
which is the required bound.
|
| 196 |
+
|
INMO/md/en-2003.md
ADDED
|
@@ -0,0 +1,194 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Solutions to INMO-2003 problems
|
| 2 |
+
|
| 3 |
+
1. Consider an acute triangle $A B C$ and let $P$ be an interior point of $A B C$. Suppose the lines $B P$ and $C P$, when produced, meet $A C$ and $A B$ in $E$ and $F$ respectively. Let $D$ be the point where $A P$ intersects the line segment $E F$ and $K$ be the foot of perpendicular from $D$ on to $B C$. Show that $D K$ bisects $\angle E K F$.
|
| 4 |
+
|
| 5 |
+
Solution: Produce $A P$ to meet $B C$ in $Q$. Join $K E$ and $K F$. Draw perpendiculars from $F$ and $E$ on to $B C$ to meet it in $M$ and $L$ respectively. Let us denote $\angle B K F$ by $\alpha$ and $\angle C K E$ by $\beta$. We show that $\alpha=\beta$ by proving $\tan \alpha=\tan \beta$. This implies that $\angle D K F=\angle D K E$.(See Figure below.)
|
| 6 |
+
|
| 7 |
+
|
| 8 |
+
|
| 9 |
+
Since the cevians $A Q, B E$ and $C F$ concur, we may write
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\frac{B Q}{Q C}=\frac{z}{y}, \frac{C E}{E A}=\frac{x}{z}, \frac{A F}{F B}=\frac{y}{x}
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
We observe that
|
| 16 |
+
|
| 17 |
+
$$
|
| 18 |
+
\frac{F D}{D E}=\frac{[A F D]}{[A E D]}=\frac{[P F D]}{[P E D]}=\frac{[A F P]}{[A E P]}
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
However standard computations involving bases give
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
[A F P]=\frac{y}{y+x}[A B P], \quad[A E P]=\frac{z}{z+x}[A C P]
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
and
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
[A B P]=\frac{z}{x+y+z}[A B C], \quad[A C P]=\frac{y}{x+y+z}[A B C]
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
Thus we obtain
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
\frac{F D}{D E}=\frac{x+z}{x+y}
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
On the other hand
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
\tan \alpha=\frac{F M}{K M}=\frac{F B \sin B}{K M}, \tan \beta=\frac{E L}{K L}=\frac{E C \sin C}{K L}
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
Using $F B=\left(\frac{x}{x+y}\right) A B, E C=\left(\frac{x}{x+z}\right) A C$ and $A B \sin B=A C \sin C$, we obtain
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
\begin{aligned}
|
| 49 |
+
\frac{\tan \alpha}{\tan \beta} & =\left(\frac{x+z}{x+y}\right)\left(\frac{K L}{K M}\right) \\
|
| 50 |
+
& =\left(\frac{x+z}{x+y}\right)\left(\frac{D E}{F D}\right) \\
|
| 51 |
+
& =\left(\frac{x+z}{x+y}\right)\left(\frac{x+y}{x+z}\right)=1
|
| 52 |
+
\end{aligned}
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
We conclude that $\alpha=\beta$.
|
| 56 |
+
|
| 57 |
+
2. Find all primes $p$ and $q$, and even numbers $n>2$, satisfying the equation
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
p^{n}+p^{n-1}+\cdots+p+1=q^{2}+q+1
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
Solution: Obviously $p \neq q$. We write this in the form
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
p\left(p^{n-1}+p^{n-2}+\cdots+1\right)=q(q+1)
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
If $q \leq p^{n / 2}-1$, then $q<p^{n / 2}$ and hence we see that $q^{2}<p^{n}$. Thus we obtain
|
| 70 |
+
|
| 71 |
+
$$
|
| 72 |
+
q^{2}+q<p^{n}+p^{n / 2}<p^{n}+p^{n-1}+\cdots+p
|
| 73 |
+
$$
|
| 74 |
+
|
| 75 |
+
since $n>2$. It follows that $q \geq p^{n / 2}$. Since $n>2$ and is an even number, $n / 2$ is a natural number larger than 1 . This implies that $q \neq p^{n / 2}$ by the given condition that $q$ is a prime. We conclude that $q \geq p^{n / 2}+1$. We may also write the above relation in the form
|
| 76 |
+
|
| 77 |
+
$$
|
| 78 |
+
p\left(p^{n / 2}-1\right)\left(p^{n / 2}+1\right)=(p-1) q(q+1)
|
| 79 |
+
$$
|
| 80 |
+
|
| 81 |
+
This shows that $q$ divides $\left(p^{n / 2}-1\right)\left(p^{n / 2}+1\right)$. But $q \geq p^{n / 2}+1$ and $q$ is a prime. Hence the only possibility is $q=p^{n / 2}+1$. This gives
|
| 82 |
+
|
| 83 |
+
$$
|
| 84 |
+
p\left(p^{n / 2}-1\right)=(p-1)(q+1)=(p-1)\left(p^{n / 2}+2\right)
|
| 85 |
+
$$
|
| 86 |
+
|
| 87 |
+
Simplification leads to $3 p=p^{n / 2}+2$. This shows that $p$ divide 2. Thus $p=2$ and hence $q=5, n=4$. It is easy to verify that these indeed satisfy the given equation.
|
| 88 |
+
|
| 89 |
+
3. Show that for every real number $a$ the equation
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
8 x^{4}-16 x^{3}+16 x^{2}-8 x+a=0
|
| 93 |
+
$$
|
| 94 |
+
|
| 95 |
+
has at least one non-real root and find the sum of all the non-real roots of the equation.
|
| 96 |
+
|
| 97 |
+
Solution: Substituting $x=y+(1 / 2)$ in the equation, we obtain the equation in $y$ :
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
8 y^{4}+4 y^{2}+a-\frac{3}{2}=0
|
| 101 |
+
$$
|
| 102 |
+
|
| 103 |
+
Using the transformation $z=y^{2}$, we get a quadratic equation in $z$ :
|
| 104 |
+
|
| 105 |
+
$$
|
| 106 |
+
8 z^{2}+4 z+a-\frac{3}{2}=0
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
The discriminant of this equation is $32(2-a)$ which is nonnegative if and only if $a \leq 2$. For $a \leq 2$, we obtain the roots
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
z_{1}=\frac{-1+\sqrt{2(2-a)}}{4}, \quad z_{2}=\frac{-1-\sqrt{2(2-a)}}{4}
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
For getting real $y$ we need $z \geq 0$. Obviously $z_{2}<0$ and hence it gives only non-real values of $y$. But $z_{1} \geq 0$ if and only if $a \leq \frac{3}{2}$. In this case we obtain two real values for $y$ and hence two real roots for the original equation (1). Thus we conclude that there are two real roots and two non-real roots for $a \leq \frac{3}{2}$ and four non-real roots for $a>\frac{3}{2}$. Obviously the sum of all the roots of the equation is 2 . For $a \leq \frac{3}{2}$, two real roots of (2) are given by $y_{1}=+\sqrt{z_{1}}$ and $y_{2}=-\sqrt{z_{1}}$. Hence the sum of real roots of (1) is given by $y_{1}+\frac{1}{2}+y_{2}+\frac{1}{2}$ which reduces to 1 . It follows the sum of the non-real roots of (1) for $a \leq \frac{3}{2}$ is also 1 . Thus
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
\text { The sum of nonreal roots }= \begin{cases}1 & \text { for } a \leq \frac{3}{2} \\ 2 & \text { for } a>\frac{3}{2}\end{cases}
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
4. Find all 7-digit numbers formed by using only the digits 5 and 7 , and divisible by both 5 and 7 .
|
| 122 |
+
|
| 123 |
+
Solution: Clearly, the last digit must be 5 and we have to determine the remaining 6 digits. For divisibility by 7 , it is sufficient to consider the number obtained by replacing 7 by 0 ; for example 5775755 is divisible by 7 if and only 5005055 is divisible by 7 . Each such number is obtained by adding some of the numbers from the set $\{50,500,5000,50000,500000,5000000\}$ along with 5 . We look at the remainders of these when divided by 7 ; they are $\{1,3,2,6,4,5\}$. Thus it is sufficient to check for those combinations of
|
| 124 |
+
remainders which add up to a number of the from $2+7 k$, since the last digit is already 5 . These are $\{2\},\{3,6\},\{4,5\},\{2,3,4\},\{1,3,5\},\{1,2,6\}$, $\{2,3,5,6\},\{1,4,5,6\}$ and $\{1,2,3,4,6\}$. These correspond to the numbers $7775775,7757575,5577775,7575575,5777555,7755755,5755575,5557755$, 755555 .
|
| 125 |
+
|
| 126 |
+
5. Let $A B C$ be a triangle with sides $a, b, c$. Consider a triangle $A_{1} B_{1} C_{1}$ with sides equal to $a+\frac{b}{2}, b+\frac{c}{2}, c+\frac{a}{2}$. Show that
|
| 127 |
+
|
| 128 |
+
$$
|
| 129 |
+
\left[A_{1} B_{1} C_{1}\right] \geq \frac{9}{4}[A B C]
|
| 130 |
+
$$
|
| 131 |
+
|
| 132 |
+
where $[X Y Z]$ denotes the area of the triangle $X Y Z$.
|
| 133 |
+
|
| 134 |
+
Solution: It is easy to observe that there is a triangle with sides $a+\frac{b}{2}$, $b+\frac{c}{2}, c+\frac{a}{2}$. Using Heron's formula, we get
|
| 135 |
+
|
| 136 |
+
$$
|
| 137 |
+
16[A B C]^{2}=(a+b+c)(a+b-c)(b+c-a)(c+a-b)
|
| 138 |
+
$$
|
| 139 |
+
|
| 140 |
+
and
|
| 141 |
+
|
| 142 |
+
$$
|
| 143 |
+
16\left[A_{1} B_{1} C_{1}\right]^{2}=\frac{3}{16}(a+b+c)(-a+b+3 c)(-b+c+3 a)(-c+a+3 b)
|
| 144 |
+
$$
|
| 145 |
+
|
| 146 |
+
Since $a, b, c$ are the sides of a triangle, there are positive real numbers $p, q, r$ such that $a=q+r, b=r+p, c=p+q$. Using these relations we obtain
|
| 147 |
+
|
| 148 |
+
$$
|
| 149 |
+
\frac{[A B C]^{2}}{\left[A_{1} B_{1} C_{1}\right]^{2}}=\frac{16 p q r}{3(2 p+q)(2 q+r)(2 r+p)}
|
| 150 |
+
$$
|
| 151 |
+
|
| 152 |
+
Thus it is sufficient to prove that
|
| 153 |
+
|
| 154 |
+
$$
|
| 155 |
+
(2 p+q)(2 q+r)(2 r+p) \geq 27 p q r
|
| 156 |
+
$$
|
| 157 |
+
|
| 158 |
+
for positive real numbers $p, q, r$. Using AM-GM inequality, we get
|
| 159 |
+
|
| 160 |
+
$$
|
| 161 |
+
2 p+q \geq 3\left(p^{2} q\right)^{1 / 3}, 2 q+r \geq 3\left(q^{2} r\right)^{1 / 3}, 2 r+p \geq 3\left(r^{2} p\right)^{1 / 3}
|
| 162 |
+
$$
|
| 163 |
+
|
| 164 |
+
Multiplying these, we obtain the desired result. We also observe that equality holds if and only if $p=q=r$. This is equivalent to the statement that $A B C$ is equilateral.
|
| 165 |
+
|
| 166 |
+
6. In a lottery, tickets are given nine-digit numbers using only the digits $1,2,3$. They are also coloured red, blue or green in such a way that two tickets whose numbers differ in all the nine places get different colours. Suppose
|
| 167 |
+
the ticket bearing the number 122222222 is red and that bearing the number 222222222 is green. Determine, with proof, the colour of the ticket bearing the number 123123123 .
|
| 168 |
+
|
| 169 |
+
Solution: The following sequence of moves lead to the colour of the ticket bearing the number 123123123:
|
| 170 |
+
|
| 171 |
+
| Line Number | Ticket Number | Colour | Reason |
|
| 172 |
+
| :---: | :--- | :--- | :--- |
|
| 173 |
+
| 1 | 122222222 | red | Given |
|
| 174 |
+
| 2 | 222222222 | green | Given |
|
| 175 |
+
| 3 | 313113113 | blue | Lines 1 \& 2 |
|
| 176 |
+
| 4 | 231331331 | green | Lines 1 \& 3 |
|
| 177 |
+
| 5 | 331331331 | blue | Lines 1 \& 2 |
|
| 178 |
+
| 6 | 123123123 | red | Lines 4 \& 5 |
|
| 179 |
+
|
| 180 |
+
If 123123123 is reached by some other root, red colour must be obtained even along that root. For if for example 123123123 gets blue from some other root, then the following sequence leads to a contradiction:
|
| 181 |
+
|
| 182 |
+
| Line Number | Ticket Number | Colour | Reason |
|
| 183 |
+
| :---: | :--- | :--- | :--- |
|
| 184 |
+
| 1 | 122222222 | red | Given |
|
| 185 |
+
| 2 | 123123123 | blue | Given |
|
| 186 |
+
| 3 | 231311311 | green | Lines 1 \& 2 |
|
| 187 |
+
| 4 | 211331311 | green | Lines 1 \& 2 |
|
| 188 |
+
| 5 | 332212212 | red | Lines 4 \& 2 |
|
| 189 |
+
| 6 | 113133133 | blue | Lines 3 \& 5 |
|
| 190 |
+
| 7 | 331331331 | green | Lines 1 \& 2 |
|
| 191 |
+
| 8 | 222222222 | red | Line 6 \& 7 |
|
| 192 |
+
|
| 193 |
+
Thus the colour of 22222222 is red contradicting that it is grren.
|
| 194 |
+
|
INMO/md/en-2004.md
ADDED
|
@@ -0,0 +1,233 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# INMO 2004 - Solutions
|
| 2 |
+
|
| 3 |
+
1. Consider a convex quadrilateral $A B C D$, in which $K, L, M, N$ are the midpoints of the sides $A B$, $B C, C D, D A$ respectively. Suppose
|
| 4 |
+
|
| 5 |
+
(a) $B D$ bisects $K M$ at $Q$;
|
| 6 |
+
|
| 7 |
+
(b) $Q A=Q B=Q C=Q D$; and
|
| 8 |
+
|
| 9 |
+
(c) $L K / L M=C D / C B$.
|
| 10 |
+
|
| 11 |
+
Prove that $A B C D$ is a square.
|
| 12 |
+
|
| 13 |
+
## Solution:
|
| 14 |
+
|
| 15 |
+
|
| 16 |
+
|
| 17 |
+
Fig. 1.
|
| 18 |
+
|
| 19 |
+
Observe that $K L M N$ is a paralellogram, $Q$ is the midpoint of $M K$ and hence $N L$ also passes through $Q$. Let $T$ be the point of intersection of $A C$ and $B D$; and let $S$ be the point of intersection of $B D$ and $M N$.
|
| 20 |
+
|
| 21 |
+
Consider the triangle $M N K$. Note that $S Q$ is parallel to $N K$ and $Q$ is the midpoint of $M K$. Hence $S$ is the mid-point of $M N$. Since $M N$ is parallel to $A C$, it follows that $T$ is the mid-point of $A C$. Now $Q$ is the circumcentre of $\triangle A B C$ and the median $B T$ passes through $Q$. Here there are two possibilities:
|
| 22 |
+
|
| 23 |
+
(i) $A B C$ is a right triangle with $\angle A B C=90^{\circ}$ and $T=Q$; and
|
| 24 |
+
|
| 25 |
+
(ii) $T \neq Q$ in which case $B T$ is perpendicular to $A C$.
|
| 26 |
+
|
| 27 |
+
Suppose $\angle A B C=90^{\circ}$ and $T=Q$. Observe that $Q$ is the circumcentre of the triangle $D C B$ and hence $\angle D C B=90^{\circ}$. Similarly $\angle D A B=90^{\circ}$. It follows that $\angle A D C=90^{\circ}$. and $A B C D$ is a rectangle. This implies that $K L M N$ is a rhombus. Hence $L K / L M=1$ and this gives $C D=C B$. Thus $A B C D$ is a square.
|
| 28 |
+
|
| 29 |
+
In the second case, observe that $B D$ is perpendicular to $A C, K L$ is parallel to $A C$ and $L M$ is parallel to $B D$. Hence it follows that $M L$ is perpendicular to $L K$. Similar reasoning shows that $K L M N$ is a rectangle.
|
| 30 |
+
|
| 31 |
+
Using $L K / L M=C D / C B$, we get that $C B D$ is similar to $L M K$. In particular, $\angle L M K=$ $\angle C B D=\alpha$ say. Since $L M$ is parallel to $D B$, we also get $\angle B Q K=\alpha$. Since $K L M N$ is a cyclic quadrilateral we also get $\angle L N K=\angle L M K=\alpha$. Using the fact that $B D$ is parallel to $N K$, we get $\angle L Q B=\angle L N K=\alpha$. Since $B D$ bisects $\angle C B A$, we also have $\angle K B Q=\alpha$. Thus
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
Q K=K B=B L=L Q
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
and $B L$ is parallel to $Q K$. This gives $Q M$ is parallel to $L C$ and
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
Q M=Q L=B L=L C
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
It follows that $Q L C M$ is a parallelogram. But $\angle L C M=90^{\circ}$. Hence $\angle M Q L=90^{\circ}$. This implies that $K L M N$ is a square. Also observe that $\angle L Q K=90^{\circ}$ and hence $\angle C B A=\angle L Q K=90^{\circ}$. This gives $\angle C D A=90^{\circ}$ and hence $A B C D$ is a rectangle. Since $B A=B C$, it follows that $A B C D$ is a square.
|
| 44 |
+
|
| 45 |
+
2. Suppose $p$ is a prime greater than 3 . Find all pairs of integers $(a, b)$ satisfying the equation
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
a^{2}+3 a b+2 p(a+b)+p^{2}=0
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
Solution: We write the equation in the form
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
a^{2}+2 a p+p^{2}+b(3 a+2 p)=0
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
Hence
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
b=\frac{-(a+p)^{2}}{3 a+2 p}
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
is an integer. This shows that $3 a+2 p$ divides $(a+p)^{2}$ and hence also divides $(3 a+3 p)^{2}$. But, we have
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
(3 a+3 p)^{2}=(3 a+2 p+p)^{2}=(3 a+2 p)^{2}+2 p(3 a+2 p)+p^{2}
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
It follows that $3 a+2 p$ divides $p^{2}$. Since $p$ is a prime, the only divisors of $p^{2}$ are $\pm 1, \pm p$ and $\pm p^{2}$. Since $p>3$, we also have $p=3 k+1$ or $3 k+2$.
|
| 70 |
+
|
| 71 |
+
Case 1: Suppose $p=3 k+1$. Obviously $3 a+2 p=1$ is not possible. Infact, we get $1=3 a+2 p=$ $3 a+2(3 k+1) \Rightarrow 3 a+6 k=-1$ which is impossible. On the other hand $3 a+2 p=-1$ gives $3 a=-2 p-1=-6 k-3 \Rightarrow a=-2 k-1$ and $a+p=-2 k-1+3 k+1=k$.
|
| 72 |
+
|
| 73 |
+
Thus $b=\frac{-(a+p)^{2}}{(3 k+2 p)}=k^{2}$. Thus $(a, b)=\left(-2 k-1, k^{2}\right)$ when $p=3 k+1$. Similarly, $3 a+2 p=p \Rightarrow$ $3 a=-p$ which is not possible. Considering $3 a+2 p=-p$, we get $3 a=-3 p$ or $a=-p \Rightarrow b=0$. Hence $(a, b)=(-3 k-1,0)$ where $p=3 k+1$.
|
| 74 |
+
|
| 75 |
+
Let us consider $3 a+2 p=p^{2}$. Hence $3 a=p^{2}-2 p=p(p-2)$ and neither $p$ nor $p-2$ is divisible by 3 . If $3 a+2 p=-p^{2}$, then $3 a=-p(p+2) \Rightarrow a=-(3 k+1)(k+1)$.
|
| 76 |
+
|
| 77 |
+
Hence $a+p=(3 k+1)(-k-1+1)=-(3 k+1) k$. This gives $b=k^{2}$. Again $(a, b)=(-(k+$ 1) $\left.(3 k+1), k^{2}\right)$ when $p=3 k+1$.
|
| 78 |
+
|
| 79 |
+
Case 2: Suppose $p=3 k-1$. If $3 a+2 p=1$, then $3 a=-6 k+3$ or $a=-2 k+1$. We also get
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
b=\frac{-(a+p)^{2}}{1}=\frac{-(-2 k+1+3 k-1)^{2}}{1}=-k^{2}
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
and we get the solution $(a, b)=\left(-2 k+1, k^{2}\right)$. On the other hand $3 a+2 p=-1$ does not have any solution integral solution for $a$. Similarly, there is no solution in the case $3 a+2 p=p$. Taking $3 a+2 p=-p$, we get $a=-p$ and hence $b=0$. We get the solution $(a, b)=(-3 k+1,0)$. If $3 a+2 p=p^{2}$, then $3 a=p(p-2)=(3 k-1)(3 k-3)$ giving $a=(3 k-1)(k-1)$ and hence $a+p=(3 k-1)(1+k-1)=k(3 k-1)$. This gives $b=-k^{2}$ and hence $(a, b)=\left(3 k-1,-k^{2}\right)$. Finally $3 a+2 p=-p^{2}$ does not have any solution.
|
| 86 |
+
|
| 87 |
+
3. If $\alpha$ is a real root of the equation $x^{5}-x^{3}+x-2=0$, prove that $\left[\alpha^{6}\right]=3$. (For any real number $a$, we denote by $[a]$ the greatest integer not exceeding $a$.)
|
| 88 |
+
|
| 89 |
+
Solution: Suppose $\alpha$ is a real root of the given equation. Then
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
\alpha^{5}-\alpha^{3}+\alpha-2=0
|
| 93 |
+
$$
|
| 94 |
+
|
| 95 |
+
This gives $\alpha^{5}-\alpha^{3}+\alpha-1=1$ and hence $(\alpha-1)\left(\alpha^{4}+\alpha^{3}+1\right)=1$. Observe that $\alpha^{4}+\alpha^{3}+1 \geq$ $2 \alpha^{2}+\alpha^{3}=\alpha^{2}(\alpha+2)$. If $-1 \leq \alpha<0$, then $\alpha+2>0$, giving $\alpha^{2}(\alpha+2)>0$ and hence $(\alpha-1)\left(\alpha^{4}+\alpha^{3}+1\right)<0$. If $\alpha<-1$, then $\alpha^{4}+\alpha^{3}=\alpha^{3}(\alpha+1)>0$ and hence $\alpha^{4}+\alpha^{3}+1>0$. This again gives $(\alpha-1)\left(\alpha^{4}+\alpha^{3}+1\right)<0$.
|
| 96 |
+
|
| 97 |
+
The above resoning shows that for $\alpha<0$, we have $\alpha^{5}-\alpha^{3}+\alpha-1<0$ and hence cannot be equal to 1 . We conclude that a real root $\alpha$ of $x^{5}-x^{3}+x-2=0$ is positive (obviously $\alpha \neq 0$ ).
|
| 98 |
+
|
| 99 |
+
Now using $\alpha^{5}-\alpha^{3}+\alpha-2=0$, we get
|
| 100 |
+
|
| 101 |
+
$$
|
| 102 |
+
\alpha^{6}=\alpha^{4}-\alpha^{2}+2 \alpha
|
| 103 |
+
$$
|
| 104 |
+
|
| 105 |
+
The statement $\left[\alpha^{6}\right]=3$ is equivalent to $3 \leq \alpha^{6}<4$.
|
| 106 |
+
|
| 107 |
+
Consider $\alpha^{4}-\alpha^{2}+2 \alpha<4$. Since $\alpha>0$, this is equivalent to $\alpha^{5}-\alpha^{3}+2 \alpha^{2}<4 \alpha$. Using the relation (1), we can write $2 \alpha^{2}-\alpha+2<4 \alpha$ or $2 \alpha^{2}-5 \alpha+2<0$. Treating this as a quadratic, we get this is equivalent to $\frac{1}{2}<\alpha<2$. Now observe that if $\alpha \geq 2$ then $1=(\alpha-1)\left(\alpha^{4}+\alpha^{3}+1\right) \geq 25$ which is impossible. If $0<\alpha \leq \frac{1}{2}$, then $1=(\alpha-1)\left(\alpha^{4}+\alpha^{3}+1\right)<0$ which again is impossible. We conlude that $\frac{1}{2}<\alpha<2$. Similarly $\alpha^{4}-\alpha^{2}+2 \alpha \geq 3$ is equivalent to $\alpha^{5}-\alpha^{3}+2 \alpha^{2}-3 \alpha \geq 0$ which is equivalent to $2 \alpha^{2}-4 \alpha+2 \geq 0$. But this is $2(\alpha-1)^{2} \geq 0$ which is valid. Hence $3 \leq \alpha^{6}<4$ and we get $\left[\alpha^{6}\right]=3$.
|
| 108 |
+
|
| 109 |
+
4. Let $R$ denote the circumradius of a triangle $A B C ; a, b, c$ its sides $B C, C A, A B$; and $r_{a}, r_{b}, r_{c}$ its exradii opposite $A, B, C$. If $2 R \leq r_{a}$, prove that
|
| 110 |
+
|
| 111 |
+
(i) $a>b$ and $a>c$;
|
| 112 |
+
|
| 113 |
+
(ii) $2 R>r_{b}$ and $2 R>r_{c}$.
|
| 114 |
+
|
| 115 |
+
Solution: We know that $2 R=\frac{a b c}{2 \triangle}$ and $r_{a}=\frac{\triangle}{s-a}$, where $a, b, c$ are the sides of the triangle $A B C$, $s=\frac{a+b+c}{2}$ and $\triangle$ is the area of $A B C$. Thus the given condition $2 R \leq r_{a}$ translates to
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
a b c \leq \frac{2 \triangle^{2}}{s-a}
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
Putting $s-a=p, s-b=q, s-c=r$, we get $a=q+r, b=r+p, c=p+q$ and the condition now is
|
| 122 |
+
|
| 123 |
+
$$
|
| 124 |
+
p(p+q)(q+r)(r+p) \leq 2 \triangle^{2}
|
| 125 |
+
$$
|
| 126 |
+
|
| 127 |
+
But Heron's formula gives, $\triangle^{2}=s(s-a)(s-b)(s-c)=p q r(p+q+r)$. We obtain $(p+q)(q+$ $r)(r+p) \leq 2 q r(p+q+r)$. Expanding and effecting some cancellations, we get
|
| 128 |
+
|
| 129 |
+
$$
|
| 130 |
+
p^{2}(q+r)+p\left(q^{2}+r^{2}\right) \leq q r(q+r)
|
| 131 |
+
$$
|
| 132 |
+
|
| 133 |
+
Suppose $a \leq b$. This implies that $q+r \leq r+p$ and hence $q \leq p$. This implies that $q^{2} r \leq p^{2} r$ and $q r^{2} \leq p r^{2}$ giving $q r(q+r) \leq p^{2} r+p r^{2}<p^{2} r+p r^{2}+p^{2} q+p q^{2}=p^{2}(q+r)+p\left(q^{2}+r^{2}\right)$ which contradicts $(\star)$. Similarly, $a \leq c$ is also not possible. This proves (i).
|
| 134 |
+
|
| 135 |
+
Suppose $2 R \leq r_{b}$. As above this takes the form
|
| 136 |
+
|
| 137 |
+
$$
|
| 138 |
+
q^{2}(r+p)+q\left(r^{2}+p^{2}\right) \leq p r(p+r)
|
| 139 |
+
$$
|
| 140 |
+
|
| 141 |
+
Since $a>b$ and $a>c$, we have $q>p, r>p$. Thus $q^{2} r>p^{2} r$ and $q r^{2}>p r^{2}$. Hence
|
| 142 |
+
|
| 143 |
+
$$
|
| 144 |
+
q^{2}(r+p)+q\left(r^{2}+p^{2}\right)>q^{2} r+q r^{2}>p^{2} r+p r^{2}=p r(p+r)
|
| 145 |
+
$$
|
| 146 |
+
|
| 147 |
+
which contradicts ( $\star \star$ ). Hence $2 R>r_{b}$. Similarly, we can prove that $2 R>r_{c}$. This proves (ii)
|
| 148 |
+
|
| 149 |
+
5. Let $S$ denote the set of all 6-tuples $(a, b, c, d, e, f)$ of positive integers such that $a^{2}+b^{2}+c^{2}+d^{2}+e^{2}=$ $f^{2}$. Consider the set
|
| 150 |
+
|
| 151 |
+
$$
|
| 152 |
+
T=\{a b c d e f:(a, b, c, d, e, f) \in S\}
|
| 153 |
+
$$
|
| 154 |
+
|
| 155 |
+
Find the greatest common divisor of all the members of $T$.
|
| 156 |
+
|
| 157 |
+
Solution: We show that the required gcd is 24 . Consider an element $(a, d, c, d, e, f) \in S$. We have
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
a^{2}+b^{2}+c^{2}+d^{2}+e^{2}=f^{2}
|
| 161 |
+
$$
|
| 162 |
+
|
| 163 |
+
We first observe that not all $a, b, c, d, e$ can be odd. Otherwise, we have $a^{2} \equiv b^{2} \equiv c^{2} \equiv d^{2} \equiv e^{2} \equiv 1$ $(\bmod 8)$ and hence $f^{2} \equiv 5(\bmod 8)$, which is impossible because no square can be congruent to 5 modulo 8. Thus at least one of $a, b, c, d, e$ is even.
|
| 164 |
+
|
| 165 |
+
Similarly if none of $a, b, c, d, e$ is divisible by 3 , then $a^{2} \equiv b^{2} \equiv c^{2} \equiv d^{2} \equiv e^{2} \equiv 1(\bmod 3)$ and hence $f^{2} \equiv 2(\bmod 3)$ which again is impossible because no square is congruent to 2 modulo 3 . Thus 3 divides $a b c d e f$.
|
| 166 |
+
|
| 167 |
+
There are several possibilities for $a, b, c, d, e$.
|
| 168 |
+
|
| 169 |
+
Case 1: Suppose one of them is even and the other four are odd; say $a$ is even, $b, c, d, e$ are odd. Then $b^{2}+c^{2}+d^{2}+e^{2} \equiv 4(\bmod 8)$. If $a^{2} \equiv 4(\bmod 8)$, then $f^{2} \equiv 0(\bmod 8)$ and hence $2|a, 4| f$ giving $8 \mid a f$. If $a^{2} \equiv 0(\bmod 8)$, then $f^{2} \equiv 4(\bmod 8)$ which again gives that $4 \mid a$ and $2 \mid f$ so that $8 \mid a f$. It follows that $8 \mid a b c d e f$ and hence $24 \mid a b c d e f$.
|
| 170 |
+
|
| 171 |
+
Case 2: Suppose $a, b$ are even and $c, d, e$ are odd. Then $c^{2}+d^{2}+e^{2} \equiv 3(\bmod 8)$. Since $a^{2}+b^{2} \equiv 0$ or 4 modulo 8 , it follows that $f^{2} \equiv 3$ or $7(\bmod 8)$ which is impossible. Hence this case does not arise.
|
| 172 |
+
|
| 173 |
+
Case 3: If three of $a, b, c, d, e$ are even and two odd, then $8 \mid a b c d e f$ and hence 24|abcdef.
|
| 174 |
+
|
| 175 |
+
Case 4: If four of $a, b, c, d, e$ are even, then again $8 \mid a b c d e f$ and 24|abcdef. Here again for any six tuple $(a, b, c, d, e, f)$ in $S$, we observe that $24 \mid a b c d e f$. Since
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
1^{2}+1^{2}+1^{2}+2^{2}+3^{2}=4^{2}
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
We see that $(1,1,1,2,3,4) \in S$ and hence $24 \in T$. Thus 24 is the gcd of $T$.
|
| 182 |
+
|
| 183 |
+
6. Prove that the number of 5 -tuples of positive integers $(a, b, c, d, e)$ satisfying the equation
|
| 184 |
+
|
| 185 |
+
$$
|
| 186 |
+
a b c d e=5(b c d e+a c d e+a b d e+a b c e+a b c d)
|
| 187 |
+
$$
|
| 188 |
+
|
| 189 |
+
is an odd integer.
|
| 190 |
+
|
| 191 |
+
Solution: We write the equation in the form:
|
| 192 |
+
|
| 193 |
+
$$
|
| 194 |
+
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}+\frac{1}{e}=\frac{1}{5}
|
| 195 |
+
$$
|
| 196 |
+
|
| 197 |
+
The number of five tuple ( $a, b, c, d, e)$ which satisfy the given relation and for which $a \neq b$ is even, because for if $(a, b, c, d, e)$ is a solution, then so is $(b, a, c, d, e)$ which is distinct from $(a, b, c, d, e)$. Similarly the number of five tuples which satisfy the equation and for which $c \neq d$ is also even. Hence it suffices to count only those five tuples $(a, b, c, d, e)$ for which $a=b, c=d$. Thus the equation reduces to
|
| 198 |
+
|
| 199 |
+
$$
|
| 200 |
+
\frac{2}{a}+\frac{2}{c}+\frac{1}{e}=\frac{1}{5}
|
| 201 |
+
$$
|
| 202 |
+
|
| 203 |
+
Here again the tuple ( $a, a, c, c, e)$ for which $a \neq c$ is even because we can associate different solution $(c, c, a, a, e)$ to this five tuple. Thus it suffices to consider the equation
|
| 204 |
+
|
| 205 |
+
$$
|
| 206 |
+
\frac{4}{a}+\frac{1}{e}=\frac{1}{5}
|
| 207 |
+
$$
|
| 208 |
+
|
| 209 |
+
and show that the number of pairs $(a, e)$ satisfying this equation is odd.
|
| 210 |
+
|
| 211 |
+
This reduces to
|
| 212 |
+
|
| 213 |
+
$$
|
| 214 |
+
a e=20 e+5 a
|
| 215 |
+
$$
|
| 216 |
+
|
| 217 |
+
or
|
| 218 |
+
|
| 219 |
+
$$
|
| 220 |
+
(a-20)(e-5)=100
|
| 221 |
+
$$
|
| 222 |
+
|
| 223 |
+
But observe that
|
| 224 |
+
|
| 225 |
+
$$
|
| 226 |
+
\begin{aligned}
|
| 227 |
+
& 100=1 \times 100=2 \times 50=4 \times 25=5 \times 20 \\
|
| 228 |
+
& \quad=10 \times 10=20 \times 5=25 \times 4=50 \times 2=100 \times 1
|
| 229 |
+
\end{aligned}
|
| 230 |
+
$$
|
| 231 |
+
|
| 232 |
+
Note that no factorisation of 100 as product of two negative numbers yield a positive tuple $(a, e)$. Hence we get these 9 solutions. This proves that the total number of five tuples $(a, b, c, d, e)$ satisfying the given equation is odd.
|
| 233 |
+
|
INMO/md/en-2005.md
ADDED
|
@@ -0,0 +1,354 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# INMO 2005: Problems and Solutions
|
| 2 |
+
|
| 3 |
+
1. Let $M$ be the midpoint of side $B C$ of a triangle $A B C$. Let the median $A M$ intersect the incircle of $A B C$ at $K$ and $L, K$ being nearer to $A$ than $L$. If $A K=K L=L M$, prove that the sides of triangle $A B C$ are in the ratio $5: 10: 13$ in some order.
|
| 4 |
+
|
| 5 |
+
## Solution:
|
| 6 |
+
|
| 7 |
+
Let $I$ be the incentre of triangle $A B C$ and $D$ be its projection on $B C$. Observe that $A B \neq A C$ as $A B=A C$ implies that $D=L=M$. So assume that $A C>A B$. Let $N$ be the projection of $I$ on $K L$. Then the perpendicular $I N$ from $I$ to $K L$ is a bisector of $K L$ and as $A K=L M$, it is a bisector of $A M$ also. Hence $A I=I M$.
|
| 8 |
+
|
| 9 |
+
|
| 10 |
+
|
| 11 |
+
Fig. 1 .
|
| 12 |
+
|
| 13 |
+
But $A I=\frac{r}{\sin (A / 2)}=r \operatorname{cosec}(A / 2)$ and
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
\begin{aligned}
|
| 17 |
+
I M^{2} & =I D^{2}+D M^{2}=r^{2}+(B M-B D)^{2} \\
|
| 18 |
+
& =r^{2}+\left(\frac{a}{2}-(s-b)\right)^{2}
|
| 19 |
+
\end{aligned}
|
| 20 |
+
$$
|
| 21 |
+
|
| 22 |
+
Hence $r^{2} \operatorname{cosec}^{2}(A / 2)=r^{2}+\left((a / 2)-(s-b)^{2}\right)^{2}$ giving $r^{2} \cot ^{2}(A / 2)=((b-c) / 2)^{2}$. Since $b>c$, we obtain $r \cot (A / 2)=((b-c) / 2)$. So $s-a=((b-c) / 2)$. This gives $a=2 c$.
|
| 23 |
+
|
| 24 |
+
As $K N=N L$ and $A K=K L=L M$, we have $N L=A M / 6$. We also have $A N=N M$. Now
|
| 25 |
+
|
| 26 |
+
$$
|
| 27 |
+
\begin{aligned}
|
| 28 |
+
r^{2}=I L^{2}=I N^{2}+N L^{2} & =A I^{2}-A N^{2}+N L^{2} \\
|
| 29 |
+
& =A I^{2}-\frac{1}{4} m_{a}^{2}+\frac{1}{36} m_{a}^{2} \\
|
| 30 |
+
& =r^{2} \operatorname{cosec}^{2}(A / 2)-\frac{2}{9} m_{a}^{2}
|
| 31 |
+
\end{aligned}
|
| 32 |
+
$$
|
| 33 |
+
|
| 34 |
+
Hence $r^{2} \cot ^{2}(A / 2)=\frac{2}{9} m_{a}^{2}$. From the above, we get
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
\left(\frac{b-c}{2}\right)^{2}=\frac{2}{9} \cdot \frac{1}{4}\left(2 b^{2}+2 c^{2}-a^{2}\right)
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
Simplification gives $5 b^{2}+13 c^{2}-18 b c=0$. This can be written as $(b-c)(5 b-13 c)=0$. As $b \neq c$, we get $5 b-13 c=0$. To conclude, $a=2 c, 5 b=13 c$ yield
|
| 41 |
+
|
| 42 |
+
$$
|
| 43 |
+
\frac{a}{10}=\frac{b}{13}=\frac{c}{5}
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
2. Let $\alpha$ and $\beta$ be positive integers such that
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
\frac{43}{197}<\frac{\alpha}{\beta}<\frac{17}{77}
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
Find the minimum possible value of $\beta$.
|
| 53 |
+
|
| 54 |
+
## Solution:
|
| 55 |
+
|
| 56 |
+
We have
|
| 57 |
+
|
| 58 |
+
$$
|
| 59 |
+
\frac{77}{17}<\frac{\beta}{\alpha}<\frac{197}{43}
|
| 60 |
+
$$
|
| 61 |
+
|
| 62 |
+
That is,
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
4+\frac{9}{17}<\frac{\beta}{\alpha}<4+\frac{25}{43}
|
| 66 |
+
$$
|
| 67 |
+
|
| 68 |
+
Thus $4<\frac{\beta}{\alpha}<5$. Since $\alpha$ and $\beta$ are positive integers, we may write $\beta=4 \alpha+x$, where $0<x<\alpha$. Now we get
|
| 69 |
+
|
| 70 |
+
$$
|
| 71 |
+
4+\frac{9}{17}<4+\frac{x}{\alpha}<4+\frac{25}{43}
|
| 72 |
+
$$
|
| 73 |
+
|
| 74 |
+
So $\frac{9}{17}<\frac{x}{\alpha}<\frac{25}{43}$; that is, $\frac{43 x}{25}<\alpha<\frac{17 x}{9}$.
|
| 75 |
+
|
| 76 |
+
We find the smallest value of $x$ for which $\alpha$ becomes a well-defined integer. For $x=1,2,3$ the bounds of $\alpha$ are respectively $\left(1 \frac{18}{25}, 1 \frac{8}{9}\right),\left(3 \frac{11}{25}, 3 \frac{7}{9}\right),\left(5 \frac{4}{9}, 5 \frac{2}{3}\right)$. None of these pairs contain an integer between them.
|
| 77 |
+
|
| 78 |
+
For $x=4$, we have $\frac{43 x}{25}=6 \frac{12}{25}$ and $\frac{17 x}{9}=7 \frac{5}{9}$. Hence, in this case $\alpha=7$, and $\beta=4 \alpha+x=28+4=32$.
|
| 79 |
+
|
| 80 |
+
This is also the least possible value, because, if $x \geq 5$, then $\alpha>\frac{43 x}{25} \geq \frac{43}{5}>8$, and so $\beta>37$.
|
| 81 |
+
|
| 82 |
+
Hence the minimum possible value of $\beta$ is 32 .
|
| 83 |
+
|
| 84 |
+
3. Let $p, q, r$ be positive real numbers, not all equal, such that some two of the equations
|
| 85 |
+
|
| 86 |
+
$$
|
| 87 |
+
p x^{2}+2 q x+r=0, \quad q x^{2}+2 r x+p=0, \quad r x^{2}+2 p x+q=0
|
| 88 |
+
$$
|
| 89 |
+
|
| 90 |
+
have a common root, say $\alpha$. Prove that
|
| 91 |
+
|
| 92 |
+
(a) $\alpha$ is real and negative; and
|
| 93 |
+
|
| 94 |
+
(b) the third equation has non-real roots.
|
| 95 |
+
|
| 96 |
+
## Solution:
|
| 97 |
+
|
| 98 |
+
Consider the discriminants of the three equations
|
| 99 |
+
|
| 100 |
+
$$
|
| 101 |
+
\begin{array}{r}
|
| 102 |
+
p x^{2}+q r+r=0 \\
|
| 103 |
+
q x^{2}+r x+p=0 \\
|
| 104 |
+
r x^{2}+p x+q=0
|
| 105 |
+
\end{array}
|
| 106 |
+
$$
|
| 107 |
+
|
| 108 |
+
Let us denote them by $D_{1}, D_{2}, D_{3}$ respectively. Then we have
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
D_{1}=4\left(q^{2}-r p\right), D_{2}=4\left(r^{2}-p q\right), D_{3}=4\left(p^{2}-q r\right)
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
We observe that
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
\begin{aligned}
|
| 118 |
+
D_{1}+D_{2}+D_{3} & =4\left(p^{2}+q^{2}+r^{2}-p q-q r-r p\right) \\
|
| 119 |
+
& =2\left\{(p-q)^{2}+(q-r)^{2}+(r-p)^{2}\right\}>0
|
| 120 |
+
\end{aligned}
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
since $p, q, r$ are not all equal. Hence at least one of $D_{1}, D_{2}, D_{3}$ must be positive. We may assume $D_{1}>0$.
|
| 124 |
+
|
| 125 |
+
Suppose $D_{2}<0$ and $D_{3}<0$. In this case both the equations (2) and (3) have only non-real roots and equation (1) has only real roots. Hence the common root $\alpha$ must be between (2) and (3). But then $\bar{\alpha}$ is the other root of both (2) and (3). Hence it follows that (2) and (3) have same set of roots. This implies that
|
| 126 |
+
|
| 127 |
+
$$
|
| 128 |
+
\frac{q}{r}=\frac{r}{p}=\frac{p}{q}
|
| 129 |
+
$$
|
| 130 |
+
|
| 131 |
+
Thus $p=q=r$ contradicting the given condition. Hence both $D_{2}$ and $D_{3}$ cannot be negative. We may assume $D_{2} \geq 0$. Thus we have
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
q^{2}-r p>0, r^{2}-p q \geq 0
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
These two give
|
| 138 |
+
|
| 139 |
+
$$
|
| 140 |
+
q^{2} r^{2}>p^{2} q r
|
| 141 |
+
$$
|
| 142 |
+
|
| 143 |
+
since $p, q, r$ are all positive. Hence we obtain $q r>p^{2}$ or $D_{3}<0$. We conclude that the common root must be between equations (1) and (2).
|
| 144 |
+
|
| 145 |
+
Thus
|
| 146 |
+
|
| 147 |
+
$$
|
| 148 |
+
\begin{aligned}
|
| 149 |
+
& p \alpha^{2}+q \alpha+r=0 \\
|
| 150 |
+
& q \alpha^{2}+r \alpha+p=0
|
| 151 |
+
\end{aligned}
|
| 152 |
+
$$
|
| 153 |
+
|
| 154 |
+
Eliminating $\alpha^{2}$, we obtain
|
| 155 |
+
|
| 156 |
+
$$
|
| 157 |
+
2\left(q^{2}-p r\right) \alpha=p^{2}-q r
|
| 158 |
+
$$
|
| 159 |
+
|
| 160 |
+
Since $q^{2}-p r>0$ and $p^{2}-q r<0$, we conclude that $\alpha<0$.
|
| 161 |
+
|
| 162 |
+
The condition $p^{2}-q r<0$ implies that the equation (3) has only non-real roots.
|
| 163 |
+
|
| 164 |
+
Alternately one can argue as follows. Suppose $\alpha$ is a common root of two equations, say, (1) and (2). If $\alpha$ is non-real, then $\bar{\alpha}$ is also a root of both (1) and (2). Hence The coefficients of (1) and (2) are proportional. This forces $p=q=r$, a contradiction. Hence the common root between any two equations cannot be non-real. Looking at the coefficients, we conclude that the common root $\alpha$ must be negative. If (1) and (2) have common root $\alpha$, then $q^{2} \geq r p$ and $r^{2} \geq p q$. Here at least one inequality is strict for $q^{2}=p r$ and $r^{2}=p q$ forces $p=q=r$. Hence $q^{2} r^{2}>p^{2} q r$. This gives $p^{2}<q r$ and hence (3) has nonreal roots.
|
| 165 |
+
|
| 166 |
+
4. All possible 6-digit numbers, in each of which the digits occur in non-increasing order (from left to right, e.g., 877550) are written as a sequence in increasing order. Find the 2005 -th number in this sequence.
|
| 167 |
+
|
| 168 |
+
## Solution I:
|
| 169 |
+
|
| 170 |
+
Consider a 6-digit number whose digits from left to right are in non increasing order. If 1 is the first digit of such a number, then the subsequent digits cannot exceed 1. The set of all such numbers with initial digit equal to 1 is
|
| 171 |
+
|
| 172 |
+
$$
|
| 173 |
+
\{100000,110000,111000,111100,111110,1111111\} .
|
| 174 |
+
$$
|
| 175 |
+
|
| 176 |
+
There are elements in this set.
|
| 177 |
+
|
| 178 |
+
Let us consider 6-digit numbers with initial digit 2. Starting form 200000, we can go up to 222222 . We count these numbers as follows:
|
| 179 |
+
|
| 180 |
+
| 200000 | - | 211111 | $:$ | 6 |
|
| 181 |
+
| :--- | :--- | :--- | :--- | :--- |
|
| 182 |
+
| 220000 | - | 221111 | $:$ | 5 |
|
| 183 |
+
| 222000 | - | 222111 | $:$ | 4 |
|
| 184 |
+
| 222200 | - | 222211 | $:$ | 3 |
|
| 185 |
+
| 222220 | - | 222221 | $:$ | 2 |
|
| 186 |
+
| 222222 | - | 222222 | $:$ | 1 |
|
| 187 |
+
|
| 188 |
+
The number of such numbers is 21. Similarly we count numbers with initial digit 3 ; the sequence starts from 300000 and ends with 333333 . We have
|
| 189 |
+
|
| 190 |
+
| 300000 | -322222 | $:$ | 21 | |
|
| 191 |
+
| :---: | :---: | :---: | :---: | :---: |
|
| 192 |
+
| 330000 | - | 332222 | $:$ | 15 |
|
| 193 |
+
| 333000 | - | 333222 | $:$ | 10 |
|
| 194 |
+
| 333300 | -333322 | $:$ | 6 | |
|
| 195 |
+
| 333330 | - | 333332 | $:$ | 3 |
|
| 196 |
+
| 333333 | -333333 | $:$ | 1 | |
|
| 197 |
+
|
| 198 |
+
We obtain the total number of numbers starting from 3 equal to 56. Similarly,
|
| 199 |
+
|
| 200 |
+
| 400000 | 433333 | 56 |
|
| 201 |
+
| :---: | :---: | :---: |
|
| 202 |
+
| 440000 | 443333 | 35 |
|
| 203 |
+
| 444000 | 444333 | 20 |
|
| 204 |
+
| 444400 | 444433 | 10 |
|
| 205 |
+
| 444440 | 444443 | 4 |
|
| 206 |
+
| 444444 | $-\quad 444444$ | 1 |
|
| 207 |
+
| | | 126 |
|
| 208 |
+
| 500000 | 544444 | 126 |
|
| 209 |
+
| 550000 | 554444 | 70 |
|
| 210 |
+
| 555000 | 555444 | 35 |
|
| 211 |
+
| 555500 | 555544 | 15 |
|
| 212 |
+
| 555550 | 555554 | 5 |
|
| 213 |
+
| 555555 | 555555 | 1 |
|
| 214 |
+
| | | 252 |
|
| 215 |
+
| 600000 | 655555 | 252 |
|
| 216 |
+
| 660000 | $-\quad 665555$ | 126 |
|
| 217 |
+
| 666000 | $-\quad 666555$ | 56 |
|
| 218 |
+
| 666600 | $-\quad 666655$ | 21 |
|
| 219 |
+
| 666660 | $-\quad 666665$ | 6 |
|
| 220 |
+
| 666666 | $-\quad 666666$ | 1 |
|
| 221 |
+
| | | $\overline{462}$ |
|
| 222 |
+
| 700000 | $-\quad 766666$ | 462 |
|
| 223 |
+
| 770000 | $-\quad 776666$ | 210 |
|
| 224 |
+
| 777000 | $-\quad 777666$ | 84 |
|
| 225 |
+
| 777700 | $-\quad 777766$ | 28 |
|
| 226 |
+
| 777770 | $-\quad 777776$ | 7 |
|
| 227 |
+
| 777777 | 777777 | 1 |
|
| 228 |
+
| | | 792 |
|
| 229 |
+
|
| 230 |
+
Thus the number of 6-digit numbers where digits are non-increasing starting from 100000 and ending with 777777 is
|
| 231 |
+
|
| 232 |
+
$$
|
| 233 |
+
792+462+252+126+56+21+6=1715
|
| 234 |
+
$$
|
| 235 |
+
|
| 236 |
+
Since $2005-1715=290$, we have to consider only 290 numbers in the sequence with initial digit 8 . We have
|
| 237 |
+
|
| 238 |
+
$$
|
| 239 |
+
\begin{aligned}
|
| 240 |
+
& 800000-855555 \quad: \quad 252 \\
|
| 241 |
+
& 860000-863333: 35 \\
|
| 242 |
+
& 864000-864110 \quad: \quad 3
|
| 243 |
+
\end{aligned}
|
| 244 |
+
$$
|
| 245 |
+
|
| 246 |
+
Thus the required number is $\underline{864110}$.
|
| 247 |
+
|
| 248 |
+
## Solution: II
|
| 249 |
+
|
| 250 |
+
It is known that the number of ways of choosing $r$ objects from $n$ different types of objects (with repetitions allowed) is $\binom{n+r-1}{r}$. In particular, if we want to write $r$-digit numbers using $n$ digits allowing for repetitions with the additional condition that the digits appear in non-increasing order, we see that this can be done in $\binom{n+r-1}{r}$ ways.
|
| 251 |
+
|
| 252 |
+
Now we group the given numbers into different classes and write the number of ways in which each class can be obtained. To keep track we also write the cumulative sums of the number of numbers so obtained. Observe that the numbers themselves are written in ascending order. So we exhaust numbers beginning with 1 , then beginning with 2 and so on.
|
| 253 |
+
|
| 254 |
+
| ㄱNumbers | Digits used other <br> than the fixed part | $n$ | $r$ | $\overline{\binom{n+r-1}{r}}$ | Cumulative <br> sum |
|
| 255 |
+
| :---: | :---: | :---: | :---: | :---: | :---: |
|
| 256 |
+
| beginning with 1 | 1,0 | 2 | 5 | $\binom{6}{5}=6$ | 6 |
|
| 257 |
+
| 2 | $2,1,0$ | 3 | 5 | $\binom{7}{5}=21$ | 27 |
|
| 258 |
+
| 3 | $3,2,1,0$ | 4 | 5 | $\binom{8}{5}=56$ | 83 |
|
| 259 |
+
| 4 | $4,3,2,1,0$ | 5 | 5 | $\binom{9}{5}=126$ | 209 |
|
| 260 |
+
| 5 | $5,4,3,2,1,0$ | 6 | 5 | $\binom{10}{5}=252$ | 461 |
|
| 261 |
+
| 6 | $6,5,4,3,2,1,0$ | 7 | 5 | $\binom{11}{5}=462$ | 923 |
|
| 262 |
+
| 7 | $7,6,5,4,3,2,1,0$ | 8 | 5 | $\binom{12}{5}=792$ | 1715 |
|
| 263 |
+
| from 800000 to 855555 | $5,4,3,2,1,0$ | 6 | 5 | $\binom{10}{5}=252$ | 1967 |
|
| 264 |
+
| from 860000 to 863333 | $3,2,1,0$ | 4 | 4 | $\binom{7}{4}=35$ | 2002 |
|
| 265 |
+
|
| 266 |
+
The next three 6-digit numbers are $864000,864100,864110$.
|
| 267 |
+
|
| 268 |
+
Hence the 2005 th number in the sequence is 864110 .
|
| 269 |
+
|
| 270 |
+
5. Let $x_{1}$ be a given positive integer. A sequence $\left\langle x_{n}\right\rangle_{n=1}^{\infty}=\left\langle x_{1}, x_{2}, x_{3}, \cdots\right\rangle$ of positive integers is such that $x_{n}$, for $n \geq 2$, is obtained from $x_{n-1}$ by adding some nonzero digit of $x_{n-1}$. Prove that
|
| 271 |
+
|
| 272 |
+
(a) the sequence has an even number;
|
| 273 |
+
|
| 274 |
+
(b) the sequence has infinitely many even numbers.
|
| 275 |
+
|
| 276 |
+
## Solution:
|
| 277 |
+
|
| 278 |
+
(a) Let us assume that there are no even numbers in the sequence. This means that $x_{n+1}$ is obtained from $x_{n}$, by adding a nonzero even digit of $x_{n}$ to $x_{n}$, for each $n \geq 1$.
|
| 279 |
+
|
| 280 |
+
Let $E$ be the left most even digit in $x_{1}$ which may be taken in the form
|
| 281 |
+
|
| 282 |
+
$$
|
| 283 |
+
x_{1}=O_{1} O_{2} \cdots O_{k} E D_{1} D_{2} \cdots D_{l}
|
| 284 |
+
$$
|
| 285 |
+
|
| 286 |
+
where $O_{1}, O_{2}, \ldots, O_{k}$ are odd digits $(k \geq 0) ; D_{1}, D_{2}, \ldots, D_{l-1}$ are even or odd; and $D_{l}$ odd, $l \geq 1$.
|
| 287 |
+
|
| 288 |
+
Since each time we are adding at least 2 to a term of the sequence to get the next term, at some stage, we will have a term of the form
|
| 289 |
+
|
| 290 |
+
$$
|
| 291 |
+
x_{r}=O_{1} O_{2} \cdots O_{k} E 999 \cdots 9 F
|
| 292 |
+
$$
|
| 293 |
+
|
| 294 |
+
where $F=3,5,7$ or 9 . Now we are forced to add $E$ to $x_{r}$ to get $x_{r+1}$, as it is the only even digit available. After at most four steps of addition, we see that some next term is of the form
|
| 295 |
+
|
| 296 |
+
$$
|
| 297 |
+
x_{s}=O_{1} O_{2} \cdots O_{k} G 000 \cdots M
|
| 298 |
+
$$
|
| 299 |
+
|
| 300 |
+
where $G$ replaces $E$ of $x_{r}, G=E+1, M=1,3,5$, or 7 . But $x_{s}$ has no nonzero even digit contradicting our assumption. Hence the sequence has some even number as its term.
|
| 301 |
+
(b) If there are only finitely many even terms and $x_{t}$ is the last term, then the sequence $\left\langle x_{n}\right\rangle_{n=t+1}^{\infty}=$ $\left\langle x_{t+1}, x_{t+2}, \ldots\right\rangle$ is obtained in a similar manner and hence must have an even term by (a), a contradiction. Thus $\left\langle x_{n}\right\rangle_{n=1}^{\infty}$, has infinitely many even terms.
|
| 302 |
+
|
| 303 |
+
6. Find all functions $f: \mathbf{R} \rightarrow \mathbf{R}$ such that
|
| 304 |
+
|
| 305 |
+
$$
|
| 306 |
+
f\left(x^{2}+y f(z)\right)=x f(x)+z f(y)
|
| 307 |
+
$$
|
| 308 |
+
|
| 309 |
+
for all $x, y, z$ in $\mathbf{R}$. (Here $\mathbf{R}$ denotes the set of all real numbers.)
|
| 310 |
+
|
| 311 |
+
Solution: Taking $x=y=0$ in (1), we get $z f(0)=f(0)$ for all $z \in \mathbf{R}$. Hence we obtain $f(0)=0$. Taking $y=0$ in (1), we get
|
| 312 |
+
|
| 313 |
+
$$
|
| 314 |
+
f\left(x^{2}\right)=x f(x)
|
| 315 |
+
$$
|
| 316 |
+
|
| 317 |
+
Similarly $x=0$ in (1) gives
|
| 318 |
+
|
| 319 |
+
$$
|
| 320 |
+
f(y f(z))=z f(y)
|
| 321 |
+
$$
|
| 322 |
+
|
| 323 |
+
Putting $y=1$ in (3), we get
|
| 324 |
+
|
| 325 |
+
$$
|
| 326 |
+
f(f(z))=z f(1) \quad \forall z \in \mathbf{R}
|
| 327 |
+
$$
|
| 328 |
+
|
| 329 |
+
Now using (2) and (4), we obtain
|
| 330 |
+
|
| 331 |
+
$$
|
| 332 |
+
f(x f(x))=f\left(f\left(x^{2}\right)\right)=x^{2} f(1)
|
| 333 |
+
$$
|
| 334 |
+
|
| 335 |
+
Put $y=z=x$ in (3) also given
|
| 336 |
+
|
| 337 |
+
$$
|
| 338 |
+
f(x f(x))=x f(x)
|
| 339 |
+
$$
|
| 340 |
+
|
| 341 |
+
Comparing (5) and (6), it follows that $x^{2} f(1)=x f(x)$. If $x \neq 0$, then $f(x)=c x$, for some constant c. Since $f(0)=0$, we have $f(x)=c x$ for $x=0$ as well. Substituting this in (1), we see that
|
| 342 |
+
|
| 343 |
+
$$
|
| 344 |
+
c\left(x^{2}+c y z\right)=c x^{2}+c y z
|
| 345 |
+
$$
|
| 346 |
+
|
| 347 |
+
or
|
| 348 |
+
|
| 349 |
+
$$
|
| 350 |
+
c^{2} y z=c y z \quad \forall y, z \in \mathbf{R}
|
| 351 |
+
$$
|
| 352 |
+
|
| 353 |
+
This implies that $c^{2}=c$. Hence $c=0$ or 1 . We obtain $f(x)=0$ for all $x$ or $f(x)=x$ for all $x$. It is easy to verify that these two are solutions of the given equation.
|
| 354 |
+
|
INMO/md/en-2006.md
ADDED
|
@@ -0,0 +1,359 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# INMO 2006: Problems and Solutions
|
| 2 |
+
|
| 3 |
+
1. In a non-equilateral triangle $A B C$, the sides $a, b, c$ form an arithmetic progression. Let $I$ and $O$ denote the incentre and circumcentre of the triangle respectively.
|
| 4 |
+
|
| 5 |
+
(i) Prove that $I O$ is perpendicular to $B I$.
|
| 6 |
+
|
| 7 |
+
(ii) Suppose $B I$ extended meets $A C$ in $K$, and $D, E$ are the midpoints of $B C, B A$ respectively. Prove that $I$ is the circumcentre of triangle $D K E$.
|
| 8 |
+
|
| 9 |
+
## Solution:
|
| 10 |
+
|
| 11 |
+
(i) Extend $B I$ to meet the circumcircle in $F$. Then we know that $F A=F I=F C$. (See Figure)
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
|
| 15 |
+
Let $B I: I F=\lambda: \mu$. Applying Stewart's theorem to triangle $B A F$, we get
|
| 16 |
+
|
| 17 |
+
$$
|
| 18 |
+
\lambda A F^{2}+\mu A B^{2}=(\lambda+\mu)\left(A I^{2}+B I \cdot I F\right)
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
Similarly, Stewart's theorem to triangle $B C F$ gives
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
\lambda C F^{2}+\mu B C^{2}=(\lambda+\mu)\left(C I^{2}+B I \cdot I F\right)
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
Since $C F=A F$, subtraction gives
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\mu\left(A B^{2}-B C^{2}\right)=(\lambda+\mu)\left(A I^{2}-C I^{2}\right)
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
Using the standard notations $A B=c, B C=a, C A=b$ and $s=(a+b+c) / 2$, we get $A I^{2}=r^{2}+(s-a)^{2}$ and $C I^{2}=r^{2}+(s-c)^{2}$ where $r$ is the in-radius of $A B C$. Thus
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
\mu\left(c^{2}-a^{2}\right)=(\lambda+\mu)\left((s-a)^{2}-(s-c)^{2}\right)=(\lambda+\mu)(c-a) b
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
It follows that either $c=a$ or $\mu(c+a)=(\lambda+\mu) b$. But $c=a$ implies that $a=b=c$ since $a, b, c$ are in arithmetic progression. However, we have taken a non-equilateral triangle $A B C$. Thus $c \neq a$ and we have $\mu(c+a)=(\lambda+\mu) b$. But $c+a=2 b$ and we obtain
|
| 40 |
+
$2 b \mu=(\lambda+\mu) b$. We conclude that $\lambda=\mu$. This in turn tells that $I$ is the mid-point of $B F$. Since $O F=O B$, we conclude that $O I$ is perpendicular to $B F$.
|
| 41 |
+
|
| 42 |
+
## Alternatively
|
| 43 |
+
|
| 44 |
+
Applying Ptolemy's theorem to the cyclic quadrilateral $A B C F$, we get
|
| 45 |
+
|
| 46 |
+
$$
|
| 47 |
+
A B \cdot C F+A F \cdot B C=B F \cdot C A
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
Since $C F=A F$, we get $C F(c+a)=B F \cdot b=B F(c+a) / 2$. This gives $B F=2 C F=2 I F$. Hence $I$ is the mid-point of $B F$ and as earlier we conclude that $O I$ is perpendicular to $B F$.
|
| 51 |
+
|
| 52 |
+
## Alternatively
|
| 53 |
+
|
| 54 |
+
Join $B O$. We have to prove that $\angle B I O=90^{\circ}$, which is equivalent to $B I^{2}+I O^{2}=B O^{2}$. Draw $I L$ perpendicular to $A B$. Let $R$ denote the circumradius of $A B C$ and let $\triangle$ denote its area. Observe that $B O=R, I O^{2}=R^{2}-2 R r$,
|
| 55 |
+
|
| 56 |
+
$$
|
| 57 |
+
B I=\frac{B L}{\cos (B / 2)}=(s-b) \sqrt{\frac{c a}{s(s-b)}}
|
| 58 |
+
$$
|
| 59 |
+
|
| 60 |
+
Thus we obtain
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
B I^{2}=a c(s-b) / s=\frac{a c}{3}
|
| 64 |
+
$$
|
| 65 |
+
|
| 66 |
+
since $a, b, c$ are in arithmetic progression. Thus we need to prove that
|
| 67 |
+
|
| 68 |
+
$$
|
| 69 |
+
\frac{a c}{3}+R^{2}-2 R r=R^{2}
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
This reduces to proving $2 R r=a c / 3$. But
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
2 R r=2 \cdot \frac{a b c}{4 \Delta} \cdot \frac{\Delta}{s}=\frac{a b c}{2 s}=\frac{a b c}{a+b+c}=\frac{a c}{3}
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
using $a+c=2 b$. This proves the claim.
|
| 79 |
+
|
| 80 |
+
(ii) Join $I D$. Note that $\angle B I O=\angle B D O=90^{\circ}$. Hence $B, D, I, O$ are concyclic and hence $\angle B I D=\angle B O D=A$. Since $\angle D B I=\angle K B A=B / 2$, it follows that triangles $B A K$ and $B I D$ are similar. This gives
|
| 81 |
+
|
| 82 |
+
$$
|
| 83 |
+
\frac{B A}{B I}=\frac{B K}{B D}=\frac{A K}{I D}
|
| 84 |
+
$$
|
| 85 |
+
|
| 86 |
+
However, we have seen earlier that $B I=a c / 3$. Moreover $A K=b c /(a+c)$. Thus we obtain
|
| 87 |
+
|
| 88 |
+
$$
|
| 89 |
+
B K=\frac{B A \cdot B D}{B I}=\frac{1}{2} \sqrt{3 a c}, \quad I D=\frac{A K \cdot B I}{B A}=\frac{1}{2} \sqrt{\frac{a c}{3}} .
|
| 90 |
+
$$
|
| 91 |
+
|
| 92 |
+
By symmetry, we must have $I E=\frac{1}{2} \sqrt{\frac{a c}{3}}$. Finally
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
I K=\frac{b}{a+b+c} \cdot B K=\frac{1}{3} B K=\frac{1}{2} \sqrt{\frac{a c}{3}}
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
Thus $I D=I E=I K$ and $I$ is the circumcentre of $D K E$.
|
| 99 |
+
|
| 100 |
+
## Alternatively
|
| 101 |
+
|
| 102 |
+
Observe that $A K=b c /(a+c)=c / 2=A E$. Since $A I$ bisects angle $A$, we see that $A I E$ is congruent to $A I K$. This gives $I E=I K$. Similarly $C I D$ is congruent to $C I K$ giving $I D=I K$. We conclude that $I D=I K=I E$.
|
| 103 |
+
|
| 104 |
+
2. Prove that for every positive integer $n$ there exists a unique ordered pair $(a, b)$ of positive integers such that
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
n=\frac{1}{2}(a+b-1)(a+b-2)+a
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
Solution: We have to prove that $f: \mathbb{N} \times \mathbb{N} \rightarrow \mathbb{N}$ defined by
|
| 111 |
+
|
| 112 |
+
$$
|
| 113 |
+
f(a, b)=\frac{1}{2}(a+b-1)(a+b-2)+a, \quad \forall a, b \in \mathbb{N}
|
| 114 |
+
$$
|
| 115 |
+
|
| 116 |
+
is a bijection. (Note that the right side is a natural number.) To this end define
|
| 117 |
+
|
| 118 |
+
$$
|
| 119 |
+
T(n)=\frac{n(n+1)}{2}, \quad n \in \mathbb{N} \cup\{0\}
|
| 120 |
+
$$
|
| 121 |
+
|
| 122 |
+
An idea of the proof can be obtained by looking at the following table of values of $f(a, b)$ for some small values of $a, b$.
|
| 123 |
+
|
| 124 |
+
|
| 125 |
+
|
| 126 |
+
We observe that the $n$-th diagonal runs from $(1, n)$-th position to $(n, 1)$-th position and the entries are $n$ consecutive integers; the first entry in the $n$-th diagonal is one more than the last entry of the $(n-1)$-th diagonal. For example the first entry in 5 -th diagonal is 11 which is one more than the last entry of 4 -th diagonal which is 10 . Observe that 5 -th diagonal starts from 11 and ends with 15 which accounts for 5 consecutive natural numbers. Thus we see that $f(n-1,1)+1=f(1, n)$. We also observe that the first $n$ diagonals exhaust all the natural numbers from 1 to $T(n)$. (Thus a kind of visual bijection is already there. We formally prove the property.)
|
| 127 |
+
|
| 128 |
+
We first observe that
|
| 129 |
+
|
| 130 |
+
$$
|
| 131 |
+
f(a, b)-T(a+b-2)=a>0
|
| 132 |
+
$$
|
| 133 |
+
|
| 134 |
+
and
|
| 135 |
+
|
| 136 |
+
$$
|
| 137 |
+
T(a+b-1)-f(a, b)=\frac{(a+b-1)(a+b)}{2}-\frac{(a+b-1)(a+b-2)}{2}-a=b-1 \geq 0
|
| 138 |
+
$$
|
| 139 |
+
|
| 140 |
+
Thus we have
|
| 141 |
+
|
| 142 |
+
$$
|
| 143 |
+
T(a+b-2)<f(a, b)=\frac{(a+b-1)(a+b-2)}{2}+a \leq T(a+b-1)
|
| 144 |
+
$$
|
| 145 |
+
|
| 146 |
+
Suppose $f\left(a_{1}, b_{1}\right)=f\left(a_{2}, b_{2}\right)$. Then the previous observation shows that
|
| 147 |
+
|
| 148 |
+
$$
|
| 149 |
+
\begin{aligned}
|
| 150 |
+
& T\left(a_{1}+b_{1}-2\right)<f\left(a_{1}, b_{1}\right) \leq T\left(a_{1}+b_{1}-1\right) \\
|
| 151 |
+
& T\left(a_{2}+b_{2}-2\right)<f\left(a_{2}, b_{2}\right) \leq T\left(a_{2}+b_{2}-1\right)
|
| 152 |
+
\end{aligned}
|
| 153 |
+
$$
|
| 154 |
+
|
| 155 |
+
Since the sequence $\langle T(n)\rangle_{n=0}^{\infty}$ is strictly increasing, it follows that $a_{1}+b_{1}=a_{2}+b_{2}$. But then the relation $f\left(a_{1}, b_{1}\right)=f\left(a_{2}, b_{2}\right)$ implies that $a_{1}=a_{2}$ and $b_{1}=b_{2}$. Hence $f$ is one-one.
|
| 156 |
+
|
| 157 |
+
Let $n$ be any natural number. Since the sequence $\langle T(n)\rangle_{n=0}^{\infty}$ is strictly increasing, we can find a natural number $k$ such that
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
T(k-1)<n \leq T(k)
|
| 161 |
+
$$
|
| 162 |
+
|
| 163 |
+
Equivalently,
|
| 164 |
+
|
| 165 |
+
$$
|
| 166 |
+
\frac{(k-1) k}{2}<n \leq \frac{k(k+1)}{2}
|
| 167 |
+
$$
|
| 168 |
+
|
| 169 |
+
Now set $a=n-\frac{k(k-1)}{2}$ and $b=k-a+1$. Observe that $a>0$. Now (1) shows that
|
| 170 |
+
|
| 171 |
+
$$
|
| 172 |
+
a=n-\frac{k(k-1)}{2} \leq \frac{k(k+1)}{2}-\frac{k(k-1)}{2}=k
|
| 173 |
+
$$
|
| 174 |
+
|
| 175 |
+
Hence $b=k-a+1 \geq 1$. Thus $a$ and $b$ are both positive integers and
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
f(a, b)=\frac{1}{2}(a+b-1)(a+b-2)+a=\frac{k(k-1)}{2}+a=n
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
This shows that every natural number is in the range of $f$. Thus $f$ is also onto. We conclude that $f$ is a bijection.
|
| 182 |
+
|
| 183 |
+
3. Let $X$ denote the set of all triples $(a, b, c)$ of integers. Define a function $f: X \rightarrow X$ by
|
| 184 |
+
|
| 185 |
+
$$
|
| 186 |
+
f(a, b, c)=(a+b+c, a b+b c+c a, a b c)
|
| 187 |
+
$$
|
| 188 |
+
|
| 189 |
+
Find all triples $(a, b, c)$ in $X$ such that $f(f(a, b, c))=(a, b, c)$.
|
| 190 |
+
|
| 191 |
+
Solution: We show that the solutionset consists of $\{(t, 0,0) ; t \in \mathbb{Z}\} \cup\{(-1,-1,1)\}$. Let us put $a+b+c=d, a b+b c+c a=e$ and $a b c=f$. The given condition $f(f(a, b, c))=(a, b, c)$ implies that
|
| 192 |
+
|
| 193 |
+
$$
|
| 194 |
+
d+e+f=a, \quad d e+e f+f d=b, d e f=c
|
| 195 |
+
$$
|
| 196 |
+
|
| 197 |
+
Thus $a b c d e f=f c$ and hence either $c f=0$ or $a b d e=1$.
|
| 198 |
+
|
| 199 |
+
Case I: Suppose $c f=0$. Then either $c=0$ or $f=0$. However $c=0$ implies $f=0$ and vice-versa. Thus we obtain $a+b=d, d+e=a, a b=e$ and $d e=b$. The first two relations give $b=-e$. Thus $e=a b=-a e$ and $d e=b=-e$. We get either $e=0$ or $a=d=-1$.
|
| 200 |
+
|
| 201 |
+
If $e=0$, then $b=0$ and $a=d=t$, say. We get the triple $(a, b, c)=(t, 0,0)$, where $t \in \mathbb{Z}$. If $e \neq 0$, then $a=d=-1$. But then $d+e+f=a$ implies that $-1+e+0=-1$ forcing $e=0$. Thus we get the solution family $(a, b, c)=(t, 0,0)$, where $t \in \mathbb{Z}$.
|
| 202 |
+
|
| 203 |
+
Case II: Suppose $c f \neq 0$. In this case $a b d e=1$. Hence either all are equal to 1 ; or two equal to 1 and the other two equal to -1 ; or all equal to -1 .
|
| 204 |
+
|
| 205 |
+
Suppose $a=b=d=e=1$. Then $a+b+c=d$ shows that $c=-1$. Similarly $f=-1$. Hence $e=a b+b c+c a=1-1-1=-1$ contradicting $e=1$.
|
| 206 |
+
|
| 207 |
+
Suppose $a=b=1$ and $d=e=-1$. Then $a+b+c=d$ gives $c=-3$ and $d+e+f=a$ gives $f=3$. But then $f=a b c=1 \cdot 1 \cdot(-3)=-3$, a contradiction. Similarly $a=b=-1$ and $d=e=1$ is not possible.
|
| 208 |
+
|
| 209 |
+
If $a=1, b=-1, d=1$, $e=-1$, then $a+b+c=d$ gives $c=1$. Similarly $f=1$. But then $f=a b c=1 \cdot 1 \cdot(-1)=-1$ a contradiction. If $a=1, b=-1, d=-1, e=1$, then $c=-1$ and $e=a b+b c+c a=-1+1-1=-1$ and a contradiction to $e=1$. The symmetry between $(a, b, c)$ and $(d, e, f)$ shows that $a=-1, b=1, d=1, e=-1$ is not possible. Finally if $a=-1, b=1, d=-1$ and $e=1$, then $c=-1$ and $f=-1$. But then $f=a b c$ is not satisfied.
|
| 210 |
+
|
| 211 |
+
The only case left is that of $a, b, d, e$ being all equal to -1 . Then $c=1$ and $f=1$. It is easy to check that $(-1,-1,1)$ is indeed a solution.
|
| 212 |
+
|
| 213 |
+
## Alternatively
|
| 214 |
+
|
| 215 |
+
$c f \neq 0$ implies that $|c| \geq 1$ and $|f| \geq 1$. Observe that
|
| 216 |
+
|
| 217 |
+
$$
|
| 218 |
+
d^{2}-2 e=a^{2}+b^{2}+c^{2}, \quad a^{2}-2 b=d^{2}+e^{2}+f^{2}
|
| 219 |
+
$$
|
| 220 |
+
|
| 221 |
+
Adding these two, we get $-2(b+e)=b^{2}+c^{2}+e^{2}+f^{2}$. This may be written in the form
|
| 222 |
+
|
| 223 |
+
$$
|
| 224 |
+
(b+1)^{2}+(e+1)^{2}+c^{2}+f^{2}-2=0
|
| 225 |
+
$$
|
| 226 |
+
|
| 227 |
+
We conclude that $c^{2}+f^{2} \leq 2$. Using $|c| \geq 1$ and $|f| \geq 1$, we obtain $|c|=1$ and $|f|=1$, $b+1=0$ and $e+1=0$. Thus $b=e=-1$. Now $a+d=d+e+f+a+b+c$ and this gives $b+c+e+f=0$. It follows that $c=f=1$ and finally $a=d=-1$.
|
| 228 |
+
|
| 229 |
+
4. Some 46 squares are randomly chosen from a $9 \times 9$ chess board and are coloured red. Show that there exists a $2 \times 2$ block of 4 squares of which at least three are coloured red.
|
| 230 |
+
|
| 231 |
+
Solution: Consider a partition of $9 \times 9$ chess board using sixteen $2 \times 2$ block of 4 squares
|
| 232 |
+
|
| 233 |
+
| 1 | 2 | | |
|
| 234 |
+
| :---: | :---: | :---: | :---: |
|
| 235 |
+
| 7 | 6 | 5 | |
|
| 236 |
+
| 8 | 9 | | 10 |
|
| 237 |
+
| | | | |
|
| 238 |
+
| 10 | | | |
|
| 239 |
+
| | 1 | 1 | 13 |
|
| 240 |
+
|
| 241 |
+
each and remaining seventeen single squares as shown in the figure below.
|
| 242 |
+
|
| 243 |
+
If any one of these 16 big squares contain 3 red squares then we are done. On the contrary, each may contain at most 2 red squares and these account for at most $16 \cdot 2=32$ red squares. Then there are 17 single squares connected in zig-zag fashion. It looks as follows:
|
| 244 |
+
|
| 245 |
+
|
| 246 |
+
We split this again in to several mirror images of L-shaped figures as shown above. There are four such forks. If all the five unit squares of the first fork are red, then we can get a $2 \times 2$ square having three red squares. Hence there can be at most four unit squares having red colour. Similarly, there can be at most three red squares from each of the remaining three forks. Together we get $4+3 \cdot 3=13$ red squares. These together with 32 from the big squares account for only 45 red squares. But we know that 46 squares have red colour. The conclusion follows.
|
| 247 |
+
|
| 248 |
+
5. In a cyclic quadrilateral $A B C D, A B=a, B C=b, C D=c, \angle A B C=120^{\circ}$, and $\angle A B D=$ $30^{\circ}$. Prove that
|
| 249 |
+
|
| 250 |
+
(i) $c \geq a+b$;
|
| 251 |
+
|
| 252 |
+
(ii) $|\sqrt{c+a}-\sqrt{c+b}|=\sqrt{c-a-b}$.
|
| 253 |
+
|
| 254 |
+
## Solution:
|
| 255 |
+
|
| 256 |
+
Applying cosine rule to triangle $A B C$, we get
|
| 257 |
+
|
| 258 |
+
$$
|
| 259 |
+
A C^{2}=a^{2}+b^{2}-2 a b \cos 120^{\circ}=a^{2}+b^{2}+a b
|
| 260 |
+
$$
|
| 261 |
+
|
| 262 |
+
Observe that $\angle D A C=\angle D B C=120^{\circ}-30^{\circ}=90^{\circ}$. Thus we get
|
| 263 |
+
|
| 264 |
+
$$
|
| 265 |
+
c^{2}=\frac{A C^{2}}{\cos ^{2} 30^{\circ}}=\frac{4}{3}\left(a^{2}+b^{2}+a b\right)
|
| 266 |
+
$$
|
| 267 |
+
|
| 268 |
+
So
|
| 269 |
+
|
| 270 |
+
$$
|
| 271 |
+
c^{2}-(a+b)^{2}=\frac{4}{3}\left(a^{2}+b^{2}+a b\right)-\left(a^{2}+b^{2}+2 a b\right)=\frac{(a-b)^{2}}{3} \geq 0
|
| 272 |
+
$$
|
| 273 |
+
|
| 274 |
+
This proves $c \geq a+b$ and thus (i) is true.
|
| 275 |
+
|
| 276 |
+
|
| 277 |
+
|
| 278 |
+
For proving (ii), consider the product
|
| 279 |
+
|
| 280 |
+
$$
|
| 281 |
+
Q=(\alpha+\beta+\gamma)(\alpha-\beta-\gamma)(\alpha+\beta-\gamma)(\alpha-\beta+\gamma)
|
| 282 |
+
$$
|
| 283 |
+
|
| 284 |
+
where $\alpha=\sqrt{c+a}, \beta=\sqrt{c+b}$ and $\gamma=\sqrt{c-a-b}$. Expanding the product, we get
|
| 285 |
+
|
| 286 |
+
$$
|
| 287 |
+
\begin{aligned}
|
| 288 |
+
Q & =(c+a)^{2}+(c+b)^{2}+(c-a-b)^{2}-2(c+a)(c+b)-2(c+a)(c-a-b)-2(c+b)(c-a-b) \\
|
| 289 |
+
& =-3 c^{2}+4 a^{2}+4 b^{2}+4 a b \\
|
| 290 |
+
& =0
|
| 291 |
+
\end{aligned}
|
| 292 |
+
$$
|
| 293 |
+
|
| 294 |
+
Thus at least one of the factors must be equal to 0 . Since $\alpha+\beta+\gamma>0$ and $\alpha+\beta-\gamma>0$, it follows that the product of the remaining two factors is 0 . This gives
|
| 295 |
+
|
| 296 |
+
$$
|
| 297 |
+
\sqrt{c+a}-\sqrt{c+b}=\sqrt{c-a-b} \text { or } \sqrt{c+a}-\sqrt{c+b}=-\sqrt{c-a-b}
|
| 298 |
+
$$
|
| 299 |
+
|
| 300 |
+
We conclude that
|
| 301 |
+
|
| 302 |
+
$$
|
| 303 |
+
|\sqrt{c+a}-\sqrt{c+b}|=\sqrt{c-a-b}
|
| 304 |
+
$$
|
| 305 |
+
|
| 306 |
+
6. (a) Prove that if $n$ is a positive integer such that $n \geq 4011^{2}$, then there exists an integer $l$ such that $n<l^{2}<\left(1+\frac{1}{2005}\right) n$.
|
| 307 |
+
|
| 308 |
+
(b) Find the smallest positive integer $M$ for which whenever an integer $n$ is such that $n \geq M$, there exists an integer $l$, such that $n<l^{2}<\left(1+\frac{1}{2005}\right) n$.
|
| 309 |
+
|
| 310 |
+
## Solution:
|
| 311 |
+
|
| 312 |
+
(a) Let $n \geq 4011^{2}$ and $m \in \mathbb{N}$ be such that $m^{2} \leq n<(m+1)^{2}$. Then
|
| 313 |
+
|
| 314 |
+
$$
|
| 315 |
+
\begin{aligned}
|
| 316 |
+
\left(1+\frac{1}{2005}\right) n-(m+1)^{2} & \geq\left(1+\frac{1}{2005}\right) m^{2}-(m+1)^{2} \\
|
| 317 |
+
& =\frac{m^{2}}{2005}-2 m-1 \\
|
| 318 |
+
& =\frac{1}{2005}\left(m^{2}-4010 m-2005\right) \\
|
| 319 |
+
& =\frac{1}{2005}\left((m-2005)^{2}-2005^{2}-2005\right) \\
|
| 320 |
+
& \geq \frac{1}{2005}\left((4011-2005)^{2}-2005^{2}-2005\right) \\
|
| 321 |
+
& =\frac{1}{2005}\left(2006^{2}-2005^{2}-2005\right) \\
|
| 322 |
+
& =\frac{1}{2005}(4011-2005)=\frac{2006}{2005}>0
|
| 323 |
+
\end{aligned}
|
| 324 |
+
$$
|
| 325 |
+
|
| 326 |
+
Thus we get
|
| 327 |
+
|
| 328 |
+
$$
|
| 329 |
+
n<(m+1)^{2}<\left(1+\frac{1}{2005}\right) n
|
| 330 |
+
$$
|
| 331 |
+
|
| 332 |
+
and $l^{2}=(m+1)^{2}$ is the desired square.
|
| 333 |
+
(b) We show that $M=4010^{2}+1$ is the required least number. Suppose $n \geq M$. Write $n=4010^{2}+k$, where $k$ is a positive integer. Note that we may assume $n<4011^{2}$ by part (a). Now
|
| 334 |
+
|
| 335 |
+
$$
|
| 336 |
+
\begin{aligned}
|
| 337 |
+
\left(1+\frac{1}{2005}\right) n-4011^{2} & =\left(1+\frac{1}{2005}\right)\left(4010^{2}+k\right)-4011^{2} \\
|
| 338 |
+
& =4010^{2}+2 \cdot 4010+k+\frac{k}{2005}-4011^{2} \\
|
| 339 |
+
& =(4010+1)^{2}+(k-1)+\frac{k}{2005}-4011^{2} \\
|
| 340 |
+
& =(k-1)+\frac{k}{2005}>0
|
| 341 |
+
\end{aligned}
|
| 342 |
+
$$
|
| 343 |
+
|
| 344 |
+
Thus we obtain
|
| 345 |
+
|
| 346 |
+
$$
|
| 347 |
+
4010^{2}<n<4011^{2}<\left(1+\frac{1}{2005}\right) n
|
| 348 |
+
$$
|
| 349 |
+
|
| 350 |
+
We check that $M=4010^{2}$ will not work. For suppose $n=4010^{2}$. Then
|
| 351 |
+
|
| 352 |
+
$$
|
| 353 |
+
\left(1+\frac{1}{2005}\right) 4010^{2}=4010^{2}+2 \cdot 4010=4011^{2}-1<4011^{2}
|
| 354 |
+
$$
|
| 355 |
+
|
| 356 |
+
Thus there is no square integer between $n$ and $\left(1+\frac{1}{2005}\right) n$.
|
| 357 |
+
|
| 358 |
+
This proves (b). $\qquad$
|
| 359 |
+
|
INMO/md/en-2007.md
ADDED
|
@@ -0,0 +1,349 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Problems and Solutions of INMO-2007
|
| 2 |
+
|
| 3 |
+
1. In a triangle $A B C$ right-angled at $C$, the median through $B$ bisects the angle between $B A$ and the bisector of $\angle B$. Prove that
|
| 4 |
+
|
| 5 |
+
$$
|
| 6 |
+
\frac{5}{2}<\frac{A B}{B C}<3
|
| 7 |
+
$$
|
| 8 |
+
|
| 9 |
+
## Solution 1:
|
| 10 |
+
|
| 11 |
+
Since $E$ is the mid-point of $A C$, we have $A E=$ $E C=b / 2$. Since $B D$ bisects $\angle A B C$, we also know that $C D=a b /(a+c)$. Since $B E$ bisects $\angle A B D$, we also have
|
| 12 |
+
|
| 13 |
+
$$
|
| 14 |
+
\frac{B D^{2}}{B A^{2}}=\frac{D E^{2}}{E A^{2}}
|
| 15 |
+
$$
|
| 16 |
+
|
| 17 |
+
However,
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
\begin{aligned}
|
| 21 |
+
B D^{2} & =B C^{2}+C D^{2}=a^{2}+\frac{a^{2} b^{2}}{(a+c)^{2}} \\
|
| 22 |
+
D E^{2} & =\left(\frac{b}{2}-\frac{a b}{a+c}\right)^{2}
|
| 23 |
+
\end{aligned}
|
| 24 |
+
$$
|
| 25 |
+
|
| 26 |
+
|
| 27 |
+
|
| 28 |
+
Using these in the above expression and simplifying, we get
|
| 29 |
+
|
| 30 |
+
$$
|
| 31 |
+
a^{2}\left\{(a+c)^{2}+b^{2}\right\}=c^{2}(c-a)^{2}
|
| 32 |
+
$$
|
| 33 |
+
|
| 34 |
+
Using $c^{2}=a^{2}+b^{2}$ and eliminating $b$, we obtain
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
c^{3}-2 a c^{2}-a^{2} c-2 a^{3}=0
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
Introducing $t=c / a$, this reduces to a cubic equation;
|
| 41 |
+
|
| 42 |
+
$$
|
| 43 |
+
t^{3}-2 t^{2}-t-2=0
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
Consider the function $f(t)=t^{3}-2 t^{2}-t-2$ for $t>0$ (as $c / a$ is positive). For $0<t \leq 2$, we see that $f(t)=t^{2}(t-2)-t-2<0$. We also observe that $f(t)=(t-2)\left(t^{2}-1\right)-4$ is strictly increasing on $(2, \infty)$. It is easy to compute
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
f(5 / 2)=-\frac{11}{8}<0, \quad \text { and } \quad f(3)=4>0
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
Hence there is a unique value of $t$ in the interval $(5 / 2,3)$ such that $f(t)=0$. We conclude that
|
| 53 |
+
|
| 54 |
+
$$
|
| 55 |
+
\frac{5}{2}<\frac{c}{a}<3
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
Solution 2: Let us take $\angle B / 4=\theta$. Then $\angle E B C=\angle D B E=\theta$ and $\angle C B D=$ $2 \theta$.Using sine rule in triangles $B E A$ and $B E C$, we get
|
| 59 |
+
|
| 60 |
+
$$
|
| 61 |
+
\begin{aligned}
|
| 62 |
+
\frac{B E}{\sin A} & =\frac{A E}{\sin \theta} \\
|
| 63 |
+
\frac{B E}{\sin 90^{\circ}} & =\frac{C E}{\sin 3 \theta}
|
| 64 |
+
\end{aligned}
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
Since $A E=C E$, we obtain $\sin 3 \theta \sin A=\sin \theta$. However $A=90^{\circ}-4 \theta$. Thus we get $\sin 3 \theta \cos 4 \theta=\sin \theta$. Note that
|
| 68 |
+
|
| 69 |
+
$$
|
| 70 |
+
\frac{c}{a}=\frac{1}{\cos 4 \theta}=\frac{\sin 3 \theta}{\sin \theta}=3-4 \sin ^{2} \theta
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
This shows that $c / a<3$. Using $c / a=3-4 \sin ^{2} \theta$, it is easy to compute $\cos 2 \theta=((c / a)-1) / 2$. Hence
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
\frac{a}{c}=\cos 4 \theta=\frac{1}{2}\left(\frac{c}{a}-1\right)^{2}-1
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
Suppose $c / a \leq 5 / 2$. Then $((c / a)-1)^{2} \leq 9 / 4$ and $a / c \geq 2 / 5$. Thus
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
\frac{2}{5} \leq \frac{a}{c}=\frac{1}{2}\left(\frac{c}{a}-1\right)^{2}-1 \leq \frac{9}{8}-1=\frac{1}{8}
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
which is absurd. We conclude that $c / a>5 / 2$.
|
| 86 |
+
|
| 87 |
+
2. Let $n$ be a natural number such that $n=a^{2}+b^{2}+c^{2}$, for some natural numbers $a, b, c$. Prove that
|
| 88 |
+
|
| 89 |
+
$$
|
| 90 |
+
9 n=\left(p_{1} a+q_{1} b+r_{1} c\right)^{2}+\left(p_{2} a+q_{2} b+r_{2} c\right)^{2}+\left(p_{3} a+q_{3} b+r_{3} c\right)^{2}
|
| 91 |
+
$$
|
| 92 |
+
|
| 93 |
+
where $p_{j}$ 's, $q_{j}$ 's, $r_{j}$ 's are all nonzero integers. Further, if 3 does not divide at least one of $a, b, c$, prove that $9 n$ can be expressed in the form $x^{2}+y^{2}+z^{2}$, where $x, y, z$ are natural numbers none of which is divisible by 3 .
|
| 94 |
+
|
| 95 |
+
Solution: It can be easily seen that
|
| 96 |
+
|
| 97 |
+
$$
|
| 98 |
+
9 n=(2 b+2 c-a)^{2}+(2 c+2 a-b)^{2}+(2 a+2 b-c)^{2}
|
| 99 |
+
$$
|
| 100 |
+
|
| 101 |
+
Thus we can take $p_{1}=p_{2}=p_{3}=2, q_{1}=q_{2}=q_{3}=2$ and $r_{1}=r_{2}=r_{3}=-1$. Suppose 3 does not divide $\operatorname{gcd}(a, b, c)$. Then 3 does divide at least one of $a, b, c$; say 3 does not divide $a$. Note that each of $2 b+2 c-a, 2 c+2 a-b$ and $2 a+2 b-c$ is either divisible by 3 or none of them is divisible by 3 , as the difference of any two sums is always divisible by 3 . If 3 does not divide $2 b+2 c-a$, then we have the required representation. If 3 divides $2 b+2 c-a$, then 3 does not divide $2 b+2 c+a$. On the other hand, we also note that
|
| 102 |
+
|
| 103 |
+
$$
|
| 104 |
+
9 n=(2 b+2 c+a)^{2}+(2 c-2 a-b)^{2}+(-2 a+2 b-c)^{2}=x^{2}+y^{2}+z^{2}
|
| 105 |
+
$$
|
| 106 |
+
|
| 107 |
+
where $x=2 b+2 c+a, y=2 c-2 a-b$ and $z=-2 a+2 b-c$. Since $x-y=3(b+a)$ and 3 does not divide $x$, it follows that 3 does not divide $y$ as well. Similarly, we conclude that 3 does not divide $z$.
|
| 108 |
+
|
| 109 |
+
3. Let $m$ and $n$ be positive integers such that the equation $x^{2}-m x+n=0$ has real roots $\alpha$ and $\beta$. Prove that $\alpha$ and $\beta$ are integers if and only if $[m \alpha]+[m \beta]$ is the square of an integer. (Here $[x]$ denotes the largest integer not exceeding $x$.)
|
| 110 |
+
|
| 111 |
+
Solution: If $\alpha$ and $\beta$ are both integers, then
|
| 112 |
+
|
| 113 |
+
$$
|
| 114 |
+
[m \alpha]+[m \beta]=m \alpha+m \beta=m(\alpha+\beta)=m^{2}
|
| 115 |
+
$$
|
| 116 |
+
|
| 117 |
+
This proves one implication.
|
| 118 |
+
|
| 119 |
+
Observe that $\alpha+\beta=m$ and $\alpha \beta=n$. We use the property of integer function: $x-1<[x] \leq x$ for any real number $x$. Thus
|
| 120 |
+
|
| 121 |
+
$m^{2}-2=m(\alpha+\beta)-2=m \alpha-1+m \beta-1<[m \alpha]+[m \beta] \leq m(\alpha+\beta)=m^{2}$.
|
| 122 |
+
|
| 123 |
+
Since $m$ and $n$ are positive integers, both $\alpha$ and $\beta$ must be positive. If $m \geq 2$, we observe that there is no square between $m^{2}-2$ and $m^{2}$. Hence, either $m=1$ or $[m \alpha]+[m \beta]=m^{2}$. If $m=1$, then $\alpha+\beta=1$ implies that both $\alpha$ and $\beta$ are positive reals smaller than 1 . Hence $n=\alpha \beta$ cannot be a positive integer. We conclude that $[m \alpha]+[m \beta]=m^{2}$. Putting $m=\alpha+\beta$ in this relation, we get
|
| 124 |
+
|
| 125 |
+
$$
|
| 126 |
+
\left[\alpha^{2}+n\right]+\left[\beta^{2}+n\right]=(\alpha+\beta)^{2}
|
| 127 |
+
$$
|
| 128 |
+
|
| 129 |
+
Using $[x+k]=[x]+k$ for any real number $x$ and integer $k$, this reduces to
|
| 130 |
+
|
| 131 |
+
$$
|
| 132 |
+
\left[\alpha^{2}\right]+\left[\beta^{2}\right]=\alpha^{2}+\beta^{2}
|
| 133 |
+
$$
|
| 134 |
+
|
| 135 |
+
This shows that $\alpha^{2}$ and $\beta^{2}$ are both integers. On the other hand,
|
| 136 |
+
|
| 137 |
+
$$
|
| 138 |
+
\alpha^{2}-\beta^{2}=(\alpha+\beta)(\alpha-\beta)=m(\alpha-\beta)
|
| 139 |
+
$$
|
| 140 |
+
|
| 141 |
+
Thus
|
| 142 |
+
|
| 143 |
+
$$
|
| 144 |
+
(\alpha-\beta)=\frac{\alpha^{2}-\beta^{2}}{m}
|
| 145 |
+
$$
|
| 146 |
+
|
| 147 |
+
is a rational number. Since $\alpha+\beta=m$ is a rational number, it follows that both $\alpha$ and $\beta$ are rational numbers. However, both $\alpha^{2}$ and $\beta^{2}$ are integers. Hence each of $\alpha$ and $\beta$ is an integer.
|
| 148 |
+
|
| 149 |
+
4. Let $\sigma=\left(a_{1}, a_{2}, a_{3}, \ldots, a_{n}\right)$ be a permutation of $(1,2,3, \ldots, n)$. A pair $\left(a_{i}, a_{j}\right)$ is said to correspond to an inversion of $\sigma$, if $i<j$ but $a_{i}>a_{j}$. (Example: In the permutation $(2,4,5,3,1)$, there are 6 inversions corresponding to the pairs $(2,1)$, $(4,3),(4,1),(5,3),(5,1),(3,1)$.) How many permutations of $(1,2,3, \ldots n)$, $(n \geq 3)$, have exactly two inversions?
|
| 150 |
+
|
| 151 |
+
Solution: In a permutation of $(1,2,3, \ldots, n)$, two inversions can occur in only one of the following two ways:
|
| 152 |
+
|
| 153 |
+
(A) Two disjoint consecutive pairs are interchanged:
|
| 154 |
+
|
| 155 |
+
$$
|
| 156 |
+
\begin{aligned}
|
| 157 |
+
& (1,2,3, j-1, j, j+1, j+2 \ldots k-1, k, k+1, k+2, \ldots, n) \\
|
| 158 |
+
& \quad \longrightarrow(1,2, \ldots j-1, j+1, j, j+2, \ldots, k-1, k+1, k, k+2, \ldots, n)
|
| 159 |
+
\end{aligned}
|
| 160 |
+
$$
|
| 161 |
+
|
| 162 |
+
(B) Each block of three consecutive integers can be permuted in any of the following 2 ways;
|
| 163 |
+
|
| 164 |
+
$$
|
| 165 |
+
\begin{aligned}
|
| 166 |
+
& (1,2,3, \ldots k, k+1, k+2, \ldots, n) \longrightarrow(1,2, \ldots, k+2, k, k+1, \ldots, n) \\
|
| 167 |
+
& (1,2,3, \ldots k, k+1, k+2, \ldots, n) \longrightarrow(1,2, \ldots, k+1, k+2, k, \ldots, n)
|
| 168 |
+
\end{aligned}
|
| 169 |
+
$$
|
| 170 |
+
|
| 171 |
+
Consider case (A). For $j=1$, there are $n-3$ possible values of $k$; for $j=2$, there are $n-4$ possibilities for $k$ and so on. Thus the number of permutations with two inversions of this type is
|
| 172 |
+
|
| 173 |
+
$$
|
| 174 |
+
1+2+\cdots+(n-3)=\frac{(n-3)(n-2)}{2}
|
| 175 |
+
$$
|
| 176 |
+
|
| 177 |
+
In case (B), we see that there are $n-2$ permutations of each type, since $k$ can take values from 1 to $n-2$. Hence we get $2(n-2)$ permutations of this type.
|
| 178 |
+
|
| 179 |
+
Finally, the number of permutations with two inversions is
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
\frac{(n-3)(n-2)}{2}+2(n-2)=\frac{(n+1)(n-2)}{2}
|
| 183 |
+
$$
|
| 184 |
+
|
| 185 |
+
5. Let $A B C$ be a triangle in which $A B=A C$. Let $D$ be the mid-point of $B C$ and $P$ be a point on $A D$. Suppose $E$ is the foot of perpendicular from $P$ on $A C$. If $\frac{A P}{P D}=\frac{B P}{P E}=\lambda, \frac{B D}{A D}=m$ and $z=m^{2}(1+\lambda)$, prove that
|
| 186 |
+
|
| 187 |
+
$$
|
| 188 |
+
z^{2}-\left(\lambda^{3}-\lambda^{2}-2\right) z+1=0
|
| 189 |
+
$$
|
| 190 |
+
|
| 191 |
+
Hence show that $\lambda \geq 2$ and $\lambda=2$ if and only if $A B C$ is equilateral.
|
| 192 |
+
|
| 193 |
+
## Solution:
|
| 194 |
+
|
| 195 |
+
Let $A D=h, P D=y$ and $B D=D C=a$. We
|
| 196 |
+
|
| 197 |
+
|
| 198 |
+
observe that $B P^{2}=a^{2}+y^{2}$. Moreover,
|
| 199 |
+
|
| 200 |
+
$P E=P A \sin \angle D A C=(h-y) \frac{D C}{A C}=\frac{a(h-y)}{b}$,
|
| 201 |
+
|
| 202 |
+
where $b=A C=A B$. Using $A P / P D=(h-$ $y) / y$, we obtain $y=h /(1+\lambda)$. Thus
|
| 203 |
+
|
| 204 |
+
$$
|
| 205 |
+
\lambda^{2}=\frac{B P^{2}}{P E^{2}}=\frac{\left(a^{2}+y^{2}\right) b^{2}}{(h-y)^{2} a^{2}}
|
| 206 |
+
$$
|
| 207 |
+
|
| 208 |
+
But $(h-y)=\lambda y=\lambda h /(1+\lambda)$ and $b^{2}=a^{2}+h^{2}$. Thus we obtain
|
| 209 |
+
|
| 210 |
+
$$
|
| 211 |
+
\lambda^{4}=\frac{\left(a^{2}(1+\lambda)^{2}+h^{2}\right)\left(a^{2}+h^{2}\right)}{a^{2} h^{2}}
|
| 212 |
+
$$
|
| 213 |
+
|
| 214 |
+
Using $m=a / h$ and $z=m^{2}(1+\lambda)$, this simplifies to
|
| 215 |
+
|
| 216 |
+
$$
|
| 217 |
+
z^{2}-z\left(\lambda^{3}-\lambda^{2}-2\right)+1=0
|
| 218 |
+
$$
|
| 219 |
+
|
| 220 |
+
Dividing by $z$, this gives
|
| 221 |
+
|
| 222 |
+
$$
|
| 223 |
+
z+\frac{1}{z}=\lambda^{3}-\lambda^{2}-2
|
| 224 |
+
$$
|
| 225 |
+
|
| 226 |
+
However $z+(1 / z) \geq 2$ for any positive real number $z$. Thus $\lambda^{3}-\lambda^{2}-4 \geq 0$. This may be written in the form $(\lambda-2)\left(\lambda^{2}+\lambda+2\right) \geq 0$. But $\lambda^{2}+\lambda+2>0$. (For example, one may check that its discriminant is negative.) Hence $\lambda \geq 2$. If $\lambda=2$, then $z+(1 / z)=2$ and hence $z=1$. This gives $m^{2}=1 / 3$ or $\tan (A / 2)=m=1 / \sqrt{3}$. Thus $A=60^{\circ}$ and hence $A B C$ is equilateral.
|
| 227 |
+
|
| 228 |
+
Conversely, if triangle $A B C$ is equilateral, then $m=\tan (A / 2)=1 / \sqrt{3}$ and hence $z=(1+\lambda) / 3$. Substituting this in the equation satisfied by $z$, we obtain
|
| 229 |
+
|
| 230 |
+
$$
|
| 231 |
+
(1+\lambda)^{2}-3(1+\lambda)\left(\lambda^{3}-\lambda^{2}-2\right)+9=0
|
| 232 |
+
$$
|
| 233 |
+
|
| 234 |
+
This may be written in the form $(\lambda-2)\left(3 \lambda^{3}+6 \lambda^{2}+8 \lambda+8\right)=0$. Here the second factor is positive because $\lambda>0$. We conclude that $\lambda=2$.
|
| 235 |
+
|
| 236 |
+
6. If $x, y, z$ are positive real numbers, prove that
|
| 237 |
+
|
| 238 |
+
$$
|
| 239 |
+
(x+y+z)^{2}(y z+z x+x y)^{2} \leq 3\left(y^{2}+y z+z^{2}\right)\left(z^{2}+z x+x^{2}\right)\left(x^{2}+x y+y^{2}\right)
|
| 240 |
+
$$
|
| 241 |
+
|
| 242 |
+
Solution 1: We begin with the observation that
|
| 243 |
+
|
| 244 |
+
$$
|
| 245 |
+
x^{2}+x y+y^{2}=\frac{3}{4}(x+y)^{2}+\frac{1}{4}(x-y)^{2} \geq \frac{3}{4}(x+y)^{2}
|
| 246 |
+
$$
|
| 247 |
+
|
| 248 |
+
and similar bounds for $y^{2}+y z+z^{2}, z^{2}+z x+x^{2}$. Thus
|
| 249 |
+
|
| 250 |
+
$$
|
| 251 |
+
3\left(x^{2}+x y+y^{2}\right)\left(y^{2}+y z+z^{2}\right)\left(z^{2}+z x+x^{2}\right) \geq \frac{81}{64}(x+y)^{2}(y+z)^{2}(z+x)^{2}
|
| 252 |
+
$$
|
| 253 |
+
|
| 254 |
+
Thus it is sufficient to prove that
|
| 255 |
+
|
| 256 |
+
$$
|
| 257 |
+
(x+y+z)(x y+y z+z x) \leq \frac{9}{8}(x+y)(y+z)(z+x)
|
| 258 |
+
$$
|
| 259 |
+
|
| 260 |
+
Equivalently, we need to prove that
|
| 261 |
+
|
| 262 |
+
$$
|
| 263 |
+
8(x+y+z)(x y+y z+z x) \leq 9(x+y)(y+z)(z+x)
|
| 264 |
+
$$
|
| 265 |
+
|
| 266 |
+
However, we note that
|
| 267 |
+
|
| 268 |
+
$$
|
| 269 |
+
(x+y)(y+z)(z+x)=(x+y+z)(y z+z x+x y)-x y z
|
| 270 |
+
$$
|
| 271 |
+
|
| 272 |
+
Thus the required inequality takes the form
|
| 273 |
+
|
| 274 |
+
$$
|
| 275 |
+
(x+y)(y+z)(z+x) \geq 8 x y z
|
| 276 |
+
$$
|
| 277 |
+
|
| 278 |
+
This follows from AM-GM inequalities;
|
| 279 |
+
|
| 280 |
+
$$
|
| 281 |
+
x+y \geq 2 \sqrt{x y}, \quad y+z \geq 2 \sqrt{y z}, \quad z+x \geq 2 \sqrt{z x}
|
| 282 |
+
$$
|
| 283 |
+
|
| 284 |
+
Solution 2: Let us introduce $x+y=c, y+z=a$ and $z+x=b$. Then $a, b, c$ are the sides of a triangle. If $s=(a+b+c) / 2$, then it is easy to calculate $x=s-a, y=s-b, z=s-c$ and $x+y+z=s$. We also observe that
|
| 285 |
+
|
| 286 |
+
$x^{2}+x y+y^{2}=(x+y)^{2}-x y=c^{2}-\frac{1}{4}(c+a-b)(c+b-a)=\frac{3}{4} c^{2}+\frac{1}{4}(a-b)^{2} \geq \frac{3}{4} c^{2}$.
|
| 287 |
+
|
| 288 |
+
Moreover, $x y+y z+z x=(s-a)(s-b)+(s-b)(s-c)+(s-c)(s-a)$. Thus it si sufficient to prove that
|
| 289 |
+
|
| 290 |
+
$$
|
| 291 |
+
s \sum(s-a)(s-b) \leq \frac{9}{8} a b c
|
| 292 |
+
$$
|
| 293 |
+
|
| 294 |
+
But, $\sum(s-a)(s-b)=r(4 R+r)$, where $r, R$ are respectively the in-radius, the circum-radius of the triangle whose sides are $a, b, c$, and $a b c=4 R r s$. Thus the inequality reduces to
|
| 295 |
+
|
| 296 |
+
$$
|
| 297 |
+
r(4 R+r) \leq \frac{9}{2} R r
|
| 298 |
+
$$
|
| 299 |
+
|
| 300 |
+
This is simply $2 r \leq R$. This follows from $I O^{2}=R(R-2 r)$, where $I$ is the incentre and $O$ the circumcentre.
|
| 301 |
+
|
| 302 |
+
Solution 3: If we set $x=\lambda a, y=\lambda b, z=\lambda c$, then the inequality changes to
|
| 303 |
+
|
| 304 |
+
$$
|
| 305 |
+
(a+b+c)^{2}(a b+b c+c a)^{2} \leq 3\left(a^{2}+a b+b^{2}\right)\left(b^{2}+b c+c^{2}\right)\left(c^{2}+c a+a^{2}\right)
|
| 306 |
+
$$
|
| 307 |
+
|
| 308 |
+
This shows that we may assume $x+y+z=1$. Let $\alpha=x y+y z+z x$. We see that
|
| 309 |
+
|
| 310 |
+
$$
|
| 311 |
+
\begin{aligned}
|
| 312 |
+
x^{2}+x y+y^{2} & =(x+y)^{2}-x y \\
|
| 313 |
+
& =(x+y)(1-z)-x y \\
|
| 314 |
+
& =x+y-\alpha=1-z-\alpha
|
| 315 |
+
\end{aligned}
|
| 316 |
+
$$
|
| 317 |
+
|
| 318 |
+
Thus
|
| 319 |
+
|
| 320 |
+
$$
|
| 321 |
+
\begin{aligned}
|
| 322 |
+
\prod\left(x^{2}+x y+y^{2}\right) & =(1-\alpha-z)(1-\alpha-x)(1-\alpha-y) \\
|
| 323 |
+
& =(1-\alpha)^{3}-(1-\alpha)^{2}+(1-\alpha) \alpha-x y z \\
|
| 324 |
+
& =\alpha^{2}-\alpha^{3}-x y z
|
| 325 |
+
\end{aligned}
|
| 326 |
+
$$
|
| 327 |
+
|
| 328 |
+
Thus we need to prove that $\alpha^{2} \leq 3\left(\alpha^{2}-\alpha^{3}-x y z\right)$. This reduces to
|
| 329 |
+
|
| 330 |
+
$$
|
| 331 |
+
3 x y z \leq \alpha^{2}(2-3 \alpha)
|
| 332 |
+
$$
|
| 333 |
+
|
| 334 |
+
However
|
| 335 |
+
|
| 336 |
+
$$
|
| 337 |
+
3 \alpha=3(x y+y z+z x) \leq(x+y+z)^{2}=1
|
| 338 |
+
$$
|
| 339 |
+
|
| 340 |
+
so that $2-3 \alpha \geq 1$. Thus it suffices to prove that $3 x y z \leq \alpha^{2}$. But
|
| 341 |
+
|
| 342 |
+
$$
|
| 343 |
+
\begin{aligned}
|
| 344 |
+
\alpha^{2}-3 x y z & =(x y+y z+z x)^{2}-3 x y z(x+y+z) \\
|
| 345 |
+
& =\sum_{\text {cyclic }} x^{2} y^{2}-x y z(x+y+z) \\
|
| 346 |
+
& =\frac{1}{2} \sum_{\text {cyclic }}(x y-y z)^{2} \geq 0
|
| 347 |
+
\end{aligned}
|
| 348 |
+
$$
|
| 349 |
+
|
INMO/md/en-2008.md
ADDED
|
@@ -0,0 +1,227 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Problems and Solutions of INMO-2008
|
| 2 |
+
|
| 3 |
+
1. Let $A B C$ be a triangle, $I$ its in-centre; $A_{1}, B_{1}, C_{1}$ be the reflections of $I$ in $B C, C A, A B$ respectively. Suppose the circum-circle of triangle $A_{1} B_{1} C_{1}$ passes through $A$. Prove that $B_{1}, C_{1}$, $I, I_{1}$ are concyclic, where $I_{1}$ is the in-centre of triangle $A_{1} B_{1} C_{1}$.
|
| 4 |
+
|
| 5 |
+
## Solution:
|
| 6 |
+
|
| 7 |
+
|
| 8 |
+
|
| 9 |
+
Note that $I A_{1}=I B_{1}=I C_{1}=2 r$, where $r$ is the in-radius of the triangle $A B C$. Hence $I$ is the circum-centre of the triangle $A_{1} B_{1} C_{1}$.
|
| 10 |
+
|
| 11 |
+
Let $K$ be the point of intersection of $I B_{1}$ and $A C$. Then $I K=r, I A=2 r$ and $\angle I K A=90^{\circ}$. It follows that $\angle I A K=30^{\circ}$ and hence $\angle I A B_{1}=60^{\circ}$. Thus $A I B_{1}$ is an equilateral triangle. Similarly triangle $A I C_{1}$ is also equilateral. We hence obtain $A B_{1}=A C_{1}=A I=I B_{1}=I C_{1}=2 r$.
|
| 12 |
+
|
| 13 |
+
We also observe that $\angle B_{1} I C_{1}=120^{\circ}$ and $I B_{1} A C_{1}$ is a rhombus. Thus $\angle B_{1} A C_{1}=120^{\circ}$ and by concyclicity $\angle A_{1}=60^{\circ}$. Since $A B_{1}=A C_{1}, A$ is the midpoint of the arc $B_{1} A C_{1}$. It follows that $A_{1} A$ bisects $\angle A_{1}$ and $I_{1}$ lies on the line $A_{1} A$. This implies that
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
\angle B_{1} I_{1} C_{1}=90^{\circ}+\angle A_{1} / 2=90^{\circ}+30^{\circ}=120^{\circ}
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
Since $\angle B_{1} I C_{1}=120^{\circ}$, we conclude that $B_{1}, I, I_{1}, C_{1}$ are concyclic. (Further $A$ is the centre.)
|
| 20 |
+
|
| 21 |
+
2. Find all triples $(p, x, y)$ such that $p^{x}=y^{4}+4$, where $p$ is a prime and $x, y$ are natural numbers.
|
| 22 |
+
|
| 23 |
+
Solution: We begin with the standard factorisation
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
y^{4}+4=\left(y^{2}-2 y+2\right)\left(y^{2}+2 y+2\right)
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
Thus we have $y^{2}-2 y+2=p^{m}$ and $y^{2}+2 y+2=p^{n}$ for some positive integers $m$ and $n$ such that $m+n=x$. Since $y^{2}-2 y+2<y^{2}+2 y+2$, we have $m<n$ so that $p^{m}$ divides $p^{n}$. Thus $y^{2}-2 y+2$ divides $y^{2}+2 y+2$. Writing $y^{2}+2 y+2=y^{2}-2 y+2+4 y$, we infer that $y^{2}-2 y+2$ divides $4 y$ and hence $y^{2}-2 y+2$ divides $4 y^{2}$. But
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
4 y^{2}=4\left(y^{2}-2 y+2\right)+8(y-1)
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
Thus $y^{2}-2 y+2$ divides $8(y-1)$. Since $y^{2}-2 y+2$ divides both $4 y$ and $8(y-1)$, we conclude that it also divides 8 . This gives $y^{2}-2 y+2=1,2,4$ or 8 .
|
| 36 |
+
|
| 37 |
+
If $y^{2}-2 y+2=1$, then $y=1$ and $y^{4}+4=5$, giving $p=5$ and $x=1$. If $y^{2}-2 y+2=2$, then $y^{2}-2 y=0$ giving $y=2$. But then $y^{4}+4=20$ is not the power of a prime. The equations $y^{2}-2 y+2=4$ and $y^{2}-2 y+2=8$ have no integer solutions. We conclude that $(p, x, y)=(5,1,1)$ is the only solution.
|
| 38 |
+
|
| 39 |
+
Alternatively, using $y^{2}-2 y+2=p^{m}$ and $y^{2}+2 y+2=p^{n}$, we may get
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
4 y=p^{m}\left(p^{n-m}-1\right)
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
If $m>0$, then $p$ divides 4 or $y$. If $p$ divides 4 , then $p=2$. If $p$ divides $y$, then $y^{2}-2 y+2=p^{m}$ shows that $p$ divides 2 and hence $p=2$. But then $2^{x}=y^{4}+4$, which shows that $y$ is even. Taking $y=2 z$, we get $2^{x-2}=4 z^{4}+1$. This implies that $z=0$ and hence $y=0$, which is a contradiction. Thus $m=0$ and $y^{2}-2 y+2=1$. This gives $y=1$ and hence $p=5, x=1$.
|
| 46 |
+
|
| 47 |
+
3. Let $A$ be a set of real numbers such that $A$ has at least four elements. Suppose $A$ has the property that $a^{2}+b c$ is a rational number for all distinct numbers $a, b, c$ in $A$. Prove that there exists a positive integer $M$ such that $a \sqrt{M}$ is a rational number for every $a$ in $A$.
|
| 48 |
+
|
| 49 |
+
Solution: Suppose $0 \in A$. Then $a^{2}=a^{2}+0 \times b$ is rational and $a b=0^{2}+a b$ is also rational for all $a, b$ in $A, a \neq 0, b \neq 0, a \neq b$. Hence $a=a_{1} \sqrt{M}$ for some rational $a_{1}$ and natural number $M$. For any $b \neq 0$, we have
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
b \sqrt{M}=\frac{a b}{a_{1}}
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
which is a rational number.
|
| 56 |
+
|
| 57 |
+
Hence we may assume 0 is not in $A$. If there is a number $a$ in $A$ such that $-a$ is also in $A$, then again we can get the conclusion as follows. Consider two other elements $c, d$ in $A$. Then $c^{2}+d a$ is rational and $c^{2}-d a$ is also rational. It follows that $c^{2}$ is rational and $d a$ is rational. Similarly, $d^{2}$ and $c a$ are also rationals. Thus $d / c=(d a) /(c a)$ is rational. Note that we can vary $d$ over $A$ with $d \neq c$ and $d \neq a$. Again $c^{2}$ is rational implies that $c=c_{1} \sqrt{M}$ for some rational $c_{1}$ and natural number $M$. We observe that $c \sqrt{M}=c_{1} M$ is rational, and
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
a \sqrt{M}=\frac{c a}{c_{1}}
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
so that $a \sqrt{M}$ is a rational number. Similarly is the case with $-a \sqrt{M}$. For any other element $d$,
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
b \sqrt{M}=M c_{1} \frac{d}{c}
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
is a rational number.
|
| 70 |
+
|
| 71 |
+
Thus we may now assume that 0 is not in $A$ and $a+b \neq 0$ for any $a, b$ in $A$. Let $a, b, c, d$ be four distinct elements of $A$. We may assume $|a|>\mid b$. Then $d^{2}+a b$ and $d^{2}+b c$ are rational numbers and so is their difference $a b-b c$. Writing $a^{2}+a b=a^{2}+b c+(a b-b c)$, and using the facts $a^{2}+b c$, $a b-b c$ are rationals, we conclude that $a^{2}+a b$ is also a rational number. Similarly, $b^{2}+a b$ is also a rational number.
|
| 72 |
+
|
| 73 |
+
Consider
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
q=\frac{a}{b}=\frac{a^{2}+a b}{b^{2}+a b}
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
Note that $a^{2}+a b>0$. Thus $q$ is a rational number and $a=b q$. This gives $a^{2}+a b=b^{2}\left(q^{2}+q\right)$. Let us take $b^{2}\left(q^{2}+q\right)=l$. Then
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
|b|=\sqrt{\frac{l}{q^{2}+q}}=\sqrt{\frac{x}{y}}
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
where $x$ and $y$ are natural numbers. Take $M=x y$. Then $|b| \sqrt{M}=x$ is a rational number. Finally, for any $c$ in $A$, we have
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
c \sqrt{M}=b \sqrt{M} \frac{c}{b}
|
| 89 |
+
$$
|
| 90 |
+
|
| 91 |
+
is also a rational number.
|
| 92 |
+
|
| 93 |
+
4. All the points with integer coordinates in the $x y$-plane are coloured using three colours, red, blue and green, each colour being used at least once. It is known that the point $(0,0)$ is coloured red and the point $(0,1)$ is coloured blue. Prove that there exist three points with integer coordinates of distinct colours which form the vertices of a right-angled triangle.
|
| 94 |
+
|
| 95 |
+
Solution: Consider the lattice points(points with integer coordinates) on the lines $y=0$ and $y=1$, other than $(0,0)$ and $(0,1)$, If one of them, say $A=(p, 1)$, is coloured green, then we have a right-angled triangle with $(0,0),(0,1)$ and $A$ as vertices, all having different colours. (See Figures 1 and 2.)
|
| 96 |
+
|
| 97 |
+
|
| 98 |
+
If not, the lattice points on $y=0$ and $y=1$ are all red or blue. We consider three different cases.
|
| 99 |
+
|
| 100 |
+
Case 1. Suppose a point $B=(c, 0)$ is blue. Consider a green point $D=(p, q)$ in the plane. Suppose $p \neq 0$. If its projection $(p, 0)$ on the $x$-axis is red, then $(p, q),(p, 0)$ and $(c, 0)$ are the vertices of a required type of right-angled triangle. If $(p, 0)$ is blue, then we can consider the triangle whose vertices are $(0,0),(p, 0)$ and $(p, q)$. If $p=0$, then the points $D,(0,0)$ and $(c, 0)$ will work.(Figure 3.)
|
| 101 |
+
|
| 102 |
+
Case 2. A point $D=(c, 1)$, on the line $y=1$, is red. A similar argument works in this case.
|
| 103 |
+
|
| 104 |
+
|
| 105 |
+
|
| 106 |
+
Fig-4
|
| 107 |
+
|
| 108 |
+
Case 3. Suppose all the lattice points on the line $y=0$ are red and all on the line $y=1$ are blue points. Consider a green point $E=(p, q)$, where $q \neq 0$ and $q \neq 1$.(See Figure 4.) Consider an isosceles right-angled triangle $E K M$ with $\angle E=90^{\circ}$ such that the hypotenuse $K M$ is a part of the $x$-axis. Let $E M$ intersect $y=$ in $L$. Then $K$ is a red point and $L$ is a blue point. Hence $E K L$ is a desired triangle.
|
| 109 |
+
|
| 110 |
+
5. Let $A B C$ be a triangle; $\Gamma_{A}, \Gamma_{B}, \Gamma_{C}$ be three equal, disjoint circles inside $A B C$ such that $\Gamma_{A}$ touches $A B$ and $A C ; \Gamma_{B}$ touches $A B$; and $B C$, and $\Gamma_{C}$ touches $B C$ and $C A$. Let $\Gamma$ be a circle touching circles $\Gamma_{A}, \Gamma_{B}, \Gamma_{C}$ externally. Prove that the line joining the circum-centre $O$ and the in-centre $I$ of triangle $A B C$ passes through the centre of $\Gamma$.
|
| 111 |
+
|
| 112 |
+
Solution: Let $O_{1}, O_{2}, O_{3}$ be the centres of the circles $\Gamma_{A}, \Gamma_{B}, \Gamma_{C}$ respectively, and let $P$ be the circum-centre of the triangle $O_{1} O_{2} O_{3}$. Let $x$ denote the common radius of three circles $\Gamma_{A}, \Gamma_{B}$, $\Gamma_{C}$. Note that $P$ is also the centre of the circle $\Gamma$, as $O_{1} P, O_{2} P, O_{3} P$ each exceed the radius of $\Gamma$ by $x$. Let $D, X, K, L, M$ be respectively the projections of $I, P, O, O_{1}, O_{2}$ on $B C$.
|
| 113 |
+
|
| 114 |
+
|
| 115 |
+
|
| 116 |
+
From $\frac{B L}{B D}=\frac{L O_{2}}{D I}$, we get $B L=x(s-b) / r$, as $I D=r$ and $B D=(s-b)$. Similarly, $C M=$ $x(s-c) / r$. Therefore, $L M=a-\frac{x}{r}(s-b+s-c)=\frac{a}{r}(r-x)$. Since $O_{2} L M O_{3}$ is a rectangle and $P X$ is the perpendicular bisector of $\mathrm{O}_{2} \mathrm{O}_{3}$, it is perpendicular bisector of $L M$ as well. Thus
|
| 117 |
+
|
| 118 |
+
$$
|
| 119 |
+
\begin{aligned}
|
| 120 |
+
L X & =\frac{1}{2} L M=\frac{a}{2 r}(r-x) \\
|
| 121 |
+
B X & =B L+L X=\frac{x}{r}(s-b)+\frac{a}{2 r}(r-x)=\frac{a}{2}-\frac{x(b-c)}{2 r} \\
|
| 122 |
+
D K & =B K-B D=\frac{a}{2}-(s-b)=\frac{b-c}{2} \\
|
| 123 |
+
X K & =B K-B X=\frac{a}{2}-\frac{a}{2}+\frac{x(b-c)}{2 r}=\frac{x(b-c)}{2 r}
|
| 124 |
+
\end{aligned}
|
| 125 |
+
$$
|
| 126 |
+
|
| 127 |
+
Hence we get
|
| 128 |
+
|
| 129 |
+
$$
|
| 130 |
+
\frac{X K}{D K}=\frac{x}{r}
|
| 131 |
+
$$
|
| 132 |
+
|
| 133 |
+
We observe that the sides of triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$ are
|
| 134 |
+
|
| 135 |
+
$$
|
| 136 |
+
O_{2} O_{3}=L M=\frac{a}{r}(r-x), \quad O_{3} O_{1}=\frac{b}{r}(r-x), \quad O_{1} O_{2}=\frac{c}{r}(r-x)
|
| 137 |
+
$$
|
| 138 |
+
|
| 139 |
+
Thus the sides of $O_{1} O_{2} O_{3}$ and those of $A B C$ are in the ratio $(r-x) / r$. Further, as the sides of $O_{1} O_{2} O_{3}$ are parallel to those of $A B C$, we see that $I$ is the in-centre of $O_{1} O_{2} O_{3}$ as well. This gives $I P / I O=(r-x) / r$, and hence $P O / I O=x / r$. Thus we obtain
|
| 140 |
+
|
| 141 |
+
$$
|
| 142 |
+
\frac{X K}{D K}=\frac{P O}{I O}
|
| 143 |
+
$$
|
| 144 |
+
|
| 145 |
+
It follows that $I, P, O$ are collinear.
|
| 146 |
+
|
| 147 |
+
Alternately, we also infer that $I$ is the centre of homothety which takes the figure $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$ to $A B C$. Hence it takes $P$ to $O$. It follows that $I, P, O$ are collinear
|
| 148 |
+
|
| 149 |
+
6. Let $P(x)$ be a given polynomial with integer coefficients. Prove that there exist two polynomials $Q(x)$ and $R(x)$, again with integer coefficients, such that (i) $P(x) Q(x)$ is a polynomial in $x^{2}$; and (ii) $P(x) R(x)$ is a polynomial in $x^{3}$.
|
| 150 |
+
|
| 151 |
+
Solution: Let $P(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}$ be a polynomial with integer coefficients.
|
| 152 |
+
|
| 153 |
+
Part (i) We may write
|
| 154 |
+
|
| 155 |
+
$$
|
| 156 |
+
P(x)=a_{0}+a_{2} x^{2}+a_{4} x^{4}+\cdots+x\left(a_{1}+a_{3} x^{2}+a_{5} x^{5}+\cdots\right)
|
| 157 |
+
$$
|
| 158 |
+
|
| 159 |
+
Define
|
| 160 |
+
|
| 161 |
+
$$
|
| 162 |
+
Q(x)=a_{0}+a_{2} x^{2}+a_{4} x^{4}+\cdots-x\left(a_{1}+a_{3} x^{2}+a_{5} x^{5}+\cdots\right)
|
| 163 |
+
$$
|
| 164 |
+
|
| 165 |
+
Then $Q(x)$ is also a polynomial with integer coefficients and
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
P(x) Q(x)=\left(a_{0}+a_{2} x^{2}+a_{4} x^{4}+\cdots\right)^{2}-x^{2}\left(a_{1}+a_{3} x^{2}+a_{5} x^{5}+\cdots\right)^{2}
|
| 169 |
+
$$
|
| 170 |
+
|
| 171 |
+
is a polynomial in $x^{2}$.
|
| 172 |
+
|
| 173 |
+
Part (ii) We write again
|
| 174 |
+
|
| 175 |
+
$$
|
| 176 |
+
P(x)=A(x)+x B(x)+x^{2} C(x)
|
| 177 |
+
$$
|
| 178 |
+
|
| 179 |
+
where
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
\begin{aligned}
|
| 183 |
+
& A(x)=a_{0}+a_{3} x^{3}+a_{6} x^{6}+\cdots \\
|
| 184 |
+
& B(x)=a_{1}+a_{4} x^{3}+a_{7} x^{6}+\cdots \\
|
| 185 |
+
& C(x)=a_{2}+a_{5} x^{3}+a_{8} x^{6}+\cdots
|
| 186 |
+
\end{aligned}
|
| 187 |
+
$$
|
| 188 |
+
|
| 189 |
+
Note that $A(x), B(x)$ and $C(x)$ are polynomials with integer coefficients and each of these is a polynomial in $x^{3}$. We may introduce
|
| 190 |
+
|
| 191 |
+
$$
|
| 192 |
+
\begin{aligned}
|
| 193 |
+
& S(x)=A(x)+\omega x B(x)+\omega^{2} x^{2} C(x) \\
|
| 194 |
+
& T(x)=A(x)+\omega^{2} x B(x)+\omega x^{2} C(x)
|
| 195 |
+
\end{aligned}
|
| 196 |
+
$$
|
| 197 |
+
|
| 198 |
+
where $\omega$ is an imaginary cube-root of unity. Then
|
| 199 |
+
|
| 200 |
+
$$
|
| 201 |
+
\begin{aligned}
|
| 202 |
+
S(x) T(x)=(A(x))^{2}+x^{2}(B(x))^{2}+x^{4}(C(x))^{2} & \\
|
| 203 |
+
& -x A(x) B(x)-x^{3} B(x) C(x)-x^{2} C(x) A(x)
|
| 204 |
+
\end{aligned}
|
| 205 |
+
$$
|
| 206 |
+
|
| 207 |
+
since $\omega^{3}=1$ and $\omega+\omega^{2}=-1$. Taking $R(x)=S(x) T(x)$, we obtain
|
| 208 |
+
|
| 209 |
+
$$
|
| 210 |
+
P(x) R(x)=(A(x))^{3}+x^{3}(B(x))^{3}+x^{6}(C(x))^{3}-3 x^{3} A(x) B(x) C(x)
|
| 211 |
+
$$
|
| 212 |
+
|
| 213 |
+
which is a polynomial in $x^{3}$. This follows from the identity
|
| 214 |
+
|
| 215 |
+
$$
|
| 216 |
+
(a+b+c)\left(a^{2}+b^{2}+c^{2}-a b-b c-c a\right)=a^{3}+b^{3}+c^{3}-3 a b c
|
| 217 |
+
$$
|
| 218 |
+
|
| 219 |
+
Alternately, $R(x)$ may be directly defined by
|
| 220 |
+
|
| 221 |
+
$$
|
| 222 |
+
\begin{aligned}
|
| 223 |
+
& R(x)=(A(x))^{2}+x^{2}(B(x))^{2}+x^{4}(C(x))^{2} \\
|
| 224 |
+
&-x A(x) B(x)-x^{3} B(x) C(x)-x^{2} C(x) A(x)
|
| 225 |
+
\end{aligned}
|
| 226 |
+
$$
|
| 227 |
+
|
INMO/md/en-2009.md
ADDED
|
@@ -0,0 +1,411 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# 24th Indian National Mathematical Olympiad, 2009
|
| 2 |
+
|
| 3 |
+
## Problems and Solutions
|
| 4 |
+
|
| 5 |
+
1. Let $A B C$ be a triangle and let $P$ be an interior point such that $\angle B P C=90^{\circ}, \angle B A P=$ $\angle B C P$. Let $M, N$ be the mid-points of $A C, B C$ respectively. Suppose $B P=2 P M$. Prove that $A, P, N$ are collinear.
|
| 6 |
+
|
| 7 |
+
## Solution:
|
| 8 |
+
|
| 9 |
+
Extend $C P$ to $D$ such that $C P=P D$. Let $\angle B C P=\alpha=\angle B A P$. Observe that $B P$ is the perpendicular bisector of $C D$. Hence $B C=B D$ and $B C D$ is an isosceles triangle. Thus $\angle B D P=\alpha$. But then $\angle B D P=$ $\alpha=\angle B A P$. This implies that $B, P, A, D$ all lie on a circle. In turn, we conclude that $\angle D A B=\angle D P B=90^{\circ}$. Since $P$ is the midpoint of $C P$ (by construction) and $M$ is the mid-point of $C A$ (given), it follows that $P M$ is parallel to $D A$ and $D A=2 P M=B P$. Thus $D B P A$ is an isosceles trapezium and $D B$ is parallel to $P A$.
|
| 10 |
+
|
| 11 |
+
|
| 12 |
+
|
| 13 |
+
We hence get
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
\angle D P A=\angle B A P=\angle B C P=\angle N P C
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
the last equality follows from the fact that $\angle B P C=90^{\circ}$, and $N$ is the mid-point of $C B$ so that $N P=N C=N B$ for the right-angled triangle $B P C$. It follows that $A, P, N$ are collinear.
|
| 20 |
+
|
| 21 |
+
## Alternate Solution:
|
| 22 |
+
|
| 23 |
+
We use coordinate geometry. Let us take $P=(0,0)$, and the coordinate axes along $P C$ and $P B$; We take $C=(c, 0)$ and $B=(0, b)$. Let $A=(u, v)$. We see that $N=(c / 2, b / 2)$ and $M=((u+c) / 2, v / 2)$. The condition $P B=2 P M$ translates to
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
(u+c)^{2}+v^{2}=b^{2}
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
We observe that the slope of $C P=0$; that of $C B$ is $-b / c$; that of $P A$ is $v / u$; and that of $B A$ is $(v-b) / u$. Taking proper signs, we can convert $\angle P C B=\angle P A B$, via tan function, to the following relation:
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
u^{2}+v^{2}-v b=-c u
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
Thus we obtain
|
| 36 |
+
|
| 37 |
+
$$
|
| 38 |
+
u(u+c)=v(b-v), \quad c(c+u)=b(b-v)
|
| 39 |
+
$$
|
| 40 |
+
|
| 41 |
+
It follows that $v / u=b / c$. But then we get that the slope of $A P$ and $P N$ are the same. We conclude that $A, P, N$ are collinear.
|
| 42 |
+
|
| 43 |
+
2. Define a sequence $\left\langle a_{n}\right\rangle_{n=1}^{\infty}$ as follows:
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
a_{n}= \begin{cases}0, & \text { if the number of positive divisors of } n \text { is odd } \\ 1, & \text { if the number of positive divisors of } n \text { is even }\end{cases}
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
(The positive divisors of $n$ include 1 as well as $n$.) Let $x=0 . a_{1} a_{2} a_{3} \ldots$ be the real number whose decimal expansion contains $a_{n}$ in the $n$-th place, $n \geq 1$. Determine, with proof, whether $x$ is rational or irrational.
|
| 50 |
+
|
| 51 |
+
## Solution:
|
| 52 |
+
|
| 53 |
+
We show that $x$ is irrational. Suppose that $x$ is rational. Then the sequence $\left\langle a_{n}\right\rangle_{n=1}^{\infty}$ is periodic after some stage; there exist natural numbers $k, l$ such that $a_{n}=a_{n+l}$ for all $n \geq k$. Choose $m$ such that $m l \geq k$ and $m l$ is a perfect square. Let
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
m=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \ldots p_{r}^{\alpha_{r}}, \quad l=p_{1}^{\beta_{1}} p_{2}^{\beta_{2}} \ldots p_{r}^{\beta_{r}}
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
be the prime decompositions of $m, l$ so that $\alpha_{j}+\beta_{j}$ is even for $1 \leq j \leq r$. Now take a prime $p$ different from $p_{1}, p_{2}, \ldots, p_{r}$. Consider $m l$ and $p m l$. Since $p m l-m l$ is divisible by $l$, we have $a_{p m l}=a_{m l}$. Hence $d(p m l)$ and $d(m l)$ have same parity. But $d(p m l)=2 d(m l)$, since $\operatorname{gcd}(p, m l)=1$ and $p$ is a prime. Since $m l$ is a square, $d(m l)$ is odd. It follows that $d(p m l)$ is even and hence $a_{p m l} \neq a_{m l}$. This contradiction implies that $x$ is irrational.
|
| 60 |
+
|
| 61 |
+
Alternative Solution: As earlier, assume that $x$ is rational and choose natural numbers $k, l$ such that $a_{n}=a_{n+l}$ for all $n \geq k$. Consider the numbers $a_{m+1}, a_{m+2}, \ldots, a_{m+l}$, where $m \geq k$ is any number. This must contain at least one 0 . Otherwise $a_{n}=1$ for all $n \geq k$. But $a_{r}=0$ if and only if $r$ is a square. Hence it follows that there are no squares for $n>k$, which is absurd. Thus every $l$ consecutive terms of the sequence $\left\langle a_{n}\right\rangle$ must contain a 0 after certain stage. Let $t=\max \{k, l\}$, and consider $t^{2}$ and $(t+1)^{2}$. Since there are no squares between $t^{2}$ and $(t+1)^{2}$, we conclude that $a_{t^{2}+j}=1$ for $1 \leq j \leq 2 t$. But then, we have $2 t(>l)$ consecutive terms of the sequence $\left\langle a_{n}\right\rangle$ which miss 0 , contradicting our earlier observation.
|
| 62 |
+
|
| 63 |
+
3. Find all real numbers $x$ such that
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
\left[x^{2}+2 x\right]=[x]^{2}+2[x]
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
(Here $[x]$ denotes the largest integer not exceeding $x$.)
|
| 70 |
+
|
| 71 |
+
## Solution:
|
| 72 |
+
|
| 73 |
+
Adding 1 both sides, the equation reduces to
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
\left[(x+1)^{2}\right]=([x+1])^{2}
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
we have used $[x]+m=[x+m]$ for every integer $m$. Suppose $x+1 \leq 0$. Then $[x+1] \leq$ $x+1 \leq 0$. Thus
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
([x+1])^{2} \geq(x+1)^{2} \geq\left[(x+1)^{2}\right]=([x+1])^{2}
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
Thus equality holds everywhere. This gives $[x+1]=x+1$ and thus $x+1$ is an integer. Using $x+1 \leq 0$, we conclude that
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
x \in\{-1,-2,-3, \ldots\}
|
| 89 |
+
$$
|
| 90 |
+
|
| 91 |
+
Suppose $x+1>0$. We have
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
(x+1)^{2} \geq\left[(x+1)^{2}\right]=([x+1])^{2}
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
Moreover, we also have
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
(x+1)^{2} \leq 1+\left[(x+1)^{2}\right]=1+([x+1])^{2}
|
| 101 |
+
$$
|
| 102 |
+
|
| 103 |
+
Thus we obtain
|
| 104 |
+
|
| 105 |
+
$$
|
| 106 |
+
[x]+1=[x+1] \leq(x+1)<\sqrt{1+([x+1])^{2}}=\sqrt{1+([x]+1)^{2}}
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
This shows that
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
x \in\left[n, \sqrt{1+(n+1)^{2}}-1\right)
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
where $n \geq-1$ is an integer. Thus the solution set is
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
\{-1,-2,-3, \ldots\} \cup\left\{\cup_{n=-1}^{\infty}\left[n, \sqrt{1+(n+1)^{2}}-1\right)\right\}
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
It is easy verify that all the real numbers in this set indeed satisfy the given equation.
|
| 122 |
+
|
| 123 |
+
4. All the points in the plane are coloured using three colours. Prove that there exists a triangle with vertices having the same colour such that either it is isosceles or its angles are in geometric progression.
|
| 124 |
+
|
| 125 |
+
## Solution:
|
| 126 |
+
|
| 127 |
+
Consider a circle of positive radius in the plane and inscribe a regular heptagon $A B C D E F G$ in it. Since the seven vertices of this heptagon are coloured by three colours, some three vertices have the same colour, by pigeon-hole principle. Consider the triangle formed by these three vertices. Let us call the part of the circumference separated by any two consecutive vertices of the heptagon an arc. The three vertices of the same colour are separated by arcs of length $l, m, n$ as we move, say counter-clockwise, along the circle, starting from a fixed vertex among these three, where $l+m+n=7$. Since, the order of $l, m, n$ does not matter for a triangle, there are four possibilities: $1+1+5=7 ; 1+2+4=7 ; 1+3+3=7 ; 2+2+3=7$. In the first, third and fourth cases, we have isosceles triangles. In the second case, we have a triangle whose angles are in geometric progression. The four corresponding figures are shown below.
|
| 128 |
+
|
| 129 |
+
|
| 130 |
+
|
| 131 |
+
(i)
|
| 132 |
+
|
| 133 |
+
|
| 134 |
+
|
| 135 |
+
(ii)
|
| 136 |
+
|
| 137 |
+
|
| 138 |
+
|
| 139 |
+
(iii)
|
| 140 |
+
|
| 141 |
+
|
| 142 |
+
|
| 143 |
+
(iv)
|
| 144 |
+
|
| 145 |
+
In (i), $A B=B C$; in (iii), $A E=B E$; in (iv), $A C=C E$; and in (ii) we see that $\angle D=\pi / 7$, $\angle A=2 \pi / 7$ and $\angle B=4 \pi / 7$ which are in geometric progression.
|
| 146 |
+
|
| 147 |
+
5. Let $A B C$ be an acute-angled triangle and let $H$ be its ortho-centre. Let $h_{\text {max }}$ denote the largest altitude of the triangle $A B C$. Prove that
|
| 148 |
+
|
| 149 |
+
$$
|
| 150 |
+
A H+B H+C H \leq 2 h_{\max }
|
| 151 |
+
$$
|
| 152 |
+
|
| 153 |
+
## Solution:
|
| 154 |
+
|
| 155 |
+
|
| 156 |
+
|
| 157 |
+
Let $\angle C$ be the smallest angle, so that $C A \geq A B$ and $C B \geq A B$. In this case the altitude through $C$ is the longest one. Let the altitude through $C$ meet $A B$ in $D$ and let $H$ be the ortho-centre of $A B C$. Let $C D$ extended meet the circum-circle of $A B C$ in $K$. We have $C D=h_{\max }$ so that the inequality to be proved is
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
A H+B H+C H \leq 2 C D
|
| 161 |
+
$$
|
| 162 |
+
|
| 163 |
+
Using $C D=C H+H D$, this reduces to $A H+B H \leq C D+H D$. However, we observe that $A H=A K, B H=B K$ and $H D=D K$.(For example $B H=B K$ and $D H=D K$ follow from the congruency of the right-angled triangles $D B K$ and $D B H$.)
|
| 164 |
+
|
| 165 |
+
Thus we need to prove that $A K+B K \leq C K$. Applying Ptolemy's theorem to the cyclic quadrilateral $B C A K$, we get
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
A B \cdot C K=A C \cdot B K+B C \cdot A K \geq A B \cdot B K+A B \cdot A K
|
| 169 |
+
$$
|
| 170 |
+
|
| 171 |
+
This implies that $C K \geq A K+B K$, which is precisely what we are looking for.
|
| 172 |
+
|
| 173 |
+
There were other beautiful solutions given by students who participated in INMO-2009. We record them here.
|
| 174 |
+
|
| 175 |
+
1. Let $A D, B E, C F$ be the altitudes and $H$ be the ortho-centre. Observe that
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
\frac{A H}{A D}=\frac{[A H B]}{[A D B]}=\frac{[A H C]}{[A D C]}
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
This gives
|
| 182 |
+
|
| 183 |
+
$$
|
| 184 |
+
\frac{A H}{A D}=\frac{[A H B]+[A H C]}{[A D B]+[A D C]}=1-\frac{[B H C]}{[A B C]}
|
| 185 |
+
$$
|
| 186 |
+
|
| 187 |
+
Similar expressions for the ratios $B H / B E$ and $C H / C F$ may be obtained. Adding, we get
|
| 188 |
+
|
| 189 |
+
$$
|
| 190 |
+
\frac{A H}{A D}+\frac{B H}{B E}+\frac{C H}{C F}=2
|
| 191 |
+
$$
|
| 192 |
+
|
| 193 |
+
Suppose $A D$ is the largest altitude. We get
|
| 194 |
+
|
| 195 |
+
$$
|
| 196 |
+
\frac{A H}{A D}+\frac{B H}{A D}+\frac{C H}{A D} \leq \frac{A H}{A D}+\frac{B H}{B E}+\frac{C H}{C F}=2
|
| 197 |
+
$$
|
| 198 |
+
|
| 199 |
+
This gives the result.
|
| 200 |
+
|
| 201 |
+
2. Let $O$ be the circum-centre and let $L, M, N$ be the mid-points of $B C, C A, A B$ respectively. Then we know that $A H=2 O L, B H=2 O M$ and $C H=2 O N$. As earlier, assume $A D$ is the largest altitude. Then $B C$ is the least side. We have
|
| 202 |
+
|
| 203 |
+
$$
|
| 204 |
+
\begin{aligned}
|
| 205 |
+
4[A B C]=4[B O C]+4[C O A]+4[A O B] & =B C \times 2 O L+C A \times 2 O M+A B \times 2 O N \\
|
| 206 |
+
& =B C \times A H+C A \times B H+A B \times C H \\
|
| 207 |
+
& \geq A B(A H+B H+C H)
|
| 208 |
+
\end{aligned}
|
| 209 |
+
$$
|
| 210 |
+
|
| 211 |
+
Thus
|
| 212 |
+
|
| 213 |
+
$$
|
| 214 |
+
A H+B H+C H \leq \frac{4[A B C]}{A B}=2 A D
|
| 215 |
+
$$
|
| 216 |
+
|
| 217 |
+
3. We make use of the fact that $A H=2 R \cos \angle A, B H=2 R \cos \angle B, C H=2 R \cos \angle C$ and $A D=2 R \sin \angle B \sin \angle C$, where $R$ is the circum-radius of $A B C$. We are assuming that $A D$ is the largest altitude so that $\angle A$ is the least angle. Thus we have to prove that
|
| 218 |
+
|
| 219 |
+
$$
|
| 220 |
+
\cos \angle A+\cos \angle B+\cos \angle C \leq 2 \sin \angle B \angle C
|
| 221 |
+
$$
|
| 222 |
+
|
| 223 |
+
under the assumption $\angle A \leq \angle B$ and $\angle A \leq \angle C$. On multiplying this by $2 \sin \angle A$, this is equivalent to
|
| 224 |
+
|
| 225 |
+
$$
|
| 226 |
+
\begin{aligned}
|
| 227 |
+
& 2(\sin \angle A \cos \angle A+\sin \angle A \cos \angle B+\sin \angle A \cos \angle C) \\
|
| 228 |
+
& \leq 4 \sin \angle A \sin \angle B \angle C=\sin 2 A+\sin 2 B+\sin 2 C
|
| 229 |
+
\end{aligned}
|
| 230 |
+
$$
|
| 231 |
+
|
| 232 |
+
This is equivalent to
|
| 233 |
+
|
| 234 |
+
$$
|
| 235 |
+
\cos \angle B(\sin \angle A-\sin \angle B)+\cos \angle C(\sin \angle A-\sin \angle C) \leq 0
|
| 236 |
+
$$
|
| 237 |
+
|
| 238 |
+
Since $A B C$ is acute-angled and $A$ is the least angle, the result follows.
|
| 239 |
+
|
| 240 |
+
6. Let $a, b, c$ be positive real numbers such that $a^{3}+b^{3}=c^{3}$. Prove that
|
| 241 |
+
|
| 242 |
+
$$
|
| 243 |
+
a^{2}+b^{2}-c^{2}>6(c-a)(c-b)
|
| 244 |
+
$$
|
| 245 |
+
|
| 246 |
+
## Solution:
|
| 247 |
+
|
| 248 |
+
The given inequality may be written in the form
|
| 249 |
+
|
| 250 |
+
$$
|
| 251 |
+
7 c^{2}-6(a+b) c-\left(a^{2}+b^{2}-6 a b\right)<0
|
| 252 |
+
$$
|
| 253 |
+
|
| 254 |
+
Putting $x=7 c^{2}, y=-6(a+b) c, z=-\left(a^{2}+b^{2}-6 a b\right)$, we have to prove that $x+y+z<0$. Observe that $x, y, z$ are not all equal $(x>0, y<0)$. Using the identity
|
| 255 |
+
|
| 256 |
+
$$
|
| 257 |
+
x^{3}+y^{3}+z^{3}-3 x y z=\frac{1}{2}(x+y+z)\left[(x-y)^{2}+(y-z)^{2}+(z-x)^{2}\right]
|
| 258 |
+
$$
|
| 259 |
+
|
| 260 |
+
we infer that it is sufficient to prove $x^{3}+y^{3}+z^{3}-3 x y z<0$. Substituting the values of $x, y, z$, we see that this is equivalent to
|
| 261 |
+
|
| 262 |
+
$$
|
| 263 |
+
343 c^{6}-216(a+b)^{3} c^{3}-\left(a^{2}+b^{2}-6 a b\right)^{3}-126 c^{3}(a+b)\left(a^{2}+b^{2}-6 a b\right)<0
|
| 264 |
+
$$
|
| 265 |
+
|
| 266 |
+
Using $c^{3}=a^{3}+b^{3}$, this reduces to
|
| 267 |
+
|
| 268 |
+
$343\left(a^{3}+b^{3}\right)^{2}-216(a+b)^{3}\left(a^{3}+b^{3}\right)-\left(a^{2}+b^{2}-6 a b\right)^{3}-126\left(\left(a^{3}+b^{3}\right)(a+b)\left(a^{2}+b^{2}-6 a b\right)<0\right.$.
|
| 269 |
+
|
| 270 |
+
This may be simplified (after some tedious calculations) to,
|
| 271 |
+
|
| 272 |
+
$$
|
| 273 |
+
-a^{2} b^{2}\left(129 a^{2}-254 a b+129 b^{2}\right)<0
|
| 274 |
+
$$
|
| 275 |
+
|
| 276 |
+
But $129 a^{2}-254 a b+129 b^{2}=129(a-b)^{2}+4 a b>0$. Hence the result follows.
|
| 277 |
+
|
| 278 |
+
Remark: The best constant $\theta$ in the inequality $a^{2}+b^{2}-c^{2} \geq \theta(c-a)(c-b)$, where $a, b, c$
|
| 279 |
+
are positive reals such that $a^{3}+b^{3}=c^{3}$, is $\theta=2\left(1+2^{1 / 3}+2^{-1 / 3}\right)$.
|
| 280 |
+
|
| 281 |
+
Here again, there were some beautiful solutions given by students.
|
| 282 |
+
|
| 283 |
+
1. We have
|
| 284 |
+
|
| 285 |
+
$$
|
| 286 |
+
a^{3}=c^{3}-b^{3}=(c-b)\left(c^{2}+c b+b^{2}\right)
|
| 287 |
+
$$
|
| 288 |
+
|
| 289 |
+
which is same as
|
| 290 |
+
|
| 291 |
+
$$
|
| 292 |
+
\frac{a^{2}}{c-b}=\frac{c^{2}+c b+b^{2}}{a}
|
| 293 |
+
$$
|
| 294 |
+
|
| 295 |
+
Similarly, we get
|
| 296 |
+
|
| 297 |
+
$$
|
| 298 |
+
\frac{b^{2}}{c-a}=\frac{c^{2}+c a+a^{2}}{b}
|
| 299 |
+
$$
|
| 300 |
+
|
| 301 |
+
We observe that
|
| 302 |
+
|
| 303 |
+
$$
|
| 304 |
+
\frac{a^{2}}{c-b}+\frac{b^{2}}{c-a}=\frac{c\left(a^{2}+b^{2}\right)-a^{3}-b^{3}}{(c-a)(c-b)}=\frac{c\left(a^{2}+b^{2}-c^{2}\right)}{(c-a)(c-b)}
|
| 305 |
+
$$
|
| 306 |
+
|
| 307 |
+
This shows that
|
| 308 |
+
|
| 309 |
+
$$
|
| 310 |
+
\frac{a^{2}+b^{2}-c^{2}}{(c-a)(c-b)}=\frac{c^{2}+c b+b^{2}}{c a}+\frac{c^{2}+c a+a^{2}}{c b}
|
| 311 |
+
$$
|
| 312 |
+
|
| 313 |
+
Thus it is sufficient to prove that
|
| 314 |
+
|
| 315 |
+
$$
|
| 316 |
+
\frac{c^{2}+c b+b^{2}}{c a}+\frac{c^{2}+c a+a^{2}}{c b} \geq 6
|
| 317 |
+
$$
|
| 318 |
+
|
| 319 |
+
However, we have $c^{2}+b^{2} \geq 2 c b$ and $c^{2}+a^{2} \geq 2 c a$. Hence
|
| 320 |
+
|
| 321 |
+
$$
|
| 322 |
+
\frac{c^{2}+c b+b^{2}}{c a}+\frac{c^{2}+c a+a^{2}}{c b} \geq 3\left(\frac{b}{a}+\frac{a}{b}\right) \geq 3 \times 2=6
|
| 323 |
+
$$
|
| 324 |
+
|
| 325 |
+
We have used AM-GM inequality.
|
| 326 |
+
|
| 327 |
+
2. Let us set $x=a / c$ and $y=b / c$. Then $x^{3}+y^{3}=1$ and the inequality to be proved is $x^{2}+y^{2}-1>6(1-x)(1-y)$. This reduces to
|
| 328 |
+
|
| 329 |
+
$$
|
| 330 |
+
(x+y)^{2}+6(x+y)-8 x y-7>0
|
| 331 |
+
$$
|
| 332 |
+
|
| 333 |
+
But
|
| 334 |
+
|
| 335 |
+
$$
|
| 336 |
+
1=x^{3}+y^{3}=(x+y)\left(x^{2}-x y+y^{2}\right)
|
| 337 |
+
$$
|
| 338 |
+
|
| 339 |
+
which gives $x y=\left((x+y)^{3}-1\right) / 3(x+y)$. Substituting this in (1) and introducing $x+y=t$, the inequality takes the form
|
| 340 |
+
|
| 341 |
+
$$
|
| 342 |
+
t^{2}+6 t-\frac{8}{3} \frac{\left(t^{3}-1\right)}{t}-7>0
|
| 343 |
+
$$
|
| 344 |
+
|
| 345 |
+
This may be simplified to $-5 t^{3}+18 t^{2}-2 t+8>0$. Equivalently
|
| 346 |
+
|
| 347 |
+
$$
|
| 348 |
+
-(5 t-8)(t-1)^{2}>0
|
| 349 |
+
$$
|
| 350 |
+
|
| 351 |
+
Thus we need to prove that $5 t<8$. Observe that $(x+y)^{3}>x^{3}+y^{3}=1$, so that $t>1$. We also have
|
| 352 |
+
|
| 353 |
+
$$
|
| 354 |
+
\left(\frac{x+y}{2}\right) \leq \frac{x^{3}+y^{3}}{2}=\frac{1}{2}
|
| 355 |
+
$$
|
| 356 |
+
|
| 357 |
+
This shows that $t^{3} \leq 4$. Thus
|
| 358 |
+
|
| 359 |
+
$$
|
| 360 |
+
\left(\frac{5 t}{8}\right)^{3} \leq \frac{125 \times 4}{512}=\frac{500}{512}<1
|
| 361 |
+
$$
|
| 362 |
+
|
| 363 |
+
Hence $5 t<8$, which proves the given inequality.
|
| 364 |
+
|
| 365 |
+
3. We write $b^{3}=c^{3}-a^{3}$ and $a^{3}=c^{3}-b^{3}$ so that
|
| 366 |
+
|
| 367 |
+
$$
|
| 368 |
+
c-a=\frac{b^{3}}{c^{2}-c a+a^{2}}, \quad c-b=\frac{a^{3}}{c^{2}-c b+b^{2}}
|
| 369 |
+
$$
|
| 370 |
+
|
| 371 |
+
Thus the inequality reduces to
|
| 372 |
+
|
| 373 |
+
$$
|
| 374 |
+
a^{2}+b^{2}-c^{2}>6 \frac{a^{3} b^{3}}{\left(c^{2}-c a+a^{2}\right)\left(c^{2}-c b+b^{2}\right)}
|
| 375 |
+
$$
|
| 376 |
+
|
| 377 |
+
This simplifies(after some lengthy calculations) to
|
| 378 |
+
|
| 379 |
+
$$
|
| 380 |
+
\begin{aligned}
|
| 381 |
+
& -c^{6}-(a+b) c^{5}-a b c^{4}+\left(a^{3}+b^{3}\right) c^{3}+\left(a^{4}+a^{3} b+a^{2} b^{2}+a b^{3}+b^{4}\right) c^{2} \\
|
| 382 |
+
& \quad\left(a^{2} b+a b^{2}+a^{3}+b^{3}\right) a b c+\left(a^{4} b^{2}-6 a^{3} b^{3}+a^{2} b^{4}\right)>0
|
| 383 |
+
\end{aligned}
|
| 384 |
+
$$
|
| 385 |
+
|
| 386 |
+
Substituting
|
| 387 |
+
|
| 388 |
+
$$
|
| 389 |
+
c^{3}=a^{3}+b^{3}, \quad c^{4}=c\left(a^{3}+b^{3}\right), \quad c^{5}=c^{2}\left(a^{3}+b^{3}\right), \quad c^{6}=\left(a^{3}+b^{3}\right)^{2}
|
| 390 |
+
$$
|
| 391 |
+
|
| 392 |
+
the inequality further reduces to
|
| 393 |
+
|
| 394 |
+
$$
|
| 395 |
+
a^{2} b^{2}\left(a^{2}+b^{2}+c^{2}+a c+b c-6 a b\right)>0
|
| 396 |
+
$$
|
| 397 |
+
|
| 398 |
+
Thus we need to prove that $a^{2}+b^{2}+c^{2}+a c+b c-6 a b>0$. Since $a^{2}+b^{2} \geq 2 a b$, it is enough to prove that $c^{2}+c(a+b)-4 a b>0$. Multiplying this by $c$ and using $a^{3}+b^{3}=c^{3}$, we need to prove that
|
| 399 |
+
|
| 400 |
+
$$
|
| 401 |
+
a^{3}+b^{3}+c^{2} a+c^{2} b>4 a b c
|
| 402 |
+
$$
|
| 403 |
+
|
| 404 |
+
Using AM-GM inequality to these 4 terms and using $c>a, c>b$ we get
|
| 405 |
+
|
| 406 |
+
$$
|
| 407 |
+
a^{3}+b^{3}+c^{2} a+c^{2} b>4\left(a^{3} b^{3} c^{2} a c^{2} b\right)^{1 / 4}=4 a b c
|
| 408 |
+
$$
|
| 409 |
+
|
| 410 |
+
which proves the inequality.
|
| 411 |
+
|
INMO/md/en-2010.md
ADDED
|
@@ -0,0 +1,270 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# INMO-2010 Problems and Solutions
|
| 2 |
+
|
| 3 |
+
1. Let $A B C$ be a triangle with circum-circle $\Gamma$. Let $M$ be a point in the interior of triangle $A B C$ which is also on the bisector of $\angle A$. Let $A M, B M, C M$ meet $\Gamma$ in $A_{1}, B_{1}, C_{1}$ respectively. Suppose $P$ is the point of intersection of $A_{1} C_{1}$ with $A B$; and $Q$ is the point of intersection of $A_{1} B_{1}$ with $A C$. Prove that $P Q$ is parallel to $B C$.
|
| 4 |
+
|
| 5 |
+
Solution: Let $A=2 \alpha$. Then $\angle A_{1} A C=\angle B A A_{1}=\alpha$. Thus
|
| 6 |
+
|
| 7 |
+
$$
|
| 8 |
+
\angle A_{1} B_{1} C=\alpha=\angle B B_{1} A_{1}=\angle A_{1} C_{1} C=\angle B C_{1} A_{1}
|
| 9 |
+
$$
|
| 10 |
+
|
| 11 |
+
We also have $\angle B_{1} C Q=\angle A A_{1} B_{1}=\beta$, say. It follows that triangles $M A_{1} B_{1}$ and $Q C B_{1}$ are similar and hence
|
| 12 |
+
|
| 13 |
+
$$
|
| 14 |
+
\frac{Q C}{M A_{1}}=\frac{B_{1} C}{B_{1} A_{1}}
|
| 15 |
+
$$
|
| 16 |
+
|
| 17 |
+
|
| 18 |
+
|
| 19 |
+
Similarly, triangles $A C M$ and $C_{1} A_{1} M$ are similar and we get
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
\frac{A C}{A M}=\frac{C_{1} A_{1}}{C_{1} M}
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
Using the point $P$, we get similar ratios:
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
\frac{P B}{M A_{1}}=\frac{C_{1} B}{A_{1} C_{1}}, \quad \frac{A B}{A M}=\frac{A_{1} B_{1}}{M B_{1}}
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
Thus,
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
\frac{Q C}{P B}=\frac{A_{1} C_{1} \cdot B_{1} C}{C_{1} B \cdot B_{1} A_{1}}
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
and
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
\begin{aligned}
|
| 41 |
+
\frac{A C}{A B} & =\frac{M B_{1} \cdot C_{1} A_{1}}{A_{1} B_{1} \cdot C_{1} M} \\
|
| 42 |
+
& =\frac{M B_{1}}{C_{1} M} \frac{C_{1} A_{1}}{A_{1} B_{1}}=\frac{M B_{1}}{C_{1} M} \frac{C_{1} B \cdot Q C}{P B \cdot B_{1} C}
|
| 43 |
+
\end{aligned}
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
However, triangles $C_{1} B M$ and $B_{1} C M$ are similar, which gives
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
\frac{B_{1} C}{C_{1} B}=\frac{M B_{1}}{M C_{1}}
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
Putting this in the last expression, we get
|
| 53 |
+
|
| 54 |
+
$$
|
| 55 |
+
\frac{A C}{A B}=\frac{Q C}{P B}
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
We conclude that $P Q$ is parallel to $B C$.
|
| 59 |
+
|
| 60 |
+
2. Find all natural numbers $n>1$ such that $n^{2}$ does not divide $(n-2)$ !.
|
| 61 |
+
|
| 62 |
+
Solution: Suppose $n=p q r$, where $p<q$ are primes and $r>1$. Then $p \geq 2, q \geq 3$ and $r \geq 2$, not necessarily a prime. Thus we have
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
\begin{aligned}
|
| 66 |
+
& n-2 \geq n-p=p q r-p \geq 5 p>p \\
|
| 67 |
+
& n-2 \geq n-q=q(p r-1) \geq 3 q>q \\
|
| 68 |
+
& n-2 \geq n-p r=p r(q-1) \geq 2 p r>p r \\
|
| 69 |
+
& n-2 \geq n-q r=q r(p-1) \geq q r
|
| 70 |
+
\end{aligned}
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
Observe that $p, q, p r, q r$ are all distinct. Hence their product divides $(n-2)$ !. Thus $n^{2}=p^{2} q^{2} r^{2}$ divides $(n-2)$ ! in this case. We conclude that either $n=p q$ where $p, q$ are distinct primes or $n=p^{k}$ for some prime $p$.
|
| 74 |
+
|
| 75 |
+
Case 1. Suppose $n=p q$ for some primes $p, q$, where $2<p<q$. Then $p \geq 3$ and $q \geq 5$. In this case
|
| 76 |
+
|
| 77 |
+
$$
|
| 78 |
+
\begin{aligned}
|
| 79 |
+
& n-2>n-p=p(q-1) \geq 4 p \\
|
| 80 |
+
& n-2>n-q=q(p-1) \geq 2 q
|
| 81 |
+
\end{aligned}
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
Thus $p, q, 2 p, 2 q$ are all distinct numbers in the set $\{1,2,3, \ldots, n-2\}$. We see that $n^{2}=p^{2} q^{2}$ divides $(n-2)!$. We conclude that $n=2 q$ for some prime $q \geq 3$. Note that $n-2=2 q-2<2 q$ in this case so that $n^{2}$ does not divide $(n-2)!$.
|
| 85 |
+
|
| 86 |
+
Case 2. Suppose $n=p^{k}$ for some prime $p$. We observe that $p, 2 p, 3 p, \ldots\left(p^{k-1}-1\right) p$ all lie in the set $\{1,2,3, \ldots, n-2\}$. If $p^{k-1}-1 \geq 2 k$, then there are at least $2 k$ multiples of $p$ in the set $\{1,2,3, \ldots, n-2\}$. Hence $n^{2}=p^{2 k}$ divides $(n-2)!$. Thus $p^{k-1}-1<2 k$.
|
| 87 |
+
|
| 88 |
+
If $k \geq 5$, then $p^{k-1}-1 \geq 2^{k-1}-1 \geq 2 k$, which may be proved by an easy induction. Hence $k \leq 4$. If $k=1$, we get $n=p$, a prime. If $k=2$, then $p-1<4$ so that $p=2$ or 3 ; we get $n=2^{2}=4$ or $n=3^{2}=9$. For $k=3$, we have $p^{2}-1<6$ giving $p=2$; $n=2^{3}=8$ in this case. Finally, $k=4$ gives $p^{3}-1<8$. Again $p=2$ and $n=2^{4}=16$. However $n^{2}=2^{8}$ divides 14! and hence is not a solution.
|
| 89 |
+
|
| 90 |
+
Thus $n=p, 2 p$ for some prime $p$ or $n=8,9$. It is easy to verify that these satisfy the conditions of the problem.
|
| 91 |
+
|
| 92 |
+
3. Find all non-zero real numbers $x, y, z$ which satisfy the system of equations:
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
\begin{aligned}
|
| 96 |
+
\left(x^{2}+x y+y^{2}\right)\left(y^{2}+y z+z^{2}\right)\left(z^{2}+z x+x^{2}\right) & =x y z \\
|
| 97 |
+
\left(x^{4}+x^{2} y^{2}+y^{4}\right)\left(y^{4}+y^{2} z^{2}+z^{4}\right)\left(z^{4}+z^{2} x^{2}+x^{4}\right) & =x^{3} y^{3} z^{3}
|
| 98 |
+
\end{aligned}
|
| 99 |
+
$$
|
| 100 |
+
|
| 101 |
+
Solution: Since $x y z \neq 0$, We can divide the second relation by the first. Observe that
|
| 102 |
+
|
| 103 |
+
$$
|
| 104 |
+
x^{4}+x^{2} y^{2}+y^{4}=\left(x^{2}+x y+y^{2}\right)\left(x^{2}-x y+y^{2}\right)
|
| 105 |
+
$$
|
| 106 |
+
|
| 107 |
+
holds for any $x, y$. Thus we get
|
| 108 |
+
|
| 109 |
+
$$
|
| 110 |
+
\left(x^{2}-x y+y^{2}\right)\left(y^{2}-y z+z^{2}\right)\left(z^{2}-z x+x^{2}\right)=x^{2} y^{2} z^{2}
|
| 111 |
+
$$
|
| 112 |
+
|
| 113 |
+
However, for any real numbers $x, y$, we have
|
| 114 |
+
|
| 115 |
+
$$
|
| 116 |
+
x^{2}-x y+y^{2} \geq|x y|
|
| 117 |
+
$$
|
| 118 |
+
|
| 119 |
+
Since $x^{2} y^{2} z^{2}=|x y||y z||z x|$, we get
|
| 120 |
+
|
| 121 |
+
$$
|
| 122 |
+
|x y||y z||z x|=\left(x^{2}-x y+y^{2}\right)\left(y^{2}-y z+z^{2}\right)\left(z^{2}-z x+x^{2}\right) \geq|x y||y z||z x|
|
| 123 |
+
$$
|
| 124 |
+
|
| 125 |
+
This is possible only if
|
| 126 |
+
|
| 127 |
+
$$
|
| 128 |
+
x^{2}-x y+y^{2}=|x y|, \quad y^{2}-y z+z^{2}=|y z|, \quad z^{2}-z x+x^{2}=|z x|
|
| 129 |
+
$$
|
| 130 |
+
|
| 131 |
+
hold simultaneously. However $|x y|= \pm x y$. If $x^{2}-x y+y^{2}=-x y$, then $x^{2}+y^{2}=0$ giving $x=y=0$. Since we are looking for nonzero $x, y, z$, we conclude that $x^{2}-x y+y^{2}=x y$ which is same as $x=y$. Using the other two relations, we also get $y=z$ and $z=x$. The first equation now gives $27 x^{6}=x^{3}$. This gives $x^{3}=1 / 27$ (since $x \neq 0$ ), or $x=1 / 3$. We thus have $x=y=z=1 / 3$. These also satisfy the second relation, as may be verified.
|
| 132 |
+
|
| 133 |
+
4. How many 6-tuples $\left(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}\right)$ are there such that each of $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}$ is from the set $\{1,2,3,4\}$ and the six expressions
|
| 134 |
+
|
| 135 |
+
$$
|
| 136 |
+
a_{j}^{2}-a_{j} a_{j+1}+a_{j+1}^{2}
|
| 137 |
+
$$
|
| 138 |
+
|
| 139 |
+
for $j=1,2,3,4,5,6$ (where $a_{7}$ is to be taken as $a_{1}$ ) are all equal to one another?
|
| 140 |
+
|
| 141 |
+
Solution: Without loss of generality, we may assume that $a_{1}$ is the largest among $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}$. Consider the relation
|
| 142 |
+
|
| 143 |
+
$$
|
| 144 |
+
a_{1}^{2}-a_{1} a_{2}+a_{2}^{2}=a_{2}^{2}-a_{2} a_{3}+a_{3}^{2}
|
| 145 |
+
$$
|
| 146 |
+
|
| 147 |
+
This leads to
|
| 148 |
+
|
| 149 |
+
$$
|
| 150 |
+
\left(a_{1}-a_{3}\right)\left(a_{1}+a_{3}-a_{2}\right)=0
|
| 151 |
+
$$
|
| 152 |
+
|
| 153 |
+
Observe that $a_{1} \geq a_{2}$ and $a_{3}>0$ together imply that the second factor on the left side is positive. Thus $a_{1}=a_{3}=\max \left\{a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}\right\}$. Using this and the relation
|
| 154 |
+
|
| 155 |
+
$$
|
| 156 |
+
a_{3}^{2}-a_{3} a_{4}+a_{4}^{2}=a_{4}^{2}-a_{4} a_{5}+a_{5}^{2}
|
| 157 |
+
$$
|
| 158 |
+
|
| 159 |
+
we conclude that $a_{3}=a_{5}$ as above. Thus we have
|
| 160 |
+
|
| 161 |
+
$$
|
| 162 |
+
a_{1}=a_{3}=a_{5}=\max \left\{a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}\right\}
|
| 163 |
+
$$
|
| 164 |
+
|
| 165 |
+
Let us consider the other relations. Using
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
a_{2}^{2}-a_{2} a_{3}+a_{3}^{2}=a_{3}^{2}-a_{3} a_{4}+a_{4}^{2}
|
| 169 |
+
$$
|
| 170 |
+
|
| 171 |
+
we get $a_{2}=a_{4}$ or $a_{2}+a_{4}=a_{3}=a_{1}$. Similarly, two more relations give either $a_{4}=a_{6}$ or $a_{4}+a_{6}=a_{5}=a_{1}$; and either $a_{6}=a_{2}$ or $a_{6}+a_{2}=a_{1}$. Let us give values to $a_{1}$ and count the number of six-tuples in each case.
|
| 172 |
+
|
| 173 |
+
(A) Suppose $a_{1}=1$. In this case all $a_{j}$ 's are equal and we get only one six-tuple $(1,1,1,1,1,1)$.
|
| 174 |
+
|
| 175 |
+
(B) If $a_{1}=2$, we have $a_{3}=a_{5}=2$. We observe that $a_{2}=a_{4}=a_{6}=1$ or $a_{2}=a_{4}=$ $a_{6}=2$. We get two more six-tuples: $(2,1,2,1,2,1),(2,2,2,2,2,2)$.
|
| 176 |
+
|
| 177 |
+
(C) Taking $a_{1}=3$, we see that $a_{3}=a_{5}=3$. In this case we get nine possibilities for $\left(a_{2}, a_{4}, a_{6}\right)$
|
| 178 |
+
|
| 179 |
+
$$
|
| 180 |
+
(1,1,1),(2,2,2),(3,3,3),(1,1,2),(1,2,1),(2,1,1),(1,2,2),(2,1,2),(2,2,1)
|
| 181 |
+
$$
|
| 182 |
+
|
| 183 |
+
(D) In the case $a_{1}=4$, we have $a_{3}=a_{5}=4$ and
|
| 184 |
+
|
| 185 |
+
$$
|
| 186 |
+
\begin{aligned}
|
| 187 |
+
\left(a_{2}, a_{4}, a_{6}\right)=(2,2,2),(4,4,4) & ,(1,1,1),(3,3,3) \\
|
| 188 |
+
& (1,1,3),(1,3,1),(3,1,1),(1,3,3),(3,1,3),(3,3,1)
|
| 189 |
+
\end{aligned}
|
| 190 |
+
$$
|
| 191 |
+
|
| 192 |
+
Thus we get $1+2+9+10=22$ solutions. Since $\left(a_{1}, a_{3}, a_{5}\right)$ and $\left(a_{2}, a_{4}, a_{6}\right)$ may be interchanged, we get 22 more six-tuples. However there are 4 common among these, namely, $(1,1,1,1,1,1),(2,2,2,2,2,2),(3,3,3,3,3,3)$ and $(4,4,4,4,4,4)$. Hence the total number of six-tuples is $22+22-4=40$.
|
| 193 |
+
|
| 194 |
+
5. Let $A B C$ be an acute-angled triangle with altitude $A K$. Let $H$ be its ortho-centre and $O$ be its circum-centre. Suppose $K O H$ is an acute-angled triangle and $P$ its circum-centre. Let $Q$ be the reflection of $P$ in the line $H O$. Show that $Q$ lies on the line joining the mid-points of $A B$ and $A C$.
|
| 195 |
+
|
| 196 |
+
Solution: Let $D$ be the mid-point of $B C ; M$ that of $H K$; and $T$ that of $O H$. Then $P M$ is perpendicular to $H K$ and $P T$ is perpendicular to $O H$. Since $Q$ is the reflection of $P$ in $H O$, we observe that $P, T, Q$ are collinear, and $P T=T Q$. Let $Q L, T N$ and $O S$ be the perpendiculars drawn respectively from $Q, T$ and $O$ on to the altitude $A K$.(See the figure.)
|
| 197 |
+
|
| 198 |
+
|
| 199 |
+
|
| 200 |
+
We have $L N=N M$, since $T$ is the mid-point of $Q P ; H N=N S$, since $T$ is the mid-point of $O H$; and $H M=M K$, as $P$ is the circum-centre of $K H O$. We obtain
|
| 201 |
+
|
| 202 |
+
$$
|
| 203 |
+
L H+H N=L N=N M=N S+S M
|
| 204 |
+
$$
|
| 205 |
+
|
| 206 |
+
which gives $L H=S M$. We know that $A H=2 O D$. Thus
|
| 207 |
+
|
| 208 |
+
$$
|
| 209 |
+
\begin{aligned}
|
| 210 |
+
A L=A H & -L H=2 O D-L H=2 S K-S M=S K+(S K-S M)=S K+M K \\
|
| 211 |
+
& =S K+H M=S K+H S+S M=S K+H S+L H=S K+L S=L K
|
| 212 |
+
\end{aligned}
|
| 213 |
+
$$
|
| 214 |
+
|
| 215 |
+
This shows that $L$ is the mid-point of $A K$ and hence lies on the line joining the midpoints of $A B$ and $A C$. We observe that the line joining the mid-points of $A B$ and $A C$ is also perpendicular to $A K$. Since $Q L$ is perpendicular to $A K$, we conclude that $Q$ also lies on the line joining the mid-points of $A B$ and $A C$.
|
| 216 |
+
|
| 217 |
+
Remark: It may happen that $H$ is above $L$ as in the adjoining figure, but the result remains true here as well. We have $H N=N S, L N=N M$, and $H M=$ $M K$ as earlier. Thus $H N=H L+L N$ and $N S=$ $S M+N M$ give $H L=S M$. Now $A L=A H+H L=$ $2 O D+S M=2 S K+S M=S K+(S K+S M)=$ $S K+M K=S K+H M=S K+H L+L M=S K+$ $S M+L M=L K$. The conclusion that $Q$ lies on the line joining the mid-points of $A B$ and $A C$ follows as earlier.
|
| 218 |
+
|
| 219 |
+
|
| 220 |
+
|
| 221 |
+
6. Define a sequence $\left\langle a_{n}\right\rangle_{n \geq 0}$ by $a_{0}=0, a_{1}=1$ and
|
| 222 |
+
|
| 223 |
+
$$
|
| 224 |
+
a_{n}=2 a_{n-1}+a_{n-2}
|
| 225 |
+
$$
|
| 226 |
+
|
| 227 |
+
for $n \geq 2$.
|
| 228 |
+
|
| 229 |
+
(a) For every $m>0$ and $0 \leq j \leq m$, prove that $2 a_{m}$ divides $a_{m+j}+(-1)^{j} a_{m-j}$.
|
| 230 |
+
|
| 231 |
+
(b) Suppose $2^{k}$ divides $n$ for some natural numbers $n$ and $k$. Prove that $2^{k}$ divides $a_{n}$.
|
| 232 |
+
|
| 233 |
+
## Solution:
|
| 234 |
+
|
| 235 |
+
(a) Consider $f(j)=a_{m+j}+(-1)^{j} a_{m-j}, 0 \leq j \leq m$, where $m$ is a natural number. We observe that $f(0)=2 a_{m}$ is divisible by $2 a_{m}$. Similarly,
|
| 236 |
+
|
| 237 |
+
$$
|
| 238 |
+
f(1)=a_{m+1}-a_{m-1}=2 a_{m}
|
| 239 |
+
$$
|
| 240 |
+
|
| 241 |
+
is also divisible by $2 a_{m}$. Assume that $2 a_{m}$ divides $f(j)$ for all $0 \leq j<l$, where $l \leq m$. We prove that $2 a_{m}$ divides $f(l)$. Observe
|
| 242 |
+
|
| 243 |
+
$$
|
| 244 |
+
\begin{aligned}
|
| 245 |
+
& f(l-1)=a_{m+l-1}+(-1)^{l-1} a_{m-l+1} \\
|
| 246 |
+
& f(l-2)=a_{m+l-2}+(-1)^{l-2} a_{m-l+2}
|
| 247 |
+
\end{aligned}
|
| 248 |
+
$$
|
| 249 |
+
|
| 250 |
+
Thus we have
|
| 251 |
+
|
| 252 |
+
$$
|
| 253 |
+
\begin{aligned}
|
| 254 |
+
a_{m+l} & =2 a_{m+l-1}+a_{m+l-2} \\
|
| 255 |
+
& =2 f(l-1)-2(-1)^{l-1} a_{m-l+1}+f(l-2)-(-1)^{l-2} a_{m-l+2} \\
|
| 256 |
+
& =2 f(l-1)+f(l-2)+(-1)^{l-1}\left(a_{m-l+2}-2 a_{m-l+1}\right) \\
|
| 257 |
+
& =2 f(l-1)+f(l-2)+(-1)^{l-1} a_{m-l}
|
| 258 |
+
\end{aligned}
|
| 259 |
+
$$
|
| 260 |
+
|
| 261 |
+
This gives
|
| 262 |
+
|
| 263 |
+
$$
|
| 264 |
+
f(l)=2 f(l-1)+f(l-2)
|
| 265 |
+
$$
|
| 266 |
+
|
| 267 |
+
By induction hypothesis $2 a_{m}$ divides $f(l-1)$ and $f(l-2)$. Hence $2 a_{m}$ divides $f(l)$. We conclude that $2 a_{m}$ divides $f(j)$ for $0 \leq j \leq m$.
|
| 268 |
+
|
| 269 |
+
(b) We see that $f(m)=a_{2 m}$. Hence $2 a_{m}$ divides $a_{2 m}$ for all natural numbers $m$. Let $n=2^{k} l$ for some $l \geq 1$. Taking $m=2^{k-1} l$, we see that $2 a_{m}$ divides $a_{n}$. Using an easy induction, we conclude that $2^{k} a_{l}$ divides $a_{n}$. In particular $2^{k}$ divides $a_{n}$.
|
| 270 |
+
|
INMO/md/en-2011.md
ADDED
|
@@ -0,0 +1,306 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Problems and Solutions, INMO-2011
|
| 2 |
+
|
| 3 |
+
1. Let $D, E, F$ be points on the sides $B C, C A, A B$ respectively of a triangle $A B C$ such that $B D=C E=A F$ and $\angle B D F=\angle C E D=\angle A F E$. Prove that $A B C$ is equilateral.
|
| 4 |
+
|
| 5 |
+
## Solution 1:
|
| 6 |
+
|
| 7 |
+
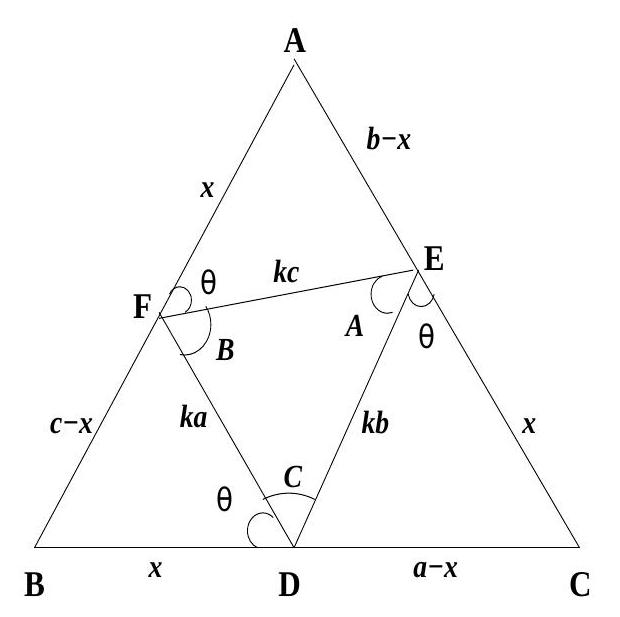
|
| 8 |
+
|
| 9 |
+
Let $B D=C E=A F=x ; \angle B D F=$ $\angle C E D=\angle A F E=\theta$. Note that $\angle A F D=$ $B+\theta$, and hence $\angle D F E=B$. Similarly, $\angle E D F=C$ and $\angle F E D=A$. Thus the triangle $E F D$ is similar to $A B C$. We may take $F D=k a, D E=k b$ and $E F=k c$, for some positive real constant $k$. Applying sine rule to triangle $B F D$, we obtain
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\frac{c-x}{\sin \theta}=\frac{k a}{\sin B}=\frac{2 R k a}{b}
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
where $R$ is the circum-radius of $A B C$. Thus we get $2 R k \sin \theta=b(c-x) / a$. Similarly, we obtain $2 R k \sin \theta=c(a-x) / b$ and $2 R k \sin \theta=$ $a(b-x) / c$. We therefore get
|
| 16 |
+
|
| 17 |
+
$$
|
| 18 |
+
\frac{b(c-x)}{a}=\frac{c(a-x)}{b}=\frac{a(b-x)}{c}
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
If some two sides are equal, say, $a=b$, then $a(c-x)=c(a-x)$ giving $a=c$; we get $a=b=c$ and $A B C$ is equilateral. Suppose no two sides of $A B C$ are equal. We may assume $a$ is the least. Since (1) is cyclic in $a, b, c$, we have to consider two cases: $a<b<c$ and $a<c<b$.
|
| 22 |
+
|
| 23 |
+
|
| 24 |
+
|
| 25 |
+
In this case $a<c$ and hence $b(c-x)<a(b-x)$, from (1). Since $b>a$ and $c-x>b-x$, we get $b(c-x)>a(b-x)$, which is a contradiction.
|
| 26 |
+
|
| 27 |
+
Case 2. $\underline{a<c<b}$.
|
| 28 |
+
|
| 29 |
+
We may write (1) in the form
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
\frac{(c-x)}{a / b}=\frac{(a-x)}{b / c}=\frac{(b-x)}{c / a}
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
Now $a<c$ gives $a-x<c-x$ so that $\frac{b}{c}<\frac{a}{b}$. This gives $b^{2}<a c$. But $b>a$ and $b>c$, so that $b^{2}>a c$, which again leads to a contradiction
|
| 36 |
+
|
| 37 |
+
Thus Case 1 and Case 2 cannot occur. We conclude that $a=b=c$.
|
| 38 |
+
|
| 39 |
+
Solution 2. We write (1) in the form (2), and start from there. The case of two equal sides is dealt as in Solution 1. We assume no two sides are equal. Using ratio properties in (2), we obtain
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
\frac{a-b}{\left(a b-c^{2}\right) / c a}=\frac{b-c}{\left(b c-a^{2}\right) / a b}
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
This may be written as $c(a-b)\left(b c-a^{2}\right)=b(b-c)\left(a b-c^{2}\right)$. Further simplification gives $a b^{3}+b c^{3}+c a^{3}=a b c(a+b+c)$. This may be further written in the form
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
a b^{2}(b-c)+b c^{2}(c-a)+c a^{2}(a-b)=0
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
If $a<b<c$, we write (3) in the form
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
0=a b^{2}(b-c)+b c^{2}(c-b+b-a)+c a^{2}(a-b)=b(c-b)\left(c^{2}-a b\right)+c(b-a)\left(b c-a^{2}\right)
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
Since $c>b, c^{2}>a b, b>a$ and $b c>a^{2}$, this is impossible. If $a<c<b$, we write (3), as in previous case, in the form
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
0=a(b-c)\left(b^{2}-c a\right)+c(c-a)\left(b c-a^{2}\right)
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
which again is impossible.
|
| 64 |
+
|
| 65 |
+
One can also use inequalities: we can show that $a b^{3}+b c^{3}+c a^{3} \geq a b c(a+b+c)$, and equality holds if and only if $a=b=c$. Here are some ways of deriving it:
|
| 66 |
+
(i) We can write the inequality in the form
|
| 67 |
+
|
| 68 |
+
$$
|
| 69 |
+
\frac{b^{2}}{c}+\frac{c^{2}}{a}+\frac{a^{2}}{b} \geq a+b+c
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
Adding $a+b+c$ both sides, this takes the form
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
\frac{b^{2}}{c}+c+\frac{c^{2}}{a}+a+\frac{a^{2}}{b}+b \geq 2(a+b+c)
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
But AM-GM inequality gives
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
\frac{b^{2}}{c}+c \geq 2 b, \quad \frac{c^{2}}{a}+a \geq 2 a, \quad \frac{a^{2}}{b}+b \geq 2 a
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
Hence the inequality follows and equality holds if and only if $a=b=c$.
|
| 85 |
+
|
| 86 |
+
(ii) Again we write the inequality in the form
|
| 87 |
+
|
| 88 |
+
$$
|
| 89 |
+
\frac{b^{2}}{c}+\frac{c^{2}}{a}+\frac{a^{2}}{b} \geq a+b+c
|
| 90 |
+
$$
|
| 91 |
+
|
| 92 |
+
We use $b / c$ with weight $b, c / a$ with weight $c$ and $a / b$ with weight $a$, and apply weighted AM-HM inequality:
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
b \cdot \frac{b}{c}+c \cdot \frac{c}{a}+a \cdot \frac{a}{b} \geq \frac{(a+b+c)^{2}}{b \cdot \frac{c}{b}+c \cdot \frac{a}{c}+a \cdot \frac{b}{a}}
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
which reduces to $a+b+c$. Again equality holds if and only if $a=b=c$.
|
| 99 |
+
|
| 100 |
+
Solution 3. Here is a pure geometric solution given by a student. Consider the triangle $B D F, C E D$ and $A F E$ with $B D, C E$ and $A F$ as bases. The sides $D F, E D$ and $F E$ make equal angles $\theta$ with the bases of respective triangles. If $B \geq C \geq A$, then it is easy to see that $F D \geq D E \geq E F$. Now using the triangle $F D E$, we see that $B \geq C \geq A$ gives $D E \geq E F \geq F D$. Combining, you get $F D=D E=E F$ and hence $A=B=\bar{C}=60^{\circ}$.
|
| 101 |
+
|
| 102 |
+
2. Call a natural number $n$ faithful, if there exist natural numbers $a<b<c$ such that $a$ divides $b, b$ divides $c$ and $n=a+b+c$.
|
| 103 |
+
|
| 104 |
+
(i) Show that all but a finite number of natural numbers are faithful.
|
| 105 |
+
|
| 106 |
+
(ii) Find the sum of all natural numbers which are not faithful.
|
| 107 |
+
|
| 108 |
+
Solution 1: Suppose $n \in \mathbb{N}$ is faithful. Let $k \in \mathbb{N}$ and consider $k n$. Since $n=a+b+c$, with $a>b>c, c \mid b$ and $b \mid a$, we see that $k n=k a+k b+k c$ which shows that $k n$ is faithful.
|
| 109 |
+
|
| 110 |
+
Let $p>5$ be a prime. Then $p$ is odd and $p=(p-3)+2+1$ shows that $p$ is faithful. If $n \in \mathbb{N}$ contains a prime factor $p>5$, then the above observation shows that $n$ is faithful. This shows that a number which is not faithful must be of the form $2^{\alpha} 3^{\beta} 5^{\gamma}$. We also observe that $2^{4}=16=12+3+1,3^{2}=9=6+2+1$ and $5^{2}=25=22+2+1$, so that $2^{4}, 3^{2}$ and $5^{2}$ are faithful. Hence $n \in \mathbb{N}$ is also faithful if it contains a factor of the form $2^{\alpha}$ where $\alpha \geq 4$; a factor of the form $3^{\beta}$ where $\beta \geq 2$; or a factor of the form $5^{\gamma}$ where $\gamma \geq 2$. Thus the numbers which are not faithful are of the form $2^{\alpha} 3^{\beta} 5^{\gamma}$, where $\alpha \leq 3, \beta \leq 1$ and $\gamma \leq 1$. We may enumerate all such numbers:
|
| 111 |
+
|
| 112 |
+
$$
|
| 113 |
+
1,2,3,4,5,6,8,10,12,15,20,24,30,40,60,120
|
| 114 |
+
$$
|
| 115 |
+
|
| 116 |
+
Among these $120=112+7+1,60=48+8+4,40=36+3+1,30=18+9+3,20=12+6+2$, $15=12+2+1$, and $10=6+3+1$. It is easy to check that the other numbers cannot be written in the required form. Hence the only numbers which are not faithful are
|
| 117 |
+
|
| 118 |
+
$$
|
| 119 |
+
1,2,3,4,5,6,8,12,24
|
| 120 |
+
$$
|
| 121 |
+
|
| 122 |
+
Their sum is 65 .
|
| 123 |
+
|
| 124 |
+
Solution 2: If $n=a+b+c$ with $a<b<c$ is faithful, we see that $a \geq 1, b \geq 2$ and $c \geq 4$. Hence $n \geq 7$. Thus $1,2,3,4,5,6$ are not faithful. As observed earlier, $k n$ is faithful whenever
|
| 125 |
+
$n$ is. We also notice that for odd $n \geq 7$, we can write $n=1+2+(n-3)$ so that all odd $n \geq 7$ are faithful. Consider $2 n, 4 n, 8 n$, where $n \geq 7$ is odd. By observation, they are all faithful. Let us list a few of them:
|
| 126 |
+
|
| 127 |
+
$$
|
| 128 |
+
\begin{aligned}
|
| 129 |
+
2 n & : \quad 14,18,22,26,30,34,38,42,46,50,54,58,62, \ldots \\
|
| 130 |
+
4 n & : \quad 28,36,44,52,60,68, \ldots \\
|
| 131 |
+
8 n & : \quad 56,72, \ldots
|
| 132 |
+
\end{aligned}
|
| 133 |
+
$$
|
| 134 |
+
|
| 135 |
+
We observe that $16=12+3+1$ and hence it is faithful. Thus all multiples of 16 are also faithful. Thus we see that $16,32,48,64, \ldots$ are faithful. Any even number which is not a multiple of 16 must be either an odd multiple of 2 , or that of 4 , or that of 8 . Hence, the only numbers not covered by this process are $8,10,12,20,24,40$. Of these, we see that
|
| 136 |
+
|
| 137 |
+
$$
|
| 138 |
+
10=1+3+6, \quad 20=2 \times 10, \quad 40=4 \times 10
|
| 139 |
+
$$
|
| 140 |
+
|
| 141 |
+
so that $10,20,40$ are faithful. Thus the only numbers which are not faithful are
|
| 142 |
+
|
| 143 |
+
$$
|
| 144 |
+
1,2,3,4,5,6,8,12,24
|
| 145 |
+
$$
|
| 146 |
+
|
| 147 |
+
Their sum is 65 .
|
| 148 |
+
|
| 149 |
+
3. Consider two polynomials $P(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$ and $Q(x)=b_{n} x^{n}+$ $b_{n-1} x^{n-1}+\cdots+b_{1} x+b_{0}$ with integer coefficients such that $a_{n}-b_{n}$ is a prime, $a_{n-1}=b_{n-1}$ and $a_{n} b_{0}-a_{0} b_{n} \neq 0$. Suppose there exists a rational number $r$ such that $P(r)=Q(r)=0$. Prove that $r$ is an integer.
|
| 150 |
+
|
| 151 |
+
Solution: Let $r=u / v$ where $\operatorname{gcd}(u, v)=1$. Then we get
|
| 152 |
+
|
| 153 |
+
$$
|
| 154 |
+
\begin{array}{r}
|
| 155 |
+
a_{n} u^{n}+a_{n-1} u^{n-1} v+\cdots+a_{1} u v^{n-1}+a_{0} v^{n}=0 \\
|
| 156 |
+
b_{n} u^{n}+b_{n-1} u^{n-1} v+\cdots+b_{1} u v^{n-1}+b_{0} v^{n}=0
|
| 157 |
+
\end{array}
|
| 158 |
+
$$
|
| 159 |
+
|
| 160 |
+
Subtraction gives
|
| 161 |
+
|
| 162 |
+
$$
|
| 163 |
+
\left(a_{n}-b_{n}\right) u^{n}+\left(a_{n-2}-b_{n-2}\right) u^{n-2} v^{2}+\cdots+\left(a_{1}-b_{1}\right) u v^{n-1}+\left(a_{0}-b_{0}\right) v^{n}=0
|
| 164 |
+
$$
|
| 165 |
+
|
| 166 |
+
since $a_{n-1}=b_{n-1}$. This shows that $v$ divides $\left(a_{n}-b_{n}\right) u^{n}$ and hence it divides $a_{n}-b_{n}$. Since $a_{n}-b_{n}$ is a prime, either $v=1$ or $v=a_{n}-b_{n}$. Suppose the latter holds. The relation takes the form
|
| 167 |
+
|
| 168 |
+
$$
|
| 169 |
+
u^{n}+\left(a_{n-2}-b_{n-2}\right) u^{n-2} v+\cdots+\left(a_{1}-b_{1}\right) u v^{n-2}+\left(a_{0}-b_{0}\right) v^{n-1}=0
|
| 170 |
+
$$
|
| 171 |
+
|
| 172 |
+
(Here we have divided through-out by $v$.) If $n>1$, this forces $v \mid u$, which is impossible since $\operatorname{gcd}(v, u)=1\left(v>1\right.$ since it is equal to the prime $\left.a_{n}-b_{n}\right)$. If $n=1$, then we get two equations:
|
| 173 |
+
|
| 174 |
+
$$
|
| 175 |
+
\begin{aligned}
|
| 176 |
+
a_{1} u+a_{0} v & =0 \\
|
| 177 |
+
b_{1} u+b_{0} v & =0
|
| 178 |
+
\end{aligned}
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
This forces $a_{1} b_{0}-a_{0} b_{1}=0$ contradicting $a_{n} b_{0}-a_{0} b_{n} \neq 0$. (Note: The condition $a_{n} b_{0}-a_{0} b_{n} \neq 0$ is extraneous. The condition $a_{n-1}=b_{n-1}$ forces that for $n=1$, we have $a_{0}=b_{0}$. Thus we obtain, after subtraction
|
| 182 |
+
|
| 183 |
+
$$
|
| 184 |
+
\left(a_{1}-b_{1}\right) u=0
|
| 185 |
+
$$
|
| 186 |
+
|
| 187 |
+
This implies that $u=0$ and hence $r=0$ is an integer.)
|
| 188 |
+
|
| 189 |
+
4. Suppose five of the nine vertices of a regular nine-sided polygon are arbitrarily chosen. Show that one can select four among these five such that they are the vertices of a trapezium.
|
| 190 |
+
|
| 191 |
+
Solution 1: Suppose four distinct points $P, Q, R, S$ (in that order on the circle) among these five are such that $\widehat{P Q}=\widehat{R S}$. Then $P Q R S$ is an isosceles trapezium, with $P S \| Q R$. We use this in our argument.
|
| 192 |
+
|
| 193 |
+
- If four of the five points chosen are adjacent, then we are through as observed earlier. (In this case four points $A, B, C, D$ are such that $\widehat{A B}=\widehat{B C}=\widehat{C D}$.) See Fig 1 .
|
| 194 |
+
|
| 195 |
+
|
| 196 |
+
|
| 197 |
+
Fig 1.
|
| 198 |
+
|
| 199 |
+
|
| 200 |
+
|
| 201 |
+
Fig 2.
|
| 202 |
+
|
| 203 |
+
|
| 204 |
+
|
| 205 |
+
Fig 3.
|
| 206 |
+
|
| 207 |
+
- Suppose only three of the vertices are adjacent, say $A, B, C$ (see Fig 2.) Then the remaining two must be among $E, F, G, H$. If these two are adjacent vertices, we can pair them with $A, B$ or $B, C$ to get equal arcs. If they are not adjacent, then they must be either $E, G$ or $F, H$ or $E, H$. In the first two cases, we can pair them with $A, C$ to get equal arcs. In the last case, we observe that $\widehat{H A}=\widehat{C E}$ and $A H E C$ is an isosceles trapezium.
|
| 208 |
+
- Suppose only two among the five are adjacent, say $A, B$. Then the remaining three are among $D, E, F, G, H$. (See Fig 3.) If any two of these are adjacent, we can combine them with $A, B$ to get equal arcs. If no two among these three vertices are adjacent, then they must be $D, F, H$. In this case $\widehat{H A}=\widehat{B D}$ and $A H D B$ is an isosceles trapezium.
|
| 209 |
+
|
| 210 |
+
Finally, if we choose 5 among the 9 vertices of a regular nine-sided polygon, then some two must be adjacent. Thus any choice of 5 among 9 must fall in to one of the above three possibilities.
|
| 211 |
+
|
| 212 |
+
Solution 2: Here is another solution used by many students. Suppose you join the vertices of the nine-sided regular polygon. You get $\binom{9}{2}=36$ line segments. All these fall in to 9 sets of parallel lines. Now using any 5 points, you get $\binom{5}{2}=10$ line segments. By pigeon-hole principle, two of these must be parallel. But, these parallel lines determine a trapezium.
|
| 213 |
+
|
| 214 |
+
5. Let $A B C D$ be a quadrilateral inscribed in a circle $\Gamma$. Let $E, F, G, H$ be the midpoints of the arcs $A B, B C, C D, D A$ of the circle $\Gamma$. Suppose $A C \cdot B D=E G \cdot F H$. Prove that $A C, B D$, $E G, F H$ are concurrent.
|
| 215 |
+
|
| 216 |
+
## Solution:
|
| 217 |
+
|
| 218 |
+
|
| 219 |
+
|
| 220 |
+
Let $R$ be the radius of the circle $\Gamma$. Observe that $\angle E D F=\frac{1}{2} \angle D$. Hence $E F=2 R \sin \frac{D}{2}$. Similarly, $H G=2 R \sin \frac{B}{2}$. But $\angle B=180^{\circ}-\angle D$. Thus $H G=2 R \cos \frac{D}{2}$. We hence get
|
| 221 |
+
|
| 222 |
+
$E F \cdot G H=4 R^{2} \sin \frac{D}{2} \cos \frac{D}{2}=2 R^{2} \sin D=R \cdot A C$.
|
| 223 |
+
|
| 224 |
+
Similarly, we obtain $E H \cdot F G=R \cdot B D$.
|
| 225 |
+
|
| 226 |
+
Therefore
|
| 227 |
+
|
| 228 |
+
$$
|
| 229 |
+
R(A C+B D)=E F \cdot G H+E H \cdot F G=E G \cdot F H
|
| 230 |
+
$$
|
| 231 |
+
|
| 232 |
+
by Ptolemy's theorem. By the given hypothesis, this gives $R(A C+B D)=A C \cdot B D$. Thus
|
| 233 |
+
|
| 234 |
+
$$
|
| 235 |
+
A C \cdot B D=R(A C+B D) \geq 2 R \sqrt{A C \cdot B D}
|
| 236 |
+
$$
|
| 237 |
+
|
| 238 |
+
using AM-GM inequality. This implies that $A C \cdot B D \geq 4 R^{2}$. But $A C$ and $B D$ are the chords of $\Gamma$, so that $A C \leq 2 R$ and $B D \leq 2 R$. We obtain $A C \cdot B D \leq 4 R^{2}$. It follows that $A C \cdot B D=4 R^{2}$, implying that $A C=B D=2 R$. Thus $A C$ and $B D$ are two diameters of $\Gamma$. Using $E G \cdot F H=A C \cdot B D$, we conclude that $E G$ and $F H$ are also two diameters of $\Gamma$. Hence $A C, B D, E G$ and $F H$ all pass through the centre of $\Gamma$.
|
| 239 |
+
|
| 240 |
+
6. Find all functions $f: \mathbf{R} \rightarrow \mathbf{R}$ such that
|
| 241 |
+
|
| 242 |
+
$$
|
| 243 |
+
f(x+y) f(x-y)=(f(x)+f(y))^{2}-4 x^{2} f(y)
|
| 244 |
+
$$
|
| 245 |
+
|
| 246 |
+
for all $x, y \in \mathbf{R}$, where $\mathbf{R}$ denotes the set of all real numbers.
|
| 247 |
+
|
| 248 |
+
Solution 1.: Put $x=y=0$; we get $f(0)^{2}=4 f(0)^{2}$ and hence $f(0)=0$.
|
| 249 |
+
|
| 250 |
+
Put $x=y$ : we get $4 f(x)^{2}-4 x^{2} f(x)=0$ for all $x$. Hence for each $x$, either $f(x)=0$ or $f(x)=x^{2}$.
|
| 251 |
+
|
| 252 |
+
Suppose $f(x) \not \equiv 0$. Then we can find $x_{0} \neq 0$ such that $f\left(x_{0}\right) \neq 0$. Then $f\left(x_{0}\right)=x_{0}^{2} \neq 0$. Assume that there exists some $y_{0} \neq 0$ such that $f\left(y_{0}\right)=0$. Then
|
| 253 |
+
|
| 254 |
+
$$
|
| 255 |
+
f\left(x_{0}+y_{0}\right) f\left(x_{0}-y_{0}\right)=f\left(x_{0}\right)^{2}
|
| 256 |
+
$$
|
| 257 |
+
|
| 258 |
+
Now $f\left(x_{0}+y_{0}\right) f\left(x_{0}-y_{0}\right)=0$ or $f\left(x_{0}+y_{0}\right) f\left(x_{0}-y_{0}\right)=\left(x_{0}+y_{0}\right)^{2}\left(x_{0}-y_{0}\right)^{2}$. If $f\left(x_{0}+\right.$ $\left.y_{0}\right) f\left(x_{0}-y_{0}\right)=0$, then $f\left(x_{0}\right)=0$, a contradiction. Hence it must be the latter so that
|
| 259 |
+
|
| 260 |
+
$$
|
| 261 |
+
\left(x_{0}^{2}-y_{0}^{2}\right)^{2}=x_{0}^{4}
|
| 262 |
+
$$
|
| 263 |
+
|
| 264 |
+
This reduces to $y_{0}^{2}\left(y_{0}^{2}-2 x_{0}^{2}\right)=0$. Since $y_{0} \neq 0$, we get $y_{0}= \pm \sqrt{2} x_{0}$.
|
| 265 |
+
|
| 266 |
+
Suppose $y_{0}=\sqrt{2} x_{0}$. Put $x=\sqrt{2} x_{0}$ and $y=x_{0}$ in (1); we get
|
| 267 |
+
|
| 268 |
+
$$
|
| 269 |
+
f\left((\sqrt{2}+1) x_{0}\right) f\left((\sqrt{2}-1) x_{0}\right)=\left(f\left(\sqrt{2} x_{0}\right)+f\left(x_{0}\right)\right)^{2}-4\left(2 x_{0}^{2}\right) f\left(x_{0}\right)
|
| 270 |
+
$$
|
| 271 |
+
|
| 272 |
+
But $f\left(\sqrt{2} x_{0}\right)=f\left(y_{0}\right)=0$. Thus we get
|
| 273 |
+
|
| 274 |
+
$$
|
| 275 |
+
\begin{aligned}
|
| 276 |
+
f\left((\sqrt{2}+1) x_{0}\right) f\left((\sqrt{2}-1) x_{0}\right) & =f\left(x_{0}\right)^{2}-8 x_{0}^{2} f\left(x_{0}\right) \\
|
| 277 |
+
& =x_{0}^{4}-8 x_{0}^{4}=-7 x_{0}^{4}
|
| 278 |
+
\end{aligned}
|
| 279 |
+
$$
|
| 280 |
+
|
| 281 |
+
Now if LHS is equal to 0 , we get $x_{0}=0$, a contradiction. Otherwise LHS is equal to $(\sqrt{2}+$ $1)^{2}(\sqrt{2}-1)^{2} x_{0}^{4}$ which reduces to $x_{0}^{4}$. We obtain $x_{0}^{4}=-7 x_{0}^{4}$ and this forces again $x_{0}=0$. Hence there is no $y \neq 0$ such that $f(y)=0$. We conclude that $f(x)=x^{2}$ for all $x$.
|
| 282 |
+
|
| 283 |
+
Thus there are two solutions: $f(x)=0$ for all $x$ or $f(x)=x^{2}$, for all $x$. It is easy to verify that both these satisfy the functional equation.
|
| 284 |
+
|
| 285 |
+
Solution 2: As earlier, we get $f(0)=0$. Putting $x=0$, we will also get
|
| 286 |
+
|
| 287 |
+
$$
|
| 288 |
+
f(y)(f(y)-f(-y))=0
|
| 289 |
+
$$
|
| 290 |
+
|
| 291 |
+
As earlier, we may conclude that either $f(y)=0$ or $f(y)=f(-y)$ for each $y \in \mathbb{R}$. Replacing $y$ by $-y$, we may also conclude that $f(-y)(f(-y)-f(y))=0$. If $f(y)=0$ and $f(-y) \neq 0$ for some $y$, then we must have $f(-y)=f(y)=0$, a contradiction. Hence either $f(y)=f(-y)=0$ or $f(y)=f(-y)$ for each $y$. This forces $f$ is an even function.
|
| 292 |
+
|
| 293 |
+
Taking $y=1$ in (1), we get
|
| 294 |
+
|
| 295 |
+
$$
|
| 296 |
+
f(x+1) f(x-1)=(f(x)+f(1))^{2}-4 x^{2} f(1)
|
| 297 |
+
$$
|
| 298 |
+
|
| 299 |
+
Replacing $y$ by $x$ and $x$ by 1 , you also get
|
| 300 |
+
|
| 301 |
+
$$
|
| 302 |
+
f(1+x) f(1-x)=(f(1)+f(x))^{2}-4 f(x)
|
| 303 |
+
$$
|
| 304 |
+
|
| 305 |
+
Comparing these two using the even nature of $f$, we get $f(x)=c x^{2}$, where $c=f(1)$. Putting $x=y=1$ in (1), you get $4 c^{2}-4 c=0$. Hence $c=0$ or 1 . We get $f(x)=0$ for all $x$ or $f(x)=x^{2}$ for all $x$.
|
| 306 |
+
|
INMO/md/en-2012.md
ADDED
|
@@ -0,0 +1,307 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Problems and Solutions: INMO-2012
|
| 2 |
+
|
| 3 |
+
1. Let $A B C D$ be a quadrilateral inscribed in a circle. Suppose $A B=$ $\sqrt{2+\sqrt{2}}$ and $A B$ subtends $135^{\circ}$ at the centre of the circle. Find the maximum possible area of $A B C D$.
|
| 4 |
+

|
| 5 |
+
|
| 6 |
+
Solution: Let $O$ be the centre of the circle in which $A B C D$ is inscribed and let $R$ be its radius. Using cosine rule in triangle $A O B$, we have
|
| 7 |
+
|
| 8 |
+
$$
|
| 9 |
+
2+\sqrt{2}=2 R^{2}\left(1-\cos 135^{\circ}\right)=R^{2}(2+\sqrt{2})
|
| 10 |
+
$$
|
| 11 |
+
|
| 12 |
+
Hence $R=1$.
|
| 13 |
+
|
| 14 |
+
Consider quadrilateral $A B C D$ as in the second figure above. Join $A C$. For $[A D C]$ to be maximum, it is clear that $D$ should be the mid-point of the arc $A C$ so that its distance from the segment $A C$ is maximum. Hence $A D=D C$ for $[A B C D]$ to be maximum. Similarly, we conclude that $B C=C D$. Thus $B C=C D=D A$ which fixes the quadrilateral $A B C D$. Therefore each of the sides $B C, C D, D A$ subtends equal angles at the centre $O$.
|
| 15 |
+
|
| 16 |
+
Let $\angle B O C=\alpha, \angle C O D=\beta$ and $\angle D O A=\gamma$. Observe that
|
| 17 |
+
|
| 18 |
+
$$
|
| 19 |
+
[A B C D]=[A O B]+[B O C]+[C O D]+[D O A]=\frac{1}{2} \sin 135^{\circ}+\frac{1}{2}(\sin \alpha+\sin \beta+\sin \gamma)
|
| 20 |
+
$$
|
| 21 |
+
|
| 22 |
+
Now $[A B C D]$ has maximum area if and only if $\alpha=\beta=\gamma=\left(360^{\circ}-\right.$ $\left.135^{\circ}\right) / 3=75^{\circ}$. Thus
|
| 23 |
+
|
| 24 |
+
$$
|
| 25 |
+
[A B C D]=\frac{1}{2} \sin 135^{\circ}+\frac{3}{2} \sin 75^{\circ}=\frac{1}{2}\left(\frac{1}{\sqrt{2}}+3 \frac{\sqrt{3}+1}{2 \sqrt{2}}\right)=\frac{5+3 \sqrt{3}}{4 \sqrt{2}}
|
| 26 |
+
$$
|
| 27 |
+
|
| 28 |
+
Alternatively, we can use Jensen's inequality. Observe that $\alpha, \beta, \gamma$ are all less than $180^{\circ}$. Since $\sin x$ is concave on $(0, \pi)$, Jensen's inequality gives
|
| 29 |
+
|
| 30 |
+
$$
|
| 31 |
+
\frac{\sin \alpha+\sin \beta+\sin \gamma}{3} \leq \sin \left(\frac{\alpha+\beta+\gamma}{3}\right)=\sin 75^{\circ}
|
| 32 |
+
$$
|
| 33 |
+
|
| 34 |
+
Hence
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
[A B C D] \leq \frac{1}{2 \sqrt{2}}+\frac{3}{2} \sin 75^{\circ}=\frac{5+3 \sqrt{3}}{4 \sqrt{2}}
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
with equality if and only if $\alpha=\beta=\gamma=75^{\circ}$.
|
| 41 |
+
|
| 42 |
+
2. Let $p_{1}<p_{2}<p_{3}<p_{4}$ and $q_{1}<q_{2}<q_{3}<q_{4}$ be two sets of prime numbers such that $p_{4}-p_{1}=8$ and $q_{4}-q_{1}=8$. Suppose $p_{1}>5$ and $q_{1}>5$. Prove that 30 divides $p_{1}-q_{1}$.
|
| 43 |
+
|
| 44 |
+
Solution: Since $p_{4}-p_{1}=8$, and no prime is even, we observe that $\left\{p_{1}, p_{2}, p_{3}, p_{4}\right\}$ is a subset of $\left\{p_{1}, p_{1}+2, p_{1}+4, p_{1}+6, p_{1}+8\right\}$. Moreover $p_{1}$ is larger than 3 . If $p_{1} \equiv 1(\bmod 3)$, then $p_{1}+2$ and $p_{1}+8$ are divisible by 3 . Hence we do not get 4 primes in the set $\left\{p_{1}, p_{1}+2, p_{1}+4, p_{1}+6, p_{1}+8\right\}$. Thus $p_{1} \equiv 2(\bmod 3)$ and $p_{1}+4$ is not a prime. We get $p_{2}=p_{1}+2, p_{3}=$ $p_{1}+6, p_{4}=p_{1}+8$.
|
| 45 |
+
|
| 46 |
+
Consider the remainders of $p_{1}, p_{1}+2, p_{1}+6, p_{1}+8$ when divided by 5 . If $p_{1} \equiv 2(\bmod 5)$, then $p_{1}+8$ is divisible by 5 and hence is not a prime. If $p_{1} \equiv 3(\bmod 5)$, then $p_{1}+2$ is divisible by 5. If $p_{1} \equiv 4(\bmod 5)$, then $p_{1}+6$ is divisible by 5 . Hence the only possibility is $p_{1} \equiv 1(\bmod 5)$.
|
| 47 |
+
|
| 48 |
+
Thus we see that $p_{1} \equiv 1(\bmod 2), p_{1} \equiv 2(\bmod 3)$ and $p_{1} \equiv 1(\bmod 5)$. We conclude that $p_{1} \equiv 11(\bmod 30)$.
|
| 49 |
+
|
| 50 |
+
Similarly $q_{1} \equiv 11(\bmod 30)$. It follows that 30 divides $p_{1}-q_{1}$.
|
| 51 |
+
|
| 52 |
+
3. Define a sequence $\left\langle f_{0}(x), f_{1}(x), f_{2}(x), \ldots\right\rangle$ of functions by
|
| 53 |
+
|
| 54 |
+
$$
|
| 55 |
+
f_{0}(x)=1, \quad f_{1}(x)=x, \quad\left(f_{n}(x)\right)^{2}-1=f_{n+1}(x) f_{n-1}(x), \text { for } n \geq 1
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
Prove that each $f_{n}(x)$ is a polynomial with integer coefficients.
|
| 59 |
+
|
| 60 |
+
Solution: Observe that
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
f_{n}^{2}(x)-f_{n-1}(x) f_{n+1}(x)=1=f_{n-1}^{2}(x)-f_{n-2}(x) f_{n}(x)
|
| 64 |
+
$$
|
| 65 |
+
|
| 66 |
+
This gives
|
| 67 |
+
|
| 68 |
+
$$
|
| 69 |
+
f_{n}(x)\left(f_{n}(x)+f_{n-2}(x)\right)=f_{n-1}\left(f_{n-1}(x)+f_{n+1}(x)\right)
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
We write this as
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
\frac{f_{n-1}(x)+f_{n+1}(x)}{f_{n}(x)}=\frac{f_{n-2}(x)+f_{n}(x)}{f_{n-1}(x)}
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
Using induction, we get
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
\frac{f_{n-1}(x)+f_{n+1}(x)}{f_{n}(x)}=\frac{f_{0}(x)+f_{2}(x)}{f_{1}(x)}
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
Observe that
|
| 85 |
+
|
| 86 |
+
$$
|
| 87 |
+
f_{2}(x)=\frac{f_{1}^{2}(x)-1}{f_{0}(x)}=x^{2}-1
|
| 88 |
+
$$
|
| 89 |
+
|
| 90 |
+
Hence
|
| 91 |
+
|
| 92 |
+
$$
|
| 93 |
+
\frac{f_{n-1}(x)+f_{n+1}(x)}{f_{n}(x)}=\frac{1+\left(x^{2}-1\right)}{x}=x
|
| 94 |
+
$$
|
| 95 |
+
|
| 96 |
+
Thus we obtain
|
| 97 |
+
|
| 98 |
+
$$
|
| 99 |
+
f_{n+1}(x)=x f_{n}(x)-f_{n-1}(x)
|
| 100 |
+
$$
|
| 101 |
+
|
| 102 |
+
Since $f_{0}(x), f_{1}(x)$ and $f_{2}(x)$ are polynomials with integer coefficients, induction again shows that $f_{n}(x)$ is a polynomial with integer coefficients.
|
| 103 |
+
|
| 104 |
+
Note: We can get $f_{n}(x)$ explicitly:
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
f_{n}(x)=x^{n}-\binom{n-1}{1} x^{n-2}+\binom{n-2}{2} x^{n-4}-\binom{n-3}{3} x^{n-6}+\cdots
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
4. Let $A B C$ be a triangle. An interior point $P$ of $A B C$ is said to be good if we can find exactly 27 rays emanating from $P$ intersecting the sides of the triangle $A B C$ such that the triangle is divided by these rays into 27 smaller triangles of equal area. Determine the number of good points for a given triangle $A B C$.
|
| 111 |
+
|
| 112 |
+
Solution: Let $P$ be a good point. Let $l, m, n$ be respetively the number of parts the sides $B C, C A, A B$ are divided by the rays starting from $P$. Note that a ray must pass through each of the vertices the triangle $A B C$; otherwise we get some quadrilaterals.
|
| 113 |
+
|
| 114 |
+
Let $h_{1}$ be the distance of $P$ from $B C$. Then $h_{1}$ is the height for all the triangles with their bases on $B C$. Equality of areas implies that all these bases have equal length. If we denote this by $x$, we get $l x=a$. Similarly, taking $y$ and $z$ as the lengths of the bases of triangles on $C A$ and $A B$ respectively, we get $m y=b$ and $n z=c$. Let $h_{2}$ and $h_{3}$ be the distances of $P$ from $C A$ and $A B$ respectively. Then
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
h_{1} x=h_{2} y=h_{3} z=\frac{2 \Delta}{27}
|
| 118 |
+
$$
|
| 119 |
+
|
| 120 |
+
where $\Delta$ denotes the area of the triangle $A B C$. These lead to
|
| 121 |
+
|
| 122 |
+
$$
|
| 123 |
+
h_{1}=\frac{2 \Delta}{27} \frac{l}{a}, \quad h_{1}=\frac{2 \Delta}{27} \frac{m}{b}, \quad h_{1}=\frac{2 \Delta}{27} \frac{n}{c}
|
| 124 |
+
$$
|
| 125 |
+
|
| 126 |
+
But
|
| 127 |
+
|
| 128 |
+
$$
|
| 129 |
+
\frac{2 \Delta}{a}=h_{a}, \quad \frac{2 \Delta}{b}=h_{b}, \quad \frac{2 \Delta}{c}=h_{c}
|
| 130 |
+
$$
|
| 131 |
+
|
| 132 |
+
Thus we get
|
| 133 |
+
|
| 134 |
+
$$
|
| 135 |
+
\frac{h_{1}}{h_{a}}=\frac{l}{27}, \quad \frac{h_{2}}{h_{b}}=\frac{m}{27}, \quad \frac{h_{3}}{h_{c}}=\frac{n}{27}
|
| 136 |
+
$$
|
| 137 |
+
|
| 138 |
+
However, we also have
|
| 139 |
+
|
| 140 |
+
$$
|
| 141 |
+
\frac{h_{1}}{h_{a}}=\frac{[P B C]}{\Delta}, \quad \frac{h_{2}}{h_{b}}=\frac{[P C A]}{\Delta}, \quad \frac{h_{3}}{h_{c}}=\frac{[P A B]}{\Delta}
|
| 142 |
+
$$
|
| 143 |
+
|
| 144 |
+
Adding these three relations,
|
| 145 |
+
|
| 146 |
+
$$
|
| 147 |
+
\frac{h_{1}}{h_{a}}+\frac{h_{2}}{h_{b}}+\frac{h_{3}}{h_{c}}=1
|
| 148 |
+
$$
|
| 149 |
+
|
| 150 |
+
Thus
|
| 151 |
+
|
| 152 |
+
$$
|
| 153 |
+
\frac{l}{27}+\frac{m}{27}+\frac{n}{27}=\frac{h_{1}}{h_{a}}+\frac{h_{2}}{h_{b}}+\frac{h_{3}}{h_{c}}=1
|
| 154 |
+
$$
|
| 155 |
+
|
| 156 |
+
We conclude that $l+m+n=27$. Thus every good point $P$ determines a partition $(l, m, n)$ of 27 such that there are $l, m, n$ equal segments respectively on $B C, C A, A B$.
|
| 157 |
+
|
| 158 |
+
Conversely, take any partition $(l, m, n)$ of 27 . Divide $B C, C A, A B$ respectively in to $l, m, n$ equal parts. Define
|
| 159 |
+
|
| 160 |
+
$$
|
| 161 |
+
h_{1}=\frac{2 l \Delta}{27 a}, \quad h_{2}=\frac{2 m \Delta}{27 b}
|
| 162 |
+
$$
|
| 163 |
+
|
| 164 |
+
Draw a line parallel to $B C$ at a distance $h_{1}$ from $B C$; draw another line parallel to $C A$ at a distance $h_{2}$ from $C A$. Both lines are drawn such that they intersect at a point $P$ inside the triangle $A B C$. Then
|
| 165 |
+
|
| 166 |
+
$$
|
| 167 |
+
[P B C]=\frac{1}{2} a h_{1}=\frac{l \Delta}{27}, \quad[P C A]=\frac{m \Delta}{27}
|
| 168 |
+
$$
|
| 169 |
+
|
| 170 |
+
Hence
|
| 171 |
+
|
| 172 |
+
$$
|
| 173 |
+
[P A B]=\frac{n \Delta}{27}
|
| 174 |
+
$$
|
| 175 |
+
|
| 176 |
+
This shows that the distance of $P$ from $A B$ is
|
| 177 |
+
|
| 178 |
+
$$
|
| 179 |
+
h_{3}=\frac{2 n \Delta}{27 c}
|
| 180 |
+
$$
|
| 181 |
+
|
| 182 |
+
Therefore each traingle with base on $C A$ has area $\frac{\Delta}{27}$. We conclude that all the triangles which partitions $A B C$ have equal areas. Hence $P$ is a good point.
|
| 183 |
+
|
| 184 |
+
Thus the number of good points is equal to the number of positive integral solutions of the equation $l+m+n=27$. This is equal to
|
| 185 |
+
|
| 186 |
+
$$
|
| 187 |
+
\binom{26}{2}=325
|
| 188 |
+
$$
|
| 189 |
+
|
| 190 |
+
5. Let $A B C$ be an acute-angled triangle, and let $D, E, F$ be points on $B C$, $C A, A B$ respectively such that $A D$ is the median, $B E$ is the internal angle bisector and $C F$ is the altitude. Suppose $\angle F D E=\angle C, \angle D E F=$ $\angle A$ and $\angle E F D=\angle B$. Prove that $A B C$ is equilateral.
|
| 191 |
+
|
| 192 |
+
Solution: Since $\triangle B F C$ is right-angled at $F$, we have
|
| 193 |
+
|
| 194 |
+
|
| 195 |
+
$F D=B D=C D=a / 2$. Hence $\angle B F D=\angle B$. Since $\angle E F D=$ $\angle B$, we have $\angle A F E=\pi-2 \angle B$. Since $\angle D E F=\angle A$, we also get $\angle C E D=\pi-2 \angle B$. Applying sine rule in $\triangle D E F$, we have
|
| 196 |
+
|
| 197 |
+
$$
|
| 198 |
+
\frac{D F}{\sin A}=\frac{F E}{\sin C}=\frac{D E}{\sin B}
|
| 199 |
+
$$
|
| 200 |
+
|
| 201 |
+
Thus we get $F E=c / 2$ and $D E=b / 2$. Sine rule in $\triangle C E D$ gives
|
| 202 |
+
|
| 203 |
+
$$
|
| 204 |
+
\frac{D E}{\sin C}=\frac{C D}{\sin (\pi-2 B)}
|
| 205 |
+
$$
|
| 206 |
+
|
| 207 |
+
Thus $(b / \sin C)=(a / 2 \sin B \cos B)$. Solving for $\cos B$, we have
|
| 208 |
+
|
| 209 |
+
$$
|
| 210 |
+
\cos B=\frac{a \sin c}{2 b \sin B}=\frac{a c}{2 b^{2}}
|
| 211 |
+
$$
|
| 212 |
+
|
| 213 |
+
Similarly, sine rule in $\triangle A E F$ gives
|
| 214 |
+
|
| 215 |
+
$$
|
| 216 |
+
\frac{E F}{\sin A}=\frac{A E}{\sin (\pi-2 B)}
|
| 217 |
+
$$
|
| 218 |
+
|
| 219 |
+
This gives (since $A E=b c /(a+c)$ ), as earlier,
|
| 220 |
+
|
| 221 |
+
$$
|
| 222 |
+
\cos B=\frac{a}{a+c}
|
| 223 |
+
$$
|
| 224 |
+
|
| 225 |
+
Comparing the two values of $\cos B$, we get $2 b^{2}=c(a+c)$. We also have
|
| 226 |
+
|
| 227 |
+
$$
|
| 228 |
+
c^{2}+a^{2}-b^{2}=2 c a \cos B=\frac{2 a^{2} c}{a+c}
|
| 229 |
+
$$
|
| 230 |
+
|
| 231 |
+
Thus
|
| 232 |
+
|
| 233 |
+
$$
|
| 234 |
+
4 a^{2} c=(a+c)\left(2 c^{2}+2 a^{2}-2 b^{2}\right)=(a+c)\left(2 c^{2}+2 a^{2}-c(a+c)\right)
|
| 235 |
+
$$
|
| 236 |
+
|
| 237 |
+
This reduces to $2 a^{3}-3 a^{2} c+c^{3}=0$. Thus $(a-c)^{2}(2 a+c)=0$. We conclude that $a=c$. Finally
|
| 238 |
+
|
| 239 |
+
$$
|
| 240 |
+
2 b^{2}=c(a+c)=2 c^{2}
|
| 241 |
+
$$
|
| 242 |
+
|
| 243 |
+
We thus get $b=c$ and hence $a=c=b$. This shows that $\triangle A B C$ is equilateral.
|
| 244 |
+
|
| 245 |
+
6. Let $f: \mathbb{Z} \rightarrow \mathbb{Z}$ be a function satisfying $f(0) \neq 0, f(1)=0$ and
|
| 246 |
+
|
| 247 |
+
(i) $f(x y)+f(x) f(y)=f(x)+f(y)$;
|
| 248 |
+
|
| 249 |
+
(ii) $(f(x-y)-f(0)) f(x) f(y)=0$,
|
| 250 |
+
|
| 251 |
+
for all $x, y \in \mathbb{Z}$, simultaneously.
|
| 252 |
+
|
| 253 |
+
(a) Find the set of all possible values of the function $f$.
|
| 254 |
+
|
| 255 |
+
(b) If $f(10) \neq 0$ and $f(2)=0$, find the set of all integers $n$ such that $f(n) \neq 0$.
|
| 256 |
+
|
| 257 |
+
Solution: Setting $y=0$ in the condition (ii), we get
|
| 258 |
+
|
| 259 |
+
$$
|
| 260 |
+
(f(x)-f(0)) f(x)=0
|
| 261 |
+
$$
|
| 262 |
+
|
| 263 |
+
for all $x$ (since $f(0) \neq 0$ ). Thus either $f(x)=0$ or $f(x)=f(0)$, for all $x \in \mathbb{Z}$. Now taking $x=y=0$ in (i), we see that $f(0)+f(0)^{2}=2 f(0)$. This shows
|
| 264 |
+
that $f(0)=0$ or $f(0)=1$. Since $f(0) \neq 0$, we must have $f(0)=1$. We conclude that
|
| 265 |
+
|
| 266 |
+
$$
|
| 267 |
+
\text { either } f(x)=0 \text { or } f(x)=1 \text { for each } x \in \mathbb{Z}
|
| 268 |
+
$$
|
| 269 |
+
|
| 270 |
+
This shows that the set of all possible value of $f(x)$ is $\{0,1\}$. This completes (a).
|
| 271 |
+
|
| 272 |
+
Let $S=\{n \in \mathbb{Z} \mid f(n) \neq 0\}$. Hence we must have $S=\{n \in \mathbb{Z} \mid f(n)=1\}$ by (a). Since $f(1)=0,1$ is not in $S$. And $f(0)=1$ implies that $0 \in S$. Take any $x \in \mathbb{Z}$ and $y \in S$. Using (ii), we get
|
| 273 |
+
|
| 274 |
+
$$
|
| 275 |
+
f(x y)+f(x)=f(x)+1
|
| 276 |
+
$$
|
| 277 |
+
|
| 278 |
+
This shows that $x y \in S$. If $x \in \mathbb{Z}$ and $y \in \mathbb{Z}$ are such that $x y \in S$, then (ii) gives
|
| 279 |
+
|
| 280 |
+
$$
|
| 281 |
+
1+f(x) f(y)=f(x)+f(y)
|
| 282 |
+
$$
|
| 283 |
+
|
| 284 |
+
Thus $(f(x)-1)(f(y)-1)=0$. It follows that $f(x)=1$ or $f(y)=1$; i.e., either $x \in S$ or $y \in S$. We also observe from (ii) that $x \in S$ and $y \in S$ implies that $f(x-y)=1$ so that $x-y \in S$. Thus $S$ has the properties:
|
| 285 |
+
|
| 286 |
+
(A) $x \in \mathbb{Z}$ and $y \in S$ implies $x y \in S$;
|
| 287 |
+
|
| 288 |
+
(B) $x, y \in \mathbb{Z}$ and $x y \in S$ implies $x \in S$ or $y \in S$;
|
| 289 |
+
|
| 290 |
+
(C) $x, y \in S$ implies $x-y \in S$.
|
| 291 |
+
|
| 292 |
+
Now we know that $f(10) \neq 0$ and $f(2)=0$. Hence $f(10)=1$ and $10 \in S$; and $2 \notin S$. Writing $10=2 \times 5$ and using (B), we conclude that $5 \in S$ and $f(5)=1$. Hence $f(5 k)=1$ for all $k \in \mathbb{Z}$ by (A).
|
| 293 |
+
|
| 294 |
+
Suppose $f(5 k+l)=1$ for some $l, 1 \leq l \leq 4$. Then $5 k+l \in S$. Choose $u \in \mathbb{Z}$ such that $l u \equiv 1(\bmod 5)$. We have $(5 k+l) u \in S$ by (A). Moreover, $l u=1+5 m$ for some $m \in \mathbb{Z}$ and
|
| 295 |
+
|
| 296 |
+
$$
|
| 297 |
+
(5 k+l) u=5 k u+l u=5 k u+5 m+1=5(k u+m)+1
|
| 298 |
+
$$
|
| 299 |
+
|
| 300 |
+
This shows that $5(k u+m)+1 \in S$. However, we know that $5(k u+m) \in S$. By (C), $1 \in S$ which is a contradiction. We conclude that $5 k+l \notin S$ for any $l, 1 \leq l \leq 4$. Thus
|
| 301 |
+
|
| 302 |
+
$$
|
| 303 |
+
S=\{5 k \mid k \in \mathbb{Z}\}
|
| 304 |
+
$$
|
| 305 |
+
|
| 306 |
+
$\qquad$
|
| 307 |
+
|
INMO/md/en-2023.md
ADDED
|
@@ -0,0 +1,428 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# INMO 2023
|
| 2 |
+
|
| 3 |
+
## Official Solutions
|
| 4 |
+
|
| 5 |
+
Problem 1. Let $S$ be a finite set of positive integers. Assume that there are precisely 2023 ordered pairs $(x, y)$ in $S \times S$ so that the product $x y$ is a perfect square. Prove that one can find at least four distinct elements in $S$ so that none of their pairwise products is a perfect square.
|
| 6 |
+
|
| 7 |
+
Note: As an example, if $S=\{1,2,4\}$, there are exactly five such ordered pairs: $(1,1),(1,4)$, $(2,2),(4,1)$, and $(4,4)$.
|
| 8 |
+
|
| 9 |
+
Solution 1. Consider the graph whose vertices are elements of $S$, with an edge between $x$ and $y$ if and only if $x y$ is a perfect square. We claim every connected component is a clique.
|
| 10 |
+
|
| 11 |
+
Indeed, take any two vertices corresponding to $x, y$ in $S$ in the same connected component. It suffices to show they are adjacent. By assumption, there is a path between them; so there is a sequence $x=a_{1}, a_{2}, \ldots, a_{n-1}, a_{n}=y$ so that $a_{i} a_{i+1}$ is a perfect square for $1 \leq i<n$. Therefore
|
| 12 |
+
|
| 13 |
+
$$
|
| 14 |
+
x y=a_{1} a_{n}=\frac{\left(a_{1} a_{2}\right)\left(a_{2} a_{3}\right) \cdots\left(a_{n-1} a_{n}\right)}{a_{2}^{2} \cdots a_{n-1}^{2}}
|
| 15 |
+
$$
|
| 16 |
+
|
| 17 |
+
is a perfect square as well. This proves our claim.
|
| 18 |
+
|
| 19 |
+
Now suppose first there are at most 3 connected components, with sizes $a, b, c$ (possibly zero). Note that for $(x, y) \in S \times S, x y$ is a perfect square if and only if $x, y$ are in the same component, which can be chosen is $a^{2}+b^{2}+c^{2}$ ways. Thus
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
a^{2}+b^{2}+c^{2}=2023
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
But since squares can only be 0,1 or $4 \bmod 8$, and 2023 is $7 \bmod 8$, the above equation is impossible. Thus our graph must have at least four components. Picking a number from each component, we can now satisfy the requirements of the problem.
|
| 26 |
+
|
| 27 |
+
Solution 2. For $a$ in $S$, let $S_{a}=\{x \in S \mid a x$ is a square $\}$. Let $a, b$ be elements of $S$. Suppose that $x$ is in $S_{a} \cap S_{b}$. Then $a x$ and $b x$ are squares and hence $a b=\frac{a x \cdot b x}{x^{2}}$ is a square. Then for any $y$ in $S$ such that $a y$ is a square it follows that by is a square, so $S_{a}=S_{b}$. Hence for two elements $a, b$ in $S$, either $S_{a}=S_{b}$ or $S_{a} \cap S_{b}=\emptyset$.
|
| 28 |
+
|
| 29 |
+
Now, $S=\cup S_{a}$ where the union runs over elements of $S$ (since $a \in S_{a}$ for any $a \in S$ ). Let $S=S_{a_{1}} \cup S_{a_{2}} \cup \cdots \cup S_{a_{n}}$ for some elements $a_{1}, a_{2}, \ldots, a_{n}$ of $S$ such that $S_{a_{i}} \cap S_{a_{j}}=\emptyset$ for $1 \leq i<j \leq n$. Then the number of distinct pairs $(x, y)$ of $S \times S$ such that $x y$ is a square is precisely $\left|S_{a_{1}}\right|^{2}+\left|S_{a_{2}}\right|^{2}+\cdots+\left|S_{a_{n}}\right|^{2}$. Since $2023 \equiv 7(\bmod 8)$ it follows that $n>3$ as in the previous solution. Thus we have four elements $a_{1}, a_{2}, a_{3}, a_{4}$ none of whose pairwise products is a square.
|
| 30 |
+
|
| 31 |
+
For those familiar with the language of linear algebra and finite fields, the above argument can be reformulated as follows:
|
| 32 |
+
|
| 33 |
+
Solution 3. Let $p_{1}<p_{2}<\ldots$ be the sequence of prime numbers. Denote by $\mathbb{F}_{2}^{\omega}$ the $\mathbb{F}_{2}$ vector space of all binary sequences $\left(a_{1}, a_{2}, \ldots\right)$ with entries in $\mathbb{F}_{2}$. Consider the set map $\Phi: \mathbb{N} \rightarrow \mathbb{F}_{2}^{\omega}$ defined by
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
\Phi(n):=\left(v_{p_{i}}(n) \quad(\bmod 2)\right)_{i \geq 1}
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
for all $n \in \mathbb{N}$. It is clear that for $x, y \in \mathbb{N}$, the product $x y$ is a perfect square if and only if $\Phi(x)=\Phi(y)$. So we want $|\Phi(S)| \geq 4$. Indeed, decompose $S$ as a union of fibres, $S=\cup_{a \in \Phi(S)} \Phi^{-1}(a)$. Each fibre with size $r$ accounts for $2\binom{r}{2}+r=r^{2}$ pairs towards the count, so if $\Phi(S)$ has at most three elements, then $a^{2}+b^{2}+c^{2}=2023$ has a solution in non-negative integers. This is a contradiction mod 8 , by simply checking that no triple formed using one of $\{0,1,4\}$ can add to $7 \bmod 8$.
|
| 40 |
+
|
| 41 |
+
Problem 2. Suppose $a_{0}, \ldots, a_{100}$ are positive reals. Consider the following polynomial for each $k$ in $\{0,1, \ldots, 100\}$ :
|
| 42 |
+
|
| 43 |
+
$$
|
| 44 |
+
a_{100+k} x^{100}+100 a_{99+k} x^{99}+a_{98+k} x^{98}+a_{97+k} x^{97}+\cdots+a_{2+k} x^{2}+a_{1+k} x+a_{k}
|
| 45 |
+
$$
|
| 46 |
+
|
| 47 |
+
where indices are taken modulo 101, i.e., $a_{100+i}=a_{i-1}$ for any $i$ in $\{1,2, \ldots, 100\}$. Show that it is impossible that each of these 101 polynomials has all its roots real.
|
| 48 |
+
|
| 49 |
+
Solution 1. Let $n=50$. For the sake of contradiction, assume that each of these polynomials has all real roots; these roots must be negative. Let
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
-\alpha_{1, k},-\alpha_{2, k}, \ldots,-\alpha_{2 n, k}
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
be the roots of the polynomial
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
a_{2 n+k} x^{2 n}+2 n a_{2 n-1+k} x^{2 n-1}+a_{2 n-2+k} x^{2 n-2}+a_{2 n-3+k} x^{2 n-3}+\cdots+a_{2+k} x^{2}+a_{1+k} x+a_{k}
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
Indices are taken modulo $2 n+1$, so $a_{2 n+k}=a_{k-1}$ and $a_{2 n-1+k}=a_{k-2}$. Then
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
\sum_{j=1}^{2 n} \alpha_{j, k}=2 n \cdot\left(\frac{a_{k-2}}{a_{k-1}}\right) ; \prod_{j=1}^{2 n} \alpha_{j, k}=\frac{a_{k}}{a_{k-1}}
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
Since the $\alpha_{j, k}$ 's are positive, AM-GM inequality can be applied and by virtue of it we are led to
|
| 68 |
+
|
| 69 |
+
$$
|
| 70 |
+
\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2 n} \geq \frac{a_{k}}{a_{k-1}}
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
for each $k$. As both sides of the inequalities are positive, multiplying them we obtain
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
\prod_{k=0}^{2 n}\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2 n} \geq \prod_{k=0}^{2 n} \frac{a_{k}}{a_{k-1}}
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
But both sides are equal to 1 . Therefore all the $2 n+1$ A.M-G.M inequalities are equalities implying that for each $k$,
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
\alpha_{1, k}=\alpha_{2, k}=\ldots=\alpha_{2 n, k}=\frac{a_{k-2}}{a_{k-1}}
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
Since $n \geq 2$, using Vieta's relations gives
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
\frac{a_{k-3}}{a_{k-1}}=\sum_{1 \leq i<j \leq 2 n} \alpha_{i, k} \alpha_{j, k}=\binom{2 n}{2}\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2}
|
| 89 |
+
$$
|
| 90 |
+
|
| 91 |
+
Simplifying leads
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
\binom{2 n}{2} a_{k-2}^{2}=a_{k-1} a_{k-3}
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
for each $k$. Multiplying all these equations yields
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
\left(\binom{2 n}{2}^{2 n+1}-1\right)\left(\prod_{k=0}^{2 n} a_{k}\right)^{2}=0
|
| 101 |
+
$$
|
| 102 |
+
|
| 103 |
+
which shows that at least one $a_{k}=0$, a contradiction.
|
| 104 |
+
|
| 105 |
+
Solution 2. As above, one proves that
|
| 106 |
+
|
| 107 |
+
$$
|
| 108 |
+
\alpha_{1, k}=\alpha_{2, k}=\ldots=\alpha_{2 n, k}=\frac{a_{k-2}}{a_{k-1}}
|
| 109 |
+
$$
|
| 110 |
+
|
| 111 |
+
This implies
|
| 112 |
+
|
| 113 |
+
$$
|
| 114 |
+
a_{2 n+k} x^{2 n}+2 n a_{2 n-1+k} x^{2 n-1}+\cdots+a_{1+k} x+a_{k}=a_{2 n+k}\left(x+\frac{a_{k-2}}{a_{k-1}}\right)^{2 n}
|
| 115 |
+
$$
|
| 116 |
+
|
| 117 |
+
For $n \geq 2$, comparing coefficients of $x^{0}$ and $x^{1}$, we see that
|
| 118 |
+
|
| 119 |
+
$$
|
| 120 |
+
a_{k}=a_{2 n+k}\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2 n}, \quad a_{k+1}=a_{2 n+k} \cdot 2 n\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2 n-1}
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
whence we obtain
|
| 124 |
+
|
| 125 |
+
$$
|
| 126 |
+
\frac{a_{k+1}}{a_{k}}=2 n \cdot \frac{a_{k-1}}{a_{k-2}}
|
| 127 |
+
$$
|
| 128 |
+
|
| 129 |
+
This must hold for all $k$. However, if we pick $k$ is such that $\frac{a_{k+1}}{a_{k}}$ is minimal, we must necessarily have
|
| 130 |
+
|
| 131 |
+
$$
|
| 132 |
+
\frac{a_{k+1}}{a_{k}} \leq \frac{a_{k-1}}{a_{k-2}}<2 n \cdot \frac{a_{k-1}}{a_{k-2}}
|
| 133 |
+
$$
|
| 134 |
+
|
| 135 |
+
a contradiction.
|
| 136 |
+
|
| 137 |
+
Several other beautiful solutions were pointed out to us; we include a few of them.
|
| 138 |
+
|
| 139 |
+
Solution 3. As usual, assume all of these polynomials have all real roots. We consider the polynomial obtained by writing the coefficients of the given polynomials in reverse order:
|
| 140 |
+
|
| 141 |
+
$$
|
| 142 |
+
a_{k} x^{100}+a_{k+1} x^{99}+a_{k+2} x^{98}+\cdots+100 a_{k+99} x+a_{k+100}
|
| 143 |
+
$$
|
| 144 |
+
|
| 145 |
+
This also has all its roots real: in fact, its roots are reciprocals of the original polynomial. By Rolle's theorem, its derivative must also have all roots real. Repeating this argument, we see that the polynomial obtained by differentiating this 98 times
|
| 146 |
+
|
| 147 |
+
$$
|
| 148 |
+
\frac{100!}{2!} a_{k} x^{2}+99!a_{k+1} x+98!a_{k+2}
|
| 149 |
+
$$
|
| 150 |
+
|
| 151 |
+
also have real roots. Therefore this must have nonnegative discriminant:
|
| 152 |
+
|
| 153 |
+
$$
|
| 154 |
+
99!^{2} a_{k+1}^{2} \geq 2 \cdot 98!\cdot 100!a_{k} a_{k+2}
|
| 155 |
+
$$
|
| 156 |
+
|
| 157 |
+
which simplifies to
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
99 a_{k+1}^{2} \geq 200 a_{k} a_{k+2}
|
| 161 |
+
$$
|
| 162 |
+
|
| 163 |
+
This holds for all $k$, so multiplying these as $k$ varies, we obtain
|
| 164 |
+
|
| 165 |
+
$$
|
| 166 |
+
99^{101} \prod_{i=0}^{100} a_{i}^{2} \geq 200^{101} \prod_{i=0}^{100} a_{i}^{2}
|
| 167 |
+
$$
|
| 168 |
+
|
| 169 |
+
which is impossible since $99<200$.
|
| 170 |
+
|
| 171 |
+
Solution 4. Choose $k$ so that $a_{k+1}$ is minimal. As before, consider the polynomial
|
| 172 |
+
|
| 173 |
+
$$
|
| 174 |
+
a_{k} x^{100}+a_{k+1} x^{99}+a_{k+2} x^{98}+\cdots+100 a_{k+99} x+a_{k+100}
|
| 175 |
+
$$
|
| 176 |
+
|
| 177 |
+
and suppose its roots are $\beta_{1}, \cdots, \beta_{100}$. We have, by Vieta's relations,
|
| 178 |
+
|
| 179 |
+
$$
|
| 180 |
+
\sum_{i=1}^{100} \beta_{i}=-\frac{a_{k+1}}{a_{k}}, \quad \sum_{1 \leq i<j \leq n} \beta_{i} \beta_{j}=\frac{a_{k+2}}{a_{k}}
|
| 181 |
+
$$
|
| 182 |
+
|
| 183 |
+
However, we note that
|
| 184 |
+
|
| 185 |
+
$$
|
| 186 |
+
\left(\sum_{i=1}^{100} \beta_{i}\right)^{2}=\sum_{i=1}^{100} \beta_{i}^{2}+2 \sum_{1 \leq i<j \leq n} \beta_{i} \beta_{j} \geq 2 \sum_{1 \leq i<j \leq n} \beta_{i} \beta_{j}
|
| 187 |
+
$$
|
| 188 |
+
|
| 189 |
+
which yields
|
| 190 |
+
|
| 191 |
+
$$
|
| 192 |
+
\left(-\frac{a_{k+1}}{a_{k}}\right)^{2} \geq \frac{2 a_{k+2}}{a_{k}}
|
| 193 |
+
$$
|
| 194 |
+
|
| 195 |
+
This simplifies to $a_{k+1}^{2} \geq 2 a_{k} a_{k+2}$. However, by the choice of $k$, we have
|
| 196 |
+
|
| 197 |
+
$$
|
| 198 |
+
a_{k+1}^{2} \leq a_{k} a_{k+2}<2 a_{k} a_{k+2}
|
| 199 |
+
$$
|
| 200 |
+
|
| 201 |
+
a contradiction.
|
| 202 |
+
|
| 203 |
+
Problem 3. Let $\mathbb{N}$ denote the set of all positive integers. Find all real numbers $c$ for which there exists a function $f: \mathbb{N} \rightarrow \mathbb{N}$ satisfying:
|
| 204 |
+
|
| 205 |
+
(a) for any $x, a \in \mathbb{N}$, the quantity $\frac{f(x+a)-f(x)}{a}$ is an integer if and only if $a=1$;
|
| 206 |
+
|
| 207 |
+
(b) for all $x \in \mathbb{N}$, we have $|f(x)-c x|<2023$.
|
| 208 |
+
|
| 209 |
+
Solution 1. We claim that the only possible values of $c$ are $k+\frac{1}{2}$ for some non-negative integer $k$. The fact that these values are possible is seen from the function $f(x)=$ $\left\lfloor\left(k+\frac{1}{2}\right) x\right\rfloor+1=k x+\left\lfloor\frac{x}{2}\right\rfloor+1$. Indeed, if you have any $x, a \in \mathbb{N}$, then
|
| 210 |
+
|
| 211 |
+
$$
|
| 212 |
+
\frac{f(x+a)-f(x)}{a}=\frac{1}{a}\left(k a+\left\lfloor\frac{x+a}{2}\right\rfloor-\left\lfloor\frac{x}{2}\right\rfloor\right)=k+\frac{1}{a}\left(\left\lfloor\frac{x+a}{2}\right\rfloor-\left\lfloor\frac{x}{2}\right\rfloor\right)
|
| 213 |
+
$$
|
| 214 |
+
|
| 215 |
+
This is clearly an integer for $a=1$. But for $a \geq 2$, we have
|
| 216 |
+
|
| 217 |
+
$$
|
| 218 |
+
\left\lfloor\frac{x+a}{2}\right\rfloor-\left\lfloor\frac{x}{2}\right\rfloor \geq\left\lfloor\frac{x+2}{2}\right\rfloor-\left\lfloor\frac{x}{2}\right\rfloor=1
|
| 219 |
+
$$
|
| 220 |
+
|
| 221 |
+
If $a=2 k$, then
|
| 222 |
+
|
| 223 |
+
$$
|
| 224 |
+
\left\lfloor\frac{x+a}{2}\right\rfloor-\left\lfloor\frac{x}{2}\right\rfloor=k<2 k=a
|
| 225 |
+
$$
|
| 226 |
+
|
| 227 |
+
and if $a=2 k+1$ for $k \geq 1$, then
|
| 228 |
+
|
| 229 |
+
$$
|
| 230 |
+
\left\lfloor\frac{x+a}{2}\right\rfloor-\left\lfloor\frac{x}{2}\right\rfloor \leq\left\lfloor\frac{x+2 k+2}{2}\right\rfloor-\left\lfloor\frac{x}{2}\right\rfloor=k+1<2 k+1=a
|
| 231 |
+
$$
|
| 232 |
+
|
| 233 |
+
So in either case, the quantity $\left\lfloor\frac{x+a}{2}\right\rfloor-\left\lfloor\frac{x}{2}\right\rfloor$ is strictly between 0 and $a$, and thus cannot be divisible by $a$. Thus condition (a) holds; condition (b) is obviously true.
|
| 234 |
+
|
| 235 |
+
Now let us show these are the only possible values, under the weaker assumption that there exists some $d \in \mathbb{N}$ so that $|f(x)-c x|<d$. It is clear that $c \geq 0$ : if $-d<f(x)-c x<d$ and $c<0$, then for large $x$ the range $[c x-d, c x+d]$ consists only of negative numbers and cannot contain $f(x)$.
|
| 236 |
+
|
| 237 |
+
Now we claim that $c \geq \frac{1}{2}$. Indeed, suppose that $0 \leq c<\frac{1}{2}$, and that $d>0$ is such that $|f(x)-c x| \leq d$. Pick $N>\frac{2 d}{1-2 c}$ so that $2(c N+d)<N$. Then the $N$ values $\{f(1), \ldots, f(N)\}$ must be all be in the range $\{1, \ldots, c N+d\}$, and by pigeonhole principle, some three values $f(i), f(j), f(k)$ must be equal. Some two of $i, j, k$ are not consecutive: suppose WLOG $i>j+1$. Then $\frac{f(i)-f(j)}{i-j}=0$, which contradicts condition (a) for $x=j$ and $a=i-j$.
|
| 238 |
+
|
| 239 |
+
Now for the general case, suppose $c=k+\lambda$, where $k \in \mathbb{Z}$ and $\lambda \in[0,1)$. Let $d \in \mathbb{N}$ be such that $-d \leq f(x)-c x \leq d$. Consider the functions
|
| 240 |
+
|
| 241 |
+
$$
|
| 242 |
+
g_{1}(x)=f(x)-k x+d+1, g_{2}(x)=x-f(x)+k x+d+1
|
| 243 |
+
$$
|
| 244 |
+
|
| 245 |
+
Note that
|
| 246 |
+
|
| 247 |
+
$$
|
| 248 |
+
\begin{gathered}
|
| 249 |
+
g_{1}(x) \geq c x-d-k x+d+1=\lambda x+1 \geq 1 \\
|
| 250 |
+
g_{2}(x) \geq x-(c x+d)+k x+d+1=(1-\lambda) x+1 \geq 1
|
| 251 |
+
\end{gathered}
|
| 252 |
+
$$
|
| 253 |
+
|
| 254 |
+
so that these are also functions from $\mathbb{N}$ to $\mathbb{N}$. They also satisfy condition (a) for $f$ :
|
| 255 |
+
|
| 256 |
+
$$
|
| 257 |
+
\frac{g_{1}(x+a)-g_{1}(x)}{a}=\frac{f(x+a)-k(x+a)+d-f(x)+k x-d}{a}=\frac{f(x+a)-f(x)}{a}-k
|
| 258 |
+
$$
|
| 259 |
+
|
| 260 |
+
is an integer if and only if $\frac{f(x+a)-f(x)}{a}$ is, which happens if and only if $a=1$. A similar argument holds for $g_{2}$.
|
| 261 |
+
|
| 262 |
+
Now note that $g_{1}(x)-\lambda x=f(x)-c x+d+1$ is bounded, and so is $g_{2}(x)-(1-\lambda) x=$ $c x-f(x)+d+1$. So they satisfy the weaker form of condition (b) as well. Thus applying the reasoning in the second paragraph, we see that $\lambda \geq \frac{1}{2}$ and $1-\lambda \geq \frac{1}{2}$. This forces $\lambda=\frac{1}{2}$, which finishes our proof.
|
| 263 |
+
|
| 264 |
+
Solution 2. We will show that for any such $c$, we have $c>0$ and $\{c\}=\frac{1}{2}$. Also 2023 can be replaced by any fixed $d \geq 1$ in condition $(b)$ which we assume now.
|
| 265 |
+
|
| 266 |
+
Clearly $c \geq 0$ else for $c<0$ and $x>\frac{d}{|c|}, c x-d<f(x)<c x+d<0$ which is a contradiction. Suppose $\{c\} \neq \frac{1}{2}$. Put $r=\lfloor c\rfloor$ and $\lambda=\min (\{c\}, 1-\{c\})$ and define
|
| 267 |
+
|
| 268 |
+
$$
|
| 269 |
+
g(x)= \begin{cases}f(x)-r x & \text { if }\{c\}<\frac{1}{2} \\ x+r x-f(x) & \text { if }\{c\}>\frac{1}{2}\end{cases}
|
| 270 |
+
$$
|
| 271 |
+
|
| 272 |
+
so that $|f(x)-c x|=|g(x)-\lambda x|$ and $g(x) \in \mathbb{Z}$ for all $x \in \mathbb{N}$. Here $0 \leq \lambda<\frac{1}{2}$. Take $N>2(\lambda N+2 d)$. Then from $|g(x)-\lambda x|=|f(x)-c x|<d$, we get
|
| 273 |
+
|
| 274 |
+
$$
|
| 275 |
+
-d \leq \lambda n-d<g(n)<\lambda n+d \leq \lambda N+d
|
| 276 |
+
$$
|
| 277 |
+
|
| 278 |
+
for all $1 \leq n \leq N$. That is $N$ integers $g(n), 1 \leq n \leq N$ can take at most $\lambda N+2 d$ values. Since $N>2(\lambda N+2 d)$, by pigeonhole principle, there are 3 positive integers $i<j<k$ such that $g(i)=g(j)=g(k)$. Then $k-i \geq 2$ and
|
| 279 |
+
|
| 280 |
+
$$
|
| 281 |
+
f(k)-f(i)= \begin{cases}g(k)+r k-(g(i)+r i)=r(k-i) & \text { if }\{c\}<\frac{1}{2} \\ (1+r) k-g(k)-((1+r) i-g(i))=(1+r)(k-i) & \text { if }\{c\}>\frac{1}{2}\end{cases}
|
| 282 |
+
$$
|
| 283 |
+
|
| 284 |
+
so that $\frac{f(k)-f(i)}{k-i}$ is an integer. This contradicts the condition $(a)$. Also for each $c=k+\frac{1}{2}$, the function $f(x)=\left\lfloor\left(k+\frac{1}{2}\right) x\right\rfloor$ satisfy the conditions $(a)$ and $(b)$.
|
| 285 |
+
|
| 286 |
+
Solution 3. We give a different proof that $\{c\}=1 / 2$. Let us first prove a claim:
|
| 287 |
+
|
| 288 |
+
Claim. For any $k \geq 1$ and any $x, f\left(x+2^{k}\right)-f(x)$ is divisible by $2^{k-1}$ but not $2^{k}$.
|
| 289 |
+
|
| 290 |
+
Proof. We prove this via induction on $k$. For $k=1$, the claim is trivial. Now assume the statement is true for some $k$, and note that $f\left(x+2^{k}\right)-f(x)=2^{k-1} y_{1}$ and $f\left(x+2^{k}+2^{k}\right)-$ $f\left(x+2^{k}\right)=2^{k-1} y_{2}$ for some odd integers $y_{1}, y_{2}$. Adding these, we see that
|
| 291 |
+
|
| 292 |
+
$$
|
| 293 |
+
f\left(x+2^{k+1}\right)-f(x)=2^{k-1}\left(y_{1}+y_{2}\right)
|
| 294 |
+
$$
|
| 295 |
+
|
| 296 |
+
which is divisible by $2^{k}$ because $y_{1}+y_{2}$ is even. The fact that this is not divisible by $2^{k+1}$ follows from the condition on $f$.
|
| 297 |
+
|
| 298 |
+
Now using this claim, we see that for any $k \geq 1, f\left(1+2^{k}\right)=f(1)+2^{k-1}\left(2 y_{k}+1\right)$ for some integer $y_{k}$, which means
|
| 299 |
+
|
| 300 |
+
$$
|
| 301 |
+
f\left(1+2^{k}\right)-c\left(1+2^{k}\right)=f(1)-c+2^{k}\left(y_{k}+\frac{1}{2}-c\right)
|
| 302 |
+
$$
|
| 303 |
+
|
| 304 |
+
Thus $2^{k}\left(y_{k}+\frac{1}{2}-c\right)$ is bounded. But $y_{k}+\frac{1}{2}-c$ has the same fractional part as $\frac{1}{2}-c$, so if this quantity is never zero, its absolute value must be at least $m=\min \left(\left\{\frac{1}{2}-c\right\},\left\{c-\frac{1}{2}\right\}\right)$ and thus we have
|
| 305 |
+
|
| 306 |
+
$$
|
| 307 |
+
2^{k}\left|y_{k}+\frac{1}{2}-c\right| \geq 2^{k} m
|
| 308 |
+
$$
|
| 309 |
+
|
| 310 |
+
contradicting boundedness. Thus we must have $y_{k}+\frac{1}{2}-c=0$ for some $k$. Since $y_{k}$ is an integer, so that $\{c\}=\frac{1}{2}$.
|
| 311 |
+
|
| 312 |
+
A more rigorous treatment is given below.
|
| 313 |
+
|
| 314 |
+
Obtain
|
| 315 |
+
|
| 316 |
+
$$
|
| 317 |
+
f\left(1+2^{k}\right)-c\left(1+2^{k}\right)=f(1)-c-2^{k}\left(y_{k}+\frac{1}{2}-c\right)
|
| 318 |
+
$$
|
| 319 |
+
|
| 320 |
+
as before. We obtain that $2^{k}\left|y_{k}+\frac{1}{2}-c\right| \leq M$ for some $M>0$ by condition (b). Suppose that $\{c\} \neq \frac{1}{2}$. Writing $y_{k}+\frac{1}{2}-c=m_{k}+\delta$ with $m_{k} \in \mathbb{Z}$ and $0 \leq \delta<1$, we have $0<\delta<1$. Then there exists $\ell>1$ such that $\min (\delta, 1-\delta) \geq \frac{1}{2^{\ell}}$. Hence
|
| 321 |
+
|
| 322 |
+
$$
|
| 323 |
+
\left|y_{k}+\frac{1}{2}-c\right|=\left|m_{k}+\delta\right| \geq \begin{cases}\delta \geq \frac{1}{2^{\ell}} & \text { if } m_{k} \geq 0 \\ -m_{k}-\delta \geq 1-\delta \geq \frac{1}{2^{\ell}} & \text { if } m_{k}<0\end{cases}
|
| 324 |
+
$$
|
| 325 |
+
|
| 326 |
+
implying $M \geq 2^{k}\left|y_{k}+\frac{1}{2}-c\right| \geq 2^{k-\ell}$ which is a contradiction for large $k$. Thus $\{c\}=\frac{1}{2}$.
|
| 327 |
+
|
| 328 |
+
Problem 4. Let $k \geq 1$ and $N>1$ be two integers. On a circle are placed $2 N+1$ coins all showing heads. Calvin and Hobbes play the following game. Calvin starts and on his move can turn any coin from heads to tails. Hobbes on his move can turn at most one coin that is next to the coin that Calvin turned just now from tails to heads. Calvin wins if at any moment there are $k$ coins showing tails after Hobbes has made his move. Determine all values of $k$ for which Calvin wins the game.
|
| 329 |
+
|
| 330 |
+
Solution 1. Calvin wins if $k \in\{1,2, \ldots, N+1\}$ and Hobbes wins otherwise.
|
| 331 |
+
|
| 332 |
+
Label the coins $1,2, \ldots, 2 N+1$. Note that if $k \geq N+2$ then Hobbes wins as follows: he pairs the coins $2 i-1$ and $2 i$ for $1 \leq i \leq N$. If Calvin in a move makes both coins in a pair tails, Hobbes in that move turns the one which was tails prior to Calvin's move back to heads. Thus, he can ensure that after his move, no pair has more than one tails. So, the number of tails after his move is $\leq 1+\frac{(2 N+1)-1}{2}=N+1$, hence Hobbes wins. If $k \leq N$, then Calvin wins by simply turning coins $2 i$ for $1 \leq i \leq N$. Now let $k=N+1$.
|
| 333 |
+
|
| 334 |
+
Let $N=2 m+\varepsilon$ where $\varepsilon \in\{0,1\}$. Now consider $m$ arcs on the circle with the $i$ th arc containing $\{4 i+1,4 i+2,4 i+3,4 i+4\}$, for all $0 \leq i<m$. Calvin makes $3 m$ moves as follows: on move $3 i+1,3 i+2$, and $3 i+3$, he turns coins numbered $4 i+2,4 i+4$, and $4 i+3$, respectively, to tails, for all $0 \leq i<m$. Thus, no matter what Hobbes does, each arc will have either $\{4 i+2,4 i+3\}$ tails (type $\widehat{23}$ ), or $\{4 i+3,4 i+4\}$ tails (type $\widehat{34}$ ), or all of $\{4 i+2,4 i+3,4 i+4\}$ tails (type $\widehat{234}$ ), by the end of these $3 \mathrm{~m}$ moves. We now split into cases:
|
| 335 |
+
|
| 336 |
+
Case 1. $\varepsilon=0$ In this case, if we have any arc of type $\widehat{234}$, we get that there are $\geq 3+2(m-1)=N+1$ tails at the end and the game is won. Assume all arcs are of type $\widehat{23}$ or $\widehat{34}$; hence we currently have $2 m$ tails. Now, if $4 m+1$ has no tails neighbours, Calvin turns it to win. So assume the arc $\{4 m-3,4 m-2,4 m-1,4 m\}$ is of type $\widehat{34}$. If $\{1,2,3,4\}$ is also of type $\widehat{34}$, Calvin can turn 1 to tails to win as it has no tails neighbours. If it is of type $\widehat{23}$, then we must have an $0 \leq i<m-1$ such that the $i$ th arc is of type $\widehat{23}$ but the $(i+1)$ th arc is of type $\widehat{34}$, which means that Calvin can turn $4 i+1$ to tails to win, as it has no tails neighbours.
|
| 337 |
+
|
| 338 |
+
Case 2. $\varepsilon=1 \quad$ Again, if we have any arc of type $\widehat{234}$, Calvin turns $4 m+2$ and we end up with $\geq 3+2(m-1)+1=N+1$ tails at the end and the game is won. Assume all arcs are of type $\widehat{23}$ or $\widehat{34}$; hence we currently have $2 m$ tails. If Calvin can turn $4 m+1$, then he wins, by turning $4 m+3$ next move; so assume the arc $\{4 m-3,4 m-2,4 m-1,4 m\}$ is of type $\widehat{34}$. If $\{1,2,3,4\}$ is of type $\widehat{34}$, then Calvin can turn 1 and $4 m+2$ to secure his win; so assume $\{1,2,3,4\}$ is of type $\widehat{23}$. Thus, there exists $0 \leq i<m-1$ such that the $i$ th arc is of type $\widehat{23}$ and the $(i+1)$ th arc is of type $\widehat{34}$, hence Calvin wins by turning $4 m+2$ and $4 i+1$, in the next two moves.
|
| 339 |
+
|
| 340 |
+
In conclusion, Calvin wins if $k=N+1$, completing the proof.
|
| 341 |
+
|
| 342 |
+
Again, we include some remarkable alternative solutions that were brought to our attention.
|
| 343 |
+
|
| 344 |
+
Solution 2. As before, we can prove that Hobbes wins for $k \geq N+2$. It remains to show that Calvin can win for $k=N+1$.
|
| 345 |
+
|
| 346 |
+
Let Calvin turn the $N$ coins labeled $1,3, \cdots, 2 N-1$ in order. Note that no two coins showing tails are adjacent at any point till now, so Hobbes cannot change any of them back to heads. On the next move, let Calvin turn coin 2 to tails. Now if Hobbes turns coin 1 to heads, Calvin can turn coin $2 N+1$ to tails and win. If Hobbes turns coin 3 to heads instead, let Calvin turn the even-numbered coins $4,6, \cdots, 2 N-2$ in order. After Calvin flips the coin $2 k$, Hobbes must respond by flipping $2 k+1$ after each move to avoid losing. Therefore after these moves, the $N$ coins $1,2,4, \cdots, 2 N-2$ are showing tails, so now Calvin can turn $2 N$ and win.
|
| 347 |
+
|
| 348 |
+
Solution 3. Again we show a procedure for Calvin to win for $k=N+1$. Let Calvin turn coins 1 and 3 tails, and then coin 2 to tails. Hobbes must respond by turning one of 1 or 3 back to heads. In any case, Calvin secures two consecutive tails at the end of Hobbes' turn. He removes these two coins and their neighbours; and from the $(2 N+1)-4=2 N-3$ remaining coins, he turns $\frac{1}{2}(2 N-3+1)=N-1$ of them tails by alternately flipping them. Hobbes never gets to make a move to stop this sequence, so Calvin wins.
|
| 349 |
+
|
| 350 |
+
Problem 5. Euler marks $n$ different points in the Euclidean plane. For each pair of marked points, Gauss writes down the number $\left\lfloor\log _{2} d\right\rfloor$ where $d$ is the distance between the two points. Prove that Gauss writes down less than $2 n$ distinct values.
|
| 351 |
+
|
| 352 |
+
Note: For any $d>0,\left\lfloor\log _{2} d\right\rfloor$ is the unique integer $k$ such that $2^{k} \leq d<2^{k+1}$.
|
| 353 |
+
|
| 354 |
+
Solution 1. We first prove that the Gauss writes down at most $n$ even numbers.
|
| 355 |
+
|
| 356 |
+
For each even number $2 k$ that Gauss writes down, choose a single pair of points whose distance $d$ satisfies $2^{2 k} \leq d<2^{2 k+1}$. Connect these points with a red edge. We claim there cannot be a cycle $\{$ of length $m, 3 \leq m \leq n\}$ : indeed, if the edges corresponding to the distinct even integers $2 k_{1}, \ldots, 2 k_{m}, 2 k_{m+1}$ form a cycle in that order, then assume without loss of generality that $2 k_{m+1}$ is the largest among these, and $2 k_{i}$ is the largest among the rest. The sum of distances for the first $m$ edges is at most
|
| 357 |
+
|
| 358 |
+
$$
|
| 359 |
+
2^{2 k_{1}+1}+\cdots+2^{2 k_{m}+1} \leq 2^{2 k_{i}+1}\left(1+2^{-2}+2^{-4}+\cdots\right) \leq \frac{2^{2 k_{i}+1}}{1-\frac{1}{2^{2}}}<2^{2 k_{i}+2} \leq 2^{2 k_{m+1}}
|
| 360 |
+
$$
|
| 361 |
+
|
| 362 |
+
i.e., less than the distance corresponding to the last edge: a contradiction to triangle inequality. So there are at most $n-1$ red edges.
|
| 363 |
+
|
| 364 |
+
This implies that Gauss only writes at most $n-1$ even numbers, and similarly at most $n-1$ odd numbers. Thus, Gauss writes down at most $2 n-2$ numbers in total.
|
| 365 |
+
|
| 366 |
+
Solution 2. Given a pair of points with distance $d$, we say their log-distance is $\left\lfloor\log _{2} d\right\rfloor$. By dilating by a suitable power of 2 , we can assume all log-distances are positive and the smallest one of them is 1 . Define a sequence of graphs $G_{0}, G_{1}, G_{2}, \cdots$ as follows: $G_{k}$ has the $n$ points as vertices, and two points are joined by an edge in it if and only if their log-distance is at most $k$. In particular, $G_{0}$ is a graph with $n$ vertices and no edges.
|
| 367 |
+
|
| 368 |
+
Now we define a second sequence of graphs $H_{0}, H_{1}, H_{2}, \cdots$ with $H_{i}$ being a subgraph of $G_{i}$ inductively as follows. We let $H_{0}$ be the same as $G_{0}$ and $H_{1}$ by adding an edge with log-distance 1. Now once we have defined $H_{k-1}, H_{k}$ is obtained from it as follows:
|
| 369 |
+
|
| 370 |
+
- If $H_{k-1}$ is a disjoint union of cliques, choose a pair of points with log-distance $k$, and add the edge between them to $H_{k-1}$ to form $H_{k}$ : such an index $k$ will be called clique-destroyer. If no such pair exists, let $H_{k}=H_{k-1}$ : in this case, the index $k$ will be called empty.
|
| 371 |
+
- If not, then $H_{k-1}$ was obtained by adding one edge between cliques $C_{1}$ and $C_{2}$ in $H_{k-2} \subseteq G_{k-2}$. We claim that all edges between $C_{1}$ and $C_{2}$ are in $G_{k}$. Indeed, if suppose the edge was added between points $A_{1} \in C_{1}$ and $A_{2} \in C_{2}$. Take any point $B_{1} \in C_{1}$ and $B_{2} \in C_{2}$. By assumption, $B_{1} A_{1}$ and $B_{2} A_{2}$ are edges in $G_{k-2}$ and $A_{1} A_{2}$ is an edge in $G_{k-1}$, so $\left|B_{1} A_{1}\right|<2^{k-1},\left|B_{2} A_{2}\right|<2^{k-1}$, and $\left|A_{1} A_{2}\right|<2^{k}$, so by triangle inequality,
|
| 372 |
+
|
| 373 |
+
$$
|
| 374 |
+
\left|B_{1} B_{2}\right|<2^{k-1}+2^{k-1}+2^{k}=2^{k+1}
|
| 375 |
+
$$
|
| 376 |
+
|
| 377 |
+
which proves our claim. Now to form $H_{k}$, we take $H_{k-1}$ and add all edges between $C_{1}$ and $C_{2}$ : this yields a disjoint union of cliques. This index $k$ will be called cliquerestorer.
|
| 378 |
+
|
| 379 |
+
Now for every clique-destroyer index $k$, either $H_{k}$ is again a disjoint union of cliques with one fewer clique than $H_{k-1}$, or it is followed by a clique-restorer index $k+1$ (as we add all the missing edges between some two disjoint cliques $C_{1}$ and $C_{2}$ connected by an edge), and $H_{k+1}$ is a disjoint union of cliques with one fewer clique than $H_{k-1}$. Initially, $H_{0}$ has $n$ cliques and the chain stops once $H_{k}$ becomes a single clique on $n$ vertices. There can be at most $2(n-1)$ indices that are one of the above two types. However, the empty indices correspond to values of $k$ that do not occur as a log-distance: therefore the number of distinct values of log-distance is at most the number of non-empty indices, i.e., at most $2 n-2$ as desired.
|
| 380 |
+
|
| 381 |
+
Problem 6. Euclid has a tool called cyclos which allows him to do the following:
|
| 382 |
+
|
| 383 |
+
- Given three non-collinear marked points, draw the circle passing through them.
|
| 384 |
+
- Given two marked points, draw the circle with them as endpoints of a diameter.
|
| 385 |
+
- Mark any intersection points of two drawn circles or mark a new point on a drawn circle.
|
| 386 |
+
|
| 387 |
+
Show that given two marked points, Euclid can draw a circle centered at one of them and passing through the other, using only the cyclos.
|
| 388 |
+
|
| 389 |
+
Solution 1. We begin by proving a series of lemmas.
|
| 390 |
+
|
| 391 |
+
Lemma 1. Given a non-right angled triangle $A B C$, we can draw the nine-point circle and mark the orthocentre $H$ using only a cyclos.
|
| 392 |
+
|
| 393 |
+
Proof. Draw circles $(B C),(C A),(A B)$ and mark their intersections to get the three feet of altitudes $D, E, F$ opposite $A, B, C$. Now draw the circle $(D E F)$ to get the nine-point circle. Draw $(B D F),(C D E),(A E F)$ and they meet at $H$, which we can also mark.
|
| 394 |
+
|
| 395 |
+
Lemma 2. Given points $A, B$, we can mark the midpoint $M$ of $A B$ using only a cyclos.
|
| 396 |
+
|
| 397 |
+
Proof. Draw the circle $(A B)$ and choose a point $X$ on it. Draw circles $(X A),(X B)$ and mark their intersection $Y$. Now mark a point $Z$ on the circle $(X A)$ apart from the marked points. Clearly, $Z$ does not lie on $A B$ nor on $(A B)$, hence we can draw $(A Z B)$. Mark five points $Z_{1}, \ldots, Z_{5}$ on this circle, each different from all previous points and verify if either $A$ lies on $\left(Z_{i} B\right)$ or $B$ lies on $\left(Z_{i} A\right)$ for each $1 \leq i \leq 5$ before marking the new point. By pigeonhole principle, for some three indices $i, j, k$, the three triangles $A Z_{i} B$ are non-right angled, hence we can draw their ninepoint circles by Lemma 1. All of them pass through $M$, and their centres are not collinear, else homothety at the centre of $(A B Z)$ implies the orthocentres of the three triangles are collinear; but they all lie on the reflection of $(A Z B)$ in $A B$, a contradiction! Thus, these three nine-point circles meet at only $M$, and we mark this point.
|
| 398 |
+
|
| 399 |
+
Lemma 3. Given points $A, B, C, D$ on the plane in general position, we can mark the intersection point $E$ of lines $A B$ and $C D$ using only a cyclos.
|
| 400 |
+
|
| 401 |
+
Proof. Draw $(A B)$ and mark five points on it, all different from previously marked points. For each marked point $X$; draw $(C X)$ and $(D X)$ and check whether they have an intersection apart from $X$ (i.e., if they are tangent, or if $X$ lies on $C D$ ). We can find three points $X_{1}, X_{2}, X_{3}$ among them not lying on $C D$. Denote by $Y_{i}$ the second intersection of $\left(A X_{i}\right),\left(B X_{i}\right)$ and by $Z_{i}$ the second intersection of $\left(C X_{i}\right),\left(D X_{i}\right)$ and mark them, for each $1 \leq i \leq 3$. Draw the circles $\left(X_{i} Y_{i} Z_{i}\right)$ and note that they all pass through $E$ and have diameters $E X_{i}$ for all $i$; so they are not coaxial as $X_{1}, X_{2}, X_{3}$ are not collinear; all lying on $(A B)$. Thus we mark $E$ as the unique point common to them all. (Note: if $C, D$ lie on $(A B)$, we can pick a point $T$ on it other than these four, then a point $X$ on $(A T)$, and continue the same argument again, avoiding all edge cases.)
|
| 402 |
+
|
| 403 |
+
Lemma 4. Given a circle $\Gamma$, we can mark the centre of $\Gamma$ using only a cyclos.
|
| 404 |
+
|
| 405 |
+
Proof. Mark points $A, B, C \in \Gamma$ and mark the midpoints of $B C, C A, A B$ to get $A_{1}, B_{1}, C_{1}$ according to Lemma 2. Draw the circles $\left(A B_{1} C_{1}\right),\left(B A_{1} C_{1}\right),\left(C B_{1} A_{1}\right)$ and mark the intersection to get the centre of $\Gamma$.
|
| 406 |
+
|
| 407 |
+
Lemma 5. Given a circle $\Gamma$ and point $A$ on $\Gamma$, we can mark a point $K$ such that line $A K$ is tangent to $\Gamma$ using only a cyclos.
|
| 408 |
+
|
| 409 |
+
Proof. Mark points $B_{1}, B_{2}, B_{3}$ and $C$ on $\Gamma$. By Lemma 4, mark the point $O$, the centre of $\Gamma$. Draw $\left(B_{i} O\right)$ and $(A O C)$ and mark the intersection denoted $F_{i}$; there exists an index $j$ for which $F_{j} \neq O$; mark the point $K$ which is the intersection of $B_{j} F_{j}$ and $O M$ where $M$ is the midpoint of $A C$ (which we mark by Lemma 2) by Lemma 3. Clearly, $K$ lies on $A$ tangent to $\Gamma$. Note that we can do this again to get multiple such points $K$ by choosing different $C$ each time.
|
| 410 |
+
|
| 411 |
+
Lemma 6. Given a circle $\Gamma$ and a point $A$ on $\Gamma$, and a point $B$ not on $\Gamma$, we can mark the point $C$ which is the second intersection of line $A B$ and $\Gamma$ using only a cyclos.
|
| 412 |
+
|
| 413 |
+
Proof. Mark the foot of perpendicular $M$ from $O$ onto line $A B$ as done in Lemma 1. Mark the intersection of line $O M$ and $A K$ by Lemma 3 , where $K$ is a point on the $A$-tangent to $\Gamma$ as constructed in Lemma 5. Draw $(O A K)$ and mark the second intersection with $\Gamma$ to obtain $C$.
|
| 414 |
+
|
| 415 |
+
Lemma 7. Given points $A, B, C$ not all on a line, we can draw the reflection of $A$ in $B C$ using only a cyclos.
|
| 416 |
+
|
| 417 |
+
Proof. Draw $(A B C)$ and mark the orthocentre $H$ of $A B C$ by Lemma 1. Mark the intersection $A^{\prime}$ of line $A H$ with $(B H C)$ using Lemma 6 , which is the $A$-reflection in line $B C$.
|
| 418 |
+
|
| 419 |
+
Lemma 8. Given points $A, B$, we can mark the point $C$ which is the reflection of $A$ in $B$ using only a cyclos.
|
| 420 |
+
|
| 421 |
+
Proof. Draw $(A B)$, and by Lemma 6, mark two points $K_{1}, K_{2}$ such that $B K_{i}$ is tangent to $(A B)$ for $i \in\{1,2\}$. By Lemma 7 , mark the reflection $C$ of $A$ in line $K_{1} K_{2}$ as desired.
|
| 422 |
+
|
| 423 |
+
Thus, a cyclos can do everything a compass can: to draw a circle with given centre $A$ and given radius $B$, we use Lemma 8 to mark the reflection $C$ of $B$ in $A$ and use the cyclos to draw $(B C)$ which has centre $A$ and passes through $B$.
|
| 424 |
+
|
| 425 |
+
Solution 2. After deriving the first two lemmas in the previous solution, one can proceed as follows: Let $C$ denote the point such that $A$ is the midpoint of $C B$.
|
| 426 |
+
|
| 427 |
+
Choose a generic point $X$. We can get the midpoint $M$ of $B X$ and the foot of perpendicular $D$ from $X$ to $A B$. Draw the circle passing through $A, D$ and $M$. This is the nine-point of circle of triangle $C B X$. Intersect this circle with the circle whose diameter is $B X$. The intersection point other than $D$ is the foot of perpendicular $E$ from $B$ to $C X$. Note that $|A E|=|A B|$. Similarly, we can construct another point $F$ such that $|A F|=|A B|$. The circle through $B, E$ and $F$ is the required circle.
|
| 428 |
+
|
INMO/md/en-INMO_2021_solutions.md
ADDED
|
@@ -0,0 +1,370 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# INMO 2021
|
| 2 |
+
|
| 3 |
+
## Official Solutions
|
| 4 |
+
|
| 5 |
+
Problem 1. Suppose $r \geq 2$ is an integer, and let $m_{1}, n_{1}, m_{2}, n_{2}, \cdots, m_{r}, n_{r}$ be $2 r$ integers such that
|
| 6 |
+
|
| 7 |
+
$$
|
| 8 |
+
\left|m_{i} n_{j}-m_{j} n_{i}\right|=1
|
| 9 |
+
$$
|
| 10 |
+
|
| 11 |
+
for any two integers $i$ and $j$ satisfying $1 \leq i<j \leq r$. Determine the maximum possible value of $r$.
|
| 12 |
+
|
| 13 |
+
Solution. Let $m_{1}, n_{1}, m_{2}, n_{2}$ be integers satisfying $m_{1} n_{2}-m_{2} n_{1}= \pm 1$. By changing the signs of $m_{2}, n_{2}$ if need be, we may assume that
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
m_{1} n_{2}-m_{2} n_{1}=1
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
If $m_{3}, n_{3}$ are integers satisfying $m_{1} n_{3}-m_{3} n_{1}= \pm 1$, again we may assume (by changing their signs if necessary) that
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
m_{1} n_{3}-m_{3} n_{1}=1
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
So $m_{1}\left(n_{2}-n_{3}\right)=n_{1}\left(m_{2}-m_{3}\right)$.
|
| 26 |
+
|
| 27 |
+
As $m_{1}, n_{1}$ are relatively prime, $m_{1}$ divides $m_{2}-m_{3}$; say, $m_{2}-m_{3}=m_{1} a$ for some integer $a$. Thus, we get $n_{2}-n_{3}=n_{1} a$. In other words,
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
m_{3}=m_{2}-m_{1} a, n_{3}=n_{2}-n_{1} a
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
Now, if $m_{2} n_{3}-n_{2} m_{3}= \pm 1$, we get
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
\pm 1=m_{2}\left(n_{2}-n_{1} a\right)-n_{2}\left(m_{2}-m_{1} a\right)=\left(m_{1} n_{2}-m_{2} n_{1}\right) a=a
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
Thus, $m_{3}=m_{2}-m_{1} a=m_{2} \pm m_{1}, n_{3}=n_{2}-n_{1} a=n_{2} \pm n_{1}$.
|
| 40 |
+
|
| 41 |
+
Now if we were to have another pair of integers $m_{4}, n_{4}$ such that
|
| 42 |
+
|
| 43 |
+
$$
|
| 44 |
+
m_{1} n_{4}-n_{1} m_{4}= \pm 1
|
| 45 |
+
$$
|
| 46 |
+
|
| 47 |
+
we may assume that $m_{1} n_{4}-n_{1} m_{4}=1$. As seen above, $m_{4}=m_{2} \mp m_{1}, n_{4}=n_{2} \mp n_{1}$. But then
|
| 48 |
+
|
| 49 |
+
$$
|
| 50 |
+
m_{3} n_{4}-n_{3} m_{4}=\left(m_{2} \pm m_{1}\right)\left(n_{2} \mp n_{1}\right)-\left(n_{2} \pm n_{1}\right)\left(m_{2} \mp m_{1}\right)= \pm 2
|
| 51 |
+
$$
|
| 52 |
+
|
| 53 |
+
Therefore, there can be only 3 pairs of such integers.
|
| 54 |
+
|
| 55 |
+
That there do exist many sets of 3 pairs is easy to see; for instance, $(1,0),(1,1),(0,1)$ is such a triple.
|
| 56 |
+
|
| 57 |
+
Alternate Solution. It is clear that $r$ can be 3 due to the valid solution $m_{1}=1, n_{1}=$ $1, m_{2}=1, n_{2}=2, m_{3}=2, n_{3}=3$.
|
| 58 |
+
|
| 59 |
+
If possible, let $r>3$. We observe that:
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
\begin{aligned}
|
| 63 |
+
& m_{1} n_{2} n_{3}-m_{2} n_{1} n_{3}= \pm n_{3} \\
|
| 64 |
+
& m_{2} n_{3} n_{1}-m_{3} n_{2} n_{1}= \pm n_{1} \\
|
| 65 |
+
& m_{3} n_{1} n_{2}-m_{1} n_{3} n_{2}= \pm n_{2}
|
| 66 |
+
\end{aligned}
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
Adding, we get $\pm n_{1} \pm n_{2} \pm n_{3}=0$; which forces at least one of $n_{1}, n_{2}, n_{3}$ to be even; WLOG let $n_{1}$ be even.
|
| 70 |
+
|
| 71 |
+
Repeating the argument for indices $2,3,4$, we deduce that at least one of $n_{2}, n_{3}, n_{4}$ is even; WLOG let $n_{2}$ be even. This leads to a contradiction, since $\left|m_{1} n_{2}-m_{2} n_{1}\right|=1$ cannot be even. Hence $r>3$ is not possible, as claimed.
|
| 72 |
+
|
| 73 |
+
Problem 2. Find all pairs of integers $(a, b)$ so that each of the two cubic polynomials
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
x^{3}+a x+b \text { and } x^{3}+b x+a
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
has all the roots to be integers.
|
| 80 |
+
|
| 81 |
+
Solution. The only such pair is $(0,0)$, which clearly works. To prove this is the only one, let us prove an auxiliary result first.
|
| 82 |
+
|
| 83 |
+
Lemma If $\alpha, \beta, \gamma$ are reals so that $\alpha+\beta+\gamma=0$ and $|\alpha|,|\beta|,|\gamma| \geq 2$, then
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
|\alpha \beta+\beta \gamma+\gamma \alpha|<|\alpha \beta \gamma|
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
Proof. Some two of these reals have the same sign; WLOG, suppose $\alpha \beta>0$. Then $\gamma=$ $-(\alpha+\beta)$, so by substituting this,
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
|\alpha \beta+\beta \gamma+\gamma \alpha|=\left|\alpha^{2}+\beta^{2}+\alpha \beta\right|,|\alpha \beta \gamma|=|\alpha \beta(\alpha+\beta)|
|
| 93 |
+
$$
|
| 94 |
+
|
| 95 |
+
So we simply need to show $|\alpha \beta(\alpha+\beta)|>\left|\alpha^{2}+\beta^{2}+\alpha \beta\right|$. Since $|\alpha| \geq 2$ and $|\beta| \geq 2$, we have
|
| 96 |
+
|
| 97 |
+
$$
|
| 98 |
+
\begin{aligned}
|
| 99 |
+
& |\alpha \beta(\alpha+\beta)|=|\alpha||\beta(\alpha+\beta)| \geq 2|\beta(\alpha+\beta)| \\
|
| 100 |
+
& |\alpha \beta(\alpha+\beta)|=|\beta||\alpha(\alpha+\beta)| \geq 2|\alpha(\alpha+\beta)| .
|
| 101 |
+
\end{aligned}
|
| 102 |
+
$$
|
| 103 |
+
|
| 104 |
+
Adding these and using triangle inequality,
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
\begin{aligned}
|
| 108 |
+
2|\alpha \beta(\alpha+\beta)| & \geq 2|\beta(\alpha+\beta)|+2|\alpha(\alpha+\beta)| \geq 2|\beta(\alpha+\beta)+\alpha(\alpha+\beta)| \\
|
| 109 |
+
& \geq 2\left(\alpha^{2}+\beta^{2}+2 \alpha \beta\right)>2\left(\alpha^{2}+\beta^{2}+\alpha \beta\right) \\
|
| 110 |
+
& =2\left|\alpha^{2}+\beta^{2}+\alpha \beta\right|
|
| 111 |
+
\end{aligned}
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
Here we have used the fact that $\alpha^{2}+\beta^{2}+2 \alpha \beta=(\alpha+\beta)^{2}$ and $\alpha^{2}+\beta^{2}+\alpha \beta=\left(\alpha+\frac{\beta}{2}\right)^{2}+\frac{3 \beta^{2}}{4}$ are both nonnegative. This proves our claim.
|
| 115 |
+
|
| 116 |
+
For our main problem, suppose the roots of $x^{3}+a x+b$ are the integers $r_{1}, r_{2}, r_{3}$ and the roots of $x^{3}+b x+a$ are the integers $s_{1}, s_{2}, s_{3}$. By Vieta's relations, we have
|
| 117 |
+
|
| 118 |
+
$$
|
| 119 |
+
\begin{gathered}
|
| 120 |
+
r_{1}+r_{2}+r_{3}=0=s_{1}+s_{2}+s_{3} \\
|
| 121 |
+
r_{1} r_{2}+r_{2} r_{3}+r_{3} r_{1}=a=-s_{1} s_{2} s_{3} \\
|
| 122 |
+
s_{1} s_{2}+s_{2} s_{3}+s_{3} s_{1}=b=-r_{1} r_{2} r_{3}
|
| 123 |
+
\end{gathered}
|
| 124 |
+
$$
|
| 125 |
+
|
| 126 |
+
If all six of these roots had an absolute value of at least 2 , by our lemma, we would have
|
| 127 |
+
|
| 128 |
+
$$
|
| 129 |
+
|b|=\left|s_{1} s_{2}+s_{2} s_{3}+s_{3} s_{1}\right|<\left|s_{1} s_{2} s_{3}\right|=\left|r_{1} r_{2}+r_{2} r_{3}+r_{3} r_{1}\right|<\left|r_{1} r_{2} r_{3}\right|=|b|
|
| 130 |
+
$$
|
| 131 |
+
|
| 132 |
+
which is absurd. Thus at least one of them is in the set $\{0,1,-1\}$; WLOG, suppose it's $r_{1}$.
|
| 133 |
+
|
| 134 |
+
1. If $r_{1}=0$, then $r_{2}=-r_{3}$, so $b=0$. Then the roots of $x^{3}+b x+a=x^{3}+a$ are precisely the cube roots of $-a$, and these are all real only for $a=0$. Thus $(a, b)=(0,0)$, which is a solution.
|
| 135 |
+
2. If $r_{1}= \pm 1$, then $\pm 1 \pm a+b=0$, so $a$ and $b$ can't both be even. If $a=-s_{1} s_{2} s_{3}$ is odd, then $s_{1}, s_{2}, s_{3}$ are all odd, so $s_{1}+s_{2}+s_{3}$ cannot be zero. Similarly, if $b$ is odd, we get a contradiction.
|
| 136 |
+
|
| 137 |
+
The proof is now complete.
|
| 138 |
+
|
| 139 |
+
Alternate Solution. The only such pair is $(0,0)$, which clearly works. Let us prove this is the only one. In what follows, we use $\nu_{2}(n)$ to denote the largest integer $k$ so that $2^{k} \mid n$ for any non-zero $n \in \mathbb{Z}$.
|
| 140 |
+
|
| 141 |
+
If one of the cubics has 0 as a root, say the first one, then $0^{3}+0 \cdot a+b=0$, so $b=0$. Then the roots of $x^{3}+b x+a=x^{3}+a$ are precisely the cube roots of $-a$, and these are all real only for $a=0$. Thus $(a, b)=(0,0)$.
|
| 142 |
+
|
| 143 |
+
So suppose none of the roots are zero. Take the cubic $x^{3}+a x+b$, and suppose its roots are $x, y, z$. We cannot have $\nu_{2}(x)=\nu_{2}(y)=\nu_{2}(z)$; indeed, if we had $x=2^{k} x_{1}, y=2^{k} y_{1}, z=$ $2^{k} z_{1}$ for odd $x_{1}, y_{1}, z_{1}$, then
|
| 144 |
+
|
| 145 |
+
$$
|
| 146 |
+
0=x+y+z=2^{k}\left(x_{1}+y_{1}+z_{1}\right)
|
| 147 |
+
$$
|
| 148 |
+
|
| 149 |
+
But $x_{1}+y_{1}+z_{1}$ is odd, and hence non-zero, so this cannot happen.
|
| 150 |
+
|
| 151 |
+
Thus we can assume WLOG that $\nu_{2}(x)>\nu_{2}(y)$. Then the third root is $-(x+y)$. Similarly, the three roots of $x^{3}+b x+a$ can be written as $p, q,-(p+q)$ where $\nu_{2}(p)>\nu_{2}(q)$. By Vieta's relations,
|
| 152 |
+
|
| 153 |
+
$$
|
| 154 |
+
\begin{gathered}
|
| 155 |
+
x y-x(x+y)-y(x+y)=-\left(x^{2}+x y+y^{2}\right)=a=p q(p+q) \\
|
| 156 |
+
p q-p(p+q)-q(p+q)=-\left(p^{2}+p q+q^{2}\right)=b=x y(x+y)
|
| 157 |
+
\end{gathered}
|
| 158 |
+
$$
|
| 159 |
+
|
| 160 |
+
Suppose $x=2^{k} x_{1}$ and $y=2^{\ell} y_{1}$ for odd $x_{1}, y_{1}$ and $k>\ell$; in particular $k>0$. Then
|
| 161 |
+
|
| 162 |
+
$$
|
| 163 |
+
x y(x+y)=2^{k} x_{1} \cdot 2^{\ell} y_{1} \cdot\left(2^{k} x_{1}+2^{\ell} y_{1}\right)=2^{k+2 \ell} x_{1} y_{1}\left(2^{k-\ell} x_{1}+y_{1}\right)
|
| 164 |
+
$$
|
| 165 |
+
|
| 166 |
+
Here $x_{1} y_{1}\left(2^{k-\ell} x_{1}+y_{1}\right)$ is clearly odd, so $\nu_{2}(x y(x+y))=k+2 \ell$.
|
| 167 |
+
|
| 168 |
+
Also,
|
| 169 |
+
|
| 170 |
+
$$
|
| 171 |
+
x^{2}+x y+y^{2}=2^{2 k} x_{1}^{2}+2^{k} x_{1} \cdot 2^{\ell} y_{1}+2^{2 \ell} y_{1}^{2}=2^{2 \ell}\left(2^{2 k-2 \ell} x_{1}^{2}+2^{k-\ell} x_{1} y_{1}+y_{1}^{2}\right)
|
| 172 |
+
$$
|
| 173 |
+
|
| 174 |
+
Again, all the terms in the second factor are even except $y_{1}^{2}$, so the entire factor is odd. This means $\nu_{2}\left(x^{2}+x y+y^{2}\right)=2 \ell$. Therefore
|
| 175 |
+
|
| 176 |
+
$$
|
| 177 |
+
\nu_{2}(x y(x+y))>\nu_{2}\left(x^{2}+x y+y^{2}\right)
|
| 178 |
+
$$
|
| 179 |
+
|
| 180 |
+
Similarly, one may show
|
| 181 |
+
|
| 182 |
+
$$
|
| 183 |
+
\nu_{2}(p q(p+q))>\nu_{2}\left(p^{2}+p q+q^{2}\right)
|
| 184 |
+
$$
|
| 185 |
+
|
| 186 |
+
But then
|
| 187 |
+
|
| 188 |
+
$$
|
| 189 |
+
\nu_{2}(b)=\nu_{2}(x y(x+y))>\nu_{2}\left(x^{2}+x y+y^{2}\right)=\nu_{2}(p q(p+q))>\nu_{2}\left(p^{2}+p q+q^{2}\right)=\nu_{2}(b)
|
| 190 |
+
$$
|
| 191 |
+
|
| 192 |
+
Here we have used the fact that $\nu_{2}(n)=\nu_{2}(-n)$ for any integer $n$. But this is a contradiction, proving our claim.
|
| 193 |
+
|
| 194 |
+
Problem 3. Betal marks 2021 points on the plane such that no three are collinear, and draws all possible line segments joining these. He then chooses any 1011 of these line segments, and marks their midpoints. Finally, he chooses a line segment whose midpoint is not marked yet, and challenges Vikram to construct its midpoint using only a straightedge. Can Vikram always complete this challenge?
|
| 195 |
+
|
| 196 |
+
Note: A straightedge is an infinitely long ruler without markings, which can only be used to draw the line joining any two given distinct points.
|
| 197 |
+
|
| 198 |
+
Solution. The answer is 'yes'. To prove this, we will first prove two lemmas:
|
| 199 |
+
|
| 200 |
+
Lemma 1 Given any two points $A, B$, their midpoint $M$, and any point $C$, Vikram can draw a line parallel to $A B$ through $C$.
|
| 201 |
+
|
| 202 |
+
Proof. If $C$ is on line $A B$ we are already done. If not, extend $B C$ to $X$ as shown, draw $P=A C \cap X M$, and then draw $D=B P \cap A X$. We claim $C D$ is the desired line. Indeed, using Ceva's theorem on triangle $A B X$ and the fact $A M=M B$, we see that
|
| 203 |
+
|
| 204 |
+
$$
|
| 205 |
+
\frac{A M}{M B} \cdot \frac{B C}{C X} \cdot \frac{X D}{D A}=1 \Longrightarrow \frac{X C}{C B}=\frac{X D}{D A}
|
| 206 |
+
$$
|
| 207 |
+
|
| 208 |
+
This means $C D \| A B$.
|
| 209 |
+
|
| 210 |
+
|
| 211 |
+
|
| 212 |
+
Lemma 1
|
| 213 |
+
|
| 214 |
+
|
| 215 |
+
|
| 216 |
+
Lemma 2
|
| 217 |
+
|
| 218 |
+
Lemma 2 Given two non-parallel segments $A B, B C$ and their midpoints $M, N$, Vikram can draw the midpoint of any other segment $X Y$.
|
| 219 |
+
|
| 220 |
+
Proof. Assume first $X Y$ is not parallel to $A B$ or $B C$. Using lemma 1, draw lines $\ell_{1}$ and $\ell_{2}$ through $X$ parallel to $A B$ and $B C$ respectively, and similarly draw $m_{1}$ and $m_{2}$ through $Y$ parallel to $A B$ and $B C$ respectively. If we draw $P=\ell_{1} \cap m_{2}$ and $Q=\ell_{2} \cap m_{1}$, then $X P Y Q$ is a parallelogram, so intersecting $P Q$ and $X Y$ gives the midpoint of $X Y$.
|
| 221 |
+
|
| 222 |
+
As for the remaining case, one can draw $A C$ and construct the midpoint $P$ of $A C$ by the construction described above. Since $X Y$ can be parallel to at most one of the sides $A B, B C$ and $A C$, we can pick the two non-parallel sides, and use the above construction to draw the midpoint of $X Y$.
|
| 223 |
+
|
| 224 |
+
Now for the main problem, note that if no two of the 1011 chosen segments share an endpoint, then we have at least $2 \cdot 1011=2022$ distinct endpoints, a contradiction. Thus there must be two segments $A B$ and $B C$ which have their midpoints marked. Since no three of the chosen 2021 points were collinear, $A B$ and $B C$ are not parallel, so using lemma 2, Vikram can construct the midpoint of any other segment, in particular, the segment chosen by Betal.
|
| 225 |
+
|
| 226 |
+
Alternate Solution As in the previous solution, note that there exist $A B$ and $A C$ whose midpoints $C^{\prime}$ and $B^{\prime}$ are marked. Using the straightedge, Vikram can draw the two medians $A C^{\prime}$ and $A B^{\prime}$ and obtain their intersection, the centroid $G$ of $\triangle A B C$. Now intersecting $A G$ with $B C$ gives $A^{\prime}$, the midpoint of $B C$.
|
| 227 |
+
|
| 228 |
+
Lemma Given a point $P$ not on $A B, A C$, Vikram can draw the midpoint of $P A$.
|
| 229 |
+
|
| 230 |
+
Proof. If $P B \| A C$ and $P C \| A B$, then $P B A C$ is a parallelogram, in which case $A^{\prime}$ constructed above is the midpoint of $P A$. Without loss of generality, we may assume $P B \nVdash A C$.
|
| 231 |
+
|
| 232 |
+
|
| 233 |
+
|
| 234 |
+
Using the straightedge, one can mark the points $D=P B \cap A C$ and $P B \cap A^{\prime} C^{\prime}=D^{\prime}$. Since $C A \| A^{\prime} C^{\prime}$, we have
|
| 235 |
+
|
| 236 |
+
$$
|
| 237 |
+
\frac{B D^{\prime}}{D^{\prime} D}=\frac{B C^{\prime}}{C^{\prime} A}=1
|
| 238 |
+
$$
|
| 239 |
+
|
| 240 |
+
so $D^{\prime}$ is the midpoint of $B D$. Now in $\triangle A B D$, two midpoints $C^{\prime}$ and $D^{\prime}$ are known, so the midpoint of $Q^{\prime}$ of $A D$ can be constructed using the centroid construction outlined before. Let $P^{\prime}=C^{\prime} Q^{\prime} \cap P A$; this exists as $C^{\prime} Q^{\prime} \| B P \nVdash A P$. As before, $C^{\prime} P^{\prime} \| B P$, so
|
| 241 |
+
|
| 242 |
+
$$
|
| 243 |
+
\frac{A P^{\prime}}{P^{\prime} P}=\frac{A C^{\prime}}{C^{\prime} B}=1
|
| 244 |
+
$$
|
| 245 |
+
|
| 246 |
+
which means $P^{\prime}$ is the desired midpoint of $P A$.
|
| 247 |
+
|
| 248 |
+
Now suppose we need to find the midpoint of $P Q$. If $P, Q$ are different points from $A$, then one can draw the midpoints of $A P$ and $A Q$ using the lemma. Then by using the centroid of $\triangle A P Q$, one can find the midpoint of $P Q$ as we did for $B C$. If $P$ or $Q$ is $A$, the above lemma immediately yields the required midpoint.
|
| 249 |
+
|
| 250 |
+
Problem 4 A Magician and a Detective play a game. The Magician lays down cards numbered from 1 to 52 face-down on a table. On each move, the Detective can point to two cards and inquire if the numbers on them are consecutive. The Magician replies truthfully. After a finite number of moves the Detective points to two cards. She wins if the numbers on these two cards are consecutive, and loses otherwise.
|
| 251 |
+
|
| 252 |
+
Prove that the Detective can guarantee a win if and only if she is allowed to ask at least 50 questions.
|
| 253 |
+
|
| 254 |
+
Solution. Strategy for the Detective: Pick a card $A$ and compare against all others except one. If he ever gets a "Yes", that pair works; else the remaining card is consecutive with A. This process takes at most 50 queries.
|
| 255 |
+
|
| 256 |
+
Strategy for the Magician: We show that it is not always possible to obtain a "Yes" in 50 turns, hence showing that 49 turns are not enough to figure out a consecutive pair. It is enough to conjure a labelling of cards for which denying all 50 inquiries is valid.
|
| 257 |
+
|
| 258 |
+
Replace 52 by any $N>3$. Think of the cards as vertices of a complete graph $K_{N}$. Delete all edges joining vertices which correspond to pairs of cards the Detective inquired about. We will show that deleting any $N-2$ edges of $K_{N}$ still leaves a graph that admits a path containing all the vertices. Labelling all cards along this path as 1 to $N$ would finish. Several proofs of this claim are possible. We present three of them.
|
| 259 |
+
|
| 260 |
+
## Proof 1 .
|
| 261 |
+
|
| 262 |
+
For any two vertices $a$ and $b$, since $\operatorname{deg} a+\operatorname{deg} b \geq 2(N-1)-(N-2)=N$, they share a common neighbour. Hence the graph is connected.
|
| 263 |
+
|
| 264 |
+
Pick the longest path $\mathcal{P}: u=u_{0} \rightarrow u_{1} \rightarrow \cdots \rightarrow u_{k}=v$. All neighbours of $u$ and $v$ must remain within the path, else we could get a longer path. Let $u$ have $x$ neighbours $\left\{u_{i_{1}}, u_{i_{2}}, \ldots, u_{i_{x}}\right\}$ with $1=i_{1}<i_{2}<\cdots<i_{x} \leq k$. Let $v$ have $y$ neighbours $\left\{u_{j_{1}}, \ldots, u_{j_{y}}\right\}$. Since $x+y \geq n$, we see that $i_{s}=j_{r}+1$ for some $r$ and $s$. Thus there exists $i$ such that $u \rightarrow u_{i+1}$ and $u_{i} \rightarrow v$ are edges. Thus the path is a cycle
|
| 265 |
+
|
| 266 |
+
$$
|
| 267 |
+
\mathcal{C}=u_{i+1} \rightarrow u_{0} \rightarrow u_{1} \cdots \rightarrow u_{i} \rightarrow v \rightarrow u_{k-1} \cdots \rightarrow u_{i+1}
|
| 268 |
+
$$
|
| 269 |
+
|
| 270 |
+
Suppose a vertex $w$ is not in the path $\mathcal{P}$. By connectedness, we have a path $\mathcal{P}^{\prime}$ from $w$ to some vertex of $\mathcal{P}$. Continue along this path via the cycle $\mathcal{C}$ to obtain a path longer than $\mathcal{P}$; contradiction! Thus the graph has a path of length $N-1$, as desired.
|
| 271 |
+
|
| 272 |
+
## Proof 2 .
|
| 273 |
+
|
| 274 |
+
Pick the longest cycle $\mathcal{C}=v_{1} \rightarrow \cdots \rightarrow v_{k} \rightarrow v_{1}$. Note that any vertex $w$ not in the cycle can be incident to no more than $\frac{k}{2}$ of the vertices in it; else there exists $i$ such that $w v_{i}$ and $w v_{i+1}$ (indices mod $k$ ) are edges, so we can put $w$ in to get a longer cycle. Thus our graph is missing at least $\frac{1}{2} k(N-k)$ edges. So $2(N-2) \geq k(N-k)$. Clearly $k>2$ so we see that $k \in\{N-2, N-1\}$.
|
| 275 |
+
|
| 276 |
+
Case 1. $k=N-1$. Pick the leftover $w$ outside $\mathcal{C}$. Not all edges from $w$ to the cycle are missing (since only $N-2$ are missing in total), so follow an edge from $w$ to $\mathcal{C}$ and continue along $\mathcal{C}$ to get a path of length $N-1$.
|
| 277 |
+
|
| 278 |
+
Case 2. $k=N-2$. Pick the leftover $a, b$ outside $\mathcal{C}$. It is clear that both of them have edges to the cycle and $a b$ is also an edge (since $k(N-k)=2(N-2)$ in this case). So starting at $a$, going to $b$, to some vertex of $\mathcal{C}$ and following along $\mathcal{C}$ gives us a path of length $N-1$.
|
| 279 |
+
|
| 280 |
+
The proof is complete.
|
| 281 |
+
|
| 282 |
+
Proof 3.
|
| 283 |
+
|
| 284 |
+
The idea is to prove the stronger claim by induction on $N \geq 3$ : a graph on $N$ vertices with $\binom{N-1}{2}+2$ edges has a cycle of length $N$. Deleting the extra edge will give a path of length $N-1$ through all the vertices.
|
| 285 |
+
|
| 286 |
+
The base case $N=3$ is trivial. Suppose it holds for all $k \leq N$, we prove it for $N+1$. Since $\frac{2\left(2+\binom{N}{2}\right)}{N+1}>N-2$ we see that some vertex $v$ has degree either $N-1$ or $N$.
|
| 287 |
+
|
| 288 |
+
Case 1. If degree of $v$ is $N-1$. Then we have an edge $e=u v$ missing among all the edges through $v$. Delete $v$ along with all the edges through it in the graph. The induced graph has a cycle of length $N$. Pick two consecutive vertices that are not $u$, and append $v$ between them.
|
| 289 |
+
|
| 290 |
+
Case 2. If degree of $v$ is $N$. Delete $v$ along with all its edges. Add an arbitrarily chosen extra edge to the graph so obtained. By induction hypothesis, this resulting graph has a cycle of length $N$. If removing the extra edge does not disrupt the cycle, append $v$ anywhere between two consecutive vertices. If it does break the cycle, use $v$ to connect the vertices it joined.
|
| 291 |
+
|
| 292 |
+
The induction is complete.
|
| 293 |
+
|
| 294 |
+
Problem 5 In a convex quadrilateral $A B C D, \angle A B D=30^{\circ}, \angle B C A=75^{\circ}, \angle A C D=25^{\circ}$ and $C D=C B$. Extend $C B$ to meet the circumcircle of triangle $D A C$ at $E$. Prove that $C E=B D$.
|
| 295 |
+
|
| 296 |
+
Solution. First we show that $\angle D E C=30^{\circ}$. Choose a point $F$ on $A B$ such that $C F=C B$. Join $F C$ and $F D$. Observe that $\angle D C B=75^{\circ}+25^{\circ}=100^{\circ}$. Since $C D=C B$, we have $\angle C D B=\angle C B D=40^{\circ}$. Therefore $\angle C B F=40^{\circ}+30^{\circ}=70^{\circ}$. This gives $\angle C F B=70^{\circ}$.
|
| 297 |
+
|
| 298 |
+
Since $C D=C B=C F$, we have the isosceles triangle $C D F$. But $\angle B C F=40^{\circ}$. Hence $\angle F C D=60^{\circ}$. Therefore we have an equilateral triangle $C D F$. This means $F D=F C=C D$ and $\angle D F C=60^{\circ}$.
|
| 299 |
+
|
| 300 |
+
|
| 301 |
+
|
| 302 |
+
Observe that $\angle A F C=110^{\circ}$ and $\angle F C A=35^{\circ}$. Hence $\angle F A C=35^{\circ}$. This means $F A=$ $F C=F D$. Thus $F$ is the circumcentre of $\triangle A D C$. This implies that
|
| 303 |
+
|
| 304 |
+
$$
|
| 305 |
+
\angle C A D=\frac{\angle C F D}{2}=30^{\circ}
|
| 306 |
+
$$
|
| 307 |
+
|
| 308 |
+
Therefore $\angle D E C=\angle D A C=30^{\circ}$. Now concentrate on triangle $D C E$.
|
| 309 |
+
|
| 310 |
+
Construct an equilateral triangle $E C G$ with $C E$ as base, on the side of $B$. Join $G D$.
|
| 311 |
+
|
| 312 |
+
|
| 313 |
+
|
| 314 |
+
We have $\angle C G E=\angle G C E=\angle C E G=60^{\circ}$ and $C E=E G=G C$. Since $\angle C E D=30^{\circ}$, we get $\angle G E D=30^{\circ}$. Thus $E D$ is the angle bisector of the isosceles triangle $G E C$. This implies that $E D$ is also the pependicular bisector of $G C$. Thus $D$ is on the pependicular bisector of $G C$. Therefore $D C=D G$ and hence $\angle D G C=\angle D C G$.
|
| 315 |
+
|
| 316 |
+
But $\angle D C G=100^{\circ}-60^{\circ}=40^{\circ}$. This implies that $\angle D G C=40^{\circ}$ and hence $\angle C D G=100^{\circ}$.
|
| 317 |
+
|
| 318 |
+
Consider the quadrilateral $G B C D$. We have $D G=D C=C B, \angle G D C=100^{\circ}=\angle D C B$. It is an isosceles trapezium. ( or we can show that $\triangle G D C \cong \triangle B C D$.) Therefore $D B=G C$. But $G C=C E$. Thus we get $D B=C E$.
|
| 319 |
+
|
| 320 |
+
Alternate Solution As in the previous solution, one shows that $F$ is the circumcenter of $\triangle A D C$. since $E$ lies on this circumcircle, this means $F E$ is equal to all of the sides $F A, F D, F C$ and thus also to $C D$ and $C B$. Now $C D B$ and $F C E$ are both isosceles triangles with base angles $40^{\circ}$, and they have $C D=F C$, so they are in fact congruent. This directly implies $C E=B D$, as required.
|
| 321 |
+
|
| 322 |
+
Problem 6. Let $\mathbb{R}[x]$ be the set of all polynomials with real coefficients, and let $\operatorname{deg} P$ denote the degree of a nonzero polynomial $P$. Find all functions $f: \mathbb{R}[x] \rightarrow \mathbb{R}[x]$ satisfying the following conditions:
|
| 323 |
+
|
| 324 |
+
- $f$ maps the zero polynomial to itself,
|
| 325 |
+
- for any non-zero polynomial $P \in \mathbb{R}[x]$, $\operatorname{deg} f(P) \leq 1+\operatorname{deg} P$, and
|
| 326 |
+
- for any two polynomials $P, Q \in \mathbb{R}[x]$, the polynomials $P-f(Q)$ and $Q-f(P)$ have the same set of real roots.
|
| 327 |
+
|
| 328 |
+
|
| 329 |
+
## Solution.
|
| 330 |
+
|
| 331 |
+
## Answer
|
| 332 |
+
|
| 333 |
+
We have $f(p)=p \forall p \in \mathbb{R}[x]$, or $f(p)=-p \forall p \in \mathbb{R}[x]$. These clearly satisfy the given conditions.
|
| 334 |
+
|
| 335 |
+
## Proof
|
| 336 |
+
|
| 337 |
+
Claim 1 For all $p \in \mathbb{R}[x], f(f(p))=p$.
|
| 338 |
+
|
| 339 |
+
Proof. Using condition 3 on the polynomials $p$ and $f(p)$, we see that $p-f(f(p))$ has the same set of real roots as $f(p)-f(p)=0$, which is $\mathbb{R}$. Therefore $p-f(f(p))$ is identically zero.
|
| 340 |
+
|
| 341 |
+
Note that this implies $f$ is bijective. In what follows, $p \sim q$ will mean that $p$ and $q$ have the same set of real roots. Note that putting $f(q)$ for $q$ in condition 2 gives $p-q \sim f(p)-f(q)$ for all $p, q$ (call this statement $(\star)$ ). In particular, putting $q=0$ here, $p \sim f(p)$ for all $p$ (call this $(\star \star))$.
|
| 342 |
+
|
| 343 |
+
Claim 2 For all non-zero $p \in \mathbb{R}[x]$, $\operatorname{deg} p-1 \leq \operatorname{deg} f(p) \leq \operatorname{deg} p+1$.
|
| 344 |
+
|
| 345 |
+
Proof. The right inequality is simply condition 2 . Now using condition 2 on the polynomial $f(p)$, we see that $\operatorname{deg} f(f(p)) \leq \operatorname{deg} f(p)+1$ which gives $\operatorname{deg} f(p) \geq \operatorname{deg} p-1$ because of claim 1 .
|
| 346 |
+
|
| 347 |
+
Claim 3 For all $p \in \mathbb{R}[x], \operatorname{deg} f(p)=\operatorname{deg} p$.
|
| 348 |
+
|
| 349 |
+
Proof. Note that nonzero constant polynomials have no root, so by ( $\star \star$ ), their image must have no root. This is impossible if that image has degree 1 ; so by condition 2 , the image has degree 0, i.e., is a constant polynomial. First consider the case when $\operatorname{deg} p$ is even; assume for now the leading coefficient of $p$ is positive. That means $p(x) \rightarrow \infty$ for $x \rightarrow \pm \infty$, so it has a global minimum, say $C$. Then the polynomial $p+k(k>C)$ has no real roots. Using ( $\star$ ) on $p$ and the constant polynomial $-k$, we see that $f(p)-f(-k)$ has no roots. But this is impossible if $\operatorname{deg} f(p)$ is odd (since $f(-k)$ is a constant), so by claim 2 , we must $\operatorname{deg} f(p)=\operatorname{deg} p$. A similar argument holds if $p$ has negative leading coefficient.
|
| 350 |
+
|
| 351 |
+
Now if $\operatorname{deg} p$ is odd, then $\operatorname{deg} f(p)$ cannot be even, otherwise $q=f(p)$ would be an even degree polynomial whose image $f(q)=f(f(p))=p$ has odd degree, contradicting the last paragraph. Thus $\operatorname{deg} f(p)$ is odd, and using claim 2, we infer than $\operatorname{deg} f(p)=\operatorname{deg} p$.
|
| 352 |
+
|
| 353 |
+
We call a polynomial $p$ ninth-grade if all $\operatorname{deg} p$ roots of $p$ are real and distinct. Clearly for any ninth-grade $p, p$ and $f(p)$ have the roots and same degree, so $f(p)=c_{p} p$ for some non-zero $c_{p} \in \mathbb{R}$.
|
| 354 |
+
|
| 355 |
+
Claim 4 Given any non-constant $q \in \mathbb{R}[x]$, we can choose $r$ with degree bigger than $q$ so that both $r$ and $q-r$ are ninth-grade.
|
| 356 |
+
|
| 357 |
+
Proof. Assume that all real roots of $q$ are inside the interval $[a, b]$. Now choose a number $n$ which has the same parity as $\operatorname{deg} q$ and is bigger than $\operatorname{deg} q$, and choose numbers $c_{1}=a<$ $c_{2}<\cdots<c_{n-1}<c_{n}=b$. Consider the polynomial $p=k\left(x-c_{1}\right)\left(x-c_{2}\right) \cdots\left(x-c_{n}\right)$, so that $k$ has the same sign as the leading coefficient of $q$ (value of $k$ will be chosen later). Clearly $p$ has alternating signs on the intervals $\left(-\infty, c_{1}\right),\left(c_{1}, c_{2}\right), \cdots,\left(c_{n-1}, c_{n}\right),\left(c_{n}, \infty\right)$, and has the same sign as $q$ outside $[a, b]$. Let $k_{1}, k_{2}, \cdots, k_{n-1}$ be the extrema of $p$ on the intervals $\left[c_{1}, c_{2}\right], \cdots\left[c_{n-1}, c_{n}\right]$ in that order, and suppose they are attained at $x_{1}, \cdots x_{n-1}$. Make $|k|$ large enough so that $\left|k_{i}\right|>\max _{x \in[a, b]}|q(x)|$ for all $i$. Then $p+q$ has degree $n$, and has alternating signs at $a-\epsilon, x_{1}, \cdots, x_{n}, b+\epsilon$ for $\epsilon>0$, so it has exactly $n$ distinct roots. Now it is enough to take $r=-p$.
|
| 358 |
+
|
| 359 |
+
Claim 5 For any $q \in \mathbb{R}[x], f(q)=c_{q} q$ for some non-zero real $c_{q}$.
|
| 360 |
+
|
| 361 |
+
Proof. We have already proved this for ninth-grade polynomials. Take ninth-grade $r$ so that $q-r$ is ninth grade and $n=\operatorname{deg}(q-r)>\operatorname{deg} q$. Then $q-r \sim f(q)-f(r)=f(q)-c_{r} r$. Since $q-r$ is ninth-grade and has the same degree as $f(q)-c_{r} r, q-r=c\left(f(q)-c_{r} r\right)=c f(q)-c_{1} r$ for non-zero reals $c, c_{1}$. Comparing the leading term (which belongs to $r$ ) on both sides, $c_{1}=1$, therefore $q=c f(q) \Longrightarrow f(q)=c_{q} q$.
|
| 362 |
+
|
| 363 |
+
Claim 6 For any $p, q \in \mathbb{R}[x], c_{p}=c_{q}$.
|
| 364 |
+
|
| 365 |
+
Proof. We note that for any two polynomials $p, q$ if $p-q$ has a real root which is not a root of $p$, then $c_{p}=c_{q}$. Indeed, if $s$ is a root of $p-q$ (meaning $p(s)=q(s) \neq 0$ ), then it's also a root of $f(p)-f(q)=c_{p} p-c_{q} q$, so that $c_{p} p(s)=c_{q} q(s) \Longrightarrow c_{p}=c_{q}$.
|
| 366 |
+
|
| 367 |
+
Now for any two $p, q$, choose odd $N$ such that $N>\max \{\operatorname{deg} p, \operatorname{deg} q\}$. Then the polynomial $r=x^{N}$ is such that $r-p$ and $r-q$ both have real roots, so $c_{q}=c_{r}=c_{p}$.
|
| 368 |
+
|
| 369 |
+
Claim 6 clearly means there is $c \in \mathbb{R}$ so that $f(p)=c p$ for all $p \in \mathbb{R}[x]$. Using the fact $f(f(p))=p$, we see that the only possibilities are $c=1$ or $c=-1$, completing the proof.
|
| 370 |
+
|
INMO/md/en-INMO_2024_final_solutions.md
ADDED
|
@@ -0,0 +1,284 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# INMO 2024
|
| 2 |
+
|
| 3 |
+
## Official Solutions
|
| 4 |
+
|
| 5 |
+
Problem 1. In triangle $A B C$ with $C A=C B$, point $E$ lies on the circumcircle of $A B C$ such that $\angle E C B=90^{\circ}$. The line through $E$ parallel to $C B$ intersects $C A$ in $F$ and $A B$ in $G$. Prove that the centre of the circumcircle of triangle $E G B$ lies on the circumcircle of triangle $E C F$.
|
| 6 |
+
|
| 7 |
+
## Solution 1.
|
| 8 |
+
|
| 9 |
+
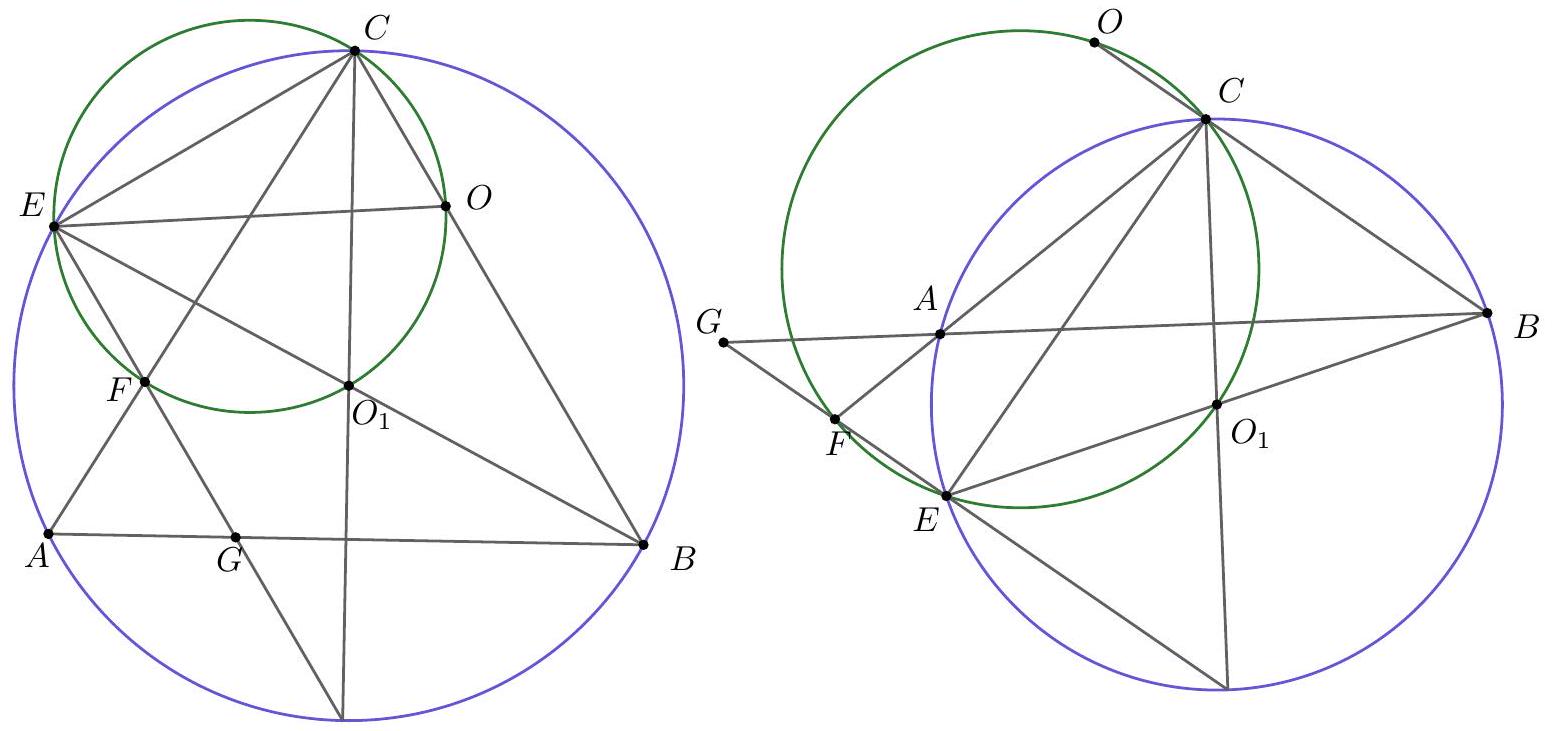
|
| 10 |
+
|
| 11 |
+
We have $F G=F A$ since $F G$ is parallel to $B C$. But also $\triangle G A E$ is a right angle triangle. Thus, if $F^{\prime}$ is the midpoint of $G E$, then $\angle G A F=\angle F G A=\angle F^{\prime} G A=\angle G A F^{\prime}$ which implies $F \equiv F^{\prime}$. Thus, $F$ is the midpoint of $G E$.
|
| 12 |
+
|
| 13 |
+
If $O$ is the circumcenter of $\triangle E B G$, then
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
\angle F O E=\angle G B E=\angle A B E=\angle A C E=\angle F C E
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
Thus, we get $\angle F O E=\angle F C E$ as desired.
|
| 20 |
+
|
| 21 |
+
Solution 2. ( $\angle B C A$ acute case) Let $O_{1}$ be the circumcenter of $\triangle A B C, O$ be the circumcenter of $\triangle E B G$ and $\omega$ be the circumcircle of $\triangle E C F$.
|
| 22 |
+
|
| 23 |
+
First, show that $F$ is the midpoint of $E G$ as in Solution 1. Next, we show that $O_{1}$ lies on $\omega$. This follows from
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
\angle E O_{1} C=2 \angle E B C=2 \angle O_{1} B C=2 \angle B C O_{1}=\angle B C A=\angle E F C
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
Now, $O_{1}$ is the midpoint of $E B$ and $F$ is the midpoint of $E G$, therefore the homothety at $E$ with ratio $1 / 2$ takes $\triangle E G B$ to $\triangle E F O_{1}$. Thus, it takes $O$, the circumcenter of $\triangle E G B$, to the circumcenter of $\triangle E F O_{1}$, thus proving that the midpoint of $E O$ is the center of $\omega$. This immediately implies that $O$ lies on $\omega$.
|
| 30 |
+
|
| 31 |
+
## Remark.
|
| 32 |
+
|
| 33 |
+
- There are two configurations possible in the above problem, one for $C$ acute and one for obtuse. One may replace all the angles in the above solutions by directed angles to obtain a solution which remains invariant in all configurations.
|
| 34 |
+
- There is a direct solution by first proving that $O$ is on $B C$ by calculating $\angle E B O$ and then proving that $\angle O C F=\angle O E F$. However, this needs more care for handling both configurations.
|
| 35 |
+
|
| 36 |
+
Problem 2. All the squares of a $2024 \times 2024$ board are coloured white. In one move, Mohit can select one row or column whose every square is white, choose exactly 1000 squares in this row or column, and colour all of them red. Find the maximum number of squares that Mohit can colour red in a finite number of moves.
|
| 37 |
+
|
| 38 |
+
Solution. Let $n=2024$ and $k=1000$. We claim that the maximum number of squares that can be coloured in this way is $k(2 n-k)$, which evaluates to 3048000 .
|
| 39 |
+
|
| 40 |
+
Indeed, call a row/column bad if it has at least one red square. After the first move, there are exactly $k+1$ bad rows and columns: if a row was picked, then that row and the $k$ columns corresponding to the chosen squares are all bad. Any subsequent move increases the number of bad rows/columns by at least 1 . Since there are only $2 n$ rows and columns, we can make at most $2 n-(k+1)$ moves after the first one, and so at most $2 n-k$ moves can be made in total. Thus we can have at most $k(2 n-k)$ red squares.
|
| 41 |
+
|
| 42 |
+
To prove this is achievable, let's choose each of the $n$ columns in the first $n$ moves, and colour the top $k$ cells in these columns. Then, the bottom $n-k$ rows are still uncoloured, so we can make $n-k$ more moves, colouring $k(n+n-k)$ cells in total.
|
| 43 |
+
|
| 44 |
+
Problem 3. Let $p$ be an odd prime number and $a, b, c$ be integers so that the integers
|
| 45 |
+
|
| 46 |
+
$$
|
| 47 |
+
a^{2023}+b^{2023}, \quad b^{2024}+c^{2024}, \quad c^{2025}+a^{2025}
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
are all divisible by $p$. Prove that $p$ divides each of $a, b$, and $c$.
|
| 51 |
+
|
| 52 |
+
Solution 1. Set $k=2023$. If one of $a, b, c$ is divisible by $p$, then all of them are. Indeed, for example, if $p \mid a$, then $p \mid a^{k}+b^{k}$ implies $p \mid b$, and then $p \mid b^{k+1}+c^{k+1}$ implies $p \mid c$. The other cases follow similarly.
|
| 53 |
+
|
| 54 |
+
So for the sake of contradiction assume none of $a, b, c$ is divisible by $p$. Then
|
| 55 |
+
|
| 56 |
+
$$
|
| 57 |
+
a^{k(k+2)} \equiv\left(a^{k}\right)^{k+2} \equiv\left(-b^{k}\right)^{k+2} \equiv-b^{k(k+2)} \quad(\bmod p)
|
| 58 |
+
$$
|
| 59 |
+
|
| 60 |
+
and
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
a^{k(k+2)} \equiv\left(a^{k+2}\right)^{k}=\left(-c^{k+2}\right)^{k} \equiv-c^{k(k+2)} \quad(\bmod p)
|
| 64 |
+
$$
|
| 65 |
+
|
| 66 |
+
So $b^{k(k+2)} \equiv c^{k(k+2)}(\bmod p)$. But then
|
| 67 |
+
|
| 68 |
+
$$
|
| 69 |
+
c^{k(k+2)} \cdot c \equiv c^{(k+1)^{2}} \equiv\left(-b^{k+1}\right)^{k+1} \equiv b^{(k+1)^{2}} \equiv b^{k(k+2)} \cdot b \equiv c^{k(k+2)} \cdot b \quad(\bmod p)
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
which forces $b \equiv c(\bmod p)$. Thus
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
0 \equiv b^{k+1}+c^{k+1}=2 b^{k+1} \quad(\bmod p)
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
implying $p \mid b$, a contradiction. Thus the proof is complete.
|
| 79 |
+
|
| 80 |
+
Solution 2. As before, we may assume $p$ divides none of $a, b$, and $c$ and set $k=2023$. Then
|
| 81 |
+
|
| 82 |
+
$$
|
| 83 |
+
\begin{aligned}
|
| 84 |
+
a^{k} & \equiv-b^{k} \quad(\bmod p) \\
|
| 85 |
+
b^{k+1} & \equiv-c^{k+1} \quad(\bmod p) \\
|
| 86 |
+
c^{k+2} & \equiv-a^{k+2} \quad(\bmod p)
|
| 87 |
+
\end{aligned}
|
| 88 |
+
$$
|
| 89 |
+
|
| 90 |
+
and multiplying these three equations yields $a^{k} b^{k+1} c^{k+2} \equiv-b^{k} c^{k+1} a^{k+2}(\bmod p)$. By cancelling the factor $a^{k} b^{k} c^{k+1}$, we get $a^{2} \equiv-b c(\bmod p)$. Now
|
| 91 |
+
|
| 92 |
+
$$
|
| 93 |
+
p \mid a^{k}+b^{k} \Longrightarrow a^{4 k} \equiv b^{4 k} \quad(\bmod p) \Longrightarrow c^{2 k} \equiv b^{2 k} \quad(\bmod p)
|
| 94 |
+
$$
|
| 95 |
+
|
| 96 |
+
so
|
| 97 |
+
|
| 98 |
+
$$
|
| 99 |
+
p \mid b^{k+1}+c^{k+1} \Longrightarrow b^{2(k+1)} \equiv c^{2(k+1)} \quad(\bmod p) \Longrightarrow b^{2} \equiv c^{2} \quad(\bmod p)
|
| 100 |
+
$$
|
| 101 |
+
|
| 102 |
+
so either $b \equiv c(\bmod p)$ or $b \equiv-c(\bmod p)$. In the latter case, $a^{2} \equiv c^{2}(\bmod p)$ so $a \equiv c$ $(\bmod p)$ or $a \equiv-c(\bmod p)$. In any case, two out of $\{a, b, c\}$ are the same $\bmod p$, so one of the equations gives $p \mid 2 x^{y}$ where $x \in\{a, b, c\}$ and $y \in\{k, k+1, k+2\}$, hence $p$ odd implies $p \mid x$ so $p \mid a b c$, the desired contradiction.
|
| 103 |
+
|
| 104 |
+
Solution 3. We have
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
\begin{aligned}
|
| 108 |
+
a^{2023} & \equiv-b^{2023} \quad(\bmod p) \\
|
| 109 |
+
b^{2024} & \equiv-c^{2024} \quad(\bmod p) \\
|
| 110 |
+
c^{2025} & \equiv-a^{2025} \quad(\bmod p)
|
| 111 |
+
\end{aligned}
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
Thus,
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
\begin{aligned}
|
| 118 |
+
a^{2023 \cdot 2024 \cdot 2025} & \equiv b^{2023 \cdot 2024 \cdot 2025} \quad(\bmod p) \quad \text { by }(1) \\
|
| 119 |
+
& \equiv-c^{2023 \cdot 2024 \cdot 2025} \quad(\bmod p) \quad \text { by }(2) \\
|
| 120 |
+
& \equiv-a^{2023 \cdot 2024 \cdot 2025} \quad(\bmod p) \quad \text { by }(3)
|
| 121 |
+
\end{aligned}
|
| 122 |
+
$$
|
| 123 |
+
|
| 124 |
+
Thus, $p \mid 2 \cdot a^{2023 \cdot 2024 \cdot 2025}$ and hence $p \mid a$ since $p$ is odd. Now, finish as before.
|
| 125 |
+
|
| 126 |
+
## Remark.
|
| 127 |
+
|
| 128 |
+
- Solution 3 is the shortest, and seems to crucially relies on 2024 being even but it can be modified to always work. In particular, instead of raising to power $k(k+1)(k+2)$, we raise it to $\operatorname{lcm}(k, k+1, k+2)$. This method even works if we have a longer chain of equations and more variables i.e. $p \mid a_{i}^{k+i}+a_{i+1}^{k+i}$ for all $i$ in $0, \cdots, n-1$ and $a_{n}=a_{0}$.
|
| 129 |
+
- There are other possible approaches: one using primitive roots and another using orders. These proceed by considering the highest power of 2 dividing the exponents of the primitive root or order of $a b^{-1} \bmod p$ respectively.
|
| 130 |
+
|
| 131 |
+
Problem 4. A finite set $S$ of positive integers is called cardinal if $S$ contains the integer $|S|$, where $|S|$ denotes the number of distinct elements in $S$. Let $f$ be a function from the set of positive integers to itself, such that for any cardinal set $S$, the set $f(S)$ is also cardinal. Here $f(S)$ denotes the set of all integers that can be expressed as $f(a)$ for some $a$ in $S$. Find all possible values of $f(2024)$.
|
| 132 |
+
|
| 133 |
+
Note: As an example, $\{1,3,5\}$ is a cardinal set because it has exactly 3 distinct elements, and the set contains 3 .
|
| 134 |
+
|
| 135 |
+
Solution 1. The possible values are 1, 2, and 2024 .
|
| 136 |
+
|
| 137 |
+
Construction. The function $f(x)=1$ for all $x \in \mathbb{N}$ works. Also, $f(x)=1$ for all $x \neq 2024$ and $f(2024)=2$, works. Finally, $f(x)=x$ for all $x \in \mathbb{N}$ works as well.
|
| 138 |
+
|
| 139 |
+
It remains to show these are the only possible values for $f(2024)$.
|
| 140 |
+
|
| 141 |
+
Proof. Denote $\operatorname{Im}(f)=\{f(x) \mid x \in \mathbb{N}\}$. The cardinal set $\{1\}$ gives $f(1)=1$. Consider the following two cases:
|
| 142 |
+
|
| 143 |
+
- $\operatorname{Im}(f)$ is unbounded. Fix any $n \in \mathbb{N}$, with $n>1$. Pick $n-1$ distinct integers $k_{1}, \ldots, k_{n-1}$ such that $f\left(k_{i}\right) \notin\{n, f(n)\}$ and $f\left(k_{i}\right)$ are all pairwise distinct, for $1 \leq i<n$. Then $\left\{n, k_{1}, \ldots, k_{n-1}\right\}$ is a cardinal set. Then $\left\{f(n), f\left(k_{1}\right), \ldots, f\left(k_{n-1}\right)\right\}$ is a cardinal set with $n$ distinct elements, so $n$ lies in this set, hence $f(n)=n$. This gives the identity function.
|
| 144 |
+
- $\operatorname{Im}(f)$ is bounded. Suppose $f(x) \leq M$ for all $x \in \mathbb{N}$ and some integer $M>0$.
|
| 145 |
+
|
| 146 |
+
Claim. For any integer $a$ satisfying $1 \leq a \leq M$, if there are infinitely many integers $n \in \mathbb{N}$ such that $f(n)=a$, then $a=1$.
|
| 147 |
+
|
| 148 |
+
Proof. Let $b>1$ be one of the integers with $f(b)=a$. Consider $b-1$ other integers $c_{1}, \ldots, c_{b-1}$, such that $f\left(c_{i}\right)=a$ for $1 \leq i<b$, and $c_{i}$ are all pairwise distinct. Then $\left\{b, c_{1}, \ldots, c_{b-1}\right\}$ is a cardinal set, so the image set, which consists of the singleton $\{a\}$ is cardinal, hence $a=1$.
|
| 149 |
+
|
| 150 |
+
So for every $2 \leq m \leq M$, there are only finitely many integers $x$ such that $f(x)=m$. Thus, there exists an integer $N>1$ such that for all $n \geq N, f(n)=1$. Now for every $1<l<N$, consider the cardinal set $\{l, N+1, N+2, \ldots, N+l-1\}$. Then the image set consists of $\{1, f(l)\}$, which can be cardinal only when $f(l)=1$ or $f(l)=2$.
|
| 151 |
+
|
| 152 |
+
By the above reasoning, $f(2024)$ can only be 1,2 , or 2024 , each of which occurs as an example.
|
| 153 |
+
|
| 154 |
+
Solution 2. We present a second proof of the fact that the proposed values are the only possibilities. Considering the singleton cardinal set $\{1\}$, we see that $f(1)=1$. The cardinal set $\{1,2\}$ gets mapped to $\{1, f(2)\}$, so $f(2)$ must be 2 or 1 .
|
| 155 |
+
|
| 156 |
+
Case 1. Suppose $f(2)=1$. Now $\{2,2024\}$ is a cardinal set, and therefore so is $\{1, f(2024)\}$. This means $f(2024)$ is 1 or 2 .
|
| 157 |
+
|
| 158 |
+
Case 2. Suppose $f(2)=2$. The cardinal set $f(\{1,2,3\})=\{1,2, f(3)\}$ shows that $f(3) \in$ $\{1,2,3\}$, but the cardinal set $f(\{2,3\})=\{2, f(3)\}$ proves $f(3)$ cannot be 2 . Thus there are two sub-cases:
|
| 159 |
+
|
| 160 |
+
2.1. $f(3)=1$. Then the set $\{1,3,2024\}$ is cardinal, hence so is $\{1, f(2024)\}$, implying, as before, $f(2024) \in\{1,2\}$.
|
| 161 |
+
|
| 162 |
+
2.2. $f(3)=3$. In this case, we show via induction that $f(n)=n$ for all $n \in \mathbb{N}$.
|
| 163 |
+
|
| 164 |
+
The base cases $n=1,2,3$ are already known. Now consider $n \geq 4$, and assume $f(k)=k$ for all $k<n$. Consider the cardinal $f(\{1,2, \ldots, n\})=\{1,2, \ldots, n-1, f(n)\}$ which implies $f(n) \in\{1,2, \ldots, n\}$.
|
| 165 |
+
|
| 166 |
+
However, consider the $n$-1-element cardinal set $\{1,2, \ldots, n\} \backslash\{n-2\}$. For its image to be cardinal $f(n)$ cannot equal any number in $\{1,2, \ldots, n-1\} \backslash\{n-2\}$; else its cardinality would be $n-2$, which isn't in the set. So $f(n) \in\{n-2, n\}$.
|
| 167 |
+
|
| 168 |
+
Finally, consider the $n-2$-element set $\{1,2, \ldots, n\} \backslash\{n-1, n-3\}$. If $f(n)=n-2$, its image would only have $n-3$ elements, and thus would not be cardinal. So we conclude that $f(n)=n$ and the induction is complete. In particular, $f(2024)=2024$.
|
| 169 |
+
|
| 170 |
+
Thus the only possible values of $f(2024)$ are 1,2 , and 2024 .
|
| 171 |
+
|
| 172 |
+
## Remark.
|
| 173 |
+
|
| 174 |
+
- There are many ways to finish Solution 2 after reaching (2.2):
|
| 175 |
+
|
| 176 |
+
1. Induct on $n$ and get $1 \leq f(n) \leq n$ as before. Now, note that $f(n) \neq 1$ for $n>3$ by considering $\{1,3, n\}$, and then if $f(n)<n$ we get a contradiction on considering $\{1,2, \ldots, f(n)-2, f(n), n\}$.
|
| 177 |
+
2. Show that $f(n) \neq 1,2,3$ for $n>3$ by considering $\{2, n\}$ and $\{1,3, n\}$. Then prove that $f$ is injective by considering $\{3, n, m\}$ if $n>m>3$. Now, finish by induction and considering $\{1,2, \ldots, n\}$.
|
| 178 |
+
3. Suppose $n_{0}$ is the smallest integer so that $f\left(n_{0}\right) \neq n_{0}$ for some $n_{0}>3$, and let $t$ be the smallest value achieved by $f(n)$ for $n \geq n_{0}$. Let $f(m)=t$. Then $t \neq 1,2,3$ and $t<n_{0} \leq m$ as before. And now consider $\{t, m, m+1, \ldots, m+t-2\}$ to get that $f$ must take on a value smaller than $t$.
|
| 179 |
+
|
| 180 |
+
Problem 5. Let points $A_{1}, A_{2}$, and $A_{3}$ lie on the circle $\Gamma$ in counter-clockwise order, and let $P$ be a point in the same plane. For $i \in\{1,2,3\}$, let $\tau_{i}$ denote the counter-clockwise rotation of the plane centred at $A_{i}$, where the angle of the rotation is equal to the angle at vertex $A_{i}$ in $\triangle A_{1} A_{2} A_{3}$. Further, define $P_{i}$ to be the point $\tau_{i+2}\left(\tau_{i}\left(\tau_{i+1}(P)\right)\right)$, where indices are taken modulo 3 (i.e., $\tau_{4}=\tau_{1}$ and $\tau_{5}=\tau_{2}$ ).
|
| 181 |
+
|
| 182 |
+
Prove that the radius of the circumcircle of $\triangle P_{1} P_{2} P_{3}$ is at most the radius of $\Gamma$.
|
| 183 |
+
|
| 184 |
+
Solution 1. Fix an index $i \in\{1,2,3\}$. Let $D_{1}, D_{2}, D_{3}$ be the points of tangency of the incircle of triangle $\triangle A_{1} A_{2} A_{3}$ with its sides $A_{2} A_{3}, A_{3} A_{1}, A_{1} A_{2}$ respectively.
|
| 185 |
+
|
| 186 |
+
The key observation is that given a line $\ell$ in the plane, the image of $\ell$ under the mapping $\tau_{i+2}\left(\tau_{i}\left(\tau_{i+1}(\ell)\right)\right)$ is a line parallel to $\ell$. Indeed, $\ell$ is rotated thrice by angles equal to the angles of $\triangle A_{1} A_{2} A_{3}$, and the composition of these rotations induces a half-turn and translation on $\ell$ as the angles of $\triangle A_{1} A_{2} A_{3}$ add to $180^{\circ}$. Since $D_{i}$ is a fixed point of this transformation (by the chain of maps $D_{i} \xrightarrow{\tau_{i+1}} D_{i+2} \xrightarrow{\tau_{i}} D_{i+1} \xrightarrow{\tau_{i+2}} D_{i}$ ), we conclude that the line $\overline{P D_{i}}$ maps to the line $\overline{P_{i} D_{i}}$. But the two lines are parallel and both of them pass through $D_{i}$ hence they must coincide, so $D_{i}$ lies on $\overline{P P_{i}}$. Further, each rotation preserves distances, hence $P_{i}$ is the reflection of $P$ in $D_{i}$.
|
| 187 |
+
|
| 188 |
+
In other words, the triangle $P_{1} P_{2} P_{3}$ is obtained by applying a homothety with ratio 2 and center $P$ to the triangle $D_{1} D_{2} D_{3}$. Thus, the radius of the circumcircle of $\triangle P_{1} P_{2} P_{3}$ is twice the radius of the circumcircle of $\triangle D_{1} D_{2} D_{3}$, i.e., twice the radius of the incircle of $\triangle A_{1} A_{2} A_{3}$, which is known to be at most the radius of the circumcircle $\Gamma$.
|
| 189 |
+
|
| 190 |
+
Solution 2. Toss the figure on the complex plane, and let $A_{1}=a, A_{2}=b, A_{3}=c$ without loss of generality. Let the angles of the triangle at $A_{1}, A_{2}, A_{3}$ be denoted by $A, B, C$.
|
| 191 |
+
|
| 192 |
+
Now, for any complex number $z$, the rotation at $z_{0}$ with angle $\theta$ counterclockwise sends $z$ to $\left(z-z_{0}\right) e^{i \theta}+z_{0}$.
|
| 193 |
+
|
| 194 |
+
Therefore, one computes that
|
| 195 |
+
|
| 196 |
+
$$
|
| 197 |
+
\begin{aligned}
|
| 198 |
+
\tau_{321}(z)=\tau_{3}\left(\tau_{1}\left(\tau_{2}(z)\right)\right) & =\tau_{3}\left(\tau_{1}\left((z-b) e^{i B}+b\right)\right) \\
|
| 199 |
+
& =\tau_{3}\left(z e^{i(A+B)}+b e^{i A}\left(1-e^{i B}\right)+a\left(1-e^{i A}\right)\right) \\
|
| 200 |
+
& =-z+b+c+b e^{i(A+C)}+a e^{i C}-a e^{i(A+C)}-c e^{i C}
|
| 201 |
+
\end{aligned}
|
| 202 |
+
$$
|
| 203 |
+
|
| 204 |
+
Thus, $\tau_{312}(z)+z$ is independent of $z$. Similarly $\tau_{123}(z)+z$ and $\tau_{231}(z)+z$ are also independent of $z$. Note that adding $z$ is the same as translation by $z$, hence we have shown that the circumradius of $\triangle P_{1} P_{2} P_{3}$ is independent of $P$.
|
| 205 |
+
|
| 206 |
+
Thus, it suffices to prove the result for $z=z_{0}=a+b+c$. Let $U=-\tau_{312}\left(z_{0}\right), V=$ $-\tau_{123}\left(z_{0}\right), W=-\tau_{231}\left(z_{0}\right)$. So, it is enough to prove that the circumradius of $\triangle U V W$ at most the radius of $\Gamma$.
|
| 207 |
+
|
| 208 |
+
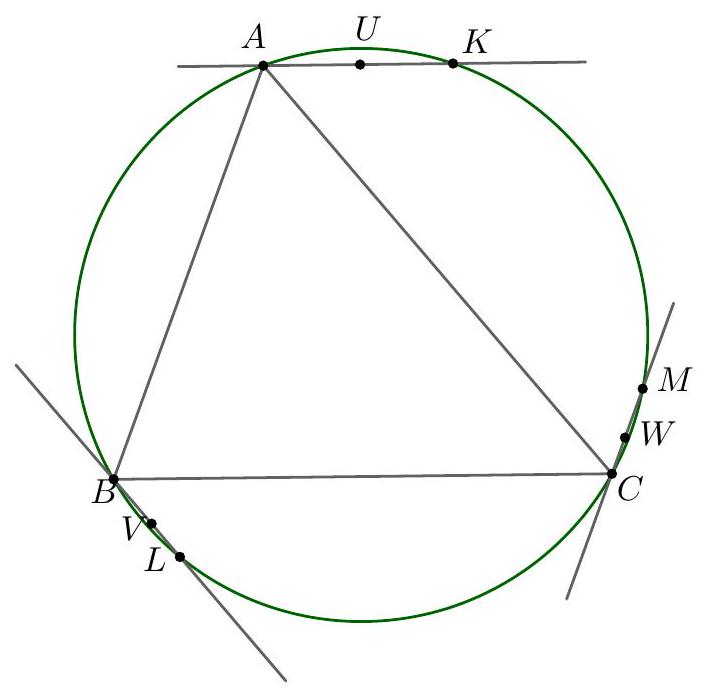
|
| 209 |
+
|
| 210 |
+
Name the vertices $A_{1}, A_{2}, A_{3}$ as $A, B, C$ for convenience. Let the parallel line to $B C$ passing through $A$ intersect $\Gamma$ again at $K$. Similarly, define $L$ as the second intersection of the line through $B$ parallel to $C A$ and finally $M$ for $C$ parallel to $A B$.
|
| 211 |
+
|
| 212 |
+
We claim that $U$ lies on the line segment $\overline{A K}$ : We have $U=a-(b-a) e^{i(A+C)}+(c-a) e^{i C}$, hence $\overrightarrow{A U}$ is parallel to $\overrightarrow{A K}$ hence $U$ lies on the line $A K$. If $A B=A C$ then $U=A$, and the claim is proven. Else suppose that $A B<A C$. Then $\overrightarrow{A U}$ points towards $K$ and $|A U|=A C-A B$, so it suffices to show that $A K>A C-A B$. But this is clear because $K C B A$ is an isosceles trapezium, so $A B=K C$, and then triangle inequality on $\triangle K A C$ to get $K A+K C>A C$.
|
| 213 |
+
|
| 214 |
+
Thus, $U \in \overline{A K}$, and similarly $V \in \overline{B L}, W \in \overline{C M}$. We claim that for any $U, V, W$ on the segments $A K, B L, C M$ respectively, the circumradius of $\triangle U V W$ is less than or equal to the radius of $\Gamma$.
|
| 215 |
+
|
| 216 |
+
Now let $X, Y$ be two fixed points on the same side of a line $\ell$. Fix a side of $\overleftarrow{X Y}$, and let $Z$ be a variable point on $\ell$ which always remains on this fixed side of $\overleftarrow{X Y}$. Then the circumradius of $\triangle X Y Z$ is minimized at the unique point $Z_{0}$ (on this fixed side of $\overleftrightarrow{X Y}$ ) for which the circumcircle of $\triangle X Y Z_{0}$ is tangent to $\ell$ and it is a increasing function as one goes further away from this unique point $Z_{0}$. Thus, the maximum circumradius of $\triangle U V W$ is achieved only if $U \in\{A, K\}, V \in\{B, L\}, W \in\{C, M\}$. For each of these, the circumradius is the radius of $\Gamma$, hence we are done.
|
| 217 |
+
|
| 218 |
+
## Remark.
|
| 219 |
+
|
| 220 |
+
- The conclusion of Solution 1 used the fact that in a triangle $A B C$ with incentre $I$ and inradius $r$, and circumcentre $O$ and circumradius $R$, we have the inequality $R \geq 2 r$. This is called Euler's Inequality. The standard proof is that $0 \leq O I^{2}=$ $R^{2}-\operatorname{Pow}(I,(O, R))=R^{2}-2 R r$. The last equality holds as $\operatorname{Pow}(I,(O, R))=I A \cdot I M$ where $M$ is the midpoint of minor arc $\widehat{B C}$ in the circumcircle of $A B C$, and because $I A=\frac{r}{\sin \frac{A}{2}}$ and $I M=M B=\frac{a}{2 \cos \frac{A}{2}}=\frac{2 R \sin A}{2 \cos \frac{A}{2}}=2 R \sin \frac{A}{2}$ by using "the trident lemma" and the double-angle sine formulas.
|
| 221 |
+
- After proving that the circumradius is independent of $P$, one can take $P=I$, for which $P_{1}$ is easily seen to be the point such that $D_{1}$ is the midpoint of $I P_{1}$. Now we again finish by Euler's Inequality.
|
| 222 |
+
|
| 223 |
+
Problem 6. For each positive integer $n \geq 3$, define $A_{n}$ and $B_{n}$ as
|
| 224 |
+
|
| 225 |
+
$$
|
| 226 |
+
\begin{gathered}
|
| 227 |
+
A_{n}=\sqrt{n^{2}+1}+\sqrt{n^{2}+3}+\cdots+\sqrt{n^{2}+2 n-1} \\
|
| 228 |
+
B_{n}=\sqrt{n^{2}+2}+\sqrt{n^{2}+4}+\cdots+\sqrt{n^{2}+2 n}
|
| 229 |
+
\end{gathered}
|
| 230 |
+
$$
|
| 231 |
+
|
| 232 |
+
Determine all positive integers $n \geq 3$ for which $\left\lfloor A_{n}\right\rfloor=\left\lfloor B_{n}\right\rfloor$.
|
| 233 |
+
|
| 234 |
+
Note. For any real number $x,\lfloor x\rfloor$ denotes the largest integer $N$ such that $N \leq x$.
|
| 235 |
+
|
| 236 |
+
Solution. Let $M=n^{2}+\frac{1}{2} n$.
|
| 237 |
+
|
| 238 |
+
Lemma 1. $B_{n}-A_{n}<\frac{1}{2}$.
|
| 239 |
+
|
| 240 |
+
Indeed,
|
| 241 |
+
|
| 242 |
+
$$
|
| 243 |
+
\begin{array}{r}
|
| 244 |
+
\left(B_{n}-A_{n}\right)=\sum_{k=1}^{n}\left(\sqrt{n^{2}+2 k}-\sqrt{n^{2}+2 k-1}\right)=\sum_{k=1}^{n} \frac{1}{\sqrt{n^{2}+2 k}+\sqrt{n^{2}+2 k-1}}<\sum_{k=1}^{n} \frac{1}{2 n} \\
|
| 245 |
+
=\frac{n}{2 n}=\frac{1}{2}
|
| 246 |
+
\end{array}
|
| 247 |
+
$$
|
| 248 |
+
|
| 249 |
+
proving the lemma.
|
| 250 |
+
|
| 251 |
+
Lemma 2. $A_{n}<M<B_{n}$.
|
| 252 |
+
|
| 253 |
+
Proof. Observe that
|
| 254 |
+
|
| 255 |
+
$$
|
| 256 |
+
\begin{aligned}
|
| 257 |
+
& \left(A_{n}-n^{2}\right)=\sum_{k=1}^{n}\left(\sqrt{n^{2}+2 k-1}-n\right)=\sum_{k=1}^{n} \frac{2 k-1}{\sqrt{n^{2}+2 k-1}+n}<\sum_{k=1}^{n} \frac{2 k-1}{n+n}=\frac{n^{2}}{2 n} \\
|
| 258 |
+
& =\frac{n}{2}
|
| 259 |
+
\end{aligned}
|
| 260 |
+
$$
|
| 261 |
+
|
| 262 |
+
as $\sum_{k=1}^{n}(2 k-1)=n^{2}$, proving $A_{n}-n^{2}<\frac{n}{2}$ or $A_{n}<M$. Similarly,
|
| 263 |
+
|
| 264 |
+
$$
|
| 265 |
+
\begin{array}{r}
|
| 266 |
+
\left(B_{n}-n^{2}\right)=\sum_{k=1}^{n}\left(\sqrt{n^{2}+2 k}-n\right)=\sum_{k=1}^{n} \frac{2 k}{\sqrt{n^{2}+2 k}+n}>\sum_{k=1}^{n} \frac{2 k}{(n+1)+n} \\
|
| 267 |
+
=\frac{n(n+1)}{2 n+1}>\frac{n}{2}
|
| 268 |
+
\end{array}
|
| 269 |
+
$$
|
| 270 |
+
|
| 271 |
+
as $\sum_{k=1}^{n}(2 k)=n(n+1)$, so $B_{n}-n^{2}>\frac{n}{2}$ hence $B_{n}>M$, as desired.
|
| 272 |
+
|
| 273 |
+
By Lemma 2, we see that $A_{n}$ and $B_{n}$ are positive real numbers containing $M$ between them. When $n$ is even, $M$ is an integer. This implies $\left\lfloor A_{n}\right\rfloor<M$, but $\left\lfloor B_{n}\right\rfloor \geq M$, which means we cannot have $\left\lfloor A_{n}\right\rfloor=\left\lfloor B_{n}\right\rfloor$.
|
| 274 |
+
|
| 275 |
+
When $n$ is odd, $M$ is a half-integer, and thus $M-\frac{1}{2}$ and $M+\frac{1}{2}$ are consecutive integers. So the above two lemmas imply
|
| 276 |
+
|
| 277 |
+
$$
|
| 278 |
+
M-\frac{1}{2}<B_{n}-\left(B_{n}-A_{n}\right)=A_{n}<B_{n}=A_{n}+\left(B_{n}-A_{n}\right)<M+\frac{1}{2}
|
| 279 |
+
$$
|
| 280 |
+
|
| 281 |
+
This shows $\left\lfloor A_{n}\right\rfloor=\left\lfloor B_{n}\right\rfloor=M-\frac{1}{2}$.
|
| 282 |
+
|
| 283 |
+
Thus, the only integers $n \geq 3$ that satisfy the conditions are the odd numbers and all of them work.
|
| 284 |
+
|
INMO/md/en-Inmo-2019-Solutions.md
ADDED
|
@@ -0,0 +1,225 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $34^{\text {th }}$ Indian National Mathematical Olympiad-2019
|
| 2 |
+
|
| 3 |
+
## Problems and Solutions
|
| 4 |
+
|
| 5 |
+
1. Let $A B C$ be a triangle with $\angle B A C>90^{\circ}$. Let $D$ be a point on the segment $B C$ and $E$ be a point on the line $A D$ such that $A B$ is tangent to the circumcircle of triangle $A C D$ at $A$ and $B E$ is perpendicular to $A D$. Given that $C A=C D$ and $A E=C E$, determine $\angle B C A$ in degrees.
|
| 6 |
+
|
| 7 |
+
Solution: Let $\angle C=2 \alpha$. Then $\angle C A D=\angle C D A=90^{\circ}-\alpha$. Moreover $\angle B A D=2 \alpha$ as $B A$ is tangent to the circumcircle of $\triangle C A D$. Since $A E=A D$, it gives $\angle A E C=2 \alpha$. Thus $\triangle A E C$ is similar to $\triangle A C D$. Hence
|
| 8 |
+
|
| 9 |
+
$$
|
| 10 |
+
\frac{A E}{A C}=\frac{A C}{A D}
|
| 11 |
+
$$
|
| 12 |
+
|
| 13 |
+
But the condition that $B E \perp A D$ gives $A E=A B \cos 2 \alpha=c \cos 2 \alpha$. It is easy to see that $\angle B=90^{\circ}-3 \alpha$. Using sine rule in triangle $A D C$, we get
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
\frac{A D}{\sin 2 \alpha}=\frac{A C}{\sin (90-\alpha)}
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
This gives $A D=2 b \sin \alpha$. Thus we get
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
b^{2}=A C^{2}=A E \cdot A D=(c \cos 2 \alpha) \cdot 2 b \sin \alpha
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
Using $b=2 R \sin B$ and $c=2 R \sin C$, this leads to
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
\cos 3 \alpha=2 \sin 2 \alpha \cos 2 \alpha \sin \alpha=\sin 4 \alpha \sin \alpha
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
Writing $\cos 3 \alpha=\cos (4 \alpha-\alpha)$ and expanding, we get $\cos 4 \alpha \cos \alpha=0$. Therefore $\alpha=90^{\circ}$ or $4 \alpha=90^{\circ}$. But $\alpha=90^{\circ}$ is not possible as $\angle C=2 \alpha$. Therefore $4 \alpha=90^{\circ}$ which gives $\angle C=2 \alpha=45^{\circ}$.
|
| 32 |
+
|
| 33 |
+
2. Let $A_{1} B_{1} C_{1} D_{1} E_{1}$ be a regular pentagon. For $2 \leq n \leq 11$,
|
| 34 |
+
|
| 35 |
+
let $A_{n} B_{n} C_{n} D_{n} E_{n}$ be the pentagon whose vertices are the midpoints of the sides of the pentagon $A_{n-1} B_{n-1} C_{n-1} D_{n-1} E_{n-1}$. All the 5 vertices of each of the 11 pentagons are arbitrarily coloured red or blue. Prove that four points among these 55 points have the same colour and form the vertices of a cyclic quadrilateral.
|
| 36 |
+
|
| 37 |
+
Solution: We first observe that all the eleven pentagons are regular. Moreover, there are 5 fixed directions and all the 55 sides are in one of these directions. If we consider any two sides which are parallel, they are the parallel sides of an isosceles trapezium, which is cyclic.
|
| 38 |
+
|
| 39 |
+
If we consider any pentagon, its two adjacent vertices have the same colour. Consider all such 11 sides whose end points are of the same colour. These are in 5 fixed directions. By pigeon-hole principle, there are 3 sides which are in the same directions and therefore parallel to each other. Among these three sides, two must have end points having one colour (again by $\mathrm{P}-\mathrm{H}$ principle). Thus there are two parallel sides among the 55 and the end points of these have one fixed colour. But these two sides are parallel sides of an isosceles trapezium. Hence the four end points are concyclic.
|
| 40 |
+
|
| 41 |
+
3. Let $m, n$ be distinct positive integers. Prove that
|
| 42 |
+
|
| 43 |
+
$$
|
| 44 |
+
\operatorname{gcd}(m, n)+\operatorname{gcd}(m+1, n+1)+\operatorname{gcd}(m+2, n+2) \leq 2|m-n|+1
|
| 45 |
+
$$
|
| 46 |
+
|
| 47 |
+
Further, determine when equality holds.
|
| 48 |
+
|
| 49 |
+
Solution: Observe that
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
\operatorname{gcd}(m+j, n+j)=\operatorname{gcd}(m+j,|m-n|)
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
for $j=0,1,2$. Hence we can find positive integers $a, b, c$ such that
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
\operatorname{gcd}(m, n)=\frac{|m-n|}{a}, \quad \operatorname{gcd}(m+1, n+1)=\frac{|m-n|}{b}, \quad \operatorname{gcd}(m+2, n+2)=\frac{|m-n|}{c}
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
It follows that $|m-n|$ divides $m a,(m+1) b$ and $(m+2) c$. Hence we can see that $|m-n|$ divides $a b$ and $b c$. We get $|m-n| \leq a b$ and $|m-n| \leq b c$. This leads to
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
b \geq \frac{|m-n|}{a}, \quad b \geq \frac{|m-n|}{c}
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
Thus
|
| 68 |
+
|
| 69 |
+
$$
|
| 70 |
+
\begin{aligned}
|
| 71 |
+
\operatorname{gcd}(m, n)+\operatorname{gcd}(m+1, n+1)+\operatorname{gcd}(m+2, & n+2) \\
|
| 72 |
+
& =\frac{|m-n|}{a}+\frac{|m-n|}{b}+\frac{|m-n|}{c} \leq 2 b+\frac{|m-n|}{b}
|
| 73 |
+
\end{aligned}
|
| 74 |
+
$$
|
| 75 |
+
|
| 76 |
+
We have to prove that
|
| 77 |
+
|
| 78 |
+
$$
|
| 79 |
+
2 b+\frac{|m-n|}{b} \leq 2|m-n|+1
|
| 80 |
+
$$
|
| 81 |
+
|
| 82 |
+
Taking $|m-n|=K$, we have to show that $2 b^{2}+K \leq b(2 K+1)$. This reduces to $(b-K)(2 b-1) \leq 0$. However
|
| 83 |
+
|
| 84 |
+
$$
|
| 85 |
+
K=|m-n| \geq b \geq 1>\frac{1}{2}
|
| 86 |
+
$$
|
| 87 |
+
|
| 88 |
+
Equality holds only when $(m, n)=(k, k+1)$ or $(2 k, 2 k+2)$ or permutations of these for some $k$.
|
| 89 |
+
|
| 90 |
+
4. Let $n$ and $M$ be positive integers such that $M>n^{n-1}$. Prove that there are $n$ distinct primes $p_{1}, p_{2}, p_{3}, \ldots, p_{n}$ such that $p_{j}$ divides $M+j$ for $1 \leq j \leq n$.
|
| 91 |
+
|
| 92 |
+
Solution: If some number $M+k, 1 \leq k \leq n$, has at least $n$ distinct prime factors, then we can associate a prime factor of $M+k$ with the number $M+k$ which is not associated with any of the remaining $n-1$ numbers.
|
| 93 |
+
|
| 94 |
+
Suppose $m+j$ has less than $n$ distinct prime factors. Write
|
| 95 |
+
|
| 96 |
+
$$
|
| 97 |
+
M+j=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \cdots p_{r}^{\alpha_{r}}, \quad r<n
|
| 98 |
+
$$
|
| 99 |
+
|
| 100 |
+
But $M+j>n^{n-1}$. Hence there exist $t, 1 \leq t \leq r$ such that $p_{t}^{\alpha_{t}}>n$. Associate $p_{t}$ with this $M+j$. Suppose $p_{t}$ is associated with some $M+l$. Let $p_{t}^{\beta_{t}}$ be the largest power of $p_{t}$ dividing $M+l$. Then $p_{t}^{\beta_{t}}>n$. Let $T=\operatorname{gcd}\left(p_{t}^{\alpha_{t}}, p_{t}^{\beta_{t}}\right)$. Then $T>n$. Since $T \mid(M+j)$ and $T \mid(M+l)$, it follows that $T \mid(|j-l|)$. But $|j-l|<n$ and $T>n$, and we get a contradiction. This shows that $p_{t}$ cannot be associated with any other $M+l$. Thus each $M+j$ is associated with different primes.
|
| 101 |
+
|
| 102 |
+
5. Let $A B$ be a diameter of a circle $\Gamma$ and let $C$ be a point on $\Gamma$ different from $A$ and $B$. Let $D$ be the foot of perpendicular from $C$ on to $A B$. Let $K$ be a point of the segment $C D$ such that $A C$ is equal to the semiperimeter of the triangle $A D K$. Show that the excircle of triangle $A D K$ opposite $A$ is tangent to $\Gamma$.
|
| 103 |
+
|
| 104 |
+
Solution: Draw another diameter $P Q \perp A B$. Let $E$ be the point at which the excircle $\Gamma_{1}$ touches the line $A D$. Join $Q E$ and extend it to meet $\Gamma$ in $L$. Draw the diameter $E N$ of $\Gamma_{1}$ and draw $Q S \perp N E$ (extended). See the figure. We also observe that $D E=E M=E N / 2$.
|
| 105 |
+
|
| 106 |
+
|
| 107 |
+
|
| 108 |
+
Since $A E$ is equal to the semiperimeter of $\triangle A D K$, we have $A C=A E$. Hence $A E^{2}=A C^{2}=$ $A D \cdot A B$ (as $A C B$ is a right-angle triangle). Thus
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
A D(A D+D E+E B)=(A D+D E)^{2}=A D^{2}+2 A D \cdot D E+D E^{2}
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
Simplification gives
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
\begin{aligned}
|
| 118 |
+
A D \cdot E B & =A D \cdot D E+D E^{2} \\
|
| 119 |
+
& =D E(A D+D E) \\
|
| 120 |
+
& =D E \cdot A E \\
|
| 121 |
+
& =D E(A B-B E)
|
| 122 |
+
\end{aligned}
|
| 123 |
+
$$
|
| 124 |
+
|
| 125 |
+
Therefore
|
| 126 |
+
|
| 127 |
+
$$
|
| 128 |
+
D E \cdot A B=E B(A D+D E)=E B \cdot A E
|
| 129 |
+
$$
|
| 130 |
+
|
| 131 |
+
But
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
D E \cdot A B=D E \cdot P Q=2 D E \cdot O Q=E N \cdot E S
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
and $E B \cdot A E=Q E \cdot E L$. Therefore we get
|
| 138 |
+
|
| 139 |
+
$$
|
| 140 |
+
Q E \cdot E L=E N \cdot E S
|
| 141 |
+
$$
|
| 142 |
+
|
| 143 |
+
It follows that $Q, S, L, N$ are concyclic. Since $\angle Q S E=90^{\circ}$, we get $\angle E L N=90^{\circ}$. Since $E N$ is a diameter, this implies that $L$ also lies on $\Gamma_{1}$. But $\angle Q L P=90^{\circ}$. Therefore $L, N, P$ are collinear. Since $N M \| P O$ and
|
| 144 |
+
|
| 145 |
+
$$
|
| 146 |
+
\frac{N M}{P O}=\frac{N E}{P Q}=\frac{L N}{L P}
|
| 147 |
+
$$
|
| 148 |
+
|
| 149 |
+
it follows that $L, M, O$ are collinear. Hence $\Gamma_{1}$ is tangent to $\Gamma$ at $L$.
|
| 150 |
+
|
| 151 |
+
Alternate solution: Let $R$ be the radius the circle $\Gamma$ and $r$ be that of the circle $\Gamma_{1}$. Let $O$ be the centre of $\Gamma$ and $M$ be that of the circle $\Gamma_{1}$. Let $E$ be the point of contact of $\Gamma_{1}$ with $A B$. Then $M E=D E=r$. Observe that $A E$ is the semiperimeter of $\triangle A D E$. We are given that $A C=A E$. Using that $\angle A C B=90^{\circ}$, we also get $A C^{2}=A D \cdot A B$. Hence $A E^{2}=A D \cdot A B$. We have to show that $R-r=O M$ for proving that $\Gamma_{1}$ is tangent to $\Gamma$. We have
|
| 152 |
+
|
| 153 |
+
$$
|
| 154 |
+
\begin{aligned}
|
| 155 |
+
& O M^{2}-(R-r)^{2}=O E^{2}+r^{2}-(R-r)^{2}=(A D+D E-A O)^{2}+r^{2}-(R-r)^{2} \\
|
| 156 |
+
&=(A D-(R-r))^{2}+r^{2}-(R-r)^{2}=A D^{2}-2 A D \cdot(R-r)+r^{2} \\
|
| 157 |
+
&=\left(A D^{2}+2 A D \cdot r+r^{2}\right)-2 A D \cdot R=(A D+r)^{2}-A D \cdot A B \\
|
| 158 |
+
&=(A D+D E)^{2}-A D \cdot A B=A E^{2}-A D \cdot A B=0
|
| 159 |
+
\end{aligned}
|
| 160 |
+
$$
|
| 161 |
+
|
| 162 |
+
Hence $O M=R-r$ and therefore $\Gamma_{1}$ is tangent to $\Gamma$.
|
| 163 |
+
|
| 164 |
+
6. Let $f$ be function defined from the set $\{(x, y): x, y$ reals, $x y \neq 0\}$ in to the set of all positive real numbers such that
|
| 165 |
+
|
| 166 |
+
(i) $\quad f(x y, z)=f(x, z) f(y, z)$, for all $x, y \neq 0$;
|
| 167 |
+
|
| 168 |
+
(ii) $\quad f(x, y z)=f(x, y) f(x, z)$, for all $x, y \neq 0$;
|
| 169 |
+
|
| 170 |
+
(iii) $\quad f(x, 1-x)=1$, for all $x \neq 0,1$.
|
| 171 |
+
|
| 172 |
+
Prove that
|
| 173 |
+
|
| 174 |
+
(a) $\quad f(x, x)=f(x,-x)=1$, for all $x \neq 0$;
|
| 175 |
+
|
| 176 |
+
(b) $\quad f(x, y) f(y, x)=1$, for all $x, y \neq 0$.
|
| 177 |
+
|
| 178 |
+
Solution: (The condition (ii) was inadvertently left out in the paper. We give the solution with condition (ii).)
|
| 179 |
+
|
| 180 |
+
Taking $x=y=1$ in (ii), weget $f(1, z)^{2}=f(1, z)$ so that $f(1, z)=1$ for all $z \neq 0$. Similarly, $x=y=-1$ gives $f(-1, z)=1$ for all $z \neq 0$. Using the second condition, we also get $f(z, 1)=$ $f(z,-1)=1$ for all $z \neq 0$. Observe
|
| 181 |
+
|
| 182 |
+
$$
|
| 183 |
+
f\left(\frac{1}{x}, y\right) f(x, y)=f(1, y)=1=f(x, 1)=f\left(x, \frac{1}{y}\right) f(x, y)
|
| 184 |
+
$$
|
| 185 |
+
|
| 186 |
+
Therefore
|
| 187 |
+
|
| 188 |
+
$$
|
| 189 |
+
f\left(x, \frac{1}{y}\right)=f\left(\frac{1}{x}, y\right)=\frac{1}{f(x, y)}
|
| 190 |
+
$$
|
| 191 |
+
|
| 192 |
+
for all $x, y \neq 0$. Now for $x \neq 0,1$, condition (iii) gives
|
| 193 |
+
|
| 194 |
+
$$
|
| 195 |
+
1=f\left(\frac{1}{x}, 1-\frac{1}{x}\right)=f\left(x, \frac{1}{1-\frac{1}{x}}\right)
|
| 196 |
+
$$
|
| 197 |
+
|
| 198 |
+
Multiplying by $1=f(x, 1-x)$, we get
|
| 199 |
+
|
| 200 |
+
$$
|
| 201 |
+
1=f(x, 1-x) f\left(x, \frac{1}{1-\frac{1}{x}}\right)=f\left(x, \frac{1-x}{1-\frac{1}{x}}\right)=f(x,-x)
|
| 202 |
+
$$
|
| 203 |
+
|
| 204 |
+
for all $x \neq 0,1$. But $f(x,-1)=1$ for all $x \neq 0$ gives
|
| 205 |
+
|
| 206 |
+
$$
|
| 207 |
+
f(x, x)=f(x,-x) f(x,-1)=f(x,-x)=1
|
| 208 |
+
$$
|
| 209 |
+
|
| 210 |
+
for all $x \neq 0,1$. Observe $f(1,1)=f(1,-1)=1$. Hence
|
| 211 |
+
|
| 212 |
+
$$
|
| 213 |
+
f(x, x)=f(x,-x)=1
|
| 214 |
+
$$
|
| 215 |
+
|
| 216 |
+
for all $x \neq 0$, which proves (a).
|
| 217 |
+
|
| 218 |
+
We have
|
| 219 |
+
|
| 220 |
+
$$
|
| 221 |
+
1=f(x y, x y)=f(x, x y) f(y, x y)=f(x, x) f(x, y) f(y, x) f(y, y)=f(x, y) f(y, x)
|
| 222 |
+
$$
|
| 223 |
+
|
| 224 |
+
for all $x, y \neq 0$, which proves (b).
|
| 225 |
+
|
INMO/md/en-inmo-2014.md
ADDED
|
@@ -0,0 +1,51 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $29^{\text {th }}$ Indian National Mathematical Olympiad-2014
|
| 2 |
+
|
| 3 |
+
## February 02, 2014
|
| 4 |
+
|
| 5 |
+
1. In a triangle $A B C$, let $D$ be a point on the segment $B C$ such that $A B+B D=A C+C D$. Suppose that the points $B, C$ and the centroids of triangles $A B D$ and $A C D$ lie on a circle. Prove that $A B=A C$.
|
| 6 |
+
|
| 7 |
+
Solution. Let $G_{1}, G_{2}$ denote the centroids of triangles $A B D$ and $A C D$. Then $G_{1}, G_{2}$ lie on the line parallel to $B C$ that passes through the centriod of triangle $A B C$. Therefore $B G_{1} G_{2} C$ is an isosceles trapezoid. Therefore it follows that $B G_{1}=C G_{2}$. This proves that $A B^{2}+B D^{2}=A C^{2}+C D^{2}$. Hence it follows that $A B \cdot B D=A C \cdot C D$. Therefore the sets $\{A B, B D\}$ and $\{A C, C D\}$ are the same (since they are both equal to the set of roots of the same polynomial). Note that if $A B=C D$ then $A C=B D$ and then $A B+A C=B C$, a contradiction. Therefore it follows that $A B=A C$.
|
| 8 |
+
|
| 9 |
+
2. Let $n$ be a natural number. Prove that
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\left[\frac{n}{1}\right]+\left[\frac{n}{2}\right]+\left[\frac{n}{3}\right]+\cdots\left[\frac{n}{n}\right]+[\sqrt{n}]
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
is even. (Here $[x]$ denotes the largest integer smaller than or equal to $x$.)
|
| 16 |
+
|
| 17 |
+
Solution. Let $f(n)$ denote the given equation. Then $f(1)=2$ which is even. Now suppose that $f(n)$ is even for some $n \geq 1$. Then
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
\begin{aligned}
|
| 21 |
+
f(n+1) & =\left[\frac{n+1}{1}\right]+\left[\frac{n+1}{2}\right]+\left[\frac{n+1}{3}\right]+\cdots\left[\frac{n+1}{n+1}\right]+[\sqrt{n+1}] \\
|
| 22 |
+
& =\left[\frac{n}{1}\right]+\left[\frac{n}{2}\right]+\left[\frac{n}{3}\right]+\cdots\left[\frac{n}{n}\right]+[\sqrt{n+1}]+\sigma(n+1)
|
| 23 |
+
\end{aligned}
|
| 24 |
+
$$
|
| 25 |
+
|
| 26 |
+
where $\sigma(n+1)$ denotes the number of positive divisors of $n+1$. This follows from $\left[\frac{n+1}{k}\right]=\left[\frac{n}{k}\right]+1$ if $k$ divides $n+1$, and $\left[\frac{n+1}{k}\right]=\left[\frac{n}{k}\right]$ otherwise. Note that $[\sqrt{n+1}]=[\sqrt{n}]$ unless $n+1$ is a square, in which case $[\sqrt{n+1}]=[\sqrt{n}]+1$. On the other hand $\sigma(n+1)$ is odd if and only if $n+1$ is a square. Therefore it follows that $f(n+1)=f(n)+2 l$ for some integer $l$. This proves that $f(n+1)$ is even.
|
| 27 |
+
|
| 28 |
+
Thus it follows by induction that $f(n)$ is even for all natural number $n$.
|
| 29 |
+
|
| 30 |
+
3. Let $a, b$ be natural numbers with $a b>2$. Suppose that the sum of their greatest common divisor and least common multiple is divisible by $a+b$. Prove that the quotient is at most $(a+b) / 4$. When is this quotient exactly equal to $(a+b) / 4$ ?
|
| 31 |
+
|
| 32 |
+
Solution. Let $g$ and $l$ denote the greatest common divisor and the least common multiple, respectively, of $a$ and $b$. Then $g l=a b$. Therefore $g+l \leq a b+1$. Suppose that $(g+l) /(a+b)>(a+b) / 4$. Then we have $a b+1>(a+b)^{2} / 4$, so we get $(a-b)^{2}<4$. Assuming, $a \geq b$ we either have $a=b$ or $a=b+1$. In the former case, $g=l=a$ and the quotient is $(g+l) /(a+b)=1 \leq(a+b) / 4$. In the latter case, $g=1$ and $l=b(b+1)$ so we get that $2 b+1$ divides $b^{2}+b+1$. Therefore $2 b+1$ divides $4\left(b^{2}+b+1\right)-(2 b+1)^{2}=3$ which implies that $b=1$ and $a=2$, a contradiction to the given assumption that $a b>2$. This shows that $(g+l) /(a+b) \leq(a+b) / 4$. Note that for the equality to hold, we need that either $a=b=2$ or, $(a-b)^{2}=4$ and $g=1, l=a b$. The latter case happens if and only if $a$ and $b$ are two consecutive odd numbers. (If $a=2 k+1$ and $b=2 k-1$ then $a+b=4 k$ divides $a b+1=4 k^{2}$ and the quotient is precisely $(a+b) / 4$.)
|
| 33 |
+
|
| 34 |
+
4. Written on a blackboard is the polynomial $x^{2}+x+2014$. Calvin and Hobbes take turns alternatively (starting with Calvin) in the following game. During his turn, Calvin should either increase or decrease the coefficient of $x$ by 1. And during his turn, Hobbes should either increase or decrease the constant coefficient by 1. Calvin wins if at any point of time the polynomial on the blackboard at that instant has integer roots. Prove that Calvin has a winning strategy.
|
| 35 |
+
|
| 36 |
+
Solution. For $i \geq 0$, let $f_{i}(x)$ denote the polynomial on the blackboard after Hobbes' $i$-th turn. We let Calvin decrease the coefficient of $x$ by 1 . Therefore $f_{i+1}(2)=f_{i}(2)-1$ or $f_{i+1}(2)=f_{i}(2)-3$ (depending on whether Hobbes increases or decreases the constant term). So for some $i$, we have $0 \leq f_{i}(2) \leq 2$. If $f_{i}(2)=0$ then Calvin has won the game. If $f_{i}(2)=2$ then Calvin wins the game by reducing the coefficient of $x$ by 1 . If $f_{i}(2)=1$ then $f_{i+1}(2)=0$ or $f_{i+1}(2)=-2$. In the former case, Calvin has won the game and in the latter case Calvin wins the game by increasing the coefficient of $x$ by 1 .
|
| 37 |
+
|
| 38 |
+
5. In an acute-angled triangle $A B C$, a point $D$ lies on the segment $B C$. Let $O_{1}, O_{2}$ denote the circumcentres of triangles $A B D$ and $A C D$, respectively. Prove that the line joining the circumcentre of triangle $A B C$ and the orthocentre of triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{D}$ is parallel to $B C$.
|
| 39 |
+
|
| 40 |
+
Solution. Without loss of generality assume that $\angle A D C \geq 90^{\circ}$. Let $O$ denote the circumcenter of triangle $A B C$ and $K$ the orthocentre of triangle $O_{1} O_{2} D$. We shall first show that the points $O$ and $K$ lie on the circumcircle of triangle $A O_{1} O_{2}$. Note that circumcircles of triangles $A B D$ and $A C D$ pass through the points $A$ and $D$, so $A D$ is perpendicular to $O_{1} O_{2}$ and, triangle $A O_{1} O_{2}$ is congruent to triangle $D O_{1} O_{2}$. In particular, $\angle A O_{1} O_{2}=\angle O_{2} O_{1} D=\angle B$ since $O_{2} O_{1}$ is the perpendicular bisector of $A D$. On the other hand since $O O_{2}$ is the perpendicular bisector of $A C$ it follows that $\angle A O O_{2}=\angle B$. This shows that $O$ lies on the circumcircle of triangle $A O_{1} O_{2}$. Note also that, since $A D$ is perpendicular to $O_{1} O_{2}$, we have $\angle O_{2} K A=90^{\circ}-\angle O_{1} O_{2} K=$ $\angle O_{2} O_{1} D=\angle B$. This proves that $K$ also lies on the circumcircle of triangle $A O_{1} O_{2}$.
|
| 41 |
+
|
| 42 |
+
Therefore $\angle A K O=180^{\circ}-\angle A O_{2} O=\angle A D C$ and hence $O K$ is parallel to $B C$.
|
| 43 |
+
|
| 44 |
+
Remark. The result is true even for an obtuse-angled triangle.
|
| 45 |
+
|
| 46 |
+
6. Let $n$ be a natural number and $X=\{1,2, \ldots, n\}$. For subsets $A$ and $B$ of $X$ we define $A \Delta B$ to be the set of all those elements of $X$ which belong to exactly one of $A$ and $B$. Let $\mathcal{F}$ be a collection of subsets of $X$ such that for any two distinct elements $A$ and $B$ in $\mathcal{F}$ the set $A \Delta B$ has at least two elements. Show that $\mathcal{F}$ has at most $2^{n-1}$ elements. Find all such collections $\mathcal{F}$ with $2^{n-1}$ elements.
|
| 47 |
+
|
| 48 |
+
Solution. For each subset $A$ of $\{1,2, \ldots, n-1\}$, we pair it with $A \cup\{n\}$. Note that for any such pair $(A, B)$ not both $A$ and $B$ can be in $\mathcal{F}$. Since there are $2^{n-1}$ such pairs it follows that $\mathcal{F}$ can have at most $2^{n-1}$ elements.
|
| 49 |
+
|
| 50 |
+
We shall show by induction on $n$ that if $|\mathcal{F}|=2^{n-1}$ then $\mathcal{F}$ contains either all the subsets with odd number of elements or all the subsets with even number of elements. The result is easy to see for $n=1$. Suppose that the result is true for $n=m-1$. We now consider the case $n=m$. Let $\mathcal{F}_{1}$ be the set of those elements in $\mathcal{F}$ which contain $m$ and $\mathcal{F}_{2}$ be the set of those elements which do not contain $m$. By induction, $\mathcal{F}_{2}$ can have at most $2^{m-2}$ elements. Further, for each element $A$ of $\mathcal{F}_{1}$ we consider $A \backslash\{m\}$. This new collection also satisfies the required property, so it follows that $\mathcal{F}_{1}$ has at most $2^{m-2}$ elements. Thus, if $|\mathcal{F}|=2^{m-1}$ then it follows that $\left|\mathcal{F}_{1}\right|=\left|\mathcal{F}_{2}\right|=2^{m-2}$. Further, by induction hypothesis, $\mathcal{F}_{2}$ contains all those subsets of $\{1,2, \ldots, m-1\}$ with (say) even number of elements. It then follows that $\mathcal{F}_{1}$ contains all those subsets of $\{1,2, \ldots, m\}$ which contain the element $m$ and which contains an even number of elements. This proves that $\mathcal{F}$ contains either all the subsets with odd number of elements or all the subsets by even number of elements.
|
| 51 |
+
|
INMO/md/en-inmo2013-solutions.md
ADDED
|
@@ -0,0 +1,94 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Problems and solutions: INMO 2013
|
| 2 |
+
|
| 3 |
+
Problem 1. Let $\Gamma_{1}$ and $\Gamma_{2}$ be two circles touching each other externally at $R$. Let $l_{1}$ be a line which is tangent to $\Gamma_{2}$ at $P$ and passing through the center $O_{1}$ of $\Gamma_{1}$. Similarly, let $l_{2}$ be a line which is tangent to $\Gamma_{2}$ at $Q$ and passing through the center $O_{2}$ of $\Gamma_{2}$. Suppose $l_{1}$ and $l_{2}$ are not parallel and interesct at $K$. If $K P=K Q$, prove that the triangle $P Q R$ is equilateral.
|
| 4 |
+
|
| 5 |
+
Solution. Suppose that $P$ and $Q$ lie on the opposite sides of line joining $O_{1}$ and $O_{2}$. By symmetry we may assume that the configuration is as shown in the figure below. Then we have $K P>K O_{1}>K Q$ since $K O_{1}$ is the hypotenuse of triangle $K Q O_{1}$. This is a contradiction to the given assumption, and therefore $P$ and $Q$ lie on the same side of the line joining $O_{1}$ and $O_{2}$.
|
| 6 |
+
|
| 7 |
+
|
| 8 |
+
|
| 9 |
+
Since $K P=K Q$ it follows that $K$ lies on the radical axis of the given circles, which is the common tangent at $R$. Therefore $K P=K Q=K R$ and hence $K$ is the cirumcenter of $\triangle P Q R$.
|
| 10 |
+
|
| 11 |
+
|
| 12 |
+
|
| 13 |
+
On the other hand, $\triangle K Q O_{1}$ and $\triangle K R O_{1}$ are both right-angled triangles with $K Q=K R$ and $Q O_{1}=R O_{1}$, and hence the two triangles are congruent. Therefore $\widehat{Q K O_{1}}=\widehat{R K O_{1}}$, so $K O_{1}$, and hence $P K$ is perpendicular to $Q R$. Similarly, $Q K$ is perpendicular to $P R$, so it follows that $K$ is the orthocenter of $\triangle P Q R$. Hence we have that $\triangle P Q R$ is equilateral.
|
| 14 |
+
|
| 15 |
+
Alternate solution. We again rule out the possibility that $P$ and $Q$ are on the opposite side of the line joining $O_{1} O_{2}$, and assume that they are on the same side.
|
| 16 |
+
|
| 17 |
+
Observe that $\triangle K P O_{2}$ is congruent to $\triangle K Q O_{1}$ (since $K P=K Q$ ). Therefore $O_{1} P=O_{2} Q=r$ (say). In $\triangle O_{1} O_{2} Q$, we have $\widehat{O_{1} Q O_{2}}=\pi / 2$ and $R$ is the midpoint of the hypotenuse, so $R Q=$ $R O_{1}=r$. Therefore $\triangle O_{1} R Q$ is equilateral, so $\widehat{Q R O_{1}}=\pi / 3$. Similarly, $P R=r$ and $\widehat{P R O_{2}}=\pi / 3$, hence $\widehat{P R Q}=\pi / 3$. Since $P R=Q R$ it follows that $\triangle P Q R$ is equilateral.
|
| 18 |
+
|
| 19 |
+
Problem 2. Find all positive integers $m, n$, and primes $p \geq 5$ such that
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
m\left(4 m^{2}+m+12\right)=3\left(p^{n}-1\right)
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
Solution. Rewriting the given equation we have
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
4 m^{3}+m^{2}+12 m+3=3 p^{n}
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
The left hand side equals $(4 m+1)\left(m^{2}+3\right)$.
|
| 32 |
+
|
| 33 |
+
Suppose that $\left(4 m+1, m^{2}+3\right)=1$. Then $\left(4 m+1, m^{2}+3\right)=\left(3 p^{n}, 1\right),\left(3, p^{n}\right),\left(p^{n}, 3\right)$ or $\left(1,3 p^{n}\right)$, a contradiction since $4 m+1, m^{2}+3 \geq 4$. Therefore $\left(4 m+1, m^{2}+3\right)>1$.
|
| 34 |
+
|
| 35 |
+
Since $4 m+1$ is odd we have $\left(4 m+1, m^{2}+3\right)=\left(4 m+1,16 m^{2}+48\right)=(4 m+1,49)=7$ or 49 . This proves that $p=7$, and $4 m+1=3 \cdot 7^{k}$ or $7^{k}$ for some natural number $k$. If $(4 m+1,49)=7$ then we have $k=1$ and $4 m+1=21$ which does not lead to a solution. Therefore $\left(4 m+1, m^{2}+3\right)=49$. If $7^{3}$ divides $4 m+1$ then it does not divide $m^{2}+3$, so we get $m^{2}+3 \leq 3 \cdot 7^{2}<7^{3} \leq 4 m+1$. This implies $(m-2)^{2}<2$, so $m \leq 3$, which does not lead to a solution. Therefore we have $4 m+1=49$ which implies $m=12$ and $n=4$. Thus $(m, n, p)=(12,4,7)$ is the only solution.
|
| 36 |
+
|
| 37 |
+
Problem 3. Let $a, b, c, d$ be positive integers such that $a \geq b \geq c \geq d$. Prove that the equation $x^{4}-a x^{3}-b x^{2}-c x-d=0$ has no integer solution.
|
| 38 |
+
|
| 39 |
+
Solution. Suppose that $m$ is an integer root of $x^{4}-a x^{3}-b x^{2}-c x-d=0$. As $d \neq 0$, we have $m \neq 0$. Suppose now that $m>0$. Then $m^{4}-a m^{3}=b m^{2}+c m+d>0$ and hence $m>a \geq d$. On the other hand $d=m\left(m^{3}-a m^{2}-b m-c\right)$ and hence $m$ divides $d$, so $m \leq d$, a contradiction. If $m<0$, then writing $n=-m>0$ we have $n^{4}+a n^{3}-b n^{2}+c n-d=n^{4}+n^{2}(a n-b)+(c n-d)>0$, a contradiction. This proves that the given polynomial has no integer roots.
|
| 40 |
+
|
| 41 |
+
Problem 4. Let $n$ be a positive integer. Call a nonempty subset $S$ of $\{1,2, \ldots, n\}$ good if the arithmetic mean of the elements of $S$ is also an integer. Further let $t_{n}$ denote the number of good subsets of $\{1,2, \ldots, n\}$. Prove that $t_{n}$ and $n$ are both odd or both even.
|
| 42 |
+
|
| 43 |
+
Solution. We show that $T_{n}-n$ is even. Note that the subsets $\{1\},\{2\}, \cdots,\{n\}$ are good. Among the other good subsets, let $A$ be the collection of subsets with an integer average which belongs to the subset, and let $B$ be the collection of subsets with an integer average which is not a member of the subset. Then there is a bijection between $A$ and $B$, because removing the average takes a member of $A$ to a member of $B$; and including the average in a member of $B$ takes it to its inverse. So $T_{n}-n=|A|+|B|$ is even.
|
| 44 |
+
|
| 45 |
+
Alternate solution. Let $S=\{1,2, \ldots, n\}$. For a subset $A$ of $S$, let $\bar{A}=\{n+1-a \mid a \in A\}$. We call a subset $A$ symmetric if $\bar{A}=A$. Note that the arithmetic mean of a symmetric subset is $(n+1) / 2$. Therefore, if $n$ is even, then there are no symmetric good subsets, while if $n$ is odd then every symmetric subset is good.
|
| 46 |
+
|
| 47 |
+
If $A$ is a proper good subset of $S$, then so is $\bar{A}$. Therefore, all the good subsets that are not symmetric can be paired. If $n$ is even then this proves that $t_{n}$ is even. If $n$ is odd, we have to show that there are odd number of symmetric subsets. For this, we note that a symmetric subset contains the element $(n+1) / 2$ if and only if it has odd number of elements. Therefore, for any natural number $k$, the number of symmetric subsets of size $2 k$ equals the number of symmetric subsets of size $2 k+1$. The result now follows since there is exactly one symmetric subset with only one element.
|
| 48 |
+
|
| 49 |
+
Problem 5. In an acute triangle $A B C, O$ is the circumcenter, $H$ is the orthocenter and $G$ is the centroid. Let $O D$ be perpendicular to $B C$ and $H E$ be perpendicular to $C A$, with $D$ on $B C$ and $E$ on $C A$. Let $F$ be the midpoint of $A B$. Suppose the areas of triangles $O D C, H E A$ and $G F B$ are equal. Find all the possible values of $\widehat{C}$.
|
| 50 |
+
|
| 51 |
+
Solution. Let $R$ be the circumradius of $\triangle A B C$ and $\Delta$ its area. We have $O D=R \cos A$ and $D C=\frac{a}{2}$, so
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
[O D C]=\frac{1}{2} \cdot O D \cdot D C=\frac{1}{2} \cdot R \cos A \cdot R \sin A=\frac{1}{2} R^{2} \sin A \cos A
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
Again $H E=2 R \cos C \cos A$ and $E A=c \cos A$. Hence
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
[H E A]=\frac{1}{2} \cdot H E \cdot E A=\frac{1}{2} \cdot 2 R \cos C \cos A \cdot c \cos A=2 R^{2} \sin C \cos C \cos ^{2} A
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
Further
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
[G F B]=\frac{\Delta}{6}=\frac{1}{6} \cdot 2 R^{2} \sin A \sin B \sin C=\frac{1}{3} R^{2} \sin A \sin B \sin C
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
Equating (1) and (2) we get $\tan A=4 \sin C \cos C$. And equating (1) and (3), and using this relation we get
|
| 70 |
+
|
| 71 |
+
$$
|
| 72 |
+
\begin{aligned}
|
| 73 |
+
3 \cos A & =2 \sin B \sin C=2 \sin (C+A) \sin C \\
|
| 74 |
+
& =2(\sin C+\cos C \tan A) \sin C \cos A \\
|
| 75 |
+
& =2 \sin ^{2} C\left(1+4 \cos ^{2} C\right) \cos A
|
| 76 |
+
\end{aligned}
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
Since $\cos A \neq 0$ we get $3=2 t(-4 t+5)$ where $t=\sin ^{2} C$. This implies $(4 t-3)(2 t-1)=0$ and therefore, since $\sin C>0$, we get $\sin C=\sqrt{3} / 2$ or $\sin C=1 / \sqrt{2}$. Because $\triangle A B C$ is acute, it follows that $\widehat{C}=\pi / 3$ or $\pi / 4$.
|
| 80 |
+
|
| 81 |
+
We observe that the given conditions are satisfied in an equilateral triangle, so $\widehat{C}=\pi / 3$ is a possibility. Also, the conditions are satisfied in a triangle where $\widehat{C}=\pi / 4, \widehat{A}=\tan ^{-1} 2$ and $\widehat{B}=\tan ^{-1} 3$. Therefore $\widehat{C}=\pi / 4$ is also a possibility.
|
| 82 |
+
|
| 83 |
+
Thus the two possible values of $\widehat{C}$ are $\pi / 3$ and $\pi / 4$.
|
| 84 |
+
|
| 85 |
+
Problem 6. Let $a, b, c, x, y, z$ be positive real numbers such that $a+b+c=x+y+z$ and abc $=x y z$. Further, suppose that $a \leq x<y<z \leq c$ and $a<b<c$. Prove that $a=x, b=y$ and $c=z$.
|
| 86 |
+
|
| 87 |
+
Solution. Let
|
| 88 |
+
|
| 89 |
+
$$
|
| 90 |
+
f(t)=(t-x)(t-y)(t-z)-(t-a)(t-b)(t-c)
|
| 91 |
+
$$
|
| 92 |
+
|
| 93 |
+
Then $f(t)=k t$ for some constant $k$. Note that $k a=f(a)=(a-x)(a-y)(a-z) \leq 0$ and hence $k \leq 0$. Similarly, $k c=f(c)=(c-x)(c-y)(c-z) \geq 0$ and hence $k \geq 0$. Combining the two, it follows that $k=0$ and that $f(a)=f(c)=0$. These equalities imply that $a=x$ and $c=z$, and then it also follows that $b=y$.
|
| 94 |
+
|
INMO/md/en-inmosol-15.md
ADDED
|
@@ -0,0 +1,261 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Problems and Solutions: INMO-2015
|
| 2 |
+
|
| 3 |
+
1. Let $A B C$ be a right-angled triangle with $\angle B=90^{\circ}$. Let $B D$ be the altitude from $B$ on to $A C$. Let $P, Q$ and $I$ be the incentres of triangles $A B D, C B D$ and $A B C$ respectively. Show that the circumcentre of of the triangle $P I Q$ lies on the hypotenuse $A C$.
|
| 4 |
+
|
| 5 |
+
Solution: We begin with the following lemma:
|
| 6 |
+
|
| 7 |
+
Lemma: Let $X Y Z$ be a triangle with $\angle X Y Z=90+\alpha$. Construct an isosceles triangle $X E Z$, externally on the side $X Z$, with base angle $\alpha$. Then $E$ is the circumcentre of $\triangle X Y Z$.
|
| 8 |
+
|
| 9 |
+
Proof of the Lemma: Draw $E D \perp$ $X Z$. Then $D E$ is the perpendicular bisector of $X Z$. We also observe that $\angle X E D=\angle Z E D=90-\alpha$. Observe that $E$ is on the perpendicular bisector of $X Z$. Construct the circumcircle of $X Y Z$. Draw perpendicular bisector of $X Y$ and let it meet $D E$ in $F$. Then $F$ is the circumcentre of $\triangle X Y Z$. Join $X F$. Then $\angle X F D=90-\alpha$. But we know
|
| 10 |
+
|
| 11 |
+
|
| 12 |
+
that $\angle X E D=90-\alpha$. Hence $E=F$. Let $r_{1}, r_{2}$ and $r$ be the inradii of the triangles $A B D, C B D$ and $A B C$ respectively. Join $P D$ and $D Q$. Observe that $\angle P D Q=90^{\circ}$. Hence
|
| 13 |
+
|
| 14 |
+
$$
|
| 15 |
+
P Q^{2}=P D^{2}+D Q^{2}=2 r_{1}^{2}+2 r_{2}^{2}
|
| 16 |
+
$$
|
| 17 |
+
|
| 18 |
+
Let $s_{1}=(A B+B D+D A) / 2$. Observe that $B D=c a / b$ and $A D=$ $\sqrt{A B^{2}-B D^{2}}=\sqrt{c^{2}-\left(\frac{c a}{b}\right)^{2}}=c^{2} / b$. This gives $s_{1}=c s / b$. But $r_{1}=$ $s_{1}-c=(c / b)(s-b)=c r / b$. Similarly, $r_{2}=a r / b$. Hence
|
| 19 |
+
|
| 20 |
+
$$
|
| 21 |
+
P Q^{2}=2 r^{2}\left(\frac{c^{2}+a^{2}}{b^{2}}\right)=2 r^{2}
|
| 22 |
+
$$
|
| 23 |
+
|
| 24 |
+
Consider $\triangle P I Q$. Observe that $\angle P I Q=90+(B / 2)=135$. Hence $P Q$ subtends $90^{\circ}$ on the circumference of the circumcircle of $\triangle P I Q$. But we have seen that $\angle P D Q=90^{\circ}$. Now construct a circle with $P Q$ as diameter. Let it cut $A C$ again in $K$. It follows that $\angle P K Q=90^{\circ}$ and the points $P, D, K, Q$ are concyclic. We also notice $\angle K P Q=\angle K D Q=45^{\circ}$
|
| 25 |
+
|
| 26 |
+
|
| 27 |
+
and $\angle P Q K=\angle P D A=45^{\circ}$.
|
| 28 |
+
|
| 29 |
+
Thus $P K Q$ is an isosceles right-angled triangle with $K P=K Q$. Therfore $K P^{2}+K Q^{2}=P Q^{2}=2 r^{2}$ and hence $K P=K Q=r$.
|
| 30 |
+
|
| 31 |
+
Now $\angle P I Q=90+45$ and $\angle P K Q=2 \times 45^{\circ}=90^{\circ}$ with $K P=K Q=r$.
|
| 32 |
+
|
| 33 |
+
Hence $K$ is the circumcentre of $\triangle P I Q$.
|
| 34 |
+
|
| 35 |
+
(Incidentally, This also shows that $K I=r$ and hence $K$ is the point of contact of the incircle of $\triangle A B C$ with $A C$.)
|
| 36 |
+
|
| 37 |
+
Solution 2: Here we use computation to prove that the point of contact $K$ of the incircle with $A C$ is the circumcentre of $\triangle P I Q$. We show that $K P=K Q=r$. Let $r_{1}$ and $r_{2}$ be the inradii of triangles $A B D$ and $C B D$ respectively. Draw $P L \perp A C$ and $Q M \perp A C$. If $s_{1}$ is the semiperimeter of $\triangle A B D$, then $A L=s_{1}-B D$.
|
| 38 |
+
|
| 39 |
+
|
| 40 |
+
|
| 41 |
+
But
|
| 42 |
+
|
| 43 |
+
$$
|
| 44 |
+
s_{1}=\frac{A B+B D+D A}{2}, \quad B D=\frac{c a}{b}, \quad A D=\frac{c^{2}}{b}
|
| 45 |
+
$$
|
| 46 |
+
|
| 47 |
+
Hence $s_{1}=c s / b$. This gives $r_{1}=s_{1}-c=c r / b, A L=s_{1}-B D=c(s-a) / b$. Hence $K L=A K-A L=(s-a)-\frac{c(s-a)}{b}=\frac{(b-c)(s-a)}{b}$. We observe that $2 r^{2}=\frac{(c+a-b)^{2}}{2}=\frac{c^{2}+a^{2}+b^{2}-2 b c-2 a b+2 c a}{2}=\left(b^{2}-b a-b c+a c\right)=(b-c)(b-a)$.
|
| 48 |
+
|
| 49 |
+
This gives
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
\begin{aligned}
|
| 53 |
+
(s-a)(b-c)=(s-b+b-a) & (b-c)=r(b-c)+(b-a)(b-c) \\
|
| 54 |
+
& =r(b-c)+2 r^{2}=r(b-c+c+a-b)=r a
|
| 55 |
+
\end{aligned}
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
Thus $K L=r a / b$. Finally,
|
| 59 |
+
|
| 60 |
+
$$
|
| 61 |
+
K P^{2}=K L^{2}+L P^{2}=\frac{r^{2} a^{2}}{b^{2}}+\frac{r^{2}+c^{2}}{b^{2}}=r^{2}
|
| 62 |
+
$$
|
| 63 |
+
|
| 64 |
+
Thus $K P=r$. Similarly, $K Q=r$. This gives $K P=K I=K Q=r$ and therefore $K$ is the circumcentre of $\triangle K I Q$.
|
| 65 |
+
|
| 66 |
+
(Incidentally, this also shows that $K L=c a / b=r_{2}$ and $K M=r_{1}$.)
|
| 67 |
+
|
| 68 |
+
2. For any natural number $n>1$, write the infinite decimal expansion of $1 / n$ (for example, we write $1 / 2=0.4 \overline{9}$ as its infinite decimal expansion, not 0.5 ). Determine the length of the non-periodic part of the (infinite) decimal expansion of $1 / n$.
|
| 69 |
+
|
| 70 |
+
Solution: For any prime $p$, let $\nu_{p}(n)$ be the maximum power of $p$ dividing $n$; ie $p^{\nu_{p}(n)}$ divides $n$ but not higher power. Let $r$ be the
|
| 71 |
+
length of the non-periodic part of the infinite decimal expansion of $1 / n$.
|
| 72 |
+
|
| 73 |
+
Write
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
\frac{1}{n}=0 . a_{1} a_{2} \cdots a_{r} \overline{b_{1} b_{2} \cdots b_{s}}
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
We show that $r=\max \left(\nu_{2}(n), \nu_{5}(n)\right)$.
|
| 80 |
+
|
| 81 |
+
Let $a$ and $b$ be the numbers $a_{1} a_{2} \cdots a_{r}$ and $b=b_{1} b_{2} \cdots b_{s}$ respectively. (Here $a_{1}$ and $b_{1}$ can be both 0.) Then
|
| 82 |
+
|
| 83 |
+
$$
|
| 84 |
+
\frac{1}{n}=\frac{1}{10^{r}}\left(a+\sum_{k \geq 1} \frac{b}{\left(10^{s}\right)^{k}}\right)=\frac{1}{10^{r}}\left(a+\frac{b}{10^{s}-1}\right)
|
| 85 |
+
$$
|
| 86 |
+
|
| 87 |
+
Thus we get $10^{r}\left(10^{s}-1\right)=n\left(\left(10^{s}-1\right) a+b\right)$. It shows that $r \geq$ $\max \left(\nu_{2}(n), \nu_{5}(n)\right)$. Suppose $r>\max \left(\nu_{2}(n), \nu_{5}(n)\right)$. Then 10 divides $b-a$. Hence the last digits of $a$ and $b$ are equal: $a_{r}=b_{s}$. This means
|
| 88 |
+
|
| 89 |
+
$$
|
| 90 |
+
\frac{1}{n}=0 . a_{1} a_{2} \cdots a_{r-1} \overline{b_{s} b_{1} b_{2} \cdots b_{s-1}}
|
| 91 |
+
$$
|
| 92 |
+
|
| 93 |
+
This contradicts the definition of $r$. Therefore $r=\max \left(\nu_{2}(n), \nu_{5}(n)\right)$.
|
| 94 |
+
|
| 95 |
+
3. Find all real functions $f$ from $\mathbb{R} \rightarrow \mathbb{R}$ satisfying the relation
|
| 96 |
+
|
| 97 |
+
$$
|
| 98 |
+
f\left(x^{2}+y f(x)\right)=x f(x+y)
|
| 99 |
+
$$
|
| 100 |
+
|
| 101 |
+
Solution: Put $x=0$ and we get $f(y f(0))=0$. If $f(0) \neq 0$, then $y f(0)$ takes all real values when $y$ varies over real line. We get $f(x) \equiv 0$. Suppose $f(0)=0$. Taking $y=-x$, we get $f\left(x^{2}-x f(x)\right)=0$ for all real $x$.
|
| 102 |
+
|
| 103 |
+
Suppose there exists $x_{0} \neq 0$ in $\mathbb{R}$ such that $f\left(x_{0}\right)=0$. Putting $x=x_{0}$ in the given relation we get
|
| 104 |
+
|
| 105 |
+
$$
|
| 106 |
+
f\left(x_{0}^{2}\right)=x_{0} f\left(x_{0}+y\right)
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
for all $y \in \mathbb{R}$. Now the left side is a constant and hence it follows that $f$ is a constant function. But the only constant function which satisfies the equation is identically zero function, which is already obtained. Hence we may consider the case where $f(x) \neq 0$ for all $x \neq 0$.
|
| 110 |
+
|
| 111 |
+
Since $f\left(x^{2}-x f(x)\right)=0$, we conclude that $x^{2}-x f(x)=0$ for all $x \neq 0$. This implies that $f(x)=x$ for all $x \neq 0$. Since $f(0)=0$, we conclude that $f(x)=x$ for all $x \in R$.
|
| 112 |
+
|
| 113 |
+
Thus we have two functions: $f(x) \equiv 0$ and $f(x)=x$ for all $x \in \mathbb{R}$.
|
| 114 |
+
|
| 115 |
+
4. There are four basket-ball players $A, B, C, D$. Initially, the ball is with $A$. The ball is always passed from one person to a different person. In how many ways can the ball come back to $A$ after seven passes? (For example $A \rightarrow C \rightarrow B \rightarrow D \rightarrow A \rightarrow B \rightarrow C \rightarrow A$ and
|
| 116 |
+
$A \rightarrow D \rightarrow A \rightarrow D \rightarrow C \rightarrow A \rightarrow B \rightarrow A$ are two ways in which the ball can come back to $A$ after seven passes.)
|
| 117 |
+
|
| 118 |
+
Solution: Let $x_{n}$ be the number of ways in which $A$ can get back the ball after $n$ passes. Let $y_{n}$ be the number of ways in which the ball goes back to a fixed person other than $A$ after $n$ passes. Then
|
| 119 |
+
|
| 120 |
+
$$
|
| 121 |
+
x_{n}=3 y_{n-1} \text {, }
|
| 122 |
+
$$
|
| 123 |
+
|
| 124 |
+
and
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
y_{n}=x_{n-1}+2 y_{n-1}
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
We also have $x_{1}=0, x_{2}=3, y_{1}=1$ and $y_{2}=2$.
|
| 131 |
+
|
| 132 |
+
Eliminating $y_{n}$ and $y_{n-1}$, we get $x_{n+1}=3 x_{n-1}+2 x_{n}$. Thus
|
| 133 |
+
|
| 134 |
+
$$
|
| 135 |
+
\begin{aligned}
|
| 136 |
+
& x_{3}=3 x_{1}+2 x_{2}=2 \times 3=6 \\
|
| 137 |
+
& x_{4}=3 x_{2}+2 x_{3}=(3 \times 3)+(2 \times 6)=9+12=21 \\
|
| 138 |
+
& x_{5}=3 x_{3}+2 x_{4}=(3 \times 6)+(2 \times 21)=18+42=60 \\
|
| 139 |
+
& x_{6}=3 x_{4}+2 x_{5}=(3 \times 21)+(2 \times 60)=63+120=183 \\
|
| 140 |
+
& x_{7}=3 x_{5}+2 x_{6}=(3 \times 60)+(2 \times 183)=180+366=546
|
| 141 |
+
\end{aligned}
|
| 142 |
+
$$
|
| 143 |
+
|
| 144 |
+
Alternate solution: Since the ball goes back to one of the other 3 persons, we have
|
| 145 |
+
|
| 146 |
+
$$
|
| 147 |
+
x_{n}+3 y_{n}=3^{n}
|
| 148 |
+
$$
|
| 149 |
+
|
| 150 |
+
since there are $3^{n}$ ways of passing the ball in $n$ passes. Using $x_{n}=$ $3 y_{n-1}$, we obtain
|
| 151 |
+
|
| 152 |
+
$$
|
| 153 |
+
x_{n-1}+x_{n}=3^{n-1}
|
| 154 |
+
$$
|
| 155 |
+
|
| 156 |
+
with $x_{1}=0$. Thus
|
| 157 |
+
|
| 158 |
+
$$
|
| 159 |
+
\begin{array}{r}
|
| 160 |
+
x_{7}=3^{6}-x_{6}=3^{6}-3^{5}+x_{5}=3^{6}-3^{5}+3^{4}-x_{4}=3^{6}-3^{5}+3^{4}-3^{3}+x_{3} \\
|
| 161 |
+
=3^{6}-3^{5}+3^{4}-3^{3}+3^{2}-x_{2}=3^{6}-3^{5}+3^{4}-3^{3}+3^{2}-3 \\
|
| 162 |
+
=\left(2 \times 3^{5}\right)+\left(2 \times 3^{3}\right)+(2 \times 3)=486+54+6=546
|
| 163 |
+
\end{array}
|
| 164 |
+
$$
|
| 165 |
+
|
| 166 |
+
5. Let $A B C D$ be a convex quadrilateral. Let the diagonals $A C$ and $B D$ intersect in $P$. Let $P E, P F, P G$ and $P H$ be the altitudes from $P$ on to the sides $A B, B C, C D$ and $D A$ respectively. Show that $A B C D$ has an incircle if and only if
|
| 167 |
+
|
| 168 |
+
$$
|
| 169 |
+
\frac{1}{P E}+\frac{1}{P G}=\frac{1}{P F}+\frac{1}{P H}
|
| 170 |
+
$$
|
| 171 |
+
|
| 172 |
+
Solution: Let $A P=p, B P=q, C P=r, D P=s ; A B=a, B C=b$, $C D=c$ and $D A=d$. Let $\angle A P B=\angle C P D=\theta$. Then $\angle B P C=\angle D P A=$ $\pi-\theta$. Let us also write $P E=h_{1}, P F=h_{2}, P G=h_{3}$ and $P H=h_{4}$.
|
| 173 |
+
|
| 174 |
+
|
| 175 |
+
|
| 176 |
+
## Observe that
|
| 177 |
+
|
| 178 |
+
$$
|
| 179 |
+
h_{1} a=p q \sin \theta, \quad h_{2} b=q r \sin \theta, \quad h_{3} c=r s \sin \theta, \quad h_{4} d=s p \sin \theta
|
| 180 |
+
$$
|
| 181 |
+
|
| 182 |
+
Hence
|
| 183 |
+
|
| 184 |
+
$$
|
| 185 |
+
\frac{1}{h_{1}}+\frac{1}{h_{3}}=\frac{1}{h_{2}}+\frac{1}{h_{4}}
|
| 186 |
+
$$
|
| 187 |
+
|
| 188 |
+
is equivalent to
|
| 189 |
+
|
| 190 |
+
$$
|
| 191 |
+
\frac{a}{p q}+\frac{c}{r s}=\frac{b}{q r}+\frac{d}{s p}
|
| 192 |
+
$$
|
| 193 |
+
|
| 194 |
+
This is the same as
|
| 195 |
+
|
| 196 |
+
$$
|
| 197 |
+
a r s+c p q=b s p+d q r
|
| 198 |
+
$$
|
| 199 |
+
|
| 200 |
+
Thus we have to prove that $a+c=b+d$ if and only if $a r s+c p q=b s p+d q r$. Now we can write $a+c=b+d$ as
|
| 201 |
+
|
| 202 |
+
$$
|
| 203 |
+
a^{2}+c^{2}+2 a c=b^{2}+d^{2}+2 b d
|
| 204 |
+
$$
|
| 205 |
+
|
| 206 |
+
But we know that
|
| 207 |
+
|
| 208 |
+
$$
|
| 209 |
+
\begin{aligned}
|
| 210 |
+
& a^{2}=p^{2}+q^{2}-2 p q \cos \theta, \quad c^{2}=r^{2}+s^{2}-2 r s \cos \theta \\
|
| 211 |
+
& b^{2}=q^{2}+r^{2}+2 q r \cos \theta, \quad d^{2}=p^{2}+s^{2}+2 p s \cos \theta
|
| 212 |
+
\end{aligned}
|
| 213 |
+
$$
|
| 214 |
+
|
| 215 |
+
Hence $a+c=b+d$ is equivalent to
|
| 216 |
+
|
| 217 |
+
$$
|
| 218 |
+
-p q \cos \theta+-r s \cos \theta+a c=p s \cos \theta+q r \cos \theta+b d
|
| 219 |
+
$$
|
| 220 |
+
|
| 221 |
+
Similarly, by squaring ars $+c p q=b s p+d q r$ we can show that it is equivalent to
|
| 222 |
+
|
| 223 |
+
$$
|
| 224 |
+
-p q \cos \theta+-r s \cos \theta+a c=p s \cos \theta+q r \cos \theta+b d
|
| 225 |
+
$$
|
| 226 |
+
|
| 227 |
+
We conclude that $a+c=b+d$ is equivalent to $c p q+a r s=b p s+d q r$. Hence $A B C D$ has an in circle if and only if
|
| 228 |
+
|
| 229 |
+
$$
|
| 230 |
+
\frac{1}{h_{1}}+\frac{1}{h_{3}}=\frac{1}{h_{2}}+\frac{1}{h_{4}}
|
| 231 |
+
$$
|
| 232 |
+
|
| 233 |
+
6. From a set of 11 square integers, show that one can choose 6 numbers $a^{2}, b^{2}, c^{2}, d^{2}, e^{2}, f^{2}$ such that
|
| 234 |
+
|
| 235 |
+
$$
|
| 236 |
+
a^{2}+b^{2}+c^{2} \equiv d^{2}+e^{2}+f^{2} \quad(\bmod 12)
|
| 237 |
+
$$
|
| 238 |
+
|
| 239 |
+
Solution: The first observation is that we can find 5 pairs of squares such that the two numbers in a pair have the same parity. We can see this as follows:
|
| 240 |
+
|
| 241 |
+
| Odd numbers | Even numbers | Odd pairs | Even pairs | Total pairs |
|
| 242 |
+
| :---: | :---: | :---: | :---: | :---: |
|
| 243 |
+
| 0 | 11 | 0 | 5 | 5 |
|
| 244 |
+
| 1 | 10 | 0 | 5 | 5 |
|
| 245 |
+
| 2 | 9 | 1 | 4 | 5 |
|
| 246 |
+
| 3 | 8 | 1 | 4 | 5 |
|
| 247 |
+
| 4 | 7 | 2 | 3 | 5 |
|
| 248 |
+
| 5 | 6 | 2 | 3 | 5 |
|
| 249 |
+
| 6 | 5 | 3 | 2 | 5 |
|
| 250 |
+
| 7 | 4 | 3 | 2 | 5 |
|
| 251 |
+
| 8 | 3 | 4 | 1 | 5 |
|
| 252 |
+
| 9 | 2 | 4 | 1 | 5 |
|
| 253 |
+
| 10 | 1 | 5 | 0 | 5 |
|
| 254 |
+
| 11 | 0 | 5 | 0 | 5 |
|
| 255 |
+
|
| 256 |
+
Let us take such 5 pairs: say $\left(x_{1}^{2}, y_{1}^{2}\right),\left(x_{2}^{2}, y_{2}^{2}\right), \ldots,\left(x_{5}^{2}, y_{5}^{2}\right)$. Then $x_{j}^{2}-y_{j}^{2}$ is divisible by 4 for $1 \leq j \leq 5$. Let $r_{j}$ be the remainder when $x_{j}^{2}-y_{j}^{2}$ is divisible by $3,1 \leq j \leq 3$. We have 5 remainders $r_{1}, r_{2}, r_{3}, r_{4}, r_{5}$. But these can be 0,1 or 2 . Hence either one of the remainders occur 3 times or each of the remainders occur once. If, for example $r_{1}=r_{2}=r_{3}$, then 3 divides $r_{1}+r_{2}+r_{3}$; if $r_{1}=0, r_{2}=1$ and $r_{3}=2$, then again 3 divides $r_{1}+r_{2}+r_{3}$. Thus we can always find three remainders whose sum is divisible by 3 . This means we can find 3 pairs, say, $\left(x_{1}^{2}, y_{1}^{2}\right),\left(x_{2}^{2}, y_{2}^{2}\right),\left(x_{3}^{2}, y_{3}^{2}\right)$ such that 3 divides $\left(x_{1}^{2}-y_{1}^{2}\right)+\left(x_{2}^{2}-y_{2}^{2}\right)+\left(x_{3}^{2}-y_{3}^{2}\right)$. Since each difference is divisible by 4 , we conclude that we can find 6 numbers $a^{2}, b^{2}, c^{2}, d^{2}, e^{2}, f^{2}$ such that
|
| 257 |
+
|
| 258 |
+
$$
|
| 259 |
+
a^{2}+b^{2}+c^{2} \equiv d^{2}+e^{2}+f^{2} \quad(\bmod 12)
|
| 260 |
+
$$
|
| 261 |
+
|
INMO/md/en-sol-inmo-20.md
ADDED
|
@@ -0,0 +1,218 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Solutions to INMO-2020 problems
|
| 2 |
+
|
| 3 |
+
1. Let $\Gamma_{1}$ and $\Gamma_{2}$ be two circles of unequal radii, with centres $O_{1}$ and $O_{2}$ respectively, in the plane intersecting in two distinct points $A$ and $B$. Assume that the centre of each of the circles $\Gamma_{1}$ and $\Gamma_{2}$ is outside the other. The tangent to $\Gamma_{1}$ at $B$ intersects $\Gamma_{2}$ again in $C$, different from $B$; the tangent to $\Gamma_{2}$ at $B$ intersects $\Gamma_{1}$ again in $D$, different from $B$. The bisectors of $\angle D A B$ and $\angle C A B$ meet $\Gamma_{1}$ and $\Gamma_{2}$ again in $X$ and $Y$, respectively, different from $A$. Let $P$ and $Q$ be the circumcentres of triangles $A C D$ and $X A Y$, respectively. Prove that $P Q$ is the perpendicular bisector of the line segment $O_{1} O_{2}$.
|
| 4 |
+
|
| 5 |
+
## Solution:
|
| 6 |
+
|
| 7 |
+
|
| 8 |
+
|
| 9 |
+
Let $\angle C B A=\alpha$ and $\angle D B A=\beta$. Then $\angle B D A=\alpha$ and $\angle B C A=\beta$. We also observe that $\angle A O_{1} O_{2}=\left(\angle A O_{1} B / 2\right)=\alpha$ and, simiarly, $\angle A O_{2} O_{1}=\beta$. Hence
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\angle O_{1} A O_{2}=180^{\circ}-(\alpha+\beta)
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
We also have
|
| 16 |
+
|
| 17 |
+
$$
|
| 18 |
+
\angle P O_{1} A=\frac{\angle D O_{1} A}{2}=\frac{2 \angle D B A}{2}=\angle D B A=\beta
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
Hence $\angle P O_{1} O_{2}=\angle P O_{1} A+\angle A O_{1} O_{2}=\beta+\alpha$. Similarly, we can get $\angle P O_{2} O_{1}=\alpha+\beta$. It follows that $P$ lies on the perpendicular bisector of $\mathrm{O}_{1} \mathrm{O}_{2}$.
|
| 22 |
+
|
| 23 |
+
Now we observe that
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
\angle X Q Y=360^{\circ}-2 \angle X A Y=360^{\circ}-2\left(180^{\circ}-\alpha-\beta\right)=2(\alpha+\beta)
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
This gives
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
\angle O_{1} Q O_{2}=\frac{1}{2}(\angle X Q A+\angle Y Q A)=\frac{\angle X Q Y}{2}=\alpha+\beta
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
This shows that $A, O_{1}, O_{2}, Q$ are concyclic. We also have
|
| 36 |
+
|
| 37 |
+
$$
|
| 38 |
+
\begin{aligned}
|
| 39 |
+
& \angle A B X=\angle A B D+\angle D B X=\beta+\angle D A X=\beta+\frac{\angle D A B}{2} \\
|
| 40 |
+
& \angle A B Y=\angle A B C+\angle C B Y=\alpha+\angle C A Y=\alpha+\frac{\angle B A C}{2}
|
| 41 |
+
\end{aligned}
|
| 42 |
+
$$
|
| 43 |
+
|
| 44 |
+
Adding we obtain
|
| 45 |
+
|
| 46 |
+
$$
|
| 47 |
+
\angle A B X+\angle A B Y=\alpha+\beta+\frac{1}{2}(\angle D A B+\angle B A C)=\alpha+\beta+\left(180^{\circ}-\alpha-\beta\right)=180^{\circ}
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
Hence $X, B, Y$ are collinear. Now
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
\begin{gathered}
|
| 54 |
+
\angle Q A X=\frac{1}{2}\left(180^{\circ}-\angle A Q X\right)=90^{\circ}-\beta \\
|
| 55 |
+
\angle X A O_{1}=\frac{1}{2}\left(180^{\circ}-\angle X O_{1} A\right)=90^{\circ}-\frac{1}{2}\left(360^{\circ}-2 \angle A B X\right)=\angle A B X-90^{\circ}
|
| 56 |
+
\end{gathered}
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
Hence
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
\angle Q A O_{1}=90^{\circ}-\beta+\angle A B X-90^{\circ}=\angle A B X-\beta=\frac{\angle D A B}{2}=\frac{\angle O_{1} A O_{2}}{2}
|
| 63 |
+
$$
|
| 64 |
+
|
| 65 |
+
This shows that $A Q$ bisects $\angle O_{1} A O_{2}$ and therefore the chords $Q O_{1}$ and $Q O_{2}$ subtend equal angles on the circumference of the circle passing through $Q O_{2} A O_{1}$. Hence $Q O_{2}=Q O_{1}$. This means $Q$ lies on the perpendicular bisector of $\mathrm{O}_{1} \mathrm{O}_{2}$.
|
| 66 |
+
|
| 67 |
+
Combining, we get that $P Q$ is the perpendicular bisector of $O_{1} O_{2}$.
|
| 68 |
+
|
| 69 |
+
2. Suppose $P(x)$ is a polynomial with real coefficients satsfying the condition $P(\cos \theta+\sin \theta)=$ $P(\cos \theta-\sin \theta)$, for every real $\theta$. Prove that $P(x)$ can be expressed in the form
|
| 70 |
+
|
| 71 |
+
$$
|
| 72 |
+
P(x)=a_{0}+a_{1}\left(1-x^{2}\right)^{2}+a_{2}\left(1-x^{2}\right)^{4}+\cdots+a_{n}\left(1-x^{2}\right)^{2 n}
|
| 73 |
+
$$
|
| 74 |
+
|
| 75 |
+
for some real numbers $a_{0}, a_{1}, a_{2}, \ldots, a_{n}$ and nonnegative integer $n$.
|
| 76 |
+
|
| 77 |
+
Solution: Changing $\theta$ to $\theta-\pi / 2$, we see that
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
P(\sin \theta+\cos \theta)=P(\sin \theta-\cos \theta)
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
This shows that $P(x)=P(-x)$ for all $x \in[-\sqrt{2}, \sqrt{2}]$ and as $\mathrm{P}$ is a polynomial, in fact,
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
P(x)=P(-x)
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
for all $x \in \mathbb{R}$. Hence $P(x)$ is an even polynomial; $P(x)=Q\left(x^{2}\right)$ for some polynomial $Q(x)$. This gives
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
Q(1+\sin (2 \theta))=P(\cos \theta+\sin \theta)=P(\cos \theta-\sin \theta)=Q(1-\sin (2 \theta))
|
| 93 |
+
$$
|
| 94 |
+
|
| 95 |
+
Taking $t=\sin (2 \theta)$, we see that $Q(1+t)=Q(1-t)$. Hence $Q(0)=Q(2)$
|
| 96 |
+
|
| 97 |
+
Consider $Q(t)-Q(0)$. This vanishes both at $t=0$ and $t=2$. Hence $t(2-t)$ is a factor of $Q(t)-Q(0)$. We obtain
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
Q(t)-Q(0)=t(2-t) h(t)
|
| 101 |
+
$$
|
| 102 |
+
|
| 103 |
+
for some polynomial $h(t)$. Using $Q(1+t)=Q(1-t)$, it follows that $h(1+t)=h(1-t)$. Hence by induction we get
|
| 104 |
+
|
| 105 |
+
$$
|
| 106 |
+
Q(t)=\sum_{k=0}^{n} b_{k} t^{k}(2-t)^{k}
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
Hence
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
P(x)=Q\left(x^{2}\right)=\sum_{k=0}^{n} b_{k}\left(x^{2}\left(2-x^{2}\right)\right)^{k}=\sum_{k=0}^{n} b_{k}\left(1-\left(1-x^{2}\right)^{2}\right)^{k}
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
Using binomial theorem, we can write this as
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
P(x)=\sum_{k=0}^{n} a_{k}\left(1-x^{2}\right)^{2 k}
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
for some coefficients $a_{k}, 0 \leq k \leq n$.
|
| 122 |
+
|
| 123 |
+
3. Let $X=\{0,1,2,3,4,5,6,7,8,9\}$. Let $S \subseteq X$ be such that any nonnegative integer $n$ can be written as $p+q$ where the nonnegative integers $p, q$ have all their digits in $S$. Find the smallest possible number of elements in $S$.
|
| 124 |
+
|
| 125 |
+
Solution: We show that 5 numbers will suffice. Take $S=\{0,1,3,4,6\}$. Observe the following splitting:
|
| 126 |
+
|
| 127 |
+
| $n$ | $a$ | $b$ |
|
| 128 |
+
| :--- | :--- | :--- |
|
| 129 |
+
| 0 | 0 | 0 |
|
| 130 |
+
| 1 | 0 | 1 |
|
| 131 |
+
| 2 | 1 | 1 |
|
| 132 |
+
| 3 | 0 | 3 |
|
| 133 |
+
| 4 | 1 | 3 |
|
| 134 |
+
| 5 | 1 | 4 |
|
| 135 |
+
| 6 | 3 | 3 |
|
| 136 |
+
| 7 | 3 | 4 |
|
| 137 |
+
| 8 | 4 | 4 |
|
| 138 |
+
| 9 | 3 | 6 |
|
| 139 |
+
|
| 140 |
+
Thus each digit in a given nonnegative integer is split according to the above and can be written as a sum of two numbers each having digits in $S$.
|
| 141 |
+
|
| 142 |
+
We show that $|S|>4$. Suppose $|S| \leq 4$. We may take $|S|=4$ as adding extra numbers to $S$ does not alter our argument. Let $S=\{a, b, c, d\}$. Since the last digit can be any one of the numbers $0,1,2, \ldots, 9$, we must be able to write this as a sum of digits from $S$, modulo 10. Thus the collection
|
| 143 |
+
|
| 144 |
+
$$
|
| 145 |
+
A=\{x+y \quad(\bmod 10) \mid x, y \in S\}
|
| 146 |
+
$$
|
| 147 |
+
|
| 148 |
+
must contain $\{0,1,2, \ldots, 9\}$ as a subset. But $A$ has at most 10 elements $\left(\binom{4}{2}+4\right)$. Thus each element of the form $x+y(\bmod 10)$, as $x, y$ vary over $S$, must give different numbers from $\{0,1,2, \ldots, 9\}$.
|
| 149 |
+
|
| 150 |
+
Consider $a+a, b+b, c+c, d+d$ modulo 10. They must give 4 even numbers. Hence the remaining even number must be from the remaining 6 elements obtained by adding two distinct members of $S$. We may assume that even number is $a+b(\bmod 10)$. Then $a, b$ must have same parity. If any one of $c, d$ has same parity as that of $a$, then its sum with $a$ gives an even number, which is impossible. Hence $c, d$ must have same parity, in which case $c+d(\bmod 10)$ is even, which leads to a contradiction. We conclude that $|S| \geq 5$.
|
| 151 |
+
|
| 152 |
+
4. Let $n \geq 3$ be an integer and let $1<a_{1} \leq a_{2} \leq a_{3} \leq \cdots \leq a_{n}$ be $n$ real numbers such that $a_{1}+a_{2}+a_{3}+\cdots+a_{n}=2 n$. Prove that
|
| 153 |
+
|
| 154 |
+
$$
|
| 155 |
+
a_{1} a_{2} \cdots a_{n-1}+a_{1} a_{2} \cdots a_{n-2}+\cdots+a_{1} a_{2}+a_{1}+2 \leq a_{1} a_{2} \cdots a_{n}
|
| 156 |
+
$$
|
| 157 |
+
|
| 158 |
+
Solution: We use Chebyshev's inequality. Observe
|
| 159 |
+
|
| 160 |
+
$$
|
| 161 |
+
\begin{aligned}
|
| 162 |
+
& n\left(a_{1} a_{2} \cdots a_{n-1}+a_{1} a_{2} \cdots a_{n-2}+\cdots+a_{1}+1\right) \\
|
| 163 |
+
& \quad=\left(a_{1} a_{2} \cdots a_{n-1}+a_{1} a_{2} \cdots a_{n-2}+\cdots+a_{1}+1\right)\left(\left(a_{n}-1\right)+\left(a_{n-1}-1\right)+\cdots+\left(a_{1}-1\right)\right) \\
|
| 164 |
+
& \quad \leq n\left(a_{1} a_{2} \cdots a_{n-1}\left(a_{n}-1\right)+\cdots+a_{1}\left(a_{2}-1\right)+1\left(a_{1}-1\right)\right) \\
|
| 165 |
+
& \quad \leq n\left(a_{1} a_{2} \cdots a_{n}-1\right)
|
| 166 |
+
\end{aligned}
|
| 167 |
+
$$
|
| 168 |
+
|
| 169 |
+
It follows that
|
| 170 |
+
|
| 171 |
+
$$
|
| 172 |
+
a_{1} a_{2} \cdots a_{n-1}+a_{1} a_{2} \cdots a_{n-2}+\cdots+a_{1}+1 \leq a_{1} a_{2} \cdots a_{n}-1
|
| 173 |
+
$$
|
| 174 |
+
|
| 175 |
+
This gives the required inequality.
|
| 176 |
+
|
| 177 |
+
5. Infinitely many equidistant parallel lines are drawn in the plane. A positive integer $n \geq 3$ is called frameable if it is possible to draw a regular polygon with $n$ sides all whose vertices lie on these lines and no line contains more than one vertex of the polygon.
|
| 178 |
+
|
| 179 |
+
(a) Show that $3,4,6$ are frameable.
|
| 180 |
+
|
| 181 |
+
(b) Show that any integer $n \geq 7$ is not frameable.
|
| 182 |
+
(c) Determine whether 5 is frameable.
|
| 183 |
+
|
| 184 |
+
Solution: For $n=3,4,6$ it is possible to draw regular polygons with vertices on the parallel lines (note that when we show a regular hexagon is a framed polygon, it includes the equilateral triangle case).
|
| 185 |
+
|
| 186 |
+
|
| 187 |
+
|
| 188 |
+
Figure 1:
|
| 189 |
+
|
| 190 |
+
|
| 191 |
+
|
| 192 |
+
Figure 2:
|
| 193 |
+
|
| 194 |
+
|
| 195 |
+
|
| 196 |
+
Figure 3:
|
| 197 |
+
|
| 198 |
+
We will prove that it is not possible for $n \geq 7$. In fact, we prove a stronger statement that we can not draw other polygons with vertices on the lines (even if we allow more than one vertex to lie on the same line).
|
| 199 |
+
|
| 200 |
+
First observe that if $A, B$ are points on the lines and $C$ is another point on a line, if we locate
|
| 201 |
+
|
| 202 |
+
|
| 203 |
+
Figure 4:
|
| 204 |
+
|
| 205 |
+
|
| 206 |
+
Figure 5:
|
| 207 |
+
|
| 208 |
+
point $D$ such that $C D$ is parallel and equal to $A B$, then $D$ also lies on a line. Suppose that we have a regular polygon $A_{1} A_{2} \ldots A_{n}$, where $n \geq 6$, with all the vertices on the grid lines. Choose a point $O$ on a grid line and draw segments $O B_{i}$ equal and parallel to $A_{i} A_{i+1}$, for $i=1,2, \ldots, n-1$ and $O B_{n}$ parallel and equal to $A_{n} A_{1}$. The points $B_{i}$ also lie on the grid lines and form a regular polygon with $n$ sides. Consider the ratio $k=\frac{B_{1} B_{2}}{A_{1} A_{2}}$. Since $n>6$, the $\angle B_{1} O B_{2}<360^{\circ} / 6$ and hence is the smallest angle in the triangle $B_{1} O B_{2}$ (note that the triangle $B_{1} O B_{2}$ is isosceles). Thus $k<1$. Hence starting with a polygon with vertices on grid lines, we obtain another polygon with ratio of side lengths $k<1$. Repeating this process, we obtain a polygon with vertices on grid lines with ratio of sides $k^{m}$ for any $m$. This is a contradiction since the length of the side of a polygon with vertices on grid lines can not be less than the distance between the parallel lines. Thus for $n>6$, we can not draw a polygon with vertices on the grid lines.
|
| 209 |
+
|
| 210 |
+
The above proof fails for $n=5$. In this case, draw $O B_{1}, O B_{1}^{\prime}$ parallel and equal to $A_{1} A_{2}$, in opposite directions (see Figure 5), and similarly for other sides. Then we obtain a regular decagon with vertices on the grid lines and we have proved that this is impossible.
|
| 211 |
+
|
| 212 |
+
6. A stromino is a $3 \times 1$ rectangle. Show that a $5 \times 5$ board divided into twenty-five $1 \times 1$ squares
|
| 213 |
+
cannot be covered by 16 strominos such that each stromino covers exactly three unit squares of the board and every unit square is covered by either one or two strominos. (A stromino can be placed either horizontally or vertically on the board.)
|
| 214 |
+
|
| 215 |
+
Solution: Suppose on the contrary that it is possible to cover the board with 16 strominos such that each unit square is covered by either one or two strominos. If there are $k$ squares that are covered by exactly one stromino then $2(25-k)+k=163=48$ and hence $k=2$. Thus there are exactly two squares which are covered by only one stromino. We colour the board with three colours red, blue, green as follows. The square corresponding to the $i$-th row and the $j$-th column is coloured red if $i+j \equiv 0(\bmod 3)$, green if $i+j \equiv 1(\bmod 3)$ and blue otherwise. Then there are 9 red squares, 8 green squares and 8 blue squares. Note that each stromino covers exactly one square of each colour. Therefore the two squares that are covered by only one stromino are both red. For each such square $i+j \equiv 0(\bmod 3)$ where $i$ and $j$ are its row and column number.
|
| 216 |
+
|
| 217 |
+
We now colour the board with a different scheme. We colour the square corresponding to the $i$-th row and the $j$-th column red if $i-j \equiv(\bmod 3)$, green if $i-j \equiv 1(\bmod 3)$ and blue otherwise. Again, there are 9 red squares and hence the two squares covered by only one stromino are both red. For each such square $i-j \equiv 0(\bmod 3)$ where $i$ and $j$ are its row and columne number Thus, each of the two squares covered by only one stromino satisfies $i+j \equiv 0(\bmod 3)$ and $i-j \equiv 0$ $(\bmod 3)$ where $i$ and $j$ are its row and column number. This implies that $i=j=3$. This is a contradiction because there is only one such square.
|
| 218 |
+
|
INMO/md/en-sol-inmo16.md
ADDED
|
@@ -0,0 +1,505 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# INMO-2016 problems and solutions
|
| 2 |
+
|
| 3 |
+
1. Let $A B C$ be triangle in which $A B=A C$. Suppose the orthocentre of the triangle lies on the in-circle. Find the ratio $A B / B C$.
|
| 4 |
+
|
| 5 |
+
Solution: Since the triangle is isosceles, the orthocentre lies on the perpendicular $A D$ from $A$ on to $B C$. Let it cut the in-circle at $H$. Now we are given that $H$ is the orthocentre of the triangle. Let $A B=A C=b$ and $B C=2 a$. Then $B D=a$. Observe that $b>a$ since $b$ is the hypotenuse and $a$ is a leg of a right-angled triangle. Let $B H$ meet $A C$ in $E$ and $C H$ meet $A B$ in $F$. By Pythagoras theorem applied to $\triangle B D H$, we get
|
| 6 |
+
|
| 7 |
+
|
| 8 |
+
|
| 9 |
+
$$
|
| 10 |
+
B H^{2}=H D^{2}+B D^{2}=4 r^{2}+a^{2}
|
| 11 |
+
$$
|
| 12 |
+
|
| 13 |
+
where $r$ is the in-radius of $A B C$. We want to compute $B H$ in another way. Since $A, F, H, E$ are con-cyclic, we have
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
B H \cdot B E=B F \cdot B A
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
But $B F \cdot B A=B D \cdot B C=2 a^{2}$, since $A, F, D, C$ are con-cyclic. Hence $B H^{2}=4 a^{4} / B E^{2}$. But
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
B E^{2}=4 a^{2}-C E^{2}=4 a^{2}-B F^{2}=4 a^{2}-\left(\frac{2 a^{2}}{b}\right)^{2}=\frac{4 a^{2}\left(b^{2}-a^{2}\right)}{b^{2}}
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
This leads to
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
B H^{2}=\frac{a^{2} b^{2}}{b^{2}-a^{2}}
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
Thus we get
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
\frac{a^{2} b^{2}}{b^{2}-a^{2}}=a^{2}+4 r^{2}
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
This simplifies to $\left(a^{4} /\left(b^{2}-a^{2}\right)\right)=4 r^{2}$. Now we relate $a, b, r$ in another way using area. We know that $[A B C]=r s$, where $s$ is the semi-perimeter of $A B C$. We have $s=(b+b+2 a) / 2=b+a$. On the other hand area can be calculated using Heron's formula::
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
[A B C]^{2}=s(s-2 a)(s-b)(s-b)=(b+a)(b-a) a^{2}=a^{2}\left(b^{2}-a^{2}\right)
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
Hence
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
r^{2}=\frac{[A B C]^{2}}{s^{2}}=\frac{a^{2}\left(b^{2}-a^{2}\right)}{(b+a)^{2}}
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
Using this we get
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
\frac{a^{4}}{b^{2}-a^{2}}=4\left(\frac{a^{2}\left(b^{2}-a^{2}\right)}{(b+a)^{2}}\right)
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
Therefore $a^{2}=4(b-a)^{2}$, which gives $a=2(b-a)$ or $2 b=3 a$. Finally,
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
\frac{A B}{B C}=\frac{b}{2 a}=\frac{3}{4}
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
## Alternate Solution 1:
|
| 62 |
+
|
| 63 |
+
We use the known facts $B H=2 R \cos B$ and $r=4 R \sin (A / 2) \sin (B / 2) \sin (C / 2)$, where $R$ is the circumradius of $\triangle A B C$ and $r$ its in-radius. Therefore
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
H D=B H \sin \angle H B D=2 R \cos B \sin \left(\frac{\pi}{2}-C\right)=2 R \cos ^{2} B
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
since $\angle C=\angle B$. But $\angle B=(\pi-\angle A) / 2$, since $A B C$ is isosceles. Thus we obtain
|
| 70 |
+
|
| 71 |
+
$$
|
| 72 |
+
H D=2 R \cos ^{2}\left(\frac{\pi}{2}-\frac{A}{2}\right)
|
| 73 |
+
$$
|
| 74 |
+
|
| 75 |
+
However $H D$ is also the diameter of the in circle. Therefore $H D=2 r$. Thus we get
|
| 76 |
+
|
| 77 |
+
$$
|
| 78 |
+
2 R \cos ^{2}\left(\frac{\pi}{2}-\frac{A}{2}\right)=2 r=8 R \sin (A / 2) \sin ^{2}((\pi-A) / 4)
|
| 79 |
+
$$
|
| 80 |
+
|
| 81 |
+
This reduces to
|
| 82 |
+
|
| 83 |
+
$$
|
| 84 |
+
\sin (A / 2)=2(1-\sin (A / 2))
|
| 85 |
+
$$
|
| 86 |
+
|
| 87 |
+
Therefore $\sin (A / 2)=2 / 3$. We also observe that $\sin (A / 2)=B D / A B$. Finally
|
| 88 |
+
|
| 89 |
+
$$
|
| 90 |
+
\frac{A B}{B C}=\frac{A B}{2 B D}=\frac{1}{2 \sin (A / 2)}=\frac{3}{4}
|
| 91 |
+
$$
|
| 92 |
+
|
| 93 |
+
## Alternate Solution 2:
|
| 94 |
+
|
| 95 |
+
Let $D$ be the mid-point of $B C$. Extend $A D$ to meet the circumcircle in $L$. Then we know that $H D=D L$. But $H D=2 r$. Thus $D L=2 r$. Therefore $I L=I D+D L=r+2 r=3 r$. We also know that $L B=L I$. Therefore $L B=3 r$. This gives
|
| 96 |
+
|
| 97 |
+
$$
|
| 98 |
+
\frac{B L}{L D}=\frac{3 r}{2 r}=\frac{3}{2}
|
| 99 |
+
$$
|
| 100 |
+
|
| 101 |
+
But $\triangle B L D$ is similar to $\triangle A B D$. So
|
| 102 |
+
|
| 103 |
+
$$
|
| 104 |
+
\frac{A B}{B D}=\frac{B L}{L D}=\frac{3}{2}
|
| 105 |
+
$$
|
| 106 |
+
|
| 107 |
+
Finally,
|
| 108 |
+
|
| 109 |
+
$$
|
| 110 |
+
\frac{A B}{B C}=\frac{A B}{2 B D}=\frac{3}{4}
|
| 111 |
+
$$
|
| 112 |
+
|
| 113 |
+
## Alternate Solution 3:
|
| 114 |
+
|
| 115 |
+
Let $D$ be the mid-point of $B C$ and $E$ be the mid-point of $D C$. Since $D I=I H(=r)$ and $D E=E C$, the mid-point theorem implies that $I E \| C H$. But $C H \perp A B$. Therefore $E I \perp A B$. Let $E I$ meet $A B$ in $F$. Then $F$ is the point of tangency of the incircle of $\triangle A B C$ with $A B$. Since the incircle is also tangent to $B C$ at $D$, we have $B F=B D$. Observe that $\triangle B F E$ is similar to $\triangle B D A$. Hence
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
\frac{A B}{B D}=\frac{B E}{B F}=\frac{B E}{B D}=\frac{B D+D E}{B D}=1+\frac{D E}{B D}=\frac{3}{2}
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
This gives
|
| 122 |
+
|
| 123 |
+
$$
|
| 124 |
+
\frac{A B}{B C}=\frac{3}{4}
|
| 125 |
+
$$
|
| 126 |
+
|
| 127 |
+
2. For positive real numbers $a, b, c$, which of the following statements necessarily implies $a=b=c$ : (I) $a\left(b^{3}+c^{3}\right)=b\left(c^{3}+a^{3}\right)=c\left(a^{3}+b^{3}\right)$, (II) $a\left(a^{3}+b^{3}\right)=b\left(b^{3}+c^{3}\right)=c\left(c^{3}+a^{3}\right)$ ? Justify your answer.
|
| 128 |
+
|
| 129 |
+
Solution: We show that (I) need not imply that $a=b=c$ where as (II) always implies $a=b=c$.
|
| 130 |
+
|
| 131 |
+
Observe that $a\left(b^{3}+c^{3}\right)=b\left(c^{3}+a^{3}\right)$ gives $c^{3}(a-b)=a b\left(a^{2}-b^{2}\right)$. This gives either $a=b$ or $a b(a+b)=c^{3}$. Similarly, $b=c$ or $b c(b+c)=a^{3}$. If $a \neq b$ and $b \neq c$, we obtain
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
a b(a+b)=c^{3}, \quad b c(b+c)=a^{3}
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
Therefore
|
| 138 |
+
|
| 139 |
+
$$
|
| 140 |
+
b\left(a^{2}-c^{2}\right)+b^{2}(a-c)=c^{3}-a^{3}
|
| 141 |
+
$$
|
| 142 |
+
|
| 143 |
+
This gives $(a-c)\left(a^{2}+b^{2}+c^{2}+a b+b c+c a\right)=0$. Since $a, b, c$ are positive, the only possibility is $a=c$. We have therefore 4 possibilities: $a=b=c ; a \neq b, b \neq c$ and $c=a ; b \neq c, c \neq a$ and $a=b$; $c \neq a, a \neq b$ and $b=c$.
|
| 144 |
+
|
| 145 |
+
Suppose $a=b$ and $b, a \neq c$. Then $b\left(c^{3}+a^{3}\right)=c\left(a^{3}+b^{3}\right)$ gives $a c^{3}+a^{4}=2 c a^{3}$. This implies that $a(a-c)\left(a^{2}-a c-c^{2}\right)=0$. Therefore $a^{2}-a c-c^{2}=0$. Putting $a / c=x$, we get the quadratic equation $x^{2}-x-1=0$. Hence $x=(1+\sqrt{5}) / 2$. Thus we get
|
| 146 |
+
|
| 147 |
+
$$
|
| 148 |
+
a=b=\left(\frac{1+\sqrt{5}}{2}\right) c, \quad c \text { arbitrary positive real number. }
|
| 149 |
+
$$
|
| 150 |
+
|
| 151 |
+
Similarly, we get other two cases:
|
| 152 |
+
|
| 153 |
+
$$
|
| 154 |
+
\begin{aligned}
|
| 155 |
+
& b=c=\left(\frac{1+\sqrt{5}}{2}\right) a, \quad a \text { arbitrary positive real number } \\
|
| 156 |
+
& c=a=\left(\frac{1+\sqrt{5}}{2}\right) b, \quad b \text { arbitrary positive real number. }
|
| 157 |
+
\end{aligned}
|
| 158 |
+
$$
|
| 159 |
+
|
| 160 |
+
And $a=b=c$ is the fourth possibility.
|
| 161 |
+
|
| 162 |
+
Consider (II): $a\left(a^{3}+b^{3}\right)=b\left(b^{3}+c^{3}\right)=c\left(c^{3}+a^{3}\right)$. Suppose $a, b, c$ are mutually distinct. We may assume $a=\max \{a, b, c\}$. Hence $a>b$ and $a>c$. Using $a>b$, we get from the first relation that $a^{3}+b^{3}<b^{3}+c^{3}$. Therefore $a^{3}<c^{3}$ forcing $a<c$. This contradicts $a>c$. We conclude that $a, b, c$ cannot be mutually distinct. This means some two must be equal. If $a=b$, the equality of the first two expressions give $a^{3}+b^{3}=b^{3}+c^{3}$ so that $a=c$. Similarly, we can show that $b=c$ implies $b=a$ and $c=a$ gives $c=b$.
|
| 163 |
+
|
| 164 |
+
Alternate for (II) by a contestant: We can write
|
| 165 |
+
|
| 166 |
+
$$
|
| 167 |
+
\begin{aligned}
|
| 168 |
+
\frac{a^{3}}{c}+\frac{b^{3}}{c} & =\frac{c^{3}}{a}+a^{2} \\
|
| 169 |
+
\frac{b^{3}}{a}+\frac{c^{3}}{a} & =\frac{a^{3}}{b}+b^{2} \\
|
| 170 |
+
\frac{c^{3}}{b}+\frac{a^{3}}{b} & =\frac{b^{3}}{c}+c^{2}
|
| 171 |
+
\end{aligned}
|
| 172 |
+
$$
|
| 173 |
+
|
| 174 |
+
Adding, we get
|
| 175 |
+
|
| 176 |
+
$$
|
| 177 |
+
\frac{a^{3}}{c}+\frac{b^{3}}{a}+\frac{c^{3}}{b}=a^{2}+b^{2}+c^{2}
|
| 178 |
+
$$
|
| 179 |
+
|
| 180 |
+
Using C-S inequality, we have
|
| 181 |
+
|
| 182 |
+
$$
|
| 183 |
+
\begin{aligned}
|
| 184 |
+
\left(a^{2}+b^{2}+c^{2}\right)^{2} & =\left(\frac{\sqrt{a^{3}}}{\sqrt{c}} \cdot \sqrt{a c}+\frac{\sqrt{b^{3}}}{\sqrt{a}} \cdot \sqrt{b a}+\frac{\sqrt{c^{3}}}{\sqrt{b}} \cdot \sqrt{c b}\right)^{2} \\
|
| 185 |
+
& \leq\left(\frac{a^{3}}{c}+\frac{b^{3}}{a}+\frac{c^{3}}{b}\right)(a c+b a+c b) \\
|
| 186 |
+
& =\left(a^{2}+b^{2}+c^{2}\right)(a b+b c+c a)
|
| 187 |
+
\end{aligned}
|
| 188 |
+
$$
|
| 189 |
+
|
| 190 |
+
Thus we obtain
|
| 191 |
+
|
| 192 |
+
$$
|
| 193 |
+
a^{2}+b^{2}+c^{2} \leq a b+b c+c a
|
| 194 |
+
$$
|
| 195 |
+
|
| 196 |
+
However this implies $(a-b)^{2}+(b-c)^{2}+(c-a)^{2} \leq 0$ and hence $a=b=c$.
|
| 197 |
+
|
| 198 |
+
3. Let $\mathbb{N}$ denote the set of all natural numbers. Define a function $T: \mathbb{N} \rightarrow \mathbb{N}$ by $T(2 k)=k$ and $T(2 k+1)=2 k+2$. We write $T^{2}(n)=T(T(n))$ and in general $T^{k}(n)=T^{k-1}(T(n))$ for any $k>1$.
|
| 199 |
+
|
| 200 |
+
(i) Show that for each $n \in \mathbb{N}$, there exists $k$ such that $T^{k}(n)=1$.
|
| 201 |
+
|
| 202 |
+
(ii) For $k \in \mathbb{N}$, let $c_{k}$ denote the number of elements in the set $\left\{n: T^{k}(n)=1\right\}$. Prove that $c_{k+2}=c_{k+1}+c_{k}$, for $k \geq 1$.
|
| 203 |
+
|
| 204 |
+
## Solution:
|
| 205 |
+
|
| 206 |
+
(i) For $n=1$, we have $T(1)=2$ and $T^{2}(1)=T(2)=1$. Hence we may assume that $n>1$.
|
| 207 |
+
|
| 208 |
+
Suppose $n>1$ is even. Then $T(n)=n / 2$. We observe that $(n / 2) \leq n-1$ for $n>1$.
|
| 209 |
+
|
| 210 |
+
Suppose $n>1$ is odd so that $n \geq 3$. Then $T(n)=n+1$ and $T^{2}(n)=(n+1) / 2$. Again we see that $(n+1) / 2 \leq(n-1)$ for $n \geq 3$.
|
| 211 |
+
|
| 212 |
+
Thus we see that in at most $2(n-1)$ steps $T$ sends $n$ to 1 . Hence $k \leq 2(n-1)$. (Here $2(n-1)$ is only a bound. In reality, less number of steps will do.)
|
| 213 |
+
|
| 214 |
+
(ii) We show that $c_{n}=f_{n+1}$, where $f_{n}$ is the $n$-th Fibonacci number.
|
| 215 |
+
|
| 216 |
+
Let $n \in \mathbb{N}$ and let $k \in \mathbb{N}$ be such that $T^{k}(n)=1$. Here $n$ can be odd or even. If $n$ is even, it can be either of the form $4 d+2$ or of the form $4 d$.
|
| 217 |
+
|
| 218 |
+
If $n$ is odd, then $1=T^{k}(n)=T^{k-1}(n+1)$. (Observe that $k>1$; otherwise we get $n+1=1$ which is impossible since $n \in \mathbb{N}$.) Here $n+1$ is even.
|
| 219 |
+
|
| 220 |
+
If $n=4 d+2$, then again $1=T^{k}(4 d+2)=T^{k-1}(2 d+1)$. Here $2 d+1=n / 2$ is odd.
|
| 221 |
+
|
| 222 |
+
Thus each solution of $T^{k-1}(m)=1$ produces exactly one solution of $T^{k}(n)=1$ and $n$ is either odd or of the form $4 d+2$.
|
| 223 |
+
|
| 224 |
+
If $n=4 d$, we see that $1=T^{k}(4 d)=T^{k-1}(2 d)=T^{k-2}(d)$. This shows that each solution of $T^{k-2}(m)=1$ produces exactly one solution of $T^{k}(n)=1$ of the form $4 d$.
|
| 225 |
+
|
| 226 |
+
Thus the number of solutions of $T^{k}(n)=1$ is equal to the number of solutions of $T^{k-1}(m)=1$ and the number of solutions of $T^{k-2}(l)=1$ for $k>2$. This shows that $c_{k}=c_{k-1}+c_{k-2}$ for $k>2$. We also observe that 2 is the only number which goes to 1 in one step and 4 is the only number which goes to 1 in two steps. Hence $c_{1}=1$ and $c_{2}=2$. This proves that $c_{n}=f_{n+1}$ for all $n \in \mathbb{N}$.
|
| 227 |
+
|
| 228 |
+
4. Suppose 2016 points of the circumference of a circle are coloured red and the remaining points are coloured blue. Given any natural number $n \geq 3$, prove that there is a regular $n$-sided polygon all of whose vertices are blue.
|
| 229 |
+
|
| 230 |
+
Solution: Let $A_{1}, A_{2}, \ldots, A_{2016}$ be 2016 points on the circle which are coloured red and the remain-
|
| 231 |
+
ing blue. Let $n \geq 3$ and let $B_{1}, B_{2}, \ldots, B_{n}$ be a regular $n$-sided polygon inscribed in this circle with the vertices chosen in anti-clock-wise direction. We place $B_{1}$ at $A_{1}$. (It is possible, in this position, some other $B$ 's also coincide with some other $A$ 's.) Rotate the polygon in anti-clock-wise direction gradually till some $B$ 's coincide with (an equal number of) $A$ 's second time. We again rotate the polygon in the same direction till some $B$ 's coincide with an equal number of $A$ 's third time, and so on until we return to the original position, i.e., $B_{1}$ at $A_{1}$. We see that the number of rotations will not be more than $2016 \times n$, that is, at most these many times some $B$ 's would have coincided with an equal number of $A$ 's. Since the interval $\left(0,360^{\circ}\right)$ has infinitely many points, we can find a value $\alpha^{\circ} \in\left(0,360^{\circ}\right)$ through which the polygon can be rotated from its initial position such that no $B$ coincides with any $A$. This gives a $n$-sided regular polygon having only blue vertices.
|
| 232 |
+
|
| 233 |
+
Alternate Solution: Consider a regular $2017 \times n$-gon on the circle; say, $A_{1} A_{2} A_{3} \cdots A_{2017 n}$. For each $j, 1 \leq j \leq 2017$, consider the points $\left\{A_{k}: k \equiv j(\bmod 2017)\right\}$. These are the vertices of a regular $n$-gon, say $S_{j}$. We get 2017 regular $n$-gons; $S_{1}, S_{2}, \ldots, S_{2017}$. Since there are only 2016 red points, by pigeon-hole principle there must be some $n$-gon among these 2017 which does not contain any red point. But then it is a blue $n$-gon.
|
| 234 |
+
|
| 235 |
+
5. Let $A B C$ be a right-angled triangle with $\angle B=90^{\circ}$. Let $D$ be a point on $A C$ such that the in-radii of the triangles $A B D$ and $C B D$ are equal. If this common value is $r^{\prime}$ and if $r$ is the in-radius of triangle $A B C$, prove that
|
| 236 |
+
|
| 237 |
+
$$
|
| 238 |
+
\frac{1}{r^{\prime}}=\frac{1}{r}+\frac{1}{B D}
|
| 239 |
+
$$
|
| 240 |
+
|
| 241 |
+
Solution: Let $E$ and $F$ be the incentres of triangles $A B D$ and $C B D$ respectively. Let the incircles of triangles $A B D$ and $C B D$ touch $A C$ in $P$ and $Q$ respectively. If $\angle B D A=\theta$, we see that
|
| 242 |
+
|
| 243 |
+
$$
|
| 244 |
+
r^{\prime}=P D \tan (\theta / 2)=Q D \cot (\theta / 2)
|
| 245 |
+
$$
|
| 246 |
+
|
| 247 |
+
Hence
|
| 248 |
+
|
| 249 |
+
$$
|
| 250 |
+
P Q=P D+Q D=r^{\prime}\left(\cot \frac{\theta}{2}+\tan \frac{\theta}{2}\right)=\frac{2 r^{\prime}}{\sin \theta}
|
| 251 |
+
$$
|
| 252 |
+
|
| 253 |
+
|
| 254 |
+
|
| 255 |
+
But we observe that
|
| 256 |
+
|
| 257 |
+
$$
|
| 258 |
+
D P=\frac{B D+D A-A B}{2}, \quad D Q=\frac{B D+D C-B C}{2}
|
| 259 |
+
$$
|
| 260 |
+
|
| 261 |
+
Thus $P Q=(b-c-a+2 B D) / 2$. We also have
|
| 262 |
+
|
| 263 |
+
$$
|
| 264 |
+
\begin{aligned}
|
| 265 |
+
\frac{a c}{2}=[A B C]=[A B D]+[C B D]=r^{\prime} \frac{(A B+B D+D A)}{2} & +r^{\prime} \frac{(C B+B D+D C)}{2} \\
|
| 266 |
+
= & r^{\prime} \frac{(c+a+b+2 B D)}{2}=r^{\prime}(s+B D)
|
| 267 |
+
\end{aligned}
|
| 268 |
+
$$
|
| 269 |
+
|
| 270 |
+
But
|
| 271 |
+
|
| 272 |
+
$$
|
| 273 |
+
r^{\prime}=\frac{P Q \sin \theta}{2}=\frac{P Q \cdot h}{2 B D}
|
| 274 |
+
$$
|
| 275 |
+
|
| 276 |
+
where $h$ is the altitude from $B$ on to $A C$. But we know that $h=a c / b$. Thus we get
|
| 277 |
+
|
| 278 |
+
$$
|
| 279 |
+
a c=2 \times r^{\prime}(s+B D)=2 \times \frac{P Q \cdot h}{2 \times B D}(s+B D)=\frac{(b-c-a+2 B D) c a(s+B D)}{2 \times B D \times b}
|
| 280 |
+
$$
|
| 281 |
+
|
| 282 |
+
Thus we get
|
| 283 |
+
|
| 284 |
+
$$
|
| 285 |
+
2 \times B D \times b=2 \times(B D-(s-b))(s+B D)
|
| 286 |
+
$$
|
| 287 |
+
|
| 288 |
+
This gives $B D^{2}=s(s-b)$. Since $A B C$ is a right-angled triangle $r=s-b$. Thus we get $B D^{2}=r s$. On the other hand, we also have $[A B C]=r^{\prime}(s+B D)$. Thus we get
|
| 289 |
+
|
| 290 |
+
$$
|
| 291 |
+
r s=[A B C]=r^{\prime}(s+B D)
|
| 292 |
+
$$
|
| 293 |
+
|
| 294 |
+
Hence
|
| 295 |
+
|
| 296 |
+
$$
|
| 297 |
+
\frac{1}{r^{\prime}}=\frac{1}{r}+\frac{B D}{r s}=\frac{1}{r}+\frac{1}{B D}
|
| 298 |
+
$$
|
| 299 |
+
|
| 300 |
+
## Alternate Solution 1: Observe that
|
| 301 |
+
|
| 302 |
+
$$
|
| 303 |
+
\frac{r^{\prime}}{r}=\frac{A P}{A X}=\frac{C Q}{C X}=\frac{A P+C Q}{A C}
|
| 304 |
+
$$
|
| 305 |
+
|
| 306 |
+
where $X$ is the point at which the incircle of $A B C$ touches the side $A C$. If $s_{1}$ and $s_{2}$ are respectively the semi-perimeters of triangles $A B D$ and $C B D$, we know $A P=s_{1}-B D$ and $C Q=s_{2}-B D$. Therefore
|
| 307 |
+
|
| 308 |
+
$$
|
| 309 |
+
\frac{r^{\prime}}{r}=\frac{\left(s_{1}-B D\right)+\left(s_{2}-B D\right)}{A C}=\frac{s_{1}+s_{2}-2 B D}{b}
|
| 310 |
+
$$
|
| 311 |
+
|
| 312 |
+
But
|
| 313 |
+
|
| 314 |
+
$$
|
| 315 |
+
s_{1}+s_{2}=\frac{A D+B D+c}{2}+\frac{C D+B D+a}{2}=\frac{(a+b+c)+2 B D}{2}=\frac{s+B D}{2}
|
| 316 |
+
$$
|
| 317 |
+
|
| 318 |
+
This gives
|
| 319 |
+
|
| 320 |
+
$$
|
| 321 |
+
\frac{r^{\prime}}{r}=\frac{s+B D-2 B D}{b}=\frac{s-B D}{b}
|
| 322 |
+
$$
|
| 323 |
+
|
| 324 |
+
We also have
|
| 325 |
+
|
| 326 |
+
$$
|
| 327 |
+
r^{\prime}=\frac{[A B D]}{s_{1}}=\frac{[C B D]}{s_{2}}=\frac{[A B D]+[C B D]}{s_{1}+s_{2}}=\frac{[A B C]}{s+B D}=\frac{r s}{s+B D}
|
| 328 |
+
$$
|
| 329 |
+
|
| 330 |
+
This implies that
|
| 331 |
+
|
| 332 |
+
$$
|
| 333 |
+
\frac{r^{\prime}}{r}=\frac{s}{s+B D}
|
| 334 |
+
$$
|
| 335 |
+
|
| 336 |
+
Comparing the two expressions for $r^{\prime} / r$, we see that
|
| 337 |
+
|
| 338 |
+
$$
|
| 339 |
+
\frac{s-B D}{b}=\frac{s}{s+B D}
|
| 340 |
+
$$
|
| 341 |
+
|
| 342 |
+
Therefore $s^{2}-B D^{2}=b s$, or $B D^{2}=s(s-b)$. Thus we get $B D=\sqrt{s(s-b)}$.
|
| 343 |
+
|
| 344 |
+
We know now that
|
| 345 |
+
|
| 346 |
+
$$
|
| 347 |
+
\frac{r^{\prime}}{r}=\frac{s}{s+B D}=\frac{s-B D}{b}=\frac{B D}{(s-b)+B D}=\frac{\sqrt{s(s-b)}}{(s-b)+\sqrt{s(s-b)}}=\frac{\sqrt{s}}{\sqrt{s-b}+\sqrt{s}}
|
| 348 |
+
$$
|
| 349 |
+
|
| 350 |
+
Therefore
|
| 351 |
+
|
| 352 |
+
$$
|
| 353 |
+
\frac{r}{r^{\prime}}=1+\sqrt{\frac{s-b}{s}}
|
| 354 |
+
$$
|
| 355 |
+
|
| 356 |
+
This gives
|
| 357 |
+
|
| 358 |
+
$$
|
| 359 |
+
\frac{1}{r^{\prime}}=\frac{1}{r}+\left(\sqrt{\frac{s-b}{s}}\right) \frac{1}{r}
|
| 360 |
+
$$
|
| 361 |
+
|
| 362 |
+
But
|
| 363 |
+
|
| 364 |
+
$$
|
| 365 |
+
\left(\sqrt{\frac{s-b}{s}}\right) \frac{1}{r}=\left(\frac{s-b}{\sqrt{s(s-b)}}\right) \frac{1}{r}=\left(\frac{s-b}{B D}\right) \frac{1}{r}
|
| 366 |
+
$$
|
| 367 |
+
|
| 368 |
+
If $\angle B=90^{\circ}$, we know that $r=s-b$. Therfore we get
|
| 369 |
+
|
| 370 |
+
$$
|
| 371 |
+
\frac{1}{r^{\prime}}=\frac{1}{r}+\left(\frac{s-b}{B D}\right) \frac{1}{r}=\frac{1}{r}+\frac{1}{B D}
|
| 372 |
+
$$
|
| 373 |
+
|
| 374 |
+
Alternate Solution 2 by a contestant: Observe that $\angle E D F=90^{\circ}$. Hence $\triangle E D P$ is similar to $\triangle D F Q$. Therefore $D P \cdot D Q=E P \cdot F Q$. Taking $D P=y_{1}$ and $D Q=x_{1}$, we get $x_{1} y_{1}=\left(r^{\prime}\right)^{2}$. We also observe that $B D=x_{1}+x_{2}=y_{1}+y_{2}$. Since $\angle E B F=45^{\circ}$, we get
|
| 375 |
+
|
| 376 |
+
$$
|
| 377 |
+
1=\tan 45^{\circ}=\tan \left(\beta_{1}+\beta_{2}\right)=\frac{\tan \beta_{1}+\tan \beta_{2}}{1-\tan \beta_{1} \tan \beta_{2}}
|
| 378 |
+
$$
|
| 379 |
+
|
| 380 |
+
|
| 381 |
+
|
| 382 |
+
But $\tan \beta_{1}=r^{\prime} / y_{2}$ and $\tan \beta_{2}=r^{\prime} / x_{2}$. Hence we obtain
|
| 383 |
+
|
| 384 |
+
$$
|
| 385 |
+
1=\frac{\left(r^{\prime} / y_{2}\right)+\left(r^{\prime} / x_{2}\right)}{1-\left(r^{\prime}\right)^{2} / x_{2} y_{2}}
|
| 386 |
+
$$
|
| 387 |
+
|
| 388 |
+
Solving for $r^{\prime}$, we get
|
| 389 |
+
|
| 390 |
+
$$
|
| 391 |
+
r^{\prime}=\frac{x_{2} y_{2}-x_{1} y_{1}}{x_{2}+y_{2}}
|
| 392 |
+
$$
|
| 393 |
+
|
| 394 |
+
We also know
|
| 395 |
+
|
| 396 |
+
$$
|
| 397 |
+
r=\frac{A B+B C-A C}{2}=\frac{x_{2}+y_{2}-\left(x_{1}+y_{1}\right)}{2}=\frac{\left(x_{2}-x_{1}\right)+\left(y_{2}-y_{1}\right)}{2}
|
| 398 |
+
$$
|
| 399 |
+
|
| 400 |
+
Finally,
|
| 401 |
+
|
| 402 |
+
$$
|
| 403 |
+
\begin{aligned}
|
| 404 |
+
\frac{1}{r}+\frac{1}{B D} & =\frac{2}{\left(x_{2}-x_{1}\right)+\left(y_{2}-y_{1}\right)}+\frac{1}{x_{1}+x_{2}} \\
|
| 405 |
+
& =\frac{2 x_{1}+2 x_{2}+\left(x_{2}-x_{1}\right)+\left(y_{2}-y_{1}\right)}{\left(x_{1}+x_{2}\right)\left(\left(x_{2}-x_{1}\right)+\left(y_{2}-y_{1}\right)\right)}
|
| 406 |
+
\end{aligned}
|
| 407 |
+
$$
|
| 408 |
+
|
| 409 |
+
But we can write
|
| 410 |
+
|
| 411 |
+
$$
|
| 412 |
+
2 x_{1}+2 x_{2}+\left(x_{2}-x_{1}\right)+\left(y_{2}-y_{1}\right)=\left(x_{1}+x_{2}+x_{2}-x_{1}\right)+\left(y_{1}+y_{2}+y_{2}-y_{1}\right)=2\left(x_{2}+y_{2}\right)
|
| 413 |
+
$$
|
| 414 |
+
|
| 415 |
+
and
|
| 416 |
+
|
| 417 |
+
$$
|
| 418 |
+
\begin{aligned}
|
| 419 |
+
\left(x_{1}+x_{2}\right)\left(\left(x_{2}-x_{1}\right)+\left(y_{2}-y_{1}\right)\right)=2\left(x_{1}+x_{2}\right) & \left(x_{2}-y_{1}\right) \\
|
| 420 |
+
& =2\left(x_{2}\left(x_{2}+x_{1}-y_{1}\right)-x_{1} y_{1}\right)=2\left(x_{2} y_{2}-x_{1} y_{1}\right)
|
| 421 |
+
\end{aligned}
|
| 422 |
+
$$
|
| 423 |
+
|
| 424 |
+
Therefore
|
| 425 |
+
|
| 426 |
+
$$
|
| 427 |
+
\frac{1}{r}+\frac{1}{B D}=\frac{2\left(x_{2}+y_{2}\right)}{2\left(x_{2} y_{2}-x_{1} y_{1}\right)}=\frac{1}{r^{\prime}}
|
| 428 |
+
$$
|
| 429 |
+
|
| 430 |
+
Remark: One can also choose $B=(0,0), A=(0, a)$ and $C=(1,0)$ and the coordinate geometry proof gets reduced considerbly.
|
| 431 |
+
|
| 432 |
+
6. Consider a non-constant arithmetic progression $a_{1}, a_{2}, \ldots, a_{n}, \ldots$ Suppose there exist relatively prime positive integers $p>1$ and $q>1$ such that $a_{1}^{2}, a_{p+1}^{2}$ and $a_{q+1}^{2}$ are also the terms of the same arithmetic progression. Prove that the terms of the arithmetic progression are all integers.
|
| 433 |
+
|
| 434 |
+
Solution: Let us take $a_{1}=a$. We have
|
| 435 |
+
|
| 436 |
+
$$
|
| 437 |
+
a^{2}=a+k d, \quad(a+p d)^{2}=a+l d, \quad(a+q d)^{2}=a+m d
|
| 438 |
+
$$
|
| 439 |
+
|
| 440 |
+
Thus we have
|
| 441 |
+
|
| 442 |
+
$$
|
| 443 |
+
a+l d=(a+p d)^{2}=a^{2}+2 p a d+p^{2} d^{2}=a+k d+2 p a d+p^{2} d^{2}
|
| 444 |
+
$$
|
| 445 |
+
|
| 446 |
+
Since we have non-constant AP, we see that $d \neq 0$. Hence we obtain $2 p a+p^{2} d=l-k$. Similarly, we get $2 q a+q^{2} d=m-k$. Observe that $p^{2} q-p q^{2} \neq 0$. Otherwise $p=q$ and $\operatorname{gcd}(p, q)=p>1$ which is a contradiction to the given hypothesis that $\operatorname{gcd}(p, q)=1$. Hence we can solve the two equations for $a, d$ :
|
| 447 |
+
|
| 448 |
+
$$
|
| 449 |
+
a=\frac{p^{2}(m-k)-q^{2}(l-k)}{2\left(p^{2} q-p q^{2}\right)}, \quad d=\frac{q(l-k)-p(m-k)}{p^{2} q-p q^{2}}
|
| 450 |
+
$$
|
| 451 |
+
|
| 452 |
+
It follows that $a, d$ are rational numbers. We also have
|
| 453 |
+
|
| 454 |
+
$$
|
| 455 |
+
p^{2} a^{2}=p^{2} a+k p^{2} d
|
| 456 |
+
$$
|
| 457 |
+
|
| 458 |
+
But $p^{2} d=l-k-2 p a$. Thus we get
|
| 459 |
+
|
| 460 |
+
$$
|
| 461 |
+
p^{2} a^{2}=p^{2} a+k(l-k-2 p a)=(p-2 k) p a+k(l-k)
|
| 462 |
+
$$
|
| 463 |
+
|
| 464 |
+
This shows that pa satisfies the equation
|
| 465 |
+
|
| 466 |
+
$$
|
| 467 |
+
x^{2}-(p-2 k) x-k(l-k)=0
|
| 468 |
+
$$
|
| 469 |
+
|
| 470 |
+
Since $a$ is rational, we see that $p a$ is rational. Write $p a=w / z$, where $w$ is an integer and $z$ is a natural numbers such that $\operatorname{gcd}(w, z)=1$. Substituting in the equation, we obtain
|
| 471 |
+
|
| 472 |
+
$$
|
| 473 |
+
w^{2}-(p-2 k) w z-k(l-k) z^{2}=0
|
| 474 |
+
$$
|
| 475 |
+
|
| 476 |
+
This shows $z$ divides $w$. Since $\operatorname{gcd}(w, z)=1$, it follows that $z=1$ and $p a=w$ an integer. (In fact any rational solution of a monic polynomial with integer coefficients is necessarily an integer.) Similarly, we can prove that $q a$ is an integer. Since $\operatorname{gcd}(p, q)=1$, there are integers $u$ and $v$ such that $p u+q v=1$. Therefore $a=(p a) u+(q a) v$. It follows that $a$ is an integer.
|
| 477 |
+
|
| 478 |
+
But $p^{2} d=l-k-2 p a$. Hence $p^{2} d$ is an integer. Similarly, $q^{2} d$ is also an integer. Since $\operatorname{gcd}\left(p^{2}, q^{2}\right)=1$, it follows that $d$ is an integer. Combining these two, we see that all the terms of the AP are integers.
|
| 479 |
+
|
| 480 |
+
Alternatively, we can prove that $a$ and $d$ are integers in another way. We have seen that $a$ and $d$ are rationals; and we have three relations:
|
| 481 |
+
|
| 482 |
+
$$
|
| 483 |
+
a^{2}=a+k d, \quad p^{2} d+2 p a=n_{1}, \quad q^{2} d+2 q a=n_{2}
|
| 484 |
+
$$
|
| 485 |
+
|
| 486 |
+
where $n_{1}=l-k$ and $n_{2}=m-k$. Let $a=u / v$ and $d=x / y$ where $u, x$ are integers and $v, y$ are natural numbers, and $\operatorname{gcd}(u, v)=1, \operatorname{gcd}(x, y)=1$. Putting this in these relations, we obtain
|
| 487 |
+
|
| 488 |
+
$$
|
| 489 |
+
\begin{aligned}
|
| 490 |
+
u^{2} y & =u v y+k x v^{2} \\
|
| 491 |
+
2 p u y+p^{2} v x & =v y n_{1} \\
|
| 492 |
+
2 q u y+q^{2} v x & =v y n_{2}
|
| 493 |
+
\end{aligned}
|
| 494 |
+
$$
|
| 495 |
+
|
| 496 |
+
Now (1) shows that $v \mid u^{2} y$. Since $\operatorname{gcd}(u, v)=1$, it follows that $v \mid y$. Similarly (2) shows that $y \mid p^{2} v x$. Using $\operatorname{gcd}(y, x)=1$, we get that $y \mid p^{2} v$. Similarly, (3) shows that $y \mid q^{2} v$. Therefore $y$ divides $\operatorname{gcd}\left(p^{2} v, q^{2} v\right)=v$. The two results $v \mid y$ and $y \mid v$ imply $v=y$, since both $v, y$ are positive.
|
| 497 |
+
|
| 498 |
+
Substitute this in (1) to get
|
| 499 |
+
|
| 500 |
+
$$
|
| 501 |
+
u^{2}=u v+k x v
|
| 502 |
+
$$
|
| 503 |
+
|
| 504 |
+
This shows that $v \mid u^{2}$. Since $\operatorname{gcd}(u, v)=1$, it follows that $v=1$. This gives $v=y=1$. Finally $a=u$ and $d=x$ which are integers.
|
| 505 |
+
|
INMO/md/en-sol-inmo_17.md
ADDED
|
@@ -0,0 +1,418 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# $32^{\text {nd }}$ Indian National Mathematical Olympiad-2017
|
| 2 |
+
|
| 3 |
+
## Problems and Solutions
|
| 4 |
+
|
| 5 |
+
1. In the given figure, $A B C D$ is a square paper. It is folded along $E F$ such that $A$ goes to a point $A^{\prime} \neq C, B$ on the side $B C$ and $D$ goes to $D^{\prime}$. The line $A^{\prime} D^{\prime}$ cuts $C D$ in $G$. Show that the inradius of the triangle $G C A^{\prime}$ is the sum of the inradii of the triangles $G D^{\prime} F$ and $A^{\prime} B E$.
|
| 6 |
+
|
| 7 |
+
|
| 8 |
+
|
| 9 |
+
Solution: Observe that the triangles $G C A^{\prime}$ and $A^{\prime} B E$ are similar to the triangle $G D^{\prime} F$. If $G F=u, G D^{\prime}=v$ and $D^{\prime} F=w$, then we have
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
A^{\prime} G=p u, C G=p v, A^{\prime} C=p w, \quad A^{\prime} E=q u, B E=q w, A^{\prime} B=q v
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
If $r$ is the inradius of $\triangle G D^{\prime} F$, then $p r$ and $q r$ are respectively the inradii of triangles $G C A^{\prime}$ and $A^{\prime} B E$. We have to show that $p r=r+q r$. We also observe that
|
| 16 |
+
|
| 17 |
+
$$
|
| 18 |
+
A E=E A^{\prime}, \quad D F=F D^{\prime}
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
Therefore
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
p w+q v=q w+q u=w+u+p v=v+p u
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
The last two equalities give $(p-1)(u-v)=w$. The first two equalities give $(p-q) w=q(u-v)$. Hence
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\frac{p-q}{q}=\frac{u-v}{w}=\frac{1}{p-1}
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
This simplifies to $p(p-q-1)=0$. Since $p \neq 0$, we get $p=q+1$. This implies that $p r=q r+r$.
|
| 34 |
+
|
| 35 |
+
2. Suppose $n \geq 0$ is an integer and all the roots of $x^{3}+\alpha x+4-\left(2 \times 2016^{n}\right)=0$ are integers. Find all possible values of $\alpha$.
|
| 36 |
+
|
| 37 |
+
Solution 1: Let $u, v, w$ be the roots of $x^{3}+\alpha x+4-\left(2 \times 2016^{n}\right)=0$. Then $u+v+w=0$ and $u v w=-4+\left(2 \times 2016^{n}\right)$. Therefore we obtain
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
u v(u+v)=4-\left(2 \times 2016^{n}\right)
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
Suppose $n \geq 1$. Then we see that $u v(u+v) \equiv 4\left(\bmod 2016^{n}\right)$. Therefore $u v(u+v) \equiv 1$ $(\bmod 3)$ and $u v(u+v) \equiv 1(\bmod 9)$. This implies that $u \equiv 2(\bmod 3)$ and $v \equiv 2(\bmod 3)$. This shows that modulo 9 the pair $(u, v)$ could be any one of the following:
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
(2,2),(2,5),(2,8),(5,2),(5,5),(5,8),(8,2),(8,5),(8,8)
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
In each case it is easy to check that $u v(u+v) \not \equiv 4(\bmod 9)$. Hence $n=0$ and $u v(u+v)=2$. It follows that $(u, v)=(1,1),(1,-2)$ or $(-2,1)$. Thus
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
\alpha=u v+v w+w u=u v-(u+v)^{2}=-3
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
for every pair $(u, v)$.
|
| 56 |
+
|
| 57 |
+
Solution 2: Let $a, b, c \in \mathbb{Z}$ be the roots of the given equation for some $n \in \mathbb{N}_{0}$. By Vieta Theorem, we know that
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
\begin{gathered}
|
| 61 |
+
a+b+c=0 \\
|
| 62 |
+
a b+b c+c a=\alpha \\
|
| 63 |
+
a b c=2 \times 2016^{n}-4
|
| 64 |
+
\end{gathered}
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
If possible, let us have $n \geq 1$. Since $7 \mid 2016$, we have that
|
| 68 |
+
|
| 69 |
+
$$
|
| 70 |
+
7|a b c+4 \Longrightarrow 7| 3(a b c+4) \Longrightarrow 7|3 a b c+12 \Longrightarrow 7| 3 a b c+5
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
Since we have $a+b+c=0$, we get that $3 a b c=a^{3}+b^{3}+c^{3}$. Substituting this in the earlier expression, we get that
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
a^{3}+b^{3}+c^{3}+5 \equiv 0 \quad(\bmod 7)
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
Consider below, a table calculating the residues of cubes modulo 7 .
|
| 80 |
+
|
| 81 |
+
| $x$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
| 82 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 83 |
+
| $x^{3}$ | 0 | 1 | 1 | -1 | 1 | -1 | -1 |
|
| 84 |
+
|
| 85 |
+
Hence, we know that if $x \in \mathbb{N}$, then we have $x^{3} \equiv 0,1,-1(\bmod 7)$. Since $a^{3}+b^{3}+c^{3} \equiv 2$ $(\bmod 7)$, we see that we must have one of the numbers divisible by 7 and the other two numbers, when cubed, must leave 1 as remainder modulo 7. Without of generality, let us assume that
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
a \equiv 0 \quad(\bmod 7), \quad b^{3}, c^{3} \equiv 1 \quad(\bmod 7)
|
| 89 |
+
$$
|
| 90 |
+
|
| 91 |
+
Hence, we have $b, c \equiv 1,2,4(\bmod 7)$. We will consider all possible values of $b+c$ modulo 7 . Since the expression is symmetric in $b, c$, modulo 7 , we will consider $b \leq c$.
|
| 92 |
+
|
| 93 |
+
| $b$ | 1 | 1 | 1 | 2 | 2 | 4 |
|
| 94 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 95 |
+
| $c$ | 1 | 2 | 4 | 2 | 4 | 4 |
|
| 96 |
+
| $b+c$ | 2 | 3 | 5 | 4 | 6 | 1 |
|
| 97 |
+
|
| 98 |
+
We see that, in all the above cases, we get $7 \nmid\langle b+c$. But this is a contradiction, since 7$| a+b+c$ and $7 \mid a$ together imply that $7 \mid b+c$. Hence, we cannot have $n \geq 1$. Hence, the only possible value is $n=0$. Substituting this value in the original equation, the equation becomes
|
| 99 |
+
|
| 100 |
+
$$
|
| 101 |
+
x^{3}+\alpha x+2=0
|
| 102 |
+
$$
|
| 103 |
+
|
| 104 |
+
Solving the equations $a+b+c=0$ and $a b c=-2$ in integers, we see that the only possible solutions $(a, b, c)$ are permutations of $(1,1,-2)$. In case of any permutation, $\alpha=-3$. Substituting this value of $\alpha$ back in the equation, we see that we indeed, get integer roots. Hence, the only possible value for $\alpha$ is -3 .
|
| 105 |
+
|
| 106 |
+
3. Find the number of triples $(x, a, b)$ where $x$ is a real number and $a, b$ belong to the set $\{1,2,3,4,5,6,7,8,9\}$ such that
|
| 107 |
+
|
| 108 |
+
$$
|
| 109 |
+
x^{2}-a\{x\}+b=0
|
| 110 |
+
$$
|
| 111 |
+
|
| 112 |
+
where $\{x\}$ denotes the fractional part of the real number $x$. (For example $\{1.1\}=0.1=$ $\{-0.9\}$.
|
| 113 |
+
|
| 114 |
+
Solution: Let us write $x=n+f$ where $n=[x]$ and $f=\{x\}$. Then
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
f^{2}+(2 n-a) f+n^{2}+b=0
|
| 118 |
+
$$
|
| 119 |
+
|
| 120 |
+
Observe that the product of the roots of (1) is $n^{2}+b \geq 1$. If this equation has to have a solution $0 \leq f<1$, the larger root of (1) is greater 1 . We conclude that the equation (1) has a real root less than 1 only if $P(1)<0$ where $P(y)=y^{2}+(2 n-a) y+n^{2}+2 b$. This gives
|
| 121 |
+
|
| 122 |
+
$$
|
| 123 |
+
1+2 n-a+n^{2}+2 b<0
|
| 124 |
+
$$
|
| 125 |
+
|
| 126 |
+
Therefore we have $(n+1)^{2}+b<a$. If $n \geq 2$, then $(n+1)^{2}+b \geq 10>a$. Hence $n \leq 1$. If $n \leq-4$, then again $(n+1)^{2}+b \geq 10>a$. Thus we have the range for $n:-3,-2,-1,0,1$. If $n=-3$ or $n=1$, we have $(n+1)^{2}=4$. Thus we must have $4+b<a$. If $a=9$, we must have $b=4,3,2,1$ giving 4 values. For $a=8$, we must have $b=3,2,1$ giving 3 values. Similarly, for $a=7$ we get 2 values of $b$ and $a=6$ leads to 1 value of $b$. In each case we get a real value of $f<1$ and this leads to a solution for $x$. Thus we get totally $2(4+3+2+1)=20$ values of the triple $(x, a, b)$.
|
| 127 |
+
|
| 128 |
+
For $n=-2$ and $n=0$, we have $(n+1)^{2}=1$. Hence we require $1+b<a$. We again count pairs $(a, b)$ such that $a-b>1$. For $a=9$, we get 7 values of $b$; for $a=8$ we get 6 values of $b$ and so on. Thus we get $2(7+6+5+4+3+2+1)=56$ values for the triple $(x, a, b)$.
|
| 129 |
+
|
| 130 |
+
Suppose $n=-1$ so that $(n+1)^{2}=0$. In this case we require $b<a$. We get $8+7+6+5+$ $4+3+2+1=36$ values for the triple $(x, a, b)$.
|
| 131 |
+
|
| 132 |
+
Thus the total number of triples $(x, a, b)$ is $20+56+36=112$.
|
| 133 |
+
|
| 134 |
+
4. Let $A B C D E$ be a convex pentagon in which $\angle A=\angle B=\angle C=\angle D=120^{\circ}$ and whose side lengths are 5 consecutive integers in some order. Find all possible values of $A B+B C+C D$.
|
| 135 |
+
|
| 136 |
+
Solution 1: Let $A B=a, B C=b$, and $C D=c$. By symmetry, we may assume that $c<a$. We show that $D E=a+b$ and $E A=b+c$.
|
| 137 |
+
|
| 138 |
+
|
| 139 |
+
|
| 140 |
+
Draw a line parallel to $B C$ through $D$. Extend $E A$ to meet this line at $F$. Draw a line parallel to $C D$ through $B$ and let it intersect $D F$ in $G$. Let $A B$ intersect $D F$ in $H$. We have $\angle F D E=60^{\circ}$ and $\angle E=60^{\circ}$. Hence $E F D$ is an equilateral triangle. Similarly $A F H$ and $B G H$ are also equilateral triangles. Hence $H G=G B=c$. Moreover, $D G=b$. Therefore $H D=b+c$. But $H D=A E$ since $F H=F A$ and $F D=F E$. Also $A H=a-B H=$ $a-B G=a-c$. Hence $E D=E F=E A+A F=b+c+A H=(b+c)+(a-c)=b+a$.
|
| 141 |
+
|
| 142 |
+
We have five possibilities:
|
| 143 |
+
|
| 144 |
+
(1) $b<c<a<b+c<a+b$;
|
| 145 |
+
|
| 146 |
+
(2) $c<b<a<b+c<a+b$;
|
| 147 |
+
|
| 148 |
+
(3) $c<a<b<b+c<a+b$;
|
| 149 |
+
|
| 150 |
+
(4) $b<c<b+c<a<a+b$;
|
| 151 |
+
|
| 152 |
+
(5) $c<b<b+c<a<a+b$.
|
| 153 |
+
|
| 154 |
+
In (1), we see that $c<a<b+c$ are three consecutive integers provided $b=2$. Hence we get $c=3$ and $a=4$. In this case $b+c=5$ and $a+b=6$ so that we have five consecutive integrs $2,3,4,5,6$ as side lengths. In (2), $b<a<b+c$ form three consecutive integrs only when $c=2$. Hence $b=3, a=4$. But then $b+c=5$ and $a+b=7$. Thus the side lengths are $2,3,4,6,7$ which are not consecutive integers. In case (3), $b<b+c$ are two consecutive integrs so that $c=1$. Hence $a=2$ and $b=3$. We get $b+c=4$ and $a+b=5$ so that the consecutive integers $1,2,3,4,5$ form the side lengths. In case (4), we have $c<b+c$ as two consecutive integers and hence $b=1$. Therefore $c=2, b+c=3, a=4$ and $a+b=5$ which is admissible. Finally, in case (5) we have $b<b+c$ as two consecutive integers, so that $c=1$. Thus $b=2, b+c=3, a=4$ and $a+b=6$. We do not get consecutive integers.
|
| 155 |
+
|
| 156 |
+
Therefore the only possibilities are $(a, b, c)=(4,2,3),(2,3,1)$ and $(4,1,2)$. This shows that $a+b+c=9,6$ or 7 . Thus there are three possible sums $A B+B C+C A$, namely, 6,7 or 9 .
|
| 157 |
+
|
| 158 |
+
Solution 2: As in the earlier solution, $E D=d=a+b$ and $E A=e=b+c$. Let the sides be $x-2, x-1, x, x+1, x+2$. Then $x \geq 3$. We also have $x+2 \geq x-1+x-2$ so that $x \leq 5$. Thus $x=3,4$ or 5 . If $x=5$, the sides are $\{3,4,5,6,7\}$ and here we do not have two pairs which add to a number in the set. Hence $x=3$ or 4 and we get the sets as $\{1,2,3,4,5\}$ or $\{2,3,4,5,6\}$. With the set $\{1,2,3,4,5\}$ we get
|
| 159 |
+
|
| 160 |
+
$$
|
| 161 |
+
(a, b, c, d, e)=(2,3,1,5,4),(4,1,2,5,3)
|
| 162 |
+
$$
|
| 163 |
+
|
| 164 |
+
From the set $\{2,3,4,5,6\}$, we get $(a, b, c, d, e)=(4,2,3,6,5)$. Thus we see that $a+b+c=6,7$ or 9 .
|
| 165 |
+
|
| 166 |
+
Solution 3: We use the same notations and we get $d=a+b$ and $e=b+c$. If $a \geq 5$, we see that $d-b \geq 5$. But the maximum difference in a set of 5 consecutive integers is 4 . Hence $a \leq 4$. Similarly, we see $b \leq 4$ and $c \leq 4$. Thus we see that $a+b+c \leq 2+3+4=9$. But $a+b+c \geq 1+2+3=6$. It follows that $a+b+c=6,7,8$ or 9 . If we take $(a, b, c, d, e)=(1,3,2,4,5)$, we get $a+b+c=6$. Similarly, $(a, b, c, d, e)=(2,1,4,3,5)$ gives $a+b+c=7$, For $a+b+c=8$, the only we we can get $1+3+4=8$. Here we cannot accommodate 2 and consecutiveness is lost. For 9 , we can have $(a, b, c, d, e)=(3,2,4,5,6)$ and $a+b+c=9$.
|
| 167 |
+
|
| 168 |
+
5. Let $A B C$ be a triangle with $\angle A=90^{\circ}$ and $A B<A C$. Let $A D$ be the altitude from $A$ on to $B C$. Let $P, Q$ and $I$ denote respectively the incentres of triangles $A B D, A C D$ and $A B C$. Prove that $A I$ is perpendicular to $P Q$ and $A I=P Q$.
|
| 169 |
+
|
| 170 |
+
Solution: Draw $P S \| B C$ and $Q S \| A D$. Then $P S Q$ is a right-angled triangle with $\angle P S Q=90^{\circ}$. Observe that $P S=r_{1}+r_{2}$ and $S Q=r_{2}-r_{1}$, where $r_{1}$ and $r_{2}$ are the inradii of triangles $A B D$ and $A C D$, respectively. We observe that triangles $D A B$ and $D C A$ are similar to triangle $A C B$.
|
| 171 |
+
|
| 172 |
+
|
| 173 |
+
|
| 174 |
+
Hence
|
| 175 |
+
|
| 176 |
+
$$
|
| 177 |
+
r_{1}=\frac{c}{a} r, \quad r_{2}=\frac{b}{a} r
|
| 178 |
+
$$
|
| 179 |
+
|
| 180 |
+
where $r$ is the inradius of triangle $A B C$. Thus we get
|
| 181 |
+
|
| 182 |
+
$$
|
| 183 |
+
\frac{P S}{S Q}=\frac{r_{2}+r_{1}}{r_{2}-r_{1}}=\frac{b+c}{b-c}
|
| 184 |
+
$$
|
| 185 |
+
|
| 186 |
+
On the otherhand $A D=h=b c / a$. We also have $B E=c a /(b+c)$ and
|
| 187 |
+
|
| 188 |
+
$$
|
| 189 |
+
B D^{2}=c^{2}-h^{2}=c^{2}-\frac{b^{2} c^{2}}{a^{2}}=\frac{c^{4}}{a^{2}}
|
| 190 |
+
$$
|
| 191 |
+
|
| 192 |
+
Hence $B D=c^{2} / a$. Therefore
|
| 193 |
+
|
| 194 |
+
$$
|
| 195 |
+
D E=B E-B D=\frac{c a}{b+c}-\frac{c^{2}}{a}=\frac{c b(b-c)}{a(b+c)}
|
| 196 |
+
$$
|
| 197 |
+
|
| 198 |
+
Thus we get
|
| 199 |
+
|
| 200 |
+
$$
|
| 201 |
+
\frac{A D}{D E}=\frac{b+c}{b-c}=\frac{P S}{S Q}
|
| 202 |
+
$$
|
| 203 |
+
|
| 204 |
+
Since $\angle A D E=90^{\circ}=\angle P S Q$, we conclude that $\triangle A D E \sim \triangle P S Q$. Since $A D \perp P S$, it follows that $A E \perp P Q$.
|
| 205 |
+
|
| 206 |
+
We also observe that
|
| 207 |
+
|
| 208 |
+
$$
|
| 209 |
+
P Q^{2}=P S^{2}+S Q^{2}=\left(r_{2}+r_{1}\right)^{2}+\left(r_{2}-r_{1}\right)^{2}=2\left(r_{1}^{2}+r_{2}^{2}\right)
|
| 210 |
+
$$
|
| 211 |
+
|
| 212 |
+
However
|
| 213 |
+
|
| 214 |
+
$$
|
| 215 |
+
r_{1}^{2}+r_{2}^{2}=\frac{c^{2}+b^{2}}{a^{2}} r^{2}=r^{2}
|
| 216 |
+
$$
|
| 217 |
+
|
| 218 |
+
Hence $P Q=\sqrt{2} r$. We also observe that $A I=r \operatorname{cosec}(A / 2)=r \operatorname{cosec}\left(45^{\circ}\right)=\sqrt{2} r$. Thus $P Q=A I$.
|
| 219 |
+
|
| 220 |
+
Solution 2: In the figure, we have made the construction as mentioned in the hint. Since $P, Q$ are the incentres of $\triangle A B D, \triangle A C D, D P, D Q$ are the internal angle bisectors of $\angle A D B, \angle A D C$ respectively. Since $A D$ is the altitude on the hypotenuse $B C$ in $\triangle A B C$, we have that $\angle P D Q=45^{\circ}+45^{\circ}=90^{\circ}$. It also implies that
|
| 221 |
+
|
| 222 |
+
$$
|
| 223 |
+
\triangle A B C \sim \triangle D B A \sim \triangle D A C
|
| 224 |
+
$$
|
| 225 |
+
|
| 226 |
+
This implies that all corresponding length in the above mentioned triangles have the same ratio.
|
| 227 |
+
|
| 228 |
+
|
| 229 |
+
|
| 230 |
+
In particular,
|
| 231 |
+
|
| 232 |
+
$$
|
| 233 |
+
\begin{aligned}
|
| 234 |
+
& \frac{A I}{B C}=\frac{D P}{A B}=\frac{D Q}{A C} \\
|
| 235 |
+
\Longrightarrow \quad & \frac{A I^{2}}{B C^{2}}=\frac{D P^{2}}{A B^{2}}=\frac{D Q^{2}}{A C^{2}}=\frac{D P^{2}+D Q^{2}}{A B^{2}+A C^{2}} \\
|
| 236 |
+
\Longrightarrow \quad & \frac{A I^{2}}{B C^{2}}=\frac{P Q^{2}}{B C^{2}}, \quad \text { by Pythagoras Theorem in } \triangle A B C, \triangle P D Q \\
|
| 237 |
+
\Longrightarrow \quad & A I=P Q
|
| 238 |
+
\end{aligned}
|
| 239 |
+
$$
|
| 240 |
+
|
| 241 |
+
as required.
|
| 242 |
+
|
| 243 |
+
For the second, part, we note that from the above relations, we have $\triangle A B C \sim \triangle D P Q$. Let us take $\angle A C B=\theta$. Then, we get
|
| 244 |
+
|
| 245 |
+
$$
|
| 246 |
+
\begin{aligned}
|
| 247 |
+
\angle P S D & =180^{\circ}-(\angle S P D+\angle S D P) \\
|
| 248 |
+
& =180^{\circ}-\left(90^{\circ}-\theta+45^{\circ}\right) \\
|
| 249 |
+
& =45^{\circ}+\theta
|
| 250 |
+
\end{aligned}
|
| 251 |
+
$$
|
| 252 |
+
|
| 253 |
+
This gives us that
|
| 254 |
+
|
| 255 |
+
$$
|
| 256 |
+
\begin{aligned}
|
| 257 |
+
\angle A R S & =180^{\circ}-(\angle A S R+\angle S A R) \\
|
| 258 |
+
& =180^{\circ}-(\angle P S D+\angle S A C-\angle I A C) \\
|
| 259 |
+
& =180^{\circ}-\left(45^{\circ}+\theta+90^{\circ}-\theta-45^{\circ}\right) \\
|
| 260 |
+
& =90^{\circ}
|
| 261 |
+
\end{aligned}
|
| 262 |
+
$$
|
| 263 |
+
|
| 264 |
+
as required. Hence, we get that $A I=P Q$ and $A I \perp P Q$.
|
| 265 |
+
|
| 266 |
+
Solution 3: We know that the angle bisector of $\angle B$ passes through $P, I$ which implies that $B, P, I$ are collinear. Similarly, $C, Q, I$ are also collinear. Since $I$ is the incentre of $\triangle A B C$, we know that
|
| 267 |
+
|
| 268 |
+
$$
|
| 269 |
+
\angle P I Q=\angle B I C=90^{\circ}+\frac{\angle A}{2}=135^{\circ}
|
| 270 |
+
$$
|
| 271 |
+
|
| 272 |
+
Join $A P, A Q$. We know that $\angle B A P=\frac{1}{2} \angle B A D=\frac{1}{2} \angle C$. Also, $\angle A B P=\frac{1}{2} \angle B$. Hence by Exterior Angle Theorem in $\triangle A B P$, we get that
|
| 273 |
+
|
| 274 |
+
$$
|
| 275 |
+
\angle A P I=\angle A B P+\angle B A P=\frac{1}{2}(\angle B+\angle C)=45^{\circ}
|
| 276 |
+
$$
|
| 277 |
+
|
| 278 |
+
Similarly in $\triangle A D C$, we get that $\angle A Q I=45^{\circ}$. Also, we have
|
| 279 |
+
|
| 280 |
+
$$
|
| 281 |
+
\angle P A I=\angle B A I-\angle B A P=45^{\circ}-\frac{\angle C}{2}=\frac{\angle B}{2}
|
| 282 |
+
$$
|
| 283 |
+
|
| 284 |
+
Similarly, we get $\angle Q A I=\frac{\angle C}{2}$.
|
| 285 |
+
|
| 286 |
+
Now applying Sine Rule in $\triangle A P I$, we get
|
| 287 |
+
|
| 288 |
+
$$
|
| 289 |
+
\frac{I P}{\sin \angle P A I}=\frac{A I}{\sin \angle A P I} \Longrightarrow I P=\sqrt{2} A I \sin \frac{B}{2}
|
| 290 |
+
$$
|
| 291 |
+
|
| 292 |
+
Similarly, applying Sine Rule in $\triangle A Q I$, we get
|
| 293 |
+
|
| 294 |
+
$$
|
| 295 |
+
\frac{I Q}{\sin \angle P A I}=\frac{A I}{\sin \angle A Q I} \Longrightarrow I Q=\sqrt{2} A I \sin \frac{C}{2}
|
| 296 |
+
$$
|
| 297 |
+
|
| 298 |
+
Applying Cosine Rule in $\triangle P I Q$ gives us that
|
| 299 |
+
|
| 300 |
+
$$
|
| 301 |
+
\begin{aligned}
|
| 302 |
+
P Q^{2} & =I P^{2}+I Q^{2}-2 \cdot I P \cdot I Q \cos \angle P I Q \\
|
| 303 |
+
& =2 A I^{2}\left(\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}+\sqrt{2} \sin \frac{B}{2} \sin \frac{C}{2}\right)
|
| 304 |
+
\end{aligned}
|
| 305 |
+
$$
|
| 306 |
+
|
| 307 |
+
We will prove that $\left(\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}+\sqrt{2} \sin \frac{B}{2} \sin \frac{C}{2}\right)=\frac{1}{2}$. In any $\triangle X Y Z$, we have that
|
| 308 |
+
|
| 309 |
+
$$
|
| 310 |
+
\sum_{c y c} \sin ^{2} \frac{X}{2}=1-2 \prod \sin \frac{X}{2}
|
| 311 |
+
$$
|
| 312 |
+
|
| 313 |
+
Using this in $\triangle A B C$, and using the fact that $\angle A=90^{\circ}$, we get
|
| 314 |
+
|
| 315 |
+
$$
|
| 316 |
+
\begin{aligned}
|
| 317 |
+
& \sin ^{2} \frac{A}{2}+\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}=1-2 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} \\
|
| 318 |
+
\Longrightarrow \quad & \frac{1}{2}+\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}=1-\sqrt{2} \sin \frac{B}{2} \sin \frac{C}{2} \\
|
| 319 |
+
\Longrightarrow \quad & \left(\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}+\sqrt{2} \sin \frac{B}{2} \sin \frac{C}{2}\right)=\frac{1}{2}
|
| 320 |
+
\end{aligned}
|
| 321 |
+
$$
|
| 322 |
+
|
| 323 |
+
which was to be proved. Hence we get $P Q=A I$.
|
| 324 |
+
|
| 325 |
+
The second part of the problem can be obtained by angle-chasing as outlined in Solution 2 .
|
| 326 |
+
|
| 327 |
+
Solution 4: Observe that $\angle A P B=\angle A Q C=135^{\circ}$. Thus $\angle A P I=\angle A Q I=45^{\circ}$ (since $B-P-I$ and $C-Q-I)$. Note $\angle P A Q=1 / 2 \angle A=45^{\circ}$. Let $X=B I \cap A Q$ and $Y=C I \cap A P$. Therefore $\angle A X P=180-\angle A P I-\angle P A Q=90^{\circ}$. Similarly $\angle A Y Q=90^{\circ}$. Hence $I$ is the orthocentre of triangle $P A Q$. Therefore $A I$ is perpendicular to $P Q$. Also $A I=2 R_{P A Q} \cos 45^{\circ}=2 R_{P A Q} \sin 45^{\circ}=P Q$.
|
| 328 |
+
|
| 329 |
+
6. Let $n \geq 1$ be an integer and consider the sum
|
| 330 |
+
|
| 331 |
+
$$
|
| 332 |
+
x=\sum_{k \geq 0}\binom{n}{2 k} 2^{n-2 k} 3^{k}=\binom{n}{0} 2^{n}+\binom{n}{2} 2^{n-2} \cdot 3+\binom{n}{4} 2^{n-4} \cdot 3^{2}+\cdots
|
| 333 |
+
$$
|
| 334 |
+
|
| 335 |
+
Show that $2 x-1,2 x, 2 x+1$ form the sides of a triangle whose area and inradius are also integers.
|
| 336 |
+
|
| 337 |
+
Solution: Consider the binomial expansion of $(2+\sqrt{3})^{n}$. It is easy to check that
|
| 338 |
+
|
| 339 |
+
$$
|
| 340 |
+
(2+\sqrt{3})^{n}=x+y \sqrt{3}
|
| 341 |
+
$$
|
| 342 |
+
|
| 343 |
+
where $y$ is also an integer. We also have
|
| 344 |
+
|
| 345 |
+
$$
|
| 346 |
+
(2-\sqrt{3})^{n}=x-y \sqrt{3}
|
| 347 |
+
$$
|
| 348 |
+
|
| 349 |
+
Multiplying these two relations, we obtain $x^{2}-3 y^{2}=1$.
|
| 350 |
+
|
| 351 |
+
Since all the terms of the expansion of $(2+\sqrt{3})^{n}$ are positive, we see that
|
| 352 |
+
|
| 353 |
+
$$
|
| 354 |
+
2 x=(2+\sqrt{3})^{n}+(2-\sqrt{3})^{n}=2\left(2^{n}+\binom{n}{2} 2^{n-2} \cdot 3+\cdots\right) \geq 4
|
| 355 |
+
$$
|
| 356 |
+
|
| 357 |
+
Thus $x \geq 2$. Hence $2 x+1<2 x+(2 x-1)$ and therefore $2 x-1,2 x, 2 x+1$ are the sides of a triangle. By Heron's formula we have
|
| 358 |
+
|
| 359 |
+
$$
|
| 360 |
+
\Delta^{2}=3 x(x+1)(x)(x-1)=3 x^{2}\left(x^{2}-1\right)=9 x^{2} y^{2}
|
| 361 |
+
$$
|
| 362 |
+
|
| 363 |
+
Hence $\Delta=3 x y$ which is an integer. Finally, its inradius is
|
| 364 |
+
|
| 365 |
+
$$
|
| 366 |
+
\frac{\text { area }}{\text { perimeter }}=\frac{3 x y}{3 x}=y
|
| 367 |
+
$$
|
| 368 |
+
|
| 369 |
+
which is also an integer.
|
| 370 |
+
|
| 371 |
+
Solution 2: We will first show that the numbers $2 x_{n}-1,2 x_{n}, 2 x_{n}+1$ form the sides of a triangle. To show that, it suffices to prove that $2 x_{n}-1+2 x_{n}>2 x_{n}+1$. If possible, let the converse hold. Then, we see that we must have $4 x_{n}-1 \leq 2 x_{n}+1$, which implies that $x_{n} \leq 1$. But we see that even for the smallest value of $n=1$, we have that $x_{n}>1$. Hence, the numbers are indeed sides of a triangle.
|
| 372 |
+
|
| 373 |
+
Let $\Delta_{n}, r_{n}, s_{n}$ denote respectively, the area, inradius and semiperimeter of the triangle with sides $2 x_{n}-1,2 x_{n}, 2 x_{n}+1$. By Heron's Formula for the area of a triangle, we see that
|
| 374 |
+
|
| 375 |
+
$$
|
| 376 |
+
\Delta_{n}=\sqrt{3 x_{n}\left(x_{n}-1\right) x_{n}\left(x_{n}+1\right)}=x_{n} \sqrt{3\left(x_{n}^{2}-1\right)}
|
| 377 |
+
$$
|
| 378 |
+
|
| 379 |
+
If possible, let $\Delta_{n}$ be an integer for all $n \in \mathbb{N}$. We see that due to the presence of the first term $\binom{n}{0} 2^{n}$, we have $3 \nmid x_{n}, \forall n \in \mathbb{N}$. Hence, we get that $3 \mid x_{n}^{2}-1$. Hence, we can write $x_{n}^{2}-1$ as $3 m$ for some $m \in \mathbb{N}$. Then, we can also write
|
| 380 |
+
|
| 381 |
+
$$
|
| 382 |
+
\Delta_{n}=3 x_{n} \sqrt{m}
|
| 383 |
+
$$
|
| 384 |
+
|
| 385 |
+
Note that we have assumed that $\Delta_{n}$ is an integer. Hence, we see that we must have $m$ to be a perfect square. Consequently, we get that
|
| 386 |
+
|
| 387 |
+
$$
|
| 388 |
+
r_{n}=\frac{\Delta_{n}}{s_{n}}=\frac{\Delta_{n}}{3 x_{n}}=\sqrt{m} \in \mathbb{Z}
|
| 389 |
+
$$
|
| 390 |
+
|
| 391 |
+
Hence, it only remains to show that $\Delta_{n} \in \mathbb{Z}, \forall n \in \mathbb{N}$. In other words, it suffices to show that $3\left(x_{n}^{2}-1\right)$ is a perfect square for all $n \in \mathbb{N}$.
|
| 392 |
+
|
| 393 |
+
We see that we can write $x_{n}$ as
|
| 394 |
+
|
| 395 |
+
$$
|
| 396 |
+
\begin{aligned}
|
| 397 |
+
x_{n} & =\frac{1}{2}\left(2 \sum_{k \geq 0}\binom{n}{2 k} 2^{n-2 k} 3^{k}\right) \\
|
| 398 |
+
& =\frac{1}{2}\left((2+\sqrt{3})^{n}+(2-\sqrt{3})^{n}\right) \\
|
| 399 |
+
3 x_{n}^{2}-3 & =\frac{3}{4}\left((2+\sqrt{3})^{2 n}+(2-\sqrt{3})^{2 n}+2(2+\sqrt{3})^{n}(2-\sqrt{3})^{n}\right)-3 \\
|
| 400 |
+
& =\frac{3}{4}\left((2+\sqrt{3})^{2 n}+(2-\sqrt{3})^{2 n}-2(2+\sqrt{3})^{n}(2-\sqrt{3})^{n}\right) \\
|
| 401 |
+
& =\left(\frac{\sqrt{3}}{2}\left((2+\sqrt{3})^{n}-(2-\sqrt{3})^{n}\right)\right)^{2}
|
| 402 |
+
\end{aligned}
|
| 403 |
+
$$
|
| 404 |
+
|
| 405 |
+
We are left to show that the quantity obtained in the above equation is an integer. But we see that if we define
|
| 406 |
+
|
| 407 |
+
$$
|
| 408 |
+
a_{n}=\frac{\sqrt{3}}{2}\left((2+\sqrt{3})^{n}-(2-\sqrt{3})^{n}\right), \quad \forall n \in \mathbb{N}
|
| 409 |
+
$$
|
| 410 |
+
|
| 411 |
+
the sequence $\left\langle a_{k}\right\rangle_{k=1}^{\infty}$ thus obtained is exactly the solution for the recursion given by
|
| 412 |
+
|
| 413 |
+
$$
|
| 414 |
+
a_{n+2}=4 a_{n+1}-a_{n}, \quad \forall n \in \mathbb{N}, \quad a_{1}=3, a_{2}=12
|
| 415 |
+
$$
|
| 416 |
+
|
| 417 |
+
Hence, clearly, each $a_{n}$ is obviously an integer, thus completing the proof. $\qquad$
|
| 418 |
+
|
INMO/raw/en-2000.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:c81c25d819ed96a8e791a02f68b36ed72bf3de241060d6c2047f5e7b3f82d9df
|
| 3 |
+
size 43782
|
INMO/raw/en-2001.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:b22b38714b01054fd9c4ec2307b281e6c855003cd7052e21891441cf70cb04ca
|
| 3 |
+
size 59388
|
INMO/raw/en-2002.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:c229c7bc9e0594d64a5b00c2c8221ddebc68d564aeb0d1bccb67d7e57c301ff9
|
| 3 |
+
size 77299
|
INMO/raw/en-2003.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:1f07a47b100b71c593da67b8f61e38d42d3c756d97d6595fdea630ab0095e333
|
| 3 |
+
size 73489
|
INMO/raw/en-2004.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:e684abd66493f1cef3875389a1f544b7e2e8f9159127f67a990737d0625543d4
|
| 3 |
+
size 72959
|
INMO/raw/en-2005.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:a0514f87904e0bb3250f52af8eddbb9b1f64c064fc5fcae9bf9003ece7341218
|
| 3 |
+
size 87085
|
INMO/raw/en-2006.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:59aa4d51e4be8fdb0950570aea34c50532ad912bfb682e231edd6cbb7a19c598
|
| 3 |
+
size 89027
|
INMO/raw/en-2007.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:c2e26e9e5464a53a0e8847693405a77e91ab5beca57a6c3b4210cc6ec90d2890
|
| 3 |
+
size 86914
|
INMO/raw/en-2008.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:525d8c656ca1883665ed4f0411c52d88bae01f4a406d5f8a1d06816e037451dc
|
| 3 |
+
size 83510
|
INMO/raw/en-2009.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:15177d43483882001b528af5cc6f83a9cab33753563e203be0cb82410c0a64fa
|
| 3 |
+
size 103869
|
INMO/raw/en-2010.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:f98b61f9d6a0c377a8583d95b2e682934f467e4aeac60f6ddde30a3822509f0a
|
| 3 |
+
size 62380
|
INMO/raw/en-2011.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:8296f07fe403e0a98b61f39238ecc94d2ed47cc1b760d1fec1b1a1f6cf30c3ec
|
| 3 |
+
size 76563
|
INMO/raw/en-2012.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:3f860c560d42f48416629b4aa12656d986385d382fd91753e7c04986a5aaf80e
|
| 3 |
+
size 84639
|
INMO/raw/en-2023.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:8ae05e992dbe6b2e064f266b820848c3ddb6f99c21a1ec78cdc4e56e4796ccf9
|
| 3 |
+
size 181833
|
INMO/raw/en-INMO_2021_solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:6e80ebe225baf23d70d84995aab853f0b290477b07be7c1f4dfacd72f564c3bc
|
| 3 |
+
size 206389
|
INMO/raw/en-INMO_2024_final_solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:c7d53c941ea8a52d3ac9233b504e0e0e2a83b8d92fc1b2ca3faed1c1f52dc76e
|
| 3 |
+
size 185214
|
INMO/raw/en-Inmo-2019-Solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:4762b8b7fd04bf487b98ebbee3096ab42b7488c7123e426b207991b0f3609e9d
|
| 3 |
+
size 151376
|
INMO/raw/en-inmo-2014.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:60dd93d90593f65cb89a0e47d59aa18815d452ab697d62b49c22bbd52b3b03d7
|
| 3 |
+
size 116069
|
INMO/raw/en-inmo2013-solutions.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:c216fc81025187fe50912dbdbe13da5bd39414be2d4d606892ec0446ddf7c071
|
| 3 |
+
size 54492
|
INMO/raw/en-inmosol-15.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:4ba0fc8af2b90bc7d96544a2624c75558fb72f76cbb3790ed525f9b5c51b7507
|
| 3 |
+
size 158993
|
INMO/raw/en-sol-inmo-20.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:62f4dda5ae4ecc940767127d8805ac2fc0d6f95cee404201f3ccaf9a81bcea43
|
| 3 |
+
size 198975
|
INMO/raw/en-sol-inmo16.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:48fc46625af588f7cad453f1792a444e14e0aa5b49f0b40d5c62a1a44a679265
|
| 3 |
+
size 193668
|
INMO/raw/en-sol-inmo_17.pdf
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:c1a14411ddc071966ffa69d24d1306c6defb684344343a16bf69f9a7b7cd3d0f
|
| 3 |
+
size 190129
|
INMO/segment_script/segment.py
ADDED
|
@@ -0,0 +1,127 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import re
|
| 2 |
+
import json
|
| 3 |
+
|
| 4 |
+
from tqdm import tqdm
|
| 5 |
+
from loguru import logger
|
| 6 |
+
|
| 7 |
+
from pathlib import Path
|
| 8 |
+
from typing import Tuple, List
|
| 9 |
+
|
| 10 |
+
|
| 11 |
+
project_root = Path(__file__).parent.parent.parent
|
| 12 |
+
|
| 13 |
+
problem_tag = 'Problem'
|
| 14 |
+
solution_tag = 'Solution'
|
| 15 |
+
|
| 16 |
+
|
| 17 |
+
prob_re = re.compile
|
| 18 |
+
sol_re = re.compile
|
| 19 |
+
def analyze(text: str) -> Tuple[List, int]:
|
| 20 |
+
"""
|
| 21 |
+
Analyze the text and return the tags and problem number.
|
| 22 |
+
Args:
|
| 23 |
+
text (str): The markdown text to analyze.
|
| 24 |
+
Returns:
|
| 25 |
+
Tuple[List, int]: A tuple containing the tags and problem number.
|
| 26 |
+
"""
|
| 27 |
+
problem_pattern = re.compile(r"(?i)(?:\n|##* )(?:Problem (\d+)\.|№(\d+)\.|(\d+)\.)")
|
| 28 |
+
solution_pattern = re.compile(r"(?i)(?:\n|##* )(?:Solution\s*(\d+)?[\.:](\s*\:)?|Alternative solution[:\.]|Solution I*[\.:]|Sol[:\.](\s*\:)?)")
|
| 29 |
+
|
| 30 |
+
tags = []
|
| 31 |
+
tags.extend([(x, problem_tag) for x in problem_pattern.finditer(text)])
|
| 32 |
+
problem_num = len(tags)
|
| 33 |
+
|
| 34 |
+
tags.extend([(x, solution_tag) for x in solution_pattern.finditer(text)])
|
| 35 |
+
|
| 36 |
+
tags.sort(key=lambda x: x[0].start())
|
| 37 |
+
return tags, problem_num
|
| 38 |
+
|
| 39 |
+
|
| 40 |
+
def segment(text: str, tags):
|
| 41 |
+
starts = []
|
| 42 |
+
ends = []
|
| 43 |
+
|
| 44 |
+
for i in range(len(tags)):
|
| 45 |
+
starts.append(tags[i][0].end())
|
| 46 |
+
if i + 1 < len(tags):
|
| 47 |
+
ends.append(tags[i + 1][0].start())
|
| 48 |
+
else:
|
| 49 |
+
ends.append(len(text))
|
| 50 |
+
|
| 51 |
+
return [text[start:end].strip().strip('#').strip() for start, end in zip(starts, ends)]
|
| 52 |
+
|
| 53 |
+
|
| 54 |
+
def join(tags, segments):
|
| 55 |
+
problem, solution = '', ''
|
| 56 |
+
problem_label, problem_match, solution_match = '', '', ''
|
| 57 |
+
pairs = []
|
| 58 |
+
|
| 59 |
+
for tag, segment in zip(tags, segments):
|
| 60 |
+
if tag[1] == problem_tag:
|
| 61 |
+
problem = segment
|
| 62 |
+
problem_match = tag[0].group(0)
|
| 63 |
+
problem_label = tag[0].group(1) or tag[0].group(2) or tag[0].group(3)
|
| 64 |
+
else:
|
| 65 |
+
solution = segment
|
| 66 |
+
solution_match = tag[0].group(0)
|
| 67 |
+
pairs.append((problem, solution, problem_label, problem_match, solution_match))
|
| 68 |
+
|
| 69 |
+
return pairs
|
| 70 |
+
|
| 71 |
+
|
| 72 |
+
def write_pairs(output_file: Path, pairs, year):
|
| 73 |
+
output_jsonl_text = ""
|
| 74 |
+
for problem, solution, problem_label, problem_match, solution_match in pairs:
|
| 75 |
+
output_jsonl_text += json.dumps(
|
| 76 |
+
{
|
| 77 |
+
'year': year,
|
| 78 |
+
'tier': "T3",
|
| 79 |
+
'problem_label': problem_label,
|
| 80 |
+
'problem_type': None,
|
| 81 |
+
'problem': problem,
|
| 82 |
+
'solution': solution,
|
| 83 |
+
'metadata': {
|
| 84 |
+
'resource_path': output_file.relative_to(project_root).as_posix(),
|
| 85 |
+
'problem_match': problem_match,
|
| 86 |
+
'solution_match': solution_match
|
| 87 |
+
}
|
| 88 |
+
},
|
| 89 |
+
ensure_ascii=False
|
| 90 |
+
) + '\n'
|
| 91 |
+
|
| 92 |
+
output_file.write_text(output_jsonl_text, encoding="utf-8")
|
| 93 |
+
|
| 94 |
+
|
| 95 |
+
def main():
|
| 96 |
+
compet_base_path = Path(__file__).resolve().parent.parent
|
| 97 |
+
compet_md_path = compet_base_path / "md"
|
| 98 |
+
seg_output_path = compet_base_path / "segmented"
|
| 99 |
+
|
| 100 |
+
total_problem_count = 0
|
| 101 |
+
total_solution_count = 0
|
| 102 |
+
|
| 103 |
+
for inmo_md in tqdm(list(compet_md_path.glob('**/*.md')), desc='Segmenting'):
|
| 104 |
+
output_file = seg_output_path / inmo_md.relative_to(compet_md_path).with_suffix('.jsonl')
|
| 105 |
+
output_file.parent.mkdir(parents=True, exist_ok=True)
|
| 106 |
+
|
| 107 |
+
text = '\n' + inmo_md.read_text(encoding="utf-8")
|
| 108 |
+
year = re.search(r'\d{4}', text).group(0)
|
| 109 |
+
|
| 110 |
+
tags, problem_num = analyze(text)
|
| 111 |
+
|
| 112 |
+
segments = segment(text, tags)
|
| 113 |
+
pairs = join(tags, segments)
|
| 114 |
+
if pairs and problem_num > 0:
|
| 115 |
+
write_pairs(output_file, pairs, year)
|
| 116 |
+
|
| 117 |
+
total_problem_count += problem_num
|
| 118 |
+
total_solution_count += len(pairs)
|
| 119 |
+
else:
|
| 120 |
+
logger.warning(f"No problem found in {inmo_md}")
|
| 121 |
+
|
| 122 |
+
logger.info(f"Total problem count: {total_problem_count}")
|
| 123 |
+
logger.info(f"Total solution count: {total_solution_count}")
|
| 124 |
+
|
| 125 |
+
|
| 126 |
+
if __name__ == '__main__':
|
| 127 |
+
main()
|
INMO/segmented/en-2000.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2000", "tier": "T3", "problem_label": "1", "problem_type": null, "problem": "The in-circle of triangle $A B C$ touches the sides $B C, C A$ and $A B$ in $K, L$ and $M$ respectively. The line through $A$ and parallel to $L K$ meets $M K$ in $P$ and the line through $A$ and parallel to $M K$ meets $L K$ in $Q$. Show that the line $P Q$ bisects the sides $A B$ and $A C$ of triangle $A B C$.", "solution": "Let $A P, A Q$ produced meet $B C$ in $D, E$ respectively.\n\n\n\nSince $M K$ is parallel to $A E$, we have $\\angle A E K=\\angle M K B$. Since $B K=B M$, both being tangents to the circle from $B, \\angle M K B=\\angle B M K$. This with the fact that $M K$ is parallel to $A E$ gives us $\\angle A E K=\\angle M A E$. This shows that $M A E K$ is an isosceles trapezoid. We conclude that $M A=K E$. Similarly, we can prove that $A L=D K$. But $A M=A L$. We get that $D K=K E$. Since $K P$ is parallel to $A E$, we get $D P=P A$ and similarly $E Q=Q A$. This implies that $P Q$ is parallel to $D E$ and hence bisects $A B, A C$ when produced.\n\n[The same argument holds even if one or both of $P$ and $Q$ lie outside triangle $A B C$.]", "metadata": {"resource_path": "INMO/segmented/en-2000.jsonl", "problem_match": "\n1.", "solution_match": "\nSolution. :"}}
|
| 2 |
+
{"year": "2000", "tier": "T3", "problem_label": "2", "problem_type": null, "problem": "Solve for integers $x, y, z$ :\n\n$$\nx+y=1-z, \\quad x^{3}+y^{3}=1-z^{2}\n$$", "solution": "Eliminating $z$ from the given set of equations, we get\n\n$$\nx^{3}+y^{3}+\\{1-(x+y)\\}^{2}=1\n$$\n\nThis factors to\n\n$$\n(x+y)\\left(x^{2}-x y+y^{2}+x+y-2\\right)=0\n$$\n\nCase 1. Suppose $x+y=0$. Then $z=1$ and $(x, y, z)=(m,-m, 1)$, where $m$ is an integer give one family of solutions.\n\nCase 2. Suppose $x+y \\neq 0$. Then we must have\n\n$$\nx^{2}-x y+y^{2}+x+y-2=0 \\text {. }\n$$\n\nThis can be written in the form\n\n$$\n(2 x-y+1)^{2}+3(y+1)^{2}=12\n$$\n\nHere there are two possibilities:\n\n$$\n2 x-y+1=0, y+1= \\pm 2 ; \\quad 2 x-y+1= \\pm 3, y+1= \\pm 1\n$$\n\nAnalysing all these cases we get\n\n$$\n(x, y, z)=(0,1,0),(-2,-3,6),(1,0,0),(0,-2,3),(-2,0,3),(-3,-2,6) .\n$$", "metadata": {"resource_path": "INMO/segmented/en-2000.jsonl", "problem_match": "\n2.", "solution_match": "\nSol. :"}}
|
| 3 |
+
{"year": "2000", "tier": "T3", "problem_label": "3", "problem_type": null, "problem": "If $a, b, c, x$ are real numbers such that $a b c \\neq 0$ and\n\n$$\n\\frac{x b+(1-x) c}{a}=\\frac{x c+(1-x) a}{b}=\\frac{x a+(1-x) b}{c}\n$$\n\nthen prove that either $a+b+c=0$ or $a=b=c$.", "solution": "Suppose $a+b+c \\neq 0$ and let the common value be $\\lambda$. Then\n\n$$\n\\lambda=\\frac{x b+(1-x) c+x c+(1-x) a+x a+(1-x) b}{a+b+c}=1\n$$\n\nWe get two equations:\n\n$$\n-a+x b+(1-x) c=0, \\quad(1-x) a-b+x c=0\n$$\n\n(The other equation is a linear combination of these two.) Using these two equations, we get the relations\n\n$$\n\\frac{a}{1-x+x^{2}}=\\frac{b}{x^{2}-x+1}=\\frac{c}{(1-x)^{2}+x}\n$$\n\nSince $1-x+x^{2} \\neq 0$, we get $a=b=c$.", "metadata": {"resource_path": "INMO/segmented/en-2000.jsonl", "problem_match": "\n3.", "solution_match": "\nSol. :"}}
|
| 4 |
+
{"year": "2000", "tier": "T3", "problem_label": "4", "problem_type": null, "problem": "In a convex quadrilateral $P Q R S, P Q=R S,(\\sqrt{3}+1) Q R=S P$ and $\\angle R S P-\\angle S P Q=$ $30^{\\circ}$. Prove that\n\n$$\n\\angle P Q R-\\angle Q R S=90^{\\circ}\n$$", "solution": "Let $[$ Fig $]$ denote the area of Fig. We have\n\n$$\n[P Q R S]=[P Q R]+[R S P]=[Q R S]+[S P Q]\n$$\n\nLet us write $P Q=p, Q R=q, R S=r, S P=s$. The above relations reduce to\n\n$$\np q \\sin \\angle P Q R+r s \\sin \\angle R S P=q r \\sin \\angle Q R S+s p \\sin \\angle S P Q\n$$\n\nUsing $p=r$ and $(\\sqrt{3}+1) q=s$ and dividing by $p q$, we get\n\n$$\n\\sin \\angle P Q R+(\\sqrt{3}+1) \\sin \\angle R S P=\\sin \\angle Q R S+(\\sqrt{3}+1) \\sin \\angle S P Q\n$$\n\nTherefore, $\\sin \\angle P Q R-\\sin \\angle Q R S=(\\sqrt{3}+1)(\\sin \\angle S P Q-\\sin \\angle R S P)$.\n\n\n\nFig. 2.\n\nThis can be written in the form\n\n$$\n\\begin{aligned}\n2 \\sin & \\frac{\\angle P Q R-\\angle Q R S}{2} \\cos \\frac{\\angle P Q R+\\angle Q R S}{2} \\\\\n& =(\\sqrt{3}+1) 2 \\sin \\frac{\\angle S P Q-\\angle R S P}{2} \\cos \\frac{\\angle S P Q+\\angle R S P}{2}\n\\end{aligned}\n$$\n\nUsing the relations\n\n$$\n\\cos \\frac{\\angle P Q R+\\angle Q R S}{2}=-\\cos \\frac{\\angle S P Q+\\angle R S P}{2}\n$$\n\nand\n\n$$\n\\sin \\frac{\\angle S P Q-\\angle R S P}{2}=-\\sin 15^{\\circ}=-\\frac{(\\sqrt{3}-1)}{2 \\sqrt{2}}\n$$\n\nwe obtain\n\n$$\n\\sin \\frac{\\angle P Q R-\\angle Q R S}{2}=(\\sqrt{3}+1)\\left[-\\frac{(\\sqrt{3}-1)}{2 \\sqrt{2}}\\right]=\\frac{1}{\\sqrt{2}}\n$$\n\nThis shows that\n\n$$\n\\frac{\\angle P Q R-\\angle Q R S}{2}=\\frac{\\pi}{4} \\quad \\text { or } \\quad \\frac{3 \\pi}{4}\n$$\n\nUsing the convexity of $P Q R S$, we can rule out the latter alternative. We obtain\n\n$$\n\\angle P Q R-\\angle Q R S=\\frac{\\pi}{2}\n$$", "metadata": {"resource_path": "INMO/segmented/en-2000.jsonl", "problem_match": "\n4.", "solution_match": "\nSol. :"}}
|
| 5 |
+
{"year": "2000", "tier": "T3", "problem_label": "5", "problem_type": null, "problem": "Let $a, b, c$ be three real numbers such that $1 \\geq a \\geq b \\geq c \\geq 0$. Prove that if $\\lambda$ is a root of the cubic equation $x^{3}+a x^{2}+b x+c=0$ (real or complex), then $|\\lambda| \\leq 1$.", "solution": "Since $\\lambda$ is a root of the equation $x^{3}+a x^{2}+b x+c=0$, we have\n\n$$\n\\lambda^{3}=-a \\lambda^{2}-b \\lambda-c\n$$\n\nThis implies that\n\n$$\n\\begin{aligned}\n\\lambda^{4} & =-a \\lambda^{3}-b \\lambda^{2}-c \\lambda \\\\\n& =(1-a) \\lambda^{3}+(a-b) \\lambda^{2}+(b-c) \\lambda+c\n\\end{aligned}\n$$\n\nwhere we have used again\n\n$$\n-\\lambda^{3}-a \\lambda^{2}-b \\lambda-c=0\n$$\n\nSuppose $|\\lambda| \\geq 1$. Then we obtain\n\n$$\n\\begin{aligned}\n|\\lambda|^{4} & \\leq(1-a)|\\lambda|^{3}+(a-b)|\\lambda|^{2}+(b-c)|\\lambda|+c \\\\\n& \\leq(1-a)|\\lambda|^{3}+(a-b)|\\lambda|^{3}+(b-c)|\\lambda|^{3}+c|\\lambda|^{3} \\\\\n& \\leq|\\lambda|^{3}\n\\end{aligned}\n$$\n\nThis shows that $|\\lambda| \\leq 1$. Hence the only possibility in this case is $|\\lambda|=1$. We conclude that $|\\lambda| \\leq 1$ is always true.", "metadata": {"resource_path": "INMO/segmented/en-2000.jsonl", "problem_match": "\n5.", "solution_match": "\nSol. :"}}
|
| 6 |
+
{"year": "2000", "tier": "T3", "problem_label": "6", "problem_type": null, "problem": "For any natural number $n,(n \\geq 3)$, let $f(n)$ denote the number of non-congruent integer-sided triangles with perimeter $n$ (e.g., $f(3)=1, f(4)=0, f(7)=2$ ). Show that\n\n(a) $f(1999)>f(1996)$\n\n(b) $f(2000)=f(1997)$.", "solution": "(a) Let $a, b, c$ be the sides of a triangle with $a+b+c=1996$, and each being a positive integer. Then $a+1, b+1, c+1$ are also sides of a triangle with perimeter 1999 because\n\n$$\na<b+c \\quad \\Longrightarrow \\quad a+1<(b+1)+(c+1)\n$$\n\nand so on. Moreover $(999,999,1)$ form the sides of a triangle with perimeter 1999, which is not obtainable in the form $(a+1, b+1, c+1)$ where $a, b, c$ are the integers and the sides of a triangle with $a+b+c=1996$. We conclude that $f(1999)>f(1996)$.\n\n(b) As in the case (a) we conclude that $f(2000) \\geq f(1997)$. On the other hand, if $x, y, z$ are the integer sides of a triangle with $x+y+z=2000$, and say $x \\geq y \\geq z \\geq 1$, then we cannot have $z=1$; for otherwise we would get $x+y=1999$ forcing $x, y$ to have opposite parity so that $x-y \\geq 1=z$ violating triangle inequality for $x, y, z$. Hence $x \\geq y \\geq z>1$. This implies that $x-1 \\geq y-1 \\geq z-1>0$. We already have $x<y+z$. If $x \\geq y+z-1$, then we see that $y+z-1 \\leq x<y+z$, showing that $y+z-1=x$. Hence we obtain $2000=x+y+z=2 x+1$ which is impossible. We conclude that $x<y+z-1$. This shows that $x-1<(y-1)+(z-1)$ and hence $x-1, y-1, z-1$ are the sides of a triangle with perimeter 1997. This gives $f(2000) \\leq f(1997)$. Thus we obtain the desired result.", "metadata": {"resource_path": "INMO/segmented/en-2000.jsonl", "problem_match": "\n6.", "solution_match": "\nSol. :"}}
|
INMO/segmented/en-2001.jsonl
ADDED
|
@@ -0,0 +1,6 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
{"year": "2001", "tier": "T3", "problem_label": "1", "problem_type": null, "problem": "Let $A B C$ be a triangle in which no angle is $90^{\\circ}$. For any point $P$ in the plane of the triangle, let $A_{1}, B_{1}, C_{1}$ denote the reflections of $P$ in the sides $B C, C A, A B$ respectively. Prove the following statements:\n\n(a) If $P$ is the incentre or an excentre of $A B C$, then $P$ is the circumcentre of $A_{1} B_{1} C_{1}$;\n\n(b) If $P$ is the circumcentre of $A B C$, then $P$ is the orthocentre of $A_{1} B_{1} C_{1}$;\n\n(c) If $P$ is the orthocentre of $A B C$, then $P$ is either the incentre or an excentre of $A_{1} B_{1} C_{1}$.", "solution": "(a)\n\n\n\nIf $P=I$ is the incentre of triangle $A B C$, and $r$ its inradius, then it is clear that $A_{1} I=B_{1} I=C_{1} I=2 r$. It follows that $I$ is the circumcentre of $A_{1} B_{1} C_{1}$. On the otherhand if $P=I_{1}$ is the excentre of $A B C$ opposite $A$ and $r_{1}$ the corresponding exradius, then again we see that $A_{1} I_{1}=B_{1} I_{1}=C_{1} I_{1}=2 r_{1}$. Thus $I_{1}$ is the circumcentre of $A_{1} B_{1} C_{1}$.\n\n\n\n(b)\n\nLet $P=O$ be the circumcentre of $A B C$. By definition, it follows that $O A_{1}$ bisects and is bisected by $B C$ and so on. Let $D, E, F$ be the mid-points of $B C, C A, A B$ respectively. Then $F E$ is parallel to $B C$. But $E, F$ are also mid-points of $O B_{1}, O C_{1}$ and hence $F E$ is parallel to $B_{1} C_{1}$ as well. We conclude that $B C$ is parallel to $B_{1} C_{1}$. Since $O A_{1}$ is perpendicular to $B C$, it follows that $O A_{1}$ is perpendicular to $B_{1} C_{1}$. Similarly $O B_{1}$ is perpendicular to $C_{1} A_{1}$ and $O C_{1}$ is perpendicular to $A_{1} B_{1}$. These imply that $O$ is the orthocentre of $A_{1} B_{1} C_{1}$. (This applies whether $O$ is inside or outside $A B C$.)\n\n(c)\n\nlet $P=H$, the orthocentre of $A B C$. We consider two possibilities; $H$ falls inside $A B C$ and $H$ falls outside $A B C$.\n\nSuppose $H$ is inside $A B C$; this happens if $A B C$ is an acute triangle. It is known that $A_{1}, B_{1}, C_{1}$ lie on the circumcircle of $A B C$. Thus $\\angle C_{1} A_{1} A=\\angle C_{1} C A=90^{\\circ}-A$. Similarly $\\angle B_{1} A_{1} A=\\angle B_{1} B A=90^{\\circ}-A$. These show that $\\angle C_{1} A_{1} A=\\angle B_{1} A_{1} A$. Thus $A_{1} A$ is an internal bisector of $\\angle C_{1} A_{1} B_{1}$. Similarly we can show that $B_{1}$ bisects $\\angle A_{1} B_{1} C_{1}$ and $C_{1} C$ bisects $\\angle B_{1} C_{1} A_{1}$. Since $A_{1} A, B_{1} B, C_{1} C$ concur at $H$, we conclude that $H$ is the incentre of $A_{1} B_{1} C_{1}$.\n\nOR If $D, E, F$ are the feet of perpendiculars of $A, B, C$ to the sides $B C, C A, A B$ respectively, then we see that $E F, F D, D E$ are respectively parallel to $B_{1} C_{1}, C_{1} A_{1}$, $A_{1} B_{1}$. This implies that $\\angle C_{1} A_{1} H=\\angle F D H=\\angle A B E=90^{\\circ}-A$, as $B D H F$ is a cyclic quadrilateral. Similarly, we can show that $\\angle B_{1} A_{1} H=90^{\\circ}-A$. It follows that $A_{1} H$ is the internal bisector of $\\angle C_{1} A_{1} B_{1}$. We can proceed as in the earlier case.\n\nIf $H$ is outside $A B C$, the same proofs go through again, except that two of $A_{1} H$, $B_{1} H, C_{1} H$ are external angle bisectors and one of these is an internal angle bisector. Thus $H$ becomes an excentre of triangle $A_{1} B_{1} C_{1}$.", "metadata": {"resource_path": "INMO/segmented/en-2001.jsonl", "problem_match": "\n1.", "solution_match": "## Solution:"}}
|
| 2 |
+
{"year": "2001", "tier": "T3", "problem_label": "2", "problem_type": null, "problem": "Show that the equation\n\n$$\nx^{2}+y^{2}+z^{2}=(x-y)(y-z)(z-x)\n$$\n\nhas infinitely many solutions in integers $x, y, z$.", "solution": "We seek solutions $(x, y, z)$ which are in arithmetic progression. Let us put $y-x=z-y=d>0$ so that the equation reduces to the form\n\n$$\n3 y^{2}+2 d^{2}=2 d^{3}\n$$\n\nThus we get $3 y^{2}=2(d-1) d^{2}$. We conclude that $2(d-1)$ is 3 times a square. This is satisfied if $d-1=6 n^{2}$ for some $n$. Thus $d=6 n^{2}+1$ and $3 y^{2}=d^{2} \\cdot 2\\left(6 n^{2}\\right)$ giving us $y^{2}=4 d^{2} n^{2}$. Thus we can take $y=2 d n=2 n\\left(6 n^{2}+1\\right)$. From this we obtain $x=y-d=(2 n-1)\\left(6 n^{2}+1\\right), z=y+d=(2 n+1)\\left(6 n^{2}+1\\right)$. It is easily verified that\n\n$$\n(x, y, z)=\\left((2 n-1)\\left(6 n^{2}+1\\right), 2 n\\left(6 n^{2}+1\\right),(2 n+1)\\left(6 n^{2}+1\\right)\\right)\n$$\n\nis indeed a solution for a fixed $n$ and this gives an infinite set of solutions as $n$ varies over natural numbers.", "metadata": {"resource_path": "INMO/segmented/en-2001.jsonl", "problem_match": "\n2.", "solution_match": "\nSolution:"}}
|
| 3 |
+
{"year": "2001", "tier": "T3", "problem_label": "3", "problem_type": null, "problem": "If $a, b, c$ are positive real numbers such that $a b c=1$, prove that\n\n$$\na^{b+c} b^{c+a} c^{a+b} \\leq 1\n$$", "solution": "Note that the inequality is symmetric in $a, b, c$ so that we may assume that $a \\geq b \\geq c$. Since $a b c=1$, it follows that $a \\geq 1$ and $c \\leq 1$. Using $b=1 / a c$, we get\n\n$$\na^{b+c} b^{c+a} c^{a+b}=\\frac{a^{b+c} c^{a+b}}{a^{c+a} c^{c+a}}=\\frac{c^{b-c}}{a^{a-b}} \\leq 1\n$$\n\nbecause $c \\leq 1, b \\geq c, a \\geq 1$ and $a \\geq b$.", "metadata": {"resource_path": "INMO/segmented/en-2001.jsonl", "problem_match": "\n3.", "solution_match": "\nSolution:"}}
|
| 4 |
+
{"year": "2001", "tier": "T3", "problem_label": "4", "problem_type": null, "problem": "Given any nine integers show that it is possible to choose, from among them, four integers $a, b, c, d$ such that $a+b-c-d$ is divisible by 20 . Further show that such a selection is not possible if we start with eight integers instead of nine.", "solution": "Suppose there are four numbers $a, b, c, d$ among the given nine numbers which leave the same remainder modulo 20 . Then $a+b \\equiv c+d(\\bmod 20)$ and we are done.\n\nIf not, there are two possibilities:\n\n(1) We may have two disjoint pairs $\\{a, c\\}$ and $\\{b, d\\}$ obtained from the given nine numbers such that $a \\equiv c(\\bmod 20)$ and $b \\equiv d(\\bmod 20)$. In this case we get $a+b \\equiv c+d$ $(\\bmod 20)$.\n\n(2) Or else there are at most three numbers having the same remainder modulo 20 and the remaining six numbers leave distinct remainders which are also different from the first remainder (i.e., the remainder of the three numbers). Thus there are at least 7 disinct remainders modulo 20 that can be obtained from the given set of nine numbers. These 7 remainders give rise to $\\binom{7}{2}=21$ pairs of numbers. By pigeonhole principle, there must be two pairs $\\left(r_{1}, r_{2}\\right),\\left(r_{3}, r_{4}\\right)$ such that $r_{1}+r_{2} \\equiv r_{3}+r_{4}(\\bmod 20)$. Going back we get four numbers $a, b, c, d$ such that $a+b \\equiv c+d(\\bmod 20)$.\n\nIf we take the numbers $0,0,0,1,2,4,7,12$, we check that the result is not true for these eight numbers.", "metadata": {"resource_path": "INMO/segmented/en-2001.jsonl", "problem_match": "\n4.", "solution_match": "## Solution:"}}
|
| 5 |
+
{"year": "2001", "tier": "T3", "problem_label": "5", "problem_type": null, "problem": "Let $A B C$ be a triangle and $D$ be the mid-point of side $B C$. Suppose $\\angle D A B=\\angle B C A$ and $\\angle D A C=15^{\\circ}$. Show that $\\angle A D C$ is obtuse. Further, if $O$ is the circumcentre of $A D C$, prove that triangle $A O D$ is equilateral.", "solution": "\n\nLet $\\alpha$ denote the equal angles $\\angle B A D=\\angle D C A$. Using sine rule in triangles $D A B$ and $D A C$, we get\n\n$$\n\\frac{A D}{\\sin B}=\\frac{B D}{\\sin \\alpha}, \\quad \\frac{C D}{\\sin 15^{\\circ}}=\\frac{A D}{\\sin \\alpha}\n$$\n\nEliminating $\\alpha$ (using $B D=D C$ and $2 \\alpha+B+15^{\\circ}=\\pi$ ), we obtain $1+\\cos \\left(B+15^{\\circ}\\right)=$ $2 \\sin B \\sin 15^{\\circ}$. But we know that $2 \\sin B \\sin 15^{\\circ}=\\cos \\left(B-15^{\\circ}\\right)-\\cos \\left(B+15^{\\circ}\\right)$. Putting $\\beta=B-15^{\\circ}$, we get a relation $1+2 \\cos (\\beta+30)=\\cos \\beta$. We write this in the form\n\n$$\n(1-\\sqrt{3}) \\cos \\beta+\\sin \\beta=1\n$$\n\nSince $\\sin \\beta \\leq 1$, it follows that $(1-\\sqrt{3}) \\cos \\beta \\geq 0$. We conclude that $\\cos \\beta \\leq 0$ and hence that $\\beta$ is obtuse. So is angle $B$ and hence $\\angle A D C$.\n\nWe have the relation $(1-\\sqrt{3}) \\cos \\beta+\\sin \\beta=1$. If we set $x=\\tan (\\beta / 2)$, then we get, using $\\cos \\beta=\\left(1-x^{2}\\right) /\\left(1+x^{2}\\right), \\sin \\beta=2 x /\\left(1+x^{2}\\right)$,\n\n$$\n(\\sqrt{3}-2) x^{2}+2 x-\\sqrt{3}=0\n$$\n\nSolving for $x$, we obtain $x=1$ or $x=\\sqrt{3}(2+\\sqrt{3})$. If $x=\\sqrt{3}(2+\\sqrt{3})$, then $\\tan (\\beta / 2)>2+\\sqrt{3}=\\tan 75^{\\circ}$ giving us $\\beta>150^{\\circ}$. This forces that $B>165^{\\circ}$ and hence $B+A>165^{\\circ}+15^{\\circ}=180^{\\circ}$, a contradiction. thus $x=1$ giving us $\\beta=\\pi / 2$. This gives $B=105^{\\circ}$ and hence $\\alpha=30^{\\circ}$. Thus $\\angle D A O=60^{\\circ}$. Since $O A=O D$, the result follows.\n\n## OR\n\nLet $m_{a}$ denote the median $A D$. Then we can compute\n\n$$\n\\cos \\alpha=\\frac{c^{2}+m_{a}^{2}-\\left(a^{2} / 4\\right)}{2 c m_{a}}, \\quad \\sin \\alpha=\\frac{2 \\Delta}{c m_{a}}\n$$\n\nwhere $\\Delta$ denotes the area of triangle $A B C$. These two expressions give\n\n$$\n\\cot \\alpha=\\frac{c^{2}+m_{a}^{2}-\\left(a^{2} / 4\\right)}{4 \\Delta}\n$$\n\nSimilarly, we obtain\n\n$$\n\\cot \\angle C A D=\\frac{b^{2}+m_{a}^{2}-\\left(a^{2} / 4\\right)}{4 \\Delta}\n$$\n\nThus we get\n\n$$\n\\cot \\alpha-\\cot 15^{\\circ}=\\frac{c^{2}-a^{2}}{4 \\Delta}\n$$\n\nSimilarly we can also obtain\n\n$$\n\\cot B-\\cot \\alpha=\\frac{c^{2}-a^{2}}{4 \\Delta}\n$$\n\ngiving us the relation\n\n$$\n\\cot B=2 \\cot \\alpha-\\cot 15^{\\circ}\n$$\n\nIf $B$ is acute then $2 \\cot \\alpha>\\cot 15^{\\circ}=2+\\sqrt{3}>2 \\sqrt{3}$. It follows that $\\cot \\alpha>\\sqrt{3}$. This implies that $\\alpha<30^{\\circ}$ and hence\n\n$$\nB=180^{\\circ}-2 \\alpha-15^{\\circ}>105^{\\circ}\n$$\n\nThis contradiction forces that angle $B$ is obtuse and consequently $\\angle A D C$ is obtuse.\n\nSince $\\angle B A D=\\alpha=\\angle A C D$, the line $A B$ is tangent to the circumcircle $\\Gamma$ of $A D C$ at $A$. Hence $O A$ is perpendicular to $A B$. Draw $D E$ and $B F$ perpendicular to $A C$, and join $O D$. Since $\\angle D A C=15^{\\circ}$, we see that $\\angle D O C=30^{\\circ}$ and hence $D E=O D / 2$. But $D E$ is parallel to $B F$ and $B D=D C$ shows that $B F=2 D E$. We conclude that\n$B F=D O$. But $D O=A O$, both being radii of $\\Gamma$. Thus $B F=A O$. Using right triangles $B F O$ and $B A O$, we infer that $A B=O F$. We conclude that $A B F O$ is a rectangle. In particular $\\angle A O F=90^{\\circ}$. It follows that\n\n$$\n\\angle A O D=90^{\\circ}-\\angle D O C=90^{\\circ}-30^{\\circ}=60^{\\circ}\n$$\n\nSince $O A=O D$, we conclude that $A O D$ is equilateral.\n\nOR\n\nNote that triangles $A B D$ and $C B A$ are similar. Thus we have the ratios\n\n$$\n\\frac{A B}{B D}=\\frac{C B}{B A}\n$$\n\nThis reduces to $a^{2}=2 c^{2}$ giving us $a=\\sqrt{2} c$. This is equivalent to $\\sin ^{2}\\left(\\alpha+15^{\\circ}\\right)=$ $2 \\sin ^{2} \\alpha$. We write this in the form\n\n$$\n\\cos 15^{\\circ}+\\cot \\alpha \\sin 15^{\\circ}=\\sqrt{2}\n$$\n\nSolving for $\\cot \\alpha$, we get $\\cot \\alpha=\\sqrt{3}$. We conclude that $\\alpha=30^{\\circ}$, and the result follows.", "metadata": {"resource_path": "INMO/segmented/en-2001.jsonl", "problem_match": "\n5.", "solution_match": "## Solution:"}}
|
| 6 |
+
{"year": "2001", "tier": "T3", "problem_label": "6", "problem_type": null, "problem": "Let $\\mathbf{R}$ denote the set of all real numbers. Find all functions $f: \\mathbf{R} \\rightarrow \\mathbf{R}$ satisfying the condition\n\n$$\nf(x+y)=f(x) f(y) f(x y)\n$$\n\nfor all $x, y$ in $\\mathbf{R}$.", "solution": "Putting $x=0, y=0$, we get $f(0)=f(0)^{3}$ so that $f(0)=0,1$ or -1 . If $f(0)=0$, then taking $y=0$ in the given equation, we obtain $f(x)=f(x) f(0)^{2}=0$ for all $x$.\n\nSuppose $f(0)=1$. Taking $y=-x$, we obtain\n\n$$\n1=f(0)=f(x-x)=f(x) f(-x) f\\left(-x^{2}\\right)\n$$\n\nThis shows that $f(x) \\neq 0$ for any $x \\in \\mathbf{R}$. Taking $x=1, y=x-1$, we obtain\n\n$$\nf(x)=f(1) f(x-1)^{2}=f(1)[f(x) f(-x) f(-x)]^{2}\n$$\n\nUsing $f(x) \\neq 0$, we conclude that $1=k f(x)(f(-x))^{2}$, where $k=$\n\n$f(1)(f(-1))^{2}$. Changing $x$ to $-x$ here, we also infer that $1=k f(-x)(f(x))^{2}$. Comparing these expressions we see that $f(-x)=f(x)$. It follows that $1=k f(x)^{3}$. Thus $f(x)$ is constant for all $x$. Since $f(0)=1$, we conclude that $f(x)=1$ for all real $x$.\n\nIf $f(0)=-1$, a similar analysis shows that $f(x)=-1$ for all $x \\in \\mathbf{R}$. We can verify that each of these functions satisfies the given functional equation. Thus there are three solutions, all of them being constant functions.", "metadata": {"resource_path": "INMO/segmented/en-2001.jsonl", "problem_match": "\n6.", "solution_match": "\nSolution:"}}
|