problem
stringlengths 28
7.48k
| solution
stringlengths 0
18.5k
| answer
stringclasses 1
value | problem_type
stringclasses 8
values | question_type
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class | source_dataset
stringclasses 1
value | source_split
stringclasses 1
value | __index_level_0__
int64 1
111k
|
|---|---|---|---|---|---|---|---|---|---|
## Problem 3.
Let $n>1$ and $p(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0}$ be a polynomial with $n$ real roots (counted with multiplicity). Let the polynomial $q$ be defined by
$$
q(x)=\prod_{j=1}^{2015} p(x+j)
$$
We know that $p(2015)=2015$. Prove that $q$ has at least 1970 different roots $r_{1}, \ldots, r_{1970}$ such that $\left|r_{j}\right|<2015$ for all $j=1, \ldots, 1970$.
|
Solution. Let $h_{j}(x)=p(x+j)$. Consider $h_{2015}$. Like $p$, it has $n$ real roots $s_{1}, s_{2}, \ldots, s_{n}$, and $h_{2015}(0)=p(2015)=2015$. By Viète, the product $\left|s_{1} s_{2} \cdots s_{n}\right|$ equals 2015. Since $n \geq 2$, there is at least one $s_{j}$ such that $\left|s_{j}\right| \leq \sqrt{2015}<\sqrt{2025}=45$. Denote this $s_{j}$ by $m$. Now for all $j=0,1, \ldots, 2014, h_{2015-j}(m+j)=p(m+j+2015-j)=p(m+2015)=$ $h_{2015}(m)=0$. So $m, m+1, \ldots, m+2014$ are all roots of $q$. Since $0 \leq|m|<45$, the condition $|m+j|<2015$ is satisfied by at least 1970 different $j, 0 \leq j \leq 2014$, and we are done.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 241 |
Problem 3. Define a sequence $\left(n_{k}\right)_{k \geq 0}$ by $n_{0}=n_{1}=1$, and $n_{2 k}=n_{k}+n_{k-1}$ and $n_{2 k+1}=n_{k}$ for $k \geq 1$. Let further $q_{k}=n_{k} / n_{k-1}$ for each $k \geq 1$. Show that every positive rational number is present exactly once in the sequence $\left(q_{k}\right)_{k \geq 1}$.
|
Solution. Clearly, all the numbers $n_{k}$ are positive integers. Moreover,
$$
q_{2 k}=\frac{n_{2 k}}{n_{2 k-1}}=\frac{n_{k}+n_{k-1}}{n_{k-1}}=q_{k}+1
$$
and similarly,
$$
\frac{1}{q_{2 k+1}}=\frac{n_{2 k}}{n_{2 k+1}}=\frac{n_{k}+n_{k-1}}{n_{k}}=\frac{1}{q_{k}}+1
$$
In particular, $q_{k}>1$ when $k$ is even, and $q_{k}s$. We know that $r / s=q_{m}$ is only possible if $m$ is even. But
$$
\frac{r}{s}=q_{2 k} \Leftrightarrow \frac{r-s}{s}=q_{k}
$$
by (1), and moreover, the latter equality holds for precisely one $k$ according to the induction hypothesis, since $\operatorname{gcd}(r-s, s)=1$ and $(r-s)+s=r \leq t$.
Next, assume that $r<s$. We know that $r / s=q_{m}$ is only possible if $m$ is odd. But
$$
\frac{r}{s}=q_{2 k+1} \Leftrightarrow \frac{s}{r}=\frac{1}{q_{2 k+1}} \Leftrightarrow \frac{s-r}{r}=\frac{1}{q_{k}}
$$
by (2), and moreover, the latter equality holds for precisely one $k$ according to the induction hypothesis, since $\operatorname{gcd}(s-r, r)=1$ and $(s-r)+r=s \leq t$.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 242 |
Problem 4. Let $A B C$ be an acute angled triangle, and $H$ a point in its interior. Let the reflections of $H$ through the sides $A B$ and $A C$ be called $H_{c}$ and $H_{b}$, respectively, and let the reflections of $H$ through the midpoints of these same sides be called $H_{c}^{\prime}$ and $H_{b}^{\prime}$, respectively. Show that the four points $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ are concyclic if and only if at least two of them coincide or $H$ lies on the altitude from $A$ in triangle $A B C$.
|
Solution. If at least two of the four points $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ coincide, all four are obviously concyclic. Therefore we may assume that these four points are distinct.
Let $P_{b}$ denote the midpoint of segment $H H_{b}, P_{b}^{\prime}$ the midpoint of segment $H H_{b}^{\prime}, P_{c}$ the midpoint of segment $H H_{c}$, and $P_{c}^{\prime}$ the midpoint of segment $H H_{c}^{\prime}$.
The triangle $H H_{b} H_{b}^{\prime}$ being right-angled in $H_{b}$, it follows that the perpendicular bisector $\ell_{b}$ of the side $H_{b} H_{b}^{\prime}$ goes through the point $P_{b}^{\prime}$. Since the segments $P_{b} P_{b}^{\prime}$ and $H_{b} H_{b}^{\prime}$ are parallel and $P_{b}^{\prime}$ is the midpoint of the side $A C$, we then conclude that $\ell_{b}$ also goes through the circumcentre $O$ of triangle $A B C$.
Similarly the perpendicular bisector $\ell_{c}$ of the segment $H_{c} H_{c}^{\prime}$ also goes through $O$. Hence the four points $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ are concyclic if and only if also the perpendicular bisector $\ell$ of the segment $H_{b}^{\prime} H_{c}^{\prime}$ goes through the point $O$. Since $H_{b}^{\prime} H_{c}^{\prime}\left\|P_{b}^{\prime} P_{c}^{\prime}\right\| B C$, this is the case if and only if $\ell$ is the perpendicular bisector $m$ of the segment $B C$.
Let $k$ denote the perpendicular bisector of the segment $P_{b}^{\prime} P_{c}^{\prime}$. Since the lines $\ell$ and $m$ are obtained from $k$ by similarities of ratio 2 and centres $H$ and $A$, respectively, they coincide if and only if $H A$ is parallel to $m$. Thus $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ are concyclic if and only if $H$ lies on the altitude from $A$ in triangle $A B C$.
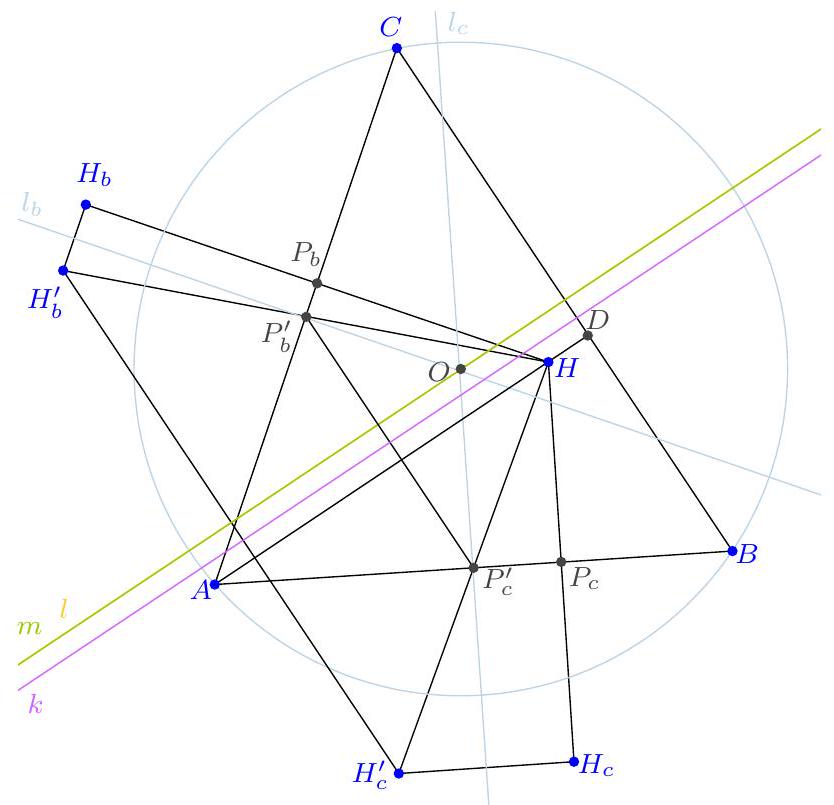
Click here to experiment with the figure in GeoGebra.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 243 |
LII OM - I - Problem 10
Prove that inside any triangle $ABC$ there exists a point $P$ with the following property:
Every line passing through point $P$ divides the perimeter of triangle $ABC$ in the same ratio as it divides its area.
|
We will show that the property described in the problem statement is possessed by the center of the inscribed circle.
om52_1r_img_17.jpg
Let $ \ell $ be any line passing through point $ P $, which is the center of the circle inscribed in triangle $ ABC $ (Fig. 1). Without loss of generality, assume that line $ \ell $ intersects sides $ AC $ and $ BC $ at points $ D $ and $ E $, respectively. We need to show that
where $ [\mathcal{F}] $ is the area of figure $ \mathcal{F} $. Denoting by $ r $ the radius of the circle inscribed in triangle $ ABC $, we get
and
Dividing the sides of equations (2) and (3), we obtain equation (1).
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 244 |
XXXVII OM - III - Problem 1
A square with a side length of 1 is covered by $ m^2 $ rectangles. Prove that the perimeter of one of these rectangles is greater than or equal to $ 4/m $.
|
Pole $ P = ab $ i obwód $ p = 2(a+b) $ prostokąta o bokach długości $ a $, $ b $ związane są nierównością
The area $ P = ab $ and the perimeter $ p = 2(a+b) $ of a rectangle with side lengths $ a $, $ b $ are related by the inequality
Gdyby więc każdy z rozważanych $ m^2 $ prostokątów miał obwód mniejszy od
$ 4/m $, to pole każdego z nich byłoby mniejsze od $ \frac{1}{16} \cdot \left( \frac{4}{m} \right)^2 $ (czyli od $ 1/m^2 $), a więc suma ich pól byłaby mniejsza od $ 1 $ - wbrew założeniu, że pokrywają one kwadrat jednostkowy.
If, therefore, each of the $ m^2 $ rectangles considered had a perimeter less than
$ 4/m $, then the area of each of them would be less than $ \frac{1}{16} \cdot \left( \frac{4}{m} \right)^2 $ (i.e., less than $ 1/m^2 $), and thus the sum of their areas would be less than $ 1 $ - contrary to the assumption that they cover the unit square.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 245 |
XI OM - II - Task 1
Prove that if real numbers $ a $ and $ b $ are not both equal to zero, then for every natural $ n $
|
When one of the numbers $ a $ and $ b $ is equal to zero or when both are of the same sign, inequality (1) is obvious, since in that case no term on the left side $ L $ of the inequality is negative. It remains to prove the case when $ a $ and $ b $ are of different signs. Due to the symmetry of $ L $ with respect to $ a $ and $ b $, it suffices to consider the case $ a > 0 $, $ b < 0 $.
If $ b = aq $, then $ q < 0 $ and
therefore, according to the known formula for the sum of a geometric progression
Since $ q < 0 $ and $ q^{2n+1} < 0 $, then $ 1 - q > 0 $ and $ 1 - q^{2n+1} > 0 $, and since $ a^{2n} > 0 $, indeed $ L > 0 $.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 248 |
XXXVII OM - I - Problem 12
Prove that if the line connecting the midpoints of two opposite edges of a tetrahedron passes through the center of the inscribed sphere of this tetrahedron, then it also passes through the center of the circumscribed sphere of this tetrahedron.
|
We will first prove a lemma.
Lemma. Given a convex dihedral angle formed by half-planes $\alpha$ and $\beta$ with a common edge $l$. Let $\pi$ be the bisecting half-plane of this dihedral angle. Suppose that point $P \in \pi$ is the midpoint of segment $AB$ with endpoints $A \in \alpha$, $B \in \beta$ (where $A$, $B$, $P \in l$). Let $O$ denote the orthogonal projection of point $P$ onto line $l$. Then the lines $OP$ and $AB$ are perpendicular.
Proof of the lemma. Lines $l$ and $AB$ are skew. Therefore, there exists exactly one plane $\sigma$ containing line $AB$ and parallel to $l$. This plane intersects the half-planes $\alpha$, $\beta$, and $\pi$ along lines $\alpha \cap \sigma$, $\beta \cap \sigma$, $\pi \cap \sigma$ parallel to $l$ (Figure 5). Lines $\pi \cap \sigma$ and $OP$ are thus perpendicular.
om37_1r_img_5.jpg
Consider triangle $OST$ located in a plane perpendicular to $l$, with vertices $S \in \alpha \cap \sigma$, $T \in \beta \cap \sigma$. Right triangles $ASP$ and $BTP$ have equal angles ($|\measuredangle SPA| = |\measuredangle TPB|$ as vertical angles) and equal hypotenuses ($|PA| = |PB|$) - they are therefore congruent and thus $|PS| = |PT|$. Therefore, segment $OP$ is the median in triangle $OST$. It is also the angle bisector of $\angle SOT$ (since the half-plane $\pi$ bisects the dihedral angle between $\alpha$ and $\beta$). It follows that this segment is also the altitude in triangle $OST$, so $OP \bot ST$. Line $OP$, being perpendicular to lines $ST$ and $\pi \cap \sigma$ lying in plane $\sigma$, is perpendicular to this plane - and thus to line $AB$.
Proof of the theorem. Let $P$ and $Q$ be the midpoints of edges $AB$ and $CD$ of tetrahedron $ABCD$ (Figure 6) and let, according to the problem's assumption, line $PQ$ pass through the center of the inscribed sphere of the tetrahedron. Then the half-plane $CDP^\rightarrow$ bisects the dihedral angle formed by faces $CDA$ and $CDB$. Denoting by $O$ the orthogonal projection of point $P$ onto line $l = CD$, we have by the lemma that $OP \bot AB$. Similarly, the half-plane $ABQ^\rightarrow$ bisects the dihedral angle between faces $ABC$ and $ABD$, and by the lemma $QR \bot CD$, where $R$ is the projection of point $Q$ onto line $AB$.
om37_1r_img_6.jpg
Thus, each of the lines $OP$ and $QR$ is perpendicular to both lines $AB$ and $CD$. But for any pair of skew lines, there is only one line that intersects both and is perpendicular to them. Consequently, lines $OP$ and $QR$ coincide. This means that line $PQ$ is perpendicular to lines $AB$ and $CD$. Therefore, planes $CDP$ and $ABQ$ are the perpendicular bisector planes of segments $AB$ and $CD$ (respectively). The center of the circumscribed sphere must lie in both of these planes, and thus on their line of intersection, which is line $PQ$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 250 |
I OM - B - Task 2
Prove that if the number $ a $ is the sum of the squares of two different natural numbers, then $ a^2 $ is the sum of the squares of two natural numbers.
|
If $ a=x^2+y^2 $, then
保留了源文本的换行和格式。请注意,最后一行的“保留了源文本的换行和格式”是中文,翻译成英文应为:“The line breaks and formatting of the source text have been preserved.” 但为了保持格式一致,这里没有将其翻译出来。
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 252 |
XXVIII - I - Problem 5
Prove that if $ P(x, y) $ is a polynomial in two variables such that $ P(x, y) = P(y, x) $ for all real $ x, y $ and the polynomial $ (x-y) $ divides $ P(x, y) $, then the polynomial $ (x - y)^2 $ also divides $ P(x, y) $.
|
By assumption, there exists a polynomial $ Q(x, y) $ such that $ P(x,y) = (x - y) \cdot Q(x, y) $. From the equality $ P(x, y) = P(y, x) $, we obtain that $ (x - y) \cdot Q(x, y) = (y - x) \cdot Q(y, x) $, which means $ (x - y) \cdot (Q(x, y) + Q(y, x)) = 0 $. Since the product of polynomials is a zero polynomial only if one of the factors is a zero polynomial, and the polynomial $ x - y $ is non-zero, it follows from the last equality that $ Q(x, y) + Q(y, x) = 0 $. By substituting $ x = y $ here, we particularly obtain that $ Q(y, y) = 0 $, i.e., $ Q(y, y) $ is a zero polynomial.
Treating the polynomials $ Q(x, y) $ and $ x - y $ as polynomials in the variable $ x $ with coefficients being polynomials in the variable $ y $, we divide $ Q(x, y) $ by $ x - y $. We obtain some quotient $ U(x, y) $ and a remainder $ R(y) $ independent of $ x $. From the division algorithm, it follows that $ U(x, y) $ and $ R(y) $ are polynomials in the variables $ x $, $ y $, and $ y $ respectively. Thus, we have $ Q(x, y) = (x - y) \cdot U(x, y) + R(y) $. Substituting $ x=y $ here, we get $ Q(y, y) = R(y) $. On the other hand, we have proven that $ Q(y, y) = 0 $. Therefore, $ R(y) = 0 $, which means $ Q(x, y) = (x - y) \cdot U(x, y) $ and hence $ P(x, y) = (x - y)^2 \cdot U(x, y) $.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 253 |
IV OM - I - Problem 11
Prove that if $ A + B + C $ or $ A + B - C $ or $ A - B + C $ or $ A - B - C $ equals an odd number of straight angles, then $ \cos^2A + \cos^2B + \cos^2C + 2 \cos A \cos B \cos C = 1 $ and that the converse theorem is also true.
|
\spos{1} We need to prove that
The task can be solved in a very simple way when it is noticed that the equation $ x = (2k + 1) \cdot 180^\circ $ is equivalent to the equation $ \cos \frac{x}{2} = 0 $. The necessary and sufficient condition for one of the angles $ A + B + C $, $ A + B - C $, $ A - B + C $, $ A - B - C $ to equal an odd multiple of a straight angle can thus be expressed by the following equation (2)
The task, therefore, reduces to showing that equality (1) is equivalent to equality (2). We will achieve this by transforming the left side of equality (2) using known formulas for sums and products of trigonometric functions:
It turns out that the left side of equality (2) is identically equal to $ \frac{1}{4} $ of the left side of equality (1). The equalities are therefore equivalent, and it follows that equality (1) holds if and only if one of the angles $ A + B + C $, $ A + B - C $, $ A - B + C $, $ A - B - C $ is an odd multiple of a straight angle.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 255 |
XL OM - III - Task 2
In the plane, there are three circles $ k_1 $, $ k_2 $, $ k_3 $. Circles $ k_2 $ and $ k_3 $ are externally tangent at point $ P $, circles $ k_3 $ and $ k_1 $ — at point $ Q $, and circles $ k_1 $ and $ k_2 $ — at point $ R $. The line $ PQ $ intersects circle $ k_1 $ again at point $ S $, and the line $ PR $ — at point $ T $. The line $ SR $ intersects circle $ k_2 $ again at point $ U $, and the line $ TQ $ intersects $ k_3 $ again at point $ V $. Prove that point $ P $ lies on the line $ UV $.
|
Let's denote the incircle of triangle $O_1O_2O_3$ by $k$, its center by $I$, and the centers of circles $k_1$, $k_2$, $k_3$ by $O_1$, $O_2$, $O_3$. Circle $k$ is tangent to the sides of triangle $O_1O_2O_3$ at points $P$, $Q$, $R$; this follows from the equalities $|O_1Q| = |O_1R|$, $|O_2R| = |O_2P|$, $|O_3P| = |O_3Q|$.
The following angle equalities hold (see Figure 6):
From these equalities, we obtain the relationship
which means that triangles $PRS$ and $PQT$ are right triangles: $PT \perp SU$, $PS \perp TY$.
Thus, angles $PRU$ and $PQV$ are right angles. These are inscribed angles in circles $k_2$ and $k_3$ and must subtend semicircles. Therefore, segments $PU$ and $PV$ are diameters of these circles; they are thus perpendicular to the common tangent (line $PI$). Hence, points $U$, $P$, $V$ are collinear.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 257 |
XV OM - II - Task 6
Prove that among any five points in a plane, one can choose three points that are not the vertices of an acute triangle.
|
If among the given points there are three collinear points, the thesis of the theorem is of course true. If, however, no three of the given points lie on a straight line, then four of these points, for example, $ A $, $ B $, $ C $, $ D $, are the vertices of a convex quadrilateral, as proven in problem 4. The angles of the quadrilateral $ ABCD $ are convex, and their sum is $ 360^\circ $, so at least one of these angles, for example, angle $ BAC $, is a convex angle not less than $ 90^\circ $. The points $ A $, $ B $, $ C $ are therefore not the vertices of an acute triangle.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 258 |
XVIII OM - II - Problem 1
Given is a sequence of numbers $ a_1, a_2, \ldots, a_n $ ($ n \geq 3 $), where $ a_1 = a_n = 0 $ and $ a_{k-1}+a_{k+1} \geq 2a_{k+1} $ for $ k = 2, 3, \ldots, (n - 1) $. Prove that this sequence does not contain any positive terms.
|
In a finite set of numbers $a_1, a_2, \ldots, a_n$, there exists at least one number not less than any of these numbers. Suppose such a number is $a_r$, i.e., $a_i \leq a_r$ for $i = 1, 2, \ldots, n$. Let $s$ be the smallest index with the property that $a_s = a_r$. We will prove that $s=1$. Indeed, if $s > 1$, then the inequalities would hold:
Adding these inequalities, we get
which contradicts the assumption of the theorem.
If, however, $s = 1$, this means that $a_r = a_1 = 0$, so $a_i \leq 0$ for $i = 1, 2, \ldots, n$.
Note. In the above proof, we relied on the theorem that in any finite set of numbers $a_1, a_2, \ldots, a_n$, there exists a number $a_r$ such that $a_i \leq a_r$ for $i = 1, 2, \ldots, n$.
This theorem, known as the maximum principle, is an easy consequence of the principle of induction. Conversely, the principle of induction follows from the maximum principle. We propose proving this equivalence as an exercise.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 259 |
XXX OM - I - Task 11
Given a positive number $ p $ and three distinct rays $ OA^{\rightarrow} $, $ OB^{\rightarrow} $, $ OC^{\rightarrow} $ contained in a plane. Prove that there exists exactly one such triplet of points $ K, L, M $, that $ K\in OA^{\rightarrow} $, $ L \in OB^{\rightarrow} $, $ M\in OC^{\rightarrow} $ and the perimeter of each of the triangles $ OKL $, $ OLM $, $ OMK $ is equal to $ 2p $.
|
For the triangles mentioned in the problem to exist, it is of course necessary to assume that no two of the given rays lie on the same line.
First, note that if points $P$ and $Q$ belong to different sides of an angle with vertex $O$ and point $Q$ moves away from $O$, then the perimeter of triangle $OPQ$ increases without bound. Indeed, let point $Q$ lie between points $O$ and $Q$ (Fig. 9).
om30_1r_img_9.jpg
Then $PQ < QQ$ and therefore
the perimeter of triangle $OPQ$ is less than the perimeter of triangle $OPQ$. Moreover, the perimeter of triangle $OPQ$ can be arbitrarily large if we choose point $Q$ appropriately on the ray $OQ^\to$.
Let the number $x$ satisfy $0 < x < p$. Let $K(x)$ be the point on the ray $OA^\to$ such that $OK(x) = x$. Such a point is unique. Next, let $L(x) \in OB^\to$ and $M(x) \in OC^\to$ be such points that the perimeter of each of the triangles $OK(x)L(x)$ and $OK(x)M(x)$ is equal to $2p$. By the initial observation, these conditions uniquely determine the points $L(x)$ and $M(x)$.
Since
when $x \to 0$, then $OK(x) \to 0$, $OL(x) \to p$, $K(x)L(x) \to p$, $OM(x) \to p$, $K(x)M(x) \to p$.
Similarly, when $x \to p$, then $OK(x) \to p$, $OL(x) \to 0$, $K(x)L(x) \to p$, $OM(x) \to 0$, $K(x)M(x) \to p$.
Therefore, when $x \to 0$, the perimeter of triangle $OL(x)M(x)$ approaches a limit greater than $2p$, and when $x \to p$, this perimeter approaches zero. Since this perimeter is a continuous function of $x$, there exists some $x = x_0$ in the interval $(0, p)$ such that the perimeter of triangle $OL(x_0)M(x_0)$ is equal to $2p$.
Thus, the points $K = K(x_0)$, $L = L(x_0)$, $M = M(x_0)$ satisfy the conditions of the problem.
We will prove that such a triplet of points is unique. If points $K$, $L$, $M$ also satisfy the conditions of the problem and, for example, $OK < OK$, then from the initial observation it follows that $OL > OL$ and $OM > OM$. In this case, however, the perimeter of triangle $OLM$ would be less than the perimeter of triangle $OL$. The obtained contradiction proves that there is only one triplet of points satisfying the conditions of the problem.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 263 |
XL OM - III - Task 4
Let $ n, k $ be natural numbers. We choose a sequence of sets $ A_0, \ldots, A_k $ such that $ A_0 = \{1, \ldots, n\} $, and for $ i = 1, \ldots, k $, the set $ A_i $ is a randomly chosen subset of $ A_{i-1} $, with each subset being equally likely. We consider the random variable equal to the number of elements in $ A_k $. Prove that its expected value is $ n2^{-k} $.
|
We introduce random variables $ X_1, \ldots , X_n $ defined as follows:
\
($ i = 1,\ldots ,n $). The random variable $ X $ (the number of elements in the set $ A_k $) considered in the problem is the sum of the variables introduced just now:
Let us fix a number $ i \in A_0 = \{1, \ldots, n\} $. Since $ A_1 $ is a randomly chosen subset of $ A_0 $, the number $ i $ will be in the set $ A_1 $ with probability
This follows from the fact that the set $ A_0 $ has as many subsets containing a fixed element $ i $ as subsets not containing this element.
With the same probability, the number $ i $ will end up in the set $ A_2 $ - provided it previously ended up in $ A_1 $:
Thus,
(To put it less formally and more vividly: the number $ i $ will be in the set $ A_2 $ if two consecutive drawings are "successful" for it.) Continuing this reasoning, we conclude inductively that
For $ j = k $, the obtained equality $ P(i \in A_k) = 2^{-k} $ means that the random variable $ X_i $ takes the value $ 1 $ with probability $ 2^{-k} $ (and the value $ 0 $ with probability $ 1-2^{-k} $). Therefore, its expected value is $ 2^{-k} $.
This conclusion is valid for any choice of $ i \in \{1,\ldots, n\} $. This means that the number $ 2^{-k} $ is the expected value of each of the random variables $ X_1, \ldots , X_n $. Therefore,
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 265 |
LI OM - II - Task 6
A polynomial $ w(x) $ of degree two with integer coefficients takes values that are squares of integers for integer $ x $. Prove that the polynomial $ w(x) $ is the square of some polynomial.
|
Let $ w(x) = ax^2 + bx + c $. Introduce the notation: $ k_n = \sqrt{w(n)} $ for any positive integer $ n $. Then $ k_n $ can be zero for at most two values of $ n $. For the remaining $ n $ we have
Dividing the numerator and the denominator of the obtained fraction by $ n $ and passing to the limit as $ n $ goes to infinity, we see that the sequence $ (k_{n+1} - k_n) $ is convergent and its limit is $ \sqrt{a} $. Since the terms of the sequence $ (k_{n+1} - k_n) $ are integers, the limit of this sequence, the number $ \sqrt{a} $, is also an integer. Moreover, there exists a natural number $ m $ such that
Let $ d = k_m - m\sqrt{a} $. From the relation (1) it follows that
Consider $ p(x) = (x\sqrt{a} + d)^2 $. By the definition of the numbers $ k_n $ and the equality (2), we obtain the equality $ p(n) = w(n) $ for $ n \geq m $. This means that $ p(x) = w(x) $, hence
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 266 |
XXXIII OM - II - Task 3
Prove that for every natural number $ n \geq 2 $ the following inequality holds
|
For non-negative numbers $ a $, $ b $, the inequality
holds.
Therefore, for $ k = 1,2,\ldots,n $ we have
From inequality (*) it also follows that
We obtain the inequalities:
and
Suppose $ n $ is an odd number. By combining the first and last terms, the second and second-to-last terms, etc., in the product $ \log_n 2 \cdot \log_n 4 \cdot \ldots \cdot \log_n (2n - 2) $, we get a product of expressions of the form $ \log_n k \log_n (2n - k) $, each of which, by the previous considerations, is a positive number not greater than $ 1 $. This leads to the desired inequality.
If $ n $ is an even number, then a similar procedure as for odd numbers leads to a product of expressions of the form $ \log_n k \cdot \log_n (2n - k) $ and the factor $ \log_n (2n - n) = \log_n n = 1 $. Therefore, in this case as well, we obtain the inequality
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 269 |
XLII OM - II - Problem 5
$ P_1, P_2, \ldots, P_n $ are distinct two-element subsets of the set $ \{1,2,\ldots,n\} $. Sets $ P_i $, $ P_j $ for $ i\neq j $ have a common element if and only if the set $ \{i,j\} $ is one of the sets $ P_1, P_2, \ldots, P_n $. Prove that each of the numbers $ 1,2,\ldots,n $ is a common element of exactly two of the sets $ P_1, P_2, \ldots, P_n $.
|
For each $ k \in \{1,2,\ldots,n\} $, let $ m_k $ be the number of sets $ P_i $ that contain the element $ k $. The sum of these numbers (as $ k $ ranges from $ 1 $ to $ n $) is $ 2n $, because each of the sets $ P_1,\ldots, P_n $ has two elements and is thus counted twice. We therefore have the equality
\[
\sum_{k=1}^n m_k = 2n.
\]
We need to prove that $ m_k = 2 $ for $ k = 1, \ldots, n $.
According to the problem statement, the family of $ n $ sets $ P_1,\ldots, P_n $ consists exactly of those pairs $ \{i,j\} $ of elements of the set $ \{1,2,\ldots,n\} $ for which the sets $ P_i $, $ P_j $ have a common element. This common element can be any number $ k \in \{1,2,\ldots,n\} $. For a fixed $ k $, there are $ m_k $ sets $ P_i $ that contain $ k $; thus, there are
\[
\binom{m_k}{2}
\]
pairs $ \{ i,j \} $ such that $ P_i \cap P_j = \{k\} $. The number of all such pairs is the sum of expressions (2) as $ k $ ranges from $ 1 $ to $ n $. Since each such pair $ \{i,j\} $ is one of the sets $ P_1,\ldots, P_n $, the number of these pairs is $ n $. We obtain the equality
\[
\sum_{k=1}^n \binom{m_k}{2} = n.
\]
Thus, in view of (1),
\[
\sum_{k=1}^n \frac{m_k(m_k-1)}{2} = n.
\]
Hence, from (1),
\[
\sum_{k=1}^n m_k^2 - \sum_{k=1}^n m_k = 2n.
\]
Therefore,
\[
\sum_{k=1}^n m_k^2 - 2n = 2n,
\]
which simplifies to
\[
\sum_{k=1}^n m_k^2 = 4n.
\]
We want to prove that all numbers $ m_k $ equal $ 2 $. Consider the differences $ m_k - 2 $. Let's compute the sum of the squares of these differences, using equations (1) and (3):
\[
\sum_{k=1}^n (m_k - 2)^2 = \sum_{k=1}^n (m_k^2 - 4m_k + 4) = \sum_{k=1}^n m_k^2 - 4 \sum_{k=1}^n m_k + 4n.
\]
Substituting the values from (1) and (3):
\[
\sum_{k=1}^n (m_k - 2)^2 = 4n - 4 \cdot 2n + 4n = 0.
\]
The sum of non-negative numbers equals zero only if all these numbers are zero. Therefore, $ m_1 = \ldots = m_n = 2 $.
This means that each number $ k \in \{1,2,\ldots,n\} $ belongs to exactly two sets $ P_i $. The proof is complete.
**Note 1.** By modifying the transformation used at the end of the solution, we can easily obtain a proof of the inequality between the *arithmetic mean*
\[
A(x_1,\ldots,x_n) = \frac{x_1 + \ldots + x_n}{n}
\]
of a system of non-negative numbers $ x_1,\ldots,x_n $ and the *quadratic mean* of these numbers, defined by the formula
\[
Q(x_1,\ldots,x_n) = \sqrt{\frac{x_1^2 + \ldots + x_n^2}{n}}.
\]
Writing $ A $ and $ Q $ instead of $ A(x_1,\ldots,x_n) $ and $ Q(x_1,\ldots,x_n) $, we have:
\[
\sum_{k=1}^n (x_k - A)^2 = \sum_{k=1}^n x_k^2 - 2A \sum_{k=1}^n x_k + nA^2 = nQ^2 - 2nA^2 + nA^2 = n(Q^2 - A^2).
\]
Thus,
\[
Q^2 \geq A^2,
\]
with equality holding only if $ x_1 = \ldots = x_n = A $.
Conversely, assuming the inequality (4) (along with the information when it becomes an equality) as a known fact, we can immediately deduce the proven theorem ($ m_1 = \ldots = m_n = 2 $) from equations (1) and (3).
**Note 2.** In this problem, we are dealing with a pair $ (V,E) $, where $ V $ is the set $ \{1,2,\ldots,n\} $, and $ E $ is a family of two-element sets $ P_1,\ldots,P_n $, each of which is contained in $ V $. This type of configuration forms a graph. Generally, a *graph* is a pair $ (V,E) $, where $ V $ is any set, and $ E $ is a certain family of distinguished two-element subsets of $ V $. (In applications, $ V $ is most often a finite set.) It is convenient to interpret $ V $ as a set of points (on a plane or in space), and each two-element set $ \{u,v\} $ belonging to the family $ E $ as a segment connecting points $ u $ and $ v $. This interpretation justifies the terminology used in graph theory: the elements of the set $ V $ are called the vertices of the graph, and the elements of the set $ E $ are called its edges (see problem 4 from the 32nd International Mathematical Olympiad).
The number of edges that have a given vertex as an endpoint is called the *degree* of that vertex.
Two edges of a graph are called *adjacent* if they have a common endpoint. Two vertices of a graph are called *adjacent* if they are connected by an edge.
It should be emphasized that this interpretation is intended only to facilitate the visualization of the given sets and their mutual relations (of a set-theoretic and combinatorial nature); there is no "geometry" involved here. The lengths of the edges and the angles between them, as well as their possible intersections outside the vertices of the graph, are abstracted away. For example, the graph $ (V_1,E_1) $, where $ V_1 $ is the set of vertices of a square, and $ E_1 $ consists of its three sides and both diagonals, is indistinguishable from the graph $ (V_2, E_2) $, where $ V_2 $ is the set of vertices of a tetrahedron, and $ E_2 $ is the set of any five of its edges.
The theorem to be proved in this problem can be formulated in the language of graphs as follows:
Given a graph $ (V,E) $, where the sets $ V $ and $ E $ have the same finite number of elements, numbered from $ 1 $ to $ n $. For each pair of different natural numbers $ i,j \in \{1,2,\ldots,n\} $, the vertices numbered $ i $ and $ j $ are adjacent if and only if the edges numbered $ i $ and $ j $ are adjacent. Under these assumptions, the degree of each vertex is $ 2 $.
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 270 |
II OM - I - Task 1
Prove that the product of two factors, each of which is the sum of the squares of two integers, is also the sum of the squares of two integers.
|
We will apply the transformation
If $ a $, $ b $, $ c $, $ d $ are integers, then $ ac + bd $ and $ ad - bc $ are also integers; the theorem has thus been proven.
Notice that a more general theorem holds:
The product of $ n $ factors, each of which is the sum of the squares of two integers, is also the sum of the squares of two integers.
We will prove this theorem using the principle of mathematical induction. Let's briefly recall how this principle can be formulated:
Let $ T_n $ denote a statement asserting some property of the natural number $ n $, and suppose it is known that:
1° The statement $ T_1 $ is true, i.e., the number $ 1 $ has this property.
2° If for some number $ k $ the statement $ T_k $ is true, then the statement $ T_{k+1} $ is also true, i.e., if some natural number $ k $ has this property, then the next natural number $ k + 1 $ also has this property.
Then the statement $ T_n $ is true for every natural number $ n $, i.e., every natural number has this property. (This conclusion is the essence of the principle of induction).
Proceeding to the proof of the theorem mentioned above, we will give it a more convenient formulation:
Theorem ($ T_n $). If the numbers $ a_1, b_1, a_2, b_2, \ldots, a_n, b_n $ are integers, then the product
equals the sum of the squares of two integers.
(We wrote the number 1 at the beginning so that the above expression also has the form of a product in the case $ n = 1 $).
The proof will consist in showing that conditions 1°-2°, appearing in the principle of induction, are satisfied. Indeed:
1° The statement $ T_1 $ is true, since
2° Suppose that for some $ k $ the statement $ T_k $ is true, i.e., that
where $ A $ and $ B $ are integers. We will prove that under this assumption, the statement $ T_{k+1} $ is also true.
Indeed,
Based on the principle of induction, we infer from premises 1° and 2° that the statement $ T_n $ is true for every natural $ n $.
Note. It can be proven that the principle of mathematical induction is equivalent to the following theorem:
In any set of natural numbers (containing at least one number), there exists a smallest number. The stipulation that the set of natural numbers under consideration contains at least one number is necessary because in mathematics, sets of numbers or other objects (called elements of the set) include the so-called empty set, i.e., a set containing no elements. This is very convenient in certain reasoning.
We will conduct the proof of the previous theorem $ T_n $ based on the theorem mentioned above.
Suppose there exist natural numbers for which the statement $ T_n $ is not true. In the set of these numbers, there exists a smallest number $ k $. There exist, therefore, integers $ a_1, b_1, a_2, b_2, \ldots, a_k, b_k $ such that the product
does not equal the sum of the squares of two integers, while at the same time
where $ A $ and $ B $ are integers. But then we can write:
According to this equality, the product (1) equals the sum of the squares of two integers, which contradicts the previous conclusion. The assumption that there exist values of $ n $ for which the statement $ T_n $ is false - led to a contradiction; therefore, the statement $ T_n $ is true for every natural $ n $.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 271 |
XLIV OM - II - Problem 2
Given a circle with center $O$ and a point $P$ lying outside this circle. Through point $P$, we draw a line $l$ intersecting the given circle at points $A$ and $B$. Let $C$ be the point symmetric to $B$ with respect to the line $OP$, and let $m$ be the line passing through points $A$ and $C$. Prove that all such lines $m$ (corresponding to different choices of line $l$) have a common point.
|
The task does not specify how points $A$ and $B$ are situated on line $l$, meaning which one is closer to point $P$; Figure 5 illustrates these two situations. Let $Q$ be the point of intersection of lines $OP$ and $AC$; the thesis of the task will be proven if we show that the position of point $Q$ on the ray $OP^\to$ does not depend on the choice of line $l$ (which would mean that $Q$ is the sought common point of all considered lines $m$).
Triangle $AOC$ is isosceles; let us adopt the notation
Thus, the convex angle $AOC$ has a measure of
om44_2r_img_5.jpg
Angle $ABC$ is an inscribed angle subtended by the same arc as the convex or concave central angle $AOC$ (depending on whether point $A$ lies between $P$ and $B$, or point $B$ lies between $P$ and $A$). In the first case,
and in the second case,
In the first case, angle $PBC$ is identical to angle $ABC$, and in the second case, angle $PBC$ complements angle $ABC$ to a straight angle. Thus, in both cases, the equality $|\measuredangle PBC| = 90^\circ - \alpha$ holds. Further reasoning does not depend on the case.
Points $B$ and $C$ are symmetric with respect to line $OP$, so triangle $BPC$ is isosceles; hence,
and therefore,
Now, let's look at triangles $OPA$ and $OAQ$. They share a common angle at vertex $O$; angles $OPA$ and $OAQ$ have the same measure $\alpha$. Therefore, these triangles are similar, and the proportion $|OP|: |OA| = |OA|: |OQ|$ holds, which means
This indicates that the position of point $Q$ on the ray $OP^\to$ is determined by the radius of the circle and the position of point $P$; more precisely: point $Q$ is the image of point $P$ under inversion with respect to the given circle. The proof is complete.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 273 |
XXXII - I - Problem 6
Given numbers $ a_1\geq a_2 \geq \ldots \geq a_n \geq 0 $ satisfying the condition $ \sum_{i=1}^n a_i = 1 $. Prove that there exist integers $ k_1\geq k_2 \geq \ldots \geq k_n \geq 0 $ such that
|
Let $ [x] $ be the greatest integer not greater than $ x $.
Assume $ \widetilde{k_j} = [2na_j] $. The numbers $ \widetilde{k_j} $ satisfy the condition $ \widetilde{k_1} \geq \widetilde{k_2} \geq \ldots \geq \widetilde{k_n} \geq 0 $, and moreover $ 2na_j-1 < \widetilde{k_j} \leq 2na_j $, so $ 2a_j - \frac{1}{n} < \frac{\widetilde{k_j}}{n} \leq 2a_j $ and therefore
It follows that $ \sum_{j=1}^n \widetilde{k_j} > n $. We will now define the numbers $ k_j $ by subtracting appropriately chosen non-negative integers from $ \widetilde{k_j} $. Let $ d_n $ be the maximum non-negative integer for which
We set $ k_n = \widetilde{k_n}-d_n $. Of course, $ \frac{k_n}{n} \leq 2a_n $. Next, we define $ d_{n-1} $ as the maximum non-negative integer for which
We set $ k_{n-1} = \widetilde{k_{n-1}}-d_{n-1} $ and so on we define $ d_j $ as the maximum non-negative integer for which
and we set $ k_j = \widetilde{k_j} -d_j $.
Of course, $ \frac{k_j}{n} \leq 2a_j $ for $ j = 1,2,\ldots,n $ and $ \sum_{j=1}^n k_j = n $, since otherwise it would be $ \sum_{j=1}^n k_j > n $, which would mean that at least one term of this sum could be decreased by $ 1 $ while maintaining the conditions of the problem, contradicting the fact that at each step we subtracted the maximum possible $ d_j $.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 275 |
LVIII OM - II - Problem 5
A convex quadrilateral $ABCD$, where $AB \ne CD$, is inscribed in a circle. Quadrilaterals $AKDL$ and $CMBN$ are rhombuses with side lengths of $a$. Prove that points $K$, $L$, $M$, $N$ lie on the same circle.
|
Since the chords $ AB $ and $ CD $ are of different lengths, the lines $ AD $ and $ BC $ are not parallel. Let's denote their intersection point by $ P $ (Fig. 10). We will show that the points $ K $, $ L $, $ M $, and $ N $ lie on a circle with center $ P $.
The line $ AD $ is the perpendicular bisector of segment $ KL $, from which we get $ PK=PL $. Similarly, $ PM=PN $. It is therefore sufficient to prove that $ PK=PN $.
Let $ Q $ be the intersection point of the diagonals of the rhombus $ AKDL $. Then, by the Pythagorean theorem, we obtain
om58_2r_img_10.jpg
Similarly, we prove that
The points $ A $, $ B $, $ C $, $ D $ lie on the same circle, so the equality
is satisfied.
Combining dependencies (1), (2), and (3), we conclude that
since $ AK=BN=a $, we obtain from this the equality $ PK=PN $, which completes the solution of the problem.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 276 |
XXXI - III - Problem 5
In a tetrahedron, the areas of the six triangles, whose sides are the edges and whose vertices are the midpoints of the opposite edges of the tetrahedron, are equal. Prove that the tetrahedron is regular.
|
The assumption of the task guarantees the equality of the areas of six triangles, each of which has a base being an edge of the tetrahedron, and the opposite vertex is the midpoint of the opposite edge. On the tetrahedron $ABCD$, we describe a parallelepiped $A_1CB_1DAC_1BD_1$, whose each face contains a certain edge of the tetrahedron and is parallel to the opposite edge of the tetrahedron. From the assumption of the equality of the areas of the six triangles, whose sides are edges and whose vertices are the midpoints of the opposite edges of the tetrahedron, it follows that the sections of the parallelepiped by planes containing opposite edges have equal areas, because, for example, the area of $A_1B_1BA$ is equal to $2 \cdot$ the area of $\triangle ABK_1$, the area of $CDD_1C_1$ is equal to $2 \cdot$ the area of $\triangle CDK$, etc., for the remaining four sections.
om31_3r_img_20.jpgom31_3r_img_21.jpg
Now, let's draw a plane perpendicular to a certain edge of the considered parallelepiped, for example, to $\overline{AA_1}$. It intersects the lines $AA_1$, $BB_1$, $CC_1$, $DD_1$ at points $A_2$, $B_2$, $C_2$, $D_2$, respectively, and $A_2C_2B_2D_2$ is a parallelogram. Since the area of $ABB_1A_1$ is equal to $AA_1 \cdot A_2B_2$ and the area of $CDD_1C_1$ is equal to $CC_1 \cdot C_2D_2$, and these areas are equal and $AA_1 = CC_1$, then $A_2B_2 = C_2D_2$. Therefore, the parallelogram $A_2C_2B_2D_2$ has diagonals of equal length, so it is a rectangle. It follows that the faces $AC_1CA_1$ and $CB_1BC_1$; $CB_1BC_1$ and $B_1DD_1B$; $B_1DD_1B$ and $A_1DD_1A$ are perpendicular to each other.
By drawing a plane perpendicular to the edge $AC_1$ and then a plane perpendicular to the edge $AD_1$, we will similarly conclude that any two faces of the parallelepiped having a common edge are perpendicular to each other, and thus the parallelepiped is a rectangular parallelepiped. If $x$, $y$, $z$ are the lengths of the edges of this rectangular parallelepiped, then since (as we determined above) the sections drawn through opposite edges have equal areas, we have
Therefore,
The first of these equalities implies $x^2z^2 = y^2z^2$, so $x = y$, and similarly from the second equality, we get $y = z$.
Therefore, the parallelepiped described on the given tetrahedron is a cube, and hence the given tetrahedron is regular.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 277 |
XV OM - III - Task 3
Given is a tetrahedron $ABCD$, whose edges $AB, BC, CD, DA$ are tangent to a certain sphere: Prove that the points of tangency lie in the same plane.
|
We distinguish two cases:
a) $ AM = CN $, thus also $ AQ = CP $. Triangles $ MBN $ and $ ABC $ are then similar with respect to point $ B $, so $ MN \parallel AC $ and similarly $ QP \parallel AC $. Therefore, $ QP \parallel MN $, which means points $ MNPQ $ lie in the same plane.
b) $ AM \ne CN $, let's say $ AM > CN $, thus also $ AQ > CP $. (Fig. 17).
A line parallel to $ MN $ drawn through point $ C $ then intersects segment $ AB $ at some point $ E $, and a line parallel to $ PQ $ drawn through $ C $ intersects segment $ AD $ at some point $ F $. Since $ BM = BN $ and $ DP = DQ $, we have $ EM = CN = CP = QF $, hence $ MQ \parallel EF $.
The lines $ PQ $, $ QM $, $ MN $ are respectively parallel to the lines $ CF $, $ FE $, $ EC $, so the planes $ PQM $ and $ QMN $ are parallel to the plane $ CFE $; since these planes have a common line $ QM $, they coincide, meaning points $ P $, $ Q $, $ M $, $ N $ lie in the same plane.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 278 |
XXVI - I - Problem 10
Let $ \alpha $ be an irrational number, $ A_1 $ - a point on the circle $ S $ with center $ O $. Consider the infinite sequence $ A_n $ of points on the circle $ S $, where the point $ A_{k+1} $ is the image of the point $ A_k $ under a rotation about the point $ O $ by an angle $ \alpha m $. Prove that every arc of the circle $ S $ contains some points of the sequence $ A_n $.
|
If for certain natural numbers $k$ and $n$, where $k \ne n$, it was $A_k = A_n$, then the rotations by angles $(k-1)\alpha\pi$ and $(n-1)\alpha\pi$ would be equal. This means that the numbers $(k-1)\alpha\pi$ and $(n-1)\alpha\pi$ would differ by an integer multiple of $2\pi$, i.e., $(n-k)\alpha\pi = 2m\pi$, where $m$ is some integer. Hence, $\alpha = \frac{2m}{n-k}$, which contradicts the irrationality of $\alpha$. Therefore, all terms of the sequence $(A_n)$ are distinct.
Let $L$ be an arc of length $d$ contained in the circle $S$ of radius $r$. Let $t$ be a natural number greater than $\frac{2\pi r}{d}$. By dividing the circle $S$ into $t$ equal arcs of length $\frac{2\pi r}{t}$, we observe that there exists among them an arc containing at least two of the points $A_1, A_2, \ldots, A_{t+1}$. Let these points be $A_i$ and $A_j$, where $i < j$. Then the arc $\widehat{A_iA_j}$ has a length no greater than $\frac{2\pi r}{t}$. Since $t > \frac{2\pi r}{d}$, it follows that $\frac{2\pi r}{t} < d$, and thus the length of the arc $\widehat{A_iA_j}$ is less than $d$. This implies that the rotation by the angle $(j-i)\alpha\pi$ maps the point $A_i$ to $A_j$ and generally maps the point $A_{i+n}$ to $A_{j+n}$ for $n = 0, 1, 2, \ldots$. Therefore, the terms of the subsequence $A_1, A_{1 + (j-i)}, A_{1+2(j-i)}, \ldots$ determine arcs of length $\leq \frac{2\pi r}{t}$, which is less than $d$. Hence, some term of this subsequence must belong to the arc $L$ of length $d$.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 279 |
XVI OM - II - Task 5
Prove that a square can be divided into any number of squares greater than 5, but it cannot be divided into 5 squares.
|
a) First, let us note that having a square divided into $ m $ squares, we can divide one of these squares into four squares by connecting the midpoints of its opposite sides. The entire square will then be divided into $ m + 3 $ squares.
Let $ n $ be a natural number greater than $ 1 $. Divide each side of the square $ Q $ into $ n $ equal parts and connect the corresponding points of division of opposite sides (two points of opposite sides of the square are called corresponding here if they lie on a line perpendicular to those sides). The square $ Q $ will then be divided into $ n^2 $ smaller squares $ Q_i $, with $ n $ squares $ Q_i $ adjacent to each side of the square $ Q $.
Consider two adjacent sides of the square $ Q $; $ 2n - 1 $ squares $ Q_i $ are adjacent to them, since one of them is adjacent to both of these sides; the remaining squares $ Q $ exactly fill a square $ R $ with a side equal to $ \frac{n-1}{n} $ of the side of the square $ Q $. When we erase all the lines of the division that are inside the square $ R $, we obtain a division of the square $ Q $ into $ 2n - 1 $ squares $ Q_i $ and the square $ R $, i.e., into $ (2n - 1) + 1 = 2n $ squares.
Thus, a square can be divided into any even number of squares greater than $ 2 $.
In that case, by the previous remark, a square can also be divided into $ 2n + 3 = 2 (n + 1) + 1 $ ($ n > 1 $) squares, i.e., into any odd number of squares greater than $ 5 $.
We have proved that a square can be divided into any number of squares greater than $ 5 $.
b) When a square is divided into squares only, in such a figure only right angles or straight angles appear, and the dividing squares have sides parallel to the sides of the entire square.
Suppose the square $ Q $ with side length $ l $ and vertices $ A $, $ B $, $ C $, $ D $ is divided into $ 5 $ squares $ Q_1 $, $ Q_2 $, $ Q_3 $, $ Q_4 $, $ Q_5 $. Each vertex of the square $ Q $ is a vertex of one of the squares $ Q_i $ ($ i = 1, 2, \ldots, 5 $), and two different vertices of the square $ Q $ cannot belong to the same square $ Q_i $, since their distance is $ \geq l $, which is greater than the side length of $ Q_i $. Let $ A $, $ B $, $ C $, $ D $ be the vertices of the squares $ Q_1 $, $ Q_2 $, $ Q_3 $, $ Q_4 $ with side lengths $ a $, $ b $, $ c $, $ d $, respectively.
If all the vertices of the square $ Q_5 $ were inside the square $ Q $, then the sides of the squares $ Q_i $ would completely cover the sides of the square $ Q $, i.e., the equality
would hold, which would imply that $ c = a $, $ d = b $,
and thus the area of $ Q $ would be expressed by the formula
as well as by the formula
from which it would follow that
which is impossible.
If one of the vertices of the square $ Q_5 $ were on one of the sides of the square $ Q $, for example, on $ AB $, then one of the sides of the square $ Q_5 $, for example, $ MN $, would lie on $ AB $. The remaining $ 2 $ vertices would lie on lines perpendicular to $ AB $ at points $ M $ and $ N $ at a distance less than $ l $ from $ AB $, i.e., inside the square $ Q_5 $. This would imply that
This system of conditions is, however, contradictory, since from the first three conditions it follows that $ (b + c) - (c + d) + (d + a) = l - l + l = l $, i.e., that $ a + b = l $, which contradicts the last one.
The assumption that the square $ Q $ was divided into $ 5 $ squares led to a contradiction. Such a division is therefore impossible.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 281 |
XLIX OM - II - Problem 2
In triangle $ABC$, angle $BCA$ is obtuse and $\measuredangle BAC = 2\measuredangle ABC$. The line passing through point $B$ and perpendicular to $BC$ intersects line $AC$ at point $D$. Point $M$ is the midpoint of side $AB$. Prove that $\measuredangle AMC = \measuredangle BMD$.
|
Let a line parallel to $ AB $ and passing through point $ C $ intersect segment $ BD $ at point $ E $. Denote by $ N $ the midpoint of segment $ CE $. Then points $ M $, $ N $, $ D $ are collinear. Triangle $ BCE $ is a right triangle, so $ N $ is the center of the circle circumscribed around it. This implies that triangle $ BCN $ is isosceles, which gives the following equalities:
Cyclic quadrilateral $ ABNC $ is thus an isosceles trapezoid, not a parallelogram. Therefore, point $ N $ is the image of point $ C $ under the reflection about the perpendicular bisector of segment $ AB $. This means that $ \measuredangle AMC =\measuredangle BMN = \measuredangle BMD $.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 283 |
XXXIX OM - II - Problem 6
A convex polyhedron is given with $ k $ faces $ S_1, \ldots, S_k $. Denote the unit vector perpendicular to the face $ S_i $ ($ i = 1, \ldots, k $) directed outward from the polyhedron by $ \overrightarrow{n_i} $, and the area of this face by $ P_i $. Prove that
|
We start with the observation that if in space a convex planar polygon $S$ and a plane $\pi$ are given, and if $\overrightarrow{n}$ is a unit vector perpendicular to the plane of the polygon $S$, and $\overrightarrow{w}$ is a unit vector perpendicular to the plane $\pi$, then denoting by $W$ the orthogonal projection of the polygon $S$ onto the plane $\pi$, we have the following relationship between the areas of the polygons $S$ and $W$:
\[
\text{Area}(W) = |\overrightarrow{n} \cdot \overrightarrow{w}| \cdot \text{Area}(S)
\]
(The dot between the vectors denotes the dot product.)
Formula (I) is obvious in the case where the considered planes are parallel or perpendicular (because in these cases, respectively, $|\overrightarrow{n} \cdot \overrightarrow{w}|$ equals $1$ or $0$). In the remaining case, when the planes intersect along a line $l$ forming an angle $\varphi (0 < \varphi < \pi/2)$, formula (1) follows from the following observations:
If $S$ is a rectangle with one side parallel and the other perpendicular to the line $l$, its projection $W$ onto the plane $\pi$ is also such a rectangle. The length of the side parallel to $l$ does not change during projection, while the length of the side perpendicular to $l$ is shortened by a factor of $|\cos \varphi|$. The area of the rectangle changes by the same factor; thus, for a rectangle $S$, we obtain formula (1), because $|\overrightarrow{n} \cdot \overrightarrow{w}| = |\cos \measuredangle (\overrightarrow{n}, \overrightarrow{w})| = |\cos \varphi|$.
From this, it immediately follows that (1) is true for any right triangle with one leg parallel and the other perpendicular to $l$, because such a triangle can be completed to a rectangle (whose two sides are the legs of the given triangle). The area of the rectangle changes during projection by a factor of $|\cos \varphi| = |\overrightarrow{n} \cdot \overrightarrow{w}|$, so the same happens to the area of the triangle, which is half the area of the rectangle (Figure 8).
It is enough to notice that any convex polygon $S$ is the sum of a finite number of right triangles with legs parallel and perpendicular to the line $l$, with disjoint interiors. The area of $S$ is the sum of the areas of these triangles, and the area of $W$ (the projection of $S$ onto $\pi$) is the sum of the areas of the projections of the individual triangles (Figure 8). The area of the projection of each of these triangles equals the area of the triangle multiplied by the same factor equal to $|\overrightarrow{n} \cdot \overrightarrow{w}|$, and by summing up, we obtain the formula (1) to be proved.
We proceed to the proof of the theorem. Let
\[
\overrightarrow{v} = \sum_{i=1}^{k} \text{Area}(S_i) \overrightarrow{n_i}
\]
We need to prove that $\overrightarrow{v}$ is the zero vector.
Choose any unit vector $\overrightarrow{w}$ in space. Let $\pi$ be any plane perpendicular to the vector $\overrightarrow{w}$. The orthogonal projection of the considered polyhedron onto the plane $\pi$ is a convex polygon $W$. The projection of any face $S_i$ is a convex polygon $W_i$ (degenerate to a segment if $\overrightarrow{n_i} \bot \overrightarrow{w}$).
We partition the set of indices $\{1, \ldots, k\}$ into three subsets:
\[
I_+ = \{i : \overrightarrow{n_i} \cdot \overrightarrow{w} > 0\}
\]
\[
I_- = \{i : \overrightarrow{n_i} \cdot \overrightarrow{w} < 0\}
\]
\[
I_0 = \{i : \overrightarrow{n_i} \cdot \overrightarrow{w} = 0\}
\]
(Looking at the polyhedron from the outside, in the direction of the vector $\overrightarrow{w}$, we see the faces $S_i$ with indices $i \in I_-$, and we do not see the faces with indices $i \in I_+$) (Figure 9). The projections of the faces with indices $i \in I_+ \cup I_0$ have no common interior points and fill the entire polygon $W$. The same can be said about the projections of the faces with indices $i \in I_- \cup I_0$. Therefore,
\[
\sum_{i \in I_+ \cup I_0} \text{Area}(W_i) = \text{Area}(W)
\]
and simultaneously,
\[
\sum_{i \in I_- \cup I_0} \text{Area}(W_i) = \text{Area}(W)
\]
Notice now that according to formula (1),
\[
\text{Area}(W_i) = |\overrightarrow{n_i} \cdot \overrightarrow{w}| \cdot \text{Area}(S_i)
\]
Therefore,
\[
\sum_{i \in I_+ \cup I_0} |\overrightarrow{n_i} \cdot \overrightarrow{w}| \cdot \text{Area}(S_i) = \text{Area}(W)
\]
and
\[
\sum_{i \in I_- \cup I_0} |\overrightarrow{n_i} \cdot \overrightarrow{w}| \cdot \text{Area}(S_i) = \text{Area}(W)
\]
Since the vector $\overrightarrow{w}$ was chosen arbitrarily, we have thus shown that the vector $\overrightarrow{v}$ is perpendicular to any unit vector. It is therefore the zero vector.
(Figure 9)
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 287 |
XXXVIII OM - III - Problem 1
In a square with side 1, there are $ n $ points ($ n > 2 $). Prove that they can be numbered $ P_1, P_2, ..., P_n $ such that \sum_{i=1}^n |P_{i-1}P_i|^2 \leq 4 (we assume $ P_0=P_n $).
|
The proof will be based on the following lemma:
Lemma. In a right-angled isosceles triangle $ABC$, where $|AB| = |BC| = a$, $|\measuredangle ABC| = 90^\circ$, there are $k$ points ($k \geq 1$). These points can then be numbered $P_1, \ldots, P_k$ such that
(we assume $P_0 = A$, $P_{k+1} = C$).
Proof. We use induction. When $k = 1$, we have one point $P$ and need to prove the inequality $|AP|^2 + |PC|^2 \leq 2a^2$, which follows from the fact that $2a^2 = |AC|^2$, and the angle $APC$ is not obtuse.
Fix a natural number $m \geq 2$ and assume that the lemma holds for any right-angled isosceles triangle and any set of $k$ points contained in it, where $k$ is any natural number less than $m$.
Consider a triangle $ABC$ ($|AB| = |BC| = a$, $|\measuredangle B| = 90^\circ$), and a set $Z$ of $m$ points. Let $A_0B_0C_0$ be the smallest triangle with sides parallel to the corresponding sides of triangle $ABC$ that contains the set $Z$. (Construction: each of the three lines containing the sides of triangle $ABC$ is translated parallel until it meets the first point of set $Z$; the translated lines form triangle $A_0B_0C_0$ as described.)
Let $E_0$ be the foot of the perpendicular from vertex $B_0$ to the hypotenuse $A_0C_0$. Of course,
Denote the triangles (closed) $A_0E_0B_0$ and $B_0E_0C_0$ by $\Delta$ and $\Delta'$, and their intersection, the segment $B_0E_0$, by $I$. Each of the triangles $\Delta$ and $\Delta'$ contains points of set $Z$; otherwise, triangle $A_0B_0C_0$ would not be minimal. We now divide the set $Z$ into two non-empty subsets $Z_1$ and $Z_2$ contained in $\Delta$ and $\Delta'$, respectively: points of the set $Z \cap \Delta$ are assigned to $Z_1$, points of the set $Z \cap \Delta'$ are assigned to $Z_2$, and points of the set $Z \cap I$ are distributed between $Z_1$ and $Z_2$ in any way, with the only condition that the resulting sets $Z_1$ and $Z_2$ are non-empty; this is possible because, by the previous conclusion, $Z \cap \Delta \neq \emptyset$, $Z \cap \Delta' \neq \emptyset$, and $m \geq 2$.
Let $k$ be the number of elements in set $Z_1$, and $m-k$ the number of elements in set $Z_2$ ($0 < k < m$). By the induction hypothesis applied to triangles $\Delta$ and $\Delta'$ and the sets $Z_1$ and $Z_2$ contained in them, we can number the points of these sets as $P_1, \ldots, P_k$ and $P_{k+1}, \ldots, P_m$ respectively, such that
Notice now that
(because $|\measuredangle P_kB_0P_{k+1}| \leq 90^\circ$), and moreover
(see Figure 17). Therefore,
This means that the numbering $P_1, \ldots, P_m$ of the points in set $Z$ satisfies the given condition. The inductive proof of the lemma is thus completed.
om38_2r_img_17.jpg
To deduce the theorem from the lemma, we divide the given square $ABCD$ (with side length 1) into two right-angled triangles by the diagonal $AC$. The given set of $n$ points is divided into two subsets, contained in one and the other triangle, respectively, and counting $k$ and $n-k$ points ($0 \leq k \leq n$); points lying on the diagonal are assigned to either of these sets.
We consider two cases:
1. $0 < k < n$. From the lemma, it follows that the points in each of these subsets can be numbered as $P_1, \ldots, P_k$ and $P_{k+1}, \ldots, P_n$ such that
Similarly, as in the proof of the lemma, we use the inequalities
which follow from the fact that $|\measuredangle P_kCP_{k+1}| \leq 90^\circ$, $|\measuredangle P_nAP_1| \leq 90^\circ$ (see Figure 18). We get the inequality
Thus, the numbering $P_1, \ldots, P_n$ satisfies the condition of the problem.
om38_3r_img_18.jpg
2. $k = 0$ or $k = n$. In this case, all given points lie in one of the triangles $ABC$ or $CDA$, and according to the lemma, we can number them as $P_1, \ldots, P_n$ such that
Therefore,
which, combined with the obvious inequality $|P_nP_1|^2 \leq 2$, gives the desired condition
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 288 |
XXV OM - II - Problem 4
In a convex quadrilateral $ABCD$ with area $S$, each side is divided into 3 equal parts, and segments connecting corresponding division points of opposite sides are drawn in such a way that the quadrilateral is divided into 9 smaller quadrilaterals. Prove that the sum of the areas of the following three quadrilaterals resulting from the division: the one containing vertex $A$, the central one, and the one containing vertex $C$ is equal to $\frac{S}{3}$.
|
We will first prove the
Lemma. The segment connecting the corresponding division points of opposite sides of the given quadrilateral intersects with analogous segments connecting the corresponding division points of the remaining sides of the quadrilateral at points that divide this segment into three equal parts.
Proof. Let points $S$, $Z$, $W$, $R$ divide the sides $\overline{AB}$, $\overline{BC}$, $\overline{DC}$, $\overline{AD}$ of the given quadrilateral $ABCD$ in the ratio $1:2$ (Fig. 16). Let $E$ be the intersection point of segments $\overline{RZ}$ and $\overline{SW}$. It suffices to prove that point $E$ divides each of these segments in the ratio $1:2$.
Since
\[
\frac{AS}{AB} = \frac{AR}{AD} = \frac{1}{3},
\]
by the converse of Thales' theorem, we have $RS \parallel DB$. It follows that triangles $ARS$ and $ADB$ are similar in the ratio $1:3$. Hence
\[
\frac{RS}{DB} = \frac{1}{3}.
\]
Similarly, from the equality $\frac{CW}{CD} = \frac{CZ}{CB} = \frac{2}{3}$, it follows that $WZ \parallel DB$. Therefore, triangles $CWZ$ and $CDB$ are similar in the ratio $2:3$. Hence
\[
\frac{WZ}{DB} = \frac{2}{3}.
\]
From (1) and (2), it follows that $\frac{RS}{WZ} = \frac{1}{2}$. Moreover, we have $RS \parallel WZ$. Therefore, triangles $RSE$ and $ZWE$ are similar in the ratio $1:2$. In particular, it follows that $\frac{RE}{EZ} = \frac{SE}{EW} = \frac{1}{2}$.
We now proceed to solve the problem. Let points $R, G \in \overline{AD}$, $W, P \in \overline{DC}$, $Q, Z \in \overline{BC}$, $S, H \in \overline{AB}$ divide each of the segments $\overline{AD}$, $\overline{DC}$, $\overline{BC}$, $\overline{AB}$ into three equal parts (Fig. 17). Then, by the lemma, points $E, U \in \overline{RZ}$, $T, F \in \overline{GQ}$, $E, T \in \overline{WS}$, $F, U \in \overline{HP}$ divide each of the segments $\overline{RZ}$, $\overline{GQ}$, $\overline{WS}$, $\overline{HP}$ into three equal parts.
\spos{1} Since $RE = EU$, $TE = ES$, it follows from the converse of Thales' theorem that $RS \parallel TU$. Therefore, triangles $ERS$ and $ETU$ are congruent. Hence $RS = TU$.
In proving the lemma, we showed that $RS \parallel DB$ and $RS = \frac{1}{3} DB$. Similarly, $PQ \parallel DB$ and $PQ = \frac{1}{3} DB$. We have then $TU \parallel RS \parallel DB \parallel PQ$ and
\[
RS = TU = PQ = \frac{1}{3} DB.
\]
By drawing the heights in triangles
\[
\triangle ARS, \triangle ETF, \triangle FPC
\]
to the bases $\overline{RS}$, $\overline{TU}$, $\overline{PQ}$, respectively, we see that the sum of the lengths of these heights is equal to the sum of the lengths of the heights $h$ and $h$ of triangles $ABD$ and $CBD$ drawn to the base $\overline{DB}$. Since the lengths of the bases of triangles (4) are equal (by (3) they are equal to $\frac{1}{3} DB$), the sum of their areas, i.e., the sum of the areas of quadrilaterals $ARSE$, $ETFU$, $FPCQ$ is equal to half the product of the number $\frac{1}{3} DB$ and the sum of their heights, i.e., the number
\[
\frac{1}{3} DB \cdot \frac{1}{2} (h + h) = \frac{1}{6} DB \cdot (h + h) = \frac{1}{6} S_{ABCD}.
\]
Note. An analogous theorem is true in the case of dividing the sides of the quadrilateral $ABCD$ into $n$ equal parts, where $n > 3$. Then the sum of the areas of the quadrilaterals located on the diagonal is equal to $\frac{1}{n} S_{ABCD}$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 290 |
VII OM - II - Problem 4
Prove that the equation $ 2x^2 - 215y^2 = 1 $ has no solutions in integers.
|
Let $ x $ and $ y $ denote integers. The number $ 215y^2 $ is divisible by $ 5 $, so the number $ 215y^2 + 1 $ gives a remainder of $ 1 $ when divided by $ 5 $. The number $ x^2 $ has one of the forms $ 5k $, $ 5k + 1 $, $ 5k + 4 $ ($ k $ - an integer, see problem 2), so the number $ 2x^2 $ has one of the forms $ 10k $, $ 10k + 2 $, $ 10k + 8 = 10k + 5 + 3 $, and thus gives one of the remainders $ 0 $, $ 2 $, or $ 3 $ when divided by $ 5 $. Therefore, the equation $ 2x^2 = 215y^2 + 1 $ cannot hold, i.e., the given equation has no integer solutions.
Note. The solution to the problem can be stated more concisely if we replace the given equation with an equivalent equation $ (2x)^2 = 430y^2 + 2 $ and consider the remainders when divided by $ 10 $, i.e., the last digits of the terms of this equation when $ x $ and $ y $ are integers. The last digit of the square of an even number $ 2x $ can only be $ 0 $, $ 4 $, or $ 6 $, and the last digit of the number $ 430y^2 $ is $ 0 $, so the last digit of the number $ 430y^2 + 2 $ is $ 2 $. Therefore, the given equation cannot have integer solutions $ (x, y) $.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 291 |
XXXV OM - I - Problem 10
In the plane, there are $3n$ points, among which no three points are collinear. Prove that there exist $n$ disjoint triangles with vertices at the given points.
|
Consider all lines, each of which passes through two points of a given set of $3n$ points. There are finitely many such lines, so there exists a line $l$ that is not perpendicular to any of them. Project all the given points perpendicularly onto the line $l$, ensuring that the projections of any two points do not coincide. Number the given points $A_1, \ldots, A_{3n}$ according to the order in which their projections are located on the line $l$. The triangles $A_{3i-2} A_{3i-1} A_{3i}$ for $i = 1, \ldots, n$ are disjoint.
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 294 |
LIII OM - II - Problem 3
In an $ n $-person association, there are six committees. Each of them includes at least $ n/4 $ people. Prove that there exist two committees and a group of at least $ n/30 $ people, who belong to both of these committees.
|
Let's number the committees by $1, 2, \ldots, 6$ and denote by $K_i$ the number of members of the $i$-th committee who are not members of any committee with a number less than $i$.
$K_1$ is the number of all members of the first committee, which gives $K_1 \geq n/4$.
Assume that the intersection of any two committees has fewer than $n/30$ members.
Since the second committee includes at least $n/4$ members, the number of members of the second committee who are not in the first committee must be greater than $n/4 - n/30$. Therefore,
\[
K_2 > \frac{n}{4} - \frac{n}{30} = \frac{7n}{30}
\]
Similarly, we conclude that
\[
K_3 > \frac{n}{4} - \frac{n}{30} = \frac{7n}{30}
\]
\[
K_4 > \frac{n}{4} - \frac{n}{30} = \frac{7n}{30}
\]
\[
K_5 > \frac{n}{4} - \frac{n}{30} = \frac{7n}{30}
\]
\[
K_6 > \frac{n}{4} - \frac{n}{30} = \frac{7n}{30}
\]
Adding these inequalities, we get
\[
K_1 + K_2 + K_3 + K_4 + K_5 + K_6 > \frac{n}{4} + 5 \cdot \frac{7n}{30} = \frac{n}{4} + \frac{35n}{30} = \frac{n}{4} + \frac{7n}{6} = \frac{3n + 14n}{12} = \frac{17n}{12}
\]
We have obtained a contradiction, since the quantity $K_1 + K_2 + \ldots + K_6$ is not greater than the total number of members of the association, which is $n$.
Thus, the intersection of some two committees must contain at least $n/30$ members.
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 298 |
V OM - II - Task 6
Prove that if $ x_1, x_2, \ldots, x_n $ are angles contained between $ 0^\circ $ and $ 180^\circ $, and $ n $ is any natural number greater than $ 1 $, then
|
We will prove a "stronger" theorem, namely, we will show that if $0^\circ < x_i < 180^\circ$ for $i = 1, 2, \ldots, n$, where $n \geq 2$, then
(If $|a| < b$, then $a < b$ (but not vice versa), so inequality (2) implies inequality (1)).
In the proof, we will use known properties of the absolute value:
as well as the fact that if $0^\circ < x < 180^\circ$, then $|\sin x| = \sin x > 0$, $|\cos x| < 1$, and for any $x$, $|\cos x| \leq 1$.
We will prove this by using the principle of mathematical induction. When $n = 2$, the theorem is true, since
so
Suppose that for some $k \geq 2$,
and let $0 < x_{k+1} < 180^\circ$. Then
By the principle of mathematical induction, we conclude that theorem (2) is true for all $n \geq 2$.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 301 |
XIX OM - III - Problem 6
Given a set of $ n > 3 $ points, no three of which are collinear, and a natural number $ k < n $. Prove the following statements:
1. If $ k \leq \frac{n}{2} $, then each point in the given set can be connected to at least $ k $ other points in the set in such a way that among the drawn segments, there are no three sides of the same triangle.
2. If $ k > \frac{n}{2} $ and each point in the given set is connected to $ k $ other points in the set, then among the drawn segments, there are three sides of the same triangle.
|
$ 1^\circ $. Suppose $ k \leq \frac{n}{2} $. From the given set $ Z $, select a part $ Z_1 $ consisting of $ \left[ \frac{n}{2} \right] $ points*); the remaining part $ Z_2 $ contains $ \left[ \frac{n}{2} \right] $ points if $ n $ is even, and $ \left[ \frac{n}{2} \right] + 1 $ points if $ n $ is odd. Since $ k $ is an integer, from the condition $ k \leq \frac{n}{2} $ it follows that $ k \leq \left[ \frac{n}{2} \right] $. Therefore, each of the sets $ Z_1 $, $ Z_2 $ contains at least $ k $ points.
Connect each point of set $ Z_1 $ with each point of set $ Z_2 $ by segments. Then each point of set $ Z $ will be connected to at least $ k $ other points of this set. No three of the drawn segments are sides of the same triangle, for if such a triangle existed, then two of its vertices, i.e., both ends of one of the segments, would lie in one of the sets $ Z_1 $, $ Z_2 $, which is impossible, since no such segment was drawn.
$ 2^\circ $ Suppose $ k > \frac{n}{2} $ and that each point of the given set is connected by $ k $ segments to $ k $ other points of the set; let $ AB $ be one of the drawn segments.
From each of the points $ A $ and $ B $, in addition to $ AB $, there are still $ k - 1 $ other segments, i.e., a total of $ 2k - 2 $ segments whose ends belong to the set of the remaining $ n - 2 $ points. But if $ k > \frac{n}{2} $, then $ 2k - 2 > n - 2 $; among those $ 2k - 2 $ segments, there are therefore two segments with a common end $ C $. In the set of drawn segments, there are thus the sides $ AB $, $ AC $, and $ BC $ of triangle $ ABC $.
Note. In a similar way, a more general theorem can be proved. Let there be given: a set $ Z $ consisting of $ n > 3 $ points, no three of which are collinear, a natural number $ p $ satisfying the inequalities $ 3 \leq p < n $, and a natural number $ k < n $. Then:
$ 1 ^\circ $ If $ k \leq \frac{p-2}{p-1}n $, then each of the points of set $ Z $ can be connected by segments to at least $ k $ other points of this set so that in any subset of set $ Z $ consisting of $ p $ points, some two points are not connected by a segment.
$ 2^\circ $ If $ k > \frac{p-2}{p-1}n $ and each point of set $ Z $ is connected by a segment to $ k $ other points of this set, then there exists a subset of set $ Z $ consisting of $ p $ points in which every two points are connected by a segment.
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 304 |
LVII OM - II - Problem 3
Positive numbers $ a, b, c $ satisfy the condition $ ab+bc+ca = abc $. Prove that
|
Dividing the equality $ ab+bc+ca = abc $ by $ abc $ on both sides, we get
Let us substitute: $ x=1/a,\ y =1/b,\ z =1/c $. Then the numbers $ x, y, z $ are positive, and their sum is 1. Moreover,
Thus, the inequality to be proved takes the form
We will show that for any positive numbers $ x, y $, the following relationship holds:
Transforming the above inequality equivalently, we get the following in sequence:
We have obtained a relationship that is true for any positive numbers $ x $ and $ y $, so the inequality (2) is satisfied. Similarly, we prove that
Adding the relations (2), (3), and using the condition $ x + y + z = 1 $, we obtain the inequality (1) to be proved.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 305 |
XXIX OM - I - Problem 10
Point $ O $ is an internal point of a convex quadrilateral $ ABCD $, $ A_1 $, $ B_1 $, $ C_1 $, $ D_1 $ are the orthogonal projections of point $ O $ onto the lines $ AB $, $ BC $, $ CD $, and $ DA $, respectively, $ A_{i+1} $, $ B_{i+1} $, $ C_{i+1} $, $ D_{i+1} $ are the orthogonal projections of point $ O $ onto the lines $ A_iB_i $, $ B_iC_i $, $ C_iD_i $, $ D_iA_i $, respectively. Prove that the quadrilaterals $ A_4B_4C_4D_4 $ and $ ABCD $ are similar.
|
The construction given in the task is not always feasible. For example, three of the points $A_{i+1}$, $B_{i+1}$, $C_{i+1}$, $D_{i+1}$ may lie on the same line. In this case, the task loses its meaning. Therefore, we will provide a solution to the task with the additional assumption that all considered quadrilaterals exist and are convex.
Since $ \measuredangle OD_1A + \measuredangle OA_1A = \frac{\pi}{2} + \frac{\pi}{2} = \pi $, a circle can be circumscribed around quadrilateral $OA_1AD_1$. The measures of angles inscribed in a circle and subtended by the same arc are equal. Therefore, $ \measuredangle OAD = \measuredangle OA_1D_1 $ (Fig. 8). Similarly, we prove that $ \measuredangle OA_2D_2 = \measuredangle OA_2D_2 = \measuredangle OA_3D_3 = \measuredangle OA_4D_4 $.
Reasoning similarly, we obtain $ \measuredangle ODA = \measuredangle OC_1D_1 = \measuredangle OB_2C_2 = \measuredangle OA_3B_3 = \measuredangle OD_4A_4 $. Triangles $OAD$ and $OA_4D_4$ are similar because two corresponding angles in these triangles have equal measures. Therefore, $ \displaystyle \frac{OA}{AD} = \frac{OA_4}{A_4D_4} $. Similarly, we prove that $ \displaystyle \frac{OA}{AB} = \frac{OA_4}{A_4B_4} $. Hence, $ \displaystyle \frac{AB}{A_4B_4} = \frac{AD}{A_4D_4} $, and similarly $ \displaystyle \frac{AB}{A_4B_4} = \frac{BC}{B_4C_4} = \frac{CD}{C_4D_4} $.
We have also proved that $ \measuredangle OAD = \measuredangle OA_4D_4 $. Similarly, we prove that $ \measuredangle OAB = \measuredangle OA_4B_4 $, and thus $ \measuredangle BAD = \measuredangle OAB + \measuredangle OAD = \measuredangle OA_4B_4 + \measuredangle OA_4D_4 = \measuredangle B_4A_4D_4 $. Similarly, we can show that the measures of the remaining angles of quadrilateral $ABCD$ are equal to the measures of the corresponding angles of quadrilateral $A_4B_4C_4D_4$.
Thus, the corresponding sides of these quadrilaterals are proportional, and the measures of the corresponding angles are equal. Therefore, these quadrilaterals are similar.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 310 |
LI OM - I - Task 4
Each point of the circle is painted one of three colors. Prove that some three points of the same color are vertices of an isosceles triangle.
|
Let $A_1, A_2, \ldots, A_{13}$ be the vertices of an arbitrary regular 13-gon inscribed in a given circle. We will show that among any five vertices of this 13-gon, there will be three that form the vertices of an isosceles triangle. Since among any thirteen points on a given circle, there will always be five colored the same color, the problem will be solved.
Suppose, then, that it is possible to choose five vertices from $A_1, A_2, \ldots, A_{13}$ such that no three of the chosen points form an isosceles triangle.
First, assume that among the chosen points, there are no two adjacent vertices of the 13-gon $A_1 A_2 \ldots A_{13}$. Then among the chosen points, we will find two separated by exactly one vertex that was not chosen. Without loss of generality, we can assume these are $A_1$ and $A_3$. Since no three chosen vertices form an isosceles triangle, none of the points $A_{12}$, $A_{13}$, $A_2$, $A_4$, $A_5$ (Fig. 1) were chosen.
om51_1r_img_3.jpg
om51_1r_img_4.jpg
Since triangle $A_1A_6A_{11}$ is isosceles, at least one of the vertices $A_6$, $A_{11}$ was not chosen. Without loss of generality, we can assume that this vertex is $A_6$. Therefore, among the five points $A_7$, $A_8$, $A_9$, $A_{10}$, $A_{11}$, exactly three were chosen, and no two of them are consecutive vertices of the 13-gon $A_1A_2\ldots A_{13}$. Thus, the points $A_7$, $A_9$, $A_{11}$ must have been chosen. However, this is not possible, as these points form an isosceles triangle (Fig. 2). We have reached a contradiction.
The remaining case to consider is when among the chosen vertices, there are two adjacent ones, say $A_1$ and $A_2$. This means that none of the vertices $A_{13}$, $A_3$, $A_8$ (Fig. 3) were chosen.
om51_1r_img_5.jpg
om51_1r_img_6.jpg
Since triangles $A_2A_4A_6$, $A_1A_6A_{11}$, $A_{11}A_1A_4$ are isosceles, at most one of the points $A_4$, $A_6$, $A_{11}$ was chosen. Similarly, we conclude that at most one of the points $A_5$, $A_{10}$, $A_{12}$ was chosen. Therefore, at least one of the points $A_7$, $A_9$ must have been chosen. Without loss of generality, assume that the point $A_7$ was chosen (Fig. 4). The isosceles nature of triangles $A_1A_4A_7$, $A_2A_{10}A_7$, $A_2A_{11}A_7$, and $A_2A_{12}A_7$ proves that the points $A_4$, $A_{10}$, $A_{11}$, and $A_{12}$ were not chosen.
Thus, among the five chosen points, there must be two from $A_5$, $A_6$, $A_9$. Given the isosceles nature of triangle $A_5A_6A_7$, only one of the points $A_5$, $A_6$ could have been chosen. Therefore, the chosen point is $A_9$ (Fig. 5). This, in turn, means that the point $A_5$ was not chosen, as triangle $A_5A_7A_9$ is isosceles.
om51_1r_img_7.jpg
om51_1r_img_8.jpg
Thus, the fifth chosen point must be $A_6$, which leads to a contradiction, as triangle $A_9A_1A_6$ is isosceles (Fig. 6).
Thus, we have shown that it is impossible to choose five vertices of the 13-gon such that no three of them form an isosceles triangle, which completes the solution of the problem.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 313 |
XXXV OM - I - Problem 8
Let $ n $ be an even natural number. Prove that a quadrilateral can be divided into $ n $ triangles, whose vertices lie at the vertices of the quadrilateral or inside the quadrilateral, and each side of the triangle is either a side of the quadrilateral or a side of another triangle.
|
At least one diagonal of the quadrilateral is contained within its interior. Let this be, for example, the diagonal $ \overline{AC} $. If $ n = 2 $, then the division of the quadrilateral $ ABCD $ into triangles $ ABC $ and $ ACD $ is the desired division. Suppose that $ n = 2k $ is an even number. Choose any points $ A_1, \ldots, A_{k-1} $ on the diagonal $ AC $ lying on it in the order consistent with the numbering and different from $ A $ and $ C $. Additionally, let $ A_0 = A $, $ A_k = C $. The division of the quadrilateral $ ABCD $ into triangles $ A_{i-1}BA_i $ and $ A_{i-1}DA_i $, $ i = 1, \ldots, k $ satisfies the given conditions.
om35_1r_img_3.jpg
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 316 |
XII OM - III - Task 4
Prove that if each side of a triangle is less than $ 1 $, then its area is less than $ \frac{\sqrt{3}}{4} $.
|
In every triangle, at least one angle does not exceed $ 60^\circ $. Suppose that in triangle $ ABC $ with sides less than one unit, $ \measuredangle C \leq 60^\circ $. Then
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 319 |
XLIII OM - I - Problem 12
On a plane, four lines are drawn such that no two of them are parallel and no three have a common point. These lines form four triangles. Prove that the orthocenters of these triangles lie on a single straight line.
Note: The orthocenter of a triangle is the point where its altitudes intersect.
|
Let's denote four given lines by $k$, $l$, $m$, $n$, and their points of intersection by $O$, $P$, $Q$, $R$, $S$, $T$, such that
None of these points coincide; this is guaranteed by the conditions of the problem.
Figure 5 shows one possible configuration; however, for the further course of reasoning, it does not matter whether the three points of intersection of any of these lines with the remaining lines lie on the chosen line in the same order as in the figure, or in any other order.
The orthocenters of the four considered triangles
we denote by $E$, $F$, $G$, $H$ respectively. The line $OE$ (see Note 1) contains the altitude of triangle $OPT$, and is therefore perpendicular to the line $PT$, which is identical to the line $QP$.
om43_1r_img_6.jpg
Similarly, we justify each of the following eight perpendicularity relations:
The thesis of the problem can be obtained using vector calculus. From the relations (1), it follows that the following scalar products are equal to zero:
And since $ \overrightarrow{QP} = \overrightarrow{OP} - \overrightarrow{OQ} $, $ \overrightarrow{PE}=\overrightarrow{OE}-\overrightarrow{OP} $, we can rewrite these equalities in the form
The relations (2), (3), (4) are written similarly:
We add the two equalities in (5) side by side:
and transform the obtained relation to the form
Similarly, by adding the two equalities in each of the pairs (6), (7), (8), we get - respectively - the dependencies
Let's denote the vector $ \overrightarrow{OP} - \overrightarrow{OQ} +\overrightarrow{OR} $ by $ \overrightarrow{\mathbf{w}} $. According to the equalities (9) - (12),
Subtracting the first two products, we get the equality , which means that the vectors $ \overrightarrow{EF} $ and $ \overrightarrow{\mathbf{w}} $ are perpendicular. Similarly, by considering the differences of any two products appearing in (13), we conclude that the vector $ \overrightarrow{\mathbf{w}} $ is perpendicular to each of the vectors whose endpoints are any two of the points $ E $, $ F $, $ G $, $ H $.
Notice that $ \overrightarrow{\mathbf{w}} = \overrightarrow{OP} -\overrightarrow{OQ} + \overrightarrow{OR} = \overrightarrow{OP} + \overrightarrow{QR} $ is not a zero vector; the equality $ \overrightarrow{OP} + \overrightarrow{QR} = \overrightarrow{\mathbf{0}} $ would mean that the quadrilateral $ OPQR $ is a parallelogram, contrary to the assumption that the lines $ OP $ and $ QR $ - i.e., $ k $ and $ m $ - are not parallel. Therefore, we can speak of a line perpendicular to $ \overrightarrow{\mathbf{w}} $ passing through a given point; let this point be, for example, $ E $. Since each of the vectors $ \overrightarrow{EF} $, $ \overrightarrow{EG} $, $ \overrightarrow{EH} $ is perpendicular to $ \overrightarrow{\mathbf{w}} $, the points $ F $, $ G $, $ H $ lie on the line defined just now. The proof is complete.
Note 1. When some of the considered lines intersect at a right angle, then the orthocenter of the corresponding triangle coincides with one of the vertices; for example, point $ E $ may be identical to $ O $. One cannot then speak of the {\it line} $ OE $; nevertheless, the equality $ \overrightarrow{OE} \bullet \overrightarrow{QP} = 0 $ is meaningful (and true) in this case as well, because $ \overrightarrow{OE} $ is a zero vector. Similarly, any of the line notations used in the relations (1) - (4) may lose its meaning; but the corresponding relations (5) - (8) are valid in every case.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 321 |
XVII OM - I - Problem 12
Prove the theorem: If the sum of the planar angles at the vertex of a regular pyramid is equal to $180^{\circ}$, then in this pyramid, the center of the circumscribed sphere coincides with the center of the inscribed sphere.
|
We introduce the following notations: $ AB $ - the edge of the base of the given regular pyramid, $ S $ - its apex, $ H $ - the projection of point $ S $ onto the base, $ O $ - the center of the sphere circumscribed around the pyramid, $ M $ - the center of the circle circumscribed around triangle $ ASB $ (Fig. 9).
To prove the theorem, it suffices to state that the distance $ OM $ from point $ O $ to the lateral face $ ASB $ is equal to the distance $ OH $ from point $ O $ to the plane of the base of the pyramid.
According to the assumption, $ \measuredangle ASB = \frac{180^\circ}{n} $ where $ n $ denotes the number of edges of the base, and $ \measuredangle AHB = \frac{360^\circ}{n} $, so $ \measuredangle AHB = 2 \measuredangle ASB $.
In the circle circumscribed around triangle $ ASB $, angle $ AMB $ is a central angle, thus $ \measuredangle AMB = 2 \measuredangle ASB $, hence $ \measuredangle AHB = \measuredangle AMB $. The isosceles triangles $ AHB $ and $ AMB $ are therefore congruent, $ AH = AM $. From the equality $ OS = AO $ and $ MS = AM = AH $, the congruence of the right triangles $ OSM $ and $ AOH $ follows, so $ OM = OH $, Q.E.D.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 322 |
XLV OM - I - Problem 4
Given a circle with center $ O $, a point $ A $ inside this circle, and a chord $ PQ $, which is not a diameter, passing through $ A $. Lines $ p $ and $ q $ are tangent to the considered circle at points $ P $ and $ Q $, respectively. Line $ l $ passing through point $ A $ and perpendicular to $ OA $ intersects lines $ p $ and $ q $ at points $ K $ and $ L $, respectively. Prove that $ |AK|=|AL| $.
|
om45_1r_img_1.jpg
We start by observing that points $P$ and $K$ lie on one side of the line $OA$, while points $Q$ and $L$ lie on the other side (regardless of whether point $A$ is closer to the endpoint $P$ or $Q$ on the chord $PQ$). The chord $PQ$ of the given circle is not a diameter, so the tangents $p$ and $q$ intersect. Let's denote the point of intersection by $S$.
We circumscribe a circle $\omega_1$ around triangle $OAK$. We circumscribe a circle $\omega_2$ around triangle $OAL$. Angles $OAK$ and $OAL$ are right angles by assumption, so the diameters of these circles are (respectively) segments $OK$ and $OL$ (see Figure 1).
The lines $p$ and $q$, tangent to the given circle, are perpendicular to its radii $OP$ and $OQ$; thus, angles $OPK$ and $OQL$ are right angles. Therefore, circle $\omega_1$ passes through point $P$, and circle $\omega_2$ passes through point $Q$. (In the special case where point $A$ is the midpoint of the chord $PQ$ and consequently points $K$ and $L$ coincide with points $P$ and $Q$, respectively, we cannot strictly speak of angles $OPK$ and $OQL$, but the conclusion that $P \in \omega_1$ and $Q \in \omega_2$ is still valid.)
Angles $OPA$ and $OKA$ are inscribed angles in circle $\omega_1$, subtending the same arc $OA$ (we use the earlier observation that points $P$ and $K$ lie on the same side of the line $OA$). Therefore, these angles have the same measure: $|\measuredangle OPA| = |\measuredangle OKA|$; similarly, $|\measuredangle OQA| = |\measuredangle OLA|$ (inscribed angles in circle $\omega_2$, subtending the same arc $OA$). Finally, note that
since triangle $POQ$ is isosceles.
From the obtained angle equalities, it follows that
Therefore, the right triangles $OAK$ and $OAL$ are congruent, and we obtain the desired equality of segments $|AK| = |AL|$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 323 |
XXVI - I - Problem 12
In space, there is a cube with side $ a $, and spheres $ B_1, B_2, \ldots, B_n $ of arbitrary radii such that every point of the cube belongs to at least one of the spheres. Prove that among these spheres, one can select pairwise disjoint spheres such that the sum of their volumes is not less than $ \left(\frac{a}{5}\right)^3 $.
|
By induction on $ N $ we will prove
Theorem. If in a space there is a set $ F $ of volume $ V $ contained in the sum of $ N $ open balls $ B_1, B_2, \ldots, B_N $, then there exists a subset $ B_{i_1}, B_{i_2}, \ldots, B_{i_r} $ of these balls such that the balls belonging to this subset are pairwise disjoint and the sum of the volumes of the balls $ B_{i_1}, B_{i_2}, \ldots, B_{i_r} $ is greater than $ \displaystyle \frac{1}{27} V $.
Proof. If $ N = 1 $, the theorem is obvious. The ball $ B_1 $ contains the figure $ F $ of volume $ V $. Then the volume of the ball $ B_1 $ is not less than $ V $, and therefore is greater than $ \displaystyle \frac{1}{27} V $.
Next, assume that the above theorem is true for some natural number $ N $. We will prove it for the number $ N+1 $. Let the set $ F $ of volume $ V $ be contained in the sum of balls $ B_1, B_2, \ldots, B_N, B_{N+1} $. We can assume that the volume $ V_{N+1} $ of the ball $ B_{N+1} $ is not less than the volume of each of the other balls. Let $ B $ be the ball with the same center as the ball $ B_{N+1} $ and with radius of length $ 3r $, where $ r $ is the length of the radius of the ball $ B_{N+1} $. Then the volume $ V $ of the ball $ B $ is equal to $ 27 V_{N+1} $. Let $ V_0 $ be the volume of the set $ F_0 = F-B $. Since the sets $ F_0 $ and $ B $ are disjoint and $ F $ is contained in the sum of the sets $ F_0 $ and $ B $, then $ V \leq V_0 + 27 V_{N+1} $.
Every point of the set $ F_0 $ belongs to at least one of the balls $ B_1, B_2, \ldots, B_N $. Without loss of generality, we can assume that for some $ k, 0 \leq k \leq N $ each of the balls $ B_1, B_2, \ldots, B_k $ has a point in common with the set $ F_0 $, and each of the balls $ B_{k+1}, B_{k+2}, \ldots, B_N $ is disjoint from $ F_0 $. Then the set $ F_0 $ is contained in the sum of the balls $ B_1, B_2, \ldots, B_k $.
The distance from the center of the ball $ B_{N+1} $ to any point of the set $ F_0 $ is not less than $ 3r $. Therefore, the distance from any point of the ball $ B_{N+1} $ to any point of the set $ F_0 $ is not less than $ 2r $. The diameter of each of the balls $ B_1, B_2, \ldots, B_k $ is not greater than the diameter of the ball $ B_{N+1} $, i.e., not greater than $ 2r $. Therefore, each of the balls $ B_1, B_2, \ldots, B_k $ is disjoint from the ball $ B_{N+1} $. The number of balls $ B_1, B_2, \ldots, B_k $ is not greater than $ N $. By the induction hypothesis, there exists a subset $ B_{i_1}, B_{i_2}, \ldots, B_{i_r} $ of the set of balls $ B_1, B_2, \ldots, B_k $ such that the balls belonging to this subset are pairwise disjoint, and the sum of their volumes is greater than $ \displaystyle \frac{1}{27} V_0 $, and therefore - greater than $ \displaystyle \frac{1}{27} V - V_{N+1} $. Since the ball $ B_{N+1} $ is disjoint from each of the balls $ B_1, B_2, \ldots, B_k $, the balls $ B_{i_1}, B_{i_2}, \ldots, B_{i_r} $ are pairwise disjoint. The sum of their volumes is greater than $ \displaystyle \left( \frac{1}{27} V - V_{N+1} \right) + V_{N+1} = \frac{1}{27} V $.
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 324 |
XXXII - I - Problem 4
On the sides of an acute triangle $ ABC $, squares $ ABED $, $ BCGF $, $ ACHI $ are constructed outside the triangle. Prove that the medians of the triangle formed by the lines $ EF $, $ GH $, $ DI $ are perpendicular to the sides of triangle $ ABC $.
|
Let $K$, $L$, $M$ be the vertices of the formed triangle lying at the squares $ABED$, $BCGF$, $ACHI$, respectively. Let $KO$ and $LO$ be lines perpendicular to segments $\overline{AB}$ and $\overline{BC}$, respectively (Fig. 8).
om32_1r_img_8.jpg
Triangles $KLO$ and $BEF$ have corresponding sides that are parallel, so they are similar. From this, we obtain
Suppose the perpendicular to $AC$ passing through point $M$ does not pass through $O$, then it intersects line $KO$ at some point $P$, and line $LO$ at some point $R$. If at the same time $KP > KO$ (the opposite case $KP < KO$ is considered analogously), then $MR > MP$ and $LO > LR$. Similarly, as stated above, we have
Dividing these equalities side by side, we get
Thus, based on the previously written inequalities, we have
The obtained contradiction is a consequence of the assumption that the perpendiculars to the sides of triangle $ABC$ drawn from the corresponding vertices of triangle $KLM$ do not intersect at one point. Therefore, $O = P = R$. We will show that $O$ is the centroid of triangle $KLM$. From equalities (1) and (2), it follows that
Considering angles $ABC$, $CBF$, $FBE$, $EBA$, we note that $\measuredangle EBF = 360^\circ - 2 \cdot 90^\circ - \measuredangle ABC = 180^\circ - \measuredangle ABC$. Therefore, $\measuredangle KOL = 180^\circ - \measuredangle ABC$, and from this, it follows that the area of triangle $KLO$ is
Similarly, we obtain that
The rays $OK^\to$, $OL^\to$, $OM^\to$ thus divide triangle $KLM$ into three triangles of equal area, which implies that $O$ is the centroid of triangle $KLM$, i.e., the lines $KO$, $LO$, $MO$ contain the medians of the corresponding sides of triangle $KLM$. Thus, the medians of this triangle are perpendicular to the corresponding sides of triangle $ABC$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 328 |
LVIII OM - III - Problem 1
In an acute triangle $ABC$, point $O$ is the center of the circumscribed circle, segment $CD$ is the altitude, point $E$ lies on side $AB$, and point $M$ is the midpoint of segment $CE$. The line perpendicular to line $OM$ and passing through point $M$ intersects lines $AC$, $BC$ at points $K$, $L$ respectively. Prove that
|
Let's draw a line through point $ M $ parallel to side $ AB $, which intersects segments $ AC $ and $ BC $ at points $ P $ and $ Q $ respectively (Fig. 12). Then points $ P $ and $ Q $ are the midpoints of sides $ AC $ and $ BC $ respectively. Since point $ O $ is the center of the circumcircle of triangle $ ABC $, we have $ \measuredangle APO=90^\circ $. Moreover, $ \measuredangle KMO=90^\circ $. Therefore, points $ K $, $ P $, $ M $, $ O $ lie on the same circle, whose diameter is segment $ KO $. Hence, $ \measuredangle OKM=\measuredangle OPM $.
Similarly, we prove that $ \measuredangle OLM=\measuredangle OQM $. From the equality of these angles, it follows that triangles $ OKL $ and $ OPQ $ are similar. Denote by $ S $ the orthogonal projection of point $ O $ onto line $ PQ $, and we obtain
om58_3r_img_12.jpg
om58_3r_img_13.jpg
Let $ X $ be the midpoint of segment $ OC $, and let $ Y $, $ R $ be the orthogonal projections of points $ X $ and $ C $ onto line $ PQ $ (Fig. 13). Since $ \measuredangle OPC=\measuredangle OQC=90^\circ $, points $ C $, $ P $, $ O $, $ Q $ lie on the same circle, whose center is point $ X $. Therefore, $ PX=XQ $, and thus $ PY=YQ $. Moreover, point $ X $ is the midpoint of segment $ OC $, so $ RY=YS $. From this, we obtain $ PR=QS $.
Therefore,
Combining equalities (1) and (2), we obtain the thesis.
Note: After obtaining relation (1), we can complete the solution in a slightly different way.
Let $ T $ be the midpoint of segment $ AB $, and let $ G $ denote the centroid of triangle $ ABC $ (Fig. 14).
om58_3r_img_14.jpg
Then point $ G $ divides each of the medians $ AQ $, $ BP $, $ CT $ of triangle $ ABC $ in the ratio $ 2:1 $. Therefore, the homothety $ j $ with center at point $ G $ and scale $ -1/2 $ maps points $ A $, $ B $, $ C $ to points $ Q $, $ P $, $ T $ respectively.
On the other hand, the line passing through point $ O $ and perpendicular to lines $ AB $ and $ QP $ contains both point $ S $ (since $ S $ is the orthogonal projection of point $ O $ onto line $ QP $) and point $ T $ (the projection of the center of the circumcircle of triangle $ ABC $ onto a side of the triangle is the midpoint of that side). In other words, segment $ TS $ is the altitude of triangle $ QPT $.
As a result, the homothety $ j $ maps the foot $ D $ of the altitude $ CD $ in triangle $ ABC $ to the foot $ S $ of the altitude $ TS $ in triangle $ QPT $. This means that $ j $ maps segments $ AD $ and $ DB $ to segments $ QS $ and $ SP $ respectively. It follows that the ratios are equal,
which, together with equality (1), implies the thesis of the problem.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 329 |
XXV OM - II - Problem 6
Given is a sequence of integers $ a_1, a_2, \ldots, a_{2n+1} $ with the following property: after discarding any term, the remaining terms can be divided into two groups of $ n $ terms each, such that the sum of the terms in the first group is equal to the sum of the terms in the second. Prove that all terms of the sequence are equal.
|
\spos{1} First, note that if a sequence of real numbers satisfies the conditions of the problem, then so does any sequence of the form
where $ k $ is any real number.
Suppose that a sequence (1) of integers satisfies the conditions of the problem and $ a_1 \ne a_2 $. Without loss of generality, we can assume that $ a_1 = 0 $. Otherwise, we would add $ -a_1 $ to each term of the sequence. Among the sequences (1) of integers that satisfy the conditions of the problem, with $ a_1 \ne a_2 $ and $ a_1 = 0 $, let us choose one in which the number $ |a_2| $ is minimal.
By discarding the term $ a_1 = 0 $, the sum of the remaining terms is even by the conditions of the problem. Therefore, the sum of all terms of the sequence (1) is even. Similarly, by discarding any term $ a_j $, the sum of the remaining terms is even. Hence, any term $ a_j $ of the sequence (1) is even.
It follows that the terms of the sequence $ b_1, b_2, \ldots, b_{2n+1} $, where $ b_i = \displaystyle \frac{1}{2} a_i $ for $ i= 1,2,\ldots, 2n+1 $, are integers. We have $ |b_2| = \displaystyle \frac{1}{2} |a_2| < |a_2| $, since $ a_2 \ne 0 $. This contradicts the minimality of the number $ |a_2| $.
The obtained contradiction proves that in every sequence of integers (1) that satisfies the conditions of the problem, all terms are equal.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 333 |
XXXVIII OM - III - Problem 3
Given is a polynomial $ W $ with non-negative integer coefficients. We define a sequence of numbers $ (p_n) $, where $ p_n $ is the sum of the digits of the number $ W(n) $. Prove that some number appears in the sequence $ (p_n) $ infinitely many times.
|
Let $ W(x) = a_mx^m + \ldots +a_1x+a_0 $ ($ a_i $ - non-negative integers) and let $ q $ be the number of digits in the decimal representation of the largest of the numbers $ a_0, \ldots, a_m $. Let $ \overline{a_i} $ denote the $ q $-digit decimal representation of $ a_i $; if $ a_i $ has fewer than $ q $ digits, we prepend zeros. Then for $ r > q $, the decimal representation of the number $ W(10^r) $ has the form
where $ \bar{b} $ is a block consisting of $ r-q $ zeros. The sum of the digits of each of these numbers equals the sum of the digits of all the coefficients of the polynomial $ W $. This is therefore the common value of all terms of the sequence $ (p_n) $ with indices $ n = 10^r $, $ r \leq q $.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 334 |
XLIX OM - I - Problem 11
In a tennis tournament, $ n $ players participated. Each played one match against each other; there were no draws. Prove that there exists a player $ A $ who has either directly or indirectly defeated every other player $ B $, i.e., player $ A $ won against $ B $ or player $ A $ defeated some player $ C $ who won against player $ B $.
|
Let $ A $ be the participant in the tournament who defeated the largest number of opponents. (If several players have the same maximum number of victories, we choose any one of them.) We claim that the player $ A $ selected in this way has defeated, directly or indirectly, all other players.
Let $ B $ be any player who has won against $ A $. We need to show that among all the players $ C_1, \ldots, C_m $ defeated by $ A $, there exists one who has won against $ B $.
Suppose this is not the case. This means that player $ B $ has defeated players $ C_1, \ldots, C_m $ as well as player $ A $ — he would then have more victories on his record than player $ A $.
However, this is not possible, since $ A $ is the player who has achieved the most victories. The obtained contradiction completes the proof.
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 337 |
XIV OM - III - Task 1
Prove that two natural numbers, whose digits are all ones, are relatively prime if and only if the numbers of their digits are relatively prime.
|
Let $ J_m $ denote the $ m $-digit number whose digits are all ones:
If $ m $ is divisible by $ d $ ($ m $, $ d $ - natural numbers), then $ J_m $ is divisible by $ J_d $. Indeed, if $ m = k \cdot d $ ($ k $ - a natural number), then
where the number $ M $ is an integer.
$ \beta $) If $ m > n $, then
Let the numbers $ J_m $ and $ J_n $ be given, where $ m > n > 1 $.
a) The proof of the theorem that if $ J_m $ and $ J_n $ are coprime, then $ m $ and $ n $ are also coprime, is immediate, because according to $ \alpha $) if $ d $ is a common divisor of the natural numbers $ m $ and $ n $, then $ J_d $ is a common divisor of the numbers $ J_m $ and $ J_n $.
b) We will prove the converse theorem. Suppose the natural numbers $ m $ and $ n $ are coprime. Applying the Euclidean algorithm, i.e., dividing $ m $ by $ m $, $ n $ by the obtained remainder $ r $, the remainder $ r $ by the new remainder $ r_1 $, etc., we get smaller and smaller remainders, so we eventually reach a remainder equal to zero:
From the sequence of equalities (1), it follows that the natural number $ r_k $ is a common divisor of the numbers $ r_{k-1}, r_{k-2}, \ldots, r, n, m $, so $ r_k = 1 $.
From the first equality (1), we infer, based on $ \beta $), that
Let $ D $ be a common divisor of the natural numbers $ J_m $ and $ J_n $. Since $ J_{nq} $ is divisible by $ J_n $ according to $ \alpha $), $ D $ is also a divisor of the number $ J_r \cdot 10^{nq} $ according to (2). The number $ 10^{nq} $ has no other prime divisors except for the numbers $ 2 $ and $ 5 $, which are not divisors of the number $ J_m $, so $ D $ is coprime with $ 10^{nq} $. Therefore, $ D $ is a divisor of $ J_r $.
In the same way, based on the next equalities (1), we will conclude successively that $ D $ is a divisor of the numbers $ J_{r_1}, J_{r_2}, \ldots, J_{r_k} $. But $ r_k = 1 $, so
This means that $ J_m $ and $ J_n $ are coprime, which is what we had to prove.
Note 1. The part b) of the above proof can be replaced by a much shorter argument, using the following well-known theorem of number theory:
If the natural numbers $ m $ and $ n $ are coprime, then there exist natural numbers $ x $ and $ y $ such that
The converse theorem also holds: if the natural numbers $ m $, $ n $, $ x $, $ y $ satisfy equation (3), then $ m $ and $ n $ are coprime. This follows from equation (3) because any common divisor of the numbers $ m $ and $ n $ is a divisor of the number $ 1 $.
Assume the natural numbers $ m $, $ n $ are coprime, so for some natural numbers $ x $ and $ y $, (3) holds. Then
and since according to ($ \alpha $): $ J_{mx} = J_m \cdot M $ and $ J_{my} = J_m \cdot N $, where the numbers $ M $ and $ N $ are natural, then:
from which it follows that $ J_m $ and $ J_n $ are coprime.
Note 2. The proof of the theorem cited in Note 1 can be derived from the sequence of equalities (1). Substituting the value of $ r $ from the first equality into the second, and then after this substitution the value of $ r_1 $ from the second equality into the third, etc., we eventually arrive, considering that $ r_k = 1 $, at an equality of the form (3).
Note 3. In the above arguments, we assumed that the base of numeration is $ 10 $. The theorem is, however, true for any base of numeration $ g $. The proof remains the same, except that everywhere $ 10 $ must be replaced by $ g $.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 340 |
LX OM - III - Task 1
Each vertex of a convex hexagon is the center of a circle with a radius equal to the length of the longer of the two sides of the hexagon containing that vertex. Prove that if the intersection of all six circles (considered with their boundaries) is non-empty, then the hexagon is regular.
|
Let's denote the consecutive vertices of the given hexagon by the letters $A, B, C, D, E$, and $F$.
Assume that the intersection of the six circles mentioned in the problem is non-empty and that point
$P$ belongs to this intersection. Consider any side of the hexagon, for the sake of argument, let it be
side $AB$. From the conditions of the problem, it follows that $AP \leqslant AB$ and $BP \leqslant AB$, so
if $P$ does not lie on the line $AB$, then segment $AB$ is the longest side of triangle $ABP$.
Angle $\measuredangle APB$ is therefore its largest angle, i.e., $\measuredangle APB \geqslant 60^{\circ}$.
If, however, point $P$ lies on the line $AB$, then it lies on segment $AB$ (otherwise $AP > AB$ or $BP > AB$).
If it is not at the end of this segment, then $\measuredangle APB = 180^{\circ}$. In summary,
if $P \neq A$ and $P \neq B$, then $\measuredangle APB \geqslant 60^{\circ}$. Similar reasoning can be
applied to the other sides of the hexagon.
We will show that point $P$ does not lie outside the hexagon $ABCDEF$. If it did, then for some
vertices $X, Y$, the convex angle $\measuredangle XPY < 180^{\circ}$ would cover the entire hexagon
(Fig. 1). Given the convexity of hexagon $ABCDEF$,
this would imply
which is contradictory to $\measuredangle XPY < 180^{\circ}$.
Since point $P$ does not lie outside the hexagon, it must lie in its interior or on its boundary.
First, consider the case where $P$ is one of the vertices of the hexagon. Without loss of
generality, we can assume that $P = A$. Then, due to the convexity of the hexagon, we have
which is impossible. If $P$ lies on the boundary of hexagon $ABCDEF$ but is not a vertex,
then it lies between some consecutive vertices. Without loss of generality, we can
assume that $P$ lies on side $AB$ of the hexagon. Then we have
which is also impossible.
Therefore, $P$ lies in the interior of the hexagon. Angles $\measuredangle APB$, $\measuredangle BPC$, $\measuredangle CPD$,
$\measuredangle DPE$, $\measuredangle EPF$, and $\measuredangle FPA$ then sum up to a full angle, and the measure
of each of them is at least $60^{\circ}$. It follows that the measure of each of them is
$60^{\circ}$ (Fig. 2). Since $\measuredangle APB = 60^{\circ}$ is the largest angle of triangle
$ABP$, the other angles also measure $60^{\circ}$. Triangle $ABP$ is therefore equilateral, and similarly,
the other triangles with vertex $P$ and base being one of the sides are also equilateral. Thus, the hexagon
is regular.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 341 |
LV OM - I - Task 8
Point $ P $ lies inside the tetrahedron $ ABCD $. Prove that
|
Let $ K $ be the point of intersection of the plane $ CDP $ with the edge $ AB $, and let $ L $ be the point of intersection of the plane $ ABP $ with the edge $ CD $ (Fig. 4).
Similarly, let $ M $ be the point of intersection of the plane $ ADP $ and the edge $ BC $, and let $ N $ denote the common point of the plane $ BCP $ and the edge $ AD $.
om55_1r_img_4.jpg
The points $ K $, $ P $, and $ L $ belong to the common part of the planes $ ABP $ and $ CDP $, so they lie on the same line. Similarly, the points $ M $, $ P $, and $ N $ lie on the same line. Therefore, the points $ K $, $ L $, $ M $, $ N $, and $ P $ lie in the same plane. This concludes the solution of the problem.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 342 |
L OM - I - Task 4
Given real numbers $ x $, $ y $, such that the numbers $ x + y $, $ x^2 + y^2 $, $ x^3 + y^3 $, and $ x^4 + y^4 $ are integers. Prove that for every positive integer $ n $, the number $ x^n + y^n $ is an integer.
|
Since $ 2xy= (x + y)^2 - (x^2 + y^2) $ and $ 2x^2y^2 = (x^2 + y^2)^2 - (x^4 + y^4) $, the numbers $ 2xy $ and $ 2x^2y^2 $ are integers. If the number $ xy $ were not an integer, then $ 2xy $ would be odd. But then the number $ 2x^2y^2 = (2xy)^2/2 $ would not be an integer. The conclusion is that the number $ xy $ is an integer.
The integrality of the number $ x^n + y^n $ is proved by induction using the identity $ x^n + y^n = (x^{n-1} +y^{n-1})(x + y)-xy(x^{n-2} +y^{n-2}) $.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 343 |
V OM - III - Task 5
Prove that if in a tetrahedron $ABCD$ the opposite edges are equal, i.e., $AB = CD$, $AC = BD$, $AD = BC$, then the lines passing through the midpoints of opposite edges are mutually perpendicular and are axes of symmetry of the tetrahedron.
|
Let $ K $, $ L $, $ M $, $ N $, $ P $, $ Q $ denote the midpoints of the edges of the tetrahedron $ ABCD $, as indicated in Fig. 42. It is sufficient to prove that any of the lines $ KL $, $ MN $, $ PQ $, for example, $ KL $, is an axis of symmetry of the tetrahedron and that it is perpendicular to one of the two remaining lines, for example, to $ PQ $.
\spos{1} Since, by assumption, $ AD = BC $ and $ BD = AC $, the triangles $ ABD $ and $ ABC $ are congruent, as they have corresponding equal sides, so the medians $ DK $ and $ CK $ of these triangles are equal, which means that triangle $ DKC $ is isosceles and the median $ KL $ of this triangle is its altitude, i.e., $ KL \bot DC $; similarly, $ KL \bot AB $. It follows that the line $ KL $ is an axis of symmetry of the tetrahedron, as point $ S $ is symmetric to point $ A $, and point $ C $ is symmetric to point $ D $ with respect to the line $ KL $. Segment $ BC $ is symmetric to segment $ AD $, so the midpoint $ Q $ of segment $ BC $ is symmetric to the midpoint $ P $ of segment $ AD $. The line $ PQ $ passing through points $ P $ and $ Q $ symmetric with respect to the line $ KL $ intersects this line and is perpendicular to it.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 345 |
XXV - I - Problem 3
Prove that the bisectors of the angles formed by the lines containing the opposite sides of a convex quadrilateral inscribed in a circle are respectively parallel to the bisectors of the angles formed by the lines containing the diagonals of this quadrilateral.
|
Let $ A $, $ B $, $ C $, $ D $ be consecutive vertices of a quadrilateral inscribed in a circle. Let $ O $ be the point of intersection of the lines $ AB $ and $ CD $, and let $ k $ be the angle bisector of $ \measuredangle AOD $ (Fig. 12). If $ A' $ and $ C' $ are the images of points $ A $ and $ C $, respectively, under reflection in the line $ k $, then the lines $ A'C' $ and $ BD $ are parallel. We have $ \measuredangle OBD = \measuredangle A'CO $ (as inscribed angles subtended by the same arc) and $ \measuredangle A'CO = \measuredangle ACO $ (symmetry preserves angle measures). Therefore, the angle bisectors of the angles formed by the lines $ AC $ and $ BD $, and $ AC $ and $ A'C' $ are parallel. The latter angle bisector is the line $ k $.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 352 |
XXXVI OM - III - Problem 6
Prove that if in a convex polyhedron with $ k $ faces there are more than $ k/2 $ faces, no two of which have a common edge, then it is impossible to inscribe a sphere in this polyhedron.
|
Suppose that a sphere can be inscribed in a given polyhedron. Let $S_1, \ldots, S_k$ be the faces of the polyhedron, and $P_1, \ldots, P_k$ the points of tangency of the respective faces with the sphere. If $A$ and $B$ are common vertices of the faces $S_i$ and $S_j$, then the triangles $ABP_i$ and $ABP_j$ are congruent (the segments $AP_i$ and $AP_j$ tangent to the sphere from point $A$ have equal lengths, similarly $|BP_i| = |BP_j|$). In this way, the full angle at vertex $P_i$ located on face $S_i$ can be represented as the sum of the corresponding angles located on faces sharing an edge with $S_i$. The sum of the measures of the angles determined in this way on all faces is $k \cdot 2\pi$. According to the assumption, there are more than $k/2$ faces, no two of which share an edge. Of course, the sum of the measures of the angles centered at the points of tangency of these faces with the sphere is more than $k\pi$. Each of these angles is equal to a corresponding angle on one of the remaining faces. But there are fewer than $k/2$ of these remaining faces, so the sum of the measures of the angles considered on them is less than $k\pi$. We have obtained a contradiction. Therefore, a sphere cannot be inscribed in such a polyhedron.
Note. The existence of polyhedra satisfying such a condition was demonstrated in problem 11 of the first stage of the competition.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 356 |
XXIII OM - III - Problem 5
Prove that all subsets of a finite set can be arranged in a sequence, where consecutive terms differ by one element.
|
Assume that a given finite set $A$ has $n$ elements. By applying induction on $n$, we will prove that there exists such a sequence of all subsets of set $A$ that
(1)
all subsets of set $A$ are included, and
(2)
for any two consecutive subsets $A_i$ and $A_{i+1}$ in the sequence, one of the sets $A_{i+1} - A_i$ and $A_i - A_{i+1}$ is empty, and the other is a singleton.
For $n = 1$, the sequence $\emptyset$, $A$ obviously satisfies (2). Assume that for some natural number $n$, there exists such a sequence (1) of all subsets of an $n$-element set $A$ that satisfies (2). We will prove that there exists a sequence of all subsets of an $(n+1)$-element set $A \cup \{b\}$ that satisfies (2).
We apply induction on $n$. If the sequence (1) of all subsets of an $n$-element set $A$ satisfies condition (2), then the following sequence of all subsets of an $(n+1)$-element set $A \cup \{b\}$ also satisfies this condition:
(5)
This sequence contains all sets $A_i$ and all sets $A_i \cup \{b\}$ for $i = 1, 2, \ldots, 2^n$, i.e., all subsets of set $A \cup \{b\}$. Consider the consecutive terms of sequence (5). From the induction hypothesis, we know that one of the sets $A_{i+1} - A_i$ and $A_i - A_{i+1}$ is empty, and the other is a singleton; it follows that one of the sets $(A_i \cup \{b\}) - (A_{i+1} \cup \{b\}) = A_i - A_{i+1}$ and $(A_{i+1} \cup \{b\}) - (A_i \cup \{b\}) = A_{i+1} - A_i$ is empty, and the other is a singleton.
Finally, $(A_{2^n} \cup \{b\}) - A_{2^n} = \{b\}$ and $A_{2^n} - (A_{2^n} \cup \{b\}) = \emptyset$. Therefore, sequence (5) satisfies condition (2).
Note. This problem has an interesting geometric interpretation. Consider the case $n = 3$. If $A = \{a_1, a_2, a_3\}$, then each subset of set $A$ can be identified with a point $(e_1, e_2, e_3)$, whose coordinates are either $0$ or $1$. Specifically, we define
(6)
The points thus defined are the vertices of a cube determined by the unit vectors of the coordinate axes.
Let $A$ and $A'$ be subsets of set $A$. One of the sets $A' - A$ and $A - A'$ is empty, and the other is a singleton if and only if the points corresponding to sets $A$ and $A'$ differ in one coordinate. Such points belong to some edge of the cube. Therefore, our problem can be formulated as follows: There exists a broken line formed by some edges of the cube that passes exactly once through each of its vertices.
In the case $n \ne 3$, an analogous interpretation of the problem can be given. Instead of a cube, one should consider an $n$-dimensional hypercube.
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 357 |
LIV OM - II - Task 5
Point $ A $ lies outside the circle $ o $ with center $ O $. From point $ A $, two tangent lines to circle $ o $ are drawn at points $ B $ and $ C $. A certain tangent to circle $ o $ intersects segments $ AB $ and $ AC $ at points $ E $ and $ F $, respectively. Lines $ OE $ and $ OF $ intersect segment $ BC $ at points $ P $ and $ Q $, respectively. Prove that from segments $ BP $, $ PQ $, and $ QC $, a triangle similar to triangle $ AEF $ can be constructed.
|
Let $ X $ be the point of tangency of circle $ o $ with line $ EF $ (Fig. 3). From the equality
of
it follows that triangles $ BEP $ and $ XEP $ are congruent. Therefore, $ BP = XP $.
Similarly, we prove the equality $ CQ = XQ $. This means that triangle $ PQX $ is constructed from segments $ BP $, $ PQ $, and $ QC $.
om54_2r_img_3.jpg
It remains to show that triangle $ PQX $ is similar to triangle $ FEA $. Let $ \measuredangle FEA = \alpha $, $ \measuredangle EFA = \beta $. Triangle $ ABC $ is isosceles, from which we calculate that $ \measuredangle ABC = \frac{1}{2} (\alpha+\beta) $. Furthermore, $ \measuredangle BEP = 90^{\circ} - \frac{1}{2} \alpha $. The last two equalities imply
that
which results in
Similarly, we prove that $ \measuredangle XQP = \alpha $, which completes the solution of the problem.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 359 |
XXXVII OM - III - Problem 3
Prove that if $ p $ is a prime number, and the integer $ m $ satisfies the inequality $ 0 \leq m < p—1 $, then $ p $ divides the number $ \sum_{j=1}^p j^m $.
|
Let's denote the sum $1^m + 2^m + \ldots + p^m$ by $A(p, m)$. We need to prove that under the given conditions
Proof is conducted by induction on $m$ (for a fixed $p$). When $m = 0$, we get the number $A(p, 0) = p$, which is clearly divisible by $p$.
Fix an integer $m$ satisfying $0 < m < p - 1$ and assume that
We want to show that $p \mid A(p, m)$.
According to the binomial theorem, for each natural number $j$ the following equality holds
Substituting $j = 1, \ldots, p$ we get a sequence of equalities
Adding these equalities side by side, we obtain
The left-hand side of equation (2) can be rewritten as . This is a number divisible by $p$. In the last sum on the right-hand side of equation (2), all terms are divisible by $p$ by the inductive hypothesis (1). Therefore, the remaining term in (2) is also divisible by $p$:
Since $p$ is a prime number, it must divide one of the factors of the obtained product. The number $m + 1$, being smaller than $p$, does not divide $p$. Therefore, ultimately $p \mid A(p, m)$, which is what we needed to prove.
By the principle of induction, the theorem given in the problem is proved.
Note. Equation (2) is a recursive formula, from which one can compute the sums of powers (with increasingly larger natural exponents) of finite sequences of consecutive natural numbers.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 360 |
XLVI OM - II - Zadanie 1
Wielomian $ P(x) $ ma współczynniki całkowite. Udowodnić, że jeżeli liczba $ P(5) $ dzieli się przez 2, a liczba $ P(2) $ dzieli się przez 5, to liczba $ P(7) $ dzieli się przez 10.
|
Dowód opiera się na spostrzeżeniu, że jeśli $ P(x) = a_0 + a_1x + \ldots + a_nx^n $ jest wielomianem o współczynnikach całkowitych, to dla każdej pary różnych liczb całkowitych $ u $, $ v $ różnica $ P(u) - P(v) $ jest podzielna przez różnicę $ u-v $. Istotnie:
a każda z różnic $ u^k - v^k $ rozkłada się na czynniki:
Przyjmując w szczególności $ u = 7 $, $ v = 5 $ widzimy, że różnica $ P(7)-P(5) $ dzieli się przez $ 2 $; przyjmując następnie $ u = 7 $, $ v = 2 $ stwierdzamy, że różnica $ P(7)-P(2) $ dzieli się przez $ 5 $. Stąd, wobec warunków danych w założeniu zadania, wnosimy, że liczba $ P(7) $ dzieli się zarówno przez $ 2 $, jak i przez $ 5 $. A ponieważ liczby $ 2 $ i $ 5 $ są względnie pierwsze, zatem liczba $ P(7) $ dzieli się przez iloczyn $ 2 \cdot 5 $, czyli przez $ 10 $.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 361 |
LIX OM - II - Task 6
Given a positive integer $ n $ not divisible by 3. Prove that there exists a number $ m $ with the following property:
Every integer not less than $ m $ is the sum of the digits of some multiple of the number $ n $.
|
A good number will be understood as a positive integer that is the sum of the digits of some multiple of the number $ n $.
First of all, note that the sum of two good numbers is also a good number. Indeed, let $ k_1, k_2 $ be multiples of the number $ n $ with the sums of their digits being $ s_1, s_2 $, respectively. Let $ t $ be an integer such that $ 10^t > k_2 $. Then the number $ k = 10^t \cdot k_1 + k_2 $ is a multiple of the number $ n $, and the sum of the digits of the number $ k $ is equal to $ s_1 + s_2 $, since when adding the numbers $ 10^t \cdot k_1 $ and $ k_2 $, non-zero digits appear in different positions.
The number $ n $ is not divisible by 3, so its sum of digits is also not divisible by 3.
Now let $ b $ be an integer such that $ 10^{3^b} > n $. Assume that the digits of the decimal representation of the number $ n $ are $ c_1, c_2, \dots, c_l $. We can of course assume that $ c_l \neq 0 $, since dividing the number $ n $ by 10 does not change the conditions of the problem. Then the digits of the decimal representation of the number
$ (10^{3^b} -1)n = \underbrace{999\dots 99}_{3^b} \cdot n $, divisible by $ n $, are the digits:
Hence, the sum of the digits of the number $ (10^{3^b} -1)n $ is $ 9 \cdot 3^b = 3^{b+2} $.
We have thus shown that the good numbers are: the number $ a $, which is not divisible by 3, and the number $ 3^d $, where $ d = b+2 $.
We will show that every integer not less than $ a \cdot 3^d $ is good. This will imply that the number
$ m = a \cdot 3^d $ satisfies the thesis of the problem.
Let $ s \geqslant a \cdot 3^d $ be any integer. The numbers
are then positive. Moreover, no two of them give the same remainder when divided by $ 3^d $ (since the divisibility
$ 3^d | (s - ia) - (s - ja) = (j - i)a $ for some indices $ 0 \leqslant i, j \leqslant 3^d - 1 $ due to the non-divisibility of the number $ a $ by 3 is only possible if $ 3^d | j - i $, which implies $ i = j $). There are $ 3d $ numbers in the sequence (*), so there exists a number among them that is divisible by $ 3^d $. Let, for example, $ s - va = w \cdot 3^d $. Then
$ v, w \geqslant 0 $ and
The numbers $ a $ and $ 3^d $ are good. Therefore, from the above representation, we conclude that the number $ s $, as the sum of good numbers, is also good, which is what we were proving.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 362 |
XXVIII - I - Problem 7
Three circles with radii equal to 1 intersect such that their common part is bounded by three arcs, each belonging to a different circle. The endpoints of these arcs are denoted by $ K, L, M $. The first circle intersects the second at points $ C $ and $ M $, the second intersects the third at points $ A $ and $ K $, and the third intersects the first at points $ B $ and $ L $.
Prove that the sum of the lengths of the arcs $ AM, BK, CL $ equals $ \pi $.
|
If two circles of equal radii intersect at points $ P $ and $ Q $, then the lengths of the arcs determined by these points on one circle are equal to the lengths of the corresponding arcs determined by these points on the other circle. By performing a symmetry with respect to the line $ PQ $, the arcs with endpoints $ P $ and $ Q $ on one circle are transformed into the corresponding arcs with endpoints $ P $ and $ Q $ on the other circle.
From this, the following equalities of the arc lengths of the circles given in the problem (Fig. 5) follow:
By adding these equalities side by side, we conclude that
The measure of an inscribed angle in a circle is half the measure of the central angle subtended by the same arc. In a circle with a radius of length $ 1 $, the measure of the central angle expressed in radians is equal to the length of the arc on which this angle is subtended. Therefore,
and similarly,
Since the sum of the measures of the angles of triangle $ KLM $ is $ \pi $, by adding these equalities side by side, we obtain, by virtue of (1),
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 364 |
XXXII - I - Problem 3
A cone $ S_1 $ is circumscribed around a sphere $ K $. Let $ A $ be the center of the circle of tangency of the cone with the sphere. A plane $ \Pi $ is drawn through the vertex of the cone $ S_1 $ perpendicular to the axis of the cone. A second cone $ S_2 $ is circumscribed around the sphere $ K $, with its vertex lying on the plane $ \Pi $. Prove that the plane of the circle of tangency of the cone $ S_2 $ with the sphere $ K $ passes through the point $ A $.
|
Let $ O $ be the center of the sphere, $ r $ - the length of its radius. $ W_1 $, $ W_2 $ are the vertices of the cones $ S_1 $ and $ S_2 $ (Fig. 7).
om32_1r_img_7.jpg
The plane determined by the points $ O $, $ W_1 $, $ W_2 $ contains the point $ A $, which is the center of the circle of tangency of the cone $ S_1 $ with the sphere $ K $ (point $ A $ lies on the segment $ \overline{OW_1} $), and also contains a certain diameter $ \overline{BC} $ of this circle, the center $ R $ of the circle of tangency of the cone $ S_2 $ with the sphere $ K $, and the diameter $ \overline{MN} $ of this circle. Let $ D $ be the point of intersection of the segment $ \overline{MN} $ and the line $ W_1O $. We will show that $ D = A $. Suppose that the point $ D $ lies between $ M $ and $ R $. Then $ MD = MR - RD $, $ ND = MR + RD $, and $ MD \cdot ND = (MR - RD) (MR + RD) = MR^2 - RD^2 $. Applying the Pythagorean theorem to triangles $ MRW_2 $ and $ DRW_2 $ we get from this
however, from the Pythagorean theorem applied to triangles $ MW_2O $ and $ W_1DW_2 $ it follows that
From the theorem of the secant and the tangent, it follows that
thus
If $ DW_1 < AW_1 $, then $ MD \cdot DN > W_1B^2 - AW_1^2 = AB^2 $, since $ AB^2 = BA \cdot AC $, so $ MD \cdot DN > BA \cdot AC $, which is not possible, because the segment $ \overline{MN} $ intersects the segment $ \overline{AB} $ at some point $ T $, such that $ MT \cdot TN = BT \cdot TC \leq AB^2 $. If $ DW_1 > AW_1 $, then $ W_1O^2 - DW_1 < W_1O^2 - AW_1^2 = AB^2 $, which is also not possible. Therefore, it must be $ DW_1 = AW_1 $, from which it follows that $ A = D $. Therefore, the point $ A $ lies on the line $ MN $, and thus in the plane of the circle of tangency of the cone $ S_2 $ with the sphere $ K $.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 365 |
XXVII OM - II - Problem 4
Inside the circle $ S $, place the circle $ T $ and the circles $ K_1, K_2, \ldots, K_n $ that are externally tangent to $ T $ and internally tangent to $ S $, with the circle $ K_1 $ tangent to $ K_2 $, $ K_2 $ tangent to $ K_3 $, and so on. Prove that the points of tangency between the circles $ K_1 $ and $ K_2 $, $ K_2 $ and $ K_3 $, and so on, lie on a circle.
|
Let circles $S$ and $T$ be concentric. We will show that the points of tangency $K_1$ with $K_2$, $K_2$ with $K_3$, etc., are equidistant from the common center $O$ of circles $S$ and $T$.
Let for $i = 1, 2, \ldots, A_i$ be the point of tangency of circles $K_i$ and $T$, $B_i$ - the point of tangency of circles $K_i$ and $K_{i+1}$, $C_i$ - the point of tangency of circles $K_i$ and $S$, $O_i$ - the center of circle $K_i$ (Fig. 14). Let $r$ and $R$ be the lengths of the radii of circles $T$ and $S$ respectively. Then the length of the radius of circle $K_i$ is equal to $\frac{1}{2} A_iC_i = \frac{1}{2}(R-r)$, and thus circles $K_1, K_2, \ldots$ have radii of equal length. Point $B_i$ is then the midpoint of segment $\overline{O_iO_{i+1}}$, and angle $OB_iO_i$ is a right angle. By the Pythagorean theorem, we then have
From this, it follows that $OB_1 = OB_2 = \ldots = \sqrt{Rr}$, and thus points $B_1, B_2, \ldots$ are equidistant from point $O$.
Suppose now that circles $S$ and $T$ are not concentric. Then, by the remark to the solution of problem 7, there exists a circle $K$ such that the inversion $\varphi$ with respect to $K$ maps circles $S$ and $T$ to concentric circles and the center $P$ of circle $K$ lies outside circle $S$.
Inversion $\varphi$ is a one-to-one transformation of the set of points of the plane without point $P$ and maps each circle not containing point $P$ to some circle not containing point $P$. The inverse transformation to inversion $\varphi$ is the same inversion, i.e., $\varphi(\varphi(A)) = A$ for any point $A$ different from $P$.
Circles $S$ and $T$ are then concentric, and circles $K_1, K_2, \ldots$ tangent to circles $S$ and $T$ are mapped by inversion $\varphi$ to circles $K_1$ tangent to circles $S$ and $T$. In this case, circle $T$ contains circle $S$, and point $P$ lies outside circle $T$. Moreover, circle $K_1$ is tangent to circle $K_2$, circle $K_2$ is tangent to $K_3$, etc. Since circles $S$ and $T$ are concentric, it follows from the case considered at the beginning that the points of tangency of $K_1$ with $K_2$, $K_2$ with $K_3$, etc., belong to some circle $U$ lying inside $T$. Therefore, point $P$ does not belong to $L$, and thus figure $\varphi(L)$ is a circle.
By performing inversion $\varphi$ again, we conclude that the points of tangency of circles $\varphi(K_1)$ with $\varphi(K_2)$, $\varphi(K_2)$ with $\varphi(K_3)$, etc., belong to circle $\varphi(L)$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 366 |
XXII OM - II - Problem 3
Given 6 lines in space, of which no 3 are parallel, no 3 pass through the same point, and no 3 are contained in the same plane. Prove that among these 6 lines, there are 3 lines that are mutually skew.
|
From the conditions of the problem, it follows that in every triple of the considered lines, there is a pair of skew lines. Let us associate the given lines with the vertices of a convex hexagon marked with the numbers $1, 2, \ldots, 6$ (Fig. 11). If two lines are skew, let us connect the corresponding vertices of the hexagon with a solid line, and if they are not skew, with a dashed line.
Thus, we have reduced the problem to the following: Six points are given. Each pair of them is connected by a solid or a dashed line. Moreover, every triangle with vertices belonging to the given set of points has at least one side that is a solid line. Prove that there exists a triangle whose all sides are solid lines.
Suppose there is no triangle whose all sides are solid lines. Therefore, there is a pair of points connected by a dashed line. Let this be, for example, the pair $1, 2$. Since in each of the triangles $1, 2, 3$; $1, 2, 4$; $1, 2, 5$; $1, 2, 6$ there is a side drawn with a solid line and the side $1, 2$ is not one of them, each of the points $3, 4, 5, 6$ is connected by a solid line to at least one of the points $1, 2$.
If one of the points $1, 2$ were connected by a solid line to at least three of the points $3, 4, 5, 6$, for example, point $1$ with points $3, 4, 5$, then considering the triangles $1, 3, 4$; $1, 4, 5$; $1, 3, 5$, in which two sides are drawn with solid lines, we conclude that the sides $3, 4$; $4, 5$ and $3, 5$ are drawn with dashed lines (Fig. 11). In the triangle $3, 4, 5$, none of the sides would be drawn with a solid line. This contradicts the conditions of the problem.
Therefore, each of the points $1$ and $2$ is connected by a solid line to exactly two of the points $3, 4, 5, 6$. Without loss of generality, we can assume that point $1$ is connected by a solid line to points $3$ and $4$, and point $2$ is connected by a solid line to points $5$ and $6$. Meanwhile, point $1$ is connected by a dashed line to points $5$ and $6$, and point $2$ is connected by a dashed line to points $3$ and $4$ (Fig. 12). Considering the triangle $2, 5, 6$, we conclude that points $5$ and $6$ are connected by a dashed line. Then, however, the triangle $1, 5, 6$ has all sides drawn with dashed lines. This contradicts the conditions of the problem. The obtained contradiction proves that there exists a triangle whose all sides are drawn with solid lines.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 371 |
XII OM - I - Problem 2
Prove that if $ a_1 \leq a_2 \leq a_3 $ and $ b_1 \leq b_2 \leq b_3 $, then
|
Inequality (1) will be replaced by an equivalent inequality
This, in turn, by the inequality
According to the assumption $ a_1 - a_2 \leq 0 $, $ b_1 -b_2 \leq 0 $, therefore
Hence
Similarly
And
Adding the above 3 inequalities side by side, we obtain inequality (2) equivalent to the desired inequality (1).
Note 1. A more general theorem can be proven. If
then
Indeed, inequality (4) is equivalent to the inequality
which can be easily proven by induction. This inequality is obviously true when $ n = 1 $, since $ a_1b_1 \leq a_1b_1 $; it is therefore sufficient to show that if this inequality holds for $ n \leq k $, where $ k $ is any chosen natural number, then it also holds for $ n = k + 1 $. We assert this as follows:
Note 2. Let the numbers $ a_i $ and $ b_i $ ($ i = 1, 2, \ldots,n $) satisfy condition (3) and let $ i_1,i_2, \ldots , i_n $ be any permutation (i.e., arrangement) of the numbers $ 1, 2, \ldots, n $. Then
Inequality (6) seems almost obvious; we suggest that the reader justify it precisely using induction. From inequality (6), inequality (5) can be deduced without using induction:
Note 3. The principle of mathematical induction is usually formulated in the following form.
$ Z_1 $: Let $ T (n) $ denote a statement expressing some property of the natural number $ n $. If
[a)] $ T (1) $ is true,
[b)] the truth of $ T (n) $ implies the truth of $ T (n + 1) $,
then the statement $ T (n) $ is true for every natural number $ n $.
In Note 1, we used the following form of this principle:
$ Z_2 $: Let $ S (n) $ denote a statement expressing some property of the natural number $ n $. If
[$ \alpha $)] $ S (1) $ is true,
[$ \beta $)] the truth of $ S(1), S(2), \ldots, S (n) $ implies the truth of $ S (n + 1) $,
then the statement $ S (n) $ is true for every natural number $ n $.
Both forms $ Z_1 $ and $ Z_2 $ are equivalent. Suppose, for instance, that the principle $ Z_2 $ is valid and that the statement $ T (n) $ satisfies conditions a) and b). If the truth of $ T (n) $ implies the truth of $ T (n + 1) $, then the truth of all statements $ T (1), T (2), \ldots, T (n) $ even more so implies the truth of $ T (n + 1) $, the statement $ T (n) $ thus satisfies conditions $ \alpha $) and $ \beta $), and by the principle $ Z_2 $, the statement $ T (n) $ is true for every natural $ n $, so the principle $ Z_1 $ is valid.
Conversely, suppose that the principle $ Z_1 $ is valid and that some statement $ S (n) $ satisfies conditions $ \alpha $) and $ \beta $). Let $ T (n) $ denote the statement asserting that each of the statements $ S (1), S (2), \ldots, S (n) $ holds. If $ T (n) $ is true for some natural $ n $, then by $ \beta $), $ S (n + 1) $ is true, and thus $ T (n + 1) $ is also true. Therefore, conditions a) and b) are satisfied, and by the principle $ Z_1 $, the statement $ T (n) $ is true for every natural $ n $; this means that $ S (n) $ is true for every natural $ n $, which means that the principle $ Z_2 $ is valid.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 372 |
LX OM - II - Zadanie 3
Rozłączne okręgi $ o_1 $ i $ o_2 $ o środkach odpowiednio $ I_1 $ i $ I_2 $ są styczne do prostej
$ k $ odpowiednio w punktach $ A_1 $ i $ A_2 $ oraz leżą po tej samej jej stronie. Punkt $ C $ leży na odcinku
$ I_1I_2 $, przy czym $ \meqsuredangle A_1CA_2 =90^{\circ} $. Dla $ i=1,2 $ niech $ B_i $ będzie punktem różnym od
$ A_i $, w którym prosta $ A_iC $ przecina okrąg $ o_i $. Dowieść, że prosta $ B_1B_2 $ jest styczna do okręgów
$ o_1 $ i $ o_2 $.
|
Niech prosta styczna do okręgu $ o_1 $ w punkcie $ B_1 $ przecina prostą $ A_1A_2 $ w punkcie $ D $.
(Punkt przecięcia istnieje, gdyż punkt $ C $ nie leży na prostej $ A_1I_1 $, a więc odcinek $ A_1B_1 $
nie jest średnicą okręgu $ o_1 $.) Trójkąt $ A_1B_1D $ jest wówczas równoramienny, gdyż dwa jego boki
są odcinkami stycznych do okręgu $ o_1 $ poprowadzonymi z punktu $ D $. Wobec tego prosta
$ DI_1 $ jako dwusieczna kąta $ \measuredangle A_1DB_1 $ jest prostopadła do cięciwy $ A_1B_1 $,
a więc równoległa do prostej $ CA_2 $.
Udowodnimy, że proste $ A_1B_1 $ i $ DI_2 $ są równoległe.
Jeżeli $ A_1A_2 || I_1I_2 $, to $ A_1A_2 = I_1I_2 $ i czworokąt $ I_1CA_2D $ jest równoległobokiem.
W takim razie $ CI_2 = A_1D $ i czworokąt $ CI_2DA_1 $ także jest równoległobokiem. W szczególności
więc $ A_1B_1 || DI_2 $.
Jeżeli natomiast proste $ A_1A_2 $ i $ I_1I_2 $ przecinają się w punkcie $ E $, to stosując dwukrotnie
twierdzenie Talesa do kąta $ \measuredangle A_1EI_1 $ przeciętego prostymi równoległymi $ I_1D $, $ CA_2 $
oraz $ I_1A_1 $, $ I_2A_2 $ otrzymujemy
co w połączeniu z twierdzeniem odwrotnym do twierdzenia Talesa znowu daje zależność $ A_1B_1 || DI_2 $.
Wykazana właśnie równoległość wraz z danym w treści zadania warunkiem $ \measuredangle A_1CA_2 = 90^{\circ} $
pozwala wnioskować, że proste $ DI_2 $ i $ B_2A_2 $ są prostopadłe. Zauważmy teraz, że prosta $ DI_2 $ przechodzi
przez środek okręgu $ o_2 $. W efekcie punkty $ B_2 $ i $ A_2 $ są symetryczne względem prostej $ DI_2 $
(gdyż są końcami cięciwy prostopadłej do tej prostej) oraz proste $ DB_2 $ i $ DA_2 $ są symetryczne
względem tej prostej. Skoro zaś prosta $ DA_2 $ jest styczna do okręgu $ o_2 $, to również prosta $ DB_2 $
jest doń styczna, co kończy rozwiązanie zadania.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 373 |
II OM - III - Problem 5
In a circle, a quadrilateral $ABCD$ is inscribed. Lines $AB$ and $CD$ intersect at point $E$, and lines $AD$ and $BC$ intersect at point $F$. The angle bisector of $\angle AEC$ intersects side $BC$ at point $M$ and side $AD$ at point $N$; and the angle bisector of $\angle BFD$ intersects side $AB$ at point $P$ and side $CD$ at point $Q$. Prove that quadrilateral $MPNQ$ is a rhombus.
|
Ignoring for now the condition that points $A$, $B$, $C$, $D$ lie on a circle, consider any convex quadrilateral $ABCD$ where the extensions of sides $AB$ and $CD$ intersect at point $E$, and the extensions of sides $AD$ and $BC$ intersect at point $F$.
Draw the angle bisectors $EO$ and $FO$ of angles $E$ and $F$, and the segment $EF$ as indicated in Figure 66, and consider triangles $EAF$, $ECF$, $EOF$ with the common base $EF$.
Each of the angles at the base $EF$ in triangle $EOF$ is the arithmetic mean of the angles of triangles $EAF$ and $ECF$ at the same vertex; it follows that the third angle $x$ of triangle $EOF$ is also the arithmetic mean of the remaining angles $\alpha$ and $\gamma$ of triangles $EAF$ and $ECF$:
We can reach the same conclusion in the following way:
From any point $M$ (Figure 67), draw rays $a_1$, $b_1$, $c_1$, $d_1$, $e_1$, $f_1$ having the directions of rays $a$, $b$, $c$, $d$, $e$, $f$ according to the labels in Figure 66.
Since $e_1$ is the bisector of the angle between $a_1$ and $c_1$, and $f_1$ is the bisector of the angle between $d_1$ and $b_1$, the angle between rays $e_1$ and $f_1$ is the arithmetic mean of the angle between rays $a_1$ and $d_1$ and the angle between rays $c_1$ and $b_1$, which we can write as:
However, $\measuredangle (e_1, f_1) = \measuredangle (e, f)$, $\measuredangle (a_1, d_1) = \measuredangle (a, d)$, $\measuredangle (c_1, b_1) = \measuredangle (c, b)$, thus
We have obtained, as is easily verified, the same equality as before.
Now assume that the quadrilateral $ABCD$ is inscribed in a circle (Figure 68).
In this case, $\alpha + \gamma = 180^\circ$ and the previous equality gives
This means that the diagonals of quadrilateral $MPNQ$ are perpendicular.
Notice that in this case, in triangle $PEQ$, the angle bisector $EO$ of angle $E$ is perpendicular to side $PQ$, so triangle $PEQ$ is isosceles, and point $O$ is the midpoint of segment $PQ$. Similarly, point $O$ is the midpoint of segment $MN$.
Quadrilateral $MPNQ$, whose diagonals bisect each other and are perpendicular, is therefore a rhombus, which is what we needed to prove.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 376 |
XLVI OM - II - Problem 5
The circles inscribed in the faces $ABC$ and $ABD$ of the tetrahedron $ABCD$ are tangent to the edge $AB$ at the same point. Prove that the points of tangency of these circles with the edges $AC$, $BC$ and $AD$, $BD$ lie on a single circle.
|
Let's assume that the circle inscribed in the face $ABC$ is tangent to the edges $AC$, $BC$, and $AB$ at points $P$, $Q$, and $T$, respectively, and the circle inscribed in the face $ABD$ is tangent to the edges $AD$, $BD$, and $AB$ at points $R$, $S$, and $T$ (the same point $T$, according to the assumption). We have the following equalities of tangent segments:
If point $T$ is the midpoint of edge $AB$, then triangles $ABC$ and $ABD$ are isosceles, and lines $PQ$ and $RS$ are parallel to line $AB$; points $P$ and $Q$ are symmetric with respect to the plane passing through $T$ and perpendicular to $AB$, and points $R$ and $S$ are also symmetric with respect to this plane, so segments $PQ$ and $RS$ are the bases of an isosceles trapezoid on which a circle can be circumscribed.
We further assume that point $T$ is not the midpoint of edge $AB$; without loss of generality, let's assume that $|AT| > |BT|$. Neither of the lines $PQ$ and $RS$ is parallel to $AB$. Points $A$, $B$, $P$, and $Q$ lie in the plane of face $ABC$, so line $PQ$ intersects line $AB$; let's denote the intersection point by $U$. Similarly, points $A$, $B$, $R$, and $S$ lie in the plane of face $ABD$, so line $RS$ intersects line $AB$; let's denote the intersection point by $V$.
Points $U$ and $V$ lie on the ray $AB^\to$, beyond segment $AB$; therefore,
(Figure 10 shows the arrangement of the considered points and lines separately on the plane $ABC$ and on the plane $ABD$.)
By the theorem of tangent and secant segments (applied to the circles inscribed in triangles $ABC$ and $ABD$), we have the equalities:
Now let's apply Menelaus' theorem to triangle $ABC$ intersected by line $PQ$ and to triangle $ABD$ intersected by line $RS$:
From relations (2) and (1), we get the proportions
Replacing $|AU|$ and $|AV|$ with the right-hand sides of equations (3), we obtain equations from which we calculate:
Thus, $|BU| = |BV|$. Therefore, point $U$ coincides with $V$; it is the intersection point of lines $PQ$ and $RS$.
A pair of intersecting lines defines a plane. Thus, points $P$, $Q$, $R$, and $S$ lie in the same plane. Since points $U$ and $V$ coincide, from relations (4) we obtain the equality $|UP| \cdot |UQ| = |UR| \cdot |US|$. It follows that points $P$, $Q$, $R$, and $S$ lie on the same circle.
Note 1. Menelaus' theorem was used only to derive equality (5); however, it is not necessary for this. We encourage readers to find other justifications for formulas (5).
Note 2. Once we conclude that points $P$, $Q$, $R$, and $S$ are coplanar, we can reason as follows: through the center of circle $PQT$, we draw a line perpendicular to the plane $ABC$, and through the center of circle $RST$, we draw a line perpendicular to the plane $ABD$. These lines lie in the same plane (perpendicular to $AB$ and passing through point $T$), and they are not parallel, so they intersect. From equality (1), it easily follows that the intersection point is equidistant from points $P$, $Q$, $T$, $R$, and $S$ - it is, therefore, the center of a sphere on which these points lie. The intersection of this sphere with the plane $PQRS$ gives the desired circle.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 382 |
LX OM - II - Task 1
Real numbers $ a_1, a_2, \cdots , a_n $ $ (n \geqslant 2) $ satisfy the condition
$ a_1 \geqslant a_2 \geqslant \cdots \geqslant a_n > 0 $. Prove the inequality
|
We will apply mathematical induction with respect to the value of the number $ n $.
For $ n = 2 $, the thesis of the problem is true, as both sides of the inequality are equal to $ 2a_2 $.
Moving on to the inductive step, consider the real numbers
$ a_1, a_2, \cdots, a_{n+1} $, for which $ a_1 \geqslant a_2 \geqslant \cdots \geqslant a_{n+1} > 0 $.
We need to prove the inequality
Let us introduce the notation
Then the left side of the inequality (1) can be written in the form
Applying the inductive hypothesis to $ n $ numbers $ a_2 \geqslant a_3 \geqslant \cdots \geqslant a_{n+1} \geqslant 0 $,
we obtain
Furthermore, for any real numbers $ x \geqslant y > 0 $, the double inequality
$ -x \leqslant -x + 2(x - y) = x - 2y < x $ holds, which implies $ |x - 2y| \leqslant x $, and consequently,
This means that the number $ K - L $ is non-negative. The number $ t = a_1 - a_2 $ is also non-negative, so
continuing the inequality (2) and using (3), we get
We have obtained the right side of the inequality (1), which completes the inductive proof.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 383 |
XVIII OM - II - Task 6
Prove that points $ A_1, A_2, \ldots, A_n $ ($ n \geq 7 $) lying on the surface of a sphere lie on a circle if and only if the tangent planes to the sphere at these points have a common point or are parallel to a single line.
|
a) Suppose that points $ A_1, A_2, \ldots, A_n $ on the surface of a sphere with center $ O $ lie on a circle $ k $. Let $ \alpha_1 $ denote the tangent plane to the sphere at point $ A_i $ ($ i= 1,2, \ldots, n $), and $ \pi $ - the plane of the circle $ k $.
If the center of the circle $ k $ is point $ O $, then the plane $ \alpha_i $ is perpendicular to the radius $ OA_i $, so it is perpendicular to the plane $ \pi $ containing the line $ OA_i $. Therefore, the plane $ \alpha_i $ is parallel to any line perpendicular to $ \pi $.
If, however, the center of the circle $ k $ is a point $ S $ different from $ O $ (Fig. 10), then the plane $ \pi $ is perpendicular to the line $ OS $, so in the triangle $ OSA_i $ the angle $ S $ is a right angle, and the angle $ O $ is acute, which means that the line $ OS $ intersects the plane $ \alpha_i $ at some point $ T_i $. In the triangle $ OA_iT_i $ the angle $ A_i $ is a right angle, hence the equality $ OA_i^2 = OT_i \cdot OS $ holds, therefore
The segment $ OA_i $ equals the radius of the sphere, so the segment $ OT_i $ has the same length for every $ i $, and since all points $ T_i $ lie on the same ray $ OS $, they coincide.
b) Suppose that all planes $ \alpha_i $ are parallel to a line $ l $ or all have a common point $ T $. In the first case, all segments $ OA_i $ are perpendicular to the line $ l $, so they lie in the same plane $ \pi $, which means that all points $ A_i $ lie on a circle $ k $, which is the intersection of the plane $ \pi $ with the surface of the given sphere. In the second case, the line $ TA_i $ is for each $ i $ tangent to the surface of the sphere, so it is perpendicular to the radius $ OA_i $. Let $ A_iS_i $ be the altitude of the right triangle $ OA_iT $ to the hypotenuse $ OT $; then $ OA_i^2 = OT \cdot OS_i $, hence
it follows that all segments $ OS_i $ are equal. Since all points $ S_i $ lie on the segment $ OT $, they coincide. Therefore, all segments $ A_iS_i $ lie in the same plane $ \pi $, which means that all points $ A_i $ lie on the intersection of the plane $ \pi $ with the surface of the sphere, i.e., on some circle $ k $.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 384 |
XI OM - I - Problem 11
Prove that if a quadrilateral is circumscribed around a circle, then a circle can be circumscribed around it if and only if the chords connecting the points of tangency of the opposite sides of the quadrilateral with the circle are perpendicular.
|
Let $ABCD$ be a quadrilateral inscribed in a certain circle, and let $M$, $N$, $P$, $Q$ denote the points of tangency of the sides $AB$, $BC$, $CD$, $DA$ with the inscribed circle, and let $S$ be the point of intersection of segments $MP$ and $NQ$ (Fig. 16).
Since tangents to a circle drawn from the ends of a chord form equal angles with that chord, if we denote $\measuredangle AMS = \delta$, $\measuredangle AQS = \varepsilon$, then $\measuredangle DPS = \delta$, $\measuredangle BNS = \varepsilon$, hence $\measuredangle CPS = 180^\circ - \delta$, $\measuredangle CNS = 180^\circ - \varepsilon$. Let $\measuredangle MSQ = \varphi$.
In quadrilateral $AMSQ$
and in quadrilateral $CNSP$
Adding these equalities, we get
A circle can be circumscribed around quadrilateral $ABCD$ if and only if the sums of the opposite angles are each $180^\circ$. From the last equality, it follows that $\measuredangle A + \measuredangle C = 180^\circ$ if and only if $\varphi = 90^\circ$, i.e., when the chords $MP$ and $NQ$ are perpendicular. Q.E.D.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 385 |
XXXVII OM - II - Problem 5
Prove that if a polynomial $ f $ not identically zero satisfies for every real $ x $ the equation $ f(x)f(x + 3) = f(x^2 + x + 3) $, then it has no real roots.
|
Suppose a polynomial $ f $ satisfying the given conditions has real roots. Let $ x_0 $ be the largest of them. The number $ y_0 = x_0^2 + x_0 + 3 > x_0 $ is also a root of the polynomial $ f $, because
- contrary to the fact that $ x_0 $ is the largest root. The obtained contradiction proves that $ f $ cannot have real roots.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 386 |
XXXIV OM - I - Problem 5
Prove the existence of a number $ C_0 $ with the property that for any sequence $ x_1, x_2, \ldots, x_N $ of positive numbers and for any positive number $ K $, if the number of terms $ x_j $ not less than $ K $ is not greater than $ \frac{N}{K} $, then
|
Suppose the sequence $ x_1, x_2, \ldots, x_N $ satisfies the given condition. By rearranging the terms if necessary, we can assume that $ x_1 \geq x_2 \geq \ldots \geq x_N $. We will show that $ x_j \leq N/j $ for $ j = 1, \ldots, N $. Suppose this is not the case, i.e., for some index $ m $, the inequality $ x_m > N/m $ holds. Take any number $ K $ such that $ N/m < K < x_m $. According to the assumption, the number of terms $ x_j $ greater than $ K $ is no more than $ N/K $, and thus is less than $ m $. This leads to a contradiction because $ x_1, \ldots, x_m > K $. Therefore, we have $ x_j \leq N/j $ for $ j = 1, \ldots, N $. We can now estimate the left-hand side of the inequality given in the problem:
We will prove by induction that for any natural number $ N $, the inequality $ N^N/N! < e^N $ holds, where $ e $ is the limit of the increasing sequence $ \left( \left(1+\frac{1}{n} \right) \right) $. For $ N = 1 $, the last inequality is satisfied. Assume the inequality holds for some $ N $. Then
\[
\frac{(N+1)^{N+1}}{(N+1)!} = \frac{(N+1)^N}{N!} = \frac{(N+1)^N}{N^N} \cdot \frac{N^N}{N!} < \left(1 + \frac{1}{N}\right)^N \cdot e^N < e \cdot e^N = e^{N+1},
\]
which completes the inductive proof. Continuing the estimation of the quantity $ L(N) $, we get
\[
L(N) = \sum_{j=1}^N \log x_j \leq \sum_{j=1}^N \log \left( \frac{N}{j} \right) = \sum_{j=1}^N \left( \log N - \log j \right) = N \log N - \sum_{j=1}^N \log j.
\]
We can use the inequality $ \sum_{j=1}^N \log j \geq \int_1^N \log x \, dx = N \log N - N + 1 $, so
\[
L(N) \leq N \log N - (N \log N - N + 1) = N - 1.
\]
Thus, we can take the constant $ C_0 $ to be $ \log e = 1 $.
Note. The problem statement did not specify whether the symbol $ \log $ denotes the common logarithm (base 10) or the natural logarithm (base $ e $). This does not matter. The theorem is valid for logarithms of any base greater than 1.
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 388 |
XXXVI OM - III - Problem 2
Given a square with side length 1 and positive numbers $ a_1, b_1, a_2, b_2, \ldots, a_n, b_n $ not greater than 1 such that $ a_1b_1 + a_2b_2 + \ldots + a_nb_n > 100 $. Prove that the square can be covered by rectangles $ P_i $ ($ i = 1,2,\ldots,n $) with side lengths $ a_i, b_i $ parallel to the sides of the square.
|
Let $ AB $ be the base of a square. We can assume that $ 1 \geq a_x \geq a_2 \geq \ldots \geq a_n $. On the ray $ AB^\to $, we sequentially lay down segments of lengths $ b_1, b_2, \ldots, b_k $ until we exceed point $ B $, and over each subsequent segment of length $ b_i $, we construct a rectangle whose other side has length $ a_i $. In this way, we obtain a layer of rectangles, the sum of whose areas $ S_1 $ satisfies the inequality
Next, we draw a line parallel to $ AB $ at a distance of $ a_k $ from it, intersecting the sides of the square at points $ A_1 $ and $ B_1 $, and on this line, we build the next layer of rectangles: we sequentially lay down segments of lengths $ b_{k+1}, b_{k+2}, \ldots, b_r $ until we exceed point $ B_1 $, and over each subsequent segment of length $ b_i $, we construct a rectangle whose other side has length $ a_i $. The sum $ S_2 $ of the areas of the rectangles in this layer satisfies the inequality
We continue this process until we exhaust all the numbers $ a_1b_1, \ldots, a_nb_n $. Suppose that as a result of this process, we do not cover the entire square. In that case,
On the other hand,
but
Thus,
contradicting inequality (1). Therefore, the method of arranging the rectangles described here leads to covering the given square.
Note. The number $ 100 $ given in the problem statement can be replaced by a smaller number. The solution presented here works when $ a_1b_1 + a_2b_2 + \ldots + a_nb_n \geq 6 $.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 389 |
XLV OM - I - Problem 8
Given natural numbers $ a $, $ b $, $ c $, such that $ a^3 $ is divisible by $ b $, $ b^3 $ is divisible by $ c $, and $ c^3 $ is divisible by $ a $. Prove that the number $ (a+b+c)^{13} $ is divisible by $ abc $.
|
The number $ (a + b + c)^{13} $ is the product of thirteen factors, each equal to $ a + b + c $. Multiplying these thirteen identical expressions, we obtain a sum of many (specifically $ 3^{13} $) terms of the form
It suffices to show that each such term is divisible by the product $ abc $. This is obvious when none of the exponents $ k $, $ m $, $ n $ is zero, because then $ a^kb^mc^n = abc \cdot a^{k-1}b^{m-1}c^{n-1} $. It remains to consider the case where at least one of these exponents is zero.
Since the system of assumptions is invariant under cyclic permutation of the variables ( $ a \mapsto b \mapsto c \mapsto a $ ), we do not lose generality by assuming that $ n = 0 $. The product (1) then has the form
The problem has been reduced to showing that for each such pair of exponents $ k $, $ m $, the number $ a^kb^m $ is divisible by $ abc $.
From the assumptions given in the problem, it follows that
A number of the form (2) can be written as the product of four factors (separated by dots):
In each of the above representations, the first factor is divisible by $ a $, the second by $ b $, and the third by $ c $; the fourth is a certain natural number. Thus, in each case, the product $ a^kb^m $ is a number divisible by the product $ abc $. In light of the previous remarks, this completes the proof.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 391 |
XLVII OM - III - Problem 3
Given a natural number $ n \geq 2 $ and positive numbers $ a_1, a_2, \ldots , a_n $, whose sum equals 1.
(a) Prove that for any positive numbers $ x_1, x_2, \ldots , x_n $ whose sum equals 1, the following inequality holds:
(b) Determine all systems of positive numbers $ x_1, x_2, \ldots , x_n $ whose sum equals 1 for which the above inequality becomes an equality.
Note: The symbol $ \sum_{i<j} x_i x_j $ denotes the sum of $ \binom{n}{2} $ terms corresponding to all pairs of indices $ i, j $ from the set $ \{1, 2, \ldots , n\} $ satisfying the condition $ i < j $.
|
From the given conditions ($ n \geq 2 $; $ a_i>0 $; $ \sum a_i =1 $), it follows that the numbers $ a_1, a_2, \ldots, a_n $ belong to the interval $ (0;\ 1) $. Let us assume
these are also numbers in the interval $ (0;\ 1) $. For them, the equality
holds.
Let $ x_1, x_2,\ldots, x_n $ be any real numbers whose sum is equal to $ 1 $. Then
The inequality to be proven takes the form
or, equivalently,
Using the notation (1), we get another equivalent form of the inequality to be proven:
For each index $ i \in \{1,2,\ldots,n\} $, we have the obvious inequality
We add these $ n $ inequalities side by side (expanding the squares of the differences):
We use formula (2) and the fact that $ \sum x_i=1 $, and we obtain
A simple transformation yields the inequality (3) from this.
We have thus proven the thesis (a).
From the reasoning conducted, it also immediately follows the resolution of issue (b): the inequality (3) (equivalent to the inequality given in the problem) becomes an equality if and only if each of the inequalities (4) (for $ i = 1,2, \ldots,n $) turns into an equality; that is, when $ x_i/c_i= c_i/(n - 1) $, or, according to notation (1), when
|
proof
|
Inequalities
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 392 |
XXIX OM - I - Problem 1
The sequence of numbers $ (p_n) $ is defined as follows: $ p_1 = 2 $, $ p_n $ is the largest prime divisor of the sum $ p_1p_2\ldots p_{n-1} + 1 $. Prove that the number 5 does not appear in the sequence $ (p_n) $.
|
We have $ p_1 = 2 $ and $ p_2 = 3 $, because $ p_2 $ is the largest prime divisor of the number $ p_1 + 1 = 3 $. Therefore, for $ n > 2 $, the number $ p_1p_2 \ldots p_{n-1} + 1 = 6p_3 \ldots p_n + 1 $ is not divisible by either $ 2 $ or $ 3 $. If, for some natural number $ n $, the largest prime divisor of the number $ p_1p_2 \ldots p_{n-1} + 1 $ were equal to $ 5 $, then it would be its only prime divisor, i.e., it would be equal to $ 5^r $ for some $ r \geq 1 $. Therefore,
The number $ 5^r - 1 $ is divisible by the number $ 5 - 1 = 4 $. Hence, from (1) it follows that $ p_k = 2 $ for some $ k \geq 3 $. This is impossible, because the number $ p_k $, by definition, is a divisor of the number $ p_1p_2 \ldots p_{k-1} + 1 = 2p_2 \ldots p_{k-1} + 1 $, and this number is odd.
The obtained contradiction proves that the number 5 does not appear in the sequence $ (p_n) $.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 393 |
XXXIV - III - Task 3
We consider a single-player game on an infinite chessboard based on the following rule. If two pieces are on adjacent squares and the next square is empty (the three squares being discussed lie on the same horizontal or vertical line), we can remove these pieces and place one piece on the third of these squares (which was empty).
Prove that if in the initial position the pieces fill a rectangle with a number of squares divisible by 3, then we cannot achieve a position where there is only one piece on the chessboard.
|
By introducing a coordinate system on the plane, we can assign a pair of integers to each square of the chessboard, such that two adjacent squares in the same column are assigned the numbers $(m, n)$ and $(m, n+1)$, and two adjacent squares in the same row are assigned the numbers $(m, n)$ and $(m+1, n)$. We can assign to each square of the chessboard the sum $m+n$ of its coordinates, and then the remainder of dividing $m+n$ by $3$. In this way, we divide all the squares into three sets:
Pawns placed in the initial position occupy a rectangle of dimensions $3k \times l$ or $l \times 3k$. In each row parallel to the side of length $3k$, every third pawn stands on a square belonging to $A_0$, every third on a square belonging to $A_1$, and every third on a square belonging to $A_2$ (the sums of the coordinates of consecutive squares are consecutive integers). Therefore, in the initial position, the number of pawns occupying squares belonging to $A_0$, to $A_1$, and to $A_2$ are equal. If in a certain position exactly $a_0$ pawns occupy squares from the set $A_0$, $a_1$ pawns - squares from the set $A_1$, and $a_2$ pawns - from the set $A_2$, and by making a move allowed in the game, we take away two pawns and place a third, and we do this on three squares that are adjacent in one row, then each of these squares belongs to a different set $A_0$, $A_1$, $A_2$. Thus, two of the numbers $a_0$, $a_1$, $a_2$ decrease by $1$, and the remaining number increases by $1$. Since in the initial position the numbers of pawns occupying squares from the sets $A_0$, $A_1$, $A_2$ were equal, after each series of allowed moves, the numbers of pawns occupying squares from the sets $A_0$, $A_1$, $A_2$ are numbers of the same parity. If there is only one pawn left on the chessboard, it belongs to one of the sets $A_0$, $A_1$, or $A_2$, for example, to $A_0$, and in this case the numbers $a_0 = 1$, $a_1 = 0$, $a_2 = 0$ do not have the same parity. It follows from this that it is not possible to reach a position in which only one pawn remains on the chessboard.
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 396 |
XXXV OM - I - Problem 12
In a trihedral angle $ W $, a ray $ L $ passing through its vertex is contained. Prove that the sum of the angles formed by $ L $ with the edges of $ W $ does not exceed the sum of the dihedral angles of $ W $.
|
Consider a sphere of radius 1 with its center at the vertex of a trihedral angle. The measure of each plane angle, whose sides are rays originating from the center of the sphere, is equal to the length of the corresponding arc of a great circle (the shorter of the two arcs defined by the points of intersection of the given rays with the surface of the sphere). All arcs on the surface of the sphere that we will discuss in the course of this solution will be arcs of the corresponding great circles.
om35_1r_img_6.jpg
om35_1r_img_7.jpg
The sum of the measures of the plane angles of the trihedral angle is equal to the sum of the lengths of the arcs $ AB $, $ BC $, and $ CA $, whose endpoints are the points of intersection of the edges of the trihedral angle and the surface of the sphere. The sum of the measures of the angles formed by $ L $ with the edges of the trihedral angle is equal to the sum of the lengths of the arcs $ AD $, $ BD $, and $ CD $, where $ D $ is the point of intersection of the ray $ L $ and the surface of the sphere.
The length of the arc (in accordance with the adopted convention - the arc of a great circle) connecting two points on the surface of the sphere satisfies the properties of distance (see, e.g., R. Courant, H. Robbins, What is Mathematics, Chapter VII), in particular the so-called triangle inequality.
Based on the triangle inequality, the lengths of the corresponding arcs satisfy
\[
\text{length}(AB) + \text{length}(BC) \geq \text{length}(AC)
\]
\[
\text{length}(BC) + \text{length}(CA) \geq \text{length}(AB)
\]
\[
\text{length}(CA) + \text{length}(AB) \geq \text{length}(BC)
\]
Thus, we have
\[
\text{length}(AD) + \text{length}(BD) \geq \text{length}(AB)
\]
By analogous reasoning, we can state that
\[
\text{length}(BD) + \text{length}(CD) \geq \text{length}(BC)
\]
and
\[
\text{length}(CD) + \text{length}(AD) \geq \text{length}(CA)
\]
Adding the last three inequalities side by side, we get
\[
2(\text{length}(AD) + \text{length}(BD) + \text{length}(CD)) \geq \text{length}(AB) + \text{length}(BC) + \text{length}(CA)
\]
Thus,
\[
\text{length}(AD) + \text{length}(BD) + \text{length}(CD) \geq \frac{1}{2} (\text{length}(AB) + \text{length}(BC) + \text{length}(CA))
\]
Therefore, the sum of the measures of the angles formed by $ L $ with the edges of the trihedral angle $ W $ does not exceed the sum of the measures of the plane angles of $ W $.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 397 |
V OM - I - Task 3
Prove that if in a quadrilateral $ABCD$ the equality $AB + CD = AD + BC$ holds, then the incircles of triangles $ABC$ and $ACD$ are tangent.
|
If the incircles of triangles $ABC$ and $ACD$ touch their common side $AC$ at points $M$ and $N$ respectively (Fig. 20), then according to known formulas we have
from which
If $AB + CD = AD + BC$, then from the above equality it follows that $AM = AN$, i.e., that points $M$ and $N$ coincide; both circles are tangent to the line $AC$ at the same point, so the circles are tangent to each other.
Note. The equality (1) also implies the converse theorem: if the incircles of triangles $ABC$ and $ACD$ are tangent, then $AM = AN$, hence $AB + CD = AD + BC$.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 398 |
XXI OM - I - Problem 6
Prove that a real number $ a $ is rational if and only if there exist integers $ p > n > m \leq 0 $ such that $ a + m, a + n, a + p $ form a geometric progression.
|
Let $ a $ be a rational number. We choose a natural number $ m $ such that $ a + m > 0 $. Then
where $ r $ and $ q $ are natural numbers.
Consider a geometric sequence with a common ratio of $ 1 + q $ and the first term $ \frac{r}{q} $. Thus, the subsequent terms of the sequence will be
Assuming then $ n = m + r $ and $ p = m + 2r + rq $, we conclude that $ m $, $ n $, $ p $ are integers satisfying the condition $ 0 \leq m < n < p $. Moreover, the numbers $ a + m $, $ a + n $, $ a + p $ form a geometric sequence.
Conversely, suppose that the integers $ m $, $ n $, $ p $ satisfy the condition $ 0 \leq m < n < p $ and that for some real number $ a $ the numbers $ a + m $, $ a + n $, $ a + p $ form a geometric sequence.
Let $ 1 + q $ be the common ratio of this sequence. Then
Therefore
Since $ n > m $, it follows from (1) that $ a + m \ne 0 $ and $ q \ne 0 $. Dividing (2) by (1) we get
Therefore, from (1) it follows that $ a = \frac{n-m}{q} - m $ is also a rational number.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 404 |
XXV OM - III - Task 5
Prove that if natural numbers $ n $, $ r $ satisfy the inequality $ r + 3 \leq n $, then the numbers $ \binom{n}{r} $, $ \binom{n}{r+1} $, $ \binom{n}{r+2} $, $ \binom{n}{r+3} $ are not consecutive terms of any arithmetic sequence.
|
We will first prove two lemmas.
Lemma 1. For a fixed natural number $n$, there are at most two natural numbers $k \leq n - 2$ such that the numbers $\binom{n}{k}$, $\binom{n}{k+1}$, $\binom{n}{k+2}$ are consecutive terms of an arithmetic sequence.
Proof. If the numbers $\displaystyle \binom{n}{k}, \binom{n}{k+1}, \binom{n}{k+2}$ are consecutive terms of an arithmetic sequence, then
Multiplying this equality by $\displaystyle \frac{(k+2)!(n-k)!}{n!}$, we get
This is a quadratic equation in terms of $k$. Therefore, it has at most two solutions.
Lemma 2. For a fixed natural number $n$, there is at most one natural number $k \leq n - 1$ such that $\displaystyle \binom{n}{k} = \binom{n}{k+1}$.
Proof. Multiplying the above equality on both sides by $\displaystyle \frac{(k+1)!(n-k)!}{n!}$, we get $k + 1 = n - k$. This is a first-degree equation in terms of $k$. Therefore, it has at most one solution in the set of natural numbers less than $n$.
We now proceed to solve the problem. For simplicity of notation, let us assume that $a_j = \displaystyle \binom{n}{j}$ for $j = 1, 2, \ldots, n$. Suppose that the numbers
are consecutive terms of an arithmetic sequence. By the formula $\displaystyle \binom{n}{k} = \binom{n}{n-k}$, i.e., $a_k = a_{n-k}$, the numbers $a_{n-r-3}, a_{n-r-2}, a_{n-r-1}, a_{n-r}$ are also consecutive terms of an arithmetic sequence. Therefore, we have the following three-term arithmetic sequences
From Lemma 1, the set $\{r, r + 1, n - r - 3, n - r - 2\}$ contains at most two different numbers. Since $r$ and $r + 1$ as well as $n - r - 3$ and $n - r - 2$ are consecutive natural numbers, we have $r = n - r - 3$ and $r + 1 = n - r - 2$.
Thus, $a_{r+1} = a_{n-r-2} = a_{r+2}$, meaning the arithmetic sequence (1) is constant. From Lemma 2, this is impossible.
The obtained contradiction proves that the numbers (1) are not consecutive terms of an arithmetic sequence.
Note. It can be proven that if for some natural numbers $n$ and $r$, where $r \leq n - 2$, the numbers $\displaystyle \binom{n}{r}, \binom{n}{r+1}, \binom{n}{r+2}$ are consecutive terms of an arithmetic sequence, then there exists a natural number $m \geq 3$ such that $n = m^2 - 2$ and $r = \displaystyle \frac{1}{2} (m^2 - m) - 2$ or $r = \displaystyle \frac{1}{2} (m^2 + m) - 2$.
Conversely, if the numbers $n$ and $r$ are defined by the above formulas, then the numbers $\displaystyle \binom{n}{k}, \binom{n}{k+1}, \binom{n}{k+2}$ are consecutive terms of an arithmetic sequence.
For example, taking $m = 3$ gives that the numbers $\displaystyle \binom{7}{1}, \binom{7}{2}, \binom{7}{3}$ form an arithmetic sequence.
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 408 |
XXXIX OM - II - Problem 4
Prove that for every natural number $ n $ the number $ n^{2n} - n^{n+2} + n^n - 1 $ is divisible by $ (n - 1)^3 $.
|
Let us denote:
Assume that $ n \geq 2 $, hence $ m \geq 1 $. According to the binomial formula,
where $ A $, $ B $, $ C $ are integers. We transform further:
Thus, $ N = Dm^3 = D(n - 1)^3 $, where $ D $ is an integer (this is also true for $ n = 1 $).
We have thus shown that $ N $ is divisible by $ (n - 1)^3 $.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 409 |
XLIV OM - III - Problem 2
Point $ O $ is the center of the circle $ k $ inscribed in the non-isosceles trapezoid $ ABCD $, whose longer base $ AB $ has midpoint $ M $. The shorter base $ CD $ is tangent to the circle $ k $ at point $ E $, and the line $ OM $ intersects the base $ CD $ at point $ F $. Prove that $ |DE| = |FC| $ if and only if $ |AB| = 2\cdot |CD| $.
|
Since the equality $ |DE| = |FC| $ (considered in the thesis of the problem) holds if and only if $ |DF| = |EC| $, the conditions of the assumptions and the thesis will not change when the roles of the legs $ AD $ and $ BC $ of the given trapezoid are swapped. Therefore, we can assume, without loss of generality, that $ |AD| > |BC| $; this is the situation depicted in Figure 9.
om44_3r_img_9.jpg
om44_3r_img_10.jpg
We extend the legs $ AD $ and $ BC $ to intersect at point $ S $. Let $ k $ be the incircle of triangle $ CDS $, $ K $ the point of tangency of circle $ k $ with side $ CD $, $ N $ the midpoint of side $ CD $, and $ L $ the point of tangency of circle $ k $ with base $ AB $. We have the equalities
the first of these equalities is a well-known formula expressing the distance from the point of tangency of the incircle (of a triangle) with a side to the vertex; the second is an analogous formula for the distance from the point of tangency of the excircle with the corresponding side to the vertex (note that $ k $ is the excircle of triangle $ CDS $); this formula may not be as widely known as the first equality in (1); we leave its proof to the Reader as a not difficult exercise.
Since $ N $ is the midpoint of segment $ CD $, it follows from the equalities (1) that $ |NK| = |NE| $, i.e.,
The homothety with center $ S $ and scale $ |AB|: |CD| $ maps triangle $ SCD $ to triangle $ SBA $, the incircle of the first of these triangles to the incircle of the second (i.e., circle $ k $ to circle $ k $), the point of tangency $ K $ to the point of tangency $ L $, and the midpoint $ N $ of side $ CD $ to the midpoint $ M $ of side $ AB $. Therefore,
The right triangles $ OLM $ and $ OEF $ are congruent (segments $ OL $ and $ OE $ are radii of circle $ k $, and angles $ OLM $ and $ OEF $ are equal as vertical angles). Therefore, the following equality holds:
By virtue of the relationships (3), (2), (4), and (1), we have
We obtain the equivalence
which is the thesis of the problem.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 410 |
XXXII - I - Problem 8
Given a point $ P $ inside a sphere $ S $. The transformation $ f: S\to S $ is defined as follows: for a point $ X \in S $, the point $ f(X) \in S $, $ f(X) \neq X $, and $ P\in \overline{Xf(X)} $. Prove that the image of any circle contained in $ S $ under the transformation $ f $ is a circle.
|
Let $ k $ be a circle contained in the sphere $ S $, and let $ S_1 $ be a sphere containing $ k $ and the point $ P $, $ P_1 $ be such a point that the segment $ \overline{PP_1} $ is a diameter of $ S_1 $. For every $ X \in k $, the angle $ PXP_1 $ is a right angle. Let $ X $ be the orthogonal projection of the point $ f(X) $ onto the line $ PP_1 $. The triangles $ f(X)PX $ and $ P_1PX $ are similar, so
The value of the last expression does not depend on the position of the point $ X $ on the circle $ k $ by a theorem stating that the product of the segments into which a fixed point divides the chords of a circle is constant. Therefore, for every point $ X \in k $, the projection of the point $ f(X) $ onto $ PP_1 $ is the same point. It follows that all images $ f(X) $ belong to a plane perpendicular to the line $ PP_1 $. Since these images belong to the sphere $ S $, they belong to the intersection of the sphere and the plane, i.e., to some circle $ o $. Therefore, $ f(k) \subset o $. Since, however, the transformation $ f $ is invertible, with $ f^{-1} = f $, and by analogous reasoning we determine that $ f(o) \subset k $, the circle $ o $ is the image of the circle $ k $ (and simultaneously $ k $ is the image of the circle $ o $).
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 411 |
LVIII OM - II - Problem 3
From $ n^2 $ tiles in the shape of equilateral triangles with a side of $ 1 $, an equilateral triangle with a side of $ n $ was formed. Each tile is white on one side and black on the other. A move consists of the following actions: We select a tile $ P $ that shares sides with at least two other tiles, whose visible sides have a color different from the visible side of tile $ P $. Then we flip tile $ P $ to the other side.
For each $ n\ge 2 $, determine whether there exists an initial arrangement of tiles that allows for an infinite sequence of moves.
|
Let's call a boundary segment the common side of two tiles whose visible sides have different colors. Of course, the number of boundary segments is non-negative and does not exceed the number $ m $ of all segments that are the common side of two tiles. We will investigate how the number of boundary segments changes as a result of performing an allowed move.
Each of the $ n^2 $ tiles shares common sides with at most three other tiles. Flipping a tile is allowed if at least two of these sides are boundary segments. Suppose we flip tile $ P $. Then boundary segments can only appear or disappear on the sides of tile $ P $. Moreover, a side of tile $ P $ is a boundary segment after flipping if and only if it was not a boundary segment before flipping. It follows that as a result of performing an allowed move, the number of boundary segments decreases.
In this way, we have proved that from any initial arrangement of tiles, no more than $ m $ moves can be made.
Answer: For no $ n\ge 2 $ does there exist an arrangement allowing an infinite sequence of moves.
|
proof
|
Combinatorics
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 412 |
XVI OM - III - Task 2
Prove that if the numbers $ x_1 $ and $ x_2 $ are roots of the equation
$ x^2 + px - 1 = 0 $, where $ p $ is an odd number, then for every natural $ n $ the numbers $ x_1^n + x_2^n $ and $ x_1^{n+1} + x_2^{n+1} $ are integers and relatively prime.
|
We will apply the method of induction. Since $ p $ is an odd number, the numbers
are integers and relatively prime. The theorem is thus true for $ n = 0 $.
Suppose that for some natural number $ n \geq 0 $ the numbers
are integers and relatively prime. We will prove that then $ x_1^{n+2} + x_2^{n+2} $ is an integer relatively prime to $ x_1^{n+1} + x_2^{n+1} $. Indeed, considering the equalities $ x_1 + x_2 = -p $, $ x_1x_2 = -1 $, we obtain from this
From this equality, it follows that 1) $ x_1^{n+2} + x_2^{n+2} $ is the sum of two integers, so it is an integer, 2) any common divisor of the numbers $ x_1^{n+2} + x_2^{n+2} $ and $ x_1^{n+1} + x_2^{n+1} $ is a divisor of the number $ x_1^{n} + x_2^{n} $, and thus is a common divisor of the relatively prime numbers $ x_1^{n+1} + x_2^{n+1} $ and $ x_1^{n} + x_2^{n} $, the numbers $ x_1^{n+2} + x_2^{n+2} $ and $ x_1^{n+1} + x_2^{n+1} $ are therefore relatively prime.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 414 |
LVI OM - II - Problem 4
Given is the polynomial $ W(x)=x^2+ax+b $, with integer coefficients, satisfying the condition:
For every prime number $ p $ there exists an integer $ k $ such that the numbers $ W(k) $ and $ W(k + 1) $ are divisible by $ p $. Prove that there exists an integer $ m $ for which
|
The condition $ W(m) = W(m +1) = 0 $ means that $ W(x)=(x-m)(x-m+1) $, i.e., $ W(x)=x^{2}-(2m+1)x+m^{2}+m $. Therefore, it is necessary to show that there exists an integer $ m $ such that
Let us fix a prime number $ p $. Then for some integer $ k $, the numbers
are divisible by $ p $. Therefore, the following numbers are divisible by $ p $:
The number $ E $ is determined by the coefficients of the polynomial $ W $ and does not depend on $ k $. By conducting this reasoning for each prime number $ p $, we conclude that the number $ E $ is divisible by every prime number $ p $, and consequently $ E = 0 $. This implies that the number $ a $ is odd, i.e., $ a = -2m-1 $ for some integer $ m $, and $ b= \frac{1}{4}(a^{2}-1)=m^{2}+m $.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 415 |
XXXVI OM - I - Problem 8
Prove that if $ (a_n) $ is a sequence of real numbers such that $ a_{n+2}=|a_{n+1}|-a_n $ for $ n = 1,2,\ldots $, then $ a_{k+9} = a_k $ for $ k = 1,2,\ldots $.
|
Let's consider the transformation $ F $ of the plane into itself given by the formula $ F(x,y) = (y,|y|-x) $. Let $ a $ be a positive number. Let $ I_0 $ be the segment with endpoints $ (0,-a) $ and $ (-a,0) $, let $ I_1 $ be the image of the segment $ I_0 $ under the transformation $ F $, and further, inductively, let $ I_n = F(I_{n-1}) $. The segment $ I_0 $ has the parametric representation
Acting on the point $ (x,y) = (-t, -a+t) $ with the transformation $ F $, we obtain
and therefore $ I_1 $ is a segment with the parametric representation
In the same way, we check that the subsequent sets $ I_n $ are segments with the following parametric representations (the parameter $ t $ always runs through the interval $ \langle 0;a \rangle $):
Thus, $ I_9 $ coincides with $ I_0 $. The sum of the segments $ I_0, \ldots, I_8 $ forms a closed broken line, which we will denote by $ L_a $. Interpreting the parameter $ t $ as time, we see that when the point $ P = (x,y) $ moves uniformly along the segment $ I_n $ in the direction indicated on the figure 4 by an arrow, its image $ F(P) $ moves uniformly along the segment $ I_{n+1} $. This means that the point $ F(P) $ divides the segment $ I_{n+1} $ in the same ratio in which $ P $ divides $ I_n $. From this and the observed cyclicity $ (I_9 = I_0) $, it follows that every point of the broken line $ L_a $, after applying the transformation $ F^9 $ (ninefold composition of the transformation $ F $), returns to its original position.
om36_1r_img_4.jpg
All broken lines $ L_a $ (for different values of $ a $) are similar sets on the plane, and their sum fills the entire plane except for the point $ (0,0) $, which is, of course, a fixed point of the transformation $ F $. Therefore, $ F^9 $ is the identity transformation.
From this, the thesis of the problem immediately follows: taking $ x $ and $ y $ as two consecutive terms of the sequence $ (a_n) $, we see that
and therefore $ F^9(a_n,a_{n+1}) = (a_{n+9}, a_{n+10}) $, and since $ F^9 $ is the identity, then $ a_{n+9} = a_n $.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 419 |
XX OM - I - Problem 11
In a convex quadrilateral $ABCD$, the sum of the distances from each vertex to the lines $AB$, $BC$, $CD$, $DA$ is the same. Prove that this quadrilateral is a parallelogram.
|
Let's denote the measures of the angles of a quadrilateral by $A$, $B$, $C$, $D$, and the lengths of the sides $AB$, $BC$, $CD$, $DA$ by $a$, $b$, $c$, $d$ respectively (Fig. 6).
The sum of the distances from vertex $A$ to the lines containing the sides of the quadrilateral is then $a \sin B + d \sin D$. Denoting this sum by $s$, we have
\[ a \sin B + d \sin D = s \]
and similarly
\[ b \sin C + a \sin A = s \]
\[ c \sin D + b \sin B = s \]
\[ d \sin A + c \sin C = s. \]
Solving the above system of equations for the sines of the angles of the quadrilateral, we obtain
\[ \sin A = \frac{s - c \sin D}{d} \]
\[ \sin B = \frac{s - d \sin A}{a} \]
\[ \sin C = \frac{s - a \sin B}{b} \]
\[ \sin D = \frac{s - b \sin C}{c}. \]
From the equalities (1)--(4), we get the equality
\[ \sin A + \sin C = \sin B + \sin D, \]
which we can write as
\[ \sin \frac{A+C}{2} \cos \frac{A-C}{2} = \sin \frac{B+D}{2} \cos \frac{B-D}{2}. \]
Since $A + B + C + D = 2\pi$, we have $\frac{B+D}{2} = \pi - \frac{A+C}{2}$, so $\sin \frac{A+C}{2} = \sin \frac{B+D}{2}$, and from equality (5) we get
\[ \cos \frac{A-C}{2} = \cos \frac{B-D}{2}. \]
Therefore,
\[ \frac{A-C}{2} = \pm \frac{B-D}{2} + 2k\pi, \quad k \in \mathbb{Z}. \]
Since $ \left| \frac{A-C}{2} \right| < \pi $ and $ \left| \frac{B-D}{2} \right| < \pi $, in equality (6) $k = 0$ holds, and one of the following cases occurs:
a) $\frac{A-C}{2} = \frac{B-D}{2}$; then $A + D = B + C$, so $A + D = \pi$, which implies that sides $AB$ and $DC$ are parallel and $\sin D = \sin A$. Therefore, from equalities (1) and (4) we get $a = c$.
b) $\frac{A-C}{2} = -\frac{B-D}{2}$; then $A + B = C + D$, so $A + B = \pi$, which implies that lines $AD$ and $BC$ are parallel and $\sin A = \sin B$. Therefore, from equalities (1) and (2) we get $b = d$.
We have thus shown that in the given quadrilateral, two opposite sides are parallel and equal, so the quadrilateral is a parallelogram.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 420 |
LII OM - I - Problem 5
Prove that for any natural number $ n \geq 2 $ and any prime number $ p $, the number $ n^{p^p} + p^p $ is composite.
|
If $ p $ is an odd prime, then by the identity
in which we set $ x = n^{p^{p-1}} $ and $ y = p $, the number $ n^{p^p} + p^p $ is composite. (For the above values of $ x $, $ y $, the inequalities $ x^p + y^p > x + y > 1 $ hold, so each of the factors on the right-hand side of formula (1) is greater than 1).
On the other hand, for $ p = 2 $ we get $ n^4 + 4 = (n^2 + 2n + 2)(n^2 - 2n + 2) $. Since $ n \geq 2 $, both factors are greater than $ 1 $. Hence, for $ n \geq 2 $ the number $ n^4 + 4 $ is composite.
|
proof
|
Number Theory
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 421 |
XXI OM - I - Problem 4
In a square $ABCD$ with side length 1, there is a convex quadrilateral with an area greater than $\frac{1}{2}$. Prove that this quadrilateral contains a segment of length $\frac{1}{2}$ parallel to $\overline{AB}$.
|
We draw through the vertices of a given quadrilateral lines parallel to line $AB$ (Fig. 4). In the case where these lines are different, the quadrilateral is divided into $3$ parts: a triangle with base $p$ and height $h_1$, a trapezoid with bases $p$ and $q$ and height $h_2$, and a triangle with base $q$ and height $h_3$. By assumption, the area of the quadrilateral $P$ is greater than $\frac{1}{2}$. On the other hand,
Therefore,
Hence,
Since $h_1 + h_2 \leq 1$ and $h_2 + h_3 \leq 1$, we obtain from this that $p + q \geq p(h_1 + h_2) + q(h_2 + h_3) > 1$.
Thus, at least one of the numbers $p$ and $q$ is greater than $\frac{1}{2}$.
In special positions of the given quadrilateral, the considered triangles or trapezoid may degenerate into a segment, i.e., it may be $h_1 = 0$ or $h_2 = 0$ or $h_3 = 0$. However, even in such a case, the above reasoning remains valid.
Remarks
1. This problem can be generalized to the case of any convex figures: If the area of a certain convex figure contained in square $ABCD$ with side $1$ is greater than $\frac{1}{2}$, then this figure contains a segment of length $\frac{1}{2}$ parallel to $\overline{AB}$.
2. Similarly, the theorem is also true for a non-convex quadrilateral; however, a similar theorem does not hold for a non-convex hexagon.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 422 |
XIII OM - I - Problem 4
Prove that the line symmetric to the median $CS$ of triangle $ABC$ with respect to the angle bisector of angle $C$ of this triangle divides the side $AB$ into segments proportional to the squares of the sides $AC$ and $BC$.
|
Let $ CM $ (Fig. 4) be the line symmetric to the median $ CS $ with respect to the angle bisector $ CD $ of angle $ C $ in triangle $ ABC $.
Since the areas of triangles with the same height are proportional to the bases of these triangles, therefore
From the equality $ \measuredangle ACD = \measuredangle DCB $ and $ \measuredangle MCD = \measuredangle DCS $, it follows that $ \measuredangle ACM = \measuredangle SCB $ and $ \measuredangle ACS = \measuredangle MCB $. The areas of triangles having one pair of equal angles are proportional to the products of the sides forming these angles, thus
From the equality (1) and (2), it follows that
Multiplying these equalities side by side and considering that $ SB = AS $, we obtain
which was to be proved.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 425 |
XL OM - I - Problem 7
In space, a finite set of points is given, any four of which are vertices of a tetrahedron with a volume less than or equal to 1. Prove that there exists a tetrahedron with a volume no greater than 27, containing all these points.
|
Let $ABCD$ be a tetrahedron of maximum volume among all tetrahedra whose vertices are points of the considered set. Denote by $O$ its centroid, that is, the point of intersection of four segments, each connecting a vertex of the tetrahedron with the centroid of the opposite face. It is known that the centroid of a tetrahedron divides each of these four segments in the ratio $3:1$.
Let $A'$ be the image of the tetrahedron $ABCD$ under a homothety with center $O$ and scale $-3$ ($A'$ - the image of point $A$ and so on). According to the remark made a moment ago, the centroid of each face of the tetrahedron is mapped to the opposite vertex in this homothety.
By the assumption of the problem, the volume of the tetrahedron $ABCD$ does not exceed $1$. Therefore, the volume of the tetrahedron $A'$ does not exceed $27$ (the ratio of the volumes of similar bodies equals the cube of the similarity ratio). We will show that the tetrahedron $A'$ contains all the considered points - it is thus the sought tetrahedron.
Suppose that one of these points - let's call it $P$ - lies outside the tetrahedron $A'$. Each tetrahedron is the intersection of four half-spaces obtained by dividing the entire space by the planes of the faces. If, therefore, the point $P$ does not belong to $A'$, it means that $P$ does not belong to one of these half-spaces; say, to the half-space determined by the plane $A'$. In other words, $P$ lies on the opposite side of the plane $A'$ from the point $O$. But the plane $A'$, parallel to the face $ABC$ of the tetrahedron $ABCD$, passes through its vertex $D$ (since, as noted above, the vertex $D$ is the image of the centroid of the face $ABC$ in the homothety defined at the beginning).
Hence, the distance from the point $P$ to the plane $ABC$ is greater than the distance from the point $D$ to this plane. Consequently, the volume of the tetrahedron $ABCP$ is greater than the volume of the tetrahedron $ABCD$. Yet, the tetrahedron $ABCD$ was defined as the one among all tetrahedra with vertices in the given points, whose volume is maximum.
The obtained contradiction proves that all points of the given set lie within the tetrahedron $A'$. The proof is complete.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 427 |
XVI OM - II - Task 6
Prove that there does not exist a polyhedron whose every planar section is a triangle.
|
Every vertex of a polyhedron is the common point of at least three of its edges. Let $ A $ be a vertex of the polyhedron, and segments $ AB $ and $ AC $ as well as $ AB $ and $ AD $ be edges of two faces. Let us choose points $ P $ and $ Q $ on segments $ AC $ and $ AD $, respectively, different from the endpoints of these segments, and draw through $ P $ and $ Q $ lines $ p $ and $ q $ parallel to line $ AB $. Lines $ p $ and $ q $ lie in the planes of two faces of the polyhedron, so there are segments $ p_1 $ and $ q_1 $ on them, belonging to these faces. The section of the polyhedron by the plane determined by lines $ p $ and $ q $ is not a triangle, since the boundary of this section contains two parallel segments $ p_1 $ and $ q_1 $.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 428 |
LVIII OM - II - Problem 1
The polynomial $ P(x) $ has integer coefficients. Prove that if the polynomials $ P(x) $ and $ P(P(P(x))) $ have a common real root, then they also have a common integer root.
|
Let the real number $ a $ be a common root of the polynomials $ P(x) $ and $ P(P(P(x))) $. From the equalities $ P(a)=0 $ and $ P(P(P(a)))=0 $, we obtain $ P(P(0))=0 $. The integer $ m=P(0) $ thus satisfies the conditions
which means that $ m $ is the desired common integer root.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 430 |
XLII OM - III - Problem 5
Non-intersecting circles $ k_1 $ and $ k_2 $ lie one outside the other. The common tangents to these circles intersect the line determined by their centers at points $ A $ and $ B $. Let $ P $ be any point on circle $ k_1 $. Prove that there exists a diameter of circle $ k_2 $, one end of which lies on the line $ PA $, and the other end on the line $ PB $.
|
Let the centers of circles $k_1$ and $k_2$ be denoted by $O_1$ and $O_2$, and their radii by $r_1$ and $r_2$. Points $A$ and $B$ lie on the line $O_1O_2$, and it does not matter which letter denotes which point. For the sake of clarity, let us agree that point $B$ lies on the segment $O_1O_2$, and point $A$ lies outside this segment.
Consider one of the common tangents to circles $k_1$ and $k_2$ passing through point $A$, and one of the common tangents passing through point $B$. The points of tangency of the first line with circles $k_1$ and $k_2$ are denoted by $U_1$ and $U_2$, and those of the second line by $V_1$ and $V_2$ (Figure 9 shows the situation when $r_1 < r_2$; but the entire subsequent reasoning does not change when $r_1 > r_2$ - we recommend the Reader to draw the corresponding figure).
om42_3r_img_9.jpg
From the similarity of right triangles $AU_1O_1$ and $AU_2O_2$ and the similarity of triangles $BV_1O_1$ and $BV_2O_2$, the following proportions follow:
Let $j_A$ be the homothety with center $A$ and ratio $r_2/r_1$; let $j_B$ denote the homothety with center $B$ and ratio $-r_2/r_1$. From the proportions obtained just now, it follows that
We see, therefore, that the image of circle $k_1$ under each of these homotheties is circle $k_2$.
Consider the points
which lie on circle $k_2$. Point $R$ is the image of point $Q$ under the transformation
The inverse transformation $j_A^{-1}$ (inverse to $j_A$) is a homothety with ratio $r_1/r_2$. Thus, $f$ is an isometry, and an even isometry (as the composition of two homotheties).
Circle $k_2$ is transformed by $j_A^{-1}$ into circle $k_1$: circle $k_1$ is transformed by $j_B$ into circle $k_2$. Therefore, the image of circle $k_2$ under transformation $f$ is the same circle $k_2$. Hence, $f$, as an even isometry, is a rotation about point $O_2$ by some angle.
To determine this angle, let $C_1$ and $D_1$ be the points of intersection of line $O_1O_2$ with circle $k_1$, and $C_2$ and $D_2$ the points of intersection of this line with circle $k_2$. Let us choose the notation so that the considered points lie on line $O_1O_2$ in the order: $C_1$, $O_1$, $D_1$, $B$, $D_2$, $O_2$, $C_2$. Then $j_A(D_1) = C_2$, $j_B(D_1) = D_2$, and thus $f(C_2) = D_2$.
Segment $C_2D_2$ is a diameter of circle $k_2$; rotation $f$ maps one of its endpoints to the other. Therefore, $f$ is a rotation by $180^\circ$.
We previously noted that $f$ maps point $Q$ to $R$. This means that segment $QR$ is also a diameter of circle $k_2$. Point $Q$ lies on line $PA$, and point $R$ on line $PB$. Therefore, segment $QR$ is a diameter, whose existence we needed to prove.
|
proof
|
Geometry
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 431 |
XLV OM - I - Problem 6
The function $ f: \mathbb{R} \to \mathbb{R} $ is continuous. Prove that if for every real number $ x $ there exists a natural number $ n $ such that $ (\underbrace{f \circ \ldots \circ f}_{n})(x) = 1 $, then $ f(1)=1 $.
|
We will denote by $ f^r $ the $ r $-th iterate of the function $ f $, that is, the $ r $-fold composition (superposition) $ f \circ f \circ \ldots \circ f $.
Suppose, contrary to the thesis, that $ f(1) \neq 1 $. Let $ m $ be the smallest positive integer for which the equality
holds (such a number exists by the condition of the problem). Since $ f(1) \neq 1 $, we have $ m \geq 2 $. Let $ x_0 = 1 $ and denote the value $ f(1) $ by $ x_1 $, the value $ f(x_1) $ by $ x_2 $, and so on, inductively, the value $ f(x_i) $ by $ x_{i+1} $ (for $ i = 1,2,\ldots,m - 1 $); then $ x_m = f^m(1) = 1 $. We obtain a sequence of real numbers $ x_0,x_1,\ldots,x_{m-1},x_m $ satisfying the conditions
Let $ x_k $ be the smallest, and $ x_l $ the largest among the numbers $ x_0,x_1, \ldots ,x_{m-1} $. Therefore, the inequalities
hold (indeed, strict inequalities hold here because the numbers $ x_0, x_1, \ldots, x_{m-1} $ are all different, which follows from the definition of $ m $ as the smallest number satisfying condition (1); but for the further reasoning, weak inequalities (2) are sufficient).
Consider the function $ g(x) = f(x) - x $; this is a continuous function. It takes the values
at the points $ x_k $ and $ x_l $
and
therefore, by the Darboux property, there exists a number $ c \in \langle x_k; x_l \rangle $ for which the equality $ g(c) = 0 $ holds, i.e., $ f(c) = c $. This implies that
Let us use the condition of the problem again, which states that for some $ n $ the value $ f^n(c) $ is equal to $ 1 $. We conclude that $ c = 1 $. The equality $ f(c) = c $ now asserts that $ f(1) = 1 $ - contrary to the initial assumption - and thus proves the incorrectness of this assumption. Therefore, ultimately, $ f(1)=1 $.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 436 |
XVII OM - I - Problem 6
Prove the theorem: If the coefficients $ a, b, c, d $ of the cubic equation $ ax^3 + bx^2 + cx + d = 0 $ are integers, where the number $ ad $ is odd and the number $ bc $ is even, then the equation cannot have three rational roots.
|
Suppose the given equation has three rational roots $x_1, x_2, x_3$. Let us transform the equation by introducing a new variable $y = ax$, i.e., substituting $\frac{y}{a}$ for $x$ in the equation.
We obtain the equation
whose roots are $y_1 = ax_1$, $y_2 = ax_2$, $y_3 = ax_3$. These numbers, being the products of the rational numbers $x_1$, $x_2$, $x_3$ by the integer $a$, are rational. Since in equation (1) the coefficient of the highest power of the unknown, i.e., of $y^3$, is equal to $1$, it follows from a known theorem that the rational roots of this equation, i.e., $y_1$, $y_2$, $y_3$, are integers.
According to Vieta's formulas,
From the assumption that the product $ad$ of the integers $a$ and $d$ is an odd number, it follows that $a$ and $d$, and therefore $a^2d$, are odd numbers, from which, in view of equation (4), we conclude that $y_1$, $y_2$, $y_3$ are odd. In this case, from equations (2) and (3), it follows that the numbers $b$ and $ac$ are odd, and hence the product $abc$ is an odd number. We have thus obtained a contradiction with the assumption that the number $bc$ is even. The assumption that the given equation has three rational roots is therefore false.
|
proof
|
Algebra
|
proof
|
olympiads
| false |
nlile/NuminaMath-1.5-proofs-only
|
train
| 440 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.