path
stringlengths 8
399
| content_id
stringlengths 40
40
| detected_licenses
sequence | license_type
stringclasses 2
values | repo_name
stringlengths 6
109
| repo_url
stringlengths 25
128
| star_events_count
int64 0
52.9k
| fork_events_count
int64 0
7.07k
| gha_license_id
stringclasses 9
values | gha_event_created_at
timestamp[us] | gha_updated_at
timestamp[us] | gha_language
stringclasses 28
values | language
stringclasses 1
value | is_generated
bool 1
class | is_vendor
bool 1
class | conversion_extension
stringclasses 17
values | size
int64 317
10.5M
| script
stringlengths 245
9.7M
| script_size
int64 245
9.7M
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
/havedata.ipynb | 290e36cf4dc9df367ff240b0f1bfc8ed331a640c | [] | no_license | choi97201/DartFss | https://github.com/choi97201/DartFss | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 29,404 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: py37
# language: python
# name: py37
# ---
# # 회원 보유종목 데이터
#
# ### 고은세님 요청사항: 운용팀에서 예상하는 보유 종목 이외의 다른 종목을 보유한 고객정보
# ### columns: 회원 아이디, 전략, 종목
#
# ### 02-26 추가사항
# ##### 1. 띄어씌기 여부와 상관없이 필터 가능
# ##### 2. 회원이름 추가
# ##### 3. 스프레드 시트로부터 보유종목 xlsx 파일 생성
# ##### 4. 생성된 파일의 종목명 오류 체크
# ##### 5. STRPURSTARTTIME 15:30 이상인 사람 제외
# ##### 6. A,C,E,S,U,N,G,T,SVIP6,VVIP1 전략 한에서 검색
# ##### 7. 전략명과 종목명 묶어서
# +
import cjw_maria
import pandas as pd
import datetime
host = "15.165.29.213"
user = "lt_user"
password = "De4IjOY32e7o"
db = "leaderstrading"
maria = cjw_maria.MariaDB(host, user, password, db)
sql = 'SELECT NAME, ID, ClientID, CompleteTime, StrategyName, TradingType, Status \
FROM trading_history \
ORDER BY ClientID, NAME, CompleteTime ASC;'
ordered_df = maria.showData(sql)
after_processed_df = ordered_df.drop_duplicates(subset=['NAME', 'ClientID'], keep='last')
after_processed_df.value_counts('TradingType')
have_df = after_processed_df[after_processed_df['TradingType']=='매수'].reset_index(drop=True)
have_df.drop_duplicates(subset=['ID', 'NAME'])[['ID', 'NAME']].to_csv('history_name.csv', index=False, encoding='utf-8-sig')
df = have_df[['ClientID', 'NAME', 'StrategyName']]
df['NAME'] = pd.DataFrame(df['NAME']).applymap(str.upper)['NAME']
tmp = list(df['NAME'])
df['NAME'] = [t.replace(' ','') for t in tmp]
boyoo = pd.read_excel('보유종목.xlsx', sheet_name='보유종목')
boyoo.columns = boyoo.iloc[3]
boyoo = boyoo.iloc[5:]
boyoo.columns = [c.replace(' ','') if type(c)==str else c for c in list(boyoo.columns)]
tmp = ['VVIP1', 'SVIP6', 'G', 'E', 'A', 'C', 'S', 'N', 'T', 'S\'']
cols = []
for i in range(len(boyoo.columns)):
if boyoo.columns[i] in tmp:
cols.append(boyoo.columns[i])
cols.append(boyoo.columns[i+1])
boyoo = boyoo[cols]
woonyong = []
print(list(boyoo.columns))
for i in range(0, len(list(boyoo.columns)), 2):
data = list(boyoo[boyoo.columns[i:i+2]].dropna()[boyoo.columns[i]])
for d in data:
if len(boyoo.columns[i])<=2:
woonyong.append(['Master.'+boyoo.columns[i], d])
else:
woonyong.append([boyoo.columns[i], d])
woonyong = pd.DataFrame(woonyong, columns=['전략명', '종목명'])
woonyong['종목명'] = pd.DataFrame(woonyong['종목명']).applymap(str.upper)['종목명']
tmp = list(woonyong['종목명'])
woonyong['종목명'] = [t.replace(' ','') for t in tmp]
woonyong = woonyong.reset_index(drop=True)
u_start = woonyong[woonyong['종목명']=='U'].index[0]
tmp = woonyong.iloc[u_start:].reset_index(drop=True)
for i in range(1, tmp.shape[0]):
if tmp['전략명'][i] != tmp['전략명'][i-1]:
break
woonyong = woonyong.drop(u_start)
woonyong = woonyong.drop(u_start+1)
woonyong.iloc[u_start:u_start+i-2]['전략명'] = ['Master.U'] * (i-2)
woonyong = woonyong.reset_index(drop=True)
nowtime = '보유종목'+str(datetime.datetime.now()).replace(' ', '_').replace(':', '.') + '.csv'
woonyong.to_csv(nowtime, encoding='utf-8-sig', index=False)
woonyong['종목명'] = pd.DataFrame(woonyong['종목명']).applymap(str.upper)['종목명']
tmp = list(woonyong['종목명'])
woonyong['종목명'] = [t.replace(' ','') for t in tmp]
woonyong = woonyong.reset_index(drop=True)
error_name = []
for i in range(woonyong.shape[0]):
if woonyong['종목명'][i] not in list(df.drop_duplicates('NAME')['NAME']):
error_name.append(woonyong['종목명'][i])
pd.DataFrame(error_name, columns=['종목명']).to_csv('error_name.csv', index=False, encoding='utf-8-sig')
stradegies = ['Master.A','Master.C','Master.E',
'Master.S','Master.U','Master.N',
'Master.G','Master.T','SVIP6', 'VVIP1']
indexNames = []
for i in range(woonyong['전략명'].shape[0]):
if woonyong['전략명'].iloc[i] in stradegies:
indexNames.append(i)
woonyong = woonyong.iloc[indexNames].reset_index(drop=True)
res = []
df['new'] = df['StrategyName'].astype(str) + df['NAME']
woonyong = woonyong.replace('Master.S\'', 'Master.S')
woonyong['new'] = woonyong['전략명'].astype(str) + woonyong['종목명']
for n in list(df.drop_duplicates('new')['new']):
if n not in list(woonyong['new']):
res.append(df[df['new']==n][['NAME', 'ClientID', 'StrategyName']])
df = pd.concat(res)
sql = "SELECT A.USER_ID, A.USER_NAME, B.STRPURSTARTTIME \
FROM TRM2200 AS A LEFT OUTER JOIN TRM2300 B \
ON A.SEQ = B.TRM2200_SEQ \
LEFT OUTER JOIN TRM1300 C \
ON B.TRM1300_SEQ = C.STRSEQ \
LEFT OUTER JOIN TRM1310 D \
ON D.STRSEQ = C.STRSEQ \
LEFT OUTER JOIN BASECODE E \
ON E.TOTAL_CODE = D.STRRANGECODE \
LEFT OUTER JOIN BASECODE F \
ON F.TOTAL_CODE = B.STRPURCODE \
LEFT OUTER JOIN BASECODE G \
ON G.TOTAL_CODE = B.STRSELLCODE \
LEFT OUTER JOIN BASECODE H \
ON H.TOTAL_CODE = B.STRPURVAL \
LEFT OUTER JOIN BASECODE I \
ON I.TOTAL_CODE = B.STRSELLVAL \
WHERE STRNAME='Master.G';"
clients = maria.showData(sql).drop_duplicates(subset='USER_ID', keep='last')
time_list = list(clients['STRPURSTARTTIME'])
time_list = ['0'+t if len(t)==4 else t for t in time_list]
clients['STRPURSTARTTIME'] = time_list
clients = clients[clients['STRPURSTARTTIME'] < '15:30'][['USER_ID', 'USER_NAME']]
clients.columns = ['ClientID', 'ClientName']
df = pd.merge(df, clients, on='ClientID')[['ClientID', 'ClientName', 'StrategyName', 'NAME']]
nowtime = str(datetime.datetime.now()).replace(' ', '_').replace(':', '.') + '.csv'
df.to_csv(nowtime, encoding='utf-8-sig', index=False)
# -
boyoo.columns[1:3]
# +
import cjw_maria
import pandas as pd
import datetime
from pykrx import stock
host = "15.165.29.213"
user = "lt_user"
password = "De4IjOY32e7o"
db = "leaderstrading"
maria = cjw_maria.MariaDB(host, user, password, db)
sql = "SELECT * FROM trading_history WHERE clientid='dnsdydqn4' and StrategyName='Master.C' ORDER BY Name, CompleteTime ASC;"
ordered_df = maria.showData(sql)
after_processed_df = ordered_df.drop_duplicates(subset=['Name'], keep='last')[['Name', 'ID', 'Quantity', 'AvgBuyPrice', 'Status', 'TradingType']]
after_processed_df = after_processed_df[after_processed_df['TradingType']=='매수']
std_date = '20210303'
df1 = stock.get_market_ohlcv_by_ticker(std_date)['종가']
df2 = stock.get_market_ohlcv_by_ticker(std_date, market='KOSDAQ')['종가']
df3 = stock.get_market_ohlcv_by_ticker(std_date, market='KONEX')['종가']
price_df = pd.concat([df1, df2, df3]).reset_index(drop=False).rename(columns={'티커': 'ID', '종가': 'NowPrice'})
df = pd.merge(after_processed_df, price_df, on=['ID'])
df['수익률'] = ((df['NowPrice'] - df['AvgBuyPrice'].astype('float')) / df['AvgBuyPrice'].astype('float')) * 100
df['매수금액'] = (df['Quantity'].astype('float') * df['AvgBuyPrice'].astype('float')).astype('int')
df['예수금'] = (df['Quantity'].astype('float') * df['NowPrice']).astype('int')
df[['ID', 'Name', 'AvgBuyPrice', 'Quantity', 'NowPrice', '수익률', '매수금액', '예수금']]
# -
df[['ID', 'Name', 'AvgBuyPrice', 'Quantity', 'NowPrice', '수익률', '매수금액', '예수금']].to_excel('보유종목C.xlsx', index=False, encoding='utf-8-sig')
price_df
df
type()
1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_1, variance_1)[1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_2, variance_2)[1:3])
plot_polys(ax, polys)
plot_polys(ax, polys_1)
plot_polys(ax, polys_2)
a = picture_cross.poly_union([polys, polys_1, polys_2])
a = picture_cross.multi_union(a, 3)
fill_between_lines(ax, a)
ax.plot(x, y, color=colors[0], label="p\u2080(x)", linewidth=4, alpha=0.5)
ax.plot(x_1, y_1, color=colors[1], label="p\u2081(x)", linewidth=4, alpha=0.5)
ax.plot(x_2, y_2, color=colors[2], label="p\u2082(x)", linewidth=4, alpha=0.5)
ax.plot(x_b, y_b, color=background_color, label="p(x)", linewidth=4)
ax.set_xlabel("x")
ax.set_ylabel("Dichte")
ax.legend()
fig.savefig("first_example.png")
# +
fig, (ax_0,ax_1, ax_2) = plt.subplots(3,1, sharex="row")
mu = -2
variance = 0.7
mu_1 = 0
variance_1 = 0.7
mu_2 = 2
variance_2 = .7
x, mu, sigma, a, b = get_gaussian(mu, variance)
y = stats.norm.pdf(x, mu, sigma)
polys = get_polys(x, y, 6, method="equal_value")
x_1, mu_1, sigma_1, a, b = get_gaussian(mu_1, variance_1)
y_1 = stats.norm.pdf(x_1, mu_1, sigma_1)
polys_1 = get_polys_vert(x_1, y_1, 6, colorscheme=colorsch[1], method="equal_density")
x_2, mu_2, sigma_2, a, b = get_gaussian(mu_2, variance_2)
y_2 = stats.norm.pdf(x_2, mu_2, sigma_2)
polys_2 = get_polys(x_2, y_2, 6, colorscheme=colorsch[2], method="equal_horizontal")
x_b = np.linspace(np.sum([mu, mu_1, mu_2])/3 - 12 * np.sum([sigma, sigma_1, sigma_2])/3,
np.sum([mu, mu_1, mu_2])/3 + 12 * np.sum([sigma, sigma_1, sigma_2])/3, 400)
y_b = stats.norm.pdf(x_b, *get_gaussian(mu, variance)[1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_1, variance_1)[1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_2, variance_2)[1:3])
plot_polys(ax_0, polys)
plot_polys(ax_0, polys_1)
plot_polys(ax_0, polys_2)
a = picture_cross.poly_union([polys, polys_1, polys_2])
fill_between_lines(ax_0, a)
a = picture_cross.multi_union(a, 3)
ax_0.plot(x, y, color=colors[0], label="value", linewidth=4, alpha=0.5)
ax_0.plot(x_1, y_1, color=colors[1], label="density", linewidth=4, alpha=0.5)
ax_0.plot(x_2, y_2, color=colors[2], label="horizontal", linewidth=4, alpha=0.5)
# ax.plot(x_b, y_b, color=background_color, label="p(x)", linewidth=4)
ax_0.set_ylabel("Dichte")
ax_0.legend()
mu = -2
variance = 0.2
mu_1 = 0
variance_1 = 0.2
mu_2 = 2
variance_2 = 0.2
x, mu, sigma, a, b = get_gaussian(mu, variance)
y = stats.norm.pdf(x, mu, sigma)
polys = get_polys(x, y, 6, method="equal_value")
x_1, mu_1, sigma_1, a, b = get_gaussian(mu_1, variance_1)
y_1 = stats.norm.pdf(x_1, mu_1, sigma_1)
polys_1 = get_polys_vert(x_1, y_1, 6, colorscheme=colorsch[1], method="equal_density")
x_2, mu_2, sigma_2, a, b = get_gaussian(mu_2, variance_2)
y_2 = stats.norm.pdf(x_2, mu_2, sigma_2)
polys_2 = get_polys(x_2, y_2, 6, colorscheme=colorsch[2], method="equal_horizontal")
x_b = np.linspace(np.sum([mu, mu_1, mu_2])/3 - 12 * np.sum([sigma, sigma_1, sigma_2])/3,
np.sum([mu, mu_1, mu_2])/3 + 12 * np.sum([sigma, sigma_1, sigma_2])/3, 400)
y_b = stats.norm.pdf(x_b, *get_gaussian(mu, variance)[1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_1, variance_1)[1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_2, variance_2)[1:3])
plot_polys(ax_1, polys)
plot_polys(ax_1, polys_1)
plot_polys(ax_1, polys_2)
a = picture_cross.poly_union([polys, polys_1, polys_2])
a = picture_cross.multi_union(a, 3)
fill_between_lines(ax_1, a)
ax_1.plot(x, y, color=colors[0], label="value", linewidth=4, alpha=0.5)
ax_1.plot(x_1, y_1, color=colors[1], label="density", linewidth=4, alpha=0.5)
ax_1.plot(x_2, y_2, color=colors[2], label="horizontal", linewidth=4, alpha=0.5)
# ax.plot(x_b, y_b, color=background_color, label="p(x)", linewidth=4)
ax_1.set_ylabel("Dichte")
ax_1.legend()
mu = -2
variance = 0.1
mu_1 = 0
variance_1 = 0.1
mu_2 = 2
variance_2 = 0.1
x, mu, sigma, a, b = get_gaussian(mu, variance)
y = stats.norm.pdf(x, mu, sigma)
polys = get_polys(x, y, 6, method="equal_value")
x_1, mu_1, sigma_1, a, b = get_gaussian(mu_1, variance_1)
y_1 = stats.norm.pdf(x_1, mu_1, sigma_1)
polys_1 = get_polys_vert(x_1, y_1, 6, colorscheme=colorsch[1], method="equal_density")
x_2, mu_2, sigma_2, a, b = get_gaussian(mu_2, variance_2)
y_2 = stats.norm.pdf(x_2, mu_2, sigma_2)
polys_2 = get_polys(x_2, y_2, 6, colorscheme=colorsch[2], method="equal_horizontal")
x_b = np.linspace(np.sum([mu, mu_1, mu_2])/3 - 12 * np.sum([sigma, sigma_1, sigma_2])/3,
np.sum([mu, mu_1, mu_2])/3 + 12 * np.sum([sigma, sigma_1, sigma_2])/3, 400)
y_b = stats.norm.pdf(x_b, *get_gaussian(mu, variance)[1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_1, variance_1)[1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_2, variance_2)[1:3])
plot_polys(ax_2, polys)
plot_polys(ax_2, polys_1)
plot_polys(ax_2, polys_2)
a = picture_cross.poly_union([polys, polys_1, polys_2])
a = picture_cross.multi_union(a, 3)
fill_between_lines(ax_2, a)
ax_2.plot(x, y, color=colors[0], label="value", linewidth=4, alpha=0.5)
ax_2.plot(x_1, y_1, color=colors[1], label="density", linewidth=4, alpha=0.5)
ax_2.plot(x_2, y_2, color=colors[2], label="horizontal", linewidth=4, alpha=0.5)
# ax.plot(x_b, y_b, color=background_color, label="p(x)", linewidth=4)
ax_2.set_xlabel("x")
ax_2.set_ylabel("Dichte")
ax_2.legend()
ax_0.set_xlim(-4, 4)
ax_0.set_ylim(0, 1.3)
ax_1.set_xlim(-4, 4)
ax_1.set_ylim(0, 1.3)
ax_2.set_xlim(-4, 4)
ax_2.set_ylim(0, 1.3)
ax_0.set_aspect('equal')
ax_1.set_aspect('equal')
ax_2.set_aspect('equal')
pos = ax_0.get_position()
pos2 = ax_1.get_position()
ax_1.set_position([pos.x0, pos2.y0, pos.width, pos2.height])
fig.savefig("iso_line_types.png")
# +
fig = plt.figure(figsize=(2,3)) #, sharex="row"
mu = -2
variance = 0.7
mu_1 = 0
variance_1 = 0.7
mu_2 = 2
variance_2 = .7
x, mu, sigma, a, b = get_gaussian(mu, variance)
y = stats.norm.pdf(x, mu, sigma)
polys = get_polys(x, y, 6, method="equal_value")
x_1, mu_1, sigma_1, a, b = get_gaussian(mu_1, variance_1)
y_1 = stats.norm.pdf(x_1, mu_1, sigma_1)
polys_1 = get_polys_vert(x_1, y_1, 6, colorscheme=colorsch[1], method="equal_density")
x_2, mu_2, sigma_2, a, b = get_gaussian(mu_2, variance_2)
y_2 = stats.norm.pdf(x_2, mu_2, sigma_2)
polys_2 = get_polys(x_2, y_2, 6, colorscheme=colorsch[2], method="equal_horizontal")
x_b = np.linspace(np.sum([mu, mu_1, mu_2])/3 - 12 * np.sum([sigma, sigma_1, sigma_2])/3,
np.sum([mu, mu_1, mu_2])/3 + 12 * np.sum([sigma, sigma_1, sigma_2])/3, 400)
y_b = stats.norm.pdf(x_b, *get_gaussian(mu, variance)[1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_1, variance_1)[1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_2, variance_2)[1:3])
plot_polys(ax_0, polys)
plot_polys(ax_0, polys_1)
plot_polys(ax_0, polys_2)
a = picture_cross.poly_union([polys, polys_1, polys_2])
fill_between_lines(ax_0, a)
a = picture_cross.multi_union(a, 3)
ax_0.plot(x, y, color=colors[0], label="value", linewidth=4, alpha=0.5)
ax_0.plot(x_1, y_1, color=colors[1], label="density", linewidth=4, alpha=0.5)
ax_0.plot(x_2, y_2, color=colors[2], label="horizontal", linewidth=4, alpha=0.5)
# ax.plot(x_b, y_b, color=background_color, label="p(x)", linewidth=4)
ax_0.set_ylabel("Dichte")
ax_0.legend()
mu = -2
variance = 0.2
mu_1 = 0
variance_1 = 0.2
mu_2 = 2
variance_2 = 0.2
x, mu, sigma, a, b = get_gaussian(mu, variance)
y = stats.norm.pdf(x, mu, sigma)
polys = get_polys(x, y, 6, method="equal_value")
x_1, mu_1, sigma_1, a, b = get_gaussian(mu_1, variance_1)
y_1 = stats.norm.pdf(x_1, mu_1, sigma_1)
polys_1 = get_polys_vert(x_1, y_1, 6, colorscheme=colorsch[1], method="equal_density")
x_2, mu_2, sigma_2, a, b = get_gaussian(mu_2, variance_2)
y_2 = stats.norm.pdf(x_2, mu_2, sigma_2)
polys_2 = get_polys(x_2, y_2, 6, colorscheme=colorsch[2], method="equal_horizontal")
x_b = np.linspace(np.sum([mu, mu_1, mu_2])/3 - 12 * np.sum([sigma, sigma_1, sigma_2])/3,
np.sum([mu, mu_1, mu_2])/3 + 12 * np.sum([sigma, sigma_1, sigma_2])/3, 400)
y_b = stats.norm.pdf(x_b, *get_gaussian(mu, variance)[1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_1, variance_1)[1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_2, variance_2)[1:3])
ax_1 = fig.add_subplot(1, 2, 1)
plot_polys(ax_1, polys)
plot_polys(ax_1, polys_1)
plot_polys(ax_1, polys_2)
a = picture_cross.poly_union([polys, polys_1, polys_2])
a = picture_cross.multi_union(a, 3)
fill_between_lines(ax_1, a)
ax_1.plot(x, y, color=colors[0], label="value", linewidth=4, alpha=0.5)
ax_1.plot(x_1, y_1, color=colors[1], label="density", linewidth=4, alpha=0.5)
ax_1.plot(x_2, y_2, color=colors[2], label="horizontal", linewidth=4, alpha=0.5)
# ax.plot(x_b, y_b, color=background_color, label="p(x)", linewidth=4)
ax_1.set_ylabel("Dichte")
ax_1.legend()
ax_2 = fig.add_subplot(2, 1, 2)
gau_1 = Gaussian(means=[mu_1, mu_1], cov_matrix=[[variance_1,0],[0,variance_1]])
picture
# -
from contour_visualization.Gaussian import Gaussian
from contour_visualization.MixingDistribution import MixingDistribution
mu_1 = 0
cov_matrix_1 = [[1.,0],[0,1.]]
eig_1 = [mu_1, mu_1]
mu_2 = 2
cov_matrix_2 = [[3.,0],[0,3.]]
eig_2 = [mu_2, mu_2]
x_min = -5
x_max = 5
y_min = -5
y_max = 5
gau_1 = Gaussian(eig_1, cov_matrix_1, x_min=x_min, x_max=x_max, y_min=y_min, y_max=y_max)
gau_2 = Gaussian(eig_2, cov_matrix_2, x_min=x_min, x_max=x_max, y_min=y_min, y_max=y_max)
mix_gau = MixingDistribution(gau_1, gau_2)
# +
ax_1 = plt.subplot(211)
ax_2 = plt.subplot(234)
ax_3 = plt.subplot(235, sharey=ax_2)
ax_4 = plt.subplot(236, sharey=ax_2)
# ax_1.grid(True)
ax_2.grid(True)
ax_3.grid(True)
ax_4.grid(True)
mu = -2
variance = 0.2
mu_1 = 0
variance_1 = 0.2
mu_2 = 2
variance_2 = 0.2
x, mu, sigma, a, b = get_gaussian(mu, variance)
y = stats.norm.pdf(x, mu, sigma)
polys = get_polys(x, y, 6, method="equal_value")
x_1, mu_1, sigma_1, a, b = get_gaussian(mu_1, variance_1)
y_1 = stats.norm.pdf(x_1, mu_1, sigma_1)
polys_1 = get_polys_vert(x_1, y_1, 6, colorscheme=colorsch[1], method="equal_density")
x_2, mu_2, sigma_2, a, b = get_gaussian(mu_2, variance_2)
y_2 = stats.norm.pdf(x_2, mu_2, sigma_2)
polys_2 = get_polys(x_2, y_2, 6, colorscheme=colorsch[2], method="equal_horizontal")
x_b = np.linspace(np.sum([mu, mu_1, mu_2])/3 - 12 * np.sum([sigma, sigma_1, sigma_2])/3,
np.sum([mu, mu_1, mu_2])/3 + 12 * np.sum([sigma, sigma_1, sigma_2])/3, 400)
y_b = stats.norm.pdf(x_b, *get_gaussian(mu, variance)[1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_1, variance_1)[1:3]) + stats.norm.pdf(x_b, *get_gaussian(mu_2, variance_2)[1:3])
plot_polys(ax_1, polys)
plot_polys(ax_1, polys_1)
plot_polys(ax_1, polys_2)
a = picture_cross.poly_union([polys, polys_1, polys_2])
a = picture_cross.multi_union(a, 3)
fill_between_lines(ax_1, a)
names = ["Eqidistant", "Quantile", "Horizontal"]
ax_1.plot(x, y, color=colors[0], label=names[0], linewidth=4, alpha=0.5)
ax_1.plot(x_1, y_1, color=colors[1], label=names[1], linewidth=4, alpha=0.5)
ax_1.plot(x_2, y_2, color=colors[2], label=names[2], linewidth=4, alpha=0.5)
ax_1.set_ylabel("Dichte")
ax_1.legend()
cov_matrix = [[0.2,0],[0,0.2]]
gau = Gaussian(means=[mu_1, mu_1], cov_matrix=cov_matrix)
ax_2.set_title(names[0])
ax_3.set_title(names[1])
ax_4.set_title(names[2])
picture_plot.plot_image(ax_2, [mix_gau], contours=True, contour_method="equal_value")
picture_plot.plot_image(ax_3, [mix_gau], contours=True, contour_method="equal_density", contour_colorscheme = color_schemes.get_colorbrewer_schemes()[1:])
picture_plot.plot_image(ax_4, [mix_gau], contours=True, contour_method="equal_horizontal", contour_colorscheme = color_schemes.get_colorbrewer_schemes()[2:])
ax_1.set_xlim(-4, 4)
ax_1.set_ylim(0, 1.3)
ax_1.set_aspect('equal')
plt.savefig("iso_line_types.png")
# -
# horizontal density --> nur limitierte anzahl an kanten --> alle im peak, der rest ist nicht dargestellt --> informationsverlust
| 18,817 |
/predictCustomerChurn/Notebooks/TelcoChurn_DSX_Cloud.ipynb | 834b5791a78552580defebf7f84946e8dccb9b8d | [] | no_license | seby408/DSX-DemoCenter | https://github.com/seby408/DSX-DemoCenter | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 204,178 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python [Root]
# language: python
# name: Python [Root]
# ---
# ## Predicting Customer Churn in Telco
# In this notebook you will learn how to build a predictive model with Spark machine learning API (SparkML) and deploy it for scoring in Machine Learning (ML).
#
# This notebook walks you through these steps:
# - Build a model with SparkML API
# - Save the model in the ML repository
# - Create a Deployment in ML (via UI)
# - Test the model (via UI)
# - Test the model (via REST API)
# ### Use Case
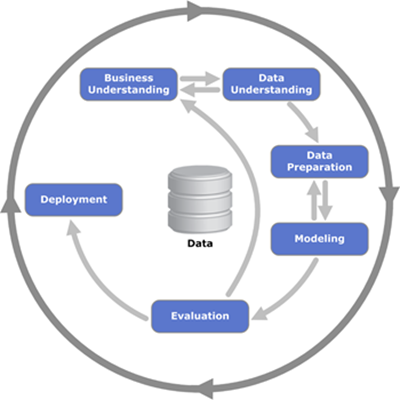
# The analytics use case implemented in this notebook is telco churn. While it's a simple use case, it implements all steps from the CRISP-DM methodolody, which is the recommended best practice for implementing predictive analytics.
# 
#
# The analytics process starts with defining the business problem and identifying the data that can be used to solve the problem. For Telco churn, we use demographic and historical transaction data. We also know which customers have churned, which is the critical information for building predictive models. In the next step, we use visual APIs for data understanding and complete some data preparation tasks. In a typical analytics project data preparation will include more steps (for example, formatting data or deriving new variables).
#
# Once the data is ready, we can build a predictive model. In our example we are using the SparkML Random Forrest classification model. Classification is a statistical technique which assigns a "class" to each customer record (for our use case "churn" or "no churn"). Classification models use historical data to come up with the logic to predict "class", this process is called model training. After the model is created, it's usually evaluated using another data set.
#
# Finally, if the model's accuracy meets the expectations, it can be deployed for scoring. Scoring is the process of applying the model to a new set of data. For example, when we receive new transactional data, we can score the customer for the risk of churn.
#
# We also developed a sample Python Flask application to illustrate deployment: http://predictcustomerchurn.mybluemix.net/. This application implements the REST client call to the model.
# ### Working with Notebooks
# If you are new to Notebooks, here's a quick overview of how to work in this environment.
#
# 1. To run the notebook, it must be in the Edit mode. If you don't see the menu in the notebook, then it's not in the edit mode. Click on the pencil icon.
# 2. The notebook has 2 types of cells - markdown (text) and code.
# 3. Each cell with code can be executed independently or together (see options under the Cell menu). When working in this notebook, we will be running one cell at a time because we need to make code changes to some of the cells.
# 4. To run the cell, position cursor in the code cell and click the Run (arrow) icon. The cell is running when you see the * next to it. Some cells have printable output.
# 5. Work through this notebook by reading the instructions and executing code cell by cell. Some cells will require modifications before you run them.
# ### Step 1: Add Data to Project and Load Into Notebook as Spark DataFrames
#
#
# 1 - **Download** the 2 data sets needed for this demo from these links:
#
# - Customer Data (Features) - https://ibm.box.com/s/i1uhwjm3ce43ou5qc5odcithrqmvdxof
# - Churn Flag Data (Labels) - https://ibm.box.com/s/1eblljquzufv3bxn6heu93mv3dorjtdf
# <br>
#
#
# 2 - Click on the 1001 image in the top right to open the data tab and **drag your files there to load** in the project.
#
# <img src="https://github.com/IBMDataScience/DSX-DemoCenter/blob/master/predictCustomerChurn/static/img/1001.png?raw=true" width = 50>
#
#
# 3 - Click in the cells below to **insert the `churn` and `customer` data sets as SparkSession DataFrames**
#
# <img src="https://github.com/IBMDataScience/DSX-DemoCenter/blob/master/predictCustomerChurn/static/img/insert_sparksession.png?raw=true" width = 250>
#
# Note that now that you have added these datasets to your project, other notebooks in your project will be able to use these datasets as well.
#
# With your cursor in the cell below, select `insert to code for customer.csv`
#
# **Important: Rename the `df_data_X` variable in the auto-generated code to `customer`**
#
# The .take(5) function shows the first 5 rows of the DataFrame.
#
# Put your cursor in the cell below, select `insert to code for churn.csv`
#
# **Important: Rename the `df_data_X` variable in the auto-generated code to `customer_churn`**
#
# The .take(5) function shows the first 5 rows of the DataFrame.
#
# If the these steps ran successfully (you saw output for each dataset), then continue reviewing the notebook and running each code cell step by step. Note that not every cell has a visual output. The cell is still running if you see a * in the brackets next to the cell.
#
# If you were not able to load in both datasets into the notebook successfully, please check with the instructor.
# ### Step 3: Merge Files
data=customer.join(customer_churn,customer['ID']==customer_churn['ID']).select(customer['*'],customer_churn['CHURN'])
# If you are having issues running the cell above, check to see that you remembered to rename the auto-generated variables to `customer` and `customer_churn`.
# ### Step 4: Rename some columns
# This step is to remove spaces from columns names, it's an example of data preparation that you may have to do before creating a model.
data = data.withColumnRenamed("Est Income", "EstIncome").withColumnRenamed("Car Owner","CarOwner")
data.toPandas().head()
# ### Step 5: Data understanding
# Data preparation and data understanding are the most time-consuming tasks in the data mining process. The data scientist needs to review and evaluate the quality of data before modeling.
#
# Visualization is one of the ways to reivew data.
#
# The Brunel Visualization Language is a highly succinct and novel language that defines interactive data visualizations based on tabular data. The language is well suited for both data scientists and business users.
# More information about Brunel Visualization: https://github.com/Brunel-Visualization/Brunel/wiki
#
# Try Brunel visualization here: http://brunel.mybluemix.net/gallery_app/renderer
import brunel
df = data.toPandas()
# %brunel data('df') bar x(CHURN) y(EstIncome) mean(EstIncome) color(LocalBilltype) stack tooltip(EstIncome) | x(LongDistance) y(Usage) point color(Paymethod) tooltip(LongDistance, Usage) :: width=1100, height=400
# **PixieDust** is a Python Helper library for Spark IPython Notebooks. One of it's main features are visualizations. You'll notice that unlike other APIs which produce just output, PixieDust creates an **interactive UI** in which you can explore data.
#
# More information about PixieDust: https://github.com/ibm-cds-labs/pixiedust?cm_mc_uid=78151411419314871783930&cm_mc_sid_50200000=1487962969
# + pixiedust={"displayParams": {"aggregation": "SUM", "chartsize": "50", "handlerId": "barChart", "keyFields": "Paymethod,International", "rendererId": "matplotlib", "rowCount": "500", "title": "Test", "valueFields": "Usage"}}
from pixiedust.display import *
display(data)
# -
# ### Step 6: Build the Spark pipeline and the Random Forest model
# "Pipeline" is an API in SparkML that's used for building models.
# Additional information on SparkML: https://spark.apache.org/docs/2.0.2/ml-guide.html
# +
from pyspark.ml.feature import OneHotEncoder, StringIndexer, VectorIndexer, IndexToString
from pyspark.ml import Pipeline
from pyspark.ml.feature import VectorAssembler
from pyspark.ml.classification import RandomForestClassifier
# Prepare string variables so that they can be used by the decision tree algorithm
# StringIndexer encodes a string column of labels to a column of label indices
SI1 = StringIndexer(inputCol='Gender', outputCol='GenderEncoded')
SI2 = StringIndexer(inputCol='Status',outputCol='StatusEncoded')
SI3 = StringIndexer(inputCol='CarOwner',outputCol='CarOwnerEncoded')
SI4 = StringIndexer(inputCol='Paymethod',outputCol='PaymethodEncoded')
SI5 = StringIndexer(inputCol='LocalBilltype',outputCol='LocalBilltypeEncoded')
SI6 = StringIndexer(inputCol='LongDistanceBilltype',outputCol='LongDistanceBilltypeEncoded')
labelIndexer = StringIndexer(inputCol='CHURN', outputCol='label').fit(data)
#Apply OneHotEncoder so categorical features aren't given numeric importance
OH1 = OneHotEncoder(inputCol="GenderEncoded", outputCol="GenderEncoded"+"classVec")
OH2 = OneHotEncoder(inputCol="StatusEncoded", outputCol="StatusEncoded"+"classVec")
OH3 = OneHotEncoder(inputCol="CarOwnerEncoded", outputCol="CarOwnerEncoded"+"classVec")
OH4 = OneHotEncoder(inputCol="PaymethodEncoded", outputCol="PaymethodEncoded"+"classVec")
OH5 = OneHotEncoder(inputCol="LocalBilltypeEncoded", outputCol="LocalBilltypeEncoded"+"classVec")
OH6 = OneHotEncoder(inputCol="LongDistanceBilltypeEncoded", outputCol="LongDistanceBilltypeEncoded"+"classVec")
# Pipelines API requires that input variables are passed in a vector
assembler = VectorAssembler(inputCols=["GenderEncodedclassVec", "StatusEncodedclassVec", "CarOwnerEncodedclassVec", "PaymethodEncodedclassVec", "LocalBilltypeEncodedclassVec", \
"LongDistanceBilltypeEncodedclassVec", "Children", "EstIncome", "Age", "LongDistance", "International", "Local",\
"Dropped","Usage","RatePlan"], outputCol="features")
# +
# instantiate the algorithm, take the default settings
rf=RandomForestClassifier(labelCol="label", featuresCol="features")
# Convert indexed labels back to original labels.
labelConverter = IndexToString(inputCol="prediction", outputCol="predictedLabel", labels=labelIndexer.labels)
pipeline = Pipeline(stages=[SI1,SI2,SI3,SI4,SI5,SI6,labelIndexer, OH1, OH2, OH3, OH4, OH5, OH6, assembler, rf, labelConverter])
# -
# Split data into train and test datasets
train, test = data.randomSplit([0.8,0.2], seed=6)
train.cache()
test.cache()
# Build models
model = pipeline.fit(train)
# ### Step 7: Score the test data set
results = model.transform(test)
results=results.select(results["ID"],results["CHURN"],results["label"],results["predictedLabel"],results["prediction"],results["probability"])
results.toPandas().head(6)
# ### Step 8: Model Evaluation
print 'Precision model1 = {:.2f}.'.format(results.filter(results.label == results.prediction).count() / float(results.count()))
# +
from pyspark.ml.evaluation import BinaryClassificationEvaluator
# Evaluate model
evaluator = BinaryClassificationEvaluator(rawPredictionCol="prediction", labelCol="label", metricName="areaUnderROC")
print 'Area under ROC curve = {:.2f}.'.format(evaluator.evaluate(results))
# -
# We have finished building and testing a predictive model. The next step is to deploy it. In production environment the model can be deployed for batch or real time scoring. The following steps explain how to deploy a model for real time scoring.
# ### Step 9: Save Model in ML repository
# ** You need to have a Bluemix account and create a WML service to complete the rest of the steps. If you don't have the account, please ask the instructor to show a demo.
#
# In this section you will store your model in the Watson Machine Learning (WML) repository by using Python client libraries.
# * <a href="https://console.ng.bluemix.net/docs/services/PredictiveModeling/index.html">WML Documentation</a>
# * <a href="http://watson-ml-api.mybluemix.net/">WML REST API</a>
# * <a href="https://watson-ml-staging-libs.mybluemix.net/repository-python/">WML Repository API</a>
# <br/>
#
# First, you must import client libraries.
from repository.mlrepositoryclient import MLRepositoryClient
from repository.mlrepositoryartifact import MLRepositoryArtifact
# Put your authentication information from your instance of the Watson Machine Learning service in <a href="https://console.ng.bluemix.net/dashboard/apps/" target="_blank">Bluemix</a> in the next cell. You can find your information in the **Service Credentials** tab of your service instance in Bluemix.
#
# 
#
# <span style="color:red">Replace the service_path and credentials with your own information</span>
#
# service_path=[your url]<br/>
# instance_id=[your instance_id]<br/>
# username=[your username]<br/>
# password=[your password]<br/>
# @hidden_cell
service_path = 'https://ibm-watson-ml.mybluemix.net'
instance_id = 'sMxnUcPTRtnQzm5uLOzMHEGL6p3pfERZdSnON3f2s4WwGq/qkYCXXmzVE20w4MO8HxGxQ3pIogjgEOjN0TGDTcL0h32gVzPkwMbmHXNpi+FQYUqQmv73SQJrb1WXWeZv'
username = 'fef42c4e-cf59-4df7-8a95-98ebf29b13bf'
password = '21309f7f-9b36-4b39-95ff-99559066d654'
# Authorize the repository client
ml_repository_client = MLRepositoryClient(service_path)
ml_repository_client.authorize(username, password)
# Create the model artifact and save it in the repository.
#
# <b>Tip:</b> The MLRepositoryArtifact method expects a trained model object, training data, and a model name. (It is this model name that is displayed by the Watson Machine Learning service).
#
# +
model_artifact = MLRepositoryArtifact(model, training_data=train, name="Predict Customer Churn")
saved_model = ml_repository_client.models.save(model_artifact)
# Print the saved model properties
print "modelType: " + saved_model.meta.prop("modelType")
print "creationTime: " + str(saved_model.meta.prop("creationTime"))
print "modelVersionHref: " + saved_model.meta.prop("modelVersionHref")
print "label: " + saved_model.meta.prop("label")
# -
# ### Step 10: Deploy and Test model with UI
# 1. Save the notebook and switch to the **Analytic Assets** tab of the project (hint: open with another tab in your browser).
# 2. Under **Models**, find and click into your deployed model. Add an **Online deployment** and use the the **Test API** option to test the model.
#
# You can use the following data for testing: ID=99, Gender=M, Status=S, Children=0, Est Income=60000, Car Owner=Y, Age=34, LongDistance=68, International=50, Local=100, Dropped=0, Paymethod=CC, LocalBilltype=Budget, LongDistanceBilltype=Intnl_discount, Usage=334, RatePlan=3
# The results of the test is displayed as follows:<br/>
# <img style="float: left;" src="https://github.com/yfphoon/dsx_local/blob/master/images/Test_Model.png?raw=true" alt="Test API" width=900 />
# ### Summary
# You have finished working on this hands-on lab. In this notebook you created a model using SparkML API, deployed it in Machine Learning service for online (real time) scoring and tested it using a test client.
#
# Created by **Sidney Phoon** and **Elena Lowery**
# <br/>
# yfphoon@us.ibm.com
# elowery@us.ibm.com
# <br/>
# July 25, 2017
| 15,100 |
/Part 3 - A slightly More Complex Agent Based Model.ipynb | 8fb592d9ef70c17057b0363fd1fbd31082e93826 | [] | no_license | vinodratre/Tutorial_Agent_Based_Models | https://github.com/vinodratre/Tutorial_Agent_Based_Models | 0 | 1 | null | 2019-07-29T04:48:51 | 2019-07-26T20:01:14 | null | Jupyter Notebook | false | false | .py | 130,334 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Machine learning with scikit-learn
# *The following materials (including text, code, and figures) were adapted from the "SciPy 2017 Scikit-learn Tutorial" by Alexandre Gramfort and Andreas Mueller. The contents of their tutorial are licensed under Creative Commons CC0 1.0 Universal License as work dedicated to the public domain, and can be found at https://github.com/amueller/scipy-2017-sklearn.*
# ## What is Machine Learning?
# Machine learning is the process of extracting knowledge from data automatically, usually with the goal of making predictions on new, unseen data. Put another way, you are giving samples of data to the machine, which tries to infer observations from the data.
#
# Two key concepts:
# - **automating decision making** from data **without the user specifying explicit rules** for how this decision should be made
# - **generalization**: the goal of a machine learning model is to predict on new, previously unseen data
#
# The data is usually presented to the algorithm as a two-dimensional array (or matrix) of numbers. Each data point (also known as a *sample* or *training instance*) is represented as a list of numbers, a so-called feature vector, and the features that comprise the vector represent the properties of this point.
#
# For instance, we can represent a dataset consisting of 150 samples and 4 features as a 2-dimensional array or matrix $\mathbb{R}^{150 \times 4}$ in the following format:
#
#
# $$\mathbf{X} = \begin{bmatrix}
# x_{1}^{(1)} & x_{2}^{(1)} & x_{3}^{(1)} & \dots & x_{4}^{(1)} \\
# x_{1}^{(2)} & x_{2}^{(2)} & x_{3}^{(2)} & \dots & x_{4}^{(2)} \\
# \vdots & \vdots & \vdots & \ddots & \vdots \\
# x_{1}^{(150)} & x_{2}^{(150)} & x_{3}^{(150)} & \dots & x_{4}^{(150)}
# \end{bmatrix}.
# $$
#
# (The superscript denotes the *i*th row, and the subscript denotes the *j*th feature, respectively.
# Data in scikit-learn, with very few exceptions, is assumed to be stored as a
# **two-dimensional array**, of shape `[n_samples, n_features]`.
#
# - **n_samples:** The number of samples: each sample is an item to process (e.g. classify).
# A sample can be a document, a picture, a sound, a video, an astronomical object,
# a row in database or CSV file,
# or whatever you can describe with a fixed set of quantitative traits.
# - **n_features:** The number of features or distinct traits that can be used to describe each
# item in a quantitative manner. Features are generally real-valued, but may be Boolean or
# discrete-valued in some cases.
#
# The number of features must be fixed in advance. However it can be very high dimensional
# (e.g. millions of features) with most of them being "zeros" for a given sample. This is a case
# where `scipy.sparse` matrices can be useful, in that they are
# much more memory-efficient than NumPy arrays.
# There are two kinds of machine learning we will talk about today: ***supervised learning*** and ***unsupervised learning***.
# ### Supervised Learning: Classification and regression
#
# In **Supervised Learning**, we have a dataset consisting of both input features (observed quantities) and a desired output (what we want to determine).
#
# Some examples are:
#
# - Given a photograph of a person, identify the person in the photo.
# - Given a list of movies a person has watched and their personal ratings
# of the movies, recommend a list of movies they would like.
# - Given a persons age, education and position, infer their salary.
#
# Supervised learning is further broken down into two categories, **classification** and **regression**:
#
# - **In classification, the label is discrete**, such as "spam" or "no spam" for an email.
#
# - **In regression, the label is continuous** (a float output).
#
# In supervised learning, there is always a distinction between a **training set** for which the desired outcome (a certain label or class) is given, and a **test set** for which the desired outcome needs to be inferred. The learning model fits the predictive model to the training set, and we use the test set to evaluate its generalization performance.
#
# ### Unsupervised Learning
#
# In **Unsupervised Learning** there is no desired output associated with the data.
# Instead, we are interested in extracting some form of knowledge or model from the given data.
# In a sense, you can think of unsupervised learning as a means of discovering labels from the data itself.
#
# Unsupervised learning comprises tasks such as *dimensionality reduction*, *clustering*, and
# *anomaly detection*. Some unsupervised learning problems are:
#
# - Given detailed observations of distant galaxies, determine which features or combinations of
# features best summarize the information.
# - Given a large collection of news articles, find recurring topics inside these articles.
# - Given a video, isolate a moving object and categorize in relation to other moving objects which have been seen.
#
# Sometimes the two types of learning may even be combined: e.g. unsupervised learning can be used to find useful
# features in heterogeneous data, and then these features can be used within a supervised
# framework.
# ### (simplified) Machine learning taxonomy
#
# <img src="Figures/ml_taxonomy.png" width="80%">
# ### A Simple Example: The Iris Dataset
# As an example of a simple dataset, we're going to take a look at the iris dataset stored by scikit-learn.
# The data consists of measurements of three different iris flower species. There are three different species of iris
# in this particular dataset: Iris-Setosa, Iris-Versicolor, and Iris-Virginica.
#
# The data consist of the following:
#
# - Features in the Iris dataset:
#
# 1. sepal length in cm
# 2. sepal width in cm
# 3. petal length in cm
# 4. petal width in cm
#
# - Target classes to predict:
#
# 1. Iris Setosa
# 2. Iris Versicolour
# 3. Iris Virginica
# ``scikit-learn`` embeds a copy of the iris CSV file along with a helper function to load it into numpy arrays:
# +
## CODE CELL 1
from sklearn.datasets import load_iris
iris = load_iris()
# -
# The resulting dataset is a ``Bunch`` object; you can see what's available using
# the method ``keys()``:
# +
## CODE CELL 2
iris.keys()
# -
# The features of each sample flower are stored in the ``data`` attribute of the dataset:
# +
## CODE CELL 3
n_samples, n_features = iris.data.shape
print('Number of samples:', n_samples)
print('Number of features:', n_features)
# the sepal length, sepal width, petal length and petal width of the first sample (first flower)
print(iris.data[0])
# -
# The information about the class of each sample is stored in the ``target`` attribute of the dataset:
# +
## CODE CELL 4
print('Target array shape:', iris.target.shape)
print('\nTarget array:', iris.target)
# +
## CODE CELL 5
import numpy as np
np.bincount(iris.target)
# -
# Using the NumPy's bincount function (above), we can see that the classes are distributed uniformly in this dataset - there are 50 flowers from each species, where
#
# - class 0: Iris-Setosa
# - class 1: Iris-Versicolor
# - class 2: Iris-Virginica
# These class names are stored in the last attribute, namely ``target_names``:
# +
## CODE CELL 6
print(iris.target_names)
# -
# This data is four dimensional, but we can visualize one or two of the dimensions
# at a time using a simple histogram. Again, we'll start by enabling
# matplotlib inline mode:
# +
## CODE CELL 7
# %matplotlib inline
import matplotlib.pyplot as plt
# +
## CODE CELL 8
x_index = 3
colors = ['red', 'blue', 'magenta']
for label, color in zip(range(len(iris.target_names)), colors):
plt.hist(iris.data[iris.target==label, x_index],
label=iris.target_names[label],
color=color)
plt.xlabel(iris.feature_names[x_index])
plt.legend(loc='upper right')
plt.show()
# -
# ## Training and Testing Data
#
# To evaluate how well our supervised models generalize, we can split our data into a training and a test set. Below, we use 50% of the data for training, and 50% for testing. Other splits - such as 2/3 training and 1/3 test - could also be used. The most important thing is to fairly evaluate your system on data it *has not* seen during training!
# +
## CODE CELL 9
from sklearn.model_selection import train_test_split
X, y = iris.data, iris.target
train_X, test_X, train_y, test_y = train_test_split(X, y,
train_size=0.5,
test_size=0.5,
random_state=123)
print("Labels for training and testing data")
print(train_y)
print(test_y)
# -
# **Tip: Stratified Split**
#
# Especially for relatively small datasets, it's better to stratify the split. Stratification means that we maintain the original class proportion of the dataset in the test and training sets. For example, after we randomly split the dataset as shown in the previous code example, we have the following class proportions in percent:
# +
## CODE CELL 10
print('All:', np.bincount(y) / float(len(y)) * 100.0)
print('Training:', np.bincount(train_y) / float(len(train_y)) * 100.0)
print('Test:', np.bincount(test_y) / float(len(test_y)) * 100.0)
# -
# So, in order to stratify the split, we can pass the label array as an additional option to the `train_test_split` function:
# +
## CODE CELL 11
train_X, test_X, train_y, test_y = train_test_split(X, y,
train_size=0.5,
test_size=0.5,
random_state=123,
stratify=y)
print('All:', np.bincount(y) / float(len(y)) * 100.0)
print('Training:', np.bincount(train_y) / float(len(train_y)) * 100.0)
print('Test:', np.bincount(test_y) / float(len(test_y)) * 100.0)
# -
# **Cross-validation**
# A common way to use more of the data to build a model, but also get a more robust estimate of the generalization performance, is cross-validation.
# In cross-validation, the data is split repeatedly into a training and non-overlapping test-sets, with a separate model built for every pair. The test-set scores are then aggregated for a more robust estimate.
#
# The most common way to do cross-validation is k-fold cross-validation, in which the data is first split into k (often 5 or 10) equal-sized folds, and then for each iteration, one of the k folds is used as test data, and the rest as training data:
# <img src="figures/cross_validation.svg" width="50%">
# This way, each data point will be in the test-set exactly once, and we can use all but a k'th of the data for training. The ``sklearn.model_selection`` module has all functions related to cross validation. For example, we can use the Stratified K-Folds cross-validator:
# +
## CODE CELL 12
from sklearn.model_selection import StratifiedKFold
# +
## CODE CELL 13
cv = StratifiedKFold(n_splits=5)
for train, test in cv.split(iris.data, iris.target):
print(test)
# -
# As you can see, there are some samples from the beginning, some from the middle, and some from the end, in each of the folds.
# This way, the class ratios are preserved. Let's visualize the split:
# +
## CODE CELL 14
def plot_cv(cv, features, labels):
masks = []
for train, test in cv.split(features, labels):
mask = np.zeros(len(labels), dtype=bool)
mask[test] = 1
masks.append(mask)
plt.matshow(masks, cmap='gray_r')
plot_cv(StratifiedKFold(n_splits=5), iris.data, iris.target)
# -
# For more information and to see other cross-validation techniques in scikit-learn, check out the documentation: http://scikit-learn.org/stable/modules/cross_validation.html.
# ## Supervised Learning: Classification Examples
# To visualize the workings of machine learning algorithms, it is often helpful to study two-dimensional or one-dimensional data, that is, data with only one or two features. While in practice, datasets usually have many more features, it is hard to plot high-dimensional data on two-dimensional screens.
#
# We will illustrate some very simple examples before we move on to more "real world" data sets.
# First, we will look at a two class classification problems in two dimensions. We use the synthetic data generated by the ``make_blobs`` function, which generates clusters of points.
# +
## CODE CELL 15
from sklearn.datasets import make_blobs
X, y = make_blobs(centers=2, random_state=0)
print('X ~ n_samples x n_features:', X.shape)
print('y ~ n_samples:', y.shape)
print('\nFirst 5 samples:\n', X[:5, :])
print('\nFirst 5 labels:', y[:5])
# -
# As the data is two-dimensional, we can plot each sample as a point in a two-dimensional coordinate system, with the first feature being the x-axis and the second feature being the y-axis.
# +
## CODE CELL 16
plt.scatter(X[y == 0, 0], X[y == 0, 1],
c='blue', s=40, label='0')
plt.scatter(X[y == 1, 0], X[y == 1, 1],
c='red', s=40, label='1', marker='s')
plt.xlabel('first feature')
plt.ylabel('second feature')
plt.legend(loc='upper right')
plt.show()
# -
# Again, we want to split our data into a training set and a test set.
# +
## CODE CELL 17
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.25,
random_state=1234,
stratify=y)
# -
# Every algorithm is exposed in scikit-learn via an ''Estimator'' object. (All models in scikit-learn have a very consistent interface). For instance, we first import the logistic regression class.
# +
## CODE CELL 18
from sklearn.linear_model import LogisticRegression
# -
# Next, we instantiate the estimator object. Practically speaking, this is how we begin implementing each machine learning technique.
# +
## CODE CELL 19
classifier = LogisticRegression()
# -
# How many instances are in the training set?
# +
## CODE CELL 20
X_train.shape
# +
## CODE CELL 21
y_train.shape
# -
# To build the model from our data, that is, to learn how to classify new points, we call the ``fit`` method with the training data and corresponding training labels (the desired output for the training data point):
# +
## CODE CELL 22
classifier.fit(X_train, y_train)
# -
# (Some estimator methods such as `fit` return `self` by default. Thus, after executing the code snippet above, you will see the default parameters of this particular instance of `LogisticRegression`. Another way of retrieving the estimator's ininitialization parameters is to execute `classifier.get_params()`, which returns a parameter dictionary.)
# We can then apply the model to unseen data and use the model to predict the estimated outcome using the ``predict`` method:
# +
## CODE CELL 23
prediction = classifier.predict(X_test)
# -
# We can compare these against the true labels:
# +
## CODE CELL 24
print('prediction:', prediction)
print('true labels:', y_test)
# -
# We can evaluate our classifier quantitatively by measuring what fraction of predictions is correct. This is called **accuracy**. There is a convenience function, ``score``, that all scikit-learn classifiers have to compute this directly from the test data:
# +
## CODE CELL 25
classifier.score(X_test, y_test)
# -
# It is often helpful to compare the generalization performance (on the test set) to the performance on the training set:
# +
## CODE CELL 26
classifier.score(X_train, y_train)
# -
# LogisticRegression is a so-called linear model,
# that means it will create a decision that is linear in the input space. In 2D, this simply means it finds a line to separate the blue from the red:
# +
## CODE CELL 27
def plot_2d_separator(classifier, X, fill=False, ax=None, eps=None):
if eps is None:
eps = X.std() / 2.
x_min, x_max = X[:, 0].min() - eps, X[:, 0].max() + eps
y_min, y_max = X[:, 1].min() - eps, X[:, 1].max() + eps
xx = np.linspace(x_min, x_max, 100)
yy = np.linspace(y_min, y_max, 100)
X1, X2 = np.meshgrid(xx, yy)
X_grid = np.c_[X1.ravel(), X2.ravel()]
try:
decision_values = classifier.decision_function(X_grid)
levels = [0]
fill_levels = [decision_values.min(), 0, decision_values.max()]
except AttributeError:
# no decision_function
decision_values = classifier.predict_proba(X_grid)[:, 1]
levels = [.5]
fill_levels = [0, .5, 1]
if ax is None:
ax = plt.gca()
if fill:
ax.contourf(X1, X2, decision_values.reshape(X1.shape),
levels=fill_levels, colors=['blue', 'red'])
else:
ax.contour(X1, X2, decision_values.reshape(X1.shape), levels=levels,
colors="black")
ax.set_xlim(x_min, x_max)
ax.set_ylim(y_min, y_max)
ax.set_xticks(())
ax.set_yticks(())
plt.scatter(X[y == 0, 0], X[y == 0, 1],
c='blue', s=40, label='0')
plt.scatter(X[y == 1, 0], X[y == 1, 1],
c='red', s=40, label='1', marker='s')
plt.xlabel("first feature")
plt.ylabel("second feature")
plot_2d_separator(classifier, X)
plt.legend(loc='upper right')
plt.show()
# -
# **Estimated parameters**: All the estimated model parameters are attributes of the estimator object ending by an underscore. Here, these are the coefficients and the offset of the line:
# +
## CODE CELL 28
print(classifier.coef_)
print(classifier.intercept_)
# -
# ### Another classifier: K Nearest Neighbors
#
# Another popular and easy to understand classifier is K nearest neighbors (kNN). It has one of the simplest learning strategies: given a new, unknown observation, look up in your reference database which ones have the closest features and assign the predominant class.
#
# The interface is exactly the same as for ``LogisticRegression above``.
# +
## CODE CELL 29
from sklearn.neighbors import KNeighborsClassifier
# -
# This time we set a parameter of the KNeighborsClassifier to tell it we want to look at three nearest neighbors:
# +
## CODE CELL 30
knn = KNeighborsClassifier(n_neighbors=3)
# -
# We fit the model with our training data:
# +
## CODE CELL 31
knn.fit(X_train, y_train)
# +
## CODE CELL 32
plt.scatter(X[y == 0, 0], X[y == 0, 1],
c='blue', s=40, label='0')
plt.scatter(X[y == 1, 0], X[y == 1, 1],
c='red', s=40, label='1', marker='s')
plt.xlabel("first feature")
plt.ylabel("second feature")
plot_2d_separator(knn, X)
plt.legend(loc='upper right')
plt.show()
# +
## CODE CELL 33
knn.score(X_test, y_test)
# -
# Let's apply the KNeighborsClassifier to the iris dataset. How does accuracy change with different values of ``n_neighbors``?
# +
## CODE CELL 34
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.50,
random_state=42)
scores = []
k_values = np.arange(1, 10)
for k in k_values:
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train, y_train)
scores.append(knn.score(X_test, y_test))
plt.plot(k_values, scores)
plt.xlabel('Num. neighbors')
plt.ylabel('Accuracy')
plt.show()
# -
# Note that changing the ``random_state`` value in `train_test_split()` will give you a different accuracy profile. This inconsistency begs the question, what other metrics besides accuracy are available for comparing model performance?
# ### Model Evaluation and Scoring Metrics
# The default scores in scikit-learn are ``accuracy`` for classification, which is the fraction of correctly classified samples, and ``r2`` for regression, with is the coefficient of determination.
#
# These are reasonable default choices in many scenarious; however, depending on our task, these are not always the definitive or recommended choices.
#
# Scikit-learn has many helpful methods in the ``sklearn.metrics`` module that can help us with model evaluation.
# +
## CODE CELL 35
# Using k=3 and fitting/predicting on the iris dataset
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.50,
random_state=42,
stratify=y)
classifier = KNeighborsClassifier(n_neighbors=3).fit(X_train, y_train)
y_test_pred = classifier.predict(X_test)
print("Accuracy: {}".format(classifier.score(X_test, y_test)))
# -
# Here, we predicted 92% of samples correctly. For multi-class problems, it is often interesting to know which of the classes are hard to predict, and which are easy, or which classes get confused. One way to get more information about misclassifications is the ``confusion_matrix``, which shows for each true class, how frequent a given predicted outcome is.
# +
## CODE CELL 36
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_test_pred)
# -
# A plot is sometimes more readable:
# +
## CODE CELL 37
plt.matshow(confusion_matrix(y_test, y_test_pred), cmap="Blues")
plt.colorbar(shrink=0.8)
plt.xticks(range(3))
plt.yticks(range(3))
plt.xlabel("Predicted label")
plt.ylabel("True label")
plt.show()
# -
# We can see that most entries are on the diagonal, which means that we predicted nearly all samples correctly. The off-diagonal entries show us that some 2s were classified as 1s.
# Another useful function is the ``classification_report`` which provides precision, recall, fscore and support for all classes.
# With TP, FP, TN, FN standing for "true positive", "false positive", "true negative" and "false negative" repectively (follow this link for more explanation: https://developers.google.com/machine-learning/crash-course/classification/true-false-positive-negative):
# Precision = TP / (TP + FP)
# Precision is a measure of how many of the predictions for a class actually belong to that class.
# Recall = TP / (TP + FN)
# Recall is how many of the true positives were recovered.
# F1-score is the geometric average of precision and recall:
#
# F1 = 2 x (precision x recall) / (precision + recall)
# The values of all these values above are in the closed interval [0, 1], where 1 means a perfect score.
# +
## CODE CELL 38
from sklearn.metrics import classification_report
print(classification_report(y_test, y_test_pred))
# -
# These metrics are helpful in two particular cases that come up often in practice:
# 1. Imbalanced classes, that is, one class might be much more frequent than the other.
# 2. Asymmetric costs, that is, one kind of error is much more "costly" than the other.
# There are several other metrics which could be used for comparing model performance; see the `sklearn.metrics` [module documentation](http://scikit-learn.org/stable/modules/classes.html#module-sklearn.metrics) for details.
# ## Unsupervised Learning Example: K-Means Clustering
# Clustering is the task of gathering samples into groups of similar
# samples according to some predefined similarity or distance (dissimilarity)
# measure, such as the Euclidean distance.
#
# <img width="60%" src='Figures/clustering.png'/>
# Here, we will use one of the simplest clustering algorithms, K-means.
# This is an iterative algorithm which searches for a pre-specified number of cluster
# centers such that the distance from each point to its cluster is
# minimized. The standard implementation of K-means uses the Euclidean distance.
# For this task, we will use the iris dataset - remember, it does come with labels in the ``target`` array, but we can perform the clustering on the ``data`` array and ignore the true labels for now.
# +
## CODE CELL 39
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3, random_state=42)
# -
# We can get the cluster labels either by calling fit and then accessing the
# ``labels_`` attribute of the K means estimator, or by calling ``fit_predict``.
# Either way, the result contains the ID of the cluster that each point is assigned to.
# +
## CODE CELL 40
# X represents the data array
clusters = kmeans.fit_predict(X)
clusters
# +
## CODE CELL 41
# What does the label/target array look like again?
y
# -
# Even though it appears that we recovered the partitioning of the data into clusters with some degree of accuracy, the cluster IDs we assigned were arbitrary (i.e. a cluster label of "0" may or may not correspond to the label "0" in the `target` array - again, we only used the `data` array for training the clustering algorithm). Therefore, if we want to compared our predicted labels with the true labels, we must use a different scoring metric, such as ``adjusted_rand_score``, which is invariant to permutations of the labels:
# +
## CODE CELL 42
from sklearn.metrics import adjusted_rand_score
adjusted_rand_score(y, clusters)
# -
# #### What value of "k" do we use?
#
# In real-world datasets, the "true labels" are often unknown. In that case, how can we pre-specify the number of clusters, and what metrics can we use to compare different models?
#
# The most important consideration is your knowledge (or a subject-matter expert's knowledge) of the data and problem at hand. In addition, there is a rule-of-thumb approach called the Elbow method which can help in finding the optimal number of clusters. The Elbow method plots the inertia, or the sum of squared distances between samples and their corresponding cluster centers, against the number of clusters.
# +
## CODE CELL 43
inertia = []
for i in range(1, 11):
km = KMeans(n_clusters=i,
random_state=0)
km.fit(X)
inertia.append(km.inertia_)
plt.plot(range(1, 11), inertia, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Within-cluster sum-of-squares')
plt.show()
# -
# Then, we pick the value that resembles the "pit of an elbow." As we can see, this would be k=3 in this case, which makes sense given our knowledge of the dataset.
# Another method of cluster model evaluation (if true labels are unknown) is called the silhouette coefficient or the silhouette score. A higher silhouette score indicates more well-defined clusters; that is, the clusters have less overlap between them.
# +
## CODE CELL 44
from sklearn.metrics import silhouette_score
def get_silhouette_score(data, model):
s_score = silhouette_score(data, model.labels_)
return s_score
ss = []
for i in range(2, 11):
km = KMeans(n_clusters=i,
random_state=0)
km_model = km.fit(X)
ss.append(get_silhouette_score(X, km_model))
plt.plot(range(2, 11), ss, 'mo-')
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Score')
plt.show()
# -
# Again, since we know we're working with data from three distinct species in this example, we don't need to go through this evaluation. However, it can be helpful when evaluating an unlabelled dataset.
# ## A recap on Scikit-learn's estimator interface
# Scikit-learn strives to have a uniform interface across all methods. Given a scikit-learn *estimator*
# object named `model`, the following methods are available (not all for each model):
#
# - Available in **all Estimators**
# + `model.fit()` : fit training data. For supervised learning applications,
# this accepts two arguments: the data `X` and the labels `y` (e.g. `model.fit(X, y)`).
# For unsupervised learning applications, `fit` takes only a single argument,
# the data `X` (e.g. `model.fit(X)`).
# - Available in **supervised estimators**
# + `model.predict()` : given a trained model, predict the label of a new set of data.
# This method accepts one argument, the new data `X_new` (e.g. `model.predict(X_new)`),
# and returns the learned label for each object in the array.
# + `model.predict_proba()` : For classification problems, some estimators also provide
# this method, which returns the probability that a new observation has each categorical label.
# In this case, the label with the highest probability is returned by `model.predict()`.
# + `model.decision_function()` : For classification problems, some estimators provide an uncertainty estimate that is not a probability. For binary classification, a decision_function >= 0 means the positive class will be predicted, while < 0 means the negative class.
# + `model.score()` : for classification or regression problems, most (all?) estimators implement
# a score method. Scores are between 0 and 1, with a larger score indicating a better fit. For classifiers, the `score` method computes the prediction accuracy. For regressors, `score` computes the coefficient of determination (R<sup>2</sup>) of the prediction.
# + `model.transform()` : For feature selection algorithms, this will reduce the dataset to the selected features. For some classification and regression models such as some linear models and random forests, this method reduces the dataset to the most informative features. These classification and regression models can therefore also be used as feature selection methods.
#
# - Available in **unsupervised estimators**
# + `model.transform()` : given an unsupervised model, transform new data into the new basis.
# This also accepts one argument `X_new`, and returns the new representation of the data based
# on the unsupervised model.
# + `model.fit_transform()` : some estimators implement this method,
# which more efficiently performs a fit and a transform on the same input data.
# + `model.predict()` : for clustering algorithms, the predict method will produce cluster labels for new data points. Not all clustering methods have this functionality.
# + `model.predict_proba()` : Gaussian mixture models (GMMs) provide the probability for each point to be generated by a given mixture component.
# + `model.score()` : Density models like KDE and GMMs provide the likelihood of the data under the model.
# ## And there's more...
# There are many more machine learning algorithms that scikit-learn covers, from support vector machines, to random forests, to neural network models. If you are interested in learning more, check out the documentation here: http://scikit-learn.org/stable/user_guide.html. The source tutorial for this notebook is also excellent - I highly recommend browsing through the notebooks and/or watching the lecture if you have time. See the link below.
# *Reference*:
#
# A. Gramfort and A. Mueller, *Scipy 2017 sklearn*, (2017), GitHub Repository, https://github.com/amueller/scipy-2017-sklearn.
| 30,983 |
/Gaussian Mixture Models.ipynb | fa69cdfb9c160557c80c87c4eaa18ae61ab4e291 | [] | no_license | aburzinski/ML_From_Scratch | https://github.com/aburzinski/ML_From_Scratch | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 75,821 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Importing the necessary packages
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Loading in the data set
df =pd.read_csv('csv_files/NBA_8YEAR.csv', header=0)
df.head()
df.shape
df.columns
df.info()
# +
# count how many missing values
names = []
val = []
# Creating a for loop to see which ones are missing
for col in df.columns:
names.append(col)
val.append(df[df.columns].isnull().sum())
break
# Printing to see the results
print(names, val)
# -
# Drop the row if it is missing a value
df = df.dropna(axis=0, how='any', subset=['W/L'])
df.shape
# +
# count how many missing values
names = []
val = []
# Creating a for loop to see which ones are missing
for col in df.columns:
names.append(col)
val.append(df[df.columns].isnull().sum())
break
# Printing to see the results
print(names, val)
# -
df.columns
# Calculating Effective Field Goal (EFG) Percentage
df['EFG%'] = ((df['FGM']-df['3PM'] + 1.5 * df['3PM'])/ df['FGA'])
# Calculating Free Throw Rate (FTR)
df['FTR'] = df['FTA'] / df['FGA']
df['TOVPerc'] = (df['TOV'] / (df['FGA'] + (.44 * df['FTA']) + df['TOV'])) * 100
# Renaming the columns in order get ride of the % signs
df.rename(columns={'FG%':'FGPerc','3P%':'ThreePPerc','FT%':'FTPerc','EFG%':'EFGPerc'}, inplace=True)
df.columns
# to change use .astype()
df['FGPerc'] = df.FGPerc.astype(float)
df['ThreePPerc'] = df.ThreePPerc.astype(float)
df['FTPerc'] = df.FTPerc.astype(float)
df['EFGPerc'] = df.EFGPerc.astype(float)
df['TOVPerc'] = df.TOVPerc.astype(float)
# Creating seperate data frames for home and away teams
home_teams = df[df.MATCHUP.str.contains('vs.')]
away_teams = df[df.MATCHUP.str.contains('@')]
# Saving these dataframes to a seperate csv
home_teams.to_csv('csv_files/home_teams.csv')
away_teams.to_csv('csv_files/away_teams.csv')
# +
#df2 = df.drop('Target_L', axis=1)
# -
df['FTPerc'].describe()
df2.shape
# +
#df2 = df.drop(['TEAM', 'DATE', 'MATCHUP', 'W/L', 'MIN', '+/', 'Target_L'], axis=1)
# -
df2.shape
# Looking at the top of the data set after droppping columns that were not needed
df2.head()
df2.columns
# ## EDA
# Looking at the target variable
fig = plt.figure()
df2['Target'].value_counts().plot(kind='bar', title="Target Variable. Win (1) vs Loss (0) ")
plt.ylabel('Number of Games')
plt.show()
fig.savefig('images/TARGET.PNG')
# Creating histograms of all of my variables to see distributions
df2.hist(figsize=(20, 20), bins=50, xlabelsize=8, ylabelsize=8)
# Looking at breakdown of 3 Pointers Made
fig = plt.figure()
df2['FGPerc'].hist()
plt.title('Field Goal Percentage')
plt.ylabel('Number of Games')
plt.xlabel('Team Field Goal Percentage')
fig.savefig('images/FGP.PNG')
# Looking at breakdown of Points
fig = plt.figure()
df2['PTS'].hist()
plt.title('Points Scored')
plt.ylabel('Number of Games')
plt.xlabel('Total Points Scored by a Team')
fig.savefig('images/PTS.PNG')
# Looking at breakdown of 3 Pointers Made
fig = plt.figure()
df2['3PM'].value_counts().plot.bar(figsize=(10,7), title='Three Pointers Made')
plt.ylabel('Number of Games')
plt.xlabel('Total Three Pointers Made')
fig.savefig('images/ThreePointersMade.PNG')
# Looking at breakdown of Turnovers
fig = plt.figure()
df2['TOV'].value_counts().plot.bar(figsize=(10,7), title='Turnovers')
plt.ylabel('Number of Games')
plt.xlabel('Turnovers Per Game')
fig.savefig('images/Turnovers.PNG')
# Looking at breakdown of Steals
fig = plt.figure()
df2['STL'].value_counts().plot.bar(figsize=(10,7), title='Steals')
fig.savefig('images/Steals.PNG')
# Looking at breakdown of Blocks
df2['BLK'].value_counts().plot.bar(figsize=(10,7), title='Blocks')
# +
#Created a heatmap to see the correlation between the different variables
#Created a figure and are able to adjust the size of the graph
plt.figure(figsize = (20,20))
#Created a heatmap using Seaborn to display the correlation based on 'Spearman' method
##Added the annotation so that the numbers appear in each box
display = sns.heatmap(df2.corr(method = 'spearman'), annot=True, fmt='.2f', cmap='BuPu', linewidth=.75, cbar_kws={'shrink': .75})
#Created a title
plt.title('Correlation Heatmap')
# -
# export working dataframe to csv
df2.to_csv('csv_files/CapstoneEDA.csv')
# ## Decision Tree
# +
# import required packages for splitting data
from sklearn import model_selection
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
# import required packages for evaluating models
from sklearn import metrics
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
from sklearn.metrics import roc_auc_score
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_recall_fscore_support
# import `logistic regression` model
from sklearn.linear_model import LogisticRegression
from sklearn.feature_selection import RFE
# import the packages needed for the Decision Tree
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
# -
# Splitting up our data into variable and target data
X = df2.iloc[:, :-1] # Variable
Y = df2.Target # Target
# Split dataset into training set and test set
# 70% training and 30% test
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=2019)
# +
# Create Decision Tree classifer object
clf = DecisionTreeClassifier()
# Train Decision Tree Classifer
clf = clf.fit(X_train,Y_train)
#Predict the response for test dataset
Y_pred = clf.predict(X_test)
# +
# Model Accuracy, how often is the Decision Tree correct?
print("Accuracy:",metrics.accuracy_score(Y_test, Y_pred))
# We are going to look at the classification report and also the confusion matrix for the Decision Tree
print(metrics.classification_report(Y_test, Y_pred))
print(metrics.confusion_matrix(Y_test, Y_pred))
# -
# define the feature importance variable
# use the feature importance values from the decision tree above, sort in descending order
feature_imp = pd.Series(clf.feature_importances_,index=df2.iloc[:,:-1].columns).sort_values(ascending=False)
# print the results
feature_imp
# ## Logistic Regression
# +
# initiate the logistic regression function
logreg = LogisticRegression()
# pass the training data into the model. This training data includes all of the independent variables
logreg.fit(X_train,Y_train)
# tell the model what to predict, or in this case classify, and what variables to use to predict the dependent variable
Y_pred=logreg.predict(X_test)
# -
# calculate accuracy, precision and recall? measures of the model
print("Accuracy:",metrics.accuracy_score(Y_test, Y_pred))
print("Precision:",metrics.precision_score(Y_test, Y_pred))
print('Recall:',metrics.recall_score(Y_test, Y_pred))
| 7,151 |
/.ipynb_checkpoints/Day 8 part 1 -checkpoint.ipynb | e2012b370d7b0590300a29b7ac833dc5ef174561 | [] | no_license | nischalstha9/pythonFundamentals | https://github.com/nischalstha9/pythonFundamentals | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 2,568 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
a=[1,2,3,4]
b=[5,6,7,8]
c=[]
for i in range(len(a)):
c=(a[i]+b[i])
print(c, end=" ")
print()
a=[1,2,3,4]
b=[5,6,7,8]
c=[]
for i in range(len(a)):
c.append(a[i]+b[i])
print(c)
# Enumerate and ZIP
#
#
a=[2,3,4,5]
for i,j in enumerate(a):
print(i,j)
# +
#enumerate gives value with index
# -
a=[1,2,3,4]
b=[5,6,7,8]
for i,j in zip(a,b):
print(i+j)
c.append(i+j)
print(c)
lets us see the plots in the notebook
# %matplotlib inline
#this uses seaborn (sns) to set the style for all the plots
sns.set(context='poster', style='whitegrid', font_scale=1.4)
from os.path import join
from scipy.stats import ttest_ind, spearmanr, pearsonr, ttest_rel, kstest
import statsmodels.formula.api as smf
import statsmodels.api as sm
from statsmodels.stats.anova import anova_lm
from sklearn.impute import KNNImputer
#import fancyimpute as fi
#less important for plotting
from glob import glob
import statsmodels.api as sm
from statsmodels.iolib.summary2 import summary_col
from statsmodels.sandbox.stats.multicomp import multipletests
# -
import pandas
pandas.__version__
def calculate_pvalues(df, correlation):
from scipy.stats import pearsonr, pearsonr
df = df.dropna()._get_numeric_data()
dfcols = pd.DataFrame(columns=df.columns)
pvalues = dfcols.transpose().join(dfcols, how='outer')
for r in df.columns:
for c in df.columns:
if correlation == 'pearson':
pvalues[r][c] = round(pearsonr(df[r], df[c])[1], 4)
if correlation == 'spearman':
pvalues[r][c] = round(spearmanr(df[r], df[c])[1], 4)
else:
raise ValueError('Invalid correlation method specified. Accpetable values are \'pearson\' and \'spearman\'.')
return pvalues
#Li & Ji (2005) method for multiple comparisons corrections
#calculating number of effective comparisons M_eff
def liji_sidak_mc(data, alpha):
import math
import numpy as np
mc_corrmat = data.corr()
eigvals, eigvecs = np.linalg.eig(mc_corrmat)
M_eff = 0
for eigval in eigvals:
if abs(eigval) >= 0:
if abs(eigval) >= 1:
M_eff += 1
else:
M_eff += abs(eigval) - math.floor(abs(eigval))
else:
M_eff += 0
print('Number of effective comparisons: {0}'.format(M_eff))
#and now applying M_eff to the Sidak procedure
sidak_p = 1 - (1 - alpha)**(1/M_eff)
if sidak_p < 0.00001:
print('Critical value of {:.3f}'.format(alpha),'becomes {:2e} after corrections'.format(sidak_p))
else:
print('Critical value of {:.3f}'.format(alpha),'becomes {:.6f} after corrections'.format(sidak_p))
return sidak_p, M_eff
fig_dir = '/Users/kbottenh/Dropbox/Projects/physics-retrieval/figures'
data_dir = '/Users/kbottenh/Dropbox/Projects/physics-retrieval/data'
df = pd.read_csv(join(data_dir, 'rescored', 'physics_learning-nonbrain_OLS-missing.csv'),
index_col=0, header=0)
post_iq = ['VCI2', 'PRI2', 'WMI2', 'PSI2', 'FSIQ2']
delta_iq = ['deltaVCI', 'deltaPRI', 'deltaWMI', 'deltaPSI', 'deltaFSIQ']
iq_vars = post_iq + delta_iq
#rsgt_df = pd.read_csv(join(data_dir, 'resting-state_graphtheory_shen+craddock_2019-05-29.csv'),
# index_col=0, header=0)
#rsgt_df = pd.read_csv(join(data_dir, 'output', 'resting-state_graphtheory_shen+craddock_2019-11-20.csv'),
# index_col=0, header=0)
head_size = pd.read_csv(join(data_dir, 'head-size_2019-05-29 15:19:53.287525.csv'), index_col=0, header=0)
head_size['normalized head size'] = (head_size['average_head_size']-np.mean(head_size['average_head_size']))/np.std(head_size['average_head_size'])
# +
fd = pd.read_csv(join(data_dir, 'avg-fd-per-condition-per-run_2019-05-29.csv'), index_col=0, header=0)
fd['normalized fd'] = (fd['average fd']-np.mean(fd['average fd']))/np.std(fd['average fd'])
retr_fd = fd[fd['task'] == 'retr']
#reas_fd = fd[fd['task'] == 'reas']
fci_fd = fd[fd['task'] == 'fci']
df_pivot = retr_fd[retr_fd['condition'] == 'high-level'].reset_index()
retr_phys_fd = df_pivot.pivot(index='subject', columns='session', values='average fd')
retr_phys_fd.rename({'pre': 'pre phys retr fd', 'post': 'post phys retr fd'}, axis=1, inplace=True)
df_pivot = retr_fd[retr_fd['condition'] == 'lower-level'].reset_index()
retr_genr_fd = df_pivot.pivot(index='subject', columns='session', values='average fd')
retr_genr_fd.rename({'pre': 'pre gen retr fd', 'post': 'post gen retr fd'}, axis=1, inplace=True)
#df_pivot = reas_fd[reas_fd['condition'] == 'high-level'].reset_index()
#reas_inf_fd = df_pivot.pivot(index='subject', columns='session', values='average fd')
#reas_inf_fd.rename({'pre': 'pre infr reas fd', 'post': 'post infr reas fd'}, axis=1, inplace=True)
#df_pivot = reas_fd[reas_fd['condition'] == 'lower-level'].reset_index()
#reas_base_fd = df_pivot.pivot(index='subject', columns='session', values='average fd')
#reas_base_fd.rename({'pre': 'pre base reas fd', 'post': 'post base reas fd'}, axis=1, inplace=True)
df_pivot = fci_fd[fci_fd['condition'] == 'high-level'].reset_index()
fci_phys_fd = df_pivot.pivot(index='subject', columns='session', values='average fd')
fci_phys_fd.rename({'pre': 'pre phys fci fd', 'post': 'post phys fci fd'}, axis=1, inplace=True)
df_pivot = fci_fd[fci_fd['condition'] == 'lower-level'].reset_index()
fci_ctrl_fd = df_pivot.pivot(index='subject', columns='session', values='average fd')
fci_ctrl_fd.rename({'pre': 'pre ctrl fci fd', 'post': 'post ctrl fci fd'}, axis=1, inplace=True)
# -
# rest_fd = pd.read_csv(join(data_dir, 'avg-fd-per-run-rest_2019-05-31.csv'), index_col=0, header=0)
# rs_fd = rest_fd.reset_index().pivot(index='subject', columns='session', values='average fd')
# rs_fd.rename({'pre': 'pre rest fd', 'post': 'post rest fd'}, axis=1, inplace=True)
# +
fci_df = pd.read_csv(join(data_dir,
'physics-learning-fci_graphtheory_shen+craddock_2019-05-31.csv'),
index_col=0, header=0)
phys_fci = fci_df[fci_df['condition'] == 'high-level']
ctrl_fci = fci_df[fci_df['condition'] == 'lower-level']
#physics fci measures per session per parcellation
df_pivot = phys_fci[phys_fci['mask'] == 'shen2015'].reset_index()
shen_eff_phys_fci_df = df_pivot.pivot(index='subject', columns='session', values='efficiency')
shen_eff_phys_fci_df.rename({0: 'pre phys fci shen eff', 1:
'post phys fci shen eff'},
axis=1, inplace=True)
#shen_cpl_phys_fci_df = df_pivot.pivot(index='subject', columns='session', values='charpath')
#shen_cpl_phys_fci_df.rename({0: 'pre phys fci shen cpl', 1: 'post phys fci shen cpl'}, axis=1, inplace=True)
shen_mod_phys_fci_df = df_pivot.pivot(index='subject', columns='session', values='modularity')
shen_mod_phys_fci_df.rename({0: 'pre phys fci shen mod', 1: 'post phys fci shen mod'}, axis=1, inplace=True)
df_pivot = phys_fci[phys_fci['mask'] == 'craddock2012'].reset_index()
crad_eff_phys_fci_df = df_pivot.pivot(index='subject', columns='session', values='efficiency')
crad_eff_phys_fci_df.rename({0: 'pre phys fci crad eff', 1: 'post phys fci crad eff'}, axis=1, inplace=True)
#crad_cpl_phys_fci_df = df_pivot.pivot(index='subject', columns='session', values='charpath')
#crad_cpl_phys_fci_df.rename({0: 'pre phys fci crad cpl', 1: 'post phys fci crad cpl'}, axis=1, inplace=True)
crad_mod_phys_fci_df = df_pivot.pivot(index='subject', columns='session', values='modularity')
crad_mod_phys_fci_df.rename({0: 'pre phys fci crad mod', 1: 'post phys fci crad mod'}, axis=1, inplace=True)
#ctrl fci measures per session per parcellation
df_pivot = ctrl_fci[ctrl_fci['mask'] == 'shen2015'].reset_index()
shen_eff_ctrl_fci_df = df_pivot.pivot(index='subject', columns='session', values='efficiency')
shen_eff_ctrl_fci_df.rename({0: 'pre ctrl fci shen eff', 1: 'post ctrl fci shen eff'}, axis=1, inplace=True)
#shen_cpl_ctrl_fci_df = df_pivot.pivot(index='subject', columns='session', values='charpath')
#shen_cpl_ctrl_fci_df.rename({0: 'pre ctrl fci shen cpl', 1: 'post ctrl fci shen cpl'}, axis=1, inplace=True)
shen_mod_ctrl_fci_df = df_pivot.pivot(index='subject', columns='session', values='modularity')
shen_mod_ctrl_fci_df.rename({0: 'pre ctrl fci shen mod', 1: 'post ctrl fci shen mod'}, axis=1, inplace=True)
df_pivot = ctrl_fci[ctrl_fci['mask'] == 'craddock2012'].reset_index()
crad_eff_ctrl_fci_df = df_pivot.pivot(index='subject', columns='session', values='efficiency')
crad_eff_ctrl_fci_df.rename({0: 'pre ctrl fci crad eff', 1: 'post ctrl fci crad eff'}, axis=1, inplace=True)
#crad_cpl_ctrl_fci_df = df_pivot.pivot(index='subject', columns='session', values='charpath')
#crad_cpl_ctrl_fci_df.rename({0: 'pre ctrl fci crad cpl', 1: 'post ctrl fci crad cpl'}, axis=1, inplace=True)
crad_mod_ctrl_fci_df = df_pivot.pivot(index='subject', columns='session', values='modularity')
crad_mod_ctrl_fci_df.rename({0: 'pre ctrl fci crad mod', 1: 'post ctrl fci crad mod'}, axis=1, inplace=True)
# +
task_df = pd.read_csv(join(data_dir, 'physics-learning-tasks_graphtheory_shen+craddock_2019-05-30.csv'), index_col=0, header=0)
retr_df = task_df[task_df['task'] == 'retr']
retr_phys_df = retr_df[retr_df['condition'] == 'high-level']
genr_phys_df = retr_df[retr_df['condition'] == 'lower-level']
#physics retrieval measures per session per parcellation
df_pivot = retr_phys_df[retr_phys_df['mask'] == 'shen2015'].reset_index()
shen_eff_retr_phys_df = df_pivot.pivot(index='subject', columns='session', values='efficiency')
shen_eff_retr_phys_df.rename({0: 'pre phys retr shen eff', 1: 'post phys retr shen eff'}, axis=1, inplace=True)
#shen_cpl_retr_phys_df = df_pivot.pivot(index='subject', columns='session', values='charpath')
#shen_cpl_retr_phys_df.rename({0: 'pre phys retr shen cpl', 1: 'post phys retr shen cpl'}, axis=1, inplace=True)
shen_mod_retr_phys_df = df_pivot.pivot(index='subject', columns='session', values='modularity')
shen_mod_retr_phys_df.rename({0: 'pre phys retr shen mod', 1: 'post phys retr shen mod'}, axis=1, inplace=True)
df_pivot = retr_phys_df[retr_phys_df['mask'] == 'craddock2012'].reset_index()
crad_eff_retr_phys_df = df_pivot.pivot(index='subject', columns='session', values='efficiency')
crad_eff_retr_phys_df.rename({0: 'pre phys retr crad eff', 1: 'post phys retr crad eff'}, axis=1, inplace=True)
#crad_cpl_retr_phys_df = df_pivot.pivot(index='subject', columns='session', values='charpath')
#crad_cpl_retr_phys_df.rename({0: 'pre phys retr crad cpl', 1: 'post phys retr crad cpl'}, axis=1, inplace=True)
crad_mod_retr_phys_df = df_pivot.pivot(index='subject', columns='session', values='modularity')
crad_mod_retr_phys_df.rename({0: 'pre phys retr crad mod', 1: 'post phys retr crad mod'}, axis=1, inplace=True)
#general retrieval measures per session per parcellation
df_pivot = genr_phys_df[genr_phys_df['mask'] == 'shen2015'].reset_index()
shen_eff_retr_genr_df = df_pivot.pivot(index='subject', columns='session', values='efficiency')
shen_eff_retr_genr_df.rename({0: 'pre gen retr shen eff', 1: 'post gen retr shen eff'}, axis=1, inplace=True)
#shen_cpl_retr_genr_df = df_pivot.pivot(index='subject', columns='session', values='charpath')
#shen_cpl_retr_genr_df.rename({0: 'pre gen retr shen cpl', 1: 'post gen retr shen cpl'}, axis=1, inplace=True)
shen_mod_retr_genr_df = df_pivot.pivot(index='subject', columns='session', values='modularity')
shen_mod_retr_genr_df.rename({0: 'pre gen retr shen mod', 1: 'post gen retr shen mod'}, axis=1, inplace=True)
df_pivot = genr_phys_df[genr_phys_df['mask'] == 'craddock2012'].reset_index()
crad_eff_retr_genr_df = df_pivot.pivot(index='subject', columns='session', values='efficiency')
crad_eff_retr_genr_df.rename({0: 'pre gen retr crad eff', 1: 'post gen retr crad eff'}, axis=1, inplace=True)
#crad_cpl_retr_genr_df = df_pivot.pivot(index='subject', columns='session', values='charpath')
#crad_cpl_retr_genr_df.rename({0: 'pre gen retr crad cpl', 1: 'post gen retr crad cpl'}, axis=1, inplace=True)
crad_mod_retr_genr_df = df_pivot.pivot(index='subject', columns='session', values='modularity')
crad_mod_retr_genr_df.rename({0: 'pre gen retr crad mod', 1: 'post gen retr crad mod'}, axis=1, inplace=True)
# -
# reas_df = task_df[task_df['task'] == 'reas']
# reas_infr_df = reas_df[reas_df['condition'] == 'high-level']
# reas_base_df = reas_df[reas_df['condition'] == 'lower-level']
#
# #infrics reasieval measures per session per parcellation
# df_pivot = reas_infr_df[reas_infr_df['mask'] == 'shen2015'].reset_index()
# shen_eff_reas_infr_df = df_pivot.pivot(index='subject', columns='session', values='efficiency')
# shen_eff_reas_infr_df.rename({0: 'pre infr reas shen eff', 1: 'post infr reas shen eff'}, axis=1, inplace=True)
#
# shen_cpl_reas_infr_df = df_pivot.pivot(index='subject', columns='session', values='charpath')
# shen_cpl_reas_infr_df.rename({0: 'pre infr reas shen cpl', 1: 'post infr reas shen cpl'}, axis=1, inplace=True)
#
# shen_mod_reas_infr_df = df_pivot.pivot(index='subject', columns='session', values='modularity')
# shen_mod_reas_infr_df.rename({0: 'pre infr reas shen mod', 1: 'post infr reas shen mod'}, axis=1, inplace=True)
#
# df_pivot = reas_infr_df[reas_infr_df['mask'] == 'craddock2012'].reset_index()
# crad_eff_reas_infr_df = df_pivot.pivot(index='subject', columns='session', values='efficiency')
# crad_eff_reas_infr_df.rename({0: 'pre infr reas crad eff', 1: 'post infr reas crad eff'}, axis=1, inplace=True)
#
# crad_cpl_reas_infr_df = df_pivot.pivot(index='subject', columns='session', values='charpath')
# crad_cpl_reas_infr_df.rename({0: 'pre infr reas crad cpl', 1: 'post infr reas crad cpl'}, axis=1, inplace=True)
#
# crad_mod_reas_infr_df = df_pivot.pivot(index='subject', columns='session', values='modularity')
# crad_mod_reas_infr_df.rename({0: 'pre infr reas crad mod', 1: 'post infr reas crad mod'}, axis=1, inplace=True)
#
# #baseeral reasieval measures per session per parcellation
# df_pivot = reas_base_df[reas_base_df['mask'] == 'shen2015'].reset_index()
# shen_eff_reas_base_df = df_pivot.pivot(index='subject', columns='session', values='efficiency')
# shen_eff_reas_base_df.rename({0: 'pre base reas shen eff', 1: 'post base reas shen eff'}, axis=1, inplace=True)
#
# shen_cpl_reas_base_df = df_pivot.pivot(index='subject', columns='session', values='charpath')
# shen_cpl_reas_base_df.rename({0: 'pre base reas shen cpl', 1: 'post base reas shen cpl'}, axis=1, inplace=True)
#
# shen_mod_reas_base_df = df_pivot.pivot(index='subject', columns='session', values='modularity')
# shen_mod_reas_base_df.rename({0: 'pre base reas shen mod', 1: 'post base reas shen mod'}, axis=1, inplace=True)
#
# df_pivot = reas_base_df[reas_base_df['mask'] == 'craddock2012'].reset_index()
# crad_eff_reas_base_df = df_pivot.pivot(index='subject', columns='session', values='efficiency')
# crad_eff_reas_base_df.rename({0: 'pre base reas crad eff', 1: 'post base reas crad eff'}, axis=1, inplace=True)
#
# crad_cpl_reas_base_df = df_pivot.pivot(index='subject', columns='session', values='charpath')
# crad_cpl_reas_base_df.rename({0: 'pre base reas crad cpl', 1: 'post base reas crad cpl'}, axis=1, inplace=True)
#
# crad_mod_reas_base_df = df_pivot.pivot(index='subject', columns='session', values='modularity')
# crad_mod_reas_base_df.rename({0: 'pre base reas crad mod', 1: 'post base reas crad mod'}, axis=1, inplace=True)
# +
#demo_df[demo_df['Strt.Level'] < 0] = np.nan
# +
all_df = pd.concat((df, head_size['normalized head size'],
shen_eff_retr_phys_df, shen_mod_retr_phys_df,
crad_eff_retr_phys_df, crad_mod_retr_phys_df,
shen_eff_retr_genr_df, shen_mod_retr_genr_df,
crad_eff_retr_genr_df, crad_mod_retr_genr_df,
shen_eff_phys_fci_df, shen_mod_phys_fci_df,
crad_eff_phys_fci_df, crad_mod_phys_fci_df,
shen_eff_ctrl_fci_df, shen_mod_ctrl_fci_df,
crad_eff_ctrl_fci_df, crad_mod_ctrl_fci_df,
retr_phys_fd, retr_genr_fd, fci_phys_fd, fci_ctrl_fd), axis=1)
missing_df = pd.DataFrame(columns=all_df.keys(), index=all_df.index)
for key in missing_df.keys():
missing_df[key] = all_df[key].isnull()
missing_df.replace({False: 0, True:1}, inplace=True)
# -
null_df = pd.read_csv(join(data_dir, 'output', 'local_efficiency/null_dist_effs.csv'),
header=0, index_col=[0,1,2,3])
null_df.head()
# +
masks = {'shen2015': 'shen', 'craddock2012': 'crad'}
tasks = ['fci', 'retr']
for mask in masks.keys():
for task in tasks:
null = null_df.loc['post', task, 'physics', mask]['mean']
vals = all_df['post phys {0} {1} eff'.format(task, masks[mask])]
all_df['post phys {0} {1} eff'.format(task, masks[mask])] = vals / null
all_df['F'] = all_df['F'] - 0.5
# -
impute_pls = KNNImputer(n_neighbors=3, weights='distance')
ols_imputed = impute_pls.fit_transform(all_df)
imp_df = pd.DataFrame(ols_imputed, columns=all_df.columns, index=all_df.index)
index = pd.MultiIndex.from_product([missing_df.keys(), all_df.keys()])
mnar = pd.DataFrame(columns=['corr', 'pval'], index=index)
sexes = ['Male', 'Female', 'All']
sessions = ['pre', 'post', 'delta']
imp_df.columns = imp_df.columns.str.replace(' ', '_')
imp_df.to_csv(join(data_dir, 'rescored', 'physics_learning-plus+brain_OLS-missing.csv'))
#compute deltas
iqs = ['VCI', 'WMI', 'PRI', 'PSI', 'FSIQ']
for iq in iqs:
imp_df['{0}2_sd'] =
imp_df['delta{0}'.format(iq)] = imp_df['{0}2'.format(iq)] - imp_df['{0}1'.format(iq)]
imp_df['delta{0}'.format(iq)] = imp_df['delta{0}'.format(iq)] /
# # For all students, all together, how is topology related to IQ?
#first things first, setting up our covariates
covariates = ['Age', 'Mod', 'StrtLvl', 'normalized head size', 'SexXClass', 'F']
# +
outcomes1 = ['post_phys_retr_crad_eff', 'post_phys_retr_crad_mod',
'post_phys_retr_shen_eff', 'post_phys_retr_shen_mod']
outcomes2 = ['post_phys_fci_shen_eff', 'post_phys_fci_shen_mod',
'post_phys_fci_crad_eff', 'post_phys_fci_crad_mod']
all_out = outcomes1 + outcomes2
adj_a,_ = liji_sidak_mc(imp_df[all_out], 0.01)
print('Shen', adj_a)
# -
# ## OLS Regressions
iterables = {'tasks': ['fci', 'retr'],
'masks': ['crad', 'shen'],
'metrics': ['mod', 'eff'],
'iq_vars': iq_vars}
simple = {}
intrxn = {}
compar = {}
for task in iterables['tasks']:
for mask in iterables['masks']:
for metric in iterables['metrics']:
for iq_meas in iterables['iq_vars']:
reg_form = '''post_phys_{0}_{1}_{2} ~
{3} + F + Mod + F*Mod + Age + StrtLvl
+ normalized_head_size + post_phys_{0}_fd'''.format(task,
mask,
metric,
iq_meas)
mod = smf.ols(formula=reg_form, data=imp_df)
res = mod.fit()
simple['{0}_{1}_{2}_{3}'.format(task,
mask,
metric,
iq_meas)] = res
if res.get_robustcov_results().f_pvalue <= adj_a:
print('\n*{0}_{1}_{2} on {3} fci_simple model IS significant'.format(task,
mask,
metric,
iq_meas))
if res.get_robustcov_results().pvalues[1] < 0.05:
print('* and {0} coefficient significant, too!'.format(iq_meas))
else:
print('x but {0} coefficient not significant.'.format(iq_meas))
#else:
#print('\n{0} on {1} fci_simple model NOT significant'.format(outcome, iq_meas))
itx_form = '''post_phys_{0}_{1}_{2} ~ {3} + {3}*F + {3}*Mod + {3}*F*Mod
+ F + Mod + F*Mod + Age + StrtLvl +
normalized_head_size + post_phys_{0}_fd'''.format(task,
mask,
metric,
iq_meas)
mod = smf.ols(formula=itx_form, data=imp_df)
res2 = mod.fit()
intrxn['{0}_{1}_{2}_{3}'.format(task,
mask,
metric,
iq_meas)] = res2
if res2.get_robustcov_results().f_pvalue <= adj_a:
print('*{0}_{1}_{2} on {3} interaction model IS significant'.format(task, mask, metric, iq_meas))
if res2.get_robustcov_results().pvalues[1] < 0.05:
print('* and {0} coefficient significant, too!'.format(iq_meas))
else:
print('x but {0} coefficient not significant.'.format(iq_meas))
#else:
#print('{0} on {1} interaction model NOT significant'.format(outcome, iq_meas))
compare = anova_lm(res.get_robustcov_results(), res2.get_robustcov_results())
compar['{0}_{1}_{2}_{3}'.format(task,
mask,
metric,
iq_meas)] = compare
if compare['Pr(>F)'][1] <= 0.05:
print(np.round(compare['Pr(>F)'][1], 3),
'interaction model fits better than nested model for {0}_{1}_{2} ~ {3}'.format(task,
mask,
metric,
iq_meas))
elif compare['Pr(>F)'][0] <= 0.05:
print('Nested model fits better than interaction model for {0}_{1}_{2} ~ {3}'.format(task,
mask,
metric,
iq_meas))
#else:
#print(np.round(fci_compare['Pr(>F)'][1], 3), 'no difference between models')
# +
columns = ['Model F (p)', 'BIC', 'WAIS-IV',
'Sex (F)', 'Class (Active)', 'Sex X Class',
'Age', 'Years in Univ.']
mi = pd.MultiIndex.from_product([iterables['tasks'],
iterables['masks'],
iterables['metrics'],
iterables['iq_vars']])
df_res_simple = pd.DataFrame(columns=columns, index=mi)
for key in simple.keys():
keys = key.split('_')
summ = simple[key].get_robustcov_results()
df_res_simple.at[(keys[0], keys[1], keys[2], keys[3]),
'Model F (p)'] = '{0} ({1})'.format(np.round(summ.fvalue[0][0],3),
np.format_float_scientific(summ.f_pvalue,
precision=3,
exp_digits=2))
df_res_simple.at[(keys[0], keys[1], keys[2], keys[3]),
'BIC'] = np.round(summ.bic,1)
if summ.pvalues[1] < 0.01:
dec = '**'
elif summ.pvalues[1] < 0.051:
dec = '*'
else:
dec=''
df_res_simple.at[(keys[0], keys[1], keys[2], keys[3]),
'WAIS-IV'] = '{0}{1}'.format(np.round(summ.params[1], 3), dec)
if summ.pvalues[2] < 0.01:
dec = '**'
elif summ.pvalues[2] < 0.051:
dec = '*'
else:
dec=''
df_res_simple.at[(keys[0], keys[1], keys[2], keys[3]),
'Sex (F)'] = '{0}{1}'.format(np.round(summ.params[2], 3), dec)
if summ.pvalues[3] < 0.01:
dec = '**'
elif summ.pvalues[3] < 0.051:
dec = '*'
else:
dec=''
df_res_simple.at[(keys[0], keys[1], keys[2], keys[3]),
'Class (Active)'] = '{0}{1}'.format(np.round(summ.params[3], 3), dec)
if summ.pvalues[4] < 0.01:
dec = '**'
elif summ.pvalues[4] < 0.051:
dec = '*'
else:
dec=''
df_res_simple.at[(keys[0], keys[1], keys[2], keys[3]),
'Sex X Class'] = '{0}{1}'.format(np.round(summ.params[4], 3), dec)
if summ.pvalues[5] < 0.01:
dec = '**'
elif summ.pvalues[5] < 0.051:
dec = '*'
else:
dec=''
df_res_simple.at[(keys[0], keys[1], keys[2], keys[3]),
'Age'] = '{0}{1}'.format(np.round(summ.params[5], 3), dec)
if summ.pvalues[6] < 0.01:
dec = '**'
elif summ.pvalues[6] < 0.051:
dec = '*'
else:
dec=''
df_res_simple.at[(keys[0], keys[1], keys[2], keys[3]),
'Years in Univ.'] = '{0}{1}'.format(np.round(summ.params[6], 3), dec)
df_res_simple.to_csv(join(data_dir, 'output', 'brain_metrics~iq-ols_robust-knn_imp-simple.csv'))
df_res_simple.head()
# +
columns = ['Model F (p)', 'BIC', 'WAIS-IV', 'WAIS X Sex', 'WAIS X Class', 'WAIS X Sex X Class',
'Sex (F)', 'Class (Active)', 'Sex X Class',
'Age', 'Years in Univ.', 'BetterThanSimple']
mi = pd.MultiIndex.from_product([iterables['tasks'],
iterables['masks'],
iterables['metrics'],
iterables['iq_vars']])
df_res_intrxn = pd.DataFrame(columns=columns, index=mi)
do_i_make_figures = pd.DataFrame(columns=columns, index=mi)
resid_df = pd.DataFrame(columns=intrxn.keys(), index=imp_df.index)
for key in intrxn.keys():
keys = key.split('_')
if compar[key]['Pr(>F)'][1] < 0.01:
df_res_intrxn.at[(keys[0], keys[1], keys[2], keys[3]),
'BetterThanSimple'] = compar[key]['Pr(>F)'][1]
summ = intrxn[key].get_robustcov_results()
resid_df[key] = intrxn[key].resid
if summ.f_pvalue < adj_a:
do_i_make_figures.at[(keys[0], keys[1], keys[2], keys[3]),
'Model F (p)'] = 10
df_res_intrxn.at[(keys[0], keys[1], keys[2], keys[3]),
'Model F (p)'] = '{0} ({1})'.format(np.round(summ.fvalue[0][0],3),
np.format_float_scientific(summ.f_pvalue,
precision=3,
exp_digits=2))
df_res_intrxn.at[(keys[0], keys[1], keys[2], keys[3]),
'BIC'] = np.round(summ.bic,1)
if summ.pvalues[1] < 0.01:
dec = '**'
elif summ.pvalues[1] < 0.051:
dec = '*'
do_i_make_figures.at[(keys[0], keys[1], keys[2], keys[3]),
'WAIS-IV'] = 10
else:
dec = ''
df_res_intrxn.at[(keys[0], keys[1], keys[2], keys[3]),
'WAIS-IV'] = '{0}{1}'.format(np.round(summ.params[1], 3), dec)
if summ.pvalues[2] < 0.01:
dec = '**'
elif summ.pvalues[2] < 0.051:
do_i_make_figures.at[(keys[0], keys[1], keys[2], keys[3]),
'Sex (F)'] = 10
dec = '*'
else:
dec = ''
df_res_intrxn.at[(keys[0], keys[1], keys[2], keys[3]),
'Sex (F)'] = '{0}{1}'.format(np.round(summ.params[2], 3), dec)
if summ.pvalues[3] < 0.01:
dec = '**'
elif summ.pvalues[3] < 0.051:
dec = '*'
do_i_make_figures.at[(keys[0], keys[1], keys[2], keys[3]),
'WAIS X Sex'] = 10
else:
dec = ''
df_res_intrxn.at[(keys[0], keys[1], keys[2], keys[3]),
'WAIS X Sex'] = '{0}{1}'.format(np.round(summ.params[3], 3), dec)
if summ.pvalues[4] < 0.01:
dec = '**'
elif summ.pvalues[4] < 0.051:
dec = '*'
do_i_make_figures.at[(keys[0], keys[1], keys[2], keys[3]),
'Class (Active)'] = 10
else:
dec = ''
df_res_intrxn.at[(keys[0], keys[1], keys[2], keys[3]),
'Class (Active)'] = '{0}{1}'.format(np.round(summ.params[4], 3), dec)
if summ.pvalues[5] < 0.01:
dec = '**'
elif summ.pvalues[5] < 0.051:
dec = '*'
do_i_make_figures.at[(keys[0], keys[1], keys[2], keys[3]),
'WAIS X Class'] = 10
else:
dec = ''
df_res_intrxn.at[(keys[0], keys[1], keys[2], keys[3]),
'WAIS X Class'] = '{0}{1}'.format(np.round(summ.params[5], 3), dec)
if summ.pvalues[6] < 0.01:
dec = '**'
elif summ.pvalues[6] < 0.051:
dec = '*'
do_i_make_figures.at[(keys[0], keys[1], keys[2], keys[3]),
'Sex X Class'] = 10
else:
dec = ''
df_res_intrxn.at[(keys[0], keys[1], keys[2], keys[3]),
'Sex X Class'] = '{0}{1}'.format(np.round(summ.params[6], 3), dec)
if summ.pvalues[7] < 0.01:
dec = '**'
elif summ.pvalues[7] < 0.051:
dec = '*'
do_i_make_figures.at[(keys[0], keys[1], keys[2], keys[3]),
'WAIS X Sex X Class'] = 10
else:
dec = ''
df_res_intrxn.at[(keys[0], keys[1], keys[2], keys[3]),
'WAIS X Sex X Class'] = '{0}{1}'.format(np.round(summ.params[7], 3), dec)
if summ.pvalues[8] < 0.01:
dec = '**'
elif summ.pvalues[8] < 0.051:
dec = '*'
do_i_make_figures.at[(keys[0], keys[1], keys[2], keys[3]),
'Age'] = 10
else:
dec = ''
df_res_intrxn.at[(keys[0], keys[1], keys[2], keys[3]),
'Age'] = '{0}{1}'.format(np.round(summ.params[8], 3), dec)
if summ.pvalues[9] < 0.01:
dec = '**'
elif summ.pvalues[9] < 0.051:
dec = '*'
do_i_make_figures.at[(keys[0], keys[1], keys[2], keys[3]),
'Years in Univ.'] = 10
else:
dec = ''
df_res_intrxn.at[(keys[0], keys[1], keys[2], keys[3]),
'Years in Univ.'] = '{0}{1}'.format(np.round(summ.params[9], 3), dec)
df_res_intrxn.to_csv(join(data_dir, 'output', 'brain_metrics~iq-ols_robust-knn_imp-interaction.csv'))
df_res_intrxn.head()
# -
do_i_make_figures.dropna(how='all').to_csv(join(data_dir, 'do_I_make_figs', 'FIGS-brain_metrics~iq-ols_robust-knn_imp-interaction.csv'))
# # time for figures!
fig_df = pd.concat([imp_df, resid_df], axis=1)
# +
crayons_l = sns.crayon_palette(['Vivid Tangerine', 'Cornflower'])
crayons_d = sns.crayon_palette(['Brick Red', 'Midnight Blue'])
f = sns.diverging_palette(8.2, 44, s=85, l=50, n=200)
m = sns.diverging_palette(243, 278, s=85, l=50, n=200)
f_2 = sns.crayon_palette(['Red Orange', 'Vivid Tangerine'])
m_2 = sns.crayon_palette(['Cerulean', 'Cornflower'])
# -
fig_df.columns[20:]
fig_df['post_phys_fci_crad_eff']
# # Physics Retrieval & PRIQ
# +
h = sns.lmplot('deltaFSIQ', 'fci_shen_eff_deltaFSIQ', data=fig_df,
hue='F', hue_order=[1.0,0.0], palette=crayons_d, height=10.)
#h.set_xlabels('Post-instruction perceptual reasoning')
#h.set_ylabels('Post-instruction efficiency')
#h.savefig(join(fig_dir, 'RETR_phys_post-cplXpost-priq_m.png'), dpi=300)
# +
h = sns.lmplot('PRI2', 'post phys retr shen cpl', data=df_f, hue='Mod',
palette=f_2, legend_out=True, height=10.)
h.set_xlabels('Post-instruction perceptual reasoning')
h.set_ylabels('Post-instruction characteristic path length')
h.savefig(join(fig_dir, 'RETR_phys_post-cplXpost-priq_f.png'), dpi=300)
# -
# # General retrieval and deltaPRIQ
# +
h = sns.lmplot('deltaPRI', 'post gen retr shen mod', data=df_m, hue='Mod',
palette=m_2, legend_out=True, height=10.)
h.set_xlabels('Change in perceptual reasoning')
h.set_ylabels('Post-instruction network modularity')
h.savefig(join(fig_dir, 'RETR_gen_post-modXdelta-priq_m.png'), dpi=300)
# +
h = sns.lmplot('deltaPRI', 'post gen retr shen mod', data=df_f, hue='Mod',
palette=f_2, legend_out=True, height=10.)
h.set_xlabels('Change in perceptual reasoning')
h.set_ylabels('Post-instruction network modularity')
h.savefig(join(fig_dir, 'RETR_gen_post-modXdelta-priq_f.png'), dpi=300)
# -
# # Physics Retrieval & FSIQ
# +
h = sns.lmplot('FSIQ2', 'post phys retr shen cpl', data=df_m, hue='Mod',
palette=m_2, legend_out=True, height=10.)
h.set_xlabels('Post-instruction full-scale IQ')
h.set_ylabels('Post-instruction network efficiency')
h.savefig(join(fig_dir, 'RETR_phys_post-cplXpost-fsiq_m.png'), dpi=300)
# +
h = sns.lmplot('FSIQ2', 'post phys retr shen cpl', data=df_m, hue='Mod',
palette=m_2, legend_out=True, height=10.)
h.set_xlabels('Post-instruction full-scale IQ')
h.set_ylabels('Post-instruction characteristic path length')
#h.savefig(join(fig_dir, 'pre_prXpre_eff_inf-m.png'), dpi=300)
# +
h = sns.lmplot('FSIQ2', 'post phys retr shen cpl', data=df_f, hue='Mod',
palette=f_2, legend_out=True, height=10.)
h.set_xlabels('Post-instruction full-scale IQ')
h.set_ylabels('Post-instruction network-efficiency')
h.savefig(join(fig_dir, 'RETR_phys_post-cplXpost-fsiq_f.png'), dpi=300)
# +
h = sns.lmplot('FSIQ2', 'post phys retr shen cpl', data=df_f, hue='Mod',
palette=f_2, legend_out=True, height=10.)
h.set_xlabels('Post-instruction full-scale IQ')
h.set_ylabels('Post-instruction characteristic path length')
#h.savefig(join(fig_dir, 'pre_prXpre_eff_inf-m.png'), dpi=300)
# -
# # FCI and PRIQ
# +
h = sns.lmplot('PRI2', 'post phys fci shen cpl', data=df_f, hue='Mod',
palette=f_2, legend_out=True, height=10.)
h.set_xlabels('Post-instruction perceptual reasoning')
h.set_ylabels('Post-instruction characteristic path length')
h.savefig(join(fig_dir, 'FCI_phys_post-cplXpost-priq_f.png'), dpi=300)
# +
h = sns.lmplot('PRI2', 'post phys fci shen cpl', data=df_m, hue='Mod',
palette=m_2, legend_out=True, height=10.)
h.set_xlabels('Post-instruction perceptual reasoning')
h.set_ylabels('Post-instruction characteristic path length')
h.savefig(join(fig_dir, 'FCI_phys_post-cplXpost-priq_m.png'), dpi=300)
# -
# # FCI and FSIQ
# +
h = sns.lmplot('FSIQ2', 'post phys fci shen cpl', data=df_m, hue='Mod',
palette=m_2, legend_out=True, height=10.)
h.set_xlabels('Post-instruction full-scale IQ')
h.set_ylabels('Post-instruction characteristic path length')
h.savefig(join(fig_dir, 'FCI_phys_post-cplXpost-fsiq_m.png'), dpi=300)
# +
h = sns.lmplot('FSIQ2', 'post phys fci shen cpl', data=df_f, hue='Mod',
palette=f_2, legend_out=True, height=10.)
h.set_xlabels('Post-instruction full-scale IQ')
h.set_ylabels('Post-instruction characteristic path length')
h.savefig(join(fig_dir, 'FCI_phys_post-cplXpost-fsiq_f.png'), dpi=300)
# +
h = sns.lmplot('deltaFSIQ', 'post phys fci shen eff', data=df_m, hue='Mod',
palette=m_2, legend_out=True, height=10.)
h.set_xlabels('Change in full-scale IQ')
h.set_ylabels('Post-instruction network efficiency')
h.savefig(join(fig_dir, 'FCI_phys_post-effXdelta-fsiq_m.png'), dpi=300)
# +
h = sns.lmplot('deltaPRI', 'post phys fci shen eff', data=df_m, hue='Mod',
palette=m_2, legend_out=True, height=10.)
h.set_xlabels('Change in perceptual reasoning')
h.set_ylabels('Post-instruction network efficiency')
h.savefig(join(fig_dir, 'FCI_phys_post-effXdelta-priq_m.png'), dpi=300)
# +
h = sns.lmplot('deltaFSIQ', 'post phys fci shen eff', data=df_f, hue='Mod',
palette=f_2, legend_out=True, height=10.)
h.set_xlabels('Change in full-scale IQ')
h.set_ylabels('Post-instruction network efficiency')
h.savefig(join(fig_dir, 'FCI_phys_post-effXdelta-fsiq_f.png'), dpi=300)
# +
h = sns.lmplot('deltaPRI', 'post phys fci shen eff', data=df_f, hue='Mod',
palette=f_2, legend_out=True, height=10.)
h.set_xlabels('Change in perceptual reasoning')
h.set_ylabels('Post-instruction network efficiency')
h.savefig(join(fig_dir, 'FCI_phys_post-effXdelta-priq_f.png'), dpi=300)
# -
# # Reasoning and WMIQ
# +
h = sns.lmplot('WMI1', 'delta infr reas shen eff', data=df_f, hue='Mod',
palette=f_2, legend_out=True, height=10.)
h.set_xlabels('Pre-instruction working memory')
h.set_ylabels('Change in network efficiency')
h.savefig(join(fig_dir, 'REAS_infr_delta-effXpre-wmiq_f.png'), dpi=300)
# +
h = sns.lmplot('WMI1', 'delta infr reas shen eff', data=df_m, hue='Mod',
palette=m_2, legend_out=True, height=10.)
h.set_xlabels('Pre-instruction working memory')
h.set_ylabels('Change in network efficiency')
h.savefig(join(fig_dir, 'REAS_infr_delta-effXpre-wmiq_m.png'), dpi=300)
# -
import seaborn as sns
sns.set()
| 38,010 |
/.ipynb_checkpoints/Fashion_Recognization-checkpoint.ipynb | 3dc380a48654b487db0c0c5890b385bbb480b5ec | [] | no_license | chrehman/Mnist_Dataset_Models | https://github.com/chrehman/Mnist_Dataset_Models | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 8,830 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="0O88LX8mS6tq"
# Importing Libraries
import tensorflow as tf
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
# %matplotlib inline
import tensorflow as tf
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.layers import Dense
from tensorflow.keras.callbacks import EarlyStopping
# + id="MO-FmOq2uPkd" colab={"base_uri": "https://localhost:8080/"} outputId="b22f16e9-26c5-4c9e-fa3c-71dd866cdbb8"
# Downloading the dataset
# !wget http://www.timeseriesclassification.com/Downloads/ECG5000.zip
# + id="nb0JSJt4TfIU" colab={"base_uri": "https://localhost:8080/"} outputId="30b27477-7e82-4b56-df0e-e898a754fa82"
# Unzipping the datasset
# !unzip ECG5000.zip
# + id="HvNPdOY5UblP"
# Concatenating the train and test file into a single file named 'ecg_final.txt'
# !cat ECG5000_TRAIN.txt ECG5000_TEST.txt > ecg_final.txt
# + colab={"base_uri": "https://localhost:8080/"} id="wLQ_IB5OVA_9" outputId="b371501b-70e9-4cf0-d669-bc50f54a218f"
# Displaying the head of the file
# !head ecg_final.txt
# + colab={"base_uri": "https://localhost:8080/"} id="Uw5I0GkpVDXo" outputId="85766cfa-fd74-464a-9d0f-fb9cb96ec785"
# Importing the finla file in pandas dataframe
df = pd.read_csv('ecg_final.txt', sep = ' ', header = None)
# + colab={"base_uri": "https://localhost:8080/", "height": 244} id="OZPhrDDHVSSM" outputId="ef44455e-0418-4e15-9429-a89e4921ee50"
df.head()
# + colab={"base_uri": "https://localhost:8080/"} id="Fzym5dVeWnk-" outputId="dba3db57-4f77-4b69-dac9-7cbb58f29727"
df.shape
# + colab={"base_uri": "https://localhost:8080/"} id="OoGCLjLXWswm" outputId="8ce1f2f1-0eb5-4b10-8854-d24b798d9344"
df.columns
# + id="TQvkVo9JW9n0"
# Adding prefix to column names so that we can easily reference them
# Original file did not contain column names so pandas creates numeric column names automatically that cannot be referenced easily
df = df.add_prefix('c')
# + colab={"base_uri": "https://localhost:8080/"} id="0P5OZXKVXB2s" outputId="5db2291b-9e93-4dca-a86f-e3b77eba6387"
df.columns
# + colab={"base_uri": "https://localhost:8080/"} id="h1npThR4WuNp" outputId="6072a912-1bb4-4774-bd15-a95a104bfef6"
# Counting the data points of diffrent labels
df['c0'].value_counts()
# + id="PtS2F_WpW2ht" colab={"base_uri": "https://localhost:8080/", "height": 333} outputId="d3406954-5c8c-466f-e028-406a169452c3"
df.describe()
# + id="LlQLRGDiMFQO"
# splitting into train test data
train_data, test_data, train_labels, test_labels = train_test_split(df.values, df.values[:, 0:1], test_size = 0.2, random_state = 111)
# + id="oCvQlVU3MFHv"
# Initializing a MinMax Scaler
scaler = MinMaxScaler()
# Fitting the train data to the scaler
data_scaled = scaler.fit(train_data)
# + id="hI8x30UHNEqC"
# Scaling dataset according to weights of train data
train_data_scaled = data_scaled.transform(train_data)
test_data_scaled = data_scaled.transform(test_data)
# + colab={"base_uri": "https://localhost:8080/"} id="wtqcxS4iNPfw" outputId="193a49f8-24e0-4c15-801d-9d1bde4f6e1e"
train_data.shape
# + id="OYOUUgmTNQ8X"
# Making pandas dataframe for the normal and anomaly train data points
normal_train_data = pd.DataFrame(train_data_scaled).add_prefix('c').query('c0 == 0').values[:, 1:]
anomaly_train_data = pd.DataFrame(train_data_scaled).add_prefix('c').query('c0 > 0').values[:, 1:]
# + colab={"base_uri": "https://localhost:8080/"} id="esn2M24NP3Em" outputId="3eeeea1b-5e75-45ed-de0f-0c7377cfb5cf"
anomaly_train_data
# + id="ITVZR-beOYvI"
# Making pandas dataframe for the normal and anomaly test data points
normal_test_data = pd.DataFrame(test_data_scaled).add_prefix('c').query('c0 == 0').values[:, 1:]
anomaly_test_data = pd.DataFrame(test_data_scaled).add_prefix('c').query('c0 > 0').values[:, 1:]
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="S2ligR14O2Yk" outputId="da6da3d0-72ca-4220-de6e-5035c3d1e5e8"
# plotting the first three normal data points
plt.plot(normal_train_data[0])
plt.plot(normal_train_data[1])
plt.plot(normal_train_data[2])
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="MTzbDn_XPVJP" outputId="760b543d-dcd2-4e67-b6b9-3541e29d5f69"
# plotting the first three anomaly data points
plt.plot(anomaly_train_data[0])
plt.plot(anomaly_train_data[1])
plt.plot(anomaly_train_data[2])
# + id="8lvdVfHGPtKB"
class Autoencoder(Model):
def __init__(self):
super(Autoencoder, self).__init__()
self.encoder = Sequential([
Dense(64, activation='relu'),
Dense(32, activation='relu'),
Dense(16, activation='relu'),
Dense(8, activation='relu')
])
self.decoder = Sequential([
Dense(16, activation='relu'),
Dense(32, activation='relu'),
Dense(64, activation='relu'),
Dense(140, activation='sigmoid')
])
def call(self,x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
# + id="EaejgzKQfrGC"
# Instantiating the Autoencoder
model = Autoencoder()
# creating an early_stopping
early_stopping = EarlyStopping(monitor='val_loss',
patience = 2,
mode = 'min')
# Compiling the model
model.compile(optimizer = 'adam',
loss = 'mae')
# + colab={"base_uri": "https://localhost:8080/"} id="5iLAZNQNg3m1" outputId="2e0ef3e6-a0db-4e7f-9ffc-ae9f82596e2d"
# Training the model
history = model.fit(normal_train_data,normal_train_data,
epochs = 50,
batch_size = 120,
validation_data = (train_data_scaled[:,1:], train_data_scaled[:,1:]),
shuffle = True,
callbacks = [early_stopping])
# + id="sJaXZqEpg8GE"
# predictions for normal test data points
encoder_out = model.encoder(normal_test_data).numpy()
decoder_out = model.decoder(encoder_out).numpy()
# + colab={"base_uri": "https://localhost:8080/"} id="zLNcwREih5BC" outputId="83f2ed6f-92c2-4824-806e-2de7151dc934"
encoder_out.shape
# + colab={"base_uri": "https://localhost:8080/"} id="V6m0WV80h6rW" outputId="4f2cc0dd-e582-428e-e33a-3a114bf5eec2"
decoder_out.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="lyGlYWPah7_h" outputId="876c8dd2-1a50-4150-d8da-20dc9c62df3a"
# plotting normal test data point and its predictiction by the autoencoder
plt.plot(normal_test_data[0], 'b')
plt.plot(decoder_out[0], 'r')
# + id="m7ZTj6saiJPr"
# predictions for anomaly test data points
encoder_out_a = model.encoder(anomaly_test_data).numpy()
decoder_out_a = model.decoder(encoder_out_a).numpy()
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="P2UI_yvOi33V" outputId="31551fd0-5eaa-42b1-c74e-67982c0b541b"
# plotting anomaly test data point and its predictiction by the autoencoder
plt.plot(anomaly_test_data[0], 'b')
plt.plot(decoder_out_a[0], 'r')
# + colab={"base_uri": "https://localhost:8080/", "height": 349} id="WKWvXpCFjAKu" outputId="a0c48128-28de-44bb-8fe9-ecc107616a09"
# reconstruction loss for normal test data
reconstructions = model.predict(normal_test_data)
train_loss = tf.keras.losses.mae(reconstructions, normal_test_data)
# Plotting histogram for recontruction loss for normal test data
plt.hist(train_loss, bins = 10)
# + colab={"base_uri": "https://localhost:8080/"} id="AdmXLSBaja5j" outputId="4550b752-0670-4a3c-a4fc-c9908f2ff246"
np.mean(train_loss)
# + colab={"base_uri": "https://localhost:8080/"} id="vtW3CBUjjiIU" outputId="e766c857-2dc6-492d-dd45-275cb5962f1b"
np.std(train_loss)
# + colab={"base_uri": "https://localhost:8080/", "height": 349} id="-r38UR6Qjw8M" outputId="ffd1278a-b299-402a-f573-65a9b7f74bc0"
# reconstruction loss for anomaly test data
reconstructions_a = model.predict(anomaly_test_data)
train_loss_a = tf.keras.losses.mae(reconstructions_a, anomaly_test_data)
# Plotting histogram for recontruction loss for anomaly test data
plt.hist(train_loss_a, bins = 10)
# + colab={"base_uri": "https://localhost:8080/"} id="K_6QYRT2kpJQ" outputId="fa0ef513-0b2e-4928-8eb0-169b68bd0d2e"
np.mean(train_loss_a)
# + colab={"base_uri": "https://localhost:8080/"} id="XQikvTQuky7-" outputId="3f139441-04ca-4166-bf53-09388142f1c2"
np.std(train_loss_a)
# + id="dy7SKgIojlJA"
# setting threshold
threshold = np.mean(train_loss) + 2*np.std(train_loss)
# + colab={"base_uri": "https://localhost:8080/"} id="yU2D1OA1ju3-" outputId="7f41e25e-0a15-435c-8141-e742c133a8b1"
threshold
# + colab={"base_uri": "https://localhost:8080/", "height": 265} id="CA9baHE3j-NT" outputId="4caee125-6bbe-449f-c519-c5ffdf8c862a"
# Plotting the normal and anomaly losses with the threshold
plt.hist(train_loss, bins = 10, label = 'Normal')
plt.hist(train_loss_a, bins = 10, label = 'Anomaly')
plt.axvline(threshold, color='r', linewidth = 3, linestyle = 'dashed', label = '{:0.3f}'.format(threshold))
plt.legend(loc = 'upper right')
plt.show()
# + id="YhkCxKbTk1eh"
# Number of correct predictions for Normal test data
preds = tf.math.less(train_loss, threshold)
# + colab={"base_uri": "https://localhost:8080/"} id="6B9m-mfnk-HH" outputId="fc3cdba3-9d8a-4aae-8b78-3e73d98c74b1"
tf.math.count_nonzero(preds)
# + id="c-zCwgsYlI0v"
# Number of correct predictions for Anomaly test data
preds_a = tf.math.greater(train_loss_a, threshold)
# + colab={"base_uri": "https://localhost:8080/"} id="DH0nTPxrlSTi" outputId="4f4af546-41b4-4bc8-8647-c98ad30c9f06"
tf.math.count_nonzero(preds_a)
# + colab={"base_uri": "https://localhost:8080/"} id="w3lKPX8tlaiW" outputId="1d5da799-7a6d-4a97-f312-3a6f1d68e7ef"
preds_a.shape
| 10,060 |
/Neural_Network_Project.ipynb | 937c712784e6bef5c7739f0235a295d95cf22a7c | [] | no_license | msrraju87/NeuralNet_Electronic_Telecom_VHSN | https://github.com/msrraju87/NeuralNet_Electronic_Telecom_VHSN | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 2,744,409 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="lyzPVoSff9b_"
# # Electronics and Telecommunication
# + [markdown] id="FjhqqhjSf9cH"
# We want to build a model that can help the company predict the signal quality using various parameters
# + [markdown] id="M_k1URphf9cJ"
# Let's now do the steps to finally build a model using Neural Nets
# + [markdown] id="QhYZNnAif9cK"
# ### Import libraries
# + id="137nGIQ6f9cM"
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
import os
# + [markdown] id="SsXi6OpBf9cO"
# ### Import data
# + [markdown] id="fn8AXP29gIXA"
# Let's first import the data from google drive
# + colab={"base_uri": "https://localhost:8080/"} id="5XlvJSbJhGmN" outputId="2cf95780-24cb-4cd5-8e1d-7bce96df8899"
from google.colab import drive
drive.mount('/content/drive')
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="d2I61j_chRE1" outputId="25b9f037-2a87-4428-b1c3-3fc2528e9db4"
os.chdir('/content/drive/My Drive/NN')
os.getcwd()
# + id="EeRdrIaof9cP"
signal_data = pd.read_csv('Part- 1 - Signal.csv')
# + [markdown] id="g6oY0_5uf9cR"
# Let' look at a sample of data
# + id="xHU0Ag7Pf9cT" colab={"base_uri": "https://localhost:8080/", "height": 223} outputId="e741e5d7-fed9-419a-ee1c-1e456e64f83e"
signal_data.head()
# + [markdown] id="8WZKbQzKf9cW"
# We can see that we have signal strength variable and that seems to be dependant on 11 parameters
# + [markdown] id="egbNlytOf9cX"
# Let's now look at the shape of the data
# + id="ZQjRtmxMf9cX" colab={"base_uri": "https://localhost:8080/"} outputId="b2682930-f72d-46e2-a0a1-83be909919c6"
signal_data.shape
# + [markdown] id="4uM7iSIjf9cY"
# So we have 11 predictors and 1 predicted variable
# + id="xc0o3Es8f9cZ" colab={"base_uri": "https://localhost:8080/"} outputId="379d345d-5eb4-44c5-93b0-1bc566a759ef"
print(signal_data['Signal_Strength'].max())
print(signal_data['Signal_Strength'].min())
# + [markdown] id="FZVHWHurf9cZ"
# Signal strength varies from 3 to 8
# + [markdown] id="wAQIvM77f9cZ"
# ### Data analysis & visualisation
# + [markdown] id="zi0fErQrf9ca"
# Let's perform a detailed statistical analysis on the data
# + id="EC7XPilhf9ca" colab={"base_uri": "https://localhost:8080/", "height": 425} outputId="48301603-fe6d-4298-f43c-c41d92091f01"
signal_data.describe().transpose()
# + [markdown] id="Pp5qlCBH7gBI"
# From the output we can see all the important statistics like mean, median, standard deviation, 25th percentile, 75th percentile, minimum and maximum
# + [markdown] id="6IUO7dFt71Bn"
# Signal_Strength is the target variable
# + [markdown] id="aP4Z6bgcf9ca"
# Except parameter 7, the other parameters and signal strength look symmetrical. We will plot graphs for these parameters to understand them better
# + [markdown] id="cBpcULNsf9cb"
# Let's now perform a detailed univariate, bivariate and multivariable analyses
# + [markdown] id="keb7CKaIf9cb"
# Univariate
# + id="hpKVPrjMf9cb" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="8259bac8-3aac-456e-9c5c-2b432543c65d"
plt.figure(figsize=(20,20))
plt.subplot(4,3,1)
sns.distplot(signal_data['Parameter 1']);
plt.subplot(4,3,2)
sns.distplot(signal_data['Parameter 2']);
plt.subplot(4,3,3)
sns.distplot(signal_data['Parameter 3']);
plt.subplot(4,3,4)
sns.distplot(signal_data['Parameter 4']);
plt.subplot(4,3,5)
sns.distplot(signal_data['Parameter 5']);
plt.subplot(4,3,6)
sns.distplot(signal_data['Parameter 6']);
plt.subplot(4,3,7)
sns.distplot(signal_data['Parameter 7']);
plt.subplot(4,3,8)
sns.distplot(signal_data['Parameter 8']);
plt.subplot(4,3,9)
sns.distplot(signal_data['Parameter 9']);
plt.subplot(4,3,10)
sns.distplot(signal_data['Parameter 10']);
plt.subplot(4,3,11)
sns.distplot(signal_data['Parameter 11']);
# + [markdown] id="buXo1Nwof9cc"
# From the above plots, it is evident that most of them are not symmetrical. Parameters 6, 7 and 11 are clearly showing signs of deviation from symmetry. Parameter 2 is bimodal and Parameter 3 is trimodal
# + [markdown] id="X9iV3fv6f9cc"
# Bivariate
# + id="vpme_-f5f9cc" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="36c08233-fa5e-444f-a7d3-7371f0390582"
plt.figure(figsize=(20,20))
plt.subplot(4,3,1)
sns.barplot('Signal_Strength','Parameter 1',data=signal_data);
plt.subplot(4,3,2)
sns.barplot('Signal_Strength','Parameter 2',data=signal_data);
plt.subplot(4,3,3)
sns.barplot('Signal_Strength','Parameter 3',data=signal_data);
plt.subplot(4,3,4)
sns.barplot('Signal_Strength','Parameter 4',data=signal_data);
plt.subplot(4,3,5)
sns.barplot('Signal_Strength','Parameter 5',data=signal_data);
plt.subplot(4,3,6)
sns.barplot('Signal_Strength','Parameter 6',data=signal_data);
plt.subplot(4,3,7)
sns.barplot('Signal_Strength','Parameter 7',data=signal_data);
plt.subplot(4,3,8)
sns.barplot('Signal_Strength','Parameter 8',data=signal_data);
plt.subplot(4,3,9)
sns.barplot('Signal_Strength','Parameter 9',data=signal_data);
plt.subplot(4,3,10)
sns.barplot('Signal_Strength','Parameter 10',data=signal_data);
plt.subplot(4,3,11)
sns.barplot('Signal_Strength','Parameter 11',data=signal_data);
# + [markdown] id="VzeJDFxcf9cd"
# We can see that parameters vary across signal strength for most of the parameters. It is only parameter 8 and probably parameter 9 that are constant across signal strength. Overall, the general parameters seem to be good predictors for signal strength
# + [markdown] id="fAtiLHq1f9cd"
# Multivariate
# + id="jnNLagbdf9cd" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="334fc0d4-5416-420d-9eaa-4a905e993213"
sns.pairplot(signal_data);
# + [markdown] id="C51Y8KWDf9cd"
# We can see from the above graph that some of the variables are correlated with each other. There are some violations in our assumptions
# + [markdown] id="6YD-htNMf9ce"
# ### Design, train, tune and test a neural network regressor
# + [markdown] id="-bDsGRLuf9ce"
# Let's now split the input data into train and test and standardize the datasets before feeding them into a neural network
# + id="u_0tyv8Sf9ce"
import tensorflow
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
# + id="IGzbDxu6f9ce"
X = signal_data.drop('Signal_Strength',axis=1)
y = signal_data['Signal_Strength']
# + id="FI6gqIfFf9ce"
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
# + [markdown] id="BjtqM9OQf9ce"
# Let's now normalize the data
# + id="0oNxNulOf9cf"
scale = MinMaxScaler()
# + id="e6cmOWTpf9cf" colab={"base_uri": "https://localhost:8080/"} outputId="deb814eb-1e4e-42dc-ea46-34eb6c0a5b86"
print(X_train.max())
print(X_train.min())
# + [markdown] id="DwiMr74U_tIK"
# We can see that the minimum and maximum values vary very much for the different parameters
# + [markdown] id="8CDaqPBfAD3Y"
# Let's standardize them
# + id="bIFr-8A-f9cf"
X_train = scale.fit_transform(X_train)
X_test = scale.fit_transform(X_test)
# + id="BvtFjcSbf9cf" colab={"base_uri": "https://localhost:8080/"} outputId="f3e330f1-cc58-4b3b-ebbc-441f790ce46d"
print(X_train.max())
print(X_train.min())
# + [markdown] id="-XtOXh95AJBL"
# We can see that the minimum and maximum values are 0 and 1
# + [markdown] id="lfvayYCEf9cg"
# Let's now design a neural network
# + [markdown] id="bzWF0l-ff9cg"
# We will use sigmoid and relu and compare their performances
# + id="puNoEnvNf9cg"
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# + [markdown] id="gMsTV7OGf9ch"
# Sigmoid
# + id="ppfZiWuPf9ch"
model = Sequential()
model.add(Dense(6,input_shape=(11,),activation='sigmoid'))
model.add(Dense(1,activation='linear'))
# + id="q4DQBItyf9ch"
model.compile(loss='mean_squared_error',optimizer='adam',metrics=['mean_squared_error'])
# + id="Bu_LUWy5f9ch" colab={"base_uri": "https://localhost:8080/"} outputId="3ad9ad23-c5b5-4b47-ade5-e5ed85a65142"
model.fit(X_train,y_train,batch_size=32,validation_data=(X_test,y_test),epochs=250)
# + [markdown] id="UrHXt1N1f9ci"
# Relu
# + id="d1L5aoImf9cj"
model = Sequential()
model.add(Dense(6,input_shape=(11,),activation='relu'))
model.add(Dense(1,activation='linear'))
# + id="zrzP3gEGf9cj"
model.compile(loss='mean_squared_error',optimizer='adam',metrics=['mean_squared_error'])
# + id="LqgE0erBf9cj" colab={"base_uri": "https://localhost:8080/"} outputId="abf22662-5521-4fba-ae9a-93be4127bfa7"
model.fit(X_train,y_train,batch_size=32,validation_data=(X_test,y_test),epochs=250)
# + [markdown] id="gykEKN1of9ck"
# We can see that both performed more or less the same
# + [markdown] id="VUcjB-wOf9ck"
# Let's now evaluate the performance. We will go ahead with RELU
# + colab={"base_uri": "https://localhost:8080/"} id="rNKqstjokHPu" outputId="84aa77c0-f5b0-4c3b-c15d-302af594d5db"
model.evaluate(x=X_test, y=y_test, batch_size=32, verbose=1)
# + [markdown] id="b2BhFtENk_4_"
# We can see that the mean squared error is 0.4457
# + [markdown] id="HYcW8-OpEKkF"
# Let's predict the outputs on the test set
# + id="25LzqgoXf9ck"
y_predict = model.predict(X_test)
# + [markdown] id="ShZC1E2vEZsX"
# We will now stack the true signal strength and predicted signal strength of the test data side by side
# + id="TS0bp26bf9cm"
Compare = pd.DataFrame(y_test.reset_index(drop=True)).join(pd.DataFrame([i[0] for i in y_predict]))
Compare.columns = ["Signal_Strength","Signal_Strength_Predict"]
# + id="9nklQMgSf9cm" colab={"base_uri": "https://localhost:8080/", "height": 423} outputId="2532e050-8011-46c4-9d3c-fa0b65d6bcf3"
Compare
# + [markdown] id="89AjGMSoEtiG"
# We will now compare the average values of the predictions to the true strength values
# + id="LkqxaqeIf9cm" colab={"base_uri": "https://localhost:8080/"} outputId="29fa4ad4-2d02-46d2-a113-0cdbd162beda"
Compare.groupby('Signal_Strength').mean()['Signal_Strength_Predict']
# + [markdown] id="yuzrA0XVwNh7"
# In the above table, the true signal strengths are on the left and the predicted signal strengths are on the right
# + [markdown] id="lBxFIMdkE-JE"
# We can see that the mean predicted signal strength shows a gradual increase as the true signal strength increases from 3 to 8 with the exception of 4 and 5 where it dipped a bit. Let's look at the counts of the signal strengths to see if that can explain the deviation
# + id="4rxHkDfcf9cn" colab={"base_uri": "https://localhost:8080/"} outputId="fdb2c470-1422-4866-e701-40231df17850"
y_train.value_counts()
# + [markdown] id="0oxOhzlfFqIp"
# We can see that the values are highly unbalanced. 5 and 6 are represented much higher than others and 4, 8 and 3 are very few. So we can expect that the outputs will be more centered around 5 and 6 and that explains the deviation we saw from the previous output
# + [markdown] id="2SvgXZw1Gm68"
# Let's now look at a scatter plot between signal strength and signal strength predict
# + id="X-HJ0Il1f9cn" colab={"base_uri": "https://localhost:8080/", "height": 280} outputId="792cc0cb-0efb-4eb2-beee-801a10e5a215"
sns.scatterplot('Signal_Strength','Signal_Strength_Predict',data=Compare);
# + [markdown] id="VZWpaaU9Gwt-"
# We can see that there is an increasing trend in the above graph which is in line with our expectations. The predicted Signal Strength values are showing an increasing trend with respect to the actual Signal Strength values. We can see that the points are spread across a lot and we can expect a more closely clustered set of predicions provided we have a more balanced input
# + [markdown] id="Iz0kabGUf9cn"
# ### Pickle the model for future use
# + [markdown] id="_PAnzVbuw3qU"
# We will now save the model for future use
# + id="dn5ebDxXHZbC"
from keras.models import load_model
model.save('/content/drive/My Drive/NN/et_pickle.h5')
# + [markdown] id="iWTWijFcIo3u"
# Deep learning models are too large and may not be pickled using pickle. We used HDF5 for storing the huge file
# + [markdown] id="6cPSEo5Jic-5"
# # Autonomous Vehicles
# + [markdown] id="TYLzkXAMmTI7"
# We will build a digit classifier on the street view housing number dataset
# + [markdown] id="BzK70yv0m54J"
# ### Import the data
# + [markdown] id="1xcQBNn8zCMb"
# Let's now import the input data
# + id="I3-JLxygf9cn"
import h5py
# + id="wZx7qNs8jWww"
f1 = h5py.File('Part - 4 - Autonomous_Vehicles_SVHN_single_grey1.h5')
# + [markdown] id="1A7ZnnLHm-ey"
# ### Data pre-processing and visualisation
# + [markdown] id="k2J5GbFnnTrI"
# Let's look at the contents of the dataset
# + colab={"base_uri": "https://localhost:8080/"} id="qU3BtDccjlpt" outputId="5e4eda33-c4ed-4d90-a080-ec7a073ed140"
list(f1)
# + id="sksZjnRKrQYt"
X_train = np.array(f1['X_train'])
y_train = np.array(f1['y_train'])
X_val = np.array(f1['X_val'])
y_val = np.array(f1['y_val'])
X_test = np.array(f1['X_test'])
y_test = np.array(f1['y_test'])
# + [markdown] id="SJ_vsoQSnl3z"
# Let's look at the shapes of the components we saw above
# + colab={"base_uri": "https://localhost:8080/"} id="vDjICEAdjop7" outputId="7b4c4534-817a-4852-dcf5-a06c4312a5e3"
print(X_train.shape)
print(y_train.shape)
print(X_val.shape)
print(y_val.shape)
print(X_test.shape)
print(y_test.shape)
# + [markdown] id="Aon0QN8coVK_"
# We can see that train data has 42000 records, val data has 60000 records and test data has 18000 records
# + [markdown] id="aV3cN40wophE"
# Let's now look at output
# + colab={"base_uri": "https://localhost:8080/"} id="hANJv7LnkSn7" outputId="13346d25-9eaf-4a82-e7eb-e8cdb4c81210"
f1['y_train'][:]
# + [markdown] id="NQwlo82Cpdnt"
# We will visualize a sample output using matplotlib
# + colab={"base_uri": "https://localhost:8080/", "height": 283} id="_ptPVweykip1" outputId="7d17657c-ac22-453f-a64b-9b4fa178714a"
print("Label : {}".format(f1['y_train'][2]))
plt.imshow(f1['X_train'][2]);
# + [markdown] id="x1hoKXNtGlZA"
# We can see that the above image is 7 and the label is also 7. We can see that the image is not very clear. This makes it challenging for us to create a model to predict it correctly
# + [markdown] id="LY460A-Kp0xY"
# ### Reshape
# + [markdown] id="ynPFrq3THXVV"
# Let's reshape the data so that it can be fed into a network
# + id="Q4H323GDktd8"
X_train = X_train.reshape(42000,1024)
X_val = X_val.reshape(60000,1024)
X_test = X_test.reshape(18000,1024)
# + [markdown] id="w7-eqRnEtc5H"
# Let's look at the maximum values of train, val and test datasets
# + colab={"base_uri": "https://localhost:8080/"} id="ZqP9LCLGqK7Q" outputId="6b32b28a-b611-422f-81e1-103b7638fea4"
print(X_train.max())
print(X_val.max())
print(X_test.max())
# + [markdown] id="GyLBjwkRtpqE"
# Let's now look at the minimum values of train,val and test datasets
# + colab={"base_uri": "https://localhost:8080/"} id="G7SFIOwntWON" outputId="d6e7e900-dc73-4c4d-cd93-19b4acb82f04"
print(X_train.min())
print(X_val.min())
print(X_test.min())
# + [markdown] id="YjVBI2WnuUGW"
# ### Normalize
# + [markdown] id="muOsS6kLuV8m"
# We will now normalize the data by dividing by 254.9745
# + colab={"base_uri": "https://localhost:8080/"} id="VPgXyTAptYgg" outputId="d6553d51-57e8-4985-bb75-4b28b7d4ab20"
print(X_train.max())
print(X_train.min())
X_train = X_train / 254.9745
X_val = X_val / 254.9745
X_test = X_test / 254.9745
print(X_train.max())
print(X_train.min())
# + [markdown] id="_iRugi7eHlwp"
# We can see from the outputs that the data has been normalized
# + [markdown] id="7hy2pAexux2t"
# ### One Hot Encode
# + [markdown] id="1XEg5ALbu0fx"
# We will now one hot encode the class variable
# + colab={"base_uri": "https://localhost:8080/"} id="sMgvzzJuugXV" outputId="12bdc2a9-e00c-4a44-f0c4-4391469266c8"
print(y_train.max())
print(y_train.min())
# + [markdown] id="T5T-1r38u_T8"
# We can see that there are a total of 10 classes starting at 0 and ending at 9
# + colab={"base_uri": "https://localhost:8080/"} id="-dr_yRyDu35q" outputId="254c7fb3-c68f-4874-c5ad-79172b82c65f"
print(y_train[10])
y_train = tensorflow.keras.utils.to_categorical(y_train,num_classes=10)
y_val = tensorflow.keras.utils.to_categorical(y_val,num_classes=10)
y_test = tensorflow.keras.utils.to_categorical(y_test,num_classes=10)
print(y_train[10])
# + [markdown] id="W2hsDWS9H0lO"
# We have converted the output to categorical
# + [markdown] id="zNyDZXrqv2v9"
# We will see some other images and their labels
# + colab={"base_uri": "https://localhost:8080/", "height": 271} id="Lm3piLJmvWMw" outputId="6cf79104-e389-4082-f6bf-4c33c0996462"
plt.figure(figsize=(10,1))
for i in range(10):
plt.subplot(1,10,i+1)
plt.imshow(X_train[i].reshape(32,32))
print('Label is:', np.argmax(y_train[i]))
# + [markdown] id="jKmVj-AXxNo5"
# We can see that the label corresponds to the central digit in each of the images
# + [markdown] id="bT8nDCUKx190"
# ### Design, train, tune and test a neural network image classifier
# + [markdown] id="e6ugyf-exYub"
# Let's start building the model now
# + id="Nh2JSSfWyWge"
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras import regularizers,optimizers
# + [markdown] id="HxwlQYNiyutW"
# We will create a function so that it can be run multiple times so as to tune it to give best performance. We will only use kernel regularizer. We will use other regularization techniques in a later iteration
# + id="F51ay0vTyjvE"
def tune_model(iterations,lr,Lambda):
iterations = iterations
learning_rate = lr
hidden_nodes = 256
output_nodes = 10
model = Sequential()
model.add(Dense(hidden_nodes,input_shape=(1024,),activation='relu'))
model.add(Dense(output_nodes,activation='softmax',kernel_regularizer=regularizers.l2(Lambda)))
adam = optimizers.Adam(learning_rate=learning_rate)
model.compile(loss='categorical_crossentropy',optimizer=adam,metrics=['accuracy'])
model.fit(X_train,y_train,epochs=iterations,validation_data=(X_val,y_val),batch_size=1000)
score = model.evaluate(X_train,y_train,verbose=0)
return score
# + [markdown] id="l8DUmKSj1Onj"
# Now let's check if the loss is reasonable
# + colab={"base_uri": "https://localhost:8080/"} id="HQa0jiUf1Kxe" outputId="e14e167b-daa7-4e19-c1a5-86236466f1a3"
lr=0.00001
Lambda=0
tune_model(1,lr,Lambda)
# + [markdown] id="DgmuIqz92G6_"
# The accuracy of around 10% seems reasonable
# + [markdown] id="i4N27MOx3BzW"
# We will now increase the Lambda value and then check what will happen to the loss
# + colab={"base_uri": "https://localhost:8080/"} id="Jx2BfOlD1ZmU" outputId="3997845f-b5f6-474f-9004-fc60b5210186"
lr=0.00001
Lambda=1e3
tune_model(1,lr,Lambda)
# + [markdown] id="wmuQEpMQ3KbH"
# The loss has gone up which is good
# + [markdown] id="PDufDThH3a1u"
# Now let's start with some random learning rate and lambda values
# + colab={"base_uri": "https://localhost:8080/"} id="H2mO6lBc3HUG" outputId="ea5af36f-e751-43eb-d567-58a12a05c9bc"
lr=1e-7
Lambda=1e-7
tune_model(20,lr,Lambda)
# + [markdown] id="RoCJ5Jyb32yM"
# The learning rate seems too low. Let's now try with a higher learning rate
# + colab={"base_uri": "https://localhost:8080/"} id="h2Qcnshs3nzr" outputId="2c9a2821-e342-4c50-c0e7-6ac1432032ee"
lr=1e7
Lambda=1e-7
tune_model(20,lr,Lambda)
# + [markdown] id="X0x0cBea4UlR"
# Even this is not good. Let's reduce it a bit and retry
# + colab={"base_uri": "https://localhost:8080/"} id="Wg39004w3-jm" outputId="5197b131-bdb5-413f-a586-cc7b9d04d1e8"
lr=1e0
Lambda=1e-7
tune_model(20,lr,Lambda)
# + [markdown] id="sO8XrZo-izPL"
# Since this also has not helped let's now search for learning rate values between 1e-7 and 1e0
# + [markdown] id="V6wwlFwzjLIq"
# Let's now run 10 iterations for different values to scout for the values that give the best accuracies. Let's loop only for 10 times each in order to save time
# + colab={"base_uri": "https://localhost:8080/"} id="fyEUj1jU4ZC_" outputId="21258793-5ea9-4451-81c8-13d4343212fc"
import math
for k in range(1,10):
learning_rate = math.pow(10,np.random.uniform(-7,0))
Lambda = math.pow(10,np.random.uniform(-8,-2))
acc = tune_model(10,learning_rate,Lambda)
print("The parameters for the {} iteration are {} and {}".format(k,learning_rate,Lambda))
# + [markdown] id="zGFqGguslT7q"
# We are getting the best accuracies at 0.0005244331947406066 and 1.4720198871425298e-08 of learning rate and lambda
# + [markdown] id="TL4KMFv4lhZ_"
# Let's now narrow down the search from 1e-7 to 1e-3
# + colab={"base_uri": "https://localhost:8080/"} id="toVKAE_Ukax9" outputId="1c8c9fe6-b04c-4138-919b-7d0461ca9cb8"
import math
for k in range(1,21):
learning_rate = math.pow(10,np.random.uniform(-7,-3))
Lambda = math.pow(10,np.random.uniform(-8,-3))
acc = tune_model(10,learning_rate,Lambda)
print("The parameters for the {} iteration are {} and {}".format(k,learning_rate,Lambda))
# + [markdown] id="JNL4ToUZn4yG"
# We got the best scores at 0.0005142086304466909 and 1.18988841561622e-08 for learning rate and lambda respectively
# + [markdown] id="Ir09iG5rmoD1"
# Let's now run 100 iterations at these values
# + colab={"base_uri": "https://localhost:8080/"} id="9BCZAUFUlvVu" outputId="26092ddc-18f6-4029-8c3a-3d80a3635bff"
learning_rate = 0.0005142086304466909
Lambda = 1.18988841561622e-08
tune_model(100,learning_rate,Lambda)
# + [markdown] id="WyBZsDcVr_7C"
# Final Model
# + colab={"base_uri": "https://localhost:8080/"} id="rEZ2d8rPm86c" outputId="914bf86f-a865-4f62-9f94-9a57dcb4eacc"
iterations = 100
learning_rate = 0.0005142086304466909
Lambda = 1.18988841561622e-08
hidden_nodes = 256
output_nodes = 10
model = Sequential()
model.add(Dense(hidden_nodes,input_shape=(1024,),activation='relu'))
model.add(Dense(output_nodes,activation='softmax',kernel_regularizer=regularizers.l2(Lambda)))
adam = optimizers.Adam(learning_rate=learning_rate)
model.compile(loss='categorical_crossentropy',optimizer=adam,metrics=['accuracy'])
history = model.fit(X_train,y_train,epochs=iterations,validation_data=(X_val,y_val),batch_size=1000)
# + [markdown] id="9RnwiZkWu4z2"
# Let's plot loss vs epochs for training and validation datasets
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="7koVKQOksXgV" outputId="0d03f41f-60cf-4cb8-f582-199757dea24a"
loss_train = history.history['loss']
loss_val = history.history['val_loss']
epochs = range(1,101)
plt.plot(epochs,loss_train,label='Training loss')
plt.plot(epochs,loss_val,label='Validation loss')
plt.title('Training and Validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
# + [markdown] id="5WCh4KcFW9DY"
# We can see that training loss is slightly lower than validation loss at 100 epochs. The difference is very small and doesn't indicate overfitting
# + colab={"base_uri": "https://localhost:8080/"} id="Bun36GC1uIst" outputId="d56c4420-71d2-41f0-aab2-ba861072a504"
for k in history.history.keys():
print(k)
# + [markdown] id="mvlQ88ipWk6l"
# Let's plot accuracy vs epochs for training and validation datasets
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="1ka_jxz6uM3N" outputId="892a2fe4-0192-4bea-a977-7ebd9d6a1596"
acc_train = history.history['accuracy']
acc_val = history.history['val_accuracy']
epochs = range(1,101)
plt.plot(epochs,acc_train,label='Training accuracy')
plt.plot(epochs,acc_val,label='Validation accuracy')
plt.title('Training and Validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
# + [markdown] id="L1k0-m33XKTY"
# The accuracy of training dataset is very slightly greater than that of validation data. Just like we have seen before, here too the difference is very small to indicate any overfit. The model seems to generalize well
# + [markdown] id="1xBCIWxEvjFA"
# Let's now do the final part of predicting on the test dataset
# + id="eknqTc1jvUW0"
y_predict = model.predict(X_test)
# + colab={"base_uri": "https://localhost:8080/"} id="elpvzTEBv1qz" outputId="3782fa00-11b1-4677-a3b0-8649b14b219c"
y_predict.argmax(axis=1)
# + colab={"base_uri": "https://localhost:8080/"} id="32n2YbOev3Fe" outputId="c0b7ace6-9fae-495c-d212-1b355cb6d7aa"
y_test.argmax(axis=1)
# + [markdown] id="nVAfqQPLWs32"
# Let's now calculate some metrics to evaluate how the model performed
# + id="nm4lo9Vrwf8F"
from sklearn.metrics import accuracy_score,confusion_matrix,classification_report
# + colab={"base_uri": "https://localhost:8080/"} id="5IpHtZq5wr2T" outputId="2001736c-ce24-4fc4-9dee-57713a8dab40"
print(accuracy_score(y_predict.argmax(axis=1),y_test.argmax(axis=1)))
# + [markdown] id="ZaONaK-0X8To"
# The overall accuracy of almost 81.22% is slightly less than the accuracy of 84.05% on train and 83.2% on val indicating slight overfitting but it is not very high to warrant our serious attention
# + [markdown] id="dpvxiSBoYSoN"
# Let's now look at confusion matrix and classification report
# + colab={"base_uri": "https://localhost:8080/"} id="vwB4ForAwzpo" outputId="6bb460a3-f811-49e1-d8d0-f2ab869ca122"
print(confusion_matrix(y_predict.argmax(axis=1),y_test.argmax(axis=1)))
# + colab={"base_uri": "https://localhost:8080/"} id="O4efYRERw30e" outputId="7172f29b-c960-4e49-b4dc-f271852d1143"
print(classification_report(y_predict.argmax(axis=1),y_test.argmax(axis=1)))
# + [markdown] id="GzgsQvbpYZPA"
# The precision, recall and f1-score all seem to be doing good
# + [markdown] id="oVzOkQnrkdBU"
# Let's now apply batch normalization and dropout to see if that can improve the results over what l2 regulatization provided. Let's also include an additional layer
# + id="4xjyVpGLnvKE"
from tensorflow.keras.layers import BatchNormalization, Dropout
# + id="a6VjMFY_kvo0"
def tune_model_regularization(iterations,lr):
iterations = iterations
learning_rate = lr
hidden_nodes = 256
output_nodes = 10
model = Sequential()
model.add(Dense(hidden_nodes,input_shape=(1024,),activation='relu'))
model.add(BatchNormalization())
model.add(Dropout(0.2))
model.add(Dense(hidden_nodes,activation='relu'))
model.add(BatchNormalization())
model.add(Dropout(0.2))
model.add(Dense(output_nodes,activation='softmax'))
adam = optimizers.Adam(learning_rate=learning_rate)
model.compile(loss='categorical_crossentropy',optimizer=adam,metrics=['accuracy'])
model.fit(X_train,y_train,epochs=iterations,validation_data=(X_val,y_val),batch_size=1000)
score = model.evaluate(X_train,y_train,verbose=0)
return score
# + [markdown] id="Ax2Uor2ma7cQ"
# Let's now implement the same things we did above
# + colab={"base_uri": "https://localhost:8080/"} id="x7e5godjnbum" outputId="cab70d39-cd78-4db9-870e-bed4dba952ad"
import math
for k in range(1,21):
learning_rate = math.pow(10,np.random.uniform(-7,-3))
acc = tune_model_regularization(10,learning_rate)
print("The learning rate for the {} iteration is {}".format(k,learning_rate))
# + [markdown] id="J355afvxrTaz"
# The best parameter is 0.0003915461454648631
# + [markdown] id="Lbt4WaYerdFu"
# Let's now train for a hundred epochs
# + colab={"base_uri": "https://localhost:8080/"} id="KSvX-xq8m7JX" outputId="0316b242-994e-46f6-f017-4559f1fca135"
learning_rate = 0.0003915461454648631
tune_model_regularization(100,learning_rate)
# + [markdown] id="wz2KrpFEbET1"
# Let's now build the final model
# + colab={"base_uri": "https://localhost:8080/"} id="ziQFh7n7stFe" outputId="4c13b9b2-c699-44f2-a012-4e9c9fee125c"
iterations = 100
learning_rate = 0.0003915461454648631
hidden_nodes = 256
output_nodes = 10
model = Sequential()
model.add(Dense(hidden_nodes,input_shape=(1024,),activation='relu'))
model.add(BatchNormalization())
model.add(Dropout(0.2))
model.add(Dense(hidden_nodes,activation='relu'))
model.add(BatchNormalization())
model.add(Dropout(0.2))
model.add(Dense(output_nodes,activation='softmax'))
adam = optimizers.Adam(learning_rate=learning_rate)
model.compile(loss='categorical_crossentropy',optimizer=adam,metrics=['accuracy'])
history = model.fit(X_train,y_train,epochs=iterations,validation_data=(X_val,y_val),batch_size=1000)
# + [markdown] id="EXeKkLFNIb8N"
# Let's now plot loss vs epochs for both training and validation datasets
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="GnPbELulss4f" outputId="b383a088-32ad-4b74-9243-01b650150578"
loss_train = history.history['loss']
loss_val = history.history['val_loss']
epochs = range(1,101)
plt.plot(epochs,loss_train,label='Training loss')
plt.plot(epochs,loss_val,label='Validation loss')
plt.title('Training and Validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
# + [markdown] id="XN46_RFyIi_y"
# We can see that the loss of validation dataset is showing a high variance. Its values are oscillating around those of the training dataset
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="fP7wtziqsstW" outputId="36aa86fb-b96e-4c5d-bb66-afbb1eb4346b"
acc_train = history.history['accuracy']
acc_val = history.history['val_accuracy']
epochs = range(1,101)
plt.plot(epochs,acc_train,label='Training accuracy')
plt.plot(epochs,acc_val,label='Validation accuracy')
plt.title('Training and Validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
# + [markdown] id="RwX5sgKJJmMG"
# We can see the same variance here as well
# + [markdown] id="0TNh33fSLFxv"
# Let's predict on the test set
# + id="ilsBF0rKssjs"
y_predict = model.predict(X_test)
# + colab={"base_uri": "https://localhost:8080/"} id="8DhQR7HAssSC" outputId="11a711b2-0f96-4a86-c999-8a235eb6e659"
print(accuracy_score(y_predict.argmax(axis=1),y_test.argmax(axis=1)))
# + [markdown] id="h2_m-6jiKIEa"
# The accuracy is 83.6% which is an imporovement over what we saw before
# + colab={"base_uri": "https://localhost:8080/"} id="nbeijZdS2QTT" outputId="5544eab0-8913-4828-ca95-1c7a06b727ef"
print(confusion_matrix(y_predict.argmax(axis=1),y_test.argmax(axis=1)))
# + colab={"base_uri": "https://localhost:8080/"} id="XjdUnyiw2QKV" outputId="99ef80e6-b305-41e2-f6d7-81cc9dfa8907"
print(classification_report(y_predict.argmax(axis=1),y_test.argmax(axis=1)))
# + [markdown] id="RIwvcALPbsJD"
# From the above results, we can see that the second model produced better accuracy but on the flipside the variance increased a bit. If accuracy is of the utmost importance for us, we can go ahead with model 2 but if stability also is needed, then perhaps we can go ahead with model 1.
# + id="VJje-oYj2QAA"
# + id="vLRxS9cZ2P0Z"
# + id="Mk1nBgIKsrsq"
# + id="3HkeKZ_8xQlN"
| 30,711 |
/homework/Day_044_HW.ipynb | 1bd24d31a74d2c2cc853507532ea78a3cd86c89b | [] | no_license | kimshih/2nd-ML100Days | https://github.com/kimshih/2nd-ML100Days | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 34,270 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## [H重點]
# 確保你了解隨機森林模型中每個超參數的意義,並觀察調整超參數對結果的影響
# ## H
#
# 1. 試著調整 RandomForestClassifier(...) 中的參數,並觀察是否會改變結果?
# 2. 改用其他資料集 (boston, wine),並與回歸模型與決策樹的結果進行比較
# ### Random Forest x Boston 效果比Decision Tree 好很多 50%
# #### RandomForestRegressor(n_estimators=30, max_depth=8) 降很多
# > MSE = 13.2
from sklearn import datasets, metrics
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
# +
boston_housing = datasets.load_boston()
# 切分訓練集/測試集
x_train, x_test, y_train, y_test = train_test_split(boston_housing.data, boston_housing.target, test_size=0.25, random_state=4)
# 建立模型 (使用 20 顆樹,每棵樹的最大深度為 4)
rlf = RandomForestRegressor(n_estimators=20, max_depth=4)
rlf.fit(x_train, y_train)
y_pred = rlf.predict(x_test)
mse = metrics.mean_squared_error(y_test, y_pred)
print("Baseline MSE: ", mse)
# -
n_estimators =[20,40,60,80,100]
mse = []
for e in n_estimators :
rlf = RandomForestRegressor(n_estimators=e, max_depth=4)
rlf.fit(x_train, y_train)
y_pred = rlf.predict(x_test)
mse.append(metrics.mean_squared_error(y_test, y_pred))
# +
import numpy as np
import matplotlib.pyplot as plt
# 將結果繪圖
plt.plot((np.array(n_estimators)),
mse, label="MSE")
plt.ylabel("MSE")
plt.xlabel("n_estimator")
plt.legend()
# -
max_depth =[2,4,6,8,10]
mse = []
for m in max_depth :
rlf = RandomForestRegressor(n_estimators=30, max_depth=m)
rlf.fit(x_train, y_train)
y_pred = rlf.predict(x_test)
mse.append(metrics.mean_squared_error(y_test, y_pred))
# +
# 將結果繪圖
plt.plot((np.array(max_depth)),
mse, label="MSE")
plt.ylabel("MSE")
plt.xlabel("max_depth")
plt.legend()
# -
rlf = RandomForestRegressor(n_estimators=30, max_depth=8)
rlf.fit(x_train, y_train)
y_pred = rlf.predict(x_test)
print(metrics.mean_squared_error(y_test, y_pred))
# ### Decision Tree x Boston
# > MSE=27.9
# +
from sklearn.tree import DecisionTreeRegressor
drg = DecisionTreeRegressor()
drg.fit(x_train, y_train)
y_pred = drg.predict(x_test)
dmse = metrics.mean_squared_error(y_test, y_pred)
print("DT MSE: ", dmse)
# -
| 2,353 |
/openCV入门/.ipynb_checkpoints/Untitled-checkpoint.ipynb | ef07fdb7a5f8ed63de8ac9ff67355f776ffd6c87 | [] | no_license | yaolinxia/ComputerView | https://github.com/yaolinxia/ComputerView | 2 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 5,297 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from PIL import Image, ImageFont, ImageDraw
import numpy as np
import cv2
height =2
width = 5
img = Image.new("1",(height, width), 1)
# img = np.ones((height, width), dtype=float) * 255
print(img)
draw = ImageDraw.Draw(img)
print(draw)
# cv2.imshow('draw', draw)
# +
#coding=utf-8
import cv2
import numpy as np
img = cv2.imread('image0.jpg',0)
#OpenCV定义的结构元素
kernel = cv2.getStructuringElement(cv2.MORPH_RECT,(3, 3))
#腐蚀图像
eroded = cv2.erode(img,kernel)
#显示腐蚀后的图像
cv2.imshow("Eroded Image",eroded);
#膨胀图像
dilated = cv2.dilate(img,kernel)
#显示膨胀后的图像
cv2.imshow("Dilated Image",dilated);
#原图像
cv2.imshow("Origin", img)
"""
#NumPy定义的结构元素
NpKernel = np.uint8(np.ones((3,3)))
Nperoded = cv2.erode(img,NpKernel)
#显示腐蚀后的图像
cv2.imshow("Eroded by NumPy kernel",Nperoded);
cv2.waitKey(0)
cv2.destroyAllWindows()
"""
# +
import numpy as np
import cv2
font = cv2.FONT_HERSHEY_SIMPLEX#默认字体
im = np.zeros((50,50,3),np.uint8)
img2 = cv2.putText(im, '3', (0, 40), font, 1.2, (255, 255, 255), 2)
cv2.imshow('dst', img2)
#img2.show()
# -
import numpy as np
import cv2
from PIL import ImageFont, ImageDraw, Image
width = 16#宽
height = 70#高
img = Image.new("1", (width, height), 1)#白色
oad image file.
from PIL import Image
import requests
from io import BytesIO
response = requests.get('https://raw.githubusercontent.com/JetBrains/lets-plot/master/docs/examples/images/fisher_boat.png')
image = Image.open(BytesIO(response.content))
img = np.asarray(image)
img.shape
# -
# ### Create 2 x 3 array of images
#
# Fill array with the same image.
rows = 2
cols = 3
X = np.empty([rows, cols], dtype=object)
X.fill(img)
# ### Display images in 2 x 3 grid
gg_image_matrix(X)
# ### Images in the grid can be of different sizes
# +
# Lets vary size of images in the matrix
X1 = np.empty([rows, cols], dtype=object)
for row in range(rows):
for col in range(cols):
v = (col + row + 1) * 10
X1[row][col] = img[v:-v,v:-v,:]
gg_image_matrix(X1)
# -
# ### Normalization in gray-scale image
#
# By default, luminosity images get normalized so that each image have values in the range [0,255].
# First, transform RGB image to grayscale image.
# Select only one `R` channel:
img_gs = img[:,:,0]
# This function will alter the range of values in an image (for demo purposes).
def _degrade(grayscale_img:np.ndarray, v:float):
# Drop all values less then v
# Subtract v from all other values
h, w = grayscale_img.shape
for row in range(h):
for col in range(w):
if grayscale_img[row][col] < v:
grayscale_img[row][col] = 0.
else:
grayscale_img[row][col] -= v
# Now lets fill a 2D array with images, applying `_degrade()` function on each iteration. The last image added is "degraded" the most.
# +
X2 = np.empty([rows, cols], dtype=object)
for row in range(rows):
for col in range(cols):
print('[%d][%d] input image range: [%f,%f]' % (row, col, img_gs.min(), img_gs.max()))
X2[row][col] = img_gs
img_gs = img_gs.copy()
_degrade(img_gs, v=.1)
# -
# ### Display images in grid with normalization (default)
gg_image_matrix(X2)
#
# ### Display images in grid with NO normalization
#
# It's important to remember that the input values are expected to be in the range [0, 255].
# In our example the values are in the range [0, 1] and without normalization the image is just too dark.
gg_image_matrix(X2, norm=False)
# ### Display images in grid with NO normalization (fixed)
#
# To be able to see images without normalization we will first map [0, 1] range to [0, 255] range and then "degrade" the images once again.
img_gs255 = np.vectorize(lambda v: v * 255.)(img[:,:,0])
X3 = np.empty([rows, cols], dtype=object)
for row in range(rows):
for col in range(cols):
print('[%d][%d] input image range: [%d,%d]' % (row, col, img_gs255.min(), img_gs255.max()))
X3[row][col] = img_gs255
img_gs255 = img_gs255.copy()
_degrade(img_gs255, v=30)
gg_image_matrix(X3, norm=False)
# ### Scaling image size
#
# In case the image size is too small or too big to show, the displayed dimentions can be changed using the parameter `scale`.
#
# For example,`digits` dataset from `sklearn` package contains very small 8x8 pictures of digits.
# Load `digits` form sklearn.
from sklearn.datasets import load_digits
digits_bunch = load_digits()
digits_data = digits_bunch.data
# Create 4x4 ndarray containing the first 16 digits in from `digits` dataset.
cols = 4
rows = 4
X4 = np.empty((rows, cols), dtype=object)
for row in range(rows):
for col in range(cols):
i = row * cols + col;
digit_data = digits_data[i]
digit_img = digit_data.reshape(8, 8)
X4[row][col] = digit_img
X4[0][0].shape
# ### Scale Up
#
# Each digit image is 8x8 px. Multiply by 15 to see 120x120 px images.
gg_image_matrix(X4, scale=15)
# ### Scale Down
#
# Use values < 1. to see smaller images.
gg_image_matrix(X, scale=.3)
| 5,249 |
/Victor.ipynb | 2f0a9b410c4ca175bc138c2296743d586bcc78c5 | [] | no_license | sostrikov/juputer | https://github.com/sostrikov/juputer | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 479,481 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# !pip install pandas
# !pip install sklearn
# !pip install matplotlib
# # Репозиторий !!!!
# UCI (UCI Machine Learning Repository)
# https://archive.ics.uci.edu/ml/datasets.php
# http://econ.sciences-po.fr/thierry-mayer/data
# https://towardsdatascience.com/top-sources-for-machine-learning-datasets-bb6d0dc3378b
#
# ## https://github.com/jupyter/jupyter/wiki/A-gallery-of-interesting-Jupyter-Notebooks#economics-and-finance
#
# https://github.com/rsvp/fecon235/blob/master/nb/fred-eurozone.ipynb
#
# Пример решения задачи множественной регрессии с помощью Python
# ## Загружаем необходимые библиотеки и файл с данными
import pandas as pd
from pandas import read_csv, DataFrame
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.svm import SVR
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
#from sklearn.cross_validation import train_test_split
from sklearn.model_selection import train_test_split
from matplotlib import pyplot as plt
plt.style.use('ggplot')
#plt.style.use('seaborn-pastel')
print(plt.style.available)
# %matplotlib inline
#Загружаем данные из файла
dataset = pd.read_csv('ENB2012_data.csv',decimal=",",delimiter=";")
# Выводим верхние строки таблицы
dataset.head()
# ## Проверяем на наличие нужных колонок и отсутствие пустых колонок
dataset.columns
# ## Проверяем корректность типов данных
print(dataset.info())
# ## Проверяем на наличие нулевых (NULL) данных
dataset.isnull().values.any()
# ## Определяем размерность данных
dataset.shape
# ## Получим некоторую сводную информацию по всей таблице.
# Это общее их количество (count), среднее значение (mean), стандартное отклонение (std), минимальное (min), макcимальное (max) значения, медиана (50%) и значения нижнего (25%) и верхнего (75%) квартилей:
# +
dataset.describe()
#dataset.groupby('Y1')['Y2'].describe()
# -
# ## Определяем корреляцию между ячейками
#
# Построим корреляционную матрицу. Все ее недиагональные положительнын значения относительно Y1 и Y2
dataset.corr()
# ## Уберем лишние столбцы
#
# ### Еще можно удалить строки или столбцы с пустыми значениями:
# удалить столбцы с такими значениями (dataset = dataset.dropna(axis=1)),
# удалить строки с такими значениями (dataset = dataset.dropna(axis=0)).
# ### Можно заполнить элементы с пустыми значениями
# dataset = dataset.fillna(dataset.median(axis=0), axis=0)
#
# +
dataset = dataset.drop(['X2','X4','X7'], axis=1)
dataset.head()
# -
# ## Построим диаграмму рассеивания
dataset.plot.scatter(x='Y1', y='Y2', color = 'green')
plt.title('Зависимость Y2 от Y1')
# Функция scatter_matrix из модуля pandas.plotting позволяет построить для каждой количественной переменной гистограмму, а для каждой пары таких переменных – диаграмму рассеяния:
from pandas.plotting import scatter_matrix
scatter_matrix(dataset, alpha=0.05, figsize=(10, 10));
# ## После обработки данных можно перейти к построению модели.
#
# Для построения модели будем использовать следующие методы:
#
# Метод наименьших квадратов
# Случайный лес
# Логистическую регрессию
# Метод опорных векторов
# Метод ближайших соседей
# Оценку будем производить с помощью коэффициента детерминации (R-квадрат). Данный коэффициент определяется следующим образом:
#
# [LaTeX:R^2 = 1 - \frac{V(y|x)}{V(y)} = 1 - \frac{\sigma^2}{\sigma_y^2}]
#
# , где image — условная дисперсия зависимой величины у по фактору х.
# Коэффициент принимает значение на промежутке [LaTeX:[0,1]] и чем он ближе к 1 тем сильнее зависимость.
# Ну что же теперь можно перейти непосредственно к построению модели и выбору модели. Давайте поместим все наши модели в один список для удобства дальнейшего анализа:
models = [LinearRegression(), # метод наименьших квадратов
RandomForestRegressor(n_estimators=100, max_features ='sqrt'), # случайный лес
KNeighborsRegressor(n_neighbors=6), # метод ближайших соседей
SVR(kernel='linear'), # метод опорных векторов с линейным ядром
LogisticRegression() # логистическая регрессия
]
# ## Разбиваем данные на обучающую (30%) и тестовую последовательность(70%) используя train_test_split
# +
#separating independent and dependent variable
trg = dataset[['Y1']] # В качестве управляемых переменных Y1,Y2
trn = dataset.drop(['Y1'], axis=1) # В качестве неуправляемых переменных все X
Xtrain, Xtest, Ytrain, Ytest = train_test_split(trn, trg, test_size=0.3, random_state = 11)
N_train = Xtrain.shape
N_test = Xtest.shape
print (N_train, N_test)
#Ytrain
#Xtrain
# -
# ## Устанавливаем разные типы регрессии, обучаем модель, проверяем модель на тестовых данных.
# ### Линейная регрессия
# +
model1 = LinearRegression()
m1 = str(model1)
model1.fit(Xtrain, Ytrain)
# Predicting the Test set results
Ypred = model1.predict(Xtest)
print("Линейная регрессия - правильность на обучающем наборе: {:.2f}".format(model1.score(Xtrain, Ytrain)))
print("Линейная регрессия - правильность на тестовом наборе: {:.2f}".format(model1.score(Xtest, Ytest)))
# +
X2 = dataset.iloc[:, 5].values # dataset.iloc[:, :-1].values Matrix of independent variables -- remove the last column in this data set
Y2 = dataset.iloc[:, 6].values # Matrix of dependent variables -- just the last column (1 == 2nd column)
# -
# ### Случайный лес
# +
model1= RandomForestRegressor(n_estimators=100, max_features ='sqrt')
m1 = str(model1)
model1.fit(Xtrain, Ytrain)
# Predicting the Test set results
#Ypred = model1.predict(Xtest)
print("Случайный лес - правильность на обучающем наборе: {:.2f}".format(model1.score(Xtrain, Ytrain)))
print("Случайный лес - правильность на тестовом наборе: {:.2f}".format(model1.score(Xtest, Ytest)))
# -
# Мы применили метод score к тестовым данным и тестовым ответам и обнаружили, что наша
# модель демонстрирует правильность около 72%. Это означает, что модель
# выдает правильные прогнозы для 72% наблюдений тестового набора.
# ## Метод ближайших соседей
# +
# SVR(kernel='linear'), # метод опорных векторов с линейным ядром
# LogisticRegression() # логистическая регрессия
model1= KNeighborsRegressor(n_neighbors=4)
m1 = str(model1)
model1.fit(Xtrain, Ytrain)
# Predicting the Test set results
Ypred = model1.predict(Xtest)
print("Ближайших соседей - правильность на обучающем наборе: {:.2f}".format(model1.score(Xtrain, Ytrain)))
print("Ближайших соседей - правильность на тестовом наборе: {:.2f}".format(model1.score(Xtest, Ytest)))
# -
# ## Метод логистическая регрессия
# +
# логистическая регрессия
# create and configure model
model1 = LogisticRegression(solver='lbfgs')
# create and configure model
#model1 = LogisticRegression(solver='lbfgs', multi_class='ovr')
m1 = str(model1)
model1.fit(Xtrain, Ytrain)
# Predicting the Test set results
Ypred = model1.predict(Xtest)
print("Метод опорных векторов с линейным ядром - правильность на обучающем наборе: {:.2f}".format(model1.score(Xtrain, Ytrain)))
print("Метод опорных векторов с линейным ядром - правильность на тестовом наборе: {:.2f}".format(model1.score(Xtest, Ytest)))
# +
#import matplotlib.pyplot as plt
plt.scatter(Xtrain, Ytrain, color = 'green')
plt.scatter(Xtest, Ytest, color = 'red')
plt.scatter(Xtest, Ypred, color = 'blue') # The predicted temperatures of the same X_test input.
plt.plot(Xtrain, model1.predict(Xtrain), color = 'gray')
plt.title('Temperature based on chirp count')
plt.xlabel('Chirps/minute')
plt.ylabel('Temperature')
plt.show()
# -
# # Пример на датасете Бостон
from sklearn.datasets import load_boston
boston = load_boston()
r = boston.data.shape
r
# +
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from distutils.version import LooseVersion
from sklearn.datasets import load_boston
from sklearn.preprocessing import QuantileTransformer, quantile_transform
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import RidgeCV
from sklearn.compose import TransformedTargetRegressor
from sklearn.metrics import median_absolute_error, r2_score
dataset = load_boston()
target = np.array(dataset.feature_names) == "DIS"
X = dataset.data[:, np.logical_not(target)]
y = dataset.data[:, target].squeeze()
y_trans = quantile_transform(dataset.data[:, target],
n_quantiles=300,
output_distribution='normal',
copy=True).squeeze()
# -
# `normed` is being deprecated in favor of `density` in histograms
if LooseVersion(matplotlib.__version__) >= '2.1':
density_param = {'density': True}
else:
density_param = {'normed': True}
X, y = make_regression(n_samples=10000, noise=100, random_state=0)
y = np.exp((y + abs(y.min())) / 200)
y_trans = np.log1p(y)
# +
f, (ax0, ax1) = plt.subplots(1, 2)
ax0.hist(y, bins=100, **density_param)
ax0.set_xlim([0, 2000])
ax0.set_ylabel('Probability')
ax0.set_xlabel('Target')
ax0.set_title('Target distribution')
ax1.hist(y_trans, bins=100, **density_param)
ax1.set_ylabel('Probability')
ax1.set_xlabel('Target')
ax1.set_title('Transformed target distribution')
f.suptitle("Synthetic data", y=0.035)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# -
# # Пример на реальных данных Бостон
# +
from sklearn.datasets import load_boston
from sklearn.preprocessing import QuantileTransformer, quantile_transform
dataset = load_boston()
target = np.array(dataset.feature_names) == "DIS"
X = dataset.data[:, np.logical_not(target)]
y = dataset.data[:, target].squeeze()
y_trans = quantile_transform(dataset.data[:, target],
n_quantiles=300,
output_distribution='normal',
copy=True).squeeze()
# +
#Делаем заготовку под две картинки
f, (ax0, ax1) = plt.subplots(1, 2)
# Атрибуты первой картинки
ax0.hist(y, bins=100, **density_param)
ax0.set_ylabel('Probability')
ax0.set_xlabel('Target')
ax0.set_title('Target distribution')
# Атрибуты второй картинки
ax1.hist(y_trans, bins=100, **density_param)
ax1.set_ylabel('Probability')
ax1.set_xlabel('Target')
ax1.set_title('Transformed target distribution')
f.suptitle("Boston housing data: distance to employment centers", y=0.035)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])
# Разбиваем данные на обучающую и тестовую последовательность
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
# +
#X_train
#y_train
# +
f, (ax0, ax1) = plt.subplots(1, 2, sharey=True)
# Определяем тип регрессии Ridge regression
regr = RidgeCV()
# Обучаем модель
regr.fit(X_train, y_train)
y_pred = regr.predict(X_test)
ax0.scatter(y_test, y_pred)
ax0.plot([0, 10], [0, 10], '--k')
ax0.set_ylabel('Target predicted')
ax0.set_xlabel('True Target')
ax0.set_title('Ridge regression \n without target transformation')
ax0.text(1, 9, r'$R^2$=%.2f, MAE=%.2f' % (
r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax0.set_xlim([0, 10])
ax0.set_ylim([0, 10])
regr_trans = TransformedTargetRegressor(
regressor=RidgeCV(),
transformer=QuantileTransformer(n_quantiles=300,
output_distribution='normal'))
# ---------------Обучаем модель----------------------------------------------
regr_trans.fit(X_train, y_train)
y_pred = regr_trans.predict(X_test)
ax1.scatter(y_test, y_pred)
ax1.plot([0, 10], [0, 10], '--k')
ax1.set_ylabel('Target predicted')
ax1.set_xlabel('True Target')
ax1.set_title('Ridge regression \n with target transformation')
ax1.text(1, 9, r'$R^2$=%.2f, MAE=%.2f' % (
r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax1.set_xlim([0, 10])
ax1.set_ylim([0, 10])
f.suptitle("Boston housing data: distance to employment centers", y=0.035)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])
plt.show()
# -
# # Пример из книжки (стр. 28). Датасет: Ирисы
from sklearn.datasets import load_iris
iris_dataset = load_iris()
print("Ключи iris_dataset: \n{}".format(iris_dataset.keys()))
print(iris_dataset['DESCR'][:193] + "\n...")
print("Названия ответов: {}".format(iris_dataset['target_names']))
print("Названия признаков: \n{}".format(iris_dataset['feature_names']))
print("Тип массива data: {}".format(type(iris_dataset['data'])))
print("Форма массива data: {}".format(iris_dataset['data'].shape))
print("Первые пять строк массива data:\n{}".format(iris_dataset['data'][:5]))
print("Тип массива target: {}".format(type(iris_dataset['target'])))
print("Форма массива target: {}".format(iris_dataset['target'].shape))
print("Ответы:\n{}".format(iris_dataset['target']))
# ### Метрики эффективности модели
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
iris_dataset['data'], iris_dataset['target'], random_state=0)
print("форма массива X_train: {}".format(X_train.shape))
print("форма массива y_train: {}".format(y_train.shape))
print("форма массива X_test: {}".format(X_test.shape))
print("форма массива y_test: {}".format(y_test.shape))
# создаем dataframe из данных в массиве X_train
# маркируем столбцы, используя строки в iris_dataset.feature_names
iris_dataframe = pd.DataFrame(X_train, columns=iris_dataset.feature_names)
# создаем матрицу рассеяния из dataframe, цвет точек задаем с помощью y_train
grr = pd.plotting.scatter_matrix(iris_dataframe, c=y_train, figsize=(15, 15), marker='o',
hist_kwds={'bins': 20}, s=60, alpha=.8)
# ### Построение модели
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
print("Правильность на тестовом наборе: {:.2f}".format(knn.score(X_test, y_test)))
# ### Получение прогнозов
# Теперь мы можем получить прогнозы, применив эту модель к новым
# данным, по которым мы еще не знаем правильные метки.
X_new = np.array([[5, 2.9, 1, 0.2]])# Создадим новый набор данных/Обратите внимание, что мы записали измерения по одному цветку в
#двумерный массив NumPy, поскольку scikit-learn работает с
#двумерными массивами данных.
print("форма массива X_new: {}".format(X_new.shape))
# Чтобы сделать прогноз, мы вызываем метод predict объекта knn:
prediction = knn.predict(X_new)
print("Прогноз: {}".format(prediction))
print("Спрогнозированная метка: {}".format(
iris_dataset['target_names'][prediction]))
# ### Оценка качества модели (стр. 37)
# Таким образом, мы можем сделать прогноз для каждого ириса в
# тестовом наборе и сравнить его с фактической меткой (уже известным
# сортом). Мы можем оценить качество модели, вычислив правильность
# (accuracy) – процент цветов, для которых модель правильно
# спрогнозировала сорта:
y_pred = knn.predict(X_test)
print("Прогнозы для тестового набора:\n {}".format(y_pred))
print("Правильность на тестовом наборе: {:.2f}".format(np.mean(y_pred == y_test)))
| 15,314 |
/open-metadata-resources/open-metadata-labs/administration-labs/understanding-cohorts.ipynb | 5e2b15275f5ec74fdaa514c3147bafdf5d03a4f6 | [
"CC-BY-4.0",
"Apache-2.0"
] | permissive | hsjung6/egeria | https://github.com/hsjung6/egeria | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 6,988 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 
#
# ### ODPi Egeria Hands-On Lab
# # Welcome to the Understanding Cohort Configuration Lab
# ## Introduction
#
# ODPi Egeria is an open source project that provides open standards and implementation libraries to connect tools,
# catalogs and platforms together so they can share information (called metadata) about data and the technology that supports it.
#
# The ODPi Egeria repository services provide APIs for understanding the make up of the cohorts that an OMAG Server
# is connected to.
# This hands-on lab steps through each of the repository services operations for understanding a cohort, providing a explaination and the code to call each operation.
# ## The Scenario
#
# Gary Geeke is the IT Infrastructure leader at Coco Pharmaceuticals. He has set up a number of OMAG Servers and
# is validating they are operating correctly.
#
# 
#
# In this hands-on lab Gary is issuing queries to the repository services. Gary's userId is `garygeeke`.
# +
import requests
adminUserId = "garygeeke"
# -
# In the **Metadata Server Configuration**, gary configured servers for the OMAG Server Platforms shown in Figure 1:
#
# 
# > **Figure 1:** Coco Pharmaceuticals' OMAG Server Platforms
#
# Below are the host name and port number for the core, data lake and development platforms and the servers that are hosted on each:
# +
import os
corePlatformURL = os.environ.get('corePlatformURL','http://localhost:8080')
dataLakePlatformURL = os.environ.get('dataLakePlatformURL','http://localhost:8081')
devPlatformURL = os.environ.get('devPlatformURL','http://localhost:8082')
server1PlatformURL = dataLakePlatformURL
server1Name = "cocoMDS1"
server2PlatformURL = corePlatformURL
server2Name = "cocoMDS2"
server3PlatformURL = corePlatformURL
server3Name = "cocoMDS3"
server4PlatformURL = dataLakePlatformURL
server4Name = "cocoMDS4"
server5PlatformURL = corePlatformURL
server5Name = "cocoMDS5"
server6PlatformURL = corePlatformURL
server6Name = "cocoMDS6"
serverXPlatformURL = devPlatformURL
serverXName = "cocoMDSx"
# -
# You can use these variables to issue the commands that follow to different servers.
#
# Figure 2 shows which metadata servers belong to each cohort.
#
# 
# > **Figure 2:** Membership of Coco Pharmaceuticals' cohorts
#
# Below are the names of the three cohorts.
cocoCohort = "cocoCohort"
devCohort = "devCohort"
iotCohort = "iotCohort"
# ## Querying a server's cohorts
#
# The command below returns the list of cohorts that a server is connected to.
#
# +
serverName = server4Name
platformURLroot = server1PlatformURL
metadataHighwayServicesURLcore = '/servers/' + serverName + '/open-metadata/repository-services/users/' + adminUserId + '/metadata-highway'
import pprint
import json
print (" ")
print ("Querying cohorts for " + serverName + " ...")
url = platformURLroot + metadataHighwayServicesURLcore + '/cohort-descriptions'
print ("GET " + url)
response = requests.get(url)
prettyResponse = json.dumps(response.json(), indent=4)
print ("Response: ")
print (prettyResponse)
print (" ")
# -
# ----
# ## Querying local registration
# +
print (" ")
print ("Querying local registration for " + serverName + " ...")
url = platformURLroot + metadataHighwayServicesURLcore + '/local-registration'
print ("GET " + url)
response = requests.get(url)
prettyResponse = json.dumps(response.json(), indent=4)
print ("Response: ")
print (prettyResponse)
print (" ")
# -
# ----
# ## Querying remote members
# +
print (" ")
print ("Querying remote members for " + serverName + " ...")
url = platformURLroot + metadataHighwayServicesURLcore + "/cohorts/cocoCohort/remote-members"
print ("GET " + url)
response = requests.get(url)
prettyResponse = json.dumps(response.json(), indent=4)
print ("Response: ")
print (prettyResponse)
print (" ")
# -
# ----
| 4,506 |
/Quantium Internship Task 1.ipynb | 5f0e35be13acfe313cb4f488820a241b60262be3 | [] | no_license | VritikaMalhotra/Quantium-Internship | https://github.com/VritikaMalhotra/Quantium-Internship | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 609,571 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#Importing required libraries
import pandas as pd
import numpy as np
import re
from datetime import date, timedelta
import matplotlib.pyplot as plt
import matplotlib.style as style
import seaborn as sns
# +
#Reading Purchase behaviour file
df_purchase_behaviour = pd.read_csv('QVI_purchase_behaviour.csv')
# +
#Reading Transaction data file
df_transaction_data = pd.read_excel('QVI_transaction_data.xlsx')
# +
#Converting the Number of days from origin to date-time in transaction data
start = date(1899,12,30)
new_date_format = []
for date in df_transaction_data["DATE"]:
days = timedelta(date)
new_date_format.append(start + days)
df_transaction_data['DATE'] = new_date_format
# +
#Generating the fequency chart for every word present in the product name in transaction data.
pname = df_transaction_data['PROD_NAME']
pname = list(pname)
product_name = []
for product in pname :
product_name.append(product[:-4])
product_freq = {}
for item in product_name:
wordList = re.sub("[^\w]", " ", item).split()
for word in wordList:
if word not in product_freq:
product_freq[word] = 0
else:
product_freq[word] += 1
product_freq
# +
#Sorting product frequency in descinding order acording to its value.
from collections import OrderedDict
product_freq = OrderedDict(sorted(product_freq.items(), key=lambda kv: kv[1], reverse=True))
# +
#Removing products from the transaction data dataframe which have Salsa present in its product name.
df_transaction_data.drop(df_transaction_data[df_transaction_data['PROD_NAME'].str.contains('Salsa')].index, inplace=True)
# +
#Summary of the data from transaction data dataframe.
summary = df_transaction_data.describe()
summary = summary.transpose()
summary
# +
#Checking if any column has a null value(NaN)?
df_transaction_data_columns = df_transaction_data.columns
for val in df_transaction_data_columns:
print(val+' : '+str(df_transaction_data[val].isnull().values.any()))
# +
# Here we have one outliner according to summary displayed above, and that it max quantity ordered for
# a packet of chips in a single go is 200 which is weird!
df_transaction_data[df_transaction_data['PROD_QTY'] == 200]
# +
#Getting the loyality card number of this customer to identify if the same customer has made other transactions.
lylty_card_no_index = df_transaction_data[df_transaction_data['PROD_QTY'] == 200].index
x = df_transaction_data['LYLTY_CARD_NBR'][df_transaction_data.index == lylty_card_no_index[0]]
val = x.get(lylty_card_no_index[0])
df_transaction_data[df_transaction_data['LYLTY_CARD_NBR'] == val]
# +
#It looks like this customer has only had the two transactions over the year and is
#not an ordinary retail customer. The customer might be buying chips for commercial
#purposes instead. We'll remove this loyalty card number from further analysis.
df_transaction_data.drop(df_transaction_data[df_transaction_data['LYLTY_CARD_NBR'] == val].index, inplace=True)
# +
#Re- examining the data.
summary = df_transaction_data.describe()
summary = summary.transpose()
summary
# +
#Counting number of transactions on each day to see if there is some missing date or not.
df_transactions = pd.DataFrame(df_transaction_data.DATE.value_counts())
df_transactions.rename(columns={'DATE':'Transactions'},inplace=True)
df_transactions.index = pd.to_datetime(df_transactions.index)
df_transactions
# +
#There's only 364 rows, meaning only 364 dates which indicates a missing date.
#Creating a sequence of dates from 1 Jul 2018 to 30 Jun 2019 and use this to create a
#chart of number of transactions over time to find the missing date.
sdate = date(2018,7,1) # start date
edate = date(2019,6,30) # end date
df_dates = pd.DataFrame(pd.date_range(sdate,edate,freq='d'))
df_dates.rename(columns={0:'Dates'},inplace=True)
df_dates.set_index('Dates',inplace=True)
df_dates
# -
#Performing join on both dataframes
df_check_date = pd.merge(df_dates, df_transactions, how='left',left_index=True, right_index=True)
df_check_date
# +
df_check_date[df_check_date['Transactions'].isnull()].index
#Missing date id 2018-12-25 i.e. 25th December 2018
# +
#Selecting dates for the month of December
start_date = pd.to_datetime('2018-12-1') # start date
end_date = pd.to_datetime('2018-12-31') # end date
mask = (df_check_date.index >= start_date) & (df_check_date.index <= end_date)
df_plot_date = df_check_date.loc[mask]
df_plot_date['Transactions'] = df_plot_date['Transactions'].fillna(0)
# -
#Zoomin in and plotting december dates with its transactions
style.use('seaborn-muted')
df_plot_date.plot(figsize=(14,4))
plt.yticks([0,200,400,600,800])
plt.xticks(df_plot_date.index,[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31])
plt.title('Transactions over time(December 2018)',fontsize=15)
plt.xlabel('Day',fontsize=15)
plt.ylabel('Number of transactions',fontsize=15);
# +
#We can see that the increase in sales occurs in the lead-up to Christmas and that
#there are zero sales on Christmas day itself. This is due to shops being closed on Christmas day.
# +
#Now that we are satisfied that the data no longer has outliers, we can move on to
#creating other features such as brand of chips or pack size from PROD_NAME. We will
#start with pack size.
# +
pack_size = []
product_name = df_transaction_data["PROD_NAME"]
for item in product_name:
if(item == 'Kettle 135g Swt Pot Sea Salt'):
pack_size.append(int(item[7:10]))
else:
pack_size.append(int(item[-4:-1]))
print('Minimum'+" : "+str(min(pack_size)))
print('Maximum'+" : "+str(max(pack_size)))
#The largest size is 380g and the smallest size is 70g - seems sensible!
# +
#Making a new column named pack size.
df_transaction_data['PACK_SIZE'] = pack_size
# -
df_transaction_data['PACK_SIZE'].hist()
plt.xlabel('Pack Sizes')
plt.ylabel('Transaction freq.')
plt.title('Freq. of size of packets sold')
# +
#Getting brand names from product names and making a seprate column for that in transaction data frame.
brand_names = []
for item in product_name:
words = item.split(' ')
brand_names.append(words[0])
# +
#Frequency of occourence of each brand.
from collections import Counter as counter
counter(brand_names)
# +
#Replacing NCC with Natural Chip Co, Natural with Natural Chip Co,Smith with Smiths, Dorito with Doritos, WW with Woolworths, RRD with Red, Snbts with Sunbites,
#Grain with Grain Waves, GrnWves with Grain Waves, Infzns with Infuzions.
for index,element in enumerate(brand_names):
if(element == 'NCC' or element == 'Natural'):
brand_names[index] = 'Natural Chip Co'
if(element == 'Smith'):
brand_names[index] = 'Smiths'
if(element == 'Dorito'):
brand_names[index] = 'Doritos'
if(element == 'WW'):
brand_names[index] = 'Woolworths'
if(element == 'RRD'):
brand_names[index] = 'Red'
if(element == 'Grain' or element == 'GrnWves'):
brand_names[index] = 'Grain Waves'
if(element == 'Infzns'):
brand_names[index] = 'Infuzions'
# +
#Frequency of occourence of each brand.
from collections import Counter as counter
brand_dict = counter(brand_names)
brand_dict
# -
#Now the results of brand names look resonable and correct.
df_transaction_data['BRAND_NAME'] = brand_names
# +
index = []
values = []
brand_dict = dict(brand_dict)
for i,v in brand_dict.items():
index.append(i)
values.append(v)
# -
plt.figure(figsize=(12,4))
plt.bar(index,values)
plt.xticks(rotation=90);
df_purchase_behaviour
# +
#Merging df_transaction_data and df_purchase_behaviour
df_merged = df_transaction_data.merge(df_purchase_behaviour,how='inner',left_on=['LYLTY_CARD_NBR'],right_on=['LYLTY_CARD_NBR'])
df_merged
# +
#Checking if any column has a null value(NaN)?
df_merged_columns = df_merged.columns
for val in df_merged_columns:
print(val+' : '+str(df_merged[val].isnull().values.any()))
#Hence we conclude that all the values from both the DataFrames were matched with each other correctly.
# +
#Saving this Dataframe for utilization in further tasks.
df_merged.to_csv('QVI_data.csv',index=False)
# -
# Now that the data is ready for analysis, we can define some metrics of interest to
# the client:
#
# - Who spends the most on chips (total sales), describing customers by lifestage and
# how premium their general purchasing behaviour is
# - How many customers are in each segment
# - How many chips are bought per customer by segment
# - What's the average chip price by customer segment
# +
#Grouping on the basis of Lifestage and Premium customers
df_grouped = df_merged.groupby(['LIFESTAGE','PREMIUM_CUSTOMER']).sum()
df_grouped
# +
#Total sales plotted based upon lifestage and premium customers
index = df_grouped.index
values = df_grouped["TOT_SALES"]
result = []
for t in index:
result.append(t[0]+"__"+t[1])
plt.figure(figsize=(10,9))
plt.barh(result,values,color='lightblue')
plt.xlabel('Total Sales',fontsize=14)
plt.title('Total sales based upon Lifestage and Premium Customer',fontsize=14)
# +
#Getting number of memebers present in each group.
group_count= pd.Series(df_merged.groupby(['LIFESTAGE', 'PREMIUM_CUSTOMER'])['DATE'].count())
df_grouped['CUSTOMER_COUNT'] = group_count.values
# +
#Collecting number of all premium, budget and mainstream customers seprately.
#also calculating their total
lifestage = ['MIDAGE SINGLES/COUPLES','NEW FAMILIES','OLDER FAMILIES','OLDER SINGLES/COUPLES','RETIREES','YOUNG FAMILIES','YOUNG SINGLES/COUPLES']
Premium = []
Budget = []
Mainstream = []
all_values = []
for index,value in group_count.iteritems():
if(index[1] == 'Premium'):
Premium.append(value)
all_values.append(value)
elif(index[1] == 'Mainstream'):
Mainstream.append(value)
all_values.append(value)
elif(index[1] == 'Budget'):
Budget.append(value)
all_values.append(value)
Total = sum(all_values)
# +
#Creating a dataframe based upon number of premium,budget and mainstream customersnumber of premium,budget and mainstream customers and calculating further for text annotation.
#Note: Here the percentage is calculated based upon number of customers in that group to total cutsomers.
df = pd.DataFrame({'Lifestage':lifestage,
'Budget': Budget,
'Mainstream': Mainstream,
'Premium':Premium})
ax_1 = df.set_index('Lifestage').plot(kind='barh', stacked=True,figsize = (14,8))
percentage_premium = []
percentage_budget = []
percentage_mainstream = []
for index,row in df.iterrows():
percentage_premium.append(round((row['Premium']/Total)*100,1))
percentage_budget.append(round((row['Budget']/Total)*100,1))
percentage_mainstream.append(round((row['Mainstream']/Total)*100,1))
all_percentage = percentage_budget+percentage_mainstream+percentage_premium
count=-1
for rec in ax_1.patches:
height = rec.get_height()
width = rec.get_width()
count = count+1
ax_1.text(rec.get_x() + rec.get_width() / 2,
rec.get_y() + height / 2,
"{:.1f}%".format(all_percentage[count]),
ha='center',
va='bottom')
plt.title('Percentage of premium, budget and mainstream customers',fontsize=16);
# -
# There are more Mainstream - young singles/couples and Mainstream - retirees who buy
# chips. This contributes to there being more sales to these customer segments but
# this is not a major driver for the Budget - Older families segment.
# Higher sales may also be driven by more units of chips being bought per customer.
# Let's have a look at this next.
#Calculating and plotting the average number of units per customer by those two dimensions.
df_grouped['UNITS_PER_CUSTOMER'] = df_grouped['PROD_QTY']/df_grouped['CUSTOMER_COUNT']
# +
average_chips_series = pd.Series(df_grouped['UNITS_PER_CUSTOMER'])
lifestage_qty = ['MIDAGE SINGLES/COUPLES','NEW FAMILIES','OLDER FAMILIES','OLDER SINGLES/COUPLES','RETIREES','YOUNG FAMILIES','YOUNG SINGLES/COUPLES']
Premium_qty = []
Budget_qty = []
Mainstream_qty = []
all_values_qty = []
for index,value in average_chips_series.iteritems():
if(index[1] == 'Premium'):
Premium_qty.append(value)
all_values_qty.append(value)
elif(index[1] == 'Mainstream'):
Mainstream_qty.append(value)
all_values_qty.append(value)
elif(index[1] == 'Budget'):
Budget_qty.append(value)
all_values_qty.append(value)
Total = sum(all_values_qty)
# +
df_qty = pd.DataFrame({'Lifestage':lifestage_qty,
'Budget': Budget_qty,
'Mainstream': Mainstream_qty,
'Premium':Premium_qty})
ax_1 = df_qty.set_index('Lifestage').plot(kind='barh', stacked=True,figsize = (14,8))
all_qty = Budget_qty+Mainstream_qty+Premium_qty
count=-1
for rec in ax_1.patches:
height = rec.get_height()
width = rec.get_width()
count = count+1
ax_1.text(rec.get_x() + rec.get_width() / 2,
rec.get_y() + height / 2,
"{:.3f} units".format(all_qty[count]),
ha='center',
va='bottom')
plt.title('Quantity of chip packets bought',fontsize=16);
# -
# This shows the average unit of chips bought by each category.
# Older families and young families in general buy more chips per customer
#Calculating and plotting the average price per chips packet by those two dimensions.
df_grouped['PRICE_PER_UNIT'] = df_grouped['TOT_SALES']/df_grouped['PROD_QTY']
# +
average_price_series = pd.Series(df_grouped['PRICE_PER_UNIT'])
lifestage_price = ['MIDAGE SINGLES/COUPLES','NEW FAMILIES','OLDER FAMILIES','OLDER SINGLES/COUPLES','RETIREES','YOUNG FAMILIES','YOUNG SINGLES/COUPLES']
Premium_price = []
Budget_price = []
Mainstream_price = []
all_values_price = []
for index,value in average_price_series.iteritems():
if(index[1] == 'Premium'):
Premium_price.append(value)
all_values_price.append(value)
elif(index[1] == 'Mainstream'):
Mainstream_price.append(value)
all_values_price.append(value)
elif(index[1] == 'Budget'):
Budget_price.append(value)
all_values_price.append(value)
Total = sum(all_values_price)
# +
df_price = pd.DataFrame({'Lifestage':lifestage_price,
'Budget': Budget_price,
'Mainstream': Mainstream_price,
'Premium':Premium_price})
ax_1 = df_price.set_index('Lifestage').plot(kind='barh', stacked=True,figsize = (14,8))
all_price = Budget_price+Mainstream_price+Premium_price
count=-1
for rec in ax_1.patches:
height = rec.get_height()
width = rec.get_width()
count = count+1
ax_1.text(rec.get_x() + rec.get_width() / 2,
rec.get_y() + height / 2,
"{:.3f} dollars".format(all_price[count]),
ha='center',
va='bottom')
plt.title('Average sale price',fontsize=16);
# -
# Mainstream midage and young singles and couples are more willing to pay more per
# packet of chips compared to their budget and premium counterparts. This may be due
# to premium shoppers being more likely to buy healthy snacks and when they buy
# chips, this is mainly for entertainment purposes rather than their own consumption.
# This is also supported by there being fewer premium midage and young singles and
# couples buying chips compared to their mainstream counterparts.
#
# +
unique_customers = pd.Series(df_merged.groupby(['LIFESTAGE','PREMIUM_CUSTOMER'])['LYLTY_CARD_NBR'].unique())
count = []
indices = []
for index,value in unique_customers.iteritems():
count.append(len(value))
indices.append(index[0]+'__'+index[1])
# -
plt.figure(figsize=(10,9))
plt.barh(indices,count,color='lightblue')
plt.xlabel('Number of unique customers',fontsize=14)
plt.title('Number of uniques customers in each category',fontsize=14);
# Young sigle/couples have large number of unique customers and the average price they spend upon each chip packet is also large and the average quantity of chip packets bought is also resonable.
#
# Midage singles/couples have lesser customers but their average price spent of chips packets and the quantity of chip packets bought is almost same as Young singls/couples.
#
# New Families (premium,budget,mainstream) have the least number of customers and leat number of unique customers but their average sale price is comparatively high
# +
df_ptest_1 = df_merged[(df_merged['LIFESTAGE'] == 'YOUNG SINGLES/COUPLES') | (df_merged['LIFESTAGE'] == 'MIDAGE SINGLES/COUPLES')]
sales_mainstream_series = pd.Series(df_ptest_1['TOT_SALES'][df_ptest_1['PREMIUM_CUSTOMER'] == 'Mainstream'])
sales_budget_premium_series = pd.Series(df_ptest_1['TOT_SALES'][(df_ptest_1['PREMIUM_CUSTOMER'] == 'Budget') | (df_ptest_1['PREMIUM_CUSTOMER'] == 'Premium')])
mainstream_list = []
budget_premium_list = []
for index,value in sales_mainstream_series.iteritems():
mainstream_list.append(value)
for index,value in sales_budget_premium_series.iteritems():
budget_premium_list.append(value)
# +
from scipy.stats import ttest_ind
stat,pvalue = ttest_ind(mainstream_list,budget_premium_list,equal_var=False)
print('Pvalue is {}'.format(pvalue))
pvalue<0.00000000001
# -
# The t-test results in a p-value of almost 0, i.e. the Total sales for mainstream,
# young and mid-age singles and couples ARE significantly higher than
# that of budget or premium, young and midage singles and couples.
# We have found quite a few interesting insights that we can dive deeper into.
# We might want to target customer segments that contribute the most to sales to
# retain them or further increase sales. Let's look at Mainstream - young
# singles/couples. For instance, let's find out if they tend to buy a particular
# brand of chips.
# +
#INSIGHTS UPON MAINSTREAM CUSTOMERS.
df_mainstream = df_merged[df_merged['PREMIUM_CUSTOMER'] == 'Mainstream']
mainstream_grouped = pd.Series(df_mainstream.groupby(['BRAND_NAME'])['LYLTY_CARD_NBR'])
brand_names = []
counts = []
for index,value in mainstream_grouped.iteritems():
brand_names.append(value[0])
counts.append(len(value[1]))
brand_names.pop(14)
counts.pop(14)
# -
plt.figure(figsize=(10,9))
plt.barh(brand_names,counts,color='lightblue')
plt.xlabel('Sales',fontsize=14)
plt.title('Number of chips from each brand sold for mainstream people',fontsize=14);
# Here we can see that mainstream people buy Kettle brand chips the most. After kettle they prefer either Doritos or Smiths.
#
# Comapny's such as French, Snbites, Burger etc have extremly low sales for mainstream category people
# +
#INSIGHTS UPON YOUNG SINGLES/COUPLES
df_young_premium = df_merged[(df_merged['LIFESTAGE'] == 'YOUNG SINGLES/COUPLES') &(df_merged['PREMIUM_CUSTOMER']=='Premium')]
df_young_mainstream = df_merged[(df_merged['LIFESTAGE'] == 'YOUNG SINGLES/COUPLES') &(df_merged['PREMIUM_CUSTOMER']=='Mainstream')]
df_young_budget = df_merged[(df_merged['LIFESTAGE'] == 'YOUNG SINGLES/COUPLES') &(df_merged['PREMIUM_CUSTOMER']=='Budget')]
# +
#for PREMIUM
premium_series = pd.Series(df_young_premium.groupby('BRAND_NAME')['LYLTY_CARD_NBR'].count())
premium_series.sort_values(inplace=True)
brand_names = []
counts = []
for index,value in premium_series.iteritems():
brand_names.append(index)
counts.append(value)
brand_names.pop(0)
counts.pop(0)
# -
plt.figure(figsize=(10,9))
plt.barh(brand_names,counts,color='lightblue')
plt.xlabel('Sales',fontsize=14)
plt.title('Number of chips from each brand sold for Young single/couples - PREMIUM people',fontsize=14);
# +
#for MAINSTREAM
mainstream_series = pd.Series(df_young_mainstream.groupby('BRAND_NAME')['LYLTY_CARD_NBR'].count())
mainstream_series.sort_values(inplace=True)
brand_names = []
counts = []
for index,value in mainstream_series.iteritems():
brand_names.append(index)
counts.append(value)
# -
plt.figure(figsize=(10,9))
plt.barh(brand_names,counts,color='lightblue')
plt.xlabel('Sales',fontsize=14)
plt.title('Number of chips from each brand sold for Young single/couples - MAINSTREAM people',fontsize=14);
# +
#for BUDGET
budget_series = pd.Series(df_young_budget.groupby('BRAND_NAME')['LYLTY_CARD_NBR'].count())
budget_series.sort_values(inplace=True)
brand_names = []
counts = []
for index,value in budget_series.iteritems():
brand_names.append(index)
counts.append(value)
# -
plt.figure(figsize=(10,9))
plt.barh(brand_names,counts,color='lightblue')
plt.xlabel('Sales',fontsize=14)
plt.title('Number of chips from each brand sold for Young single/couples - BUDGET people',fontsize=14);
# +
#Most bought pack size for mainstream people
import statistics
from statistics import mode
brands_mstream = df_mainstream['PROD_NAME']
pack_size_mstream = []
for item in brands_mstream:
if(item == 'Kettle 135g Swt Pot Sea Salt'):
pack_size_mstream.append(int(item[7:10]))
else:
pack_size_mstream.append(int(item[-4:-1]))
print('Most frequently bought pack size for MAINSTREAM people is {}g'.format(mode(pack_size_mstream)))
# +
#Histogram of all pack sizes
plt.figure(figsize=(10,5))
plt.hist(pack_size_mstream,color='lightseagreen')
plt.xticks(rotation=60)
plt.title("Pack sizes of mainstream people",fontsize=14)
plt.xlabel('Pack size in grams',fontsize=13)
plt.ylabel('Frequency',fontsize=13);
# -
#
# +
#YOUNG - PREMIUM
import statistics
from statistics import mode
brands_yp = df_young_premium['PROD_NAME']
pack_size_yp = []
for item in brands_yp:
if(item == 'Kettle 135g Swt Pot Sea Salt'):
pack_size_yp.append(int(item[7:10]))
else:
pack_size_yp.append(int(item[-4:-1]))
print('Most frequently bought pack size for young premium people is {}g'.format(mode(pack_size_yp)))
# -
#Histogram of all pack sizes
plt.figure(figsize=(10,5))
plt.hist(pack_size_yp,color='yellowgreen')
plt.xticks(rotation=60)
plt.title("Pack sizes of Young(couples/singles)-PREMIUM people",fontsize=14)
plt.xlabel('Pack size in grams',fontsize=13)
plt.ylabel('Frequency',fontsize=13);
# +
#YOUNG - MAINSTREAM
import statistics
from statistics import mode
brands_ym = df_young_mainstream['PROD_NAME']
pack_size_ym = []
for item in brands_ym:
if(item == 'Kettle 135g Swt Pot Sea Salt'):
pack_size_ym.append(int(item[7:10]))
else:
pack_size_ym.append(int(item[-4:-1]))
print('Most frequently bought pack size for young mainstream people is {}g'.format(mode(pack_size_ym)))
# -
#Histogram of all pack sizes
plt.figure(figsize=(10,5))
plt.hist(pack_size_ym,color='darksalmon')
plt.xticks(rotation=60)
plt.title("Pack sizes of Young(couples/singles)-MAINSTREAM people",fontsize=14)
plt.xlabel('Pack size in grams',fontsize=13)
plt.ylabel('Frequency',fontsize=13);
# +
#YOUNG -BUDGET
import statistics
from statistics import mode
brands_yb = df_young_budget['PROD_NAME']
pack_size_yb = []
for item in brands_yb:
if(item == 'Kettle 135g Swt Pot Sea Salt'):
pack_size_yb.append(int(item[7:10]))
else:
pack_size_yb.append(int(item[-4:-1]))
print('Most frequently bought pack size for young budget people is {}g'.format(mode(pack_size_yb)))
# -
#Histogram of all pack sizes
plt.figure(figsize=(10,5))
plt.hist(pack_size_yb,color='steelblue')
plt.xticks(rotation=60)
plt.title("Pack sizes of Young(couples/singles)-MAINSTREAM people",fontsize=14)
plt.xlabel('Pack size in grams',fontsize=13)
plt.ylabel('Frequency',fontsize=13);
# We can see that :
#
# [INSIGHTS]
#
# 1.Kettles, Pringles, Doritos, Smiths are the brands which are loved by all customers of all age groups wether singles or couples. These brands are also affodable and genrally preffered by Budget , Mainstream and Premium all 3 of them.
#
# 2.The sales to Young single/couple(mainstream),older families(budget), retirees(mainstream) is the highest.
#
# 3.There are more Mainstream - young singles/couples and Mainstream - retirees who buy chips. This contributes to there being more sales to these customer segments but this is not a major driver for the Budget - Older families segment.
#
# 4.The average quantity of chip packets bought by each category is almost the same.
#
# 5.Young singles/couples(Mainstream), Retiress(mainstream) have the largest number of unique customers.
#
# 6.Young sigle/couples have large number of unique customers and the average price they spend upon each chip packet is also large and the average quantity of chip packets bought is also resonable.
#
# 7.Midage singles/couples have lesser customers but their average price spent of chips packets and the quantity of chip packets bought is almost same as Young singls/couples.
#
# 8.New Families (premium,budget,mainstream) have the least number of customers and leat number of unique customers but their average sale price is comparatively high.
#
# 9.The t-test results in a p-value of almost 0, i.e. the Total sales for mainstream, young and mid-age singles and couples ARE significantly higher than that of budget or premium, young and midage singles and couples.
#
# 10.Most sold chips brands for mainstream people are Kettles,Smiths, Doritos, Pringles repectively.
#
# In depth insights about Young(singles/couples) as they are major customers.
#
# 11.['French','Sunbites','Burger','Cheetos', 'Cheezels','Tyrrells', 'CCs','Grain Waves', 'Twisties', 'Tostitos','Natural Chip Co','Cobs','Infuzions', 'Thins', 'Woolworths', 'Red', 'Doritos', 'Pringles','Smiths', 'Kettle']
#
# From the least sold brands to the most sold brands for Young (single/couples) PREMIUM.
#
# 12.['Sunbites', 'Burger', 'Snbts', 'French', 'Cheetos', 'CCs', 'Cheezels', 'Natural Chip Co', 'Woolworths', 'Tyrrells', 'Grain Waves', 'Cobs', 'Red', 'Tostitos', 'Twisties', 'Thins', 'Infuzions', 'Smiths', 'Pringles', 'Doritos', 'Kettle']
#
# From the least sold brands to the most sold brands for Young (single/couples) MAINSTREAM.
#
# 13.['Burger', 'Sunbites', 'Snbts', 'French', 'Cheetos', 'Cheezels', 'Tyrrells', 'CCs', 'Grain Waves', 'Tostitos', 'Cobs', 'Twisties', 'Natural Chip Co', 'Infuzions', 'Thins', 'Woolworths', 'Red', 'Doritos', 'Pringles', 'Smiths', 'Kettle']
#
# 14.Most frequently bought pack size for young budget,young mainstream,youn premium, all Mainstream people is 175g. The histogram trends for pack sizes of all groups is almost same(Tested ones with max customers).Hence we can say that the sale of packets of 175g is highest for all groups.
#
#
takes care of the backward pass, so most deep learning engineers don't need to bother with the details of the backward pass. The backward pass for convolutional networks is complicated. If you wish, you can work through this optional portion of the notebook to get a sense of what backprop in a convolutional network looks like.
#
# When in an earlier course you implemented a simple (fully connected) neural network, you used backpropagation to compute the derivatives with respect to the cost to update the parameters. Similarly, in convolutional neural networks you can calculate the derivatives with respect to the cost in order to update the parameters. The backprop equations are not trivial and we did not derive them in lecture, but we will briefly present them below.
#
# ### 5.1 - Convolutional layer backward pass
#
# Let's start by implementing the backward pass for a CONV layer.
#
# #### 5.1.1 - Computing dA:
# This is the formula for computing $dA$ with respect to the cost for a certain filter $W_c$ and a given training example:
#
# $$ dA += \sum _{h=0} ^{n_H} \sum_{w=0} ^{n_W} W_c \times dZ_{hw} \tag{1}$$
#
# Where $W_c$ is a filter and $dZ_{hw}$ is a scalar corresponding to the gradient of the cost with respect to the output of the conv layer Z at the hth row and wth column (corresponding to the dot product taken at the ith stride left and jth stride down). Note that at each time, we multiply the the same filter $W_c$ by a different dZ when updating dA. We do so mainly because when computing the forward propagation, each filter is dotted and summed by a different a_slice. Therefore when computing the backprop for dA, we are just adding the gradients of all the a_slices.
#
# In code, inside the appropriate for-loops, this formula translates into:
# ```python
# da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i, h, w, c]
# ```
#
# #### 5.1.2 - Computing dW:
# This is the formula for computing $dW_c$ ($dW_c$ is the derivative of one filter) with respect to the loss:
#
# $$ dW_c += \sum _{h=0} ^{n_H} \sum_{w=0} ^ {n_W} a_{slice} \times dZ_{hw} \tag{2}$$
#
# Where $a_{slice}$ corresponds to the slice which was used to generate the activation $Z_{ij}$. Hence, this ends up giving us the gradient for $W$ with respect to that slice. Since it is the same $W$, we will just add up all such gradients to get $dW$.
#
# In code, inside the appropriate for-loops, this formula translates into:
# ```python
# dW[:,:,:,c] += a_slice * dZ[i, h, w, c]
# ```
#
# #### 5.1.3 - Computing db:
#
# This is the formula for computing $db$ with respect to the cost for a certain filter $W_c$:
#
# $$ db = \sum_h \sum_w dZ_{hw} \tag{3}$$
#
# As you have previously seen in basic neural networks, db is computed by summing $dZ$. In this case, you are just summing over all the gradients of the conv output (Z) with respect to the cost.
#
# In code, inside the appropriate for-loops, this formula translates into:
# ```python
# db[:,:,:,c] += dZ[i, h, w, c]
# ```
#
# **Exercise**: Implement the `conv_backward` function below. You should sum over all the training examples, filters, heights, and widths. You should then compute the derivatives using formulas 1, 2 and 3 above.
def conv_backward(dZ, cache):
"""
Implement the backward propagation for a convolution function
Arguments:
dZ -- gradient of the cost with respect to the output of the conv layer (Z), numpy array of shape (m, n_H, n_W, n_C)
cache -- cache of values needed for the conv_backward(), output of conv_forward()
Returns:
dA_prev -- gradient of the cost with respect to the input of the conv layer (A_prev),
numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
dW -- gradient of the cost with respect to the weights of the conv layer (W)
numpy array of shape (f, f, n_C_prev, n_C)
db -- gradient of the cost with respect to the biases of the conv layer (b)
numpy array of shape (1, 1, 1, n_C)
"""
### START CODE HERE ###
# Retrieve information from "cache"
(A_prev, W, b, hparameters) = cache
# Retrieve dimensions from A_prev's shape
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
# Retrieve dimensions from W's shape
(f, f, n_C_prev, n_C) = W.shape
# Retrieve information from "hparameters"
stride = hparameters['stride']
pad = hparameters['pad']
# Retrieve dimensions from dZ's shape
(m, n_H, n_W, n_C) = dZ.shape
# Initialize dA_prev, dW, db with the correct shapes
dA_prev = np.zeros((m, n_H_prev, n_W_prev, n_C_prev))
dW = np.zeros((f, f, n_C_prev, n_C))
db = np.zeros((1, 1, 1, n_C))
# Pad A_prev and dA_prev
A_prev_pad = zero_pad(A_prev, pad)
dA_prev_pad = zero_pad(dA_prev, pad)
for i in range(m): # loop over the training examples
# select ith training example from A_prev_pad and dA_prev_pad
a_prev_pad = A_prev_pad[i]
da_prev_pad = dA_prev_pad[i]
for h in range(n_H): # loop over vertical axis of the output volume
for w in range(n_W): # loop over horizontal axis of the output volume
for c in range(n_C): # loop over the channels of the output volume
# Find the corners of the current "slice"
vert_start = h * stride
vert_end = h * stride + f
horiz_start = w * stride
horiz_end = w * stride + f
# Use the corners to define the slice from a_prev_pad
a_slice = a_prev_pad[vert_start:vert_end,horiz_start:horiz_end,:]
# Update gradients for the window and the filter's parameters using the code formulas given above
da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i, h, w, c]
dW[:,:,:,c] += a_slice * dZ[i, h, w, c]
db[:,:,:,c] += dZ[i, h, w, c]
# Set the ith training example's dA_prev to the unpadded da_prev_pad (Hint: use X[pad:-pad, pad:-pad, :])
dA_prev[i, :, :, :] = da_prev_pad[pad:-pad, pad:-pad, :]
### END CODE HERE ###
# Making sure your output shape is correct
assert(dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev))
return dA_prev, dW, db
# +
# We'll run conv_forward to initialize the 'Z' and 'cache_conv",
# which we'll use to test the conv_backward function
np.random.seed(1)
A_prev = np.random.randn(10,4,4,3)
W = np.random.randn(2,2,3,8)
b = np.random.randn(1,1,1,8)
hparameters = {"pad" : 2,
"stride": 2}
Z, cache_conv = conv_forward(A_prev, W, b, hparameters)
# Test conv_backward
dA, dW, db = conv_backward(Z, cache_conv)
print("dA_mean =", np.mean(dA))
print("dW_mean =", np.mean(dW))
print("db_mean =", np.mean(db))
# -
# ** Expected Output: **
# <table>
# <tr>
# <td>
# **dA_mean**
# </td>
# <td>
# 1.45243777754
# </td>
# </tr>
# <tr>
# <td>
# **dW_mean**
# </td>
# <td>
# 1.72699145831
# </td>
# </tr>
# <tr>
# <td>
# **db_mean**
# </td>
# <td>
# 7.83923256462
# </td>
# </tr>
#
# </table>
#
# ## 5.2 Pooling layer - backward pass
#
# Next, let's implement the backward pass for the pooling layer, starting with the MAX-POOL layer. Even though a pooling layer has no parameters for backprop to update, you still need to backpropagation the gradient through the pooling layer in order to compute gradients for layers that came before the pooling layer.
#
# ### 5.2.1 Max pooling - backward pass
#
# Before jumping into the backpropagation of the pooling layer, you are going to build a helper function called `create_mask_from_window()` which does the following:
#
# $$ X = \begin{bmatrix}
# 1 && 3 \\
# 4 && 2
# \end{bmatrix} \quad \rightarrow \quad M =\begin{bmatrix}
# 0 && 0 \\
# 1 && 0
# \end{bmatrix}\tag{4}$$
#
# As you can see, this function creates a "mask" matrix which keeps track of where the maximum of the matrix is. True (1) indicates the position of the maximum in X, the other entries are False (0). You'll see later that the backward pass for average pooling will be similar to this but using a different mask.
#
# **Exercise**: Implement `create_mask_from_window()`. This function will be helpful for pooling backward.
# Hints:
# - [np.max()]() may be helpful. It computes the maximum of an array.
# - If you have a matrix X and a scalar x: `A = (X == x)` will return a matrix A of the same size as X such that:
# ```
# A[i,j] = True if X[i,j] = x
# A[i,j] = False if X[i,j] != x
# ```
# - Here, you don't need to consider cases where there are several maxima in a matrix.
def create_mask_from_window(x):
"""
Creates a mask from an input matrix x, to identify the max entry of x.
Arguments:
x -- Array of shape (f, f)
Returns:
mask -- Array of the same shape as window, contains a True at the position corresponding to the max entry of x.
"""
### START CODE HERE ### (≈1 line)
mask = (x == np.max(x))
### END CODE HERE ###
return mask
np.random.seed(1)
x = np.random.randn(2,3)
mask = create_mask_from_window(x)
print('x = ', x)
print("mask = ", mask)
# **Expected Output:**
#
# <table>
# <tr>
# <td>
#
# **x =**
# </td>
#
# <td>
#
# [[ 1.62434536 -0.61175641 -0.52817175] <br>
# [-1.07296862 0.86540763 -2.3015387 ]]
#
# </td>
# </tr>
#
# <tr>
# <td>
# **mask =**
# </td>
# <td>
# [[ True False False] <br>
# [False False False]]
# </td>
# </tr>
#
#
# </table>
# Why do we keep track of the position of the max? It's because this is the input value that ultimately influenced the output, and therefore the cost. Backprop is computing gradients with respect to the cost, so anything that influences the ultimate cost should have a non-zero gradient. So, backprop will "propagate" the gradient back to this particular input value that had influenced the cost.
# ### 5.2.2 - Average pooling - backward pass
#
# In max pooling, for each input window, all the "influence" on the output came from a single input value--the max. In average pooling, every element of the input window has equal influence on the output. So to implement backprop, you will now implement a helper function that reflects this.
#
# For example if we did average pooling in the forward pass using a 2x2 filter, then the mask you'll use for the backward pass will look like:
# $$ dZ = 1 \quad \rightarrow \quad dZ =\begin{bmatrix}
# 1/4 && 1/4 \\
# 1/4 && 1/4
# \end{bmatrix}\tag{5}$$
#
# This implies that each position in the $dZ$ matrix contributes equally to output because in the forward pass, we took an average.
#
# **Exercise**: Implement the function below to equally distribute a value dz through a matrix of dimension shape. [Hint](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.ones.html)
def distribute_value(dz, shape):
"""
Distributes the input value in the matrix of dimension shape
Arguments:
dz -- input scalar
shape -- the shape (n_H, n_W) of the output matrix for which we want to distribute the value of dz
Returns:
a -- Array of size (n_H, n_W) for which we distributed the value of dz
"""
### START CODE HERE ###
# Retrieve dimensions from shape (≈1 line)
(n_H, n_W) = shape
# Compute the value to distribute on the matrix (≈1 line)
average = dz / (n_H * n_W)
# Create a matrix where every entry is the "average" value (≈1 line)
a = np.full((n_H, n_W), average)
### END CODE HERE ###
return a
a = distribute_value(2, (2,2))
print('distributed value =', a)
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# distributed_value =
# </td>
# <td>
# [[ 0.5 0.5]
# <br\>
# [ 0.5 0.5]]
# </td>
# </tr>
# </table>
# ### 5.2.3 Putting it together: Pooling backward
#
# You now have everything you need to compute backward propagation on a pooling layer.
#
# **Exercise**: Implement the `pool_backward` function in both modes (`"max"` and `"average"`). You will once again use 4 for-loops (iterating over training examples, height, width, and channels). You should use an `if/elif` statement to see if the mode is equal to `'max'` or `'average'`. If it is equal to 'average' you should use the `distribute_value()` function you implemented above to create a matrix of the same shape as `a_slice`. Otherwise, the mode is equal to '`max`', and you will create a mask with `create_mask_from_window()` and multiply it by the corresponding value of dA.
def pool_backward(dA, cache, mode = "max"):
"""
Implements the backward pass of the pooling layer
Arguments:
dA -- gradient of cost with respect to the output of the pooling layer, same shape as A
cache -- cache output from the forward pass of the pooling layer, contains the layer's input and hparameters
mode -- the pooling mode you would like to use, defined as a string ("max" or "average")
Returns:
dA_prev -- gradient of cost with respect to the input of the pooling layer, same shape as A_prev
"""
### START CODE HERE ###
# Retrieve information from cache (≈1 line)
(A_prev, hparameters) = cache
# Retrieve hyperparameters from "hparameters" (≈2 lines)
stride = hparameters['stride']
f = hparameters['f']
# Retrieve dimensions from A_prev's shape and dA's shape (≈2 lines)
m, n_H_prev, n_W_prev, n_C_prev = A_prev.shape
m, n_H, n_W, n_C = dA.shape
# Initialize dA_prev with zeros (≈1 line)
dA_prev = np.zeros(A_prev.shape)
for i in range(m): # loop over the training examples
# select training example from A_prev (≈1 line)
a_prev = A_prev[i]
for h in range(n_H): # loop on the vertical axis
for w in range(n_W): # loop on the horizontal axis
for c in range(n_C): # loop over the channels (depth)
# Find the corners of the current "slice" (≈4 lines)
vert_start = h * stride
vert_end = h * stride + f
horiz_start = w * stride
horiz_end = w * stride + f
# Compute the backward propagation in both modes.
if mode == "max":
# Use the corners and "c" to define the current slice from a_prev (≈1 line)
a_prev_slice = a_prev[vert_start:vert_end,horiz_start:horiz_end,c]
# Create the mask from a_prev_slice (≈1 line)
mask = create_mask_from_window(a_prev_slice)
# Set dA_prev to be dA_prev + (the mask multiplied by the correct entry of dA) (≈1 line)
dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += mask * dA[i,h,w,c]
elif mode == "average":
# Get the value a from dA (≈1 line)
da = dA[i,h,w,c]
# Define the shape of the filter as fxf (≈1 line)
shape = (f,f)
# Distribute it to get the correct slice of dA_prev. i.e. Add the distributed value of da. (≈1 line)
dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += distribute_value(da, shape)
### END CODE ###
# Making sure your output shape is correct
assert(dA_prev.shape == A_prev.shape)
return dA_prev
# +
np.random.seed(1)
A_prev = np.random.randn(5, 5, 3, 2)
hparameters = {"stride" : 1, "f": 2}
A, cache = pool_forward(A_prev, hparameters)
dA = np.random.randn(5, 4, 2, 2)
dA_prev = pool_backward(dA, cache, mode = "max")
print("mode = max")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1,1])
print()
dA_prev = pool_backward(dA, cache, mode = "average")
print("mode = average")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1,1])
# -
# **Expected Output**:
#
# mode = max:
# <table>
# <tr>
# <td>
#
# **mean of dA =**
# </td>
#
# <td>
#
# 0.145713902729
#
# </td>
# </tr>
#
# <tr>
# <td>
# **dA_prev[1,1] =**
# </td>
# <td>
# [[ 0. 0. ] <br>
# [ 5.05844394 -1.68282702] <br>
# [ 0. 0. ]]
# </td>
# </tr>
# </table>
#
# mode = average
# <table>
# <tr>
# <td>
#
# **mean of dA =**
# </td>
#
# <td>
#
# 0.145713902729
#
# </td>
# </tr>
#
# <tr>
# <td>
# **dA_prev[1,1] =**
# </td>
# <td>
# [[ 0.08485462 0.2787552 ] <br>
# [ 1.26461098 -0.25749373] <br>
# [ 1.17975636 -0.53624893]]
# </td>
# </tr>
# </table>
# ### Congratulations !
#
# Congratulations on completing this assignment. You now understand how convolutional neural networks work. You have implemented all the building blocks of a neural network. In the next assignment you will implement a ConvNet using TensorFlow.
| 44,237 |
/Entrega3_ProyectoIntegrador_A00833791.ipynb | 25709737e2c164a91f23bdf3799d56371999d074 | [] | no_license | RolandoGallardo/Etapa3ProyectoIntegrador | https://github.com/RolandoGallardo/Etapa3ProyectoIntegrador | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 58,612 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/RolandoGallardo/Etapa3ProyectoIntegrador/blob/main/Entrega3_ProyectoIntegrador_A00833791.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="HxfNnphlXJoG"
# # **Entrega Etapa 3 del Proyecto Integrador:**
#
# Rolando Adolfo Martin Gallardo Galvez
#
# A00833791
#
# 11/10/2021
#
# Link Collab: https://colab.research.google.com/drive/1M1ezntmkyoZox8OSKmjD_YlQc3TVPK7t?usp=sharing
#
# Link Github: https://github.com/RolandoGallardo/Etapa3ProyectoIntegrador/blob/main/Entrega3_ProyectoIntegrador_A00833791.ipynb
#
#
# **Descripcion de Problematica, Solución y Programa:**
#
#
# A causa de la aparición de la Covid 19 en México enfermedades causadas por los malos hábitos alimenticios y poca actividad física como la obesidad, la diabetes, la hipertensión entre otras han sido puestas en un foco. Estas enfermedades presentan un problema al bienestar de la comunidad en el ámbito de la salud con el objetivo de desarrollo sostenible número 3 (Salud y bienestar).
#
# El objetivo de este Proyecto Integrador es utilizar la programación para promover un estilo de vida saludable. Este proyecto intenta poner en perspectiva la importancia de una vida saludable, colaborando a mejorar la salud pública en los tiempos de pandemia. Objetivos que tienen que ser considerados son la sensibilización de las masas, concientización de los peligros y presentación de la información de manera simple y concisa.
#
# El proyecto planea solucionar esta problemática con un programa que ayudará a compañías a monitorear el estado de salud de sus empleados, ambos de forma individual y en base a departamento. El programa operará como una base de datos de los empleados en los que se almacenará información en cuanto a su estado de salud. En esta base de datos se listará su peso, estatura, imc y su estado de vacunación a la Covid 19. También se le cuestionara sobre su diagnóstico de enfermedades como la diabetes, hipertensión, cáncer, tabaquismo y problemas en el corazón. Esta información será de uso para que se realice un análisis de estos mismos y medidas informadas puedan ser tomadas al respecto.
#
# Este programa será capaz de organizar la información por individuo con el fin de poder identificar a empleados que pueda ser necesario un seguimiento más profundo para su propia salud y bienestar. Su interfaz será simple para que personas no familiarizadas con la programación sean capaces de utilizarla eficientemente. La clave es un diseño simple e intuitivo.
#
# En resumen la pandemia ha puesto en evidencia las enfermedades causadas por los malos hábitos en la nación y a base de la programación voy a ayudar a resolver este problema con este proyecto integrador. El proyecto será un programa que organiza de forma eficiente la información de empleados y con ello asistir a especialistas a identificar, informar y mejorar la salud pública de las compañías y gradualmente el país. Esta información puede ser actualizada en cualquier momento por la persona operando el programa para marcar cambios en el diagnóstico del empleado. Todo esto apoyaría en el ODS número tres (salud y bienestar).
#
# **Reflexión Final:**
#
# Durante el desarrollo de este proyecto mi conocimiento en la programación en Python ha crecido en magnitudes exponenciales. Para poder realizar este proyecto tuve que aprender a manejar listas y matrices con cohesión. Tuve que aprender a diferenciar strings, de int, tuples, floats entre otros y manipularlos entre sí para realizar procesos y manipular los datos.
#
# Yo creo que lo que he hecho bien ha sido demostrar iniciativa. En este proyecto, sobre todo en la entrega 2, sufrí mucho con la impresión en el formato indicado. El método que era recomendado era uno con strings en el que se determinaban los caracteres para el formato. Yo, al no tener mucha maestría en este método desarrollé uno diferente utilizando conceptos que tenía más consolidados. Además diría que la interfaz del programa es simple y intuitiva al únicamente requerir números para operarse.
#
# En cuanto a los aspectos en los que podría mejorar diría que el problema principal de mi código es que no está optimizado. Un aspecto que muestra esto es la función de alta_empleado(). El inicio de esta función es muy similar al de la función consultar_empleado() ya que ambas usan el ID como para identificar el empleado al que la función va a ser aplicada. Una solución a ese problema sería crear una función que cumpla esto y luego pueda ser llamada en estas mismas sería una forma de no tener esa redundancia en el código. Otro aspecto que podría mejorar en mi código sería en el formato de impresión. Al no utilizar el método con los caracteres mi codigo se hizo mucho mas grande (como 150 líneas) de lo que pudo haber sido demandando más recursos de la computadora y demorando el tiempo en el que se procesa la información (el efecto fue mínimo pero podría ser importante en proyectos de mayor escala).
#
#
# + colab={"base_uri": "https://localhost:8080/"} id="0W_bpuP6WHqF" outputId="7e114755-20c9-4472-ff53-ea9b0b45c4fe"
def guardar_archivo(nombre,empleados):
with open(nombre,"w") as archivo:
for empleado in empleados:
empleado[0] = str(empleado[0])
empleado[3] = str(empleado[3])
empleado[4] = str(empleado[4])
texto = ",".join(empleado)
archivo.write(texto + "\n")
def leer_archivo(nombre):
empleados = []
with open(nombre,"r") as archivo:
contenido = archivo.readlines()
for elemento in contenido:
linea = elemento.split(",")
linea[11] = linea[11][:-1]
if linea[5] == "1":
linea[5] = "Diabetes"
if linea[6] == "1":
linea[6] = "Hipertension"
if linea[7] == "1":
linea[7] = "Corazon"
if linea[8] == "1":
linea[8] = "Cancer"
if linea[9] == "1":
linea[9] = "Tabaquismo"
if linea[10] == "1":
linea[10] = "Con Vacuna"
empleados.append(linea)
return empleados
def alta_empleado(nombre):
empleados = leer_archivo(nombre)
# DATOS USUARIO
ID = int(input("Teclea el ID del empleado: "))
nombre = input("Teclea el nombre del empleado: ")
edad = input("Teclea edad del empleado: ")
peso = int(input("Teclea el peso (kg): "))
estatura = float(input("Teclea la estatura (mts): "))
diabetes = input("Diabetes? 1.Si 0.No: ")
hipertension = input("Hipertension? 1.Si 0.No: ")
corazon = input("Enfermedad al corazon? 1.Si 0.No: ")
cancer = input("Cancer? 1.Si 0.No: ")
tabaquismo = input("Tabaquismo? 1.Si 0.No: ")
vacuna = input("Vacuna Covid? 1.Si 0.No: ")
departamento = input("Teclea el departamento del empleado: ")
# TRANSFORMAR ENFERMEDAD
if diabetes == "1":
diabetes = "Diabetes"
if hipertension == "1":
hipertension = "Hipertension"
if corazon == "1":
corazon = "Corazon"
if cancer == "1":
cancer = "Cancer"
if tabaquismo == "1":
tabaquismo = "Tabaquismo"
if vacuna == "1":
vacuna = "Con Vacuna"
# GUARDAR LISTA
info = [ID, nombre, edad, peso, estatura, diabetes, hipertension, corazon, cancer, tabaquismo, vacuna, departamento]
empleados.append(info)
guardar_archivo("info_empleados.txt",empleados)
def calcular_IMC_empleado(empleado):
peso = int(empleado[3])
altura = float(empleado[4])
imc = round((peso / (altura * altura)), 2)
if imc < 16:
return imc, "Delgadez Severa"
elif 16 <= imc and imc < 17:
return imc, "Delgadez Moderada"
elif 17 <= imc and imc < 18.5:
return imc, "Delgadez Aceptable"
elif 18.5 <= imc and imc < 25:
return imc, "Peso Normal"
elif 25 <= imc and imc < 30:
return imc, "Sobrepeso"
elif 30 <= imc and imc < 35:
return imc, "Obeso"
elif 35 <= imc and imc < 40:
return imc, "Obeso"
elif 40 < imc:
return imc, "Obeso"
def imprimir_IMC(tabla_uno, tabla_dos, numero_de_empleados):
encabezados = ["Clasificación IMC", "IMC", "ID", "Nombre", "Peso", "Altura", "Enfermedades", "Vacuna"]
espacios = [25, 5, 5, 20, 10, 10, 65, 15]
encabezado_tabla = ""
for x in range(len(encabezados)):
encabezado = encabezados[x]
espacio = espacios[x]
falta = espacio - len(encabezado)
encabezado_tabla = encabezado_tabla + encabezado + ' ' * falta + ' '
print(encabezado_tabla)
for linea in tabla_uno:
linea_contenido = ""
for x in range(len(linea)):
if x == 6:
enfermedades = linea[x]
espacios_enfermedades = [10, 15, 10, 10, 15]
contenido = ""
for x in range(len(enfermedades)):
enfermedad = enfermedades[x]
espacio = espacios_enfermedades[x]
if enfermedad == "0":
contenido = contenido + '-' * espacio + ' '
else:
falta = espacio - len(enfermedad)
contenido = contenido + enfermedad + ' ' * falta + ' '
linea_contenido = linea_contenido + contenido + ' '
elif x == 7:
vacuna = linea[x]
espacio = 15
contenido = ""
if vacuna == "0":
contenido = contenido + '-' * espacio + ' '
else:
contenido = vacuna
linea_contenido = linea_contenido + contenido
else:
contenido = str(linea[x])
espacio = espacios[x]
falta = espacio - len(contenido)
linea_contenido = linea_contenido + contenido + ' ' * falta + ' '
print(linea_contenido)
print()
print()
encabezados_dos = ["Diagnostico", "Cantidad", "Porcentaje"]
espacios_dos = [25, 10, 15]
encabezado_tabla_dos = ""
for x in range(len(encabezados_dos)):
encabezado = encabezados_dos[x]
espacio = espacios_dos[x]
falta = espacio - len(encabezado)
encabezado_tabla_dos = encabezado_tabla_dos + encabezado + ' ' * falta + ' '
print(encabezado_tabla_dos)
for linea in tabla_dos:
linea_contenido = ""
for x in range(len(linea)):
contenido = str(linea[x])
espacio = espacios_dos[x]
falta = espacio - len(contenido)
linea_contenido = linea_contenido + contenido + ' ' * falta + ' '
print(linea_contenido)
print("Total empleados " + str(numero_de_empleados))
def calcular_IMC(nombre):
empleados = leer_archivo(nombre)
numero_de_empleados = len(empleados)
delgadez_severa = 0
delgadez_moderada = 0
delgadez_aceptable = 0
peso_normal = 0
sobrepeso = 0
obeso = 0
tabla_uno = []
for x in range(numero_de_empleados):
if x != 0:
empleado = empleados[x]
imc, categoria = calcular_IMC_empleado(empleado)
if categoria == "Delgadez Severa":
delgadez_severa = delgadez_severa + 1
elif categoria == "Delgadez Moderada":
delgadez_moderada = delgadez_moderada + 1
elif categoria == "Delgadez Aceptable":
delgadez_aceptable = delgadez_aceptable + 1
elif categoria == "Peso Normal":
peso_normal = peso_normal + 1
elif categoria == "Sobrepeso":
sobrepeso = sobrepeso + 1
elif categoria == "Obeso":
obeso = obeso + 1
id, nombre, edad, peso, estatura, diabetes, hipertension, corazon, cancer, tabaquismo, vacuna, departamento = empleado
linea = [categoria, imc, id, nombre, peso, estatura, [diabetes, hipertension, corazon, cancer, tabaquismo], vacuna]
tabla_uno.append(linea)
numero_de_empleados = numero_de_empleados - 1
porcentaje_delgadez_severa = str(delgadez_severa / numero_de_empleados * 100) + "%"
porcentaje_delgadez_moderada = str(delgadez_moderada / numero_de_empleados * 100) + "%"
porcentaje_delgadez_aceptable = str(delgadez_aceptable / numero_de_empleados * 100) + "%"
porcentaje_peso_normal = str(peso_normal / numero_de_empleados * 100) + "%"
porcentaje_sobrepeso = str(sobrepeso / numero_de_empleados * 100) + "%"
porcentaje_obeso = str(obeso / numero_de_empleados * 100) + "%"
tabla_dos = [["Delgadez Severa", delgadez_severa, porcentaje_delgadez_severa],
["Delgadez Moderada", delgadez_moderada, porcentaje_delgadez_moderada],
["Delgadez Aceptable", delgadez_aceptable, porcentaje_delgadez_aceptable],
["Peso Normal", peso_normal, porcentaje_peso_normal],
["Sobrepeso", sobrepeso, porcentaje_sobrepeso],
["Obeso", obeso, porcentaje_obeso]]
imprimir_IMC(tabla_uno, tabla_dos, numero_de_empleados)
def consultar_empleado(nombre):
empleados = leer_archivo(nombre)
ID_consulta = input("Cual es el ID del empleado? ")
found = False
indice = 0
for x in range(len(empleados)):
empleado = empleados[x]
id = empleado[0]
if ID_consulta == id:
found = True
indice = x
if found != True:
print("ID invalido")
consultar_empleado(nombre)
else:
print(empleados[indice])
def actualizar_empleado(nombre):
empleados = leer_archivo(nombre)
ID_consulta = input("ID de empleado a ser actualizado")
found = False
indice = 0
for x in range(len(empleados)):
empleado = empleados[x]
id = empleado[0]
if ID_consulta == id:
found = True
indice = x
if found != True:
print("ID invalido")
else:
empleado = empleados[indice]
actualizar_nombre = input("Actualizar Nombre? 1.Si 0.No: ")
if actualizar_nombre == "1":
nombre = input("Teclea el nombre del empleado: ")
empleado[1] = nombre
actualizar_edad = input("Actualizar Edad? 1.Si 0.No: ")
if actualizar_edad == "1":
edad = input("Teclea edad del empleado: ")
empleado[2] = edad
actualizar_peso = input("Actualizar Peso? 1.Si 0.No: ")
if actualizar_peso == "1":
peso = int(input("Teclea el peso (kg): "))
empleado[3] = peso
actualizar_estatura = input("Actualizar Estatura? 1.Si 0.No: ")
if actualizar_estatura == "1":
estatura = float(input("Teclea la estatura (mts): "))
empleado[4] = estatura
actualizar_diabetes = input("Actualizar Diabetes? 1.Si 0.No: ")
if actualizar_diabetes == "1":
diabetes = input("Diabetes? 1.Si 0.No: ")
if diabetes == "1":
diabetes = "Diabetes"
empleado[5] = diabetes
actualizar_hipertension = input("Actualizar Hipertension? 1.Si 0.No: ")
if actualizar_hipertension == "1":
hipertension = input("Hipertension? 1.Si 0.No: ")
if hipertension == "1":
hipertension = "Hipertension"
empleado[6] = hipertension
actualizar_corazon = input("Actualizar Corazon? 1.Si 0.No: ")
if actualizar_corazon == "1":
corazon = input("Enfermedad al corazon? 1.Si 0.No: ")
if corazon == "1":
corazon = "Corazon"
empleado[7] = corazon
actualizar_tabaquismo = input("Actualizar Tabaquismo? 1.Si 0.No: ")
if actualizar_tabaquismo == "1":
tabaquismo = input("Tabaquismo? 1.Si 0.No: ")
if tabaquismo == "1":
tabaquismo = "Tabaquismo"
empleado[8] = tabaquismo
actualizar_vacuna = input("Actualizar Vacuna? 1.Si 0.No: ")
if actualizar_vacuna == "1":
vacuna = input("Vacuna? 1.Si 0.No: ")
if vacuna == "1":
vacuna = "Con Vacuna"
empleado[9] = vacuna
actualizar_cancer = input("Actualizar Cancer? 1.Si 0.No: ")
if actualizar_cancer == "1":
cancer = input("Cancer? 1.Si 0.No: ")
if cancer == "1":
cancer = "Cancer"
empleado[10] = cancer
actualizar_departamento = input("Actualizar Departamento? 1.Si 0.No: ")
if actualizar_departamento == "1":
departamento = input("Departamento? 1.Si 0.No: ")
if departamento == "1":
departamento = input("Teclea Departamento")
empleado[11] = departamento
guardar_archivo(nombre,empleados)
def crear_archivo_reporte(nombre,tabla):
with open(nombre,"w") as archivo:
for x in range(len(tabla)):
linea = tabla[x]
if len(linea) == 6 and x != 0:
texto = ",".join(linea[:4]) + ",".join(linea[4]) + "," + ",".join(linea[5:])
else:
texto = ",".join(linea)
archivo.write(texto + "\n")
def crear_reporte_empleados(nombre):
empleados = leer_archivo(nombre)
tabla_uno = []
diabetes_cuenta = 0
hipertension_cuenta = 0
corazon_cuenta = 0
cancer_cuenta = 0
tabaquismo_cuenta = 0
vacuna_cuenta = 0
numero_de_empleados = len(empleados)
for x in range(numero_de_empleados):
if x != 0:
empleado = empleados[x]
id, nombre, edad, peso, estatura, diabetes, hipertension, corazon, cancer, tabaquismo, vacuna, departamento = empleado
if diabetes != "0":
diabetes_cuenta = diabetes_cuenta + 1
if hipertension != "0":
hipertension_cuenta = hipertension_cuenta + 1
if corazon != "0":
corazon_cuenta = corazon_cuenta + 1
if cancer != "0":
cancer_cuenta = cancer_cuenta + 1
if tabaquismo != "0":
tabaquismo_cuenta = tabaquismo_cuenta + 1
if vacuna != "0":
vacuna_cuenta = vacuna_cuenta + 1
empleado_formatado = [id, nombre, peso, estatura, [diabetes, hipertension, corazon, cancer, tabaquismo], vacuna]
tabla_uno.append(empleado_formatado)
numero_de_empleados = numero_de_empleados - 1
diabetes_porcentage = str(diabetes_cuenta / numero_de_empleados * 100) + "%"
hipertension__porcentage = str(hipertension_cuenta / numero_de_empleados * 100) + "%"
corazon__porcentage = str(corazon_cuenta / numero_de_empleados * 100) + "%"
cancer__porcentage = str(cancer_cuenta / numero_de_empleados * 100) + "%"
tabaquismo__porcentage = str(tabaquismo_cuenta / numero_de_empleados * 100) + "%"
vacuna__porcentage = str(vacuna_cuenta / numero_de_empleados * 100) + "%"
encabezados = ["ID", "Nombre", "Peso", "Altura", "Enfermedades", "Vacuna"]
espacios = [5, 20, 10, 10, 65, 15]
encabezado_tabla = ""
for x in range(len(encabezados)):
encabezado = encabezados[x]
espacio = espacios[x]
falta = espacio - len(encabezado)
encabezado_tabla = encabezado_tabla + encabezado + ' ' * falta + ' '
print(encabezado_tabla)
for linea in tabla_uno:
linea_contenido = ""
for x in range(len(linea)):
if x == 4:
enfermedades = linea[x]
espacios_enfermedades = [10, 15, 10, 10, 15]
contenido = ""
for x in range(len(enfermedades)):
enfermedad = enfermedades[x]
espacio = espacios_enfermedades[x]
if enfermedad == "0":
contenido = contenido + '-' * espacio + ' '
else:
falta = espacio - len(enfermedad)
contenido = contenido + enfermedad + ' ' * falta + ' '
linea_contenido = linea_contenido + contenido + ' '
elif x == 5:
vacuna = linea[x]
espacio = 15
contenido = ""
if vacuna == "0":
contenido = contenido + '-' * espacio + ' '
else:
contenido = vacuna
linea_contenido = linea_contenido + contenido
else:
contenido = str(linea[x])
espacio = espacios[x]
falta = espacio - len(contenido)
linea_contenido = linea_contenido + contenido + ' ' * falta + ' '
print(linea_contenido)
tabla_uno = [encabezados] + tabla_uno
print()
print()
tabla_dos = [["Diabetes", str(diabetes_cuenta), diabetes_porcentage],
["Hipertension", str(hipertension_cuenta), hipertension__porcentage],
["Corazon", str(corazon_cuenta), corazon__porcentage],
["Cancer", str(cancer_cuenta), cancer__porcentage],
["Tabaquismo", str(tabaquismo_cuenta), tabaquismo__porcentage],
["Vacunados", str(vacuna_cuenta), vacuna__porcentage]]
encabezados_dos = ["Enfermedad", "Cantidad", "Porcentaje"]
espacios_dos = [25, 10, 15]
encabezado_tabla_dos = ""
for x in range(len(encabezados_dos)):
encabezado = encabezados_dos[x]
espacio = espacios_dos[x]
falta = espacio - len(encabezado)
encabezado_tabla_dos = encabezado_tabla_dos + encabezado + ' ' * falta + ' '
print(encabezado_tabla_dos)
for linea in tabla_dos:
linea_contenido = ""
for x in range(len(linea)):
contenido = str(linea[x])
espacio = espacios_dos[x]
falta = espacio - len(contenido)
linea_contenido = linea_contenido + contenido + ' ' * falta + ' '
print(linea_contenido)
print("Total empleados " + str(numero_de_empleados))
tabla_dos = [encabezados_dos] + tabla_dos + [["Total Empleados", str(numero_de_empleados)]]
tabla = tabla_uno + tabla_dos
crear_archivo_reporte("reporte_empleados.txt",tabla)
def menu():
while True:
print("1. Alta de empleado")
print("2. Calcular imc de empleado")
print("3. Cambia información del empleado")
print("4. Consulta un empleado")
print("5. Reporte de todos los empleados")
print("6. Salir")
funcion = input("Teclea la opcion: ")
if funcion == "1":
alta_empleado("info_empleados.txt")
elif funcion == "2":
calcular_IMC("info_empleados.txt")
elif funcion == "3":
actualizar_empleado("info_empleados.txt")
elif funcion == "4":
consultar_empleado("info_empleados.txt")
elif funcion == "5":
crear_reporte_empleados("info_empleados.txt")
elif funcion == "6":
break
else:
print("opcion incorrecta")
def main():
menu()
main()
# + [markdown] id="__10UacBU7or"
# # **Plan de Pruebas y Descripcion de Funciones**
# + id="7EM7fsHAY_k5"
#Descripcion de funciones
#main()
#Esta funcion llama la funcion menu() y empieza el codigo, es el catalizador de todo el programa
#menu()
#Esta funcion abre un menu de opciones el cual llama las otras funciones a base de el numero que el ususario indica
#Esta funcion se repite al final de cada funcion o input invalido al tener el while true
#Esta funcion finaliza al llamar usar el input 6 ya que este usa el comando break para finalizar el programa
#1: alta_empleado
#Esta funcion abre el archivo "info_empleados.txt" con el uso de leer_archivo y añade un nuevo empleado cuya informacion
# es ingresada a base de preguntas que el usuario responde
#Luego esta utiliza la funcion guardar_archivo para añadir al archivo informacion del nuevo empleado
#2: calcular_IMC()
#Esta funcion abre el archivo "info_empleados.txt" con el uso de leer_archivo
#La funcion usa contadores para calcular los porcentajes de personas en clases de peso
#Esta funcin imprime una tabla de informacion de los empleados donde muestra su imc
#Luego imprime una tabal de informacion que muestra los porcentajes de cada clase de peso y su numero
#Hace esto llamando a las funciones calcular_IMC_empleado que calcula los valores individuales de imc de cada empleado
# y la funcion imprimir_IMC que imprime la informacion en el formato deseado
#3: actualizar_empleado()
#Esta funcion abre el archivo "info_empleados.txt" con el uso de leer_archivo
#Esta funcion utiliza un input para identificar que empleado va a ser actualizado
#Hace esto con un ciclo for revisando los elementos de cada linea de la matriz
#Luego la funcion pregunta indivualmente la variables que se desean cambiar del empleado
#Finalmente se utiliza la funcion guardar_archivo para actualizar el archivo con la informacion del empleado
#4: consultar_empleado()
#Esta funcion abre el archivo "info_empleados.txt" con el uso de leer_archivo
#Esta funcion utiliza un input para identificar que empleado va a ser actualizado
#Hace esto con un ciclo for revisando los elementos de cada linea de la matriz
#La funcion luego imprime la informacion de ese empleado
#5: crear_reporte_empleados()
#Esta funcion abre el archivo "info_empleados.txt" con el uso de leer_archivo
#La funciona utiliza contadores para conseguir la informacion que se despliega en la segunda tabla
#Esta funcion imprime una tabla organizada con la informacion de cada empleado
#Incluye una segunda tabla en la que despliega las enfermedades, cantidad de empleados por enfermedad y porcenteages
#Finalmente incluye el total de empleados
#plan pruebas
#usar menu para desplegar opciones
#seleccionar opcion 1 y añadir 2 empleados (dos pruebas)
#usar la opcion 4 para verificar que han sido salvados (dos pruebas)
#usar opcion 2 dos veces para demonstrar su uso
#usar opcion 3 para actualizar informacion de 2 empleados (dos pruebas)
#verificar utilidad de opcion 3 con la opcion 4
#imprimir tabla con informacion con opcion 5 (dos pruebas)
#salir con opcion 6 y acabar plan pruebas
# + id="0CQEw1GKkY4M"
| 26,331 |
/notebook/least squares method with kernel.ipynb | 721126c9e0cc8eee07cc3e75442856638cdccb66 | [] | no_license | zizi0429/machine_learning | https://github.com/zizi0429/machine_learning | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 27,488 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from brian2 import *
import numpy as np
import random
import time
# ### Reduced Traub-Miles E-cells
# +
# params
start_scope()
N = 1
Cm = 1*ufarad/cm**2
El = -67*mV
ENa = 50*mV
EK = -100*mV
gl = 0.1*msiemens/cm**2
gNa = 100*msiemens/cm**2
gK = 80*msiemens/cm**2
# +
# H-H eqs for cell
eqs = '''
dv/dt = ( (gl * (El-v) + gNa * m**3 * h * (ENa-v) + gK * n**4 * (EK-v) + I))/Cm : volt
I : amp*meter**-2
m = alpham / (alpham + betam) :1
dn/dt = alphan * (1-n) - betan * n : 1
dh/dt = alphah * (1-h) - betah * h : 1
alpham = (0.32/mV) * (v+54*mV) / (-exp((-v-54*mV) / (4*mV)) + 1)/ms : Hz
betam = (0.28/mV) * (v+27*mV)/ (exp((v+27*mV)/(5*mV)) - 1)/ms : Hz
alphah = (0.128) * exp(-(v+50*mV)/(18*mV))/ms : Hz
betah = 4/(exp((-v-27*mV) / (5*mV)) + 1)/ms : Hz
alphan = (0.032/mV) * (v+52*mV) / (-exp(-(v+52*mV) / (5*mV)) + 1)/ms : Hz
betan = 0.5*exp(-(v+57*mV)/(40*mV))/ms : Hz
'''
# +
start_scope()
G = NeuronGroup(N, eqs, threshold='v>0*mV',
method='exponential_euler')
M = StateMonitor(G, 'v', record=0)
G.I = 1*uA*cm**-2
G.v = -60*mV
# -
run(40*ms)
plot(M.t/ms, 1000*M.v[0], 'C0', label='Brian')
# plot(M.t/ms, 1-exp(-M.t/tau), 'C1--',label='Analytic')
xlabel('Time (ms)')
ylabel('mv')
legend();
# ### Wang-Buzsaki I-cells
# +
# params
start_scope()
N = 1
Cm = 1*ufarad/cm**2
El = -65*mV
ENa = 55*mV
EK = -90*mV
gl = 0.1*msiemens/cm**2
gNa = 35*msiemens/cm**2
gK = 9*msiemens/cm**2
# -
# H-H eqs for cell
eqs = '''
dv/dt = ( (gl * (El-v) + gNa * m**3 * h * (ENa-v) + gK * n**4 * (EK-v) + I))/Cm : volt
I : amp*meter**-2
m = alpham / (alpham + betam) :1
dn/dt = alphan * (1-n) - betan * n : 1
dh/dt = alphah * (1-h) - betah * h : 1
alpham = (0.1/mV) * (v+35*mV) / (-exp((-v-35*mV) / (10*mV)) + 1)/ms : Hz
betam = 4 * exp(-(v+60*mV)/(18*mV))/ms : Hz
alphah = (0.35) * exp(-(v+58*mV)/(20*mV))/ms : Hz
betah = 5/(exp((-v-28*mV) / (10*mV)) + 1)/ms : Hz
alphan = (0.05/mV) * (v+34*mV) / (-exp(-(v+34*mV) / (10*mV)) + 1)/ms : Hz
betan = (0.625)*exp(-(v+44*mV)/(80*mV))/ms : Hz
'''
# +
start_scope()
G = NeuronGroup(N, eqs, threshold='v>0*mV',
method='exponential_euler')
M = StateMonitor(G, 'v', record=0)
G.I = 1*uA*cm**-2
G.v = -60*mV
run(40*ms)
# -
plot(M.t/ms, 1000*M.v[0], 'C0', label='Brian')
# plot(M.t/ms, 1-exp(-M.t/tau), 'C1--',label='Analytic')
xlabel('Time (ms)')
ylabel('mv')
legend();
# ### Synapses
# +
# E cells
start_scope()
N = 1
Cm = 1*ufarad/cm**2
El = -67*mV
ENa = 50*mV
EK = -100*mV
gl = 0.1*msiemens/cm**2
gNa = 100*msiemens/cm**2
gK = 80*msiemens/cm**2
gampa = 0.6*msiemens/cm**2
ggaba = 0.6*msiemens/cm**2
eqs = '''
dv/dt = ( (gl * (El-v) + gNa * m**3 * h * (ENa-v) + gK * n**4 * (EK-v) + Isyn))/Cm : volt
Isyn = Igaba : amp*meter**-2
Igaba = ggaba * (V_I - v) * sgaba_tot : amp*meter**-2
sgaba_tot : 1
m = alpham / (alpham + betam) :1
dn/dt = alphan * (1-n) - betan * n : 1
dh/dt = alphah * (1-h) - betah * h : 1
alpham = (0.32/mV) * (v+54*mV) / (-exp((-v-54*mV) / (4*mV)) + 1)/ms : Hz
betam = (0.28/mV) * (v+27*mV)/ (exp((v+27*mV)/(5*mV)) - 1)/ms : Hz
alphah = (0.128) * exp(-(v+50*mV)/(18*mV))/ms : Hz
betah = 4/(exp((-v-27*mV) / (5*mV)) + 1)/ms : Hz
alphan = (0.032/mV) * (v+52*mV) / (-exp(-(v+52*mV) / (5*mV)) + 1)/ms : Hz
betan = 0.5*exp(-(v+57*mV)/(40*mV))/ms : Hz
'''
Ecells = NeuronGroup(N, eqs, threshold='v>0*mV',
method='exponential_euler')
Me = StateMonitor(Ecells, 'v', record=1)
N = 1
Cm = 1*ufarad/cm**2
El = -65*mV
ENa = 55*mV
EK = -90*mV
gl = 0.1*msiemens/cm**2
gNa = 35*msiemens/cm**2
gK = 9*msiemens/cm**2
# a diff ggaba
ggaba = 0.2*msiemens/cm**2
eqs = '''
dv/dt = ( (gl * (El-v) + gNa * m**3 * h * (ENa-v) + gK * n**4 * (EK-v) + Isyn))/Cm : volt
Isyn = Igaba + Iampa : amp*meter**-2
Igaba = ggaba * (V_I - v) * sgaba_tot : amp*meter**-2
Iampa = gampa * (V_E - v) * sampa_tot : amp*meter**-2
sampa_tot : 1
sgaba_tot : 1
m = alpham / (alpham + betam) :1
dn/dt = alphan * (1-n) - betan * n : 1
dh/dt = alphah * (1-h) - betah * h : 1
alpham = (0.1/mV) * (v+35*mV) / (-exp((-v-35*mV) / (10*mV)) + 1)/ms : Hz
betam = 4 * exp(-(v+60*mV)/(18*mV))/ms : Hz
alphah = (0.35) * exp(-(v+58*mV)/(20*mV))/ms : Hz
betah = 5/(exp((-v-28*mV) / (10*mV)) + 1)/ms : Hz
alphan = (0.05/mV) * (v+34*mV) / (-exp(-(v+34*mV) / (10*mV)) + 1)/ms : Hz
betan = (0.625)*exp(-(v+44*mV)/(80*mV))/ms : Hz
'''
Icells = NeuronGroup(N, eqs, threshold='v>0*mV',
method='exponential_euler')
MI = StateMonitor(Icells, 'v', record=True)
# Synapses
tausampar = 0.2*ms
tausampad = 2*ms
tausgabar = 0.5*ms
tausgabad = 10*ms
eqs_ampa = '''
sampa_tot_post = w*sampa : 1 (summed)
dsampa/dt= (1+tanh(v_pre/10))/2 * (1-sampa)/tausampar - sampa/tausampad : 1 (clock-driven)
w : 1 # synaptic weight
'''
eqs_gaba = '''
sgaba_tot_post = w*sgaba : 1 (summed)
dsgaba/dt= (1+tanh(v_pre/10))/2 * (1-sgaba)/tausgabar - sgaba/tausgabad : 1 (clock-driven)
w : 1 # synaptic weight
'''
# E to I, ampa
C_E_I = Synapses(Ecells, Icells, model=eqs_ampa, method='euler')
# C_E_I = Synapses(Ecells, Icells, model=eqs_ampa, method='euler')
C_E_I.connect()
C_E_I.w[:] = 1
# I to I
C_I_I = Synapses(Icells, Icells, on_pre=eqs_gaba, method='euler')
C_I_I.connect('i != j')
# I to E
C_I_E = Synapses(Icells, Ecells, on_pre=eqs_gaba, method='euler')
C_I_E.connect()
sp_E = SpikeMonitor(Ecells)
sp_I = SpikeMonitor(Icells)
#dv/dt = ( (gl * (El-v) + gNa * m**3 * h * (ENa-v) + gK * n**4 * (EK-v) + I +
# gei*(ve - v)))/Cm : volt
# -
# +
start_scope()
# net = Network(collect())
# net.add(sp_E)
# net.add(sp_I)
# # M = SpikeMonitor(G)
# net.run(4 * ms, report='stdout')
# gmax = 0.01
# taupre = 20*ms
# taupost = taupre
# dApre = .01
# dApost = -dApre * taupre / taupost * 1.05
# dApost *= gmax
# dApre *= gmax
# S = Synapses(Ecells, Icells,
# '''w : 1
# dApre/dt = -Apre / taupre : 1 (event-driven)
# dApost/dt = -Apost / taupost : 1 (event-driven)''',
# on_pre='''ge += w
# Apre += dApre
# w = clip(w + Apost, 0, gmax)''',
# on_post='''Apost += dApost
# w = clip(w + Apre, 0, gmax)''',
# )
# S.connect()
# S.w = 'rand() * gmax'
# mon = StateMonitor(S, 'w', record=[0, 1])
# w=1.0*volt
# S = Synapses(Ecells, Icells, model='w : volt', on_pre='v += w')
# S.connect()
# run(10*ms, report='text')
run(10*ms)
# subplot(311)
# plot(S.w / gmax, '.k')
# ylabel('Weight / gmax')
# xlabel('Synapse index')
# subplot(312)
# hist(S.w / gmax, 20)
# xlabel('Weight / gmax')
# subplot(313)
# plot(mon.t/second, mon.w.T/gmax)
# xlabel('Time (s)')
# ylabel('Weight / gmax')
# tight_layout()
# show()
# -
C_E_I
plot(sp_I.t/ms)
# +
from brian2 import *
# populations
N = 1000
N_E = int(N * 0.8) # pyramidal neurons
N_I = int(N * 0.2) # interneurons
# voltage
V_L = -70. * mV
V_thr = -50. * mV
V_reset = -55. * mV
V_E = 0. * mV
V_I = -70. * mV
# membrane capacitance
C_m_E = 0.5 * nF
C_m_I = 0.2 * nF
# membrane leak
g_m_E = 25. * nS
g_m_I = 20. * nS
# refractory period
tau_rp_E = 2. * ms
tau_rp_I = 1. * ms
# external stimuli
rate = 3 * Hz
C_ext = 800
# synapses
C_E = N_E
C_I = N_I
# AMPA (excitatory)
g_AMPA_ext_E = 2.08 * nS
g_AMPA_rec_E = 0.104 * nS * 800. / N_E
g_AMPA_ext_I = 1.62 * nS
g_AMPA_rec_I = 0.081 * nS * 800. / N_E
tau_AMPA = 2. * ms
# NMDA (excitatory)
g_NMDA_E = 0.327 * nS * 800. / N_E
g_NMDA_I = 0.258 * nS * 800. / N_E
tau_NMDA_rise = 2. * ms
tau_NMDA_decay = 100. * ms
alpha = 0.5 / ms
Mg2 = 1.
# GABAergic (inhibitory)
g_GABA_E = 1.25 * nS * 200. / N_I
g_GABA_I = 0.973 * nS * 200. / N_I
tau_GABA = 10. * ms
# subpopulations
f = 0.1
p = 5
N_sub = int(N_E * f)
N_non = int(N_E * (1. - f * p))
w_plus = 2.1
w_minus = 1. - f * (w_plus - 1.) / (1. - f)
# modeling
eqs_E = '''
dv / dt = (- g_m_E * (v - V_L) - I_syn) / C_m_E : volt (unless refractory)
I_syn = I_AMPA_ext + I_AMPA_rec + I_NMDA_rec + I_GABA_rec : amp
I_AMPA_ext = g_AMPA_ext_E * (v - V_E) * s_AMPA_ext : amp
I_AMPA_rec = g_AMPA_rec_E * (v - V_E) * 1 * s_AMPA : amp
ds_AMPA_ext / dt = - s_AMPA_ext / tau_AMPA : 1
ds_AMPA / dt = - s_AMPA / tau_AMPA : 1
I_NMDA_rec = g_NMDA_E * (v - V_E) / (1 + Mg2 * exp(-0.062 * v / mV) / 3.57) * s_NMDA_tot : amp
s_NMDA_tot : 1
I_GABA_rec = g_GABA_E * (v - V_I) * s_GABA : amp
ds_GABA / dt = - s_GABA / tau_GABA : 1
'''
eqs_I = '''
dv / dt = (- g_m_I * (v - V_L) - I_syn) / C_m_I : volt (unless refractory)
I_syn = I_AMPA_ext + I_AMPA_rec + I_NMDA_rec + I_GABA_rec : amp
I_AMPA_ext = g_AMPA_ext_I * (v - V_E) * s_AMPA_ext : amp
I_AMPA_rec = g_AMPA_rec_I * (v - V_E) * 1 * s_AMPA : amp
ds_AMPA_ext / dt = - s_AMPA_ext / tau_AMPA : 1
ds_AMPA / dt = - s_AMPA / tau_AMPA : 1
I_NMDA_rec = g_NMDA_I * (v - V_E) / (1 + Mg2 * exp(-0.062 * v / mV) / 3.57) * s_NMDA_tot : amp
s_NMDA_tot : 1
I_GABA_rec = g_GABA_I * (v - V_I) * s_GABA : amp
ds_GABA / dt = - s_GABA / tau_GABA : 1
'''
P_E = NeuronGroup(N_E, eqs_E, threshold='v > V_thr', reset='v = V_reset', refractory=tau_rp_E, method='euler')
P_E.v = V_L
P_I = NeuronGroup(N_I, eqs_I, threshold='v > V_thr', reset='v = V_reset', refractory=tau_rp_I, method='euler')
P_I.v = V_L
eqs_glut = '''
s_NMDA_tot_post = w * s_NMDA : 1 (summed)
ds_NMDA / dt = - s_NMDA / tau_NMDA_decay + alpha * x * (1 - s_NMDA) : 1 (clock-driven)
dx / dt = - x / tau_NMDA_rise : 1 (clock-driven)
w : 1
'''
eqs_pre_glut = '''
s_AMPA += w
x += 1
'''
eqs_pre_gaba = '''
s_GABA += 1
'''
eqs_pre_ext = '''
s_AMPA_ext += 1
'''
# E to E
C_E_E = Synapses(P_E, P_E, model=eqs_glut, on_pre=eqs_pre_glut, method='euler')
C_E_E.connect('i != j')
C_E_E.w[:] = 1
for pi in range(N_non, N_non + p * N_sub, N_sub):
# internal other subpopulation to current nonselective
C_E_E.w[C_E_E.indices[:, pi:pi + N_sub]] = w_minus
# internal current subpopulation to current subpopulation
C_E_E.w[C_E_E.indices[pi:pi + N_sub, pi:pi + N_sub]] = w_plus
# E to I
C_E_I = Synapses(P_E, P_I, model=eqs_glut, on_pre=eqs_pre_glut, method='euler')
C_E_I.connect()
C_E_I.w[:] = 1
# I to I
C_I_I = Synapses(P_I, P_I, on_pre=eqs_pre_gaba, method='euler')
C_I_I.connect('i != j')
# I to E
C_I_E = Synapses(P_I, P_E, on_pre=eqs_pre_gaba, method='euler')
C_I_E.connect()
# external noise
C_P_E = PoissonInput(P_E, 's_AMPA_ext', C_ext, rate, '1')
C_P_I = PoissonInput(P_I, 's_AMPA_ext', C_ext, rate, '1')
# at 1s, select population 1
C_selection = int(f * C_ext)
rate_selection = 25 * Hz
stimuli1 = TimedArray(np.r_[np.zeros(40), np.ones(2), np.zeros(100)], dt=25 * ms)
input1 = PoissonInput(P_E[N_non:N_non + N_sub], 's_AMPA_ext', C_selection, rate_selection, 'stimuli1(t)')
# at 2s, select population 2
stimuli2 = TimedArray(np.r_[np.zeros(80), np.ones(2), np.zeros(100)], dt=25 * ms)
input2 = PoissonInput(P_E[N_non + N_sub:N_non + 2 * N_sub], 's_AMPA_ext', C_selection, rate_selection, 'stimuli2(t)')
# at 4s, reset selection
stimuli_reset = TimedArray(np.r_[np.zeros(120), np.ones(2), np.zeros(100)], dt=25 * ms)
input_reset_I = PoissonInput(P_E, 's_AMPA_ext', C_ext, rate_selection, 'stimuli_reset(t)')
input_reset_E = PoissonInput(P_I, 's_AMPA_ext', C_ext, rate_selection, 'stimuli_reset(t)')
# monitors
N_activity_plot = 15
sp_E_sels = [SpikeMonitor(P_E[pi:pi + N_activity_plot]) for pi in range(N_non, N_non + p * N_sub, N_sub)]
sp_E = SpikeMonitor(P_E[:N_activity_plot])
sp_I = SpikeMonitor(P_I[:N_activity_plot])
r_E_sels = [PopulationRateMonitor(P_E[pi:pi + N_sub]) for pi in range(N_non, N_non + p * N_sub, N_sub)]
r_E = PopulationRateMonitor(P_E[:N_non])
r_I = PopulationRateMonitor(P_I)
# simulate, can be long >120s
net = Network(collect())
net.add(sp_E_sels)
net.add(r_E_sels)
net.run(4 * second, report='stdout')
# plotting
title('Population rates')
xlabel('ms')
ylabel('Hz')
plot(r_E.t / ms, r_E.smooth_rate(width=25 * ms) / Hz, label='nonselective')
plot(r_I.t / ms, r_I.smooth_rate(width=25 * ms) / Hz, label='inhibitory')
for i, r_E_sel in enumerate(r_E_sels[::-1]):
plot(r_E_sel.t / ms, r_E_sel.smooth_rate(width=25 * ms) / Hz, label='selective {}'.format(p - i))
legend()
figure()
title('Population activities ({} neurons/pop)'.format(N_activity_plot))
xlabel('ms')
yticks([])
plot(sp_E.t / ms, sp_E.i + (p + 1) * N_activity_plot, '.', markersize=2, label='nonselective')
plot(sp_I.t / ms, sp_I.i + p * N_activity_plot, '.', markersize=2, label='inhibitory')
for i, sp_E_sel in enumerate(sp_E_sels[::-1]):
plot(sp_E_sel.t / ms, sp_E_sel.i + (p - i - 1) * N_activity_plot, '.', markersize=2, label='selective {}'.format(p - i))
legend()
show()
# -
| 12,728 |
/india_&_states_2011 - Machine Learning - decision tree .ipynb | bd7d010cad090f638fb882a1184c6e5eb8585121 | [] | no_license | meenujomi/Research_Thesis_mortality_fertility | https://github.com/meenujomi/Research_Thesis_mortality_fertility | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 6,063,431 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
csv_name = "tmp5c00jrqx.csv"
df = pd.read_csv(csv_name)
df.OFFENSE_CODE.unique()
# +
years = [2015, 2016, 2017, 2018, 2019]
offense_codes = ["413", "3301", "802", "311"]
# to filter by districts, add a predicate like `& df["DISTRICT"].isin(districts)`
df = df[df["YEAR"].isin(years) & df["OFFENSE_CODE"].isin(offense_codes)]
df
# -
groups = df.groupby(["YEAR", "DISTRICT", "OFFENSE_CODE"]).groups
# +
counts = {}
for name, group in groups.items():
counts[name] = len(group)
counts
return (f(x) - f(x-h))/h
def cfd(f, x, h):
return (f(x+h) - f(x-h))/h/2
# + [markdown] id="IlKQiYM4E0rX" colab_type="text"
# I want to see for $f(x)=sin(x)$, the approximations for $f'(x)$
# + id="8bRv5NNCFHd7" colab_type="code" colab={}
f = lambda x: np.sin(x)
# + id="NWRijP0AFLnW" colab_type="code" colab={}
def f1(x):
return np.sin(x)
# + id="QSVpuyPoFPqg" colab_type="code" colab={}
fprime = lambda x: np.cos(x)
# + id="wsePdBETFTOS" colab_type="code" outputId="e0db1f82-e757-4a20-c79d-4548fe36f955" colab={"base_uri": "https://localhost:8080/", "height": 34}
#f'(x) is
print(fprime(1))
# + id="Ca8asOqCFX3F" colab_type="code" outputId="8094a002-0af7-4b17-de48-caf44c82e590" colab={"base_uri": "https://localhost:8080/", "height": 34}
#by ffd it gives
print(ffd(f, 1, .5))
# + id="XK4t6uGTFfmA" colab_type="code" outputId="f4205f74-0b8f-4b3a-8871-6e7f2f2bff5a" colab={"base_uri": "https://localhost:8080/", "height": 347}
h = .5 #step size
x_co = np.linspace(0, 2*np.pi, 100)
plt.plot(x_co, np.cos(x_co), label = 'cosine');
plt.plot(x_co, ffd(np.sin, x_co, h), label = 'FFD');
plt.plot(x_co, bfd(np.sin, x_co, h), label = 'BFD');
plt.plot(x_co, cfd(np.sin, x_co, h), label = 'CFD');
plt.legend();
# + id="8EJBI_WCF6ZS" colab_type="code" outputId="0fa9e19a-81a4-4411-977d-ef838fa563ac" colab={"base_uri": "https://localhost:8080/", "height": 34}
nn = np.arange(5,11)
nn
# + id="H_AibI0QTTUa" colab_type="code" outputId="62cf7872-64f0-4a9a-9ecb-c945c2ee5c10" colab={"base_uri": "https://localhost:8080/", "height": 50}
hh = 1/np.power(2,nn) #Note: np.power does not take negative numbers - use 1/() instead!
hh
# + [markdown] id="1WIbl_1EaNX_" colab_type="text"
# BSM
# Python coding central theme: class
# + id="sDsv52gXhpo6" colab_type="code" colab={}
class HumanBeing:
def __init__(self, yourname, yourage):
self.name = yourname
self.age = yourage
def print_name(self):
print('My name is ' + self.name)
def print_age(self, n):
print(str(n) + 'years after, I turn to ' + str(self.age + n))
# + id="Bh5CjrhAiY8h" colab_type="code" colab={}
std1 = HumanBeing('Emily', 21)
# + id="5eEnK9PSjTuy" colab_type="code" outputId="2113b572-03bf-4f40-f2a2-3a4c1439fe82" colab={"base_uri": "https://localhost:8080/", "height": 50}
std1.name
std1.print_name()
std1.print_age(5)
# + id="3qWM5MYUTxPw" colab_type="code" colab={}
'''=========
option class init
=========='''
class VanillaOption:
def __init__( #initialize the class
self,
otype = 1, # 1: 'call'
# -1: 'put'
strike = 110.,
maturity = 1.,
market_price = 10.):
self.otype = otype
self.strike = strike
self.maturity = maturity
self.market_price = market_price #this will be used for calibration
def payoff(self, s): #s: excercise price
otype = self.otype
k = self.strike
maturity = self.maturity
return np.max([0, (s - k)*otype])
| 3,745 |
/ImageClassification_CNN.ipynb | 666d756b9e5833f12d6b1e3514f20fa542fde181 | [] | no_license | marcvilella/ImageClassificationCNN | https://github.com/marcvilella/ImageClassificationCNN | 1 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 2,100,941 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="w6lduZruX9qM" colab_type="text"
# # **Setup and resources**
# + id="wl2Ayb5NXeR9" colab_type="code" colab={}
import torch
import torchvision
import torch.optim as optim
import torch.nn as nn
import torchvision.transforms as transforms
from torch.utils.data import Dataset
from sklearn.metrics import confusion_matrix
from skimage import io, transform
import matplotlib.pyplot as plt
from tqdm import tqdm
from PIL import Image
import pandas as pd
import numpy as np
import csv
import os
import math
import cv2
# + [markdown] id="kZ4VvGGPMVig" colab_type="text"
# Import google drive to save and load models
# + id="w3kF-PFYMYc0" colab_type="code" outputId="84ddf164-b37a-4864-9f7c-45b50e02e416" colab={"base_uri": "https://localhost:8080/", "height": 126}
from google.colab import drive
drive.mount('/content/gdrive')
# + [markdown] id="fdtI3g00YJ1p" colab_type="text"
# The first part of the assignment is to build a CNN and train it on a subset of the ImageNet dataset. We will first create a dataframe with all the references to the images and their labels.
# + id="scy9KkQNYUj7" colab_type="code" outputId="98f844e0-36ab-43d3-cc16-5f1dcdc4d202" colab={"base_uri": "https://localhost:8080/", "height": 124}
#To download the images into your work environment, clone into a git respository containing the images.
# ! git clone https://github.com/MohammedAlghamdi/imagenet10.git
# + id="sY1HikEGYXL3" colab_type="code" outputId="e31ddb54-67ba-40c0-d070-d011a4f28344" colab={"base_uri": "https://localhost:8080/", "height": 35}
# Check that the repository is there:
# ! dir
root_dir = "imagenet10/train_set/"
class_names = [
"baboon",
"banana",
"canoe",
"cat",
"desk",
"drill",
"dumbbell",
"football",
"mug",
"orange",
]
# + [markdown] id="FpotUi56YZsD" colab_type="text"
# A helper function for reading in images and assigning labels.
# + id="2A0qjUfJX4WZ" colab_type="code" colab={}
def get_meta(root_dir, dirs):
""" Fetches the meta data for all the images and assigns labels.
"""
paths, classes = [], []
for i, dir_ in enumerate(dirs):
for entry in os.scandir(root_dir + dir_):
if (entry.is_file()):
paths.append(entry.path)
classes.append(i)
return paths, classes
# + [markdown] id="72Os9bZcYexZ" colab_type="text"
# Now we create a dataframe using all the data.
# + id="TjLoNFojYfIV" colab_type="code" colab={}
# Benign images we will assign class 0, and malignant as 1
paths, classes = get_meta(root_dir, class_names)
data = {
'path': paths,
'class': classes
}
data_df = pd.DataFrame(data, columns=['path', 'class'])
data_df = data_df.sample(frac=1).reset_index(drop=True) # Shuffles the data
# + [markdown] id="SHzdOrbkYfTW" colab_type="text"
# View some sample data.
# + id="zcDzJpcdYffN" colab_type="code" outputId="78e3c69c-aef9-4767-927f-34ff6a0e3f6c" colab={"base_uri": "https://localhost:8080/", "height": 224}
print("Found", len(data_df), "images.")
data_df.head()
# + [markdown] id="LvmFDinvWD77" colab_type="text"
# # **Building the network**
# + [markdown] id="oeMOKX47YfqX" colab_type="text"
# Now we will create the Dataset class.
# + id="pIyljQHvYf0o" colab_type="code" colab={}
class ImageNet10(Dataset):
""" ImageNet10 dataset. """
def __init__(self, df, transform=None):
"""
Args:
image_dir (string): Directory with all the images
df (DataFrame object): Dataframe containing the images, paths and classes
transform (callable, optional): Optional transform to be applied
on a sample.
"""
self.df = df
self.transform = transform
def __len__(self):
return len(self.df)
def __getitem__(self, index):
# Load image from path and get label
x = Image.open(self.df['path'][index])
try:
x = x.convert('RGB') # To deal with some grayscale images in the data
except:
pass
y = torch.tensor(int(self.df['class'][index]))
if self.transform:
x = self.transform(x)
return x, y
# + [markdown] id="T2ewxlNXY-md" colab_type="text"
# Compute what we should normalise the dataset to.
# + id="nkQf9nB2Y-xl" colab_type="code" outputId="6391228c-c2b5-42f2-d9a4-b89d922616d3" colab={"base_uri": "https://localhost:8080/", "height": 88}
def compute_img_mean_std(image_paths):
"""
Author: @xinruizhuang. Computing the mean and std of three channel on the whole dataset,
first we should normalize the image from 0-255 to 0-1
"""
img_h, img_w = 224, 224
imgs = []
means, stdevs = [], []
for i in tqdm(range(len(image_paths))):
img = cv2.imread(image_paths[i])
img = cv2.resize(img, (img_h, img_w))
imgs.append(img)
imgs = np.stack(imgs, axis=3)
print(imgs.shape)
imgs = imgs.astype(np.float32) / 255.
for i in range(3):
pixels = imgs[:, :, i, :].ravel() # resize to one row
means.append(np.mean(pixels))
stdevs.append(np.std(pixels))
means.reverse() # BGR --> RGB
stdevs.reverse()
print("normMean = {}".format(means))
print("normStd = {}".format(stdevs))
return means, stdevs
norm_mean, norm_std = compute_img_mean_std(paths)
# + [markdown] id="5RxsThtdY--g" colab_type="text"
# Now let's create the transforms to normalise and turn our data into tensors.
# + id="p2zqP6BXY_Jm" colab_type="code" colab={}
data_transform = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(256),
transforms.ToTensor(),
transforms.Normalize(norm_mean, norm_std),
])
# + [markdown] id="Rib7zgBhY_Um" colab_type="text"
# Let's split the data into train and test sets and instantiate our new ISIC_Dataset objects.
# + id="zQN9mhTTY_gh" colab_type="code" colab={}
train_split = 0.70 # Defines the ratio of train/valid/test data.
valid_split = 0.10
train_size = int(len(data_df)*train_split)
valid_size = int(len(data_df)*valid_split)
ins_dataset_train = ImageNet10(
df=data_df[:train_size],
transform=data_transform,
)
ins_dataset_valid = ImageNet10(
df=data_df[train_size:(train_size + valid_size)].reset_index(drop=True),
transform=data_transform,
)
ins_dataset_test = ImageNet10(
df=data_df[(train_size + valid_size):].reset_index(drop=True),
transform=data_transform,
)
# + [markdown] id="2WNDtyIjZzKH" colab_type="text"
# DataLoaders for the datasets.
# + id="zF9zc22MZzXu" colab_type="code" colab={}
train_loader = torch.utils.data.DataLoader(
ins_dataset_train,
batch_size=8,
shuffle=True,
num_workers=2,
pin_memory=True
)
valid_loader = torch.utils.data.DataLoader(
ins_dataset_valid,
batch_size=8,
shuffle=False,
num_workers=2,
pin_memory=True
)
test_loader = torch.utils.data.DataLoader(
ins_dataset_test,
batch_size=8, # Forward pass only so batch size can be larger
shuffle=False,
num_workers=2,
pin_memory=True
)
# + [markdown] id="FnCY4k-Jdvzd" colab_type="text"
# You can optionally seed the Random Number Generator across all devices for testing purposes.
# + id="49xxL6eedv9m" colab_type="code" outputId="e3f3c2e9-60b5-4f6b-a832-6ed098aeeb8e" colab={"base_uri": "https://localhost:8080/", "height": 35}
torch.manual_seed(1)
# + [markdown] id="lNbp5VsuZ9Pb" colab_type="text"
# We can now create device where we refer to GPU or CPU.
# + id="f7hzCHGAaIzQ" colab_type="code" colab={}
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
# + [markdown] id="uOX67G7paJMr" colab_type="text"
# Define Accuracy function
# + id="-iKTy9LIaJVr" colab_type="code" colab={}
def compute_validation_stats(loader):
global model
# Accuracy parameters
correct = 0
total = 0
accuracy = 0
labels_total = torch.tensor([], dtype=torch.long)
predicted_total = torch.tensor([], dtype=torch.long)
# Loss parameters
validation_loss = 0
model.eval()
with torch.no_grad():
# Iterate over the validation set
for data in loader:
images, labels = data
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
# Accuracy
# torch.max is an argmax operation
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
labels_total = torch.cat((labels_total, labels.cpu()))
predicted_total = torch.cat((predicted_total, predicted.cpu()))
# Loss
logps = model.forward(images)
batch_loss = criterion(logps, labels)
validation_loss += batch_loss.item()
model.train()
return labels_total, predicted_total, (100 * correct / total), (validation_loss / len(loader))
# + [markdown] id="2BXAa3AHacSf" colab_type="text"
# Define Train function
# + id="ePttVmxfacb1" colab_type="code" colab={}
import matplotlib.pyplot as plt
import copy
def train_model_epochs(num_epochs):
""" Copy of function train_model_epochs but explicitly copying data to device
during training.
"""
global model
best_model_loss = 9
best_model = []
train_losses, validation_losses, validation_accuracies = [], [], []
for epoch in range(num_epochs):
# Train data
running_loss = 0.0
for i, data in enumerate(train_loader, 0):
images, labels = data
# Explicitly specifies that data is to be copied onto the device!
images = images.to(device) # <----------- And note it's NOT an in-place operation; original
labels = labels.to(device) # <----------- variables still exist on CPU
optimizer.zero_grad()
outputs = model(images)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if i % 100 == 99: # print every 100 mini-batches
print('Epoch / Batch [%d / %d]' %
(epoch + 1, i + 1))
# Validation data
_, _, validation_accuracy, validation_loss = compute_validation_stats(valid_loader)
running_loss = running_loss / len(train_loader)
train_losses.append(running_loss)
validation_losses.append(validation_loss)
validation_accuracies.append(validation_accuracy)
if best_model_loss > validation_loss:
best_model_loss = validation_loss
best_model = copy.deepcopy(model)
print(f"-------------------------------- \n"
f" Epoch {epoch+1}/{num_epochs} \n"
f" Train loss: {running_loss:.3f} \n"
f" Validation loss: {validation_loss:.3f} \n"
f" Validation accuracy: {validation_accuracy:.3f}% \n"
f"--------------------------------")
model.train()
plt.plot(train_losses, label='Training loss')
plt.plot(validation_losses, label='Validation loss')
plt.legend(frameon=False)
#path = f"/content/gdrive/My Drive/Escola/Master/Semester 2/Artificial Intelligence/Coursework 1/Experiments/model_{getNumberLayers(model)}_loss.png"
#plt.savefig(F"{path}", bbox_inches='tight')
plt.show()
print("Train losses")
print(train_losses)
print("Validation losses")
print(validation_losses)
plt.plot(validation_accuracies, label='Validation accuracy')
plt.legend(frameon=False)
#path = f"/content/gdrive/My Drive/Escola/Master/Semester 2/Artificial Intelligence/Coursework 1/Experiments/model_{getNumberLayers(model)}_accuracy.png"
#plt.savefig(F"{path}", bbox_inches='tight')
plt.show()
print("Validation accuracies")
print(validation_accuracies)
model = best_model.to(device)
# + [markdown] id="fuGLYJO4YgVi" colab_type="text"
# Create view confusion matrix
# + id="JHwMtRRqYggf" colab_type="code" colab={}
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import itertools
def plot_confusion_matrix(cm,
classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix very prettily.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
# Specify the tick marks and axis text
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=90)
plt.yticks(tick_marks, classes)
# The data formatting
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
# Print the text of the matrix, adjusting text colour for display
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout()
#path = f"/content/gdrive/My Drive/Escola/Master/Semester 2/Artificial Intelligence/Coursework 1/Experiments/model_{getNumberLayers(model)}_matrix.png"
#plt.savefig(F"{path}")
plt.show()
# + id="aypUj4HDlTYM" colab_type="code" colab={}
# Return number of layers
def getNumberLayers(model):
n = 0
for idx, x in enumerate(model.modules()):
if '.conv.' in str(type(x)):
n += 1
return n
# + [markdown] id="rLoD8iPoWTMQ" colab_type="text"
# # **1. Experiments**
# + [markdown] id="YoYY2xHKW7U_" colab_type="text"
# ### How does the number of layers affect the training process and test performance? Try between 2 and 5 layers.
# + [markdown] id="3qCUwkauhJzU" colab_type="text"
# #### Two layers
# + id="jmIn6Y0p1ZkK" colab_type="code" colab={}
# Create Convolution Network
class ConvNet(nn.Module):
def __init__(self, num_classes=10):
super(ConvNet, self).__init__() #3x256x256
self.conv1 = nn.Sequential(
nn.Conv2d(3, 16, 3), #16x254x254
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #16x127x127
nn.Dropout(p = 0.3)
)
self.conv2 = nn.Sequential(
nn.Conv2d(16, 24, 4), #24x124x124
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #24x62x62=92256
nn.Dropout(p = 0.3)
)
self.fc1 = nn.Linear(24*62*62, 512)
self.fc2 = nn.Linear(512, num_classes)
def forward(self, x):
out = self.conv1(x)
out = self.conv2(out)
out = out.reshape(out.size(0), -1)
out = self.fc1(out)
out = self.fc2(out)
return out
# + id="J82GJPfA8cAy" colab_type="code" colab={}
# Initialize
torch.manual_seed(1)
model = ConvNet().to(device)
# + id="DG527vWA8cJ_" colab_type="code" colab={}
# Define the loss and optimiser
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
# + id="CX3CsxCC-Yzq" colab_type="code" outputId="65e2379a-2926-4bff-db0a-8fd727bba457" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# Run
import timeit
gpu_train_time = timeit.timeit(
"train_model_epochs(num_epochs)",
setup="num_epochs=60",
number=1,
globals=globals(),
)
labels, predicted, a, l = compute_validation_stats(test_loader)
print(a)
print(l)
print(gpu_train_time)
# + id="u758VuMt-nvw" colab_type="code" outputId="344f6b63-3f92-4af9-b12b-fae977a3daec" colab={"base_uri": "https://localhost:8080/", "height": 315}
# Show confusion matrix
cm = confusion_matrix(labels, predicted)
plot_confusion_matrix(cm, class_names)
# + id="0JARbWSS-l_a" colab_type="code" outputId="a4740d02-bec6-4d85-9246-7c51285d8fb4" colab={"base_uri": "https://localhost:8080/", "height": 74}
# Save model
path = f"/content/gdrive/My Drive/Escola/Master/Semester 2/Artificial Intelligence/Coursework 1/Models/model_2___{a:.1f}_{l:.3f}.py"
torch.save(model, F"{path}")
# + [markdown] id="FCooHEPZhJAm" colab_type="text"
# #### Three layers
# + id="oj2iqnF0hPIg" colab_type="code" colab={}
# Convolutional neural network
class ConvNet(nn.Module):
def __init__(self, num_classes=10):
super(ConvNet, self).__init__() #3x256x256
self.conv1 = nn.Sequential(
nn.Conv2d(3, 16, 3), #16x254x254 #parameters = 3 * (16 + 1(bias)) * 3^2
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #16x127x127
nn.Dropout(p = 0.3)
)
self.conv2 = nn.Sequential(
nn.Conv2d(16, 24, 4), #24x124x124
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #24x62x62
nn.Dropout(p = 0.3)
)
self.conv3 = nn.Sequential(
nn.Conv2d(24, 32, 4), #32x59x59
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #32x29x29=26912
nn.Dropout(p = 0.3)
)
self.fc1 = nn.Linear(32*29*29, 512) # #parameters = 26912 * (512 + 1 (bias))
self.fc2 = nn.Linear(512, num_classes)
#self.final = nn.Softmax(dim=1) # We shouldn't use this because CrossEntropyLoss is softmax, so we're already using it
def forward(self, x):
out = self.conv1(x)
out = self.conv2(out)
out = self.conv3(out)
out = out.reshape(out.size(0), -1)
out = self.fc1(out)
out = self.fc2(out)
return out
# + id="mFsMgBWvV4W6" colab_type="code" colab={}
# Initialize
torch.manual_seed(1)
model = ConvNet().to(device)
# + id="5KCs_GhXV4aZ" colab_type="code" colab={}
# Define the loss and optimiser
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
# + id="r3mXlPptV9p2" colab_type="code" outputId="a46a103f-f57e-40ba-e430-9b4646179d3b" colab={}
# Run
import timeit
gpu_train_time = timeit.timeit(
"train_model_epochs(num_epochs)",
setup="num_epochs=60",
number=1,
globals=globals(),
)
labels, predicted, a, l = compute_validation_stats(test_loader)
print(a)
print(l)
print(gpu_train_time)
# + id="xynzmWmcWJhl" colab_type="code" outputId="15b66107-6f05-474d-8e1d-468486653f36" colab={"base_uri": "https://localhost:8080/", "height": 315}
# Show confusion matrix
cm = confusion_matrix(labels, predicted)
plot_confusion_matrix(cm, class_names)
# + id="YAg2IYo6WOHe" colab_type="code" outputId="bd9692c0-4eae-4c25-d186-ec2b866e6cd0" colab={}
# Save model
path = f"/content/gdrive/My Drive/Escola/Master/Semester 2/Artificial Intelligence/Coursework 1/Models/model_3___{a:.1f}_{l:.3f}.py"
torch.save(model, F"{path}")
# + [markdown] id="_ExzwTx4hPXU" colab_type="text"
# #### Four layers
# + id="qvWTwEzlhPh_" colab_type="code" colab={}
# Convolutional neural network
class ConvNet(nn.Module):
def __init__(self, num_classes=10):
super(ConvNet, self).__init__() #3x256x256
self.conv1 = nn.Sequential(
nn.Conv2d(3, 16, 3), #16x254x254
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #16x127x127
nn.Dropout(p = 0.3)
)
self.conv2 = nn.Sequential(
nn.Conv2d(16, 24, 4), #24x124x124
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #24x62x62
nn.Dropout(p = 0.3)
)
self.conv3 = nn.Sequential(
nn.Conv2d(24, 32, 4), #32x59x59
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #32x29x29
nn.Dropout(p = 0.3)
)
self.conv4 = nn.Sequential(
nn.Conv2d(32, 40, 4), #40x26x26
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #40x13x13=6760
nn.Dropout(p = 0.3)
)
self.fc1 = nn.Linear(40*13*13, 512)
self.fc2 = nn.Linear(512, num_classes)
def forward(self, x):
out = self.conv1(x)
out = self.conv2(out)
out = self.conv3(out)
out = self.conv4(out)
out = out.reshape(out.size(0), -1)
out = self.fc1(out)
out = self.fc2(out)
return out
# + id="bNjyHfVTe-qy" colab_type="code" colab={}
# Initialize
torch.manual_seed(1)
model = ConvNet().to(device)
# + id="cJTS2s2Qe-3M" colab_type="code" colab={}
# Define the loss and optimiser
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
# + id="pUKZXaBge_AI" colab_type="code" outputId="ad716cad-b721-4ef0-aa1a-b58ca30a77da" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# Run
import timeit
gpu_train_time = timeit.timeit(
"train_model_epochs(num_epochs)",
setup="num_epochs=60",
number=1,
globals=globals(),
)
labels, predicted, a, l = compute_validation_stats(test_loader)
print(a)
print(l)
print(gpu_train_time)
# + id="R9ReFkXEe_JV" colab_type="code" outputId="6d062da4-e0f8-460e-b6e2-bf43825a5ac2" colab={"base_uri": "https://localhost:8080/", "height": 315}
# Show confusion matrix
cm = confusion_matrix(labels, predicted)
plot_confusion_matrix(cm, class_names)
# + id="VR0CCVvEfLH3" colab_type="code" outputId="8214fc8d-fe57-48a9-be1e-a6226a451708" colab={"base_uri": "https://localhost:8080/", "height": 74}
# Save model
path = f"/content/gdrive/My Drive/Escola/Master/Semester 2/Artificial Intelligence/Coursework 1/Models/model_4___{a:.1f}_{l:.3f}.py"
torch.save(model, F"{path}")
# + [markdown] id="RoHZGpwxhPwb" colab_type="text"
# #### Five layers
# + id="nHg52A3KhP7L" colab_type="code" colab={}
# Convolutional neural network
class ConvNet(nn.Module):
def __init__(self, num_classes=10):
super(ConvNet, self).__init__() #3x256x256
self.conv1 = nn.Sequential(
nn.Conv2d(3, 16, 3), #16x254x254
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #16x127x127
nn.Dropout(p = 0.3)
)
self.conv2 = nn.Sequential(
nn.Conv2d(16, 24, 4), #24x124x124
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #24x62x62
nn.Dropout(p = 0.3)
)
self.conv3 = nn.Sequential(
nn.Conv2d(24, 32, 4), #32x59x59
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #32x29x29
nn.Dropout(p = 0.3)
)
self.conv4 = nn.Sequential(
nn.Conv2d(32, 40, 4), #40x26x26
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #40x13x13
nn.Dropout(p = 0.3)
)
self.conv5 = nn.Sequential(
nn.Conv2d(40, 48, 4), #48x10x10
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #48x5x5=1200
nn.Dropout(p = 0.3)
)
self.fc1 = nn.Linear(48*5*5, 512)
self.fc2 = nn.Linear(512, num_classes)
def forward(self, x):
out = self.conv1(x)
out = self.conv2(out)
out = self.conv3(out)
out = self.conv4(out)
out = self.conv5(out)
out = out.reshape(out.size(0), -1)
out = self.fc1(out)
out = self.fc2(out)
return out
# + id="vtPdRk4igIoV" colab_type="code" colab={}
# Initialize
torch.manual_seed(1)
model = ConvNet().to(device)
# + id="qsw-TOA0gIwB" colab_type="code" colab={}
# Define the loss and optimiser
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
# + id="ko4k8wxZgIy8" colab_type="code" outputId="46a80c72-00c4-4e05-9218-053ea5c73a0f" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# Run
import timeit
gpu_train_time = timeit.timeit(
"train_model_epochs(num_epochs)",
setup="num_epochs=100",
number=1,
globals=globals(),
)
labels, predicted, a, l = compute_validation_stats(test_loader)
print(a)
print(l)
print(gpu_train_time)
# + id="FXn5mHOIgI1r" colab_type="code" outputId="5b2b1c61-953c-41c9-8936-e2d38100535e" colab={"base_uri": "https://localhost:8080/", "height": 315}
# Show confusion matrix
cm = confusion_matrix(labels, predicted)
plot_confusion_matrix(cm, class_names)
# + id="aaZhzYdGgI4f" colab_type="code" outputId="c871067d-c9bb-44fd-9a2f-7ec15b8c9c5b" colab={"base_uri": "https://localhost:8080/", "height": 74}
# Save model
path = f"/content/gdrive/My Drive/Escola/Master/Semester 2/Artificial Intelligence/Coursework 1/Models/model_5___{a:.1f}_{l:.3f}.py"
torch.save(model, F"{path}")
# + [markdown] id="2TqkpZqyW8ej" colab_type="text"
# ## Choose one more architectural element to test (filter size, max-pool kernel size, number/dimensions of fully-connected layers, etc.).
# + id="hZTI7uE9W81x" colab_type="code" colab={}
# Convolutional neural network
class ConvNet(nn.Module):
def __init__(self, num_classes=10):
super(ConvNet, self).__init__() #3x256x256
self.conv1 = nn.Sequential(
nn.Conv2d(3, 16, 4), #16x253x253
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #16x126x126
nn.Dropout(p = 0.3)
)
self.conv2 = nn.Sequential(
nn.Conv2d(16, 24, 5), #24x122x122
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #24x61x61
nn.Dropout(p = 0.3)
)
self.conv3 = nn.Sequential(
nn.Conv2d(24, 32, 5), #32x57x57
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #32x28x28=25088
nn.Dropout(p = 0.3)
)
self.fc1 = nn.Linear(32*28*28, 512)
self.fc2 = nn.Linear(512, num_classes)
def forward(self, x):
out = self.conv1(x)
out = self.conv2(out)
out = self.conv3(out)
out = out.reshape(out.size(0), -1)
out = self.fc1(out)
out = self.fc2(out)
return out
# + id="QkXU1jxrzfFC" colab_type="code" colab={}
# Initialize
torch.manual_seed(1)
model = ConvNet().to(device)
# + id="Mj8osI4TzfK9" colab_type="code" colab={}
# Define the loss and optimiser
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
# + id="vC8CQ48izfNu" colab_type="code" outputId="918067c8-df4b-4ab1-ed37-986d51205e10" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# Run
import timeit
gpu_train_time = timeit.timeit(
"train_model_epochs(num_epochs)",
setup="num_epochs=60",
number=1,
globals=globals(),
)
labels, predicted, a, l = compute_validation_stats(test_loader)
print(a)
print(l)
print(gpu_train_time)
# + id="0m0SUeWtzfQA" colab_type="code" outputId="2f8726e7-ff6d-4079-a091-8c72548d9b1e" colab={"base_uri": "https://localhost:8080/", "height": 315}
# Show confusion matrix
cm = confusion_matrix(labels, predicted)
plot_confusion_matrix(cm, class_names)
# + id="Q9SNB1grzfTV" colab_type="code" outputId="dd1e41f3-3428-4d5a-ef77-cab915fe21ba" colab={"base_uri": "https://localhost:8080/", "height": 74}
# Save model
path = f"/content/gdrive/My Drive/Escola/Master/Semester 2/Artificial Intelligence/Coursework 1/Models/model_3_mod___{a:.1f}_{l:.3f}.py"
torch.save(model, F"{path}")
# + [markdown] id="87UZSeITWY7R" colab_type="text"
# # **2. Filter visualisation**
# + [markdown] id="sJ4Rz8IkUJBS" colab_type="text"
# The best model is the one with 5 layers at epoch 26
# + id="mSLEL_2IYewY" colab_type="code" colab={}
import matplotlib.pyplot as plt
def normalize (layer):
f_min, f_max = layer.min(), layer.max()
return (layer - f_min) / (f_max - f_min)
def getFilters (model):
filters = []
for idx, x in enumerate(model.modules()):
if '.conv.' in str(type(x)):
filters.append(normalize(x.weight.data))
return filters
def showFilters (filter):
fig = plt.figure()
plt.figure(figsize=(22,6))
size = filter.size() # Out (filters) - In - 4x4
for idx, filt in enumerate(filter):
for layer in range(size[1]):
plt.subplot(size[1],size[0], idx + 1 + size[0]*layer)
plt.imshow(filt[layer, :, :], cmap="gray")
plt.axis('off')
fig.show()
# + [markdown] id="YELob1BTVrGL" colab_type="text"
# Show filters before training
# + id="c0pG2UQDVxrn" colab_type="code" outputId="2f58d596-dbcc-4307-d48b-bfca6c59db5f" colab={"base_uri": "https://localhost:8080/", "height": 344}
filters = getFilters(model.cpu())
showFilters(filters[0])
# + [markdown] id="4TkOH1hgVyGF" colab_type="text"
# Show filters at halfway during training (after epoch 13)
# + id="PzGMuI4FWZNV" colab_type="code" outputId="aed87f02-3bb1-4f05-961d-2e06a2cec673" colab={"base_uri": "https://localhost:8080/", "height": 1000}
import timeit
torch.manual_seed(1)
model = model.to(device)
gpu_train_time = timeit.timeit(
"train_model_epochs(num_epochs)",
setup="num_epochs=26//2",
number=1,
globals=globals(),
)
filters = getFilters(model.cpu())
showFilters(filters[0])
# + [markdown] id="ALA3cyUjVqWA" colab_type="text"
# Show filters after training (after epoch 26)
# + id="oRCrcm8oWofx" colab_type="code" outputId="83fcae17-274c-4096-d985-57d68d3ca3f6" colab={"base_uri": "https://localhost:8080/", "height": 1000}
model = model.to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
gpu_train_time = timeit.timeit(
"train_model_epochs(num_epochs)",
setup="num_epochs=26//2",
number=1,
globals=globals(),
)
filters = getFilters(model.cpu())
showFilters(filters[0])
# + [markdown] id="lrc0jyrJWZbx" colab_type="text"
# # **3. Feature map visualisation**
# + [markdown] id="yFox_k4reSrH" colab_type="text"
# Load best model
# + id="5uQzRYLPeS0e" colab_type="code" colab={}
model = torch.load(F"/content/gdrive/My Drive/Escola/Master/Semester 2/Artificial Intelligence/Coursework 1/Models/model_5___62.7_1.097.py")
model = model.to(device)
# + id="9c2zqSJJBRGI" colab_type="code" colab={}
import matplotlib.pyplot as plt
import numpy as np
import random
# Select 'num' random images but from different class, it does not check 'num'
def getDifferenClassesImages(num):
dataloader_iterator = iter(test_loader)
images = torch.tensor([], dtype=torch.float)
labels = []
for i in range(num):
tmp1, tmp2 = next(dataloader_iterator)
tmp3 = random.randint(0, len(tmp1) - 1)
while tmp3 in labels:
tmp3 = random.randint(0, len(tmp1) - 1)
images = torch.cat((images, tmp1[tmp3:(tmp3+1),:,:,:].detach()))
labels = np.append(labels, tmp2[tmp3].detach().numpy())
return images, labels
# Show 'fm_number' Feature Map for input
def showFeatureMaps (input, fm_number):
fig = plt.figure()
plt.figure(figsize=(max(round(input.size()[1]/14), 9),6))
for i in range(fm_number):
plt.subplot(1,fm_number, i + 1)
plt.imshow(input[i, :, :], cmap="gray")
fig.tight_layout()
fig.show()
# Special function for hook
def Get_Features_and_Show(self, input, output):
showFeatureMaps(output.data[0].detach().cpu(), 4)
showFeatureMaps(output.data[1].detach().cpu(), 4)
return None
# + id="MQbW5aq3R6pp" colab_type="code" colab={}
# Set to show feature maps after each convolution
for idx, x in enumerate(model.modules()):
if '.conv.' in str(type(x)):
x.register_forward_hook(Get_Features_and_Show)
# + id="vOLkt3abKRLD" colab_type="code" outputId="e9c9d543-db61-4052-ec5f-6d64cee70ef8" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# Run
#images, labels = getDifferenClassesImages(2)
print(labels)
images = images.cpu()
for im in images:
plt.figure()
plt.imshow(im[0, :, :], cmap="gray")
images = images.to(device)
model(images)
# + [markdown] id="ZARs-LRmWZ1L" colab_type="text"
# # **4. Improving network performance**
# + id="dNJihDGB2LcU" colab_type="code" colab={}
data_transform_train = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(256),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize(norm_mean, norm_std),
transforms.RandomErasing(),
])
ins_dataset_train = ImageNet10(
df=data_df[:train_size],
transform=data_transform_train,
)
ins_dataset_valid = ImageNet10(
df=data_df[train_size:(train_size + valid_size)].reset_index(drop=True),
transform=data_transform,
)
ins_dataset_test = ImageNet10(
df=data_df[(train_size + valid_size):].reset_index(drop=True),
transform=data_transform,
)
train_loader = torch.utils.data.DataLoader(
ins_dataset_train,
batch_size=8,
shuffle=True,
num_workers=2,
pin_memory=True
)
valid_loader = torch.utils.data.DataLoader(
ins_dataset_valid,
batch_size=8,
shuffle=False,
num_workers=2,
pin_memory=True
)
test_loader = torch.utils.data.DataLoader(
ins_dataset_test,
batch_size=8,
shuffle=False,
num_workers=2,
pin_memory=True
)
# + id="ZTpGQ9XOWaIZ" colab_type="code" colab={}
# Convolutional neural network
class ConvNet(nn.Module):
def __init__(self, num_classes=10):
super(ConvNet, self).__init__() #3x256x256
# 1st NET
self.conv1_1 = nn.Sequential(
nn.Conv2d(3, 16, 3), #16x254x254
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #16x127x127
nn.Dropout(p = 0.3)
)
self.conv1_2 = nn.Sequential(
nn.Conv2d(16, 24, 3), #24x125x125
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #24x62x62
nn.Dropout(p = 0.3)
)
self.conv1_3 = nn.Sequential(
nn.Conv2d(24, 32, 3), #32x60x60
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #32x30x30
nn.Dropout(p = 0.3)
)
self.conv1_4 = nn.Sequential(
nn.Conv2d(32, 40, 3), #40x28x28
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #40x14x14
nn.Dropout(p = 0.3)
)
self.conv1_5 = nn.Sequential(
nn.Conv2d(40, 48, 3), #48x12x12
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #48x6x6=1728
nn.Dropout(p = 0.3)
)
self.fc1_1 = nn.Linear(48*6*6, 512)
self.fc1_2 = nn.Linear(512, num_classes)
# 2nd NET
self.conv2_1 = nn.Sequential(
nn.Conv2d(3, 16, 5), #16x252x252
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #16x126x126
nn.Dropout(p = 0.3)
)
self.conv2_2 = nn.Sequential(
nn.Conv2d(16, 24, 5), #24x122x122
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #24x61x61
nn.Dropout(p = 0.3)
)
self.conv2_3 = nn.Sequential(
nn.Conv2d(24, 32, 5), #32x57x57
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #32x28x28
nn.Dropout(p = 0.3)
)
self.conv2_4 = nn.Sequential(
nn.Conv2d(32, 40, 5), #40x24x24
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #40x12x12
nn.Dropout(p = 0.3)
)
self.conv2_5 = nn.Sequential(
nn.Conv2d(40, 48, 5), #48x8x8
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2), #48x4x4=768
nn.Dropout(p = 0.3)
)
self.fc2_1 = nn.Linear(48*4*4, 512)
self.fc2_2 = nn.Linear(512, num_classes)
def forward(self, x):
y = x
x = self.conv1_1(x)
x = self.conv1_2(x)
x = self.conv1_3(x)
x = self.conv1_4(x)
x = self.conv1_5(x)
x = x.reshape(x.size(0), -1)
x = self.fc1_1(x)
x = self.fc1_2(x)
y = self.conv2_1(y)
y = self.conv2_2(y)
y = self.conv2_3(y)
y = self.conv2_4(y)
y = self.conv2_5(y)
y = y.reshape(y.size(0), -1)
y = self.fc2_1(y)
y = self.fc2_2(y)
return (x + y) / 2
# + id="EFqkWM-xicQc" colab_type="code" colab={}
# Initialize
torch.manual_seed(1)
model = ConvNet().to(device)
# + id="5q0Nn3LNiXb8" colab_type="code" colab={}
# Define the loss and optimiser
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
# + id="FUt0xtuGif_K" colab_type="code" colab={} outputId="689b05ac-cd26-40ad-d862-a7214cba3462"
# Run
import timeit
gpu_train_time = timeit.timeit(
"train_model_epochs(num_epochs)",
setup="num_epochs=100",
number=1,
globals=globals(),
)
labels, predicted, a, l = compute_validation_stats(test_loader)
print(a)
print(l)
print(gpu_train_time)
# + id="nvIFyO-gkMbq" colab_type="code" outputId="4b39d109-9823-4991-e992-aeee2b589e29" colab={"base_uri": "https://localhost:8080/", "height": 315}
# Show confusion matrix
cm = confusion_matrix(labels, predicted)
plot_confusion_matrix(cm, class_names)
# + id="iAo2o4_diHVW" colab_type="code" colab={} outputId="66c3e077-daaf-4293-9364-d4e8d496fc52"
# Save model
path = f"/content/gdrive/My Drive/Escola/Master/Semester 2/Artificial Intelligence/Coursework 1/Models/model_Improvement___{a:.1f}_{l:.3f}.py"
torch.save(model, F"{path}")
sklearn.metrics import classification_report
print('Logistic Regression:')
print(classification_report(y_test, y_pred_log_reg))
print('KNears Neighbors:')
print(classification_report(y_test, y_pred_knear))
print('Support Vector Classifier:')
print(classification_report(y_test, y_pred_svc))
print('Support Vector Classifier:')
print(classification_report(y_test, y_pred_tree))
# -
| 38,529 |
/Webscrapper_fuzzy (1).ipynb | c0338a098a6af0a627a3455ae66bb84f5b719bc9 | [] | no_license | Kimo-Gandall101/LIWC-General-Assembly | https://github.com/Kimo-Gandall101/LIWC-General-Assembly | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 59,832 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import xml.etree.ElementTree as ET
XML_PATH = "../data/IFRS_Texte_6.0_2017_06.xml"
etree = ET.parse(XML_PATH)
root = etree.getroot()
for child in root:
for child2 in child.getchildren():
if child2.tag == "text" and child2.attrib["left"] in ["105", "106", "107"]:
print(child2)
root = tree.getroot()
root
# +
# left="106" (104-108?)
# -
# !howdoi parse xml etree by attribute
for text in root.findall("text"):
print(text)
inding this data in the real world (not to mention how hard it was to model in SIR to begin with), I'll stick with synthetic data for now. Using MCMC and SVI methods to estimate epidemic parameters and see if intervention helps, and to what extent.
# +
import os
import matplotlib.pyplot as plt
import seaborn as sns
import torch
import pyro
import pyro.distributions as dist
from pyro.contrib.epidemiology import CompartmentalModel, binomial_dist, infection_dist
# %matplotlib inline
#assert pyro.__version__.startswith('1.5.0') # I have 1.5.1, hopefully not a problem to comment this out.
torch.set_default_dtype(torch.double) # Required for MCMC inference.
pyro.enable_validation(True) # Always a good idea.
smoke_test = ('CI' in os.environ)
# -
pyro.__version__
# +
class SimpleSEIRModel(CompartmentalModel):
"""
Susceptible-Exposed-Infected-Recovered model.
To customize this model we recommend forking and editing this class.
This is a stochastic discrete-time discrete-state model with four
compartments: "S" for susceptible, "E" for exposed, "I" for infected,
and "R" for recovered individuals (the recovered individuals are
implicit: ``R = population - S - E - I``) with transitions
``S -> E -> I -> R``.
:param int population: Total ``population = S + E + I + R``.
:param float incubation_time: Mean incubation time (duration in state
``E``). Must be greater than 1.
:param float recovery_time: Mean recovery time (duration in state
``I``). Must be greater than 1.
:param iterable data: Time series of new observed infections. Each time
step is Binomial distributed between 0 and the number of ``S -> E``
transitions. This allows false negative but no false positives.
"""
def __init__(self, population, incubation_time, recovery_time, data):
compartments = ("S", "E", "I") # R is implicit.
duration = len(data)
super().__init__(compartments, duration, population)
assert isinstance(incubation_time, float)
assert incubation_time > 1
self.incubation_time = incubation_time
assert isinstance(recovery_time, float)
assert recovery_time > 1
self.recovery_time = recovery_time
self.data = data
def global_model(self):
tau_e = self.incubation_time
tau_i = self.recovery_time
R0 = pyro.sample("R0", dist.LogNormal(0., 1.))
rho = pyro.sample("rho", dist.Beta(10, 10))
return R0, tau_e, tau_i, rho
def initialize(self, params):
# Start with a single infection.
return {"S": self.population - 1, "E": 0, "I": 1}
def transition(self, params, state, t):
R0, tau_e, tau_i, rho = params
# Sample flows between compartments.
S2E = pyro.sample("S2E_{}".format(t),
infection_dist(individual_rate=R0 / tau_i, ## TODO: it seems like in paper, (1-u) * (b1*_i1 + b2*_i2 + b3*_i3)/_n*_s
num_susceptible=state["S"],
num_infectious=state["I"],
population=self.population))
E2I = pyro.sample("E2I_{}".format(t),
binomial_dist(state["E"], 1 / tau_e))
I2R = pyro.sample("I2R_{}".format(t),
binomial_dist(state["I"], 1 / tau_i))
# Update compartments with flows.
state["S"] = state["S"] - S2E
state["E"] = state["E"] + S2E - E2I
state["I"] = state["I"] + E2I - I2R
# Condition on observations.
t_is_observed = isinstance(t, slice) or t < self.duration
pyro.sample("obs_{}".format(t),
binomial_dist(S2E, rho),
obs=self.data[t] if t_is_observed else None)
# -
# ## Generating Data
#
# What if I don't want to do this?
# +
population = 329064930
recovery_time = 10.
incubation_time = 14.
empty_data = [None] * 300
model = SimpleSEIRModel(population, incubation_time, recovery_time, empty_data)
# We'll repeatedly generate data until a desired number of infections is found.
pyro.set_rng_seed(20200709)
for attempt in range(100):
synth_data = model.generate({"R0": 1.7})
total_infections = synth_data["S2E"].sum().item()
# if 4000 <= total_infections <= 6000:
break
print("Simulated {} infections after {} attempts".format(total_infections, 1 + attempt))
# -
# For the model to work, it requires S, S2I, I, I2R, obs (noisy S2I), R0, and rho.
#
#
# At the moment, all of these things are synthetically generated, after we first specify R0, rho and population.
#
# For real world, I'll try this now, but we set:
#
# S2I = obs, and use reported values for the others. In essence we no longer use the noisy observations and assume whatever is reported is right?
#
# I'm not sure if the model will work if we do not specify R0 or rho, so will have to try this and find out.
# #### Swapneel's comments: I think you mean we have to specify a prior for R0 and rho and the model will update that into a posterior estimate based on the data that it observes.
for key, value in sorted(synth_data.items()):
print("{}.shape = {}".format(key, tuple(value.shape)))
plt.figure(figsize=(8,4))
for name, value in sorted(synth_data.items()):
if value.dim():
plt.plot(value, label=name)
plt.xlim(0, len(empty_data) - 1)
plt.ylim(0.8, None)
plt.xlabel("time step")
plt.ylabel("individuals")
plt.yscale("log")
plt.legend(loc="best")
plt.title("Synthetic time series")
plt.tight_layout()
# ## Inference
# what if we only have obs? can we estimate using just that?
obs = synth_data["obs"]
model = SimpleSEIRModel(population, incubation_time, recovery_time, obs)
# %%time
losses = model.fit_svi(num_steps=101 if smoke_test else 2001,
jit=True)
plt.figure(figsize=(8, 3))
plt.plot(losses)
plt.xlabel("SVI step")
plt.ylabel("loss")
plt.ylim(min(losses), max(losses[50:]));
for key, value in sorted(model.samples.items()):
print("{}.shape = {}".format(key, tuple(value.shape)))
# %%time
samples = model.predict()
names = ["R0", "rho"]
fig, axes = plt.subplots(2, 1, figsize=(5, 5))
axes[0].set_title("Posterior estimates of global parameters")
for ax, name in zip(axes, names):
truth = synth_data[name]
sns.distplot(samples[name], ax=ax, label="posterior")
ax.axvline(truth, color="k", label="truth")
ax.set_xlabel(name)
ax.set_yticks(())
ax.legend(loc="best")
plt.tight_layout()
# ## MCMC
mcmc = model.fit_mcmc(num_samples=4 if smoke_test else 200,
jit_compile=True,)
# ## Prediction
# %%time
samples = model.predict()
for key, value in sorted(samples.items()):
print("{}.shape = {}".format(key, tuple(value.shape)))
names = ["R0", "rho"]
fig, axes = plt.subplots(2, 1, figsize=(5, 5))
axes[0].set_title("Posterior estimates of global parameters")
for ax, name in zip(axes, names):
truth = synth_data[name]
sns.distplot(samples[name], ax=ax, label="posterior")
ax.axvline(truth, color="k", label="truth")
ax.set_xlabel(name)
ax.set_yticks(())
ax.legend(loc="best")
plt.tight_layout()
# ## Forecasting
# %time
samples = model.predict(forecast=30)
# +
def plot_forecast(samples):
duration = len(empty_data)
forecast = samples["S"].size(-1) - duration
num_samples = len(samples["R0"])
time = torch.arange(duration + forecast)
S2E = samples["S2E"]
median = S2E.median(dim=0).values
p05 = S2E.kthvalue(int(round(0.5 + 0.05 * num_samples)), dim=0).values
p95 = S2E.kthvalue(int(round(0.5 + 0.95 * num_samples)), dim=0).values
plt.figure(figsize=(8, 4))
plt.fill_between(time, p05, p95, color="red", alpha=0.3, label="90% CI")
plt.plot(time, median, "r-", label="median")
plt.plot(time[:duration], obs, "k.", label="observed")
plt.plot(time[:duration], synth_data["S2E"], "k--", label="truth")
plt.axvline(duration - 0.5, color="gray", lw=1)
plt.xlim(0, len(time) - 1)
plt.ylim(0, None)
plt.xlabel("day after first infection")
plt.ylabel("new infections per day")
plt.title("New infections in population of {}".format(population))
plt.legend(loc="upper left")
plt.tight_layout()
plot_forecast(samples)
# -
# A suggestion of the authors is to use MCMC rather than SVI to estimate, and this will produce better results with only a little longer compute time. I will avoid doing that for the moment, because I would consider it a higher priority to figure out how to run this model with actual data, rather than manufactured.
synth_data
| 9,379 |
/Python_assignments/Exo36_VowelOrConsonant.ipynb | b3e7794b20531358fa7024de0d4fece62f0769da | [] | no_license | ModoukpeA/FemCodeAfrica_DS_Training | https://github.com/ModoukpeA/FemCodeAfrica_DS_Training | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 1,533 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
vowels=["a","e","i","o","u"]
consonants=["b","c","d","f","g","h","j","k","l","m","n","p","q","r","s","t","v","w","x","z"]
user=input("Type one letter of the alphabet:")
if(user=="y"):
print("This letter is sometimes a vowel, sometimes a consonant")
elif (user in vowels):
print("This is a vowel")
elif (user in consonants):
print("This is a consonant")
else:
print("You should type a letter of the alphabet")
| 695 |
/11_segment_tree.ipynb | d22cbcf9eb04072e7191225ae2caaf5b216de79a | [] | no_license | z-sector/algorithms-course | https://github.com/z-sector/algorithms-course | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 6,274 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Решение задачи "Сумма на отрезке"
import random
import os
import math
# - N - число элементов массива: [1, 100000]
# - K - число запросов: [0, 100000]
# - i - номер элемента в массиве: [1, 100000]
# - x - значение: [0, 1000000000]
# - A i x - присвоить значение
# - Q l r - найти сумму
# ## Вспомогательные функции
# +
def generate_files(N_min, N_max, K_min, K_max, x_max):
N = random.randint(N_min, N_max)
K = random.randint(K_min, K_max)
array = [0 for i in range(N+1)]
with open('sum.in', 'w') as fi, open('sum_right.out', 'w') as fo:
fi.write(f'{N} {K}\n')
if K != 0:
for k in range(K):
operation = random.choice(['A', 'Q'])
if operation == 'A':
i = random.randint(1, N)
x = random.randint(0, x_max)
array[i] = x
fi.write(f'A {i} {x}\n')
if operation == 'Q':
l = random.randint(1, N)
r = random.randint(l, N)
s = sum(array[l:r+1])
fi.write(f'Q {l} {r}\n')
fo.write(str(s)+'\n')
def compare_files():
with open('sum_right.out', 'r') as fr, open('sum.out', 'r') as fo:
if not (fr.read() == fo.read()):
print('False')
return
# -
# ## Реализация
# +
def get_data():
with open('sum.in', 'r') as fi:
for line in fi:
yield line
def get_sum(array, ind_l, ind_r):
result = 0
while ind_l <= ind_r:
# если элемент с индексом ind_l - правый потомок (нечетный индекс), добавляем к результату
if ind_l % 2 == 1:
result += array[ind_l]
# если элемент с индексом ind_r - левый потомок (четный индекс), добавляем к результату
if ind_r % 2 == 0:
result += array[ind_r]
ind_l = (ind_l + 1) // 2
ind_r = (ind_r - 1) // 2
return result
def get_results():
lines = get_data()
line = next(lines).split()
N, K = int(line[0]), int(line[1])
if K == 0:
return results
#array_n = [0 for i in range(N+1)]
shift = 2**math.ceil(math.log(N, 2))
array = [0 for i in range(2*shift)]
with open('sum.out', 'w') as fo:
for i in range(K):
line = next(lines).split()
if line[0] == 'A':
i = int(line[1]) + shift - 1
x = int(line[2])
diff = x - array[i]
array[i] = x
while i != 1:
array[i//2] += diff
i //= 2
if line[0] == 'Q':
l, r = int(line[1]), int(line[2])
s = get_sum(array, l+shift-1, r+shift-1)
fo.write(str(s)+'\n')
# -
# ## Тестирование
N_min = 10**5
N_max = 10**5
K_min = 10**5
K_max = 10**5
x_max = 10**9
generate_files(N_min, N_max, K_min, K_max, x_max)
# %%timeit -r 1 -n 1 -o -q
get_results()
compare_files()
# %%timeit -r 1 -n 1 -o -q
# !./algorithms_cpp/11_segment_tree.out
compare_files()
os.remove('sum.in')
os.remove('sum_right.out')
os.remove('sum.out')
| 3,416 |
/10_3_xor_tensorflow_ipynb의_사본.ipynb | b5581201feb84777d35897079cb193a99062bb85 | [] | no_license | ealsk/2020_AI | https://github.com/ealsk/2020_AI | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 17,646 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# What is Pandas?
# ---
#
# From https://pandas.pydata.org/pandas-docs/stable:
#
# > pandas is a Python package providing fast, flexible, and expressive data structures designed to make working with “relational” or “labeled” data both easy and intuitive. It aims to be the fundamental high-level building block for doing practical, real world data analysis in Python. Additionally, it has the broader goal of becoming the most powerful and flexible open source data analysis / manipulation tool available in any language. It is already well on its way toward this goal.
# >
# > pandas is well suited for many different kinds of data:
# >
# > - Tabular data with heterogeneously-typed columns, as in an SQL table or Excel spreadsheet
# > - Ordered and unordered (not necessarily fixed-frequency) time series data.
# > - Arbitrary matrix data (homogeneously typed or heterogeneous) with row and column labels
# > - Any other form of observational / statistical data sets. The data actually need not be labeled at all to be placed into a pandas data structure
#
# Why would you want to choose Pandas over a spreadsheet program (e.g. Excel)?
#
# - Pandas is open-source and free 👍
# - One can store __reproducible__ steps to get from an input to an output
# - Excel will only store the final state, not the steps to get there!
# - It is less memory intensive and you can work with larger datasets
# - It is fast and libraries exist (e.g. dask, ray, RAPIDS) to scale far beyond one core
#
# ### Pandas is built with NumPy
#
# NumPy provides multi-dimensional list-like data structures which are __typed__ and much faster than Python lists. The interface to the pandas data structures, to be discussed in this workshop, is very similar to the one provided by NumPy. In many cases the methods provided have the same, or similar, names. Therefore, I will skip a detailed discussion of NumPy and simply point you to the [documentation](https://docs.scipy.org/doc/numpy/reference/) for later use.
# Importing Pandas
# ---
#
# First, you need to `import pandas`. By convention, it is imported using the _alias_ `pd`. To import using an alias use the following syntax:
#
# ```python
# import <library> as <alias>
# ```
#
# - Many popular libraries try to define an alias convention, check their documentation
#
# #### Tasks:
#
# 1. Try to import `pandas` using the alias convention?
# Data Structures
# ---
#
# Similar to the Python data structures (e.g. `list, dictionary, set`), Pandas provides three fundamental data structures:
#
# 1. `Series`: For one-dimensional data, similar to a Python list
# 2. `DataFrame`: For two-dimensional data, similar to a Python list of lists
# 3. `Index`: Similar to a `Series`, but for naming, selecting, and transforming data within a `Series` or `DataFrame`
#
# ### Series
#
# You can create a Pandas `Series` in a variety of ways, e.g.:
#
# - From an assigned Python list:
a = ['a', 'b', 'c']
series = pd.Series(a)
series
# - From an unnamed Python list:
series = pd.Series([4, 5, 6])
series
# - Using a specific index (similar to a `dict` where `index` are the keys):
series = pd.Series([4, 5, 6], index=["a", "b", "c"])
series
# - Directly from a dictionary (exactly the same as above):
series = pd.Series({"a": 4, "b": 5, "c": 6})
series
# ### DataFrame
#
# This is the data structure that makes Pandas shine. A `DataFrame` is essentially a dictionary of `Series` objects. In a `DataFrame`, the `keys` map to `Series` objects which share a common `index`. We should start with an example:
rock_bands = ["Pink Floyd", "Rush", "Yes"]
year_formed = [1965, 1968, 1968]
location_formed = ["London, England", "Ontario, Canada", "London, England"]
df = pd.DataFrame({"year_formed": year_formed, "location_formed": location_formed}, index=rock_bands)
df
# ### Breaking Down the Result
#
# - The indicies are `"Pink Floyd"`, `"Rush"`, and `"Yes"`
# - The keys to the DataFrame are `"year_formed"` and `"location_formed"`
# - The lists are converted to `Series` objects which share the indices
#
# This might not seem very powerful, except that `DataFrame`s can be constructed from files! In a previous task, you were asked to read a file `states.csv` then parse it manually and do some statistics. In the following cell, I will read the file and generate statistics in two lines!
df = pd.read_csv("states.csv")
df.describe()
# ### Tasks
#
# 1. Use `pd.read_csv` to read in the csv file: `example.bsv`
# - It does not contain a header (add `header=None` to the arguments)
# - When working with a single dataframe it is assigned to the name `df`, by convention
# - The file is bar separated (add `sep='|'` to the arguments)
# - Lastly set the column names (add `names=["First", "Second"]`)
# Viewing DataFrames
# ---
#
# Jupyter has built in support for viewing `DataFrame` objects in a nice format. Example:
import pandas as pd
df = pd.DataFrame([0, 1, 2], index=[5, 6, 7], columns=["Example"])
df
# The result should have been a nice looking table. Reminders:
#
# - The above `DataFrame` contains a single `Series` with the key `Example`
# - The indices are on the left (in bold)
# - The values are in columns underneath the key
#
# If you only want to view a subset of the DataFrame, you can use the syntax `<df>.head()`. By default it will print only 5 rows from the top of your DataFrame. This is very useful when trying to view the _shape_ of your data. You can print fewer rows by adding `n=<number>` to the arguments of `head`.
#
# ### Tasks
#
# - Run the definitions cell below
# - Print the DataFrame in the following ways:
# - Using the built in Jupyter view
# - The head
# - The first row
# definitions
l = list(range(10))
df = pd.DataFrame({"a": l, "b": l, "c": l})
# ### Access and Types
#
# You can access individual `Series` from `DataFrame`s using two syntax:
#
# - Like a dictionary: `<df>["<key>"]`
# - Like a data member, `<df>.<key>`
#
# Important notes about the data member style:
#
# - doesn't support keys with spaces
# - can't be used to assign values to a non-existent key
#
# For these reasons, I tend to prefer the dictionary style for everything. You will see both styles in this document simply to increase your familiarity with both, but it is important to know the limitations.
#
# If you want to know the types of your `DataFrame`'s `Series`s using `<df>.dtypes`
#
# ### Tasks
#
# - Run the definitions cell below
# - Access the `b` Series of `df` using both accessor syntax
# - Why are two columns printed?
# - What is the type of `df["b"]`?
# - What are the `dtypes` of `df`?
# definitions
df = pd.DataFrame({"a": [0, 1, 2], "b": [0.0, 1.0, 2.0], "c": ["pandas", "is", "great"]})
df
# Slicing and Indexing
# ---
#
# There are many ways to slice and dice DataFrames. Let's start with the least flexible option, selecting multiple columns. Let's make a new DataFrame in the following cell.
example = pd.DataFrame({"a": [1, 2, 3], "b": [4, 5, 6], "c": [7, 8, 9]})
example
# To slice columns `a` and `c` we'll use a similar syntax to dictionary access, shown before, but instead we will ask for a list of columns instead of a single one, e.g.
example[["a", "c"]]
# One can also slice rows using the `list` slicing syntax. Note you are __required__ to specify a slice (something containing '`:`'). For example,
# zeroth row only
example[0:1]
# first row to end
example[1:]
# every other row
example[::2]
# this will fail with `KeyError`
# -> remember this is dictionary style access and `0` isn't a key!
example[0]
# More Complicated Access Patterns
# ---
#
# You can narrow down rows and columns using `loc`, some examples:
# only row 1, columns 'a' and 'c'
example.loc[1:1, ["a", "c"]]
# all rows, columns 'a' to 'b'
example.loc[:, "a":"b"]
# single row, single column
example.loc[0, "a"]
# ### Tasks
#
# Using `loc` and the `example` DataFrame,
#
# 1. Run the definitions cell below
# 2. Try to print every other row
# 3. Try to print columns `b` to `c`
# 4. Try to print all columns of the final row
# definitions
example = pd.DataFrame({"a": [1, 2, 3], "b": [4, 5, 6], "c": [7, 8, 9]})
example
# ### Note
#
# `loc` is all about index/key access, what if the indices are characters? Run the following cell and then complete the tasks
example2 = pd.DataFrame({"a": [1, 2, 3], "b": [4, 5, 6], "c": [7, 8, 9]}, index=["A", "B", "C"])
example2.head()
# ### Tasks
#
# Use `loc` and DataFrame `example2`, to
#
# - Print rows `B` to `C` and columns `a` to `b`.
# - What happens if you try to access the index numerically?
# ### Notes
#
# To access `example2` w/ numerical indices, we need `iloc`.
#
# ### Tasks
#
# 1. Using `iloc` and `example2`, get rows `B` to `C` and columns `a` to `b`.
# ### Notes
#
# You can also use the `list` style access I showed before, e.g.
example2.iloc[[1, 2], [0, 1]]
# Access by Boolean Arrays
# ---
#
# - One can use a boolean array to access subsets of `DataFrame`s
# - First, I will define a `DataFrame`
df = pd.DataFrame({"hello": [0, 1, 2], "world": [3, 4, 5]}, index=["top", "middle", "bottom"])
df
# - I can generate a boolean array using _dispatch_
#
# Aside: Dispatch
# ---
#
# Dispatch is automatically used when you use the built-in operators, e.g. `==`. It essentially creates a new `Series` where it distributes the function to every element in the original `Series`. We should start with an example:
df.index == "middle"
# - The concept of dispatch can be a little tricky, what is the type and dtype?
arr = (df.index == "middle")
type(arr), arr.dtype
# - One can use these `bool` arrays to downselect `DataFrame`s
df[df.index == "middle"]
# - You can also compose multiple criterion together, e.g.
# - `|` is `or`
# - `&` is `and`
df[(df.index == "middle") | (df.index == "top")]
# ### Tasks
#
# - Run the definitions cell
# - Access the `DataFrame` where column `"a"` is greater than or equal to 2
# - Access row `"B"` where row `"B"` is greater than or equal to 5
# - Access the `DataFrame` where column `"a"` is greater than 2 and column `"b"` is less than 6
df = pd.DataFrame({"a": [1, 2, 3], "b": [4, 5, 6], "c": [7, 8, 9]}, index=["A", "B", "C"])
df
# Built-in Statistics
# ---
#
# Coming back to the original example:
states = pd.read_csv("states.csv", index_col=0)
states.head()
# - One can easily access the statistics of the entire `DataFrame`
states.describe()
# - There are 52 states according to the `count`. The `mean` population is about 6.3 million people for 2016 and 2017
# - It is also possible to down select the statistics, e.g. if I want the mean for the key `Population (2016)`
states["Population (2016)"].mean()
# ### Tasks
#
# - Find the state with
# - the minimum (`min`) population in 2016
# - the maximum (`max`) population in 2017
# Adding New Columns
# ---
#
# How would we find the average population _per state_ for 2016 and 2017?
#
# - We can use a dispatched operation similar to the `==` example previous to generate the averages
(states["Population (2016)"] + states["Population (2017)"]) / 2
# - The above is a `Series` object. We can assign it to a `key` in the `DataFrame`
states["Average Population"] = (states["Population (2016)"] + states["Population (2017)"]) / 2
states["Average Population"].head()
# - Finally the overall mean
states["Average Population"].mean()
# Viewing Data
# ---
#
# Pandas plugs into `matplotlib` very nicely. I am going to iteratively build a plot which is easy to read. First, run the following cell.
# %matplotlib inline
import matplotlib.pyplot as plt
states = pd.read_csv("states.csv", index_col=0)
states.plot()
# This is something, but not very helpful. What would we like:
#
# - X axis should be labeled with the state
ax = states.plot(subplots=True, xticks=range(states.shape[0]))
# Notes
# ---
#
# 1. `subplots=True`: separates the 2 plots from one another
# 2. `xticks=range(states.shape[0])`: sets all of the ticks on the x-axis
# 3. `ax = ...`: is a list containing both plots
# 4. `ax[0].set_xticklables` changes the numeric index to the State name, should only be necessary for the 0th plot
# 5. `suppressing_output = ...`, I use this to supress the output from `set_xticklabels`
#
#
# Neat, but I can't read the labels...
ax = states.plot(subplots=True, xticks=range(states.shape[0]), figsize=(20, 10))
# - The line plots are a little awkward because the points aren't connected in anyway
ax = states.plot(subplots=True, xticks=range(states.shape[0]), figsize=(20, 10), kind='bar')
# - Not bad!
# Apply + Lambda
# ---
#
# I want to briefly show you a decent idiom for doing more complicated work on a `Series` object.
#
# This is a contrived example, but it shows the utility of `apply` + `lambda`. What if we wanted wanted to figure out if all letters A-Z are in the names of the states? First, we could create a `set` of characters in each state's name:
# +
# don't use the names of states an the index!
states = pd.read_csv("states.csv")
def set_of_chars(s):
return set(list(s.lower()))
series_of_sets = states.State.apply(lambda s: set_of_chars(s))
series_of_sets
# -
# Reminder: Lambdas
# ---
#
# Reminder, a _lambda_ constructs an ephemeral unnamed function. This is opposed to the named function `set_of_chars` above. The point is the `apply` method takes a function. We could have done the following:
#
# ```
# series_of_sets = states.State.apply(lambda s: set(list(s.lower())))
# ```
#
# Or, simply:
#
# ```
# series_of_sets = states.State.apply(set_of_chars)
# ```
# Getting Back to the Problem
# ---
#
# Now we have a `Series` of `set`s each containing the unique characters contained in each state's name. Next, we need to combine all of these sets into a single one!
#
# - First, an example of combining sets
a = {1, 2, 3}
b = {2, 4}
a.union(b)
# Now, we are going to __reduce__ the `Series` of `set`s by taking the union of each entry. If done step by step:
#
# ```python
# _tmp = <zeroth_set>.union(<first_set>)
# _tmp = _tmp.union(<second_set>)
# _tmp = _tmp.union(<third_set>)
# ...
# _tmp = _tmp.union(<final_set>)
# ```
#
# Imagine if we had a million rows! Luckily, Python includes functions for this! It is called `reduce` and comes from the `functools` package.
# All we need to do is provide a function which combines two elements and it will recursively apply the function until there is only one value.
# Try the cell below:
from functools import reduce
chars_used_in_states_name = reduce(lambda x, y: x.union(y), series_of_sets)
chars_used_in_states_name
# Lastly, we need to remove any non-alphanumeric characters
#
# - `ascii_lowercase` from `string` is simply a string of all of the characters
# - We can test if something is part of this set by using the `in` function, try the cell below:
from string import ascii_lowercase
print(" " in ascii_lowercase) # Should print `False`
print("a" in ascii_lowercase) # Should print `True`
# - We can use a set comprehension to filter the non-ascii characters
chars_used_in_states_name = {x for x in chars_used_in_states_name if x in ascii_lowercase}
chars_used_in_states_name
# - Now we can answer our question!
#
# Are all of the characters used in the states names?
alphabet_set = set(list(ascii_lowercase))
alphabet_set.difference(chars_used_in_states_name)
# The concepts of reductions and anonymous functions can be very useful when doing data analysis! Many times you can use comprehensions to do something similar, but I personally enjoy the `reduce` style. No tasks for this section. I would suggest prodding the above code to make sure you understand it!
# Built-in Methods and Axis
# ---
#
# There are many built-in methods in Pandas, for example `.mean()`. By default, these methods operate on the columns with an argument called the `axis` with a default value of `0`. You can generate row based means with `axis=1`.
#
# ### Tasks
#
# - Run the definitions cell
# - Generate the column and row means for `states` using the axis argument
# - Generate the DataFrame mean, i.e. a single value, for `states`
# definitions
states = pd.read_csv("states.csv", index_col=0)
# Writing Files
# ---
#
# CSV files are a standard way to share data, one can write a `DataFrame` to a CSV file using the syntax:
#
# ```python
# <df>.to_csv(<filename.csv>)
# ```
#
# Notes:
#
# - The seperator, by default, is a comma. Try `sep="|"` argument, use a '.bsv' ending
# - To not include the index, use `index=None`
# - To not include a header, use `header=None`
#
# ### Tasks
#
# - Run the definitions cell
# - Write the `states` DataFrame to a file called "intro.bsv"
# definitions
states = pd.read_csv("states.csv", index_col=0)
# Combining DataFrames
# ---
#
# ### Merge
#
# A `merge` operation takes two dataframes and tries to combine them side by side. We should start with a basic example. The names below are first names for current Vancouver Canucks.
left = pd.DataFrame({"id": [1, 2, 3], "names": ["Elias", "Jake", "Bo"]})
left
right = pd.DataFrame({"id": [1, 2, 3], "names": ["Brock", "Quinn", "Nikolay"]})
right
pd.merge(left, right, on="id")
# The keyword `on` takes a column from both dataframes and creates a new `DataFrame` sharing that column. By default it will only merge columns where values are shared between the `DataFrame`s, i.e. an _inner join_. Example:
left = pd.DataFrame({"id": [1, 3], "names": ["Elias", "Bo"]})
right = pd.DataFrame({"id": [1, 2], "names": ["Brock", "Quinn"]})
pd.merge(left, right, on="id")
# There are a few different choices for _how_ you can join two `DataFrame`s
#
# - Using the keys from the `left` `DataFrame`:
pd.merge(left, right, on="id", how="left")
# - Using the keys from the `right` `DataFrame`:
pd.merge(left, right, on="id", how="right")
# - Use all of the keys, an `outer` join:
pd.merge(left, right, on="id", how="outer")
# ### Join
#
# The `join` operation is essentially the same as `merge` with one change, the default `how` parameter is `"left"`.
# ### Concatenate
#
# `concat` is used to stack `DataFrame`s on top of one-another. It takes a list of `DataFrame`s. Let's look at a simple example:
top = pd.DataFrame({"letters": ["a", "b", "c"], "numbers": [1, 2, 3]})
bottom = pd.DataFrame({"letters": ["g", "h", "i"], "numbers": [7, 8, 9]})
pd.concat([top, bottom])
# ### Tasks
#
# 1. Run the definitions cell below
# 2. Try to merge `top` and `middle` using an `outer` join on the `"numbers"` column
# 3. Guess what will happen if you do an `inner` join? Test your hypothesis
# 4. Try to concatenate `top`, `middle`, and `bottom`
# definitions
top = pd.DataFrame({"letters": ["a", "b", "c"], "numbers": [1, 2, 3]})
middle = pd.DataFrame({"letters": ["d", "e", "f"], "numbers": [4, 5, 6]})
bottom = pd.DataFrame({"letters": ["g", "h", "i"], "numbers": [7, 8, 9]})
# Reshaping DataFrames
# ---
#
# ### Grouping Data
#
# Let's work with some real data from Pittsburgh in this example. I got this data from [Western Pennslyvania Regional Data Center](http://www.wprdc.org/). First, we should get an idea of the shape of the data:
df = pd.read_csv("311.csv")
df.head()
# This data was collected by the city of Pittsburgh from 311 calls. We are going to use the `groupby` functionality to extract some information from this data.
#
# I want you to extract some data for your neighborhood. First we will create a `groupby` object for the column `"NEIGHBORHOOD"`.
neighborhood = df.groupby(by="NEIGHBORHOOD")
# - To get the groups, you can use the `groups` data member.
# - We can determine the number of 311 calls from each group by using the `count` method on the grouped `DataFrame` (I use head below to reduce the amount of output)
neighborhood.count().head()
# ### Tasks
#
# 1. Select one of the columns from the grouped `DataFrame` and print the counts for all neighborhoods
# 2. Did your neighborhood make the list?
# 3. Which neighborhood has the most 311 calls?
# For the neighborhood with the most 311 calls, lets group again by the `"REQUEST_TYPE"`
#
# To get a group from a `DataFrame` you can use the `get_group` method, example:
neighborhood.get_group("Allegheny Center")
# ### Tasks
#
# 1. Using the `get_group` and `groupby` functions, downselect the `neighborhood` `DataFrame` to the neighborhood with the most 311 calls and determine how many different types of requests were made
# - If we wanted to see all 311 calls for a particular neighborhood and request type we could simply make a groupby object for both columns!
requests_by_neighborhood = df.groupby(by=["NEIGHBORHOOD", "REQUEST_TYPE"])
requests_by_neighborhood.get_group(("Allegheny Center", "Potholes"))
# - Grouping is very useful when you want to aggregrate based on duplicate entries
#
# ### Pivoting
#
# - We can use pivoting to change the shape of our data. For example, if we wanted the police zones as our columns and neighborhood as our values.
police_zones = df.pivot(values="NEIGHBORHOOD", columns="POLICE_ZONE")
police_zones.head()
# - Now we have a new `DataFrame` with a few columns: `nan`, `1.0`, `2.0`, `3.0`, `4.0`, `5.0`, and `6.0`
# - My guess is the `nan` is because there are cases where the police zone is not specified, let's remove it
police_zones = police_zones.iloc[:, 1:]
police_zones.head()
# - For each column, let's get the unique entries:
for col in police_zones.columns:
print(col)
print(police_zones[col].unique())
# Dealing with Strings
# ---
#
# If your working with string data there is a special method which allows you to apply normal string methods on the entire column.
#
# This data set comes from the city of Pittsburgh. It is all of the trees that the city maintains. The dataset can be found at https://data.wprdc.org/dataset/city-trees
df = pd.read_csv("trees.csv")
df.head()
# First, a very simple example where we convert the `"street"` columns to lower case
df["street"].str.lower().head()
# Tasks
# ---
#
# Strings have a `split` method. Given a string it will split the string up by that character into a list of strings. An example,
"Maple: Red".split(":")
# - Generate a `Series` which contains the tree type, in the above example `"Maple"`. Hint: use the `str` method and a `lambda`.
# Quick Survey
# ---
#
# - `<Ctrl-Enter>` the following cell
from IPython.display import IFrame
IFrame("https://forms.gle/5MXeyx6VYU2A96Du7", width=760, height=500)
| 22,627 |
/_misc/geron_2ed/ch13_data_api/data_api_intro.ipynb | 399a5e197ee55225cc2c89111c42b6406b703fcb | [] | no_license | ilyarudyak/cs230_project_keras | https://github.com/ilyarudyak/cs230_project_keras | 1 | 0 | null | 2022-11-22T01:40:22 | 2020-01-15T13:42:32 | Jupyter Notebook | Jupyter Notebook | false | false | .py | 14,047 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # CLX Cheat Sheets sample code
#
# (c) 2020 NVIDIA, Blazing SQL
#
# Distributed under Apache License 2.0
# # Workflow
# #### clx.workflow.workflow.Workflow() Yes
# +
from clx.workflow.workflow import Workflow
import cudf
import s3fs
from os import path
from clx.analytics.cybert import Cybert
class SimpleWorkflow(Workflow):
def workflow(self, dataframe):
dataframe['length'] = dataframe['raw'].str.len()
dataframe['ip'] = dataframe['raw'].str.extract(
'([0-9]+\.[0-9]+\.[0-9]+\.[0-9]+)', expand=True)
return dataframe
# +
DATA_DIR = '../data'
APACHE_SAMPLE_CSV = 'apache_sample_1k.csv'
source = {
"type": "fs",
"input_format": "csv",
"input_path": f'{DATA_DIR}/{APACHE_SAMPLE_CSV}',
"schema": ["raw"],
"delimiter": ",",
"usecols": ["raw"],
"dtype": ["str"],
"header": 0,
}
destination = {
"type": "fs",
"output_format": "csv",
"output_path": f'{DATA_DIR}/{APACHE_SAMPLE_CSV.split(".")[0]}_workflow.csv',
"index": False
}
# -
workflow = SimpleWorkflow(
name='SimpleWorkflow'
, source=source
, destination=destination
)
# #### clx.workflow.workflow.Workflow.run_workflow() Yes
![ -e ../data/apache_sample_1k_workflow.csv ] && rm ../data/apache_sample_1k_workflow.csv
workflow.run_workflow()
# !head ../data/apache_sample_1k_workflow.csv
# #### clx.workflow.workflow.Workflow.destination() Yes
workflow.destination
# #### clx.workflow.workflow.Workflow.name() Yes
workflow.name
# #### clx.workflow.workflow.Workflow.set_destination() Yes
workflow.set_destination(destination=destination)
# #### clx.workflow.workflow.Workflow.set_source() Yes
workflow.set_source(source=source)
# #### clx.workflow.workflow.Workflow.source() Yes
workflow.source
# #### clx.workflow.workflow.Workflow.stop_workflow() Yes
workflow.stop_workflow()
# #### clx.workflow.workflow.Workflow.workflow() Yes
df = cudf.read_csv(f'{DATA_DIR}/{APACHE_SAMPLE_CSV}')[['raw']]
workflow.workflow(df)
# #### clx.workflow.workflow.Workflow.benchmark()
# #### clx.workflow.splunk_alert_workflow.SplunkAlertWorkflow()
# #### clx.workflow.splunk_alert_workflow.SplunkAlertWorkflow.interval()
# #### clx.workflow.splunk_alert_workflow.SplunkAlertWorkflow.raw_data_col_name()
# #### clx.workflow.splunk_alert_workflow.SplunkAlertWorkflow.threshold()
# #### clx.workflow.splunk_alert_workflow.SplunkAlertWorkflow.window()
# #### clx.workflow.splunk_alert_workflow.SplunkAlertWorkflow.workflow()
t:8080/"} executionInfo={"elapsed": 420, "status": "ok", "timestamp": 1625123976367, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="fftUmyjS0ERD" outputId="32537176-6a8b-4dd5-9fb3-76f24806dc91"
# Example 1 - working
arr1 = [[1, 2],
[3, 4.]]
arr2 = [[5, 6, 7],
[8, 9, 10]]
np.concatenate((arr1, arr2) , axis=1)
# + [markdown] id="IqzYGg6A0ERD"
# > In this example two arrays `arr1` and `arr2` are joined along the columns due to `axis=1` property.
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 418, "status": "ok", "timestamp": 1625124721826, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="GtwToF_j0ERD" outputId="793a4c45-559f-466e-a1bf-a91037b9ca58"
# Example 2 - working
arr1 = [[1, 2],
[3, 4.]]
arr2 = [[5, 6, 7],
[8, 9, 10]]
np.concatenate((arr1, arr2) , axis=None)
# + [markdown] id="fGAhcs3p0ERE"
# > In this example, with `axis=None` property the arrays are joined but are flattened.
#
#
# + id="_hbXW4Us0ERE" outputId="c5cf69e9-880a-4f1f-a1ea-0412862e7e65"
# Example 3 - breaking (to illustrate when it breaks)
arr1 = [[1, 2],
[3, 4.]]
arr2 = [[5, 6, 7],
[8, 9, 10]]
np.concatenate((arr1, arr2), axis=0)
# + [markdown] id="1POSwvaf0ERE"
# > In this example `axis=0` property is used which means that arrays are intended to be joined along the rows but the no of columns in both the arrays are not same which give us the error. To remove this error simply increase the no of columns of smaller array.
#
#
#
# + [markdown] id="9n5dYAss0ERF"
# >When you want to join arrays , you can this function but keep in mind that while using `axis=0` property, no of coulmns in arrays must be same. Similarily while using `axis=1` property, no of rows in arrays must be same.
# + [markdown] id="W6AbGKdz0ERF"
#
#
# ## Function 2 - np.reciprocal
#
# It is used to return the reciprocal of the argument, element-wise.
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 420, "status": "ok", "timestamp": 1625126269917, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="vYrB9dVf0ERF" outputId="e08cfe75-7889-4bec-c638-4d9f7a07cf8b"
# Example 1 - working
np.reciprocal([2., 3., 5., 6.])
# + [markdown] id="HWMN2Gt70ERF"
# > It can be clearly seen from the example that it returns the reciprocal of the elements in the array.
#
#
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 416, "status": "ok", "timestamp": 1625126753946, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="RZG4vT-U0ERG" outputId="fa939ba4-6d18-4642-df8d-50ee7517490e"
# Example 2 - working
np.reciprocal([[2., 4., 22., 6., 91.],
[4.1, 5.3, 4.22, 1.09, 7.99]])
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 422, "status": "ok", "timestamp": 1625126630876, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="wZGOBM7p0ERG" outputId="932a22ac-ad0c-474b-b2fc-a92af40466d3"
# Example 3 - breaking (to illustrate when it breaks)
np.reciprocal([2, 4, 22, 6, 91]), np.reciprocal([0, 0, 0])
# + [markdown] id="iANS8Ad50ERG"
# > It displays 0 for all the elements of first array because all of them are integers and this fucntion does not work on integers. Hence their reciprocal is 0.
#
# > Also, on the array containing 0, it displays a RunTimeWarning as it cannont find the reciprocal of zero
# + [markdown] id="JU0G64Ib0ERG"
# >So when you want to find the recipriocal of arrays containg `float` type numbers, you can use this `numpy.reciprocal` function.
#
#
#
#
# + [markdown] id="5j4k6oQJ0ERH"
# ## Function 3 - np.unravel_index
#
# It is used to convert a flat index or array of flat indices into a tuple of coordinate arrays.
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 520, "status": "ok", "timestamp": 1625127719388, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="u7Gia1qn0ERH" outputId="c522bfe4-6a92-4cf7-f317-5db3982fc069"
# Example 1 - working
np.unravel_index(100, (6,7,8), order='F')
# + [markdown] id="QiuoHyd80ERH"
# > In the above example, function `np.unravel_index` finds the index of 100th element in the array of size (6, 7, 8) and displays it in column-major style because of `order='F'` property.
#
#
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 669, "status": "ok", "timestamp": 1625127722760, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="zlkYKqU80ERH" outputId="7a4c5030-28cd-4abf-910b-afd26fb615bd"
# Example 2 - working
np.unravel_index(100, (6,7,8), order='C')
# + [markdown] id="CgStx_fm0ERH"
# >In the above example, function `np.unravel_index` finds the index of 100th element in the array of size (6, 7, 8) and displays it in row-major style because of `order='C'` property. It is different from the example 1.
# + colab={"base_uri": "https://localhost:8080/", "height": 212} executionInfo={"elapsed": 427, "status": "error", "timestamp": 1625127931161, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="T80LdT1-0ERI" outputId="b2a64a1e-76ec-4abc-cebd-d071544241af"
# Example 3 - breaking (to illustrate when it breaks)
np.unravel_index(np.array([]), (6,7,8))
# + [markdown] id="syQH_WQlLLPY"
# > In the above, example we are getting a `TypeError` because `[]` in numpy is a `float` value by default and `float` indices are not permitted. To avoid getting this error, use `np.array([], dtype='int')` instead of `np.array([])`
# + [markdown] id="qlocpyfuMm3B"
# > So , when you want to find out the index of $nth$ element in a $(i, j, k)$ shaped array , u can use this function
# + [markdown] id="BXl0l1bL0ERL"
# ## Function 4 - np.tile
#
# It is used to construct an array by repeating A the number of times given by reps.
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 423, "status": "ok", "timestamp": 1625130224196, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="ZzF1sxea0ERL" outputId="f1b1cd1c-0081-42ac-b382-d8847c345cb7"
# Example 1 - working
np.tile(np.array([1, 3, 5 ,6]) , reps=5)
# + [markdown] id="ycK1JFBy0ERL"
# > In the above example, the array is reapeated 5 times in one direction
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 407, "status": "ok", "timestamp": 1625130314398, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="ND-uXZlp0ERL" outputId="1e2b76eb-d2ff-46b3-b038-99eff9445fba"
# Example 2 - working
np.tile(np.array([1, 3, 5, 6]), reps=(3,3,3,3))
# + [markdown] id="uRtwnnjc0ERL"
# >In the above example, the array is repeated in 4-dimnesions unlike in the first example, where it was repeated only in 1-dimension
# + colab={"base_uri": "https://localhost:8080/", "height": 296} executionInfo={"elapsed": 429, "status": "error", "timestamp": 1625130493204, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="V7hXEtZW0ERM" outputId="d237141a-01db-4559-e888-364fb8571217"
# Example 3 - breaking (to illustrate when it breaks)
np.tile(np.array([1, 3, 5 ,6]) , reps=5.3)
# + [markdown] id="GN1eVubL0ERM"
# > The above error is generated due to the use of `float` type value for `reps` attribute, instead it should be `int` value.
# + [markdown] id="ifjOm2EK0ERM"
# > This function can be used when a particular array is to repeated a particular number of times.
#
#
# + [markdown] id="31n_Ph-s0ERM"
# ## Function 5 - np.pad
#
# It is used to pad an array
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 16, "status": "ok", "timestamp": 1625131150914, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="VYWkt-aZW6a_" outputId="ed6985f3-92e3-48d1-d472-f48a6f8ab3bb"
arr = np.array([[1,3, 4],[5,4,7],[1,4,6]])
arr
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 401, "status": "ok", "timestamp": 1625131384119, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="7bBtha2x0ERN" outputId="72d8b319-b309-4b1a-ff93-33cc79c318dc"
# Example 1 - working
np.pad(arr, pad_width=2, mode='constant', constant_values = 0)
# + [markdown] id="ic8eGh2C0ERN"
# > In the above example, a border of $0's$ of width 2 is added to the following array.
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 413, "status": "ok", "timestamp": 1625131586716, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="uYYQiqTQ0ERN" outputId="00d86cdf-d929-4d21-a01c-c43848ec561e"
# Example 2 - working
np.pad(arr, (2,3) , 'wrap')
# + [markdown] id="LlTLezdG0ERN"
# > In the above example, the first values are used to pad the end and the end values are used to pad the beginning.
# + colab={"base_uri": "https://localhost:8080/", "height": 387} executionInfo={"elapsed": 719, "status": "error", "timestamp": 1625133142797, "user": {"displayName": "Dikshant kalotra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GizJbuok-R4gMPHWAfoZjjXOH-Z-hZ7ojZuG5CJ=s64", "userId": "17465417811836548495"}, "user_tz": -330} id="OL8Of_-80ERN" outputId="99fc6e5f-e5a8-4e0f-d0cb-8ca2584bb28d"
# Example 3 - breaking (to illustrate when it breaks)
np.pad(arr,(3,3,3), mode='constant', constant_values=0)
# + [markdown] id="VreR0XhL0ERN"
# We got the `ValueError` because the original array was of `2-d` but on `np.pad` function we were requesting to create a `3-d` array.
# + [markdown] id="GnolW9i10ERO"
# So , when you want to pad an array you can always use `np.pad` function
# + [markdown] id="1p9yE4yQ0ERO"
# ## Conclusion
#
# In this notebook, 5 functions of numpy are studied and experimented on different values. The functions are broken down to the cases where they show different types of errors and
| 14,416 |
/MN-CuadernoNotas-Introducción.ipynb | 97155bed498d776cea715ea6629039d5c748db5a | [] | no_license | facomprivate/MetodosNumericos | https://github.com/facomprivate/MetodosNumericos | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 16,599 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # dataset plot with zoom insets
import sys
sys.path.append('..')
import os
import random
import numpy as np
import unidecode
import numpy.ma as ma
import pylab as pl
import skimage
import agronn.classif2 as classif2
import matplotlib.cm as cm
import skimage.color as skcolor
import sklearn.cross_validation as skcross
import scipy.stats as stats
from osgeo import gdal
from osgeo import ogr
# %pylab inline --no-import-all
img_rgb = classif2.load_image('2013_10_08', 'rgb')
img_rgb = skimage.img_as_float(img_rgb).astype(np.float32)
pl.imshow(img_rgb)
# white background
vimg = img_rgb.copy()
vimg[np.all(img_rgb == 0, axis=2)] = 1
pl.imshow(vimg)
# +
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1.inset_locator import zoomed_inset_axes
from mpl_toolkits.axes_grid1.inset_locator import mark_inset
fig, ax = pl.subplots(figsize=([8, 8]))
ax.imshow(vimg, interpolation='nearest')
ax.axis('off')
#axins1 = zoomed_inset_axes(ax, 8, loc=1) # zoom = 6
axins1 = zoomed_inset_axes(
ax, 8, loc=4,
bbox_to_anchor=(1.2, 0.6),
bbox_transform=ax.figure.transFigure) # zoom = 6
axins1.imshow(vimg, interpolation='nearest')
axins1.set_xlim(897, 977)
axins1.set_ylim(533, 455)
axins1.axis('off')
# https://ocefpaf.github.io/python4oceanographers/blog/2013/12/09/zoom/
#axins2 = zoomed_inset_axes(ax, 8, loc=4) # zoom = 6
axins2 = zoomed_inset_axes(
ax, 8, loc=4,
bbox_to_anchor=(1.2, 0.2),
bbox_transform=ax.figure.transFigure) # zoom = 6
axins2.imshow(vimg, interpolation='nearest')
axins2.set_xlim(1850, 1930)
axins2.set_ylim(1373, 1293)
axins2.axis('off')
mark_inset(ax, axins1, loc1=2, loc2=3, fc="none", ec=(0.2,0.2,0.8))
mark_inset(ax, axins2, loc1=2, loc2=3, fc="none", ec=(0.2,0.2,0.8))
pl.savefig('../../latex/figs/dataset_with_zoom.pdf', bbox_inches='tight', dpi=150)
# -
nformación.
# - ¿Cómo evaluaremos el curso?.
# - Herramientas de comunicación e interacción con el profesor.
# + [markdown] id="oCsHFetU_ezu"
# ## Presentaciones
# + [markdown] id="pyFUXFsrIe1Y"
# ### Presentación del profesor
# + [markdown] id="0-H26Zwp_lGt"
# - Mi nombre es Jorge I. Zuluaga, soy físico y tengo un doctorado en física de la Universidad de Antioquia.
# + [markdown] id="syJlSd-NEgOt"
# - Mis áreas de especialidad técnica son los métodos numéricos y computacionales aplicados en ciencias, la programación científica, y la computación de alto rendimiento.
#
# <center><img src="https://github.com/JorgeZuluaga/NotasMetodosNumericos/raw/master/figuras/ejemplo-computacion-cientifica2.gif" width=400></br></center>
# + [markdown] id="H0s_YbhtEkZo"
# - Mis áreas de especialidad científica astrofísica, ciencias planetarias, exoplanetas, astrobiología.
#
#
# <center><img src="https://github.com/JorgeZuluaga/NotasMetodosNumericos/raw/master/figuras/exoplanetas.jpeg" width=400></br></center>
#
# + [markdown] id="H2YMggrU_xyi"
# - Mi gran pasión (además de la investigación científica y la programación) es la divulgación científica. Durante unos años realicé un programa para Telemedellín que se llamaba [Eso no tiene ciencia](https://www.youtube.com/watch?v=_e9t6Qdt8yo&list=PL2hl1l-cy3EJVCLCFSHnEPgV8e2klVMTQ)
#
# <center><img src="https://github.com/JorgeZuluaga/NotasMetodosNumericos/raw/master/figuras/zuluaga-divulgacion.jpg" width=400></center>
#
# - También hago divulgación en redes sociales, [TikTok, @zuluagajorge](tiktok.com/@zuluagajorge), [Twitter, @zuluagajorge](https://twitter.com/zuluagajorge) e [Instagram](https://www.instagram.com/jorgeizuluagac/), aunque en estas dos últimas público especialmente cosas personales.
#
#
# + [markdown] id="oN8yJQYBIhWw"
# ### Presentación de los estudiantes
# + [markdown] id="kTCpcvHGIb-5"
# - ¿Quiénes son los estudiantes de este grupo?
#
# Por favor presentarse diciendo:
#
# - Nombre.
# - Carrera y nivel (semestre).
# + [markdown] id="xf8wqXzsDMWq"
# ## ¿Qué son los métodos y el análisis numérico?
# + [markdown] id="XJUVKlRcJvIn"
# ### Motivación
# + [markdown] id="ETIsIXpzDq0A"
# - Desde tiempos de Galileo sabemos que el mundo funciona obedeciendo reglas matemáticas. No sabemos exactamente porque, pero eso nos ha permitido explotar lo que sabemos de matemáticas para entender y manipular el mundo.
# + [markdown] id="yh1_JLeeJFJA"
# - Ejemplos:
#
# - Es posible saber la longitud de la diagonal de un televisor sin necesidad de medirla, sabiendo solamente cuánto miden sus lados:
#
# $$
# diagonal=\sqrt{ancho^2+alto^2}
# $$
#
# - Se puede predecir en que momento exacto llega un tren a una estación sabiendo la distancia a la que esta de otra estación, su velocidad y aceleración, si se resuelve la ecuación algebraica:
#
# $$
# d=v_o t + \frac{1}{2} a t^2
# $$
#
# - Se puede predecir cuál será la temperatura en cualquier lugar en Medellín si se resuelve el sistema de ecuaciones diferenciales:
#
# $$
# \begin{gathered}
# \frac{d \rho}{d t}+\rho(\nabla \cdot \mathbf{u})=0 \\
# \rho \frac{d \mathbf{u}}{d t}=\nabla \cdot \sigma+\mathbf{F} \\
# \rho C_{\mathrm{p}} \frac{d T}{d t}-\alpha_{\mathrm{p}} T \frac{d p}{d t}=-\nabla \cdot \mathbf{q}+\phi+Q
# \end{gathered}
# $$
#
# - Los métodos numéricos y el análisis numérico, son una disciplina de las matemáticas. Este es **un curso de matemáticas**.
# + [markdown] id="tNqwJSi6Mjad"
# ### Los problemas de la academia son solubles
# + [markdown] id="bBd2tVyGMnUo"
# - La mayoría de los cursos de matemáticas que vemos permiten definir las entidades abstractas que manipulamos en las ciencias (números, variables, funciones, operadores, figuras geom´
# etricas, etc.) y sus relaciones (axiomas, postulados, teoremas, etc.)
#
# - También nos permiten resolver muchos problemas:
#
# - Cuál es la raíz cuadrada de 100.
#
# - Cuál es el valor de x que cumple esta ecuación algebraica:
#
# $$
# x+2 = -\frac{1}{x}, x = ?
# $$
#
# - Cuánto vale está integral:
#
# $$
# \int_0^1 2x e^{x^2} dx =
# $$
#
# - Cuál es la solución a esta ecuación diferencial:
#
# $$
# \frac{dy}{dx}=y, y(x) = ?
# $$
# + [markdown] id="l83wsjTHJ2f8"
# ### No todos los problemas pueden resolverse
# + [markdown] id="7ruwjoGcJ5fG"
# - Pero hay muchos problemas, incluso sencillos que no pueden resolverse fácilmente:
#
# - Cuál es la raíz cuadrada de 10.
#
# - Cuál es el valor de x que cumple esta ecuación algebraica:
#
# $$
# \sin x = x, x = ?
# $$
#
# - Cuánto vale está integral:
#
# $$
# \int_{-1}^{1} \sqrt{\tan x} dx =
# $$
#
# - Cuál es la solución a esta ecuación diferencial:
#
# $$
# \frac{dy}{dx}=y^2, y(x) = ?
# $$
# + [markdown] id="xB8aRbxYNjeS"
# - En estas situaciones los **métodos matemáticos convencionales** no son útiles.
# + [markdown] id="lWzKmyFANzVU"
# ### Un ejemplo de método numérico
# + [markdown] id="yV_p2fsTUgEK"
# - Es posible que el método numérico más antiguo haya sido inventado por los egipcios para resolver problemas del tipo cuál es la raíz cuadrada de 10 (los egipcios no tenían calculadoras).
#
# - El método fue legado a mesopotamia de donde finalmente llegó a occidente como el **método babilónico**.
#
# - La *receta informal* del método babilónico es así:
#
# 1. Suponga que la raíz de $N=10$ es $r=N/2=5$.
# 2. A continuación haga esta operación: $(r + N/r )/2$
# 3. El resultado de la operación llamelo $r$.
# 4. Repita desde el paso 2 hasta que este content@ con la respuesta.
# + [markdown] id="pAGDPz1UUcIL"
# #### Pongámoslo a prueba:
# + [markdown] id="RVcOgX-BUi1W"
# 1. Empezamos con: r = 5
# 2. Calculamos: $(r + N/r )/2=(5+10/5)/2=3.5$
# 3. Ahora $r = 3.5$.
# 4. Repito desde 2.
# 2. Calculamos: $(r + N/r )/2=(3.5+10/3.5)/2=3.17857$
# 3. Ahora $r = 3.17857$.
# 4. Repito desde 2.
# 2. Calculamos: $(r + N/r )/2=(3.17857+10/3.17857)/2=3.1623194$
# 3. Ahora $r = 3.1623194$.
# 4. Repito desde 2.
# 2. Calculamos: $(r + N/r )/2=(3.1623194+10/3.1623194)/2=3.16227766$
# 3. Ahora $r = 3.16227766$.
# 4. Repito desde 2.
# 2. Calculamos: $(r + N/r )/2=(3.16227766+10/3.16227766)/2=3.16227766$
# + [markdown] id="g9YH5Ed5qUR6"
# #### ¿Cómo se hace esto en `Python`?
# + colab={"base_uri": "https://localhost:8080/"} id="O4fMGPGVofpR" executionInfo={"status": "ok", "timestamp": 1643825576146, "user_tz": 300, "elapsed": 500, "user": {"displayName": "JORGE IVAN ZULUAGA CALLEJAS", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhJohWOSPnt7P2OtNZz-4Lyge_uD-JJD8C_2KR1dH-ePlYUNskYcQpe1btZ1bqnVgk5kWedyE5xHhaYiPgSAXerAr4qYa7BWwaM7IEMvoUA-2WS6SKkRPKN5WX2oDzxxGZEraAU2ibNAPVEMvJlWsQg7EDLbhNd8OYHLr1ngZFGxKy6X-A9SkU-G-V3jYG8y2t-LlocKdd4civlohDwu9l6xPJhLeCu83Fw9MwntQG3kkumphu5IRQOMiQ3ATHSH8utGDVQ1h5Z9fYjejXVS7Sc4RwkXxlIKsj2y91GvVhZ-YTgfMON6BOj0ZaG5QnHieogqK-GHogXAx-fvCi7VLAJz1FvQOKC15wpcUZAotzs9QSHHDUz8qEUU64r3sgi0TsPrCvoEHxfXF7hhbygkg9S-4tn7DCB9024B1s4zblvOpMabbCZomNkUjDS9W3q6F0hILLmUST-x-Rsu_FOJpxljTyCrJrFsqsNVq7zVAyDCOFbG5Q99zYdYRGTjDTqFVy1kFq1a7V2sqRhSs0GFtQI1tRB3eXGPXuB0j5ZRxXKn0CnJqA8pQv2e2v79A0I2m-XePiycJ8_ciPAhKSoP8V4yt5WTBktqCoTzwRGZhjn2kqnei2ni8lA3JXKWSAMnzOVOARqLJeEcweTyGGjN2-Ty0lmBXkoP5lJIsbG95TpHvAkcyWfCi_ynevSMWLZOLazoGbixrerePmobHKUkgbCNL1ce4JXa-1kxixoVVE_Z3OVjvtW_QH09zxKqP-thvvMEHc=s64", "userId": "14268130563590845195"}} outputId="74ef3380-957d-4adb-bb4a-000077cd8398"
N = 10
r = N/2
for paso in 1,2,3,4,5,6:
r=(r+N/r)/2
print(r)
# + [markdown] id="RLtCS7VIRmBw"
# #### Criterios de parada
# + [markdown] id="o6SsXZ4PRnpH"
# - La pregunta es: *¿qué significa estar content@?*
#
# - Hay dos resultados posibles:
#
# - Si conozco la respuesta, la raíz de 10 es 3.16227766, entonces puede seguir haciendo la receta hasta que el número se parezca mucho a este.
#
# - ¿Si no conozco la respuesta que puedo hacer? Puedo comparar los valores de $r$ en cada paso con el del paso anterior:
#
# - Primera respuesta: r = 5
# - Segunda respuesta: r = 3.5
# - Tercera respuesta: r = 3.17857
# - Cuarta respuesta: r = 3.1623194
# - Quinta respuesta: r = 3.16227766
# - Sexta respuesta: r = 3.16227766
#
# se ve que a partir de la quinta respuesta el r no cambia, así que es casi seguro que esa es la raíz cuadrada de 10, como en efecto lo es.
# + [markdown] id="rNT6Ut0_SM_i"
# ### Métodos y Análisis
# + [markdown] id="MDV4-WJXSPca"
# - Llamamos métodos numéricos a las *recetas*, estrategias que se usan para resolver un problema matemático que no se puede resolver por métodos convencionales.
#
# - El método babilónico es un método numérico.
#
# - El adjetivo numérico hace referencia a que la respuesta que se obtiene con estos métodos siempre es... numérica (números) y casi nunca simbólica (variables o funciones).
#
# - Adicionalmente los métodos numéricos producen respuestas *aproximadas*.
#
# - Llamamos **Análisis numérico** a la teoría en matemáticas que permite:
#
# 1. Demostrar que un método numérico funciona y bajo que condiciones lo hace.
#
# 2. Encontrar el margen de error de la respuesta de un método numérico, es decir un estimado de qué tan lejos estamos de la respuesta.
# + [markdown] id="SWKOKQs_D39V"
# ## Fuentes de información
# + [markdown] id="mmmgRw39D7Cq"
# - Muchos estudiantes de la Universidad toman este curso y muchos profesores distintos lo dictan, de modo que es necesario que todos estemos seguros de ver los mismos temas.
#
# - Para ello se ha elegido un libro guía: **Análisis Numérico** de Burden et al.
#
# <center><img src="https://github.com/JorgeZuluaga/NotasMetodosNumericos/raw/master/figuras/portada-burden.jpeg" width=400></br></center>
# + [markdown] id="FTjyFTJlQS5T"
# - Se recomienda comprar el libro físico. Todo científico y científica en el mundo debería tener un libro de métodos y análisis numérico en su biblioteca.
#
# - Adicionalmente el profesor estará proveyendo las notas de clase en la forma de *Cuadernos de Colaboratory*.
# + [markdown] id="N9YuEjwzD8Aa"
# ## ¿Cómo evaluaremos el curso?
# + [markdown] id="7aKes0K_D-aN"
# - Los mecanismos de evaluación de este curso son dos a grandes rasgos:
#
# - **Seguimiento [75%]**: actividades de evaluación exclusivas del curso y del profesor.
#
# - **Examen final [25%]**: evaluación de facultad. Es un examen que presentan todos los estudiantes que están viendo métodos numéricos en la Facultad.
#
# - Para el seguimiento usaremos estos mecanismos:
#
# - **3 Quices** [15%,15%,15%]. Examenes cortos realizados en la clase. Individuales y en pareja.
#
# - **2 Trabajos** [15%,15%]: Se asignaran 2 problemas que exigen una solución usando programación en `Python`. Los problemas deben entregarse usando Cuaderno de Google Colab. Se resolveran de forma individual y en pareja.
#
# - Para ver la programación de las evaluaciones vaya a la información disponible en U. Virtual.
#
# - El detalle de las políticas de evaluación lo pueden encontrar en [este archivo](https://docs.google.com/document/d/1SBJmKX8x2V7OTPApXjqxXooc0lPlJCsv/edit)
#
# + [markdown] id="aCBUUZj4D-23"
# ## Herramientas de comunicación e interacción con el profesor
# + [markdown] id="-SPvpA4wEC9I"
# - La principal herramienta de comunicación con el profesor es U. Virutal.
#
# - También usaremos el Grupo de WhatsApp para comunicaciones urgentes o para facilitar la asesoría de estudiantes.
# + [markdown] id="q0hnhCylED33"
# -------
# *Esta historia continuará...*
| 13,537 |
/MDP/policy and value iteration analysis.ipynb | 39c79a043d9fcfa52d1c36988a5c01c4a210d0c6 | [] | no_license | alofgreen/ml7641 | https://github.com/alofgreen/ml7641 | 0 | 1 | null | null | null | null | Jupyter Notebook | false | false | .py | 97,843 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import matplotlib.pylab as plt
import matplotlib
from vectorDiff import *
from scipy.stats import chisquare
# +
#This file is checking by not removing all of the events but just the ones that are larger than 200 meters.
# -
df = pd.read_csv('Events_iron.csv')
df2 = pd.read_csv('Events.csv')
df = df.loc[(df['chi2']>0)&(df['chi2']<10)&(df['zenith']<35*np.pi/180)]
df2 = df2.loc[(df2['chi2']>0)&(df['chi2']<10)&(df['zenith']<35*np.pi/180)]
events = df['Unnamed: 0'].unique()
events2 = df2['Unnamed: 0'].unique()
df.keys()
c = .299
def get_delta(r,a,b,sigma):
b_start = 19.51
sigma_start = 83.5
delta = a * r**2.0 #+ b_start * (1-np.exp(-(r**2.0)/(2*(sigma_start**2.0))))
return delta
def get_n(x,y,z):
x,y,z = np.array([x,y,z])/(x**2.0+y**2.0+z**2.0)**0.5
return [x,y,z]
def get_n_cos(zen,az):
x = -np.sin(zen) * np.cos(az)
y = -np.sin(zen) * np.sin(az)
z = -np.cos(zen)
return x,y,z
def rotation(X,az,zen):
R1 = np.array([[np.cos(az),-np.sin(az),0],
[np.sin(az),np.cos(az),0],
[0,0,1]])
y_new = np.dot(R1,[0,1,0])
R2_1 = np.cos(zen)*np.array([[1,0,0],[0,1,0],[0,0,1]])
R2_2 = np.sin(zen)*(np.outer(np.cross(y_new,[1,0,0]),[1,0,0]) + np.outer(np.cross(y_new,[0,1,0]),[0,1,0]) + np.outer(np.cross(y_new,[0,0,1]),[0,0,1]))
R2_3 = (1 - np.cos(zen)) * np.outer(y_new,y_new)
R2 = R2_1+R2_2+R2_3
X_prime = np.dot(R2,np.dot(R1,X))
return X_prime
def new_basis(az,zen):
x_prime = rotation([1,0,0],az,zen)
y_prime = rotation([0,1,0],az,zen)
z_prime = rotation([0,0,1],az,zen)
return x_prime,y_prime,z_prime
def new_vector(X,az,zen):
x_prime,y_prime,z_prime = new_basis(az,zen)
vector_x_prime = np.dot(x_prime,X)
vector_y_prime = np.dot(y_prime,X)
vector_z_prime = np.dot(z_prime,X)
rho = ((vector_x_prime**2.0)+(vector_y_prime**2.0))**0.5
return np.array([rho,vector_z_prime])
x_values = [[df['x'].values[i]-df['ShowerCOG_x'].values[i],
df['y'].values[i]-df['ShowerCOG_y'].values[i],
df['z'].values[i]-df['ShowerCOG_z'].values[i]] for i in range(len(df['x'].values))]
x_values2 = [[df2['x'].values[i]-df2['ShowerCOG_x'].values[i],
df2['y'].values[i]-df2['ShowerCOG_y'].values[i],
df2['z'].values[i]-df2['ShowerCOG_z'].values[i]] for i in range(len(df2['x'].values))]
difference = [new_vector(x_values[i],df['Laputop_dir_azimuth'].values[i],df['Laputop_dir_zenith'].values[i]) for i in range(len(x_values))]
difference2 = [new_vector(x_values2[i],df2['Laputop_dir_azimuth'].values[i],df2['Laputop_dir_zenith'].values[i]) for i in range(len(x_values2))]
df['rho'] = [i[0] for i in difference]
df['z_new'] = [i[1] for i in difference]
df2['rho'] = [i[0] for i in difference2]
df2['z_new'] = [i[1] for i in difference2]
def get_t(X,x1,y1,z1,a,b,sigma,xc,yc,zc,tc):
x,y,z,r = X
n = get_n(x1,y1,z1)
x_new = np.array([(i-xc)*n[0] for i in x])
y_new = np.array([(i-yc)*n[1] for i in y])
z_new = np.array([(i-zc)*n[2] for i in z])
new = x_new + y_new + z_new
tc = np.array([tc for i in range(len(z_new))])
t = tc + (1/c)*new + get_delta(r,a,b,sigma)
return t
def get_ang_diff(x1,y1,z1,x2,y2,z2):
n1 = np.array(get_n(x1,y1,z1))
n2 = np.array(get_n(x2,y2,z2))
if np.dot(n1,n2)>1:
value = 1
angular_diff = np.arccos(value)*180/np.pi
else:
angular_diff = np.arccos(np.dot(n1,n2))*180/np.pi
return angular_diff
def ldf(r,S125,beta):
k = 0.30264
VEM = S125*(r/125)**(-beta-k*np.log10(r/125))
return VEM
def magnitude_spherical(theta,d_theta,d_phi):
dl = (d_theta)**2.0 + (np.sin(theta)**2.0)*(d_phi)**2.0
return dl
df.keys()
from scipy.optimize import curve_fit
from functools import partial
from random import choice
laputop_zenith = []
laputop_azimuth = []
laputop_new_zen = []
laputop_new_az = []
mc_zenith = []
mc_azimuth = []
angular_resolution = []
for event in events:
event1 = df.loc[df['Unnamed: 0'] == event]
laputop_zenith.append(event1['Laputop_dir_zenith'].values[0])
laputop_azimuth.append(event1['Laputop_dir_azimuth'].values[0])
mc_zenith.append(event1['zenith'].values[0])
mc_azimuth.append(event1['azimuth'].values[0])
laputop_new_zen.append(event1['Laputop_new_zenith'].values[0])
laputop_new_az.append(event1['Laputop_new_azimuth'].values[0])
n_lap = [get_n_cos(i,j) for i,j in zip(laputop_zenith,laputop_azimuth)]
n_lap_new = [get_n_cos(i,j) for i,j in zip(laputop_new_zen,laputop_new_az)]
n_mc = [get_n_cos(i,j) for i,j in zip(mc_zenith,mc_azimuth)]
ang_resolution = np.array([get_ang_diff(i[0],i[1],i[2],j[0],j[1],j[2]) for i,j in zip(n_lap,n_mc)])
ang_resolution_new = np.array([get_ang_diff(i[0],i[1],i[2],j[0],j[1],j[2]) for i,j in zip(n_lap_new,n_mc)])
plt.hist(ang_resolution[ang_resolution<3],color='r',alpha=0.5,bins=30,label='old')
plt.hist(ang_resolution_new[ang_resolution_new<3],color='b',alpha=0.5,bins=30,label='new')
plt.xlabel('Degrees')
plt.legend()
plt.savefig('Old_vs_new.png')
np.percentile(ang_resolution_new,50)
np.percentile(ang_resolution,50)
df.keys()
import matplotlib
plt.hist2d(abs(df['z_new'])[(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)],df['m'][(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)],bins=100,norm=matplotlib.colors.LogNorm())
plt.show()
plt.hist2d(df['rho'][(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)],df['m'][(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)],bins=100,norm=matplotlib.colors.LogNorm())
plt.xlabel('rho [m]')
plt.ylabel('m')
plt.savefig('check_rho.png')
plt.hist2d(df['s'][(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)],df['sigmas'][(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)],bins=100,norm=matplotlib.colors.LogNorm())
plt.show()
plt.hist2d(df['rho'][(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)],df['sigmas'][(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)],bins=50,norm=matplotlib.colors.LogNorm())
plt.show()
plt.hist2d(df['s'][(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)],df['m'][(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)],bins=100,norm=matplotlib.colors.LogNorm())
plt.xlabel('s')
plt.ylabel('m')
plt.savefig('check_s.png')
plt.hist2d(abs(df['z_new'])[(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)],df['s'][(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)],bins=100,norm=matplotlib.colors.LogNorm())
plt.show()
thingy = (np.log10(df['chargeVEM'].values)>0.25)
plt.hist2d(df['rho'][(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)&thingy],df['s'][(df['sigmam']<0.1)&(df['rho']<400)&(df['sigmas']<0.1)&thingy],bins=100,norm=matplotlib.colors.LogNorm())
plt.show()
plt.hist(df['sigmam'][df['sigmam']<0.1],bins=100)
plt.show()
plt.hist(df2['sigmam'][df2['sigmam']<0.1],bins=100)
plt.show()
plt.hist(df['sigmas'][df['sigmas']<0.1],bins=100)
plt.show()
print(df.iloc[np.argmax(df['energy'].values)])
event1 = df.loc[df['Unnamed: 0']=='event_672']
#event1 = df2.loc[df2['Unnamed: 0']=='event_828']
def get_t(t,X,x1,y1,z1,xc,yc,zc,tc):
x,y,z,r = X
n = get_n(x1,y1,z1)
x1 = (x-xc)*n[0]
x2 = (y-yc)*n[1]
x3 = (z-zc)*n[2]
new = x1 + x2 + x3
get_delta = t - tc - (1/c)*np.array(new)
return t
print((event1['Laputop_dir_zenith'].values[0])*(180/np.pi))
print((event1['Laputop_dir_azimuth'].values[0])*(180/np.pi))
# +
def func_s(rho,m,b):
y = m*rho + b
return y
def func_m(X,A,B,C,D):
s,rho = X
y = A + B*rho +D*(s-C)**2
return y
def chisquare_value(observed,true):
chi2 = np.sum([((i-j)**2)/abs(j) for i,j in zip(observed,true)])
return chi2
# -
from sklearn.utils import resample
def get_check(function,z,rho,m,chi2,charge,sigma):
value = []
value2 = []
list_values = [240,260,280,300]
charge_values = [0,0.25,0.5]
try:
for charge_value in charge_values:
check = (np.log10(charge)>charge_value)&(rho<300)
fit_m = curve_fit(func_m,xdata=[z[check],rho[check]],ydata=m[check],bounds=((1e-10,1e-10,1e-10,1e-10),np.inf),sigma=chi2[check]**0.5)
chi2_m = chisquare_value(m[check],func_m(np.array([z[check],rho[check]]),fit_m[0][0],fit_m[0][1],fit_m[0][2],fit_m[0][3]))
value2.append(abs(chi2_m))
min_charge = charge_values[np.argmin(value2)]
for max_value in list_values:
check = (np.log10(charge)>min_charge)&(rho<max_value)
fit_m = curve_fit(func_m,xdata=[z[check],rho[check]],ydata=m[check],bounds=((1e-10,1e-10,1e-10,1e-10),np.inf),sigma=chi2[check]**0.5)
chi2_m = chisquare_value(m[check],func_m(np.array([z[check],rho[check]]),fit_m[0][0],fit_m[0][1],fit_m[0][2],fit_m[0][3]))
value.append(abs(chi2_m))
max_rho = list_values[np.argmax(value)]
except:
min_charge = 0
max_rho = 300
value_new = np.mean(sigma) + np.std(sigma)
check = (np.log10(charge)>min_charge)&(rho<list_values[np.argmax(value)])&(sigma<value_new)
final_fit = curve_fit(func_m,xdata=[z[check],rho[check]],ydata=m[check],bounds=((1e-10,1e-10,1e-10,1e-10),np.inf))
final_out = func_m([z[check],rho[check]],final_fit[0][0],final_fit[0][1],final_fit[0][2],final_fit[0][3])
chi2_m = chisquare_value(m[check],func_m(np.array([z[check],rho[check]]),final_fit[0][0],final_fit[0][1],final_fit[0][2],final_fit[0][3]))
print(chi2_m)
residual = [(i-j) for i,j in zip(m[check],final_out)]
return check
from functools import partial
def get_check(func_m,rho,m,s,sigma,sigma1,charge):
check = (rho<400)&(sigma<0.1)&(sigma1<0.1)&(charge>0.25)
error = np.array([1/i for i in sigma])
fit_m = curve_fit(func_m,xdata=[s[check],rho[check]],ydata=m[check],bounds=((1e-10,1e-10,1e-10,1e-10),np.inf))
new_m = func_m([s,rho],fit_m[0][0],fit_m[0][1],fit_m[0][2],fit_m[0][3])
check = (np.array([(abs(i-j)/j)*100 for i,j in zip(new_m,m)])<=10)&check
return check
def get_check_s(function,rho,s,sigmas,check):
error = np.array([1/i for i in sigmas])
fit_s = curve_fit(function,xdata=rho[check],ydata=s[check],bounds=((1e-10,1e-10),np.inf))
new_s = function(rho,fit_s[0][0],fit_s[0][1])
check = (np.array([(abs(i-j)/j)*100 for i,j in zip(new_s,s)])<=10)
return check
check = get_check(func_m,event1['rho'].values,event1['m'].values,event1['s'].values,event1['sigmam'].values,event1['sigmas'].values,event1['chargeVEM'].values)
check_s = get_check_s(func_s,event1['rho'].values,event1['s'].values,event1['sigmas'].values,check)
check_s = check
np.mean(event1['s'][check]),np.std(event1['s'][check])
error = np.sqrt(event1['chi2'][check])
plt.hist(df['rho'],bins=100)
plt.show()
plt.errorbar(event1['z_new'][check],event1['m'][check],fmt='o')
plt.show()
plt.errorbar(event1['rho'],event1['m'],fmt='o')
plt.xlabel('rho')
plt.ylabel('m')
plt.savefig('m_vs_rho.png')
plt.scatter(event1['rho'][check],np.log10(event1['chargeVEM'][check]))
plt.ylabel('log10(chargeVEM)')
plt.xlabel('rho')
plt.savefig('charge_vs_rho.png')
plt.scatter(event1['rho'][check_s],np.log10(event1['chargeVEM'])[check_s])
plt.ylabel('log10(chargeVEM)')
plt.xlabel('rho')
plt.show()
plt.errorbar(event1['rho'][check_s],event1['s'][check_s],fmt='o')
plt.xlabel('rho')
plt.ylabel('s')
plt.savefig('s_vs_rho.png')
plt.errorbar(event1['rho'][check],event1['chi2'][check],fmt='o')
plt.xlabel('rho')
plt.ylabel('chi2')
plt.show()
plt.errorbar(event1['s'][check],event1['m'][check],fmt='o')
plt.show()
plt.errorbar(event1['s'][check_s],event1['m'][check_s],fmt='o')
plt.show()
error = [1/i for i in event1['chi2'].values[check_s]]
X_new = [event1['s'][check],event1['rho'][check]]
fit = curve_fit(func_m,xdata = X_new,ydata=event1['m'][check])
from functools import partial
X_new1 = [event1['rho'][check],event1['z'][check]]
error = [1/i**0.5 for i in event1['chi2'].values[check]]
fit2 = curve_fit(func_s,xdata = event1['rho'][check],ydata=event1['s'][check],sigma=error,p0 = [1e-4,fit[0][3]])
print(fit)
print(fit2)
m_new = func_m(X_new,fit[0][0],fit[0][1],fit[0][2],fit[0][3])
s_new = func_s(event1['rho'][check_s],fit2[0][0],fit2[0][1])
residual_m = event1['m'][check].values-(m_new)
residual_s = event1['s'][check_s].values-(s_new)
plt.scatter(event1['rho'][check],residual_m)
plt.xlabel('rho')
plt.ylabel('residual')
plt.show()
plt.scatter(event1['rho'][check_s],residual_s)
plt.xlabel('rho')
plt.ylabel('residual')
plt.show()
plt.scatter(event1['z_new'][check],residual_m)
plt.xlabel('z')
plt.ylabel('residual')
plt.show()
plt.scatter(event1['z_new'][check_s],residual_s)
plt.xlabel('z')
plt.ylabel('residual')
plt.show()
plt.scatter(event1['m'][check],residual_m)
plt.ylabel('residual')
plt.xlabel('m')
plt.show()
plt.scatter(event1['s'][check_s],residual_s)
plt.ylabel('residual')
plt.xlabel('s')
plt.show()
plt.scatter(event1['m'][check],m_new)
plt.errorbar(event1['m'][check],event1['m'][check])
plt.show()
plt.scatter(event1['s'][check_s],s_new)
plt.errorbar(event1['s'][check_s],event1['s'][check_s])
plt.show()
chisquare(event1['m'][check],m_new)[0]
plt.hist(residual_m,bins=20)
plt.xlabel('Residual')
plt.savefig('Residual_event.png')
np.mean(residual_m),np.std(residual_m)
plt.hist(residual_s,bins=20)
plt.show()
plt.scatter(event1['rho'][check],m_new)
plt.errorbar(event1['rho'][check],event1['m'][check],fmt='o',color='r')
plt.savefig('m_vs_rho.png')
plt.scatter(event1['s'][check],m_new)
plt.errorbar(event1['s'][check],event1['m'][check],fmt='o',color='r')
plt.show()
plt.scatter(abs(event1['z_new'][check]),m_new)
plt.errorbar(abs(event1['z_new'][check]),event1['m'][check],fmt='o',color='r')
plt.show()
plt.scatter(event1['rho'][check_s],s_new)
plt.errorbar(event1['rho'][check_s],event1['s'][check_s],fmt='o',color='r')
plt.xlabel('rho')
plt.ylabel('s')
plt.savefig('s_rho.png')
plt.scatter(event1['z_new'][check_s],s_new)
plt.errorbar(event1['z_new'][check_s],event1['s'][check_s],fmt='o',color='r')
plt.xlabel('rho')
plt.ylabel('z')
plt.show()
plt.scatter(event1['rho'][check],np.log10(event1['chargeVEM'][check]))
plt.show()
plt.errorbar(event1['m'][check_s],event1['s'][check_s],fmt='o',color='r')
plt.scatter(event1['m'][check_s],s_new)
plt.savefig('m_vs_s.png')
from scipy.stats import chisquare
# +
A = []
B = []
C = []
m125_1 = []
Xmax = []
rho_value = []
z_value = []
energy = []
s_mean = []
s_std = []
chi2_1 = []
A1 = []
B1 = []
C1 = []
m125_2 = []
Xmax1 = []
rho_value1 = []
z_value1 = []
energy1 = []
s1_mean= []
s1_std = []
chi2_2 = []
for i in events:
event1 = df.loc[df['Unnamed: 0']==i]
try:
check = get_check(func_m,event1['rho'].values,event1['m'].values,event1['s'].values,event1['sigmam'].values,event1['sigmas'].values,event1['chargeVEM'].values)
except (TypeError,ValueError,RuntimeError,KeyError) as err:
continue
X_new = [event1['s'].values[check],event1['rho'].values[check]]
if np.sum(check) < 4:
continue
try:
fit = curve_fit(func_m,xdata=X_new,ydata=event1['m'].values[check])
chi2_1.append(chisquare(event1['m'][check],func_m(X_new,fit[0][0],fit[0][1],fit[0][2],fit[0][3]))[0])
except RuntimeError:
continue
m125_1.append(func_m([fit[0][2],125],fit[0][0],fit[0][1],fit[0][2],fit[0][3]))
A.append(fit[0][0])
B.append(fit[0][1])
C.append(fit[0][2])
Xmax.append(event1['Xmax'].values[0])
z_value.append(event1['z_new'].values)
rho_value.append(event1['rho'].values)
energy.append(event1['energy'].values[0])
s_mean.append(np.mean(event1['s'].values[check]))
s_std.append(np.std(event1['s'].values[check]))
for i in events2:
event1 = df2.loc[df2['Unnamed: 0']==i]
check = (np.log10(event1['chargeVEM'].values)>0)&(event1['rho'].values<300)&(event1['sigmam']<np.mean(event1['sigmam'])+np.std(event1['sigmam']))
try:
check = get_check(func_m,event1['rho'].values,event1['m'].values,event1['s'].values,event1['sigmam'],event1['sigmas'].values,event1['chargeVEM'].values)
except (TypeError,ValueError,RuntimeError,KeyError) as err:
continue
error = np.sqrt(event1['chi2'][check])
X_new = [event1['s'][check],event1['rho'][check]]
if np.sum(check)<4:
continue
try:
fit = curve_fit(func_m,xdata=X_new,ydata=event1['m'][check])
chi2_2.append(chisquare(event1['m'][check],func_m(X_new,fit[0][0],fit[0][1],fit[0][2],fit[0][3]))[0])
except RuntimeError:
continue
m125_2.append(func_m([fit[0][2],125],fit[0][0],fit[0][1],fit[0][2],fit[0][3]))
A1.append(fit[0][0])
B1.append(fit[0][1])
C1.append(fit[0][2])
Xmax1.append(event1['Xmax'].values[0])
z_value1.append(event1['z_new'].values)
rho_value1.append(event1['rho'].values)
energy1.append(event1['energy'][check].values[0])
s1_mean.append(np.mean(event1['s'].values[check]))
s1_std.append(np.std(event1['s'].values[check]))
# -
len(A)
len(A1)
energy = np.array(energy)
energy1 = np.array(energy1)
A = np.array(A)
B = np.array(B)
C = np.array(C)
A1 = np.array(A1)
B1 = np.array(B1)
C1 = np.array(C1)
m125_1 = np.array(m125_1)
m125_2 = np.array(m125_2)
Xmax = np.array(Xmax)
Xmax1 = np.array(Xmax1)
s_mean = np.array(s_mean)[energy>7]
s1_mean = np.array(s1_mean)[energy1>7]
s_std = np.array(s_std)[energy>7]
s1_std = np.array(s1_std)[energy1>7]
plt.hist(C,bins=100)
plt.show()
print(np.corrcoef(A,Xmax)[0][1],np.corrcoef(B,Xmax)[0][1],np.corrcoef(C,Xmax)[0][1])
0.21574939174672653 0.231497101470742 0.019306044299974907
print(np.corrcoef(A1,Xmax1)[0][1],np.corrcoef(B1,Xmax1)[0][1],np.corrcoef(C1,Xmax1)[0][1])
0.08720071845531845 0.21504764945263605 0.018907957460036564
np.corrcoef(B,chi2_1)
plt.hist(A[(A>0)&(A<10)],bins=50,facecolor='w',edgecolor='r',alpha=0.5)
plt.hist(A1[(A1>0)&(A1<10)],bins=50,facecolor='w',edgecolor='g',alpha=0.5)
plt.xlabel('A')
plt.show()
np.mean(A),np.mean(A1)
plt.hist(B,bins=50,facecolor='w',edgecolor='r',alpha=0.5,density=True)
plt.hist(B1,bins=50,facecolor='w',edgecolor='g',alpha=0.5,density=True)
plt.xlabel('B')
plt.show()
np.mean(B[np.isfinite(B)]),np.mean(B1[np.isfinite(B1)])
plt.hist(C,bins=50,facecolor='w',edgecolor='r',alpha=0.5,density=True)
plt.hist(C1,bins=50,facecolor='w',edgecolor='g',alpha=0.5,density=True)
plt.show()
np.mean(C),np.mean(C1)
plt.hist(np.hstack(rho_value),bins=100)
plt.hist(np.hstack(rho_value1),bins=100)
plt.xlabel('rho')
plt.savefig('rho_distribution.png')
plt.hist(np.hstack(z_value),bins=100)
plt.hist(np.hstack(z_value1),bins=100)
plt.xlabel('z')
plt.savefig('z_value.png')
import matplotlib
plt.hist2d(np.array(Xmax),A,bins=30,norm =matplotlib.colors.LogNorm() )
plt.show()
check = (A1>0)&(A1<10)
plt.hist2d(np.array(Xmax1)[check],A1[check],bins=50,norm =matplotlib.colors.LogNorm() )
plt.show()
def line(m,x,b):
y = m * x + b
return y
# +
B_new = np.append(B,B1)
new_xmax = np.append(Xmax,Xmax1)
#fit_new = curve_fit(line,B_new,new_xmax)
plt.hist2d(new_xmax[np.isfinite(B_new)],B_new[np.isfinite(B_new)],bins=100,norm =matplotlib.colors.LogNorm())
#plt.plot(B_new,line(B_new,fit_new[0][0],fit_new[0][1]))
plt.xlabel('slope')
plt.ylabel('Xmax')
plt.savefig('Xmax_vs_slope.png')
# -
np.corrcoef(np.append(C,C1)[np.isfinite(B_new)],new_xmax[np.isfinite(B_new)])[0][1]
new_C = np.append(C,C1)
plt.hist2d(new_C,new_xmax,bins=100,norm =matplotlib.colors.LogNorm() )
plt.show()
plt.hist(np.array(m125_1)[(m125_1>3)&(m125_1<5)],bins=50,alpha=0.5)
plt.hist(np.array(m125_2)[(m125_2>3)&(m125_2<5)],bins=50,alpha=0.5)
plt.show()
np.mean(m125_1),np.mean(m125_2)
m_125_new = np.append(m125_1,m125_2)
plt.hist2d(m_125_new,new_xmax,bins=20,norm =matplotlib.colors.LogNorm() )
plt.xlabel('m_125')
plt.ylabel('Xmax')
plt.savefig('Xmax_vs_m_125.png')
np.corrcoef(m_125_new,new_xmax)[0][1]
plt.hist2d(m_125_new,np.append(energy,energy1),bins=20,norm =matplotlib.colors.LogNorm() )
plt.show()
plt.hist(m125_1,bins=100,alpha=0.5)
plt.hist(m125_2,bins=100,alpha=0.5)
plt.show()
| 20,306 |
/SecmentClusterAssignment_p1.ipynb | ff7e861596629d9c5328b34eb6ec21cac73afdc8 | [] | no_license | glazerm/Clustering | https://github.com/glazerm/Clustering | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 24,032 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Bankrupt data
#
#
# Importing the libraries
from numpy import loadtxt
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.layers.experimental import preprocessing
# load the dataset
dataset = loadtxt('bankruptTrain.csv', delimiter=',')
# split into input (X) and output (y) variables
train_x = dataset[:,0:4]
train_y = dataset[:,4]
print(train_x.shape)
print(train_y.shape)
# normalization
normalizer = preprocessing.Normalization()
normalizer.adapt(np.array(train_x))
print(normalizer.mean.numpy())
# define the keras model
model = tf.keras.models.Sequential([
normalizer,
tf.keras.layers.Dense(24, activation='relu'),
tf.keras.layers.Dense(24, activation='relu'),
layers.Dropout(0.1),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.summary()
# compile the keras model
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# fit the keras model on the dataset
model.fit(train_x, train_y, epochs=150, batch_size=10)
# evaluate the keras model
_, accuracy = model.evaluate(train_x, train_y, verbose=1)
print('Accuracy: %.2f' % (accuracy*100))
# load test data
dataset_test = loadtxt('bankruptTest.csv', delimiter=',')
# split into input (X) and output (y) variables
test_x = dataset_test[:,0:4]
test_y = dataset_test[:,4]
print(test_x.shape)
print(test_y.shape)
test_results = model.evaluate(test_x, test_y, verbose=1)
test_results
rint(dtc_prediction)
dtc_accuracy=accuracy_score(test_target,dtc_prediction)
print("Accuracy=",dtc_accuracy)
# -
from sklearn.ensemble import RandomForestClassifier
obj_rf=RandomForestClassifier()
obj_rf.fit(rf_train_data,train_target)
rf_prediction=obj_rf.predict(rf_test_data)
print(rf_prediction)
rf_accuracy=accuracy_score(test_target,rf_prediction)
print("Accuracy=",rf_accuracy)
from sklearn.ensemble import GradientBoostingClassifier
obj_gbc=GradientBoostingClassifier()
obj_gbc.fit(gbc_train_data,train_target)
gbc_prediction=obj_gbc.predict(gbc_test_data)
print(gbc_prediction)
gbc_accuracy=accuracy_score(test_target,gbc_prediction)
print("Accuracy=",gbc_accuracy)
# +
prediction_final=[]
for i in range(0,len(test_target)):
l=[]
count_0=count_1=count_2=0
l.append(knn_prediction[i])
l.append(dtc_prediction[i])
l.append(rf_prediction[i])
l.append(gbc_prediction[i])
for j in l:
if(j==0):
count_0=count_0+1
elif(j==1):
count_1=count_1+1
elif(j==2):
count_2=count_2+1
if(count_0>count_1 and count_0>count_2):
prediction_final.append(0)
elif(count_1>count_0 and count_1>count_2):
prediction_final.append(1)
elif(count_2>count_0 and count_2>count_1):
prediction_final.append(2)
elif(count_0==count_1 and (count_0>count_2 or count_1>count_2)):
prediction_final.append(random.choice([0,1]))
elif(count_0==count_2 and (count_0>count_1 or count_2>count_1)):
prediction_final.append(random.choice([0,2]))
elif(count_2==count_1 and (count_1>count_0 or count_2>count_0)):
prediction_final.append(random.choice([2,1]))
final_accuracy=accuracy_score(test_target,prediction_final)
print("Final Accuracy=",final_accuracy)
# -
--', label=cond, color=color_bar[i])
plt.title("Loss")
plt.legend()
plt.show()
plt.figure(figsize=(8,6))
for i, cond in enumerate(results.keys()):
plt.plot(range(len(results[cond]['train-acc'])),results[cond]['train-acc'], '-', label=cond, color=color_bar[i])
plt.plot(range(len(results[cond]['valid-acc'])),results[cond]['valid-acc'], '--', label=cond, color=color_bar[i])
plt.title("Accuracy")
plt.legend()
plt.show()
# -
results = {}
"""
建立你的訓練與實驗迴圈並蒐集資料
"""
results = {}
"""Code Here
撰寫你的訓練流程並將結果用 dictionary 紀錄
"""
"""
使用迴圈,建立不同 Learning rate 的模型並訓練
"""
for lr in LEARNING_RATE:
keras.backend.clear_session() # 把舊的 Graph 清掉
print("Experiment with LR = %.6f" % (lr))
model = build_mlp(input_shape=x_train.shape[1:])
model.summary()
optimizer = keras.optimizers.SGD(lr=lr, nesterov=True, momentum=MOMENTUM)
model.compile(loss="categorical_crossentropy", metrics=["accuracy"], optimizer='RMSprop')
model.fit(x_train, y_train,
epochs=EPOCHS,
batch_size=BATCH_SIZE,
validation_data=(x_test, y_test),
shuffle=True)
# Collect results
train_loss = model.history.history["loss"]
valid_loss = model.history.history["val_loss"]
train_acc = model.history.history["accuracy"]
valid_acc = model.history.history["val_accuracy"]
exp_name_tag = "exp-lr-%s" % str(lr)
results[exp_name_tag] = {'train-loss': train_loss,
'valid-loss': valid_loss,
'train-acc': train_acc,
'valid-acc': valid_acc}
# +
import matplotlib.pyplot as plt
# %matplotlib inline
"""
將實驗結果繪出
"""
color_bar = ["r", "g", "b", "y", "m", "k"]
plt.figure(figsize=(8,6))
for i, cond in enumerate(results.keys()):
plt.plot(range(len(results[cond]['train-loss'])),results[cond]['train-loss'], '-', label=cond, color=color_bar[i])
plt.plot(range(len(results[cond]['valid-loss'])),results[cond]['valid-loss'], '--', label=cond, color=color_bar[i])
plt.title("Loss")
plt.legend()
plt.show()
plt.figure(figsize=(8,6))
for i, cond in enumerate(results.keys()):
plt.plot(range(len(results[cond]['train-acc'])),results[cond]['train-acc'], '-', label=cond, color=color_bar[i])
plt.plot(range(len(results[cond]['valid-acc'])),results[cond]['valid-acc'], '--', label=cond, color=color_bar[i])
plt.title("Accuracy")
plt.legend()
plt.show()
# -
results = {}
"""
建立你的訓練與實驗迴圈並蒐集資料
"""
results = {}
"""Code Here
撰寫你的訓練流程並將結果用 dictionary 紀錄
"""
"""
使用迴圈,建立不同 Learning rate 的模型並訓練
"""
for lr in LEARNING_RATE:
keras.backend.clear_session() # 把舊的 Graph 清掉
print("Experiment with LR = %.6f" % (lr))
model = build_mlp(input_shape=x_train.shape[1:])
model.summary()
optimizer = keras.optimizers.SGD(lr=lr, nesterov=True, momentum=MOMENTUM)
model.compile(loss="categorical_crossentropy", metrics=["accuracy"], optimizer='AdaGrad')
model.fit(x_train, y_train,
epochs=EPOCHS,
batch_size=BATCH_SIZE,
validation_data=(x_test, y_test),
shuffle=True)
# Collect results
train_loss = model.history.history["loss"]
valid_loss = model.history.history["val_loss"]
train_acc = model.history.history["accuracy"]
valid_acc = model.history.history["val_accuracy"]
exp_name_tag = "exp-lr-%s" % str(lr)
results[exp_name_tag] = {'train-loss': train_loss,
'valid-loss': valid_loss,
'train-acc': train_acc,
'valid-acc': valid_acc}
# +
import matplotlib.pyplot as plt
# %matplotlib inline
"""
將實驗結果繪出
"""
color_bar = ["r", "g", "b", "y", "m", "k"]
plt.figure(figsize=(8,6))
for i, cond in enumerate(results.keys()):
plt.plot(range(len(results[cond]['train-loss'])),results[cond]['train-loss'], '-', label=cond, color=color_bar[i])
plt.plot(range(len(results[cond]['valid-loss'])),results[cond]['valid-loss'], '--', label=cond, color=color_bar[i])
plt.title("Loss")
plt.legend()
plt.show()
plt.figure(figsize=(8,6))
for i, cond in enumerate(results.keys()):
plt.plot(range(len(results[cond]['train-acc'])),results[cond]['train-acc'], '-', label=cond, color=color_bar[i])
plt.plot(range(len(results[cond]['valid-acc'])),results[cond]['valid-acc'], '--', label=cond, color=color_bar[i])
plt.title("Accuracy")
plt.legend()
plt.show()
# -
| 8,007 |
/Daniel/Outlier Analysis/OA_Endometrial_Proteomics.ipynb | 492651c43bd4fa4a851742f44158ea98f819e78c | [] | no_license | thomashmolina/WhenMutationsMatter | https://github.com/thomashmolina/WhenMutationsMatter | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 469,459 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="VRtcA8J29L7D"
# Kimlik doğrulama
# + colab={"base_uri": "https://localhost:8080/"} id="n_G9X5Xk827n" executionInfo={"status": "ok", "timestamp": 1622372828044, "user_tz": -180, "elapsed": 17987, "user": {"displayName": "\u0130smail \u00d6zdere", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGk3QzQtOA4pNSRRaCMWCcX4YisHfLwlFlv47xDQ=s64", "userId": "01635209815510460280"}} outputId="4e9c899b-2c88-4d03-b443-50adeef31070"
from google.colab import drive
drive.mount("/gdrive")
# %cd / gdrive
# + [markdown] id="PVlQ1RhX9Qbv"
# # Kütüphane kurulumları ve ağların oluşturulması
# + id="sFTronKs9HuB" executionInfo={"status": "ok", "timestamp": 1622372897657, "user_tz": -180, "elapsed": 487, "user": {"displayName": "\u0130smail \u00d6zdere", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGk3QzQtOA4pNSRRaCMWCcX4YisHfLwlFlv47xDQ=s64", "userId": "01635209815510460280"}}
from keras import Input , layers
# + id="7dhzxSf49c_O" executionInfo={"status": "ok", "timestamp": 1622372991905, "user_tz": -180, "elapsed": 5988, "user": {"displayName": "\u0130smail \u00d6zdere", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGk3QzQtOA4pNSRRaCMWCcX4YisHfLwlFlv47xDQ=s64", "userId": "01635209815510460280"}}
input_tensor = Input((32 , ) )
dense = layers.Dense(32 , activation= "relu")
output_tensor = dense(input_tensor)
# + id="tLe2ArG-9ypO" executionInfo={"status": "ok", "timestamp": 1622373054615, "user_tz": -180, "elapsed": 599, "user": {"displayName": "\u0130smail \u00d6zdere", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGk3QzQtOA4pNSRRaCMWCcX4YisHfLwlFlv47xDQ=s64", "userId": "01635209815510460280"}}
from keras.models import Sequential ,Model
# + [markdown] id="Usm2YHve-DsF"
# ## Sequantial Model
# + colab={"base_uri": "https://localhost:8080/"} id="7_CMbzNo-DPM" executionInfo={"status": "ok", "timestamp": 1622373376694, "user_tz": -180, "elapsed": 498, "user": {"displayName": "\u0130smail \u00d6zdere", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGk3QzQtOA4pNSRRaCMWCcX4YisHfLwlFlv47xDQ=s64", "userId": "01635209815510460280"}} outputId="982bfdb9-9f56-4d7d-f051-d25a1e4b0b17"
seq_model = Sequential()
seq_model.add(layers.Dense(32 , activation= "relu" , input_shape = (64, )))
seq_model.add(layers.Dense(32 , activation= "relu"))
seq_model.add(layers.Dense(10 , activation= "softmax"))
seq_model.summary()
# + [markdown] id="SIITOHiw_V5r"
# ### ``` functional ``` Model
#
#
#
# + colab={"base_uri": "https://localhost:8080/"} id="OZe3RNWK_G46" executionInfo={"status": "ok", "timestamp": 1622373835555, "user_tz": -180, "elapsed": 470, "user": {"displayName": "\u0130smail \u00d6zdere", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGk3QzQtOA4pNSRRaCMWCcX4YisHfLwlFlv47xDQ=s64", "userId": "01635209815510460280"}} outputId="ee476e5c-256f-499b-b05c-77c2ef207e55"
input_tensor = Input(shape = 64 , )
x = layers.Dense(32 , activation= "relu" )(input_tensor)
x = layers.Dense(32 , activation= "relu")(x)
output_tensor = layers.Dense(10 , activation= "softmax")(x)
model = Model(input_tensor , output_tensor)
model.summary()
# + [markdown] id="BTQ2DOBxBKoQ"
# ## Modelin Derlenmesi
# + id="rv1L8Mp9BB2-" executionInfo={"status": "ok", "timestamp": 1622373916990, "user_tz": -180, "elapsed": 330, "user": {"displayName": "\u0130smail \u00d6zdere", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGk3QzQtOA4pNSRRaCMWCcX4YisHfLwlFlv47xDQ=s64", "userId": "01635209815510460280"}}
model.compile(optimizer= "rmsprop" , loss= "categorical_crossentropy")
# + [markdown] id="4sZM36wDBWb8"
# Eğitim için rasgele bir küme oluşturmak
# + id="bVV6voVGBV3O" executionInfo={"status": "ok", "timestamp": 1622373956783, "user_tz": -180, "elapsed": 501, "user": {"displayName": "\u0130smail \u00d6zdere", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGk3QzQtOA4pNSRRaCMWCcX4YisHfLwlFlv47xDQ=s64", "userId": "01635209815510460280"}}
import numpy as np
# + id="7ZE3utGTBfj0" executionInfo={"status": "ok", "timestamp": 1622374075582, "user_tz": -180, "elapsed": 529, "user": {"displayName": "\u0130smail \u00d6zdere", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGk3QzQtOA4pNSRRaCMWCcX4YisHfLwlFlv47xDQ=s64", "userId": "01635209815510460280"}}
x_train = np.random.random((1000 , 64))
y_train = np.random.random((1000 , 10))
# + [markdown] id="f2zgeRM4BwXA"
# ## Modelin Eğitilmesi
# + colab={"base_uri": "https://localhost:8080/"} id="yZ8Xk1x-Bsqo" executionInfo={"status": "ok", "timestamp": 1622374165363, "user_tz": -180, "elapsed": 19384, "user": {"displayName": "\u0130smail \u00d6zdere", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGk3QzQtOA4pNSRRaCMWCcX4YisHfLwlFlv47xDQ=s64", "userId": "01635209815510460280"}} outputId="e81f41fc-40ba-4dce-a4db-0720b918c1a7"
model.fit(x_train , y_train , epochs= 10 , batch_size= 128)
score = model.evaluate(x_train , y_train)
# + id="z6-C2N0tCN0X"
plot(ax=ax)
plt.show()
# Oops! Where did the bike lanes go? Well, python uses a default color for all plots, so the bike paths were plotted on top of the polygon in the exact same color. Let's try to plot the bike lanes yellow.
fig, ax = plt.subplots(figsize = (10,8))
berkeley.plot(ax=ax)
bikes.plot(ax=ax, color="yellow")
plt.show()
# Now we have a map that shows where the bike network of the City of Berkeley is located.
# <a id="section4"></a>
# ## 10.4 Read in data via a Python library (OSMnx)
#
# OSMnx is a Python library that lets you access Open Street Map's street networks through an API.
#
# You can explore more of Open Street Maps [here](https://www.openstreetmap.org/)
#
# You can access the full documentation of OSMnx [here](https://osmnx.readthedocs.io/en/stable/index.html)
# +
# Uncomment to install library
# # !pip install osmnx
# -
# If the below cell does not run, you need to install the library first, by uncommmenting and running the cell above
#
# > **Note**
# >
# > If you get a `numpy` associated error you may need to uninstall and reinstall `numpy` as well as set up tools. Run the following lines of code in your terminal:
# ><code>
# pip uninstall -y numpy
# pip uninstall -y setuptools
# pip install setuptools
# pip install numpy</code>
import osmnx as ox
# Now we can use the osmnx library to access data from Open Street Maps. Let's try to load the Berkeley street map.
# We are using the graph_from_place function. To see the full documentation for the function, go to this link: https://osmnx.readthedocs.io/en/stable/osmnx.html#osmnx.graph.graph_from_place.
#
#
# We need to define two arguments for the function: the **query** and the **network type**
#
# - **Query**: For cities in the US, the query should follow the following format: "City Name, State Abbreviation, USA"
#
#
# - **Network Type**: This is where we define which network we are interested in. Some of the available options are:
# - all
# - drive
# - walk
# - bike
#
# Let's try to read the data for the vehicular network for Berkeley
place = "Berkeley, CA, USA"
graph = ox.graph_from_place(place, network_type='drive')
# This took a while to read. Let's take a look at how many elements were loaded from OSM for Berkeley
len(graph)
# Let's check the data type
type(graph)
# This is a new format. To get this into something that is familiar to us, we are going to extract the nodes and links by using the *graph_to_gdfs* function, which converts our data from a graph to two geodataframes. Because a street network is made up from nodes and links, and our geodatraframes can only have one geography type, the *graph_to_gdfs* returns 2 geodataframes: a node (point) and a street (line) geodataframe.
nodes, streets = ox.graph_to_gdfs(graph)
streets.plot();
# Now, let's try to put everything together in the same map (the limits of the city, the bike lanes and the streets)
fig, ax = plt.subplots(figsize = (10,8))
berkeley.plot(ax=ax)
streets.plot(ax=ax, color="grey")
bikes.plot(ax=ax, color="yellow")
plt.show()
# Another feature that we can extract form OSMnx is the bus stops. To do this, we use the pois_from_place function (see full documentation [here](https://osmnx.readthedocs.io/en/stable/osmnx.html#osmnx.pois.pois_from_place))
#
# This function requires two arguments: the **query** (same as above) and the **tag**:
#
# - **Query**: For cities in the US, the query should follow the following format: "City Name, State Abbreviation, USA"
#
#
# - **Tag**: This is where we define which tags we are interested in. There are many options available. You can find a list of tag features [here](https://wiki.openstreetmap.org/wiki/Map_Features#Highway). These tags are coded as dictionaries. Bus stops are a value defined under the key highway, therefore, the format to call for bus stops looks like this: {'highway':'bus_stop'}
# Let's access the bus stops using the same query defined for Berkeley
#
# > **Note**
# >
# >If you are using an older version of `osmnx` you would be able to use the function `pois_from_place`. This and other functions such as `footprints_from_place` are deprecated as of July 2020. `geometries_from_place` is meant to replace these functions.
### fetch and map POIs from osmnx
busstops = ox.geometries_from_place(place, tags = {'highway':'bus_stop'})
# Now, let's check the data type busstops was read as
type(busstops)
# As we can see, busstops is already a geodataframe. Therefore, we can plot it as it is unto out map.
fig, ax = plt.subplots(figsize = (10,8))
berkeley.plot(ax=ax)
streets.plot(ax=ax, color="grey")
bikes.plot(ax=ax, color="yellow")
busstops.plot(ax=ax, color="white")
plt.show()
# <a id="section5"></a>
# ## 10.5 Exercise
#
# Repeat above for SF. The link for accessing the bikeways for SF is already given to you below.
#
# ### SF Open Data portal
#
# https://datasf.org/opendata/
#
# #### SF Bike Network data
# https://data.sfgov.org/Transportation/SFMTA-Bikeway-Network/ygmz-vaxd
sf_bike_ways = "https://data.sfgov.org/api/geospatial/ygmz-vaxd?method=export&format=GeoJSON"
# +
# Your code here
# -
# ## Double-click here to see solution!
#
# <!--
#
# # SOLUTION:
#
# sf_bikes = gpd.read_file(sf_bike_ways)
#
# # Limit places data to San Francisco
# sf = places[places['NAME']=='San Francisco']
#
# # Set place to be for SF
# place = "San Francisco, CA, USA"
# # Pull in networtk from OSM
# graph = ox.graph_from_place(place, network_type='bike')
# # Extract nodes and streets as geodataframes
# nodes, streets = ox.graph_to_gdfs(graph)
#
# # Plot results
# fig, ax = plt.subplots(figsize = (10,8))
# sf.plot(ax=ax)
# streets.plot(ax=ax, color="grey")
# sf_bikes.plot(ax=ax, color="yellow")
# plt.show()
#
#
# -->
# <a id="section6"></a>
# ## 10.6 Read in Data from a CSV and convert to geodataframe
#
# In this example, we'll learn how to read a csv file with latitude and longitude coordinates and convert it to a geodataframe for plotting.
# Read in CSV file
stations = pd.read_csv("notebook_data/transportation/bart.csv")
stations.head()
# We now want to convert the csv file into a Point geodataframe, so we can produce maps and access the geospatial analysis tools.
#
# We do this below with the geopandas `GeoDataFrame` function which takes as input
#
# 1. a pandas dataframe here `stations`, and
# 2. `geometry` for each row in the dataframe.
#
# We create the geometry using the geopandas `points_from_xy` function, using the data in the `lon` and `lat` columns of the pandas dataframe.
# +
#Convert the DataFrame to a GeoDataFrame.
bart_gdf = gpd.GeoDataFrame(stations, geometry=gpd.points_from_xy(stations.lon, stations.lat))
# and take a look
bart_gdf.plot();
# -
# Now we have a map of BART stations! You can use this approach with any CSV file that has columns of x,y coordinates.
# ### 10.7 Exercises
#
#
#
# Set the CRS for `bart_gdf` to WGS84
# Below is the url for the 2018 census county geographic boundary file.
#
# * Read in the county file
# * Subset on Marin County
# * Plot Marin County with the Bart stations you transformed
# * Question: what should do if the county name is not unique?
# Census Counties file for the USA
county_file = "https://www2.census.gov/geo/tiger/GENZ2018/shp/cb_2018_us_county_500k.zip"
# +
# Your code here
# -
# ## Double-click here to see solution!
#
# <!--
#
# # SOLUTION:
#
# # Set CRS of Bart since it's missing
# bart_gdf.crs ='epsg:4326'
#
# # Bring in counties
# counties = gpd.read_file(county_file)
# counties.head()
#
# # Subset to marin
# marin = counties[counties['NAME']=='Marin']
# marin.crs
#
# # Figure
# fig,ax = plt.subplots(figsize=(8,8))
# marin.plot(ax=ax,color='tan')
# bart_gdf.plot(ax=ax,color='k')
#
# -->
# ---
# <div style="display:inline-block;vertical-align:middle;">
# <a href="https://dlab.berkeley.edu/" target="_blank"><img src ="assets/images/dlab_logo.png" width="75" align="left">
# </a>
# </div>
#
# <div style="display:inline-block;vertical-align:middle;">
# <div style="font-size:larger"> D-Lab @ University of California - Berkeley</div>
# <div> Team Geo<div>
# </div>
#
#
| 13,350 |
/w6_lda.ipynb | f0b4afcab37cddf6e1e2bb43ee2d53782696fbe7 | [] | no_license | neda0/uw_biol359_spr21 | https://github.com/neda0/uw_biol359_spr21 | 0 | 1 | null | null | null | null | Jupyter Notebook | false | false | .py | 20,962 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] pycharm={}
# # Submitting and Managing Jobs
#
# Launch this tutorial in a Jupyter Notebook on Binder:
# [](https://mybinder.org/v2/gh/htcondor/htcondor-python-bindings-tutorials/master?urlpath=lab/tree/introductory/Submitting-and-Managing-Jobs.ipynb)
#
# The two most common HTCondor command line tools are `condor_q` and `condor_submit`; in the previous module, we learning the `xquery()` method that corresponds to `condor_q`. Here, we will learn the Python binding equivalent of `condor_submit`.
#
# We start by importing the relevant modules:
# + pycharm={}
import htcondor
# + [markdown] pycharm={}
# Submitting Jobs
# ---------------
#
# We will submit jobs utilizing the dedicated `Submit` object.
#
# **Note** the Submit object was introduced in 8.5.6, which might be newer than your home cluster. The original API, using the `Schedd.submit` method, utilizes raw ClassAds and is not covered here.
#
# `Submit` objects consist of key-value pairs. Unlike ClassAds, the values do not have an inherent type (such as strings, integers, or booleans); they are evaluated with macro expansion at submit time. Where reasonable, they behave like Python dictionaries:
# + pycharm={}
sub = htcondor.Submit({"foo": "1", "bar": "2", "baz": "$(foo)"})
sub.setdefault("qux", "3")
print("=== START ===\n{}\n=== END ===".format(sub))
print(sub.expand("baz"))
# + [markdown] pycharm={}
# The available attribuets - and their semantics - are relatively well documented in the `condor_submit` [online help](http://research.cs.wisc.edu/htcondor/manual/v8.5/condor_submit.html); we won’t repeat them here. A minimal, but realistic submit object may look like the following:
# + pycharm={}
sub = htcondor.Submit({"executable": "/bin/sleep", "arguments": "5m"})
# + [markdown] pycharm={}
# To go from a submit object to job in a schedd, one must do three things:
#
# 1. Create a new transaction in the schedd using `transaction()`.
# 2. Call the `queue()` method, passing the transaction object.
# 3. Commit the transaction.
#
# Since the transaction object is a Python context, (1) and (3) can be achieved using Python's with statement:
# + pycharm={}
schedd = htcondor.Schedd() # Create a schedd object using default settings.
with schedd.transaction() as txn: # txn will now represent the transaction.
print(sub.queue(txn)) # Queues one job in the current transaction; returns job's cluster ID
# + [markdown] pycharm={}
# If the code block inside the `with` statement completes successfully, the transaction is automatically committed. If an exception is thrown (or Python abruptly exits), the transaction is aborted.
#
# By default, each invocation of `queue` will submit a single job. A more common use case is to submit many jobs at once - often identical. Suppose we don't want to submit a single "sleep" job, but 10; instead of writing a `for`-loop around the `queue` method, we can use the `count` argument:
# -
schedd = htcondor.Schedd() # Create a fresh Schedd object, pointint at the current schedd.
with schedd.transaction() as txn: # Start a new transaction
cluster_id = sub.queue(txn, count=10) # Submit 10 identical jobs
print(cluster_id)
# We can now query for all the jobs we have in the queue:
schedd.query(constraint='ClusterId=?={}'.format(cluster_id),
attr_list=["ClusterId", "ProcId", "JobStatus", "EnteredCurrentStatus"])
# It's not entirely useful to submit many identical jobs -- but rather each one needs to vary slightly based on its ID (the "process ID") within the job cluster. For this, the `Submit` object in Python behaves similarly to submit files: references within the submit command are evaluated as macros at submit time.
#
# For example, suppose we want the argument to `sleep` to vary based on the process ID:
sub = htcondor.Submit({"executable": "/bin/sleep", "arguments": "$(Process)s"})
# Here, the `$(Process)` string will be substituted with the process ID at submit time.
with schedd.transaction() as txn: # Start a new transaction
cluster_id = sub.queue(txn, count=10) # Submit 10 identical jobs
print(cluster_id)
schedd.query(constraint='ClusterId=?={}'.format(cluster_id),
attr_list=["ClusterId", "ProcId", "JobStatus", "Args"])
# The macro evaluation behavior (and the various usable tricks and techniques) are identical between the python bindings and the `condor_submit` executable.
# ## Submitting Jobs with Unique Inputs
# While it's useful to submit jobs which each differ by an integer, it is sometimes difficult to make your jobs fit into this paradigm. A common case is to process unique files in a directory. Let's start by creating a directory with 10 input files:
# +
# generate 10 input files, each with unique content.
import pathlib
input_dir = pathlib.Path("input_directory")
input_dir.mkdir(exist_ok=True)
for idx in range(10):
input_file = input_dir / "job_{}.txt".format(idx)
input_file.write_text("Hello from job {}".format(idx))
# -
# Next, we want to create a python dictionary of all the filenames in the `input_directory` and pass the iterator to the `queue_with_itemdata`.
# +
sub = htcondor.Submit({"executable": "/bin/cat"})
sub["arguments"] = "$(filename)"
sub["transfer_input_files"] = "input_directory/$(filename)"
sub["output"] = "results.$(Process)"
# filter to select only the the job files
itemdata = [{"filename": path.name} for path in input_dir.iterdir() if 'job' in path.name]
for item in itemdata:
print(item)
# +
with schedd.transaction() as txn:
# Submit one job per entry in the iterator.
results = sub.queue_with_itemdata(txn, 1, iter(itemdata))
print(results.cluster())
# -
# *Warning*:
# As of the time of writing (HTCondor 8.9.2), this function takes an _iterator_ and not an _iterable_. Therefore, `[1,2,3,4]` is not a valid third argument but `iter([1,2,3,4])` is; this restriction is expected to be relaxed in the future.
#
# Note that the results of the method is a `SubmitResults` object and not a plain integer as before.
#
# Next, we can make sure our arguments were applied correctly:
schedd.query(constraint='ClusterId=?={}'.format(results.cluster()),
attr_list=["ClusterId", "ProcId", "JobStatus", "TransferInput", "Out", "Args"])
# + [markdown] pycharm={}
# ## Managing Jobs
#
# Once a job is in queue, the schedd will try its best to execute it to completion. There are several cases where a user may want to interrupt the normal flow of jobs. Perhaps the results are no longer needed; perhaps the job needs to be edited to correct a submission error. These actions fall under the purview of _job management_.
#
# There are two `Schedd` methods dedicated to job management:
#
# * `edit()`: Change an attribute for a set of jobs to a given expression. If invoked within a transaction, multiple calls to `edit` are visible atomically.
# * The set of jobs to change can be given as a ClassAd expression. If no jobs match the filter, _then an exception is thrown_.
# * `act()`: Change the state of a job to a given state (remove, hold, suspend, etc).
#
# Both methods take a _job specification_: either a ClassAd expression (such as `Owner=?="janedoe"`)
# or a list of job IDs (such as `["1.1", "2.2", "2.3"]`). The `act` method takes an argument
# from the `JobAction` enum. Commonly-used values include:
#
# * `Hold`: put a job on hold, vacating a running job if necessary. A job will stay in the hold
# state until explicitly acted upon by the admin or owner.
# * `Release`: Release a job from the hold state, returning it to Idle.
# * `Remove`: Remove a job from the Schedd's queue, cleaning it up first on the remote host (if running).
# This requires the remote host to acknowledge it has successfully vacated the job, meaning ``Remove`` may
# not be instantaneous.
# * `Vacate`: Cause a running job to be killed on the remote resource and return to idle state. With
# `Vacate`, jobs may be given significant time to cleanly shut down.
#
# Here's an example of job management in action:
# + pycharm={}
with schedd.transaction() as txn:
clusterId = sub.queue(txn, 5) # Queues 5 copies of this job.
schedd.edit(["%d.0" % clusterId, "%d.1" % clusterId], "foo", '"bar"') # Sets attribute foo to the string "bar".
print("=== START JOB STATUS ===")
for job in schedd.xquery(requirements="ClusterId == %d" % clusterId, projection=["ProcId", "foo", "JobStatus"]):
print("%d: foo=%s, job_status = %d" % (job.get("ProcId"), job.get("foo", "default_string"), job["JobStatus"]))
print("=== END ===")
schedd.act(htcondor.JobAction.Hold, 'ClusterId==%d && ProcId >= 2' % clusterId)
print("=== START JOB STATUS ===")
for job in schedd.xquery(requirements="ClusterId == %d" % clusterId, projection=["ProcId", "foo", "JobStatus"]):
print("%d: foo=%s, job_status = %d" % (job.get("ProcId"), job.get("foo", "default_string"), job["JobStatus"]))
print("=== END ===")
# -
# Finally, let's clean up after ourselves (this will remove all of the jobs you own from the queue).
# + jupyter={"outputs_hidden": false} pycharm={"name": "#%%\n"}
import getpass
schedd.act(htcondor.JobAction.Remove, f'Owner=="{getpass.getuser()}"')
# + [markdown] pycharm={}
# ## That's It!
#
# You've made it through the very basics of the Python bindings. While there are many other features the Python
# module has to offer, we have covered enough to replace the command line tools of `condor_q`, `condor_submit`,
# `condor_status`, `condor_rm` and others.
#
# Head back to the top-level notebook and try out one of our advanced tutorials.
,15)
fig.legend(handles=handles, loc='lower center', ncol=2, labels=['benign','malignant'], frameon=False)
fig.suptitle('Swarm Plot with Box Plot', weight='bold', size='xx-large')
plt.show()
# +
fig, axs = plt.subplots(2)
sns.histplot(ax=axs[0], data=lda_breast, x='LD1', hue='tumor', alpha=.4, fill=True, legend=False)
sns.despine()
sns.histplot(ax=axs[1], data=pca_breast, x='PC1', hue='tumor', alpha=.4, fill=True, legend=False)
sns.despine()
axs[0].text(-5.6, 60, 'LDA', weight='bold', size='xx-large')
axs[1].text(-14, 60, 'PCA', weight='bold', size='xx-large')
axs[0].set_xlim(-6,6)
axs[1].set_xlim(-15,15)
fig.legend(handles=handles, loc='lower center', ncol=2, labels=['benign','malignant'], frameon=False)
fig.suptitle('Histograms', weight='bold', size='xx-large')
plt.show()
# -
fig, axs = plt.subplots(2)
sns.kdeplot(ax=axs[0], data=lda_breast, x='LD1', hue='tumor', alpha=.4, fill=True, legend=False)
sns.despine()
sns.kdeplot(ax=axs[1], data=pca_breast, x='PC1', hue='tumor', alpha=.4, fill=True, legend=False)
sns.despine()
axs[0].text(-5.6, .15, 'LDA', weight='bold', size='xx-large')
axs[1].text(-14, .08, 'PCA', weight='bold', size='xx-large')
axs[0].set_xlim(-6,6)
axs[1].set_xlim(-15,15)
fig.legend(handles=handles, loc='lower center', ncol=2, labels=['benign','malignant'], frameon=False)
fig.suptitle('Kernel Density Plot', weight='bold', size='xx-large')
plt.show()
# ### Now let's try to use LDA to predict whether or not a tumor is benign or malignant.
#
# First we will split our data into an 80% training set and a 20% test set.
# +
from sklearn.model_selection import train_test_split
split = 0.2
X_train, X_test, y_train, y_test = train_test_split(StandardScaler().fit_transform(features),
tumor, test_size=split, random_state=5)
print(f"My training set has {X_train.shape[0]} observations, where my test set has {X_test.shape[0]}.")
# -
# ### How can we evaluate our classification?
#
# An ubiquitous metric is "accuracy" which is the percentage of the set (training or test) that the algorithm was able to predict correctly. The training set is the data where the algorithm "sees" the target/response class. The test set is the one where we withhold the class data until the algorithm makes the prediction.
#
# Remember: we have the ground truth of benign v. malignant to compare to, and we just need to give the algorithm the features. Please do be critical of any biases for your ground truth data, as your algorithm will only be as effective as the data you provide.
# +
def PerformLDA(X, y):
"""
Uses sklearn LinearDiscriminantAnalysis tool to perform LDA
input:
X: Pandas Dataframe or Numpy Array of features
y: Pandas Series or Numpy Vector of target
n_dimensions: Number of LDs to fit
output:
X_lda: Pandas dataframe with column titles of LD1,...,LDn
"""
X_standardized = StandardScaler().fit_transform(X)
lda = LinearDiscriminantAnalysis()
lda.fit(X,y)
X_lda_array = lda.transform(X)
column_names = ['LD{}'.format(i+1) for i in range(X_lda_array.shape[1])]
X_lda = pd.DataFrame(X_lda_array, columns=column_names)
return X_lda, lda
lda_train, lda_model = PerformLDA(X_train, y_train)
train_accuracy = lda_model.score(X_train, y_train)
print(f"Training classification accuracy of {train_accuracy*100:0.1f}%")
test_accuracy = lda_model.score(X_test, y_test)
print(f"Test classification accuracy of {test_accuracy*100:0.1f}%")
# -
lda_train
# +
train = pd.DataFrame(lda_model.transform(X_train), columns=['LD1'])
train['tumor'] = y_train.values
train['train'] = 'train'
test = pd.DataFrame(lda_model.transform(X_test), columns=['LD1'])
test['tumor'] = y_test.values
test['train'] = 'test'
test['predict'] = lda_model.predict(X_test)
total_set = pd.concat([train, test], ignore_index=True)
total_set = total_set.replace({'tumor': {0: 'benign', 1: 'malignant'}})
total_set = total_set.replace({'predict': {0: 'benign', 1: 'malignant'}})
sns.swarmplot(data=total_set, x='LD1', y='train', hue='tumor', hue_order=['benign','malignant'],alpha=.7)
# sns.swarmplot(data=total_set[total_set['guess']!=total_set['guess']], x='LD1', y='train', color='red', size=3, alpha=.2)
sns.despine()
misses=total_set[total_set['predict']!=total_set['tumor']].dropna()
plt.axvline(misses['LD1'].min(), linestyle='--', color='r', linewidth=1)
plt.axvline(misses['LD1'].max(), linestyle='--', color='r', linewidth=1)
plt.show()
# -
misses[['LD1','tumor','predict']]
| 14,448 |
/.ipynb_checkpoints/adult_dataset_analysis-checkpoint.ipynb | 6742e31047c644765cb8d9b5d16ac66c67621edf | [] | no_license | TheTuringExperience/adult-dataset-exploration | https://github.com/TheTuringExperience/adult-dataset-exploration | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 269,075 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import OneHotEncoder
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# -
path_to_data =r"\adult.csv"
data = pd.read_csv(path_to_data)
data.columns = ['age', 'workclass', 'fnlwgt', 'education', 'education_num', 'marital_status', 'ocuppation',
'relantionship', 'race', 'sex', 'capital_gain', 'capital_loss', 'hours_per_week', 'native_country', 'income']
#I do not know what this filds represent, also they are mostly ceros
data.drop(['fnlwgt'],axis=1, inplace=True)
data.drop(['capital_gain', 'capital_loss'], axis=1, inplace=True)
#It will be easier to process like this
data['income'] = data.income.map({' <=50K':0, ' >50K':1})
data.head(20)
# ## Data Exploration
data.describe()
data[['sex', 'income']].groupby('sex', as_index=False).mean().sort_values('income', ascending=False)
data[['workclass', 'income']].groupby('workclass', as_index=False).mean().sort_values('income', ascending=False)
data[['education', 'income']].groupby('education', as_index=False).mean().sort_values(by='income', ascending=False)
sns.set(rc={'figure.figsize':(11.7,8.27)})#Set the sizes for the figures
sns.barplot(x=data['income'],y= data['education'])
# ### Unsurprisingly the higher the education the larger the income, out of the people how did not finish preschool not a sigle one makes over 50K
data[['marital_status', 'income']].groupby('marital_status', as_index=False).mean().sort_values(by='income', ascending=False)
# ### People that have never married gain less than the rest, but this can also be due to the fact that they are the youngest in the data set and younger people on avarage make less
sns.barplot(x=data['marital_status'], y=data['age'])
sns.barplot(data['income'], data['age'])
# ### 1 = >50K
# ### 0 = <=50K
# ### Older people make usually make more
sns.barplot(x=data['income'], y = data['workclass'])
# ### Self employed people are the ones that have more individuasl how's income is over 50K, people who never worked and people that don't get paid clearly don't make over 50K
male_over_50 = []
male_under_50 = []
for i,x in enumerate(data['sex']):
if x.strip() == 'Male' and data['income'][i] == 1:
male_over_50.append(x)
elif x.strip() == 'Male' and data['income'][i] == 0:
male_under_50.append(x)
male = [len(male_over_50), len(male_under_50)]
male
female_over_50 = []
female_under_50 = []
for i,x in enumerate(data['sex']):
if x.strip() == 'Female' and data['income'][i] == 1:
female_over_50.append(x)
elif x.strip() == 'Female' and data['income'][i] == 0:
female_under_50.append(x)
female = [len(female_over_50), len(female_under_50)]
female
sns.barplot(x=["Men", "Women"], y=[male[0], female[0]]).set_title("People how earn more than 50K by gender")
# ### Man are much more likely to make over 50K than women
sns.barplot(x=["Men", "Women"], y=[male[1], female[1]]).set_title("People how earn less than 50K by gender")
# ### Man are also more likely than women to make under 50K, but this distribution is much more balanced
sns.barplot(x=data['sex'], y=data['hours_per_week'])
# ### Man work more hours a week than women, and as we are about to see the people that work more hours are more likely to earn over 50K, however the difference in work hours, and how much the amount of work hours a week influences the income, are not that big so this alone can't explain why men are much more likely to earn over 50K than women.
sns.barplot(x=data['income'], y=data['hours_per_week'])
# ### 1 = >50K
# ### 0 = <=50K
# ### People that work more hours make more money
sns.barplot(x = data['race'], y =data['income'])
def get_frequencies(df, field):
"""Returns the frequencies and levels of a categorical field"""
frequencies = list(data[field].value_counts())
levels = dict(data[field].value_counts()).keys()
levels = list(levels)
return frequencies, levels
education_frequencies, education_levels = get_frequencies(data, 'education')
sns.barplot(x=np.log(education_frequencies), y=education_levels).set_title('In logaritmic scale')
# ### The frequencies of each education level in logaritmic scale
workclass_frequencies, workclass_levels = get_frequencies(data, 'workclass')
sns.barplot(x=np.log(workclass_frequencies), y = workclass_levels).set_title("In logaritmic scale")
# ### The frequencies of each workclass in logaritmic scale
# ## Data Preprocessing
# +
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(data, test_size=0.2, random_state=42)
# I used the number 42 as the random seed simple
# because is the answer to the ultimate question about life the universe and everything
# +
#Separe the target value from the dataset
X_train = train_set.drop(['income'], axis=1)
y_train = train_set['income']
X_test = test_set.drop(['income'], axis=1)
y_test = test_set['income']
# +
from sklearn.base import BaseEstimator, TransformerMixin
#creating custom transformer
class DataFrameSelector(BaseEstimator, TransformerMixin):
"""Selects the specified columns from the dataframe and returns it as a numpy array"""
def __init__(self, attribute_names):
self.attribute_names = attribute_names
def fit(self, X, y=None):
return self
def transform(self,X):
return X[self.attribute_names].values
# -
data.head()
X_train.info()
# +
num_attributes = ['age', 'education_num', 'hours_per_week']
cat_atrributes = list(X_train.drop(num_attributes, axis=1))
cat_pipeline = Pipeline([
('selector', DataFrameSelector(cat_atrributes)),
('lblbinarizer', OneHotEncoder(sparse=False))
])
num_pipeline = Pipeline([
('selector', DataFrameSelector(num_attributes)),
('std_scaler', StandardScaler())
])
# +
from sklearn.pipeline import FeatureUnion
full_pipeline = FeatureUnion(transformer_list=[
('num_pipeline', num_pipeline),
('cat_pipeline', cat_pipeline)
])
# -
X_train_prepared = full_pipeline.fit_transform(X_train)
y_train = np.array(y_train)
X_test_prepared = full_pipeline.transform(X_test)
y_test = np.array(y_test)
X_test_prepared.shape
# ## Data modeling
# Import all the machine learning models
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import SGDClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn import svm
from sklearn.ensemble import RandomForestClassifier
# ### Decision tree
decision_tree = DecisionTreeClassifier()
decision_tree.fit(X_train_prepared, y_train)
acc_decision_tree = decision_tree.score(X_test_prepared, y_test)
acc_decision_tree
# ### Logistic regression
log_reg = LogisticRegression()
log_reg.fit(X_train_prepared, y_train)
acc_log_reg = log_reg.score(X_test_prepared, y_test)
acc_log_reg
# ### SGD Classifier
sgd = SGDClassifier()
sgd.fit(X_train_prepared, y_train)
acc_sgd = sgd.score(X_test_prepared, y_test)
acc_sgd
# ### K nearest neighbors
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train_prepared, y_train)
acc_knn = knn.score(X_test_prepared, y_test)
acc_knn
# ### Support vector machines
# #### SVC
#This one took a long time to execute for some reason
svc_cls = svm.SVC()
svc_cls.fit(X_train_prepared, y_train)
acc_svc = svc_cls.score(X_test_prepared, y_test)
acc_svc
# #### LinearSVC
linear_svc = svm.LinearSVC()
linear_svc.fit(X_train_prepared, y_train)
acc_lin_svc = linear_svc.score(X_test_prepared, y_test)
acc_lin_svc
# ### Random forest
rnd_forest = RandomForestClassifier()
rnd_forest.fit(X_train_prepared, y_train)
acc_rnd_forest = rnd_forest.score(X_test_prepared, y_test)
acc_rnd_forest
# ### The model with the best acc in the test set is the Linear_svc so I we will save by serializing it with pickle
# +
import pickle
pickle.dump(linear_svc, open('linear_svc.pkl', 'wb'))
# -
# # That's All Folks!!
| 8,319 |
/ML_11012021/ex2.ipynb | 8c912bc36c4f8cbe70cafbe26367836f7ee8496c | [] | no_license | NhutNguyen236/Intro-to-Machine-learning | https://github.com/NhutNguyen236/Intro-to-Machine-learning | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 3,557 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="DS60dQxoQEDy"
import numpy as np
import pandas
from google.colab import files
uploaded = files.upload()
excel_data_df = pandas.read_excel('data1.xlsx', sheet_name='Sheet1')
# print whole sheet data
print("\n Data from Excel file")
print(excel_data_df)
programming = []
programming = excel_data_df['Programming'].tolist()
english = []
english = excel_data_df['English'].tolist()
philosophy = []
philosophy = excel_data_df['Philosophy'].tolist()
ID = []
ID = excel_data_df['ID'].tolist()
name = []
name = excel_data_df['Name'].tolist()
KQ = []
# Calculate KQ
for i in range(0, len(programming)):
KQ.append(round((programming[i] + english[i] + philosophy[i])/3,2))
#print("KQ = ", KQ)
# Write KQ into data frame
df = pandas.DataFrame({'ID':ID, 'Name':name , 'KQ': KQ})
df.to_excel('./KQ.xlsx')
# Question 4: Read top 4 lines
# Question 5: Visualization with 4 scores (Programming, English, Philosophy, Result)
import matplotlib.pyplot as plt
plt.plot(programming)
plt.title("Programming scores")
plt.show()
plt.plot(english)
plt.title("English scores")
plt.show()
plt.plot(philosophy)
plt.title("Philosophy scores")
plt.show()
# Question 6: Show Min, Max, Average of 4 scores
print("\n Describe data from excel file")
print(excel_data_df.describe())
# Question 7: Print out top 5 students with the highest result score
KQ_sheet = pandas.read_excel('KQ.xlsx', sheet_name='Sheet1')
# print whole sheet data
print("\n Data from KQ file")
print(KQ_sheet)
kq_value = []
kq_value = KQ_sheet['KQ'].tolist()
print(kq_value)
from operator import itemgetter
lst = dict(zip(name,kq_value))
top5_lst = dict(sorted(lst.items(), key=itemgetter(1), reverse=True)[:5])
print("\nTop 5 students:")
print(top5_lst)
# Question 8: Calculate Pearson and Spearman (handmade function & Libarary) between Age, Programming, English, Philosophy and Result
# Question 9: 9- Using heatmap to visualize the result of the question 8
"]), "b.")
plt.plot(ancho[i//10-6],float(comp[llaves_t[i]]["media"]), "r.", label="Media")
plt.plot(ancho[i//10-6],float(comp[llaves_t[i]]["mediana"]), "b.", label="Mediana")
plt.legend(loc='best')
plt.grid()
plt.title("Series t")
plt.xticks(ancho)
plt.ylabel("complejidad(ua)")
plt.xlabel("Ancho del pulso (us)")
plt.savefig("series_t.png")
ancho = [1, 1.5, 2.5, 3]
for i in range(60, len(llaves_v)):
plt.plot(ancho[i//10-6],float(comp[llaves_v[i]]["media"]), "r.")
plt.plot(ancho[i//10-6],float(comp[llaves_v[i]]["mediana"]), "b.")
plt.plot(ancho[i//10-6],float(comp[llaves_v[i]]["media"]), "r.", label="Media")
plt.plot(ancho[i//10-6],float(comp[llaves_v[i]]["mediana"]), "b.", label="Mediana")
plt.legend(loc='best')
plt.grid()
plt.title("Series V")
plt.xticks(ancho)
plt.ylabel("complejidad(ua)")
plt.xlabel("Ancho del pulso (us)")
plt.savefig("series_V.png")
f = open('./post_analisis/resultados_2.csv')
resultados_nists = f.read()
sr = resultados_nists.split('\n')[1:-2]
comp = {}
for linea in sr:
l = linea.split(";")
nombre = l[0][:18].replace('20210407-','')
comp[nombre] = []
for i in range(1,len(l)):
resultado = l[i].split(',')[-1].replace(')','').replace(']','').strip()
comp[nombre].append(resultado)
llaves_ordenadas = sorted(comp)
llaves_v = llaves_ordenadas[::2]
llaves_t = llaves_ordenadas[1::2]
for i in llaves_t:
#print(comp[i])
count = 0
for element in comp[i]:
if element == 'True':
count += 1
if count > 5:
print(count)
print(i)
for i in llaves_v:
#print(comp[i])
count = 0
for element in comp[i][:-2]:
if element == 'True':
count += 1
if count > 4:
print(count)
print(i)
comp['0010_04_V']
sr[51].split(';')[-1].split('),')
) and len(translate) == 2, \
"translate should be a list or tuple and it must be of length 2."
for t in translate:
if not (0.0 <= t <= 1.0):
raise ValueError("translation values should be between 0 and 1")
self.translate = translate
if scale is not None:
assert isinstance(scale, (tuple, list)) and len(scale) == 2, \
"scale should be a list or tuple and it must be of length 2."
for s in scale:
if s <= 0:
raise ValueError("scale values should be positive")
self.scale = scale
if shear is not None:
if isinstance(shear, numbers.Number):
if shear < 0:
raise ValueError("If shear is a single number, it must be positive.")
self.shear = (-shear, shear)
else:
assert isinstance(shear, (tuple, list)) and \
(len(shear) == 2 or len(shear) == 4), \
"shear should be a list or tuple and it must be of length 2 or 4."
# X-Axis shear with [min, max]
if len(shear) == 2:
self.shear = [shear[0], shear[1], 0., 0.]
elif len(shear) == 4:
self.shear = [s for s in shear]
else:
self.shear = shear
self.resample = resample
self.fillcolor = fillcolor
@staticmethod
def get_params(degrees, translate, scale_ranges, shears, img_size):
"""Get parameters for affine transformation
Returns:
sequence: params to be passed to the affine transformation
"""
if degrees == 0:
angle = 0
else:
angle = random.uniform(degrees[0], degrees[1])
if translate is not None:
max_dx = translate[0] * img_size[0]
max_dy = translate[1] * img_size[1]
translations = (np.round(random.uniform(-max_dx, max_dx)),
np.round(random.uniform(-max_dy, max_dy)))
else:
translations = (0, 0)
if scale_ranges is not None:
scale = random.uniform(scale_ranges[0], scale_ranges[1])
else:
scale = 1.0
if shears is not None:
if len(shears) == 2:
shear = [random.uniform(shears[0], shears[1]), 0.]
elif len(shears) == 4:
shear = [random.uniform(shears[0], shears[1]),
random.uniform(shears[2], shears[3])]
else:
shear = 0.0
return angle, translations, scale, shear
def __call__(self, img):
"""
img (PIL Image): Image to be transformed.
Returns:
PIL Image: Affine transformed image.
"""
ret = self.get_params(self.degrees, self.translate, self.scale, self.shear, img[0].shape)
if ret[0] == 0:
total_img = []
for m in img:
m = np.array([m])
m1 = torch.tensor(m, dtype=torch.float32)
m2 = transforms.ToPILImage()(m1)
m_crop = transforms.CenterCrop(m2.size[0]//2)(m2)
m3 = transforms.ToTensor()(m_crop)
m_np = np.array(m3.tolist())[0]
total_img.append(m_np)
total_img_np = np.array(total_img)
return np.array(total_img_np)
else:
total_img = []
for c in img:
c = np.array([c])
c1 = torch.tensor(c, dtype=torch.float32)
c2 = transforms.ToPILImage()(c1)
af = F.affine(c2, *ret, resample=self.resample, fillcolor=self.fillcolor)
af_crop = transforms.CenterCrop(af.size[0]//2)(af)
af1 = transforms.ToTensor()(af_crop)
af_np = np.array(af1.tolist())[0]
total_img.append(af_np)
total_img_np = np.array(total_img)
return total_img_np
def __repr__(self):
s = '{name}(degrees={degrees}'
if self.translate is not None:
s += ', translate={translate}'
if self.scale is not None:
s += ', scale={scale}'
if self.shear is not None:
s += ', shear={shear}'
if self.resample > 0:
s += ', resample={resample}'
if self.fillcolor != 0:
s += ', fillcolor={fillcolor}'
s += ')'
d = dict(self.__dict__)
d['resample'] = _pil_interpolation_to_str[d['resample']]
return s.format(name=self.__class__.__name__, **d)
# + colab_type="code" id="7o3VEujZiQZR" outputId="0ebac8aa-e1af-4ba9-8519-ebeaf92a4afb" colab={"base_uri": "https://localhost:8080/", "height": 52}
import scipy
import numpy as np
import seaborn as sns
import fiona
import rasterio
import matplotlib.pyplot as plt
from shapely import geometry
from rasterio.mask import mask
from tqdm import tqdm_notebook
from extractor_helper import extractor
# + id="V7OP4-W2m-Rk" colab_type="code" colab={}
class TreesData():
def __init__(self, X, y, transform, duplicate={}):
super().__init__()
self.transform = transform
for k, v in duplicate.items():
idx = y == k
X = np.concatenate([X, np.repeat(X[idx], int(v), 0)])
y = np.concatenate([y, np.repeat(y[idx], int(v), 0)])
self.X, self.y = shuffle(X, y)
def __len__(self):
return self.X.shape[0]
def __getitem__(self, idx):
x = self.transform(self.X[idx])
y = self.y[idx]
return torch.tensor(x, dtype=torch.float32), torch.tensor(y, dtype=torch.long)
# + [markdown] colab_type="text" id="i0nYJcyhiQbr"
# ## Inference
# + colab_type="code" id="CTJi0TVriQbr" colab={}
test2_img = rasterio.open("/content/drive/My Drive/Weak_Learners_ML2020/Eval/test2/pp_2_sat_modified.tif")
test2_points = fiona.open("/content/drive/My Drive/Weak_Learners_ML2020/Eval/test2/points_2_modified_Copy.shp", "r")
test3_img = rasterio.open("/content/drive/My Drive/Weak_Learners_ML2020/Eval/test3/pp_3_sat_modified.tif")
test3_points = fiona.open("/content/drive/My Drive/Weak_Learners_ML2020/Eval/test3/targets_Copy.shp", "r")
test4_img = rasterio.open("/content/drive/My Drive/Weak_Learners_ML2020/Eval/test4/pp_4_sat_modified_spline.tif")
test4_points = fiona.open("/content/drive/My Drive/Weak_Learners_ML2020/Eval/test4/modified_points_Copy.shp", "r")
# + colab_type="code" id="fw3dDGcgVOZa" outputId="9e3b408f-eb6e-4fe5-bdcd-511fc91e7e18" colab={"base_uri": "https://localhost:8080/", "height": 621}
from extractor_helper import extractor
size___ = 14
patch2,coordinates2,labels2, = extractor(test2_img,test2_points,size___ ,normalize=True,labeling=True)
patch3,coordinates3,labels3, = extractor(test3_img,test3_points,size___ ,normalize=True,labeling=True)
patch4,coordinates4,labels4, = extractor(test4_img,test4_points,size___ ,normalize=True,labeling=True)
# + colab_type="code" id="ibTf9NsXdN6S" outputId="c278de33-bd63-40ca-87f9-8be3c834819b" colab={"base_uri": "https://localhost:8080/", "height": 88}
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
patch2,patch3, patch4 = np.array(patch2), np.array(patch3), np.array(patch4)
print(patch2.shape)
labels2, labels3, labels4 = np.array(labels2), np.array(labels3), np.array(labels4)
patch2, patch3, patch4 = np.moveaxis(patch2,3,1), np.moveaxis(patch3,3,1), np.moveaxis(patch4,3,1)
print(patch2.shape)
patch = np.concatenate((patch2, patch3, patch4),axis=0)
labels = np.concatenate((labels2,labels3,labels4),axis=0)
print(patch.shape)
print(labels.shape)
# + colab_type="code" id="bXdckpt3u-63" outputId="c3db332d-4108-474b-c167-b2ed4630e72f" colab={"base_uri": "https://localhost:8080/", "height": 52}
weight_0 = len(labels) / np.sum(labels == 0)
weight_1 = len(labels) / np.sum(labels == 1)
weight_2 = len(labels) / np.sum(labels == 2)
weight_3 = len(labels) / np.sum(labels == 3)
print(weight_0, weight_1, weight_2, weight_3)
duplicate1 = {0: round(weight_0 - 1), 1: round(weight_1 - 1), 2: round(weight_2 -1), 3: round(weight_3 -1)}
weight = np.array([weight_0, weight_1, weight_2, weight_3])
weight = weight / np.sum(weight) # normalized, just in case this is not done automatically
duplicate1
# + id="su3D1ESEE7ze" colab_type="code" colab={}
x_train,x_test,y_train,y_test = train_test_split(patch, labels, test_size=.2, shuffle=True, random_state = 12)
# + id="JRvmBnbhE7zg" colab_type="code" outputId="2f519135-7f48-4cac-9092-b9d705a7085b" colab={"base_uri": "https://localhost:8080/", "height": 300}
sam = x_train[0].copy()
print(type(sam))
sss = RandomAffine(degrees = 0)(sam)
type(sss[0])
plt.imshow(sss[0,:,:])
# + id="KRq-s5KME7zj" colab_type="code" outputId="a77b721b-afbd-41ca-c2b8-dbaf00b73ecd" colab={"base_uri": "https://localhost:8080/", "height": 300}
sam = x_train[0].copy()
print(type(sam))
sss = RandomAffine(degrees = 20)(sam)
type(sss[0])
plt.imshow(sss[0,:,:])
# + id="bCOz3TzJE7zl" colab_type="code" colab={}
train_data = TreesData(x_train,y_train, RandomAffine(degrees = 60, translate = (0.1, 0.2), shear = 20), duplicate1)
test_data = TreesData(x_test,y_test,RandomAffine(degrees = 0))
# + id="2jNREqUWE7z1" colab_type="code" colab={}
train_loader = torch_data.DataLoader(train_data,batch_size=64, shuffle=True)
val_loader = torch_data.DataLoader(test_data,batch_size=250,shuffle=True)
# + id="GEAx-Vn8EIWk" colab_type="code" colab={}
new_train = []
j=0
for a,b in train_data:
new_train.append(b.tolist())
j+=1
import seaborn as sns
sns.countplot(np.array(new_train))
# + colab_type="code" id="9SByHP79vxMW" colab={}
import torch
import torch.nn as nn
__all__ = [
'VGG', 'vgg11', 'vgg11_bn', 'vgg13', 'vgg13_bn', 'vgg16', 'vgg16_bn',
'vgg19_bn', 'vgg19',
]
class VGG(nn.Module): # 256 * 7 * 7
def __init__(self, features, num_classes=4, init_weights=True):
super(VGG, self).__init__()
self.features = features
#self.avgpool = nn.AdaptiveAvgPool2d((7, 7))
self.classifier = nn.Sequential(
nn.Linear(16384, 4096),
nn.ReLU(True),
nn.Dropout(p=0.01),
nn.Linear(4096, 1024),
nn.ReLU(True),
nn.Dropout(),
nn.Linear(1024, 128),
nn.ReLU(True),
nn.Linear(128, num_classes),
nn.ReLU(True)
)
if init_weights:
self._initialize_weights()
def forward(self, x):
#print(x.shape)
x = self.features(x)
#print(x.shape)
x = torch.flatten(x, 1)
#print(x.shape)
x = self.classifier(x)
return x
def _initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
if m.bias is not None:
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.BatchNorm2d):
nn.init.constant_(m.weight, 1)
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
nn.init.normal_(m.weight, 0, 0.01)
nn.init.constant_(m.bias, 0)
def make_layers(cfg, batch_norm=False):
layers = []
in_channels = 8
for v in cfg:
if v == 'M':
layers += [nn.MaxPool2d(kernel_size=2, stride=2, padding=1)]
else:
conv2d = nn.Conv2d(in_channels, v, kernel_size=2, padding=1, stride=1)
if batch_norm:
layers += [conv2d, nn.BatchNorm2d(v), nn.ReLU(inplace=True)]
else:
layers += [conv2d, nn.ReLU(inplace=True)]
in_channels = v
return nn.Sequential(*layers)
cfgs = {'A': [32, 64, 'M', 128, 128, 'M', 256, 256]}
def _vgg(arch, cfg, batch_norm, pretrained, progress, **kwargs):
if pretrained:
kwargs['init_weights'] = False
model = VGG(make_layers(cfgs[cfg], batch_norm=batch_norm), **kwargs) #, batch_norm=batch_norm
if pretrained:
state_dict = load_state_dict_from_url(model_urls[arch],
progress=progress)
model.load_state_dict(state_dict)
return model
def vgg11(pretrained=False, progress=True, **kwargs):
r"""VGG 11-layer model (configuration "A") from
`"Very Deep Convolutional Networks For Large-Scale Image Recognition" <https://arxiv.org/pdf/1409.1556.pdf>`_
Args:
pretrained (bool): If True, returns a model pre-trained on ImageNet
progress (bool): If True, displays a progress bar of the download to stderr
"""
return _vgg('vgg11', 'A', True, pretrained, progress, **kwargs)
model = vgg11(pretrained=False, progress=False)
# + colab_type="code" id="p4lqYUulvw9m" colab={}
def train(model, optimizer, loss_function, train_loader, val_loader, device, epochs_n=1, plot_each=10):
# send the model to that device
model = model.to(device)
# initialize some visualization code that you don't need to care about
monitor = Monitor()
# Reduce the lr every 50 epochs
#scheduler = StepLR(optimizer, 50, 0.5, last_epoch=-1)
# one full cycle on train data is called epoch
for epoch in trange(epochs_n):
# switch the model to the train mode
# later on we will have some blocks that behave differently in train and test mode
model.train()
for model_input, target in train_loader:
# send data to device
model_input = model_input.to(device)
target = target.to(device)
# calculate outputs and loss
model_output = model(model_input)
loss = loss_function(model_output, target)
# update model weights
optimizer.zero_grad()
loss.backward()
optimizer.step()
# do some visualization
monitor.add_loss_value(loss.item())
# evaluate our model
model.eval()
train_accuracy = get_accuracy(model, train_loader, device)
val_accuracy = get_accuracy(model, val_loader, device)
val_f1 = f1_score_(model, val_loader, device) ###########
monitor.add_train_accuracy_value(train_accuracy)
monitor.add_val_accuracy_value(val_accuracy)
monitor.add_val_f1_value(val_f1) ##############
#scheduler.step()
if epoch % plot_each == 0:
monitor.show()
# + [markdown] id="mxoLVw5kRxMi" colab_type="text"
#
# + id="SogKz_XhE7z_" colab_type="code" outputId="f7fc78bb-0ed7-479b-8d78-37fcbed56630" colab={"base_uri": "https://localhost:8080/", "height": 243}
#from utils import get_accuracy, Monitor, set_random_seeds
from tqdm import trange
loss_function = torch.nn.CrossEntropyLoss() # weight = torch.tensor(weight, dtype=torch.float32)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-5)#torch.optim.SGD(model.parameters(), lr=1e-3, momentum=0.9)
# train
train(model, optimizer, loss_function, train_loader, val_loader, device, epochs_n=200)
# + id="om3RXLYrsLvp" colab_type="code" colab={}
| 19,261 |
/2021-1/Linge-Ch4/Linge-Ch4.3.3.ipynb | 7214208ae41e5d4218269306fda797683c5c1585 | [] | no_license | yhkimlab/class-YHKlab-arXiv | https://github.com/yhkimlab/class-YHKlab-arXiv | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 32,482 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# %matplotlib inline
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
# %load_ext autoreload
# %aimport basket_db
# %aimport evaluator
# %aimport predictor
from basket_db import BasketDB
from evaluator import TrainEvaluator
from predictor import PreviousOrderPredictor
ops_train = pd.read_csv('dat/order_products__train.csv')
ops_prior = pd.read_csv('dat/order_products__prior.csv')
orders = pd.read_csv('dat/orders.csv') # index_col = 'order_id'
# or
# orders.set_index('order_id', drop=0)
products = pd.read_csv('dat/products.csv')
aisles = pd.read_csv('dat/aisles.csv')
departments = pd.read_csv('dat/departments.csv')
db = BasketDB(
ops_train=ops_train,
ops_prior=ops_prior,
orders=orders,
products=products,
aisles=aisles,
departments=departments,
)
foo = db.snoop()
foo
# 13, 18
# 6376
zoo = db.snoop(uid=2455)
zoo
[n] + dt*v[n]
v[n+1] = v[n] - dt*omega**2*u[n]
fig = plt.figure(figsize=[14,4])
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
ax1.plot(t, u, 'b-', label='numerical')
ax1.plot(t, X_0*cos(omega*t), 'r--', label='exact')
ax1.set_xlabel('t')
#ax1.set_ylim(-3,3)
ax1.legend(loc='upper left')
# Plot the last three periods to illustrate the accuracy in long time simulations
N3l = int(round(3*P/dt)) # No of intervals to be plotted
ax2.plot(t[-N3l:], u[-N3l:], 'b-', label='numerical')
ax2.plot(t[-N3l:], X_0*cos(omega*t)[-N3l:], 'r--', label='exact')
ax2.set_xlabel('t')
#ax2.set_ylim(-3,3)
ax2.legend(loc='upper left')
plt.show()
#plt.savefig('tmp.pdf'); plt.savefig('tmp.png')
# -
# Since we already know the exact solution as $u(t) = X_0 cos \omega t$, we have reasoned as follows to find an appropriate simulation interval $[0, T]$ and also how many points we should choose. The solution has a period $P = 2\pi/\omega$ (The period $P$ is the time difference between two peaks of the $u(t) ~ cos\omega t$ curve.
# Simulating for three periods of the cosine function, $ T = 3P$, and choosing $\Delta t$ such that there are 20 intervals per period gives $\Delta = P/20$ and a total of $N_t = T/\Delta t$ intervals. The rest of the program is a straightforward coding of the Forward Euler scheme.
# The discretization parameter $\Delta t$ and see if the reusults become more accurate. The numerical and exact solution for the cases $\Delta t = P/40, P/160, P/2000$.
# The conclusion is that the Forward Euler method has a fundamental problem with its growing amplitudes, and that a very small $\Delta t$ is required to achieve satisfactory results. The longer the simulation is, the smaller $\Delta t$ has to be. It is certainly time to look for more effective numerical methods!
lt()
X_display,y_display = shap.datasets.adult(display=True)
# create a train/test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=7)
d_train = lgb.Dataset(X_train, label=y_train)
d_test = lgb.Dataset(X_test, label=y_test)
# -
# まずはトレーニングする。
# +
params = {
"max_bin": 512,
"learning_rate": 0.05,
"boosting_type": "gbdt",
"objective": "binary",
"metric": "binary_logloss",
"num_leaves": 10,
"verbose": -1,
"min_data": 100,
"boost_from_average": True
}
model = lgb.train(params, d_train, 10000, valid_sets=[d_test], early_stopping_rounds=50, verbose_eval=1000)
# -
# ## shap value を計算する
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X)
shap.force_plot(explainer.expected_value, shap_values[0,:], X_display.iloc[0,:])
shap.force_plot(explainer.expected_value, shap_values[:1000,:], X_display.iloc[:1000,:])
shap_values.shape
explainer_valid = shap.TreeExplainer(model)
shap_values_valid = explainer.shap_values(X_test, y_test)
shap.force_plot(explainer_valid.expected_value, shap_values_valid[0,:], X_display.iloc[0,:])
shap.summary_plot(shap_values, X)
for name in X_train.columns:
shap.dependence_plot(name, shap_values, X, display_features=X_display)
import matplotlib.colors as colors
print(hasattr(colors, "to_rgba"))
import matplotlib
matplotlib.__version__
# +
params = {
"max_bin": 512,
"learning_rate": 0.1,
"boosting_type": "gbdt",
"objective": "binary",
"metric": "binary_logloss",
"num_leaves": 2,
"verbose": -1,
"min_data": 100,
"boost_from_average": True
}
model_ind = lgb.train(params, d_train, 20000, valid_sets=[d_test], early_stopping_rounds=50, verbose_eval=1000)
# -
| 4,704 |
/notebook/von Mises distribution.ipynb | bdc03e4897491e026b015bdcd77f69932438b694 | [] | no_license | zizi0429/machine_learning | https://github.com/zizi0429/machine_learning | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 107,050 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: nlp
# language: python
# name: nlp
# ---
# # 문자 단위 RNN (char RNN)
# 모든 시점의 입력에 대해서 출력하는 many-to-many RNN 구현
#
# ## 문자 단위 RNN(Char RNN)
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
# ### 데이터 전처리
sentence = ("if you want to build a ship, don't drum up people together to "
"collect wood and don't assign them tasks and work, but rather "
"teach them to long for the endless immensity of the sea.")
# 문자들에 고유한 정수를 부여
char_set = list(set(sentence)) # 중복을 제거한 문자 집합 생성
print(char_set)
char_dic = {c: i for i, c in enumerate(char_set)} # 각 문자에 정수 인코딩
print(char_dic) # 공백도 여기서는 하나의 원소
dic_size = len(char_dic)
print('문자 집합의 크기 : {}'.format(dic_size))
# 문자 집합의 크기 = 입력으로 사용할 원핫 벡터의 크기
#
# 문장을 임의의 sequence_length로 잘라서 데이터를 만듬
# +
sequence_length = 10 # 임의 숫자 지정
x_data = []
y_data = []
for i in range(0, len(sentence) - sequence_length):
x_str = sentence[i:i + sequence_length]
y_str = sentence[i + 1: i + sequence_length + 1]
print(i, x_str, '->', y_str)
x_data.append([char_dic[c] for c in x_str]) # x str to index
y_data.append([char_dic[c] for c in y_str]) # y str to index
print(x_data[0])
print(y_data[0])
# -
# 원핫 인코딩을 수행
x_one_hot = [np.eye(dic_size)[x] for x in x_data] # x 데이터는 원-핫 인코딩
# 데이터를 텐서로 변환
# +
X = torch.FloatTensor(x_one_hot)
Y = torch.LongTensor(y_data)
print('훈련 데이터의 크기 : {}'.format(X.shape))
print('레이블의 크기 : {}'.format(Y.shape))
print(X[0])
print(Y[0])
# -
# ### 하이퍼 파라미터
hidden_size = dic_size
sequence_length = 10 # 임의 숫자 지정
learning_rate = 0.1
# ### 모델 구현
# +
class Net(torch.nn.Module):
def __init__(self, input_dim, hidden_dim, layers): # 현재 hidden_size는 dic_size와 같음.
super(Net, self).__init__()
self.rnn = torch.nn.RNN(input_dim, hidden_dim, num_layers=layers, batch_first=True)
self.fc = torch.nn.Linear(hidden_dim, hidden_dim, bias=True)
def forward(self, x):
x, _status = self.rnn(x)
x = self.fc(x)
return x
net = Net(dic_size, hidden_size, 2) # 이번에는 층을 두 개 쌓습니다.
# -
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.Adam(net.parameters(), learning_rate)
outputs = net(X)
print(outputs.shape) # 3차원 텐서
print(Y.shape)
print(Y.view(-1).shape)
for i in range(100):
optimizer.zero_grad()
outputs = net(X) # (170, 10, 25) 크기를 가진 텐서를 매 에포크마다 모델의 입력으로 사용
loss = criterion(outputs.view(-1, dic_size), Y.view(-1))
loss.backward()
optimizer.step()
# results의 텐서 크기는 (170, 10)
results = outputs.argmax(dim=2)
predict_str = ""
for j, result in enumerate(results):
if j == 0: # 처음에는 예측 결과를 전부 가져오지만
predict_str += ''.join([char_set[t] for t in result])
else: # 그 다음에는 마지막 글자만 반복 추가
predict_str += char_set[result[-1]]
print(predict_str)
0*rm2*(2.0*rm12-rm6) # 24[2/r^14 - 1/r^8]
ene_pot[i] = ene_pot[i]+0.5*phi # Accumulate energy
ene_pot[j] = ene_pot[j]+0.5*phi # Accumulate energy
virial = virial - dphi*Rsqij # Virial is needed to calculate the pressure
acc[i,:] = acc[i,:]+dphi*Sij # Accumulate forces
acc[j,:] = acc[j,:]-dphi*Sij # (Fji=-Fij)
return acc, np.sum(ene_pot)/N, -virial/DIM # return the acceleration vector, potential energy and virial coefficient
def Compute_Forces(pos,acc,ene_pot,epsilon,N,DIM):
"""Compute forces on positions using the Lennard-Jones potential without periodic boundaries"""
Rij = np.zeros(DIM) # Real space units
#Set all variables to zero
ene_pot = ene_pot*0
acc = acc*0
virial=0
# Loop over all pairs of particles
for i in range(N-1):
for j in range(i+1,N):
Rij = pos[i,:]-pos[j,:]
Rsqij = np.dot(Rij,Rij) # Calculate the square of the distance
if(Rsqij < Rcutoff**2):
# Calculate LJ potential inside cutoff
# We can calculate parts of the LJ potential at a time to improve the efficieny of the computation
rm2 = 1/Rsqij # 1/r^2
rm6 = rm2**3 # 1/r^6
rm12 = rm6**2 # 1/r^12
phi = epsilon*(4*(rm12-rm6)-phicutoff) # 4[1/r^12 - 1/r^6] - phi(Rc) - we are using the shifted LJ potential
# The following is dphi = -(1/r)(dV/dr)
dphi = epsilon*24*rm2*(2*rm12-rm6) # 24[2/r^14 - 1/r^8]
ene_pot[i] = ene_pot[i]+0.5*phi # Accumulate energy
ene_pot[j] = ene_pot[j]+0.5*phi # Accumulate energy
virial = virial - dphi*Rsqij # Virial is needed to calculate the pressure
acc[i,:] = acc[i,:]+dphi*Sij # Accumulate forces
acc[j,:] = acc[j,:]-dphi*Sij # (Fji=-Fij)
return acc, np.sum(ene_pot)/N, -virial/DIM # return the acceleration vector, potential energy and virial coefficient
# ## Temperature
#
# Temperature is a macroscopic quantity. Microscopically it is less well defined due to the low number of particles. However, if we use the kinetic energy of the parameters we can calculate the temperature.
#
# $$E_K = \frac{1}{2}mv^2$$
#
# $$k_bT=\frac{2}{3}\sum_{N}E_K$$
#
# Where we sum over all $N$ atoms. We will use this in order to scale the velocities to maintain a constant temperature (we are using reduced units so $k_B=1$ and $m=1$).
def Calculate_Temperature_PB(vel,BoxSize,DIM,N):
ene_kin = 0
for i in range(N):
real_vel = BoxSize*vel[i,:]
ene_kin = ene_kin + 0.5*np.dot(real_vel,real_vel)
ene_kin_aver = 1.0*ene_kin/N
temperature = 2.0*ene_kin_aver/DIM
return ene_kin_aver,temperature
def Calculate_Temperature(vel,BoxSize,DIM,N):
ene_kin = 0
for i in range(N):
real_vel = vel[i,:]
ene_kin = ene_kin + 0.5*np.dot(real_vel,real_vel)
ene_kin_aver = ene_kin/N
temperature = 2*ene_kin_aver/DIM
return ene_kin_aver,temperature
# ## Initialise the particles
# +
DIM = 2 # Dimensions
N = 128
BoxSize = 10.0#6.35
volume = BoxSize**DIM
density = N / volume
print("volume = ", volume, " density = ", density)
pos = np.zeros([N,DIM])
pos = np.random.uniform(0,10,(N,DIM))
pos = pos[:,:DIM]/BoxSize
MassCentre = np.sum(pos,axis=0)/N
for i in range(DIM):
pos[:,i] = pos[:,i]-MassCentre[i]
# -
# ## Integrate equations of motion
#
# The velocity Verlet algorithm spilts the velocity update into two steps intially doing a half step then modifing the acceleration and then doing the second velocity update. Written in full, this gives:
#
# $$x(t+\Delta t) = x(t) + v(t+1/2\Delta t)\Delta t$$
# $$v(t+1/2 \Delta t) = v(t) + 1/2a(t) \Delta t$$
# $$\text{Derive } a( t + \Delta t ) \text{ from the interaction potential using } x(t+ \Delta t)$$
# $$ v( t + \Delta t ) = v ( t + 1/2 \Delta t ) + 1/2 a ( t + \Delta t ) \Delta t$$
#
# Between step 1 and 2 we rescale the velocities to maintain the temperature at the requested value.
# +
# Setting up the simulation
NSteps=10000 # Number of steps
deltat = 0.0032 # Time step in reduced time units
TRequested = 0.5# #Reduced temperature
DumpFreq = 100 # plot every DumpFreq seconds
epsilon = 1.0 # LJ parameter for the energy between particles
# Main MD loop
def main(pos,NSteps,deltat,TRequested,DumpFreq,epsilon,BoxSize,DIM):
# Vectors to store parameter values at each step
N = np.size(pos[:,1])
ene_kin_aver = np.ones(NSteps)
ene_pot_aver = np.ones(NSteps)
temperature = np.ones(NSteps)
virial = np.ones(NSteps)
pressure = np.ones(NSteps)
ene_pot = np.ones(N)
vel = (np.random.randn(N,DIM)-0.5)
acc = (np.random.randn(N,DIM)-0.5)
for k in range(NSteps):
# Refold positions according to periodic boundary conditions
for i in range(DIM):
period = np.where(pos[:,i] > 0.5)
pos[period,i]=pos[period,i]-1
period = np.where(pos[:,i] < -0.5)
pos[period,i]=pos[period,i]+1
# r(t+dt) modify positions according to velocity and acceleration
pos = pos + deltat*vel + 0.5*(deltat**2)*acc # Step 1
# Calculate temperature
ene_kin_aver[k],temperature[k] = Calculate_Temperature_PB(vel,BoxSize,DIM,N)
# Rescale velocities and take half step
chi = np.sqrt(TRequested/temperature[k])
vel = chi*vel + 0.5*deltat*acc # v(t+dt/2) Step 2
# Compute forces a(t+dt),ene_pot,virial
acc, ene_pot_aver[k], virial[k] = Compute_Forces_PB(pos,acc,ene_pot,epsilon,N, DIM, BoxSize) # Step 3
# Complete the velocity step
vel = vel + 0.5*deltat*acc # v(t+dt/2) Step 4
# Calculate temperature
ene_kin_aver[k],temperature[k] = Calculate_Temperature_PB(vel,BoxSize,DIM,N)
# Calculate pressure
pressure[k]= density*temperature[k] + virial[k]/volume
if(k%DumpFreq==0):
if(DIM==2):
plt.cla()
plt.xlim(-0.5*BoxSize,0.5*BoxSize)
plt.ylim(-0.5*BoxSize,0.5*BoxSize)
for i in range(N):
plt.plot(pos[i,0]*BoxSize,pos[i,1]*BoxSize,'o',markersize=2)
display.clear_output(wait=True)
display.display(plt.gcf())
#print(ene_kin_aver[k], ene_pot_aver[k], temperature[k], pressure[k])
return ene_kin_aver, ene_pot_aver, temperature, pressure, pos
# -
ene_kin_aver, ene_pot_aver, temperature, pressure, pos = main(pos,NSteps,deltat,TRequested,DumpFreq,epsilon,BoxSize,DIM)
# +
# Plot all of the quantities
def plot():
plt.figure(figsize=[7,12])
plt.rc('xtick', labelsize=15)
plt.rc('ytick', labelsize=15)
plt.subplot(4, 1, 1)
plt.plot(ene_kin_aver,'k-')
plt.ylabel(r"$E_{K}", fontsize=20)
plt.subplot(4, 1, 2)
plt.plot(ene_pot_aver,'k-')
plt.ylabel(r"$E_{P}$", fontsize=20)
plt.subplot(4, 1, 3)
plt.plot(temperature,'k-')
plt.ylabel(r"$T$", fontsize=20)
plt.subplot(4, 1, 4)
plt.plot(pressure,'k-')
plt.ylabel(r"$P$", fontsize=20)
plt.show()
plot()
| 10,303 |
/Basic Python Programs for Practice .ipynb | 4c6e4f4b8c45465017ce7a6839861bc612e4a719 | [] | no_license | profthyagu/Mathematical-Fundamentals-for-Artificial-Intelligence | https://github.com/profthyagu/Mathematical-Fundamentals-for-Artificial-Intelligence | 0 | 1 | null | null | null | null | Jupyter Notebook | false | false | .py | 12,214 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Basic Python Programs for Practice
# ### 1. Write a Python Program to read and print integer,float and string
# +
x = int(input("Enter Integer : "))
print("Entered integer value is:",x)
y = float(input("Enter Floating point Number"))
print("\n Entered floating point value is : ",y)
s = input("Enter String : ")
print("\n Entered string is : ",s)
# -
# ### 2. Write a Program to perform addition , subtraction , multiplication ,division ,modulor division and exponentiation.
# +
x,y = input("Enter two values").split()
x = int(x)
y = int(y)
print(" Sum = {}".format(x+y))
print(" Diff = {}".format(x-y))
print(" Prod = {}".format(x*y))
print(" Div = {}".format(x/y))
print(" MOD Div = {}".format(x%y))
print(" Exponent = {}".format(x**y))
# -
# ### 3.What will be output of the following program.
x = 4
y = x + 1
x = 2
print(x,y)
# ### 4. What will be the output of the following program.
x, y = 2, 6
x, y = y, x + 2
print(x, y)
# ### 5. What will be the output of the following program
a, b = 2, 3
c, b = a, b + 1
print(a,b,c)
# ### 6. What will be the output of the following program
# +
x = 1
def f():
return x
print(x)
print(f())
# -
x = 1
def f():
x = 2
return x
print(x)
print(f())
print(x)
# ### 7. What will be the output of the following program
x = 2
def f(a):
x = a * a
return x
y = f(3)
print(x, y)
cube = lambda x: x ** 3
print(cube(3))
square = lambda x: x*x
print(square(2))
# ### 8. What will be the output of the following program
print(2 < 3 and 3 > 1)
print(2 < 3 or 3 > 1)
print(2 < 3 or not 3 > 1)
print(2 < 3 and not 3 > 1)
x = 4
y = 5
p = x < y or x < z
print (p)
# ### 9. What will be the output of the following program
x = 2
if x == 2:
print (x)
else:
print(y)
import time
time.asctime()
import sys
print(sys.argv[1])
import math
math.sqrt(4)
# ### 10. What will be the output of the following program
x = [0, 1, [2]]
x[2][0] = 3
print(x)
x[2].append(4)
print(x)
x[2] = 2
print(x)
# ### 11. What will be the output of the following program
x = zip(["a", "b", "c"], [1, 2, 3])
print(list(x))
x = zip(["a", "b", "c"], [1, 2, 3])
print(set(x))
x = zip(["a", "b", "c"], [1, 2, 3])
print(dict(x))
x = zip(["a", "b", "c"], [1, 2, 3])
print(tuple(x))
# ### 12. What will be the output of the following program
x = sum([1, 2, 3])
print(x)
a = [2, 10, 4, 3, 7]
a.sort()
print(a)
a.reverse()
print(a)
b= [1,3,2,5,4]
print(sorted(b))
print(b)
# ### 13. What will be the output of the following program
def square(x):
return x * x
y=map(square, range(5))
list(y)
def even(x):
return x %2 == 0
f=filter(even, range(10))
list(f)
x = enumerate(["a", "b", "c"])
list(x)
for index, value in enumerate(["a", "b", "c"]):
print(index, value)
# +
### What will be the output of the following program
# +
### What will be the output of the following program
# +
### What will be the output of the following program
# +
### What will be the output of the following program
| 3,244 |
/Loan Underwriting UI/loanUnderwritingUI.ipynb | 5ca6cfa3b81d73a859eb35ae2c0b36b1323df9a7 | [] | no_license | Pratik-Bhujade/Loan-underwriting | https://github.com/Pratik-Bhujade/Loan-underwriting | 3 | 1 | null | null | null | null | Jupyter Notebook | false | false | .py | 5,747 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, f1_score, precision_score
from flask import Flask, render_template, request
from matplotlib import pyplot as plt
from flask import json
app = Flask(__name__, static_url_path='/static')
@app.route('/')
def upload_file():
return render_template('index.html')
@app.route('/result', methods = ['GET', 'POST'])
def fn():
if request.method == 'POST':
f = request.files['file']
print(f.filename)
# For importing the data into environment
application = pd.read_csv("app_train.csv")
val_data = pd.read_csv(f.filename)
# Diving data into feature and target set
X = application.drop(['TARGET'], axis=1)
y = application.TARGET
feature_name = X.columns.tolist()
#Divinding dta into test and train set
X_train,X_test,y_train,y_test = train_test_split(X, y, test_size=0.25, random_state=42)
# ## Deep Q-Learning
# Setting data
num_data = len(X_train)
rf= DecisionTreeClassifier()
rf.fit(X_train,y_train)
#Set Reward
def getReward(accuracy):
if accuracy>=0.90:
return 10
else:
return 0
#Q Matrix for q-netwrok
Q = np.matrix(np.zeros([1]))
#Training the model with provided dataset
def generateQ(x,y):
reward=0
ypred=rf.predict(x)
acc=accuracy_score(y,ypred)
f1=f1_score(ypred,y)
ps= precision_score(y, ypred, average='weighted')
reward=getReward(acc)+reward
Q=[acc,f1,ps]
return Q,reward,ypred
# Testing the Deep Q network model
Q,reward,ypred = generateQ(X_test,y_test)
print("Q is",Q)
print("reward is ", reward)
# Accuracy of deep Q networking with training data
QAcc = Q[0]
QAcc*100
# F1 Score of deep Q networking with training data
Qf1 = Q[1]
Qf1*100
# Precision Score of deep Q networking with training data
QPrec = Q[2]
QPrec*100
X_val=val_data.drop(['TARGET'], axis=1)
Y_val=val_data['TARGET']
Q,reward,ypred = generateQ(X_val,Y_val)
data1=pd.DataFrame({'Actual value':Y_val, 'Predicted value':ypred})
acc=Q[0]*100
f1=Q[1]*100
prec=Q[2]*100
count_1 = 0
count_0 = 0
for index in data1.index:
if(data1['Actual value'][index] == data1['Predicted value'][index]):
count_1 += 1
else:
count_0 += 1
# return render_template("result.html",result = data1.to_html(header = 'true'), acc=acc,f1=f1,prec=prec, reward=reward)
return render_template("result.html", table=data1.to_html(header='true'), result = json.dumps([count_0,count_1]), acc=acc,f1=f1,prec=prec, reward=reward)
if __name__ == '__main__':
app.run()
# -
| 3,396 |
/qiancheng_spider/1_Crawler_list_page.ipynb | db03ba6e5fe244026ed9c8e0fa18d46941c4e39a | [] | no_license | lhang662543608/python_crawler | https://github.com/lhang662543608/python_crawler | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 64,198 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import requests
from lxml import etree
# 设置请求头,防止反爬
headers={
'User-Agent': 'Mozilla/5.0 (Windows NT 10.0; WOW64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/72.0.3626.109 Safari/537.36'
}
def qiancheng_keyword_urlcode(keyword=""):
'''
生成51job“专属”的url编码
Examples:
---------
>>>qiancheng_keyword_urlcode('深度学习')
'%25E6%25B7%25B1%25E5%25BA%25A6%25E5%25AD%25A6%25E4%25B9%25A0'
'''
from urllib.parse import quote
return quote(keyword,'utf-8').replace("%","%25")
def generate_url(keyword=None,loc="全国",page_num='1'):
'''
生成url链接
Parameters:
-----------
keyword: str,default = None
-岗位关键字
loc: str,default = "全国"
-岗位所在省份或城市
Examples:
'''
# 位置对应的url代码,全国默认为‘000000’。这些数据是从51网站上整理的,只整理了部分省份和直辖市,想要具体的自己整理。
loc_dict ={"北京":"010000","上海":"020000","广东省":"030000","深圳":"040000","天津":"050000","重庆":"060000","江苏省":"070000","浙江省":"080000","四川省":"090000","海南省":"100000","福建省":"110000","山东省":"120000","江西省":"130000","广西省":"140000","安徽省":"150000","河北省":"160000","河南省":"170000","湖北省":"180000","湖南省":"190000","陕西省":"200000","山西省":"210000","黑龙江省":"220000","辽宁省":"230000","吉林省":"240000","云南省":"250000","贵州省":"260000","甘肃省":"270000","内蒙古":"280000","宁夏":"290000","西藏":"300000","新疆":"310000","青海省":"320000","香港":"330000","澳门":"340000","台湾":"350000"}
keyword = qiancheng_keyword_urlcode(keyword)
try:
loc = loc_dict[loc]
page_num = str(page_num)
except:
loc = "000000" # 默认为全国
page_num ='1'
url = 'https://search.51job.com/list/'+loc+',000000,0000,00,9,99,'+keyword+',2,'+page_num+'.html'
return url
href_list = [] # 用于存放抓取到的详情页链接
jobName_list = [] # 用于存放抓取到的职位名
companyName_list = [] # 用于存放抓取到的公司名
workAddress_list = [] # 用于存放抓取到的工作地点
salary_list = [] # 用于存放抓取到的薪资 ---> 若是招聘信息没公布招聘薪资,则对应薪资默认值为''
releaseTime_list = [] # 用于存放抓取到的发布时间
keyword = '深度学习' # 所要搜的关键字 ex:深度学习
location = '北京' # 你想要所搜索的职位所在的省份 ex:全国:000000
pageNum = 10 # 所有抓取的页数
for index in range(pageNum):
print("*"*30+"开始下载第"+str(index+1)+"页"+"*"*30)
url = generate_url(keyword,location,index+1) # 生成要抓取的url链接
print(url)
response=requests.get(url,headers =headers)
html = response.content.decode('gbk')
html = etree.HTML(html)
list_length=len(html.xpath('//*[@id="resultList"]/div[@class="el"]'))
print("本页共"+str(list_length)+"条招聘信息")
for i in range(list_length):
print("-"*15+"开始下载第"+str(i+1)+"条招聘信息"+"-"*15)
href = html.xpath('//*[@id="resultList"]/div[@class="el"]/p/span/a/@href')[i] # 本条招聘信息的详情页链接地址
href_list.append(href)
jobName = html.xpath('//*[@id="resultList"]/div[@class="el"]/p/span/a/text()')[i].strip() # 本条招聘信息的职位名
jobName_list.append(jobName)
companyName = html.xpath('//*[@id="resultList"]/div[@class="el"]/span[@class="t2"]/*')[i].xpath('string(.)') # 公司名
companyName_list.append(companyName)
workAddress = html.xpath('//*[@id="resultList"]/div[@class="el"]/span[@class="t3"]')[i].xpath('string(.)') # 工作地点
workAddress_list.append(workAddress)
salary = html.xpath('//*[@id="resultList"]/div[@class="el"]/span[@class="t4"]')[i].xpath('string(.)') # 薪资
salary_list.append(salary)
releaseTime = html.xpath('//*[@id="resultList"]/div[@class="el"]/span[@class="t5"]')[i].xpath('string(.)') # 发布时间
releaseTime_list.append(releaseTime)
print("-"*15+"第"+str(i+1)+"条招聘信息下载已完成"+"-"*15)
print("*"*30+"第"+str(index+1)+"页已下载完成"+"*"*30)
# 数据字典
data ={
"详情页链接":href_list,
"职位名":jobName_list,
"公司名":companyName_list,
"工作地点":workAddress_list,
"薪资":salary_list,
"发布时间":releaseTime_list
}
import pandas as pd
df = pd.DataFrame(data=data)
df.to_csv("51job_"+location+"_"+keyword+"_列表页.csv",mode='w',index=None) # 数据持久化:下入文件
| 4,174 |
/Cousera/DeepLearning.AI TensorFlow Developer Professional Certificate/C2-CNN/w4/Course_2_Part_8_Lesson_2_Notebook_(RockPaperScissors).ipynb | 9c3e0ff27fb94e0d8401d25b9a2ae5fce6a15b59 | [] | no_license | nghiabeooo/tfdevcert | https://github.com/nghiabeooo/tfdevcert | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 8,451 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Python 2 examples for porting to Python 3
# This notebook contains some Python 2 examples for things that you can do with the `print` statement.
# * Try to find the best translation to Python 3
# * Note that you can easily add cells for with the `+` button in the toolbar and move them with the arrow buttons. You can create one or more cells for the Python 3 solution or for any experiments just below the Python 2 example.
# * Note that the magic command `%%python2` has been used to switch the example cells to Python 2 mode. If you start a new cell, it should be in Python 3 mode by default.
# * Feel free to look at the Python 3 documentation. Note that you can quickly look at the docstring of a function by typing, e.g., `?print` in a cell.
# # 1. `print`
# The most notable change about `print` is that it is a function in Python 3, such that you need parentheses when invoking it:
#
# print "A", 1
#
# becomes
#
# print("A", 1)
#
# in Python 3. However, there a a few more changes which we will investigate in the following examples.
#
# Note that you can easily get the Python 3 behavior in Python 2 if you want to make future porting efforts easier:
#
# from __future__ import print_function
# ## Example 1.1: `print` without line break
# + language="python2"
# print "Hello",
# print "world!"
# -
# ## Example 1.2: `print` without spaces between individual values
# By default, `print` separates values that are printed in a single `print` command with spaces:
# + language="python2"
# print 1, 2, 3
# -
# If you prefer to print the values without a separator, `print` cannot help easily in Python 2:
# + language="python2"
# import sys
# for i in range(5):
# sys.stdout.write(str(i))
# + language="python2"
# # This is a solution with print, but it builds the entire string in memory - this can be avoided in Python 3 :-)
# print "".join(str(i) for i in range(5))
# -
# ## Example 1.3: `print` to standard error
# Python 2 allows to redirect the output of a `print` statement to any stream instead of the default `sys.stdout` with `>>`. Note how the things that go to standard error are formatted in the notebook:
# + language="python2"
# import sys
# print >>sys.stderr, "This is an error message"
# -
# ## Example 1.4: `print` to a file
# Python 2 allows to `print` directly to a file:
# + language="python2"
# filename = "test.txt"
# with open(filename, "w") as f:
# print >>f, "This is the first line of the file :-)"
# print >>f, "This is line number", 2
# -
# Commands that are prepended with ! are treated as shell commands
# !cat test.txt
# # 2. Functions which return a `list` in Python 2
# In many functions which return a `list` in Python 2 have been modified such that they return a generator in Python 3. The cell below contains some examples. Try to copy the cell without the `%%python2` magic to a new Python 3 cell and see what happens.
# + language="python2"
# from __future__ import print_function
#
# def print_type_and_value(x):
# print(type(x), x)
#
# print_type_and_value(range(10))
#
# l = [0, 1, 2, 3, 4, 5]
# print_type_and_value(filter(lambda x: x%2 == 0, l))
# print_type_and_value(map(lambda x: 2*x, l))
# print_type_and_value(zip(l, l))
#
# d = {"a": 1, "b": 2}
# print_type_and_value(d.keys())
# print_type_and_value(d.values())
# print_type_and_value(d.items())
# -
# For a few of these functions, Python 2 has replacements which return generators instead of ranges. These functions have been removed in Python 3:
# + language="python2"
# from __future__ import print_function
#
# def print_type_and_value(x):
# print(type(x), x)
#
# print_type_and_value(xrange(10))
#
# d = {"a": 1, "b": 2}
# print_type_and_value(d.iterkeys())
# print_type_and_value(d.itervalues())
# print_type_and_value(d.iteritems())
# -
# ## Example 2.1: Iterate more than once through a `list`
# Since the result of `map`, `filter`, etc. is a `list` in Python 2, it can be iterated over multiple times. However, generators can be iterated over only once, such that the following code does not work in Python 3. Try to change the function `min_max` such that it works in both versions:
# + language="python2"
# def min_max(items):
# return min(items), max(items)
#
# def is_even(n):
# return n % 2 == 0
#
# print(min_max(filter(is_even, [1, 2, 3, 4, 5])))
# -
# ## Example 2.2: Modifying a `dict` during iteration
# In Python 2, the `keys()` method of a `dict` returns a `list`. This list remains unchanged if the `dict` is modified in any way. Therefore, the `dict` can be safely modified in a loop over the `list` of keys.
#
# Try to run the example code in Python 3, see what happens, and modify it such that it works as expected.
# + language="python2"
# def delete_false_items(d):
# for k in d.keys():
# if not d[k]:
# del d[k]
#
# d = {1: True, 2: False, 3: True, 4: False, 5: True, 6: False}
# delete_false_items(d)
# print(d)
# -
# # 3. Integer division
# In Python 2, applying the division operator `/` to two ints returns an int:
# + language="python2"
# print type(3 / 2), 3 / 2
# -
# In Python 3, the result is a float. Integer division can now be done with `//`:
print(type(3 / 2), 3 / 2)
print(type(3 // 2), 3 // 2)
# The new behavior can be enabled in Python 2 with
#
# from __future__ import division
# ## Example 3.1: Binary search in a sorted list
# The new behavior can be a problem if the result of the division is to be used as a `list` or `tuple` index:
# + language="python2"
# def binary_search(x, items, start=None, end=None):
# """Returns True if and only if x is found in items[start:end]. If start"""
# if start is None:
# start = 0
# if end is None:
# end = len(items)
# if start >= end:
# return False
# middle = (start + end) / 2
# if items[middle] == x:
# return True
# elif items[middle] < x:
# return binary_search(x, items, middle + 1, end)
# else:
# return binary_search(x, items, start, middle)
#
# items = (2, 3, 4, 6, 7, 9, 12)
#
# # Find numbers between 1 and 13 which are not in 'items'
# print(tuple(x for x in range(1, 14) if not binary_search(x, items)))
# -
# # 4. Rounding
# In Python 2, `round` returns a `float`. In Python 3, the return type is `int`. Moreover, the rounding behavior has changed. Try to run this code in Python 3 and see what happens:
# + language="python2"
# def print_and_round(x):
# print("round({}) == {}".format(x, round(x)))
#
# for x in (-3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5):
# print_and_round(x)
| 6,878 |
/1. 调整gamma对比.ipynb | 3db4b25c0ab7c2739781ae6f04d1f744b7a2754d | [] | no_license | dichangyan/MG_Qlearning | https://github.com/dichangyan/MG_Qlearning | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 596,920 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## 实验1,调整gamma,观察
#
# ### 环境及智能体
#
# - 环境: MinorityGame_1, 少数派游戏,101人博弈,无穷博弈,创建环境时可自定义环境承载量,本实验中固定为50
# - 智能体:QLearningAgent,创建智能体时支持自定义学习率、折扣因子以及探索系数,本实验中固定学习率和探索系数,观察不同折扣因子对玩家决策及收益的影响
#
# ### 实验结果
#
# 101人少数博弈,固定环境承载量为50,学习率为0.1,探索系数为0.1时,选取不同的折扣因子,观察玩家决策和平均收益未发现明显影响。
#
# ### 实验内容
# #### 实验准备
# +
# MG环境
import gym
from gym import spaces
from gym.utils import seeding
import random
import numpy as np
import copy
import math, random
from collections import deque
import matplotlib.pyplot as plt
import numpy as np
# # %matplotlib inline
class MinorityGame_1(gym.Env):
'''
Minority Game, we have some agent, every agent can choose 1 or 0 every day.
In midnight, all of the day to make a few choices of the agent to get +1 reward.
'''
def __init__(self, env_max=50):
'''
环境初始化:
玩家数固定101;
env_max 环境承载量,选择1能获取收益的最大人数,默认为50;
action_space 动作空间,大小为2,玩家只能选择0或1;
observation_space 观测空间,这个环境使用2,玩家立足于上一次博弈的状态;
'''
self.env_max = env_max
self.action_space = spaces.Discrete(2)
self.observation_space = spaces.Discrete(2)
self.seed()
def seed(self, seed=None):
'''
设置seed
'''
self.np_random, seed = seeding.np_random(seed)
return [seed]
def step(self, action_101):
'''
每一步博弈:
1. 检查输入是否合法
2. 统计选择1的人数allpick,allpick不超过env_max则1获胜,否则0获胜
3. 返回S(玩家本回合动作), R(所有玩家的奖励列表), done(False,无尽博弈)
'''
assert len(action_101) == 101
assert all(map(lambda x:self.action_space.contains(x), action_101))
allpick = sum(action_101)
reward_101 = []
for action in action_101:
if action == 1 and allpick <= self.env_max or action == 0 and allpick > self.env_max:
reward_101.append(1)
else:
reward_101.append(0)
done = True
return action_101, reward_101, done, {}
def reset(self):
'''
重置环境,每轮第一次博弈给所有玩家一个随机状态
'''
# return [0]*101
return [random.randint(0,1) for _ in range(101)]
# -
# Qlearning智能体
class QLearningAgent:
'''
Q-learning智能体实现
'''
def __init__(self, env, gamma=0.9, learning_rate=0.1, epsilon=0.1):
'''
Q-learning智能体初始化:
env 智能体的博弈环境;
gamma 折扣因子,n步后的奖励为 pow(gamma, n)*Rn, gamma越大表示越重视长期收益。
learning_rata 学习率,Qlearning 更新过程为:Q(s,a) += learning_rate * (R + gamma * Qmax - Q(s,a)),
学习率越大表示越不依赖过去学习的结果
'''
self.gamma = gamma
self.learning_rate = learning_rate
self.epsilon = epsilon
self.action_n = env.action_space.n
self.q = np.zeros((env.observation_space.n, env.action_space.n))
def decide(self, state):
'''
epsilon-greedy策略,另外Q表所有值相等表示智能体还没有学到任何经验,这时也鼓励探索。
'''
if np.random.uniform() > self.epsilon and self.q[state].argmax() != self.q[state].argmin():
action = self.q[state].argmax()
else:
action = 0 if np.random.randint(self.action_n) < 0.5 else 1
return action
def learn(self, state, action, reward, next_state, done):
'''
Q(s,a) += learning_rate * (R + gamma * Qmax - Q(s,a)
'''
u = reward + self.gamma * self.q[next_state].max()
td_error = u - self.q[state, action]
self.q[state, action] += self.learning_rate * td_error
def play_qlearning(env, agent_101, episodes,render=False):
'''
Qlearning智能体一次游戏
参数:
env: 游戏环境
agent_101:101个智能体列表
episodes: 最大轮数
render:是否图形显示
返回值:
episode_reward
'''
episode_rewards = []
episode_actions = []
# 初始化S
observation_101 = env.reset()
for _ in range(episodes):
# 各智能体根据环境选择动作
action_101 = [agent.decide(observation) for agent, observation in zip(agent_101, observation_101)]
# 执行动作后得到环境奖励和新状态
next_observation_101, reward_101, done, _ = env.step(action_101)
# 为所有智能体更新Q表
for agent, observation, action, reward, next_observation in zip(agent_101, observation_101, action_101, reward_101, next_observation_101):
agent.learn(observation, action, reward, next_observation,done)
# 更新状态
observation = next_observation
# 上面是Q-learning完整的一步,下面是数据统计
# 统计动作
episode_actions.append(action_101)
# 统计奖励
episode_rewards.append(reward_101)
return episode_rewards, episode_actions
# +
def moving_average(lst, N):
'''
计算移动平均
参数:
lst: 输入列表
N: 窗口大小
返回值:
res: 移动平均列表
'''
res = []
for i in range(len(lst)):
l = max(i-N+1, 0)
r = i+1
res.append(sum(lst[l:r])/(r-l))
return res
def density(lst):
'''
将玩家决策原始数据转换成密度数据
参数:
lst: 玩家决策原始数据
返回值:
res: 玩家决策密度数据
例:
输入: [1,1,2,3]
输出: [0,2,1,1] + [0]*98
'''
from collections import Counter
res = [0] * 102
tbl = Counter(lst)
for i in tbl:
res[i] = tbl[i]/len(lst)
return res
# -
# ### 实验过程
# 1. 基础测试:gamma = 0.1, learning_rate=0.1, epislon=0,1, 博弈3000次,观察玩家收益和动作
# 创建环境
env = MinorityGame_1(50)
# 创建玩家
agent_101 = [QLearningAgent(env,gamma=0.1,learning_rate=0.1,epsilon=0.1) for _ in range(101)]
rewards_0, actions_0 = play_qlearning(env,agent_101,3000)
# 玩家总收益(仅绘制前500轮)
plt.clf()
plt.plot(moving_average([sum(reward) for reward in rewards_0],1))
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
# 选择1的人数(仅绘制前500轮)
plt.clf()
plt.plot([sum(action) for action in actions_0])
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
# 玩家总收益10轮移动平均(仅绘制前500轮)
plt.clf()
plt.plot(moving_average([sum(reward) for reward in rewards_0],10))
plt.plot([50]*3000)
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
# 2. 调整gamma,观测对结果的影响
# 创建环境
env = MinorityGame_1(50)
# 创建玩家
agent_101 = [QLearningAgent(env,gamma=0.05,learning_rate=0.1,epsilon=0.1) for _ in range(101)]
# 博弈
rewards_1a, actions_1a = play_qlearning(env,agent_101,3000)
print("玩家总收益")
# 玩家总收益(仅绘制前500轮)
plt.clf()
plt.plot(moving_average([sum(reward) for reward in rewards_1a],1))
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
print("选择1的人数")
# 选择1的人数(仅绘制前500轮)
plt.clf()
plt.plot([sum(action) for action in actions_1a])
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
print("玩家总收益10轮移动平均")
# 玩家总收益10轮移动平均(仅绘制前500轮)
plt.clf()
plt.plot(moving_average([sum(reward) for reward in rewards_1a],10))
plt.plot([50]*3000)
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
# 创建环境
env = MinorityGame_1(50)
# 创建玩家
agent_101 = [QLearningAgent(env,gamma=0.3,learning_rate=0.1,epsilon=0.1) for _ in range(101)]
# 博弈
rewards_1b, actions_1b = play_qlearning(env,agent_101,3000)
print("玩家总收益")
# 玩家总收益(仅绘制前500轮)
plt.clf()
plt.plot(moving_average([sum(reward) for reward in rewards_1b],1))
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
print("选择1的人数")
# 选择1的人数(仅绘制前500轮)
plt.clf()
plt.plot([sum(action) for action in actions_1b])
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
print("玩家总收益10轮移动平均")
# 玩家总收益10轮移动平均(仅绘制前500轮)
plt.clf()
plt.plot(moving_average([sum(reward) for reward in rewards_1b],10))
plt.plot([50]*3000)
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
# 创建环境
env = MinorityGame_1(50)
# 创建玩家
agent_101 = [QLearningAgent(env,gamma=0.6,learning_rate=0.1,epsilon=0.1) for _ in range(101)]
# 博弈
rewards_1c, actions_1c = play_qlearning(env,agent_101,3000)
print("玩家总收益")
# 玩家总收益(仅绘制前500轮)
plt.clf()
plt.plot(moving_average([sum(reward) for reward in rewards_1c],1))
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
print("选择1的人数")
# 选择1的人数(仅绘制前500轮)
plt.clf()
plt.plot([sum(action) for action in actions_1c])
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
print("玩家总收益10轮移动平均")
# 玩家总收益10轮移动平均(仅绘制前500轮)
plt.clf()
plt.plot(moving_average([sum(reward) for reward in rewards_1c],10))
plt.plot([50]*3000)
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
# 创建环境
env = MinorityGame_1(50)
# 创建玩家
agent_101 = [QLearningAgent(env,gamma=0.9,learning_rate=0.1,epsilon=0.1) for _ in range(101)]
# 博弈
rewards_1d, actions_1d = play_qlearning(env,agent_101,3000)
print("玩家总收益")
# 玩家总收益(仅绘制前500轮)
plt.clf()
plt.plot(moving_average([sum(reward) for reward in rewards_1d],1))
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
print("选择1的人数")
# 选择1的人数(仅绘制前500轮)
plt.clf()
plt.plot([sum(action) for action in actions_1d])
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
print("玩家总收益10轮移动平均")
# 玩家总收益10轮移动平均(仅绘制前500轮)
plt.clf()
plt.plot(moving_average([sum(reward) for reward in rewards_1d],10))
plt.plot([50]*3000)
plt.ylim(0,101)
plt.xlim(0,500)
plt.pause(0.1)
# 玩家总收益10轮移动平均,不同gamma对比
print("不同gamma对平均收益的影响")
plt.clf()
plt.xlabel("Round")
plt.ylabel("Reward")
plt.plot(moving_average([sum(reward) for reward in rewards_1d],10),label ='0.9')
plt.plot(moving_average([sum(reward) for reward in rewards_1c],10),label ='0.6')
plt.plot(moving_average([sum(reward) for reward in rewards_1b],10),label ='0.3')
# plt.plot(moving_average([sum(reward) for reward in rewards_0],10),label ='0.1')
plt.plot(moving_average([sum(reward) for reward in rewards_1a],10),label ='0.05')
plt.plot([50]*3000)
plt.ylim(35,65)
plt.xlim(0,500)
plt.legend()
plt.show()
# +
# 玩家决策,不同gamma对比
print("不同gamma对玩家决策的影响")
plt.clf()
plt.plot(moving_average([sum(reward) for reward in actions_1d],1),label ='0.9')
plt.plot(moving_average([sum(reward) for reward in actions_1c],1),label ='0.6')
plt.plot(moving_average([sum(reward) for reward in actions_1b],1),label ='0.3')
plt.plot(moving_average([sum(reward) for reward in actions_0],1),label ='0.1')
plt.plot(moving_average([sum(reward) for reward in actions_1a],1),label ='0.05')
plt.plot([50]*3000)
plt.ylim(0,101)
plt.xlim(0,3000)
plt.legend()
plt.show()
# +
# 玩家决策,不同gamma对比
print("不同gamma对玩家决策的影响")
plt.clf()
plt.plot(moving_average([sum(reward) for reward in actions_1d],1),label ='0.9', alpha = .7)
plt.plot(moving_average([sum(reward) for reward in actions_1c],1),label ='0.6', alpha = .7)
plt.plot(moving_average([sum(reward) for reward in actions_1b],1),label ='0.3', alpha = .7)
plt.plot(moving_average([sum(reward) for reward in actions_0],1),label ='0.1', alpha = .7)
plt.plot(moving_average([sum(reward) for reward in actions_1a],1),label ='0.05', alpha = .7)
plt.plot([50]*3000)
plt.ylim(0,101)
plt.xlim(0,3000)
plt.legend()
plt.show()
# +
# 玩家决策,不同gamma对比
print("不同gamma对玩家决策的影响")
plt.clf()
plt.plot(moving_average([sum(reward) for reward in actions_1d[0:1000]],1),label ='0.9')
plt.plot(moving_average([sum(reward) for reward in actions_1c[0:1000]],1),label ='0.6')
plt.plot(moving_average([sum(reward) for reward in actions_1b[0:1000]],1),label ='0.3')
# plt.plot(moving_average([sum(reward) for reward in actions_0[900:1000]],1),label ='0.1')
plt.plot(moving_average([sum(reward) for reward in actions_1a[0:1000]],1),label ='0.05')
plt.plot([50]*3000)
plt.ylim(0,101)
plt.xlim(0,500)
plt.legend()
plt.show()
# -
print("平均收益对比")
print(" 0.05",sum(sum(r) for r in rewards_1a[400:500])/len(rewards_1a[400:500]))
print(" 0.1",sum(sum(r) for r in rewards_0[400:500])/len(rewards_0[400:500]))
print(" 0.3",sum(sum(r) for r in rewards_1b[400:500])/len(rewards_1b[400:500]))
print(" 0.6",sum(sum(r) for r in rewards_1c[400:500])/len(rewards_1c[400:500]))
print(" 0.9",sum(sum(r) for r in rewards_1d[400:500])/len(rewards_1d[400:500]))
len(rewards_0)
# 玩家决策,不同gamma对比
print("不同gamma对玩家决策的影响")
plt.clf()
plt.plot(density([sum(reward) for reward in actions_1d]),label ='0.9')
plt.plot(density([sum(reward) for reward in actions_1c]),label ='0.6')
plt.plot(density([sum(reward) for reward in actions_1b]),label ='0.3')
plt.plot(density([sum(reward) for reward in actions_0]),label ='0.1')
plt.plot(density([sum(reward) for reward in actions_1a]),label ='0.05')
plt.xlim(0,102)
plt.ylim(0,0.5)
# plt.axvline(51)
plt.legend()
plt.show()
def variance(lst, N):
'''
序列转为方差序列
参数:
lst: 输入序列
N: 计算方差所需元素数
返回值:
res: 方差序列
'''
import numpy as np
res = []
for i in range(len(lst)):
l = max(i-N+1, 0)
r = i+1
res.append(np.var(lst[l:r]) if l else 0)
return res
# 玩家决策,不同gamma对比
print("不同gamma对玩家决策的影响")
plt.clf()
plt.xlabel("Round")
plt.ylabel("Variance")
plt.plot(variance([sum(reward) for reward in actions_1d],10),label ='0.9')
plt.plot(variance([sum(reward) for reward in actions_1c],10),label ='0.6')
plt.plot(variance([sum(reward) for reward in actions_1b],10),label ='0.3')
# plt.plot(variance([sum(reward) for reward in actions_0],10),label ='0.1')
plt.plot(variance([sum(reward) for reward in actions_1a],10),label ='0.05')
plt.xlim(0,500)
# plt.axvline(51)
plt.legend()
plt.show()
# 玩家决策,不同gamma对比
print("不同gamma对玩家决策的影响")
plt.clf()
plt.plot(moving_average(variance([sum(reward) for reward in actions_1d],10),10),label ='0.9')
plt.plot(moving_average(variance([sum(reward) for reward in actions_1c],10),10),label ='0.6')
plt.plot(moving_average(variance([sum(reward) for reward in actions_1b],10),10),label ='0.3')
# plt.plot(variance([sum(reward) for reward in actions_0],10),label ='0.1')
plt.plot(moving_average(variance([sum(reward) for reward in actions_1a],10),10),label ='0.05')
plt.xlim(0,3000)
# plt.axvline(51)
plt.legend()
plt.show()
print("平均收益对比")
print(" 0.9",sum(sum(r) for r in rewards_1d[100:500])/len(rewards_1d[100:500]))
print(" 0.6",sum(sum(r) for r in rewards_1c[100:500])/len(rewards_1c[100:500]))
print(" 0.3",sum(sum(r) for r in rewards_1b[100:500])/len(rewards_1b[100:500]))
print(" 0.1",sum(sum(r) for r in rewards_0[100:500])/len(rewards_0[100:500]))
print(" 0.05",sum(sum(r) for r in rewards_1a[100:500])/len(rewards_1a[100:500]))
# print(" 0.6",sum(sum(r) for r in rewards_1c[400:500])/len(rewards_1c[400:500]))
# print(" 0.9",sum(sum(r) for r in rewards_1d[400:500])/len(rewards_1d[400:500]))
# print("random",sum(sum(r) for r in rewards_sp[100:500])/len(rewards_sp[100:500]))
print("决策方差对比")
print(" 0.9",np.var([sum(r) for r in actions_1d[100:500]]))
print(" 0.6",np.var([sum(r) for r in actions_1c[100:500]]))
print(" 0.3",np.var([sum(r) for r in actions_1b[100:500]]))
print(" 0.1",np.var([sum(r) for r in actions_0[100:500]]))
print(" 0.05",np.var([sum(r) for r in actions_1a[100:500]]))
np.var([sum(r) for r in rewards_1d[100:500]])
plt.xlabel("γ")
plt.ylabel("Reward")
plt.xlim(0,1)
plt.ylim(40,60)
xData = [0.05, 0.1, 0.3, 0.6, 0.9]
yData = [48.30 , 48.31 , 48.33 , 48.56 , 48.35]
print(np.corrcoef(xData, yData))
plt.scatter(xData, yData, s=40, c="#ff1212", marker='o')
parameter = np.polyfit(xData, yData, 1) # n=1为一次函数,返回函数参数
f = np.poly1d(parameter) # 拼接方程
plt.plot([0,1], f([0,1]),"b--")
plt.xlabel("γ")
plt.ylabel("Variance")
plt.xlim(0,1)
plt.ylim(0,20)
xData = [0.05, 0.1, 0.3, 0.6, 0.9]
yData = [8.25 , 8.70 , 7.23 , 5.85 , 6.27]
print(np.corrcoef(xData, yData))
plt.scatter(xData, yData, s=40, c="#12ff12", marker='o')
parameter = np.polyfit(xData, yData, 1) # n=1为一次函数,返回函数参数
f = np.poly1d(parameter) # 拼接方程
plt.plot([0,1], f([0,1]),"y--")
plt.xlabel("α")
plt.ylabel("Reward")
plt.xlim(0,1)
plt.ylim(40,60)
xData = [0.05, 0.1, 0.3, 0.6, 0.9]
yData = [48.80 , 48.39 , 46.43 , 44.43 , 44.98 ]
print(np.corrcoef(xData, yData))
plt.scatter(xData, yData, s=40, c="#ff1212", marker='o')
parameter = np.polyfit(xData, yData, 1) # n=1为一次函数,返回函数参数
f = np.poly1d(parameter) # 拼接方程
plt.plot([0,1], f([0,1]),"b--")
plt.xlabel("α")
plt.ylabel("Variance")
plt.xlim(0,1)
plt.ylim(0,60)
xData = [0.05, 0.1, 0.3, 0.6, 0.9]
yData = [4.53 , 7.19 , 27.92 , 49.33 , 40.68]
print(np.corrcoef(xData, yData))
plt.scatter(xData, yData, s=40, c="#12ff12", marker='o')
parameter = np.polyfit(xData, yData, 1) # n=1为一次函数,返回函数参数
f = np.poly1d(parameter) # 拼接方程
plt.plot([0,1], f([0,1]),"y--")
plt.xlabel("ε")
plt.ylabel("Reward")
plt.xlim(0,0.12)
plt.ylim(40,60)
xData = [0.01 , 0.02 , 0.05 , 0.1]
yData = [49.75 , 49.57 , 49.06 , 48.34 ]
print(np.corrcoef(xData, yData))
plt.scatter(xData, yData, s=40, c="#ff1212", marker='o')
parameter = np.polyfit(xData, yData, 1) # n=1为一次函数,返回函数参数
f = np.poly1d(parameter) # 拼接方程
plt.plot([0,1], f([0,1]),"b--")
plt.xlabel("ε")
plt.ylabel("Variance")
plt.xlim(0,0.12)
plt.ylim(0,10)
xData = [0.01, 0.02, 0.05, 0.1]
yData = [0.80 , 1.39 , 3.20 , 7.09 ]
print(np.corrcoef(xData, yData))
plt.scatter(xData, yData, s=40, c="#12ff12", marker='o')
parameter = np.polyfit(xData, yData, 1) # n=1为一次函数,返回函数参数
f = np.poly1d(parameter) # 拼接方程
plt.plot([0,1], f([0,1]),"y--")
xData=[3,2,1]
yData=[1,2,3]
print(np.corrcoef(xData, yData))
# +
class MinorityGame_1(gym.Env):
'''
Minority Game, we have some agent, every agent can choose 1 or 0 every day.
In midnight, all of the day to make a few choices of the agent to get +1 reward.
'''
def __init__(self, env_max=2000):
'''
环境初始化:
玩家数固定101;
env_max 环境承载量,选择1能获取收益的最大人数,默认为50;
action_space 动作空间,大小为2,玩家只能选择0或1;
observation_space 观测空间,这个环境使用2,玩家立足于上一次博弈的状态;
'''
self.env_max = env_max
self.action_space = spaces.Discrete(2)
self.observation_space = spaces.Discrete(2)
self.seed()
def seed(self, seed=None):
'''
设置seed
'''
self.np_random, seed = seeding.np_random(seed)
return [seed]
def step(self, action_4001):
'''
每一步博弈:
1. 检查输入是否合法
2. 统计选择1的人数allpick,allpick不超过env_max则1获胜,否则0获胜
3. 返回S(玩家本回合动作), R(所有玩家的奖励列表), done(False,无尽博弈)
'''
assert len(action_4001) == 4001
assert all(map(lambda x:self.action_space.contains(x), action_4001))
allpick = sum(action_4001)
reward_4001 = []
for action in action_4001:
if action == 1 and allpick <= self.env_max or action == 0 and allpick > self.env_max:
reward_4001.append(1)
else:
reward_4001.append(0)
done = True
return action_4001, reward_4001, done, {}
def reset(self):
'''
重置环境,每轮第一次博弈给所有玩家一个随机状态
'''
# return [0]*101
return [random.randint(0,1) for _ in range(4001)]
# -
def play_qlearning(env, agent_4001, episodes,render=False):
episode_rewards = []
episode_actions = []
# 初始化S
observation_101 = env.reset()
for _ in range(episodes):
# 各智能体根据环境选择动作
# print(len(agent_4001))
action_101 = [agent.decide(observation) for agent, observation in zip(agent_4001, observation_101)]
# 执行动作后得到环境奖励和新状态
next_observation_101, reward_101, done, _ = env.step(action_101)
# 为所有智能体更新Q表
for agent, observation, action, reward, next_observation in zip(agent_4001, observation_101, action_101, reward_101, next_observation_101):
agent.learn(observation, action, reward, next_observation,done)
# 更新状态
observation = next_observation
# 上面是Q-learning完整的一步,下面是数据统计
# 统计动作
episode_actions.append(action_101)
# 统计奖励
episode_rewards.append(reward_101)
return episode_rewards, episode_actions
env = MinorityGame_1()
# 创建玩家
agent_4001 = [QLearningAgent2(env,gamma=0.9,learning_rate=0.9,epsilon=0.02) for _ in range(4001)]
rewards_0, actions_0 = play_qlearning(env,agent_4001,1000)
plt.plot([sum(i) for i in actions_0])
env = MinorityGame_1()
# 创建玩家
agent_4001 = [QLearningAgent2(env,gamma=0.9,learning_rate=0.9,epsilon=0.01) for _ in range(101)]
rewards_0, actions_0 = play_qlearning(env,agent_4001,1000)
plt.plot([sum(i) for i in rewards_0])
# Qlearning智能体
class QLearningAgent2:
'''
Q-learning智能体实现
'''
def __init__(self, env, gamma=0.9, learning_rate=0.1, epsilon=0.1):
'''
Q-learning智能体初始化:
env 智能体的博弈环境;
gamma 折扣因子,n步后的奖励为 pow(gamma, n)*Rn, gamma越大表示越重视长期收益。
learning_rata 学习率,Qlearning 更新过程为:Q(s,a) += learning_rate * (R + gamma * Qmax - Q(s,a)),
学习率越大表示越不依赖过去学习的结果
'''
self.gamma = gamma
self.learning_rate = learning_rate
self.epsilon = epsilon
self.action_n = env.action_space.n
self.q = np.zeros((env.observation_space.n, env.action_space.n))
def decide(self, state):
'''
epsilon-greedy策略,另外Q表所有值相等表示智能体还没有学到任何经验,这时也鼓励探索。
'''
if np.random.uniform() > self.epsilon :
action = self.q[state].argmax()
else:
action = 0 if np.random.randint(self.action_n) < 0.5 else 1
return action
def learn(self, state, action, reward, next_state, done):
'''
Q(s,a) += learning_rate * (R + gamma * Qmax - Q(s,a)
'''
u = reward + self.gamma * self.q[next_state].max()
td_error = u - self.q[state, action]
self.q[state, action] += self.learning_rate * td_error
| 21,019 |
/numpy/.ipynb_checkpoints/Udemy - Numpy Arrays -checkpoint.ipynb | a0a2e39e5811224c467cf85b6ae2936af7df2690 | [] | no_license | shivakrishnak/python | https://github.com/shivakrishnak/python | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 10,515 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
my_list = [1,2,3]
arr = np.array(my_list)
arr
my_mat = [[1,2,3],[4,5,6],[7,8,9]]
np.array(my_mat)
np.arange(0,10)
np.arange(0,11,2)
np.zeros(3)
np.zeros((2,3))
np.ones(5)
np.ones((3,4))
np.linspace(0,5,10)
np.linspace(0,8,10)
np.eye(4) #Identitiy Matrix
np.random.rand(5)
np.random.rand(5,5)
np.random.randn(2)
np.random.randint(1,100,10)
ranarr = np.random.randint(0,50,10)
ranarr
ranarr.reshape(2,5)
arr_new = np.arange(25)
arr_new.reshape(5,5)
ranarr.max()
ranarr.min()
ranarr.argmax()
ranarr.argmin()
ranarr.shape
ranarr = ranarr.reshape(2,5)
ranarr.shape
ranarr.dtype
ranarr
| 896 |
/06-PyViz/1/Activities/07-Ins_Viz_Options/Solved/viz_options.ipynb | dc57f02b7d8cbc69044250f467acc61224a3020e | [] | no_license | CPix18/MyFinTechRepo | https://github.com/CPix18/MyFinTechRepo | 0 | 1 | null | null | null | null | Jupyter Notebook | false | false | .py | 2,977,171 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from pathlib import Path
import pandas as pd
import hvplot.pandas
# ### Prep Data
# +
# Read in data, filter, and slice
home_sale_prices = pd.read_csv(
Path("../Resources/housing_sale_data.csv"), index_col="salesHistoryKey"
)
home_sale_prices = home_sale_prices.loc[
(home_sale_prices["saleDate"] > "2019-06-01")
& (home_sale_prices["saleDate"] < "2019-06-31")
]
# Slice data
sale_prices_by_year = (
home_sale_prices[["saleAmt", "saleDate"]]
.groupby("saleDate")
.mean()
.sort_values("saleDate")
)
# -
# ### Plot data
# Plot data without rotation
sale_prices_by_year.hvplot.bar(x='saleDate', y='saleAmt')
# ### Rotate x axis labels
# Plot data with rotation
sale_prices_by_year.hvplot.bar(x='saleDate', y='saleAmt', rot=40)
# ### Format axis labels
# Use string formatting to show no decimal places for saleAmt
# Use string formatting to show no decimal places for saleAmt
sale_prices_by_year.hvplot.bar(x="saleDate", y="saleAmt", rot=45).opts(
yformatter="%.0f"
)
# ### Set title
# Set title
sale_prices_by_year.hvplot.bar(x="saleDate", y="saleAmt", rot=90).opts(
yformatter="%.0f", title="Arlington, VA Housing Sale Prices June 2016"
)
# ### Invert axes
# Invert axes
sale_prices_by_year.hvplot.bar(x="saleDate", y="saleAmt").opts(
xformatter="%.0f",
title="Arlington, VA Housing Sale Prices June 2016",
invert_axes=True,
)
| 1,667 |
/timeseries/.ipynb_checkpoints/Data_science_exercise-checkpoint.ipynb | a6339c6be4cc3e26c425c53974cbfadf5b6f5bf5 | [] | no_license | varshinireddyt/Python-for-DataScience | https://github.com/varshinireddyt/Python-for-DataScience | 0 | 1 | null | null | null | null | Jupyter Notebook | false | false | .py | 229,624 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="blXAIWH0h5QX" colab_type="text"
# # Assignment on Feature Engineering (L6)
#
# This assignment has been adapted from the course **Feature Engineering for Machine Learning in Python** On DataCamp.
#
# We will explore what feature engineering is and how to get started with applying it to real-world data. We will be working with a modified subset of the [Stackoverflow survey response data](https://insights.stackoverflow.com/survey/2018/#overview). This data set records the details, and preferences of thousands of users of the StackOverflow website.
# + [markdown] id="V8OJHHSFhkVo" colab_type="text"
# ## Creating Features
# ---
# + id="xxrLsTxvi4Ef" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 73} outputId="91c8aa61-494d-4d23-e175-91edf1d056a3"
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# + [markdown] id="lw55w5YsB6jE" colab_type="text"
# ---
# ### Inspect your data
# ---
#
# + id="fCpuZS41h35f" colab_type="code" colab={}
# Load the data which has been stored as a CSV on the URL given below:
so_survey_csv = 'https://assets.datacamp.com/production/repositories/3752/datasets/19699a2441073ad6459bf5e3e17690e2cae86cf1/Combined_DS_v10.csv'
# Import so_survey_csv into so_survey_df
so_survey_df = pd.read_csv(so_survey_csv)
# + [markdown] id="yO7TR7EGBgDP" colab_type="text"
# Instructions: For the `so_survey_df` DataFrame,
# * Print its shape and its first five rows.
# * Print the data type of each column.
# + [markdown] id="1MzXp3T8Cl8W" colab_type="text"
# ---
# ### Selecting specific data types
# ---
# Often a data set will contain columns with several different data types (like the one we are working with). The majority of machine learning models require us to have a consistent data type across features. Similarly, most feature engineering techniques are applicable to only one type of data at a time.
# + [markdown] id="glnEQlrVCobL" colab_type="text"
# Instructions:
#
# * Create a subset of `so_survey_df` consisting of only the numeric (int and float) columns and save it as `so_numeric_df`.
# * Print the column names contained in `so_numeric_df`.
# + [markdown] id="O_4kpncQDXuj" colab_type="text"
# ---
# ### One-hot encoding and dummy variables
# ---
# To use categorical variables in a machine learning model, we first need to represent them in a quantitative way. The two most common approaches are to one-hot encode the variables using or to use dummy variables.
# + [markdown] id="oRQM6bVaDhnT" colab_type="text"
# Instructions:
#
# * One-hot encode the `Country` column of `so_survey_df` DataFrame, adding "OH" as a prefix for each column.
# * Create dummy variables for the `Country` column, adding "DM" as a prefix for each column.
# + [markdown] id="UZ56-6j9oz4H" colab_type="text"
# ---
# ### Dealing with uncommon categories
# ---
# Some features can have many different categories but a very uneven distribution of their occurrences. Take for example Data Science's favorite languages to code in, some common choices are Python, R, and Julia, but there can be individuals with bespoke choices, like FORTRAN, C etc. In these cases, we may not want to create a feature for each value, but only the more common occurrences.
# + [markdown] id="1z1TCKQ7EHcb" colab_type="text"
# Instructions:
#
# * Extract the `Country` column of `so_survey_df` as a series and assign it to `countries`.
# * Find the counts of each category in the newly created `countries` series.
# + [markdown] id="lKxW1Z70EW5W" colab_type="text"
# Instructions:
#
# * Create a mask for values occurring less than 10 times in `country_counts`.
# * Print the first 5 rows of the mask.
# + [markdown] id="6Zro-imOEiwt" colab_type="text"
# Instructions:
#
# * Label values occurring less than the `mask` cutoff as 'Other'.
# * Print the new category counts in `countries`.
# + [markdown] id="w0j7IlzLpke5" colab_type="text"
# ---
# ### Binarizing columns
# ---
# While numeric values can often be used without any feature engineering, there will be cases when some form of manipulation can be useful. For example on some occasions, we might not care about the magnitude of a value but only care about its direction, or if it exists at all. In these situations, we will want to binarize a column. In the `so_survey_df` data, we have a large number of survey respondents that are working voluntarily (without pay). We will create a new column titled `Paid_Job` indicating whether each person is paid (their salary is greater than zero).
# + [markdown] id="HdCPaTzFExzS" colab_type="text"
# Instructions:
#
# * Create a new column called `Paid_Job` filled with zeros.
# * Replace all the `Paid_Job` values with a 1 where the corresponding `ConvertedSalary` is greater than 0.
# + [markdown] id="7lJTmpvzq_NJ" colab_type="text"
# ---
# ### Binning values
# ---
# For many continuous values we will care less about the exact value of a numeric column, but instead care about the bucket it falls into. This can be useful when plotting values, or simplifying your machine learning models. It is mostly used on continuous variables where accuracy is not the biggest concern e.g. age, height, wages.
#
# Bins are created using `pd.cut(df['column_name'], bins)` where bins can be an integer specifying the number of evenly spaced bins, or a list of bin boundaries.
# + [markdown] id="GglGS3NkFtU3" colab_type="text"
# Instructions:
#
# * Bin the value of the `ConvertedSalary` column in `so_survey_df` into 5 equal bins, in a new column called `equal_binned`.
# * Print the first five rows of both columns: `ConvertedSalary` and `equal_binned`.
# + [markdown] id="-o_1_UiiF1dc" colab_type="text"
# Instructions:
#
# * Bin the `ConvertedSalary` column using the boundaries in the list bins and label the bins using `labels` in a new column called `boundary_binned`.
# * Print the first 5 rows of the `boundary_binned` column.
# + id="UZyNvV6krVLJ" colab_type="code" colab={}
# Specify the boundaries of the bins
bins = [-np.inf, 10000, 50000, 100000, 150000, np.inf]
# Bin labels
labels = ['Very low', 'Low', 'Medium', 'High', 'Very high']
# + [markdown] id="cIkFDAVUGhcQ" colab_type="text"
# ## Dealing with Messy Data
# ---
# + [markdown] id="m8o-Z4YEsYF9" colab_type="text"
# ---
# ### How sparse is my data?
# ---
# Most data sets contain missing values, often represented as NaN (Not a Number). If we are working with Pandas, we can easily check how many missing values exist in each column.
#
# Let's find out how many of the developers taking the survey chose to enter their age (found in the `Age` column of `so_survey_df`) and their gender (`Gender` column of `so_survey_df`).
# + [markdown] id="1n0JDxzMHMwD" colab_type="text"
# Instructions:
#
# * Subset the `so_survey_df` DataFrame to only include the `Age` and `Gender` columns.
# * Print the number of non-missing values in both columns.
# + [markdown] id="STDb03R3swA4" colab_type="text"
# ---
# ### Finding the missing values
# ---
# While having a summary of how much of your data is missing can be useful, often we will need to find the exact locations of these missing values. Using the same subset of the StackOverflow data from the last exercise (`sub_df`), we will show how a value can be flagged as missing.
# + [markdown] id="E5XbMPSrHhY4" colab_type="text"
# Instructions:
#
# * Print the first 10 entries of the `sub_df` DataFrame.
# * Print the locations of the missing values in the first 10 rows of this DataFrame.
# * Print the locations of the non-missing values in the first 10 rows.
# + [markdown] id="CgR_uodEtS2o" colab_type="text"
# ---
# ### Listwise deletion
# ---
# The simplest way to deal with missing values in our dataset when they are occurring entirely at random is to remove those rows, also called 'listwise deletion'.
#
# Depending on the use case, we will sometimes want to remove all missing values in our data while other times we may want to only remove a particular column if too many values are missing in that column.
# + [markdown] id="kIioVg70H8fY" colab_type="text"
# Instructions:
#
# * Print the number of rows and columns in `so_survey_df`.
# * Drop all rows with missing values in `so_survey_df`.
# * Drop all columns with missing values in `so_survey_df`.
# * Drop all rows in `so_survey_df` where `Gender` is missing.
# + [markdown] id="9C1H8JwhtxHU" colab_type="text"
# ---
# ### Replacing missing values with constants
# ---
# While removing missing data entirely maybe a correct approach in many situations, this may result in a lot of information being omitted from your models.
#
# We may find categorical columns where the missing value is a valid piece of information in itself, such as someone refusing to answer a question in a survey. In these cases, we can fill all missing values with a new category entirely, for example 'No response given'.
# + [markdown] id="cPq_Ae40IUnY" colab_type="text"
# Instructions:
#
# * Print the count of occurrences of each category in `so_survey_df`'s `Gender` column.
# * Replace all missing values in the `Gender` column with the string 'Not Given'. Make changes to the original DataFrame.
# * Print the count of occurrences of updated category in `so_survey_df`'s `Gender` column.
# + [markdown] id="Rn2h-F8IuI0C" colab_type="text"
# ---
# ### Filling continuous missing values
# ---
# Earlier, we dealt with different methods of removing data missing values and filling in missing values with a fixed string. These approaches are valid in many cases, particularly when dealing with categorical columns but have limited use when working with continuous values. In these cases, it may be most valid to fill the missing values in the column with a value calculated from the entries present in the column.
# + [markdown] id="_S9YZ2GsIyLx" colab_type="text"
# Instructions:
#
# * Print the first five rows of the `StackOverflowJobsRecommend` column of `so_survey_df`.
# * Replace the missing values in the `StackOverflowJobsRecommend` column with its mean. Make changes directly to the original DataFrame.
# * Round the decimal values that we introduced in the `StackOverflowJobsRecommend` column.
# + [markdown] id="SKcC12f0vCuh" colab_type="text"
# ---
# ### Dealing with stray characters (I)
# ---
# In this exercise, we will work with the `RawSalary` column of so_survey_df which contains the wages of the respondents along with the currency symbols and commas, such as $42,000. When importing data from Microsoft Excel, more often that not we will come across data in this form.
# + [markdown] id="tz0CGSQkJI03" colab_type="text"
# Instructions:
#
# * Remove the commas (,) from the `RawSalary` column.
# * Remove the dollar ($) signs from the `RawSalary` column.
# * Print the first five rows of updated `RawSalary` column.
# + [markdown] id="UpayqY5IwMBl" colab_type="text"
# ---
# ### Dealing with stray characters (II)
# ---
# In the last exercise, we could tell quickly based off of the `df.head()` call which characters were causing an issue. In many cases this will not be so apparent. There will often be values deep within a column that are preventing us from casting a column as a numeric type so that it can be used in a model or further feature engineering.
#
# One approach to finding these values is to force the column to the data type desired using `pd.to_numeric()`, coercing any values causing issues to `NaN`, Then filtering the DataFrame by just the rows containing the `NaN` values.
#
# Try to cast the `RawSalary` column as a float and it will fail as an additional character can now be found in it. Find the character and remove it so the column can be cast as a float.
# + [markdown] id="Z7Duf4v7JpPv" colab_type="text"
# Instructions:
#
# * Attempt to convert the `RawSalary` column of `so_survey_df` to numeric values coercing all failures into null values.
# * Find the indexes of the rows containing `NaN`s.
# * Print the rows in `RawSalary` based on these indexes.
# + id="AYuh53vbv5_d" colab_type="code" outputId="7f02eefc-b7da-485b-c391-dcab68a352c2" colab={"base_uri": "https://localhost:8080/", "height": 233}
# Attempt to convert the column to numeric values
numeric_vals = pd.to_numeric(so_survey_df['RawSalary'], errors='coerce')
# + [markdown] id="vyllnJ5NKEwy" colab_type="text"
# Instructions:
#
# * Did you notice the pound (£) signs in the `RawSalary` column? Remove these signs like we did in the previous exercise.
# + [markdown] id="feXhsa94wtBz" colab_type="text"
# ---
# ### Method chaining
# ---
# When applying multiple operations on the same column (like in the previous exercises), you made the changes in several steps, assigning the results back in each step. However, when applying multiple successive operations on the same column, you can "chain" these operations together for clarity and ease of management. This can be achieved by calling multiple methods sequentially:
# ```
# # Method chaining
# df['column'] = df['column'].method1().method2().method3()
#
# # Same as
# df['column'] = df['column'].method1()
# df['column'] = df['column'].method2()
# df['column'] = df['column'].method3()
# ```
# + [markdown] id="yo-JUG77KTRi" colab_type="text"
# Instructions:
#
# * Remove the commas (`,`) from the `RawSalary` column of `so_survey_df`.
# * Remove the dollar (`$`) signs from the `RawSalary` column.
# * Remove the pound (`£`) signs from the `RawSalary` column.
# * Convert the `RawSalary` column to float.
# + [markdown] id="CqpCNv72Kl_1" colab_type="text"
# ## Conforming to Statistical Assumptions
# ---
# + [markdown] id="hYwlN2FyyBml" colab_type="text"
# ---
# ### What does your data look like?
# ---
# Up until now we have focused on creating new features and dealing with issues in our data. Feature engineering can also be used to make the most out of the data that we already have and use it more effectively when creating machine learning models.
# Many algorithms may assume that our data is normally distributed, or at least that all our columns are on the same scale. This will often not be the case, e.g. one feature may be measured in thousands of dollars while another would be number of years. In this exercise, we will create plots to examine the distributions of some numeric columns in the `so_survey_df` DataFrame.
# + id="LHMvrvwxyTQu" colab_type="code" colab={}
so_numeric_df = so_survey_df[['ConvertedSalary', 'Age', 'Years Experience']]
# + [markdown] id="i8Ch5slQy6B-" colab_type="text"
# Instructions:
#
# * Generate a histogram of all columns in the `so_numeric_df` DataFrame.
# * Generate box plots of the `Age` and `Years Experience` columns in the `so_numeric_df` DataFrame.
# * Generate a box plot of the `ConvertedSalary` column in the `so_numeric_df`.
# * Plot pairwise relationships (using `sns.pairplot`) in the `so_numeric_df`.
# + [markdown] id="op7uFM-70CW5" colab_type="text"
# ---
# ### Normalization
# ---
# In normalization we linearly scale the entire column between 0 and 1, with 0 corresponding with the lowest value in the column, and 1 with the largest. When using scikit-learn (the most commonly used machine learning library in Python) we can use a `MinMaxScaler` to apply normalization. (It is called this as it scales our values between a minimum and maximum value.)
# + [markdown] id="ME9djjbu0K83" colab_type="text"
# Instructions:
#
# * Fit the `MinMaxScaler` on the `Age` column of `so_numeric_df`.
# * Transform the same column with the scaler you just fit.
# + id="jNgwBJRp0Zgl" colab_type="code" colab={}
# Import MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
# + id="iYeEJLVQ0HCU" colab_type="code" colab={}
# Instantiate MinMaxScaler
MM_scaler = MinMaxScaler()
# + [markdown] id="lBKJrNv60m2p" colab_type="text"
# ---
# ### Standardization
# ---
# While normalization can be useful for scaling a column between two data points, it is hard to compare two scaled columns if even one of them is overly affected by outliers. One commonly used solution to this is called standardization, where instead of having a strict upper and lower bound, you center the data around its mean, and calculate the number of standard deviations away from mean each data point is.
# + [markdown] id="gFyXLW3v0rU9" colab_type="text"
# Instructions:
#
# * Fit the `StandardScaler` on the `Age` column of `so_numeric_df`.
# * Transform the same column with the scaler we just fit.
# + id="TL8N_V9n03jy" colab_type="code" colab={}
# Import StandardScaler
from sklearn.preprocessing import StandardScaler
# + id="lOoRs_vR0qmJ" colab_type="code" colab={}
# Instantiate StandardScaler
SS_scaler = StandardScaler()
# + [markdown] id="QLntVWcp1aZ1" colab_type="text"
# ---
# ### Log transformation
# ---
# In the previous exercises we scaled the data linearly, which will not affect the data's shape. This works great if our data is normally distributed (or closely normally distributed), an assumption that a lot of machine learning models make. Sometimes we will work with data that closely conforms to normality, e.g the height or weight of a population. On the other hand, many variables in the real world do not follow this pattern e.g, wages or age of a population.
#
# Now, we will use a log transform on the `ConvertedSalary` column in the `so_numeric_df` DataFrame as it has a large amount of its data centered around the lower values, but contains very high values also. These distributions are said to have a long right tail.
# + [markdown] id="NMQB-F4e1lMK" colab_type="text"
# Instructions:
#
# * Fit the `PowerTransformer` on the `ConvertedSalary` column of `so_numeric_df`.
# * Transform the same column with the scaler we just fit.
# + id="N95T8tjM1h5A" colab_type="code" colab={}
# Import PowerTransformer
from sklearn.preprocessing import PowerTransformer
# + id="9CNzVVOg1ueY" colab_type="code" colab={}
# Instantiate PowerTransformer
pow_trans = PowerTransformer()
# + [markdown] id="VhlDOrtb18uG" colab_type="text"
# ---
# ### Percentage based outlier removal
# ---
# One way to ensure a small portion of data is not having an overly adverse effect is by removing a certain percentage of the largest and/or smallest values in the column. This can be achieved by finding the relevant quantile and trimming the data using it with a mask. This approach is particularly useful if we are concerned that the highest values in our dataset should be avoided. When using this approach, we must remember that even if there are no outliers, this will still remove the same top N percentage from the dataset.
# + [markdown] id="AhiOqx-v2CFB" colab_type="text"
# Instructions:
#
# * Find the 95th quantile of the `ConvertedSalary` column in `so_numeric_df` DataFrame.
# * Trim the `so_numeric_df` DataFrame to retain all rows where `ConvertedSalary` is less than it's 95th quantile and store this as `trimmed_df`.
# * Plot the histogram of `so_numeric_df[['ConvertedSalary']]`.
# * Plot the histogram of `trimmed_df[['ConvertedSalary']]`
# + id="G1_-eGVu1_JA" colab_type="code" colab={}
# Find the 95th quantile
quantile = so_numeric_df['ConvertedSalary'].quantile(0.95)
# + [markdown] id="Lgva617FNqZy" colab_type="text"
# ## Dealing with Text Data
# ---
# + [markdown] id="IuHUqVR03PJV" colab_type="text"
# ---
# ### Cleaning up your text
# ---
# Unstructured text data cannot be directly used in most analyses. Multiple steps need to be taken to go from a long free form string to a set of numeric columns in the right format that can be ingested by a machine learning model. The first step of this process is to standardize the data and eliminate any characters that could cause problems later on in your analytic pipeline.
#
# Here, we will be working with a new dataset containing the inaugural speeches of the presidents of the United States loaded as `speech_df`, with the speeches stored in the `text` column.
# + id="dFmYNs7W3hYj" colab_type="code" outputId="e5915ecf-c1d6-4d24-8953-35d4afc04e8a" colab={"base_uri": "https://localhost:8080/", "height": 204}
speech_df = pd.read_csv('https://raw.githubusercontent.com/shala2020/shala2020.github.io/master/Lecture_Materials/Assignments/MachineLearning/L6/inaugural_speeches.csv')
speech_df.head()
# + [markdown] id="qvbCog623SDx" colab_type="text"
# Instructions:
#
# * Print the first 5 rows of the `text` column in `speech_df` DataFrame to see the free text fields.
# * Replace all non letter characters in the `text` column with a whitespace and add it as a new column `text_clean` in the `speech_df` DataFrame.
# * Make all characters in the newly created `text_clean` column lower case.
# * Print the first 5 rows of the `text_clean` column.
# + [markdown] id="Ag6i4ijT4tcM" colab_type="text"
# ---
# ### High level text features
# ---
# Once the text has been cleaned and standardized we can begin creating features from the data. The most fundamental information we can calculate about free form text is its size, such as its length and number of words.
# + [markdown] id="q4jPqRmA4zRA" colab_type="text"
# Instructions:
#
# * Record the character length of each speech (`speech_df['text_clean']`) and store it in a new `char_count` column.
# * Record the word count of each speech in the `word_count` column.
# * Record the average word length of each speech in the `avg_word_length` column.
# * Print the first 5 rows of the columns: `text_clean`, `char_cnt`, `word_cnt`, `avg_word_length`
#
# + [markdown] id="Wi2hOh045bsm" colab_type="text"
# ---
# ### Counting words (I)
# ---
# Once high level information has been recorded we can begin creating features based on the actual content of each text, as given below:
#
# * For each unique word in the dataset a column is created.
# * For each entry, the number of times this word occurs is counted and the count value is entered into the respective column.
#
# These "count" columns can then be used to train machine learning models.
# + [markdown] id="b6sMPuHi5nB7" colab_type="text"
# Instructions:
#
# * Import `CountVectorizer` from `sklearn.feature_extraction.text`.
# * Instantiate `CountVectorizer` and assign it to 'cv'.
# * Fit the vectorizer to the `text_clean` column.
# * Print the feature names generated by the vectorizer and find the number of features.
#
# + id="nomeBUIc5lA2" colab_type="code" colab={}
# Import CountVectorizer
from sklearn.feature_extraction.text import CountVectorizer
# Instantiate CountVectorizer
cv = CountVectorizer()
# + [markdown] id="bAm6_JHr6Cto" colab_type="text"
# ---
# ### Counting words (II)
# ---
# Once the vectorizer has been fit to the data, it can be used to transform the text to an array representing the word counts.
# + [markdown] id="JcFMh9k_6Hu4" colab_type="text"
# Instructions:
#
# * Apply the vectorizer ('cv' in the previous exercise) to the `text_clean` column.
# * Convert this transformed (sparse) array into a `numpy` array with counts and print it.
# + [markdown] id="vUQAwgOV73BB" colab_type="text"
# ---
# ### Limiting your features
# ---
# As we have seen, using the `CountVectorizer` with its default settings creates a feature for every single word in our corpus. This can create far too many features, often including ones that will provide very little analytical value.
#
# For this purpose `CountVectorizer` has parameters that you can set to reduce the number of features:
#
# * `min_df` : Use only words that occur in more than this percentage of documents. This can be used to remove outlier words that will not generalize across texts.
# * `max_df` : Use only words that occur in less than this percentage of documents. This is useful to eliminate very common words that occur in every corpus without adding value such as "and" or "the".
# + [markdown] id="I9X2x50g8Dfd" colab_type="text"
# Instructions:
#
# * Limit the number of features in the `CountVectorizer` by setting the minimum number of documents a word can appear to 20% and the maximum to 80%.
# * Fit and apply the vectorizer on `text_clean` column in one step.
# * Convert this transformed (sparse) array into a `numpy` array with counts and print the dimensions of the new reduced array.
# * Did you notice that the number of features (unique words) greatly reduced from 9043 to 818?
#
# + id="RqNCtZu-8NbI" colab_type="code" colab={}
# Import CountVectorizer
from sklearn.feature_extraction.text import CountVectorizer
# Specify arguements to limit the number of features generated
cv = CountVectorizer(min_df=0.2, max_df=0.8)
# + [markdown] id="KKZ4xX3L9IxL" colab_type="text"
# ---
# ### Text to DataFrame
# ---
# Now that we have generated these count based features in an array we will need to reformat them so that they can be combined with the rest of the dataset. This can be achieved by converting the array into a pandas DataFrame, with the feature names you found earlier as the column names, and then concatenate it with the original DataFrame.
#
# + [markdown] id="rvioGe8x9Olj" colab_type="text"
# Instructions:
#
# * Create a DataFrame `cv_df` containing the `cv_array` as the values and the feature names as the column names.
# * Add the prefix `Counts_` to the column names for ease of identification.
# * Concatenate this DataFrame (`cv_df`) to the original DataFrame (`speech_df`) column wise.
#
# + [markdown] id="Rpo0ek00-dsr" colab_type="text"
# ---
# ### Tf-idf
# ---
# While counts of occurrences of words can be useful to build models, words that occur many times may skew the results undesirably. To limit these common words from overpowering your model a form of normalization can be used. In this lesson we will be using **Term frequency-inverse document frequency** (**Tf-idf**). Tf-idf has the effect of reducing the value of common words, while increasing the weight of words that do not occur in many documents.
# + [markdown] id="c29xSq9Q-mcH" colab_type="text"
# Instructions:
#
# * Import `TfidfVectorizer` from `sklearn.feature_extraction.text`.
# * Instantiate `TfidfVectorizer` while limiting the number of features to 100 and removing English stop words.
# * Fit and apply the vectorizer on `text_clean` column in one step.
# * Create a DataFrame `tv_df` containing the weights of the words and the feature names as the column names.
# * Add the prefix `TFIDF_` to the column names for ease of identification.
# + id="-F0vdfx9-yIq" colab_type="code" colab={}
# Import TfidfVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
# Instantiate TfidfVectorizer
tv = TfidfVectorizer(max_features=100, stop_words='english')
# + [markdown] id="qzcGgNmS_Yc5" colab_type="text"
# ---
# ### Inspecting Tf-idf values
# ---
# After creating Tf-idf features we will often want to understand what are the most highest scored words for each corpus. This can be achieved by isolating the row we want to examine and then sorting the the scores from high to low.
# + [markdown] id="MP0QjLZJ_cvX" colab_type="text"
# * Assign the first row of `tv_df` to `sample_row`.
# * `sample_row` is now a series of weights assigned to words. Sort these values to print the top 5 highest-rated words.
# + id="g800sJg2_j2x" colab_type="code" colab={}
# Isolate the row to be examined
sample_row = tv_df.iloc[0]
# + [markdown] id="A7WK0CHgH_3J" colab_type="text"
# ---
# ### Sentiment analysis
# ---
# You have been given the tweets about US airlines. Making use of this data, your task is to predict whether a tweet contains
#
# * positive,
# * negative, or
# * neutral sentiment
#
# about the airline.
# + id="mupsP8kXIFld" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 445} outputId="6e45ae9b-bbca-47c0-c351-ae719400989b"
data_source_url = "https://raw.githubusercontent.com/shala2020/shala2020.github.io/master/Lecture_Materials/Assignments/MachineLearning/L6/Tweets.csv"
airline_tweets = pd.read_csv(data_source_url)
airline_tweets.head()
# + [markdown] id="AYlKJmRzIHlu" colab_type="text"
# Instructions:
#
# * Apply suitable data pre-processing steps to get rid of undesired symbols.
# * Using `TfidfVectorizer` class, convert text features into TF-IDF feature vectors.
# * `airline_sentiment` is the label and `text` is the feature. Apply suitable `train_test_split`, implement suitable machine learning classifier, and show the accuracy.
#
| 28,493 |
/notebooks/03_ResultAnalysis.ipynb | 0781613aa8d275e5444cd957df2e2f8de43c790e | [] | no_license | PetarZecevic97/automatic-stock-trading-system | https://github.com/PetarZecevic97/automatic-stock-trading-system | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 417,531 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
df_results = pd.read_csv('../results/results.csv')
df_results.head()
df_results.drop(['Unnamed: 0'], axis=1, inplace=True)
# +
# Plot total capital based on metaparam values
def plot(df, feature):
plt.scatter(x = df[feature], y = df['TotalCap'])
plt.xlabel(feature)
plt.ylabel("total capital")
plt.show()
plot(df_results, 'AdjustmentPeriod')
plot(df_results, 'ShortSig')
plot(df_results, 'LongSig')
# -
# Best metaparams based on sharpe ratio
df_results.sort_values(by='SR').iloc[-25:]
# Best metaparams based on total capital
df_results.sort_values(by='TotalCap').iloc[-25:]
colors_30 = ["#E5F5F9", "#1D91C0", "#67001F", "#F7FCFD", "#CB181D", "#78C679", "#F46D43", "#A6CEE3", "#FD8D3C", "#A6D854", "#D4B9DA", "#6A51A3", "#7F0000", "#D9D9D9", "#FFF7BC", "#000000", "#F0F0F0", "#C7EAE5", "#003C30", "#F16913", "#FFF7FB", "#8C6BB1", "#C7E9B4", "#762A83", "#FC9272", "#AE017E", "#F7F7F7", "#DF65B0", "#EF3B2C", "#74C476"]
# +
# Correlation between short signal and long signal
groups = df_results.groupby('ShortSig')
i = 0
fig = plt.figure(figsize=(10, 10), dpi=150)
plt.xticks(df_results['LongSig'].unique())
for name, group in groups:
plt.plot(group['LongSig'], group['TotalCap'], marker='x', linestyle='', c = colors_30[i], markersize=12, label=name)
i += 1
plt.legend()
plt.show()
# +
# Correlation between adjusment persio and long signal
groups = df_results.groupby('AdjustmentPeriod')
i = 0
fig = plt.figure(figsize=(10, 10), dpi=150)
plt.xticks(df_results['LongSig'].unique())
for name, group in groups:
plt.plot(group['LongSig'], group['TotalCap'], marker='x', linestyle='', c = colors_30[i], markersize=12, label=name)
i += 1
plt.legend()
plt.show()
# -
| 2,077 |
/lab2/notebooks/02-look-at-emnist-lines.ipynb | a31045543eab91d2010ca0ac01bbd53796ec99d1 | [
"MIT"
] | permissive | emsansone/fsdl-text-recognizer-project | https://github.com/emsansone/fsdl-text-recognizer-project | 0 | 0 | null | 2018-08-03T18:13:47 | 2018-08-03T18:07:20 | null | Jupyter Notebook | false | false | .py | 175,632 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from collections import defaultdict
import itertools
import string
import re
import matplotlib.pyplot as plt
import nltk
import numpy as np
import sys
sys.path.append('..')
from text_recognizer.datasets.emnist_lines import EmnistLinesDataset, construct_image_from_string, get_samples_by_char
from text_recognizer.datasets.sentences import SentenceGenerator
# %load_ext autoreload
# %autoreload 2
# %matplotlib inline
# -
# ## Dataset
dataset = EmnistLinesDataset()
dataset.load_or_generate_data()
print(dataset)
# Training is 28 images repeated 34 times
# Testing is 28 images repeated 34 times
print('Mapping:', dataset.mapping)
# +
def convert_y_label_to_string(y, dataset=dataset):
return ''.join([dataset.mapping[i] for i in np.argmax(y, axis=-1)])
convert_y_label_to_string(dataset.y_train[0])
# +
num_samples_to_plot = 9
for i in range(num_samples_to_plot):
plt.figure(figsize=(20, 20))
sentence = convert_y_label_to_string(dataset.y_train[i])
print(sentence)
plt.title(sentence)
plt.imshow(dataset.x_train[i], cmap='gray')
# -
| 1,343 |
/exercise2/1_FullyConnectedNets.ipynb | 4dd7daa1996746bf65da20cdfbec0ca953790d34 | [] | no_license | raincrash/i2dl | https://github.com/raincrash/i2dl | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 370,077 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# %matplotlib inline
#
# Autograd: automatic differentiation
# ===================================
#
# Central to all neural networks in PyTorch is the ``autograd`` package.
# Let’s first briefly visit this, and we will then go to training our
# first neural network.
#
#
# The ``autograd`` package provides automatic differentiation for all operations
# on Tensors. It is a define-by-run framework, which means that your backprop is
# defined by how your code is run, and that every single iteration can be
# different.
#
# Let us see this in more simple terms with some examples.
#
# Variable
# --------
#
# ``autograd.Variable`` is the central class of the package. It wraps a
# Tensor, and supports nearly all of operations defined on it. Once you
# finish your computation you can call ``.backward()`` and have all the
# gradients computed automatically.
#
# You can access the raw tensor through the ``.data`` attribute, while the
# gradient w.r.t. this variable is accumulated into ``.grad``.
#
# .. figure:: /_static/img/Variable.png
# :alt: Variable
#
# Variable
#
# There’s one more class which is very important for autograd
# implementation - a ``Function``.
#
# ``Variable`` and ``Function`` are interconnected and build up an acyclic
# graph, that encodes a complete history of computation. Each variable has
# a ``.creator`` attribute that references a ``Function`` that has created
# the ``Variable`` (except for Variables created by the user - their
# ``creator is None``).
#
# If you want to compute the derivatives, you can call ``.backward()`` on
# a ``Variable``. If ``Variable`` is a scalar (i.e. it holds a one element
# data), you don’t need to specify any arguments to ``backward()``,
# however if it has more elements, you need to specify a ``grad_output``
# argument that is a tensor of matching shape.
#
#
import torch
from torch.autograd import Variable
# Create a variable:
#
#
x = Variable(torch.ones(2, 2), requires_grad=True)
print(x)
print(x.data)
print(x.grad)
print(x.creator)
# Do an operation of variable:
#
#
# +
y = x + 2
print(y.creator)
#y = x*x
#print(y.creator)
# -
# ``y`` was created as a result of an operation, so it has a creator.
#
#
print(y.creator)
# Do more operations on y
#
#
# +
z = y * y * 3
out = z.mean()
print(z, out, z.creator, out.creator)
# -
# Gradients
# ---------
# let's backprop now
# ``out.backward()`` is equivalent to doing ``out.backward(torch.Tensor([1.0]))``
#
#
out.backward(torch.Tensor([1.0]))
# print gradients d(out)/dx
#
#
#
print(x.grad)
# You should have got a matrix of ``4.5``. Let’s call the ``out``
# *Variable* “$o$”.
# We have that $o = \frac{1}{4}\sum_i z_i$,
# $z_i = 3(x_i+2)^2$ and $z_i\bigr\rvert_{x_i=1} = 27$.
# Therefore,
# $\frac{\partial o}{\partial x_i} = \frac{3}{2}(x_i+2)$, hence
# $\frac{\partial o}{\partial x_i}\bigr\rvert_{x_i=1} = \frac{9}{2} = 4.5$.
#
#
# You can do many crazy things with autograd!
#
#
# +
x = torch.randn(3)
x = Variable(x, requires_grad=True)
y = x * 2
while y.data.norm() < 1000:
y = y * 2
print(y)
# +
gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)
print(x.grad)
# -
# **Read Later:**
#
# Documentation of ``Variable`` and ``Function`` is at
# http://pytorch.org/docs/autograd
#
#
torch.cuda.is_available()
ffine_forward` function.
#
# Once you are done you can test your implementaion by running the following:
# +
# Test the affine_forward function
num_inputs = 2
input_shape = (4, 5, 6)
output_dim = 3
input_size = num_inputs * np.prod(input_shape)
weight_size = output_dim * np.prod(input_shape)
x = np.linspace(-0.1, 0.5, num=input_size).reshape(num_inputs, *input_shape)
w = np.linspace(-0.2, 0.3, num=weight_size).reshape(np.prod(input_shape), output_dim)
b = np.linspace(-0.3, 0.1, num=output_dim)
out, _ = affine_forward(x, w, b)
correct_out = np.array([[ 1.49834967, 1.70660132, 1.91485297],
[ 3.25553199, 3.5141327, 3.77273342]])
# Compare your output with ours. The error should be around 1e-9.
print('Testing affine_forward function:')
print('difference: ', rel_error(out, correct_out))
# -
# # Affine layer: backward
# Now implement the `affine_backward` function and test your implementation using numeric gradient checking.
# +
# Test the affine_backward function
x = np.random.randn(10, 2, 3)
w = np.random.randn(6, 5)
b = np.random.randn(5)
dout = np.random.randn(10, 5)
dx_num = eval_numerical_gradient_array(lambda x: affine_forward(x, w, b)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: affine_forward(x, w, b)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: affine_forward(x, w, b)[0], b, dout)
_, cache = affine_forward(x, w, b)
dx, dw, db = affine_backward(dout, cache)
# The error should be around 1e-10
print('Testing affine_backward function:')
print('dx error: ', rel_error(dx_num, dx))
print('dw error: ', rel_error(dw_num, dw))
print('db error: ', rel_error(db_num, db))
# -
# # ReLU layer: forward
# Implement the forward pass for the ReLU activation function in the `relu_forward` function and test your implementation using the following:
# +
# Test the relu_forward function
x = np.linspace(-0.5, 0.5, num=12).reshape(3, 4)
out, _ = relu_forward(x)
correct_out = np.array([[ 0., 0., 0., 0., ],
[ 0., 0., 0.04545455, 0.13636364,],
[ 0.22727273, 0.31818182, 0.40909091, 0.5, ]])
# Compare your output with ours. The error should be around 1e-8
print('Testing relu_forward function:')
print('difference: ', rel_error(out, correct_out))
# -
# # ReLU layer: backward
# Now implement the backward pass for the ReLU activation function in the `relu_backward` function and test your implementation using numeric gradient checking:
# +
x = np.random.randn(10, 10)
dout = np.random.randn(*x.shape)
dx_num = eval_numerical_gradient_array(lambda x: relu_forward(x)[0], x, dout)
_, cache = relu_forward(x)
dx = relu_backward(dout, cache)
# The error should be around 1e-12
print('Testing relu_backward function:')
print('dx error: ', rel_error(dx_num, dx))
# -
# # "Sandwich" layers
# There are some common patterns of layers that are frequently used in neural nets. For example, affine layers are frequently followed by a ReLU nonlinearity. To make these common patterns easy, we define several convenience layers in the file `exercise_code/layer_utils.py`.
#
# For now take a look at the `affine_relu_forward` and `affine_relu_backward` functions, and run the following to numerically gradient check the backward pass:
# +
from exercise_code.layer_utils import affine_relu_forward, affine_relu_backward
x = np.random.randn(2, 3, 4)
w = np.random.randn(12, 10)
b = np.random.randn(10)
dout = np.random.randn(2, 10)
out, cache = affine_relu_forward(x, w, b)
dx, dw, db = affine_relu_backward(dout, cache)
dx_num = eval_numerical_gradient_array(lambda x: affine_relu_forward(x, w, b)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: affine_relu_forward(x, w, b)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: affine_relu_forward(x, w, b)[0], b, dout)
print('Testing affine_relu_forward:')
print('dx error: ', rel_error(dx_num, dx))
print('dw error: ', rel_error(dw_num, dw))
print('db error: ', rel_error(db_num, db))
# -
# # Loss layers: Softmax
# You implemented this loss function in the last assignment, so we'll give them to you for free here. You should still make sure you understand how they work by looking at the implementations in `exercise_code/layers.py`.
#
# You can make sure that the implementations are correct by running the following:
# +
num_classes, num_inputs = 10, 50
x = 0.001 * np.random.randn(num_inputs, num_classes)
y = np.random.randint(num_classes, size=num_inputs)
dx_num = eval_numerical_gradient(lambda x: softmax_loss(x, y)[0], x, verbose=False)
loss, dx = softmax_loss(x, y)
# Test softmax_loss function. Loss should be 2.3 and dx error should be 1e-8
print('\nTesting softmax_loss:')
print('loss: ', loss)
print('dx error: ', rel_error(dx_num, dx))
# -
# # Two-layer network
# In the previous assignment you implemented a two-layer neural network in a single monolithic class. Now that you have implemented modular versions of the necessary layers, you will reimplement the two layer network using these modular implementations.
#
# Open the file `exercise_code/classifiers/fc_net.py` and complete the implementation of the `TwoLayerNet` class. This class will serve as a model for the other networks you will implement in this assignment, so read through it to make sure you understand the API. You can run the cell below to test your implementation.
# +
N, D, H, C = 3, 5, 50, 7
X = np.random.randn(N, D)
y = np.random.randint(C, size=N)
std = 1e-2
model = TwoLayerNet(input_dim=D, hidden_dim=H, num_classes=C, weight_scale=std)
print('Testing initialization ... ')
W1_std = abs(model.params['W1'].std() - std)
b1 = model.params['b1']
W2_std = abs(model.params['W2'].std() - std)
b2 = model.params['b2']
assert W1_std < std / 10, 'First layer weights do not seem right'
assert np.all(b1 == 0), 'First layer biases do not seem right'
assert W2_std < std / 10, 'Second layer weights do not seem right'
assert np.all(b2 == 0), 'Second layer biases do not seem right'
print('Testing test-time forward pass ... ')
model.params['W1'] = np.linspace(-0.7, 0.3, num=D*H).reshape(D, H)
model.params['b1'] = np.linspace(-0.1, 0.9, num=H)
model.params['W2'] = np.linspace(-0.3, 0.4, num=H*C).reshape(H, C)
model.params['b2'] = np.linspace(-0.9, 0.1, num=C)
X = np.linspace(-5.5, 4.5, num=N*D).reshape(D, N).T
scores = model.loss(X)
correct_scores = np.asarray(
[[11.53165108, 12.2917344, 13.05181771, 13.81190102, 14.57198434, 15.33206765, 16.09215096],
[12.05769098, 12.74614105, 13.43459113, 14.1230412, 14.81149128, 15.49994135, 16.18839143],
[12.58373087, 13.20054771, 13.81736455, 14.43418138, 15.05099822, 15.66781506, 16.2846319 ]])
scores_diff = np.abs(scores - correct_scores).sum()
assert scores_diff < 1e-6, 'Problem with test-time forward pass'
print('Testing training loss')
y = np.asarray([0, 5, 1])
loss, grads = model.loss(X, y)
correct_loss = 3.4702243556
assert abs(loss - correct_loss) < 1e-10, 'Problem with training-time loss'
model.reg = 1.0
loss, grads = model.loss(X, y)
correct_loss = 26.5948426952
assert abs(loss - correct_loss) < 1e-10, 'Problem with regularization loss'
for reg in [0.0, 0.7]:
print('Running numeric gradient check with reg = ', reg)
model.reg = reg
loss, grads = model.loss(X, y)
assert grads != {}, 'Problem with gradients (empty dict)'
for name in sorted(grads):
f = lambda _: model.loss(X, y)[0]
grad_num = eval_numerical_gradient(f, model.params[name], verbose=False)
print('%s relative error: %.2e' % (name, rel_error(grad_num, grads[name])))
# -
# # Solver
# In the previous assignment, the logic for training models was coupled to the models themselves. Following a more modular design, for this assignment we have split the logic for training models into a separate class.
#
# Open the file `exercise_code/solver.py` and read through it to familiarize yourself with the API. After doing so, use a `Solver` instance to train a `TwoLayerNet` that achieves at least `50%` accuracy on the validation set.
# +
model = TwoLayerNet(hidden_dim=150, reg=1e-3, weight_scale=1e-3)
solver = None
##############################################################################
# TODO: Use a Solver instance to train a TwoLayerNet that achieves at least #
# 50% accuracy on the validation set. #
##############################################################################
solver = Solver(model,
data=data,
num_epochs=10,
lr_decay=0.95,
batch_size=300,
print_every=100,
optim_config={
'learning_rate': 0.00123456,
})
solver.train()
##############################################################################
# END OF YOUR CODE #
##############################################################################
# +
# Run this cell to visualize training loss and train / val accuracy
plt.subplot(2, 1, 1)
plt.title('Training loss')
plt.plot(solver.loss_history, 'o')
plt.xlabel('Iteration')
plt.subplot(2, 1, 2)
plt.title('Accuracy')
plt.plot(solver.train_acc_history, '-o', label='train')
plt.plot(solver.val_acc_history, '-o', label='val')
plt.plot([0.5] * len(solver.val_acc_history), 'k--')
plt.xlabel('Epoch')
plt.legend(loc='lower right')
plt.gcf().set_size_inches(15, 12)
plt.show()
# -
# # Multilayer network
# Next you will implement a fully-connected network with an arbitrary number of hidden layers.
#
# Read through the `FullyConnectedNet` class in the file `exercise_code/classifiers/fc_net.py`.
#
# Implement the initialization, the forward pass, and the backward pass. For the moment don't worry about implementing batch normalization.
# ## Initial loss and gradient check
# As a sanity check, run the following to check the initial loss and to gradient check the network both with and without regularization. Do the initial losses seem reasonable?
#
# For gradient checking, you should expect to see errors around 1e-6 or less.
# +
N, D, H1, H2, C = 2, 15, 20, 30, 10
X = np.random.randn(N, D)
y = np.random.randint(C, size=(N,))
for reg in [0, 3.14]:
print('Running check with reg = ', reg)
model = FullyConnectedNet([H1, H2], input_dim=D, num_classes=C,
reg=reg, weight_scale=5e-2, dtype=np.float64)
loss, grads = model.loss(X, y)
print('Initial loss: ', loss)
for name in sorted(grads):
f = lambda _: model.loss(X, y)[0]
grad_num = eval_numerical_gradient(f, model.params[name], verbose=False, h=1e-5)
print('%s relative error: %.2e' % (name, rel_error(grad_num, grads[name])))
# -
# As another sanity check, make sure you can overfit a small dataset of 50 images. First we will try a three-layer network with 100 units in each hidden layer. You will need to tweak the learning rate and initialization scale, but you should be able to overfit and achieve 100% **training** accuracy within 20 epochs.
# +
# TODO: Use a three-layer Net to overfit 50 training examples.
num_train = 50
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
#############################################################################
# TODO: Maybe tweak values #
#############################################################################
weight_scale = 1e-3
learning_rate = 1e-2
model = FullyConnectedNet([100, 100],
weight_scale=weight_scale, dtype=np.float64)
solver = Solver(model, small_data,
print_every=10, num_epochs=20, batch_size=25,
update_rule='sgd',
optim_config={
'learning_rate': learning_rate,
}
)
solver.train()
##############################################################################
# END OF YOUR CODE #
##############################################################################
plt.plot(solver.loss_history, 'o')
plt.title('Training loss history')
plt.xlabel('Iteration')
plt.ylabel('Training loss')
plt.show()
# -
# Now try to use a five-layer network with 100 units on each layer to overfit 50 training examples. Again you will have to adjust the learning rate and weight initialization, but you should be able to achieve 100% training accuracy within 20 epochs.
# +
# TODO: Use a five-layer Net to overfit 50 training examples.
num_train = 50
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
#############################################################################
# TODO: Maybe tweak values #
#############################################################################
learning_rate = 2e-3
weight_scale = 1e-5
model = FullyConnectedNet([100, 100, 100, 100],
weight_scale=weight_scale, dtype=np.float64)
solver = Solver(model, small_data,
print_every=10, num_epochs=20, batch_size=25,
update_rule='sgd',
optim_config={
'learning_rate': learning_rate,
}
)
solver.train()
##############################################################################
# END OF YOUR CODE #
##############################################################################
plt.plot(solver.loss_history, 'o')
plt.title('Training loss history')
plt.xlabel('Iteration')
plt.ylabel('Training loss')
plt.show()
# -
# <div class="alert alert-info">
# <h3>Inline Question</h3>
# <p>Did you notice anything about the comparative difficulty of training the three-layer net vs training the five layer net?</p>
# </div>
#
# # Update rules
# So far we have used vanilla stochastic gradient descent (SGD) as our update rule. More sophisticated update rules can make it easier to train deep networks. We will implement a few of the most commonly used update rules and compare them to vanilla SGD.
# # SGD+Momentum
# Stochastic gradient descent with momentum is a widely used update rule that tends to make deep networks converge faster than vanilla stochstic gradient descent.
#
# Open the file `exercise_code/optim.py` and read the documentation at the top of the file to make sure you understand the API. Implement the SGD+momentum update rule in the function `sgd_momentum` and run the following to check your implementation. You should see errors less than 1e-8.
# +
from exercise_code.optim import sgd_momentum
N, D = 4, 5
w = np.linspace(-0.4, 0.6, num=N*D).reshape(N, D)
dw = np.linspace(-0.6, 0.4, num=N*D).reshape(N, D)
v = np.linspace(0.6, 0.9, num=N*D).reshape(N, D)
config = {'learning_rate': 1e-3, 'velocity': v}
next_w, _ = sgd_momentum(w, dw, config=config)
expected_next_w = np.asarray([
[ 0.1406, 0.20738947, 0.27417895, 0.34096842, 0.40775789],
[ 0.47454737, 0.54133684, 0.60812632, 0.67491579, 0.74170526],
[ 0.80849474, 0.87528421, 0.94207368, 1.00886316, 1.07565263],
[ 1.14244211, 1.20923158, 1.27602105, 1.34281053, 1.4096 ]])
expected_velocity = np.asarray([
[ 0.5406, 0.55475789, 0.56891579, 0.58307368, 0.59723158],
[ 0.61138947, 0.62554737, 0.63970526, 0.65386316, 0.66802105],
[ 0.68217895, 0.69633684, 0.71049474, 0.72465263, 0.73881053],
[ 0.75296842, 0.76712632, 0.78128421, 0.79544211, 0.8096 ]])
print('next_w error: ', rel_error(next_w, expected_next_w))
print('velocity error: ', rel_error(expected_velocity, config['velocity']))
# -
# Once you have done so, run the following to train a six-layer network with both SGD and SGD+momentum. You should see the SGD+momentum update rule converge faster.
# +
num_train = 4000
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
solvers = {}
for update_rule in ['sgd', 'sgd_momentum']:
print('running with ', update_rule)
model = FullyConnectedNet([100, 100, 100, 100, 100], weight_scale=3e-2)
solver = Solver(model, small_data,
num_epochs=10, batch_size=100,
update_rule=update_rule,
optim_config={'learning_rate': 1e-2},
verbose=True)
solvers[update_rule] = solver
solver.train()
print()
plt.subplot(3, 1, 1)
plt.title('Training loss')
plt.xlabel('Iteration')
plt.subplot(3, 1, 2)
plt.title('Training accuracy')
plt.xlabel('Epoch')
plt.subplot(3, 1, 3)
plt.title('Validation accuracy')
plt.xlabel('Epoch')
for update_rule, solver in solvers.items():
plt.subplot(3, 1, 1)
plt.plot(solver.loss_history, 'o', label=update_rule)
plt.subplot(3, 1, 2)
plt.plot(solver.train_acc_history, '-o', label=update_rule)
plt.subplot(3, 1, 3)
plt.plot(solver.val_acc_history, '-o', label=update_rule)
for i in [1, 2, 3]:
plt.subplot(3, 1, i)
plt.legend(loc='upper center', ncol=4)
plt.gcf().set_size_inches(15, 15)
plt.show()
# -
# # Adam
# Adam [1] is an update rule that sets per-parameter learning rates by using a running average of the second moments of gradients.
#
# In the file `exercise_code/optim.py`, we have implemented the update rule `adam` for you. Check this implementation and make sure you understand what the optimizer is doing. Then train the fully connected net below to see how Adam affects the learning process.
#
# [1] Diederik Kingma and Jimmy Ba, "Adam: A Method for Stochastic Optimization", ICLR 2015.
# +
learning_rates = {'adam': 1e-3}
update_rule = 'adam'
print('running with ', update_rule)
model = FullyConnectedNet([100, 100, 100, 100, 100], weight_scale=5e-2)
solver = Solver(model, small_data,
num_epochs=5, batch_size=100,
update_rule=update_rule,
optim_config={
'learning_rate': learning_rates[update_rule]
},
verbose=True)
solvers[update_rule] = solver
solver.train()
print()
plt.subplot(3, 1, 1)
plt.title('Training loss')
plt.xlabel('Iteration')
plt.subplot(3, 1, 2)
plt.title('Training accuracy')
plt.xlabel('Epoch')
plt.subplot(3, 1, 3)
plt.title('Validation accuracy')
plt.xlabel('Epoch')
for update_rule, solver in solvers.items():
plt.subplot(3, 1, 1)
plt.plot(solver.loss_history, 'o', label=update_rule)
plt.subplot(3, 1, 2)
plt.plot(solver.train_acc_history, '-o', label=update_rule)
plt.subplot(3, 1, 3)
plt.plot(solver.val_acc_history, '-o', label=update_rule)
for i in [1, 2, 3]:
plt.subplot(3, 1, i)
plt.legend(loc='upper center', ncol=4)
plt.gcf().set_size_inches(15, 15)
plt.show()
# -
# # Train a good model!
# Train the best fully-connected model that you can on CIFAR-10, storing your best model in the `best_model` variable. We require you to get at least __50%__ accuracy on the validation set using a fully-connected net.
#
# You might find it useful to complete the `2_BatchNormalization.ipynb` and the `3_Dropout.ipynb` notebooks before completing this part, since these techniques can help you train powerful models.
# +
best_model = None
################################################################################
# TODO: Train the best FullyConnectedNet that you can on CIFAR-10. You might #
# batch normalization and dropout useful. Store your best model in the #
# best_model variable. #
# Note that dropout is not required to pass beyond the linear scoring regime #
################################################################################
best_model = None
best_solver = None
best_val_acc = -1
weight_scales = [0.04, 0.05]
learning_rates = [0.001, 0.007]
for weight_scale in weight_scales:
for learning_rate in learning_rates:
model = FullyConnectedNet([100, 75, 50, 25],
weight_scale=weight_scale,
dtype=np.float64, use_batchnorm=True)
solver = Solver(model, data,
print_every=100,
num_epochs=10,
batch_size=200,
update_rule='adam',
verbose=True,
optim_config={
'learning_rate': learning_rate,
}
)
solver.train()
if solver.val_acc_history[-1] > best_val_acc:
best_model = model
best_solver = solver
################################################################################
# END OF YOUR CODE #
################################################################################
# -
# # Test your model
# Run your best model on the validation and test sets. You should achieve score of above __50%__ accuracy on the validation set.
# +
X_test = data['X_test']
X_val = data['X_val']
y_val = data['y_val']
y_test = data['y_test']
y_test_pred = np.argmax(best_model.loss(X_test), axis=1)
y_val_pred = np.argmax(best_model.loss(X_val), axis=1)
print('Validation set accuracy: ', (y_val_pred == y_val).mean())
print('Test set accuracy: ', (y_test_pred == y_test).mean())
# -
# ## Save the model
#
# When you are satisfied with your training, save the model for submission.
from exercise_code.model_savers import save_fully_connected_net
save_fully_connected_net(best_model)
| 25,404 |
/cratering.ipynb | 95a7416332516d1cd085728e1d65eb6fe48928bb | [] | no_license | UChicagoPhysicsLabs/Physics131 | https://github.com/UChicagoPhysicsLabs/Physics131 | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 337,590 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.linear_model import LogisticRegression
# +
# Read in the data
data = pd.read_csv('Full_Data.csv', encoding = "ISO-8859-1")
data.head(1)
# -
train = data[data['Date'] < '20150101']
test = data[data['Date'] > '20141231']
# +
# Removing punctuations
slicedData= train.iloc[:,2:27]
slicedData.replace(to_replace="[^a-zA-Z]", value=" ", regex=True, inplace=True)
# Renaming column names for ease of access
list1= [i for i in range(25)]
new_Index=[str(i) for i in list1]
slicedData.columns= new_Index
slicedData.head(5)
# Convertng headlines to lower case
for index in new_Index:
slicedData[index]=slicedData[index].str.lower()
slicedData.head(1)
# -
headlines = []
for row in range(0,len(slicedData.index)):
headlines.append(' '.join(str(x) for x in slicedData.iloc[row,0:25]))
headlines[0]
basicvectorizer = CountVectorizer(ngram_range=(1,1))
basictrain = basicvectorizer.fit_transform(headlines)
print(basictrain.shape)
basicmodel = LogisticRegression()
basicmodel = basicmodel.fit(basictrain, train["Label"])
testheadlines = []
for row in range(0,len(test.index)):
testheadlines.append(' '.join(str(x) for x in test.iloc[row,2:27]))
basictest = basicvectorizer.transform(testheadlines)
predictions = basicmodel.predict(basictest)
predictions
pd.crosstab(test["Label"], predictions, rownames=["Actual"], colnames=["Predicted"])
# +
from sklearn.metrics import classification_report
from sklearn.metrics import f1_score
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
print (classification_report(test["Label"], predictions))
print (accuracy_score(test["Label"], predictions))
# +
basicvectorizer2 = CountVectorizer(ngram_range=(1,2))
basictrain2 = basicvectorizer2.fit_transform(headlines)
print(basictrain2.shape)
basicmodel2 = LogisticRegression()
basicmodel2 = basicmodel2.fit(basictrain2, train["Label"])
basictest2 = basicvectorizer2.transform(testheadlines)
predictions2 = basicmodel2.predict(basictest2)
pd.crosstab(test["Label"], predictions2, rownames=["Actual"], colnames=["Predicted"])
print (classification_report(test["Label"], predictions2))
print (accuracy_score(test["Label"], predictions2))
print (classification_report(test["Label"], predictions2))
print (accuracy_score(test["Label"], predictions2))
# +
basicvectorizer3 = CountVectorizer(ngram_range=(2,3))
basictrain3 = basicvectorizer3.fit_transform(headlines)
print(basictrain3.shape)
basicmodel3 = LogisticRegression()
basicmodel3 = basicmodel3.fit(basictrain3, train["Label"])
basictest3 = basicvectorizer3.transform(testheadlines)
predictions3 = basicmodel3.predict(basictest3)
pd.crosstab(test["Label"], predictions3, rownames=["Actual"], colnames=["Predicted"])
print (classification_report(test["Label"], predictions3))
print (accuracy_score(test["Label"], predictions3))
# -
`list of numbers`])`**
#
#
#
#
#
# + id="1rgTfXZrBmyy"
# This creates empty lists
Energy = []
Crater_Width = []
# This is where you add the energy value and diameters for your first energy
# NOTE THE FORMATTING: the energy value is a single number, but the diameters is a list of number
# enclosed in square brackets [...]. Don't forget the square brackets!
Energy.append(0.60)
Crater_Width.append([5.9, 5.8, 6.0, 6.05, 5.8, 5.9, 5.9])
# This is where you add the energy value and diameters for your second energy
Energy.append(0.51)
Crater_Width.append([5.6, 5.4, 5.6, 5.7, 5.8, 5.7, 6.0])
#This is your third energy and list of diameters, etc.
Energy.append(0.35)
Crater_Width.append([4.9, 5.0, 4.95, 5.1, 5.4, 5.0, 5.2])
Energy.append(0.17)
Crater_Width.append([4.3, 4.55, 4.5, 4.4, 4.5, 4.75, 4.4, 4.5])
Energy.append(0.12)
Crater_Width.append([3.75, 3.6, 3.8, 3.7, 3.55, 3.8, 3.85, 3.7])
Energy.append(0.08)
Crater_Width.append([3.55, 3.65, 3.6, 3.65, 3.45, 3.4])
Energy.append(0.05)
Crater_Width.append([2.9, 3.15, 3.0, 3.05, 3.05, 3.1, 3.0, 3.1])
# To add more data, copy and paste additional pairs of the `append` commands from above... one for each energy
# Energy.append()
# Crater_Width.append([])
# + [markdown] id="l8QyziZOZJ88"
# Next we'll quickly plot each data set to make sure that we haven't done anything strange.
#
# Re-run this plot every time you add values for a new energy to see how things are evolving!
# + id="osaNHhO_jr-v" colab={"base_uri": "https://localhost:8080/", "height": 629} outputId="7b9ff346-9fd8-4609-a0db-c88265242279"
fig,ax = plt.subplots()
# This is a loop that plots each energy in a different color
for n, Width in enumerate(Crater_Width):
ax.scatter(np.full_like(Width,Energy[n]),Width,marker='.')
ax.set_title('Raw Data Plot')
ax.set_xlabel('Impactor Kinetic Energy (J)')
ax.set_ylabel('Crater Diameter (cm)')
plt.show()
# + [markdown] id="urbN0-fHefBC"
# Now that we've checked our data, let's find the average and uncertainty for each energy value.
# + id="eT2zdtx6k76S" colab={"base_uri": "https://localhost:8080/", "height": 880, "referenced_widgets": ["d455c45c4e764387b7fd2348c154f9d9", "6cc10efe6c004041abecb367fff4a5ee", "4993363e44ef40a68259dc9d72bccb6a", "1e2f97d44df94333bcaafbb53e9692c7", "6c99b76b1f8d4921a063a2645f74a439", "072ee2822d254c03927f249411eda808", "c8a24b30d45942d280664936f1103558", "b16004c7f75c4fe0bab79ed680491626", "d700610166984a849657fdea245268e9", "5c490cdb6315444196c686452e7b77ae", "252271cc4b5446e09a2d5ad8f4caae21", "80059b8c69d14a8bbee76e0f4721c521", "83071188dafa4ab1a982845675596ab4", "b4b88a2e0ff24be28fe9a90387a3ec22", "5c2d7d5d344e4f78b024fccb931b521f", "df14ac8d20674822ac66d048caae1eef"]} outputId="54c1ecc2-dd58-48b7-9114-520a772fb058"
Crater_Width_Average = []
Crater_Width_Uncertainty = []
for n, Width in enumerate(Crater_Width):
Crater_Width_Average.append(average(Width))
Crater_Width_Uncertainty.append(standard_error(Width))
print(Energy[n],"J ", Crater_Width_Average[n],"+-",Crater_Width_Uncertainty[n],"cm")
@widgets.interact(A = widgets.FloatSlider(min=1, max=20, step=0.1, value=2),
B = widgets.FloatSlider(min=1, max=20, step=0.1, value=2),
maxK = widgets.FloatSlider(min=0, max=2, step=0.1, value=1),
logplot = widgets.Checkbox(value=False,
description= 'log-log plot?'))
def update(A, B, maxK, logplot):
fig,ax = plt.subplots()
ax.errorbar(Energy, Crater_Width_Average, Crater_Width_Uncertainty, fmt='k.',
markersize=2, capsize=3)
X = np.linspace(0, maxK, 1000)
ax.plot(X, A*X**(1/3), label='$A*K^{1/3}$')
ax.plot(X, B*X**(1/4), label='$B*K^{1/4}$')
if logplot == True:
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_title('Average Data Plot')
ax.set_xlabel('Impactor Kinetic Energy, $K$, (J)')
ax.set_ylabel('Crater Diameter (cm)')
ax.legend()
# + [markdown] id="2B5s8j4eK3wz"
# Record your average values, and don't forget to save your plots (right click and select "save as") and put copies in your lab notebook!
# + [markdown] id="VVg9kc19KZfO"
# # Part 2 -- Understanding and applying the model
#
# This part will fit your data to the competing models and help you make predictions for new craters.
# + [markdown] id="xgGF-bZ-tm0M"
# Type in your energies, as well as the corresponding crater width averages and uncertainties. (You wrote those down last time, right? If not, you'll have to re-run the code in part one to calculate them again.)
# + id="_ilH06eatgDe"
Energy = [0.0523, 0.032, 0.0665, 0.01, 0.0196, 0.0083, 0.004]
Crater_Width_Average = [5.723, 5.079, 5.917, 3.718, 4.488, 3.550, 3.044]
Crater_Width_Uncertainty = [0.10, 0.095, 0.089, 0.057, 0.087, 0.053, 0.067]
# + [markdown] id="hcb3UUUESnJa"
# Next we define our two possible model functions,
# - The "1/3-power model": $D = A*K^{1/3}$
# - The "1/4-power model": $D = B*K^{1/4}$
#
# and our residual function (which calculates the difference between the data and the fit function),
# - Residual on point $i$: $\chi_i = \frac{D_{fit} - D_i}{\delta D_i}$.
#
# We can also define a general power law function that may be useful later,
# - The "general-power model": $D = C*K^x$.
# + id="0e93gikCuYf-"
#Defines fit functions
def third_power(p, x):
return(p[0]*np.array(x)**(1/3)).tolist()
def quarter_power(p, x):
return(p[0]*np.array(x)**(1/4)).tolist()
def gen_power(p,x):
return(p[0]*np.array(x)**p[1]).tolist()
def residual(p, function, x, y, dy):
return ((function(p, np.array(x)) - np.array(y))/np.array(dy))
# + [markdown] id="Rf-X-UIu--Yb"
# Next, we define a function that will perform a least-squares fit to a set of data. **This code is quite complex and you DO NOT need to understand it!**
#
# The fit returns the best fit values (e.g. $A$ or $B$) and the uncertainties on that value (e.g. $\delta A$ or $\delta B$). It also returns the number of degrees of freedom, the chi-squared value, and the reduced chi-squared value:
# - Number of degrees of freedom, dof: $\nu$ = "number of data points" - "number of fit parameters"
# - Chi-square: $\chi^2 = \sum_i^N \frac{(D_{fit} - D_i)^2}{\delta D_i^2}$
# - Reduced chi-square: $\chi^2/\nu$
# + id="LvZSqinR4qvI"
# The code below defines our data fitting function.
# Inputs are:
# a list of variable names
# initial guess for parameters p0
# the function we're fitting to
# the x,y, and dy variables
# tmi can be set to 1 or 2 if more intermediate data is needed
def data_fit(varnames, p0, func, xvar, yvar, err, tmi=0):
try:
fit = optimize.least_squares(residual, p0, args=(func,xvar, yvar, err),
verbose=tmi)
except Exception as error:
print("Something has gone wrong:", error)
return p0, np.zeros_like(p0), -1, -1
pf = fit['x']
try:
cov = np.linalg.inv(fit['jac'].T.dot(fit['jac']))
# This computes a covariance matrix by finding the inverse of the Jacobian times its transpose
# We need this to find the uncertainty in our fit parameters
except:
# If the fit failed, print the reason
print('Fit did not converge')
print('Result is likely a local minimum')
print('Try changing initial values')
print('Status code:', fit['status'])
print(fit['message'])
return pf,np.zeros_like(pf), -1, -1
#You'll be able to plot with this, but it will not be a good fit.
chisq = sum(residual(pf,func,xvar, yvar, err) **2)
dof = len(xvar) - len(pf)
red_chisq = chisq/dof
pferr = np.sqrt(np.diagonal(cov)) # finds the uncertainty in fit parameters by squaring diagonal elements of the covariance matrix
print('Converged with chi-squared: {:.2f}'.format(chisq))
print('Number of degrees of freedom, dof: {:.0f}'.format(dof))
print('Reduced chi-squared (chi-squared/dof): {:.2f}'.format(red_chisq))
print()
Columns = ["Parameter", "Best fit values:", "Uncertainties in the best fit values:"]
print('{:<11}'.format(Columns[0]),'|','{:<24}'.format(Columns[1]),"|",'{:<24}'.format(Columns[2]))
for num in range(len(pf)):
print('{:<11}'.format(varnames[num]),'|','{:<24.4f}'.format(pf[num]),'|','{:<24.4f}'.format(pferr[num]))
print()
return pf, pferr, chisq, dof
# + [markdown] id="blMZD5nK006P"
# At the heart of this function is the idea of a **residual**. Residuals are a function of our data and the function we're fitting the data to. The residual for a point is the difference between the y-value of that datapoint and that of the function at the same point. It's a quantitative way of measuring how well a data and function agree with one another.
#
# Often formulas will use the residual squared as a way of avoiding negative numbers since undershooting and overshooting points are equally bad.
#
# The fitting algorithm above will vary function parameters `p` repeatedly and keep changes that make the sum of the residuals (squared) smaller until it can't make any meaningful improvements. It also weights points by their uncertainties: points with large uncertanties are likely to be less representative of the underlying behavior than points with small uncertanties.
#
# Let's see what it comes up with, and how far our data is from the fits.
# + [markdown] id="e-9K_IADoFcg"
# Try to fit your data to the two models. Can you tell yet whether you have better agreement with one model over the other?
# + colab={"base_uri": "https://localhost:8080/"} id="eovatUbl5Yzt" outputId="39a7ba27-be7c-4b89-eead-e1469c2ac521"
# Fits
print('FIT: D = A*K^(1/3)')
print('-----')
third_fit, third_err, third_chisq, third_dof = data_fit(['A'], [1], third_power,
Energy, Crater_Width_Average, Crater_Width_Uncertainty)
print('FIT: D = B*K^(1/4)')
print('-----')
quarter_fit, quarter_err, quarter_chisq, quarter_dof = data_fit(['B'], [1], quarter_power,
Energy, Crater_Width_Average, Crater_Width_Uncertainty)
# + [markdown] id="1zIDaFX7154o"
# Next, let's plot the fits to see how they look compared to the data.
# + colab={"base_uri": "https://localhost:8080/", "height": 661, "referenced_widgets": ["e1b72c2ba96945b29301e62cc6c24fc0", "635ccf2d637947b2ab216ea0f8d3f0bf", "6d0ded7e3e1649af9e91c949dcdef858", "7ae992d9a44949bda3433ed9b80809ba", "2afffe0edea64064bb556fda7ecc876f", "1bb8f68f1a4641eea1aea208b01409da", "badb5f5441a34fc2b03dc0b2bf44ddb6"]} id="jmmw-S1w16gW" outputId="c149d24b-906c-4a5f-abb4-d411499b95e3"
#Plots
@widgets.interact(logplot = widgets.Checkbox(value=False,
description= 'log-log plot?'))
def update(logplot):
fig,ax = plt.subplots()
ax.errorbar(Energy, Crater_Width_Average, Crater_Width_Uncertainty, fmt='k.',
label="Data", capsize=2)
X = np.linspace(min(Energy), max(Energy), 5000)
X_longer = np.linspace(0.25*min(Energy), 1.2*max(Energy), 5000)
ax.plot(X_longer, third_power(third_fit, X_longer), 'b--')
ax.plot(X, third_power(third_fit, X), 'b-', label="$A*K^{1/3}$")
ax.plot(X_longer, quarter_power(quarter_fit, X_longer), 'r--')
ax.plot(X, quarter_power(quarter_fit, X), 'r-', label="$B*K^{1/4}$")
if logplot == True:
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_title("Power law fit Comparison")
ax.set_ylabel("Crater Diameter (cm)")
ax.set_xlabel("Energy (J)")
ax.legend()
# + [markdown] id="EKl6Bo7AxZsy"
# It might still be a little hard to tell how far the data is from the fits, so let's make a plot of residuals for each of the two functions below. We'll also include the sum of the residuals squared (i.e. $\chi^2$) as a title so we don't have to do that by hand.
# + colab={"base_uri": "https://localhost:8080/", "height": 641} id="18Mb-U1fxUCV" outputId="7e8de47d-48f7-466f-9f87-fc575e4acd93"
fig,(ax,ay) = plt.subplots(2,1,sharex=True,sharey=True)
ax.plot(Energy,residual(third_fit,third_power,Energy,Crater_Width_Average,Crater_Width_Uncertainty),'b.',label='third power')
ax.vlines(Energy,0,residual(third_fit,third_power,Energy,Crater_Width_Average,Crater_Width_Uncertainty),'b')
ax.hlines(0,min(Energy),max(Energy),'b',alpha=0.25)
third_sum_residuals = sum(residual(third_fit,third_power,Energy,Crater_Width_Average,Crater_Width_Uncertainty)**2)
ay.plot(Energy,residual(quarter_fit,quarter_power,Energy,Crater_Width_Average,Crater_Width_Uncertainty),'r.',label='quarter power')
ay.vlines(Energy,0,residual(quarter_fit,quarter_power,Energy,Crater_Width_Average,Crater_Width_Uncertainty),'r')
ay.hlines(0,min(Energy),max(Energy),'r',alpha=0.25)
quarter_sum_residuals = sum(residual(quarter_fit,quarter_power,Energy,Crater_Width_Average,Crater_Width_Uncertainty)**2)
ax.set_ylabel("Residual")
ax.set_xlabel("Energy (J)")
ax.set_title("$\chi^2$ = {:.2f}".format(third_sum_residuals))
ax.legend(loc=2)
ay.set_ylabel("Residual")
ay.set_xlabel("Energy (J)")
ay.set_title("$\chi^2$ = {:.2f}".format(quarter_sum_residuals))
ay.legend(loc=2)
fig.tight_layout()
plt.show()
# + [markdown] id="GzyCzd3vo9Px"
# Do you find better agreement with one model over the other? What criteria are you using to make that decision?
#
# Does either of your models show a trend in the residuals? (That is, do the residuals all fall too low in one part then too high in another part rather than randomly up and down all over?) What does this indicate about the quality of the fit?
# + [markdown] id="eXHyW_Tlzmkc"
# Does it help to fit to a more general function where the exponent is itself a fit parameter? Maybe the best fit isn't to a 1/3- or 1/4-power law, but to something else?
# + colab={"base_uri": "https://localhost:8080/", "height": 831, "referenced_widgets": ["d7dca86335404762a425d3e6c74c1b1b", "4218fcb462614ee0ab0a180987173e41", "8257d11eaf08419a8caa94e42ee0f1fc", "c43fe1f7f5ca4b69bdf6f1f7ba04f30b", "b7c0e60cd8d24ff4a554dad3d36e4bc4", "fc2053ce9b84409fbb0c3215344e6dbd", "ffb117c507fe494aa68c90d315457c04"]} id="5uCf1tCE8UHo" outputId="cf814373-13e0-44d6-a2a1-0f3a868a05a2"
#Fit
print('FIT: D = C*K^x')
print('-----')
gen_fit, gen_err, gen_chisq, gen_dof = data_fit(['C', 'x'], [1, 0.5], gen_power,
Energy, Crater_Width_Average, Crater_Width_Uncertainty)
#Plots
@widgets.interact(logplot = widgets.Checkbox(value=False,
description= 'log-log plot?'))
def update(logplot):
fig,ax = plt.subplots()
ax.errorbar(Energy, Crater_Width_Average, Crater_Width_Uncertainty, fmt='k.',
label="Data", capsize=2)
X = np.linspace(min(Energy), max(Energy), 5000)
X_longer = np.linspace(0.1*min(Energy), 1.2*max(Energy), 5000)
ax.plot(X_longer, third_power(third_fit, X_longer), 'b--')
ax.plot(X, third_power(third_fit, X), 'b-', label="$A*K^{1/3}$")
ax.plot(X_longer, quarter_power(quarter_fit, X_longer), 'r--')
ax.plot(X, quarter_power(quarter_fit, X), 'r-', label="$B*K^{1/4}$")
ax.plot(X_longer, gen_power(gen_fit, X_longer), 'g--')
ax.plot(X, gen_power(gen_fit, X), 'g-', label="$C*K^x$")
if logplot == True:
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_title("Power law fit Comparison")
ax.set_ylabel("Crater Diameter (cm)")
ax.set_xlabel("Energy (J)")
ax.legend()
# + colab={"base_uri": "https://localhost:8080/", "height": 641} id="XOFBrsFPzygB" outputId="34b9c185-17ac-4c82-b022-8fd2d856c8fb"
fig,ax = plt.subplots()
ax.plot(Energy,residual(gen_fit,gen_power,Energy,Crater_Width_Average,Crater_Width_Uncertainty),'b.',label='general power')
ax.vlines(Energy,0,residual(gen_fit,gen_power,Energy,Crater_Width_Average,Crater_Width_Uncertainty),'b')
ax.hlines(0,min(Energy),max(Energy),'b',alpha=0.25)
gen_sum_residuals = sum(residual(gen_fit,gen_power,Energy,Crater_Width_Average,Crater_Width_Uncertainty)**2)
ax.set_ylabel("Residual")
ax.set_xlabel("Energy (J)")
ax.set_title("$\chi^2$ = {:.2f}".format(gen_sum_residuals))
ax.legend(loc=2)
fig.tight_layout()
plt.show()
# + [markdown] id="CCdm4rdZ_rt4"
# Now, let's use our model to make predictions. Input an energy to predict a crater diameter.
# + id="uVdNWf7NqJTR" colab={"base_uri": "https://localhost:8080/"} outputId="f1cf4b40-07ca-4b9f-e1a8-d9610cf0a08f"
val = input("Enter an energy (in J) to see what your models predict for the crater diameter: ")
test_K = float(val)
D_third = third_power(third_fit, test_K)
dD_third = D_third*third_err[0]/third_fit[0]
D_quarter = quarter_power(quarter_fit, test_K)
dD_quarter = D_quarter*quarter_err[0]/quarter_fit[0]
D_gen = gen_power(gen_fit, test_K)
dD_gen = D_gen*np.sqrt((gen_err[0]/gen_fit[0])**2 + (gen_fit[1]*gen_err[1]/test_K)**2)
print("1/3-power prediction: ", D_third, " +/- ", dD_third, "cm")
print("1/4-power prediction: ", D_quarter," +/- ", dD_quarter, "cm")
print("general-power prediction: ", D_gen, " +/- ", dD_gen, "cm")
# + id="6CdDIwnF_zBS"
| 20,081 |
/OpenCVBasics/Green Screen Car.ipynb | 8454d2f97f21175230f414f0460ce52cde2386db | [] | no_license | srikanthadya/CV | https://github.com/srikanthadya/CV | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 431,549 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Color Masking, Green Screen
# ### Import resources
# +
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import numpy as np
import cv2
# %matplotlib inline
# -
# ### Read in and display the image
# +
# Read in the image
image = mpimg.imread('images/car_green_screen.jpg')
# Print out the image dimensions (height, width, and depth (color))
print('Image dimensions:', image.shape)
# Display the image
plt.imshow(image)
# -
# ### Define the color threshold
# Define our color selection boundaries in RGB values
lower_green = np.array([0,180,0])
upper_green = np.array([100,255,100])
# ### Create a mask
# +
# Define the masked area
mask = cv2.inRange(image, lower_green, upper_green)
# Vizualize the mask
plt.imshow(mask, cmap='gray')
# +
# Mask the image to let the car show through
masked_image = np.copy(image)
masked_image[mask != 0] = [0, 0, 0]
# Display it!
plt.imshow(masked_image)
# -
# ## TODO: Mask and add a background image
# +
# Load in a background image, and convert it to RGB
background_image = mpimg.imread('images/sky.jpg')
## TODO: Crop it or resize the background to be the right size (450x660)
# Hint: Make sure the dimensions are in the correct order!
background_image = cv2.resize(background_image,(660,450))
## TODO: Mask the cropped background so that the car area is blocked
# Hint: mask the opposite area of the previous image
masked_back = background_image.copy()
masked_back[mask==0]=[0,0,0]
## TODO: Display the background and make sure
plt.imshow(masked_back)
plt.show()
# -
# ### TODO: Create a complete image
# +
## TODO: Add the two images together to create a complete image!
# complete_image = masked_image + crop_background
complete_image = masked_back+masked_image
plt.imshow(complete_image)
plt.show()
# -
間也越久
# # 作業
# * 將原始資料集換為S型圖, 觀察不同 perplexity 下的流形還原結果
| 2,115 |
/Investigate_a_Dataset.ipynb | 98663746e8cebba4d561455a75b4b00114fda49b | [] | no_license | gabriela99/Investigating-Gapminder-Datasets | https://github.com/gabriela99/Investigating-Gapminder-Datasets | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 602,086 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Задание по программированию: Предобработка данных в Pandas
import pandas
data = pandas.read_csv('./data/titanic.csv', index_col='PassengerId')
print(len(data))
data.head()
# data.tail()
# ## 1. Какое количество мужчин и женщин ехало на корабле? В качестве ответа приведите два числа через пробел.
# count male and female
print(f"{len(data[data['Sex'] == 'male'])} {len(data[data['Sex'] == 'female'])}")
# ## 2. Какой части пассажиров удалось выжить? Посчитайте долю выживших пассажиров. Ответ приведите в процентах (число в интервале от 0 до 100, знак процента не нужен), округлив до двух знаков.
print(f"{round(100 * len(data[data['Survived'] == 1]) / len(data), 2)}")
# ## 3. Какую долю пассажиры первого класса составляли среди всех пассажиров? Ответ приведите в процентах (число в интервале от 0 до 100, знак процента не нужен), округлив до двух знаков.
print(f"{round(100 * len(data[data['Pclass'] == 1]) / len(data), 2)}")
# ## 4. Какого возраста были пассажиры? Посчитайте среднее и медиану возраста пассажиров. В качестве ответа приведите два числа через пробел.
print(f"{round(data['Age'].mean(), 2)} {data['Age'].median()}")
# ## 5. Коррелируют ли число братьев/сестер/супругов с числом родителей/детей? Посчитайте корреляцию Пирсона между признаками SibSp и Parch.
# print(f"{data[5:6, :]}")
print(f"{data[['SibSp', 'Parch']].corr()}")
# ## 6. Какое самое популярное женское имя на корабле? Извлеките из полного имени пассажира (колонка Name) его личное имя (First Name). Это задание — типичный пример того, с чем сталкивается специалист по анализу данных. Данные очень разнородные и шумные, но из них требуется извлечь необходимую информацию. Попробуйте вручную разобрать несколько значений столбца Name и выработать правило для извлечения имен, а также разделения их на женские и мужские.
female_name = data[data['Sex'] == 'female']['Name']
female_name.head()
female_name[3].split('.')
# +
import collections
c = collections.Counter()
for str_ in female_name:
_ = str_.split('(')
if len(_) == 1:
_ = str_.split(' ')[2]
c[_] += 1
else:
_ = _[1].split(' ')[0]
c[_] += 1
print(c.most_common(1)[0][0])
| 2,453 |
/Output In Construction 1.ipynb | 1d3cab767c04d88eea2fc3c1883581930be9ab6f | [] | no_license | GSS-Cogs/mock-transformations | https://github.com/GSS-Cogs/mock-transformations | 0 | 3 | null | 2021-01-28T10:29:51 | 2020-10-02T16:00:52 | Jupyter Notebook | Jupyter Notebook | false | false | .py | 2,571 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Output In The Construction Industry
#
# -----
#
# ### Requirements
#
# We're looking to transform **tabs 1 and 2 only**.
#
# #### Observations & Dimensions
#
# The `observations` should be apparent.
#
# The required dimensions are:
#
# * **Geography** - it's all UK level data (the code for UK is "K02000001")
# * **Time** - either a simple year, or a year followed by a quarter, i.e "2002 Q2"
# * **Adjustment** - either seasonal or non-seasonal
# * **Business** - concatenation of rows 6-9 around hyphens. i.e 'Other New Work - Excluding Infrastructure - Private Commercial'
# * **CDID** - ONS specific 4 letter codes. Typically on row 10
#
# -----
# Notes:
#
# * Getting the **Business** dimension cleanly is going to be tricky (read - cant see an obvious way to do it), I'd perhaps leave this one until last.
# * It's always worth getting the file out of /sources and having a look over.
# * You can't really take CDID as a dimension (dimension items needs to be repeating, not unqiue), it's a good exercise though as if doing this for real we'd likely be taking it as meta/supporting data.
# +
from databaker.framework import *
tabs = loadxlstabs("./sources/OIC.xls") # load tabs
# -
| 1,464 |
/Assignments/intro_into_Python/assignment_module_3.ipynb | b27062fd2b73cf31df54f0d5e4dcd4f7d61392f1 | [] | no_license | mmehmadi94/Data_Science_Bootcamp_codingDojo | https://github.com/mmehmadi94/Data_Science_Bootcamp_codingDojo | 1 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 82,138 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="6c9fsJpqCC2b"
# ### In each cell complete the task using pandas
# + id="hg_sIkv_CC2e" executionInfo={"status": "ok", "timestamp": 1603973500398, "user_tz": 240, "elapsed": 326, "user": {"displayName": "Daniel Oostra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjoFqfaFDmBwsQMk-5iKq2nP59iwzw_tLWSkGcj=s64", "userId": "11468040424360387869"}}
import pandas as pd
import numpy as np
# + [markdown] id="BX874lK4CC2s"
# Read in the titanic.csv file in the `~/data` directory as a pandas dataframe called **df**
#
# Or you can also use this link: https://raw.githubusercontent.com/daniel-dc-cd/data_science/master/module_3_Python/data/titanic.csv
#
#
# + id="ojgJ3wqUCC2x" executionInfo={"status": "ok", "timestamp": 1603973575902, "user_tz": 240, "elapsed": 561, "user": {"displayName": "Daniel Oostra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjoFqfaFDmBwsQMk-5iKq2nP59iwzw_tLWSkGcj=s64", "userId": "11468040424360387869"}}
df = pd.read_csv('https://raw.githubusercontent.com/daniel-dc-cd/data_science/master/module_3_Python/data/titanic.csv')
# + [markdown] id="R8Oq_qrCCC2-"
# Display the head of the dataframe
# -
df.head()
df.info()
df.shape
df.describe()
# + [markdown] id="ikD3XVZnCC3K"
# What is the percentage of people who survived? (hint find the mean of the survival column)
# -
print(round(df.Survived.mean()*100,4), "%")
# How many women and how many man survived?
survived_per_gender = df.groupby(['Sex','Survived']).Survived.count()
print(survived_per_gender)
survived_per_gender.unstack()
# + [markdown] id="KufP8fcFCC3c"
# What is the percentage of people that survived who paid a fare less than 10?
# -
df1 = df[(df.Fare <10)]
df1.head(2)
survived_fare_less_10 = df1[df1.Survived == 1]
Survived = df[df.Survived == 1]
print("percentage of people that survived who paid a fare less than 10: ",
(len(survived_fare_less_10)/len(Survived))*100,"%")
# + [markdown] id="ZjEHLwflCC3m"
# What is the average age of those who didn't survive?
# -
df[df.Survived == 0].Age.mean()
# + [markdown] id="2VSXhYtRCC3s"
# What is the average age of those who did survive?
# -
df[df.Survived == 1].Age.mean()
# + [markdown] id="KXOFWFyYCC32"
# What is the average age of those who did and didn't survive grouped by gender?
# -
age_mean = df.groupby(['Sex','Survived']).Age.mean()
print(age_mean)
age_mean.unstack()
# + [markdown] id="vqf5OGCiCC38"
# ## Tidy GDP
# + [markdown] id="hcUYOSgrCC39"
# Manipulate the GDP.csv file and make it tidy, the result should be a pandas dataframe with the following columns:
# * Country Name
# * Country Code
# * Year
# * GDP
#
# https://raw.githubusercontent.com/daniel-dc-cd/data_science/master/module_3_Python/data/GDP.csv
#
# + id="Df3tU4ruX3Xp"
df = pd.read_csv('https://raw.githubusercontent.com/daniel-dc-cd/data_science/master/module_3_Python/data/GDP.csv', skiprows=4)
df.head(2)
# -
df.shape
df.drop(['Indicator Name' , 'Indicator Code'], axis=1)
formatted_df = pd.melt(df,
["Country Name","Country Code"],
var_name="Year",
value_name="GDP")
formatted_df = formatted_df.sort_values(by=["Country Name","Year"]).set_index("Country Name")
formatted_df.head(10)
| 3,516 |
/6.classification-1/Ch4_classification .ipynb | b9251471ca770ef28e6ff8c9620a8747d7238557 | [] | no_license | chunghyunhee/python_ml_perfect_guide | https://github.com/chunghyunhee/python_ml_perfect_guide | 1 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 311,671 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Collision Avoidance - Live Demo
#
# In this notebook we'll use the model we trained to detect whether the robot is ``free`` or ``blocked`` to enable a collision avoidance behavior on the robot.
#
# ## Load the trained model
#
# We'll assumed that you've already downloaded the ``best_model.pth`` to your workstation as instructed in the training notebook. Now, you should upload this model into this notebook's
# directory by using the Jupyter Lab upload tool. Once that's finished there should be a file named ``best_model.pth`` in this notebook's directory.
#
# > Please make sure the file has uploaded fully before calling the next cell
#
# Execute the code below to initialize the PyTorch model. This should look very familiar from the training notebook.
# +
import torch
import torchvision
model = torchvision.models.alexnet(pretrained=False)
model.classifier[6] = torch.nn.Linear(model.classifier[6].in_features, 2)
# -
# Next, load the trained weights from the ``best_model.pth`` file that you uploaded
model.load_state_dict(torch.load('best_model.pth'))
# Currently, the model weights are located on the CPU memory execute the code below to transfer to the GPU device.
device = torch.device('cuda')
model = model.to(device)
# ### Create the preprocessing function
#
# We have now loaded our model, but there's a slight issue. The format that we trained our model doesnt *exactly* match the format of the camera. To do that,
# we need to do some *preprocessing*. This involves the following steps
#
# 1. Convert from BGR to RGB
# 2. Convert from HWC layout to CHW layout
# 3. Normalize using same parameters as we did during training (our camera provides values in [0, 255] range and training loaded images in [0, 1] range so we need to scale by 255.0
# 4. Transfer the data from CPU memory to GPU memory
# 5. Add a batch dimension
# +
import cv2
import numpy as np
mean = 255.0 * np.array([0.485, 0.456, 0.406])
stdev = 255.0 * np.array([0.229, 0.224, 0.225])
normalize = torchvision.transforms.Normalize(mean, stdev)
def preprocess(camera_value):
global device, normalize
x = camera_value
x = cv2.cvtColor(x, cv2.COLOR_BGR2RGB)
x = x.transpose((2, 0, 1))
x = torch.from_numpy(x).float()
x = normalize(x)
x = x.to(device)
x = x[None, ...]
return x
# -
# Great! We've now defined our pre-processing function which can convert images from the camera format to the neural network input format.
#
# Now, let's start and display our camera. You should be pretty familiar with this by now. We'll also create a slider that will display the
# probability that the robot is blocked.
# +
import traitlets
from IPython.display import display
import ipywidgets.widgets as widgets
from jetbot import Camera, bgr8_to_jpeg
camera = Camera.instance(width=224, height=224)
image = widgets.Image(format='jpeg', width=224, height=224)
blocked_slider = widgets.FloatSlider(description='blocked', min=0.0, max=1.0, orientation='vertical')
camera_link = traitlets.dlink((camera, 'value'), (image, 'value'), transform=bgr8_to_jpeg)
display(widgets.HBox([image, blocked_slider]))
# -
# We'll also create our robot instance which we'll need to drive the motors.
# +
from jetbot import Robot
robot = Robot(driver_board = "dfrobot")
# -
# Next, we'll create a function that will get called whenever the camera's value changes. This function will do the following steps
#
# 1. Pre-process the camera image
# 2. Execute the neural network
# 3. While the neural network output indicates we're blocked, we'll turn left, otherwise we go forward.
# +
import torch.nn.functional as F
import time
def update(change):
global blocked_slider, robot
x = change['new']
x = preprocess(x)
y = model(x)
# we apply the `softmax` function to normalize the output vector so it sums to 1 (which makes it a probability distribution)
y = F.softmax(y, dim=1)
prob_blocked = float(y.flatten()[0])
blocked_slider.value = prob_blocked
if prob_blocked < 0.5:
robot.forward(0.4)
else:
robot.left(0.4)
time.sleep(0.001)
update({'new': camera.value}) # we call the function once to intialize
# -
# Cool! We've created our neural network execution function, but now we need to attach it to the camera for processing.
#
# We accomplish that with the ``observe`` function.
#
# > WARNING: This code will move the robot!! Please make sure your robot has clearance. The collision avoidance should work, but the neural
# > network is only as good as the data it's trained on!
camera.observe(update, names='value') # this attaches the 'update' function to the 'value' traitlet of our camera
# Awesome! If your robot is plugged in it should now be generating new commands with each new camera frame. Perhaps start by placing your robot on the ground and seeing what it does when it reaches an obstacle.
#
# If you want to stop this behavior, you can unattach this callback by executing the code below.
# +
import time
camera.unobserve(update, names='value')
time.sleep(0.1) # add a small sleep to make sure frames have finished processing
robot.stop()
# -
# Perhaps you want the robot to run without streaming video to the browser. You can unlink the camera as below.
camera_link.unlink() # don't stream to browser (will still run camera)
# To continue streaming call the following.
camera_link.link() # stream to browser (wont run camera)
# ### Conclusion
#
# That's it for this live demo! Hopefully you had some fun and your robot avoided collisions intelligently!
#
# If your robot wasn't avoiding collisions very well, try to spot where it fails. The beauty is that we can collect more data for these failure scenarios
# and the robot should get even better :)
visualize_boundary(dt_clf, X_features, y_labels)
# -
#(min_samples_leaf=6)으로 제약조건 추가 시
dt_clf=DecisionTreeClassifier(min_samples_leaf=6).fit(X_features, y_labels)
visualize_boundary(dt_clf, X_features, y_labels)
# 결정트리 실습: 사용자 행동인식 데이터셋에 대한 예측분류를 수행하기 (결정나무 이용)
# +
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
#(features.txt)에는 피처이름 인덱스와 피처명이 공백으로 분리돼 있음 (이를 데이터프레임으로 불러옴)
feature_name_df=pd.read_csv('human_activity/features.txt',sep='\s+', #걍 띄어쓰기 한 번 되면서, 엔터는 검은네모 안에 흰 원 기호로 껴있음
header=None, names=['column_index','column_name'])
#피처명 인덱스 제거 후, 피처명만 리스트 객체로 생성해서, 샘플 10개 추출
feature_name=feature_name_df.iloc[:,1].values.tolist() #(.iloc[행,열]): 모든행, 2열만 선택해 오기
print('전체 피처명에서 10개만 추출:', feature_name[:10]) #0번째부터 (10-1=)9번째까지 (맨 앞에서부터) 총 10개
# +
import pandas as pd
def get_human_dataset():
feature_name_df=pd.read_csv('./human_activity/features.txt',sep='\s+',header=None,names=['column_index','column_name'])
feature_name=feature_name_df.iloc[:,1].values.tolist()
X_train=pd.read_csv('./human_activity/train/X_train.txt', sep='\s+', names=feature_name)
X_test=pd.read_csv('./human_activity/test/X_test.txt', sep='\s+', names=feature_name)
y_train=pd.read_csv('./human_activity/train/y_train.txt', sep='\s+', header=None, names=['action'])
y_test=pd.read_csv('./human_activity/test/y_test.txt', sep='\s+', header=None, names=['action'])
return X_train, X_test, y_train, y_test
X_train, X_test, y_train, y_test = get_human_dataset()
# -
print('## 학습 피처 데이터셋 info()')
print(X_train.info())
print(y_train['action'].value_counts()) #['action'] 안 쓰면 에러남
# +
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
dt_clf=DecisionTreeClassifier(random_state=156)
dt_clf.fit(X_train, y_train)
pred=dt_clf.predict(X_test)
accuracy=accuracy_score(y_test, pred)
print('결정나무 예측 정확도:{0:.4f}'.format(accuracy))
print('DecisionTreeClassifier 기본 하이퍼 모수:\n', dt_clf.get_params())
# +
#트리 깊이가 예측 정확도에 미치는 영향을 비교하기
from sklearn.model_selection import GridSearchCV
params={'max_depth': [6,8,10,12,16,20,24]}
grid_cv=GridSearchCV(dt_clf, param_grid=params, scoring='accuracy',cv=5, verbose=1)
grid_cv.fit(X_train, y_train)
print('GridSearchCV 최고 평균 정확도 수치: {0:.4f}'.format(grid_cv.best_score_))
print('GridSearchCV 최적 하이퍼 모수:', grid_cv.best_params_)
# -
cv_results_df=pd.DataFrame(grid_cv.cv_results_)
cv_results_df[['param_max_depth','mean_test_score','mean_train_score']] #(cv_results_df) 데이터셋 내 3개 열만 선택해 출력
#검증 데이터셋 (mean_test_score) 기준: 깊이가 8일 때, 0.852로 정확도가 최상이고, 더 깊어질수록 정확도가 계속 하락함 (과적합에 따른 성능저하)
# +
max_depths=[6,8,10,12,16,20,24]
for depth in max_depths: #위에 7가지 max_depths 각 값마다 순서대로 for문에 넣어 print까지 돌아감 (7번 출력시킴)
dt_clf=DecisionTreeClassifier(max_depth=depth, random_state=156)
dt_clf.fit(X_train, y_train)
pred=dt_clf.predict(X_test)
accuracy=accuracy_score(y_test, pred)
print('max_depth={0} 정확도: {1:.4f}'.format(depth, accuracy))
# +
#(max_depth), (min_samples_split) 변경하면서 정확도 성능 비교/평가하기
params={'max_depth':[8,12,16,20],
'min_samples_split':[16,24]}
grid_cv=GridSearchCV(dt_clf, param_grid=params, scoring='accuracy', cv=5, verbose=1)
grid_cv.fit(X_train, y_train)
print('GridSearchCV 최고 평균정확도 값: {0:.4f}'.format(grid_cv.best_score_))
print('GridSearchCV 최적 하이퍼 모수:', grid_cv.best_params_)
# -
#분리된 테스트 데이터셋에 위 최적 하이퍼 모수를 적용하기
best_df_clf=grid_cv.best_estimator_
pred1=best_df_clf.predict(X_test)
accuracy=accuracy_score(y_test, pred1)
print('결정나무 예측정확도:{0:.4f}'.format(accuracy))
# +
#결정나무에서 각 피처의 중요도 Top 20 막대그래프로 시각화하기
import seaborn as sns
ftr_importances_values=best_df_clf.feature_importances_
ftr_importances=pd.Series(ftr_importances_values, index=X_train.columns)
ftr_top20=ftr_importances.sort_values(ascending=False)[:20]
plt.figure(figsize=(8,6))
plt.title('피처 중요도 상위 20개')
sns.barplot(x=ftr_top20, y=ftr_top20.index)
plt.show()
# -
# 03) 앙상블 학습 (Ensemble Learning)
# - 여러개의 분류기 (Classifier)를 생성하고, 그 예측을 결합하여, 더 정확한 예측을 달성할 수 있음 (단일 분류기보다 신뢰성이 높음)
# - 전통적인 대표 알고리즘: 랜덤 포레스트 (배깅 방법), 그래디언트 부스팅 알고리즘
# - 새로운 알고리즘: XGBoost, LightGBM, 스태킹(Staking: 여러 다른 모델의 예측 결과에 기반해 다시 학습데이터로 만들어 다른모델 즉, 메타모형로 재학습시켜 예측함) 등
#
# - 앙상블 학습의 유형:
# 1) 보팅 (Voting): 다양한 알고리즘을 가진 분류기들을 투표로 결합해 최종 예측
# 2) 배깅 (Bagging): 하나의 같은 알고리즘을 샘플링을 여러번 하면서 (Bootstrapping 분할방식: 중복추출 허용) 다른 샘플을 가지고 반복한 후
# 투표로 결합해 최종 예측
# 3) 부스팅 (Boosting): 여러 분류기가 순차적으로 학습을 하되, 이전 분류기에서 예측이 틀린 데이터에 대해 다음 분류기에서 가중치(w)를 부여하면서 예측을 진행 (예. 그래디언트 부스트, XGBoost, LightGBM 등)
#
# - 보팅 유형:
# 1) 하드 보팅 (:각 분류기마다 결정한 예측값(Y)를 다수결의 원칙에 의해 최종 선정)
# 2) 소프트 보팅 (더 정확하여 많이 활용되는 방법, 각 분류기마다 레이블 값 예측 확률
# (ex. Y=1,2 두 가지가 존재하는데, 분류기1이 Y=1으로 예측할 확률 0.7, Y=2로 예측할 확률 0.3 (각 분류기별로 확률 값 계산))이 존재할 때, 레이블 값마다 모든 분류기들의 예측확률을 단순평균하여, Y=1으로 예측할 (평균) 확률 0.65 > Y=2으로 예측할 (평균) 확률 0.35 -> Y=1으로 최종 보팅함)
#
# - 보팅 분류기 (VotingClassifier 클래스 활용): 위스콘신 유방암 데이터셋을 예측 분석하기 (로지스틱회귀, KNN을 기반으로 보팅 분류기를 만듬)
# +
import pandas as pd
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
cancer=load_breast_cancer()
data_df=pd.DataFrame(cancer.data, columns=cancer.feature_names)
data_df.head(3)
# +
#개별 모형: 1) 로지스틱회귀, 2) KNN
lr_clf=LogisticRegression()
knn_clf=KNeighborsClassifier(n_neighbors=8)
#개별모형을 소프트 보팅 기반 앙상블 모델로 구현한 분류기
vo_clf=VotingClassifier(estimators=[('LR',lr_clf),('KNN',knn_clf)], voting='soft')
X_train, X_test, y_train, y_test=train_test_split(cancer.data, cancer.target, test_size=0.2, random_state=156)
#VotingClassifier 학습/예측/평가하기
vo_clf.fit(X_train, y_train)
pred=vo_clf.predict(X_test)
print('Voting 분류기 정확도: {0:.4f}'.format(accuracy_score(y_test, pred)))
#개별모형의 학습/예측/평가하기
classifiers=[lr_clf, knn_clf]
for classifier in classifiers:
classifier.fit(X_train, y_train)
pred=classifier.predict(X_test)
class_name=classifier.__class__.__name__ #2가지: 1) 로지스틱회귀, 2)KNN의 명칭들을 (class_name) 변수에 대입시킴
print('{0} 정확도: {1:.4f}'.format(class_name, accuracy_score(y_test, pred)))
#결과: 3가지 중, 보팅 분류기의 정확도가 가장 높게 나타남 (대체로 그렇지만, 반드시 그렇지는 않음)
# -
# 04) 랜덤포레스트 (Bagging의 대표적인 알고리즘)
# +
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
import pandas as pd
import warnings
warnings.filterwarnings('ignore')
X_train, X_test, y_train, y_test = get_human_dataset()
rf_clf=RandomForestClassifier(random_state=0)
rf_clf.fit(X_train, y_train)
pred=rf_clf.predict(X_test)
accuracy=accuracy_score(y_test, pred)
print('랜덤포레스트 정확도:{0:.4f}'.format(accuracy))
# -
# <랜덤포레스트 하이퍼 모수 및 튜닝하기>
# - 트리기반 앙상블 알고리즘의 단점: 하이퍼 모수가 많고, 튜닝을 위한 시간이 많이 소모됨
# - 다른 방법: GridSearchCV를 이용해 랜덤포레스트의 하이퍼모수를 튜닝하기 (아래 코드 참조)
# +
from sklearn.model_selection import GridSearchCV
params={'n_estimators':[100], 'max_depth':[6,8,10,12], 'min_samples_leaf':[8,12,18], 'min_samples_split':[8,16,20]}
#랜덤포레스트 분류기 객체 생성 후, GridSearchCV 수행하기
rf_clf=RandomForestClassifier(random_state=0, n_jobs=-1) #(n_jobs=-1을 하면 속도 향상됨)
grid_cv=GridSearchCV(rf_clf, param_grid=params, cv=2, n_jobs=-1)
grid_cv.fit(X_train, y_train)
print('최적 하이퍼모수:\n', grid_cv.best_params_)
print('최고 예측 정확도:{0:.4f}'.format(grid_cv.best_score_))
# -
# - 위에서 출력한 하이퍼 모수들을 직접 지정한 후, RandomForestClassifier를 재수행하면 된다 (코드 생략).
#
# 05) GBM (Gradient Boosting Machine, 그래디언트 부스트)
# - 여러 약한 학습기(Learner)를 순차적으로 학습/예측하며, 잘못 예측한 데이터에 가중치를 주어 오류를 개선해가며 학습하는 방식
# - 가중치 업데이트를 경사 하강법 (Gradient Descent)을 이용
# - 즉, 반복수행을 통해 오류를 최소화하도록 가중치 업데이트값을 도출하는 기법
# +
from sklearn.ensemble import GradientBoostingClassifier
import time
import warnings
warnings.filterwarnings('ignore')
X_train, X_test, y_train, y_test=get_human_dataset()
#GBM 수행시간 출력위함: 시작시간 설정
start_time=time.time()
gb_clf=GradientBoostingClassifier(random_state=0)
gb_clf.fit(X_train, y_train)
gb_pred=gb_clf.predict(X_test)
gb_accuracy=accuracy_score(y_test, gb_pred)
print('GBM 정확도: {0:.4f}'.format(gb_accuracy)) #이전 랜덤포레스트보다 개선됨
print('GBM 수행시간: {0:.1f}'.format(time.time()-start_time))
# -
# <GBM 하이퍼 모수 및 튜닝> (생략, P.220~222)
# 06) XGBoost (eXtra Gradient Boost)
# - 트리기반 앙상블학습 중, 유명한 한 알고리즘 (뛰어난 예측성능, 병렬학습이 가능하므로 빠른 학습이 가능)
# - XGBoost의 파이썬 패키지명: xgboost > 1) XGBoost 전용 파이썬 패키지 + 2) 사이킷런과 호환되는 래퍼용 XGBoost
# - 래퍼 클래스 (Wrapper class): 1) XGBClassifier + 2) XGBRegressor
# (래퍼 클래스 덕분에 사이킷런과 연동 가능; 즉, fit(), predict() 등 활용 가능)
# +
#(1) XGBoost 설치하기
#conda install -c anaconda py-xgboost
import xgboost as xgb
from xgboost import XGBClassifier
#conda install -c conda-forge xgboost
#(2) 파이썬 래퍼 XGBoost 하이퍼 모수:
import xgboost
print(xgboost.__version__)
# -
# <파이썬 래퍼 XGBoost 적용하기: 위스콘신 유방암 예측>
# +
import xgboost as xgb
from xgboost import plot_importance
import pandas as pd
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')
dataset=load_breast_cancer()
X_features=dataset.data
y_label=dataset.target
cancer_df=pd.DataFrame(data=X_features, columns=dataset.feature_names)
cancer_df['target']=y_label
cancer_df.head(3)
# -
print(dataset.target_names)
print(cancer_df['target'].value_counts()) #malignant(=0, 악성), benign(=1, 양성)
X_train, X_test, y_train, y_test=train_test_split(X_features, y_label, test_size=0.2, random_state=156)
print(X_train.shape, X_test.shape)
# +
#파이썬 래퍼 XGBoost: 학습/테스트용 데이터셋 만들기 위해, 별도의 객체 DMatrix
#(모수: 1) data (피처 데이터셋), 2) label (레이블 데이터셋(분류일 때) or 숫자형인 종속값 데이터셋(회귀일 때)를 생성함)
#넘파이 형식의 데이터셋을 DMatrix로 변환하기
dtrain=xgb.DMatrix(data=X_train, label=y_train)
dtest=xgb.DMatrix(data=X_test, label=y_test)
# +
#XGBoost 하이퍼모수 설정하기 (딕셔너리 형태로 입력)
params={'max_depth':3, 'eta':0.1, 'objective':'binary:logistic', 'eval_metric':'logloss', 'early_stoppings':100}
num_rounds=400
#XGBoost 모델 학습하기
#(1) train()에서 필요한 한 모수 wlist 변수를 미리 만들기
wlist=[(dtrain, 'train'), (dtest, 'eval')] #dtrain: 훈련(train) 데이터, dtest: 검증(test)데이터 (dtest 써야 조기중단 기능 작동함)
#(2) xgboost 모듈의 train()함수를 호출: 학습하기 (학습이 완료된 모델객체를 반환해 줌)
xgb_model=xgb.train(params=params, dtrain=dtrain, num_boost_round=num_rounds, evals=wlist)
#결과: 계속 오류가 감소함
# +
#(3) 학습이 완료되었으므로, 테스트 데이터셋을 가지고 예측 수행하기 (확률값을 반환해 줌)
pred_probs=xgb_model.predict(dtest)
print('predict() 수행 결과값을 10개만 표시, 예측 확률값으로 표사됨')
print(np.round(pred_probs[:10],3))
#예측확률이 0.5보다 크면 1 (아니면 0)으로 예측값 결정해 리스트 객체 (preds)에 저장하기
preds=[1 if x>0.5 else 0 for x in pred_probs]
print('예측값 10개만 표시:', preds[:10])
# +
#모델의 예측성능을 평가하기
from sklearn.metrics import confusion_matrix, accuracy_score
from sklearn.metrics import precision_score, recall_score
from sklearn.metrics import f1_score, roc_auc_score
# 수정된 get_clf_eval() 함수
def get_clf_eval(y_test, pred=None, pred_proba=None):
confusion = confusion_matrix( y_test, pred)
accuracy = accuracy_score(y_test , pred)
precision = precision_score(y_test , pred)
recall = recall_score(y_test , pred)
f1 = f1_score(y_test,pred)
# ROC-AUC 추가
roc_auc = roc_auc_score(y_test, pred_proba)
print('오차 행렬')
print(confusion)
# ROC-AUC print 추가
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f},\
F1: {3:.4f}, AUC:{4:.4f}'.format(accuracy, precision, recall, f1, roc_auc))
#get_clf_eval(y_test, preds) #(1) y_test: 테스트 실제 레이블 값, (2) preds: 예측 레이블
get_clf_eval(y_test , preds, pred_probs)
# +
import matplotlib.pyplot as plt #중요도 출력하기 (시각화)
# %matplotlib inline
fig, ax = plt.subplots(figsize=(10, 12))
plot_importance(xgb_model, ax=ax) #f0: 1번째 피처, f1: 2번째 피처
# -
# <사이킷런 래퍼 XGBoost 개요/적용하기>
# - 알고리즘 클래스만 XGBoost 래퍼 클래스로 바꾸면, 기존 명령어를 그대로 활용 가능
# - 즉, 사이킷런을 위한 래퍼 XGBoost: 1) XGBClassifier (분류), 2) XGBRegressor (회귀)
# - 사이킷런 래퍼 XGBoost는, 전통(기본)적인 파이썬 래퍼 XGBoost와 모수에서 약간 다름
#
# <앞 데이터셋을 XGBClassifier로 예측하기>
# +
#사이킷런 래퍼 XGBoost 클래스인 XGBClassifier 불러오기
from xgboost import XGBClassifier
xgb_wrapper=XGBClassifier(n_estimators=400, learning_rate=0.1, max_depth=3)
xgb_wrapper.fit(X_train, y_train)
w_preds= xgb_wrapper.predict(X_test)
w_pred_proba = xgb_wrapper.predict_proba(X_test)[:, 1] #교재에 없는데 추가해야 됨
get_clf_eval(y_test , w_preds, w_pred_proba) #3번째 인자 추가해야 함
#결과는 이전과 동일함
# +
#early stopping을 100으로 설정하고 재 학습/예측/평가
from xgboost import XGBClassifier
xgb_wrapper = XGBClassifier(n_estimators=400, learning_rate=0.1, max_depth=3)
evals = [(X_test, y_test)]
xgb_wrapper.fit(X_train, y_train, early_stopping_rounds=100, eval_metric="logloss",
eval_set=evals, verbose=True)
ws100_preds = xgb_wrapper.predict(X_test)
ws100_pred_proba = xgb_wrapper.predict_proba(X_test)[:, 1] #교재에 없는데 추가해야 됨
# -
get_clf_eval(y_test , ws100_preds, ws100_pred_proba) #3번째 인자 추가해야 함
#211번 반복 시 logloss=0.085593인데, 이후 100회동안 이보다 낮아지면서 개선되지가 않아 멈춤 (311번까지 하다가 마침)
# +
from xgboost import plot_importance
import matplotlib.pyplot as plt
# %matplotlib inline
fig, ax = plt.subplots(figsize=(10, 12))
# 사이킷런 래퍼 클래스를 입력해도 무방.
plot_importance(xgb_wrapper, ax=ax)
# -
| 19,027 |
/Cloth Shop Linear Regression Project.ipynb | dc2743ba115d56d4009e909ed4f90e1346ea7666 | [] | no_license | poojakelkar/Data-Science-Study | https://github.com/poojakelkar/Data-Science-Study | 0 | 0 | null | 2020-03-31T19:52:07 | 2020-03-31T19:47:23 | null | Jupyter Notebook | false | false | .py | 497,169 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # DS106 Machine Learning : Lesson Three Companion Notebook
# ### Table of Contents <a class="anchor" id="DS106L3_toc"></a>
#
# * [Table of Contents](#DS106L3_toc)
# * [Page 1 - Introduction](#DS106L3_page_1)
# * [Page 2 - Quadratic Relationships](#DS106L3_page_2)
# * [Page 3 - Quadratic Modeling in R](#DS106L3_page_3)
# * [Page 4 - Exponential Relationships](#DS106L3_page_4)
# * [Page 5 - Exponential Modeling in R](#DS106L3_page_5)
# * [Page 6 - Key Terms](#DS106L3_page_6)
# * [Page 7 - Lesson 3 Hands-On](#DS106L3_page_7)
#
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
#
# # Page 1 - Overview of this Module<a class="anchor" id="DS106L3_page_1"></a>
#
# [Back to Top](#DS106L3_toc)
#
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
from IPython.display import VimeoVideo
# Tutorial Video Name: Non-Linear Modeling
VimeoVideo('246121345', width=720, height=480)
# # Introduction
#
# Previously, you looked at linear models with one predictor and logistic models with one predictor. In this lesson, you will start to look at models that are neither linear nor logistic! There are many non-linear models that exist, but you will only look quadratic and exponential modeling. You will also add on to your work in linear and logistic regression by adding additional predictors (IVs). By the end of this lesson, you should be able to:
#
# * Recognize by shape quadratic and exponential relationships
# * Conduct quadratic modeling in R
# * Conduct exponential modeling in R
#
# This lesson will culminate with a hands-on in which you test data to determine its shape and then run the appropriate non-linear model.
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
#
# # Page 2 - Quadratic Relationships<a class="anchor" id="DS106L3_page_2"></a>
#
# [Back to Top](#DS106L3_toc)
#
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
#
# # Quadratic Relationships
#
# There are many real world situations that can be modeled with a quadratic equation. Any time a ball is thrown, or a projectile is shot, or an arrow is shot, the path of the object will take on the shape of a parabola, or u-shape. The u-shape can be right side up (looking like a smiley mouth) or upside down (looking like a frowny mouth). It may be a full U, or it may only be a partial U. Any parabola can be modeled with an equation of the form y = ax<sup>2</sup> + bx + c.
#
# Here are a few examples of some quadratic relationships:
#
# * Some chemical reactions that will progress based on the square of the concentration of the reagents.
# * The ideal model for profit vs. price in economics.
# * The stopping distance of a car.
#
# Below is the general shape that a quadratic relationship will take in the data:
#
# 
#
# ---
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
#
# # Page 3 - Quadratic Modeling in R<a class="anchor" id="DS106L3_page_3"></a>
#
# [Back to Top](#DS106L3_toc)
#
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
#
# # Quadratic Modeling in R
#
# Now that you're in good *shape* with understanding what quadratic data looks like, you'll learn how to model with quadratic data in R.
#
# ---
#
# ## Load Libraries
#
# All you will need to complete a quadratic model in R is ```ggplot2```, so that you can graph the shape of the data.
#
# ```{r}
# library("ggplot2")
# ```
#
# ---
#
# ## Read in Data
#
# Researchers conducted a study of bluegill fish. They had been tagging fish for years, and were interested in their growth. The data file can be found **[here](https://repo.exeterlms.com/documents/V2/DataScience/Modeling-Optimization/bluegill_fish.zip)**.
#
# ---
#
# ## Question Setup
#
# The question you will be answering is: ```Does the age of the bluegill fish influence their length?```
#
# ---
#
# ## Graph a Quadratic Relationship
#
# If you were unsure whether you had a quadratic relationship with your data, you would want to try to graph it against a best-fit quadratic line to see if your data really was quadratic in nature. You can do that in good 'ol ```ggplot```!
#
# ```{r}
# quadPlot <- ggplot(bluegill_fish, aes(x = age, y=length)) + geom_point() + stat_smooth(method = "lm", formula = y ~x + I(x^2), size =1)
# quadPlot
# ```
#
# You will use ```bluegill_fish``` as your dataset, specify ```age``` as your ```x=``` variable, and specify ```length``` as your ```y=``` variable. Then you can add dots with ```geom_point()```, and add a best fit line with ```stat_smooth()```. As arguments, you will add ```method="lm"```, then write out the quadratic formula, which is ```y ~ x + I(x^2)```.
#
# Here is the end result:
#
# 
#
# Looks like a quadratic line is a pretty good fit for the data!
#
# ---
#
# ## Model the Quadratic Relationship
#
# Now that you are sure you have a quadratic relationship, you can go ahead and model it! You will need to square the x term, however, first. In this example, your x is ```age```. Simply square it like this and save it as its own variable, ```Agesq```:
#
# ```{r}
# Agesq <- bluegill_fish$age^2
# ```
#
# Then you're ready to dust off that favorite tool of yours, ```lm()```. This time, however, you'll use specify a slightly more sophisticated model so that you can make it quadratic in nature! You'll do the y, which is ```length```, by the x, which is ```age```, and then add in the ```Agesq``` variable that you created above.
#
# ```{r}
# quadModel <- lm(bluegill_fish$length~bluegill_fish$age+Agesq)
# summary(quadModel)
# ```
#
# And here is the result you get from the ```summary()``` function:
#
# ```text
# Call:
# lm(formula = bluegill_fish$length ~ bluegill_fish$age + Agesq)
#
# Residuals:
# Min 1Q Median 3Q Max
# -18.6170 -5.7699 -0.6662 5.6881 18.1085
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 2.4242 9.5976 0.253 0.801
# bluegill_fish$age 50.4923 5.2141 9.684 7.53e-15 ***
# Agesq -3.6511 0.6951 -5.253 1.36e-06 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 7.911 on 75 degrees of freedom
# Multiple R-squared: 0.8954, Adjusted R-squared: 0.8926
# F-statistic: 320.9 on 2 and 75 DF, p-value: < 2.2e-16
# ```
#
# Looking at the overall ```F-statistic``` shown on the bottom and associated ```p-value```, this quadratic model is significant! This means that age is a significant quadratic predictor of bluegill fish length.
#
# <div class="panel panel-success">
# <div class="panel-heading">
# <h3 class="panel-title">Additional Info!</h3>
# </div>
# <div class="panel-body">
# <p>If you would like to learn about exponential regression in Python, <a href="https://www.youtube.com/watch?v=ro5ftxuD6is"> click here.</a> If you would like to learn about exponential regression in Google Sheets, <a href="https://www.youtube.com/watch?v=30yEVjbeq0o"> click here! </a></p>
# </div>
# </div>
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
#
# # Page 4 - Exponential Relationships<a class="anchor" id="DS106L3_page_4"></a>
#
# [Back to Top](#DS106L3_toc)
#
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
#
# # Exponential Relationships
#
# There are natural phenomena that will either increase or decrease exponentially. In today's vernacular, the word "viral" is a sort of substitution for the word exponential. If your Tweet goes "viral," it might simply mean that you told 4 followers, and each of those 4 friends retweeted it to their 4 followers, etc. Before you know it, the tweet has been retweeted tens or even hundreds of thousands of times.
#
# Exponential changes can either be growth or decay. Through the magic of compound interest, your investment account can grow exponentially. On the other hand, radioactive materials typically decay exponentially.
#
# Graphed in statistics, an exponential relationship will usually look something like this:
#
# 
#
# ---
#
# ## Decibel Scale Example
#
# There are some common things with which you are probably familiar that are exponential. For example, noise is on an exponential scale called the decibel (dB) scale. In fact, the noise scale is exponential both in intensity, and 'loudness.' For instance, a sound at 40 dB would be quiet talking, whereas a sound at 50 dB (louder conversation) would be 10 times as intense, and twice as loud.
#
# A change of 10 dB is not that big of a deal, but a change of 40 dB (for instance) is a pretty big change. Again starting at 40 dB, a change to 80 dB (loud highway noise at close range) is change of intensity of 10,000x, and a change in loudness of 16x. An 80 dB sound is much more than just twice the intensity or loudness of a 40 dB sound. Take a look:
#
# 
#
# ---
#
# ## Richter Scale Example
#
# Another common measurement that is also exponential is the Richter scale, which measures magnitude of an earthquake. The scale goes from 1 to 9, but each increase of 1 on the Richter scale translates to an earthquake that has a shaking amplitude that is 10 times higher, and the energy released is 31.6 times as high. A magnitude 5 earthquake is usually felt by those at the epicenter, but the damage is usually minimal unless the buildings are poorly constructed. They rarely get reported unless they are felt in heavily populated areas. On average, there are usually 3 to 5 of these earthquakes every day. On the other hand, a magnitude 6 earthquake can usually be felt up to a couple hundred miles from the epicenter, and damage will vary depending on the quality of the construction at the epicenter. However, they still happen at least a couple times a week.
#
# An earthquake that measures 7 on the Richter scale is considered to be a major quake. Buildings at the center will suffer major damage to complete collapse, and buildings as much as 150 miles away will have some damage. These occur 1 - 2 times per month. At 8, an earthquake causes major damage to total destruction to even the most sturdy structures at the epicenter, and damage will be widespread. These can be felt several hundred miles away. You get about one of these each year. An earthquake that measures 9 or more on the Richter scale will happen once every 10 to 20 years, usually causes total destruction at the epicenter, and can cause permanent changes in the local topography. The most recent earthquake 9 or higher was in Japan in 2011. Prior to that was the earthquake is Sumatra on the day after Christmas in 2004 (9.1 on the Richter scale); the tsunami that followed killed nearly a quarter of a million people. Prior to these two, the last earthquake of magnitude 9 or higher was way back in the 1960's.
#
# 
#
# ---
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
#
# # Page 5 - Exponential Modeling in R<a class="anchor" id="DS106L3_page_5"></a>
#
# [Back to Top](#DS106L3_toc)
#
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
#
# # Exponential Modeling in R
#
# Now that you have an idea of what to expect in an exponential model, you will try one in R!
#
# ---
#
# ## Load Libraries
#
# Believe it or not, you won't need any additional libraries outside of what's included in base R.
#
# ---
#
# ## Read in Data
#
# A certain strain of bacteria was grown in a controlled environment. Most organisms will grow exponentially until something else starts to inhibit that growth - whether it be predators, or limited food. The exponential growth can be modeled using a regression equation. The Bacteria count was recorded for evenly spaced time periods, and **[the data are shown here](https://repo.exeterlms.com/documents/V2/DataScience/Modeling-Optimization/bacteria.zip)**
#
# ---
#
# ## Question Setup
#
# You are trying to answer the question of how does much does bacteria grow over time. You will examine the change in ```Count```, your y variable, over time ```Period```, your x variable.
#
# ---
#
# ## Exponential Modeling
#
# As with quadratic modeling, you will start by using the ```lm()``` function. However, you will need to take the log of the y variable using the ```log()``` function:
#
# ```{r}
# exMod <- lm(log(bacteria$Count)~bacteria$Period)
# summary(exMod)
# ```
#
# Calling a summary on this model results in this:
#
# ```text
# Call:
# lm(formula = log(bacteria$Count) ~ bacteria$Period)
#
# Residuals:
# Min 1Q Median 3Q Max
# -0.106956 -0.038992 0.002216 0.025141 0.076005
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 2.703652 0.024358 111.00 <2e-16 ***
# bacteria$Period 0.164782 0.002647 62.25 <2e-16 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 0.05106 on 16 degrees of freedom
# Multiple R-squared: 0.9959, Adjusted R-squared: 0.9956
# F-statistic: 3875 on 1 and 16 DF, p-value: < 2.2e-16
# ```
#
# By looking at the bottom ```F-statistic``` and associated ```p-value```, you see that this model is significant! That means that this particular bacteria does demonstrate exponential growth over time. Looking at the ```Estimate``` column, you can see that for every one additional time b in, the bacteria has increased by 16%!
#
# <div class="panel panel-success">
# <div class="panel-heading">
# <h3 class="panel-title">Additional Info!</h3>
# </div>
# <div class="panel-body">
# <p>If you would like to learn about exponential regression in Python, <a href="https://plot.ly/python/exponential-fits/"> check out Plotly. </a></p>
# </div>
# </div>
#
# ---
#
# ## Summary
#
# * Quadratic regression can be used to model data that shows a non-linear relationship.
# * Exponential regression can be used to model phenomena that exhibit bounding growth or exponential decay.
#
# ---
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
#
# # Page 6 - Key Terms<a class="anchor" id="DS106L3_page_6"></a>
#
# [Back to Top](#DS106L3_toc)
#
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
#
# # Key Terms
#
# Below is a list and short description of the important keywords learned in this lesson. Please read through and go back and review any concepts you do not fully understand. Great Work!
#
# <table class="table table-striped">
# <tr>
# <th>Keyword</th>
# <th>Description</th>
# </tr>
# <tr>
# <td style="font-weight: bold;" nowrap>Quadratic Relationship</td>
# <td>A parabola, or U-shaped curve, in the data.</td>
# </tr>
# <tr>
# <td style="font-weight: bold;" nowrap>Exponential Relationship</td>
# <td>A graph that continues upward or downward at a non-steady rate, gathering steam as it goes.</td>
# </tr>
# </table>
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
#
# # Page 7 - Lesson 3 Hands-On<a class="anchor" id="DS106L3_page_7"></a>
#
# [Back to Top](#DS106L3_toc)
#
# <hr style="height:10px;border-width:0;color:gray;background-color:gray">
#
#
#
# # Nonlinear Regression Hands-On
#
# This Hands-On **will** be graded. The best way to become a data scientist is to practice!
#
# <div class="panel panel-danger">
# <div class="panel-heading">
# <h3 class="panel-title">Caution!</h3>
# </div>
# <div class="panel-body">
# <p>Do not submit your project until you have completed all requirements, as you will not be able to resubmit.</p>
# </div>
# </div>
#
# Data from **[the following spreadsheet](https://repo.exeterlms.com/documents/V2/DataScience/Modeling-Optimization/nonlinear.zip)** will be used throughout this hands on. You have two sets of X and Y variables here; graph and analyze both and determine what non-linear form they best follow. These two sets of X and Ys might both be exponential relationships or quadratic relationships, or there might be one of each. The best way to figure it out is to try and fit both a quadratic function and an exponential function to each pair of variables, and then model each to determine which model is a better fit.
#
# To complete this hands on, you will need to:
#
# 1. Create a scatterplot of the data with the Y variable on the vertical axis, and the X variable on the horizontal axis.
# 2. Using eyeball analysis, make a guess about what type of model will work best for the dataset. You can add the best fit quadratic line as well to determine if it's a good fit.
# 3. Using the chosen model from step 2, complete the steps to perform the analysis that were listed in the lesson.
#
#
# <div class="panel panel-danger">
# <div class="panel-heading">
# <h3 class="panel-title">Caution!</h3>
# </div>
# <div class="panel-body">
# <p>Be sure to zip and submit your entire directory when finished!</p>
# </div>
# </div>
#
#
| 19,031 |
/Copy_of_Weekly_Project_MNIST.ipynb | 159cead6ef10d8a7183a470d5327d2c6fba71f9a | [] | no_license | mong-pnh/DS24-CoderSchool2020 | https://github.com/mong-pnh/DS24-CoderSchool2020 | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 120,149 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] id="lLy5PsIql9A5"
# # 5. Validation & Testing
# + [markdown] id="P6L-ynOvokKT"
# Welcome to the fifth notebook of our six part series part of our tutorial on Deep Learning for Human Activity Recognition. Within the last notebook you learned:
#
# - How do I define a sample neural network architecture in PyTorch?
# - What additional preprocessing do I need to apply to my data to fed it into my network?
# - How do I define a train loop which trains my neural network?
#
# This notebook will teach you everything you need to know about validation and testing. When building a predictive pipeline there are a lot of parameters which one needs to set before comencing the actual training. Coming up with a suitable set of hyperparameters is called hypertuning. In order to gain feedback whether the applied hyperparameters are a good choice, we check the predictive performance of our model on the validation set. This is called validation.
#
# Now you might ask yourself: Solely relying and tuning based on the validation scores would inherit that your trained model would end up being too well optimized on the validation set and thus not general anymore, right? If asked yourself that question, then you are 100% right in your assumption! This is what we call overfitting and is one of the major pitfalls in Machine Learning.Overfitting your model results in bad prediction performance on unseen data.
#
# We therefore need a third dataset, called the test dataset. The test dataset is a part of the initial dataset which you keep separate from all optimization steps. It is only used to gain insights on the predictive performance of the model and must not (!) be used as a reference for tuning hyperparameters. As we mentioned in during the theoretical parts of this tutorial, (supervised) Deep Learning, in our opinion, is just a fancy word for function approximation. If your model performs both well during validation and testing, it is a general function which properly approximates the underlying function.
#
# After completing this notebook you will be answer the following questions:
# - How do I split my initial dataset into a train, validation and test dataset?
# - What validation methods exist in Human Activity Recognition? How are they performed?
# - How is testing usually performed?
# + [markdown] id="G4fWjW5V0_MT"
# ## 5.1. Important Remarks
# + [markdown] id="pkhCF6Pd1B1Z"
# If you are accessing this tutorial via [Google Colab](https://colab.research.google.com/github/mariusbock/dl-for-har/blob/main/tutorial_notebooks/training.ipynb), first make sure to use Google Colab in English. This will help us to better assist you with issues that might arise during the tutorial. There are two ways to change the default language if it isn't English already:
# 1. On Google Colab, go to `Help` -> `View in English`
# 2. Change the default language of your browser to `English`.
#
# To also ease the communication when communicating errors, enable line numbers within the settings of Colab.
#
# 1. On Google Colab, go to `Tools` -> `Settings` -> `Editor` -> `Show line numbers`
#
# In general, we strongly advise you to use Google Colab as it provides you with a working Python distribution as well as free GPU resources. To make Colab use GPUs, you need to change the current notebooks runtime type via:
#
# - `Runtime` -> `Change runtime type` -> `Dropdown` -> `GPU` -> `Save`
#
# **Hint:** you can auto-complete code in Colab via `ctrl` + `spacebar`
#
# For the live tutorial, we require all participants to use Colab. If you decide to rerun the tutorial at later points and rather want to have it run locally on your machine, feel free to clone our [GitHub repository](https://github.com/mariusbock/dl-for-har).
#
# To get started with this notebook, you need to first run the code cell below. Please set `use_colab` to be `True` if you are accessing this notebook via Colab. If not, please set it to `False`. This code cell will make sure that imports from our GitHub repository will work.
# + id="si3n5Sc51L-D"
import os, sys
use_colab = True
module_path = os.path.abspath(os.path.join('..'))
if use_colab:
# move to content directory and remove directory for a clean start
# %cd /content/
# %rm -rf dl-for-har
# clone package repository (will throw error if already cloned)
# !git clone https://github.com/mariusbock/dl-for-har.git
# navigate to dl-for-har directory
# %cd dl-for-har/
else:
os.chdir(module_path)
# this statement is needed so that we can use the methods of the DL-ARC pipeline
if module_path not in sys.path:
sys.path.append(module_path)
# + [markdown] id="BIjrK-KE1iDL"
# ## 5.1. Splitting your data
# + [markdown] id="HrLU2e9H1oAX"
# Within the first part of this notebook we will split our data in the above mentioned three datasets, namely the train, validation and test dataset. There are multiple ways how to split the data into the two respective datasets, for example:
#
# - **Subject-wise:** split according to participants within the dataset. This means that we are reserving certain subjects to be included in the train, validation and test set respectively. For example, given that there are a total of 10 subjects, you could use 6 subjects for trainig, 2 subjects for validation and 2 subjects for testing.
# - **Percentage-wise:** state how large percentage-wise your train, validation and test dataset should be compared to the full dataset. For example, you could use 60% of your data for training, 20% for validation and 20% for testing. The three splits can also be chosen to be stratified, meaning that the relative label distribution within each of the two dataset is kept the same as in the full dataset. Note that stratifiying your data would require the data to be shuffled.
# - **Record-wise:** state how many records should be in your train, validation and test dataset should be contained, i.e. define two cutoff points. For example, given that there are 1 million records in your full dataset, you could have the first 600 thousand records to be contained in the train dataset, the next 200 thousand in the validation dataset and the remaining 200 thousand records to be contained in the test dataset.
#
# **WARNING:** shuffling your dataset during splitting (which is e.g. needed for stratified splits) will destroy the time-dependencies among the data records. To minimize this effect, apply a sliding window on top of your data before splitting. This way, time-dependencies will at least be preserved within the windows. While working on this notebook, we will notify you when this is necessary.
#
# To keep things simple and fast, we will be splitting our data subject-wise. We will use the first data of the first subject for training, the data of the second subject for validation and the data of the third subject for testing. Your first task will be to perform said split. Note that we already imported the dataset for you using the `load_dataset()` function, which is part of the DL-ARC feature stack.
# + [markdown] id="MIAoSI0Ql9BC"
# ### Task 1: Split the data into train, validation and test data
# + [markdown] id="1_QkR_bHl9BC"
# 1. Define the `train` dataset to be the data of the first subject, i.e. with `subject_identifier = 0`. (`lines 13-14`)
# 2. Define the `valid` dataset to be the data of the second subject, i.e. with `subject_identifier = 1`. (`lines 15-16`)
# 3. Define the `test` dataset to be the data of the third subject, i.e. with `subject_identifier = 2`. (`lines 17-18`)
# 4. Define a fourth dataset being a concatenated version of the `train` and `valid` dataset called `train_valid`. You will need this dataset for some of the validation methods. Use `pd.concat()` in order to concat the two Pandas dataframes along `axis=0`. (`lines 20-21`)
# + id="el2x8KMJl9BE"
import numpy as np
import warnings
warnings.filterwarnings("ignore")
from data_processing.preprocess_data import load_dataset
# data loading (we are using a predefined method called load_dataset, which is part of the DL-ARC feature stack)
X, y, num_classes, class_names, sampling_rate, has_null = load_dataset('rwhar_3sbjs', include_null=True)
# since the method returns features and labels separatley, we need to concat them
data = np.concatenate((X, y[:, None]), axis=1)
# define the train data to be the data of the first subject
train_data =
# define the valid data to be the data of the second subject
valid_data =
# define the test data to be the data of the third subject
test_data =
# define the train_valid_data by concatenating the train and validation dataset
train_valid_data =
print('\nShape of the train, validation and test dataset:')
print(train_data.shape, valid_data.shape, test_data.shape)
print('\nShape of the concatenated train_valid dataset:')
print(train_valid_data.shape)
# + [markdown] id="HzCPsMcd4koA"
# ## 5.2. Define the hyperparameters
# + [markdown] id="u_q8TpPal9BE"
# Before we go over talking about how to perform validation in Human Activtiy Recognition, we need to define our hyperparameters again. As you know from the previous notebook, it is common practice to track all your settings and parameters in a compiled `config` object. Due to fact that we will be using pre-implemented methods of the feature stack of the DL-ARC GitHub, we will now need to define a more complex `config` object.
#
# Within the next code block we defined a sample `config` object for you. It contains some parameters which you already know from previous notebooks, but also lots which you don't know. We will not cover all of them during this tutorial, but encourage you to check out the complete implementation of the DL-ARC. We also separated the parameters into two groups for you, once which you can play around with and ones which you should handle with care and rather leave as is.
# + id="jjZYXFX6l9BF"
config = {
#### TRY AND CHANGE THESE PARAMETERS ####
# sliding window settings
'sw_length': 50,
'sw_unit': 'units',
'sampling_rate': 50,
'sw_overlap': 30,
# network settings
'nb_conv_blocks': 2,
'conv_block_type': 'normal',
'nb_filters': 64,
'filter_width': 11,
'nb_units_lstm': 128,
'nb_layers_lstm': 1,
'drop_prob': 0.5,
# training settings
'epochs': 10,
'batch_size': 100,
'loss': 'cross_entropy',
'use_weights': True,
'weights_init': 'xavier_uniform',
'optimizer': 'adam',
'lr': 1e-4,
'weight_decay': 1e-6,
### UP FROM HERE YOU SHOULD RATHER NOT CHANGE THESE ####
'batch_norm': False,
'dilation': 1,
'pooling': False,
'pool_type': 'max',
'pool_kernel_width': 2,
'reduce_layer': False,
'reduce_layer_output': 10,
'nb_classes': 8,
'seed': 1,
'gpu': 'cuda:0',
'verbose': False,
'print_freq': 10,
'save_gradient_plot': False,
'print_counts': False,
'adj_lr': False,
'adj_lr_patience': 5,
'early_stopping': False,
'es_patience': 5,
'save_test_preds': False
}
# + [markdown] id="T0WRQj1dl9BF"
# ## 5.3. Validation
# + [markdown] id="GhwdRETQ8t9D"
# Within the next segment we will explain the most prominent validation methods used in Human Activity Recognition. These are:
#
# - Train-Valid Split
# - k-Fold Cross-Validation
# - Cross-Participant Cross-Validation
# + [markdown] id="kQPUaRRE8AC9"
# ### 5.3.1. Train-Valid Split
# + [markdown] id="r8BS4Qf3l9BF"
# The train-valid split is one of the most basic validation method, which you already did yourself. Instead of varying the validation set and getting a more holistic view, we define it to be a set part of the data. As mentioned above there are multiple ways how to do so. For simplicity purposes, we chose to use a subject-wise split. Within the next task you will be asked to train your network using the `train` data and obtain predictions on the `valid` data. We do not ask you to define the training loop again and allow you to use the built-in `train` function of the DL-ARC.
# + [markdown] id="dOcMYLvTl9BF"
# #### Task 2: Implementing the train-valid split validation loop
# + [markdown] id="XsRp7hDNl9BF"
# 1. As you already defined the train and valid dataset you can go ahead and apply a sliding window on top of both datasets. You can use the predefined method `apply_sliding_window()`, which is part of the DL-ARC pipeline, to do so. It is already be imported for you. We will give you hints on what to pass the method. (`lines 21-27`)
# 2. (*Optional*) Omit the first feature column (subject_identifier) from the train and validation dataset. (`lines 29-31`)
# 3. Within the `config` object, set the parameters `window_size` and `nb_channels` accordingly. (`lines 33-37`)
# 4. Using the windowed features and labels of both the train and valid set to train a model and obtain validation results. You can use the `DeepConvLSTM` object and `train` function of the DL-ARC pipeline. It is already imported for you. As this is quite a complex task, we will give you hints along the way. (`lines 39-48`)
# + id="61uZSoSdl9BG"
import time
import numpy as np
import torch
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_score, recall_score, f1_score, jaccard_score
from model.train import train
from model.DeepConvLSTM import DeepConvLSTM
from data_processing.sliding_window import apply_sliding_window
# in order to get reproducible results, we need to seed torch and other random parts of our implementation
seed_torch(config['seed'])
# needed for saving results
log_date = time.strftime('%Y%m%d')
log_timestamp = time.strftime('%H%M%S')
print(train_data.shape, valid_data.shape)
# apply the sliding window on top of both the train and validation data; use the "apply_sliding_window" function
# found in data_processing.sliding_window
X_train, y_train =
print(X_train.shape, y_train.shape)
X_valid, y_valid =
print(X_valid.shape, y_valid.shape)
# (optional) omit the first feature column (subject_identifier) from the train and validation dataset
# you can do it if you want to as it is not a useful feature
X_train, X_valid =
# within the config file, set the parameters 'window_size' and 'nb_channels' accordingly
# window_size = size of the sliding window in units
# nb_channels = number of feature channels
config['window_size'] =
config['nb_channels'] =
# define the network to be a DeepConvLSTM object; can be imported from model.DeepConvLSTM
# pass it the config object
net =
# defines the loss and optimizer
loss = torch.nn.CrossEntropyLoss()
opt = torch.optim.Adam(net.parameters(), lr=config['lr'], weight_decay=config['weight_decay'])
# convert the features of the train and validation to float32 and labels to uint8 for GPU compatibility
X_train, y_train =
X_valid, y_valid =
# feed the datasets into the train function; can be imported from model.train
train_valid_net, val_output, train_output =
# the next bit prints out your results if you did everything correctly
cls = np.array(range(config['nb_classes']))
print('\nVALIDATION RESULTS: ')
print("\nAvg. Accuracy: {0}".format(jaccard_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("Avg. Precision: {0}".format(precision_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("Avg. Recall: {0}".format(recall_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("Avg. F1: {0}".format(f1_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("\nVALIDATION RESULTS (PER CLASS): ")
print("\nAccuracy:")
for i, rslt in enumerate(jaccard_score(val_output[:, 1], val_output[:, 0], average=None, labels=cls)):
print(" {0}: {1}".format(class_names[i], rslt))
print("\nPrecision:")
for i, rslt in enumerate(precision_score(val_output[:, 1], val_output[:, 0], average=None, labels=cls)):
print(" {0}: {1}".format(class_names[i], rslt))
print("\nRecall:")
for i, rslt in enumerate(recall_score(val_output[:, 1], val_output[:, 0], average=None, labels=cls)):
print(" {0}: {1}".format(class_names[i], rslt))
print("\nF1:")
for i, rslt in enumerate(f1_score(val_output[:, 1], val_output[:, 0], average=None, labels=cls)):
print(" {0}: {1}".format(class_names[i], rslt))
print("\nGENERALIZATION GAP ANALYSIS: ")
print("\nTrain-Val-Accuracy Difference: {0}".format(jaccard_score(train_output[:, 1], train_output[:, 0], average='macro') -
jaccard_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("Train-Val-Precision Difference: {0}".format(precision_score(train_output[:, 1], train_output[:, 0], average='macro') -
precision_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("Train-Val-Recall Difference: {0}".format(recall_score(train_output[:, 1], train_output[:, 0], average='macro') -
recall_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("Train-Val-F1 Difference: {0}".format(f1_score(train_output[:, 1], train_output[:, 0], average='macro') -
f1_score(val_output[:, 1], val_output[:, 0], average='macro')))
# + [markdown] id="_BepnQk8l9BH"
# ### 5.3.2. K-Fold Cross-Validation
# + [markdown] id="5OlOGi55l9BJ"
# The k-fold cross-validation is the most popular form of cross-validation. Instead of only splitting our data once into a train and validation dataset, like we did in the previous validation method, we take the average of k different train-valid splits. To do so we take our concatenated version of the train and validation set and split it into k equal-sized chunks of data. A so-called fold is now that we train our network using all but one of these chunks of data and validate it using the chunk we excluded (thus being unseen data). The process is repeated k-times, i.e. k-folds, so that each chunk of data is the validation dataset exactly once. Note that with each fold, the network needs to be reinitialized, i.e. trained from scratch, to ensure that it is not predicting already seen data.
#
#
# **Note:** It is recommended to use stratified k-fold cross-validation, i.e. each of the k chunks of data has the same distribution of labels as the original full dataset. This avoids the risk, especially for unbalanced datasets, of having certain labels missing within the train dataset, which would cause the validation process to break. Nevertheless, as also stated above, stratification requires shuffeling and thus one should always first apply the sliding window before applying the split.
#
# The next task will lead you through the implementation of the k-fold cross-validation loop. In order to chunk your data and also apply stratification, we recommend you to use the scikit-learn helper object for stratified k-fold cross-validation called `StratifiedKFold`.
# + [markdown] id="1sK2SCNYl9BJ"
# #### Task 3: Implementing the k-fold CV loop
# + [markdown] id="iirq5yFll9BK"
# 1. Define the scikit-learn helper object for stratified k-fold cross-validation called `StratifiedKFold`. It is already imported for you. We will also give you hints what to pass it as arguments. (`lines 14-16`)
# 2. Apply the `apply_sliding_window()` function on top of the `train_valid_data` object which you previously defined. (`lines 20-24`)
# 3. (*Optional*) Omit the first feature column (subject_identifier) from the `train_valid_data` dataset. (`lines 26-28`)
# 4. Define the k-fold loop; use the `split()` function of the `StratifiedKFold` object to obtain indeces to split the `train_valid_data` (`lines 42-49`)
# 5. Having split the data, run the train function with it and add up obtained results to the accumulated result objects. (`lines 51-66`)
# + id="Wnh-tBGAl9BK"
from sklearn.model_selection import StratifiedKFold
# number of splits, i.e. folds
config['splits_kfold'] = 10
# in order to get reproducible results, we need to seed torch and other random parts of our implementation
seed_torch(config['seed'])
# needed for saving results
log_date = time.strftime('%Y%m%d')
log_timestamp = time.strftime('%H%M%S')
# define the stratified k-fold object; it is already imported for you
# pass it the number of splits, i.e. folds, and seed as well as set shuffling to true
skf =
print(train_valid_data.shape)
# apply the sliding window on top of both the train_valid_data; use the "apply_sliding_window" function
# found in data_processing.sliding_window
X_train_valid, y_train_valid =
print(X_train_valid.shape, y_train_valid.shape)
# (optional) omit the first feature column (subject_identifier) from the train _valid_data
# you can do it if you want to as it is not a useful feature
X_train_valid =
# result objects used for accumulating the scores across folds; add each fold result to these objects so that they
# are averaged at the end of the k-fold loop
kfold_accuracy = np.zeros(config['nb_classes'])
kfold_precision = np.zeros(config['nb_classes'])
kfold_recall = np.zeros(config['nb_classes'])
kfold_f1 = np.zeros(config['nb_classes'])
kfold_accuracy_gap = 0
kfold_precision_gap = 0
kfold_recall_gap = 0
kfold_f1_gap = 0
# k-fold validation loop; for each loop iteration return fold identifier and indeces which can be used to split
# the train + valid data into train and validation data according to the current fold
for j, (train_index, valid_index) in enumerate():
print('\nFold {0}/{1}'.format(j + 1, config['splits_kfold']))
# split the data into train and validation data; to do so, use the indeces produces by the split function
X_train, X_valid =
y_train, y_valid =
# within the config file, set the parameters 'window_size' and 'nb_channels' accordingly
# window_size = size of the sliding window in units
# nb_channels = number of feature channels
config['window_size'] =
config['nb_channels'] =
# define the network to be a DeepConvLSTM object; can be imported from model.DeepConvLSTM
# pass it the config object
net =
# defines the loss and optimizer
loss = torch.nn.CrossEntropyLoss()
opt = torch.optim.Adam(net.parameters(), lr=config['lr'], weight_decay=config['weight_decay'])
# convert the features of the train and validation to float32 and labels to uint8 for GPU compatibility
X_train, y_train =
X_valid, y_valid =
# feed the datasets into the train function; can be imported from model.train
kfold_net, val_output, train_output =
# in the following validation and train evaluation metrics are calculated
cls = np.array(range(config['nb_classes']))
val_accuracy = jaccard_score(val_output[:, 1], val_output[:, 0], average=None, labels=cls)
val_precision = precision_score(val_output[:, 1], val_output[:, 0], average=None, labels=cls)
val_recall = recall_score(val_output[:, 1], val_output[:, 0], average=None, labels=cls)
val_f1 = f1_score(val_output[:, 1], val_output[:, 0], average=None, labels=cls)
train_accuracy = jaccard_score(train_output[:, 1], train_output[:, 0], average=None, labels=cls)
train_precision = precision_score(train_output[:, 1], train_output[:, 0], average=None, labels=cls)
train_recall = recall_score(train_output[:, 1], train_output[:, 0], average=None, labels=cls)
train_f1 = f1_score(train_output[:, 1], train_output[:, 0], average=None, labels=cls)
# add up the fold results
kfold_accuracy += val_accuracy
kfold_precision += val_precision
kfold_recall += val_recall
kfold_f1 += val_f1
# add up the generalization gap results
kfold_accuracy_gap += train_accuracy - val_accuracy
kfold_precision_gap += train_precision - val_precision
kfold_recall_gap += train_recall - val_recall
kfold_f1_gap += train_f1 - val_f1
# the next bit prints out the average results across folds if you did everything correctly
print("\nK-FOLD VALIDATION RESULTS: ")
print("Accuracy: {0}".format(np.mean(kfold_accuracy / config['splits_kfold'])))
print("Precision: {0}".format(np.mean(kfold_precision / config['splits_kfold'])))
print("Recall: {0}".format(np.mean(kfold_recall / config['splits_kfold'])))
print("F1: {0}".format(np.mean(kfold_f1 / config['splits_kfold'])))
print("\nVALIDATION RESULTS (PER CLASS): ")
print("\nAccuracy:")
for i, rslt in enumerate(kfold_accuracy / config['splits_kfold']):
print(" {0}: {1}".format(class_names[i], rslt))
print("\nPrecision:")
for i, rslt in enumerate(kfold_precision / config['splits_kfold']):
print(" {0}: {1}".format(class_names[i], rslt))
print("\nRecall:")
for i, rslt in enumerate(kfold_recall / config['splits_kfold']):
print(" {0}: {1}".format(class_names[i], rslt))
print("\nF1:")
for i, rslt in enumerate(kfold_f1 / config['splits_kfold']):
print(" {0}: {1}".format(class_names[i], rslt))
print("\nGENERALIZATION GAP ANALYSIS: ")
print("\nAccuracy: {0}".format(kfold_accuracy_gap / config['splits_kfold']))
print("Precision: {0}".format(kfold_precision_gap / config['splits_kfold']))
print("Recall: {0}".format(kfold_recall_gap / config['splits_kfold']))
print("F1: {0}".format(kfold_f1_gap / config['splits_kfold']))
# + [markdown] id="jI5ztrFyl9BL"
# ### 5.3.3. Cross-Participant Cross-Validation
# + [markdown] id="vgc5fBYMl9BL"
# Cross-participant cross-validation, also known as Leave-One-Subject-Out (LOSO) cross-validation is the most complex, but also most expressive validation method one can apply when dealing with multi-subject data. In general, it can be seen as a variation of the k-fold cross-validation with k being the number of subjects. Within each fold, you train your network on the data of all but one subject and validate it on the left-out subject. The process is repeated as many times as there are subjects so that each subject becomes the validation set exaclty once. This way, each subject is treated as the unseen data at least once.
#
# Leaving one subject out each fold ensures that the overall evaluation of the algorithm does not overfit on subject-specific traits, i.e. how subjects performed the activities individually. It is therefore a great method to obtain a model which is good at predicting activities no matter which person performs them, i.e. a more general model!
#
# The next task will lead you through the implementation of the cross-participant cross-validation loop.
# + [markdown] id="xxmMLN71l9BM"
# #### Task 4: Implementing the cross-participant CV loop
# + [markdown] id="3yaGaXanl9BM"
# 1. Define a loop which iterates over the identifiers of all subjects. (`lines 8-10`)
# 2. Define the `train` data to be everything but the current subject's data and the `valid` data to be the current subject's data by filtering the `train_valid_data`. (`lines 12-15`)
# 3. Apply the `apply_sliding_window()` function on top of the filtered datasets you just defined. (`lines 19-27`)
# 4. (*Optional*) Omit the first feature column (subject_identifier) from the train and validation dataset. (`lines 29-31`)
# 5. Use both datasets to run the `train()` function. (`lines 33-47`)
# + id="vcUekkJal9BM"
# needed for saving results
log_date = time.strftime('%Y%m%d')
log_timestamp = time.strftime('%H%M%S')
# in order to get reproducible results, we need to seed torch and other random parts of our implementation
seed_torch(config['seed'])
# iterate over all subjects
for i, sbj in enumerate():
print('\n VALIDATING FOR SUBJECT {0} OF {1}'.format(int(sbj) + 1, int(np.max(train_valid_data[:, 0])) + 1))
# define the train data to be everything, but the data of the current subject
train_data =
# define the validation data to be the data of the current subject
valid_data =
print(train_data.shape, valid_data.shape)
# apply the sliding window on top of both the train and validation data; use the "apply_sliding_window" function
# found in data_processing.sliding_window
X_train, y_train =
print(X_train.shape, y_train.shape)
X_valid, y_valid =
print(X_valid.shape, y_valid.shape)
# (optional) omit the first feature column (subject_identifier) from the train and validation dataset
# you can do it if you want to as it is not a useful feature
X_train, X_valid =
# within the config file, set the parameters 'window_size' and 'nb_channels' accordingly
# window_size = size of the sliding window in units
# nb_channels = number of feature channels
config['window_size'] =
config['nb_channels'] =
# define the network to be a DeepConvLSTM object; can be imported from model.DeepConvLSTM
# pass it the config object
net =
# defines the loss and optimizer
loss = torch.nn.CrossEntropyLoss()
opt = torch.optim.Adam(net.parameters(), lr=config['lr'], weight_decay=config['weight_decay'])
# convert the features of the train and validation to float32 and labels to uint8 for GPU compatibility
X_train, y_train =
X_valid, y_valid =
cross_participant_net, val_output, train_output =
# the next bit prints out the average results per subject if you did everything correctly
cls = np.array(range(config['nb_classes']))
print('\nVALIDATION RESULTS FOR SUBJECT {0}: '.format(int(sbj) + 1))
print("\nAvg. Accuracy: {0}".format(jaccard_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("Avg. Precision: {0}".format(precision_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("Avg. Recall: {0}".format(recall_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("Avg. F1: {0}".format(f1_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("\nVALIDATION RESULTS (PER CLASS): ")
print("\nAccuracy:")
for i, rslt in enumerate(jaccard_score(val_output[:, 1], val_output[:, 0], average=None, labels=cls)):
print(" {0}: {1}".format(class_names[i], rslt))
print("\nPrecision:")
for i, rslt in enumerate(precision_score(val_output[:, 1], val_output[:, 0], average=None, labels=cls)):
print(" {0}: {1}".format(class_names[i], rslt))
print("\nRecall:")
for i, rslt in enumerate(recall_score(val_output[:, 1], val_output[:, 0], average=None, labels=cls)):
print(" {0}: {1}".format(class_names[i], rslt))
print("\nF1:")
for i, rslt in enumerate(f1_score(val_output[:, 1], val_output[:, 0], average=None, labels=cls)):
print(" {0}: {1}".format(class_names[i], rslt))
print("\nGENERALIZATION GAP ANALYSIS: ")
print("\nTrain-Val-Accuracy Difference: {0}".format(jaccard_score(train_output[:, 1], train_output[:, 0], average='macro') -
jaccard_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("Train-Val-Precision Difference: {0}".format(precision_score(train_output[:, 1], train_output[:, 0], average='macro') -
precision_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("Train-Val-Recall Difference: {0}".format(recall_score(train_output[:, 1], train_output[:, 0], average='macro') -
recall_score(val_output[:, 1], val_output[:, 0], average='macro')))
print("Train-Val-F1 Difference: {0}".format(f1_score(train_output[:, 1], train_output[:, 0], average='macro') -
f1_score(val_output[:, 1], val_output[:, 0], average='macro')))
# + [markdown] id="jTFNUytOl9BM"
# ## 5.4 Testing
# + [markdown] id="RXvP175Tl9BM"
# Now, after having implemented each of the validation techniques we want to get an unbiased view of how our trained algorithm perfoms on unseen data. To do so we use the testing set which we split off the original dataset within the first step of this notebook.
# + [markdown] id="r4cmr2Tll9BM"
# ### Task 5: Testing your trained networks
# + [markdown] id="mHRkzAaul9BM"
# 1. Apply the `apply_sliding_window()` function on top of the `test` data. (`lines 6-8`)
# 2. (*Optional*) Omit the first feature column (subject_identifier) from the test dataset. (`lines 11-13`)
# 2. Using the `predict()` function of the DL-ARC GitHub to obtain results on the `test` data using each of the trained networks as input. The function is already imported for you. (`lines 19-28`)
# 3. Which model does perform the best and why? Was this expected? Can you make out a reason why that is?
# 4. What would you change about the pipeline we just created if your goal was to get the best predictions possible? Hint: think about the amount of data which actually trained your model in the end!
# + id="L9s6kwjul9BM"
from model.train import predict
# in order to get reproducible results, we need to seed torch and other random parts of our implementation
seed_torch(config['seed'])
# apply the sliding window on top of both the test data; use the "apply_sliding_window" function
# found in data_processing.sliding_window
X_test, y_test =
print(X_test.shape, y_test.shape)
# (optional) omit the first feature column (subject_identifier) from the test dataset
# you need to do it if you did so during training and validation!
X_test =
# convert the features of the test to float32 and labels to uint8 for GPU compatibility
X_test, y_test =
# the next lines will print out the test results for each of the trained networks
print('COMPILED TEST RESULTS: ')
print('\nTest results (train-valid-split): ')
predict()
print('\nTest results (k-fold): ')
predict()
print('\nTest results (cross-participant): ')
predict()
| 33,915 |
/FASA/events/EDA Events.ipynb | 75e8f8e17b96ed4110f9c921eeba1127acba7754 | [] | no_license | aizatrosli/MANB1123 | https://github.com/aizatrosli/MANB1123 | 0 | 0 | null | 2019-09-21T04:33:39 | 2018-06-04T00:13:59 | null | Jupyter Notebook | false | false | .py | 674,562 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# + [markdown] nbgrader={"grade": false, "grade_id": "intro_1", "locked": false, "solution": false}
# # Assignment 1: Markov Decision Processes
#
#
# <br />
# <div class="alert alert-warning">
# All your answers should be written inside this notebook.
# Look for four instances of "YOUR CODE HERE".
# If you want to clear all variables from the current session, follow these steps:
# <br/>1. Find the ``Kernel`` menu (on top) and click ``Kernel - Restart`` and choose ``Clear all Outputs and Restart``.
# <br/>2. Find the ``Cell`` menu (on top) and click ``Cell - Run`` All to re-run all of your code in order"
# </div>
# <div class="alert alert-danger">
# Before turning in the homework, you should check that your code works when this notebook is run in order from a clean start. To do so, please clear and re-run the notebook as described above.
# </div>
# + [markdown] nbgrader={"grade": false, "grade_id": "intro_2", "locked": false, "solution": false}
#
# This assignment will review exact methods for solving Markov Decision Processes (MDPs) with finite state and action spaces.
# We will implement value iteration (VI) and policy iteration (PI) for a finite MDP, both of which find the optimal policy in a finite number of iterations.
#
# For this assignment, we will consider discounted infinite-horizon MDPs. Recall that the MDP is defined by the tuple $(S, A, R, P, \rho, \gamma)$, where
#
# - S: state space (set)
# - A: action space (set)
# - R(s,a,s'): reward function, $S \times A \times S \rightarrow \mathbb{R}$, where $s$ is current state and $s'$ is next state
# - P(s,a,s'): transition probability distribution $Pr(s' | s, a)$, $S \times A \times S \rightarrow \mathbb{R}$
# - $\rho(s)$: initial state distribution, $S \rightarrow \mathbb{R}$
# - $\gamma$: discount $\in (0,1)$
#
# Here we will consider MDPs where $S,A$ are finite sets, hence $R$ and $P$ are 3D arrays.
#
# We'll randomly generate an MDP which your algorithms should be able to solve.
# Using randomly generated MDPs is a bit dry, but it emphasizes that policy iteration can be expressed with a few array operations.
# + nbgrader={"grade": false, "grade_id": "init_1", "locked": false, "solution": false}
import numpy as np, numpy.random as nr
import hw_utils
# + [markdown] nbgrader={"grade": false, "grade_id": "4", "locked": false, "solution": false}
# ## Part 1: Value Iteration
# + nbgrader={"grade": false, "grade_id": "gen_mdp", "locked": true, "solution": false}
nr.seed(0) # seed random number generator
nS = 10
nA = 2
# nS: number of states
# nA: number of actions
R_rand = nr.rand(nS, nA, nS) # reward function
# R[i,j,k] := R(s=i, a=j, s'=k),
# i.e., the dimensions are (current state, action, next state)
P_rand = nr.rand(nS, nA, nS)
# P[i,j,k] := P(s'=k | s=i, a=j)
# i.e., dimensions are (current state, action, next state)
P_rand /= P_rand.sum(axis=2,keepdims=True) # normalize conditional probabilities
gamma = 0.90
# + [markdown] nbgrader={"grade": false, "locked": false, "solution": false}
# <div class="alert alert-danger">
# Be careful that you don't mix up the 0th and 2nd dimension of R and P--here we follow the convention that the axes correspond to s,a,s', not s',a,s.
# </div>
#
#
# ### Problem 1a: implement value iteration update
# You'll implement the Bellman backup operator value operator, called `vstar_backup` below. It should compute $V^{(n+1)}$, defined as
# $$V^{(n+1)}(s) = \max_a \sum_{s'} P(s,a,s') [ R(s,a,s') + \gamma V^{(n)}(s')]$$
#
# This update is often called a **backup**, since we are updating the state $s$ based on possible future states $s'$, i.e., we are propagating the value function *backwards in time*, in a sense.
# The function is called **vstar**_backup because this update converges to the optimal value function, which is conventionally called $V^*$.
# + nbgrader={"grade": false, "grade_id": "vstar_backup", "locked": false, "solution": true}
def vstar_backup(v_n, P_pan, R_pan, gamma):
"""
Apply Bellman backup operator V -> T[V], i.e., perform one step of value iteration
:param v_n: the state-value function (1D array) for the previous iteration, i.e. V^(n).
:param P_pan: the transition function (3D array: S*A*S -> R)
:param R_pan: the reward function (3D array: S*A*S -> R)
:param gamma: the discount factor (scalar)
:return: a pair (v_p, a_p), where v_p is the updated state-value function and should be a 1D array (S -> R),
and a_p is the updated (deterministic) policy, which should also be a 1D array (S -> A)
We're using the subscript letters to label the axes
E.g., "pan" refers to "Previous state", "Action", "Next state"
"""
nS = P_pan.shape[0] # number of states
### BEGIN SOLUTION
q_sa = np.sum(P_pan * R_pan + gamma * (P_pan * np.reshape(v_n, (1, 1, -1))), axis=2)
v_p = np.max(q_sa, axis=1)
a_p = np.argmax(q_sa, axis=1)
### END SOLUTION
assert v_p.shape == (nS,)
assert a_p.shape == (nS,)
return (v_p, a_p)
# -
# Now, let's test value iteration on a randomly generated MDP.
# + nbgrader={"grade": false, "grade_id": "value_iteration", "locked": true, "solution": false}
# DO NOT CHANGE THIS PART!
def value_iteration(P, R, gamma, n_iter, verbose=False):
nS = P.shape[0]
Vprev = np.zeros(nS)
Aprev = None
chg_actions_seq = []
if verbose:
print(hw_utils.fmt_row(13, ["iter", "max|V-Vprev|", "# chg actions", "V[0]"], header=True))
for i in range(n_iter):
V, A = vstar_backup(Vprev, P, R, gamma)
chg_actions = "N/A" if Aprev is None else (A != Aprev).sum()
chg_actions_seq.append(chg_actions)
if verbose:
print(hw_utils.fmt_row(13, [i+1, np.abs(V-Vprev).max(), chg_actions, V[0]]))
Vprev, Aprev = V, A
return V, A, chg_actions_seq
value_iteration(P_rand, R_rand, gamma, n_iter=20, verbose=True);
# Expected output:
# iter | max|V-Vprev| | # chg actions | V[0]
# -------------------------------------------------------------
# 1 | 0.707147 | N/A | 0.618258
# 2 | 0.514599 | 1 | 1.13286
# 3 | 0.452404 | 0 | 1.58322
# 4 | 0.405723 | 0 | 1.98855
# 5 | 0.364829 | 0 | 2.35327
# 6 | 0.328307 | 0 | 2.68157
# 7 | 0.295474 | 0 | 2.97704
# 8 | 0.265926 | 0 | 3.24297
# 9 | 0.239333 | 0 | 3.4823
# 10 | 0.2154 | 0 | 3.6977
# 11 | 0.19386 | 0 | 3.89156
# 12 | 0.174474 | 0 | 4.06604
# 13 | 0.157026 | 0 | 4.22306
# 14 | 0.141324 | 0 | 4.36439
# 15 | 0.127191 | 0 | 4.49158
# 16 | 0.114472 | 0 | 4.60605
# 17 | 0.103025 | 0 | 4.70908
# 18 | 0.0927225 | 0 | 4.8018
# 19 | 0.0834503 | 0 | 4.88525
# 20 | 0.0751053 | 0 | 4.96035
# -
# You'll notice that value iteration only takes two iterations to converge to the right actions everywhere. (However, note that the actual values converge rather slowly.) That's because most randomly generated MDPs aren't very interesting.
# Also, note that the value of any particular state (e.g., V[0], shown in the rightmost column) increases monotonically. Under which conditions is that true? [question will not be graded]
#
# ### Problem 1b: create an MDP such for which value iteration takes a long time to converge
# Specifically, the requirement is that your MDP should have 10 states and 2 actions, and the policy should be updated for each of the first 10 iterations.
#
# Here's a hint for one solution: arrange the states on a line, so that state `i` can only transition to one of `{i-1, i, i+1}`.
# You should create 3D arrays P,R in `hw1.py` that define the MDP.
# + nbgrader={"grade": false, "grade_id": "slow_mdp", "locked": false, "solution": true}
Pslow = np.zeros((10, 2, 10)) # YOUR CODE SHOULD FILL IN THE VALUES OF Pslow
Rslow = np.zeros((10, 2, 10)) # YOUR CODE SHOULD FILL IN THE VALUES OF Rslow
# Problem 1b
### BEGIN SOLUTION
for i in range(10):
Pslow[i, 0, max(i-1, 0)] = 1
Pslow[i, 1, min(i+1, 9)] = 1
Rslow = np.zeros((10,2,10))
Rslow[:, 1, :] = -1
Rslow[9, :, :] = 100
### END SOLUTION
assert Pslow.shape == (10,2,10), "P has the wrong shape"
assert Rslow.shape == (10,2,10), "R has the wrong shape"
assert np.allclose(Pslow.sum(axis=2), np.ones((10,2))), "Transition probabilities should sum to 1"
value_iteration(Pslow, Rslow, gamma, n_iter=20, verbose=True);
# The first 10 rows of the third column of the output should be something like
# # chg actions
# -------------
# N/A
# 2
# 1
# 1
# 1
# 1
# 1
# 1
# 1
# 1
# The actual numbers can differ, as long as they are > 0.
# -
# ## Part 2: Policy Iteration
#
# The next task is to implement exact policy iteration (PI).
#
# PI first initializes the policy $\pi_0(s)$, and then it performs the following two steps on the $n$th iteration:
# 1. Compute state-action value function $Q^{\pi_{n-1}}(s,a)$ of policy $\pi_{n-1}$
# 2. Compute new policy $\pi_n(s) = \operatorname*{argmax}_a Q^{\pi_{n-1}}(s,a)$
#
# We'll break step 1 into two parts.
#
# ### Problem 2a: state value function
#
# First you'll write a function called `compute_vpi` that computes the state-value function $V^{\pi}$ for an arbitrary policy $\pi$.
# Recall that $V^{\pi}$ satisfies the following linear equation:
# $$V^{\pi}(s) = \sum_{s'} P(s,\pi(s),s')[ R(s,\pi(s),s') + \gamma V^{\pi}(s')]$$
# You'll have to solve a linear system in your code.
# + nbgrader={"grade": false, "grade_id": "compute_vpi", "locked": false, "solution": true}
def compute_vpi(pi, P, R, gamma):
"""
:param pi: a deterministic policy (1D array: S -> A)
:param P: the transition probabilities (3D array: S*A*S -> R)
:param R: the reward function (3D array: S*A*S -> R)
:param gamma: the discount factor (scalar)
:return: vpi, the state-value function for the policy pi
"""
nS = P.shape[0]
### BEGIN SOLUTION
Ppi = P[np.arange(nS), pi]
Rpi = R[np.arange(nS), pi]
b = np.sum(Ppi * Rpi, axis=1)
a = np.eye(nS) - gamma * Ppi
vpi = np.linalg.solve(a, b)
### END SOLUTION
assert vpi.shape == (nS,)
return vpi
pi0 = np.zeros(nS,dtype='i')
compute_vpi(pi0, P_rand, R_rand, gamma)
# Expected output:
# array([ 5.206217 , 5.15900351, 5.01725926, 4.76913715, 5.03154609,
# 5.06171323, 4.97964471, 5.28555573, 5.13320501, 5.08988046])
# -
# ### Problem 2b: state-action value function
#
# Next, you'll write a function to compute the state-action value function $Q^{\pi}$, defined as follows
#
# $$Q^{\pi}(s, a) = \sum_{s'} P(s,a,s')[ R(s,a,s') + \gamma V^{\pi}(s')]$$
#
# + nbgrader={"grade": false, "grade_id": "compute_qpi", "locked": false, "solution": true}
def compute_qpi(vpi, pi, P, R, gamma):
"""
:param pi: a deterministic policy (1D array: S -> A)
:param T: the transition function (3D array: S*A*S -> R)
:param R: the reward function (3D array: S*A*S -> R)
:param gamma: the discount factor (scalar)
:return: qpi, the state-action-value function for the policy pi
"""
nS = P.shape[0]
nA = P.shape[1]
### BEGIN SOLUTION
qpi = np.sum(P * (R + gamma * vpi.reshape((1, 1, -1))), axis=2)
### END SOLUTION
assert qpi.shape == (nS, nA)
return qpi
vpi = compute_vpi(pi0, P_rand, R_rand, gamma)
compute_qpi(vpi, pi0, P_rand, R_rand, gamma)
# Expected output:
# array([[ 5.206217 , 5.20238706],
# [ 5.15900351, 5.1664316 ],
# [ 5.01725926, 4.99211906],
# [ 4.76913715, 4.98080235],
# [ 5.03154609, 4.89448888],
# [ 5.06171323, 5.29418621],
# [ 4.97964471, 5.06868986],
# [ 5.28555573, 4.9156956 ],
# [ 5.13320501, 4.97736801],
# [ 5.08988046, 5.00511597]])
# -
# Now we're ready to run policy iteration!
# + nbgrader={"grade": false, "locked": false, "solution": false}
def policy_iteration(P, R, gamma, n_iter):
pi_prev = np.zeros(P.shape[0],dtype='i')
print(hw_utils.fmt_row(13, ["iter", "# chg actions", "Q[0,0]"], header=True))
for i in range(n_iter):
vpi = compute_vpi(pi_prev, P_rand, R_rand, gamma)
qpi = compute_qpi(vpi, pi_prev, P, R, gamma)
pi = qpi.argmax(axis=1)
print(hw_utils.fmt_row(13, [i+1, (pi != pi_prev).sum(), qpi[0,0]]))
pi_prev = pi
policy_iteration(P_rand, R_rand, gamma, 10);
# Expected output:
# iter | # chg actions | Q[0,0]
# ---------------------------------------------
# 1 | 4 | 5.20622
# 2 | 2 | 5.59042
# 3 | 0 | 5.6255
# 4 | 0 | 5.6255
# 5 | 0 | 5.6255
# 6 | 0 | 5.6255
# 7 | 0 | 5.6255
# 8 | 0 | 5.6255
# 9 | 0 | 5.6255
# 10 | 0 | 5.6255
# -
# <div class="alert alert-info">
# The following cells will just be used by instructors for grading. Please ignore them.
# </div>
try:
import autograder
instructor=True
except ImportError:
instructor=False
# + nbgrader={"grade": true, "grade_id": "value_iteration_test", "locked": true, "points": 1, "solution": false}
"""Check that value iteration computes the correct result"""
# INSTRUCTOR ONLY -- DO NOT CHANGE THIS PART
if instructor: autograder.grade_value_iteration(value_iteration)
# + nbgrader={"grade": true, "grade_id": "slow_mdp_test", "locked": true, "points": 1, "solution": false}
"""Check that Pslow and Rslow updates the policy for each of the first 10 iterations"""
# INSTRUCTOR ONLY -- DO NOT CHANGE THIS PART
if instructor: autograder.grade_slow_mdp(value_iteration, Pslow, Rslow, gamma)
# + nbgrader={"grade": true, "grade_id": "compute_vpi_test", "locked": true, "points": 1, "solution": false}
"""Check that compute_vpi computes the correct result"""
# INSTRUCTOR ONLY -- DO NOT CHANGE THIS PART
if instructor: autograder.grade_compute_vpi(compute_vpi)
# + nbgrader={"grade": true, "grade_id": "compute_qpi_test", "locked": true, "points": 1, "solution": false}
"""Check that compute_qpi computes the correct result"""
# INSTRUCTOR ONLY -- DO NOT CHANGE THIS PART
if instructor: autograder.grade_compute_qpi(compute_qpi)
| 15,178 |
/Glushenko_497_9_2.ipynb | 103959bd719e2e87e625462252c78ffbafe47ae2 | [] | no_license | glutolik/MathStatisticsPractice | https://github.com/glutolik/MathStatisticsPractice | 2 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 3,435 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import scipy.stats as sps
import matplotlib.pyplot as plt
import numpy as np
# %matplotlib inline
f = open('497 Глушенко Анатолий 9_2.txt', 'r')
X = list(map(float, f.readlines()))
# Считаем оценки $ \hat{\beta1} $ $ \hat{\beta2} $ $ \hat{\sigma^2} $ по методу наименьших квадратов. <br>
# Выражаем оценку $ \hat{\sigma^2_t} $ = $ \frac{\hat{\sigma^2}}{(\hat{\beta2})^2} $ из условия $ \varepsilon_i = \varepsilon_i^t * \beta2 $
# +
Y = np.zeros(len(X))
Y[0] = X[0]
for i in range (1, len(X)):
Y[i] = X[i] - X[i-1]
Z = np.zeros((len(X), 2))
Z[0][0] = 1
for i in range (1, len(X)):
Z[i][1] = 1
theta_w_cap = np.matrix(np.dot(Z.T, Z))
theta_w_cap = np.dot(theta_w_cap.I, Z.T)
theta_w_cap = np.array(np.dot(theta_w_cap, Y))
theta_w_cap = theta_w_cap.ravel()
sigma_w_cap = Y - np.dot(Z, theta_w_cap)
sigma_w_cap = np.dot(sigma_w_cap.T, sigma_w_cap)/(len(X) - 2)
sigma_w_cap_t = sigma_w_cap/theta_w_cap[1]**2
# -
print("beta1_w_cap:", "\t", theta_w_cap[0])
print("beta2_w_cap:", "\t", theta_w_cap[1])
print("sigma_w_cap:", "\t", sigma_w_cap)
print("sigma_w_cap_t:", "\t", sigma_w_cap_t)
# # Вывод:
# Т.к. дисперсия небольшая - оценка наименьших квадратов - хорошая.
output = open("497 Глушенко Анатолий.txt", 'w')
output.write(str(theta_w_cap[0]) + "\n")
output.write(str(theta_w_cap[1]) + "\n")
output.write(str(sigma_w_cap) + "\n")
output.write(str(sigma_w_cap_t))
output.close()
initial state
#
# A good starting point for solving this problem is the Hartree-Fock (HF) method. This method approximates a N-body problem into N one-body problems where each electron evolves in the mean-field of the others. Classically solving the HF equations is efficient and leads to the exact exchange energy but does not include any electron correlation. Therefore, it is usually a good starting point to start adding correlation.
#
# The Hamiltonian can then be re-expressed in the basis of the solutions of the HF method, also called Molecular Orbitals (MOs):
#
# $$
# \hat{H}_{elec}=\sum_{pq} h_{pq} \hat{a}^{\dagger}_p \hat{a}_q +
# \frac{1}{2} \sum_{pqrs} h_{pqrs} \hat{a}^{\dagger}_p \hat{a}^{\dagger}_q \hat{a}_r \hat{a}_s
# $$
# with the 1-body integrals
# $$
# h_{pq} = \int \phi^*_p(r) \left( -\frac{1}{2} \nabla^2 - \sum_{I} \frac{Z_I}{R_I- r} \right) \phi_q(r)
# $$
# and 2-body integrals
# $$
# h_{pqrs} = \int \frac{\phi^*_p(r_1) \phi^*_q(r_2) \phi_r(r_2) \phi_s(r_1)}{|r_1-r_2|}.
# $$
#
# The MOs ($\phi_u$) can be occupied or virtual (unoccupied). One MO can contain 2 electrons. However, in what follows we actually work with Spin Orbitals which are associated with a spin up ($\alpha$) of spin down ($\beta$) electron. Thus Spin Orbitals can contain one electron or be unoccupied.
#
# We now show how to concretely realise these steps with Qiskit.
# Qiskit is interfaced with different classical codes which are able to find the HF solutions. Interfacing between Qiskit and the following codes is already available:
# * Gaussian
# * Psi4
# * PyQuante
# * PySCF
#
# In the following we set up a PySCF driver, for the hydrogen molecule at equilibrium bond length (0.735 angstrom) in the singlet state and with no charge.
from qiskit_nature.drivers import PySCFDriver, UnitsType, Molecule
molecule = Molecule(geometry=[['H', [0., 0., 0.]],
['H', [0., 0., 0.735]]],
charge=0, multiplicity=1)
driver = PySCFDriver(molecule = molecule, unit=UnitsType.ANGSTROM, basis='sto3g')
# For further information about the drivers see https://qiskit.org/documentation/nature/apidocs/qiskit_nature.drivers.html
# ## The mapping from fermions to qubits
#
# <img src="aux_files/jw_mapping.png" width="500">
#
# The Hamiltonian given in the previous section is expressed in terms of fermionic operators. To encode the problem into the state of a quantum computer, these operators must be mapped to spin operators (indeed the qubits follow spin statistics).
#
# There exist different mapping types with different properties. Qiskit already supports the following mappings:
# * The Jordan-Wigner 'jordan_wigner' mapping (über das paulische äquivalenzverbot. In The Collected Works of Eugene Paul Wigner (pp. 109-129). Springer, Berlin, Heidelberg (1993)).
# * The Parity 'parity' (The Journal of chemical physics, 137(22), 224109 (2012))
# * The Bravyi-Kitaev 'bravyi_kitaev' (Annals of Physics, 298(1), 210-226 (2002))
#
# The Jordan-Wigner mapping is particularly interesting as it maps each Spin Orbital to a qubit (as shown on the Figure above).
#
# Here we set up the Electronic Structure Problem to generate the Second quantized operator and a qubit converter that will map it to a qubit operator.
from qiskit_nature.problems.second_quantization import ElectronicStructureProblem
from qiskit_nature.converters.second_quantization import QubitConverter
from qiskit_nature.mappers.second_quantization import JordanWignerMapper, ParityMapper
es_problem = ElectronicStructureProblem(driver)
second_q_op = es_problem.second_q_ops()
print(second_q_op[0])
# If we now transform this Hamiltonian for the given driver defined above we get our qubit operator:
qubit_converter = QubitConverter(mapper=JordanWignerMapper())
qubit_op = qubit_converter.convert(second_q_op[0])
print(qubit_op)
# In the minimal (STO-3G) basis set 4 qubits are required. We can reduce the number of qubits by using the Parity mapping, which allows for the removal of 2 qubits by exploiting known symmetries arising from the mapping.
qubit_converter = QubitConverter(mapper = ParityMapper(), two_qubit_reduction=True)
qubit_op = qubit_converter.convert(second_q_op[0], num_particles=es_problem.num_particles)
print(qubit_op)
# This time only 2 qubits are needed.
# Now that the Hamiltonian is ready, it can be used in a quantum algorithm to find information about the electronic structure of the corresponding molecule. Check out our tutorials on Ground State Calculation and Excited States Calculation to learn more about how to do that in Qiskit!
import qiskit.tools.jupyter
# %qiskit_version_table
# %qiskit_copyright
| 6,343 |
/ipynb/pow(x,0).ipynb | 025ec8c993f499054c7087777455002cc29f82f6 | [
"MIT"
] | permissive | lepy/phuzzy | https://github.com/lepy/phuzzy | 2 | 3 | MIT | 2020-12-07T17:22:07 | 2020-12-03T18:40:32 | Jupyter Notebook | Jupyter Notebook | false | false | .py | 116,592 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Ettoday 網路爬蟲實作練習
#
#
# * 能夠利用 Request + BeatifulSour 撰寫爬蟲,並存放到合適的資料結構
#
# ## 作業目標
#
# 根據範例:
#
# 1. 取出今天所有的新聞
# 2. 取出現在時間兩小時內的新聞
# 3. 根據範例,取出三天前下午三點到五點的新聞
# ## 1. 取出今天所有的新聞
pip install -U selenium
from selenium import webdriver
from selenium.webdriver.support.ui import Select
from bs4 import BeautifulSoup
import time
from datetime import datetime as dt
from datetime import timedelta as td
# +
browser = webdriver.Chrome(executable_path='./chromedriver')
browser.get("https://www.ettoday.net/news/news-list.htm")
for i in range(10):
time.sleep(2)
browser.execute_script("window.scrollTo(0, 10000);")
html_source = browser.page_source
soup = BeautifulSoup(html_source, "html5lib")
fmt = '%Y/%m/%d %H:%M'
for d in soup.find(class_="part_list_2").find_all('h3'):
if dt.strptime(d.find(class_="date").text, fmt).date() == dt.today().date():
print(d.find(class_="date").text, d.find_all('a')[-1].text)
# -
# ## 2. 取出現在時間兩小時內的新聞
for d in soup.find(class_="part_list_2").find_all('h3'):
if (dt.now() - dt.strptime(d.find(class_="date").text, fmt)) <= td(hours=2):
print(d.find(class_="date").text, d.find_all('a')[-1].text)
# ## 3. 根據範例,取出三天前下午三點到五點的新聞
# +
day = dt.now().day -3
selectSite = Select(browser.find_element_by_id("selD"))
selectSite.select_by_value(str(day))
browser.find_element_by_id('button').click()
for i in range(35):
time.sleep(2)
browser.execute_script("window.scrollTo(0, 25000);")
# +
html_source = browser.page_source
soup = BeautifulSoup(html_source, "html5lib")
for d in soup.find(class_="part_list_2").find_all('h3'):
news_dt = dt.strptime(d.find(class_="date").text, fmt)
if news_dt.date().day == day:
if 15 <= news_dt.hour <= 17:
print(d.find(class_="date").text, d.find_all('a')[-1].text)
| 2,069 |
/.ipynb_checkpoints/Partnership Kit (Anchor Buyer)-checkpoint.ipynb | 22f4527bf3e72241da148a43c4ee2667f9ae8f88 | [] | no_license | muarrikh-at-investree/partnership-kit | https://github.com/muarrikh-at-investree/partnership-kit | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 165,489 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Import packages and load the data
import numpy as np
import pandas as pd
import time
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import Markdown, display
import plotly.graph_objects as go
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score,confusion_matrix
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from xgboost import XGBClassifier
from sklearn import svm
# %matplotlib inline
traindata = pd.read_csv("C:/Users/Shivani Reddy/Desktop/MyStuff/MS/UCMO/Data Mining/Dataset/fashion-mnist_train.csv")
testdata = pd.read_csv("C:/Users/Shivani Reddy/Desktop/MyStuff/MS/UCMO/Data Mining/Dataset/fashion-mnist_test.csv")
# Seperate data and label
data_train = traindata.iloc[:,1:785]/ 255.0
label_train = pd.DataFrame([traindata.iloc[:,0]]).T
data_test = testdata.iloc[:,0:784]/ 255.0
# View image data
pd.value_counts(label_train.values.flatten())
categoryMap = {0 :'T-shirt/Top',
1 :'Trouser',
2 :'Pullover',
3 :'Dress',
4 :'Coat',
5 :'Sandal',
6 :'Shirt',
7 :'Sneaker',
8 :'Bag',
9 :'Ankle boot'}
label_train['category']=label_train['label'].map(categoryMap)
# +
L = 5
W = 6
fig, axes = plt.subplots(L, W, figsize = (12,12))
axes = axes.ravel()
for i in range(30):
axes[i].imshow(data_train.values.reshape((data_train.shape[0], 28, 28))[i], cmap=plt.get_cmap('gray'))
axes[i].set_title("class " + str(label_train['label'][i]) + ": "+ label_train['category'][i])
axes[i].axis('off')
plt.show()
# -
# # Feature Engineering
# Check for null and missing values
print("check for data_train:\n",data_train.isnull().any().describe(),"\n\ncheck for label_train:\n",label_train.isnull().any().describe(),"\n\ncheck for data_test:\n",data_test.isnull().any().describe())
# Split training and validation set
l_train=pd.DataFrame([traindata.iloc[:,0]]).T
X_train, X_val, Y_train, Y_val = train_test_split(data_train, l_train, test_size = 0.25, random_state=255)
X_train=StandardScaler().fit_transform(X_train)
X_val=StandardScaler().fit_transform(X_val)
column_name=['pixel'+str(i) for i in range(1,785)]
X_train = pd.DataFrame(X_train,columns =column_name)
X_val = pd.DataFrame(X_val,columns =column_name)
# Dimensionality Reduction
pca = PCA(n_components=0.9,copy=True, whiten=False)
X_train = pca.fit_transform(X_train)
X_val = pca.transform(X_val)
print(pca.explained_variance_ratio_)
var=np.cumsum(np.round(pca.explained_variance_ratio_, decimals=3)*100)
fig = go.Figure(data=go.Scatter(x=list(range(1,len(var)+1)), y=var))
fig.update_layout(title='PCA Variance Explained',
xaxis_title='# Of Features',
yaxis_title='% Variance Explained')
pcn=X_train.shape[1]
X_train = pd.DataFrame(X_train,columns =column_name[0:pcn])
X_val = pd.DataFrame(X_val,columns =column_name[0:pcn])
# # Evaluate the model
# KNN
start_time = time.time()
knn = KNeighborsClassifier(n_neighbors=8)
knn.fit(X_train, Y_train.values.ravel())
y_train_prd = knn.predict(X_train)
y_val_prd = knn.predict(X_val)
acc_train_knn=accuracy_score(Y_train,y_train_prd )
acc_val_knn=accuracy_score(Y_val,y_val_prd)
print("accuracy on train set:{:.4f}\naccuracy on validation set:{:.4f}".format(acc_train_knn, acc_val_knn))
print("--- %s seconds ---" % (time.time() - start_time))
con_matrix = pd.crosstab(pd.Series(Y_val.values.flatten(), name='Actual' ),pd.Series(y_val_prd, name='Predicted'))
plt.figure(figsize = (9,6))
plt.title("Confusion Matrix on KNN")
sns.heatmap(con_matrix, cmap="Greys", annot=True, fmt='g')
plt.show()
# Gaussian Naive Bayes
start_time = time.time()
NB = GaussianNB()
NB.fit(X_train, Y_train.values.ravel())
y_train_prd = NB.predict(X_train)
y_val_prd = NB.predict(X_val)
acc_train_nb=accuracy_score(Y_train,y_train_prd )
acc_val_nb=accuracy_score(Y_val,y_val_prd)
print("accuracy on train set:{:.4f}\naccuracy on validation set:{:.4f}".format(acc_train_nb,
acc_val_nb))
print("--- %s seconds ---" % (time.time() - start_time))
con_matrix = pd.crosstab(pd.Series(Y_val.values.flatten(), name='Actual' ),pd.Series(y_val_prd, name='Predicted'))
plt.figure(figsize = (9,6))
plt.title("Confusion Matrix on Gaussian Naive Bayes")
sns.heatmap(con_matrix, cmap="Greys", annot=True, fmt='g')
plt.show()
# Logistic Regression
start_time = time.time()
lg = LogisticRegression(solver='liblinear', multi_class='auto')
lg.fit(X_train, Y_train.values.ravel())
y_train_prd = lg.predict(X_train)
y_val_prd = lg.predict(X_val)
acc_train_lg=accuracy_score(Y_train,y_train_prd )
acc_val_lg=accuracy_score(Y_val,y_val_prd)
print("accuracy on train set:{:.4f}\naccuracy on validation set:{:.4f}".format(acc_train_lg,
acc_val_lg))
print("--- %s seconds ---" % (time.time() - start_time))
con_matrix = pd.crosstab(pd.Series(Y_val.values.flatten(), name='Actual' ),pd.Series(y_val_prd, name='Predicted'))
plt.figure(figsize = (9,6))
plt.title("Confusion Matrix on Logistic Regression")
sns.heatmap(con_matrix, cmap="Greys", annot=True, fmt='g')
plt.show()
# Random Forest Classifier
start_time = time.time()
rfc = RandomForestClassifier(random_state=0)
rfc.fit(X_train, Y_train.values.ravel())
y_train_prd = rfc.predict(X_train)
y_val_prd = rfc.predict(X_val)
acc_train_rfc=accuracy_score(Y_train,y_train_prd )
acc_val_rfc=accuracy_score(Y_val,y_val_prd)
print("accuracy on train set:{:.4f}\naccuracy on validation set:{:.4f}".format(acc_train_rfc,
acc_val_rfc))
print("--- %s seconds ---" % (time.time() - start_time))
con_matrix = pd.crosstab(pd.Series(Y_val.values.flatten(), name='Actual' ),pd.Series(y_val_prd, name='Predicted'))
plt.figure(figsize = (9,6))
plt.title("Confusion Matrix on Random Forest Classifier")
sns.heatmap(con_matrix, cmap="Greys", annot=True, fmt='g')
plt.show()
# SVM Classifier
start_time = time.time()
svc = svm.SVC(decision_function_shape='ovo', gamma='auto')
svc.fit(X_train, Y_train.values.ravel())
y_train_prd = svc.predict(X_train)
y_val_prd = svc.predict(X_val)
acc_train_svc=accuracy_score(Y_train,y_train_prd )
acc_val_svc=accuracy_score(Y_val,y_val_prd)
print("accuracy on train set:{:.4f}\naccuracy on validation set:{:.4f}".format(acc_train_svc,
acc_val_svc))
print("--- %s seconds ---" % (time.time() - start_time))
con_matrix = pd.crosstab(pd.Series(Y_val.values.flatten(), name='Actual' ),pd.Series(y_val_prd, name='Predicted'))
plt.figure(figsize = (9,6))
plt.title("Confusion Matrix on SVM Classifier")
sns.heatmap(con_matrix, cmap="Greys", annot=True, fmt='g')
plt.show()
# XGBoost
start_time = time.time()
xgb = XGBClassifier()
xgb.fit(X_train, Y_train.values.ravel())
y_train_prd = xgb.predict(X_train)
y_val_prd = xgb.predict(X_val)
acc_train_xgb=accuracy_score(Y_train,y_train_prd )
acc_val_xgb=accuracy_score(Y_val,y_val_prd)
print("accuracy on train set:{:.4f}\naccuracy on validation set:{:.4f}".format(acc_train_xgb,
acc_val_xgb))
print("--- %s seconds ---" % (time.time() - start_time))
con_matrix = pd.crosstab(pd.Series(Y_val.values.flatten(), name='Actual' ),pd.Series(y_val_prd, name='Predicted'))
plt.figure(figsize = (9,6))
plt.title("Confusion Matrix on XGBoost Classifier")
sns.heatmap(con_matrix, cmap="Greys", annot=True, fmt='g')
plt.show()
# Model Comparision
acc_combine = {'Model': ['KNN', 'Gaussian Naive Bayes','Logistic Regression','Random Forest Classifier','SVM Classifier','XGBoost'],
'Accuracy_Tra': [acc_train_knn, acc_train_nb,acc_train_lg,acc_train_rfc,acc_train_svc,acc_train_xgb],
'Accuracy_Val': [acc_val_knn, acc_val_nb,acc_val_lg,acc_val_rfc,acc_val_svc,acc_val_xgb]
}
# +
fig = go.Figure(data=[
go.Bar(name='train set', x=acc_combine['Model'], y=acc_combine['Accuracy_Tra'],text=np.round(acc_combine['Accuracy_Tra'],2),textposition='outside'),
go.Bar(name='validation set', x=acc_combine['Model'], y=acc_combine['Accuracy_Val'],text=np.round(acc_combine['Accuracy_Val'],2),textposition='outside')
])
fig.update_layout(barmode='group',title_text='Accuracy Comparison On Different Models',yaxis=dict(
title='Accuracy'))
fig.show()
# -
oc[missing_data['Percent']>0]
print(missing_data)
if missing_data.shape[0]!=0:
f, ax = plt.subplots(figsize=(5, 5))
plt.xticks(rotation='90')
sns.barplot(y=missing_data.index, x=missing_data['Percent'])
plt.ylabel('Features', fontsize=15)
plt.xlabel('Percent of missing values', fontsize=15)
plt.xlim(0, 1)
plt.title('Percent missing data by feature', fontsize=15)
return missing_data
else:
print('Tidak ada missing value!!!')
# +
all_df = [df_po, df_buyer]
for data in all_df:
check_missing_value(data)
# + [markdown] id="NFiznqSgqS5l"
# <h5 align='center'>--- This is the end of <u>Data Info</u> section ---</h5>
# + [markdown] id="CfTn71pEqS5m"
# <h5 align='center'>.</h5>
# + [markdown] id="vUHb-bJX3JQZ"
# # 3. Modeling
# + [markdown] id="kLeR2-NFqS5o"
# This section gives modeling strategy to predict either limit or potential borrower performance in Investree product
# + [markdown] id="7b44KefuuUPX"
# Purchase Order Total Based on Date
# + id="cioebYimqS5p"
try:
df_pivot = df_po
df_pivot['ACT_SETTLE_DATE'] = df_pivot['ACT_SETTLE_DATE'].apply(pd.to_datetime)
df_pivot['ACT_SETTLE_DATE'] = df_pivot['ACT_SETTLE_DATE'].dt.strftime('%Y-%m')
except:
print('ACT_SETTLE_DATE is not available')
# +
try:
fig = plt.figure(figsize=(17,8))
df_calc = df_pivot.groupby(['ACT_SETTLE_DATE'], as_index=False)['PO_TOTAL'].sum()
sns.lineplot(data=df_calc[['PO_TOTAL', 'ACT_SETTLE_DATE']], x='ACT_SETTLE_DATE',y='PO_TOTAL')
plt.ticklabel_format(style='plain', axis='y')
except Exception as e:
print(e)
# -
# Quantity Based on Date
try:
fig = plt.figure(figsize=(17,8))
df_calc = df_pivot.groupby(['ACT_SETTLE_DATE'], as_index=False)['QTY'].sum()
sns.lineplot(data=df_calc[['QTY', 'ACT_SETTLE_DATE']], x='ACT_SETTLE_DATE',y='QTY')
plt.ticklabel_format(style='plain', axis='y')
except Exception as e:
print(e)
# + [markdown] id="pfDqNNJw0n7h"
# The Segmentation of Borrower Location
# -
#Merge with data kodepos
try:
postcode = pd.read_csv('Data Kodepos Indonesia.csv', sep=';')
postcode['KABUPATEN'] = postcode['JENIS'] + ' ' + postcode['KABUPATEN']
df_merged_loc = pd.merge(df_supplier, postcode, left_on='DELIVERY_POSTCODE', right_on='POSTCODE', how='left')
except Exception as e:
print(e)
# + id="wGcUJXyCqsEl"
#Provinsi
try:
count_per_loc = df_merged_loc['PROVINSI'].value_counts().rename_axis('PROVINSI').reset_index(name='JUMLAH')
print(count_per_loc)
except Exception as e:
print(e)
# + id="9sSTHJfhmsa4"
try:
fig = plt.figure(figsize=(17,8))
ax = plt.subplot(111)
ax.bar(count_per_loc.iloc[:, 0], count_per_loc.iloc[:, 1])
props = {"rotation" : 90}
plt.setp(ax.get_xticklabels(), **props)
plt.show()
except Exception as e:
print(e)
# -
#KABUPATEN
try:
count_per_loc = df_merged_loc['KABUPATEN'].value_counts().rename_axis('KABUPATEN').reset_index(name='JUMLAH')
print(count_per_loc)
except Exception as e:
print(e)
try:
fig = plt.figure(figsize=(17,8))
ax = plt.subplot(111)
ax.bar(count_per_loc.iloc[:, 0], count_per_loc.iloc[:, 1])
props = {"rotation" : 90}
plt.setp(ax.get_xticklabels(), **props)
plt.show()
except Exception as e:
print(e)
# + [markdown] id="32fg57GD1NQG"
# Payment Type Preference
# -
##Buyer
try:
count_per_paytype = df_buyer['BUYER_PAYMENT_TYPE_PREF'].value_counts().rename_axis('BUYER_PAYMENT_TYPE_PREF').reset_index(name='JUMLAH')
print(count_per_paytype)
fig = plt.figure(figsize=(10,8))
ax = plt.subplot(111)
ax.bar(count_per_paytype.iloc[:, 0], count_per_paytype.iloc[:, 1])
plt.show()
except Exception as e:
print(e)
# + [markdown] id="A12Ebrap1RMT"
# Tenure Preference
# + id="WWsEZtJ23k5a"
##Buyer
try:
df_buyer['BUYER_TENURE_PREF'] = df_buyer['BUYER_TENURE_PREF'].astype('str')
count_per_tenpref = df_buyer['BUYER_TENURE_PREF'].value_counts().rename_axis('BUYER_TENURE_PREF').reset_index(name='JUMLAH')
print(count_per_tenpref)
fig = plt.figure(figsize=(10,8))
ax = plt.subplot(111)
ax.bar(count_per_tenpref.iloc[:, 0], count_per_tenpref.iloc[:, 1])
plt.show()
except Exception as e:
print(e)
# + [markdown] id="hLGopLwr2VGz"
# Demographic of Borrower
# PT CV
#
# + id="DLefzi8F34Bt"
#buyer
try:
count_per_sex = df_buyer['BUYER_ENTITY'].value_counts().rename_axis('BUYER_ENTITY').reset_index(name='JUMLAH')
print(count_per_entity)
fig = plt.figure(figsize=(10,8))
ax = plt.subplot(111)
ax.bar(count_per_entity.iloc[:, 0], count_per_entity.iloc[:, 1])
plt.show()
except Exception as e:
print(e)
# -
#buyer
try:
count_per_age = df_buyer['BUYER_AGE'].value_counts().rename_axis('BUYER_AGE').reset_index(name='JUMLAH')
print(count_per_age)
fig = plt.figure(figsize=(10,8))
ax = plt.subplot(111)
ax.bar(count_per_age.iloc[:, 0], count_per_age.iloc[:, 1])
plt.show()
except Exception as e:
print(e)
# + [markdown] id="tma92-QQNI0N"
# Borrower Sector
# + id="PHuZ-t69NWRq"
# #buyer
# try:
# count_per_sector = df_buyer['BUYER_INDUSTRY'].value_counts().rename_axis('BUYER_INDUSTRY').reset_index(name='JUMLAH')
# print(count_per_sector)
# fig = plt.figure(figsize=(10,8))
# ax = plt.subplot(111)
# ax.bar(count_per_sector.iloc[:, 0], count_per_sector.iloc[:, 1])
# # ax.set_xticklabels(count_per_sector.loc[:,0], rotation = 90, ha="right")
# props = {"rotation" : 90}
# plt.setp(ax.get_xticklabels(), **props)
# plt.show()
# except Exception as e:
# print(e)
# -
# Term of Payment
try:
count_per_top = df_po['TERM_OF_PAYMENT'].value_counts().rename_axis('TERM_OF_PAYMENT').reset_index(name='JUMLAH')
print(count_per_top)
fig = plt.figure(figsize=(10,8))
ax = plt.subplot(111)
ax.bar(count_per_top.iloc[:, 0], count_per_top.iloc[:, 1])
plt.show()
except Exception as e:
print(e)
# Period
# +
##Buyer
try:
df_buyer['BUYER_PERIOD'] = None
for i in range(0, len(df_buyer['BUYER_FIRST_TRANSACTION_DATE'])):
df_buyer['BUYER_PERIOD'][i] = (refer_analysis_time.year - df_buyer['BUYER_FIRST_TRANSACTION_DATE'][i].year) * 12 + (refer_analysis_time.month - df_buyer['BUYER_FIRST_TRANSACTION_DATE'][i].month)
# count_per_period = df_buyer['BUYER_PERIOD'].value_counts().rename_axis('PERIOD').reset_index(name='JUMLAH')
# print(count_per_period)
# fig = plt.figure(figsize=(10,8))
# ax = plt.subplot(111)
# ax.bar(count_per_period.iloc[:, 0], count_per_period.iloc[:, 1])
difference = round((max(df_buyer['BUYER_PERIOD']) - min(df_buyer['BUYER_PERIOD']))/5)
group_1 = '< '+str(min(df_buyer['BUYER_PERIOD'])+difference)+' Bulan'
group_2 = str(min(df_buyer['BUYER_PERIOD'])+difference)+' Bulan - '+str(min(df_buyer['BUYER_PERIOD'])+2*difference-1)+' Bulan'
group_3 = str(min(df_buyer['BUYER_PERIOD'])+2*difference)+' Bulan - '+str(min(df_buyer['BUYER_PERIOD'])+3*difference-1)+' Bulan'
group_4 = str(min(df_buyer['BUYER_PERIOD'])+3*difference)+' Bulan - '+str(min(df_buyer['BUYER_PERIOD'])+4*difference-1)+' Bulan'
group_5 = '> '+str(min(df_buyer['BUYER_PERIOD'])+4*difference-1)+' Bulan'
df_buyer['BUYER_PERIOD_GROUP'] = None
for i in range(0, len(df_buyer['BUYER_PERIOD'])):
if df_buyer['BUYER_PERIOD'][i] < (min(df_buyer['BUYER_PERIOD'])+difference):
df_buyer['BUYER_PERIOD_GROUP'][i] = group_1
elif df_buyer['BUYER_PERIOD'][i] < (min(df_buyer['BUYER_PERIOD'])+2*difference):
df_buyer['BUYER_PERIOD_GROUP'][i] = group_2
elif df_buyer['BUYER_PERIOD'][i] < (min(df_buyer['BUYER_PERIOD'])+3*difference):
df_buyer['BUYER_PERIOD_GROUP'][i] = group_3
elif df_buyer['BUYER_PERIOD'][i] < (min(df_buyer['BUYER_PERIOD'])+4*difference):
df_buyer['BUYER_PERIOD_GROUP'][i] = group_4
else:
df_buyer['BUYER_PERIOD_GROUP'][i] = group_5
count_per_period = df_buyer['BUYER_PERIOD_GROUP'].value_counts().rename_axis('PERIOD_GROUP').reset_index(name='JUMLAH')
order = [group_1, group_2, group_3, group_4, group_5]
count_per_period['PERIOD_GROUP'] = pd.Categorical(count_per_period['PERIOD_GROUP'], order)
count_per_period.sort_values(by=['PERIOD_GROUP'], inplace=True)
print(count_per_period)
fig = plt.figure(figsize=(10,8))
ax = plt.subplot(111)
ax.barh(count_per_period.iloc[:, 0], count_per_period.iloc[:, 1])
except Exception as e:
print(e)
# -
# Ceritified Documents (KYC)
##Buyer
try:
count_ktp = 0
count_npwp = 0
count_siup = 0
count_tdp = 0
for i in df_buyer['BUYER_CERTIFIED_DOCUMENTS']:
ktp = i.count('KTP')
count_ktp = count_ktp+ktp
npwp = i.count('NPWP')
count_npwp = count_npwp+npwp
siup = i.count('SIUP')
count_siup = count_siup+siup
tdp = i.count('TDP')
count_tdp = count_tdp+tdp
fig = plt.figure(figsize=(10,8))
ax = plt.subplot(111)
ax.bar(['KTP', 'NPWP', 'SIUP', 'TDP'], [count_ktp, count_npwp, count_siup, count_tdp])
plt.show()
except Exception as e:
print(e)
| 17,693 |
/.ipynb_checkpoints/make_colormnist-checkpoint.ipynb | 1662fde6c242107da8187012b1ebaa3af997f158 | [
"MIT"
] | permissive | minhtannguyen/ffjord | https://github.com/minhtannguyen/ffjord | 0 | 0 | MIT | 2019-02-07T05:10:16 | 2019-02-07T00:01:39 | null | Jupyter Notebook | false | false | .py | 13,405 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from __future__ import print_function
import torchvision.datasets as dset
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
# from matplotlib import rcParams
# rcParams.update({'figure.autolayout': True})
import torchvision.datasets as dset
import torchvision.transforms as tforms
import torch.utils.data as data
from torch.utils.data import Dataset
from IPython.core.debugger import Tracer
from PIL import Image
import os
import os.path
import errno
import numpy as np
import torch
import codecs
path_to_mnist = '/tancode/repos/data'
# -
class ColorMNIST(data.Dataset):
"""`MNIST <http://yann.lecun.com/exdb/mnist/>`_ Dataset.
Args:
root (string): Root directory of dataset where ``processed/training.pt``
and ``processed/test.pt`` exist.
train (bool, optional): If True, creates dataset from ``training.pt``,
otherwise from ``test.pt``.
download (bool, optional): If true, downloads the dataset from the internet and
puts it in root directory. If dataset is already downloaded, it is not
downloaded again.
transform (callable, optional): A function/transform that takes in an PIL image
and returns a transformed version. E.g, ``transforms.RandomCrop``
target_transform (callable, optional): A function/transform that takes in the
target and transforms it.
"""
urls = [
'http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz',
'http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz',
'http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz',
'http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz',
]
raw_folder = 'raw'
processed_folder = 'processed'
training_file = 'training.pt'
test_file = 'test.pt'
def __init__(self, root, train=True, transform=None, target_transform=None, download=False):
self.root = os.path.expanduser(root)
self.transform = transform
self.target_transform = target_transform
self.train = train # training set or test set
if download:
self.download()
if not self._check_exists():
raise RuntimeError('Dataset not found.' +
' You can use download=True to download it')
if self.train:
self.train_data, self.train_labels = torch.load(
os.path.join(self.root, self.processed_folder, self.training_file))
self.train_data = np.tile(self.train_data[:, :, :, np.newaxis], 3)
else:
self.test_data, self.test_labels = torch.load(
os.path.join(self.root, self.processed_folder, self.test_file))
self.test_data = np.tile(self.test_data[:, :, :, np.newaxis], 3)
self.pallette = [[31, 119, 180],
[255, 127, 14],
[44, 160, 44],
[214, 39, 40],
[148, 103, 189],
[140, 86, 75],
[227, 119, 194],
[127, 127, 127],
[188, 189, 34],
[23, 190, 207]]
def __getitem__(self, index):
"""
Args:
index (int): Index
Returns:
tuple: (image, target) where target is index of the target class.
"""
if self.train:
img, target = self.train_data[index], self.train_labels[index]
else:
img, target = self.test_data[index], self.test_labels[index]
# doing this so that it is consistent with all other datasets
# to return a PIL Image
y_color_digit = np.random.randint(0, 10)
c_digit = self.pallette[y_color_digit]
img[:, :, 0] = img[:, :, 0] / 255 * c_digit[0]
img[:, :, 1] = img[:, :, 1] / 255 * c_digit[1]
img[:, :, 2] = img[:, :, 2] / 255 * c_digit[2]
img = Image.fromarray(img)
if self.transform is not None:
img = self.transform(img)
if self.target_transform is not None:
target = self.target_transform(target)
return img, [target,torch.from_numpy(np.array(y_color_digit))]
def __len__(self):
if self.train:
return len(self.train_data)
else:
return len(self.test_data)
def _check_exists(self):
return os.path.exists(os.path.join(self.root, self.processed_folder, self.training_file)) and \
os.path.exists(os.path.join(self.root, self.processed_folder, self.test_file))
def download(self):
"""Download the MNIST data if it doesn't exist in processed_folder already."""
from six.moves import urllib
import gzip
if self._check_exists():
return
# download files
try:
os.makedirs(os.path.join(self.root, self.raw_folder))
os.makedirs(os.path.join(self.root, self.processed_folder))
except OSError as e:
if e.errno == errno.EEXIST:
pass
else:
raise
for url in self.urls:
print('Downloading ' + url)
data = urllib.request.urlopen(url)
filename = url.rpartition('/')[2]
file_path = os.path.join(self.root, self.raw_folder, filename)
with open(file_path, 'wb') as f:
f.write(data.read())
with open(file_path.replace('.gz', ''), 'wb') as out_f, \
gzip.GzipFile(file_path) as zip_f:
out_f.write(zip_f.read())
os.unlink(file_path)
# process and save as torch files
print('Processing...')
training_set = (
read_image_file(os.path.join(self.root, self.raw_folder, 'train-images-idx3-ubyte')),
read_label_file(os.path.join(self.root, self.raw_folder, 'train-labels-idx1-ubyte'))
)
test_set = (
read_image_file(os.path.join(self.root, self.raw_folder, 't10k-images-idx3-ubyte')),
read_label_file(os.path.join(self.root, self.raw_folder, 't10k-labels-idx1-ubyte'))
)
with open(os.path.join(self.root, self.processed_folder, self.training_file), 'wb') as f:
torch.save(training_set, f)
with open(os.path.join(self.root, self.processed_folder, self.test_file), 'wb') as f:
torch.save(test_set, f)
print('Done!')
def __repr__(self):
fmt_str = 'Dataset ' + self.__class__.__name__ + '\n'
fmt_str += ' Number of datapoints: {}\n'.format(self.__len__())
tmp = 'train' if self.train is True else 'test'
fmt_str += ' Split: {}\n'.format(tmp)
fmt_str += ' Root Location: {}\n'.format(self.root)
tmp = ' Transforms (if any): '
fmt_str += '{0}{1}\n'.format(tmp, self.transform.__repr__().replace('\n', '\n' + ' ' * len(tmp)))
tmp = ' Target Transforms (if any): '
fmt_str += '{0}{1}'.format(tmp, self.target_transform.__repr__().replace('\n', '\n' + ' ' * len(tmp)))
return fmt_str
# +
def add_noise(x):
"""
[0, 1] -> [0, 255] -> add noise -> [0, 1]
"""
noise = x.new().resize_as_(x).uniform_()
x = x * 255 + noise
x = x / 256
return x
def get_train_loader(train_set, epoch):
if args.batch_size_schedule != "":
epochs = [0] + list(map(int, args.batch_size_schedule.split("-")))
n_passed = sum(np.array(epochs) <= epoch)
current_batch_size = int(args.batch_size * n_passed)
else:
current_batch_size = args.batch_size
train_loader = torch.utils.data.DataLoader(
dataset=train_set, batch_size=current_batch_size, shuffle=True, drop_last=True, pin_memory=True
)
logger.info("===> Using batch size {}. Total {} iterations/epoch.".format(current_batch_size, len(train_loader)))
return train_loader
trans = lambda im_size: tforms.Compose([tforms.Resize(im_size), tforms.ToTensor(), add_noise])
im_dim = 1
im_size = 28
train_set = ColorMNIST(root="../data", train=True, transform=trans(im_size), download=True)
test_set = ColorMNIST(root="../data", train=False, transform=trans(im_size), download=True)
data_shape = (im_dim, im_size, im_size)
test_loader = torch.utils.data.DataLoader(dataset=test_set, batch_size=500, shuffle=False, drop_last=True)
for epoch in range(1, 11):
train_loader = torch.utils.data.DataLoader(dataset=train_set, batch_size=10, shuffle=True, drop_last=True, pin_memory=True)
for _, (x, y) in enumerate(train_loader):
ximg = x.numpy().transpose([1, 2, 0])
plt.imshow(ximg)
plt.show()
Tracer()()
# +
dataloader = ColorMNIST('back', 'train', path_to_mnist, randomcolor=False)
x_all = []
for i in [1, 3, 5, 7, 2, 0, 13, 15, 17, 4]:
x_all.append(dataloader[i][0].numpy().transpose([1, 2, 0]))
x_all = np.hstack(x_all)
plt.imshow(x_all)
plt.show()
# +
dataloader = ColorMNIST('num', 'train', path_to_mnist, randomcolor=False)
x_all = []
for i in [1, 3, 5, 7, 2, 0, 13, 15, 17, 4]:
x_all.append(dataloader[i][0].numpy().transpose([1, 2, 0]))
x_all = np.hstack(x_all)
plt.imshow(x_all)
plt.show()
# +
dataloader = ColorMNIST('both', 'train', path_to_mnist, randomcolor=False)
x_all = []
for i in [1, 3, 5, 7, 2, 0, 13, 15, 17, 4]:
x_all.append(dataloader[i][0].numpy().transpose([1, 2, 0]))
x_all = np.hstack(x_all)
plt.imshow(x_all)
plt.show()
# +
dataloader = ColorMNIST('both', 'train', path_to_mnist, randomcolor=True)
x_all = []
for i in [1, 3, 5, 7, 2, 0, 13, 15, 17, 4]:
x_all.append(dataloader[i][0].numpy().transpose([1, 2, 0]))
x_all = np.hstack(x_all)
plt.imshow(x_all)
plt.show()
| 10,068 |
/modified-dr-jason-cnn-with-pso-new abdallah lasttttttttttttttttttttt .ipynb | de4c68515109820cabfee023da8602454c40da0c | [] | no_license | lamiaaAliSaid/lamiaaphd | https://github.com/lamiaaAliSaid/lamiaaphd | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 14,577 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="0MRC0e0KhQ0S"
# # Random Forest Classification
# + [markdown] colab_type="text" id="LWd1UlMnhT2s"
# ## Importing the libraries
# + colab={} colab_type="code" id="YvGPUQaHhXfL"
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# + [markdown] colab_type="text" id="K1VMqkGvhc3-"
# ## Importing the dataset
# + colab={} colab_type="code" id="M52QDmyzhh9s"
dataset = pd.read_csv('Data.csv')
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
# + [markdown] colab_type="text" id="YvxIPVyMhmKp"
# ## Splitting the dataset into the Training set and Test set
# + colab={} colab_type="code" id="AVzJWAXIhxoC"
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" executionInfo={"elapsed": 1300, "status": "ok", "timestamp": 1588269343329, "user": {"displayName": "Hadelin de Ponteves", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="P3nS3-6r1i2B" outputId="e4a38929-7ac1-4895-a070-4f241ad247c0"
print(X_train)
# + colab={"base_uri": "https://localhost:8080/", "height": 171} colab_type="code" executionInfo={"elapsed": 1294, "status": "ok", "timestamp": 1588269343330, "user": {"displayName": "Hadelin de Ponteves", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="8dpDLojm1mVG" outputId="2a9b0425-9e6d-480f-b32a-ebae6f413dbe"
print(y_train)
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" executionInfo={"elapsed": 1613, "status": "ok", "timestamp": 1588269343657, "user": {"displayName": "Hadelin de Ponteves", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="qbb7i0DH1qui" outputId="b10e7737-ae02-4c0c-b49f-8d961e2921b4"
print(X_test)
# + colab={"base_uri": "https://localhost:8080/", "height": 68} colab_type="code" executionInfo={"elapsed": 1608, "status": "ok", "timestamp": 1588269343658, "user": {"displayName": "Hadelin de Ponteves", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="kj1hnFAR1s5w" outputId="1f3a92ea-9844-4d4c-ca5f-075fa4ba98e0"
print(y_test)
# + [markdown] colab_type="text" id="kW3c7UYih0hT"
# ## Feature Scaling
# + colab={} colab_type="code" id="9fQlDPKCh8sc"
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" executionInfo={"elapsed": 1600, "status": "ok", "timestamp": 1588269343659, "user": {"displayName": "Hadelin de Ponteves", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="syrnD1Op2BSR" outputId="b1fa2925-b7de-4530-b015-01bb51e742b4"
print(X_train)
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" executionInfo={"elapsed": 1595, "status": "ok", "timestamp": 1588269343659, "user": {"displayName": "Hadelin de Ponteves", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="JUd6iBRp2C3L" outputId="48320ca4-33e0-4bfe-92ba-91c06bcf714e"
print(X_test)
# + [markdown] colab_type="text" id="bb6jCOCQiAmP"
# ## Training the Random Forest Classification model on the Training set
# + colab={"base_uri": "https://localhost:8080/", "height": 154} colab_type="code" executionInfo={"elapsed": 1589, "status": "ok", "timestamp": 1588269343659, "user": {"displayName": "Hadelin de Ponteves", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="e0pFVAmciHQs" outputId="79719013-2ffa-49f6-b49c-886d9ba19525"
from sklearn.ensemble import RandomForestClassifier
classifier = RandomForestClassifier(n_estimators = 10, criterion = 'entropy', random_state = 0)
classifier.fit(X_train, y_train)
# + [markdown] colab_type="text" id="yyxW5b395mR2"
# ## Predicting a new result
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 1584, "status": "ok", "timestamp": 1588269343660, "user": {"displayName": "Hadelin de Ponteves", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="f8YOXsQy58rP" outputId="81727e50-9f85-49ad-a41e-5891aa34e6bb"
print(classifier.predict(sc.transform([[30,87000]])))
# + [markdown] colab_type="text" id="vKYVQH-l5NpE"
# ## Predicting the Test set results
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" executionInfo={"elapsed": 1578, "status": "ok", "timestamp": 1588269343660, "user": {"displayName": "Hadelin de Ponteves", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="p6VMTb2O4hwM" outputId="f160d9d3-e4cd-4484-db9d-99028dfed42d"
y_pred = classifier.predict(X_test)
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))
# + [markdown] colab_type="text" id="h4Hwj34ziWQW"
# ## Making the Confusion Matrix
# + colab={"base_uri": "https://localhost:8080/", "height": 68} colab_type="code" executionInfo={"elapsed": 1898, "status": "ok", "timestamp": 1588269343985, "user": {"displayName": "Hadelin de Ponteves", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="D6bpZwUiiXic" outputId="b4ab126b-4118-461e-f02a-cfe538ae6a71"
from sklearn.metrics import confusion_matrix, accuracy_score
cm = confusion_matrix(y_test, y_pred)
print(cm)
# -
# ## Determining Accuracy
accuracy_score(y_test, y_pred)
# + [markdown] colab_type="text" id="6OMC_P0diaoD"
# ## Visualising the Training set results
# + colab={"base_uri": "https://localhost:8080/", "height": 349} colab_type="code" executionInfo={"elapsed": 87793, "status": "ok", "timestamp": 1588269429885, "user": {"displayName": "Hadelin de Ponteves", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="_NOjKvZRid5l" outputId="7efb744e-3ecb-4303-8543-8fabf49f64bc"
from matplotlib.colors import ListedColormap
X_set, y_set = sc.inverse_transform(X_train), y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 10, stop = X_set[:, 0].max() + 10, step = 0.25),
np.arange(start = X_set[:, 1].min() - 1000, stop = X_set[:, 1].max() + 1000, step = 0.25))
plt.contourf(X1, X2, classifier.predict(sc.transform(np.array([X1.ravel(), X2.ravel()]).T)).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Random Forest Classification (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# + [markdown] colab_type="text" id="SZ-j28aPihZx"
# ## Visualising the Test set results
# + colab={"base_uri": "https://localhost:8080/", "height": 349} colab_type="code" executionInfo={"elapsed": 172477, "status": "ok", "timestamp": 1588269514574, "user": {"displayName": "Hadelin de Ponteves", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="qeTjz2vDilAC" outputId="f1a33b1a-e8b6-4b3e-e98a-a0c7c66fed56"
from matplotlib.colors import ListedColormap
X_set, y_set = sc.inverse_transform(X_test), y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 10, stop = X_set[:, 0].max() + 10, step = 0.25),
np.arange(start = X_set[:, 1].min() - 1000, stop = X_set[:, 1].max() + 1000, step = 0.25))
plt.contourf(X1, X2, classifier.predict(sc.transform(np.array([X1.ravel(), X2.ravel()]).T)).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Random Forest Classification (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
| 9,345 |
/作業/.ipynb_checkpoints/10.23數軟作業一 因式分解-checkpoint.ipynb | 099052863b26f3e3b50876ebac4ae8e529a5507f | [] | no_license | amyyang17/mywork | https://github.com/amyyang17/mywork | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 2,356 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import sympy as sp
from sympy.abc import x,y,z
from sympy import factor
sp.factor(x**3 - x**2 + x - 1)
sp.factor(x**2+6*x+8)
f=(x+5)**5
sp.apart(f)
(y)
# ### Problem 18
x=2
if x == 2:
print (x)
else:
x +
# ### Problem 20
x = [0, 1, [2]]
x[2][0] = 3
print (x)
x[2].append(4)
print (x)
x[2] = 2
print (x)
'dog', 'horse', 'motorbike',
'person', 'pottedplant', 'sheep', 'sofa', 'train', 'tvmonitor')
label_map = {k: v+1 for v, k in enumerate(voc_labels)}
#Inverse mapping
rev_label_map = {v: k for k, v in label_map.items()}
#Colormap for bounding box
CLASSES = 20
distinct_colors = ["#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])
for i in range(CLASSES)]
label_color_map = {k: distinct_colors[i] for i, k in enumerate(label_map.keys())}
# +
def parse_annot(annotation_path):
tree = ET.parse(annotation_path)
root = tree.getroot()
boxes = list()
labels = list()
difficulties = list()
for object in root.iter("object"):
difficult = int(object.find("difficult").text == "1")
label = object.find("name").text.lower().strip()
if label not in label_map:
print("{0} not in label map.".format(label))
assert label in label_map
bbox = object.find("bndbox")
xmin = int(bbox.find("xmin").text)
ymin = int(bbox.find("ymin").text)
xmax = int(bbox.find("xmax").text)
ymax = int(bbox.find("ymax").text)
boxes.append([xmin, ymin, xmax, ymax])
labels.append(label_map[label])
difficulties.append(difficult)
return {"boxes": boxes, "labels": labels, "difficulties": difficulties}
def draw_PIL_image(image, boxes, labels):
'''
Draw PIL image
image: A PIL image
labels: A tensor of dimensions (#objects,)
boxes: A tensor of dimensions (#objects, 4)
'''
if type(image) != PIL.Image.Image:
image = F.to_pil_image(image)
new_image = image.copy()
labels = labels.tolist()
draw = ImageDraw.Draw(new_image)
boxes = boxes.tolist()
for i in range(len(boxes)):
draw.rectangle(xy= boxes[i], outline= label_color_map[rev_label_map[labels[i]]])
display(new_image)
# -
# ## Original Image
image = Image.open("./data/000144.jpg", mode= "r")
image = image.convert("RGB")
objects= parse_annot("./data/000144.xml")
boxes = torch.FloatTensor(objects['boxes'])
labels = torch.LongTensor(objects['labels'])
difficulties = torch.ByteTensor(objects['difficulties'])
draw_PIL_image(image, boxes, labels)
# ### Adjust Contrast
def Adjust_contrast(image):
return F.adjust_contrast(image,2)
new_image = Adjust_contrast(image)
draw_PIL_image(new_image, boxes, labels)
# ### Adjust Brightness
def Adjust_brightness(image):
return F.adjust_brightness(image, 2)
new_image = Adjust_brightness(image)
draw_PIL_image(new_image, boxes, labels)
# ### Adjust saturation
def Adjust_saturation(image):
return F.adjust_saturation(image, 2)
new_image = Adjust_saturation(image)
draw_PIL_image(new_image, boxes, labels)
# ### Lighting Noise
# +
def lighting_noise(image):
'''
color channel swap in image
image: A PIL image
'''
new_image = image
perms = ((0, 1, 2), (0, 2, 1), (1, 0, 2),
(1, 2, 0), (2, 0, 1), (2, 1, 0))
swap = perms[random.randint(0, len(perms)- 1)]
new_image = F.to_tensor(new_image)
new_image = new_image[swap, :, :]
new_image = F.to_pil_image(new_image)
return new_image
new_image = lighting_noise(image)
draw_PIL_image(new_image, boxes, labels)
# -
# ### Flip
# +
def flip(image, boxes):
'''
Flip image horizontally.
image: a PIL image
boxes: Bounding boxes, a tensor of dimensions (#objects, 4)
'''
new_image = F.hflip(image)
#flip boxes
new_boxes = boxes.clone()
new_boxes[:, 0] = image.width - boxes[:, 0]
new_boxes[:, 2] = image.width - boxes[:, 2]
new_boxes = new_boxes[:, [2, 1, 0, 3]]
return new_image, new_boxes
new_image, new_boxes = flip(image, boxes)
draw_PIL_image(new_image, new_boxes, labels)
# -
# ### Rotate
def rotate(image, boxes, angle):
'''
Rotate image and bounding box
image: A Pil image (w, h)
boxes: A tensors of dimensions (#objects, 4)
Out: rotated image (w, h), rotated boxes
'''
new_image = image.copy()
new_boxes = boxes.clone()
#Rotate image, expand = True
w = image.width
h = image.height
cx = w/2
cy = h/2
new_image = new_image.rotate(angle, expand= True)
angle = np.radians(angle)
alpha = np.cos(angle)
beta = np.sin(angle)
#Get affine matrix
AffineMatrix = torch.tensor([[alpha, beta, (1-alpha)*cx - beta*cy],
[-beta, alpha, beta*cx + (1-alpha)*cy]])
#Rotation boxes
box_width = (boxes[:,2] - boxes[:,0]).reshape(-1,1)
box_height = (boxes[:,3] - boxes[:,1]).reshape(-1,1)
#Get corners for boxes
x1 = boxes[:,0].reshape(-1,1)
y1 = boxes[:,1].reshape(-1,1)
x2 = x1 + box_width
y2 = y1
x3 = x1
y3 = y1 + box_height
x4 = boxes[:,2].reshape(-1,1)
y4 = boxes[:,3].reshape(-1,1)
corners = torch.stack((x1,y1,x2,y2,x3,y3,x4,y4), dim= 1)
corners.reshape(8, 8) #Tensors of dimensions (#objects, 8)
corners = corners.reshape(-1,2) #Tensors of dimension (4* #objects, 2)
corners = torch.cat((corners, torch.ones(corners.shape[0], 1)), dim= 1) #(Tensors of dimension (4* #objects, 3))
cos = np.abs(AffineMatrix[0, 0])
sin = np.abs(AffineMatrix[0, 1])
nW = int((h * sin) + (w * cos))
nH = int((h * cos) + (w * sin))
AffineMatrix[0, 2] += (nW / 2) - cx
AffineMatrix[1, 2] += (nH / 2) - cy
#Apply affine transform
rotate_corners = torch.mm(AffineMatrix, corners.t()).t()
rotate_corners = rotate_corners.reshape(-1,8)
x_corners = rotate_corners[:,[0,2,4,6]]
y_corners = rotate_corners[:,[1,3,5,7]]
#Get (x_min, y_min, x_max, y_max)
x_min, _ = torch.min(x_corners, dim= 1)
x_min = x_min.reshape(-1, 1)
y_min, _ = torch.min(y_corners, dim= 1)
y_min = y_min.reshape(-1, 1)
x_max, _ = torch.max(x_corners, dim= 1)
x_max = x_max.reshape(-1, 1)
y_max, _ = torch.max(y_corners, dim= 1)
y_max = y_max.reshape(-1, 1)
new_boxes = torch.cat((x_min, y_min, x_max, y_max), dim= 1)
scale_x = new_image.width / w
scale_y = new_image.height / h
#Resize new image to (w, h)
new_image = new_image.resize((500, 333))
#Resize boxes
new_boxes /= torch.Tensor([scale_x, scale_y, scale_x, scale_y])
new_boxes[:, 0] = torch.clamp(new_boxes[:, 0], 0, w)
new_boxes[:, 1] = torch.clamp(new_boxes[:, 1], 0, h)
new_boxes[:, 2] = torch.clamp(new_boxes[:, 2], 0, w)
new_boxes[:, 3] = torch.clamp(new_boxes[:, 3], 0, h)
return new_image, new_boxes
new_image, new_boxes= rotate(image, boxes, 10)
draw_PIL_image(new_image, new_boxes, labels)
# ### Random crop
def intersect(boxes1, boxes2):
'''
Find intersection of every box combination between two sets of box
boxes1: bounding boxes 1, a tensor of dimensions (n1, 4)
boxes2: bounding boxes 2, a tensor of dimensions (n2, 4)
Out: Intersection each of boxes1 with respect to each of boxes2,
a tensor of dimensions (n1, n2)
'''
n1 = boxes1.size(0)
n2 = boxes2.size(0)
max_xy = torch.min(boxes1[:, 2:].unsqueeze(1).expand(n1, n2, 2),
boxes2[:, 2:].unsqueeze(0).expand(n1, n2, 2))
min_xy = torch.max(boxes1[:, :2].unsqueeze(1).expand(n1, n2, 2),
boxes2[:, :2].unsqueeze(0).expand(n1, n2, 2))
inter = torch.clamp(max_xy - min_xy , min=0) # (n1, n2, 2)
return inter[:, :, 0] * inter[:, :, 1] #(n1, n2)
def find_IoU(boxes1, boxes2):
'''
Find IoU between every boxes set of boxes
boxes1: a tensor of dimensions (n1, 4) (left, top, right , bottom)
boxes2: a tensor of dimensions (n2, 4)
Out: IoU each of boxes1 with respect to each of boxes2, a tensor of
dimensions (n1, n2)
Formula:
(box1 ∩ box2) / (box1 u box2) = (box1 ∩ box2) / (area(box1) + area(box2) - (box1 ∩ box2 ))
'''
inter = intersect(boxes1, boxes2)
area_boxes1 = (boxes1[:, 2] - boxes1[:, 0]) * (boxes1[:, 3] - boxes1[:, 1])
area_boxes2 = (boxes2[:, 2] - boxes2[:, 0]) * (boxes2[:, 3] - boxes2[:, 1])
area_boxes1 = area_boxes1.unsqueeze(1).expand_as(inter) #(n1, n2)
area_boxes2 = area_boxes2.unsqueeze(0).expand_as(inter) #(n1, n2)
union = (area_boxes1 + area_boxes2 - inter)
return inter / union
def random_crop(image, boxes, labels, difficulties):
'''
image: A PIL image
boxes: Bounding boxes, a tensor of dimensions (#objects, 4)
labels: labels of object, a tensor of dimensions (#objects)
difficulties: difficulties of detect object, a tensor of dimensions (#objects)
Out: cropped image , new boxes, new labels, new difficulties
'''
if type(image) == PIL.Image.Image:
image = F.to_tensor(image)
original_h = image.size(1)
original_w = image.size(2)
while True:
mode = random.choice([0.1, 0.3, 0.5, 0.9, None])
if mode is None:
return image, boxes, labels, difficulties
new_image = image
new_boxes = boxes
new_difficulties = difficulties
new_labels = labels
for _ in range(50):
# Crop dimensions: [0.3, 1] of original dimensions
new_h = random.uniform(0.3*original_h, original_h)
new_w = random.uniform(0.3*original_w, original_w)
# Aspect ratio constraint b/t .5 & 2
if new_h/new_w < 0.5 or new_h/new_w > 2:
continue
#Crop coordinate
left = random.uniform(0, original_w - new_w)
right = left + new_w
top = random.uniform(0, original_h - new_h)
bottom = top + new_h
crop = torch.FloatTensor([int(left), int(top), int(right), int(bottom)])
# Calculate IoU between the crop and the bounding boxes
overlap = find_IoU(crop.unsqueeze(0), boxes) #(1, #objects)
overlap = overlap.squeeze(0)
# If not a single bounding box has a IoU of greater than the minimum, try again
if overlap.max().item() < mode:
continue
#Crop
new_image = image[:, int(top):int(bottom), int(left):int(right)] #(3, new_h, new_w)
#Center of bounding boxes
center_bb = (boxes[:, :2] + boxes[:, 2:])/2.0
#Find bounding box has been had center in crop
center_in_crop = (center_bb[:, 0] >left) * (center_bb[:, 0] < right
) *(center_bb[:, 1] > top) * (center_bb[:, 1] < bottom) #( #objects)
if not center_in_crop.any():
continue
#take matching bounding box
new_boxes = boxes[center_in_crop, :]
#take matching labels
new_labels = labels[center_in_crop]
#take matching difficulities
new_difficulties = difficulties[center_in_crop]
#Use the box left and top corner or the crop's
new_boxes[:, :2] = torch.max(new_boxes[:, :2], crop[:2])
#adjust to crop
new_boxes[:, :2] -= crop[:2]
new_boxes[:, 2:] = torch.min(new_boxes[:, 2:],crop[2:])
#adjust to crop
new_boxes[:, 2:] -= crop[:2]
return F.to_pil_image(new_image), new_boxes, new_labels, new_difficulties
new_image,new_boxes, new_labels, new_difficulties = random_crop(image, boxes,labels, difficulties)
draw_PIL_image(new_image, new_boxes, new_labels)
# ### Zoom out (expand image)
def zoom_out(image, boxes):
'''
Zoom out image (max scale = 4)
image: A PIL image
boxes: bounding boxes, a tensor of dimensions (#objects, 4)
Out: new_image, new_boxes
'''
if type(image) == PIL.Image.Image:
image = F.to_tensor(image)
original_h = image.size(1)
original_w = image.size(2)
max_scale = 4
scale = random.uniform(1, max_scale)
new_h = int(scale*original_h)
new_w = int(scale*original_w)
#Create an image with the filler
filler = [0.485, 0.456, 0.406]
filler = torch.FloatTensor(filler) #(3)
new_image = torch.ones((3, new_h, new_w), dtype= torch.float) * filler.unsqueeze(1).unsqueeze(1)
left = random.randint(0, new_w - original_w)
right = left + original_w
top = random.randint(0, new_h - original_h)
bottom = top + original_h
new_image[:, top:bottom, left:right] = image
#Adjust bounding box
new_boxes = boxes + torch.FloatTensor([left, top, left, top]).unsqueeze(0)
return new_image, new_boxes
new_image, new_boxes = zoom_out(image, boxes)
draw_PIL_image(new_image, new_boxes, labels)
# ### Rotate only bouding box (optional)
def rotate_only_bboxes(image, boxes, angle):
new_image = image.copy()
new_image = F.to_tensor(new_image)
for i in range(boxes.shape[0]):
x_min, y_min, x_max, y_max = map(int, boxes[i,:].tolist())
bbox = new_image[:, y_min:y_max+1, x_min:x_max+1]
bbox = F.to_pil_image(bbox)
bbox = bbox.rotate(angle)
new_image[:,y_min:y_max+1, x_min:x_max+1] = F.to_tensor(bbox)
return F.to_pil_image(new_image)
new_image = rotate_only_bboxes(image, boxes, 5)
draw_PIL_image(new_image, boxes, labels)
# ### Cutout
def cutout(image, boxes, labels, fill_val= 0, bbox_remove_thres= 0.4):
'''
Cutout augmentation
image: A PIL image
boxes: bounding boxes, a tensor of dimensions (#objects, 4)
labels: labels of object, a tensor of dimensions (#objects)
fill_val: Value filled in cut out
bbox_remove_thres: Theshold to remove bbox cut by cutout
Out: new image, new_boxes, new_labels
'''
if type(image) == PIL.Image.Image:
image = F.to_tensor(image)
original_h = image.size(1)
original_w = image.size(2)
original_channel = image.size(0)
new_image = image
new_boxes = boxes
new_labels = labels
for _ in range(50):
#Random cutout size: [0.15, 0.5] of original dimension
cutout_size_h = random.uniform(0.15*original_h, 0.5*original_h)
cutout_size_w = random.uniform(0.15*original_w, 0.5*original_w)
#Random position for cutout
left = random.uniform(0, original_w - cutout_size_w)
right = left + cutout_size_w
top = random.uniform(0, original_h - cutout_size_h)
bottom = top + cutout_size_h
cutout = torch.FloatTensor([int(left), int(top), int(right), int(bottom)])
#Calculate intersect between cutout and bounding boxes
overlap_size = intersect(cutout.unsqueeze(0), boxes)
area_boxes = (boxes[:, 2] - boxes[:, 0]) * (boxes[:, 3] - boxes[:, 1])
ratio = overlap_size / area_boxes
#If all boxes have Iou greater than bbox_remove_thres, try again
if ratio.min().item() > bbox_remove_thres:
continue
cutout_arr = torch.full((original_channel,int(bottom) - int(top),int(right) - int(left)), fill_val)
new_image[:, int(top):int(bottom), int(left):int(right)] = cutout_arr
#Create new boxes and labels
boolean = ratio < bbox_remove_thres
new_boxes = boxes[boolean[0], :]
new_labels = labels[boolean[0]]
return F.to_pil_image(new_image), new_boxes, new_labels
new_image,new_boxes, new_labels = cutout(image, boxes,labels)
draw_PIL_image(new_image, new_boxes, new_labels)
# ### Mixup
# #### Images
image1 = Image.open("./data/000144.jpg", mode= "r")
image1 = image1.convert("RGB")
objects1= parse_annot("./data/000144.xml")
boxes1 = torch.FloatTensor(objects1['boxes'])
labels1 = torch.LongTensor(objects1['labels'])
difficulties1 = torch.ByteTensor(objects1['difficulties'])
draw_PIL_image(image1, boxes1, labels1)
image2 = Image.open("./data/000055.jpg", mode= "r")
image2 = image2.convert("RGB")
objects2= parse_annot("./data/000055.xml")
boxes2 = torch.FloatTensor(objects2['boxes'])
labels2 = torch.LongTensor(objects2['labels'])
difficulties2 = torch.ByteTensor(objects2['difficulties'])
draw_PIL_image(image2, boxes2, labels2)
image_info_1 = {"image": F.to_tensor(image1), "label": labels1, "box": boxes1, "difficult": difficulties1}
image_info_2 = {"image": F.to_tensor(image2), "label": labels2, "box": boxes2, "difficult": difficulties2}
def mixup(image_info_1, image_info_2, lambd):
'''
Mixup 2 image
image_info_1, image_info_2: Info dict 2 image with keys = {"image", "label", "box", "difficult"}
lambd: Mixup ratio
Out: mix_image (Temsor), mix_boxes, mix_labels, mix_difficulties
'''
img1 = image_info_1["image"] #Tensor
img2 = image_info_2["image"] #Tensor
mixup_width = max(img1.shape[2], img2.shape[2])
mix_up_height = max(img1.shape[1], img2.shape[1])
mix_img = torch.zeros(3, mix_up_height, mixup_width)
mix_img[:, :img1.shape[1], :img1.shape[2]] = img1 * lambd
mix_img[:, :img2.shape[1], :img2.shape[2]] += img2 * (1. - lambd)
mix_labels = torch.cat((image_info_1["label"], image_info_2["label"]), dim= 0)
mix_difficulties = torch.cat((image_info_1["difficult"], image_info_2["difficult"]), dim= 0)
mix_boxes = torch.cat((image_info_1["box"], image_info_2["box"]), dim= 0)
return mix_img, mix_boxes, mix_labels, mix_difficulties
lambd = random.uniform(0, 1)
mix_img, mix_boxes, mix_labels, mix_difficulties = mixup(image_info_1, image_info_2, lambd)
draw_PIL_image(F.to_pil_image(mix_img), mix_boxes, mix_labels)
print("Lambda: ",lambd)
| 18,821 |
/US_Ecommerce/US_Ecommerce.ipynb | a6e134f7370cf9c71cc0ff575107ee6295f2437e | [] | no_license | huyvofjh/PortfolioProject | https://github.com/huyvofjh/PortfolioProject | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 20,206 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
df = pd.read_excel('US_Ecommerce.xlsx')
df.head()
df.isnull().sum()
df.dtypes
# Changing 'Order Date' variable to datetime data type
df['Order Date'] = df['Order Date'].astype('datetime64[ns]')
df.dtypes
df['Category'].unique()
df.head()
df.to_excel('US_Ecommerce2020.xlsx', sheet_name='sheet1', index=False)
| 603 |
/notebooks/shreeshet/explore-and-classify-birds-by-their-bones.ipynb | 237c19ff23853ec40f007d18c93500c2b16d90ab | [] | no_license | Sayem-Mohammad-Imtiaz/kaggle-notebooks | https://github.com/Sayem-Mohammad-Imtiaz/kaggle-notebooks | 5 | 6 | null | null | null | null | Jupyter Notebook | false | false | .py | 23,893 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] _cell_guid="61cf3171-40ef-1d38-6b67-ec1679509167"
# Explore the dataset and try some classification algorithm.
# ----------------------------------------------------------
# + _cell_guid="ef75ddb1-cb1c-69f2-7b34-16f4cf577851"
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory
from subprocess import check_output
print(check_output(["ls", "../input"]).decode("utf8"))
import warnings
warnings.filterwarnings("ignore", category=np.VisibleDeprecationWarning)
import seaborn as sns
import matplotlib.pyplot as plt
plt.style.use("ggplot")
# Any results you write to the current directory are saved as output.
# + _cell_guid="19aaf69f-c4a7-1a02-e8f6-d50e2f300496"
bird = pd.read_csv(
"../input/bird.csv",
dtype={"id": "str"}
).dropna(axis=0, how="any")
bird.shape
# + [markdown] _cell_guid="b8371c70-8779-6ccd-2e08-2f4c854e4d3e"
# Summary of the data.
# + _cell_guid="baeda003-5bb9-e60b-8a59-5fab30733ca4"
bird.describe()
# + [markdown] _cell_guid="e85aa780-f773-33d8-98df-a9409ee58af7"
# Number of birds in each ecological group.
# + _cell_guid="73b7a0a6-71f7-f06f-1097-7ad2e1af948e"
size_of_each_group = bird.groupby("type").size()
ax = size_of_each_group.plot(
kind="bar",
title="Number of birds in each ecological group",
color="#00304e",
figsize=((6, 4)),
rot=0
)
ax.set_title("Number of birds in each ecological group", fontsize=10)
_ = ax.set_xlabel("Ecological Group", fontsize=8)
for x, y in zip(np.arange(0, len(size_of_each_group)), size_of_each_group):
_ = ax.annotate("{:d}".format(y), xy=(x-(0.14 if len(str(y)) == 3 else 0.1), y-6), fontsize=10, color="#eeeeee")
# + _cell_guid="88b8e936-c244-832c-f267-e7c5ac26c3fa"
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler(with_mean=False) # Do not centralize the features, keep them positive.
bird_raw = bird.copy() # Make a copy of original data.
feature_columns = ['huml', 'humw', 'ulnal', 'ulnaw', 'feml', 'femw', 'tibl', 'tibw', 'tarl', 'tarw'] # numeric feature columns.
bird[feature_columns] = scaler.fit_transform(bird_raw[feature_columns]) # standardlize the numeric features.
# + [markdown] _cell_guid="620df605-10f0-001e-07ee-8b69bd2dbe17"
# The correlation matrix of 10 features.
# + _cell_guid="908bd037-8ea2-88a4-adec-5aec8639df31"
corr = bird_raw[feature_columns].corr()
_, ax = plt.subplots(figsize=(5, 5))
mask = np.zeros_like(corr)
mask[np.triu_indices_from(mask)] = True
_ = sns.heatmap(
corr,
cmap=sns.light_palette("#00304e", as_cmap=True),
square=True,
cbar=False,
ax=ax,
annot=True,
annot_kws={"fontsize": 8},
mask=mask
)
# + [markdown] _cell_guid="1354363f-7a11-d045-4c3f-c923598f5114"
# We can see that these features are highly correlated. That's natural: big birds has longer and thicker bones than small birds no matter what kinds of birds they are.
#
# Draw scatter plots for 10 features.
# + _cell_guid="23801085-50f7-3a0f-4bc3-27865a966a6f"
_ = sns.pairplot(
data=bird_raw,
kind="scatter",
vars=feature_columns,
hue="type",
diag_kind="hist",
palette=sns.color_palette("Set1", n_colors=6, desat=.5)
)
# + [markdown] _cell_guid="59ef04eb-6ccb-111f-1ad9-6bc4c0320733"
# Most feature-pairs present strong linear relationship.
# + [markdown] _cell_guid="a603d6c9-7f69-8dec-b520-bd47a196e920"
# The box-plots of each kind of bones.
# + _cell_guid="827de9fd-1e3d-f3f6-5a66-f78e425a1956"
_, axes = plt.subplots(nrows=4, ncols=3, figsize=(15, 20))
for f, ax in zip(feature_columns, axes.ravel()):
_ = sns.boxplot(
data=bird_raw,
y=f,
x='type',
ax=ax,
palette=sns.color_palette("Set1", n_colors=6, desat=.5)
)
_ = axes[3, 1].annotate("No Data", xy=(.42, .48))
_ = axes[3, 2].annotate("No Data", xy=(.42, .48))
# + [markdown] _cell_guid="230cc569-63de-30fd-80e6-0b2866ccc85a"
# Compute the ratios of limbs and hinds of all birds, and plot them.
# + _cell_guid="b7a49a90-5ade-1e8f-2c2a-4c191faf064c"
limb_hind_ratio = pd.DataFrame(
{"ratio": (bird_raw.huml + bird_raw.ulnal) / (bird_raw.feml + bird_raw.tibl + bird_raw.tarl),
"type": bird_raw.type})
_, axes = plt.subplots(nrows=2, ncols=3, figsize=(12, 8))
for t, ax, c in zip(limb_hind_ratio.type.unique(), axes.ravel(), sns.color_palette("Set1", n_colors=6, desat=.5)):
_ = sns.distplot(
limb_hind_ratio.loc[limb_hind_ratio.type == t, 'ratio'],
rug=True,
axlabel=t,
bins=20,
ax=ax,
color=c
)
# + [markdown] _cell_guid="5556f318-7855-5d68-cb83-6f240c9cf10e"
# ## Principle Components Analysis ##
# + _cell_guid="e9971a57-44d3-5e67-430d-7fc91a5d1491"
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(bird[feature_columns])
explained_variance = pd.DataFrame({"evr": pca.explained_variance_ratio_, "evrc": pca.explained_variance_ratio_.cumsum()},
index=pd.Index(["pc{:d}".format(i) for i in np.arange(1, len(feature_columns) + 1)], name="principle components"))
_, ax = plt.subplots(figsize=(8, 4))
_ = explained_variance.evrc.plot(kind="line", color="#ee7621", ax=ax, linestyle="-", marker="h")
_ = explained_variance.evr.plot(kind="bar", ax=ax, color="#00304e", alpha=0.8, rot=0)
_ = ax.set_title("Explained Variance Ratio of Principle Components", fontsize=10)
_ = ax.set_ylim([0.0, 1.1])
for x, y in zip(np.arange(0, len(explained_variance.evrc)), explained_variance.evrc):
_ = ax.annotate("{:.1f}%".format(y * 100.0), xy=(x-0.2, y+0.03), fontsize=7)
for x, y in zip(np.arange(1, len(explained_variance.evr)), explained_variance.evr[1:]):
_ = ax.annotate("{:.1f}%".format(y * 100.0), xy=(x-0.15, y+0.02), fontsize=7)
# + [markdown] _cell_guid="1cf6fd1e-d09b-0281-1c4a-25fdbcf2eb76"
# We see that first principle component take almost all variance. This means our dataset is nearly 1-dimension. Not surprising, birds are all "bird-shaped", size of all their bones change almost synchronously.
#
# Scatter the principle components.
# + _cell_guid="fa2f55c0-eee0-0e14-d8e8-ba7267649779"
pc_df = pd.DataFrame(
pca.transform(bird[feature_columns]),
columns=["pc{:d}".format(i) for i in np.arange(1, len(feature_columns) + 1)]
)
pc_df["type"] = bird.type
_ = sns.pairplot(
data=pc_df,
vars=["pc{:d}".format(i) for i in np.arange(1, 6)],
hue="type",
diag_kind="kde",
palette=sns.color_palette("Set1", n_colors=6, desat=.5)
)
# + [markdown] _cell_guid="26a196b0-8113-946b-6dad-f8d6ae1b807b"
# How about the robustness of the bones. Let's define the robustness of a bone is the ratio of its diameter and length.
# + _cell_guid="9a9c5567-3ade-9539-7ea6-c21ec8e775c1"
robust = pd.DataFrame({
"humr": bird_raw.humw / bird_raw.huml,
"ulnar": bird_raw.ulnaw / bird_raw.ulnal,
"femr": bird_raw.femw / bird_raw.feml,
"tibr": bird_raw.tibw / bird_raw.tibl,
"tarr": bird_raw.tarw / bird_raw.tarl,
"type": bird_raw.type}
)
_, axes = plt.subplots(nrows=3, ncols=2, figsize=(8, 12))
for f, ax in zip(["humr", "ulnar", "femr", "tibr", "tarr"], axes.ravel()):
_ = sns.boxplot(
data=robust,
y=f,
x='type',
ax=ax,
palette=sns.color_palette("Set1", n_colors=6, desat=.5)
)
if f == "tibr":
ax.set_ylim((0.0, 0.1))
_ = axes[2, 1].annotate("No Data", xy=(.42, .5), fontsize=8)
# + [markdown] _cell_guid="b8fa72b1-9ff9-4d68-b35b-7518a86b2dee"
# Add these new features to original dataset.
# + _cell_guid="1dd7ddbe-a25e-3cda-8064-95b4ae5fbde0"
bird_extended = pd.concat([bird_raw, robust[["humr", "ulnar", "femr", "tibr", "tarr"]], limb_hind_ratio["ratio"]], axis=1)
feature_columns_extended = ["huml", "humw", "ulnal", "ulnaw", "feml", "femw", "tibl", "tibw", "tarl", "tarw", "humr", "ulnar", "femr", "tibr", "tarr", "ratio"]
bird_extended[feature_columns_extended] = scaler.fit_transform(bird_extended[feature_columns_extended])
# + [markdown] _cell_guid="f980c7c7-46b7-81b6-bd79-8207f5363f1c"
# Now compute features' chi2 significances.
# + _cell_guid="6501a47d-aa6d-7ded-5007-913878e050c0"
from sklearn.feature_selection import chi2
chi2_result = chi2(bird_extended[feature_columns_extended], bird_extended.type)
chi2_result = pd.DataFrame({"feature": feature_columns_extended, "chi2_statics": chi2_result[0], "p_values": chi2_result[1]})
chi2_result.sort_values(by="p_values", ascending=False, inplace=True)
chi2_result.set_index(keys="feature", inplace=True)
ax = chi2_result["p_values"].plot(kind="barh", logx=True, color="#00304e")
_ = ax.annotate("{:3.2f}".format(chi2_result.chi2_statics[chi2_result.shape[0] - 1]), xy=(chi2_result.p_values[chi2_result.shape[0] - 1], len(feature_columns_extended) - 1), xytext=(0, -3), textcoords="offset pixels", fontsize=8, color="#00304e")
for y, x, c in zip(np.arange(0, len(feature_columns_extended) - 1), chi2_result.p_values[:-1], chi2_result.chi2_statics[:-1]):
_ = ax.annotate("{:3.2f}".format(c), xy=(x, y), xytext=(-35, -3), textcoords="offset pixels", fontsize=8, color="#eeeeee")
_ = ax.set_xlabel("p-value (chi2 value)")
_ = ax.set_title("chi2 values and p-values of features", fontsize=10)
# + [markdown] _cell_guid="717278e5-e38f-c5b5-14f2-299463ccd92f"
# More large the chi2 value (*more small the p-value*), more significant the feature (*to be different in different groups*)
# + [markdown] _cell_guid="f645d991-9dd4-ca73-bcf8-389bfc3a1fa5"
# Try classification
# ------------------
# + _cell_guid="074047f0-a88f-6004-50ed-3a03f737fee2"
from sklearn.model_selection import train_test_split
train_f, test_f, train_l, test_l = train_test_split(bird_extended[feature_columns_extended], bird_extended.type, train_size=0.6)
# + _cell_guid="3ab27fcb-dd4f-d551-e587-34776f97a085"
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
lr = LogisticRegression()
params = {
"penalty": ["l1", "l2"],
"C": [0.1, 1.0, 5.0, 10.0],
"class_weight": [None, "balanced"]
}
gs = GridSearchCV(estimator=lr, param_grid=params, scoring="accuracy", cv=5, refit=True)
_ = gs.fit(train_f, train_l)
# + [markdown] _cell_guid="0635bb9f-60b9-0467-c14c-0274c49d9f36"
# Best params found by grid search.
# + _cell_guid="e44017a4-d840-b369-21a3-960b44397149"
print('\nBest parameters:')
for param_name, param_value in gs.best_params_.items():
print('{}:\t{}'.format(param_name, str(param_value)))
print('\nBest score (accuracy): {:.3f}'.format(gs.best_score_))
# + [markdown] _cell_guid="f08216c0-eadd-f9f8-c16f-f32ff83b2811"
# Classification metrics.
# + _cell_guid="9a296f6b-51c0-5cfb-a7da-caa1fada627d"
from sklearn.metrics import confusion_matrix, classification_report
predict_l = gs.predict(test_f)
print(classification_report(test_l, predict_l))
# + _cell_guid="6b72b02f-3624-e150-ef90-6feee9caebab"
cm = confusion_matrix(test_l, predict_l)
_ = sns.heatmap(
cm,
square=True,
xticklabels=["P", "R", "SO", "SW", "T", "W"],
annot=True,
annot_kws={"fontsize": 8},
yticklabels=["P", "R", "SO", "SW", "T", "W"],
cbar=False,
cmap=sns.light_palette("#00304e", as_cmap=True)
).set(xlabel = "predicted ecological group", ylabel = "real ecological group", title = "Confusion Matrix")
# + _cell_guid="adf5056a-473e-b6eb-8b8a-bdcdac9b72ca"
from sklearn.metrics import accuracy_score
print("Accuracy: {:.3f}".format(accuracy_score(y_true=test_l, y_pred=predict_l)))
# + [markdown] _cell_guid="220d9ff6-0bc9-7e74-3d7d-b70b5f3e875e"
# Features' weights (*absolute values*).
# + _cell_guid="f1551321-f46f-a7c3-b668-7c646eed4bfc"
_, ax = plt.subplots(nrows=1, ncols=1, figsize=(16, 8))
_ = sns.heatmap(
abs(gs.best_estimator_.coef_),
ax=ax,
square=True,
xticklabels=feature_columns_extended,
annot=True,
annot_kws={"fontsize": 10},
yticklabels=gs.best_estimator_.classes_,
cbar=False,
cmap=sns.light_palette("#00304e", as_cmap=True)
).set(xlabel = "Features", ylabel = "Ecological Group", title = "Absolute Feature Weights")
# + [markdown] _cell_guid="ce887f6c-ce98-55bf-7385-6c2a610f4e93"
# Try random forest algorithm.
# + _cell_guid="abe6cec6-1493-f70a-ec18-5e61ce91047c"
from sklearn.ensemble import RandomForestClassifier
rfc = RandomForestClassifier()
params = {
"n_estimators": [5, 10, 20, 50],
"criterion": ["gini", "entropy"],
"max_depth": [5, 10, 15],
"class_weight": [None, "balanced"]
}
rfc_gs = GridSearchCV(estimator=rfc, param_grid=params, scoring="accuracy", cv=5, refit=True)
_ = rfc_gs.fit(train_f, train_l)
# + _cell_guid="d1811ad5-239e-f9ef-f763-b1b1dee4be98"
print('\nBest parameters:')
for param_name, param_value in rfc_gs.best_params_.items():
print('{}:\t{}'.format(param_name, str(param_value)))
print('\nBest score (accuracy): {:.3f}'.format(rfc_gs.best_score_))
# + [markdown] _cell_guid="2f2526bf-109d-9c17-152d-cea03e6ed8a3"
# Metrics.
# + _cell_guid="f8a6c247-2c20-1632-93b2-ace7565b7823"
predict_l = rfc_gs.predict(test_f)
print(classification_report(test_l, predict_l))
# + _cell_guid="de8a5201-fbdf-62ff-1d30-5e1d618f5333"
cm = confusion_matrix(test_l, predict_l)
_ = sns.heatmap(
cm,
square = True,
xticklabels = ["P", "R", "SO", "SW", "T", "W"],
annot = True,
annot_kws = {"fontsize": 8},
yticklabels = ["P", "R", "SO", "SW", "T", "W"],
cbar = False,
cmap=sns.light_palette("#00304e", as_cmap=True)
).set(xlabel = "Predicted Ecological Group", ylabel = "Real Ecological Group", title = "Confusion Matrix")
# + [markdown] _cell_guid="2336cbb9-a0b0-f314-5437-857ca2d098c9"
# Accuracy.
# + _cell_guid="98cd9ce2-c0fe-839a-2b3b-54715d807336"
print("Accuracy: {:.3f}".format(accuracy_score(y_true=test_l, y_pred=predict_l)))
# + [markdown] _cell_guid="0e381a60-1fd1-fa0b-ec6a-50b201831717"
# Features' importances
# + _cell_guid="c87c6446-ae25-348f-fdb7-e481842063a6"
feature_importances = pd.DataFrame(
{
"importance": rfc_gs.best_estimator_.feature_importances_
},
index=pd.Index(feature_columns_extended, name="feature")
).sort_values(by="importance")
ax = feature_importances.plot(kind="barh", legend=False, color="#00304e")
for y, x in zip(np.arange(0, feature_importances.shape[0]), feature_importances.importance):
_ = ax.annotate("{:.3f}".format(x), xy=(x-0.008, y-0.1), fontsize=8, color="#eeeeee")
_ = ax.set_xlabel("importance")
# + [markdown] _cell_guid="ba6bd0be-d27b-a98b-40ec-8bb0cb245a2c"
# The two classifiers perform poorly on wading birds. The recall is low. From charts (scatter/box-plot) we see that wading birds is difficult to tell from other kids of birds. We scatter wading birds and others here.
# + _cell_guid="c2ca75d8-7030-0d44-bebd-f34e4c95b03d"
bird_raw["is_w"] = bird_raw.type == "W"
_ = sns.pairplot(
data=bird_raw,
kind="scatter",
vars=feature_columns,
hue="is_w",
diag_kind="hist",
palette=sns.color_palette("Set1", n_colors=6, desat=.5)
)
# + [markdown] _cell_guid="73cc36c2-0d44-f3ab-1fd7-bf03ea17bd63"
# Use a support vector machine to tell wading birds from others.
# + _cell_guid="efacf49c-cf82-27ed-80bd-e3d4ac86b685"
from sklearn.svm import SVC
from sklearn.metrics import roc_curve, accuracy_score, precision_score, recall_score, auc, precision_recall_curve
# use extended feature set.
bird_extended["is_w"] = (bird_extended.type == "W").astype("int32")
# parameter grid
params = {
'C': [1, 10, 100],
'kernel': ['poly', 'rbf'],
'degree': [2, 4, 6],
'gamma': ['auto', 1, 5, 10]
}
# SVM for separate ghoul from others.
svc = SVC(probability=True)
# split the train and test set.
train_features, test_features, train_labels, test_labels = train_test_split(bird_extended[feature_columns_extended], bird_extended.is_w,
train_size=0.6)
# grid search.
gs = GridSearchCV(estimator=svc, param_grid=params, cv=3, refit=True, scoring='accuracy')
gs.fit(train_features, train_labels)
svc = gs.best_estimator_
print('\nBest parameters:')
for param_name, param_value in gs.best_params_.items():
print('{}:\t{}'.format(param_name, str(param_value)))
print('\nBest score (accuracy): {:.3f}'.format(gs.best_score_))
# + _cell_guid="ecd879c9-938a-d5a9-5577-efd86cc9b97d"
# merics.
predict_labels = gs.predict(test_features)
predict_proba = gs.predict_proba(test_features)
fpr, rc, th = roc_curve(test_labels, predict_proba[:, 1])
precision, recall, threshold = precision_recall_curve(test_labels, predict_proba[:, 1])
roc_auc = auc(fpr, rc)
print('\nMetrics: Accuracy: {:.3f}, Precision: {:.3f}, Recall: {:.3f}, AUC: {:.3f}'.format(accuracy_score(test_labels, predict_labels), precision_score(test_labels, predict_labels), recall_score(test_labels, predict_labels), roc_auc))
print('\nClassification Report:')
print(classification_report(test_labels, predict_labels, target_names=['no wading birds', 'wading birds']))
# ROC curve.
fig = plt.figure(figsize=(12, 3))
ax = fig.add_subplot(131)
ax.set_xlabel('False Positive Rate')
ax.set_ylabel('Recall')
ax.set_title('ROC Curve')
ax.plot(fpr, rc, '#00304e')
ax.fill_between(fpr, [0.0] * len(rc), rc, facecolor='#00304e', alpha=0.3)
ax.plot([0.0, 1.0], [0.0, 1.0], '--', color='#ee7621', alpha=0.6)
ax.text(0.80, 0.05, 'auc: {:.2f}'.format(roc_auc))
# ax.set_xlim([-0.01, 1.01])
# ax.set_ylim([-0.01, 1.01])
# Precision & recall change with response to threshold.
ax = fig.add_subplot(132)
ax.set_xlabel('Threshold')
ax.set_ylabel('Precision & Recall')
ax.set_title('Precsion & Recall')
ax.set_xlim([threshold.min(), threshold.max()])
ax.set_ylim([0.0, 1.0])
ax.plot(threshold, precision[:-1], '#00304e', label='Precision')
ax.plot(threshold, recall[:-1], '#ee7621', label='Recall')
ax.legend(loc='best')
# ax.set_xlim([-0.01, 1.01])
# ax.set_ylim([-0.01, 1.01])
# Accuracy changes with response to threshold.
ts = np.arange(0, 1.02, 0.02)
accuracy = []
for t in ts:
predict_label = (predict_proba[:, 1] >= t).astype(np.int)
accuracy_score(test_labels, predict_label)
accuracy.append(accuracy_score(test_labels, predict_label))
ax = fig.add_subplot(133)
ax.set_xlabel("Threshold")
ax.set_ylabel("Accuracy")
ax.set_ylim([0.0, 1.0])
ax.set_title('Accuracy')
ax.plot([0.0, 1.0], [0.5, 0.5], '--', color="#ee7621", alpha=0.6)
ax.plot(ts, accuracy, '#00304e')
_ = ax.annotate(
"max accuracy: {:.2f}".format(max(accuracy)),
xy=[ts[accuracy.index(max(accuracy))], max(accuracy)],
xytext=[ts[accuracy.index(max(accuracy))]-0.1, max(accuracy)-0.2],
# textcoords="offset points",
arrowprops={"width": 1.5, "headwidth": 6.0}
)
# ax.fill_between(ts, [0.0] * len(accuracy), accuracy, facecolor='#00304e', alpha=0.4)
# ax.set_xlim([-0.01, 1.01])
# _ = ax.set_ylim([-0.01, 1.01])
# + [markdown] _cell_guid="9a47e512-546e-3cba-f9ac-430da7527df6"
# Because the number of positive instances and negative instances are unequal (*64:349*), high accuracy is not as a good news as we may think. From the metric chart we see the recall curve falls down steeply meanwhile the precision curve keeps low. It is a difficult unbalanced two-class classification.
#
# **To Be Continued ...**
| 19,890 |
/HW9/.ipynb_checkpoints/HW9_B87772-checkpoint.ipynb | 462e728242f85b8cd2f443114100aa08b14d64ce | [] | no_license | saidk/algorithmics | https://github.com/saidk/algorithmics | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 336,040 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
#for GC36 change +
filename = "GC36/Schpo1_chrome_1_annotation.gff"
output_path = "GC36/Schpo1_converted_fixed.gtf"
seqname = "chromosome_1"
# +
result = ""
annotation = dict()
with open(filename) as handle:
for line in handle:
temp = line.split('\t')
# print temp[2]
# if 'exon' in temp[2]:continue
part1 = "\t".join(temp[:8])
name = temp[8].split(";")[0].split()[1][1:-1]
part2 = 'gene_id "{}"; transcript_id "{}";'.format(name,name)
result+= part1+"\t"+part2+"\n"
if name not in annotation:
annotation[name] = []
annotation[name].append(temp)
with open(output_path,'w') as handle: handle.write(result)
| 984 |
/Sample sine wave.ipynb | 650905f513d0fdaa83e68ad6eeaca80409ba42a9 | [] | no_license | venkat0990/Venky-coding-work | https://github.com/venkat0990/Venky-coding-work | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 128,746 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python [conda env:root] *
# language: python
# name: conda-root-py
# ---
import numpy as np
from scipy.fftpack import fft, ifft
x = np.random.random(16)
x = x-np.mean(x)
xk = fft(x)
xi = ifft(xk)
np.allclose(x, xi)
t_energy = np.sum(x*x)
f_energy = np.sum(abs(xk)*abs(xk)/len(xk))
print("time domain energy: {}".format(t_energy))
print("freq domain energy: {}".format(f_energy))
= 1200
output = 24
def generate_sequence(length, period, decay):
return [sin(2 * pi * output * (i/length)) for i in range(length)]
# define model
model = Sequential()
model.add(LSTM(20, return_sequences=True, input_shape=(length, 1)))
model.add(LSTM(20))
model.add(Dense(output))
model.compile(loss= 'mae' , optimizer= 'adam' )
print(model.summary())
# generate input and output pairs of sine waves
def generate_examples(length, n_patterns, output):
X, y = list(), list()
for _ in range(n_patterns):
p = randint(10, 20)
d = uniform(0.01, 0.1)
sequence = generate_sequence(length + output, p, d)
X.append(sequence[:-output])
y.append(sequence[-output:])
X = array(X).reshape(n_patterns, length, 1)
y = array(y).reshape(n_patterns, output)
return X, y
# test problem generation
X, y = generate_examples(260, 5, 5)
for i in range(len(X)):
pyplot.plot([x for x in X[i, :, 0]] + [x for x in y[i]], '-o' )
pyplot.show()
# fit model
X, y = generate_examples(length, 1000, output)
history = model.fit(X, y, batch_size=10, epochs=1)
# evaluate model
X, y = generate_examples(length, 1000, output)
loss = model.evaluate(X, y, verbose=0)
print( 'MAE: %f' % loss)
# prediction on new data
X, y = generate_examples(length, 1, output)
yhat = model.predict(X, verbose=0)
pyplot.plot(y[0], label= y )
pyplot.plot(yhat[0], label= yhat )
pyplot.legend()
pyplot.show()
| 2,031 |
/P_generosa/07-EPI-Bismark.ipynb | 43421b5ac17cdc4253d2317fa9ba847b1ee53861 | [] | no_license | sr320/nb-2018 | https://github.com/sr320/nb-2018 | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 1,165 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
data = np.load('data.npy')
target = np.load('target.npy')
# -
print(data.shape)
print(target.shape)
# +
from sklearn.model_selection import train_test_split as tts
train_data,test_data,train_target,test_target = tts(data,target,test_size=0.3)
# -
print(train_data.shape,train_target.shape)
print(test_data.shape,test_target.shape)
from sklearn.svm import SVC
model = SVC()
model.fit(train_data,train_target)
predicted_target = model.predict(test_data)
from sklearn.metrics import accuracy_score
acc = accuracy_score(test_target,predicted_target)
print('Accuracy:',acc*100)
from sklearn.metrics import confusion_matrix
from matplotlib import pyplot as plt
import seaborn as sns
mat = confusion_matrix(test_target,predicted_target)
sns.heatmap(mat, square=True, annot=True, cbar=False)
plt.savefig('cm_hrd.png',dpi=300)
plt.xlabel('predicted values')
plt.ylabel('actual values');
import joblib
joblib.dump(model,'English_Char_SVC.sav')
# +
from sklearn.metrics import classification_report
classi_report = classification_report(test_target,predicted_target)
print('Classification Report:',classi_report)
# -
ape
# # Load dataset ids
dt = pd.read_csv('extras/dataset_id_name.txt', sep='\t', header=None)
dt.head()
dt.set_index(1, inplace=True)
dt = dt.reindex(index=original_data.columns.values)
dt = dt.loc[dt[0].notnull()]
dt[0] = dt[0].astype(int)
dt
dataset_ids = dt[0].values
original_data = original_data.reindex(columns=dt.index.values)
# # Prepare the final dataset
data = original_data.copy()
datasets = datasets.reindex(index=dataset_ids)
lst = [datasets.index.values, ['value']*datasets.shape[0]]
tuples = list(zip(*lst))
idx = pd.MultiIndex.from_tuples(tuples, names=['dataset_id','data_type'])
data.columns = idx
data.head()
# ## Subset to the genes currently in SGD
genes = pd.read_csv(path_to_genes, sep='\t', index_col='id')
genes = genes.reset_index().set_index('systematic_name')
gene_ids = genes.reindex(index=data.index.values)['id'].values
num_missing = np.sum(np.isnan(gene_ids))
print('ORFs missing from SGD: %d' % num_missing)
# +
data['gene_id'] = gene_ids
data = data.loc[data['gene_id'].notnull()]
data['gene_id'] = data['gene_id'].astype(int)
data = data.reset_index().set_index(['gene_id','orf'])
data.head()
# -
# # Normalize
data_norm = normalize_phenotypic_scores(data, has_tested=True)
# Assign proper column names
lst = [datasets.index.values, ['valuez']*datasets.shape[0]]
tuples = list(zip(*lst))
idx = pd.MultiIndex.from_tuples(tuples, names=['dataset_id','data_type'])
data_norm.columns = idx
# +
data_norm[data.isnull()] = np.nan
data_all = data.join(data_norm)
data_all.head()
# -
# # Print out
for f in ['value','valuez']:
df = data_all.xs(f, level='data_type', axis=1).copy()
df.columns = datasets['name'].values
df = df.droplevel('gene_id', axis=0)
df.to_csv(paper_name + '_' + f + '.txt', sep='\t')
# # Save to DB
from IO.save_data_to_db3 import *
save_data_to_db(data_all, paper_pmid)
UMP INTO CONCLUSIONS THAT FAST)
#
# Again, please be careful, we are not suggesting causation. Moreover, we assumed everything is fixed when interpreted TV and Radio ads. In reality, companies who spend on TV ads tend to also spend on other means of ad.
AdData['Radio'].describe() #Let's explore Radio Data
# First of all, we just observed that in comparison to TV ads, only little has been spent on Radio ads. Median expenditure on TV ads is 7 times more than Radio ads. Second, may be only those companies who spend a lot in TV are interested in spending money in Radio ads. Let's explore it with a scatterplot.
AdData.plot(kind= 'scatter', x = 'TV',y = 'Radio')
# Fortunately, the scatter plot does not suggest that much of association between TV ads and Radio ads. That's good! Actually, corr() matrix suggested that there were no linear relationship.
# So, how can we interpret the result?
#
# May be there is synergy between TV and Radio. In other words, may be, Radio ads are effective only if we have spent enough in TV and visa-versa. In marketing, it is being said that an ad is effective if a potential customer is exposed to it at least 5 times. So, synergy effect is yet to be tested! This is what we are going to explore next session. Also, may be the types of businesses who spend money on TV are completely different from those who spend money on Radio ads.
# #### What is your prediction for a company that has spent 150000 dollars on TV ads and 30000 on Radio ads?
#
print(linreg.predict([150,30])) #we predict 15423 units
# ** This was just a demo. Very important assumptions were not checked in this study. For example we did not check p-values, significancy of variables, Error, and confidence interval of our predictions and coefficients. We also did not check synergy effects. All of these very important topics will be covered in future lectures. **
| 5,166 |
/workshop/DM_only_5533_widget.ipynb | 019241f10e20bcfabfd7f4cea862e947d6deb803 | [] | no_license | villano-lab/grav_project | https://github.com/villano-lab/grav_project | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 11,311 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#Imports
import sys
sys.path.append('../python/')
import NGC5533_functions as nf
import noordermeer as noord
import fitting_NGC5533 as fitting
import dataPython as dp
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
from ipywidgets import interactive, fixed, FloatSlider, HBox, Layout, Button, Label, Output, VBox
from IPython.display import display, clear_output
from IPython.display import Javascript
import scipy.stats as stats
import warnings
warnings.filterwarnings("ignore") #ignore warnings
# -
#TRACING:**************************************
#data points:
data = dp.getXYdata_wXYerr('data/final/nord-120kpc-datapoints.txt')
r_dat = np.asarray(data['xx'])
v_dat = np.asarray(data['yy'])
v_err0 = np.asarray(data['ex'])
v_err1 = np.asarray(data['ey'])
# +
# Define components
M = fitting.f_M
bpref = fitting.f_c
dpref = fitting.f_pref
rc = fitting.f_rc
rho00 = fitting.f_hrho00
gpref = fitting.f_gpref
def blackhole(r):
return nf.bh_v(r,M,load=False)
def bulge(r):
return bpref*nf.b_v(r,load=True)
def disk(r):
return dpref*nf.d_thief(r)
def halo(r,rc,rho00):
return nf.h_v(r,rc,rho00,load=False)
def gas(r):
return gpref*nf.g_thief(r)
def totalcurve(r,rc,rho00):
total = np.sqrt(blackhole(r)**2
+ bulge(r)**2
+ disk(r)**2
+ halo(r,rc,rho00)**2
+ gas(r)**2)
return total
# +
#best fitted prefactor values for each component, to be used as default (initial) values for widget sliders
best_rc = fitting.f_rc
best_rho00 = fitting.f_hrho00
import scipy.integrate as si # for integration
# Equation for isothermal density
def density_iso(r,rho00,rc):
density = rho00 * (1 + (r/rc)**2)**(-1)
return density
# Equation for mass as a function of radius
def mass_function(r,rho00,rc):
mass = 4 * np.pi * density_iso(r,rho00,rc) * r**2
return mass
# Integrate to calculate total mass enclosed
Mass = lambda r,rho00,rc: si.quad(mass_function, 0, r, args=(rho00,rc))[0]
radius = 100 # in kpc, approximation of infinity; the radius within which the total mass of the halo is being calculated
'''
##finding mass?
rr=max(r_dat) #kpc
h=8.9/2 #kpc; is this the thickness of the galaxy???
volume=np.pi*2*rr**2*h
def Mass(rc,rho00):
density=rho00*(1+(rr/rc)**2)**-1
Mass = volume*density
return Mass
'''
print(Mass(1,1,1))
# -
# Define plotting function
def f(rc,rho00):
# Define r
r = np.linspace(0.1,13,1000)
# Plot
plt.figure(figsize=(12,8))
plt.xlim(0,13)
plt.ylim(0,360)
plt.errorbar(r_dat,v_dat,yerr=v_err1,fmt='bo',label='Data')
plt.plot(r,blackhole(r),label=("Black Hole"),color='black')
plt.plot(r,bulge(r),label=("Bulge"),color='orange')
plt.plot(r,disk(r),label=("Disk"),color='purple')
plt.plot(r,halo(r,rc,rho00),label=("Halo"),color='green')
plt.plot(r,gas(r),label=("Gas"),color='blue')
plt.plot(r,totalcurve(r,rc,rho00),label=("Total Curve"),color='red')
plt.plot(r,(blackhole(r)**2+bulge(r)**2+disk(r)**2+gas(r)**2)**(1/2),label=("All Luminous Matter"),linestyle='--')
plt.fill_between(r,
noord.greyb_bottom(r),noord.greyb_top(r),
color='#dddddd')
plt.title("Interactive Rotation Curve - Galaxy: NGC 5533")
plt.xlabel("Radius (kpc)")
plt.ylabel("Velocity (km/s)")
# Chi squared and reduced chi squared
# Residuals
r = np.linspace(0.1,100,69)
residuals = v_dat - totalcurve(r_dat,rc,rho00)
residuals[0] = v_dat[0] #set totalcurve to 0 at 0 - currently going to infinity which results in fitting issues.
# Determining errors
errors = v_err1 #np.sqrt(v_err1**2 + noord.band**2) #inclination uncertainty shouldn't apply to this galaxy as we don't have one given.
# Chi squared
chisquared = np.sum(residuals**2/errors**2)
#chisquared = stats.chisquare(v_dat,totalcurve(r,M,bpref,dpref,rc,rho00,gpref))
reducedchisquared = chisquared * (1/(len(r_dat)-6))
props = dict(boxstyle='round', facecolor='white', alpha=0.5)
plt.text(10.15,325,r"$\chi^2$: {:.5f}".format(chisquared)+'\n'+r"Reduced: {:.5f}".format(reducedchisquared),bbox=props)
#plt.text(80,150,,bbox=props)
TotalMass = Mass(radius,rho00,rc)
props = dict(boxstyle='round', facecolor='white', alpha=0.5)
plt.text(6,325,r"Total Dark Matter Mass: {:.2e}".format(TotalMass)+'$M_{\odot}$',bbox=props)
plt.legend(loc='lower right')
plt.annotate('Data source: E. Noordermeer. The rotation curves of flattened Sérsic bulges. MNRAS,385(3):1359–1364, Apr 2008',
xy=(0, 0), xytext=(0,5),
xycoords=('axes fraction', 'figure fraction'),
textcoords='offset points',
size=10, ha='left', va='bottom')
plt.show()
# +
# Appearance
style = {'description_width': 'initial'}
layout = {'width':'600px'}
# Define slides
rc = FloatSlider(min=0.1, max=5, step=0.1,
value=0.01,
description='Halo Core Radius [kpc]',
readout_format='.2f',
orientation='horizontal',
style=style, layout=layout)
rho00 = FloatSlider(min=0, max=1e9, step=1e7,
value=.1,
description=r'Halo Surface Density [$M_{\odot} / pc^3$]',
readout_format='.2e',
orientation='horizontal',
style=style, layout=layout)
# Interactive widget
def interactive_plot(f):
interact = interactive(f,
rc = rc,
rho00 = rho00,
continuous_update=False)
return interact
# Button to revert back to Best Fit
button = Button(
description="Best Fit",
button_style='warning', # 'success', 'info', 'warning', 'danger' or ''
icon='check')
out = Output()
def on_button_clicked(_):
#display(Javascript('IPython.notebook.execute_cells_below()'))
rc.value=best_rc
rho00.value = best_rho00
button.on_click(on_button_clicked)
# -
# ## What do rotation curves look like without dark matter?
# In this activity, you can visualize how important dark matter is to accurately describing observed data (marked in blue points with error bars below)
#
# So how much mass does a dark matter halo need to contain (i.e. how much dark matter is in a given galaxy) to account for our observations?
# displaying button and its output together
VBox([button,out,interactive_plot(f)])
# ## Slider Key
#
#
# The halo surface density behaves as a prefactor for the **dark matter "halo"** in and around the galaxy.
# Its units are solar masses per cubic parsec (and in this fit is on the scale of hundreds of millions).
# This represents how much dark matter we think there is overall.
#
# Play around with the halo parameters and see how incorporating a dark matter component allows us to more accurately match our observations.
#
# **Rembember, a reduced $\chi^2$ close to 1 is generally considered a good fit. So reduced $\chi^2$ far higher or lower than 1 suggests a poor theoretical model (that is, the model probably doesn't accurately describe the real universe).**
#
# *key*
#
# kpc = kiloparsec, equal to 3.26 light years, or $1.917 \times 10^{16}$ miles <br>
# km/s = kilometers per second (this is a velocity) <br>
# $M_{\odot}$ = solar masses (X number of masses equal to our sun), approximately equal to $1.989 \times 10^{30}$ kilograms <br>
# $M_{\odot} / pc^3$ = solar masses per parsec cubed (this is a 3D density) <br>
#
og\left(1- a^{[L](i)}\right) \large{)} }_\text{cross-entropy cost} + \underbrace{\frac{1}{m} \frac{\lambda}{2} \sum\limits_l\sum\limits_k\sum\limits_j W_{k,j}^{[l]2} }_\text{L2 regularization cost} \tag{2}$$
#
# Let's modify your cost and observe the consequences.
#
# **Exercise**: Implement `compute_cost_with_regularization()` which computes the cost given by formula (2). To calculate $\sum\limits_k\sum\limits_j W_{k,j}^{[l]2}$ , use :
# ```python
# np.sum(np.square(Wl))
# ```
# Note that you have to do this for $W^{[1]}$, $W^{[2]}$ and $W^{[3]}$, then sum the three terms and multiply by $ \frac{1}{m} \frac{\lambda}{2} $.
# +
# GRADED FUNCTION: compute_cost_with_regularization
def compute_cost_with_regularization(A3, Y, parameters, lambd):
"""
Implement the cost function with L2 regularization. See formula (2) above.
Arguments:
A3 -- post-activation, output of forward propagation, of shape (output size, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
parameters -- python dictionary containing parameters of the model
Returns:
cost - value of the regularized loss function (formula (2))
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
cross_entropy_cost = compute_cost(A3, Y) # This gives you the cross-entropy part of the cost
### START CODE HERE ### (approx. 1 line)
L2_regularization_cost = lambd / (2 * m) * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3)))
### END CODER HERE ###
cost = cross_entropy_cost + L2_regularization_cost
return cost
# +
A3, Y_assess, parameters = compute_cost_with_regularization_test_case()
print("cost = " + str(compute_cost_with_regularization(A3, Y_assess, parameters, lambd = 0.1)))
# -
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# **cost**
# </td>
# <td>
# 1.78648594516
# </td>
#
# </tr>
#
# </table>
# Of course, because you changed the cost, you have to change backward propagation as well! All the gradients have to be computed with respect to this new cost.
#
# **Exercise**: Implement the changes needed in backward propagation to take into account regularization. The changes only concern dW1, dW2 and dW3. For each, you have to add the regularization term's gradient ($\frac{d}{dW} ( \frac{1}{2}\frac{\lambda}{m} W^2) = \frac{\lambda}{m} W$).
# +
# GRADED FUNCTION: backward_propagation_with_regularization
def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
Implements the backward propagation of our baseline model to which we added an L2 regularization.
Arguments:
X -- input dataset, of shape (input size, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- cache output from forward_propagation()
lambd -- regularization hyperparameter, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
### START CODE HERE ### (approx. 1 line)
dW3 = 1./m * np.dot(dZ3, A2.T) + lambd / m * W3
### END CODE HERE ###
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
### START CODE HERE ### (approx. 1 line)
dW2 = 1./m * np.dot(dZ2, A1.T) + lambd / m * W2
### END CODE HERE ###
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
### START CODE HERE ### (approx. 1 line)
dW1 = 1./m * np.dot(dZ1, X.T) + lambd / m * W1
### END CODE HERE ###
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
# +
X_assess, Y_assess, cache = backward_propagation_with_regularization_test_case()
grads = backward_propagation_with_regularization(X_assess, Y_assess, cache, lambd = 0.7)
print ("dW1 = "+ str(grads["dW1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("dW3 = "+ str(grads["dW3"]))
# -
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# **dW1**
# </td>
# <td>
# [[-0.25604646 0.12298827 -0.28297129]
# [-0.17706303 0.34536094 -0.4410571 ]]
# </td>
# </tr>
# <tr>
# <td>
# **dW2**
# </td>
# <td>
# [[ 0.79276486 0.85133918]
# [-0.0957219 -0.01720463]
# [-0.13100772 -0.03750433]]
# </td>
# </tr>
# <tr>
# <td>
# **dW3**
# </td>
# <td>
# [[-1.77691347 -0.11832879 -0.09397446]]
# </td>
# </tr>
# </table>
# Let's now run the model with L2 regularization $(\lambda = 0.7)$. The `model()` function will call:
# - `compute_cost_with_regularization` instead of `compute_cost`
# - `backward_propagation_with_regularization` instead of `backward_propagation`
parameters = model(train_X, train_Y, lambd = 0.7)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
# Congrats, the test set accuracy increased to 93%. You have saved the French football team!
#
# You are not overfitting the training data anymore. Let's plot the decision boundary.
plt.title("Model with L2-regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
# **Observations**:
# - The value of $\lambda$ is a hyperparameter that you can tune using a dev set.
# - L2 regularization makes your decision boundary smoother. If $\lambda$ is too large, it is also possible to "oversmooth", resulting in a model with high bias.
#
# **What is L2-regularization actually doing?**:
#
# L2-regularization relies on the assumption that a model with small weights is simpler than a model with large weights. Thus, by penalizing the square values of the weights in the cost function you drive all the weights to smaller values. It becomes too costly for the cost to have large weights! This leads to a smoother model in which the output changes more slowly as the input changes.
#
# <font color='blue'>
# **What you should remember** -- the implications of L2-regularization on:
# - The cost computation:
# - A regularization term is added to the cost
# - The backpropagation function:
# - There are extra terms in the gradients with respect to weight matrices
# - Weights end up smaller ("weight decay"):
# - Weights are pushed to smaller values.
# ## 3 - Dropout
#
# Finally, **dropout** is a widely used regularization technique that is specific to deep learning.
# **It randomly shuts down some neurons in each iteration.** Watch these two videos to see what this means!
#
# <!--
# To understand drop-out, consider this conversation with a friend:
# - Friend: "Why do you need all these neurons to train your network and classify images?".
# - You: "Because each neuron contains a weight and can learn specific features/details/shape of an image. The more neurons I have, the more featurse my model learns!"
# - Friend: "I see, but are you sure that your neurons are learning different features and not all the same features?"
# - You: "Good point... Neurons in the same layer actually don't talk to each other. It should be definitly possible that they learn the same image features/shapes/forms/details... which would be redundant. There should be a solution."
# !-->
#
#
# <center>
# <video width="620" height="440" src="images/dropout1_kiank.mp4" type="video/mp4" controls>
# </video>
# </center>
# <br>
# <caption><center> <u> Figure 2 </u>: Drop-out on the second hidden layer. <br> At each iteration, you shut down (= set to zero) each neuron of a layer with probability $1 - keep\_prob$ or keep it with probability $keep\_prob$ (50% here). The dropped neurons don't contribute to the training in both the forward and backward propagations of the iteration. </center></caption>
#
# <center>
# <video width="620" height="440" src="images/dropout2_kiank.mp4" type="video/mp4" controls>
# </video>
# </center>
#
# <caption><center> <u> Figure 3 </u>: Drop-out on the first and third hidden layers. <br> $1^{st}$ layer: we shut down on average 40% of the neurons. $3^{rd}$ layer: we shut down on average 20% of the neurons. </center></caption>
#
#
# When you shut some neurons down, you actually modify your model. The idea behind drop-out is that at each iteration, you train a different model that uses only a subset of your neurons. With dropout, your neurons thus become less sensitive to the activation of one other specific neuron, because that other neuron might be shut down at any time.
#
# ### 3.1 - Forward propagation with dropout
#
# **Exercise**: Implement the forward propagation with dropout. You are using a 3 layer neural network, and will add dropout to the first and second hidden layers. We will not apply dropout to the input layer or output layer.
#
# **Instructions**:
# You would like to shut down some neurons in the first and second layers. To do that, you are going to carry out 4 Steps:
# 1. In lecture, we dicussed creating a variable $d^{[1]}$ with the same shape as $a^{[1]}$ using `np.random.rand()` to randomly get numbers between 0 and 1. Here, you will use a vectorized implementation, so create a random matrix $D^{[1]} = [d^{[1](1)} d^{[1](2)} ... d^{[1](m)}] $ of the same dimension as $A^{[1]}$.
# 2. Set each entry of $D^{[1]}$ to be 0 with probability (`1-keep_prob`) or 1 with probability (`keep_prob`), by thresholding values in $D^{[1]}$ appropriately. Hint: to set all the entries of a matrix X to 0 (if entry is less than 0.5) or 1 (if entry is more than 0.5) you would do: `X = (X < 0.5)`. Note that 0 and 1 are respectively equivalent to False and True.
# 3. Set $A^{[1]}$ to $A^{[1]} * D^{[1]}$. (You are shutting down some neurons). You can think of $D^{[1]}$ as a mask, so that when it is multiplied with another matrix, it shuts down some of the values.
# 4. Divide $A^{[1]}$ by `keep_prob`. By doing this you are assuring that the result of the cost will still have the same expected value as without drop-out. (This technique is also called inverted dropout.)
# +
# GRADED FUNCTION: forward_propagation_with_dropout
def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
"""
Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
Arguments:
X -- input dataset, of shape (2, number of examples)
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape (20, 2)
b1 -- bias vector of shape (20, 1)
W2 -- weight matrix of shape (3, 20)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (1, 3)
b3 -- bias vector of shape (1, 1)
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
A3 -- last activation value, output of the forward propagation, of shape (1,1)
cache -- tuple, information stored for computing the backward propagation
"""
np.random.seed(1)
# retrieve parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
### START CODE HERE ### (approx. 4 lines) # Steps 1-4 below correspond to the Steps 1-4 described above.
D1 = np.random.rand(A1.shape[0], A1.shape[1]) # Step 1: initialize matrix D1 = np.random.rand(..., ...)
D1 = D1 < keep_prob # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
A1 = np.multiply(A1, D1) # Step 3: shut down some neurons of A1
A1 = A1 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
### END CODE HERE ###
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
### START CODE HERE ### (approx. 4 lines)
D2 = np.random.rand(A2.shape[0], A2.shape[1]) # Step 1: initialize matrix D2 = np.random.rand(..., ...)
D2 = D2 < keep_prob # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold)
A2 = np.multiply(A2, D2) # Step 3: shut down some neurons of A2
A2 = A2 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
### END CODE HERE ###
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
# +
X_assess, parameters = forward_propagation_with_dropout_test_case()
A3, cache = forward_propagation_with_dropout(X_assess, parameters, keep_prob = 0.7)
print ("A3 = " + str(A3))
# -
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# **A3**
# </td>
# <td>
# [[ 0.36974721 0.00305176 0.04565099 0.49683389 0.36974721]]
# </td>
#
# </tr>
#
# </table>
# ### 3.2 - Backward propagation with dropout
#
# **Exercise**: Implement the backward propagation with dropout. As before, you are training a 3 layer network. Add dropout to the first and second hidden layers, using the masks $D^{[1]}$ and $D^{[2]}$ stored in the cache.
#
# **Instruction**:
# Backpropagation with dropout is actually quite easy. You will have to carry out 2 Steps:
# 1. You had previously shut down some neurons during forward propagation, by applying a mask $D^{[1]}$ to `A1`. In backpropagation, you will have to shut down the same neurons, by reapplying the same mask $D^{[1]}$ to `dA1`.
# 2. During forward propagation, you had divided `A1` by `keep_prob`. In backpropagation, you'll therefore have to divide `dA1` by `keep_prob` again (the calculus interpretation is that if $A^{[1]}$ is scaled by `keep_prob`, then its derivative $dA^{[1]}$ is also scaled by the same `keep_prob`).
#
# +
# GRADED FUNCTION: backward_propagation_with_dropout
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
"""
Implements the backward propagation of our baseline model to which we added dropout.
Arguments:
X -- input dataset, of shape (2, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- cache output from forward_propagation_with_dropout()
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
### START CODE HERE ### (≈ 2 lines of code)
dA2 = np.multiply(dA2, D2) # Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation
dA2 = dA2 / keep_prob # Step 2: Scale the value of neurons that haven't been shut down
### END CODE HERE ###
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
### START CODE HERE ### (≈ 2 lines of code)
dA1 = np.multiply(dA1, D1) # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation
dA1 = dA1 / keep_prob # Step 2: Scale the value of neurons that haven't been shut down
### END CODE HERE ###
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
# +
X_assess, Y_assess, cache = backward_propagation_with_dropout_test_case()
gradients = backward_propagation_with_dropout(X_assess, Y_assess, cache, keep_prob = 0.8)
print ("dA1 = " + str(gradients["dA1"]))
print ("dA2 = " + str(gradients["dA2"]))
# -
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# **dA1**
# </td>
# <td>
# [[ 0.36544439 0. -0.00188233 0. -0.17408748]
# [ 0.65515713 0. -0.00337459 0. -0. ]]
# </td>
#
# </tr>
# <tr>
# <td>
# **dA2**
# </td>
# <td>
# [[ 0.58180856 0. -0.00299679 0. -0.27715731]
# [ 0. 0.53159854 -0. 0.53159854 -0.34089673]
# [ 0. 0. -0.00292733 0. -0. ]]
# </td>
#
# </tr>
# </table>
# Let's now run the model with dropout (`keep_prob = 0.86`). It means at every iteration you shut down each neurons of layer 1 and 2 with 14% probability. The function `model()` will now call:
# - `forward_propagation_with_dropout` instead of `forward_propagation`.
# - `backward_propagation_with_dropout` instead of `backward_propagation`.
# +
parameters = model(train_X, train_Y, keep_prob = 0.86, learning_rate = 0.3)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
# -
# Dropout works great! The test accuracy has increased again (to 95%)! Your model is not overfitting the training set and does a great job on the test set. The French football team will be forever grateful to you!
#
# Run the code below to plot the decision boundary.
plt.title("Model with dropout")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
# **Note**:
# - A **common mistake** when using dropout is to use it both in training and testing. You should use dropout (randomly eliminate nodes) only in training.
# - Deep learning frameworks like [tensorflow](https://www.tensorflow.org/api_docs/python/tf/nn/dropout), [PaddlePaddle](http://doc.paddlepaddle.org/release_doc/0.9.0/doc/ui/api/trainer_config_helpers/attrs.html), [keras](https://keras.io/layers/core/#dropout) or [caffe](http://caffe.berkeleyvision.org/tutorial/layers/dropout.html) come with a dropout layer implementation. Don't stress - you will soon learn some of these frameworks.
#
# <font color='blue'>
# **What you should remember about dropout:**
# - Dropout is a regularization technique.
# - You only use dropout during training. Don't use dropout (randomly eliminate nodes) during test time.
# - Apply dropout both during forward and backward propagation.
# - During training time, divide each dropout layer by keep_prob to keep the same expected value for the activations. For example, if keep_prob is 0.5, then we will on average shut down half the nodes, so the output will be scaled by 0.5 since only the remaining half are contributing to the solution. Dividing by 0.5 is equivalent to multiplying by 2. Hence, the output now has the same expected value. You can check that this works even when keep_prob is other values than 0.5.
# ## 4 - Conclusions
# **Here are the results of our three models**:
#
# <table>
# <tr>
# <td>
# **model**
# </td>
# <td>
# **train accuracy**
# </td>
# <td>
# **test accuracy**
# </td>
#
# </tr>
# <td>
# 3-layer NN without regularization
# </td>
# <td>
# 95%
# </td>
# <td>
# 91.5%
# </td>
# <tr>
# <td>
# 3-layer NN with L2-regularization
# </td>
# <td>
# 94%
# </td>
# <td>
# 93%
# </td>
# </tr>
# <tr>
# <td>
# 3-layer NN with dropout
# </td>
# <td>
# 93%
# </td>
# <td>
# 95%
# </td>
# </tr>
# </table>
# Note that regularization hurts training set performance! This is because it limits the ability of the network to overfit to the training set. But since it ultimately gives better test accuracy, it is helping your system.
# Congratulations for finishing this assignment! And also for revolutionizing French football. :-)
# <font color='blue'>
# **What we want you to remember from this notebook**:
# - Regularization will help you reduce overfitting.
# - Regularization will drive your weights to lower values.
# - L2 regularization and Dropout are two very effective regularization techniques.
| 29,305 |
/Applied Text Mining/3_Spam_or_NotSpam_Assignment.ipynb | b544ffd52db20294ed508dba9d640499597ab0c5 | [] | no_license | Keulando/Applied_Data_Science | https://github.com/Keulando/Applied_Data_Science | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 27,679 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="VBNHzOrf_eWj"
# ### Denoising Autoencoders And Where To Find Them
#
# Today we're going to train deep autoencoders and deploy them to faces and search for similar images.
#
# Our new test subjects are human faces from the [lfw dataset](http://vis-www.cs.umass.edu/lfw/).
# + [markdown] colab_type="text" id="H4hWkdhe_eWl"
# **Collab setting**
# + colab={"base_uri": "https://localhost:8080/", "height": 224} colab_type="code" id="C9GUvLcu_eWm" outputId="31b0e443-c0cd-4e5c-89ea-5a55ab7abf42"
# if you're running in colab,
# 1. go to Runtime -> Change Runtimy Type -> GPU
# 2. uncomment this:
# !wget https://raw.githubusercontent.com/yandexdataschool/Practical_DL/hw3_19/homework03/lfw_dataset.py -O lfw_dataset.py
# + colab={} colab_type="code" id="o7jFIMZd_eWp"
import torch
import numpy as np
from torch.utils.data import Dataset, DataLoader
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
EPOCHS = 100
BATCH_SIZE = 32
LEARNING_RATE = 1e-3
LATENT_DIMENSION = 4
BATCH_SIZE = 32
device = torch.device("cuda")
# + colab={"base_uri": "https://localhost:8080/", "height": 68} colab_type="code" id="CRWV1ryH_eWv" outputId="c650995b-26a8-4d68-8bf6-06ee86d2f32b"
import numpy as np
from lfw_dataset import fetch_lfw_dataset
from sklearn.model_selection import train_test_split
X, attr = fetch_lfw_dataset(use_raw=True,dimx=38,dimy=38)
X = X.transpose([0,3,1,2]).astype('float32') / 256.0
img_shape = X.shape[1:]
X_train, X_test = train_test_split(X, test_size=0.1,random_state=42)
# + colab={} colab_type="code" id="3fAdhPn2_eWy"
X_train_tensor = torch.from_numpy(X_train).type(torch.DoubleTensor)
X_test_tensor = torch.Tensor(X_test).type(torch.DoubleTensor)
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="FV1efJSM_eW0" outputId="63e88269-1c11-44f1-8222-0e075b4e819e"
img_shape
# + colab={"base_uri": "https://localhost:8080/", "height": 302} colab_type="code" id="MSVm1sIK_eW4" outputId="185b4bc8-2106-4ac5-c20d-8842ff224150"
# %matplotlib inline
import matplotlib.pyplot as plt
plt.title('sample image')
for i in range(6):
plt.subplot(2,3,i+1)
plt.imshow(X[i].transpose([1,2,0]))
print("X shape:",X.shape)
print("attr shape:",attr.shape)
# + [markdown] colab_type="text" id="csBv6bf1_eW7"
# ### Autoencoder architecture
#
# Let's design autoencoder as a single lasagne network, going from input image through bottleneck into the reconstructed image.
#
# <img src="http://nghiaho.com/wp-content/uploads/2012/12/autoencoder_network1.png" width=640px>
#
#
# + [markdown] colab_type="text" id="O6fFezL-_eW8"
# ## First step: PCA
#
# Principial Component Analysis is a popular dimensionality reduction method.
#
# Under the hood, PCA attempts to decompose object-feature matrix $X$ into two smaller matrices: $W$ and $\hat W$ minimizing _mean squared error_:
#
# $$\|(X W) \hat{W} - X\|^2_2 \to_{W, \hat{W}} \min$$
# - $X \in \mathbb{R}^{n \times m}$ - object matrix (**centered**);
# - $W \in \mathbb{R}^{m \times d}$ - matrix of direct transformation;
# - $\hat{W} \in \mathbb{R}^{d \times m}$ - matrix of reverse transformation;
# - $n$ samples, $m$ original dimensions and $d$ target dimensions;
#
# In geometric terms, we want to find d axes along which most of variance occurs. The "natural" axes, if you wish.
#
# 
#
#
# PCA can also be seen as a special case of an autoencoder.
#
# * __Encoder__: X -> Dense(d units) -> code
# * __Decoder__: code -> Dense(m units) -> X
#
# Where Dense is a fully-connected layer with linear activaton: $f(X) = W \cdot X + \vec b $
#
#
# Note: the bias term in those layers is responsible for "centering" the matrix i.e. substracting mean.
# + colab={} colab_type="code" id="2JTeWcCc_eW9"
# this class corresponds to view-function and may be used as a reshape layer
class View(nn.Module):
def __init__(self, *shape):
super(View, self).__init__()
self.shape = shape
def forward(self, input):
return input.view(input.size(0),*self.shape)
class Flatten(nn.Module):
def forward(self, input):
return input.view(input.size(0), -1)
# + colab={} colab_type="code" id="gB5hwVLe_eW_"
class pca_autoencoder(nn.Module):
"""
Here we define a simple linear autoencoder as described above.
We also flatten and un-flatten data to be compatible with image shapes
"""
def __init__(self, code_size=32):
super(pca_autoencoder, self).__init__()
layers_1 = [
Flatten(),
nn.Linear(38*38*3,code_size,bias=True)
]
self.enc = nn.Sequential(*layers_1)
self.dec = nn.Sequential(nn.Linear(code_size,38*38*3,bias=True),
View(3,38,38))
def batch_loss(self, batch):
reconstruction = self.enc(batch)
reconstruction = self.dec(reconstruction)
return torch.mean((batch - reconstruction)**2)
# + [markdown] colab_type="text" id="69_Da_I7_eXB"
# ### Train the model
#
# As usual, iterate minibatches of data and call train_step, then evaluate loss on validation data.
#
# __Note to py2 users:__ you can safely drop `flush=True` from any code below.
# + colab={} colab_type="code" id="7sbvg3Z__eXD"
def train(model, dataset, num_epoch=32):
model.double()
model.to(device)
gd = optim.Adamax(model.parameters(), lr=0.002)
dataloader = DataLoader(dataset, batch_size=BATCH_SIZE, shuffle=True)
losses = []
for epoch in range(num_epoch):
for i, (batch) in enumerate(dataloader):
gd.zero_grad()
loss = model.batch_loss(batch.cuda())
(loss).backward()
losses.append(loss.detach().cpu().numpy())
gd.step()
gd.zero_grad()
print("#%i, Train loss: %.7f"%(epoch+1,np.mean(losses)),flush=True)
# + colab={} colab_type="code" id="wj7YPamq_eXF"
def visualize(img, model):
"""Draws original, encoded and decoded images"""
code = model.enc(img[None].cuda())
reco = model.dec(code)
plt.subplot(1,3,1)
plt.title("Original")
plt.imshow(img.cpu().numpy().transpose([1, 2, 0]).clip(0, 1))
plt.subplot(1,3,2)
plt.title("Code")
plt.imshow(code.cpu().detach().numpy().reshape([code.shape[-1] // 2, -1]))
plt.subplot(1,3,3)
plt.title("Reconstructed")
plt.imshow(reco[0].cpu().detach().numpy().transpose([1, 2, 0]).clip(0, 1))
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 697} colab_type="code" id="4jkVqhLd_eXI" outputId="f7958ff8-9f9b-43df-a0e8-e17ec2c52036"
aenc = pca_autoencoder()
train(aenc, X_train_tensor, 40)
# + colab={"base_uri": "https://localhost:8080/", "height": 136} colab_type="code" id="Xy4JXn36YC3c" outputId="5d5082ab-f2a6-4b31-e5ed-4e82bcbd8e54"
list(aenc.named_children())
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="RqTUvLp8_eXM" outputId="ecc76752-f8e5-40f2-dda0-4e9df5e3809a"
dataloader_test = DataLoader(X_test_tensor, batch_size=BATCH_SIZE, shuffle=True)
scores = []
for i, (batch) in enumerate(dataloader_test):
scores.append(aenc.batch_loss(batch.cuda()).data.cpu().numpy())
print (np.mean(scores))
# + colab={"base_uri": "https://localhost:8080/", "height": 1337} colab_type="code" id="cvljk13x_eXP" outputId="ee665936-6cd4-4ae9-f2e1-66d814439802"
for i in range(5):
img = X_test_tensor[i]
visualize(img,aenc)
# + [markdown] colab_type="text" id="NIurZSFN_eXV"
# ### Going deeper
#
# PCA is neat but surely we can do better. This time we want you to build a deep autoencoder by... stacking more layers.
#
# In particular, your encoder and decoder should be at least 3 layers deep each. You can use any nonlinearity you want and any number of hidden units in non-bottleneck layers provided you can actually afford training it.
#
# 
#
# A few sanity checks:
# * There shouldn't be any hidden layer smaller than bottleneck (encoder output).
# * Don't forget to insert nonlinearities between intermediate dense layers.
# * Convolutional layers are good idea. To undo convolution use L.Deconv2D, pooling - L.UpSampling2D.
# * Adding activation after bottleneck is allowed, but not strictly necessary.
# + colab={} colab_type="code" id="tV1pvZsXYC3r"
class pca_autoencoder_deep(nn.Module):
def __init__(self, code_size=32):
super(pca_autoencoder_deep, self).__init__()
layers_enc = [
nn.Conv2d(in_channels=3,out_channels=8,kernel_size=3,padding=1),
nn.ELU(),
nn.MaxPool2d(2),
nn.Conv2d(in_channels=8,out_channels=16,kernel_size=3,padding=1),
nn.ELU(),
nn.Conv2d(in_channels=16,out_channels=32,kernel_size=3,padding=1),
nn.ELU(),
Flatten(),
nn.Linear(19*19*32,code_size,bias=True)
]
self.enc = nn.Sequential(*layers_enc)
layers_dec = [
nn.Linear(code_size,19*19*32,bias=True),
View(32,19,19),
nn.ConvTranspose2d(in_channels=32,out_channels=16,kernel_size=3,padding=1),
nn.ELU(),
# nn.Upsample(scale_factor=2,mode='bilinear', align_corners=True),#16,16,32
nn.ConvTranspose2d(in_channels=16,out_channels=8,kernel_size=3,padding=1),
nn.ELU(),
nn.Upsample(scale_factor=2,mode='bilinear', align_corners=True),
nn.ConvTranspose2d(in_channels=8,out_channels=3,kernel_size=3,padding=1),
nn.ELU(),
# nn.Upsample(scale_factor=2,mode='bilinear', align_corners=True)
]
self.dec = nn.Sequential(*layers_dec)
def batch_loss(self, batch):
reconstruction = self.enc(batch)
reconstruction = self.dec(reconstruction)
return torch.mean((batch - reconstruction)**2)
# + colab={"base_uri": "https://localhost:8080/", "height": 374} colab_type="code" id="xkCUWecvYC3u" outputId="de722abc-92ab-484d-c60c-3d92d6733e57"
aenc_deep = pca_autoencoder_deep()
list(aenc_deep.named_children())
# + colab={"base_uri": "https://localhost:8080/", "height": 921} colab_type="code" id="vtSWYDsB_eXc" outputId="52b22632-9cf8-40ca-e123-ac5a87787285"
train(aenc_deep, X_train_tensor, 50)
# + [markdown] colab_type="text" id="tLkLF1hC_eXh"
# Training may take long, it's okay.
# + [markdown] colab_type="text" id="twGO5gAa4n7Y"
# **Check autoencoder shapes along different code_sizes. Check architecture of you encoder-decoder network is correct**
# + colab={"base_uri": "https://localhost:8080/", "height": 190} colab_type="code" id="HmR7ot5__eXi" outputId="5f15ede8-5feb-45b8-dbd9-af0abefd0e1c"
get_dim = lambda layer: np.prod(layer.output_shape[1:])
for code_size in [1,8,32,128,512,1024]:
help_tensor = next(iter(DataLoader(X_train_tensor, batch_size=BATCH_SIZE)))
model = pca_autoencoder_deep(code_size).to(device)
encoder_out = model.enc(help_tensor.type('torch.FloatTensor').cuda())
decoder_out = model.dec(encoder_out)
print("Testing code size %i" % code_size)
assert encoder_out.shape[1:]==torch.Size([code_size]),"encoder must output a code of required size"
assert decoder_out.shape[1:]==img_shape, "decoder must output an image of valid shape"
assert (len(list(model.dec.children())) >= 6), "decoder must contain at least 3 dense layers"
print("All tests passed!")
# + [markdown] colab_type="text" id="GiNYsxJQ_eXk"
# __Hint:__ if you're getting "Encoder layer is smaller than bottleneck" error, use code_size when defining intermediate layers.
#
# For example, such layer may have code_size*2 units.
# + [markdown] colab_type="text" id="tkJCskEvyixo"
# ** Lets check you model's score. You should beat value of 0.005 **
# + colab={"base_uri": "https://localhost:8080/", "height": 1408} colab_type="code" id="khcs90Yi_eXl" outputId="83c18acc-2c32-424f-fd52-0f9cc6dea5f6"
dataloader_test = DataLoader(X_test_tensor, batch_size=BATCH_SIZE, shuffle=True)
scores = []
for i, (batch) in enumerate(dataloader_test):
scores.append(aenc_deep.batch_loss(batch.cuda(device = device)).data.cpu().numpy())
encoder_out = aenc_deep.enc(batch.cuda(device = device))
reconstruction_mse = np.mean(scores)
assert reconstruction_mse <= 0.005, "Compression is too lossy. See tips below."
assert len(encoder_out.shape)==2 and encoder_out.shape[1]==32, "Make sure encoder has code_size units"
print("Final MSE:", reconstruction_mse)
for i in range(5):
img = X_test_tensor[i]
visualize(img,aenc_deep)
# + [markdown] colab_type="text" id="KNlhwrtc_eXo"
# __Tips:__ If you keep getting "Compression to lossy" error, there's a few things you might try:
#
# * Make sure it converged. Some architectures need way more than 32 epochs to converge. They may fluctuate a lot, but eventually they're going to get good enough to pass. You may train your network for as long as you want.
#
# * Complexity. If you already have, like, 152 layers and still not passing threshold, you may wish to start from something simpler instead and go in small incremental steps.
#
# * Architecture. You can use any combination of layers (including convolutions, normalization, etc) as long as __encoder output only stores 32 numbers per training object__.
#
# A cunning learner can circumvent this last limitation by using some manual encoding strategy, but he is strongly recommended to avoid that.
# + [markdown] colab_type="text" id="JQkFuzTz_eXp"
# ## Denoising AutoEncoder
#
# Let's now make our model into a denoising autoencoder.
#
# We'll keep your model architecture, but change the way it trains. In particular, we'll corrupt it's input data randomly before each epoch.
#
# There are many strategies to apply noise. We'll implement two popular one: adding gaussian noise and using dropout.
# + colab={} colab_type="code" id="sQUS359N_eXq"
def apply_gaussian_noise(X,sigma=0.1):
"""
adds noise from normal distribution with standard deviation sigma
:param X: image tensor of shape [batch,height,width,3]
"""
noise = np.random.normal(scale=sigma, size=X.shape)
return X + noise
# + [markdown] colab_type="text" id="xy71ZmuPz1il"
# **noise tests**
# + colab={} colab_type="code" id="pslPEzXS_eXs"
theoretical_std = (X[:100].std()**2 + 0.5**2)**.5
our_std = apply_gaussian_noise(X[:100],sigma=0.5).std()
assert abs(theoretical_std - our_std) < 0.01, "Standard deviation does not match it's required value. Make sure you use sigma as std."
assert abs(apply_gaussian_noise(X[:100],sigma=0.5).mean() - X[:100].mean()) < 0.01, "Mean has changed. Please add zero-mean noise"
# + colab={"base_uri": "https://localhost:8080/", "height": 141} colab_type="code" id="unMfBi8q_eXu" outputId="ac889429-fa2b-4ba9-d1a9-cef83b6482fa"
plt.subplot(1,4,1)
plt.imshow(X[0].transpose([1,2,0]))
plt.subplot(1,4,2)
plt.imshow(apply_gaussian_noise(X[:1],sigma=0.01)[0].transpose([1,2,0]).clip(0, 1))
plt.subplot(1,4,3)
plt.imshow(apply_gaussian_noise(X[:1],sigma=0.1)[0].transpose([1,2,0]).clip(0, 1))
plt.subplot(1,4,4)
plt.imshow(apply_gaussian_noise(X[:1],sigma=0.5)[0].transpose([1,2,0]).clip(0, 1))
# + colab={} colab_type="code" id="LBKl4RbDYC4O"
def train(model, dataset, num_epoch=32):
model.double()
model.to(device)
gd = optim.Adamax(model.parameters(), lr=0.002)
dataloader = DataLoader(dataset, batch_size=BATCH_SIZE, shuffle=True)
losses = []
for epoch in range(num_epoch):
for i, (batch) in enumerate(dataloader):
gd.zero_grad()
loss = model.batch_loss(batch.cuda())
(loss).backward()
losses.append(loss.detach().cpu().numpy())
gd.step()
gd.zero_grad()
print("#%i, Train loss: %.7f"%(epoch+1,np.mean(losses)),flush=True)
# + colab={} colab_type="code" id="9hHGK_Wr_eXx"
def train_noise(model, dataset, num_epoch=50):
model.double()
model.to(device)
gd = optim.Adamax(model.parameters(), lr=0.002)
dataloader = DataLoader(dataset, batch_size=BATCH_SIZE, shuffle=True)
losses = []
for epoch in range(num_epoch):
for i, (batch) in enumerate(dataloader):
noise_batch=apply_gaussian_noise(batch.data.numpy())
noise_batch=torch.from_numpy(noise_batch).type(torch.DoubleTensor)
gd.zero_grad()
loss = model.batch_loss(batch.cuda())
(loss).backward()
losses.append(loss.detach().cpu().numpy())
gd.step()
gd.zero_grad()
print("#%i, Train loss: %.7f"%(epoch+1,np.mean(losses)),flush=True)
#<Your code: define train function for denoising autoencoder as train function above>
# + colab={} colab_type="code" id="MKQK4HJL_eX2"
X_train_noise = apply_gaussian_noise(X_train)
X_test_noise = apply_gaussian_noise(X_test)
# + colab={} colab_type="code" id="8ClYTlpa_eX4"
X_train_tensor_n = torch.from_numpy(X_train_noise).type(torch.DoubleTensor)
X_test_tensor_n = torch.Tensor(X_test_noise).type(torch.DoubleTensor)
# + colab={"base_uri": "https://localhost:8080/", "height": 867} colab_type="code" id="fVD2-ujS_eX8" outputId="2eceb307-e042-4723-db3e-dafcdc97d4f5"
aenc = pca_autoencoder()
train(aenc, X_train_tensor_n, 50)
# + [markdown] colab_type="text" id="mlekH4ww_eX_"
# __Note:__ if it hasn't yet converged, increase the number of iterations.
#
# __Bonus:__ replace gaussian noise with masking random rectangles on image.
# + [markdown] colab_type="text" id="HVj0NPXV3liL"
# ** Let's evaluate!!! **
# + colab={"base_uri": "https://localhost:8080/", "height": 1354} colab_type="code" id="pr1Drxb1_eX_" outputId="4971825c-ec6e-4cab-f6b4-2ce89c81f837"
dataloader_test = DataLoader(X_test_tensor_n, batch_size=BATCH_SIZE, shuffle=True)
scores = []
for i, (batch) in enumerate(dataloader_test):
scores.append(aenc.batch_loss(batch.cuda(device = device)).data.cpu().numpy())
encoder_out = aenc.enc(batch.cuda(device = device))
reconstruction_mse = np.mean(scores)
print("Final MSE:", reconstruction_mse)
for i in range(5):
img = X_test_tensor_n[i]
visualize(img,aenc)
# + [markdown] colab_type="text" id="weU6quCI_eYE"
# ### Image retrieval with autoencoders
#
# So we've just trained a network that converts image into itself imperfectly. This task is not that useful in and of itself, but it has a number of awesome side-effects. Let's see it in action.
#
# First thing we can do is image retrieval aka image search. We we give it an image and find similar images in latent space.
#
# To speed up retrieval process, we shall use Locality-Sensitive Hashing on top of encoded vectors. We'll use scikit-learn's implementation for simplicity. In practical scenario, you may want to use [specialized libraries](https://erikbern.com/2015/07/04/benchmark-of-approximate-nearest-neighbor-libraries.html) for better performance and customization.
# + colab={} colab_type="code" id="afiR-pC3_eYG"
codes = aenc.enc(X_train_tensor.to(device))
#<Your code:encode all images in X_train_tensor>
# + colab={} colab_type="code" id="nojmuKtb_eYI"
assert codes.shape[0] == X_train_tensor.shape[0]
# + colab={"base_uri": "https://localhost:8080/", "height": 71} colab_type="code" id="GfGatyHi_eYK" outputId="c0af72f5-b81e-4100-aecd-c866999269fa"
from sklearn.neighbors import LSHForest
lshf = LSHForest(n_estimators=50).fit(codes.detach().cpu().numpy())
# + colab={} colab_type="code" id="FYhbhxLz_eYN"
images = torch.from_numpy(X_train).type(torch.DoubleTensor)
# + colab={} colab_type="code" id="shw1V6Zn_eYP"
def get_similar(image, n_neighbors=5):
assert len(image.shape)==3,"image must be [batch,height,width,3]"
# code = aenc.enc(image.cuda(device)).detach().cpu().numpy()
code = aenc.enc(image.cuda(device).view(1, *image.size())).cpu().detach().numpy()
(distances,),(idx,) = lshf.kneighbors(code,n_neighbors=n_neighbors)
return distances,images[idx]
# + colab={} colab_type="code" id="5JkabL1A_eYQ"
def show_similar(image):
distances,neighbors = get_similar(image,n_neighbors=11)
plt.figure(figsize=[8,6])
plt.subplot(3,4,1)
plt.imshow(image.cpu().numpy().transpose([1,2,0]))
plt.title("Original image")
for i in range(11):
plt.subplot(3,4,i+2)
plt.imshow(neighbors[i].cpu().numpy().transpose([1,2,0]))
plt.title("Dist=%.3f"%distances[i])
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 390} colab_type="code" id="VG_0tXSq_eYT" outputId="086318e4-48eb-4982-bf26-d1ca50942136"
#smiles
show_similar(X_test_tensor[2])
# + colab={"base_uri": "https://localhost:8080/", "height": 390} colab_type="code" id="4Z25ZSQO_eYV" outputId="a5925fb0-fef5-4074-cab2-00d6b6c3dd06"
#ethnicity
show_similar(X_test_tensor[500])
# + colab={"base_uri": "https://localhost:8080/", "height": 390} colab_type="code" id="uPyK6-vk_eYf" outputId="5d582bd6-3297-47ef-aad9-23fe9902595d"
#glasses
show_similar(X_test_tensor[66])
# + [markdown] colab_type="text" id="piVrNWXZ_eYn"
# ## Cheap image morphing
#
# + [markdown] colab_type="text" id="DYqDtg6K2z5e"
# Here you should take two full-sized objects, code it and obtain intermediate object by decoding an intermixture code.
#
# $Code_{mixt} = a1\cdot code1 + a2\cdot code2$
# + colab={"base_uri": "https://localhost:8080/", "height": 884} colab_type="code" id="IFDk4E7N_eYr" outputId="76a77c6a-1bdc-43a6-8587-6bc7424e1d9a"
for _ in range(5):
image1,image2 = torch.from_numpy(X_test[np.random.randint(0,X_test.shape[0],size=2)]).double()
#<Your code:choose two image randomly>
code1 = aenc.enc(image1.cuda(device).view(1, *image1.size()))
code2 = aenc.enc(image2.cuda(device).view(1, *image2.size()))
plt.figure(figsize=[10,4])
for i,a in enumerate(np.linspace(0,1,num=7)):
output_code = a*code1 +(1-a)*code2
#<Your code:define intermixture code>
output_image = aenc.dec(output_code[None])[0]
plt.subplot(1,7,i+1)
plt.imshow(output_image.cpu().detach().numpy().transpose([1,2,0]))
plt.title("a=%.2f"%a)
plt.show()
# + [markdown] colab_type="text" id="lKZTo47L_eYu"
# Of course there's a lot more you can do with autoencoders.
#
# If you want to generate images from scratch, however, we recommend you our honor track seminar about generative adversarial networks.
| 22,740 |
/LinearAlgebra.ipynb | 1f792eb9fe9cb674ea5ed39f33b0ef8aecd3f6b7 | [] | no_license | khodeprasad/LinearAlgebra | https://github.com/khodeprasad/LinearAlgebra | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 19,253 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
import numpy as np
import pandas as pd
import seaborn as sns
from pandas.api.types import is_numeric_dtype
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from sklearn.cluster import DBSCAN, KMeans
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.metrics import silhouette_score
from yellowbrick.cluster import SilhouetteVisualizer
df = pd.read_csv("Dataset//Attrition.csv")
# +
to_push = ['Age', 'DistanceFromHome','Education','EnvironmentSatisfaction',
'JobInvolvement','JobLevel','JobSatisfaction','MonthlyIncome',
'NumCompaniesWorked','RelationshipSatisfaction','TotalWorkingYears',
'WorkLifeBalance','YearsAtCompany','YearsInCurrentRole',
'YearsSinceLastPromotion','YearsWithCurrManager']
to_push_2 = ['Age', 'DistanceFromHome','Education','JobLevel','MonthlyIncome',
'NumCompaniesWorked','TotalWorkingYears','YearsAtCompany',
'YearsInCurrentRole','YearsSinceLastPromotion','YearsWithCurrManager']
to_push_3 = ['Age', 'DistanceFromHome','Education','JobLevel','MonthlyIncome',
'NumCompaniesWorked','TotalWorkingYears','YearsAtCompany',
'YearsMean']
to_push_4 = ['Age', 'DistanceFromHome','MonthlyIncome','NumCompaniesWorked',
'TotalWorkingYears','YearsAtCompany']
to_push_5 = ['Age', 'DistanceFromHome', 'MonthlyIncome']
# +
pd.factorize(df['Attrition'])
to_clusterize = df[to_push_4]
for column in to_clusterize.columns:
if not is_numeric_dtype(to_clusterize[column]):
item = to_clusterize[column]
unique = list(to_clusterize[column].unique())
mapping = dict(zip(unique, range(0, len(unique) + 1)))
to_clusterize[column] = item.map(mapping).astype(int)
to_clusterize.head()
# -
#Executing kmeans on Train dataset, saving sse values on sse_values list
sse_values = list()
max_k = 30
for k in range(2, max_k + 1):
kmeans = KMeans(n_clusters = k, max_iter = 100)
kmeans.fit(to_clusterize)
sse_values.append(kmeans.inertia_)
#Plotting values obtained calculating SSE
plt.plot(range(2, max_k + 1), sse_values, marker = "o")
plt.grid(True)
plt.title("SSE variations with different clusters number")
plt.xlabel("Number of Ks")
plt.ylabel("SSE values")
plt.show()
# +
#Calculating best number of clusters using Silhouette score
from sklearn.metrics import silhouette_score
silh_values = list()
for k in range(2, max_k + 1):
kmeans = KMeans(n_clusters = k, max_iter=100, n_init=10)
kmeans.fit(to_clusterize)
labels_k = kmeans.labels_
score_k = silhouette_score(to_clusterize, labels_k)
silh_values.append(score_k)
# -
#Plotting Silhouette Score
plt.plot(range(2, max_k + 1), silh_values, marker = "o")
plt.grid(True)
plt.title("SSE variations with different clusters number")
plt.xlabel("Number of Ks")
plt.ylabel("Silhouette values")
plt.show()
fig, ax = plt.subplots(3, 3, figsize=(20, 20))
for i in range(2, 11):
kmeans = KMeans(n_clusters=i, max_iter=100, n_init=10)
visualizer = SilhouetteVisualizer(kmeans, colors='yellowbrick', ax = ax[int((i - 2)/3)][(i - 2) % 3])
visualizer.fit(to_clusterize)
visualizer.show()
#Computes KMeans with the selected number of clusters
kmeans = KMeans(n_clusters = 6, max_iter = 100)
kmeans.fit(to_clusterize[to_push_5])
to_clusterize['cluster'] = kmeans.labels_ #saves the cluster where each entry has been inserted
to_clusterize.head()
#Displays the elements contained into each cluster
barlist = to_clusterize['cluster'].value_counts().plot(kind='bar', title='Distribution of attributes between clusters')
barlist.get_children()[0].set_color('violet')
barlist.get_children()[1].set_color('fuchsia')
barlist.get_children()[2].set_color('yellow')
barlist.get_children()[3].set_color('green')
barlist.get_children()[4].set_color('orange')
barlist.get_children()[5].set_color('blue')
plt.xticks(rotation=0)
plt.show()
# +
import seaborn as sns
sns.pairplot(data = to_clusterize, hue = "cluster", palette = "Accent", corner=True, markers=['.', 's', 'p', 'P', 'D', 'd'])
plt.show()
# +
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize = (13,8))
sns.scatterplot(x = "Age", y = "MonthlyIncome", hue = 'cluster', data = to_clusterize, palette = "Accent", ax = ax1)
sns.scatterplot(x = "DistanceFromHome", y = "YearsAtCompany", hue = 'cluster', data = to_clusterize, palette = "Accent", ax = ax2)
sns.scatterplot(x = "DistanceFromHome", y = "Age", hue = 'cluster', data = to_clusterize, palette = "Accent", ax = ax3)
sns.scatterplot(x = "MonthlyIncome", y = "DistanceFromHome", hue = 'cluster', data = to_clusterize, palette = "Accent", ax = ax4)
plt.tight_layout()
plt.show()
# -
# +
###DBSCAN - NEW
# %matplotlib inline
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.neighbors import NearestNeighbors
#from sklearn import metrics
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler, RobustScaler
# +
to_push = ['Age', 'DistanceFromHome','Education','EnvironmentSatisfaction',
'JobInvolvement','JobLevel','JobSatisfaction','MonthlyIncome',
'NumCompaniesWorked','RelationshipSatisfaction','TotalWorkingYears',
'WorkLifeBalance','YearsAtCompany','YearsInCurrentRole',
'YearsSinceLastPromotion','YearsWithCurrManager']
to_push_2 = ['Age', 'DistanceFromHome','Education','JobLevel','MonthlyIncome',
'NumCompaniesWorked','TotalWorkingYears','YearsAtCompany',
'YearsInCurrentRole','YearsSinceLastPromotion','YearsWithCurrManager']
subset_3 = ['Age', 'DistanceFromHome','Education','JobLevel','MonthlyIncome',
'NumCompaniesWorked','TotalWorkingYears','YearsAtCompany',
'YearsMean']
to_push_4 = ['Age', 'DistanceFromHome','MonthlyIncome','NumCompaniesWorked',
'TotalWorkingYears','YearsAtCompany']
to_push_5 = ['Age', 'DistanceFromHome','Education','JobLevel',
'NumCompaniesWorked','TotalWorkingYears','YearsAtCompany',
'YearsMean']
SUBSET = ['HourlyRate','DailyRate','MonthlyRate','DistanceFromHome',
'MonthlyIncome','TotalWorkingYears','Age','YearsAtCompany']
df = pd.read_csv("./Dataset/attrition.csv")
cleaned_df=df[SUBSET]
X = StandardScaler().fit_transform(cleaned_df.values)
scaled_df = pd.DataFrame( X, columns = cleaned_df.columns )
# +
eps_to_test = [round(eps,1) for eps in np.arange(0.1, 2.5, 0.1)]
min_samples_to_test = range(5, 15, 1)
print("EPS:", eps_to_test)
print("MIN_SAMPLES:", list(min_samples_to_test))
# -
def get_metrics(eps, min_samples, dataset, iter_):
# Fitting
dbscan_model_ = DBSCAN( eps = eps, min_samples = min_samples)
dbscan_model_.fit(dataset)
# Mean Noise Point Distance metric
noise_indices = dbscan_model_.labels_ == -1
if True in noise_indices:
neighboors = NearestNeighbors(n_neighbors = 5).fit(dataset)
distances, indices = neighboors.kneighbors(dataset)
noise_distances = distances[noise_indices, 1:]
noise_mean_distance = round(noise_distances.mean(), 3)
else:
noise_mean_distance = None
# Number of found Clusters metric
number_of_clusters = len(set(dbscan_model_.labels_[dbscan_model_.labels_ >= 0]))
# Log
print("%3d | Tested with eps = %3s and min_samples = %3s | %5s %4s" % (iter_, eps, min_samples, str(noise_mean_distance), number_of_clusters))
return(noise_mean_distance, number_of_clusters)
# +
# Dataframe per la metrica sulla distanza media dei noise points dai K punti più vicini
results_noise = pd.DataFrame(
data = np.zeros((len(eps_to_test),len(min_samples_to_test))), # Empty dataframe
columns = min_samples_to_test,
index = eps_to_test
)
# Dataframe per la metrica sul numero di cluster
results_clusters = pd.DataFrame(
data = np.zeros((len(eps_to_test),len(min_samples_to_test))), # Empty dataframe
columns = min_samples_to_test,
index = eps_to_test
)
# +
iter_ = 0
print("ITER| INFO%s | DIST CLUS" % (" "*39))
print("-"*65)
for eps in eps_to_test:
for min_samples in min_samples_to_test:
iter_ += 1
# Calcolo le metriche
noise_metric, cluster_metric = get_metrics(eps, min_samples, scaled_df, iter_)
# Inserisco i risultati nei relativi dataframe
results_noise.loc[eps, min_samples] = noise_metric
results_clusters.loc[eps, min_samples] = cluster_metric
# +
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16,8) )
sns.heatmap(results_noise, annot = True, ax = ax1, cbar = False).set_title("METRIC: Mean Noise Points Distance")
sns.heatmap(results_clusters, annot = True, ax = ax2, cbar = False).set_title("METRIC: Number of clusters")
ax1.set_xlabel("N"); ax2.set_xlabel("N")
ax1.set_ylabel("EPSILON"); ax2.set_ylabel("EPSILON")
plt.tight_layout(); plt.show()
# +
#NEW
from scipy.spatial.distance import pdist, squareform
dist = pdist(X,"euclidean")
dist = squareform(dist)
k=5
kth_distances = []
for d in dist:
index_kth_distance = np.argsort(d)[k]
kth_distances.append(d[index_kth_distance])
plt.plot( range(0,len(kth_distances)), sorted(kth_distances) )
plt.ylabel('distance from 5th neighbor',fontsize=10)
plt.xlabel('sorted distances',fontsize=10)
# -
for k in np.arange(0.8,3,0.1):
for m in np.arange(5,16,1):
# Istantiating with eps = 1 and min_samples = 9
best_dbscan_model = DBSCAN( eps = k, min_samples = m)
# Fitting
best_dbscan_model.fit(scaled_df)
# Balance
print(f"eps:{k} min:{m}")
print(np.unique(best_dbscan_model.labels_,return_counts=True))
print("\n")
# +
# Istantiating with eps = 1.8 and min_samples = 11
best_dbscan_model = DBSCAN( eps = 1.8, min_samples = 11)
# Fitting
best_dbscan_model.fit(scaled_df)
# silhouette
labels_k = best_dbscan_model.labels_
score_k = silhouette_score(scaled_df, labels_k)
silh_values.append(score_k)
# Balance
print(np.unique(best_dbscan_model.labels_,return_counts=True))
print("\n")
# +
import statistics
statistics.mean(silh_values)
# +
# Extracting labels
scaled_df["LABEL"] = best_dbscan_model.labels_
cleaned_df["LABEL"] = best_dbscan_model.labels_
# Pairplot
sns.pairplot( cleaned_df, hue = "LABEL" ); plt.show()
# +
# Pairplot
sns.pairplot( cleaned_df, y_vars=['Age'],
x_vars=['YearsAtCompany'],
hue = "LABEL" );
sns.pairplot( cleaned_df, y_vars=['MonthlyIncome'],
x_vars=['Age'],
hue = "LABEL" );
sns.pairplot( cleaned_df, y_vars=['DailyRate'],
x_vars=['MonthlyIncome'],
hue = "LABEL" );
sns.pairplot( cleaned_df, y_vars=['YearsAtCompany'],
x_vars=['DistanceFromHome'],
hue = "LABEL" );
plt.show()
# +
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize = (13,8))
sns.scatterplot(x = "Age", y = "DistanceFromHome", data = cleaned_df, hue = "LABEL", palette = "Accent", ax = ax1)
sns.scatterplot(x = "Age", y = "TotalWorkingYears", data = cleaned_df, hue = "LABEL", palette = "Accent", ax = ax2)
sns.scatterplot(x = "MonthlyRate", y = "TotalWorkingYears", data = cleaned_df, hue = "LABEL", palette = "Accent", ax = ax3)
sns.scatterplot(x = "MonthlyIncome", y = "DistanceFromHome", data = cleaned_df, hue = "LABEL", palette = "Accent", ax = ax4)
plt.tight_layout()
plt.show()
# -
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster, cophenet
from scipy.spatial.distance import pdist
from sklearn.cluster import AgglomerativeClustering
import sklearn.metrics as sm
df = pd.read_csv("Dataset/attrition.csv")
cleaned_df=df[SUBSET]
X = StandardScaler().fit_transform(cleaned_df.values)
# led_df = pd.DataFrame( X, columns = cleaned_df.columns )
Z = linkage(X,'ward')
dendrogram(Z,truncate_mode='lastp',p=17,leaf_rotation=45,leaf_font_size=10,show_contracted=False)
plt.title('Hierarchical Clustering Dendrogram - Ward')
plt.xlabel('Cluster Size')
plt.ylabel('Distance')
#plt.axhline(y=25)
#plt.axhline(y=35)
Z = linkage(X,'single')
dendrogram(Z,truncate_mode='lastp',p=17,leaf_rotation=45,leaf_font_size=10,show_contracted=False)
plt.title('Hierarchical Clustering Dendrogram - Single Euclidean')
plt.xlabel('Cluster Size')
plt.ylabel('Distance')
plt.axhline(y=500)
plt.axhline(y=150)
Z = linkage(X,'single',metric='cosine')
dendrogram(Z,truncate_mode='lastp',p=17,leaf_rotation=45,leaf_font_size=10,show_contracted=False)
plt.title('Hierarchical Clustering Dendrogram - single cosine')
plt.xlabel('Cluster Size')
plt.ylabel('Distance')
plt.axhline(y=500)
plt.axhline(y=150)
Z = linkage(X,'complete')
dendrogram(Z,truncate_mode='lastp',p=17,leaf_rotation=45,leaf_font_size=10,show_contracted=False)
plt.title('Hierarchical Clustering Dendrogram - complete')
plt.xlabel('Cluster Size')
plt.ylabel('Distance')
plt.axhline(y=500)
plt.axhline(y=150)
Z = linkage(X,'complete',metric='cosine')
dendrogram(Z,truncate_mode='lastp',p=17,leaf_rotation=45,leaf_font_size=10,show_contracted=False)
plt.title('Hierarchical Clustering Dendrogram - complete cosine')
plt.xlabel('Cluster Size')
plt.ylabel('Distance')
plt.axhline(y=500)
plt.axhline(y=150)
Z = linkage(X,'average')
dendrogram(Z,truncate_mode='lastp',p=17,leaf_rotation=45,leaf_font_size=10,show_contracted=False)
plt.title('Hierarchical Clustering Dendrogram - avg euc')
plt.xlabel('Cluster Size')
plt.ylabel('Distance')
plt.axhline(y=500)
plt.axhline(y=150)
Z = linkage(X,'average',metric='cosine')
dendrogram(Z,truncate_mode='lastp',p=17,leaf_rotation=45,leaf_font_size=10,show_contracted=False)
plt.title('Hierarchical Clustering Dendrogram - avg cosine')
plt.xlabel('Cluster Size')
plt.ylabel('Distance')
plt.axhline(y=500)
plt.axhline(y=150)
#Silhouette on Ward method
from statistics import mean
hierc = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='ward')
hierc.fit(X)
labels_k = hierc.labels_
score_k = silhouette_score(cleaned_df, labels_k)
silh_values.append(score_k)
mean(silh_values)
hierc = AgglomerativeClustering(n_clusters=6, affinity='euclidean', linkage='average')
hierc.fit(X)
labels_k = hierc.labels_
score_k = silhouette_score(cleaned_df, labels_k)
silh_values.append(score_k)
mean(silh_values)
hierc = AgglomerativeClustering(n_clusters=6, affinity='euclidean', linkage='complete')
hierc.fit(X)
labels_k = hierc.labels_
score_k = silhouette_score(cleaned_df, labels_k)
silh_values.append(score_k)
mean(silh_values)
Инициализируем вектор весов
w = w_init
# Сюда будем записывать ошибки на каждой итерации
errors = []
# Счетчик итераций
iter_num = 0
# Будем порождать случайные числа
# (номер объекта, который будет менять веса), а для воспроизводимости
# этой последовательности случайных чисел используем seed.
np.random.seed(seed)
# Основной цикл
while weight_dist > min_weight_dist and iter_num < max_iter:
# порождаем случайный
# индекс объекта обучающей выборки
random_ind = np.random.randint(X.shape[0])
# текущий(новый) вектор весов
w_cur = stochastic_gradient_step(X, y, w, random_ind)
# находим растояние между векторами весов
weight_dist = np.linalg.norm(w - w_cur)
# обновляем вектор весов
w = w_cur
# делаем предсказание на основе нового вектора весов
y_predict = linear_prediction(X, w)
# находим ошибку (ср. кв. отклонение) и записываем в массив
errors.append(mserror(y, y_predict))
# след. итерация
iter_num += 1
return w, errors
# **Запустите $10^5$ (!) итераций стохастического градиентного спуска. Используйте длину шага $\eta$=0.01 и вектор начальных весов, состоящий из нулей.**
# %%time
w_init = np.array([0,0,0,0])
stoch_grad_desc_weights, stoch_errors_by_iter = stochastic_gradient_descent(X, y, w_init)
import matplotlib.pyplot as plt
plt.plot(range(len(stoch_errors_by_iter)), stoch_errors_by_iter)
plt.xlabel('Iteration number')
plt.ylabel('MSE')
plt.show()
# **Посмотрим на вектор весов, к которому сошелся метод.**
stoch_grad_desc_weights
# **Посмотрим на среднеквадратичную ошибку на последней итерации.**
stoch_errors_by_iter[-1]
# **Какова среднеквадратичная ошибка прогноза значений Sales в виде линейной модели с весами, найденными с помощью градиентного спуска? Запишите ответ в файл '4.txt'.**
y_predict_grad = linear_prediction(X, stoch_grad_desc_weights)
answer4 = mserror(y, y_predict_grad)
print(answer4)
write_answer_to_file(answer4, '4.txt')
# -----
#
# Ответами к заданию будут текстовые файлы, полученные в ходе этого решения. Обратите внимание, что отправленные файлы не должны содержать пустую строку в конце. Данный нюанс является ограничением платформы Coursera. Мы работаем над исправлением этого ограничения.
| 17,161 |
/postman-checkpoint.ipynb | 2f83cb330df9eeb977e755d95a777b3cfa557353 | [] | no_license | jminaeva/jminaeva | https://github.com/jminaeva/jminaeva | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 6,061 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
point_1 = (0, 2)
point_2 = (2, 5)
point_3 = (5, 2)
point_4 = (6, 6)
point_5 = (8, 3)
dest1_2 = (((point_2[0] - point_1[0])**2 + (point_2[1] - point_1[1])**2)**0.5)
print("Расстояние от 1й до 2й точки:", dest1_2)
dest1_3 = (((point_3[0] - point_1[0])**2 + (point_3[1] - point_1[1])**2)**0.5)
print("Расстояние от 1й до 3й точки:", dest1_3)
dest1_4 = (((point_4[0] - point_1[0])**2 + (point_4[1] - point_1[1])**2)**0.5)
print("Расстояние от 1й до 4й точки:", dest1_4)
dest1_5 = (((point_5[0] - point_1[0])**2 + (point_5[1] - point_1[1])**2)**0.5)
print("Расстояние от 1й до 5й точки:", dest1_5)
dest2_3 = (((point_3[0] - point_2[0])**2 + (point_3[1] - point_2[1])**2)**0.5)
print("Расстояние от 2й до 3й точки:", dest2_3)
dest2_4 = (((point_4[0] - point_2[0])**2 + (point_4[1] - point_2[1])**2)**0.5)
print("Расстояние от 2й до 4й точки:", dest2_4)
dest2_5 = (((point_5[0] - point_2[0])**2 + (point_5[1] - point_2[1])**2)**0.5)
print("Расстояние от 2й до 5й точки:", dest2_5)
dest3_4 = (((point_4[0] - point_3[0])**2 + (point_4[1] - point_3[1])**2)**0.5)
print("Расстояние от 3й до 4й точки:", dest3_4)
dest3_5 = (((point_5[0] - point_3[0])**2 + (point_5[1] - point_3[1])**2)**0.5)
print("Расстояние от 3й до 5й точки:", dest3_5)
dest4_5 = (((point_5[0] - point_4[0])**2 + (point_5[1] - point_4[1])**2)**0.5)
print("Расстояние от 4й до 5й точки:", dest4_5)
my_dict_point1 = {'точка_2': dest1_2, 'точка_3': dest1_3, 'точка_4': dest1_4, 'точка_5': dest1_5}
dest_min_from_point1 = my_dict_point1['точка_2']
for dest in my_dict_point1.values():
if dest < dest_min_from_point1:
dest_min_from_point1 = dest
print("Кратчайшее расстояние от точки 1:", dest_min_from_point1, "->", )
my_dict_point2 = {'точка_3': dest2_3, 'точка_4': dest2_4, 'точка_5': dest2_5}
dest_min_from_point2 = my_dict_point2['точка_3']
for dest in my_dict_point2.values():
if dest < dest_min_from_point2:
dest_min_from_point2 = dest
print("Кратчайшее расстояние от точки 2:", dest_min_from_point2, "->", )
my_dict_point4 = {'точка_3': dest3_4, 'точка_5': dest4_5}
dest_min_from_point4 = my_dict_point4['точка_3']
for dest in my_dict_point4.values():
if dest < dest_min_from_point4:
dest_min_from_point4 = dest
print("Кратчайшее расстояние от точки 4:", dest_min_from_point4, "->", )
my_dict_point5 = {'точка_3': dest3_5}
dest_min_from_point5 = my_dict_point5['точка_3']
for dest in my_dict_point5.values():
if dest < dest_min_from_point5:
dest_min_from_point5 = dest
print("Кратчайшее расстояние от точки 5:", dest_min_from_point5, "->", )
my_dict_point3 = {'точка_1': dest1_3}
dest_min_from_point3 = my_dict_point3['точка_1']
for dest in my_dict_point3.values():
if dest < dest_min_from_point3:
dest_min_from_point3 = dest
print("Кратчайшее расстояние от точки 3:", dest_min_from_point3, "->", )
dest1_2 = (((point_2[0] - point_1[0])**2 + (point_2[1] - point_1[1])**2)**0.5)
print("Расстояние от 1й до 2й точки:", dest1_2)
a = dest_min_from_point1 + dest_min_from_point4 + dest_min_from_point5 + dest_min_from_point3 + dest1_2
print(a)
# -
s[2]) / 2),
zoom=6
)
geo_json = GeoJSON(
data=geojson,
style={
'opacity': 1, 'dashArray': '1', 'fillOpacity': 0, 'weight': 1
},
)
m.add_layer(geo_json)
m
# -
# ### 5. Create Mosaic
titiler_endpoint = "https://api.cogeo.xyz/" # Devseed temporary endpoint
username = "anonymous" # Update this
layername = "dgopendata_CAfire_2020_post" # WARNING, you can overwrite Mosaics
# ###### 5.1. Create Token
#
# Note: Right now everyone can create a token to upload or create a mosaic in DevSeed infrastructure
#
# Docs: https://api.cogeo.xyz/docs#/Token/create_token_tokens_create_post
r = requests.post(
f"{titiler_endpoint}/tokens/create",
json={
"username": username,
"scope": ["mosaic:read", "mosaic:create"]
}
).json()
token = r["token"]
print(token)
# ###### 5.2. Create Mosaic
#
# Docs: https://api.cogeo.xyz/docs#/MosaicJSON/create_mosaic_mosaicjson_create_post
r = requests.post(
f"{titiler_endpoint}/mosaicjson/create",
json={
"username": username,
"layername": layername,
"files": [f["path"] for f in post_event]
},
params={
"access_token": r["token"]
}
).json()
print(r)
# ###### You can also `upload` a mosaic
# +
# from cogeo_mosaic.mosaic import MosaicJSON
# mosaicdata = MosaicJSON.from_urls([f["path"] for f in post_event])
# print(mosaicdata)
# r = requests.post(
# f"{titiler_endpoint}/mosaicjson/upload",
# json={
# "username": username,
# "layername": layername,
# "mosaic": mosaicdata.dict(exclude_none=True)
# },
# params={
# "access_token": token
# }
# ).json()
# -
# ###### 5.3. Display Tiles
#
# Docs: https://api.cogeo.xyz/docs#/MosaicJSON/tilejson_mosaicjson__layer__tilejson_json_get
# +
r = requests.get(
f"{titiler_endpoint}/mosaicjson/{username}.{layername}/tilejson.json",
).json()
print(r)
m = Map(
center=((bounds[1] + bounds[3]) / 2,(bounds[0] + bounds[2]) / 2),
zoom=10
)
tiles = TileLayer(
url=r["tiles"][0],
min_zoom=r["minzoom"],
max_zoom=r["maxzoom"],
opacity=1
)
geo_json = GeoJSON(
data=geojson,
style={
'opacity': 1, 'dashArray': '1', 'fillOpacity': 0, 'weight': 1
},
)
m.add_layer(geo_json)
m.add_layer(tiles)
m
| 5,637 |
/Foundation/04-pandas-intro/exercises/01-harry-potter.ipynb | e8319c4c4d32de6544d0d9c1fc42fc14eeaf8dba | [] | no_license | ohjho/ftds_oct_2018 | https://github.com/ohjho/ftds_oct_2018 | 5 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 194,807 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pymongo
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
course_cluster_uri = 'mongodb://analytics-student:analytics-password@cluster0-shard-00-00-jxeqq.mongodb.net:27017,cluster0-shard-00-01-jxeqq.mongodb.net:27017,cluster0-shard-00-02-jxeqq.mongodb.net:27017/?ssl=true&replicaSet=Cluster0-shard-0&authSource=admin'
course_client = pymongo.MongoClient(course_cluster_uri)
weather_data = course_client['100YWeatherSmall'].data
# remove outliers that are clearly bad data
query = {
'pressure.value': { '$lt': 9999 },
'airTemperature.value': { '$lt': 9999 },
'wind.speed.rate': { '$lt': 500 },
}
# convert our cursor into a list
l = list(weather_data.find(query).limit(1000))
# pull out the 3 variables we care about into their own respective lists
pressures = [x['pressure']['value'] for x in l]
air_temps = [x['airTemperature']['value'] for x in l]
wind_speeds = [x['wind']['speed']['rate'] for x in l]
# +
# here you'll write the code to plot pressures, air_temps, and wind_speeds in a 3D plot
# +
plt.clf()
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(pressures, air_temps, wind_speeds)
plt.title('Movie Ratings vs. Runtime vs. Year')
ax.set_xlabel('pressures')
ax.set_ylabel('air_temps')
ax.set_zlabel('wind_speeds')
plt.show()
# -
ce",mean_bed)
nan_list = data[data.bedrooms.isna()].index.tolist()
data.loc[data.bedrooms.isna(), 'bedrooms'] = np.ceil(data.loc[data.bedrooms.isna(), 'price']/mean_bed)
geometry = [Point(xy) for xy in zip(data.longitude, data.latitude)]
crs = {'init': 'epsg:4326'}
gdf = gpd.GeoDataFrame(data, crs=crs, geometry=geometry)
meter_500 = 0.00899928/2
# make the geometry a multipolygon if it's not already
geometry = city['geometry'].iloc[0]
if isinstance(geometry, Polygon):
geometry = MultiPolygon([geometry])
# quadrat_width is in the units the geometry is in, so we'll do a tenth of a degree
geometry_cut = ox.quadrat_cut_geometry(geometry, quadrat_width=meter_500)
city['coords'] = city['geometry'].apply(lambda x: x.representative_point().coords[:])
city['coords'] = [coords[0] for coords in city['coords']]
polylist = [p for p in geometry_cut]
polyframe = gpd.GeoDataFrame(geometry=polylist)
polyframe.crs = city.geometry.crs
polyframe['center_lon'] = polyframe['geometry'].apply(lambda x: x.centroid.coords[0][0])
polyframe['center_lat'] = polyframe['geometry'].apply(lambda x: x.centroid.coords[0][1])
pointInPoly = gpd.sjoin(polyframe, gdf, op='contains')
print("pointinpoly length:",len(pointInPoly))
#pointInPoly.sort_values(['PlateID', 'Time'], inplace=True)
pointInPoly['index'] = pointInPoly.index
pointInPoly.reset_index(drop=True, inplace=True)
present_ind = list(pointInPoly['index_right'])
gdf_test_dropped = gdf.iloc[present_ind,:]
gdf_dropped = gdf_test_dropped.copy()
gdf_dropped.reset_index(drop=True, inplace=True)
print("check contains:",polyframe.iloc[pointInPoly.loc[len(pointInPoly)-1, 'index']].geometry.contains(gdf_dropped.loc[len(pointInPoly)-1,'geometry']))
gdf_dropped['pindex'] = pointInPoly['index']
print("check if there are NAs:", gdf_dropped.isna().values.any())
pindex = gdf_dropped.pindex.unique()
airbnb_dict = dict(gdf_dropped.pindex.value_counts())
counts = pd.DataFrame(list(airbnb_dict.items()), columns=['key', 'count'])
counts = counts[counts['count']>6]
counts = counts.copy()
airbnb_dict = dict(zip(list(counts['key']), list(counts['count'])))
polyair = polyframe.copy()
polyair['count'] = 0
polyair['count'].update(pd.Series(airbnb_dict))
# plot the city
west, south, east, north = city.unary_union.bounds
fig, ax = plt.subplots(figsize=(40,26))
polyframe.plot(ax=ax, color='#000004')
polyair.plot(column='count', legend=True, cmap='magma', ax=ax)
ax.set_xlim(west, east)
ax.set_ylim(south, north)
#ax.axis('off')
plt.show()
gdf_dropped = gdf_dropped[gdf_dropped.pindex.isin(airbnb_dict.keys())]
gdf_dropped = gdf_dropped.copy()
gdf_dropped = gdf_dropped[gdf_dropped['price'] > 0]
gdf_dropped = gdf_dropped.copy()
gdf_dropped['price_normalized'] = gdf_dropped.price.divide(gdf_dropped.bedrooms)
gdf_dropped = gdf_dropped[gdf_dropped.price_normalized<270]
gdf_dropped = gdf_dropped.copy()
gdf_dropped.reset_index(drop=True, inplace=True)
gdf_dropped.price_normalized.hist(bins=100)
prices_dict = dict(gdf_dropped.groupby('pindex')['price_normalized'].mean())
from scipy import stats
hmean_prices_dict = dict(gdf_dropped.groupby('pindex')['price_normalized'].apply(lambda x: stats.hmean(x)))
median_prices_dict = dict(gdf_dropped.groupby('pindex')['price_normalized'].median())
polyair['prices'] = 0
polyair['hmean_prices'] = 0
polyair['median_prices'] = 0
polyair['prices'].update(pd.Series(prices_dict))
polyair['hmean_prices'].update(pd.Series(hmean_prices_dict))
polyair['median_prices'].update(pd.Series(median_prices_dict))
# plot the city
west, south, east, north = city.unary_union.bounds
fig, ax = plt.subplots(figsize=(40,26))
polyframe.plot(ax=ax, color='#000004')
polyair.plot(column='prices', legend=True, cmap='magma', ax=ax)
ax.set_xlim(west, east)
ax.set_ylim(south, north)
#ax.axis('off')
plt.show()
# plot the city
west, south, east, north = city.unary_union.bounds
fig, ax = plt.subplots(figsize=(40,30))
polyframe.plot(ax=ax, color='#000004')
polyair.plot(column='hmean_prices', legend=True, cmap='magma', ax=ax)
ax.set_xlim(west, east)
ax.set_ylim(south, north)
#ax.axis('off')
plt.show()
# plot the city
west, south, east, north = city.unary_union.bounds
fig, ax = plt.subplots(figsize=(40,20))
polyframe.plot(ax=ax, color='#000004')
polyair.plot(column='median_prices', legend=True, cmap='magma', ax=ax)
ax.set_xlim(west, east)
ax.set_ylim(south, north)
#ax.axis('off')
plt.show()
# +
# plot the city
west, south, east, north = city.unary_union.bounds
#fig, ax = plt.subplots(figsize=(40,20))
# for polygon, n in zip(geometry_cut, np.arange(len(polylist))):
# p = polygon.representative_point().coords[:][0]
# patch = PolygonPatch(polygon, fc='#ffffff', ec='#000000', zorder=2)
# ax.add_patch(patch)
# plt.annotate(s=n, xy=p,
# horizontalalignment='center', size=7)
fig, ax = plt.subplots(figsize=(45,30))
for polygon, n in zip(geometry_cut, np.arange(len(polylist))):
p = polygon.representative_point().coords[:][0]
patch = PolygonPatch(polygon, fc='#ffffff', ec='#000000', alpha=0.5)
ax.add_patch(patch)
plt.annotate(s=n, xy=p,
horizontalalignment='center', size=7)
polyframe.plot(ax=ax, color='#000004', alpha=0.5)
polyair.plot(column='prices', legend=True, cmap='magma', ax=ax, alpha=0.7, zorder=2)
ax.set_xlim(west, east)
ax.set_ylim(south, north)
#ax.axis('off')
plt.show()
# +
import plotly.plotly as py
import plotly.graph_objs as go
# MatPlotlib
import matplotlib.pyplot as plt
from matplotlib import pylab
from mpl_toolkits.mplot3d import Axes3D
#x, y = np.array(polyair.center_lon), np.array(polyair.center_lat)
x = np.array(polyair.center_lon)*500/meter_500
x = x-x.min()
x = x/1000
y = np.array(polyair.center_lat)*500/meter_500
y = y-y.min()
y = y/1000
# Plot the 3D figure of the fitted function and the residuals.
fig = plt.figure(figsize=(14,12))
ax = fig.gca(projection='3d')
ax.scatter(x, y, np.array(polyair.prices), cmap='plasma', s=5)
ax.set_zlim(0,np.max(np.array(polyair.median_prices))+2)
ax.view_init(30, 300)
plt.show()
plt.style.use('ggplot')
fig, ax = plt.subplots(figsize=(14,10))
scat = ax.scatter(x, y, c=np.array(polyair.prices), s=50, cmap='hot')
cbar = fig.colorbar(scat)
#cbar.set_clim(0, 250)
plt.savefig('images/Aarhus_observed.jpg')
plt.show()
# -
polyair[polyair.prices==polyair.prices.max()]
cdf = polyair[polyair.index.isin([594, 2506, 1788])]
cdf["cen_lon_km"] = cdf['center_lon'].apply(lambda x: (x*500/meter_500 - (polyair.center_lon*500/meter_500).min())/1000)
cdf["cen_lat_km"] = cdf['center_lat'].apply(lambda x: (x*500/meter_500 - (polyair.center_lat*500/meter_500).min())/1000)
cdf
# +
alphas = {}
xy = np.vstack([x, y])
zobs = np.array(polyair.prices)
#zobs = np.where(zobs>0, zobs, 0.1*zobs.max())
import scipy.optimize as opt
import matplotlib.pyplot as plt
def _gaussian(M, *args):
xy = M
arr = np.zeros(len(zobs))
for i in range(len(args)//7):
arr += twoD_Gaussian_alpha(xy, *args[i*7:i*7+7])
return arr
guess_prms = [(79.5,30.838323,18.704364, 1, 1.8,3.8, 1),
#(45,27.390274,19.832074,0.5, 1,0.5),
(61,28.888689,17.848290, 3, 4,3, 2)
]
# Flatten the initial guess parameter list.
p0 = [p for prms in guess_prms for p in prms]
def twoD_Gaussian_alpha(xy, amplitude, xo, yo, sigma_x, sigma_y, theta, alpha):
x, y = xy
xo = float(xo)
yo = float(yo)
a = (np.cos(theta)**2)/(2*sigma_x**2) + (np.sin(theta)**2)/(2*sigma_y**2)
b = -(np.sin(2*theta))/(4*sigma_x**2) + (np.sin(2*theta))/(4*sigma_y**2)
c = (np.sin(theta)**2)/(2*sigma_x**2) + (np.cos(theta)**2)/(2*sigma_y**2)
g = amplitude*np.exp( - (a*((x-xo)**2) + 2*b*(x-xo)*(y-yo)
+ c*((y-yo)**2))**alpha)
return g.ravel()
popt, pcov = opt.curve_fit(_gaussian, xy, zobs, p0)
#pred_params, uncert_cov = opt.curve_fit(gauss2d, xy, zobs, p0=guess)
zpred = np.zeros(len(zobs))
for i in range(len(popt)//7):
zpred += twoD_Gaussian_alpha(xy, *popt[i*7:i*7+7])
# for i in range(len(popt)//5):
# fit += gaussian(X, Y, *popt[i*5:i*5+5])
print('Fitted parameters:')
print(popt)
rms = np.sqrt(np.mean((zobs - zpred)**2))
print('RMS residual =', rms)
fig, ax = plt.subplots(figsize=(14,12))
scat = ax.scatter(x, y, c=zpred, vmin=0, vmax=zobs.max(), s=25, cmap='hot')
fig.colorbar(scat)
plt.savefig('Aarhus_fitted.jpg')
plt.show()
#x, y = np.array(polyair.center_lon), np.array(polyair.center_lat)
# Plot the 3D figure of the fitted function and the residuals.
fig = plt.figure(figsize=(14,12))
ax = fig.gca(projection='3d')
ax.scatter(x, y, zpred, cmap='plasma', s=10, alpha=0.5)
ax.scatter(x, y, zobs, color='green', s=5, alpha=0.4)
ax.set_zlim(0,np.max(np.array(polyair.median_prices))+2)
ax.view_init(35, 150)
plt.show()
alphas['Aarhus'] = np.mean(popt[6::7])
print(alphas)
# -
import pickle
pickle_in = open("alphas.pickle","rb")
alphas_dict = pickle.load(pickle_in)
#prices_params_dict = {}
alphas_dict['Aarhus'] = 1.87621535
print(alphas_dict)
pickle_out = open("alphas.pickle","wb")
pickle.dump(alphas_dict, pickle_out)
pickle_out.close()
# +
xy = np.vstack([x, y])
zobs = np.array(polyair.prices)
#zobs = np.where(zobs>0, zobs, 0.1*zobs.max())
import scipy.optimize as opt
import matplotlib.pyplot as plt
def _gaussian(M, *args):
xy = M
arr = np.zeros(len(zobs))
for i in range(len(args)//6):
arr += twoD_Gaussian(xy, *args[i*6:i*6+6])
return arr
guess_prms = [(79.5,30.838323,18.704364, 1, 1.8,3.8),
#(45,27.390274,19.832074,0.5, 1,0.5),
(61,28.888689,17.848290, 3, 4,3)
]
# Flatten the initial guess parameter list.
p0 = [p for prms in guess_prms for p in prms]
def twoD_Gaussian(xy, amplitude, xo, yo, sigma_x, sigma_y, theta):
x, y = xy
xo = float(xo)
yo = float(yo)
a = (np.cos(theta)**2)/(2*sigma_x**2) + (np.sin(theta)**2)/(2*sigma_y**2)
b = -(np.sin(2*theta))/(4*sigma_x**2) + (np.sin(2*theta))/(4*sigma_y**2)
c = (np.sin(theta)**2)/(2*sigma_x**2) + (np.cos(theta)**2)/(2*sigma_y**2)
g = amplitude*np.exp( - (a*((x-xo)**2) + 2*b*(x-xo)*(y-yo)
+ c*((y-yo)**2)))
return g.ravel()
popt, pcov = opt.curve_fit(_gaussian, xy, zobs, p0)
#pred_params, uncert_cov = opt.curve_fit(gauss2d, xy, zobs, p0=guess)
zpred = np.zeros(len(zobs))
for i in range(len(popt)//6):
zpred += twoD_Gaussian(xy, *popt[i*6:i*6+6])
# for i in range(len(popt)//5):
# fit += gaussian(X, Y, *popt[i*5:i*5+5])
print('Fitted parameters:')
print(popt)
rms = np.sqrt(np.mean((zobs - zpred)**2))
print('RMS residual =', rms)
fig, ax = plt.subplots(figsize=(14,12))
scat = ax.scatter(x, y, c=zpred, vmin=0, vmax=zobs.max(), s=50, cmap='hot')
fig.colorbar(scat)
plt.savefig('Aarhus_fitted.jpg')
plt.show()
#x, y = np.array(polyair.center_lon), np.array(polyair.center_lat)
# Plot the 3D figure of the fitted function and the residuals.
fig = plt.figure(figsize=(14,12))
ax = fig.gca(projection='3d')
ax.scatter(x, y, zpred, cmap='plasma', s=5, alpha=0.5)
ax.scatter(x, y, zobs, color='green', s=2, alpha=0.2)
ax.set_zlim(0,np.max(np.array(polyair.median_prices))+2)
ax.view_init(25, 100)
plt.show()
# +
def is_pos_def(x):
return np.all(np.linalg.eigvals(x) > 0)
sqrt_eigs_long = np.array([])
sqrt_eigs_short = np.array([])
for i in range(0, len(popt), 6):
a = (np.cos(popt[i+5])**2)/(2*popt[i+3]**2) + (np.sin(popt[i+5])**2)/(2*popt[i+4]**2)
b = -(np.sin(2*popt[i+5]))/(4*popt[i+3]**2) + (np.sin(2*popt[i+5]))/(4*popt[i+4]**2)
c = (np.sin(popt[i+5])**2)/(2*popt[i+3]**2) + (np.cos(popt[i+5])**2)/(2*popt[i+4]**2)
cov = np.array([a, b, b, c]).reshape(-1, 2)
print("Is cov_{} positive definite?: ".format(i//6+1), is_pos_def(cov))
eigenvalues = np.linalg.eigvals(cov)
eigenvalues = eigenvalues[eigenvalues>0]
if eigenvalues.size!=0:
stds = np.sqrt(eigenvalues)/popt[i]
#stds = stds[stds>=0]
sqrt_eigs_long = np.append(sqrt_eigs_long,max(stds))
sqrt_eigs_short = np.append(sqrt_eigs_short,min(stds))
print('long stds: ', sqrt_eigs_long, 'mean: ', np.mean(sqrt_eigs_long))
print('short stds: ', sqrt_eigs_short, 'mean: ', np.mean(sqrt_eigs_short))
# +
polyair['zpred'] = zpred
# plot the city
west, south, east, north = city.unary_union.bounds
fig, ax = plt.subplots(figsize=(40,20))
polyframe.plot(ax=ax, color='#000004')
polyair.plot(column='zpred', legend=True, cmap='magma', ax=ax)
ax.set_xlim(west, east)
ax.set_ylim(south, north)
#ax.axis('off')
plt.show()
# +
import pickle
pickle_in = open("Prices_params.pickle","rb")
prices_params_dict = pickle.load(pickle_in)
#prices_params_dict = {}
prices_params_dict['Aarhus'] = popt
pickle_out = open("Prices_params.pickle","wb")
pickle.dump(prices_params_dict, pickle_out)
pickle_out.close()
#average_slopes = {}
pickle_in_long = open("Average_price_slopes_long.pickle","rb")
average_slopes_long = pickle.load(pickle_in_long)
average_slopes_long['Aarhus'] = np.mean(sqrt_eigs_long)
pickle_out_long = open("Average_price_slopes_long.pickle","wb")
pickle.dump(average_slopes_long, pickle_out_long)
pickle_out_long.close()
pickle_in_short = open("Average_price_slopes_short.pickle","rb")
average_slopes_short = pickle.load(pickle_in_short)
average_slopes_short['Aarhus'] = np.mean(sqrt_eigs_short)
pickle_out_short = open("Average_price_slopes_short.pickle","wb")
pickle.dump(average_slopes_short, pickle_out_short)
pickle_out_short.close()
print('long: ', average_slopes_long, '\n', '\n', ' short: ', average_slopes_short)
# +
polyair['zpred'] = zpred
# plot the city
west, south, east, north = city.unary_union.bounds
fig, ax = plt.subplots(figsize=(40,20))
polyframe.plot(ax=ax, color='#000004')
polyair.plot(column='zpred', legend=True, cmap='magma', ax=ax)
ax.set_xlim(west, east)
ax.set_ylim(south, north)
#ax.axis('off')
plt.show()
# -
# download and project a street network
G = ox.graph_from_place('Aarhus Municipality, Denmark', network_type="walk")
#G = ox.project_graph(G)
fig, ax = ox.plot_graph(G, fig_height=20, bgcolor='k', node_size=2, node_color='#999999', node_edgecolor='none', node_zorder=2,
edge_color='#555555', edge_linewidth=0.5, edge_alpha=1)
# +
centers = {}
for i in range(0, len(popt), 6):
lon = popt[i+1]*1000 + (np.array(polyair.center_lon)*500/meter_500).min()
lon = lon*meter_500/500
lat = popt[i+2]*1000 + (np.array(polyair.center_lat)*500/meter_500).min()
lat = lat*meter_500/500
centers['center_node_{}'.format(i//6+1)] = ox.get_nearest_node(G, (lat,lon))
centers
# +
import networkx as nx
#center_node = ox.get_nearest_node(G, (popt[8],popt[7]))
center_node = centers['center_node_1']
# list of distances from center
dists = np.arange(500, 2000, 500)
dists
# get one color for each isochrone
iso_colors = ox.get_colors(n=len(dists), cmap='Reds', start=0.3, return_hex=True)
# color the nodes according to isochrone then plot the street network
node_colors = {}
for dist, color in zip(sorted(dists, reverse=True), iso_colors):
subgraph = nx.ego_graph(G, center_node, radius=dist, distance='length')
for node in subgraph.nodes():
node_colors[node] = color
nc = [node_colors[node] if node in node_colors else 'none' for node in G.nodes()]
ns = [20 if node in node_colors else 0 for node in G.nodes()]
fig, ax = ox.plot_graph(G, fig_height=20,show=False, close=False, node_color=nc, node_size=ns, node_alpha=0.8, node_zorder=2)
plt.close()
# to this matplotlib axis, add the place shape as descartes polygon patches
for geometry in city['geometry'].tolist():
if isinstance(geometry, (Polygon, MultiPolygon)):
if isinstance(geometry, Polygon):
geometry = MultiPolygon([geometry])
for polygon in geometry:
patch = PolygonPatch(polygon, fc='#cccccc', ec='k', linewidth=3, alpha=0.1, zorder=-1)
ax.add_patch(patch)
fig
# +
from tqdm import tqdm_notebook
#poly_prices = polyair[polyair.median_prices>0]
poly_prices = polyair.copy()
print(len(poly_prices))
poly_prices['zpred'] = zpred
lorentz_vals = poly_prices.zpred.to_dict()
s = [(k, lorentz_vals[k]) for k in sorted(lorentz_vals, key=lorentz_vals.get)]
keys = []
vals = []
for k,v in s:
keys.append(k)
vals.append(v)
vals = np.array(vals)
keys = np.array(keys)
vals_cut = vals[vals>0.05*vals.max()]
print(len(vals), len(vals_cut))
L = np.cumsum(vals_cut)/np.sum(vals_cut)
keys = keys[vals>0.05*vals.max()]
print('Number of cells with price above 5th percentile: ', len(keys))
mat = np.zeros(shape=(len(geometry_cut), len(geometry_cut)))
for pair in tqdm_notebook(combinations(sorted(keys), 2)):
mat[pair[0], pair[1]] = geometry_cut[pair[0]].centroid.distance(geometry_cut[pair[1]].centroid)
print(mat)
def isuppertriangular(M):
for i in range(1, len(M)):
for j in range(0, i):
if(M[i][j] != 0):
return False
return True
if isuppertriangular(mat):
print ("Yes")
else:
print ("No")
L1= L
F1 = np.arange(1, len(L1)+1)/len(L1)
L1 = (L1 - L1.min())/(L1.max()-L1.min())
from scipy import interpolate
tck = interpolate.splrep(F1,L1)
x0_1 =1
y0_1 = interpolate.splev(x0_1,tck)
dydx = interpolate.splev(x0_1,tck,der=1)
tngnt1 = lambda x: dydx*x + (y0_1-dydx*x0_1)
plt.plot(F1, L1)
plt.plot(x0_1,y0_1, "or")
plt.plot(F1[tngnt1(F1)>0],tngnt1(F1[tngnt1(F1)>0]), label="tangent")
plt.show()
indlist = poly_prices.index.tolist()
loubar_val = vals_cut[np.where(tngnt1(F1)>0)[0][0]]
print('Loubar price: ', loubar_val)
print('Average price: ', np.mean(vals_cut))
if loubar_val > np.mean(vals_cut):
loubar_keys = keys[vals_cut>loubar_val]
else:
loubar_keys = keys[vals_cut>np.mean(vals_cut)]
#loubar_keys = keys[vals_cut>loubar_val]
dist_mat = mat[keys.reshape(-1,1), keys]
total_dist = dist_mat.sum()
dist_corr = dist_mat[dist_mat>0]
loubar_dist_mat = mat[loubar_keys.reshape(-1,1), loubar_keys]
loubar_dist = loubar_dist_mat.sum()
loubar_dist_corr = loubar_dist_mat[loubar_dist_mat>0]
eta_loubar = loubar_dist_corr.mean()/dist_corr.mean()
x = np.array(polyair.center_lon)*500/meter_500
x = x-x.min()
x = x/1000
avg_dist_meters = (dist_corr.mean()/0.00899928)*1000
print('average city distance: ', avg_dist_meters)
print('eta = ', eta_loubar)
# +
pickle_in = open("City_spreading_index.pickle","rb")
spreading_index_dict = pickle.load(pickle_in)
#spreading_index_dict = {}
spreading_index_dict['Aarhus'] = eta_loubar
pickle_out = open("City_spreading_index.pickle","wb")
pickle.dump(spreading_index_dict, pickle_out)
pickle_out.close()
spreading_index_dict
# +
pickle_in = open("avg_distances_dict.pickle","rb")
avg_distances_dict = pickle.load(pickle_in)
#avg_distances_dict = {}
avg_distances_dict['Aarhus'] = avg_dist_meters
pickle_out = open("avg_distances_dict.pickle","wb")
pickle.dump(avg_distances_dict, pickle_out)
pickle_out.close()
avg_distances_dict
# +
# plot the city
west, south, east, north = city.unary_union.bounds
fig, ax = plt.subplots(figsize=(40,26))
polyframe.plot(ax=ax, color='#000004')
#polyair.plot(column='prices', legend=True, cmap='magma', ax=ax)
poly_prices[poly_prices.index.isin(loubar_keys)].plot(ax=ax, column='zpred')
ax.set_xlim(west, east)
ax.set_ylim(south, north)
#ax.axis('off')
plt.show()
# +
indlist = poly_prices.index.tolist()
mat = np.zeros(shape=(len(geometry_cut), len(geometry_cut)))
for pair in tqdm_notebook(combinations(sorted(indlist), 2)):
mat[pair[0], pair[1]] = geometry_cut[pair[0]].centroid.distance(geometry_cut[pair[1]].centroid)
print(mat)
def isuppertriangular(M):
for i in range(1, len(M)):
for j in range(0, i):
if(M[i][j] != 0):
return False
return True
if isuppertriangular(mat):
print ("Yes")
else:
print ("No")
# +
from tqdm import tqdm_notebook
#poly_prices = polyair[polyair.median_prices>0]
poly_prices = polyair.copy()
print(len(poly_prices))
poly_prices['zpred'] = zpred
lorentz_vals = poly_prices.zpred.to_dict()
s = [(k, lorentz_vals[k]) for k in sorted(lorentz_vals, key=lorentz_vals.get)]
keys = []
vals = []
for k,v in s:
keys.append(k)
vals.append(v)
vals = np.array(vals)
keys_initial = np.array(keys)
perc_vals = np.linspace(0.01, 1, 100)
etas_cut = []
for i in tqdm_notebook(perc_vals):
keys = keys_initial
vals_cut = vals[vals>=i*vals.max()]
print(len(vals), len(vals_cut))
L = np.cumsum(vals_cut)/np.sum(vals_cut)
keys = keys[vals>=i*vals.max()]
print('Number of cells with price above {}th percentile: '.format(i*100), len(keys))
L1= L
F1 = np.arange(1, len(L1)+1)/len(L1)
L1 = (L1 - L1.min())/(L1.max()-L1.min())
loubar_val = vals_cut[np.where(tngnt1(F1)>0)[0][0]]
print('Loubar price: ', loubar_val)
print('Average price: ', np.mean(vals_cut))
loubar_keys = keys[vals_cut>loubar_val]
dist_mat = mat[keys.reshape(-1,1), keys]
total_dist = dist_mat.sum()
dist_corr = dist_mat[dist_mat>0]
loubar_dist_mat = mat[loubar_keys.reshape(-1,1), loubar_keys]
loubar_dist = loubar_dist_mat.sum()
loubar_dist_corr = loubar_dist_mat[loubar_dist_mat>0]
eta = loubar_dist_corr.mean()/dist_corr.mean()
etas_cut.append(eta)
print('eta = ', eta)
etas_cut = np.array(etas_cut)
etas_cut = np.where(np.isnan(etas_cut), 0, etas_cut)
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(perc_vals, etas_cut, color='r', linestyle='--', marker='o', markersize=4, linewidth=1)
plt.xlabel("Cutting threshold")
plt.ylabel("eta")
plt.show()
# +
pickle_in = open("etas_cut_dict.pickle","rb")
etas_cut_dict = pickle.load(pickle_in)
#etas_cut_dict = {}
etas_cut_dict['Aarhus'] = etas_cut
pickle_out = open("etas_cut_dict.pickle","wb")
pickle.dump(etas_cut_dict, pickle_out)
pickle_out.close()
etas_cut_dict
# -
fig, ax = plt.subplots(figsize=(8, 6))
for key in etas_cut_dict:
print(len(etas_cut_dict[key]))
etas = etas_cut_dict[key]#[1:]
vals = etas/etas[0]
plt.plot(np.linspace(0.01, 1, 100), vals, linestyle='-', linewidth=1)
plt.xlabel("Price cutting threshold")
plt.ylabel("eta/eta_0")
plt.show()
# +
lval = np.linspace(0, max(vals_cut), 100)
etas = []
lorentz_vals = poly_prices.zpred.to_dict()
s = [(k, lorentz_vals[k]) for k in sorted(lorentz_vals, key=lorentz_vals.get)]
keys = []
vals = []
for k,v in s:
keys.append(k)
vals.append(v)
vals = np.array(vals)
keys = np.array(keys)
vals_cut = vals[vals>0.05*vals.max()]
print(len(vals), len(vals_cut))
L = np.cumsum(vals_cut)/np.sum(vals_cut)
keys = keys[vals>0.05*vals.max()]
print('Number of cells with price above 5th percentile: ', len(keys))
for i in tqdm_notebook(lval):
loubar_keys = keys[vals_cut>=i]
dist_mat = mat[keys.reshape(-1,1), keys]
total_dist = dist_mat.sum()
dist_corr = dist_mat[dist_mat>0]
loubar_dist_mat = mat[loubar_keys.reshape(-1,1), loubar_keys]
loubar_dist = loubar_dist_mat.sum()
loubar_dist_corr = loubar_dist_mat[loubar_dist_mat>0]
eta = loubar_dist_corr.mean()/dist_corr.mean()
etas.append(eta)
print('eta = ', eta)
etas = np.array(etas)
etas = np.where(np.isnan(etas), 0, etas)
lval = lval/lval.max()
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(lval, etas, color='r', linestyle='--', marker='o', markersize=4, linewidth=1)
plt.xlabel("Price threshold")
plt.ylabel("eta")
plt.show()
etas_cut_threshold = etas
# +
pickle_in = open("etas_cut_threshold_dict.pickle","rb")
etas_cut_threshold_dict = pickle.load(pickle_in)
#etas_cut_threshold_dict = {}
etas_cut_threshold_dict['Aarhus'] = etas_cut_threshold
pickle_out = open("etas_cut_threshold_dict.pickle","wb")
pickle.dump(etas_cut_threshold_dict, pickle_out)
pickle_out.close()
etas_cut_threshold_dict
# +
import math
# Euclidean distance.
def euc_dist(pt1,pt2):
return math.sqrt((pt2[0]-pt1[0])*(pt2[0]-pt1[0])+(pt2[1]-pt1[1])*(pt2[1]-pt1[1]))
def _c(ca,i,j,P,Q):
if ca[i,j] > -1:
return ca[i,j]
elif i == 0 and j == 0:
ca[i,j] = euc_dist(P[0],Q[0])
elif i > 0 and j == 0:
ca[i,j] = max(_c(ca,i-1,0,P,Q),euc_dist(P[i],Q[0]))
elif i == 0 and j > 0:
ca[i,j] = max(_c(ca,0,j-1,P,Q),euc_dist(P[0],Q[j]))
elif i > 0 and j > 0:
ca[i,j] = max(min(_c(ca,i-1,j,P,Q),_c(ca,i-1,j-1,P,Q),_c(ca,i,j-1,P,Q)),euc_dist(P[i],Q[j]))
else:
ca[i,j] = float("inf")
return ca[i,j]
""" Computes the discrete frechet distance between two polygonal lines
Algorithm: http://www.kr.tuwien.ac.at/staff/eiter/et-archive/cdtr9464.pdf
P and Q are arrays of 2-element arrays (points)
"""
def frechetDist(P,Q):
ca = np.ones((len(P),len(Q)))
ca = np.multiply(ca,-1)
return _c(ca,len(P)-1,len(Q)-1,P,Q)
# +
etas_dict['Paris']
a = []
for i in range(0, 50):
a.append(())
# -
frechetDist(etas_dict['Paris'], etas_dict['Aarhus'])
# +
import numpy as np
import similaritymeasures
import matplotlib.pyplot as plt
# Generate random experimental data
x = np.random.random(100)
y = np.random.random(100)
exp_data = np.zeros((100, 2))
exp_data[:, 0] = x
exp_data[:, 1] = y
# Generate random numerical data
x = np.random.random(100)
y = np.random.random(100)
num_data = np.zeros((100, 2))
num_data[:, 0] = x
num_data[:, 1] = y
# quantify the difference between the two curves using PCM
pcm = similaritymeasures.pcm(exp_data, num_data)
# quantify the difference between the two curves using
# Discrete Frechet distance
df = similaritymeasures.frechet_dist(exp_data, num_data)
# quantify the difference between the two curves using
# area between two curves
area = similaritymeasures.area_between_two_curves(exp_data, num_data)
# quantify the difference between the two curves using
# Curve Length based similarity measure
cl = similaritymeasures.curve_length_measure(exp_data, num_data)
# quantify the difference between the two curves using
# Dynamic Time Warping distance
dtw, d = similaritymeasures.dtw(exp_data, num_data)
# print the results
print(pcm, df, area, cl, dtw)
# plot the data
plt.figure()
plt.plot(exp_data[:, 0], exp_data[:, 1])
plt.plot(num_data[:, 0], num_data[:, 1])
plt.show()
# -
paris_data = np.zeros((50, 2))
paris_data[:,0] = np.arange(50)
paris_data[:,1] = etas_dict['Paris']
paris_data
Aarhus_data = np.zeros((50, 2))
Aarhus_data[:,0] = np.arange(50)
Aarhus_data[:,1] = etas_dict['Aarhus']
Aarhus_data
# +
# quantify the difference between the two curves using PCM
pcm = similaritymeasures.pcm(Aarhus_data, paris_data)
# quantify the difference between the two curves using
# Discrete Frechet distance
df = similaritymeasures.frechet_dist(Aarhus_data, paris_data)
# quantify the difference between the two curves using
# area between two curves
area = similaritymeasures.area_between_two_curves(Aarhus_data, paris_data)
# quantify the difference between the two curves using
# Curve Length based similarity measure
cl = similaritymeasures.curve_length_measure(Aarhus_data, paris_data)
# quantify the difference between the two curves using
# Dynamic Time Warping distance
dtw, d = similaritymeasures.dtw(Aarhus_data, paris_data)
# print the results
print(pcm, df, area, cl, dtw)
# plot the data
plt.figure()
plt.plot(Aarhus_data[:, 0], Aarhus_data[:, 1])
plt.plot(paris_data[:, 0], paris_data[:, 1])
plt.show()
# -
for key in etas_dict:
curve = np.zeros((50, 2))
curve[:,0] = np.arange(50)
curve[:,1] = etas_dict[key]
# quantify the difference between the two curves using PCM
pcm = similaritymeasures.pcm(curve, paris_data)
# quantify the difference between the two curves using
# Discrete Frechet distance
df = similaritymeasures.frechet_dist(curve, paris_data)
# quantify the difference between the two curves using
# area between two curves
area = similaritymeasures.area_between_two_curves(curve, paris_data)
# quantify the difference between the two curves using
# Curve Length based similarity measure
cl = similaritymeasures.curve_length_measure(curve, paris_data)
# quantify the difference between the two curves using
# Dynamic Time Warping distance
dtw, d = similaritymeasures.dtw(curve, paris_data)
# print the results
print('----------', key, '----------')
print('PCM distance: ', pcm, '\n')
print('Discrete Frechet distance: ', df, '\n')
print('Are between the curves: ', area, '\n')
print('Curve Length based similarity measure: ', cl, '\n')
print('Dynamic Time Warping distance: ', dtw, '\n')
# plot the data
plt.figure()
plt.plot(curve[:, 0], curve[:, 1])
plt.plot(paris_data[:, 0], paris_data[:, 1])
plt.title('Paris vs {}'.format(key))
plt.show()
fig, ax = plt.subplots(figsize=(8, 6))
for key in etas_dict:
plt.plot(np.arange(50), etas_dict[key], linestyle='-', linewidth=1)
plt.xlabel("Price threshold")
plt.ylabel("eta")
plt.show()
# +
lorentz_vals = poly_prices.zpred.to_dict()
s = [(k, lorentz_vals[k]) for k in sorted(lorentz_vals, key=lorentz_vals.get)]
keys = []
vals = []
for k,v in s:
keys.append(k)
vals.append(v)
vals = np.array(vals)
#keys = np.array(keys)
keys_initial = np.array(keys)
perc_vals = np.linspace(0.01, 1, 100)
etas_2d = []
for i in tqdm_notebook(perc_vals):
keys = keys_initial
vals_cut = vals[vals>=i*vals.max()]
print(len(vals), len(vals_cut))
L = np.cumsum(vals_cut)/np.sum(vals_cut)
keys = keys[vals>=i*vals.max()]
print('Number of cells with price above {}th percentile: '.format(i*100), len(keys))
etas = []
lval = np.linspace(min(vals_cut), max(vals_cut), 100)
for k in tqdm_notebook(lval):
loubar_keys = keys[vals_cut>=k]
dist_mat = mat[keys.reshape(-1,1), keys]
total_dist = dist_mat.sum()
dist_corr = dist_mat[dist_mat>0]
loubar_dist_mat = mat[loubar_keys.reshape(-1,1), loubar_keys]
loubar_dist = loubar_dist_mat.sum()
loubar_dist_corr = loubar_dist_mat[loubar_dist_mat>0]
eta = loubar_dist_corr.mean()/dist_corr.mean()
etas.append(eta)
print('eta = ', eta)
etas_array = np.array(etas)
etas_array = np.where(np.isnan(etas_array), 0, etas_array)
lval = (lval - lval.min())/(lval - lval.min()).max()
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(lval, etas_array, color='r', linestyle='--', marker='o', markersize=4, linewidth=1)
plt.xlabel("Price threshold")
plt.ylabel("eta")
plt.show()
etas_2d.append(etas)
etas_2d = np.array(etas_2d)
etas_2d = np.where(np.isnan(etas_2d), 0, etas_2d)
lval = lval/lval.max()
# -
X,Y = np.meshgrid(np.linspace(0,1, 100),np.linspace(0,1, 100))
etas_surface = etas_2d
fig, ax = plt.subplots(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
# Plot a 3D surface
ax.plot_surface(X, Y, etas_surface)
ax.view_init(45, 45)
plt.show()
# +
pickle_in = open("etas_surface_dict.pickle","rb")
etas_surface_dict = pickle.load(pickle_in)
#etas_surface_dict = {}
etas_surface_dict['Aarhus'] = etas_surface
pickle_out = open("etas_surface_dict.pickle","wb")
pickle.dump(etas_surface_dict, pickle_out)
pickle_out.close()
etas_surface_dict
# +
from tqdm import tqdm_notebook
lorentz_vals = poly_prices.zpred.to_dict()
s = [(k, lorentz_vals[k]) for k in sorted(lorentz_vals, key=lorentz_vals.get)]
keys = []
vals = []
for k,v in s:
keys.append(k)
vals.append(v)
vals = np.array(vals)
keys = np.array(keys)
vals_cut = vals[vals>0.05*vals.max()]
print(len(vals), len(vals_cut))
L = np.cumsum(vals_cut)/np.sum(vals_cut)
keys = keys[vals>0.05*vals.max()]
print('Number of cells with price above 5th percentile: ', len(keys))
print('total number of cells: ', len(polylist))
times_names = ['times_{}'.format(c) for c in range(1, len(centers)+1)]
times_dict = {name:[] for name in times_names}
plist = poly_prices[poly_prices.index.isin(keys)].geometry.tolist()
print('number of cells within urban airbnb territory: ', len(plist))
for poly in tqdm_notebook(plist):
origin = ox.get_nearest_node(G, poly.centroid.coords[0][::-1])
dists_to_centers = []
for node, target in centers.items():
try:
if origin!=target:
path = nx.shortest_path(G, origin, target, weight='length')
edges = [ tuple( path[i:i+2] ) for i in range( len(path) - 1 ) ]
dist = np.sum([G.get_edge_data(*edge)[0]['length'] for edge in edges])
dists_to_centers.append(dist)
except:
pass
if len(dists_to_centers) != 0:
dists_to_centers = sorted(dists_to_centers)
#print('distance list length equal to # of centers: ', len(dists_to_centers)==len(centers))
if len(dists_to_centers)==len(centers):
for n, dist in enumerate(dists_to_centers):
time = (dist/3.7)/60
times_dict['times_{}'.format(n+1)].append(time)
#print(times_dict['times_{}'.format(n+1)][-1])
else:
print('Distance list length NOT equal to # of centers')
#print(distances_dict)
for center in range(1, len(centers)+1):
print("Mean travel times in minutes: ", np.mean(times_dict['times_{}'.format(center)]))
for center in range(1, len(centers)+1):
plt.hist(times_dict['times_{}'.format(center)], bins=20, alpha=0.5)
plt.show()
# +
for center in range(1, len(centers)+1):
times_dict['times_{}'.format(center)] = np.array(times_dict['times_{}'.format(center)])
for center in range(1, len(centers)+1):
print("Mean travel times in minutes: ", np.mean(times_dict['times_{}'.format(center)]))
fig, ax = plt.subplots(figsize=(10,8))
for center in range(1, len(centers)+1):
plt.hist(times_dict['times_{}'.format(center)], bins=20, alpha=1, label='to {} closest center'.format(center))
plt.title('Travel time distributions to closest center in Aarhus')
plt.xlabel('Time')
plt.ylabel('Frequency')
plt.legend()
plt.show()
# +
pickle_in = open("City_Accessibility.pickle","rb")
access_dict = pickle.load(pickle_in)
#access_dict = {}
access_dict['Aarhus'] = times_dict
pickle_out = open("City_Accessibility.pickle","wb")
pickle.dump(access_dict, pickle_out)
pickle_out.close()
access_dict
# -
x = times_dict['times_{}'.format(1)]
y = times_dict['times_{}'.format(2)]
c_xy = np.histogram2d(x, y, 20)[0]
c_xx = np.histogram2d(x, x, 20)[0]
plt.imshow(c_xy, cmap='hot', interpolation='nearest')
plt.show()
# +
from sklearn.metrics import mutual_info_score
def calc_MI(x, y, bins):
c_xy = np.histogram2d(x, y, bins)[0]
mi = mutual_info_score(None, None, contingency=c_xy)
return mi
mi_list = []
for center in range(1, len(centers)+1):
mi_list.append(times_dict['times_{}'.format(center)])
mis = []
for pair in combinations_with_replacement(mi_list, 2):
MI = calc_MI(pair[0], pair[1], 20)
print(MI)
mis.append(MI)
mis = np.array(mis)
avg_mi = np.mean(mis)
print('average mutual information = ', avg_mi)
# -
mis
# +
pickle_in = open("Time_distribution_mutual_information.pickle","rb")
MI_dict = pickle.load(pickle_in)
#MI_dict = {}
MI_dict['Aarhus'] = avg_mi
pickle_out = open("Time_distribution_mutual_information.pickle","wb")
pickle.dump(MI_dict, pickle_out)
pickle_out.close()
MI_dict
# -
| 36,766 |
/Gradient_Descent_Assignment.ipynb | e3d6433502171f2de6834a7cb5b990867d400bf8 | [] | no_license | dcarter-ds/DS-Unit-2-Sprint-2-Linear-Regression | https://github.com/dcarter-ds/DS-Unit-2-Sprint-2-Linear-Regression | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 46,065 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# sdfger NameError
# ergvd sdfe SyntaxError
# 0/0 ZeroDivisionError
# a = {'b':'b'}
# a['c'] KeyError
# -
try:
# asdfaeewf
0/0
# a = {'b':'b'}
# a['c']
except NameError as nameError:
print ("Name error, variable no declarada")
except (ZeroDivisionError, KeyError) as errorComun:
print ("Error Comun en Python")
except Exception as error:
print (error)
ge!!
#
# ## Use gradient descent to find the optimal parameters of a **multiple** regression model. (We only showed an implementation for a bivariate model during lecture.)
#
# A note: Implementing gradient descent in any context is not trivial, particularly the step where we calculate the gradient will change based on the number of parameters that we're trying to optimize for. You will need to research what the gradient of a multiple regression model looks like. This challenge is pretty open-ended but I hope it will be thrilling. Please work together, help each other, share resources and generally expand your understanding of gradient descent as you try and achieve this implementation.
#
# ## Suggestions:
#
# Start off with a model that has just two $X$ variables You can use any datasets that have at least two $x$ variables. Potential candidates might be the blood pressure dataset that we used during lecture on Monday: [HERE](https://college.cengage.com/mathematics/brase/understandable_statistics/7e/students/datasets/mlr/excel/mlr02.xls) or any of the housing datasets. You would just need to select from them the two $x$ variables and one $y$ variable that you want to work with.
#
# Use Sklearn to find the optimal parameters of your model first. (like we did during the lecture.) So that you can compare the parameter estimates of your gradient-descent linear regression to the estimates of OLS linear regression. If implemented correctly they should be nearly identical.
#
# Becoming a Data Scientist is all about striking out into the unknown, getting stuck and then researching and fighting and learning until you get yourself unstuck. Work together! And fight to take your own learning-rate fueled step towards your own optimal understanding of gradient descent!
#
# + id="_Xzf_Wfvgsek" colab_type="code" colab={}
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from pandas.plotting import scatter_matrix
# + id="7oH0JU4HhLMd" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 195} outputId="59ea92b5-068d-4bee-9539-b50c79590321"
# Importing dataset and reading data
df = pd.read_csv('https://raw.githubusercontent.com/ryanleeallred/datasets/master/car_regression.csv')
df.head()
# + id="UsJT-uY-kqU6" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 314} outputId="2422c865-d682-4103-887c-a91f36226082"
df.corr()
# + id="rsXnOy1JrSPw" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 195} outputId="fc6f4f6b-d8ec-4359-f19a-489eb2f03836"
# Standardizing/normalize the data
df = (df - df.mean()) / df.std()
df.head()
# + id="xXTBGjPiZ5Mm" colab_type="code" outputId="482d2c21-a4c8-4036-b7ba-2198c4d002bc" colab={"base_uri": "https://localhost:8080/", "height": 50}
# Sklearn to find the optimal parameters
# Creating X matrix
X = df[['year', 'drive']]
# Adding ones column to X
X = np.c_[np.ones(X.shape[0]), X]
# Setting y/dependent variable
y = df[['price']].values
# Fitting model
lr = LinearRegression()
lr.fit(X, y)
# Making coefficient and intercept variables
beta_1 = lr.coef_
beta_0 = lr.intercept_
# Looking at coefs and intercept
print('Coefficients:', beta_1)
print('Intercept:', beta_0)
# + id="_tWzF6IqXIIq" colab_type="code" colab={}
##### Solve by implementing a "multiple variable" Gradient Descent Function #####
# + id="qpBC32l0r9Ri" colab_type="code" colab={}
# Setting hyperparameters
alpha = 0.02 # size of step
iters = 1000 # number of steps
theta = np.zeros([1,3]) # starting position of theta -- all zeros
# + id="jwAjgPSC4um7" colab_type="code" colab={}
# Making compute cost function
def computeCost(X,y,theta):
tobesummed = ((X @ theta.T)-y) ** 2 # Part of the cost function (https://chrisjmccormick.files.wordpress.com/2014/03/gradientdescentofmsetable.png)
return np.sum(tobesummed)/(2 * len(X)) # Summation and (1/2m) of cost function
# + id="BcpWojEU4uwC" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="12409061-1630-4e20-fe8d-17d2401fa46e"
# making gradient descent function
def gradientDescent(X,y,theta,iters,alpha):
cost = np.zeros(iters)
for i in range(iters):
theta = theta - (alpha/len(X)) * np.sum(X * (X @ theta.T - y), axis=0) # This is bulk of the gradient descent function -- still having trouble comprehending
cost[i] = computeCost(X, y, theta) # The cost of each iteration
return theta,cost
# running the gd and cost function
g,cost = gradientDescent(X,y,theta,iters,alpha)
print(g)
# print(cost)
# finalCost = computeCost(X,y,g)
# print(finalCost)
# Got the same result as the sklearn LinearRegression model
# + id="y-kO4-jN4utv" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 376} outputId="84f4e914-1696-4170-e795-84b2a74f9ff3"
# Plotting the cost against iterations
fig, ax = plt.subplots()
ax.plot(np.arange(iters), cost, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch');
# + [markdown] id="RCs6EmWhYPM-" colab_type="text"
# ## Stretch Goals
#
# If you happen upon the most useful resources for accomplishing this challenge first, I want you to spend time today studying other variations of Gradient Descent-Based Optimizers. A good list of the most common optimizers can be found in the Keras Documentation: <https://keras.io/optimizers/>
#
# - Try and write a function that can perform gradient descent for arbitarily large (in dimensionality) multiple regression models.
# - Create a notebook for yourself exploring the different gradient descent based optimizers.
# - How do the above differ from the "vanilla" gradient descent we explored today?
# - How do these different gradient descent-based optimizers seek to overcome the challenge of finding the global minimum among various local minima?
# - Write a blog post that reteaches what you have learned about these other gradient descent-based optimizers.
#
# [Overview of GD-based optimizers](http://ruder.io/optimizing-gradient-descent/)
#
# [Siraj Raval - Evolution of Gradient Descent-Based Optimizers](https://youtu.be/nhqo0u1a6fw)
| 6,855 |
/Project/HNSC/.ipynb_checkpoints/sub_em_structure-checkpoint.ipynb | e365f6a3783da64ba6565d7bd6366e82e2ed4709 | [] | no_license | Arcade0/TCI | https://github.com/Arcade0/TCI | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .r | 8,300 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# +
#####
install.packages("bnlearn")
install.packages("http://www.bnlearn.com/releases/bnlearn_latest.tar.gz")
install.packages("http://www.bnlearn.com/releases/bnlearn_latest.tar.gz")
if (!requireNamespace("BiocManager", quietly = TRUE))
install.packages("BiocManager")
BiocManager::install()
source("http://bioconductor.org/biocLite.R")
biocLite(c("graph", "Rgraphviz", "RBGL"))
install.packages("gRain")
#####
library(bnlearn)
library(gRain)
library(graph)
library(Rgraphviz)
library(RBGL)
library(reshape2)
setwd('/Users/xinzhuo/Desktop/TCI/TCI')
#####
stem = function(node, random){
if (node=='all'){
#####
##### read data
if (simu==1){
S_Am = read.table('SIMU5/S_Am_sm.csv', header=T, row.names=1, check.names = F, sep=',')
co = c()
for (i in 0:(dim(S_Am)[2]-1)){
co = c(co,paste('o',i, sep ='-' ))
}
colnames(S_Am) = co
S_Ad = read.table('SIMU5/S_Ad_sm.csv', header=T, row.names=1, check.names = F, sep=',')
S_Dm = read.table('SIMU5/S_Dm_sm.csv', header=T, row.names=1, check.names = F, sep=',')
if (random==0){
A_Dm = read.table('SIMU5/A_D_sm.csv', header=T, check.names = F, sep=',')
}
else{
A_Dm = read.table('SIMU5/A_D_rd.csv', header=T, check.names = F, sep=',')
}
}
else{
S_Am = read.table('Pre/S_Amrn.csv', header=T, row.names=1, check.names = F, sep=',')
S_Dm = read.table('Pre/S_Dmrn.csv', header=T, row.names=1, check.names = F, sep=',')
S_Dm[] = lapply(S_Dm, as.numeric)
shai = read.table('RB1mu/Output/run0/completeMatrixn.csv', header=T,check.names = F, sep=',')
S_Am = S_Am[, colnames(S_Am)%in%colnames(shai)]
S_Dm = S_Dm[, colnames(S_Dm)%in%colnames(shai)]
S_Ad = S_Am
co = c()
for (i in 1:(dim(S_Am)[2])){
co = c(co,paste('o',colnames(S_Ad)[i], sep ='-' ))
}
colnames(S_Am) = co
A_Dm = read.table('Pre/A_Drn.csv', header=T, check.names = F, sep=',')
}
TAD = melt(A_Dm, c(''))
TAD1 = TAD[TAD['value']==1,][,1:2]
TAD1 = TAD1[TAD1[,1]%in%colnames(S_Ad),]
TAD0 = TAD[TAD['value']==1,][,1:2]
TAD0 = TAD0[TAD0[,1]%in%colnames(S_Ad),]
#####
###### construct knowledge
ac = dim(S_Am)[2]
dc = dim(S_Dm)[2]
sc = dim(S_Am)[1]
# from sga-protein
ap = colnames(S_Am)
pa = colnames(S_Ad)
whitelist = data.frame(from=c(ap), to=c(pa))
#colnames(TAD1) = colnames(whitelist)
#whitelist = rbind(whitelist, TAD1)
# from protein-sga, sga-protein
paf = rep(colnames(S_Ad), each = ac-1)
apf = c()
for (i in 1:ac){
print(i)
for (j in 1:ac){
if (j!=i){
print(j)
apf = c(apf, colnames(S_Am)[j])
}
}
}
# from sga-sga
aaff = rep(colnames(S_Am), each= ac)
aaft = rep(colnames(S_Am), times=ac)
# from deg-sga, deg-protein
dfff = rep(colnames(S_Dm), times = ac)
adft = rep(colnames(S_Am), each = dc)
pdft = rep(colnames(S_Ad), each = dc)
# from dge-deg
ddff = rep(colnames(S_Dm), each = dc)
ddft = rep(colnames(S_Dm), times = dc)
blacklist = data.frame(from = c(paf, apf, aaff, adft, dfff,dfff, ddff), to = c(apf, paf, aaft,dfff, adft, pdft, ddft))
# from protein-deg
colnames(TAD0) = colnames(blacklist)
blacklist= rbind(blacklist, TAD0)
#####
#### run data
S_APD = cbind(S_Am, S_Ad, S_Dm)
for (i in 1:ac){
S_APD[sample(nrow(S_APD),sc*0.90 ), colnames(S_Ad)[i]] = NA
}
graph = structural.em(S_APD, maximize = "hc", maximize.args = list(whitelist = whitelist, blacklist = blacklist), fit = "mle", fit.args = list(), impute="parents", impute.args = list(), return.all = TRUE, start = NULL, max.iter = 5, debug = FALSE)
}
if (node=='sga'){
#####
##### read data
S_Am = read.table('SIMU5/S_Am_sm.csv', header=T, row.names=1, check.names = F, sep=',')
S_Ad = read.table('SIMU5/S_Ad_sm.csv', header=T, row.names=1, check.names = F, sep=',')
co = c()
for (i in 0:(dim(S_Ad)[2]-1)){
co = c(co,paste('pro',i, sep =':' ))
}
colnames(S_Ad) = co
#####
###### construct knowledge
# from sga-sga
ap = colnames(S_Am)
pa = colnames(S_Ad)
whitelist = data.frame(from=c(ap), to=c(pa))
# from protein-sga, sga-protein
paf = rep(colnames(S_Ad), each = ac-1)
apf = c()
for (i in 1:ac){
print(i)
for (j in 1:ac){
if (j!=i){
print(j)
apf = c(apf, colnames(S_Am)[j])
}
}
}
aaff = rep(colnames(S_Am), each= ac)
aaft = rep(colnames(S_Am), times=ac)
blacklist = data.frame(from = c(paf, apf, aaff), to = c(apf, paf, aaft))
#####
# run data
S_AP = cbind(S_Am, S_Ad)
for (i in 1:ac){
S_AP[sample(nrow(S_AP),sc*0.99 ), colnames(S_Ad)[i]] = NA
}
graph = structural.em(S_AP, maximize = "hc", maximize.args = list(whitelist = whitelist, blacklist = blacklist), fit = "mle", fit.args = list(), impute="parents", impute.args = list(), return.all = TRUE, start = NULL, max.iter = 5, debug = FALSE)
}
#####################################################
# from sga-protein
ap = colnames(S_Am)
pa = colnames(S_Ad)
whitelist = data.frame(from=c(ap), to=c(pa))
# from protein-sga, sga-protein
paf = rep(colnames(S_Ad), each = ac-1)
apf = c()
for (i in 1:ac){
print(i)
for (j in 1:ac){
if (j!=i){
print(j)
apf = c(apf, colnames(S_Am)[j])
}
}
}
# from sga-sga
aaff = rep(colnames(S_Am), each= ac)
aaft = rep(colnames(S_Am), times=ac)
blacklist = data.frame(from = c(paf, apf, aaff), to = c(apf, paf, aaft))
S_AP = cbind(S_Am, S_Ad)
for (i in 1:ac){
S_AP[sample(nrow(S_AP),sc*0.95 ), colnames(S_Ad)[i]] = NA
}
graph = structural.em(S_AP, maximize = "hc", maximize.args = list(whitelist = whitelist, blacklist = blacklist), fit = "mle", fit.args = list(), impute="parents", impute.args = list(), return.all = TRUE, start = NULL, max.iter = 5, debug = FALSE)
}
| 6,335 |
/CNN.ipynb | 55914d47d9f41fe82dfa59c6f42ef9a2ea64fcaa | [] | no_license | DaDaCheng/NeuralLandscap | https://github.com/DaDaCheng/NeuralLandscap | 2 | 1 | null | null | null | null | Jupyter Notebook | false | false | .py | 77,022 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <div class="alert alert-block alert-info" style="margin-top: 20px">
# <a href="https://cocl.us/corsera_da0101en_notebook_top">
# <img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DA0101EN/Images/TopAd.png" width="750" align="center">
# </a>
# </div>
#
# <a href="https://www.bigdatauniversity.com"><img src = "https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DA0101EN/Images/CCLog.png" width = 300, align = "center"></a>
#
# <h1 align=center><font size=5>Data Analysis with Python</font></h1>
# <h1>Module 4: Model Development</h1>
# <p>In this section, we will develop several models that will predict the price of the car using the variables or features. This is just an estimate but should give us an objective idea of how much the car should cost.</p>
# Some questions we want to ask in this module
# <ul>
# <li>do I know if the dealer is offering fair value for my trade-in?</li>
# <li>do I know if I put a fair value on my car?</li>
# </ul>
# <p>Data Analytics, we often use <b>Model Development</b> to help us predict future observations from the data we have.</p>
#
# <p>A Model will help us understand the exact relationship between different variables and how these variables are used to predict the result.</p>
# <h4>Setup</h4>
# Import libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# load data and store in dataframe df:
# This dataset was hosted on IBM Cloud object click <a href="https://cocl.us/DA101EN_object_storage">HERE</a> for free storage.
# path of data
path = 'https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DA0101EN/automobileEDA.csv'
df = pd.read_csv(path)
df.head()
# <h3>1. Linear Regression and Multiple Linear Regression</h3>
# <h4>Linear Regression</h4>
#
# <p>One example of a Data Model that we will be using is</p>
# <b>Simple Linear Regression</b>.
#
# <br>
# <p>Simple Linear Regression is a method to help us understand the relationship between two variables:</p>
# <ul>
# <li>The predictor/independent variable (X)</li>
# <li>The response/dependent variable (that we want to predict)(Y)</li>
# </ul>
#
# <p>The result of Linear Regression is a <b>linear function</b> that predicts the response (dependent) variable as a function of the predictor (independent) variable.</p>
#
#
# $$
# Y: Response \ Variable\\
# X: Predictor \ Variables
# $$
#
# <b>Linear function:</b>
# $$
# Yhat = a + b X
# $$
# <ul>
# <li>a refers to the <b>intercept</b> of the regression line0, in other words: the value of Y when X is 0</li>
# <li>b refers to the <b>slope</b> of the regression line, in other words: the value with which Y changes when X increases by 1 unit</li>
# </ul>
# <h4>Lets load the modules for linear regression</h4>
from sklearn.linear_model import LinearRegression
# <h4>Create the linear regression object</h4>
lm = LinearRegression()
lm
# <h4>How could Highway-mpg help us predict car price?</h4>
# For this example, we want to look at how highway-mpg can help us predict car price.
# Using simple linear regression, we will create a linear function with "highway-mpg" as the predictor variable and the "price" as the response variable.
X = df[['highway-mpg']]
Y = df['price']
# Fit the linear model using highway-mpg.
lm.fit(X,Y)
# We can output a prediction
Yhat=lm.predict(X)
Yhat[0:5]
# <h4>What is the value of the intercept (a)?</h4>
lm.intercept_
# <h4>What is the value of the Slope (b)?</h4>
lm.coef_
# <h3>What is the final estimated linear model we get?</h3>
# As we saw above, we should get a final linear model with the structure:
# $$
# Yhat = a + b X
# $$
# Plugging in the actual values we get:
# <b>price</b> = 38423.31 - 821.73 x <b>highway-mpg</b>
# <div class="alert alert-danger alertdanger" style="margin-top: 20px">
# <h1>Question #1 a): </h1>
#
# <b>Create a linear regression object?</b>
# </div>
# Write your code below and press Shift+Enter to execute
lm1 = LinearRegression()
lm1
# Double-click <b>here</b> for the solution.
#
# <!-- The answer is below:
#
# lm1 = LinearRegression()
# lm1
#
# -->
# <div class="alert alert-danger alertdanger" style="margin-top: 20px">
# <h1> Question #1 b): </h1>
#
# <b>Train the model using 'engine-size' as the independent variable and 'price' as the dependent variable?</b>
# </div>
# Write your code below and press Shift+Enter to execute
lm1.fit(df[['highway-mpg']], df[['price']])
lm1
# Double-click <b>here</b> for the solution.
#
# <!-- The answer is below:
#
# lm1.fit(df[['highway-mpg']], df[['price']])
# lm1
#
# -->
#
# <div class="alert alert-danger alertdanger" style="margin-top: 20px">
# <h1>Question #1 c):</h1>
#
# <b>Find the slope and intercept of the model?</b>
# </div>
# <h4>Slope</h4>
# Write your code below and press Shift+Enter to execute
lm1.coef_
# <h4>Intercept</h4>
# Write your code below and press Shift+Enter to execute
lm1.intercept_
# Double-click <b>here</b> for the solution.
#
# <!-- The answer is below:
#
# # Slope
# lm1.coef_
# # Intercept
# lm1.intercept_
#
# -->
# <div class="alert alert-danger alertdanger" style="margin-top: 20px">
# <h1>Question #1 d): </h1>
#
# <b>What is the equation of the predicted line. You can use x and yhat or 'engine-size' or 'price'?</b>
# </div>
# # You can type you answer here
#
# Double-click <b>here</b> for the solution.
#
# <!-- The answer is below:
#
# # using X and Y
# Yhat=-7963.34 + 166.86*X
#
# Price=-7963.34 + 166.86*engine-size
#
# -->
# <h4>Multiple Linear Regression</h4>
# <p>What if we want to predict car price using more than one variable?</p>
#
# <p>If we want to use more variables in our model to predict car price, we can use <b>Multiple Linear Regression</b>.
# Multiple Linear Regression is very similar to Simple Linear Regression, but this method is used to explain the relationship between one continuous response (dependent) variable and <b>two or more</b> predictor (independent) variables.
# Most of the real-world regression models involve multiple predictors. We will illustrate the structure by using four predictor variables, but these results can generalize to any integer:</p>
# $$
# Y: Response \ Variable\\
# X_1 :Predictor\ Variable \ 1\\
# X_2: Predictor\ Variable \ 2\\
# X_3: Predictor\ Variable \ 3\\
# X_4: Predictor\ Variable \ 4\\
# $$
# $$
# a: intercept\\
# b_1 :coefficients \ of\ Variable \ 1\\
# b_2: coefficients \ of\ Variable \ 2\\
# b_3: coefficients \ of\ Variable \ 3\\
# b_4: coefficients \ of\ Variable \ 4\\
# $$
# The equation is given by
# $$
# Yhat = a + b_1 X_1 + b_2 X_2 + b_3 X_3 + b_4 X_4
# $$
# <p>From the previous section we know that other good predictors of price could be:</p>
# <ul>
# <li>Horsepower</li>
# <li>Curb-weight</li>
# <li>Engine-size</li>
# <li>Highway-mpg</li>
# </ul>
# Let's develop a model using these variables as the predictor variables.
Z = df[['horsepower', 'curb-weight', 'engine-size', 'highway-mpg']]
# Fit the linear model using the four above-mentioned variables.
lm.fit(Z, df['price'])
# What is the value of the intercept(a)?
lm.intercept_
# What are the values of the coefficients (b1, b2, b3, b4)?
lm.coef_
# What is the final estimated linear model that we get?
# As we saw above, we should get a final linear function with the structure:
#
# $$
# Yhat = a + b_1 X_1 + b_2 X_2 + b_3 X_3 + b_4 X_4
# $$
#
# What is the linear function we get in this example?
# <b>Price</b> = -15678.742628061467 + 52.65851272 x <b>horsepower</b> + 4.69878948 x <b>curb-weight</b> + 81.95906216 x <b>engine-size</b> + 33.58258185 x <b>highway-mpg</b>
# <div class="alert alert-danger alertdanger" style="margin-top: 20px">
# <h1> Question #2 a): </h1>
# Create and train a Multiple Linear Regression model "lm2" where the response variable is price, and the predictor variable is 'normalized-losses' and 'highway-mpg'.
# </div>
# Write your code below and press Shift+Enter to execute
lm2 = LinearRegression()
lm2.fit(df[['normalized-losses' , 'highway-mpg']],df['price'])
# Double-click <b>here</b> for the solution.
#
# <!-- The answer is below:
#
# lm2 = LinearRegression()
# lm2.fit(df[['normalized-losses' , 'highway-mpg']],df['price'])
#
# -->
# <div class="alert alert-danger alertdanger" style="margin-top: 20px">
# <h1>Question #2 b): </h1>
# <b>Find the coefficient of the model?</b>
# </div>
# Write your code below and press Shift+Enter to execute
lm2.coef_
# Double-click <b>here</b> for the solution.
#
# <!-- The answer is below:
#
# lm2.coef_
#
# -->
# <h3>2) Model Evaluation using Visualization</h3>
# Now that we've developed some models, how do we evaluate our models and how do we choose the best one? One way to do this is by using visualization.
# import the visualization package: seaborn
# import the visualization package: seaborn
import seaborn as sns
# %matplotlib inline
# <h3>Regression Plot</h3>
# <p>When it comes to simple linear regression, an excellent way to visualize the fit of our model is by using <b>regression plots</b>.</p>
#
# <p>This plot will show a combination of a scattered data points (a <b>scatter plot</b>), as well as the fitted <b>linear regression</b> line going through the data. This will give us a reasonable estimate of the relationship between the two variables, the strength of the correlation, as well as the direction (positive or negative correlation).</p>
# Let's visualize Horsepower as potential predictor variable of price:
width = 12
height = 10
plt.figure(figsize=(width, height))
sns.regplot(x="highway-mpg", y="price", data=df)
plt.ylim(0,)
# <p>We can see from this plot that price is negatively correlated to highway-mpg, since the regression slope is negative.
# One thing to keep in mind when looking at a regression plot is to pay attention to how scattered the data points are around the regression line. This will give you a good indication of the variance of the data, and whether a linear model would be the best fit or not. If the data is too far off from the line, this linear model might not be the best model for this data. Let's compare this plot to the regression plot of "peak-rpm".</p>
plt.figure(figsize=(width, height))
sns.regplot(x="peak-rpm", y="price", data=df)
plt.ylim(0,)
# <p>Comparing the regression plot of "peak-rpm" and "highway-mpg" we see that the points for "highway-mpg" are much closer to the generated line and on the average decrease. The points for "peak-rpm" have more spread around the predicted line, and it is much harder to determine if the points are decreasing or increasing as the "highway-mpg" increases.</p>
# <div class="alert alert-danger alertdanger" style="margin-top: 20px">
# <h1>Question #3:</h1>
# <b>Given the regression plots above is "peak-rpm" or "highway-mpg" more strongly correlated with "price". Use the method ".corr()" to verify your answer.</b>
# </div>
# Write your code below and press Shift+Enter to execute
df[["peak-rpm","highway-mpg","price"]].corr()
# Double-click <b>here</b> for the solution.
#
# <!-- The answer is below:
#
# The variable "peak-rpm" has a stronger correlation with "price", it is approximate -0.704692 compared to "highway-mpg" which is approximate -0.101616. You can verify it using the following command:
# df[["peak-rpm","highway-mpg","price"]].corr()
#
# -->
# <h3>Residual Plot</h3>
#
# <p>A good way to visualize the variance of the data is to use a residual plot.</p>
#
# <p>What is a <b>residual</b>?</p>
#
# <p>The difference between the observed value (y) and the predicted value (Yhat) is called the residual (e). When we look at a regression plot, the residual is the distance from the data point to the fitted regression line.</p>
#
# <p>So what is a <b>residual plot</b>?</p>
#
# <p>A residual plot is a graph that shows the residuals on the vertical y-axis and the independent variable on the horizontal x-axis.</p>
#
# <p>What do we pay attention to when looking at a residual plot?</p>
#
# <p>We look at the spread of the residuals:</p>
#
# <p>- If the points in a residual plot are <b>randomly spread out around the x-axis</b>, then a <b>linear model is appropriate</b> for the data. Why is that? Randomly spread out residuals means that the variance is constant, and thus the linear model is a good fit for this data.</p>
width = 12
height = 10
plt.figure(figsize=(width, height))
sns.residplot(df['highway-mpg'], df['price'])
plt.show()
# <i>What is this plot telling us?</i>
#
# <p>We can see from this residual plot that the residuals are not randomly spread around the x-axis, which leads us to believe that maybe a non-linear model is more appropriate for this data.</p>
# <h3>Multiple Linear Regression</h3>
# <p>How do we visualize a model for Multiple Linear Regression? This gets a bit more complicated because you can't visualize it with regression or residual plot.</p>
#
# <p>One way to look at the fit of the model is by looking at the <b>distribution plot</b>: We can look at the distribution of the fitted values that result from the model and compare it to the distribution of the actual values.</p>
# First lets make a prediction
Y_hat = lm.predict(Z)
# +
plt.figure(figsize=(width, height))
ax1 = sns.distplot(df['price'], hist=False, color="r", label="Actual Value")
sns.distplot(Yhat, hist=False, color="b", label="Fitted Values" , ax=ax1)
plt.title('Actual vs Fitted Values for Price')
plt.xlabel('Price (in dollars)')
plt.ylabel('Proportion of Cars')
plt.show()
plt.close()
# -
# <p>We can see that the fitted values are reasonably close to the actual values, since the two distributions overlap a bit. However, there is definitely some room for improvement.</p>
# <h2>Part 3: Polynomial Regression and Pipelines</h2>
# <p><b>Polynomial regression</b> is a particular case of the general linear regression model or multiple linear regression models.</p>
# <p>We get non-linear relationships by squaring or setting higher-order terms of the predictor variables.</p>
#
# <p>There are different orders of polynomial regression:</p>
# <center><b>Quadratic - 2nd order</b></center>
# $$
# Yhat = a + b_1 X^2 +b_2 X^2
# $$
#
#
# <center><b>Cubic - 3rd order</b></center>
# $$
# Yhat = a + b_1 X^2 +b_2 X^2 +b_3 X^3\\
# $$
#
#
# <center><b>Higher order</b>:</center>
# $$
# Y = a + b_1 X^2 +b_2 X^2 +b_3 X^3 ....\\
# $$
# <p>We saw earlier that a linear model did not provide the best fit while using highway-mpg as the predictor variable. Let's see if we can try fitting a polynomial model to the data instead.</p>
# <p>We will use the following function to plot the data:</p>
def PlotPolly(model, independent_variable, dependent_variabble, Name):
x_new = np.linspace(15, 55, 100)
y_new = model(x_new)
plt.plot(independent_variable, dependent_variabble, '.', x_new, y_new, '-')
plt.title('Polynomial Fit with Matplotlib for Price ~ Length')
ax = plt.gca()
ax.set_facecolor((0.898, 0.898, 0.898))
fig = plt.gcf()
plt.xlabel(Name)
plt.ylabel('Price of Cars')
plt.show()
plt.close()
# lets get the variables
x = df['highway-mpg']
y = df['price']
# Let's fit the polynomial using the function <b>polyfit</b>, then use the function <b>poly1d</b> to display the polynomial function.
# Here we use a polynomial of the 3rd order (cubic)
f = np.polyfit(x, y, 3)
p = np.poly1d(f)
print(p)
# Let's plot the function
PlotPolly(p, x, y, 'highway-mpg')
np.polyfit(x, y, 3)
# <p>We can already see from plotting that this polynomial model performs better than the linear model. This is because the generated polynomial function "hits" more of the data points.</p>
# <div class="alert alert-danger alertdanger" style="margin-top: 20px">
# <h1>Question #4:</h1>
# <b>Create 11 order polynomial model with the variables x and y from above?</b>
# </div>
# Write your code below and press Shift+Enter to execute
f1 = np.polyfit(x, y, 11)
p1 = np.poly1d(f1)
print(p)
PlotPolly(p1,x,y, 'Highway MPG')
# Double-click <b>here</b> for the solution.
#
# <!-- The answer is below:
#
# # calculate polynomial
# # Here we use a polynomial of the 11rd order (cubic)
# f1 = np.polyfit(x, y, 11)
# p1 = np.poly1d(f1)
# print(p)
# PlotPolly(p1,x,y, 'Highway MPG')
#
# -->
# <p>The analytical expression for Multivariate Polynomial function gets complicated. For example, the expression for a second-order (degree=2)polynomial with two variables is given by:</p>
# $$
# Yhat = a + b_1 X_1 +b_2 X_2 +b_3 X_1 X_2+b_4 X_1^2+b_5 X_2^2
# $$
# We can perform a polynomial transform on multiple features. First, we import the module:
from sklearn.preprocessing import PolynomialFeatures
# We create a <b>PolynomialFeatures</b> object of degree 2:
pr=PolynomialFeatures(degree=2)
pr
Z_pr=pr.fit_transform(Z)
# The original data is of 201 samples and 4 features
Z.shape
# after the transformation, there 201 samples and 15 features
Z_pr.shape
# <h2>Pipeline</h2>
# <p>Data Pipelines simplify the steps of processing the data. We use the module <b>Pipeline</b> to create a pipeline. We also use <b>StandardScaler</b> as a step in our pipeline.</p>
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# We create the pipeline, by creating a list of tuples including the name of the model or estimator and its corresponding constructor.
Input=[('scale',StandardScaler()), ('polynomial', PolynomialFeatures(include_bias=False)), ('model',LinearRegression())]
# we input the list as an argument to the pipeline constructor
pipe=Pipeline(Input)
pipe
# We can normalize the data, perform a transform and fit the model simultaneously.
pipe.fit(Z,y)
# Similarly, we can normalize the data, perform a transform and produce a prediction simultaneously
ypipe=pipe.predict(Z)
ypipe[0:4]
# <div class="alert alert-danger alertdanger" style="margin-top: 20px">
# <h1>Question #5:</h1>
# <b>Create a pipeline that Standardizes the data, then perform prediction using a linear regression model using the features Z and targets y</b>
# </div>
# Write your code below and press Shift+Enter to execute
# </div>
# Double-click <b>here</b> for the solution.
#
# <!-- The answer is below:
#
# Input=[('scale',StandardScaler()),('model',LinearRegression())]
#
# pipe=Pipeline(Input)
#
# pipe.fit(Z,y)
#
# ypipe=pipe.predict(Z)
# ypipe[0:10]
#
# -->
# <h2>Part 4: Measures for In-Sample Evaluation</h2>
# <p>When evaluating our models, not only do we want to visualize the results, but we also want a quantitative measure to determine how accurate the model is.</p>
#
# <p>Two very important measures that are often used in Statistics to determine the accuracy of a model are:</p>
# <ul>
# <li><b>R^2 / R-squared</b></li>
# <li><b>Mean Squared Error (MSE)</b></li>
# </ul>
#
# <b>R-squared</b>
#
# <p>R squared, also known as the coefficient of determination, is a measure to indicate how close the data is to the fitted regression line.</p>
#
# <p>The value of the R-squared is the percentage of variation of the response variable (y) that is explained by a linear model.</p>
#
#
#
# <b>Mean Squared Error (MSE)</b>
#
# <p>The Mean Squared Error measures the average of the squares of errors, that is, the difference between actual value (y) and the estimated value (ŷ).</p>
# <h3>Model 1: Simple Linear Regression</h3>
# Let's calculate the R^2
#highway_mpg_fit
lm.fit(X, Y)
# Find the R^2
print('The R-square is: ', lm.score(X, Y))
# We can say that ~ 49.659% of the variation of the price is explained by this simple linear model "horsepower_fit".
# Let's calculate the MSE
# We can predict the output i.e., "yhat" using the predict method, where X is the input variable:
Yhat=lm.predict(X)
print('The output of the first four predicted value is: ', Yhat[0:4])
# lets import the function <b>mean_squared_error</b> from the module <b>metrics</b>
from sklearn.metrics import mean_squared_error
# we compare the predicted results with the actual results
mse = mean_squared_error(df['price'], Yhat)
print('The mean square error of price and predicted value is: ', mse)
# <h3>Model 2: Multiple Linear Regression</h3>
# Let's calculate the R^2
# fit the model
lm.fit(Z, df['price'])
# Find the R^2
print('The R-square is: ', lm.score(Z, df['price']))
# We can say that ~ 80.896 % of the variation of price is explained by this multiple linear regression "multi_fit".
# Let's calculate the MSE
# we produce a prediction
Y_predict_multifit = lm.predict(Z)
# we compare the predicted results with the actual results
print('The mean square error of price and predicted value using multifit is: ', \
mean_squared_error(df['price'], Y_predict_multifit))
# <h3>Model 3: Polynomial Fit</h3>
# Let's calculate the R^2
# let’s import the function <b>r2_score</b> from the module <b>metrics</b> as we are using a different function
from sklearn.metrics import r2_score
# We apply the function to get the value of r^2
r_squared = r2_score(y, p(x))
print('The R-square value is: ', r_squared)
# We can say that ~ 67.419 % of the variation of price is explained by this polynomial fit
# <h3>MSE</h3>
# We can also calculate the MSE:
mean_squared_error(df['price'], p(x))
# <h2>Part 5: Prediction and Decision Making</h2>
# <h3>Prediction</h3>
#
# <p>In the previous section, we trained the model using the method <b>fit</b>. Now we will use the method <b>predict</b> to produce a prediction. Lets import <b>pyplot</b> for plotting; we will also be using some functions from numpy.</p>
# +
import matplotlib.pyplot as plt
import numpy as np
# %matplotlib inline
# -
# Create a new input
new_input=np.arange(1, 100, 1).reshape(-1, 1)
# Fit the model
lm.fit(X, Y)
lm
# Produce a prediction
yhat=lm.predict(new_input)
yhat[0:5]
# we can plot the data
plt.plot(new_input, yhat)
plt.show()
# <h3>Decision Making: Determining a Good Model Fit</h3>
# <p>Now that we have visualized the different models, and generated the R-squared and MSE values for the fits, how do we determine a good model fit?
# <ul>
# <li><i>What is a good R-squared value?</i></li>
# </ul>
# </p>
#
# <p>When comparing models, <b>the model with the higher R-squared value is a better fit</b> for the data.
# <ul>
# <li><i>What is a good MSE?</i></li>
# </ul>
# </p>
#
# <p>When comparing models, <b>the model with the smallest MSE value is a better fit</b> for the data.</p>
#
#
# <h4>Let's take a look at the values for the different models.</h4>
# <p>Simple Linear Regression: Using Highway-mpg as a Predictor Variable of Price.
# <ul>
# <li>R-squared: 0.49659118843391759</li>
# <li>MSE: 3.16 x10^7</li>
# </ul>
# </p>
#
# <p>Multiple Linear Regression: Using Horsepower, Curb-weight, Engine-size, and Highway-mpg as Predictor Variables of Price.
# <ul>
# <li>R-squared: 0.80896354913783497</li>
# <li>MSE: 1.2 x10^7</li>
# </ul>
# </p>
#
# <p>Polynomial Fit: Using Highway-mpg as a Predictor Variable of Price.
# <ul>
# <li>R-squared: 0.6741946663906514</li>
# <li>MSE: 2.05 x 10^7</li>
# </ul>
# </p>
# <h3>Simple Linear Regression model (SLR) vs Multiple Linear Regression model (MLR)</h3>
# <p>Usually, the more variables you have, the better your model is at predicting, but this is not always true. Sometimes you may not have enough data, you may run into numerical problems, or many of the variables may not be useful and or even act as noise. As a result, you should always check the MSE and R^2.</p>
#
# <p>So to be able to compare the results of the MLR vs SLR models, we look at a combination of both the R-squared and MSE to make the best conclusion about the fit of the model.
# <ul>
# <li><b>MSE</b>The MSE of SLR is 3.16x10^7 while MLR has an MSE of 1.2 x10^7. The MSE of MLR is much smaller.</li>
# <li><b>R-squared</b>: In this case, we can also see that there is a big difference between the R-squared of the SLR and the R-squared of the MLR. The R-squared for the SLR (~0.497) is very small compared to the R-squared for the MLR (~0.809).</li>
# </ul>
# </p>
#
# This R-squared in combination with the MSE show that MLR seems like the better model fit in this case, compared to SLR.
# <h3>Simple Linear Model (SLR) vs Polynomial Fit</h3>
# <ul>
# <li><b>MSE</b>: We can see that Polynomial Fit brought down the MSE, since this MSE is smaller than the one from the SLR.</li>
# <li><b>R-squared</b>: The R-squared for the Polyfit is larger than the R-squared for the SLR, so the Polynomial Fit also brought up the R-squared quite a bit.</li>
# </ul>
# <p>Since the Polynomial Fit resulted in a lower MSE and a higher R-squared, we can conclude that this was a better fit model than the simple linear regression for predicting Price with Highway-mpg as a predictor variable.</p>
# <h3>Multiple Linear Regression (MLR) vs Polynomial Fit</h3>
# <ul>
# <li><b>MSE</b>: The MSE for the MLR is smaller than the MSE for the Polynomial Fit.</li>
# <li><b>R-squared</b>: The R-squared for the MLR is also much larger than for the Polynomial Fit.</li>
# </ul>
# <h2>Conclusion:</h2>
# <p>Comparing these three models, we conclude that <b>the MLR model is the best model</b> to be able to predict price from our dataset. This result makes sense, since we have 27 variables in total, and we know that more than one of those variables are potential predictors of the final car price.</p>
# <h1>Thank you for completing this notebook</h1>
# <div class="alert alert-block alert-info" style="margin-top: 20px">
#
# <p><a href="https://cocl.us/corsera_da0101en_notebook_bottom"><img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DA0101EN/Images/BottomAd.png" width="750" align="center"></a></p>
# </div>
#
# <h3>About the Authors:</h3>
#
# This notebook was written by <a href="https://www.linkedin.com/in/mahdi-noorian-58219234/" target="_blank">Mahdi Noorian PhD</a>, <a href="https://www.linkedin.com/in/joseph-s-50398b136/" target="_blank">Joseph Santarcangelo</a>, Bahare Talayian, Eric Xiao, Steven Dong, Parizad, Hima Vsudevan and <a href="https://www.linkedin.com/in/fiorellawever/" target="_blank">Fiorella Wenver</a> and <a href=" https://www.linkedin.com/in/yi-leng-yao-84451275/ " target="_blank" >Yi Yao</a>.
#
# <p><a href="https://www.linkedin.com/in/joseph-s-50398b136/" target="_blank">Joseph Santarcangelo</a> is a Data Scientist at IBM, and holds a PhD in Electrical Engineering. His research focused on using Machine Learning, Signal Processing, and Computer Vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.</p>
# <hr>
# <p>Copyright © 2018 IBM Developer Skills Network. This notebook and its source code are released under the terms of the <a href="https://cognitiveclass.ai/mit-license/">MIT License</a>.</p>
| 27,226 |
/CIFAR10Assignment.ipynb | 6c667345e199483cac9193c66b1cfd1dfb3407ff | [] | no_license | supritag/CSYE_7245 | https://github.com/supritag/CSYE_7245 | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 216,133 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="kZjtqoq2Xmnm" colab_type="text"
# # Hyperparameters tuning
# + [markdown] id="2zg3inwajtI1" colab_type="text"
# # MLP Model
# + id="Viend_C0XfSB" colab_type="code" outputId="25994e72-bf3c-4350-e88e-6ad8dfef25cb" colab={"base_uri": "https://localhost:8080/", "height": 51}
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.models import Sequential
from keras.utils import np_utils
from keras.layers import Dense, Dropout,Activation#, Flatten
from keras.optimizers import RMSprop
import pandas as pd
import numpy as np
batchsizes = [50,70,100,200]
num_classes = 10
epochs = [5,10,20,50,100, 200]
dropouts=[0.3,0.45, 0.5]
activationfuncs=['relu', 'sigmoid','tanh']
optimizers=['adam', 'sgd', 'rmsprop']
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train = x_train.reshape(-1, 3072)
x_test = x_test.reshape(-1, 3072)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
# + [markdown] id="epTqyvJNCurX" colab_type="text"
# # Function For MLP with base hyperparameters and 2 Hidden Layers.
# + id="J1z9jKVemBUp" colab_type="code" colab={}
def function(x_train, y_train, x_test, y_test,activationfunc,batchsize,epoch, optimizer,loss, dropout):
model = Sequential()
model.add(Dense(512, activation=activationfunc, input_shape=(3072,)))
model.add(Dropout(dropout))
model.add(Dense(512, activation=activationfunc))
model.add(Dropout(dropout))
model.add(Dense(num_classes, activation='softmax'))
model.summary()
model.compile(loss=loss,
optimizer=optimizer,
metrics=['accuracy'])
history = model.fit(x_train, y_train,
batch_size=batchsize,
epochs=epoch,
verbose=0,
validation_data=(x_test, y_test))
score = model.evaluate(x_test, y_test, verbose=0)
print('Activation Function ',activationfunc,', Batch Size ',batchsize,', Epoch ',epoch,', Optimizer ', optimizer,', Loss ',loss,', Dropout ', dropout)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
# + [markdown] id="snd2JBmhDOMl" colab_type="text"
# #Changing activation functions keeping other hyperparameters constant
# + id="qWgvzDwqnk3J" colab_type="code" outputId="3460ada3-9e36-49cc-d476-bd87e6d52f6f" colab={"base_uri": "https://localhost:8080/", "height": 710}
for activationfunc in activationfuncs:
function(x_train, y_train, x_test, y_test,activationfunc,batchsize=100,epoch=30, optimizer='rmsprop',loss='categorical_crossentropy', dropout=0.3)
# + [markdown] id="-ttXliz6DZwz" colab_type="text"
# #Changing batchsize keeping other hyperparameters constant
# + id="DtjNK99xoen4" colab_type="code" outputId="7068cf61-7dc0-47fe-89ab-d11d533c25c9" colab={"base_uri": "https://localhost:8080/", "height": 1423}
activationfunc='relu'
epoch=30
optimizer='rmsprop'
loss='categorical_crossentropy'
dropout=0.3
for batchsize in batchsizes:
function(x_train, y_train, x_test, y_test,activationfunc, batchsize,epoch, optimizer,loss, dropout)
# + [markdown] id="xNnXd9KmDf6M" colab_type="text"
# #Changing epochs keeping other hyperparameters constant
# + id="rHTpxvnuohW_" colab_type="code" outputId="d5b898b2-d462-4fba-9497-400b9b3ead07" colab={"base_uri": "https://localhost:8080/", "height": 2097}
activationfunc='relu'
batchsize=200
optimizer='rmsprop'
loss='categorical_crossentropy'
dropout=0.3
for epoch in epochs:
function(x_train, y_train, x_test, y_test,activationfunc, batchsize,epoch, optimizer,loss, dropout)
# + id="i_RFYNko3e-q" colab_type="code" colab={}
# + [markdown] id="ph8j0ZFrDl0s" colab_type="text"
# #Changing optimizers keeping other hyperparameters constant
# + id="_nbNePCUojnE" colab_type="code" outputId="97da7bb7-7f87-49b6-8f9f-bc66726f18b4" colab={"base_uri": "https://localhost:8080/", "height": 1057}
activationfunc='relu'
batchsize=200
epoch=30
loss='categorical_crossentropy'
dropout=0.3
for optimizer in optimizers:
function(x_train, y_train, x_test, y_test,activationfunc, batchsize,epoch, optimizer,loss, dropout)
# + [markdown] id="3K6kZr-4Dz9p" colab_type="text"
# #Changing dropout keeping other hyperparameters constant
# + id="jOGXS0_honpT" colab_type="code" outputId="7bd83670-6599-46e5-c8dd-a050fe270b13" colab={"base_uri": "https://localhost:8080/", "height": 1057}
activationfunc='relu'
batchsize=200
epoch=30
optimizer='rmsprop'
loss='categorical_crossentropy'
for dropout in dropouts:
function(x_train, y_train, x_test, y_test,activationfunc, batchsize,epoch, optimizer,loss, dropout)
# + [markdown] id="AUi_KtYfNeHS" colab_type="text"
# #Changing learning rates keeping other hyperparameters constant
# + id="ieChEec-zPNP" colab_type="code" outputId="8bb8d327-8f90-47e1-d7a4-f0ae6eedf967" colab={"base_uri": "https://localhost:8080/", "height": 2325}
learningrates=[0.0001,0.001, 0.005, 0.015, 0.01, 0.03]
for lr in learningrates:
rmsprop=keras.optimizers.RMSprop(lr=lr)
activationfunc='relu'
batchsize=200
epoch=30
optimizer=rmsprop
loss='categorical_crossentropy'
dropout=0.3
print("\nLearning Rate= ", lr)
function(x_train, y_train, x_test, y_test,activationfunc, batchsize,epoch, optimizer,loss, dropout)
# + [markdown] id="hxVo454hEax6" colab_type="text"
# #Changing number of neurons per hidden layer keeping other hyperparameters constant
# + id="esjtFqA95LM5" colab_type="code" outputId="fb264c3d-989b-4399-a82d-f00bf98e13a9" colab={"base_uri": "https://localhost:8080/", "height": 2305}
neuronvalues=[100,200,512, 784, 1024, 2000]
activationfunc='relu'
batchsize=200
epoch=30
optimizer='rmsprop'
loss='categorical_crossentropy'
dropout=0.3
for neuron in neuronvalues:
print("\n 3 Hidden Layers , Number of neuron in every hidden Layer= ", neuron)
model = Sequential()
model.add(Dense(neuron, activation=activationfunc, input_shape=(3072,)))
model.add(Dropout(dropout))
model.add(Dense(neuron, activation=activationfunc))
model.add(Dropout(dropout))
model.add(Dense(num_classes, activation='softmax'))
model.summary()
model.compile(loss=loss,
optimizer=optimizer,
metrics=['accuracy'])
history = model.fit(x_train, y_train,
batch_size=batchsize,
epochs=epoch,
verbose=0,
validation_data=(x_test, y_test))
score = model.evaluate(x_test, y_test, verbose=0)
print('Activation Function ',activationfunc,', Batch Size ',batchsize,', Epoch ',epoch,', Optimizer ', optimizer,', Loss ',loss,', Dropout ', dropout)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
# + [markdown] id="3jFYR5S8Ei_T" colab_type="text"
# #Changing number of hidden layers keeping other hyperparameters constant
# + id="Fk6LX-UR8JLS" colab_type="code" outputId="fe3ad541-4c34-4dd6-8bce-f8d825ce56c6" colab={"base_uri": "https://localhost:8080/", "height": 2270}
activationfunc='relu'
batchsize=200
epoch=30
optimizer='rmsprop'
loss='categorical_crossentropy'
dropout=0.3
for x in range(1, 6):
print("\n Number of Hidden Layers ", x+1)
model = Sequential()
model.add(Dense(512, activation=activationfunc, input_shape=(3072,)))
model.add(Dropout(dropout))
for y in range (0,x-1):
model.add(Dense(512, activation=activationfunc))
model.add(Dropout(dropout))
model.add(Dense(num_classes, activation='softmax'))
model.summary()
model.compile(loss=loss,
optimizer=optimizer,
metrics=['accuracy'])
history = model.fit(x_train, y_train,
batch_size=batchsize,
epochs=epoch,
verbose=0,
validation_data=(x_test, y_test))
score = model.evaluate(x_test, y_test, verbose=0)
print('Activation Function ',activationfunc,', Batch Size ',batchsize,', Epoch ',epoch,', Optimizer ', optimizer,', Loss ',loss,', Dropout ', dropout)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
# + [markdown] id="sYIBFZIFma-j" colab_type="text"
# #CNN ALGORITHM
# + [markdown] id="uZ9QTMeEoT4V" colab_type="text"
# ## Effect of Change in epoch
# + [markdown] id="Q1z71NuZ9hH3" colab_type="text"
# ###Epoch =10
# + id="DHogM09Ns1gg" colab_type="code" outputId="a7a50634-9efb-4eee-eb92-b95296f02a24" colab={"base_uri": "https://localhost:8080/", "height": 502}
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
import os
batch_size = 32
num_classes = 10
epochs = 10
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="BXuNQ2Ps9wWy" colab_type="text"
# ###Epoch =20
# + id="gB5hsxBYnFuK" colab_type="code" outputId="c01c49cb-d2ff-47cb-d6ff-719764f2ff92" colab={"base_uri": "https://localhost:8080/", "height": 849}
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
import os
batch_size = 32
num_classes = 10
epochs = 20
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="XwlFcEzP96rv" colab_type="text"
# ###Epoch =50
# + id="YrrsF1plnFxS" colab_type="code" outputId="ffea48ef-0562-4907-ed47-386abb233b0b" colab={"base_uri": "https://localhost:8080/", "height": 1889}
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
import os
batch_size = 32
num_classes = 10
epochs = 50
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="6wulZbjkogmF" colab_type="text"
# ## Effect of Change in batchsize
# + [markdown] id="hLjHTDLk-Xgq" colab_type="text"
# ###Batchsize =50
# + id="UKgu23rMnF0k" colab_type="code" outputId="7ddb9ee3-62d1-4127-caa6-87a145dfaaed" colab={"base_uri": "https://localhost:8080/", "height": 849}
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
import os
batch_size = 50
num_classes = 10
epochs = 50
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="QhMjcMDG-rhD" colab_type="text"
# ###Batchsize =70
# + id="yZId2wZVnF4o" colab_type="code" outputId="9941b6cb-847a-4eb0-e988-0d73f5601f72" colab={"base_uri": "https://localhost:8080/", "height": 849}
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
import os
batch_size = 70
num_classes = 10
epochs = 50
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="NOLW06-eompx" colab_type="text"
# ## Effect of Change in Activation Function
# + [markdown] id="2C7MxSnnFAc8" colab_type="text"
# Activation relu
# + id="rpiUmpa8nF_H" colab_type="code" outputId="90957acb-5f1c-4cd9-de10-a730ca5f289a" colab={"base_uri": "https://localhost:8080/", "height": 849}
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
import os
batch_size = 100
num_classes = 10
epochs = 20
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="i-wfKGjW-7NQ" colab_type="text"
# ###Activation=tanh
# + id="mmhwlVw2nGCS" colab_type="code" outputId="2eef98a1-009d-4719-d75f-836751554893" colab={"base_uri": "https://localhost:8080/", "height": 554}
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
import os
batch_size = 500
num_classes = 10
epochs = 10
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('tanh'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('tanh'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('tanh'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('tanh'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('tanh'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="6rne-pkoots4" colab_type="text"
# ## Effect of Change in Learning Rate
# + [markdown] id="_pT_FBSo_UE0" colab_type="text"
# ###Learning rate=0.001
# + id="OYictYtAn0uQ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 502} outputId="d7d88fd9-b47a-4471-a473-abd179475e75"
batch_size = 500
num_classes = 10
epochs = 10
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="-uHTyMVT_beK" colab_type="text"
# ###Learning rate=0.005
# + id="eRaIPIw4n0rz" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 849} outputId="26c82196-3340-435b-e1ed-e548edf9fb60"
batch_size = 500
num_classes = 10
epochs = 20
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0005, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="teDxEzrAo4Lr" colab_type="text"
# ## Effect of Change in number of layers
# + id="bkDKva3F_st7" colab_type="code" colab={}
# + [markdown] id="7F5vRZkbOEdB" colab_type="text"
# ##Number of layers=
# + id="g7gbN8Dtn0mF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 398} outputId="400d0360-b71b-485b-fa9e-cd15ba5a7d53"
batch_size = 500
num_classes = 10
epochs = 10
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="pyhU4ant_4mu" colab_type="text"
# ##Number of layers=5
# + id="I1aSMJnbn0hx" colab_type="code" colab={}
batch_size = 500
num_classes = 10
epochs = 10
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="NZGI8ThK_75R" colab_type="text"
# ##Number of layers=6
# + id="MWu-b9T3n0f4" colab_type="code" colab={}
batch_size = 500
num_classes = 10
epochs = 10
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="Gw3_F1mpo-vL" colab_type="text"
# ## Effect of Change in number of neurons per layer
# + [markdown] id="_uyW_CrD_-58" colab_type="text"
# ##Number of neurons per layer=512
# + id="UDYT_2ORn0dl" colab_type="code" colab={}
batch_size = 500
num_classes = 10
epochs = 10
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="ib9pmFl6AY8n" colab_type="text"
# ##Number of neurons per layer=1000
# + id="wHixwQ1Hn0Lt" colab_type="code" colab={}
batch_size = 500
num_classes = 10
epochs = 10
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(1000))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="W9fWAr5_AwLc" colab_type="text"
# ##Dropout rate= 0.25
# + id="6zOeX92vAurI" colab_type="code" colab={}
batch_size = 500
num_classes = 10
epochs = 10
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
# + [markdown] id="ayj6FyC3A-rf" colab_type="text"
# ##Dropout rate= 0.5
# + id="EVTV-tUxAvCd" colab_type="code" colab={}
batch_size = 500
num_classes = 10
epochs = 10
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.5))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.5))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_augmentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set input mean to 0 over the dataset
samplewise_center=False, # set each sample mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_std_normalization=False, # divide each input by its std
zca_whitening=False, # apply ZCA whitening
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=0.1,
# randomly shift images vertically (fraction of total height)
height_shift_range=0.1,
shear_range=0., # set range for random shear
zoom_range=0., # set range for random zoom
channel_shift_range=0., # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
vertical_flip=False, # randomly flip images
# set rescaling factor (applied before any other transformation)
rescale=None,
# set function that will be applied on each input
preprocessing_function=None,
# image data format, either "channels_first" or "channels_last"
data_format=None,
# fraction of images reserved for validation (strictly between 0 and 1)
validation_split=0.0)
# Compute quantities required for feature-wise normalization
# (std, mean, and principal components if ZCA whitening is applied).
datagen.fit(x_train)
# Fit the model on the batches generated by datagen.flow().
model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,steps_per_epoch=x_train.shape[0]/batch_size,
validation_data=(x_test, y_test),
workers=4)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
| 84,161 |
/examples/Country Dissimilarities.ipynb | daf35ca563af1762fe0ceb728f6185e772be90aa | [] | no_license | vlad3996/The-Elements-of-Statistical-Learning-Python-Notebooks | https://github.com/vlad3996/The-Elements-of-Statistical-Learning-Python-Notebooks | 3 | 0 | null | 2019-12-03T12:36:57 | 2019-12-03T12:36:53 | null | Jupyter Notebook | false | false | .py | 59,859 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python [conda env:Python64]
# language: python
# name: conda-env-Python64-py
# ---
# # Country Dissimilarities
# This example, taken from Kaufman and Rousseeuw (1990), comes from a study in which political science students were asked to provide pairwise dissimilarity measures for 12 countries: Belgium, Brazil, Chile, Cuba, Egypt, France, India, Israel, United States, Union of Soviet Socialist Republics, Yugoslavia and Zaire.
# +
import pandas as pd
from matplotlib import transforms, pyplot as plt
from matplotlib.colors import LinearSegmentedColormap, BoundaryNorm
import numpy as np
# %matplotlib inline
# define plots common properties and color constants
plt.rcParams['font.family'] = 'Arial'
plt.rcParams['axes.linewidth'] = 0.5
GRAY1, GRAY4, GRAY7 = '#231F20', '#646369', '#929497'
# -
# ## Load and Prepare Data
# PAGE 517. TABLE 14.3. Data from a political science survey: values are
# average pairwise dissimilarities of countries from a questionnaire
# given to political science students.
df = pd.read_csv("../data/Countries.txt", sep=' ')
countries = np.array([
'BEL', 'BRA', 'CHI', 'CUB', 'EGY', 'FRA',
'IND', 'ISR', 'USA', 'USS', 'YUG', 'ZAI'])
df
# ## K-medoids Clustering
from pyclustering.cluster.kmedoids import kmedoids
from sklearn.manifold import MDS
# PAGE 517. We applied 3-medoid clustering to these dissimilarities. Note that
# K-means clustering could not be applied because we have only
# distances rather than raw observations.
matrix = df[countries].values
initial_medoids = [0, 1, 2]
kmedoids_instance = kmedoids(
matrix, initial_medoids, data_type='distance_matrix')
kmedoids_instance.process()
clusters = kmedoids_instance.get_clusters()
medoids = kmedoids_instance.get_medoids()
# PAGE 570. Multidimensional scaling seeks values z1,z2,... ,zN ∈ R^k to
# minimize the so-called stress function (14.98). This is known as
# least squares or Kruskal–Shephard scaling. The idea is to find a
# lower-dimensional representation of the data that preserves the
# pairwise distances as well as possible.
mds = MDS(
n_components=2,
dissimilarity='precomputed',
random_state=14
).fit_transform(matrix)
# +
# PAGE 518. FIGURE 14.10. Survey of country dissimilarities. (Left panel:)
# dissimilarities reordered and blocked according to 3-medoid
# clustering. Heat map is coded from most similar (dark red) to least
# similar (bright red). (Right panel:) two-dimensional
# multidimensional scaling plot, with 3-medoid clusters indicated by
# different colors.
fig, axarr = plt.subplots(1, 2, figsize=(7, 3.3), dpi=150)
ax = axarr[0]
rows = ['USA', 'ISR', 'FRA', 'EGY', 'BEL', 'ZAI',
'IND', 'BRA', 'YUG', 'USS', 'CUB']
cols = ['CHI', 'CUB', 'USS', 'YUG', 'BRA', 'IND',
'ZAI', 'BEL', 'EGY', 'FRA', 'ISR']
row_ids = [list(countries).index(c) for c in rows]
col_ids = [list(countries).index(c) for c in cols]
m = matrix[row_ids, :][:, col_ids]
pct = np.percentile(np.unique(m), [3, 5, 8, 20, 30, 40, 50, 60, 70, 80, 90])
for i in range(m.shape[0]):
for j in range(m.shape[1]-i, m.shape[1]):
m[i, j] = np.nan
cmap = LinearSegmentedColormap.from_list('cm', ['black', '#CF0000'], N=256)
norm = BoundaryNorm(pct, cmap.N)
ax.imshow(m, interpolation='none', norm=norm, cmap=cmap)
ax.axhline(4.5, color='white')
ax.axhline(7.5, color='white')
ax.axvline(3.5, color='white')
ax.axvline(6.5, color='white')
ax.tick_params(bottom=False, labelbottom=False, top=True, labeltop=True)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_visible(False)
_ = plt.setp(ax,
yticks=range(12), yticklabels=rows+[''],
xticks=range(12), xticklabels=cols+[''])
ax.set_xlim(-1, 12)
ax.set_ylim(12, -1)
ax.spines['top'].set_bounds(0, 11)
ax.spines['left'].set_bounds(0, 11)
for i in ax.get_yticklabels() + ax.get_xticklabels():
i.set_fontsize(6)
ax.set_xlabel('Reordered Dissimilarity Matrix', color=GRAY4, fontsize=8)
ax.set_aspect('equal', 'datalim')
ax = axarr[1]
mds_rev = -mds
for i, txt in enumerate(countries):
cluster = [t for t in range(3) if i in clusters[t]][0]
plt.annotate(txt, (mds_rev[i, 0], mds_rev[i, 1]), ha='center',
color=['b', 'g', 'r'][cluster])
ax.set_xlabel('First MDS Coordinate', color=GRAY4, fontsize=8)
ax.set_ylabel('Second MDS Coordinate', color=GRAY4, fontsize=8)
ax.set_xlim(-4.5, 4.5)
ax.set_ylim(-4.5, 4.5)
ax.set_aspect('equal', 'datalim')
| 4,743 |
/Lab1/Lab1_2.ipynb | e27a22ba291f55b5c41cef27906d4749eb957394 | [] | no_license | Aakashko/Machine-Learning | https://github.com/Aakashko/Machine-Learning | 1 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 111,900 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="oPhtHHRCff41" colab_type="code" colab={}
import numpy
import pandas
# + id="9IaS9BglgEpw" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="8055b27e-e9c6-421d-a4f5-0a24920849f0"
from pandas import read_csv
path='/content/cancer_dataset.csv'
data=read_csv(path)
colnames=['id','diagnosis','radius_mean','texture_mean','perimeter_mean','area_mean','smoothness_mean','compactness_mean','concavity_mean','concave points_mean','symmetry_mean','fractal_dimension_mean','radius_se','texture_se','perimeter_se','area_se','smoothness_se','compactness_se','concavity_se','concave points_se','symmetry_se','fractal_dimension_se','radius_worst','texture_worst','perimeter_worst','area_worst','smoothness_worst','compactness_worst','concavity_worst','concave points_worst','symmetry_worst','fractal_dimension_worst']
print (data.shape)
# + id="gV4_WObrgIVt" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 212} outputId="19ea2e67-79bf-4558-d16e-a752d2e7ede4"
description = data.describe()
print(description)
# + id="H5oyEcDDgLgu" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="142b2ae7-f8a5-4dc5-de83-f46025567336"
print(data.shape)
# + id="fTYqGl9OgNbE" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 141} outputId="652f55d3-e7aa-4023-d92a-0a50a65eabb7"
print(data.head(4))
# + id="6JJ_dvZ4gPD-" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 87} outputId="edb04990-4042-401c-90f6-004a64439f7b"
print(data.groupby("diagnosis").size())
# + id="ay31OE6VgRPQ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 290} outputId="a327f846-8aeb-40d4-c654-df57a5ce2eb8"
import matplotlib.pyplot as plt
import pandas
from pandas.plotting import scatter_matrix
scatter_matrix(data[['perimeter_mean','area_mean']])
plt.show()
# + id="lXh3tua4gUFL" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 533} outputId="bf40f34a-1cb9-4ca9-fcf0-ae6250ae5ec9"
import matplotlib.pyplot as plt
import pandas
from pandas.plotting import scatter_matrix
try:
scatter_matrix(data) #scatter plot
except ValueError: #raised if `y` is empty.
pass
plt.show()
data.hist() #histogram
plt.show()
# + id="j7XhJ5eGgU-F" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 87} outputId="bb18c4f9-5023-461b-9522-859a74fd69d2"
from sklearn.preprocessing import StandardScaler
import pandas
import numpy
arr=data.values #convert data frame to array
X=arr[:,numpy.r_[0,2:8]] #split columns
Y=arr[:,8]
scaler=StandardScaler().fit(X) #fit data for standardization
rescaledX=scaler.transform(X) #convert the data as per (x-µ)/σ
numpy.set_printoptions(precision=3)
print(rescaledX[0:2,:])
print(X[0:2,:])
# + id="zEsUYTN3gYUY" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 194} outputId="521824ae-1e8e-4090-dc7c-5a69a21c8c56"
myarray=numpy.array([1,3,-10,4,5,7,-4,-2,10])
mydataframe = pandas.DataFrame(myarray)
print(mydataframe)
# + id="aM6iKkTNgbfH" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 262} outputId="c7564acb-d413-45b6-9b8c-a9c3402f0894"
mydataframe.plot(kind='bar')
plt.show()
# + id="QlRdfZErgeYJ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 440} outputId="391c4198-540d-43bd-e2d2-26122280d6f0"
from sklearn import preprocessing
fl_x=mydataframe.values.astype(float)
#fl_x=mydataframe[['f1']].values.astype(float) #If specific feature name is to be converted
min_max_scaler=preprocessing.MinMaxScaler()
X_scaled=min_max_scaler.fit_transform(fl_x)
df_normalized=pandas.DataFrame(X_scaled)
print(df_normalized)
df_normalized.plot(kind='bar')
plt.show()
# + id="fI8dqQKlllDJ" colab_type="code" colab={}
ionrSq',
'DOWNTOWN COMMERCIAL': 'Blltwn/Dwntwn/PionrSq',
'PIONEER SQUARE': 'Blltwn/Dwntwn/PionrSq',
}
odf = df.copy()
odf['Neighborhood'] = odf['Neighborhood'].apply(lambda neighborhood: neighborhood_map.get(neighborhood, neighborhood))
odf = odf[odf.Category != 'GAMBLE']
odf.head()
# Note: There are too many neighborhoods, so I picked the ones that Abbie highlighted in her talk, and included the downtown area just out of my own curiosity.
neighborhoods = ['Fmt/Wfd/GW', 'QUEEN ANNE', 'BH/GT', 'Ballard', 'MAGNOLIA', 'CapitolH/Eastlk', 'Blltwn/Dwntwn/PionrSq']
odf = odf[odf.Neighborhood.isin(neighborhoods)]
odf.head(10)
fig = plt.figure(figsize=(20, 160))
for i, crime_type in enumerate(odf.Category.unique()):
crime_type_data = odf[odf.Category == crime_type]
crime_type_data = crime_type_data.groupby(['Neighborhood', 'Occurred'])['Incidents'].sum().reset_index()
fig.add_subplot(30, 2, i + 1)
sns.lineplot(x="Occurred", y="Incidents", hue="Neighborhood", data=crime_type_data)
ax = plt.gca()
ax.set_title(crime_type)
# Note: Not surprisingly, the downtown/Belltown/Pinoneer Square area has had more incidents than other neighborhoods in general.
# # Combining all years, are there crime types that are more common within each neighborhood?
fig = plt.figure(figsize=(15, 22))
for i, neighborhood in enumerate(odf.Neighborhood.unique()):
neighborhood_data = odf[odf.Neighborhood == neighborhood]
neighborhood_data = neighborhood_data.groupby(['Neighborhood', 'Category'])['Incidents'].sum().reset_index()
fig.add_subplot(4, 2, i + 1)
chart = sns.barplot(data= neighborhood_data, x= 'Category', y= 'Incidents')
chart.set_xticklabels(chart.get_xticklabels(), rotation=45, horizontalalignment='right')
ax = plt.gca()
ax.set_title(neighborhood)
plt.tight_layout()
# Note: In all neighborhoods, theft is the most common type of crime.
# # Combining all years, were there more incidents in some neighborhoods than others (by crime type)?
# +
fig = plt.figure(figsize=(15, 40))
for i, crime_type in enumerate(odf.Category.unique()):
crime_type_data = odf[odf.Category == crime_type]
crime_type_data = crime_type_data.groupby(['Neighborhood', 'Category'])['Incidents'].sum().reset_index()
fig.add_subplot(7, 2, i + 1)
chart = sns.barplot(data=crime_type_data, x='Neighborhood', y='Incidents')
chart.set_xticklabels(chart.get_xticklabels(), rotation=45, horizontalalignment='right')
ax = plt.gca()
ax.set_title(crime_type)
plt.tight_layout()
# -
# Note: Again, the downtown area has had more incidents than other neighborhoods, followed by the Fremont/Wallingoford/Greenwood area and Capitol Hill/East Lake area.
ff = pd.read_pickle('../../../WIDS_FIFI_groupproject/generated_datasets/data_final.pkl')
ff.head()
abbie_neighborhoods = list(ff['neighborhood'].unique())
sorted(abbie_neighborhoods, key = str.lower)
#sorted(subcategories, key = str.lower)
ff_neighborhood = ['Ballard/SunsetH',
'BeaconH/MtBaker/Leschi',
'BH/GT/SP',
'Belltown',
'CapitolH/Eastlk',
'CD/CH/Madrona',
'CH/MadisonPkVy',
'ColCity/SewardP/RainierV',
'Dt/FirstH',
'Fmt/Wfd/GL/GW',
'HarborIs/IndustD',
'HighPt/Delridge',
'Magnolia',
'NAdmiral/Alki',
'NBd/LH/CH/WH/NB',
'Northgate/LkCity',
'PioneerS/FirstH/ID',
'QA/InterBay',
'Ravenna/ML/GL',
'Riverview/Delridge',
'Shoreline/Bitterlake',
'SLU/QA/WL',
'Udist/LarHur',
'UW_main']
ff = ff[ff.neighborhood.isin(ff_neighborhood)]
ff = ff.rename(columns = {
'Service_Request_Number': 'RequestNum',
})
ff = ff[['Created_Date', 'date', 'year', 'month', 'day', 'neighborhood', 'FIFI_category', 'RequestNum']]
ff.head()
ff = ff[ff.neighborhood != 'WA']
ff.shape
ffdf = ff.groupby([pd.Grouper(key='Created_Date', freq='MS'), 'neighborhood', 'FIFI_category']).size().to_frame('Incidents').reset_index()
ffdf.head()
# # Re-sorting neighborhoods in the crime dataset
c_neighborhood_map = {
'BALLARD NORTH': 'Ballard/SunsetH',
'BALLARD SOUTH': 'Ballard/SunsetH',
'MID BEACON HILL': 'BeaconH/MtBaker/Leschi',
'NORTH BEACON HILL': 'BeaconH/MtBaker/Leschi',
'MOUNT BAKER': 'BeaconH/MtBaker/Leschi',
'JUDKINS PARK/NORTH BEACON HILL': 'BeaconH/MtBaker/Leschi',
'SOUTH BEACON HILL': 'BeaconH/MtBaker/Leschi',
'GEORGETOWN': 'BH/GT/SP',
'BELLTOWN': 'Belltown',
'CAPITOL HILL': 'CapitolH/Eastlk',
'EASTLAKE - EAST': 'CapitolH/Eastlk',
'EASTLAKE - WEST': 'CapitolH/Eastlk',
'MADRONA/LESCHI':'CD/CH/Madrona',
'CHINATOWN/INTERNATIONAL DISTRICT': 'ID/SODO',
'SODO': 'ID/SODO',
'MADISON PARK': 'CH/MadisonPkVy',
'COLUMBIA CITY': 'ColCity/SewardP/RainierV',
'RAINIER VIEW': 'ColCity/SewardP/RainierV',
'DOWNTOWN COMMERCIAL': 'Dt/FirstH',
'FIRST HILL': 'Dt/FirstH',
'FREMONT': 'Fmt/Wfd/GL/GW',
'WALLINGFORD': 'Fmt/Wfd/GL/GW',
'GREENWOOD': 'Fmt/Wfd/GL/GW',
'COMMERCIAL HARBOR ISLAND': 'HarborIs/IndustD',
'HIGH POINT': 'HighPt/Delridge',
'MAGNOLIA': 'Magnolia',
'ALKI': 'NAdmiral/Alki',
'NORTHGATE': 'Northgate/LkCity',
'LAKECITY': 'Northgate/LkCity',
'PIONEER SQUARE': 'PioneerS/FirstH/ID',
'QUEEN ANNE': 'QA/InterBay',
'MONTLAKE/PORTAGE BAY': 'Ravenna/ML/GL',
'ROOSEVELT/RAVENNA': 'Ravenna/ML/GL',
'NORTH DELRIDGE': 'Riverview/Delridge',
'SOUTH DELRIDGE': 'Riverview/Delridge',
'BITTERLAKE': 'Shoreline/Bitterlake',
'SLU/CASCADE': 'SLU/QA/WL',
'UNIVERSITY': 'Udist/LarHur'
}
mdf = df.copy()
mdf.head()
mdf['Neighborhood'] = mdf['Neighborhood'].apply(lambda neighborhood: c_neighborhood_map.get(neighborhood, neighborhood))
mdf.head()
# # Merging Fifi and crime datasets
# +
ff_crime = pd.merge(
ffdf,
mdf,
left_on='Neighborhood',
)
# -
mdf.head()
pmdf = mdf.pivot_table(
values=['Incidents'],
index=['Occurred', 'Neighborhood'],
# columns=['Category'],
aggfunc='sum')
pmdf.head()
pffdf = ffdf.pivot_table(
values=['Incidents'],
index=['Created_Date', 'neighborhood'],
aggfunc='sum')
pffdf.index.set_names(['Occurred', 'Neighborhood'], inplace=True)
pffdf.head()
jdf = pd.merge(pmdf, pffdf, left_index=True, right_index=True)
jdf = jdf.rename({'Incidents_x': 'Crime_Incidents', 'Incidents_y': 'Fifi_Requests'}, axis=1)
jdf = jdf.reset_index()
jdf.head(10)
# # The total number of Fifi requests and crime reports (2013-2019) per neighborhood
sdf = jdf.groupby(['Neighborhood']).sum()
sdf.plot.bar()
# # The trend in Fifi requests and crime reports (all neighborhoods combined) from 2013 - 2019
sdf = jdf.groupby(['Occurred']).sum()
sdf.plot()
# # The trend in Fifi requests and crime reports (all neighborhoods combined) from 2013 - 2019
jdf.head()
neighborhoods = jdf['Neighborhood'].unique()
fig, axes = plt.subplots(nrows=-(-len(neighborhoods) // 2), ncols=2, figsize=(20, 80))
for i, neighborhood in enumerate(neighborhoods):
gdf = jdf[jdf['Neighborhood'] == neighborhood]
gdf = gdf.groupby(['Occurred']).sum()
gdf.plot(ax=axes[i // 2, i % 2])
axes[i // 2, i % 2].set_title(neighborhood)
| 10,939 |
/16S/Notebooks/.ipynb_checkpoints/Relative_Abundances-checkpoint.ipynb | ec40acbcff52e94e54e7b14e849bb42ed9f0159f | [] | no_license | zazalews/WoodBuffalo | https://github.com/zazalews/WoodBuffalo | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .r | 3,597,379 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# ## This notebook is to compare the relative abundances of various phyla across samples and treatments
# Loading R packages
library(reshape)
library(ggplot2)
library(phyloseq)
library(plyr)
library(dplyr)
library(plotly)
library(wesanderson)
# ### Importing and prepping the data
# Importing the dataset
ps = import_biom("../OTU_table/feature-table-metaD-tax.biom",parseFunction=parse_taxonomy_greengenes,"../OTU_table/Trees/fulltree.tre")
# Setting various parameters as combined values
sample_data(ps)$pH = as.numeric(sample_data(ps)$pH)
sample_data(ps)$Total_C_pct = as.numeric(sample_data(ps)$TC_pct)
sample_data(ps)$Total_N_pct = as.numeric(sample_data(ps)$Total_N_pct)
sample_data(ps)$Total_S_pct = as.numeric(sample_data(ps)$Total_S_pct)
sample_data(ps)$Burn_Severity_Index= as.numeric(sample_data(ps)$Burn_Severity_Index)
sample_data(ps)$CBI= as.numeric(sample_data(ps)$CBI)
sample_data(ps)$RBR= as.numeric(sample_data(ps)$RBR)
sample_data(ps)$CFSI= as.numeric(sample_data(ps)$CFSI)
sample_data(ps)$Mean_Duff_Depth_cm = as.numeric(sample_data(ps)$Mean_Duff_Depth_cm)
sample_data(ps)$Understory_CBI= as.numeric(sample_data(ps)$Understory_CBI)
sample_data(ps)$Overstory_CBI= as.numeric(sample_data(ps)$Overstory_CBI)
sample_data(ps)$Overstory_CBI= as.numeric(sample_data(ps)$Overstory_CBI)
sample_data(ps)$Dead_Trees= as.numeric(sample_data(ps)$Dead_Trees)
sample_data(ps)$Pct_Exposed_Mineral= as.numeric(sample_data(ps)$Pct_Exposed_Mineral)
sample_data(ps)$dc = as.numeric(sample_data(ps)$dc)
sample_data(ps)$fwi = as.numeric(sample_data(ps)$fwi)
sample_data(ps)$dmc = as.numeric(sample_data(ps)$dmc)
sample_data(ps)$ffmc = as.numeric(sample_data(ps)$ffmc)
sample_data(ps)$TotalSeqs=sample_sums(ps)
# Pulling out samples from this project only
ps.wb = prune_samples(sample_data(ps)$Project_ID=="WB15", ps)
# +
# Merging lab replicates for analysis
ps.merged = merge_samples(ps.wb, "Sample_ID")
# This sums the OTUs for each sample ID, and averages the sample data
# That's an issue for the non-numeric sample data, so we have to add it back in.
# The code below is probably inefficient, but it works correctly.
names=colnames(sample_data(ps.wb))
notcommonnames = c('Sample_Name','Replicate','Project_ID','Fwd_Primer_Barcode','Rev_Primer_Barcode','Revcomp_Rev_Primer_Barcode')
commonnames = names[(names %in% notcommonnames)]
common_sample_data = sample_data(ps.wb)[ , -which(names(sample_data(ps.wb)) %in% commonnames)]
commonrownames=row.names(sample_data(ps.merged))
common_sample_data2 = common_sample_data[which(common_sample_data$Sample_ID %in% commonrownames),]
common_sample_data2 = common_sample_data2[!duplicated(common_sample_data2$Sample_ID), ]
row.names(common_sample_data2) = common_sample_data2$Sample_ID
sample_data(ps.merged)=common_sample_data2
# -
ps.merged.norm = transform_sample_counts(ps.merged, function(x) x / sum(x) )
ps.merged.norm
# ## Making the classic stacked bar plot
options(repr.plot.width=15, repr.plot.height=10)
plot_bar(ps.merged.norm, fill="Phylum") + geom_bar(aes(color=Phylum, fill=Phylum), stat="identity", position="stack")
options(repr.plot.width=15, repr.plot.height=15)
plot_bar(ps.merged.norm, fill="Phylum") + geom_bar(aes(color=Phylum, fill=Phylum), stat="identity", position="stack") + facet_wrap(~Org_or_Min,scales="free",ncol=1)
d = psmelt(ps.merged.norm)
# +
df = d %>%
group_by(Sample,Phylum)%>%
mutate(Relabund=sum(Abundance))
cutoff=0.01
CommonPhyla = df %>%
group_by(Phylum)%>%
summarize(MeanRelabund=mean(Relabund), MaxRelabund = max(Relabund))%>%
filter(MeanRelabund>cutoff | MaxRelabund>cutoff)
print(c(paste(dim(CommonPhyla)[1],"most abundant phyla")))
CommonPhyla = as.matrix(CommonPhyla)[,1]
df = df %>%
filter(Phylum %in% CommonPhyla)%>%
filter(Org_or_Min != "B")
# -
options(repr.plot.width=10, repr.plot.height=10)
p = ggplot(df,aes(x=Org_or_Min, y=Relabund, color=Burned_Unburned))
p = p + geom_boxplot() + facet_wrap(~Phylum, scales="free")
p = p + scale_color_manual(values=wes_palette("Darjeeling"))
p
# +
df = d %>%
group_by(Sample,Order)%>%
mutate(Relabund=sum(Abundance))
cutoff=0.001
CommonTax = df %>%
group_by(Order)%>%
summarize(MeanRelabund=mean(Relabund), MaxRelabund = max(Relabund))%>%
filter(MeanRelabund>cutoff | MaxRelabund>cutoff)
print(c(paste(dim(CommonTax)[1],"most abundant taxa")))
CommonTax = as.matrix(CommonTax)[,1]
df = df %>%
group_by(Sample)%>%
filter(Order %in% CommonTax)
# -
p = ggplot(df)
p = p + geom_point(aes(x=CBI, y=Relabund, color=Order)) + facet_wrap(~Phylum, scales="free")
p = p + guides(color=FALSE)
p
# ## Zooming in on individual phyla
# Actinobacteria class may increase with burn severity; AlphaProteo down; Betaproteo up?
# +
minseqs = 750
df = d %>%
filter(Phylum=="Proteobacteria")%>%
filter(TotalSeqs>minseqs)%>%
group_by(Sample,Class)%>%
mutate(Relabund=sum(Abundance))%>%
filter(Org_or_Min != "B")
p = ggplot(df, aes(x=CBI, y=Relabund, color=Veg_Comm, shape=Org_or_Min)) + geom_point() + facet_wrap(~Class, scales="free")
#p = p + guides(color=FALSE)
p
# -
# ## Zooming in on classes
# Rhizobiales may decrease with increasing burn severity; Actinomycetes up with burn severity
# +
minseqs = 50
df = d %>%
filter(Class=="Actinobacteria")%>%
filter(TotalSeqs>minseqs)%>%
group_by(Sample,Order)%>%
mutate(Relabund=sum(Abundance))%>%
filter(Org_or_Min != "B")
p = ggplot(df, aes(x=CBI, y=Relabund, color=Veg_Comm, shape=Org_or_Min)) + geom_point() + facet_wrap(~Order, scales="free")
#p = p + guides(color=FALSE)
p
# +
options(repr.plot.width=15, repr.plot.height=15)
minseqs = 50
df = d %>%
filter(Order=="Actinomycetales")%>%
filter(TotalSeqs>minseqs)%>%
group_by(Sample,Family)%>%
mutate(Relabund=sum(Abundance))%>%
filter(Org_or_Min != "B")
p = ggplot(df, aes(x=CBI, y=Relabund, color=Veg_Comm, shape=Org_or_Min)) + geom_point() + facet_wrap(~Family, scales="free")
#p = p + guides(color=FALSE)
p
# +
options(repr.plot.width=7, repr.plot.height=5)
df = d %>%
filter(Genus=="Bacillus")%>%
group_by(Sample,OTU)%>%
mutate(Relabund=sum(Abundance))%>%
filter(Org_or_Min != "B")%>%
arrange(-Relabund)
p = ggplot(df, aes(x=CBI, y=Relabund, color=Veg_Comm, shape=Org_or_Min)) + geom_point() + facet_wrap(~Species, scales="free")
#p = p + guides(color=FALSE)
p
# -
head(df)
df = d %>%
group_by(Sample,OTU)%>%
mutate(Relabund=sum(Abundance))%>%
arrange(-Relabund)%>%
group_by(Sample)%>%
select(Sample,Abundance,TotalSeqs,Kingdom,Phylum,Class,Order,Family,Genus,Species)
df
| 6,840 |
/functions_Finkel.ipynb | be690fa84d48ae31bd2153ef66b98706a9b5ad34 | [] | no_license | SvetlanaF1147/python_HW5 | https://github.com/SvetlanaF1147/python_HW5 | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 14,222 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 21. Escribir un programa que determine si el año es bisiesto. Un año es bisiesto si es
# múltiplo de 4 (1988), excepto los múltiplos de 100 que no son bisiestos salvo que a su
# vez también sean múltiplos de 400 (1800no es bisiesto, 2000 sí).
anio = int(input("Año: "))
if anio % 4 == 0:
if anio % 100 ==0:
if anio % 400 == 0:
print(f"{anio} es bisiesto")
else:
print(f"{anio} no es bisiesto")
else:
print(f"{anio} es bisiesto")
else:
print(f"{anio} no es bisiesto")
# 22. Dado los valores de A, B, C que son los coeficientes de la ecuación de segundo grado,
# hallar sus raíces reales, desplegar los resultados.
import math
print("ECUACIÓN A X² + B X + C = 0")
a = float(input("Escriba el valor del coeficiente a: "))
b = float(input("Escriba el valor del coeficiente b: "))
c = float(input("Escriba el valor del coeficiente c: "))
d = b**2 - 4*a*c
if d==0:
sol = (-b)/(2*a)
print(f"La ecuacion tiene una solucion: {sol:.2f}")
elif d>0:
sol1= ((-b)+ math.sqrt(d))/(2*a)
sol2= ((-b)- math.sqrt(d))/(2*a)
print(f"La ecuacion tiene dos soluciones: {sol1:.2f} y {sol2:.2f}")
else:
com1 = complex(-b, math.sqrt(-d))
com2 = complex(-b, -math.sqrt(-d))
sol1 = (com1)/((2*a) +0j)
sol2= (com2)/((2*a) +0j)
print(f"La ecuacion tiene dos soluciones: {sol1:.2f} y {sol2:.2f}")
# 23. Dado dos valores A y B, realizar el producto de los dos números por sumas sucesivas,
# almacenar el resultado en una variable P, mostrar el resultado.
A = int(input("A: "))
B = int(input("B: "))
P = 0
if B < 0:
while B < 0:
P -= A
B += 1
else:
while B > 0:
P += A
B -= 1
print(f"El producto es igual a {P}")
# 24. Dado un número X, determinar el número de dígitos del que esta compuesto y
# desplegar el resultado.
# +
X = input("X: ")
X = X.split(".")
x1 = int(X[0])
cont = 0
if len(X) > 1:
x2 = int(X[1])
while x2 > 0:
x2 //= 10
cont += 1
while x1 > 0:
x1 //= 10
cont += 1
print(f"Digitos: {cont}")
# -
# 25. Escribir un programa que calcule y visualice el más grande, el más pequeño y la media
# de N números. El valor de N se solicitará al principio del programa y los números
# serán introducidos por el usuario.
N = int(input("N: "))
if N <= 0:
print("Imposible")
else:
numeros = []
suma = 0
while N > 0:
numero = int(input("Numero: "))
suma += numero
numeros.append(numero)
N -= 1
mayor = max(numeros)
menor = min(numeros)
media = suma / len(numeros)
print(f"Mayor: {mayor} Menor: {menor} Media: {media}")
# 26. Dado dos números A y B enteros mayores a cero, hallar A^B por sumas. Desplegar los
# números y el resultado.
A = int(input("A: "))
B = int(input("B: "))
if A <= 0 or B <= 0:
print("Imposible")
else:
cont = 0
pot = 0
aux = A
while cont < B:
pot += aux
cont += 1
print(f"{A}^{B} = {pot}")
# 27. La constante pi (3.1441592...) es muy utilizada en matemáticas. Un método sencillo
# de calcular su valor es:
# pi = 2 * (2/1)* (2/3) * (4/3) * (4/5) * (6/5) * (6/7) * (8/7) * (8/9) ...
#
# Escribir un programa que efectúe este cálculo con un número de términos
# especificando por el usuario.
# +
n = int(input("Numero de terminos: "))
if n <= 0:
print("Imposible")
else:
par = 2
impar = 1
pi = 1
usa2 = False
for i in range(0,n):
if i == 0:
pi = 2
else:
if usa2:
impar += 2
pi *= (par/impar)
par += 2
usa2 = False
else:
pi *= (par/impar)
usa2 = True
print(pi)
# -
# 28. El valor de e^x se puede aproximar por la suma
#
# 1+x+(x^2/2!) + (x^3/3!) + (x^4/4!) + (x^5/5!) + (x^n/n!)
#
# Escribir un programa que tome un valor de x como entrada y visualice la suma para
# cada uno de los valores de 1 a 100.
x = int(input("X: "))
def factorial(n):
fact = 1
for i in range(1, n+1):
fact *= i
return fact
e = 1
for i in range(1,101):
e += (x**i/factorial(i))
print(f"{e}")
# 29. Calcular la suma de todos los elementos de un vector, así como la media aritmética.
N = int(input("Tamano del vector: "))
if N <= 0:
print("Imposible")
else:
numeros = []
while N > 0:
numero = int(input("Elemento: "))
numeros.append(numero)
N -= 1
media = sum(numeros) / len(numeros)
print(f"Suma: {sum(numeros)} Media: {media}")
# 30. Multiplicar dos matrices.
import numpy
f1 = int(input("Numero de filas de la primera matriz: "))
c1 = int(input("Numero de columnas de la primera matriz: "))
m1 = numpy.zeros(shape=(f1,c1))
for i in range(0,f1):
for y in range(0,c1):
valor = int(input(f"Valor posicion ({i+1},{y+1}): "))
m1[i,y] = valor
f2 = int(input("Numero de filas de la segunda matriz: "))
c2 = int(input("Numero de columnas de la segunda matriz: "))
if c1 != f2:
print("No se pueden multiplicar estas matrices")
else:
m2 = numpy.zeros(shape=(f2,c2))
for i in range(0,f2):
for y in range(0,c2):
valor = int(input(f"Valor posicion ({i+1},{y+1}): "))
m2[i,y] = valor
mat = numpy.zeros(shape=(f1,c2))
for i in range(0,f1):
for y in range(0,c2):
for w in range(0,f2):
mat[i][y] += m1[i][w] * m2[w][y]
print(mat)
if input_shelf_num not in directories:
directories.setdefault(input_shelf_num, [])
else:
print('Такой номер полки уже существует')
return directories
add_shelf()
# +
# задание 5: d – delete – команда, которая спросит номер документа и удалит его из каталога и из перечня полок.
#Предусмотрите сценарий, когда пользователь вводит несуществующий документ;
def delite_doc():
input_doc_number = input('Введите номер документа ')
for string in documents:
#print(string)
list_number = (string['number'])
#print(list_number)
if input_doc_number == (string['number']):
string['number'] = None
for values in directories.values():
#print(values)
if input_doc_number in values:
values.remove(input_doc_number)
return documents, directories
else:
print('Такого номера документа не существует')
# -
delite_doc()
# +
# задание 6: m – move – команда, которая спросит номер документа и целевую полку и переместит его с текущей полки на целевую.
# Корректно обработайте кейсы, когда пользователь пытается переместить
#несуществующий документ или переместить документ на несуществующую полку;
def move_number():
input_doc_numb = input('Введите номер документа ')
input_wish_shelf = input('Введите номер целевой полки ')
if input_wish_shelf not in directories:
print('нет полки')
return
for key, value in directories.items():
if input_doc_numb in value:
value.remove(input_doc_numb)
directories[input_wish_shelf].append(input_doc_numb)
return directories
else:
print('нет номера')
# -
move_number()
# +
# задание 7: a – add – команда, которая добавит новый документ в каталог и в перечень полок,
# спросив его номер, тип, имя владельца и номер полки, на котором он будет храниться.
#Корректно обработайте ситуацию, когда пользователь будет пытаться добавить документ на несуществующую полку.
def add_doc():
new_people = {}
input_new_doc_number = input('Введите номер нового документа ')
input_new_doc_type = input('Введите тип нового документа ')
input_new_doc_name = input('Введите имя владельца нового документа ')
input_new_doc_shelf = input('Введите номер полки, на которой будет храниться новый документ ')
if input_new_doc_shelf in directories:
new_people['type'] = input_new_doc_type
new_people['number'] = input_new_doc_number
new_people['name'] = input_new_doc_name
documents.append(new_people)
directories[input_new_doc_shelf].append(input_new_doc_number)
else:
print('Такой полки не существует!')
return documents, directories
# -
add_doc()
#Итоговая программа:
def menu ():
while True:
user_input = input('Введите команду: ')
if user_input == 'p':
print_name()
elif user_input == 's':
print_shelf_number()
elif user_input == 'l':
print_list()
elif user_input == 'as':
add_shelf()
elif user_input == 'd':
delite_doc()
elif user_input == 'm':
move_number()
elif user_input == 'a':
add_doc()
else:
print('Такой команды не существует')
break
menu ()
| 9,151 |
/houghlines.ipynb | 6701ad32642359356ebb7bd9eba9c3910a69f8ee | [] | no_license | cheapthrillandwine/exercise_source | https://github.com/cheapthrillandwine/exercise_source | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 16,696 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import cv2
import numpy as np
IMAGE_PATH = "images/gauge-1.jpg"
def avg_circles(circles, b):
avg_x=0
avg_y=0
avg_r=0
for i in range(b):
#optional - average for multiple circles (can happen when a gauge is at a slight angle)
avg_x = avg_x + circles[0][i][0]
avg_y = avg_y + circles[0][i][1]
avg_r = avg_r + circles[0][i][2]
avg_x = int(avg_x/(b))
avg_y = int(avg_y/(b))
avg_r = int(avg_r/(b))
return avg_x, avg_y, avg_r
def dist_2_pts(x1, y1, x2, y2):
#print np.sqrt((x2-x1)^2+(y2-y1)^2)
return np.sqrt((x2 - x1)**2 + (y2 - y1)**2)
def calibrate_gauge(gauge_number, file_type):
# img = cv2.imread('image/gauge-%s.%s' %(gauge_number, file_type))
img = cv2.imread('image/gauge-%s.%s' %(gauge_number, file_type))
height, width = img.shape[:2]
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) #convert to gray
cv2.imwrite('gauge-%s-bw.%s' %(gauge_number, file_type),gray)
circles = cv2.HoughCircles(gray, cv2.HOUGH_GRADIENT, 1, 20, np.array([]), 100, 50, int(height*0.35), int(height*0.48))
# average found circles, found it to be more accurate than trying to tune HoughCircles parameters to get just the right one
a, b, c = circles.shape
x,y,r = avg_circles(circles, b)
#draw center and circle
cv2.circle(img, (x, y), r, (0, 0, 255), 3, cv2.LINE_AA) # draw circle
cv2.circle(img, (x, y), 2, (0, 255, 0), 3, cv2.LINE_AA) # draw center of circle
#for testing, output circles on image
cv2.imwrite('gauge-%s-circles.%s' % (gauge_number, file_type), img)
#for calibration, plot lines from center going out at every 10 degrees and add marker
separation = 10.0 #in degrees
interval = int(360 / separation)
p1 = np.zeros((interval,2)) #set empty arrays
p2 = np.zeros((interval,2))
p_text = np.zeros((interval,2))
for i in range(0,interval):
for j in range(0,2):
if (j%2==0):
p1[i][j] = x + 0.9 * r * np.cos(separation * i * 3.14 / 180) #point for lines
else:
p1[i][j] = y + 0.9 * r * np.sin(separation * i * 3.14 / 180)
text_offset_x = 10
text_offset_y = 5
for i in range(0, interval):
for j in range(0, 2):
if (j % 2 == 0):
p2[i][j] = x + r * np.cos(separation * i * 3.14 / 180)
p_text[i][j] = x - text_offset_x + 1.2 * r * np.cos((separation) * (i+9) * 3.14 / 180) #point for text labels, i+9 rotates the labels by 90 degrees
else:
p2[i][j] = y + r * np.sin(separation * i * 3.14 / 180)
p_text[i][j] = y + text_offset_y + 1.2* r * np.sin((separation) * (i+9) * 3.14 / 180) # point for text labels, i+9 rotates the labels by 90 degrees
#add the lines and labels to the image
for i in range(0,interval):
cv2.line(img, (int(p1[i][0]), int(p1[i][1])), (int(p2[i][0]), int(p2[i][1])),(0, 255, 0), 2)
cv2.putText(img, '%s' %(int(i*separation)), (int(p_text[i][0]), int(p_text[i][1])), cv2.FONT_HERSHEY_SIMPLEX, 0.3,(0,0,0),1,cv2.LINE_AA)
cv2.imwrite('gauge-%s-calibration.%s' % (gauge_number, file_type), img)
#get user input on min, max, values, and units
print('gauge number: %s' %gauge_number)
# min_angle = input('Min angle (lowest possible angle of dial) - in degrees: ') #the lowest possible angle
# max_angle = input('Max angle (highest possible angle) - in degrees: ') #highest possible angle
# min_value = input('Min value: ') #usually zero
# max_value = input('Max value: ') #maximum reading of the gauge
# units = input('Enter units: ')
#for testing purposes: hardcode and comment out raw_inputs above
min_angle = 45
max_angle = 320
min_value = 0
max_value = 200
units = "PSI"
return min_angle, max_angle, min_value, max_value, units, x, y, r
def get_current_value(img, min_angle, max_angle, min_value, max_value, x, y, r, gauge_number, file_type):
#for testing purposes
img = cv2.imread('image/gauge-%s.%s' % (gauge_number, file_type))
gray2 = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Set threshold and maxValue
thresh = 175
maxValue = 255
th, dst2 = cv2.threshold(gray2, thresh, maxValue, cv2.THRESH_BINARY_INV);
# found Hough Lines generally performs better without Canny / blurring, though there were a couple exceptions where it would only work with Canny / blurring
#dst2 = cv2.medianBlur(dst2, 5)
#dst2 = cv2.Canny(dst2, 50, 150)
#dst2 = cv2.GaussianBlur(dst2, (5, 5), 0)
# for testing, show image after thresholding
cv2.imwrite('gauge-%s-tempdst2.%s' % (gauge_number, file_type), dst2)
# find lines
minLineLength = 10
maxLineGap = 0
lines = cv2.HoughLinesP(image=dst2, rho=3, theta=np.pi / 180, threshold=100,minLineLength=minLineLength, maxLineGap=0) # rho is set to 3 to detect more lines, easier to get more then filter them out later
#for testing purposes, show all found lines
# for i in range(0, len(lines)):
# for x1, y1, x2, y2 in lines[i]:
# cv2.line(img, (x1, y1), (x2, y2), (0, 255, 0), 2)
# cv2.imwrite('gauge-%s-lines-test.%s' %(gauge_number, file_type), img)
# remove all lines outside a given radius
final_line_list = []
#print "radius: %s" %r
diff1LowerBound = 0.15 #diff1LowerBound and diff1UpperBound determine how close the line should be from the center
diff1UpperBound = 0.25
diff2LowerBound = 0.5 #diff2LowerBound and diff2UpperBound determine how close the other point of the line should be to the outside of the gauge
diff2UpperBound = 1.0
for i in range(0, len(lines)):
for x1, y1, x2, y2 in lines[i]:
diff1 = dist_2_pts(x, y, x1, y1) # x, y is center of circle
diff2 = dist_2_pts(x, y, x2, y2) # x, y is center of circle
#set diff1 to be the smaller (closest to the center) of the two), makes the math easier
if (diff1 > diff2):
temp = diff1
diff1 = diff2
diff2 = temp
# check if line is within an acceptable range
if (((diff1<diff1UpperBound*r) and (diff1>diff1LowerBound*r) and (diff2<diff2UpperBound*r)) and (diff2>diff2LowerBound*r)):
line_length = dist_2_pts(x1, y1, x2, y2)
# add to final list
final_line_list.append([x1, y1, x2, y2])
#testing only, show all lines after filtering
# for i in range(0,len(final_line_list)):
# x1 = final_line_list[i][0]
# y1 = final_line_list[i][1]
# x2 = final_line_list[i][2]
# y2 = final_line_list[i][3]
# cv2.line(img, (x1, y1), (x2, y2), (0, 255, 0), 2)
# assumes the first line is the best one
x1 = final_line_list[0][0]
y1 = final_line_list[0][1]
x2 = final_line_list[0][2]
y2 = final_line_list[0][3]
cv2.line(img, (x1, y1), (x2, y2), (0, 255, 0), 2)
#for testing purposes, show the line overlayed on the original image
#cv2.imwrite('gauge-1-test.jpg', img)
cv2.imwrite('gauge-%s-lines-2.%s' % (gauge_number, file_type), img)
#find the farthest point from the center to be what is used to determine the angle
dist_pt_0 = dist_2_pts(x, y, x1, y1)
dist_pt_1 = dist_2_pts(x, y, x2, y2)
if (dist_pt_0 > dist_pt_1):
x_angle = x1 - x
y_angle = y - y1
else:
x_angle = x2 - x
y_angle = y - y2
# take the arc tan of y/x to find the angle
res = np.arctan(np.divide(float(y_angle), float(x_angle)))
#np.rad2deg(res) #coverts to degrees
# print x_angle
# print y_angle
# print res
# print np.rad2deg(res)
#these were determined by trial and error
res = np.rad2deg(res)
if x_angle > 0 and y_angle > 0: #in quadrant I
final_angle = 270 - res
if x_angle < 0 and y_angle > 0: #in quadrant II
final_angle = 90 - res
if x_angle < 0 and y_angle < 0: #in quadrant III
final_angle = 90 - res
if x_angle > 0 and y_angle < 0: #in quadrant IV
final_angle = 270 - res
#print final_angle
old_min = float(min_angle)
old_max = float(max_angle)
new_min = float(min_value)
new_max = float(max_value)
old_value = final_angle
old_range = (old_max - old_min)
new_range = (new_max - new_min)
new_value = (((old_value - old_min) * new_range) / old_range) + new_min
return new_value
# +
def main():
gauge_number = 1
file_type='jpg'
# name the calibration image of your gauge 'gauge-#.jpg', for example 'gauge-5.jpg'. It's written this way so you can easily try multiple images
min_angle, max_angle, min_value, max_value, units, x, y, r = calibrate_gauge(gauge_number, file_type)
#feed an image (or frame) to get the current value, based on the calibration, by default uses same image as calibration
img = cv2.imread('image/gauge-%s.%s' % (gauge_number, file_type))
val = get_current_value(img, min_angle, max_angle, min_value, max_value, x, y, r, gauge_number, file_type)
print("Current reading: %s %s" %(val, units))
if __name__=='__main__':
main()
# -
| 9,432 |
/.ipynb_checkpoints/Python Class - Database Intro 1-checkpoint.ipynb | 3da1a1e484f97d0c4eddf1bfb90ccfd289dc6595 | [] | no_license | fatmas1982/iPythonNotebook | https://github.com/fatmas1982/iPythonNotebook | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 2,223 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
import sqlite3
# Note My sqlite3 database is located and running on raspberry pi 04, which is mapped to s on this computer
conn=sqlite3.connect('s:/mydatabase.db')
curs=conn.cursor()
print "\nEntire database contents:\n"
for row in curs.execute("SELECT * FROM temps"):
print row
print "\nDatabase entries for the garage:\n"
for row in curs.execute("SELECT * FROM temps WHERE zone='garage'"):
print row
conn.close()
# -
dom noise vector**
random_dim = 105
# **Defining a function that would return Normalized MNIST data off the bat**
def load_mnist_data():
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = (x_train.astype(np.float32) - 127.5)/127.5 #normalizing
x_train = x_train.reshape(60000, 784) # Reshaping from (60000, 28, 28) to (60000, 784)
return (x_train, y_train, x_test, y_test)
# ** function that
# returns Adam optimizer.
# with params
# lr
# beta_1
# **
def get_optimizer(lr=0.0002, beta_1=0.5):
return Adam(lr=lr, beta_1=beta_1)
#
# **Generator Function**
#
def get_generator(optimizer):
generator = Sequential()
generator.add(Dense(256, input_dim=random_dim,kernel_initializer=initializers.RandomNormal(stddev=0.02)))
generator.add(LeakyReLU(0.2))
generator.add(Dense(512))
generator.add(LeakyReLU(0.2))
generator.add(Dense(1024))
generator.add(LeakyReLU(0.2))
generator.add(Dense(784, activation='tanh'))
generator.compile(loss='binary_crossentropy', optimizer=optimizer)
return generator
# **Discriminator function**
def get_discriminator(optimizer):
discriminator = Sequential()
discriminator.add(Dense(1024, input_dim=784,
kernel_initializer=initializers.RandomNormal(stddev=0.02)))
discriminator.add(LeakyReLU(0.2))
discriminator.add(Dropout(0.3))
discriminator.add(Dense(512))
discriminator.add(LeakyReLU(0.2))
discriminator.add(Dropout(0.3))
discriminator.add(Dense(256))
discriminator.add(LeakyReLU(0.2))
discriminator.add(Dropout(0.3))
discriminator.add(Dense(1, activation='sigmoid'))
discriminator.compile(loss='binary_crossentropy', optimizer=optimizer)
return discriminator
# **Gan Network that takes in Parameters Discriminator, Generator, Random dim and Optimizer**
def gan_network(discriminator, generator, random_dim, optimizer):
discriminator.trainable = False
gan_input = Input(shape=(random_dim,))
x = generator(gan_input)
gan_output = discriminator(x)
gan = Model(inputs=gan_input, outputs=gan_output)
gan.compile(loss='binary_crossentropy', optimizer=optimizer)
return gan
# **This function plots all the images generator out of the generator at the end**
def plot_generated_images(epoch, generator, examples=100, dim=(10, 10), figsize=(10, 10)):
noise = np.random.normal(0, 1, size=[examples, random_dim])
generated_images = generator.predict(noise)
generated_images = generated_images.reshape(examples, 28, 28)
plt.figure(figsize=figsize)
for i in range(generated_images.shape[0]):
plt.subplot(dim[0], dim[1], i+1)
plt.imshow(generated_images[i],
interpolation='nearest',
cmap='gray_r')
plt.axis('off')
plt.tight_layout()
plt.savefig('generated_images/gan_generated_image_epoch_%d.png' % epoch)
# **Training the GAN**
def train_GAN(epochs=1, batch_size=128):
x_train, y_train, x_test, y_test = load_mnist_data()
batch_count = int(x_train.shape[0] / batch_size)
adam = get_optimizer()
generator = get_generator(adam)
discriminator = get_discriminator(adam)
gan = gan_network(discriminator, generator, random_dim, adam)
for e in range(1, epochs+1):
print('-'*15, 'Epoch %d' % e, '-'*15)
for _ in tqdm(range(batch_count)):
noise = np.random.normal(0, 1, size=[batch_size, random_dim])
image_batch = x_train[np.random.randint(0, x_train.shape[0],
size=batch_size)]
generated_images = generator.predict(noise)
X = np.concatenate([image_batch, generated_images])
y_dis = np.zeros(2*batch_size)
y_dis[:batch_size] = 0.9
discriminator.trainable = True
discriminator.train_on_batch(X, y_dis)
noise = np.random.normal(0, 1, size=[batch_size, random_dim])
y_gen = np.ones(batch_size)
discriminator.trainable = False
gan.train_on_batch(noise, y_gen)
if e == 1 or e % 20 == 0:
plot_generated_images(e, generator)
if __name__=='__main__':
train_GAN(400, 128)
ab_type="code" id="CiX2FI4gZtTt" colab={}
column_names = ['MPG','Cylinders','Displacement','Horsepower','Weight', 'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(dataset_path, names=column_names, na_values="?", comment="\t", sep=" ", skipinitialspace=True)
dataset = raw_dataset.copy()
dataset.tail()
# + [markdown] colab_type="text" id="3MWuJTKEDM-f"
# ### Clean the data
#
# The dataset contains a few unknown values.
# + colab_type="code" id="JEJHhN65a2VV" colab={}
dataset.isna().sum()
# + [markdown] colab_type="text" id="9UPN0KBHa_WI"
# To keep this initial tutorial simple drop those rows.
# + colab_type="code" id="4ZUDosChC1UN" colab={}
dataset = dataset.dropna()
# + [markdown] colab_type="text" id="8XKitwaH4v8h"
# The `"Origin"` column is really categorical, not numeric. So convert that to a one-hot:
# + colab_type="code" id="gWNTD2QjBWFJ" colab={}
origin = dataset.pop('Origin')
# + colab_type="code" id="ulXz4J7PAUzk" colab={}
dataset['USA'] = (origin == 1)*1.0
dataset['Europe'] = (origin == 2)*1.0
dataset['Japan'] = (origin == 3)*1.0
dataset.tail()
# + [markdown] colab_type="text" id="Cuym4yvk76vU"
# ### Split the data into train and test
#
# Now split the dataset into a training set and a test set.
#
# We will use the test set in the final evaluation of our model.
# + colab_type="code" id="qn-IGhUE7_1H" colab={}
train_dataset = dataset.sample(frac=0.8, random_state=0)
test_dataset = dataset.drop(train_dataset.index)
# + [markdown] colab_type="text" id="J4ubs136WLNp"
# ### Inspect the data
#
# Have a quick look at the joint distribution of a few pairs of columns from the training set.
# + colab_type="code" id="oRKO_x8gWKv-" colab={}
sns.pairplot(train_dataset[["MPG", "Cylinders", "Displacement", "Weight"]], diag_kind="kde")
# + [markdown] colab_type="text" id="gavKO_6DWRMP"
# Also look at the overall statistics:
# + colab_type="code" id="yi2FzC3T21jR" colab={}
train_stats = train_dataset.describe()
train_stats.pop("MPG")
train_stats = train_stats.transpose()
train_stats
# + [markdown] colab_type="text" id="Db7Auq1yXUvh"
# ### Split features from labels
#
# Separate the target value, or "label", from the features. This label is the value that you will train the model to predict.
# + colab_type="code" id="t2sluJdCW7jN" colab={}
train_labels = train_dataset.pop('MPG')
test_labels = test_dataset.pop('MPG')
# + [markdown] colab_type="text" id="mRklxK5s388r"
# ### Normalize the data
#
# Look again at the `train_stats` block above and note how different the ranges of each feature are.
# + [markdown] colab_type="text" id="-ywmerQ6dSox"
# It is good practice to normalize features that use different scales and ranges. Although the model *might* converge without feature normalization, it makes training more difficult, and it makes the resulting model dependent on the choice of units used in the input.
#
# Note: Although we intentionally generate these statistics from only the training dataset, these statistics will also be used to normalize the test dataset. We need to do that to project the test dataset into the same distribution that the model has been trained on.
# + colab_type="code" id="JlC5ooJrgjQF" colab={}
def norm(x):
return ((x - train_stats['mean']) / train_stats['std'])
normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)
# + [markdown] colab_type="text" id="BuiClDk45eS4"
# This normalized data is what we will use to train the model.
#
# Caution: The statistics used to normalize the inputs here (mean and standard deviation) need to be applied to any other data that is fed to the model, along with the one-hot encoding that we did earlier. That includes the test set as well as live data when the model is used in production.
# + [markdown] colab_type="text" id="SmjdzxKzEu1-"
# ## The model
# + [markdown] colab_type="text" id="6SWtkIjhrZwa"
# ### Build the model
#
# Let's build our model. Here, we'll use a `Sequential` model with two densely connected hidden layers, and an output layer that returns a single, continuous value. The model building steps are wrapped in a function, `build_model`, since we'll create a second model, later on.
# + colab_type="code" id="c26juK7ZG8j-" colab={}
def build_model():
model = keras.Sequential([
layers.Dense(64, activation=tf.nn.relu, input_shape=[len(train_dataset.keys())]),
layers.Dense(64, activation=tf.nn.relu),
layers.Dense(1)
])
optimizer = tf.keras.optimizers.RMSprop(0.001)
model.compile(loss='mse', optimizer=optimizer, metrics=['mae', 'mse'])
return model
# + colab_type="code" id="cGbPb-PHGbhs" colab={}
model = build_model()
# + [markdown] colab_type="text" id="Sj49Og4YGULr"
# ### Inspect the model
#
# Use the `.summary` method to print a simple description of the model
# + colab_type="code" id="ReAD0n6MsFK-" colab={}
model.summary()
# + [markdown] colab_type="text" id="Vt6W50qGsJAL"
#
# Now try out the model. Take a batch of `10` examples from the training data and call `model.predict` on it.
# + colab_type="code" id="-d-gBaVtGTSC" colab={}
example_batch = normed_train_data[:10]
example_result = model.predict(example_batch)
example_result
# + [markdown] colab_type="text" id="QlM8KrSOsaYo"
# It seems to be working, and it produces a result of the expected shape and type.
# + [markdown] colab_type="text" id="0-qWCsh6DlyH"
# ### Train the model
#
# Train the model for 1000 epochs, and record the training and validation accuracy in the `history` object.
# + colab_type="code" id="sD7qHCmNIOY0" colab={}
# Display training progress by printing a single dot for each completed epoch
class PrintDot(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
if epoch % 100 == 0: print ('')
print('.', end='')
EPOCHS = 1000
history = model.fit(normed_train_data, train_labels, epochs=EPOCHS, validation_split=0.2, verbose=0, callbacks=[PrintDot()])
# + [markdown] colab_type="text" id="tQm3pc0FYPQB"
# Visualize the model's training progress using the stats stored in the `history` object.
# + colab_type="code" id="4Xj91b-dymEy" colab={}
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
# + colab_type="code" id="B6XriGbVPh2t" colab={}
import matplotlib.pyplot as plt
def plot_history(history):
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
plt.figure()
plt.xlabel('Epoch')
plt.ylabel(' Mean absolute error [MPG]')
plt.plot(hist['epoch'], hist['mean_absolute_error'], label ='Train error')
plt.plot(hist['epoch'], hist['val_mean_absolute_error'], label = 'Val Error')
plt.legend()
plt.ylim([0,5])
plt.figure()
plt.xlabel('Epochs')
plt.ylabel(' Mean Square Error [$MPG^2$]')
plt.plot(hist['epoch'], hist['mean_squared_error'], label='Train Error')
plt.plot(hist['epoch'], hist['val_mean_squared_error'], label= 'Val Error')
plt.legend()
plt.ylim([0,20])
plot_history(history)
# + [markdown] colab_type="text" id="AqsuANc11FYv"
# This graph shows little improvement, or even degradation in the validation error after about 100 epochs. Let's update the `model.fit` call to automatically stop training when the validation score doesn't improve. We'll use an *EarlyStopping callback* that tests a training condition for every epoch. If a set amount of epochs elapses without showing improvement, then automatically stop the training.
#
# You can learn more about this callback [here](https://www.tensorflow.org/versions/master/api_docs/python/tf/keras/callbacks/EarlyStopping).
# + colab_type="code" id="fdMZuhUgzMZ4" colab={}
model = build_model()
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
history = model.fit(normed_train_data, train_labels, epochs=EPOCHS, validation_split=0.2, verbose=0, callbacks=[early_stop, PrintDot()])
plot_history(history)
# + [markdown] colab_type="text" id="3St8-DmrX8P4"
# The graph shows that on the validation set, the average error is usually around +/- 2 MPG. Is this good? We'll leave that decision up to you.
#
# Let's see how well the model generalizes by using the **test** set, which we did not use when training the model. This tells us how well we can expect the model to predict when we use it in the real world.
# + colab_type="code" id="jl_yNr5n1kms" colab={}
loss, mae, mse = model.evaluate(normed_test_data, test_labels, verbose=0)
print("Testing set Mean Abs Error: {:5.2f} MPG". format(mae))
# + [markdown] colab_type="text" id="ft603OzXuEZC"
# ### Make predictions
#
# Finally, predict MPG values using data in the testing set:
# + colab_type="code" id="Xe7RXH3N3CWU" colab={}
test_predictions = model.predict(normed_test_data).flatten()
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions[ MPG]')
plt.axis('equal')
plt.axis('square')
plt.xlim([0,plt.xlim()[1]])
plt.ylim([0,plt.ylim()[1]])
_ = plt.plot([-100, 100], [-100, 100])
# + [markdown] colab_type="text" id="OrkHGKZcusUo"
# It looks like our model predicts reasonably well. Let's take a look at the error distribution.
# + colab_type="code" id="f-OHX4DiXd8x" colab={}
error = test_predictions - test_labels
plt.hist(error, bins = 25)
plt.xlabel("Prediction Error [MPG]")
_ = plt.ylabel("Count")
# + [markdown] colab_type="text" id="r9_kI6MHu1UU"
# It's not quite gaussian, but we might expect that because the number of samples is very small.
# + [markdown] colab_type="text" id="vgGQuV-yqYZH"
# ## Conclusion
#
# This notebook introduced a few techniques to handle a regression problem.
#
# * Mean Squared Error (MSE) is a common loss function used for regression problems (different loss functions are used for classification problems).
# * Similarly, evaluation metrics used for regression differ from classification. A common regression metric is Mean Absolute Error (MAE).
# * When numeric input data features have values with different ranges, each feature should be scaled independently to the same range.
# * If there is not much training data, one technique is to prefer a small network with few hidden layers to avoid overfitting.
# * Early stopping is a useful technique to prevent overfitting.
| 15,347 |
/lessons/l29_dashboards_test.ipynb | 63dcaf5ec0c17a698a7b6e8d07c7eeac6a778d58 | [] | no_license | faymanns/bootcamp_site | https://github.com/faymanns/bootcamp_site | 0 | 2 | null | null | null | null | Jupyter Notebook | false | false | .py | 321,641 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# +
def generate_sample_data(theta0, theta1):
x = np.random.uniform(0, 10, 50)
y = theta0 + theta1 * x + np.random.randn(50)
return x, y
def create_hypothesis(theta0, theta1):
return lambda x: theta0 + theta1 * x
# -
def create_cost_function(x, y):
return lambda h: np.sum((h(x) - y) ** 2) / (2.0 * len(x))
# +
x, y = generate_sample_data(0, 1)
cf = create_cost_function(x, y)
t0, t1 = np.meshgrid(np.linspace(-10, 10, 100), np.linspace(-10, 10, 100))
hv = np.array([
cf(create_hypothesis(theta0, theta1))
for theta0, theta1
in zip(t0.ravel(), t1.ravel())
])
df = pd.DataFrame(list(zip(t0.ravel(), t1.ravel(), hv)), columns=['theta0', 'theta1', 'cf'])
df.sort_values(['cf'], ascending=True).head(10)
rint(len("spam"));
print(len("SpamAndEggs"));
for ch in "Spam!":
print(ch, end=" ");
# +
#Basic operations for strings:
import pandas as pd
data = [["+","concatination"],["*","repitition"],["<string>[]","indexing"],["<string>[:]","slicing"],["for <var> in <string>","iteration through characters"]]
pd.DataFrame(data, columns=["Operation","Meaning"])
# +
def main():
print("This program generates computer usernames.\n")
#get users first and last names
first = input("Please enter your first name (all lowercase): ")
last = input("Please enter your last name (all lowercase): ")
#concatinate first initial with 7 chars of the last name.
uname = first[0] + last[:7]
#output the username
print("Your username is:", uname)
main();
# +
def main():
#months is sued as a lookup table
months = "JanFebMarAprMayJunJulAugSepOctNovDec"
n = int(input("Enter your month's number (1-12): "))
# compute starting position of month n in months
pos = (n-1) * 3
#grab the appropriate slice from months
monthAbbrev = months[pos:pos+3]
#print the result
print("The month abbreviation is", monthAbbrev + ".")
main()
# -
print([1,2] + [3,4]);
print([1,2]*3);
grades = ['A','B','C','D','F'];
print(grades[0]);
print(grades[2:4]);
print(len(grades));
myList = [1, 'Spam', 4, 'E'];
print(myList);
# +
#Program to print the month abbreviation, given it's number
def main():
#months is a list used as a lookup table
months = ["Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec"];
n = int(input("Enter the month you want as a number (1-12): "));
print("the month abbreviation is", months[n-1] +'.');
main();
# -
print(ord('A'));
print(ord('a'));
print(chr(65));
print(chr(97));
# +
def main():
print("This program converts a textual message into a sequence");
print("of numbers representing the Unicode encoding of the message");
#get message to encode
message = input("Please enter the message to encode: ");
print("\nHere are the Unicode codes:");
#Loop through the message and print out the Unicode values
for ch in message:
print(ord(ch), end=" ")
print() #blank line before prompt
main();
# -
myString = 'Hello, string methods!'
myString.split()
"32,24,25,57".split(",")
coords = input("Enter the point coordinates (x,y): ").split(",")
x,y = float(coords[0]), float(coords[1])
print(coords)
print(coords[0])
print(coords[1])
print(x)
print(y)
# +
def main():
print("This program converts a sequence of Unicode numbers into")
print("the string text that it represents. \n")
# Get the message to encode
inString = input("Please enter the Unicode-encoded message: ")
# Loop through each substring and build Unicode message
message = ""
for numStr in inString.split():
codeNum = int(numStr) #convert digits to a number
message = message + chr(codeNum) #concatenate character to message
print("\nThe decoded message is:", message)
main()
# -
s = 'Hello, I am here'
print(s.capitalize())
print(s.title())
print(s.lower())
print(s.upper())
print(s.replace("I","you"))
print(s.center(30))
print(s.count('e'))
print(s.find(','))
print(' '.join(["Number", "one", "the", "Larch"]))
print('why '.join(["Number", "one", "the", "Larch"]))
# +
#Basic methods for strings:
import pandas as pd
data = [["s.capitalize()","Copy of s, first character capitalized"],["s.center(width)","Copy of s, centered by width"],["s.count(sub)","count occurences of sub in s"],["s.find(sub)","finds first position of sub in s"],["s.join(list)","Concatinates list as string, s as seperator"],["s.ljust(width)","Like center but left justified"],["s.lower()","copy of s but all lowercase"],["s.lstrip","copy of s without leading space"],["s.replace(oldsub, newsub)","replaces occurences of oldsub with newsub"],["s.rfind(sub)","like find but returns rightmost position"],["s.rjust(width)","like center but right-justified"],["s.rstrip()","copy of s but end space removed"],["s.split()","splits s into list of substrings"],["s.title()","copy of s but first character of each word capitalized"],["s.upper()","copy of s with all characters converted uppercase"]]
pd.DataFrame(data, columns=["Method","Meaning"])
# -
#mini program to make a list of squared numbers going up to 100 (from 1)
squares = []
for x in range(1,101):
squares.append(x*x)
print(squares)
# +
#same version of decoder from before, just now we use a list to concatinate characters instead of many strings
def main():
print("This program converts a sequence of Unicode numbers into")
print("the string text that it represents (efficient version using list accumulator). \n")
# Get the message to encode
inString = input("Please enter the Unicode-encoded message: ")
# Loop through each substring and build Unicode message
chars = []
for numStr in inString.split():
codeNum = int(numStr) #convert digits to a number
chars.append(chr(codeNum)) #accumulates new character into list
message = "".join(chars)
print("\nThe decoded message is:", message)
main()
#both string concatination and append/join techniques are efficient
# -
# - encryption: 'process of encoding information for the purpose of keeping it a secret or transmitting it privatly
# - cryptography: sub-field of mathematics and comp-sci, study of encryption methods
# - substitution ciphor: weak form of encryption given a plaintext and replacing each character by a ciphor aplhabet
# - plaintext: original message
# - cipher alphabet: characters to use as replacements for old characters
# - ciphertext: new message
# - private key (shared key) system: same key is used for encrypting and decrypting messages.
# - public key system: having seperate/related keys for encryption/decryption.
# +
#Date conversion program
def main():
#get the date
dateStr = input("Enter a date (mm/dd/yyyy): ")
#split into components
monthStr, dayStr, yearStr = dateStr.split("/")
#convert monthStr to the month name
months = ["January", "February", "March", "April", "May", "June", "July", "August", "September", "October", "November", "December"]
monthStr = months[int(monthStr)-1]
#Output result in month day, year format
print("The converted date is:", monthStr, dayStr+',', yearStr)
main()
# +
#Basic functions for casting:
import pandas as pd
data = [["float(<expr>)","convert expr to float"],["int(<expr>)","convert expr to integer"],["str(<expr>)","convert expr to string"],["eval(<string>)","evaluate string as an expression"]]
pd.DataFrame(data, columns=["Function","Meaning"])
# -
# #String formatting form
# <template-string>.format(<values>)
# {<index>:<format-specifier>}
# 0.2f <width>.<precision><type>
"Hello {0} {1}, you my have won ${2}".format("Mr.","Smith", 10000)
"This int, {0:5}, was placed in a field of width 5".format(7)
"This int, {0:10}, was placed in a field of width 10".format(7)
"This float, {0:10.5}, has width 10 and precision 5".format(3.1415926)
"This float, {0:10.5f}, is fixed at 5 decimal places".format(3.1415926)
"This float, {0:0.5}, has width 0 and precision 5".format(3.1415926)
"Compare {0} and {0:0.20}".format(3.14)
"left justification: {0:<5}".format("Hi!")
"right justification: {0:>5}".format("Hi!")
"centered: {0:^5}".format("Hi!")
# +
#Better version of the change calculator
#Program to calculate the value of some change in dollars
#This version represents the total of cash in cents
def main():
print("Change Counter\n")
print("Please enter the count of each coin type.")
quarters = int(input("Quarters: "))
dimes = int(input("Dimes: "))
nickels = int(input("Nickles: "))
pennies = int(input("Pennies: "))
total = quarters * 25 + dimes * 10 + nickels * 5 + pennies
print("The total value of your change is ${0}.{1:0>2}".format(total//100, total%100))
main()
# -
import pandas as pd
data = [["<file>.read()","Returns entire file content as single string"],["<file>.readline()","returns next line of file (all text up to and including next line)"],["<file>.readlines()","returns list of remaining lines in file (each item being a line)"]]
pd.DataFrame(data, columns=["File Operation","Meaning"])
# +
#example program that prints content of file into screen
#I made a txt file named EXAMPLE.txt and put it with my jupyter python note files.
def main():
fname = input("Enter filename: ")
infile = open(fname, "r")
data = infile.read()
print(data)
main()
# -
# # Chapter 5 Summary
#
# - Strings are sequences of characters. String literals can be delimited with either single or double quotes
# - Strings and lists can be manipulated by operations for concatination (+), repitition (*), indexing([]), slicing([:]), and length(len())
# - Lists are more general than strings
# - Strings are always sequences of characters, lists can contain anything however
# - Lists are mutable, Strings are immutable, lists can be modified by assingning new values
# - Strings are represented by numeric codes. ASCII and Unicode are compatible standards used for specifying and correspondance.
# - Process to keep data private is encryption. 2 types of encryption types (public key and private key)
# - Program input/output often involves string processing. String formatting is useful for nicely formatted output.
# - Text files are multi-line strings stored in secondary memory.
size=2,
color=color,
nonselection_alpha=nonselection_alpha,
)
plots[i][i].y_range = plots[i][i].x_range
# Build each scatter plot
for j, x in enumerate(dims):
for i, y in enumerate(dims):
if i != j:
x_axis_label = abbrev[x] if i == len(dims) - 1 else None
y_axis_label = abbrev[y] if j == 0 else None
plots[i][j] = bokeh.plotting.figure(
frame_height=125,
frame_width=125,
x_axis_label=x_axis_label,
y_axis_label=y_axis_label,
tools=tools,
align="end",
x_range=plots[j][j].x_range,
y_range=plots[i][i].x_range,
)
plots[i][j].circle(
source=source,
x=x,
y=y,
alpha=0.7,
size=2,
color=color,
nonselection_alpha=nonselection_alpha,
)
# Only show tick labels on edges
for i in range(len(dims) - 1):
for j in range(1, len(dims)):
plots[i][j].axis.visible = False
for j in range(1, len(dims)):
plots[-1][j].yaxis.visible = False
for i in range(0, len(dims) - 1):
plots[i][0].xaxis.visible = False
return bokeh.layouts.gridplot(plots)
# Now let's re-do the layout. The responsiveness will be a bit slow because every time we change a checkbox or the color by field, the HoloViews dashboard above also gets updated. For a more performant dashboard, re-run the notebook, but do not invoke the HoloViews-based dashboard.
pn.Row(
gridmatrix,
pn.Spacer(width=15),
pn.Column(
pn.Spacer(height=15),
dims_selector,
pn.Spacer(height=15),
colorby_selector,
pn.Spacer(height=15),
alpha_selector,
),
)
# ### Putting it all together
#
# The scatter plots are useful, but we would like to have a clear comparison of individual variables across insomnia conditions and across gender. We can therefore add plots of the ECDFs below the gridmatrix. We will add one more checkbox, enabling us to select whether or not we want confidence intervals on the ECDF.
# +
conf_int_selector = pn.widgets.Checkbox(
name="ECDF confidence interval", value=True
)
@pn.depends(
dims_selector.param.value,
colorby_selector.param.value,
conf_int_selector.param.value,
)
def ecdfs(dims, cat, conf_int):
if cat == "gender":
order = ["f", "m"]
elif cat == "insomnia":
order = [False, True]
elif cat == "none":
cat = None
order = None
plots = []
for i, dim in enumerate(dims):
plots.append(
iqplot.ecdf(
df,
q=dim,
cats=cat,
frame_height=150,
frame_width=250,
show_legend=(i == len(dims) - 1),
order=order,
style="staircase",
conf_int=conf_int,
)
)
return bokeh.layouts.gridplot(plots, ncols=2)
# -
# Now we can construct the final layout of the dashboard. We will place the check boxes and selectors on top, followed by the ECDFs, and finally the grid matrix.
# +
layout = pn.Column(
pn.Row(
dims_selector,
pn.Spacer(width=15),
pn.Column(
colorby_selector,
pn.Spacer(height=15),
alpha_selector,
pn.Spacer(height=15),
conf_int_selector,
),
),
pn.Spacer(height=15),
gridmatrix,
pn.Spacer(height=15),
ecdfs,
)
layout.servable()
# -
# ## Conclusions
#
# There are many more directions you can go with dashboards. In particular, if there is a type of experiment you do often in which you have multifaceted data, you may want to build a dashboard into which you can automatically load your data and display it for you to explore. This can greatly expedite your work, and can also be useful for sharing your data with others, enabling them to rapidly explore it as well.
#
# That said, it is important to constantly be rethinking how you visualize and analyze the data you collect. You do not want the displays of a dashboard you set up a year ago have undo influence on your thinking right now.
# ## Computing environment
# + tags=["hide-input"]
# %load_ext watermark
# %watermark -v -p numpy,scipy,pandas,skimage,bootcamp_utils,iqplot,bokeh,holoview,panel,colorcet,jupyterlab
| 15,383 |
/Coursera_Capstone week_1.ipynb | 548800c92398716c890a7bf7808adb1662f53b37 | [] | no_license | Raghav-Arora-01/Coursera_Capstone | https://github.com/Raghav-Arora-01/Coursera_Capstone | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 1,179 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Вы работаете секретарем и вам постоянно приходят различные документы. Вы должны быть очень внимательны, чтобы не потерять ни один документ. Каталог документов хранится в следующем виде:
documents = [
{'type': 'passport', 'number': '2207 876234', 'name': 'Василий Гупкин'},
{'type': 'invoice', 'number': '11-2', 'name': 'Геннадий Покемонов'},
{'type': 'insurance', 'number': '10006', 'name': 'Аристарх Павлов'}
]
# Перечень полок, на которых находятся документы хранится в следующем виде:
directories = {
'1': ['2207 876234', '11-2'],
'2': ['10006'],
'3': []
}
# Необходимо реализовать пользовательские команды (внимание! это не название функций, которые должны быть выразительными, а команды, которые вводит пользователь, чтобы получить необходимый результат):
#
# - p – people – команда, которая спросит номер документа и выведет имя человека, которому он принадлежит;
# - s – shelf – команда, которая спросит номер документа и выведет номер полки, на которой он находится
# *Правильно обработайте ситуации, когда пользователь будет вводить несуществующий документ*.
# - l – list – команда, которая выведет список всех документов в формате
# **passport "2207 876234" "Василий Гупкин"**
# - as – add shelf – команда, которая спросит номер новой полки и добавит ее в перечень. *Предусмотрите случай, когда пользователь добавляет полку, которая уже существует*.
# - d – delete – команда, которая спросит номер документа и удалит его из каталога и из перечня полок. *Предусмотрите сценарий, когда пользователь вводит несуществующий документ*;
# - m – move – команда, которая спросит номер документа и целевую полку и переместит его с текущей полки на целевую. *Корректно обработайте кейсы, когда пользователь пытается переместить несуществующий документ или переместить документ на несуществующую полку*;
# - a – add – команда, которая добавит новый документ в каталог и в перечень полок, спросив его номер, тип, имя владельца и номер полки, на котором он будет храниться. *Корректно обработайте ситуацию, когда пользователь будет пытаться добавить документ на несуществующую полку*.
# +
def search_people_by_num(documents_db=documents):
doc_number = input('Введите номер документа для поиска ФИО владельца: ')
for document in documents_db:
if document['number'] == doc_number:
return f'ФИО владельца: {document["name"]}'
return f'Документ с номером {doc_number} в каталоге отсутствует'
def search_shelf_by_num(directories_db=directories):
doc_number = input('Введите номер документа для поиска полки: ')
for shelf, number_list in directories_db.items():
if doc_number in number_list:
return f'Документ с номером {doc_number} находится на полке "{shelf}"'
return f'Документ с номером {doc_number} на полках отсутствует'
def get_documents_list(documents_db=documents):
for document in documents_db:
print(f'{document["type"]} "{document["number"]}" "{document["name"]}"')
return f'Всего {len(documents_db)} записи'
def add_new_shelf(directories_db=directories):
new_shelf = input('Введите номер новой полки для добавления: ')
if str(new_shelf) not in directories_db.keys():
directories_db[str(new_shelf)] = []
return f'Полка с номером "{new_shelf}" добавлена'
else:
return f'полка с номером "{new_shelf}" уже существует, укажите другой номер отличный от {list(directories_db.keys())}'
def del_document(documents_db=documents, directories_db=directories):
doc_number = input('Введите номер документа для удаления: ')
for index, document in enumerate(documents_db):
if document['number'] == doc_number:
del(documents_db[index])
print(f'Документ {doc_number} удален из каталога!')
for shelf, number_list in directories_db.items():
if doc_number in number_list:
number_list.remove(doc_number)
return f'Документ {doc_number} удален с полки "{shelf}"!'
return f'Документ с номером {doc_number} не найден. Проверьте введеный номер!'
def move_document(directories_db=directories):
doc_number = input('Введите номер перемещаемого документа: ')
shelf_number = input('Введите номер целевой полки: ')
for number_list in directories_db.values():
if doc_number in number_list:
number_list.remove(doc_number)
directories_db[str(shelf_number)].append(str(doc_number))
return f'Документ {doc_number} перемещен на полку "{shelf_number}"'
return f'Документ {doc_number} не найден, проверьте правильность указанного номера'
def add_new_document(documents_db=documents, directories_db=directories):
shelf_number = input('Введите номер полки для размещения нового документа: ')
if str(shelf_number) not in directories_db.keys():
return f'Полка с номером "{shelf_number}" отсутствует. Сначала добавьте новую полку через команду add shelf'
doc_number = input('Введите номер нового документа: ')
doc_type = input('Введите тип нового документа: ')
doc_name = input('Введите ФИО владельца документа: ')
for document in documents_db:
if document['number'] == doc_number and document['number'] == doc_number:
return f'Документ {doc_type} {doc_number} уже существует в каталоге'
documents_db.append({'type': doc_type, 'number': doc_number, 'name': doc_name})
directories_db[str(shelf_number)].append(str(doc_number))
return f'Документ {doc_type} {doc_number} внесён в каталог и размещён на полке "{shelf_number}"'
def command_list():
print("Список допустимых команд :",
'p – people - поиск ФИО владельца документа в каталоге',
's – shelf - поиск полки по номеру документа',
'l – list - перечень документов в каталоге',
'as – add shelf - добавление новой полки',
'd – delete - удаление документа из каталога и полки',
'm – move - перемещение документа между полками',
'a – add - добавление нового документа',
' ',
sep='\n')
# -
def secretary_system ():
while True:
user_input = input('Введите команду (посмотреть список команд "c - command"):')
if user_input == 'p' or user_input == 'people':
print(search_people_by_num(), " ", sep='\n')
elif user_input == 's' or user_input == 'shelf':
print(search_shelf_by_num(), " ", sep='\n')
elif user_input == 'l' or user_input == 'list':
print(get_documents_list(), " ", sep='\n')
elif user_input == 'as' or user_input == 'add shelf':
print(add_new_shelf(), " ", sep='\n')
elif user_input == 'd' or user_input == 'delete':
print(del_document(), " ", sep='\n')
elif user_input == 'm' or user_input == 'move':
print(move_document(), " ", sep='\n')
elif user_input == 'a' or user_input == 'add':
print(add_new_document(), " ", sep='\n')
elif user_input == 'c' or user_input == 'command' or user_input == '':
command_list()
elif user_input == 'q' or user_input == 'quit':
print('Завершение работы!')
break
secretary_system()
if 'date' in tuple[1].keys() and len(question.dates):
for date in question.dates:
dstrs = set()
for d in question.dates:
dstrs.add(str(d))
if not len(set(tuple[1]['date']).intersection(dstrs)):
skip = True
if skip or not is_num(tuple[1]['value']):
continue
prediction = q_predicted[0][0]
if prediction == 1:
if not (tuple[1]['relation'] == rel):
if q_predicted[1][0][1] > p_match:
total_gt += 1
if q_predicted[1][0][1] >= p_match:
total_geq += 1
total_match += 1
if found_match:
print("matched - ")
print(total_gt)
print(total_geq)
print(total_match)
return (1,total_gt,total_match,total_geq)
rs = set()
for tuple in tuples:
if not is_num(tuple[1]['value']):
pass
rs.add(tuple[1]['relation'])
if rel not in rs:
return (-1,0,0,0)
return (0,0,0,0)
for filename in os.listdir(base):
if filename.endswith(".tsv"):
with open(base+"/"+filename,encoding = "ISO-8859-1") as tsv:
for line in tsv.readlines():
row = line.split("\t")
if(len(row) == 12) and len(row[5].strip())>0:
if(row[0].lower().strip()=='y') or (row[1].lower().strip()=='y') :
rels.append({"claim":row[2],"relation":row[5],"entity":row[3],"num":row[9],"parsed":row[8]})
elif len(row) == 11:
if(row[0].lower().strip()=='y') and len(row[4].strip())>0:
rels.append({"claim":row[1],"relation":row[4],"entity":row[2],"num":row[8],"parsed":row[7]})
property_names = dict()
property_names['fertility_rate'] = "Fertility rate, total (births per woman)"
property_names['gdp_growth_rate'] = "GDP growth (annual %)"
property_names['gdp_nominal'] = "GDP (current US$)"
property_names['gdp_nominal_per_capita'] = "GDP per capita (current US$)"
property_names['gni_per_capita_in_ppp_dollars'] = "GNI per capita, PPP (current international $)"
property_names['life_expectancy'] = "Life expectancy at birth, total (years)"
property_names['cpi_inflation_rate'] = "Inflation, consumer prices (annual %)"
property_names['consumer_price_index'] = "Consumer price index (2010 = 100)"
property_names['diesel_price_liter'] = "Pump price for diesel fuel (US$ per liter)"
property_names['gni_in_ppp_dollars'] = "GNI (current US$)"
property_names['population_growth_rate'] = "Population growth (annual %)"
property_names['population'] = "Population, total"
property_names['prevalence_of_undernourisment'] = "Prevalence of undernourishment (% of population)"
property_names['renewable_freshwater_per_capita'] = "Renewable internal freshwater resources per capita (cubic meters)"
property_names['health_expenditure_as_percent_of_gdp'] = "Health expenditure, total (% of GDP)"
property_names['internet_users_percent_population'] = "Internet users (per 100 people)"
tested = defaultdict(int)
results = defaultdict(int)
pr = defaultdict(int)
num_better = defaultdict(int)
num_total = defaultdict(int)
num_better_or_equal = defaultdict(int)
print(len(rels))
claim_loc = re.compile(r'<location[^>]*>([^<]+)</location>')
claim_num = re.compile(r'<number[^>]*>([^<]+)</number>')
class NewQuestion():
def __init__(self,text,entity,number):
self.text = text
self.nes = {entity}
self.numbers = {num(number)}
self.dates = set()
self.nps = set()
def parse(self):
pass
qs = []
for rel in rels:
if len(claim_loc.findall(rel['claim'])) > 0:
rel['num'] = claim_num.findall(rel['claim'])[0]
start_claim_idx = rel['claim'].index(rel['entity'])
end_claim_idx = start_claim_idx + len(rel['entity'])
start_num_idx = rel['claim'].index(rel['num'])
end_num_idx = start_num_idx + len(rel['num'])
span = ""
if end_claim_idx < start_num_idx:
span = (rel['claim'][end_claim_idx:start_num_idx])
else:
span =(rel['claim'][start_num_idx:end_claim_idx])
span = re.sub('<[^<]+?>', '', span)
#print(normalise(span).split())
spanwords = span.split()
if(rel['parsed'][0]=="\""):
rel['parsed'] = rel['parsed'][1:-1]
dep_parse = ast.literal_eval(rel['parsed'])
tokens = []
for token in dep_parse:
for w in (token.replace("*extend*","").split("+")):
we = w.split("~")[0].replace("\"","")
if "," in we:
for t in we.split(","):
if not(t == "NUMBER_SLOT" or t == "LOCATION_SLOT"):
tokens.append(t)
elif not(we == "NUMBER_SLOT" or we == "LOCATION_SLOT"):
tokens.append(we)
tokens = " ".join(tokens).replace("DATE","1000").replace("PERCENT","10").replace("MISC","$")
tokens += " "
tokens += " ".join(spanwords).replace("DATE","1000").replace("PERCENT","10").replace("MISC","$")
q = NewQuestion(rel['claim'],rel['entity'],rel['num'])
words = normalise_keep_nos(q.text).split()
qs.append((q,rel))
done= 0
for item in qs:
done += 1
print(rel['claim'])
print(rel['relation'])
rel = item[1]
q = item[0]
result = fact_check_and_test(q, property_names[rel['relation']])
if result[0] == 1:
results[rel['relation']] += 1
if result[1] == 0:
pr[rel['relation']] += result[3]
num_better[rel['relation']] += result[1]
num_better_or_equal[rel['relation']] += result[3]
num_total[rel['relation']] += result[2]
if result[0] != -1:
tested[rel['relation']] += 1
print(result)
print("done" + str(done) )
print("")
if done%5000 == 0:
for key in tested.keys():
print(key + " " + str(results[key]) + " " + str(num_better[key]) + " " + str(num_better_or_equal[key]) + " " + str(num_total[key]) + " " + str(pr[key]) + " " + str(tested[key]) + " " + str(results[key] / tested[key]))
print("Done")
for key in tested.keys():
print(key + " " + str(results[key]) + " " + str(num_better[key]) + " " + str(num_better_or_equal[key]) + " " + str(num_total[key]) + " " + str(pr[key]) + " " + str(tested[key]) + " " + str(results[key] / tested[key]))
| 14,337 |
/ML Foundations/Week 2/.ipynb_checkpoints/Predicting house prices-checkpoint.ipynb | 0f74787c4f71462f1b97a4e3d2b741f77e363e1a | [] | no_license | josh-alley/Coursera-Machine-Learning | https://github.com/josh-alley/Coursera-Machine-Learning | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 16,767 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# #Fire up graphlab create
import graphlab
# #Load some house sales data
#
# Dataset is from house sales in King County, the region where the city of Seattle, WA is located.
sales = graphlab.SFrame('home_data.gl/')
sales
# #Exploring the data for housing sales
# The house price is correlated with the number of square feet of living space.
graphlab.canvas.set_target('ipynb')
sales.show(view="Scatter Plot", x="sqft_living", y="price")
# #Create a simple regression model of sqft_living to price
# Split data into training and testing.
# We use seed=0 so that everyone running this notebook gets the same results. In practice, you may set a random seed (or let GraphLab Create pick a random seed for you).
train_data,test_data = sales.random_split(.8,seed=0)
# ##Build the regression model using only sqft_living as a feature
sqft_model = graphlab.linear_regression.create(train_data, target='price', features=['sqft_living'],validation_set=None)
# #Evaluate the simple model
print test_data['price'].mean()
print sqft_model.evaluate(test_data)
# RMSE of about \$255,170!
# #Let's show what our predictions look like
# Matplotlib is a Python plotting library that is also useful for plotting. You can install it with:
#
# 'pip install matplotlib'
import matplotlib.pyplot as plt
# %matplotlib inline
plt.plot(test_data['sqft_living'],test_data['price'],'.',
test_data['sqft_living'],sqft_model.predict(test_data),'-')
# Above: blue dots are original data, green line is the prediction from the simple regression.
#
# Below: we can view the learned regression coefficients.
sqft_model.get('coefficients')
# #Explore other features in the data
#
# To build a more elaborate model, we will explore using more features.
my_features = ['bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot', 'floors', 'zipcode']
sales[my_features].show()
sales.show(view='BoxWhisker Plot', x='zipcode', y='price')
# Pull the bar at the bottom to view more of the data.
#
# 98039 is the most expensive zip code.
# #Build a regression model with more features
my_features_model = graphlab.linear_regression.create(train_data,target='price',features=my_features,validation_set=None)
print my_features
# ##Comparing the results of the simple model with adding more features
print sqft_model.evaluate(test_data)
print my_features_model.evaluate(test_data)
# The RMSE goes down from \$255,170 to \$179,508 with more features.
# #Apply learned models to predict prices of 3 houses
# The first house we will use is considered an "average" house in Seattle.
house1 = sales[sales['id']=='5309101200']
house1
# <img src="http://info.kingcounty.gov/Assessor/eRealProperty/MediaHandler.aspx?Media=2916871">
print house1['price']
print sqft_model.predict(house1)
print my_features_model.predict(house1)
# In this case, the model with more features provides a worse prediction than the simpler model with only 1 feature. However, on average, the model with more features is better.
# ##Prediction for a second, fancier house
#
# We will now examine the predictions for a fancier house.
house2 = sales[sales['id']=='1925069082']
house2
# <img src="https://ssl.cdn-redfin.com/photo/1/bigphoto/302/734302_0.jpg">
print sqft_model.predict(house2)
print my_features_model.predict(house2)
# In this case, the model with more features provides a better prediction. This behavior is expected here, because this house is more differentiated by features that go beyond its square feet of living space, especially the fact that it's a waterfront house.
# ##Last house, super fancy
#
# Our last house is a very large one owned by a famous Seattleite.
bill_gates = {'bedrooms':[8],
'bathrooms':[25],
'sqft_living':[50000],
'sqft_lot':[225000],
'floors':[4],
'zipcode':['98039'],
'condition':[10],
'grade':[10],
'waterfront':[1],
'view':[4],
'sqft_above':[37500],
'sqft_basement':[12500],
'yr_built':[1994],
'yr_renovated':[2010],
'lat':[47.627606],
'long':[-122.242054],
'sqft_living15':[5000],
'sqft_lot15':[40000]}
# <img src="https://upload.wikimedia.org/wikipedia/commons/thumb/d/d9/Bill_gates%27_house.jpg/2560px-Bill_gates%27_house.jpg">
print my_features_model.predict(graphlab.SFrame(bill_gates))
# The model predicts a price of over $13M for this house! But we expect the house to cost much more. (There are very few samples in the dataset of houses that are this fancy, so we don't expect the model to capture a perfect prediction here.)
| 4,986 |
/nbs/04_evaluation.causal.ipynb | de19465d94776f9d19fa579624d6ce13a15c4f62 | [
"Apache-2.0"
] | permissive | ArtificialSoftwareEngineering/AnonyCodeGen | https://github.com/ArtificialSoftwareEngineering/AnonyCodeGen | 0 | 1 | null | null | null | null | Jupyter Notebook | false | false | .py | 128,131 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
from sklearn.model_selection import cross_val_score
from xgboost import XGBClassifier, XGBRFClassifier
from sklearn.ensemble import RandomForestClassifier, StackingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split, StratifiedKFold
from sklearn.metrics import accuracy_score
from sklearn.ensemble import VotingClassifier
# Silence warnings
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
df = pd.read_csv('cab_rides.csv', nrows=10000)
df.head()
df.info()
df[df.isna().any(axis=1)]
df.dropna(inplace=True)
df['date'] = pd.to_datetime(df['time_stamp'])
df.head()
df['date'] = pd.to_datetime(df['time_stamp']*(10**6))
df.head()
import datetime as dt
df['month'] = df['date'].dt.month
df['hour'] = df['date'].dt.hour
df['dayofweek'] = df['date'].dt.dayofweek
# +
def weekend(row):
if row['dayofweek'] in [5,6]:
return 1
else:
return 0
df['weekend'] = df.apply(weekend, axis=1)
# +
def rush_hour(row):
if (row['hour'] in [6,7,8,9,15,16,17,18]) & (row['weekend'] == 0):
return 1
else:
return 0
df['rush_hour'] = df.apply(rush_hour, axis=1)
# -
df.tail()
df['cab_type'].value_counts()
df['cab_freq'] = df.groupby('cab_type')['cab_type'].transform('count')
df['cab_freq'] = df['cab_freq']/len(df)
df.tail()
from category_encoders.target_encoder import TargetEncoder
encoder = TargetEncoder()
df['cab_type_mean'] = encoder.fit_transform(df['cab_type'], df['price'])
df.tail()
from sklearn.datasets import load_breast_cancer
X, y = load_breast_cancer(return_X_y=True)
kfold = StratifiedKFold(n_splits=5)
# +
from sklearn.model_selection import cross_val_score
def classification_model(model):
# Obtain scores of cross-validation using 5 splits
scores = cross_val_score(model, X, y, cv=kfold)
# Return mean score
return scores.mean()
# -
classification_model(XGBClassifier())
classification_model(XGBClassifier(booster='gblinear'))
classification_model(XGBClassifier(booster='dart', one_drop=True))
classification_model(RandomForestClassifier(random_state=2))
classification_model(LogisticRegression(max_iter=10000))
classification_model(XGBClassifier(n_estimators=800, max_depth=4, colsample_bylevel=0.8))
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=2)
def y_pred(model):
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
score = accuracy_score(y_pred, y_test)
print(score)
return y_pred
y_pred_gbtree = y_pred(XGBClassifier())
y_pred_dart = y_pred(XGBClassifier(booster='dart', one_drop=True))
y_pred_forest = y_pred(RandomForestClassifier(random_state=2))
y_pred_logistic = y_pred(LogisticRegression(max_iter=10000))
y_pred_xgb = y_pred(XGBClassifier(max_depth=2, n_estimators=500, learning_rate=0.1))
df_pred = pd.DataFrame(data= np.c_[y_pred_gbtree, y_pred_dart, y_pred_forest, y_pred_logistic, y_pred_xgb],
columns=['gbtree', 'dart', 'forest', 'logistic', 'xgb'])
df_pred.corr()
estimators = []
logistic_model = LogisticRegression(max_iter=10000)
estimators.append(('logistic', logistic_model))
xgb_model = XGBClassifier(max_depth=2, n_estimators=500, learning_rate=0.1)
estimators.append(('xgb', xgb_model))
rf_model = RandomForestClassifier(random_state=2)
estimators.append(('rf', rf_model))
ensemble = VotingClassifier(estimators)
scores = cross_val_score(ensemble, X, y, cv=kfold)
print(scores.mean())
base_models = []
base_models.append(('lr', LogisticRegression()))
base_models.append(('xgb', XGBClassifier()))
base_models.append(('rf', RandomForestClassifier(random_state=2)))
# define meta learner model
meta_model = LogisticRegression()
# define the stacking ensemble
clf = StackingClassifier(estimators=base_models, final_estimator=meta_model)
scores = cross_val_score(clf, X, y, cv=kfold)
print(scores.mean())
| 4,196 |
/Intermediate Machine Learning/2 - missing values.ipynb | 4f82d7bd4d290aec8812293cf3c8510b2565fbca | [] | no_license | Moretti-eus/Kaggle-Courses | https://github.com/Moretti-eus/Kaggle-Courses | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 24,267 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **This notebook is an exercise in the [Intermediate Machine Learning](https://www.kaggle.com/learn/intermediate-machine-learning) course. You can reference the tutorial at [this link](https://www.kaggle.com/alexisbcook/missing-values).**
#
# ---
#
# Now it's your turn to test your new knowledge of **missing values** handling. You'll probably find it makes a big difference.
#
# # Setup
#
# The questions will give you feedback on your work. Run the following cell to set up the feedback system.
# Set up code checking
import os
if not os.path.exists("../input/train.csv"):
os.symlink("../input/home-data-for-ml-course/train.csv", "../input/train.csv")
os.symlink("../input/home-data-for-ml-course/test.csv", "../input/test.csv")
from learntools.core import binder
binder.bind(globals())
from learntools.ml_intermediate.ex2 import *
print("Setup Complete")
# In this exercise, you will work with data from the [Housing Prices Competition for Kaggle Learn Users](https://www.kaggle.com/c/home-data-for-ml-course).
#
# 
#
# Run the next code cell without changes to load the training and validation sets in `X_train`, `X_valid`, `y_train`, and `y_valid`. The test set is loaded in `X_test`.
# +
import pandas as pd
from sklearn.model_selection import train_test_split
# Read the data
X_full = pd.read_csv('../input/train.csv', index_col='Id')
X_test_full = pd.read_csv('../input/test.csv', index_col='Id')
# Remove rows with missing target, separate target from predictors
X_full.dropna(axis=0, subset=['SalePrice'], inplace=True)
y = X_full.SalePrice
X_full.drop(['SalePrice'], axis=1, inplace=True)
# To keep things simple, we'll use only numerical predictors
X = X_full.select_dtypes(exclude=['object'])
X_test = X_test_full.select_dtypes(exclude=['object'])
# Break off validation set from training data
X_train, X_valid, y_train, y_valid = train_test_split(X, y, train_size=0.8, test_size=0.2,
random_state=0)
# -
# Use the next code cell to print the first five rows of the data.
X_train.head()
# You can already see a few missing values in the first several rows. In the next step, you'll obtain a more comprehensive understanding of the missing values in the dataset.
#
# # Step 1: Preliminary investigation
#
# Run the code cell below without changes.
# +
# Shape of training data (num_rows, num_columns)
print(X_train.shape)
# Number of missing values in each column of training data
missing_val_count_by_column = (X_train.isnull().sum())
print(missing_val_count_by_column[missing_val_count_by_column > 0])
# -
# ### Part A
#
# Use the above output to answer the questions below.
# +
# Fill in the line below: How many rows are in the training data?
num_rows = 1168
# Fill in the line below: How many columns in the training data
# have missing values?
num_cols_with_missing = 3
# Fill in the line below: How many missing entries are contained in
# all of the training data?
tot_missing = 276
# Check your answers
step_1.a.check()
# +
# Lines below will give you a hint or solution code
#step_1.a.hint()
#step_1.a.solution()
# -
# ### Part B
# Considering your answers above, what do you think is likely the best approach to dealing with the missing values?
# +
# Check your answer (Run this code cell to receive credit!)
#inputation of mean
step_1.b.check()
# +
#step_1.b.hint()
# -
# To compare different approaches to dealing with missing values, you'll use the same `score_dataset()` function from the tutorial. This function reports the [mean absolute error](https://en.wikipedia.org/wiki/Mean_absolute_error) (MAE) from a random forest model.
# +
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
# Function for comparing different approaches
def score_dataset(X_train, X_valid, y_train, y_valid):
model = RandomForestRegressor(n_estimators=100, random_state=0)
model.fit(X_train, y_train)
preds = model.predict(X_valid)
return mean_absolute_error(y_valid, preds)
# -
# # Step 2: Drop columns with missing values
#
# In this step, you'll preprocess the data in `X_train` and `X_valid` to remove columns with missing values. Set the preprocessed DataFrames to `reduced_X_train` and `reduced_X_valid`, respectively.
# +
# Fill in the line below: get names of columns with missing values
cols_with_missing = [col for col in X_train.columns
if X_train[col].isnull().any()] # Your code here
print(cols_with_missing)
# Fill in the lines below: drop columns in training and validation data
reduced_X_train = X_train.drop(cols_with_missing, axis=1)
reduced_X_valid = X_valid.drop(cols_with_missing, axis=1)
# Check your answers
step_2.check()
print(reduced_X_train.shape)
# +
# Lines below will give you a hint or solution code
#step_2.hint()
#step_2.solution()
# -
# Run the next code cell without changes to obtain the MAE for this approach.
print("MAE (Drop columns with missing values):")
print(score_dataset(reduced_X_train, reduced_X_valid, y_train, y_valid))
# # Step 3: Imputation
#
# ### Part A
#
# Use the next code cell to impute missing values with the mean value along each column. Set the preprocessed DataFrames to `imputed_X_train` and `imputed_X_valid`. Make sure that the column names match those in `X_train` and `X_valid`.
# +
from sklearn.impute import SimpleImputer
# Fill in the lines below: imputation
my_imputer = SimpleImputer() # Your code here
imputed_X_train = pd.DataFrame(my_imputer.fit_transform(X_train))
imputed_X_valid = pd.DataFrame(my_imputer.transform(X_valid))
# Fill in the lines below: imputation removed column names; put them back
imputed_X_train.columns = X_train.columns
imputed_X_valid.columns = X_valid.columns
# Check your answers
step_3.a.check()
# +
# Lines below will give you a hint or solution code
#step_3.a.hint()
#step_3.a.solution()
# -
# Run the next code cell without changes to obtain the MAE for this approach.
print("MAE (Imputation):")
print(score_dataset(imputed_X_train, imputed_X_valid, y_train, y_valid))
# ### Part B
#
# Compare the MAE from each approach. Does anything surprise you about the results? Why do you think one approach performed better than the other?
# +
# Check your answer (Run this code cell to receive credit!)
# Yes, we do have a surprise. Method 1 got better results than method 2. Probably the mean has altered more the values than dropping those missing.
# Probably because there are only 3 columns with missing data. One has 20% of missings,other 4% and the last less than 1%
step_3.b.check()
# +
#step_3.b.hint()
# -
# # Step 4: Generate test predictions
#
# In this final step, you'll use any approach of your choosing to deal with missing values. Once you've preprocessed the training and validation features, you'll train and evaluate a random forest model. Then, you'll preprocess the test data before generating predictions that can be submitted to the competition!
#
# ### Part A
#
# Use the next code cell to preprocess the training and validation data. Set the preprocessed DataFrames to `final_X_train` and `final_X_valid`. **You can use any approach of your choosing here!** in order for this step to be marked as correct, you need only ensure:
# - the preprocessed DataFrames have the same number of columns,
# - the preprocessed DataFrames have no missing values,
# - `final_X_train` and `y_train` have the same number of rows, and
# - `final_X_valid` and `y_valid` have the same number of rows.
# +
missing_val_count_by_column = (X_train.isnull().sum())
print(missing_val_count_by_column[missing_val_count_by_column > 0])
X_train.columns
# +
# Name of columns with missing values
cols_with_missing = [col for col in X_train.columns
if X_train[col].isnull().any()] # Your code here
X_train_missings = X_train[cols_with_missing]
print(X_train_missings.describe()) # Há tres colunas com NAs: LotFrontage, MasVnrArea, GarageYrBlt
# +
#Ajustando coluna 1/3: GarageYrBlt
X_train.GarageYrBlt = X_train.GarageYrBlt.fillna(X_train.YearBuilt)
X_valid.GarageYrBlt = X_valid.GarageYrBlt.fillna(X_valid.YearBuilt)
# Testando:
cols_with_missing = [col for col in X_train.columns
if X_train[col].isnull().any()] # Your code here
X_train_missings = X_train[cols_with_missing]
print(X_train_missings.describe()) # Realmente não há mais NA nessa coluna.
#Ajustando colunas: LotFrontage, MasVnrArea - vou puxar média mesmo
my_imputer = SimpleImputer()
final_X_train = pd.DataFrame(my_imputer.fit_transform(X_train))
final_X_valid = pd.DataFrame(my_imputer.transform(X_valid))
#recolocando nome colunas
final_X_train.columns = X_train.columns
final_X_valid.columns = X_valid.columns
# Check your answers
step_4.a.check()
cols_with_missing = [col for col in X_train.columns
if X_train[col].isnull().any()] # Your code here
X_train_missings = X_train[cols_with_missing]
print(X_train_missings.describe())
# +
# Lines below will give you a hint or solution code
#step_4.a.hint()
#step_4.a.solution()
# -
# Run the next code cell to train and evaluate a random forest model. (*Note that we don't use the `score_dataset()` function above, because we will soon use the trained model to generate test predictions!*)
# +
#Definindo modelos:
model_1 = RandomForestRegressor(random_state=1)
model_2 = RandomForestRegressor(n_estimators=100, random_state=0)
model_3 = RandomForestRegressor(n_estimators=100, criterion='mae', random_state=0)
model_4 = RandomForestRegressor(n_estimators=200, min_samples_split=20, random_state=0)
model_5 = RandomForestRegressor(n_estimators=100, max_depth=7, random_state=0)
models = [model_1, model_2, model_3, model_4, model_5]
# Função que irá fazer fit, prever e retornar MAE
def score_model(model, X_t=final_X_train, X_v=final_X_valid, y_t=y_train, y_v=y_valid):
model.fit(X_t, y_t)
preds = model.predict(X_v)
return mean_absolute_error(y_v, preds)
for i in range(0, len(models)):
mae = score_model(models[i])
print("Model %d MAE: %d" % (i+1, mae))
# -
# ### Part B
#
# Use the next code cell to preprocess your test data. Make sure that you use a method that agrees with how you preprocessed the training and validation data, and set the preprocessed test features to `final_X_test`.
#
# Then, use the preprocessed test features and the trained model to generate test predictions in `preds_test`.
#
# In order for this step to be marked correct, you need only ensure:
# - the preprocessed test DataFrame has no missing values, and
# - `final_X_test` has the same number of rows as `X_test`.
# +
#Ajustando coluna 1/3: GarageYrBlt
X_test.GarageYrBlt = X_test.GarageYrBlt.fillna(X_test.YearBuilt)
#Ajustando colunas: LotFrontage, MasVnrArea - vou puxar média mesmo
my_imputer = SimpleImputer()
final_X_test = pd.DataFrame(my_imputer.fit_transform(X_test))
#recolocando nome colunas
final_X_test.columns = X_train.columns
# Fill in the line below: get test predictions
preds_test = model_1.predict(final_X_test)
# Check your answers
step_4.b.check()
# +
# Lines below will give you a hint or solution code
#step_4.b.hint()
#step_4.b.solution()
# -
# Run the next code cell without changes to save your results to a CSV file that can be submitted directly to the competition.
# Save test predictions to file
output = pd.DataFrame({'Id': X_test.index,
'SalePrice': preds_test})
output.to_csv('submission.csv', index=False)
# # Submit your results
#
# Once you have successfully completed Step 4, you're ready to submit your results to the leaderboard! (_You also learned how to do this in the previous exercise. If you need a reminder of how to do this, please use the instructions below._)
#
# First, you'll need to join the competition if you haven't already. So open a new window by clicking on [this link](https://www.kaggle.com/c/home-data-for-ml-course). Then click on the **Join Competition** button.
#
# 
#
# Next, follow the instructions below:
# 1. Begin by clicking on the **Save Version** button in the top right corner of the window. This will generate a pop-up window.
# 2. Ensure that the **Save and Run All** option is selected, and then click on the **Save** button.
# 3. This generates a window in the bottom left corner of the notebook. After it has finished running, click on the number to the right of the **Save Version** button. This pulls up a list of versions on the right of the screen. Click on the ellipsis **(...)** to the right of the most recent version, and select **Open in Viewer**. This brings you into view mode of the same page. You will need to scroll down to get back to these instructions.
# 4. Click on the **Output** tab on the right of the screen. Then, click on the file you would like to submit, and click on the **Submit** button to submit your results to the leaderboard.
#
# You have now successfully submitted to the competition!
#
# If you want to keep working to improve your performance, select the **Edit** button in the top right of the screen. Then you can change your code and repeat the process. There's a lot of room to improve, and you will climb up the leaderboard as you work.
#
#
# # Keep going
#
# Move on to learn what **[categorical variables](https://www.kaggle.com/alexisbcook/categorical-variables)** are, along with how to incorporate them into your machine learning models. Categorical variables are very common in real-world data, but you'll get an error if you try to plug them into your models without processing them first!
| 13,993 |
/theatre.ipynb | 29fb0840fde3b053e47aaf681fcb953454217655 | [] | no_license | ShahMusaev/Anomaly-Detection-with-LSTM | https://github.com/ShahMusaev/Anomaly-Detection-with-LSTM | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 267,013 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python36
# ---
# # Импорт библиотек
# +
# import libraries
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from sklearn.externals import joblib
import seaborn as sns
sns.set(color_codes=True)
import matplotlib.pyplot as plt
# %matplotlib inline
import tensorflow as tf
from keras.layers import Input, Dropout, Dense, LSTM, TimeDistributed, RepeatVector
from keras.models import Model
from keras import regularizers
# -
from pylab import rcParams
rcParams['figure.figsize'] = 22, 10
# # Загрузка данных
# В качестве данных мы берем показатели датчиков двигателей, которые вращают шкив, измеряющий угол от 0 до 3600. В последствии, этот угол, в зависимости от кол-ва оборотов, преобразуется в позицию (в см) декорации.
Position_df = pd.read_csv('Position.csv',sep=',', encoding='UTF-8')
Position_df['Time'] = pd.to_datetime(Position_df['time'])
def print_position(df, number):
i = 0
while i < number:
name = 'theatre.D'+str(i)+'_Position_AS'
item = df[df.name == name]
if(len(item) > 100):
plt.plot(item.Time, item.value, label=name)
plt.legend()
i = i + 1
COUNT = 15
print_position(Position_df, COUNT)
# На графике хорошо видно, что датчик на двигателе №14 имеет анамальное значение. Именно его мы и возьмем для обучения нашей модели
Position_D14 = Position_df[Position_df.name == 'theatre.D14_Position_AS1']
Position_D14 = pd.DataFrame(Position_D14, columns = ['Time', 'value'])
Position_D14 = Position_D14.set_index('Time')
# # Подготовка данных
# Определяем наборы данных для обучения и тестирования нашей модели. Разделяем наши данные на две части. Первая часть (train), в котором мы тренируемся в набора данных, которая представляет нормальные условия работы. Вторая часть (test), которая содержит аномалии.
train_size = int(len(Position_D14) * 0.82)
test_size = len(Position_D14) - train_size
train, test = Position_D14.iloc[2:train_size], Position_D14.iloc[train_size:len(Position_D14)]
print("Training dataset shape:", train.shape)
print("Test dataset shape:", test.shape)
# # Нормализация и стандартизация данных
# normalize the data
scaler = MinMaxScaler()
X_train = scaler.fit_transform(train)
X_test = scaler.transform(test)
X_train.shape
# # Преобразование данных для LTSM
# Затем мы преобразуем наши данные в формат, подходящий для ввода в сеть LSTM. Ячейки LSTM ожидают трехмерный тензор формы [выборки данных, временные шаги, особенности]
# reshape inputs for LSTM [samples, timesteps, features]
X_train = X_train.reshape(X_train.shape[0], 1, X_train.shape[1])
print("Training data shape:", X_train.shape)
X_test = X_test.reshape(X_test.shape[0], 1, X_test.shape[1])
print("Test data shape:", X_test.shape)
# # Построение нейронной сети LSTM
# Для нашей модели обнаружения аномалий мы будем использовать архитектуру нейроконтроллеров с автоматическим кодированием.
# Архитектура автоэнкодера по существу изучает функцию «идентичности». Он примет входные данные,
# создаст сжатое представление основных движущих характеристик этих данных, а затем научится восстанавливать их снова.
# Основанием для использования этой архитектуры для обнаружения аномалий является то, что мы обучаем модель «нормальным» данным и определяем полученную ошибку реконструкции.
# Затем, когда модель встретит данные, которые находятся за пределами нормы, и попытается восстановить их, мы увидим увеличение ошибки восстановления,
# поскольку модель никогда не обучалась для точного воссоздания элементов вне нормы.
# define the autoencoder network model
def autoencoder_model(X):
inputs = Input(shape=(X.shape[1], X.shape[2]))
L1 = LSTM(16, activation='relu', return_sequences=True,
kernel_regularizer=regularizers.l2(0.00))(inputs)
L2 = LSTM(4, activation='relu', return_sequences=False)(L1)
L3 = RepeatVector(X.shape[1])(L2)
L4 = LSTM(4, activation='relu', return_sequences=True)(L3)
L5 = LSTM(16, activation='relu', return_sequences=True)(L4)
output = TimeDistributed(Dense(X.shape[2]))(L5)
model = Model(inputs=inputs, outputs=output)
return model
# create the autoencoder model
model = autoencoder_model(X_train)
model.compile(optimizer='adam', loss='mae')
model.summary()
# fit the model to the data
nb_epochs = 100
batch_size = 10
history = model.fit(X_train, X_train, epochs=nb_epochs, batch_size=batch_size,validation_split=0.05).history
# plot the training losses
fig, ax = plt.subplots(figsize=(14, 6), dpi=80)
ax.plot(history['loss'], 'b', label='Train', linewidth=2)
ax.plot(history['val_loss'], 'r', label='Validation', linewidth=2)
ax.set_title('Model loss', fontsize=16)
ax.set_ylabel('Loss (mae)')
ax.set_xlabel('Epoch')
ax.legend(loc='upper right')
plt.show()
fig.savefig('Model less.png')
# График тренировочных потерь для оценки производительности модели
# plot the loss distribution of the training set
X_pred = model.predict(X_train)
X_pred = X_pred.reshape(X_pred.shape[0], X_pred.shape[2])
X_pred = pd.DataFrame(X_pred, columns=train.columns)
X_pred.index = train.index
xx = X_train.reshape(X_train.shape[0], X_train.shape[2])
xx = pd.DataFrame(xx, columns=train.columns)
xx.index = train.index
plt.plot(X_pred, color='blue', label='pred')
plt.plot(xx,color='red', label='real')
plt.legend()
# # Распределение убытков
# Составляя график распределения вычисленных потерь в обучающем наборе, мы можем определить подходящее пороговое значение для выявления аномалии.
# При этом можно убедиться, что этот порог установлен выше «уровня шума», чтобы ложные срабатывания не срабатывали.
scored = pd.DataFrame(index=train.index)
Xtrain = X_train.reshape(X_train.shape[0], X_train.shape[2])
scored['Loss_mae'] = np.mean(np.abs(X_pred-Xtrain), axis = 1)
plt.figure(figsize=(16,9), dpi=80)
plt.title('Loss Distribution', fontsize=16)
sns.distplot(scored['Loss_mae'], bins = 100, kde= True, color = 'blue')
plt.savefig('Loss Distribution.png')
# Исходя из приведенного выше распределения потерь, возьмем пороговое значение 0,01 для обозначения аномалии. Затем мы рассчитываем потери на реконструкцию в обучающем и тестовом наборах, чтобы определить, когда показания датчика пересекают порог аномалии.
# calculate the loss on the test set
X_pred = model.predict(X_test)
X_pred = X_pred.reshape(X_pred.shape[0], X_pred.shape[2])
X_pred = pd.DataFrame(X_pred, columns=test.columns)
X_pred.index = test.index
xtest = X_test.reshape(X_test.shape[0], X_test.shape[2])
xtest = pd.DataFrame(xtest, columns=test.columns)
xtest.index = test.index
plt.plot(X_pred, color='blue')
plt.plot(xtest,color='red')
plt.savefig('Prediction.png')
# # Аномалии
scored_test = pd.DataFrame(index=test.index)
Xtest = X_test.reshape(X_test.shape[0], X_test.shape[2])
scored_test['Loss_mae'] = np.mean(np.abs(X_pred-Xtest), axis = 1)
scored_test['Threshold'] = 0.01
scored_test['Anomaly'] = scored_test['Loss_mae'] > scored_test['Threshold']
# scored['value'] = test.value
scored_test.head()
# +
# calculate the same metrics for the training set
# and merge all data in a single dataframe for plotting
X_pred_train = model.predict(X_train)
X_pred_train = X_pred_train.reshape(X_pred_train.shape[0], X_pred_train.shape[2])
X_pred_train = pd.DataFrame(X_pred_train, columns=train.columns)
X_pred_train.index = train.index
scored_train = pd.DataFrame(index=train.index)
scored_train['Loss_mae'] = np.mean(np.abs(X_pred_train-Xtrain), axis = 1)
scored_train['Threshold'] = 0.01
scored_train['Anomaly'] = scored_train['Loss_mae'] > scored_train['Threshold']
# scored_train['value'] = train.value
scored = pd.concat([scored_train, scored_test])
# -
# Чтобы визуализировать результаты с течением времени. Красная линия указывает на наше пороговое значение 0,01.
# plot bearing failure time plot
scored.plot(logy=True, figsize=(16,9), color=['blue','red'])
plt.savefig('Threshold.png')
test_score_df = scored_test
test_score_df['value'] = test.value
anomalies = test_score_df[test_score_df.Anomaly == True]
anomalies
# +
plt.plot(
test.index,
test.value,
label='value'
)
sns.scatterplot(
anomalies.index,
anomalies.value,
color=sns.color_palette()[3],
s=52,
label='anomaly'
)
plt.xticks(rotation=25)
plt.legend()
plt.savefig('Anomalies.png')
# -
# по графику видно, какие значения двигателя приводят к анамалии, а значит в дальyейшем мы можем заранее определять по первым показателям, когда у нас возникают анамалии
model.save('model.h5')
| 8,691 |
/notebooks/vfsousas/question-answer-npl-exercise.ipynb | 0ba0a83f3f595bac0e06e07e3cb4f3081a7a5c0c | [] | no_license | Sayem-Mohammad-Imtiaz/kaggle-notebooks | https://github.com/Sayem-Mohammad-Imtiaz/kaggle-notebooks | 5 | 6 | null | null | null | null | Jupyter Notebook | false | false | .py | 4,674 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5" _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19"
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory
import os
print(os.listdir("../input"))
# Any results you write to the current directory are saved as output.
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a" _kg_hide-input=false
dfS08_question= pd.read_csv('../input/S08_question_answer_pairs.txt', sep="\t")
# -
# **Excluindo as colunas que nao contem as perguntas**
dfS08_question= pd.read_csv('../input/S08_question_answer_pairs.txt', sep="\t")
dfS08_question.drop(labels=['ArticleTitle', 'DifficultyFromQuestioner', 'DifficultyFromAnswerer', 'ArticleFile', 'Answer'], axis=1, inplace=True)
dfS08_question.head()
# **Convertendo o Dataframe para txt para depois importar como array de texto ja dentro do Numpy**
# +
import nltk
import numpy as np
from nltk.tokenize import sent_tokenize
dfS08_question.to_csv("./csvfile.txt", sep=";", index=False, header=False)
print(os.listdir("."))
rawText = np.genfromtxt("./csvfile.txt", dtype='str', delimiter=';', usecols=np.arange(0,1))
csvFile.shape
# +
from nltk import pos_tag
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer
from nltk.tokenize import word_tokenize
import string
from nltk.corpus import wordnet
stopwords_list = stopwords.words('english')
lemmatizer = WordNetLemmatizer()
def my_tokenizer(doc):
words = word_tokenize(doc)
pos_tags = pos_tag(words)
non_stopwords = [w for w in pos_tags if not w[0].lower() in stopwords_list]
non_punctuation = [w for w in non_stopwords if not w[0] in string.punctuation]
lemmas = []
for w in non_punctuation:
if w[1].startswith('J'):
pos = wordnet.ADJ
elif w[1].startswith('V'):
pos = wordnet.VERB
elif w[1].startswith('N'):
pos = wordnet.NOUN
elif w[1].startswith('R'):
pos = wordnet.ADV
else:
pos = wordnet.NOUN
lemmas.append(lemmatizer.lemmatize(w[0], pos))
return lemmas
# +
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf_vectorizer = TfidfVectorizer(tokenizer=my_tokenizer)
tfs = tfidf_vectorizer.fit_transform(rawText)
print(tfs.shape)
# -
# **Aqui começa o chatbot, quando se esta em modo de edição do kaggle é possivel entrar com as perguntas e receber a frase mais similar como resposta.**
from sklearn.metrics.pairwise import cosine_similarity
while True:
answer = input("Digite sua pesquisa")
if answer == 'Sair':
break
elif answer !='Sair':
query_vect = tfidf_vectorizer.transform([answer])
positions = cosine_similarity(query_vect, tfs)[0]
print('O texto mais proximo localizado foi: ', rawText[np.argmax(positions)])
| 3,616 |
/Day4_B35.ipynb | becb62e78f54c6172988f6d297cfe61c92a90b7a | [] | no_license | cyclonstar/python_fundamentals | https://github.com/cyclonstar/python_fundamentals | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 8,775 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
Today_topic = ['list'] Important note : it's an mutable datatype.
print(Today_topic)
Defination: A list is a collection of items in a particular order
how to define it ?------------[]
colors = ['red','green','yellow','blue','orange','black'] ---- #0,1,2,3,4,5,6-------------
print(colors)
type(colors) -----------------same as string to check with type of datatype
Indexing:-- 0,1,2,3...............
# +
# i want to access only blue color in the output
# -
print(colors[3])
# +
important points here in list as
1. how to add the element in the list
2. how to modify the element in the list
3. how to delete the element in the list
# -
1.. 'add element -- for eg want to add Purple color to the list'
colors.append('purple')== we use as any variable.append to add any element to the current list (but only at the end of the list)
print(colors)
adding white now ..
colors.append('white')
print(colors)
1.. 'continue -- want to add magenta to the 3 index of the list' ..
colors.insert(3,'magenta') ==== so we use variable.insert to add element any desired index to the list ..
print(colors)
print(colors[3])
print(colors[3].upper())
# +
Q-- diff n/w append and insert ?
append to add just any element to the list and that element will be added to end of the list.
whereas insert is to add any element to desired index no. to the list .
# -
2. "modify the element of the list"
-- want to modify 'purple' to 'pink'
print(colors)
# +
colors[8] = 'pink'
print(colors)
# -
3. 'to delete the element from the list'
# +
# want to delete magenta , magent ,magenta from the list ---
# -
colors = ['red','green','yellow','magenta', 'magent','magenta','blue','orange','black','pink','white']
print(colors)
del colors[3:6]
print(colors)
now to delete green from the list
del colors[1]
print(colors)
#
# Build a data pipeline from features stored in a CSV file. For this example, Titanic dataset will be used as a toy dataset stored in CSV format.
# + pycharm={"name": "#%%\n"}
# Download Titanic dataset (in csv format).
d = requests.get("https://raw.githubusercontent.com/tflearn/tflearn.github.io/master/resources/titanic_dataset.csv")
with open("titanic_dataset.csv", "wb") as f:
f.write(d.content)
# + pycharm={"name": "#%%\n"}
# Load Titanic dataset.
# Original features: survived,pclass,name,sex,age,sibsp,parch,ticket,fare
# Select specific columns: survived,pclass,name,sex,age,fare
column_to_use = [0, 1, 2, 3, 4, 8]
record_defaults = [tf.int32, tf.int32, tf.string, tf.string, tf.float32, tf.float32]
# Load the whole dataset file, and slice each line.
data = tf.data.experimental.CsvDataset("titanic_dataset.csv", record_defaults, header=True, select_cols=column_to_use)
# Refill data indefinitely.
data = data.repeat()
# Shuffle data.
data = data.shuffle(buffer_size=1000)
# Batch data (aggregate records together).
data = data.batch(batch_size=2)
# Prefetch batch (pre-load batch for faster consumption).
data = data.prefetch(buffer_size=1)
# + pycharm={"name": "#%%\n"}
for survived, pclass, name, sex, age, fare in data.take(1):
print(survived.numpy())
print(pclass.numpy())
print(name.numpy())
print(sex.numpy())
print(age.numpy())
print(fare.numpy())
# + [markdown] pycharm={"name": "#%% md\n"}
# # Load Images
#
# Build a data pipeline by loading images from disk. For this example, Oxford Flowers dataset will be used.
# + pycharm={"name": "#%%\n"}
# Download Oxford 17 flowers dataset
d = requests.get("http://www.robots.ox.ac.uk/~vgg/data/flowers/17/17flowers.tgz")
with open("17flowers.tgz", "wb") as f:
f.write(d.content)
# Extract archive.
with tarfile.open("17flowers.tgz") as t:
t.extractall()
# + pycharm={"name": "#%%\n"}
with open('jpg/dataset.csv', 'w') as f:
c = 0
for i in range(1360):
f.write("jpg/image_%04i.jpg,%i\n" % (i+1, c))
if (i+1) % 80 == 0:
c += 1
# + pycharm={"name": "#%%\n"}
# Load Images
with open("jpg/dataset.csv") as f:
dataset_file = f.read().splitlines()
# Load the whole dataset file, and slice each line.
data = tf.data.Dataset.from_tensor_slices(dataset_file)
# Refill data indefinitely.
data = data.repeat()
# Shuffle data.
data = data.shuffle(buffer_size=1000)
# Load and pre-process images.
def load_image(path):
# Read image from path.
image = tf.io.read_file(path)
# Decode the jpeg image to array [0, 255].
image = tf.image.decode_jpeg(image)
# Resize images to a common size of 256x256.
image = tf.image.resize(image, [256, 256])
# Rescale values to [-1, 1].
image = 1. - image / 127.5
return image
# Decode each line from the dataset file.
def parse_records(line):
# File is in csv format: "image_path,label_id".
# TensorFlow requires a default value, but it will never be used.
image_path, image_label = tf.io.decode_csv(line, ["", 0])
# Apply the function to load images.
image = load_image(image_path)
return image, image_label
# Use 'map' to apply the above functions in parallel.
data = data.map(parse_records, num_parallel_calls=4)
# Batch data (aggregate images-array together).
data = data.batch(batch_size=2)
# Prefetch batch (pre-load batch for faster consumption).
data = data.prefetch(buffer_size=1)
# + pycharm={"name": "#%%\n"}
for batch_x, batch_y in data.take(1):
print(batch_x, batch_y)
# + [markdown] pycharm={"name": "#%% md\n"}
# # Load data from a Generator
# + pycharm={"name": "#%%\n"}
# Create a dummy generator.
def generate_features():
# Function to generate a random string.
def random_string(length):
return ''.join(random.choice(string.ascii_letters) for m in range(length))
# Return a random string, a random vector, and a random int.
yield random_string(4), np.random.uniform(size=4), random.randint(0, 10)
# + pycharm={"name": "#%%\n"}
# Load a numpy array using tf data api with `from_tensor_slices`.
data = tf.data.Dataset.from_generator(generate_features, output_types=(tf.string, tf.float32, tf.int32))
# Refill data indefinitely.
data = data.repeat()
# Shuffle data.
data = data.shuffle(buffer_size=100)
# Batch data (aggregate records together).
data = data.batch(batch_size=4)
# Prefetch batch (pre-load batch for faster consumption).
data = data.prefetch(buffer_size=1)
# + pycharm={"name": "#%%\n"}
# Display data.
for batch_str, batch_vector, batch_int in data.take(5):
print(batch_str, batch_vector, batch_int)
# + pycharm={"name": "#%%\n"}
| 6,802 |
/Libraries_Installation.ipynb | a54e83af778b5831f1d0399ee038ce767e7cea64 | [] | no_license | yassineaitmalek/DW_project | https://github.com/yassineaitmalek/DW_project | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 26,044 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1>Libraries Installation</h1>
#
# +
# ! pip3 install pandas
# ! pip3 install pandasql
# ! pip3 install datetime
# ! pip3 install chart_studio
# ! pip3 install cufflinks
# ! sudo apt-get install python-psycopg2 -y
# ! sudo apt-get install libpq-dev -y
# ! pip3 install psycopg2-binary
# ! pip install pandas
# ! pip install pandasql
# ! pip install datetime
# ! pip install psycopg2-binary
# -
import numpy as np
from spacy.lang.en import English
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator
nlp = English()
# + id="X_c6BkB8my1u"
pd.set_option('display.max_rows', None)
pd.set_option('display.max_columns', None)
pd.set_option('display.width', None)
colWidth = pd.get_option('display.max_colwidth')
# + [markdown] id="0iImvnhOs7ia"
# # Class and function definitions
# + id="Fdwy9FpK7bCG"
class Corpus:
def __init__(self, filePath, encoding, maxTokens):
self.bagOfWords = Counter()
self.listOfWords = ["removeMe"] # So that the list is not empty
self.wordInDocIndex = np.zeros(1, dtype=int) # So that array is not empty
self.docLen = list()
self.numDocs = 0
docNumber = 0
numActualToken = 0
fileHandler = open(filePath, encoding=encoding)
with fileHandler:
for doc in fileHandler:
self.numDocs += 1
tokens = doc.lower().split()
numActualToken += len(tokens)
numTokenTemp = 0
for iToken in tokens:
if not nlp.vocab[iToken].is_stop and iToken not in ['.', '&', '...', '-', ';', '/', '!', ',', '(',
')', "'", '"', ':', "?",
'....'] and not iToken.isdigit():
self.bagOfWords[iToken] += 1
self.listOfWords = self.listOfWords + [iToken]
numTokenTemp += 1
self.docLen.append(numTokenTemp)
tempArray = docNumber * np.ones(numTokenTemp, dtype=int)
self.wordInDocIndex = np.concatenate((self.wordInDocIndex, tempArray), axis=None)
docNumber += 1
if numActualToken >= maxTokens + 1:
self.listOfWords.pop(0) # Removed "removeMe"
self.wordInDocIndex = np.delete(self.wordInDocIndex, 0)
break
fileHandler.close()
def most_common_word(self, numOfMostCommonWords):
self.corpusMostCommonWords = Counter(self.bagOfWords).most_common(numOfMostCommonWords)
class IntegerVocabulary:
def __init__(self, mostCommonWords, maxVocabSize):
self.integerVocab = dict() # Changed from list to dict - See assignment 1
wordCode = 0
for iWord in range(maxVocabSize):
self.integerVocab[mostCommonWords[iWord][0]] = wordCode
wordCode += 1
# + id="phCXu4mG7eMu"
def estimateDocTopicProb(docId):
numerator = docTopicFreq[docId] + topicParameter
denominator = books.docLen[docId] - 1 + numTopics * topicParameter
return numerator / denominator
def estimateTopicWordProb(wordIndex, prevWordIndex):
numerator = bigramTopicFreq[wordIndex, prevWordIndex] + dirParameter
sumWordsinToken = np.sum(wordTopicFreq, axis=0)
denominator = sumWordsinToken + numUniqueWords * dirParameter
return numerator / denominator
def estimateTopicWordProbUnPairedWords(wordIndex): # The first words don't have preceeding word so this function is
# picked from task 1 of this assignment.
numerator = wordTopicFreq[wordIndex] + dirParameter
sumWordsinToken = wordTopicFreq.sum(axis=0)
denominator = sumWordsinToken + numUniqueWords * dirParameter # Need to check if should be commented or included.
return numerator / denominator
# + [markdown] id="9iFz8dAhtK19"
# **Variable Defifnition**
# + id="y24HiBuZ8Cxv"
filePath = "/content/drive/My Drive/MLNLP/Assignment2/books.txt"
fileEncoding = "ISO-8859-1"
# + id="NfwfapCw96BL"
maxGibbsIterations = 200
maxTokens = 100000
desiredWordsToBePrinted = 20
# + id="NOWNf8zX8h_P"
books = Corpus(filePath, fileEncoding, maxTokens)
maxTokens = len(books.listOfWords)
numUniqueWords = len(books.bagOfWords)
numDocs = len(books.docLen)
maxVocabSize = numUniqueWords
numOfMostCommonWords = maxVocabSize # Not considering padding and out-of-vocabulary - See assignment 1
books.most_common_word(numOfMostCommonWords)
booksIV = IntegerVocabulary(books.corpusMostCommonWords, maxVocabSize)
# + id="SUM5iO7OPwKe"
documentTopicsDF = pd.DataFrame()
figureNum = 0
numTopicsList = [10, 50]
parameterList = [(0.1, 0.1), (0.01, 0.01)]
wordTopicResultsT1 = list()
sumWordsinTokenResultsT1 = list()
# + [markdown] id="FidJuiapuHFd"
# # Execution loop
# + id="cDop8R3N_InD" colab={"base_uri": "https://localhost:8080/"} outputId="78461d40-3ed1-490f-99f8-245266c0e9c0"
iCase = 0
for iTopicList in range(len(numTopicsList)):
for iParameterList in range(len(parameterList)):
print(iCase, end=" ")
numTopics = numTopicsList[iTopicList]
dirParameter = parameterList[iParameterList][0]
topicParameter = parameterList[iParameterList][1]
wordTopicResultsT1.append(list())
sumWordsinTokenResultsT1.append(np.zeros(numTopics))
wordTopic = np.random.randint(0, numTopics, maxTokens)
wordTopicFreq = np.zeros((numUniqueWords, numTopics), dtype=int)
docId = np.arange(0, numDocs, 1)
docTopicFreq = np.zeros((numDocs, numTopics), dtype=int)
# Random initialization matrix updates
jDocId = 0
for iNumber, iWord in enumerate(books.listOfWords):
wordIdentity = booksIV.integerVocab[iWord]
wordTopicFreq[wordIdentity, wordTopic[iNumber]] += 1
jDocId = books.wordInDocIndex[iNumber]
docTopicFreq[jDocId, wordTopic[iNumber]] += 1
iGibbs = 0
while iGibbs < maxGibbsIterations:
iGibbs += 1
iDocId = 0
for iNumber, iWord in enumerate(books.listOfWords):
topicNumber = wordTopic[iNumber]
wordIdentity = booksIV.integerVocab[iWord]
wordTopicFreq[wordIdentity, topicNumber] -= 1
iDocId = books.wordInDocIndex[iNumber]
docTopicFreq[iDocId, topicNumber] -= 1
docTopicProb = estimateDocTopicProb(iDocId)
wordTopicProb = estimateTopicWordProbUnPairedWords(
wordIdentity) # Notice we have passed the integer index
probWordInToken = np.multiply(docTopicProb, wordTopicProb)
selectedTopic = np.random.multinomial(1, probWordInToken / probWordInToken.sum()).argmax()
wordTopicFreq[booksIV.integerVocab[iWord], selectedTopic] += 1
docTopicFreq[iDocId, selectedTopic] += 1
wordTopic[iNumber] = selectedTopic
wordTopicResultsT1[iCase] = wordTopic
sumWordsinTokenResultsT1[iCase] = wordTopicFreq.sum(axis=0)
iCase += 1
# + [markdown] id="Un8Fy89Qtf8E"
# # Results
# + [markdown] id="VL0UPmwYuXRF"
# The next cell contains all the infomartion required to analyse results and draw conclusions. The cell contains 1 figure and 2 tables each for one of the 4 cases. The figure represents the fraction of words present in the topic as compared to total number of words considered for execution. The two tables represents words in each topic and words in the dominant topic of each document. Both the tables are trimmed to display 5 top topics and 15 documents respectively.
#
# In general, the abstract format of output is figure, top 5 topics table and dominant topic in document table.
#
# The table with top 5 topics portrays words that settled in topic by raw count, relative count and a mixture of raw and relative count. Raw count implies the words that are dominant within the topic, relative implies the words that are unique within corpus but ended under the highlighted topic and "relraw" implies the words first sorted based on raw count and then top 20 words were picked which were sorted by their relative count in the corpus.
#
# The table related to documents and dominant topic in the document goes through every document and looks for the topic that is dominant within the document and prints how much percentage of document exists in the topic and some of the words in this intersection.
#
# The observations are explained after printing all the outputs below.
# + id="pIW8wMUBXR7r" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="c6d58688-5b84-4e07-ca41-c1234ae64e25"
# Results
topTopicsSize = 5
iCase = 0
for iTopicList in range(len(numTopicsList)):
for iParameterList in range(len(parameterList)):
numTopics = numTopicsList[iTopicList]
dirParameter = parameterList[iParameterList][0]
topicParameter = parameterList[iParameterList][1]
print("Case %d, \u03B1 = %.2f, \u03B2 = %.2f, K = %d\n\n" % (iCase + 1, topicParameter, dirParameter, numTopics))
# Result part - 1. Plots
sumWordsinToken = sumWordsinTokenResultsT1[iCase].copy()
figureNum += 1
ax = plt.figure(figureNum).gca()
plt.scatter(np.arange(0, numTopics), sumWordsinToken / maxTokens)
plt.xlabel("Topic Number")
plt.ylabel("fraction of words")
plt.title(r"Fraction of words, $\alpha = {}, \beta$ = {}, K = {}".format(str(topicParameter), str(dirParameter),
str(numTopics)))
ax.xaxis.set_major_locator(MaxNLocator(integer=True))
plt.show()
# Result part - 2
topicWordRelationByRawCount = list()
topicWordRelationByRelativeCount = list()
topicWordRelationByRelInMaxRaw = list()
for iTopic in range(numTopics):
topicWordRelationByRawCount.append(Counter())
topicWordRelationByRelInMaxRaw.append(Counter())
for iNumber, iWord in enumerate(books.listOfWords):
topicWordRelationByRawCount[wordTopicResultsT1[iCase][iNumber]][iWord] += 1
for iTopic in range(numTopics):
topicWordRelationByRelativeCount.append(topicWordRelationByRawCount[iTopic].copy())
for iTopic in range(numTopics):
for iWord in topicWordRelationByRawCount[iTopic].keys():
temp = topicWordRelationByRawCount[iTopic][iWord]
topicWordRelationByRelativeCount[iTopic][iWord] = temp / books.bagOfWords[
iWord]
for iTopic in range(numTopics):
tempDict = [topicWordRelationByRawCount[iTopic], topicWordRelationByRelativeCount[iTopic]]
for iWord in topicWordRelationByRawCount[iTopic].keys():
topicWordRelationByRelInMaxRaw[iTopic][iWord] = tuple(i[iWord] for i in tempDict)
backupRel = list()
for iTopic in range(numTopics):
backupRel.append(topicWordRelationByRelativeCount[iTopic].copy())
for iTopic in range(numTopics):
topicWordRelationByRawCount[iTopic] = sorted(topicWordRelationByRawCount[iTopic].items(),
key=lambda x: x[1],
reverse=True)
topicWordRelationByRelativeCount[iTopic] = sorted(topicWordRelationByRelativeCount[iTopic].items(),
key=lambda x: x[1], reverse=True)
topicWordRelationByRelInMaxRaw[iTopic] = sorted(topicWordRelationByRelInMaxRaw[iTopic].items(),
key=lambda x: x[1][0], reverse=True)
maxWordsCanBePrinted = list()
for iMax in range(numTopics):
maxWordsCanBePrinted.append(len(topicWordRelationByRawCount[iMax]))
numWordsToPrint = list()
for iMin in range(numTopics):
numWordsToPrint.append(min(maxWordsCanBePrinted[iMin], desiredWordsToBePrinted))
topicWordRelationByRelInMaxRaw[iMin] = topicWordRelationByRelInMaxRaw[iMin][:numWordsToPrint[iMin]]
topicWordRelationByRelInMaxRaw[iMin] = sorted(topicWordRelationByRelInMaxRaw[iMin],
key=lambda x: x[1][1], reverse=True)
uniqueWordsinToken = [len(topicWordRelationByRelativeCount[iTopic]) for iTopic in range(numTopics)]
uniqueWordsinToken = np.array(uniqueWordsinToken)
topTopics = sumWordsinToken.argsort()[numTopics - topTopicsSize:]
listHeader = ["removeMe"]
for i in range(len(topTopics)):
listHeader = listHeader + ["Topic {}".format(topTopics[i])]
listHeader.pop(0)
colHeaders = pd.MultiIndex.from_product([listHeader, ['Raw', 'Rel', 'RelRaw']])
resultTopicDF = pd.DataFrame()
# for iDFRow in range(min(numWordsToPrint)): # For all topics
for iDFRow in range(desiredWordsToBePrinted):
tempRow = list()
for iDFCell in range(len(topTopics)):
try:
tempRow.append(topicWordRelationByRawCount[topTopics[iDFCell]][iDFRow][0])
except:
tempRow.append("NA")
try:
tempRow.append(topicWordRelationByRelativeCount[topTopics[iDFCell]][iDFRow][0])
except:
tempRow.append("NA")
try:
tempRow.append(topicWordRelationByRelInMaxRaw[topTopics[iDFCell]][iDFRow][0])
except:
tempRow.append("NA")
tempDF = pd.DataFrame([tempRow])
if len(tempRow) > 0:
resultTopicDF = resultTopicDF.append(tempDF, ignore_index=True)
tempRow.clear()
resultTopicDF.columns = colHeaders
display(resultTopicDF.head(desiredWordsToBePrinted).transpose())
print("\n\n")
# Result part - 3. Works fine(Hopefully)
topicCount = list()
topicCountPerc = list()
maxTopicNumPerc = np.zeros((numDocs, 2), dtype=float)
wordsInMaxTopic = list()
iPosition = 0
jPosition = 0
for iDoc in range(numDocs):
topicCountPerc.append(np.zeros(numTopics, dtype=float))
topicCount.append(np.zeros(numTopics, dtype=int))
wordsInMaxTopic.append(list())
for iWord in range(jPosition, jPosition + books.docLen[iDoc]):
topicCount[iDoc][wordTopicResultsT1[iCase][iWord]] += 1
jPosition += books.docLen[iDoc]
topicCountPerc[iDoc] = topicCount[iDoc] / books.docLen[iDoc]
maxTopicNumPerc[iDoc][0] = int(topicCount[iDoc].argmax())
maxTopicNumPerc[iDoc][1] = max(topicCountPerc[iDoc])
for iWord in range(iPosition, iPosition + books.docLen[iDoc]):
if wordTopicResultsT1[iCase][iWord] == maxTopicNumPerc[iDoc][0]:
wordsInMaxTopic[iDoc].append(books.listOfWords[iWord])
iPosition += books.docLen[iDoc]
documentTopicsDF = pd.DataFrame()
documentTopicsDF.insert(0, "Document Number", np.arange(0, numDocs, 1))
documentTopicsDF.insert(1, "Dominant Topic", maxTopicNumPerc[:, 0])
documentTopicsDF.insert(2, "Percentage", maxTopicNumPerc[:, 1])
documentTopicsDF.insert(3, "Words In Dominant Topic", wordsInMaxTopic)
documentTopicsDF = documentTopicsDF.sort_values("Percentage", ascending=False)
pd.set_option('display.max_colwidth', 150)
documentTopicsDF.style.hide_index()
display(documentTopicsDF.head(15))
pd.set_option('display.max_colwidth', colWidth)
print("\n\n")
iCase += 1
# + [markdown] id="zlBINwjDu01k"
# # Inferences
# + [markdown] id="teKXZ3vWfQAz"
# The key inferences are listed here:
#
#
# 1. The plots represent that a good fraction of words end up in fewer topics. However, this essentially means that the raw count in few topics is higher than other topics, however, the number of distinct words can have a differnt distribution.
# 2. Some of the topics forms a good cluster of words that closely resemble each other.
# 3. The doucment dominant topic table plays a good role in finding the key words under a particular topic.
#
# One examples explaining these phenomenon is:
# In case 4, form the first table, the dominant topics contains words that cosely relates to
#
# Topic | Meaning | Relation
# --- | --- | ---
# 43 | Family | **
# 38 | Worklife | *
# 6 | Academic docs | ***
# 25 | Terrorism and war | ****
# 19 | Generic | *
#
# Similarly, in case 4 second table, we can find an interesting observation that the documnet 15 contains good number of words related to topic Drug and ends up in topic 9. Topic 9 isn't very dominant in terms of raw frequency but we may infer that it contains words that resembles to drugs.
#
# Lastly, from the figures, it is quite clear that the distribution of words in topic is affected by changing the parameters from 0.1 to 0.01. It is noted that there is high variance in fraction of words in case of parameters 0.1 as compared to 0.01.
#
| 17,613 |
/Burgers_approximate.ipynb | 0860a7ad6e2e2f2dcb07ad9bde78720449a87da5 | [] | no_license | dksprabhu/riemann_book | https://github.com/dksprabhu/riemann_book | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 15,104 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] tags=["raw"]
# $$
# \newcommand{\wave}{{\cal W}}
# \newcommand{\amdq}{{\cal A}^-\Delta Q}
# \newcommand{\apdq}{{\cal A}^+\Delta Q}
# $$
# -
# # An approximate solver for Burgers' equation
# As a first example, we return to the inviscid Burgers' equation that we studied in [Burgers_equation.ipynb](Burgers_equation.ipynb):
# \begin{align} \label{burgers}
# q_t + \left(\frac{1}{2}q^2\right)_x & = 0.
# \end{align}
# Although it is easy to solve the Riemann problem for \eqref{burgers} exactly, it is nevertheless interesting to consider approximate solvers because a numerical scheme does not make use of the full Riemann solution. Furthermore, Burgers' equation provides a simple setting in which some of the intricacies of more complicated approximate solvers can be introduced. Recall that we are interested in **approximate solutions that consist entirely of traveling discontinuities**.
# ## Shock wave solutions
#
# Recall that the exact Riemann solution for \eqref{burgers} consists of a single shock or rarefaction wave. We have a shock if $q_l>q_r$ and we have a rarefaction if $q_l < q_r$. In the case of a shock wave, we can simply use the exact solution as our approximation. We have a single wave of strength $q_r-q_l$ traveling at speed $s=(q_r+q_l)/2$.
#
# In terms of fluxes, the numerical flux is $F=f(q_l)$ if $s>0$ and $F=f(q_r)$ if $s<0$. In the special case $s=0$ we have a stationary shock, and it must be that $f(q_l)=f(q_r) (=F)$.
# ## Rarefaction wave solutions
#
# As discussed in [Approximate_solvers.ipynb](Approximate_solvers.ipynb), for numerical purposes it is convenient to approximate a rarefaction wave by a traveling discontinuity. For Burgers' equation this may seem unnecessary, but for more complicated solvers for systems of equations it will be essential.
#
# We will approximate the effect of the rarefaction wave by a fictitious shock:
# $$\wave = q_r-q_l$$
# whose speed is given by the Rankine-Hugoniot jump condition:
# $$s = \frac{f(q_r)-f(q_l)}{q_r-q_l} = \frac{q_r + q_l}{2}.$$
# Recall that this is indeed a weak solution of the Riemann problem. This fictitious shock is not entropy-satisfying, but as long as it's traveling entirely to the left or entirely to the right, the effect on the numerical solution will be the same as if we used a (entropy-satisfying) rarefaction wave. The numerical flux is again $F=f(q_l)$ if $s>0$ and $F=f(q_r)$ if $s<0$.
# Because this is a scalar equation with convex flux, both the Roe and HLL approaches will simplify to what we have already described. But we briefly discuss them here to further illustrate the main ideas.
# ## A Roe solver
# Let us consider a linearized solver, in which we replace our nonlinear hyperbolic system with a linearization about some intermediate state $\hat{q}$. For Burgers' equation, the quasilinear form is $q_t + q q_x = 0$ and the linearization gives
# $$q_t + \hat{q}q_x = 0.$$
# This is simply the advection equation with velocity $\hat{q}$. The solution of the Riemann problem for this equation consists of a wave $\wave = q_r - q_l$ traveling at speed $\hat{q}$. It remains only to determine the state $\hat{q}$, and thus the wave speed.
#
# The defining feature of a Roe linearization is that it gives the exact solution in case the states $(q_r, q_l)$ lie on a single Hugoniot locus -- i.e., when the solution is a single shock. We can achieve this by choosing
# $$\hat{q} = \frac{q_r + q_l}{2}.$$
# This is equivalent to using the approximate solver described already in the sections above.
# ### Examples
# Below we show solutions for three examples; the first involves a shock, the second a (non-transonic) rarefaction, and the third a transonic rarefaction. In the first row we plot the exact solution in terms of the waves in the x-t plane; in the second row we plot numerical solutions obtained by using a simple first-order method combined with the Riemann solver.
# + tags=["hide"]
# %matplotlib inline
# %config InlineBackend.figure_format = 'svg'
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from ipywidgets import interact
from ipywidgets import widgets
sns.set_style('white',{'legend.frameon':'True'});
from exact_solvers import burgers
from utils import riemann_tools
# -
def setup(q_l, q_r, N=500, efix=False, solver_type='classic', order=1, lang='Python'):
from clawpack import pyclaw
from clawpack import riemann
if lang == 'Python':
rs = riemann.burgers_1D_py.burgers_1D
else:
rs = riemann.burgers_1D
if solver_type == 'classic':
solver = pyclaw.ClawSolver1D(rs)
solver.order = order
else:
solver = pyclaw.SharpClawSolver1D(rs)
solver.kernel_language = lang
solver.bc_lower[0]=pyclaw.BC.extrap
solver.bc_upper[0]=pyclaw.BC.extrap
x = pyclaw.Dimension(-1.0,1.0,N,name='x')
domain = pyclaw.Domain([x])
state = pyclaw.State(domain,1)
state.problem_data['efix'] = efix
xc = state.grid.p_centers[0]
state.q[0 ,:] = (xc<=0)*q_l + (xc>0)*q_r
claw = pyclaw.Controller()
claw.tfinal = 0.5
claw.solution = pyclaw.Solution(state,domain)
claw.solver = solver
claw.num_output_times = 10
claw.keep_copy = True
claw.verbosity=0
return claw
# +
shock = setup(2.,1.)
shock.run()
shocksol = burgers.exact_riemann_solution(2.,1.)
raref = setup(1.,2.)
raref.run()
rarefsol = burgers.exact_riemann_solution(1.,2.)
transonic = setup(-1.,2.)
transonic.run()
transonicsol = burgers.exact_riemann_solution(-1.,2.)
def plot_frame(i):
fig, axes = plt.subplots(2,3,figsize=(8,4))
for ax in axes[0]:
ax.set_xlim((-1,1)); ax.set_ylim((-1.1,2.1))
axes[1][0].plot(shock.frames[0].grid.x.centers, shock.frames[i].q[0,:],'-k',lw=2)
axes[1][0].set_title('Shock')
axes[1][1].plot(raref.frames[0].grid.x.centers, raref.frames[i].q[0,:],'-k',lw=2)
axes[1][1].set_title('Rarefaction')
axes[1][2].plot(transonic.frames[0].grid.x.centers, transonic.frames[i].q[0,:],'-k',lw=2)
axes[1][2].set_title('Transonic rarefaction')
t = i/10.
riemann_tools.plot_waves(*shocksol,ax=axes[0][0],t=t)
riemann_tools.plot_waves(*rarefsol,ax=axes[0][1],t=t)
riemann_tools.plot_waves(*transonicsol,ax=axes[0][2],t=t)
plt.tight_layout()
plt.show()
interact(plot_frame, i=widgets.IntSlider(min=0, max=10, description='Frame'));
# -
# The solutions obtained for the shock wave and for the first rarefaction wave are good approximations of the true solution. In the case of the transonic rarefaction, however, we see that part of the rarefaction has been replaced by an entropy-violating shock. At the end of this chapter we will show how to apply an *entropy fix* so that the solver gives a good approximation also in the transonic case.
# ## Two-wave solvers
# For Burgers' equation, the Riemann solution consists only of a single wave. It is thus natural to modify the HLL approach by assuming that one of the waves vanishes, and denote the speed of the other wave simply by $s$. Then the conservation condition discussed in [Approximate_solvers.ipynb](Approximate_solvers.ipynb#Two-wave-solvers) reduces to
# $$f(q_r) - f(q_l) = s (q_r - q_l),$$
# which is just the Rankine-Hugoniot condition and again leads to the speed discussed above. Since the solution involves only one wave, that wave must carry the entire jump $q_r - q_l$, so this solver is entirely equivalent to that already described.
#
# It is also possible to follow the full HLL approach, taking
# \begin{align*}
# s_1 & = \min f'(q) = \min(q_l, q_r) \\
# s_2 & = \max f'(q) = \max(q_l, q_r).
# \end{align*}
# Regardless of the values of $q_l$ and $q_r$, this leads to
# $$q_m = \frac{q_r + q_l}{2},$$
# so that each of the two waves carries half of the jump.
#
# *DK: Has anybody ever tried this solver?*
# ## Transonic rarefactions
#
# In the approaches above, the solution was approximated by a single wave traveling either to the left or right. For this scalar problem, this "approximation" is, in fact, an exact weak solution of the Riemann problem. As discussed already, we do not typically need to worry about the fact that it may be entropy-violating, since the effect on the numerical solution (after averaging) is identical to that of the entropy-satisfying solution.
#
# However, if $q_l < 0 < q_r$, then the true solution is a transonic rarefaction, in which part of the wave travels to the left and part travels to the right. In this case, the true Riemann solution would lead to changes to both the left and right adjacent cells, whereas an approximate solution with a single wave will only modify one or the other. This leads to an incorrect numerical solution (on the macroscopic level). It is therefore necessary to modify the Riemann solver, imposing what is known as an *entropy fix* in the transonic case.
#
# Specifically, we use a solution consisting of two waves, each of which captures the net effect of the corresponding rarefaction wave that appears in the exact solution:
#
# \begin{align}
# \wave_1 & = q_m - q_l, & s_1 = \frac{q_l + q_m}{2} \\
# \wave_2 & = q_r - q_m, & s_2 = \frac{q_m + q_r}{2}.
# \end{align}
#
# For Burgers' equation, the value $q_s=0$ is the *sonic point* satisfying $f(q_s)=0$. A transonic rarefaction wave takes the value $q_s$ along $x/t = 0$ and so it makes sense to choose $q_m = 0$. The formulas above then simplify to
#
# \begin{align}
# \wave_1 & = - q_l, & s_1 = \frac{q_l}{2} \\
# \wave_2 & = q_r, & s_2 = \frac{q_r}{2}.
# \end{align}
#
# Note that this can also be viewed as an HLL solver, although not with the usual choice of wave speeds. Choosing the waves speeds $s^1=q_l/2$ and $s^2=q_r/2$ and then solving for $q_m$ by requiring conservation gives $q_m=0$.
# We now repeat the example given above, but with the entropy fix applied.
# +
shock = setup(2.,1.,efix=True)
shock.run()
shocksol = burgers.exact_riemann_solution(2.,1.)
raref = setup(1.,2.,efix=True)
raref.run()
rarefsol = burgers.exact_riemann_solution(1.,2.)
transonic = setup(-1.,2.,efix=True)
transonic.run()
transonicsol = burgers.exact_riemann_solution(-1.,2.)
def plot_frame(i):
fig, axes = plt.subplots(2,3,figsize=(8,4))
for ax in axes[0]:
ax.set_xlim((-1,1)); ax.set_ylim((-1.1,2.1))
axes[1][0].plot(shock.frames[0].grid.x.centers, shock.frames[i].q[0,:],'-k',lw=2)
axes[1][0].set_title('Shock')
axes[1][1].plot(raref.frames[0].grid.x.centers, raref.frames[i].q[0,:],'-k',lw=2)
axes[1][1].set_title('Rarefaction')
axes[1][2].plot(transonic.frames[0].grid.x.centers, transonic.frames[i].q[0,:],'-k',lw=2)
axes[1][2].set_title('Transonic rarefaction')
t = i/10.
riemann_tools.plot_waves(*shocksol,ax=axes[0][0],t=t)
riemann_tools.plot_waves(*rarefsol,ax=axes[0][1],t=t)
riemann_tools.plot_waves(*transonicsol,ax=axes[0][2],t=t)
plt.tight_layout()
plt.show()
interact(plot_frame, i=widgets.IntSlider(min=0, max=10, description='Frame'));
# -
# The entropy fix has no effect on the first two solutions, since it is applied only in the case of a transonic rarefaction. The third solution is greatly improved, and will converge to the correct weak solution as the grid is refined.
| 11,573 |
/examples/CountriesGeoJSON.ipynb | a6b5ec790a8d20d2d1bcbe74816e1975e6bbdcbe | [
"MIT"
] | permissive | jasongrout/ipyleaflet | https://github.com/jasongrout/ipyleaflet | 0 | 0 | null | 2017-05-04T06:38:26 | 2017-05-04T02:48:38 | null | Jupyter Notebook | false | false | .py | 1,807 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import ipyleaflet as ipyl
import ipywidgets as ipyw
import json
# +
# Map and label widgets
map = ipyl.Map(center=[53.88, 27.45], zoom=4)
label = ipyw.Label(layout=ipyw.Layout(width="100%"))
# geojson layer with hover handler
with open("./europe_110.geo.json") as f:
data = json.load(f)
for feature in data["features"]:
feature["properties"]["style"] = {
"color": "grey",
"weight": 1,
"fillColor": "grey",
"fillOpacity": 0.5,
}
layer = ipyl.GeoJSON(data=data, hover_style={"fillColor": "red"})
def hover_handler(event=None, feature=None, id=None, properties=None):
label.value = properties["geounit"]
layer.on_hover(hover_handler)
map.add(layer)
ipyw.VBox([map, label])
# -
| 1,010 |
/05_回归算法案例(二):波士顿房屋租赁价格预测.ipynb | 7fae2d411276485f78e73910ba32dc453526f543 | [] | no_license | HunterArley/MLDemo | https://github.com/HunterArley/MLDemo | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 144,451 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
import warnings
import sklearn
from sklearn.linear_model import LinearRegression, LassoCV, RidgeCV, ElasticNetCV
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.linear_model.coordinate_descent import ConvergenceWarning
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import GridSearchCV
from sklearn import metrics
def notEmpty(s):
return s != ''
## 加载数据
names = ['CRIM','ZN', 'INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT']
path = "datas/boston_housing.data"
## 由于数据文件格式不统一,所以读取的时候,先按照一行一个字段属性读取数据,然后再安装每行数据进行处理
fd = pd.read_csv(path,header=None)
fd.head()
## 设置字符集,防止中文乱码
mpl.rcParams['font.sans-serif']=[u'simHei']
mpl.rcParams['axes.unicode_minus']=False
## 拦截异常
warnings.filterwarnings(action = 'ignore', category=ConvergenceWarning)
## 加载数据
names = ['CRIM','ZN', 'INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT']
path = "datas/boston_housing.data"
## 由于数据文件格式不统一,所以读取的时候,先按照一行一个字段属性读取数据,然后再安装每行数据进行处理
fd = pd.read_csv(path,header=None)
# print (fd.shape)
data = np.empty((len(fd), 14))
data.shape
data
for i, d in enumerate(fd.values):#enumerate生成一列索 引i,d为其元素
d = map(float, filter(notEmpty, d[0].split(' ')))#filter一个函数,一个list
#根据函数结果是否为真,来过滤list中的项。
data[i] = list(d)
data
# +
## 分割数据
x, y = np.split(data, (13,), axis=1)
print (x[0:5])
# print(y)
y = y.ravel() # 转换格式 拉直操作
# -
print (y[0:5])
ly=len(y)
print(y.shape)
print ("样本数据量:%d, 特征个数:%d" % x.shape)
print ("target样本数据量:%d" % y.shape[0])
# +
## Pipeline常用于并行调参
models = [
Pipeline([
('ss', StandardScaler()),
('poly', PolynomialFeatures()),
('linear', RidgeCV(alphas=np.logspace(-3,1,20)))
]),
Pipeline([
('ss', StandardScaler()),
('poly', PolynomialFeatures()),
('linear', LassoCV(alphas=np.logspace(-3,1,20)))
])
]
# 参数字典
parameters = {
"poly__degree": [3,2,1],
"poly__interaction_only": [True, False],#只额外产生交互项x1*x2
"poly__include_bias": [True, False],#多项式幂为零的特征作为线性模型中的截距
"linear__fit_intercept": [True, False]
}
# -
rf=PolynomialFeatures(2,interaction_only=True)
a=pd.DataFrame({
'name':[1,2,3,4,5],
'score':[2,3,4,4,5]
})
b=rf.fit_transform(a)
b
# 数据分割
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)
# +
## Lasso和Ridge模型比较运行图表展示
titles = ['Ridge', 'Lasso']
colors = ['g-', 'b-']
plt.figure(figsize=(16,8), facecolor='w')
ln_x_test = range(len(x_test))
plt.plot(ln_x_test, y_test, 'r-', lw=2, label=u'真实值')
for t in range(2):
# 获取模型并设置参数
model = GridSearchCV(models[t], param_grid=parameters,cv=5, n_jobs=1)#五折交叉验证
# 模型训练-网格搜索
model.fit(x_train, y_train)
# 模型效果值获取(最优参数)
print ("%s算法:最优参数:" % titles[t],model.best_params_)
print ("%s算法:R值=%.3f" % (titles[t], model.best_score_))
# 模型预测
y_predict = model.predict(x_test)
# 画图
plt.plot(ln_x_test, y_predict, colors[t], lw = t + 3, label=u'%s算法估计值,$R^2$=%.3f' % (titles[t],model.best_score_))
# 图形显示
plt.legend(loc = 'upper left')
plt.grid(True)
plt.title(u"波士顿房屋价格预测")
plt.show()
# -
stan = StandardScaler()
x_train1 = stan.fit_transform(x_train, y_train)
x_train2 = stan.fit_transform(x_train)
print(x_train1 )
print(x_train2)
# +
## 模型训练 ====> 单个Lasso模型(一阶特征选择)<2参数给定1阶情况的最优参数>
model = Pipeline([
('ss', StandardScaler()),
('poly', PolynomialFeatures(degree=1, include_bias=True, interaction_only=True)),
('linear', LassoCV(alphas=np.logspace(-3,1,20), fit_intercept=False))
])
# 模型训练
model.fit(x_train, y_train)
a = model.get_params()
# 模型评测
## 数据输出
print ("参数:", list(zip(names,model.get_params('linear')['linear'].coef_)))
print ("截距:", model.get_params('linear')['linear'].intercept_)
a
# +
# L1-norm是可以做特征选择的,主要原因在于:通过Lasso模型训练后,
# 有的参数是有可能出现为0的或者接近0的情况; 针对于这一批的特征,可以进行特征的删除操作
# df.drop(xx)
# NOTE: 自己实现参数值绝对值小于10^-1的所有特征属性删除;要求:不允许明确给定到底删除那一个特征属性
# df.drop(['CHAS', 'DIS']) ==> 不允许这样写
# 实际工作中,一般情况下,除非低于10^-6才会删除
# -
| 4,496 |
/Mini-Projects/Classification Practice/classification_metrics.ipynb | 041dc2fb037df65725af0c89a2aaccf639c1620c | [
"MIT"
] | permissive | ronv94/MachineLearning | https://github.com/ronv94/MachineLearning | 1 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 65,969 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Our Mission
#
# In this lesson you gained some insight into a number of techniques used to understand how well our model is performing. This notebook is aimed at giving you some practice with the metrics specifically related to classification problems. With that in mind, we will again be looking at the spam dataset from the earlier lessons.
#
# First, run the cell below to prepare the data and instantiate a number of different models.
# +
# Import our libraries
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
from sklearn.ensemble import BaggingClassifier, RandomForestClassifier, AdaBoostClassifier
from sklearn.svm import SVC
import tests as t
from sklearn.metrics import confusion_matrix
# Read in our dataset
df = pd.read_table('smsspamcollection/SMSSpamCollection',
sep='\t',
header=None,
names=['label', 'sms_message'])
# Fix our response value
df['label'] = df.label.map({'ham':0, 'spam':1})
# Split our dataset into training and testing data
X_train, X_test, y_train, y_test = train_test_split(df['sms_message'],
df['label'],
random_state=1)
# Instantiate the CountVectorizer method
count_vector = CountVectorizer()
# Fit the training data and then return the matrix
training_data = count_vector.fit_transform(X_train)
# Transform testing data and return the matrix. Note we are not fitting the testing data into the CountVectorizer()
testing_data = count_vector.transform(X_test)
# Instantiate a number of our models
naive_bayes = MultinomialNB()
bag_mod = BaggingClassifier(n_estimators=200)
rf_mod = RandomForestClassifier(n_estimators=200)
ada_mod = AdaBoostClassifier(n_estimators=300, learning_rate=0.2)
svm_mod = SVC()
# -
# > **Step 1**: Now, fit each of the above models to the appropriate data. Answer the following question to assure that you fit the models correctly.
# Fit each of the 4 models
# This might take some time to run
naive_bayes.fit(training_data, y_train)
bag_mod.fit(training_data, y_train)
rf_mod.fit(training_data, y_train)
ada_mod.fit(training_data, y_train)
svm_mod.fit(training_data, y_train)
# +
# The models you fit above were fit on which data?
a = 'X_train'
b = 'X_test'
c = 'y_train'
d = 'y_test'
e = 'training_data'
f = 'testing_data'
# Change models_fit_on to only contain the correct string names
# of values that you oassed to the above models
models_fit_on = {e, c} # update this to only contain correct letters
# Checks your solution - don't change this
t.test_one(models_fit_on)
# -
# > **Step 2**: Now make predictions for each of your models on the data that will allow you to understand how well our model will extend to new data. Then correctly add the strings to the set in the following cell.
# Make predictions using each of your models
preds_nb = naive_bayes.predict(testing_data)
preds_bag = bag_mod.predict(testing_data)
preds_rf = rf_mod.predict(testing_data)
preds_ada = ada_mod.predict(testing_data)
preds_svm = svm_mod.predict(testing_data)
# +
# Which data was used in the predict method to see how well your
# model would work on new data?
a = 'X_train'
b = 'X_test'
c = 'y_train'
d = 'y_test'
e = 'training_data'
f = 'testing_data'
# Change models_predict_on to only contain the correct string names
# of values that you oassed to the above models
models_predict_on = {f} # update this to only contain correct letters
# Checks your solution - don't change this
t.test_two(models_predict_on)
# -
# Now that you have set up all your predictions, let's get to topics addressed in this lesson - measuring how well each of your models performed. First, we will focus on how each metric was calculated for a single model, and then in the final part of this notebook, you will choose models that are best based on a particular metric.
#
# You will be writing functions to calculate a number of metrics and then comparing the values to what you get from sklearn. This will help you build intuition for how each metric is calculated.
#
# > **Step 3**: As an example of how this will work for the upcoming questions, run the cell below. Fill in the below function to calculate accuracy, and then compare your answer to the built in to assure you are correct.
# +
# accuracy is the total correct divided by the total to predict
def accuracy(actual, preds):
'''
INPUT
preds - predictions as a numpy array or pandas series
actual - actual values as a numpy array or pandas series
OUTPUT:
returns the accuracy as a float
'''
return np.sum(preds == actual)/len(actual)
print("ACCURACY SCORE")
print("Naive Bayes:")
print(accuracy(y_test, preds_nb))
print(accuracy_score(y_test, preds_nb))
print()
print("Bagging:")
print(accuracy(y_test, preds_bag))
print(accuracy_score(y_test, preds_bag))
print()
print("Random Forests:")
print(accuracy(y_test, preds_rf))
print(accuracy_score(y_test, preds_rf))
print()
print("AdaBoost:")
print(accuracy(y_test, preds_ada))
print(accuracy_score(y_test, preds_ada))
print()
print("SVM:")
print(accuracy(y_test, preds_svm))
print(accuracy_score(y_test, preds_svm))
print()
print("Since these match, we correctly calculated our metric!")
# -
# **Step 4**: Fill in the below function to calculate precision, and then compare your answer to the built in to assure you are correct.
# +
# precision is the true positives over the predicted positive values; precision = tp / (tp + fp)
def precision(actual, preds):
'''
INPUT
(assumes positive = 1 and negative = 0)
preds - predictions as a numpy array or pandas series
actual - actual values as a numpy array or pandas series
OUTPUT:
returns the precision as a float
'''
print("Confusion Matrix: ")
print(confusion_matrix(actual, preds))
print()
#getting values from the confusion matrix
tn, fp, fn, tp = confusion_matrix(actual, preds).ravel()
return tp/(tp + fp) # calculate precision here
print("PRECISION SCORE")
print("Naive Bayes:")
print(precision(y_test, preds_nb))
print(precision_score(y_test, preds_nb))
print()
print("Bagging:")
print(precision(y_test, preds_bag))
print(precision_score(y_test, preds_bag))
print()
print("Random Forests:")
print(precision(y_test, preds_rf))
print(precision_score(y_test, preds_rf))
print()
print("AdaBoost:")
print(precision(y_test, preds_ada))
print(precision_score(y_test, preds_ada))
print()
print("SVM:")
print(precision(y_test, preds_svm))
print(precision_score(y_test, preds_svm))
print()
print("If the above match, you got it!")
# -
# > **Step 5**: Fill in the below function to calculate recall, and then compare your answer to the built in to assure you are correct.
# +
# recall is true positives over all actual positive values; recall = tp / (tp + fn)
def recall(actual, preds):
'''
INPUT
preds - predictions as a numpy array or pandas series
actual - actual values as a numpy array or pandas series
OUTPUT:
returns the recall as a float
'''
#getting values from the confusion matrix
tn, fp, fn, tp = confusion_matrix(actual, preds).ravel()
return tp/(tp + fn) # calculate recall here
print("RECALL SCORE")
print("Naive Bayes:")
print(recall(y_test, preds_nb))
print(recall_score(y_test, preds_nb))
print()
print("Bagging:")
print(recall(y_test, preds_bag))
print(recall_score(y_test, preds_bag))
print()
print("Random Forests:")
print(recall(y_test, preds_rf))
print(recall_score(y_test, preds_rf))
print()
print("AdaBoost:")
print(recall(y_test, preds_ada))
print(recall_score(y_test, preds_ada))
print()
print("SVM:")
print(recall(y_test, preds_svm))
print(recall_score(y_test, preds_svm))
print()
print("If the above match, you got it!")
# -
# > **Step 6**: Fill in the below function to calculate f1-score, and then compare your answer to the built in to assure you are correct.
# +
# f1_score is 2*(precision*recall)/(precision+recall))
def f1(preds, actual):
'''
INPUT
preds - predictions as a numpy array or pandas series
actual - actual values as a numpy array or pandas series
OUTPUT:
returns the f1score as a float
'''
Precision = precision(actual, preds)
Recall = recall(actual, preds)
f1_score = 2 * ((Precision * Recall) / (Precision + Recall))
return f1_score # calculate f1-score here
print("F1-SCORE")
print("Naive Bayes:")
print(f1(y_test, preds_nb))
print(f1_score(y_test, preds_nb))
print()
print("Bagging:")
print(f1(y_test, preds_bag))
print(f1_score(y_test, preds_bag))
print()
print("Random Forests:")
print(f1(y_test, preds_rf))
print(f1_score(y_test, preds_rf))
print()
print("AdaBoost:")
print(f1(y_test, preds_ada))
print(f1_score(y_test, preds_ada))
print()
print("SVM:")
print(f1(y_test, preds_svm))
print(f1_score(y_test, preds_svm))
print()
print("If the above match, you got it!")
# -
# > **Step 7:** Now that you have calculated a number of different metrics, let's tie that to when we might use one versus another. Use the dictionary below to match a metric to each statement that identifies when you would want to use that metric.
# +
# add the letter of the most appropriate metric to each statement
# in the dictionary
a = "recall"
b = "precision"
c = "accuracy"
d = 'f1-score'
seven_sol = {
'We have imbalanced classes, which metric do we definitely not want to use?': c, # letter here,
'We really want to make sure the positive cases are all caught even if that means we identify some negatives as positives': a, # letter here,
'When we identify something as positive, we want to be sure it is truly positive': b, # letter here,
'We care equally about identifying positive and negative cases': d # letter here
}
t.sol_seven(seven_sol)
# -
# > **Step 8:** Given what you know about the metrics now, use this information to correctly match the appropriate model to when it would be best to use each in the dictionary below.
# +
# use the answers you found to the previous questiona, then match the model that did best for each metric
a = "naive-bayes"
b = "bagging"
c = "random-forest"
d = 'ada-boost'
e = "svm"
eight_sol = {
'We have imbalanced classes, which metric do we definitely not want to use?': a, # letter here,
'We really want to make sure the positive cases are all caught even if that means we identify some negatives as positives': a, # letter here,
'When we identify something as positive, we want to be sure it is truly positive': c, # letter here,
'We care equally about identifying positive and negative cases': a # letter here
}
t.sol_eight(eight_sol)
# +
# cells for work
# +
# If you get stuck, also notice there is a solution available by hitting the orange button in the top left
# -
# As a final step in this workbook, let's take a look at the last three metrics you saw, f-beta scores, ROC curves, and AUC.
#
# **For f-beta scores:** If you decide that you care more about precision, you should move beta closer to 0. If you decide you care more about recall, you should move beta towards infinity.
#
# > **Step 9:** Using the fbeta_score works similar to most of the other metrics in sklearn, but you also need to set beta as your weighting between precision and recall. Use the space below to show that you can use [fbeta in sklearn](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.fbeta_score.html) to replicate your f1-score from above. If in the future you want to use a different weighting, [this article](http://mlwiki.org/index.php/Precision_and_Recall) does an amazing job of explaining how you might adjust beta for different situations.
# +
# import fbeta_score
from sklearn.metrics import fbeta_score
# Show that you can produce the same f1_score results using fbeta_score
print("F-BETA SCORE")
print("Naive Bayes:")
print(fbeta_score(y_test, preds_nb, beta = 1.0))
print()
print("Bagging:")
print(fbeta_score(y_test, preds_bag, beta = 1.0))
print()
print("Random Forests:")
print(fbeta_score(y_test, preds_rf, beta = 1.0))
print()
print("AdaBoost:")
print(fbeta_score(y_test, preds_ada, beta = 1.0))
print()
print("SVM:")
print(fbeta_score(y_test, preds_svm, beta = 1.0))
# -
# > **Step 10:** Building ROC curves in python is a pretty involved process on your own. I wrote the function below to assist with the process and make it easier for you to do so in the future as well. Try it out using one of the other classifiers you created above to see how it compares to the random forest model below.
#
# Run the cell below to build a ROC curve, and retrieve the AUC for the random forest model.
# +
# Function for calculating auc and roc
def build_roc_auc(model, X_train, X_test, y_train, y_test):
'''
INPUT:
model - an sklearn instantiated model
X_train - the training data
y_train - the training response values (must be categorical)
X_test - the test data
y_test - the test response values (must be categorical)
OUTPUT:
auc - returns auc as a float
prints the roc curve
'''
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle
from sklearn.metrics import roc_curve, auc, roc_auc_score
from scipy import interp
y_preds = model.fit(X_train, y_train).predict_proba(X_test)
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(len(y_test)):
fpr[i], tpr[i], _ = roc_curve(y_test, y_preds[:, 1])
roc_auc[i] = auc(fpr[i], tpr[i])
# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_preds[:, 1].ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
plt.plot(fpr[2], tpr[2], color='darkorange',
lw=2, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.show()
return roc_auc_score(y_test, np.round(y_preds[:, 1]))
# Finding roc and auc for the random forest model
build_roc_auc(rf_mod, training_data, testing_data, y_train, y_test)
# +
# Your turn here - choose another classifier to see how it compares
build_roc_auc(naive_bayes, training_data, testing_data, y_train, y_test)
# -
| 15,041 |
/master_thesis/fiber/.ipynb_checkpoints/pressure_discharge-checkpoint.ipynb | 746a9c15c8852539ddef4fa7484d64ae0c9d66f7 | [] | no_license | bbuusshh/physics_lab | https://github.com/bbuusshh/physics_lab | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 817,819 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # model 3-3における$X_{i}$の数$N$に対する平均ステップ間距離$\phi$のプロットとフィッティング
# ※時間がかかるので注意
# +
# %matplotlib inline
import numpy as np
from scipy.spatial.distance import euclidean as euc
import matplotlib.pyplot as plt
class Person:
def __init__(self, S, a, p=0.5):
self.S = S
self.a = a
self.p = p
def gather(self):
"""make person to participate the meeting.
"""
self.ideas = self.has_idea()
def has_idea(self):
"""a person has self.S ideas with self.a dimension.
"""
return list(np.random.rand(self.S, self.a))
def chose_idea(self, idea, idea2=None):
def nearness1(x, y, z):
"""calculate nearness of x for (y, z)
by calculating a linear combination.
"""
alpha = 1.
beta = 1.
return alpha*euc(x, y) + beta*euc(x, z)
def nearness2(x, y, z):
"""calculate nearness of x for (y, z)
by distance between x and the dividing point of (y, z) with t.
"""
# t > 0
# t <= 1: interior division
# t > 1: exterior division
t = 0.5
x, y, z = np.array(x), np.array(y), np.array(z)
return euc(t*(y-x) + (1.-t)*(z-x), (0., 0.))
if len(self.ideas) == 0:
return False
# return min(d) and its idea_id
if idea2 == None:
return min([(euc(vec, idea), idea_id) for idea_id, vec in enumerate(self.ideas)])
else:
return min([(nearness1(vec, idea, idea2), idea_id)
for idea_id, vec in enumerate(self.ideas)])
class Meeting:
"""Simulate a meeting with "simple3" situation.
Give keyword arguments:
K = 20 # Time limit
N = 6 # a number of participants
S = 10 # a number of ideas for each participants
a = 2 # the dimension of an idea
p = 0.5 # probability that a person speak
draw = True # draw image or don't
Output:
self.minutes: list of
( idea(which is vector with a dimension)
, who(person_id in the list "self.membes"))
self.k: stopped time (=len(self.minutes))
"""
def __init__(self, K=20, N=6, S=10, a=2, p=0.5, case=2):
self.K = K
self.N = N
self.S = S
self.a = a
self.p = p
self.case = case # case in the above cell: 2, 3, 4 or 5
if not self.case in [2, 3, 4, 5]:
raise ValueError
self.members = []
self.minutes = [] # list of (idea, who)
self.k = 0
def gather_people(self):
"""gather people for the meeting.
You can edit what ideas they have in here.
"""
for n in range(self.N):
person = Person(self.S, self.a, self.p)
# person.has_idea = some_function()
# some_function: return list of self.S arrays with dim self.a.
person.gather()
self.members.append(person)
self.members = np.array(self.members)
def progress(self):
"""meeting progress
"""
self.init()
preidea = self.subject
prepreidea = None
self.k = 1
while self.k < self.K + 1:
# l: (distance, speaker, idea_id) list for who can speak
l = []
for person_id, person in enumerate(self.members):
# chosed: (distance, idea_id)
chosed = person.chose_idea(preidea, prepreidea)
if chosed:
l.append((chosed[0], person_id, chosed[1]))
# if no one can speak: meeting ends.
if len(l) == 0:
print "no one can speak."
break
i = np.array([(person_id, idea_id)
for distance, person_id, idea_id in sorted(l)])
for person_id, idea_id in i:
rn = np.random.rand()
if rn < self.members[person_id].p:
idea = self.members[person_id].ideas.pop(idea_id)
self.minutes.append((idea, person_id))
if self.case == 3:
preidea = idea
elif self.case == 4:
prepreidea = idea
elif self.case == 5:
prepreidea = preidea
preidea = idea
self.k += 1
break
else:
self.minutes.append((self.subject, self.N))
self.k += 1
self.minutes = np.array(self.minutes)
def init(self):
self.gather_people()
self.subject = np.random.rand(self.a)
self.minutes.append((self.subject, self.N))
# -
def myplot1(x, y, xfit=np.array([]), yfit=np.array([]), param=None,
scale=['linear', 'linear', 'log', 'log'], case=[2, 3, 4, 5]):
"""my plot function
x: {'label_x', xdata}
xdata: numpy array of array
y: {'label_y', ydata}
ydata: numpy array of array
param: {'a': 10, 'b': 20}
"""
if param:
s = [r'$%s = %f$' % (k, v) for k, v in param.items()]
label = s[0]
for _s in s[1:]:
label += ", " + _s
label_x, xdata = x.items()[0]
label_y, ydata = y.items()[0]
if len(scale)%2 == 1:
raise ValueError("'scale' must be even number")
fignum = len(scale)/2
figsize_y = 7 * fignum
fig = plt.figure(figsize=(10, figsize_y))
ax = []
for num in range(fignum):
ax.append(fig.add_subplot(fignum, 1, num+1))
for i, data in enumerate(zip(xdata, ydata)):
ax[num].plot(data[0], data[1], label="case: %d" % case[i])
if len(xfit):
ax[num].plot(xfit, yfit, label=label)
ax[num].legend(loc='best')
ax[num].set_xlabel(label_x)
ax[num].set_ylabel(label_y)
ax[num].set_xscale(scale[2*(num)])
ax[num].set_yscale(scale[2*(num)+1])
plt.show()
# +
def calc_ave_dist_btw_nodes(case, trial, N):
_tmp = []
for t in range(trial):
meeting = Meeting(K=30, N=N, S=50, a=2, p=1.0, case=case)
meeting.progress()
tmp = 0
dist_btw_nodes= []
p0 = meeting.minutes[0]
for p1 in meeting.minutes[1:]:
if p1[1] != N:
dist_btw_nodes.append(euc(p0[0], p1[0]))
p0 = p1
_tmp.append(np.average(dist_btw_nodes))
_tmp = np.array(_tmp)
return np.average(_tmp)
def N_phi2(N, case=2, trial=100):
ave_dist_btw_nodes = [calc_ave_dist_btw_nodes(case, trial, _N) for _N in N]
return ave_dist_btw_nodes
# +
import multiprocessing
case = [2, 3, 4, 5]
N = np.array([2**a for a in range(11)])
def wrapper(arg):
return arg[0](arg[1], arg[2], arg[3])
jobs = [(N_phi2, N, c, 100) for c in case]
process = multiprocessing.Pool(6)
ydata = np.array(process.map(wrapper, jobs))
# -
myplot1({r'$N$': np.array([N]*len(case))}, {r'$\phi$':ydata}, case=case)
from scipy.optimize import leastsq
def myfit(fit_func, parameter, x, y, xmin, xmax, du=0, scale=['linear', 'linear', 'log', 'log']):
"""my fitting and plotting function.
fit_func: function (parameter(type:list), x)
parameter: list of tuples: [('param1', param1), ('param2', param2), ...]
x, y: dict
xmin, xmax: float
du: dataused --- index of the data used for fitting
"""
xkey, xdata = x.items()[0]
ykey, ydata = y.items()[0]
def fit(parameter, x, y):
return y - fit_func(parameter, x)
# use x : xmin < x < xmax
i = 0
while xdata[du][i] < xmin:
i += 1
imin, imax = i, i
while xdata[du][i] < xmax:
i += 1
imax = i
paramdata = [b for a, b in parameter]
paramkey = [a for a, b in parameter]
res = leastsq(fit, paramdata, args=(xdata[du][imin:imax], ydata[du][imin:imax]))
for i, p in enumerate(res[0]):
print parameter[i][0] + ": " + str(p)
fitted = fit_func(res[0], xdata[du][imin:imax])
fittedparam = dict([(k, v) for k, v in zip(paramkey, res[0])])
myplot1(x, y, xdata[du][imin:imax], fitted, param=fittedparam, scale=scale)
# +
param = [('a', -0.5), ('b', 0.)]
xmin, xmax = 0., 1024
x = {r'$N$': np.array([N]*len(case))}
y = {r'$\phi$': ydata}
def fit_func(parameter, x):
a = parameter[0]
b = parameter[1]
return np.power(x, a)*np.power(10, b)
myfit(fit_func, param, x, y, xmin, xmax, du=2, scale=['log', 'log'])
ble(False)
# bar average sales per customer
ax = fig.add_subplot(2,2,4)
ax.set_title('Average sales per customer [$]')
country_sales.iloc[:-1,:].plot(ax=ax,kind='bar',x='country',y='average_sales_per_customer',rot=45,colors=colors[0:-1],legend=False,use_index=False)
ax.set_xticklabels(country_sales['country'][0:-1],rotation=45)
ax.spines["right"].set_visible(False)
ax.spines["left"].set_visible(False)
ax.spines["top"].set_visible(False)
ax.spines["bottom"].set_visible(False)
# -
# As we can see on the graphs currently the biggest market is in the USA skaring over 22% of total sales. The second market is Canada with over 13% of total sales.
# Czech, Portugal, India and Brazil are on top in terms of average sales per customer. If we look at average order as percentage of difference from mean of all orders we can see that Czech spend over 15% more per order then others following by India and UK where customers spend over 10% more per order then the average. Taking into account the amount of population, India may be the best choice to expand the advertising campaigns.
# ### Behavior of customers: Albums vs Tracks
# Categorize each invoice as either an album purchase or not.
run_command('''
CREATE VIEW invoice_whole_album AS
WITH
invoice_tracks AS
(SELECT
il.invoice_id,
il.track_id,
t.album_id
FROM invoice_line as il
LEFT JOIN track as t ON t.track_id = il.track_id ),
album_tracks AS
(SELECT
track_id,
album_id
FROM track)
SELECT
il.invoice_id,
CASE
WHEN
(
SELECT at.track_id
FROM album_tracks as at
WHERE album_id = (
SELECT album_id
FROM invoice_tracks as it
WHERE it.invoice_id = il.invoice_id
GROUP BY invoice_id
)
EXCEPT
SELECT track_id
FROM invoice_tracks as it
WHERE it.invoice_id =il.invoice_id
) IS NULL
AND
(SELECT count(at.track_id)
FROM album_tracks as at
WHERE album_id = (
SELECT album_id
FROM invoice_tracks as it
WHERE it.invoice_id = il.invoice_id
GROUP BY invoice_id
)
) >2
THEN 'yes'
ELSE 'no'
END AS album_purchase
FROM invoice_line as il
GROUP BY invoice_id
''')
# Print summary statistic
run_query('''
SELECT
album_purchase,
COUNT(album_purchase) as total_invoices,
COUNT(album_purchase)/ (SELECT CAST(COUNT(*) as Float) FROM invoice_whole_album) as percentage_of_invoices
FROM invoice_whole_album
GROUP BY album_purchase
''')
# As we can see basend on summary statistic over 80 % of invoices consist of individual tracks insted of the whole album. Almost 20% of the market is turned by customers buying whole albums. So would suggest to perform some futher analysis in order to recommend any movements. Introducting a new functionality may cost us loosing some of the revenue if customers would buy only most popular songs alumns insted of whole ones.
# Potential questions:
# - Which artist is used in the most playlists?
# - How many tracks have been purchased vs not purchased?
# - Is the range of tracks in the store reflective of their sales popularity?
# - Do protected vs non-protected media types have an effect on popularity?
rns a bunch of weaker decision
# models into a more powerful ensemble model
def random_forest_classifier(train_X, train_Y, test_X, test_Y):
fitted_model = RandomForestClassifier().fit(train_X, train_Y)
print "Successfully fitted random forest classifier"
assess_supervised_classifier(train_X, train_Y, test_X, test_Y, fitted_model)
# +
train_X, train_Y, test_X, test_Y = getData(BFS_model, 0.8)
logistic_regression(train_X, train_Y, test_X, test_Y, {0:1, 1:2})
mlp_classifier(train_X, train_Y, test_X, test_Y)
knn_classifier(train_X, train_Y, test_X, test_Y, 10)
decision_tree_classifier(train_X, train_Y, test_X, test_Y)
random_forest_classifier(train_X, train_Y, test_X, test_Y)
# -
# UNSUPERVISED LEARNING:
#
# We'll now use the node2vec embeddings to identify clusters within the graph
def assess_clustering_model(fitted_model, train_X, test_X=None):
train_is_whole_dataset = True if test_X == None else False
train_cluster_assignments = fitted_model.predict(train_X)
test_cluster_assignments = None if train_is_whole_dataset else fitted_model.predict(test_X)
# Compute the mean silhoutte score across all samples
# For silhouette scores, the best value is 1 and the worst value is -1
# Values near 0 indicate overlapping clusters
train_silhouette_score = silhouette_score(train_X, train_cluster_assignments)
test_silhouette_score = None if train_is_whole_dataset else silhouette_score(test_X, test_cluster_assignments)
print "Train silhouette score:"
print train_silhouette_score
print "Test silhouette score:"
print test_silhouette_score
# Compute the mean Calinski-Harabasz index for all samples
# For Calinski-Harabasz, the higher the better
train_ch_score = calinski_harabaz_score(train_X, train_cluster_assignments)
test_ch_score = None if train_is_whole_dataset else calinski_harabaz_score(test_X, test_cluster_assignments)
print "Train Calinski-Harabasz score:"
print train_ch_score
print "Test Calinski-Harabasz score:"
print test_ch_score
print ""
return train_silhouette_score
# Let's assume we don't know anything about the companies
# We'll use k-means to cluster their node2vec embeddings
def k_means(train_X, test_X, k):
fitted_model = KMeans(n_clusters=k).fit(train_X)
print "Successfully fitted K Means"
assess_clustering_model(fitted_model, train_X, test_X)
# Now we try agglomerative clustering
# Note that agglomerative clustering has no concept of training
def agglomerative_clustering(train_X, test_X, k):
data = np.concatenate((train_X, test_X))
fitted_model = AgglomerativeClustering(n_clusters=k).fit_predict(data)
print "Successfully fitted agglomerative clustering"
assess_clustering_model(fitted_model, data)
# +
# DFS appears to be the best for clustering
train_X, train_Y, test_X, test_Y = getData(DFS_model, 0.8)
k_means(train_X, test_X, 2)
agglomerative_clustering(train_X, test_X, 2)
# -
| 15,749 |
/IntroNumpyScipy.ipynb | 776588c1e12e5367f73e616e954867450abdbe8a | [] | no_license | georgsmeinung/datascience101 | https://github.com/georgsmeinung/datascience101 | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 2,690,451 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3.8.5 64-bit
# metadata:
# interpreter:
# hash: 31f2aee4e71d21fbe5cf8b01ff0e069b9275f58929596ceb00d14d90e3e16cd6
# name: Python 3.8.5 64-bit
# ---
# # [An introduction to Numpy and Scipy](https://sites.engineering.ucsb.edu/~shell/che210d/numpy.pdf)
# NumPy and SciPy are open-source add-on modules to Python that providecommon mathematical and numerical routines inpre-compiled, fast functions. These are growing into highly mature packages that provide functionality that meets, or perhaps exceeds, that associated with common commercial software like MatLab.The NumPy (Numeric Python) package provides basic routines for manipulating large arrays and matrices of numeric data. The SciPy (Scientific Python) package extends the functionality of NumPy with a substantial collection of useful algorithms, like minimization, Fourier transformation, regression, and other applied mathematical techniques.
# ## Arrays
# The central feature of NumPy is the arrayobject class. Arrays are similar to lists in Python, except that every element of an array must be of the same type, typically a numeric type like floator int. Arrays make operations with large amounts of numeric data very fast and are generally much more efficient than lists.An array can be created from a list:
import numpy as np
a = np.array([1, 4, 5, 8], float)
print(a)
type(a)
# Here, the function arraytakes two arguments: the list to be converted into the array and the type of each member of the list.Array elements are accessed, sliced, and manipulated just like lists:
a[:2]
a[3]
a[0] = 5.
a
# Arrays can be multidimensional. Unlike lists, different axes are accessed using commas insidebracket notation. Here is an example with a two-dimensional array (e.g., a matrix):
a = np.array([[1, 2, 3], [4, 5, 6]], float)
print (a)
print(a[0,0])
print(a[0,1])
# Array slicing works with multiple dimensions in the same way as usual, applying each slice specification as a filter to a specified dimension. Use of a single ":" in a dimension indicates the use of everything along that dimension:
a[1,:]
a[:,2]
a[-1,-2]
# The shape property of an array returns a tuple with the size of each array dimension:
a.shape
# The dtype property tells you what type of values are stored by the array:
a.dtype
# Here, float64 is a numeric type that NumPy uses to store double-precision (8-byte) real numbers, similar to the floattype in Python.When used with an array, the lenfunction returns the length of the first axis:
len(a)
len(a[0])
# The instatement can be used to test if values are present in an array:
2 in a
0 in a
# Arrays can be reshaped using tuples that specify new dimensions. In the following example, we turn a ten-element one-dimensional array into a two-dimensional one whose first axis has five elements andwhose second axis has two elements
a = np.array(range(10), float)
print(a)
a = a.reshape(5,2)
print(a)
a.shape
# Notice that the reshapefunction creates a new array and does not itself modify the original array.Keep in mind that Python's name-binding approach still applies to arrays.
# The copy function can be used to create a new, separate copy of an array in memory if needed:
a = np.array([1, 2, 3], float)
b = a
c = a.copy()
b[0] = 0
a
b
c
# Lists can also be created from arrays:
a = np.array([1,2,3], float)
a.tolist()
list(a)
# One can convert the raw data in an array to a binary string (i.e., not in human-readable form) using the tostring function. The fromstring function then allows an array to be created from this data later on. These routines are sometimes convenient for saving large amount of array data in files that can be read later on:
a = np.array([1,2,3],float)
s = a.tostring()
s
np.fromstring(s)
# One can fill an array with a single value:
a = np.array([1,2,3], float)
a
a.fill(0)
a
# Transposed versions of arrays can also be generated, which will create a new array with the final two axes switched:
a = np.array(range(6), float).reshape(2,3)
a
a.transpose()
# One-dimensional versions of multi-dimensional arrays can be generated with flatten:
a = np.array([[1,2,3],[4,5,6]],float)
a
a.flatten()
# Two or more arrays can be concatenated together using the concatenate function with a tuple of the arrays to be joined:
a = np.array([1,2], float)
b = np.array([3,4,5,6], float)
c = np.array([8,9], float)
np.concatenate((a,b,c))
# If an array has more than one dimension, it is possible to specify the axis along which multiple arrays are concatenated. By default (without specifying the axis), NumPy concatenates along the first dimension:
a = np.array([[1,2],[3,4]],float)
b = np.array([[5,6],[7,8]],float)
np.concatenate((a,b))
np.concatenate((a,b), axis=0)
np.concatenate((a,b), axis=1)
# Finally, the dimensionality of an array can be increased using the newaxis constant in bracket notation:
a = np.array([1,2,3], float)
a
a[:,np.newaxis]
a[:,np.newaxis].shape
a = np.array([1,2,3], float)
a
a[np.newaxis,:]
a[np.newaxis,:].shape
# Notice here that in each case the new array has two dimensions; the one created by newaxishas a length of one. The newaxis approach is convenient for generating the proper-dimensioned arrays for vector and matrix mathematics.
#
# ## Other ways to create arrays
# The arange function is similar to the range function but returns an array:
np.arange(5, dtype=float)
np.arange(1, 6, 2, dtype=int)
# The functions zeros and ones create new arrays of specified dimensions filled with these
# values. These are perhaps the most commonly used functions to create new arrays:
np.ones((2,3), dtype=float)
np.zeros(7, dtype=int)
# The zeros_like and ones_like functions create a new array with the same dimensions
# and type of an existing one:
a = np.array([[1, 2, 3], [4, 5, 6]], float)
np.zeros_like(a)
np.ones_like(a)
# There are also a number of functions for creating special matrices (2D arrays). To create an
# identity matrix of a given size,
np.identity(4, dtype=float)
# The eye function returns matrices with ones along the kth diagonal:
np.eye(4, k=2, dtype=int)
# ## Array mathematics
# When standard mathematical operations are used with arrays, they are applied on an element-by-element basis. This means that the arrays should be the same size during addition,subtraction, etc.:
a = np.array([1,2,3], float)
b = np.array([5,2,6], float)
a + b
a - b
a * b
a / b
a % b
a ** b
# For two-dimensional arrays, multiplication remains elementwise and does not correspond to
# matrix multiplication.
a = np.array([[1,2], [3,4]], float)
b = np.array([[2,0], [1,3]], float)
a * b
# Errors are thrown if arrays do not match in size:
a = np.array([1,2,3], float)
b = np.array([4,5], float)
a * b
# However, arrays that do not match in the number of dimensions will be broadcasted by Python to perform mathematical operations. This often means that the smaller array will be repeated as necessary to perform the operation indicated. Consider the following:
a = np.array([[1, 2], [3, 4], [5, 6]], float)
b = np.array([-1, 3], float)
a + b
# Here, the one-dimensional array b was broadcasted to a two-dimensional array that matched the size of a. In essence, b was repeated for each item in a, as if it were given by
# ```
# array([[-1.,3.],
# [-1.,3.],
# [-1.,3.]])
# ```
# Python automatically broadcasts arrays in this manner. Sometimes, however, how we should broadcast is ambiguous. In these cases, we can use the newaxis constant to specify how we want to broadcast:
a = np.zeros((2,2), float)
b = np.array([-1., 3.], float)
a + b
a + b[np.newaxis,:]
a + b[:,np.newaxis]
# In addition to the standard operators, NumPy offers a large library of common mathematical functions that can be applied elementwise to arrays. Among these are the functions: abs, sign, sqrt, log, log10, exp, sin, cos, tan, arcsin, arccos, arctan, sinh, cosh, tanh, arcsinh, arccosh, and arctanh.
a = np.array([1, 4, 9], float)
np.sqrt(a)
# The functions floor, ceil, and rint give the lower, upper, or nearest (rounded) integer:
a = np.array([1.1, 1.5, 1.9], float)
np.floor(a)
np.ceil(a)
np.rint(a)
# Also included in the NumPy module are two important mathematical constants:
np.pi
np.e
# ## Array iteration
# It is possible to iterate over arrays in a manner similar to that of lists:
a = np.array([1, 4, 5], int)
for x in a:
print(x)
# For multidimensional arrays, iteration proceeds over the first axis such that each loop returns a subsection of the array:
a = np.array([[1, 2], [3, 4], [5, 6]], float)
for x in a:
print(x)
# Multiple assignment can also be used with array iteration:
a = np.array([[1, 2], [3, 4], [5, 6]], float)
for (x, y) in a:
print (x * y)
# ## Basic array operations
# Many functions exist for extracting whole-array properties. The items in an array can be summed or multiplied:
a = np.array([2, 4, 3], float)
a.sum()
a.prod()
# For most of the routines described below, both standalone and member functions are available.
#
# A number of routines enable computation of statistical quantities in array datasets, such as the mean (average), variance, and standard deviation:
a = np.array([2, 1, 9], float)
a.mean()
a.var()
a.std()
# It's also possible to find the minimum and maximum element values:
a.min()
a.max()
# The argmin and argmax functions return the array indices of the minimum and maximum values:
a.argmin()
a.argmax()
# For multidimensional arrays, each of the functions thus far described can take an optional argument axis that will perform an operation along only the specified axis, placing the results in a return array:
a = np.array([[0, 2], [3, -1], [3, 5]], float)
a.mean(axis=0)
a.mean(axis=1)
a.max(axis=0)
# Like lists, arrays can be sorted:
a = np.array([6, 2, 5, -1, 0], float)
sorted(a)
# Values in an array can be "clipped" to be within a prespecified range. This is the same as applying min(max(x, minval), maxval) to each element x in an array.
a = np.array([6, 2, 5, -1, 0], float)
a.clip(0,5)
# Unique elements can be extracted from an array:
a = np.array([1, 1, 4, 5, 5, 5, 7], float)
np.unique(a)
# For two dimensional arrays, the diagonal can be extracted:
a = np.array([[1, 2], [3, 4]], float)
a.diagonal()
# ## Comparison operators and value testing
# Boolean comparisons can be used to compare members elementwise on arrays of equal size. The return value is an array of Boolean True / False values:
a = np.array([1, 3, 0], float)
b = np.array([0, 3, 2], float)
a > b
a == b
a <= b
# The results of a Boolean comparison can be stored in an array:
c = a > b
c
# Arrays can be compared to single values using broadcasting:
a > 2
# The any and all operators can be used to determine whether or not any or all elements of a Boolean array are true:
any (c)
all (c)
# Compound Boolean expressions can be applied to arrays on an element-by-element basis using special functions logical_and, logical_or, and logical_not.
a = np.array([1, 3, 0], float)
np.logical_and(a>0, a<3)
b = np.array([True, False, True], bool)
np.logical_not(b)
c = np.array([False, True, False], bool)
np.logical_or(b,c)
# The where function forms a new array from two arrays of equivalent size using a Boolean filter to choose between elements of the two. Its basic syntax is where(boolarray, truearray, falsearray):
a = np.array([1, 3, 0], float)
np.where(a!=0,1/a,a)
# Broadcasting can also be used with the where function:
np.where(a > 0, 3, 2)
# A number of functions allow testing of the values in an array. The nonzero function gives a tuple of indices of the nonzero values in an array. The number of items in the tuple equals the number of axes of the array:
a = np.array([[0, 1], [3, 0]], float)
a.nonzero()
# It is also possible to test whether or not values are NaN ("not a number") or finite:
a = np.array([1, np.NaN, np.Inf], float)
a
np.isnan(a)
np.isfinite(a)
# Although here we used NumPy constants to add the NaN and infinite values, these can result from standard mathematical operations.
# ## Array item selection and manipulation
# We have already seen that, like lists, individual elements and slices of arrays can be selected using bracket notation. Unlike lists, however, arrays also permit selection using other arrays. That is, we can use array selectors to filter for specific subsets of elements of other arrays.
#
# Boolean arrays can be used as array selectors:
a = np.array([[6, 4], [5, 9]], float)
a >= 6
a[a >= 6]
# Notice that sending the Boolean array given by a>=6 to the bracket selection for a, an array with only the True elements is returned. We could have also stored the selector array in a variable:
a = np.array([[6, 4], [5, 9]], float)
sel = (a >= 6)
a[sel]
# More complicated selections can be achieved using Boolean expressions:
a[np.logical_and(a > 5, a < 9)]
# In addition to Boolean selection, it is possible to select using integer arrays. Here, the integer arrays contain the indices of the elements to be taken from an array. Consider the following one-dimensional example:
a = np.array([2, 4, 6, 8], float)
b = np.array([0, 0, 1, 3, 2, 1], int)
a[b]
# In other words, we take the 0 th , 0 th , 1 st , 3 rd , 2 nd , and 1 st elements of a, in that order, when we use b to select elements from a. Lists can also be used as selection arrays:
a = np.array([2, 4, 6, 8], float)
a[[0, 0, 1, 3, 2, 1]]
# For multidimensional arrays, we have to send multiple one-dimensional integer arrays to the selection bracket, one for each axis. Then, each of these selection arrays is traversed in sequence: the first element taken has a first axis index taken from the first member of the first selection array, a second index from the first member of the second selection array, and so on.
#
# An example:
a = np.array([[1, 4], [9, 16]], float)
b = np.array([0, 0, 1, 1, 0], int)
c = np.array([0, 1, 1, 1, 1], int)
a[b,c]
# A special function take is also available to perform selection with integer arrays. This works in an identical manner as bracket selection:
a = np.array([2, 4, 6, 8], float)
b = np.array([0, 0, 1, 3, 2, 1], int)
a.take(b)
# take also provides an axis argument, such that subsections of an multi-dimensional array can be taken across a given dimension.
a = np.array([[0, 1], [2, 3]], float)
b = np.array([0, 0, 1], int)
a.take(b, axis=0)
a.take(b, axis=1)
# The opposite of the take function is the put function, which will take values from a source
# array and place them at specified indices in the array calling put.
a = np.array([0, 1, 2, 3, 4, 5], float)
b = np.array([9, 8, 7], float)
a.put([0, 3], b)
a
# Note that the value 7 from the source array b is not used, since only two indices \[0, 3\] are specified. The source array will be repeated as necessary if not the same size:
a = np.array([0, 1, 2, 3, 4, 5], float)
a.put([0, 3], 5)
a
# ## Vector and matrix mathematics
# NumPy provides many functions for performing standard vector and matrix multiplication routines. To perform a dot product,
a = np.array([1, 2, 3], float)
b = np.array([0, 1, 1], float)
np.dot(a,b)
# The dot function also generalizes to matrix multiplication:
a = np.array([[0, 1], [2, 3]], float)
b = np.array([2, 3], float)
c = np.array([[1, 1], [4, 0]], float)
a
np.dot(b,a)
np.dot(a,b)
np.dot(a,c)
np.dot(c,a)
# It is also possible to generate inner, outer, and cross products of matrices and vectors. For vectors, note that the inner product is equivalent to the dot product:
a = np.array([1, 4, 0], float)
b = np.array([2, 2, 1], float)
np.outer(a, b)
np.inner(a, b)
np.cross(a, b)
# NumPy also comes with a number of built-in routines for linear algebra calculations. These can be found in the sub-module linalg. Among these are routines for dealing with matrices and their inverses. The determinant of a matrix can be found:
a = np.array([[4, 2, 0], [9, 3, 7], [1, 2, 1]], float)
a
np.linalg.det(a)
# One can find the eigenvalues and eigenvectors of a matrix:
vals, vecs = np.linalg.eig(a)
vals
vecs
# The inverse of a matrix can be found:
a = np.array([[4, 2, 0], [9, 3, 7], [1, 2, 1]], float)
b = np.linalg.inv(a)
b
np.dot(a,b)
# Singular value decomposition (analogous to diagonalization of a nonsquare matrix) can also be performed:
a = np.array([[1, 3, 4], [5, 2, 3]], float)
U, s, Vh = np.linalg.svd(a)
U
s
Vh
# ## Polynomial mathematics
# NumPy supplies methods for working with polynomials. Given a set of roots, it is possible to show the polynomial coefficients:
np.poly([-1, 1, 1, 10])
# Here, the return array gives the coefficients corresponding to $ x^4 − 11x^3 + 9x^2 + 11x − 10 $.
# The opposite operation can be performed: given a set of coefficients, the root function returns all of the polynomial roots:
np.roots([1, 4, -2, 3])
# Notice here that two of the roots of $ x^3 + 4x^2 − 2x + 3 $ are imaginary.
# Coefficient arrays of polynomials can be integrated. Consider integrating $ x^3 + x^2 + x + 1 $ to
# $ x^4 ⁄ 4 + x^3 ⁄ 3 + x^2 ⁄ 2 + x + C $ . By default, the constant $ C $ is set to zero:
np.polyint([1, 1, 1, 1])
# Similarly, derivatives can be taken:
np.polyder([1./4., 1./3., 1./2., 1., 0.])
# The functions polyadd, polysub, polymul, and polydiv also handle proper addition, subtraction, multiplication, and division of polynomial coefficients, respectively.
#
# The function polyval evaluates a polynomial at a particular point. Consider $x^3 − 2x^2 + 2$ evaluated at $x = 4$:
np.polyval([1, -2, 0, 2], 4)
# Finally, the polyfit function can be used to fit a polynomial of specified order to a set of data using a least-squares approach:
x = [1, 2, 3, 4, 5, 6, 7, 8]
y = [0, 2, 1, 3, 7, 10, 11, 19]
np.polyfit(x, y, 2)
# The return value is a set of polynomial coefficients. More sophisticated interpolation routines
# can be found in the SciPy package.
# ## Statistics
# In addition to the mean, var, and std functions, NumPy supplies several other methods for
# returning statistical features of arrays.
#
# The median can be found:
a = np.array([1, 4, 3, 8, 9, 2, 3], float)
np.median(a)
# The correlation coefficient for multiple variables observed at multiple instances can be found for arrays of the form $[[x1, x2, ...], [y1, y2, ...], [z1, z2, ...], ...]$ where $x, y, z$ are different observables and the numbers indicate the observation times:
a = np.array([[1, 2, 1, 3], [5, 3, 1, 8]], float)
c = np.corrcoef(a)
c
# Here the return array `c[i,j]` gives the correlation coefficient for the ith and jth observables.
#
# Similarly, the covariance for data can be found:
np.cov(a)
# ## Random numbers
# An important part of any simulation is the ability to draw random numbers. For this purpose, we use NumPy's built-in pseudorandom number generator routines in the sub-module `random`. The numbers are pseudo random in the sense that they are generated deterministically from a seed number, but are distributed in what has statistical similarities to random fashion. NumPy uses a particular algorithm called the Mersenne Twister to generate pseudorandom numbers.
#
# The random number seed can be set:
np.random.seed(293423)
# The seed is an integer value. Any program that starts with the same seed will generate exactly
# the same sequence of random numbers each time it is run. This can be useful for debugging
# purposes, but one does not need to specify the seed and in fact, when we perform multiple
# runs of the same simulation to be averaged together, we want each such trial to have a
# different sequence of random numbers. If this command is not run, NumPy automatically
# selects a random seed (based on the time) that is different every time a program is run.
#
# An array of random numbers in the half-open interval $[0.0, 1.0)$ can be generated:
np.random.rand(5)
# The `rand` function can be used to generate two-dimensional random arrays, or the `resize`
# function could be employed here:
np.random.rand(2,3)
np.random.rand(6).reshape((2,3))
# To generate a single random number in $[0.0, 1.0)$,
np.random.random()
# To generate random integers in the range $[min, max)$ use `randint(min, max)`:
np.random.randint(5, 10)
# In each of these examples, we drew random numbers form a uniform distribution. NumPy also
# includes generators for many other distributions, including the Beta, binomial, chi-square,
# Dirichlet, exponential, F, Gamma, geometric, Gumbel, hypergeometric, Laplace, logistic, log-
# normal, logarithmic, multinomial, multivariate, negative binomial, noncentral chi-square,
# noncentral F, normal, Pareto, Poisson, power, Rayleigh, Cauchy, student's t, triangular, von
# Mises, Wald, Weibull, and Zipf distributions. Here we only give examples for two of these.
#
# To draw from the discrete Poisson distribution with $λ = 6.0$,
np.random.poisson(6.0)
# To draw from a continuous normal (Gaussian) distribution with mean $μ = 1.5$ and standard deviation $σ = 4.0$:
np.random.normal(1.5, 4.0)
# To draw from a standard normal distribution ($μ = 0$, $σ = 1$), omit the arguments:
np.random.normal()
# To draw multiple values, use the optional `size` argument:
np.random.normal(size=5)
# The random module can also be used to randomly shuffle the order of items in a list. This is
# sometimes useful if we want to sort a list in random order:
l = list(range(10))
l
np.random.shuffle(l)
l
# Notice that the shuffle function modifies the list in place, meaning it does not return a new list
# but rather modifies the original list itself.
# ## Other functions to know about
# NumPy contains many other built-in functions that we have not covered here. In particular,
# there are routines for discrete Fourier transforms, more complex linear algebra operations, size
# / shape / type testing of arrays, splitting and joining arrays, histograms, creating arrays of
# numbers spaced in various ways, creating and evaluating functions on grid arrays, treating
# arrays with special (NaN, Inf) values, set operations, creating various kinds of special matrices,
# and evaluating special mathematical functions (e.g., Bessel functions). You are encouraged to
# consult the NumPy documentation at http://docs.scipy.org/doc/ for more details.
#
# ## Modules available in SciPy
# SciPy greatly extends the functionality of the NumPy routines. We will not cover this module in
# detail but rather mention some of its capabilities. Many SciPy routines can be accessed by
# simply importing the module:
import scipy
help(scipy)
# Notice that a number of sub-modules in SciPy require explicit import, as indicated by the star
# notation above:
import scipy.interpolate
# The functions in each module are well-documented in both the internal docstrings and at the
# SciPy documentation website. Many of these functions provide instant access to common
# numerical algorithms, and are very easy to implement. Thus, SciPy can save tremendous
# amounts of time in scientific computing applications since it offers a library of pre-written, pre-
# tested routines.
#
# A large community of developers continually builds new functionality into SciPy. A good rule of
# thumb is: if you are thinking about implementing a numerical routine into your code, check the
# SciPy documentation website first. Chances are, if it's a common task, someone will have
# added it to SciPy.
| 23,807 |
/Project 2 - Modeling.ipynb | f33a5145e3fb64b03cc6103b277bb5dbc227ddc8 | [] | no_license | yichenhu577/Ames | https://github.com/yichenhu577/Ames | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 137,709 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Pre-Processing - (continued) / Modeling ##
# Notebook to finish pre-processing and model the data from my EDA notebook
# **Imports**
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import ElasticNet, LinearRegression, RidgeCV, LassoCV
from sklearn.model_selection import train_test_split, cross_val_score, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error,r2_score
# **Pre-processing (continued)**
train = pd.read_csv('clean_train.csv')
test = pd.read_csv('clean_test.csv')
# The column drops and below were created after running my previous data through a LASSO model, identifying the columns that had 0 coeeficients and dropping those
train.drop(['Garage Cars','Sale Type_CWD','TotRms AbvGrd','Functional_Sev','Sale Type_WD ','Mo Sold_Aug','Neighborhood_NPkVill',\
'Functional_Min2','Mo Sold_Dec','House Style_SLvl','Neighborhood_NAmes','Mo Sold_Nov','House Style_1.5Unf','Neighborhood_Blmngtn',\
'Bldg Type_Duplex','Neighborhood_BrkSide','Neighborhood_CollgCr','Neighborhood_Landmrk','Neighborhood_Mitchel','Sale Type_VWD'],axis=1,inplace=True)
test.drop(['Garage Cars','Sale Type_CWD','TotRms AbvGrd','Functional_Sev','Sale Type_WD ','Mo Sold_Aug','Neighborhood_NPkVill',\
'Functional_Min2','Mo Sold_Dec','House Style_SLvl','Neighborhood_NAmes','Mo Sold_Nov','House Style_1.5Unf','Neighborhood_Blmngtn',\
'Bldg Type_Duplex','Neighborhood_BrkSide','Neighborhood_CollgCr','Neighborhood_Landmrk','Neighborhood_Mitchel','Sale Type_VWD'],axis=1,inplace=True)
train.drop(['Mo Sold_Sep','Sale Type_ConLD','Neighborhood_Blueste','Neighborhood_SWISU','House Style_1Story'],axis=1,inplace=True)
test.drop(['Mo Sold_Sep','Sale Type_ConLD','Neighborhood_Blueste','Neighborhood_SWISU','House Style_1Story'],axis=1,inplace=True)
# The interactions below were created after looking at the highest weighted features from a LASSO model of my data and then identifying features from that set that seemed like they may be co-linear
train['SF interaction']=train['SF']*train['Gr Liv Area']
train['overall interaction']=train['Overall Qual']*train['Gr Liv Area']
train['overall garage interaction']=train['Overall Qual']*train['garage interaction']
test['SF interaction']=test['SF']*test['Gr Liv Area']
test['overall interaction']=test['Overall Qual']*test['Gr Liv Area']
test['overall garage interaction']=test['Overall Qual']*test['garage interaction']
# **Modeling**
y = train['SalePrice']
features = [name for name in train.columns if name != 'SalePrice']
X = train[features]
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
#Scale our data
ss = StandardScaler()
ss.fit(X_train)
X_train = ss.transform(X_train)
X_test = ss.transform(X_test)
# **Baseline model**
# The baseline model in our case is just the mean value of houses in our train dataset
baseline = y_train.mean()
baseline
base_pred = pd.Series(baseline,index=range((y_test).size))
base_pred.head()
#R2 score
print(r2_score(y_test, base_pred))
#RMSE
np.sqrt(mean_squared_error(y_test,base_pred))
# **Linear Regression**
lr = LinearRegression()
lr.fit(X_train,y_train)
# +
#R2 scores
y_pred_lr_train = lr.predict(X_train)
y_pred_lr_test = lr.predict(X_test)
print(r2_score(y_train, y_pred_lr_train))
print(r2_score(y_test, y_pred_lr_test))
# -
#RMSE
np.sqrt(mean_squared_error(y_test,y_pred_lr_test))
# **Ridge Model**
r_alphas = np.logspace(-2, 5, 100)
ridge_model = RidgeCV(alphas=r_alphas, scoring='r2', cv=5)
ridge_model = ridge_model.fit(X_train, y_train)
ridge_model.alpha_
# This is my lowest possible alpha in my range which means that I'm essentially employing no regularization. I would expect the scores from Ridge to be very similar to my Linear Regression model which they are
# +
y_pred_train_ridge = ridge_model.predict(X_train)
y_pred_test_ridge = ridge_model.predict(X_test)
print(r2_score(y_train, y_pred_train_ridge))
print(r2_score(y_test, y_pred_test_ridge))
# -
np.sqrt(mean_squared_error(y_test,y_pred_test_ridge))
# **LASSO Model**
lasso = LassoCV(n_alphas=200,cv=10)
lasso.fit(X_train,y_train)
print(lasso.alpha_)
lasso.score(X_train,y_train)
lasso.score(X_test,y_test)
lasso_pred = lasso.predict(X_test)
np.sqrt(mean_squared_error(y_test,lasso_pred))
# +
#Create a residual plot
plt.figure(figsize=(15,10))
plt.title('Plot of Predicted Home Sale Price vs Error in Sale Price Prediction', fontsize = 20)
plt.xlabel('Predicted Sale Price ($)', fontsize = 10)
plt.ylabel('Error in Sale Price ($)', fontsize = 10);
plt.hlines(0,y_test.min(),y_test.max())
plt.scatter(lasso_pred,y_test-lasso_pred);
# -
# The above residual plot shows some heteroscedasticity so my model could be improved if I had more time
# +
#Create a presentation friendly residual plot
plt.figure(figsize=(15,10))
plt.title('Plot of Predicted Home Sale Price vs Actual Home Sale Price', fontsize = 20)
plt.xlabel('Actual Sale Price ($)', fontsize = 10)
plt.ylabel('Predicted Sale Price ($)', fontsize = 10);
plt.scatter(y_test,lasso_pred)
plt.plot([0, np.max(y_test)], [0, np.max(y_test)], c='k');
# -
# The above is my final LASSO run but i used the below code with previous LASSO runs to identify the highest weighted and lowest weighted coeeficients and ended up removing those at the top of this notebook
# +
lasso_coefs = pd.DataFrame({
'feature_name':X.columns,
'coefficients':lasso.coef_,
'abs_coef':np.abs(lasso.coef_)
})
lasso_coefs.sort_values('abs_coef',ascending=False, inplace=True)
# -
lasso_coefs.tail()
lasso_coefs.head(15)
# **Elastic Net / Grid-Searching**
enet = ElasticNet()
enet.fit(X_train,y_train)
enet_params = {
'alpha':np.linspace(.2,1,15),
'l1_ratio': np.linspace(0,1,15)
}
enet_gridsearch = GridSearchCV(
ElasticNet(),
enet_params,
cv=5,
n_jobs=2,
return_train_score=False
)
enet_gridsearch.fit(X_train,y_train)
enet_gridsearch.best_params_
# l1 ratio of 1 indicates pure LASSO, expecting this to be very close or equivalent to my LASSO score
best_enet = enet_gridsearch.best_estimator_
best_enet.score(X_train, y_train)
best_enet.score(X_test, y_test)
enet_pred = best_enet.predict(X_test)
np.sqrt(mean_squared_error(y_test,enet_pred))
# **Generate Kaggle Submission**
# Kaggle requires the Id column but my model can't take the Id so need to remove this column before I run my predictions
testnoid = test[[name for name in test.columns if name != 'Id']]
# Due to a number of my modifications and the order they were done in, my columns are out of order which will cause StandardScaler to misbehave, running the below code to re-order my column to how my training dataset it.
testnoid = testnoid[features]
testnoid_scaled = ss.transform(testnoid)
submit_col = lasso.predict(testnoid_scaled)
#time to submit
submit = pd.DataFrame({
'Id':test['Id'],
'SalePrice':submit_col
})
submit.head()
submit.to_csv('final_submission.csv',index=False)
# **Analysis / Explanation**
# The baseline model has an around 80,000 so we definitely want our model to be better than that. However, our model is predicting home sale prices so errors in the tens of thousands should also be somewhat expected.
#
# My approach on this project was a bit scattershot in that I started with my EDA but half-way through decided I wanted to get some modeling results and ended up guessing on or using many of the columns that I was planning on doing my EDA on. This surprisingly generated a fairly good RMSE score. I then proceeded to finish my EDA and to my suprise, ended up with a worse RMSE score. I then looked back at my first models and identified a number a columns using LASSO that had high correlations that I subsequently eliminated and proceeded to add those back in which lowered my RMSE scores. Finally, I used a LASSO regression to identify higher and zero coefficient features. I removed the zero coefficient features and ended up creating interactions for stronger coefficient features that appeared like they may be co-linear.
#
# The result of removing the zero coefficient features caused my linear regression and Ridge model scores to be essentially the same. This makes sense since those extra coefficients were screwing up my linear regression and without them, I didn't need any regularization on my model. My elastic net regression didn't converge but showed an l1 ratio of 1 indicating pure LASSO. This means that LASSO is purely the best model for my data and not a combination of the two.
#
# The creation of interactions makes the analysis of individual coefficients difficult to do, especially relative to other features. Instead, we can draw conclusions from the process of generating our final model. My initial thought process was to use EDA to identify correlated features and then generate a model with only those features. Through interaction using LASSO though, I realized that many of the features I didn't think had value actually ended up helping my model. I believe the reasoning for this is that features that don't appear predictive of sale price when combined with other features actually become predictive. If I was to re-do this or do this project again, I would try to remove less features prior to running LASSO and then use the results of that first run to remove features and generate interactions to iterate to a better model.
| 9,697 |
/05.係り受け解析/047.機能動詞構文のマイニング.ipynb | cd078f4d574c7740a654c0f0a2447231f0d50475 | [] | no_license | YoheiFukuhara/nlp100 | https://github.com/YoheiFukuhara/nlp100 | 1 | 1 | null | null | null | null | Jupyter Notebook | false | false | .py | 7,101 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 動詞のヲ格にサ変接続名詞が入っている場合のみに着目したい.46のプログラムを以下の仕様を満たすように改変せよ.
#
# - 「サ変接続名詞+を(助詞)」で構成される文節が動詞に係る場合のみを対象とする
# - 述語は「サ変接続名詞+を+動詞の基本形」とし,文節中に複数の動詞があるときは,最左の動詞を用いる
# - 述語に係る助詞(文節)が複数あるときは,すべての助詞をスペース区切りで辞書順に並べる
# - 述語に係る文節が複数ある場合は,すべての項をスペース区切りで並べる(助詞の並び順と揃えよ)
#
# 例えば「別段くるにも及ばんさと、主人は手紙に返事をする。」という文から,以下の出力が得られるはずである.
#
# ```
# 返事をする と に は 及ばんさと 手紙に 主人は
# ```
#
# このプログラムの出力をファイルに保存し,以下の事項をUNIXコマンドを用いて確認せよ.
#
# - コーパス中で頻出する述語(サ変接続名詞+を+動詞)
# - コーパス中で頻出する述語と助詞パターン
import re
# +
# 区切り文字
separator = re.compile('\t|,')
# 係り受け
dependancy = re.compile(r'''(?:\*\s\d+\s) # キャプチャ対象外
(-?\d+) # 数字(係り先)
''', re.VERBOSE)
# -
class Morph:
def __init__(self, line):
#タブとカンマで分割
cols = separator.split(line)
self.surface = cols[0] # 表層形(surface)
self.base = cols[7] # 基本形(base)
self.pos = cols[1] # 品詞(pos)
self.pos1 = cols[2] # 品詞細分類1(pos1)
class Chunk:
def __init__(self, morphs, dst):
self.morphs = morphs
self.srcs = [] # 係り元文節インデックス番号のリスト
self.dst = dst # 係り先文節インデックス番号
self.phrase = ''
self.verb = ''
self.joshi = ''
self.sahen = '' # サ変+を+動詞のパターン対象か否か
for i, morph in enumerate(morphs):
if morph.pos != '記号':
self.phrase += morph.surface # 記号以外の場合文節作成
self.joshi = '' # 記号を除いた最終行の助詞を取得するため、記号以外の場合はブランク
if morph.pos == '動詞' and self.verb == '':
self.verb = morph.base
if morphs[-1].pos == '助詞':
self.joshi = morphs[-1].base
try:
if morph.pos1 == 'サ変接続' and \
morphs[i+1].surface == 'を':
self.sahen = morph.surface + morphs[i+1].surface
except IndexError:
pass
# 係り元を代入し、Chunkリストを文のリストを追加
def append_sentence(chunks, sentences):
# 係り元を代入
for i, chunk in enumerate(chunks):
if chunk.dst != -1:
chunks[chunk.dst].srcs.append(i)
sentences.append(chunks)
return sentences, []
# +
# %time
morphs = []
chunks = []
sentences = []
with open('./neko.txt.cabocha') as f:
for line in f:
dependancies = dependancy.match(line)
# EOSまたは係り受け解析結果でない場合
if not (line == 'EOS\n' or dependancies):
morphs.append(Morph(line))
# EOSまたは係り受け解析結果で、形態素解析結果がある場合
elif len(morphs) > 0:
chunks.append(Chunk(morphs, dst))
morphs = []
# 係り受け結果の場合
if dependancies:
dst = int(dependancies.group(1))
# EOSで係り受け結果がある場合
if line == 'EOS\n' and len(chunks) > 0:
sentences, chunks = append_sentence(chunks, sentences)
# -
def output_file(out_file, sahen, sentence, chunk):
# 係り元助詞のリストを作成
sources = [[sentence[source].joshi, sentence[source].phrase] \
for source in chunk.srcs if sentence[source].joshi != '']
if len(sources) > 0:
sources.sort()
joshi = ' '.join([row[0] for row in sources])
phrase = ' '.join([row[1] for row in sources])
out_file.write(('{}\t{}\t{}\n'.format(sahen, joshi, phrase)))
# %%time
with open('./047.result_python.txt', 'w') as out_file:
for sentence in sentences:
for chunk in sentence:
if chunk.sahen != '' and \
chunk.dst != -1 and \
sentence[chunk.dst].verb != '':
output_file(out_file, chunk.sahen+sentence[chunk.dst].verb,
sentence, sentence[chunk.dst])
# +
# 述語でソートして重複除去し、その件数でソート
# !cut --fields=1 047.result_python.txt | sort | uniq --count \
# | sort --numeric-sort --reverse > 047.result_unix1.txt
# 述語と助詞でソートして重複除去し、その件数でソート
# !cut --fields=1,2 047.result_python.txt | sort | uniq --count \
# | sort --numeric-sort --reverse > 047.result_unix2.txt
# -
| 4,305 |
/image_classification.ipynb | 9ea1675ef3bf9b7ae27969323a6ba2e72a448879 | [] | no_license | prashan1/Dress-Clasification- | https://github.com/prashan1/Dress-Clasification- | 1 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 33,068 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import tensorflow as tf
from tensorflow import keras
from matplotlib import pyplot as plt
import numpy as np
tf.__version__
keras.__version__
fashion_mnist = keras.datasets.mnist
fashion_mnist
(X_train_full, y_train_full) ,( x_test , y_test) = fashion_mnist.load_data()
X_train_full.shape
X_train_full.dtype
x_test.shape
x_valid , x_train = X_train_full[:5000]/255 , X_train_full[5000 : ]/255
y_valid , y_train = y_train_full[:5000] , y_train_full[5000:]
class_names = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat",
"Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"]
class_names[y_train[0]]
y_train_full.shape
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28,28]))
model.add(keras.layers.Dense(300,activation='relu'))
model.add(keras.layers.Dense(300,activation='relu'))
model.add(keras.layers.Dense(10,activation='softmax'))
model.summary()
model.layers
weight , bias = model.layers[1].get_weights()
weight.shape
bias.shape
model.compile(loss='sparse_categorical_crossentropy',optimizer = 'sgd' , metrics =['accuracy'])
history = model.fit(x_train , y_train , epochs = 30 , validation_data=(x_valid , y_valid) )
import pandas as pd
pd.DataFrame(history.history).plot(figsize=(8,5))
plt.grid(True)
plt.show()
model.evaluate(x_test ,y_test)
print(X_train_full.shape)
print(x_train.shape)
print(x_valid.shape)
print(x_test.shape)
x_predict = x_test[:3]
y_predict = model.predict(x_predict)
y_predict,round(2)
y_predict = model.predict_classes(x_predict)
y_predict
np.array(class_names)[y_predict]
np.array(class_names)[y_test[:3]]
model.save('my_keras_classification_model.h5')
# +
# TO load model
# model = keras.model.load_model(my_keall)
g[0,0].cpu().numpy())
ax.set_title("Corrupted:")
ax.axis("off")
ax = plt.subplot(1,2,2)
ax.imshow(torch.sigmoid(model(img)[0,0].detach().cpu()).numpy())
ax.set_title("Recovered:")
_ = ax.axis("off")
rvice), but also would create a high number of dummy variables that could make the Neural Network processing svery lower. I'm deciding to drop it.
#
# The output variable is 'Exited', 1 means the customer exited the bank (churned), o means still a customer of the bank.
#
# Making copies of the database for use downstream
df2=df.copy(deep=True)
df2=df2.drop(['RowNumber','CustomerId','Surname'],axis=1)# droping vatriables that are unique for all users
df3=df2.copy(deep=True)
df3=df3.drop(['Geography','Gender','Exited'],axis=1)# droping categorical and output variables for plotting
print("Shape: ",df2.shape) # to know the shape of the data
df.dtypes # - understand the data types
# There is a mix of numerical and categorical variables, some of which need to be one-hot encoded and scaled
df2.head()
# #### 3.- Distinguish the features and target variable(5points)
#
# The output variable is 'Exited', 1 means the customer exited the bank (churned), o means still a customer of the bank.
print(sns.countplot(df2['Exited']))
# The data is imbalanced: 20% of the customers exited
#
#
# #### I will perform regular EDA:
# (Exploratory Data Analysis)
# look for null values:
df.isnull().sum().sum()
# No null values
df2.describe().transpose() #obtaning mean, min, max, quantiles and standard deviation
# There are variables (Balance, Estimated Salary) that need to be scaled for the neural network to work properly
dupes = df.duplicated()
sum(dupes)
# There are no duplicated rows
# Getting univariate plots to understand the distribution and bias of each variable
import itertools
cols = [i for i in df3.columns]
fig = plt.figure(figsize=(15, 20))
for i,j in itertools.zip_longest(cols, range(len(cols))):
plt.subplot(4,2,j+1)
ax = sns.distplot(df2[i],color='b',rug=True)
plt.axvline(df2[i].mean(),linestyle="dashed",label="mean", color='black')
plt.legend()
plt.title(i)
plt.xlabel("")
# +
# there are several outliers in Age, Balance and HasCard , however I will not treat them as we will probably use scaling
# -
# Review the 'Exited' relation with categorical variables
fig, axarr = plt.subplots(2, 2, figsize=(20, 12))
sns.countplot(x='Geography', hue = 'Exited',data = df, ax=axarr[0][0])
sns.countplot(x='Gender', hue = 'Exited',data = df, ax=axarr[0][1])
sns.countplot(x='HasCrCard', hue = 'Exited',data = df, ax=axarr[1][0])
sns.countplot(x='IsActiveMember', hue = 'Exited',data = df, ax=axarr[1][1])
sns.pairplot(df,diag_kind='hist', hue='Exited')
# Pair-ploting the variables to see their relationship and visual grouping and correlation
# Plotting correlations between the variables
plt.subplots(figsize=(12, 6))
corr = df.corr('spearman')
mask = np.zeros_like(corr)
mask[np.triu_indices_from(mask)] = True
ax = sns.heatmap(data=corr, cmap='mako', annot=True, mask=mask)
ax.set_xticklabels(ax.get_xticklabels(), rotation=45);
# No significant correlation between variables
# only Age seems to have a moderate correlation with the output variable and Balance has a mild negative correlation with number of products, no action needed.
# #### 4.- Divide the data set into training and test sets (5points)
#
df4=df2.copy(deep=True) # df4 will contain the data used in the analysis
# +
from sklearn.model_selection import train_test_split
X = df4.iloc[:, :-1]
y = df4.iloc[:, -1]
X = pd.get_dummies(X, drop_first=True) # creating the dummy variables for esch value of categorical variables
# splitting data into training and test set for independent attributes
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=.3, random_state=33)
print(X_train.shape, X_test.shape)
# -
# #### 5.- Normalize the train and test data (10points)
#
# doing box plot to see scale comparison and identify outliers:
plt.subplots(figsize=(12, 6))
ax = sns.boxplot(data=X_train)
ax.set_xticklabels(ax.get_xticklabels(), rotation=45);
# As saw during EDA, Balance and Estimated Salary need scaling
# For that, I will try two types of normalization. I choose ZScore and also MinMax Scaling and run the models with both.
# normalizing database with Zscore:
from scipy.stats import zscore
XTrZ = X_train.apply(zscore)
XTeZ = X_test.apply(zscore)
# doing box plot to see scale, comparison and identify outliers:
plt.subplots(figsize=(12, 6))
ax = sns.boxplot(data=XTrZ)
ax.set_xticklabels(ax.get_xticklabels(), rotation=45);
# normalizing database using minmax_scale
from sklearn import preprocessing
from sklearn.preprocessing import minmax_scale # Tried Normalize, MinMax
X_trainN = preprocessing.minmax_scale(X_train)
X_testN = preprocessing.minmax_scale(X_test)
# doing box plot to see scale, comparison and identify outliers:
plt.subplots(figsize=(12, 6))
ax = sns.boxplot(data=X_trainN)
ax.set_xticklabels(ax.get_xticklabels(), rotation=45);
# Although there are some outliers, the features seem more even in both cases. The difference is that, in scaling, I'm changing the range the data while in normalization I'm changing the shape of the distribution of the data
# #### 6.- Initialize & build the model. Identify the points of improvement and implement the same. Note that you need to demonstrate at least two models(the original and the improved one) and highlight the differences to complete this point. You can also demonstrate more models. (20points)
#
# Import additional libraries:
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, BatchNormalization
from tensorflow.keras.metrics import Recall, Accuracy
tf.keras.metrics.Recall(thresholds=None, top_k= None, class_id=None, name='recall', dtype=None)
from tensorflow.keras import optimizers
from sklearn.metrics import (accuracy_score, f1_score,average_precision_score, confusion_matrix,
average_precision_score, precision_score, recall_score, roc_auc_score, )
# Normalizing using Zscore:
X_train1 = np.asarray(XTrZ)
y_train = np.asarray(y_train)
X_test1 = np.asarray(XTeZ)
y_test = np.asarray(y_test)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
# using the data from minmax_scaler to normalize:
X_train2 = np.asarray(X_trainN)
y_train = np.asarray(y_train)
X_test2 = np.asarray(X_testN)
y_test = np.asarray(y_test)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
# I will create three diferent models and compare the results:
# - The first Model is small in number of layers and number of neurons per layer and using sigmoid activation function
# - Second Model is a large model with reducing size of layers and using various types of activation functions
# - Third model is mid size, but using only tanh activation function
# #### First Pass: Run the models using the data normalized with ZScore:
# ###### First Model (small in layers and neurons per layer)
# +
model = Sequential(layers=None, name=None) # creating new network with default plus two hiden layers:
model.add(Dense(10, input_shape = (11,), activation = 'sigmoid'))
model.add(Dense(10, activation = 'sigmoid'))
model.add(Dense(10, activation = 'sigmoid'))
model.add(Dense(1, activation = 'sigmoid'))
sgd = optimizers.Adam(lr = 0.025)# Set the optimizer and learning rate
model.compile(optimizer = sgd, loss = 'binary_crossentropy', metrics=['accuracy', Recall()]) # Compile the model
model.fit(X_train1, y_train, batch_size = 7000, epochs = 500, verbose=1) # Run the Network
results1= model.evaluate(X_train1, y_train, verbose=0) # create a results table:
results2 = model.evaluate(X_test1, y_test, verbose=0)
resultsDf = pd.DataFrame( # create a results table:
{'Model': ['Small model >'],'TrainAccuracy': results1[1], 'TrainRecall': results1[2],
'TestAccuracy': results2[1], 'TestRecall': results2[2]})
resultsDf = resultsDf[['Model','TrainAccuracy','TrainRecall','TestAccuracy','TestRecall']]
resultsDf
# -
# This initial model reaches around .87 of Accuracy, but only around 0.5 of Recall for training data, which due to the imbalance nature of the Output data, is very small, is not a good result
# ##### Second Model (larger)
# +
model = Sequential(layers=None, name=None) # In this model I use a combination of types of activation function layers
model.add(Dense(100, input_shape = (11,), activation = 'relu'))
model.add(Dense(75, activation = 'relu'))
model.add(Dense(60, activation = 'relu'))
model.add(Dense(40, activation = 'tanh'))
model.add(Dense(26, activation = 'elu'))
model.add(Dense(17, activation = 'relu'))
model.add(Dense(11, activation = 'exponential'))
model.add(Dense(7, activation = 'relu'))
model.add(Dense(1, activation = 'sigmoid'))
sgd = optimizers.Adamax(lr = 0.025) # using Adamax as gave sligh better results with mixed types of activation functions
model.compile(optimizer = sgd, loss = 'binary_crossentropy', metrics=['accuracy', Recall()])
model.fit(X_train1, y_train, batch_size = 7000, epochs = 500, verbose = 1)
results1= model.evaluate(X_train1, y_train, verbose=0)
results2 = model.evaluate(X_test1, y_test, verbose=0)
tempResultsDf = pd.DataFrame({'Model':['Larger >'],
'TrainAccuracy': results1[1], 'TrainRecall': results1[2],
'TestAccuracy': results2[1], 'TestRecall': results2[2]})
resultsDf = pd.concat([resultsDf, tempResultsDf])
resultsDf
# -
# We see some improvement, using more brute-force with this larger model in number of neurons per layer, and more layers than the previous model, we achieve a significant improvement in Accuracy and Recall on training data, which could be acceptable, but can still improve.
# ##### Third model ( Mid size)
# +
model = Sequential(layers=None, name=None) # Using tanh as activation function through the model, except the output layer
model.add(Dense(80, input_shape = (11,), activation = 'tanh'))
model.add(Dense(60, activation = 'tanh'))
model.add(Dense(40, activation = 'tanh'))
model.add(Dense(20, activation = 'tanh'))
model.add(Dense(1, activation = 'sigmoid'))
sgd = optimizers.Adam(lr = 0.025) # Adam works better than Adamax od SGD in this particular case
model.compile(optimizer = sgd, loss = 'binary_crossentropy', metrics=['accuracy', Recall()])
model.fit(X_train1, y_train, batch_size = 7000, epochs = 500, verbose = 1)
results1= model.evaluate(X_train1, y_train, verbose=0)
results2 = model.evaluate(X_test1, y_test, verbose=0)
tempResultsDf = pd.DataFrame({'Model': ['Small but improved >'],
'TrainAccuracy': results1[1], 'TrainRecall': results1[2],
'TestAccuracy': results2[1], 'TestRecall': results2[2]})
resultsDf = pd.concat([resultsDf, tempResultsDf])
# -
resultsDf # Obtain the results
# The accuracy and recall for training data improve significantly, but as we can compare to the test data measurements, shows overfiting.
# ##### Running again the same models, but now using MinMax Data:
# +
# First Model (small):
model = Sequential(layers=None, name=None) # creating new network with default plus two hiden layers:
model.add(Dense(10, input_shape = (11,), activation = 'sigmoid'))
model.add(Dense(10, activation = 'sigmoid'))
model.add(Dense(10, activation = 'sigmoid'))
model.add(Dense(1, activation = 'sigmoid'))
sgd = optimizers.Adam(lr = 0.025)# Set the optimizer and learning rate
model.compile(optimizer = sgd, loss = 'binary_crossentropy', metrics=['accuracy', Recall()]) # Compile the model
model.fit(X_train2, y_train, batch_size = 7000, epochs = 500, verbose=0) # Run the Network
results1= model.evaluate(X_train2, y_train, verbose=0) # create a results table:
results2 = model.evaluate(X_test2, y_test, verbose=0)
resultsDf = pd.DataFrame( # create a results table:
{'Model': ['Small model >'],'TrainAccuracy': results1[1], 'TrainRecall': results1[2],
'TestAccuracy': results2[1], 'TestRecall': results2[2]})
resultsDf = resultsDf[['Model','TrainAccuracy','TrainRecall','TestAccuracy','TestRecall']]
# Second model (Large) :
model = Sequential(layers=None, name=None) # In this model I use a combination of types of activation function layers
model.add(Dense(100, input_shape = (11,), activation = 'relu'))
model.add(Dense(75, activation = 'relu'))
model.add(Dense(60, activation = 'relu'))
model.add(Dense(40, activation = 'tanh'))
model.add(Dense(26, activation = 'elu'))
model.add(Dense(17, activation = 'relu'))
model.add(Dense(11, activation = 'exponential'))
model.add(Dense(7, activation = 'relu'))
model.add(Dense(1, activation = 'sigmoid'))
sgd = optimizers.Adamax(lr = 0.025) # using Adamax as gave sligh better results with mixed types of activation functions
model.compile(optimizer = sgd, loss = 'binary_crossentropy', metrics=['accuracy', Recall()])
model.fit(X_train2, y_train, batch_size = 7000, epochs = 500, verbose = 0)
results1= model.evaluate(X_train2, y_train, verbose=0)
results2 = model.evaluate(X_test2, y_test, verbose=0)
tempResultsDf = pd.DataFrame({'Model':['Larger >'],
'TrainAccuracy': results1[1], 'TrainRecall': results1[2],
'TestAccuracy': results2[1], 'TestRecall': results2[2]})
resultsDf = pd.concat([resultsDf, tempResultsDf])
# Third model (Small but improved):
model = Sequential(layers=None, name=None) # Using tanh as activation function through the model, except the output layer
model.add(Dense(11, input_shape = (11,), activation = 'tanh'))
model.add(Dense(60, activation = 'tanh'))
model.add(Dense(40, activation = 'tanh'))
model.add(Dense(20, activation = 'tanh'))
model.add(Dense(1, activation = 'sigmoid'))
sgd = optimizers.Adam(lr = 0.025) # Adam works better than Adamax od SGD in this particular case
model.compile(optimizer = sgd, loss = 'binary_crossentropy', metrics=['accuracy', Recall()])
model.fit(X_train2, y_train, batch_size = 7000, epochs = 500, verbose = 0)
results1= model.evaluate(X_train2, y_train, verbose=0)
results2 = model.evaluate(X_test2, y_test, verbose=0)
tempResultsDf = pd.DataFrame({'Model': ['Small but improved >'],
'TrainAccuracy': results1[1], 'TrainRecall': results1[2],
'TestAccuracy': results2[1], 'TestRecall': results2[2]})
resultsDf = pd.concat([resultsDf, tempResultsDf])
# -
resultsDf # Results from data normalized using minmax scaler:
# These results show lower scores for training data than previous pass, but higher scores for test data: particularly for test Recall, which is important because of the imbalanced output variable.
# Appears that we could use less layers and still get acceptable results by using tanh activation function.
# This model achieves >.90 of Accuracy and .7 of Recall consistently on training data, reducing the overfitting, which could be the best result out of these three models. However, it could be overfitted, but as compared to other types of machine learning regressors is a good result, even more considering the un-balanced data.
model.save("my_bestChurn_model.h5") # Saving last model
# #### 7.- Predict the results using 0.5 as a threshold. Note that you need to first predict the probability and then predict classes using the given threshold (10points)
#
# Obtaining predicted probabilities of test data:
y_pred = model.predict_proba(X_test2, batch_size=2000, verbose=0)
y_pred
# Predicting the results using 0.5 as a threshold:
y_predict = []
for val in y_pred:
y_predict.append(np.where(val>=0.5,1,0))
# output is Binary : 1 if probability is over the threshold and 0 if lower than threshold
# #### 8.- Print the Accuracy score and confusion matrix (5points)
TT=0
for i in range(0,len(y_predict)):
if y_predict[i]==y_test[i]:
TT=TT+1
Accur=TT/len(y_test)
print("Calculated Accuracy :",Accur)
print("Recall:",recall_score(y_test,y_predict)) # Printing recall from the thereshold of 0.5
# printing the confusion matrix, based on the threshold
def draw_cm( actual, predicted ):
cm = confusion_matrix( actual, predicted)
sns.heatmap(cm, annot=True, fmt='.2f', xticklabels = [0,1] , yticklabels = [0,1] )
plt.ylabel('Observed')
plt.xlabel('Predicted')
plt.show()
print('Confusion Matrix')
print(draw_cm(y_test,y_predict))
# to confirm these values, we can exctract them directly from the model:
results = model.evaluate(X_test2, y_test, verbose=0)
print(model.metrics_names)
print(results)
# The Accuracy is >0.81 for this last model
# Now, I will change the Threshold and plot hot it influences the scores:
sensDf = pd.DataFrame( # create a results table:
{'Thres':[0],'TAccuracy': [0],'TRecall': [1]})
sensDf = sensDf[['Thres','TAccuracy','TRecall']]
for j in range(1,100):
y_predict = []
for val in y_pred:
y_predict.append(np.where(val>=(j/100),1,0))
TT=0
for i in range(0,len(y_predict)):
if y_predict[i]==y_test[i]:
TT=TT+1
Accur=TT/len(y_test)
tempSensDf = pd.DataFrame({'Thres':[j/100],'TAccuracy': [Accur],'TRecall': [recall_score(y_test,y_predict)]})
sensDf = pd.concat([sensDf, tempSensDf])
plt.plot(sensDf['Thres'],sensDf['TAccuracy'],'r',sensDf['Thres'],sensDf['TRecall'],'b')
plt.xlabel('Threshold')
plt.ylabel('Red=Accuracy, Blue=Recall')
#There is a tradeoff point at 0.13
y_pred = model.predict_proba(X_test2, batch_size=2000, verbose=0)
y_predict = []
for val in y_pred:
y_predict.append(np.where(val>=0.13,1,0))
TT=0
for i in range(0,len(y_predict)):
if y_predict[i]==y_test[i]:
TT=TT+1
Accur=TT/len(y_test)
print("Calculated Accuracy :",Accur)
print("Recall:",recall_score(y_test,y_predict)) # Printing recall from the thereshold of 0.5
# This is th highest recall thereshold, but the Accuracy diminishes to .7 (still not so bad)
# ### Conclusions:
# Type of normalization/scaling has a big impact in the behaviour of the model(s), Zscore with untreated outliers can overfit the model. Using MinMax scaling can yield to a model that can generalize better and be usable, for this database.
#
# The bank can use this model to predict who will exit with an Accuracy between of around 80%
# We could apply tunning to improve the model, but if we could get from the bank more features or even make a customer satisfaction survey, these results could improve.
#
| 20,420 |
/4_Class_Analysis/1. Updated Normalization.ipynb | 81d8a80300a017f323c1b3c70715254f2c0d834c | [] | no_license | Arnab-Sarker/WatChMaL_analysis | https://github.com/Arnab-Sarker/WatChMaL_analysis | 1 | 0 | null | 2022-03-15T05:34:02 | 2021-02-22T18:24:07 | null | Jupyter Notebook | false | false | .py | 261,281 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %load_ext autoreload
# %matplotlib inline
# %autoreload 2
import numpy as np
import matplotlib.pyplot as plt
import os
import sys
# +
#sys.path.append("../..")
sys.path.append("..")
from WatChMaL.analysis.multi_plot_utils import multi_disp_learn_hist, multi_compute_roc, multi_plot_roc
from WatChMaL.analysis.comparison_utils import multi_get_masked_data, multi_collapse_test_output
from WatChMaL.analysis.plot_utils import plot_classifier_response, plot_reduced_classifier_response
# +
label_dict = {"$\gamma$":0, "$e$":1, "$\mu$":2}
inverse_label_dict = {0:"$\gamma$", 1:"$e$", 2:"$\mu$"}
muon_softmax_index_dict = {"e/gamma":0, "mu":1}
c = plt.cm.viridis(np.linspace(0,1,10)) #plt.rcParams['axes.prop_cycle'].by_key()['color']
# +
############# define run locations #############
locs = ['/home/jtindall/WatChMaL/outputs/2021-02-16/full_veto_train_full_veto_test/outputs'
#'/home/jtindall/WatChMaL/outputs/2021-02-08/no_veto_train_full_veto_test/outputs' # trained with no veto
]
titles = ['Short Tank No Veto Run 1',
'Short Tank No Veto Run 2']
# -
linecolor = [c[0] for _ in locs]
linestyle = ['--' for _ in locs]
############# load short tank run data #############
raw_output_softmax = [np.load(loc + "/softmax.npy") for loc in locs]
raw_actual_labels = [np.load(loc + "/labels.npy") for loc in locs]
raw_actual_indices = [np.load(loc + "/indices.npy") for loc in locs]
# +
############# compute short tank multi e/gamma ROC #############
fprs, tprs, thrs = multi_compute_roc(raw_output_softmax, raw_actual_labels,
true_label=label_dict["$e$"],
false_label=label_dict["$\gamma$"],
normalize=False)
figs = multi_plot_roc(fprs, tprs, thrs, "$e$", "$\gamma$",
fig_list=[1], ylims=[[0,3e6]],
linestyles=linestyle,linecolors=linecolor,
plot_labels=titles, show=False)
# +
############# compute short tank multi e/gamma ROC #############
fprs, tprs, thrs = multi_compute_roc(raw_output_softmax, raw_actual_labels,
true_label=label_dict["$e$"],
false_label=label_dict["$\gamma$"],
normalize=True)
figs = multi_plot_roc(fprs, tprs, thrs, "$e$", "$\gamma$",
fig_list=[1], ylims=[[0,3e6]],
linestyles=linestyle,linecolors=linecolor,
plot_labels=titles, show=False)
figs = multi_plot_roc(fprs, tprs, thrs, "$e$", "$\gamma$",
fig_list=[1],
xlims=[[0.2,1.0]],ylims=[[1e0,2e1]],
linestyles=linestyle,linecolors=linecolor,
plot_labels=titles, show=False)
# -
linecolor = [c[0] for _ in range(20)]
linestyle = ['-' for _ in range(20)]
plot_classifier_response(raw_output_softmax[0], raw_actual_labels[0],
label_dict=label_dict,
linestyles=linestyle,
particle_names = ["$e$","$\gamma$",'$\mu$']
)
plot_reduced_classifier_response(raw_output_softmax[0], raw_actual_labels[0],
comparisons_list = [{'independent':['$e$'],
'dependent':['$e$',"$\gamma$",'$\mu$']},
{'independent':['$e$','$\gamma$'],
'dependent':['$e$',"$\gamma$",'$\mu$']},],
label_dict=label_dict,
linestyles=linestyle
)
plot_reduced_classifier_response(raw_output_softmax[0], raw_actual_labels[0],
comparisons_list = [{'independent':['$e$'],
'dependent':['$e$',"$\gamma$",'$\mu$']},
{'independent':['$e$'],
'dependent':['$e$',"$\gamma$"]},],
label_dict=label_dict,
linestyles=linestyle
)
plot_reduced_classifier_response(raw_output_softmax[0], raw_actual_labels[0],
comparisons_list = [{'independent':['$e$'],
'dependent':['$e$',"$\gamma$"]},
{'independent':['$e$'],
'dependent':['$e$',"$\gamma$",'$\mu$']},
],
label_dict=label_dict,
linestyles=linestyle,
normalize=True
)
| 5,530 |
/Feature Matching.ipynb | acdee5a2739aad337519ec1b8e1c2e721832d989 | [] | no_license | mayank0802/computer-vision | https://github.com/mayank0802/computer-vision | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 4,275 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#this is the notebook to generate the model
# -
import numpy as np
square root of x using your own function.
#
# **Hint**:
#
# + Do we need to iterate through all the values from 0 to x-1 and check whether the square of them?
# + Actually it is interesting to note that: $( \frac{x}{2} + 1) ^{2} = x + \frac{ x^{2}}{4} + 1 > x$
# + To make the algorithm runs even faster, binary search is your friend. http://interactivepython.org/runestone/static/pythonds/SortSearch/TheBinarySearch.html
# + You can assume that all the inputs have square root.
# +
#### Your code here
def sqrt(x):
square_j = 0
j = 0
while square_j != x:
j+= 1
square_j = j*j
return j
# -
sqrt(0) # 0
sqrt(64) # 8
sqrt(121) # 11
# ### Problem 2. Two Sum II - Input array is sorted
#
# Given an array of integers that is already sorted in ascending order, find two numbers such that they add up to a specific target number.
#
# The function twoSum should return indices of the two numbers such that they add up to the target, where index1 must be less than index2.
#
# **Hint**:
#
# + Last time we introduced a tricky solution using a dictionary. However, this time the input arrary is sorted, which means we can make our solution even faster using a similar approach like binary search.
# + We will have two pointers pointing to the beginning and the end of the list. For each iteration, we check the sum of the values of two pointers. If it equals to the target, we just return the index of those two pointers. Otherwise we either move the left pointer or the right one accordingly.
# + You may assume that each input would have exactly one solution.
# +
def twoSum(numbers, target):
"""
:type numbers: List[int]
:type target: int
:rtype: List[int]
"""
for i in range(0,len(numbers)):
for j in range(i + 1,len(numbers)):
if numbers[i] + numbers[j] == target:
if i < j:
return [i,j]
return [j,i]
return None
# -
twoSum([1,2,3,3], 6) # [2, 3]
twoSum([4,5,8,9], 12) # [0, 2]
twoSum([1,2,4], 8) # None
# ### Problem 3. Linked List Cycle
#
# Given a linked list, determine if it has a cycle in it.
#
# **Hint**: One trick to find whether there is a linked list has cycle is to set up two pointers, one called slow and the other one called fast. Slow pointer moves one step once a time and fast pointer moves twice a time. If they meet with each other at some point, then there is a cycle.
# +
# The definition of node and linkedlist from the previous code review
class Node(object):
def __init__(self, data, next_node=None):
self.next_ = next_node
self.data = data
def __str__(self):
return str(self.data)
class LinkedList(object):
def __init__(self, head=None):
self.head = head
def append(self, data, next_node=None):
if data is None:
return
node = Node(data, next_node)
if self.head is None:
self.head = node
else:
curr_node = self.head
while curr_node.next_ is not None:
curr_node = curr_node.next_
curr_node.next_ = node
return
# +
#### Your code here
def hasCycle(lst):
"""
:type lst: LinedList
:rtype: Boolean
"""
slow = lst.head
fast = lst.head
while fast:
slow = slow.next_
fast = fast.next_.next_
if slow == fast:
return True
return False
# +
#### Here we create two LinkedLists with one of them containing a cycle
lst_1=LinkedList()
for i in [1, 2, 3, 4, 5, 6]:
lst_1.append(i)
A = Node(1)
B = Node(2)
C = Node(3)
D = Node(4)
lst_2 = LinkedList(A)
curr = lst_2.head
for i in [B, C, B]:
curr.next_ = i
curr = curr.next_
# -
hasCycle(lst_2) # True
hasCycle(lst_1) # False
# ### Problem 4. Longest Palindromic Substring (Homework)
#
# Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.
#
# **Hint**:
#
# + We have already known how to check whether a string is palindromic or not. That is simply s == s[::-1]
# + The idea stays the same when we want to find out the longest palindromic substring.
# + When we have a new character in our string, if it contributes to a palindromic substring, then there are two cases:
#
# 1. odd case, like "aba"
# 2. even case, like "abba"
#
# + So we can iterate through all the characters in the string and for each character, we check whether it is case 1 or 2. If the length of palindromic substring we get is longer than the previous one, we just update our return value
def longestPalindrome(s):
"""
:type s: string
:rtype: string
"""
longestPalindrome('hjtyabcddcbafsadf') # abcddcba
longestPalindrome('abccba') # abccba
longestPalindrome('yabcdchjfsdsf') # cdc
# ### Problem 5. Find Peak Element (Homework)
#
# A peak element is an element that is greater than its neighbors.
#
# Given an input array where num[i] ≠ num[i+1], find a peak element and return its index.
#
# The array may contain multiple peaks, in that case return the index to any one of the peaks is fine.
#
# You may imagine that num[-1] = num[n] = -∞.
#
# For example, in array [1, 2, 3, 1], 3 is a peak element and your function should return the index number 2.
#
# ** Again, binary search is your friend. **
def findPeakElement(nums):
"""
:type nums: List[int]
:rtype: int
"""
findPeakElement([4,3,2,1]) # 0
findPeakElement([1,2,3,4]) # 3
findPeakElement([1,4,3,5,8,2]) # 4
| 5,996 |
/Multi-Layer Perceptron Attack 1.ipynb | d2e9e5a6a2eecbdd8817b500b8ca8ffc037ba8a9 | [] | no_license | tj-kim/privacy_project | https://github.com/tj-kim/privacy_project | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 10,472 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# This notebooks tests the spatial reasoning architecture with the simulation of one supplied sentence and plots most of the neural fields to observe the behavior.
import sys
sys.path.append('../cedar_utils/')
sys.path.append('../simulations/')
from read_json import load_from_json
from parse_cedar_objects import parse_cedar_params, make_connection
import nengo
import numpy as np
import matplotlib.pyplot as plt
from plotting import plot_0d, plot_1d, plot_2d
PROBE_ALL = False
SAVE_SIMULATION = False
objects, connections = load_from_json('../JSON/mental_imagery_extended.json')
# +
model = nengo.Network()
tau_factor = 0.15
with model:
nengo_objects = {}
# create the nodes
for ob_key in objects:
name, instance = parse_cedar_params(objects[ob_key])
if instance.__class__.__name__ == 'NeuralField':
instance.tau *= tau_factor
instance.make_node()
nengo_objects[name] = instance
# create the connections
for connection in connections:
make_connection(connection[0][1], connection[1][1], nengo_objects)
# -
# the list contains all nodes that are plotted in the plotting widget of the cedar architecture
objects_to_probe = ['Reference Behavior.intention node', # Reference processes
'Reference Behavior.CoS node',
'Reference Field & Reference Production Nodes.intention node',
'Reference Field & Reference Production Nodes.CoS node',
'Reference Memory Nodes & Color Field.intention node',
'Reference Memory Nodes & Color Field.CoS node',
'Target Behavior.intention node', # Target processes
'Target Behavior.CoS node',
'Target Field & Target Production Nodes.intention node',
'Target Field & Target Production Nodes.CoS node',
'Reference Memory Nodes & Color Field 2.intention node',
'Reference Memory Nodes & Color Field 2.CoS node',
'Match Field.intention node',
'Match Field.CoS node',
'Relational Behavior.intention node', # Spatial processes
'Relational Behavior.CoS node',
'OC Field and Spatial Production Nodes .intention node',
'OC Field and Spatial Production Nodes .CoS node',
'Condition of Dissatisfaction .intention node',
'Condition of Dissatisfaction .CoS node',
'Spatial Memory Nodes.intention node',
'Spatial Memory nodes.CoS node',
'Colour', # Color attention
'Projection', # Attention (space)
'Indeterminent ', # Spatial scene representation
'Reference', # Reference
'Target', # Target
'Object-centered ', # Relational
'Reference Red Memory', # Reference color memory
'Reference Blue Memory',
'Reference Cyan Memory',
'Reference Green Memory',
'Reference Orange Memory',
'To the left of Memory', # Spatial relation memory
'To the Right of Memory',
'Above Memory',
'Below Memory',
'Target Red Memory', # Target color memory
'Target Blue Memory',
'Target Cyan Memory',
'Target Green Memory',
'Target Orange Memory ',
'Reference Red Production', # Reference color production
'Reference Blue Production',
'Reference Cyan Production',
'Reference Green Production',
'Reference Orange Production',
'To the left of Production', # Spatial relation production
'To the Right of Production',
'Above Production',
'Below Production',
'Target Red Production', # Target color production
'Target Blue Production',
'Target Cyan Production',
'Target Green Production',
'Target Orange Production']
with model:
probes = {}
for key in nengo_objects:
if not PROBE_ALL:
if key in objects_to_probe:
probes[key] = nengo.Probe(nengo_objects[key].node, sample_every=0.01)
else:
probes[key] = nengo.Probe(nengo_objects[key].node, sample_every=0.05)
sim = nengo.Simulator(model)
# +
# Supply sentence
nengo_objects['Reference: Blue'].strength = 5.1
nengo_objects['Reference: Blue'].active = True
nengo_objects['Target: Cyan'].active = True
nengo_objects['Spatial relation: Left'].active = True
sim.run_steps(int(500*tau_factor))
# +
# Activate imagine node
nengo_objects['Reference: Blue'].active = False
nengo_objects['Target: Cyan'].active = False
nengo_objects['Spatial relation: Left'].active = False
nengo_objects['Action: Imagine'].active = True
sim.run_steps(int(9500*tau_factor))
# -
sim.close()
# +
# save simulation results
from datetime import datetime
import os
timestamp = str(datetime.now()).rsplit('.',1)[0]
print(timestamp)
if SAVE_SIMULATION:
os.mkdir('../simulation_data/%s' %timestamp)
for ob_key in probes:
file_name = ob_key.replace('/','_')
np.save('../simulation_data/%s/%s_%s' %(timestamp, file_name, timestamp), sim.data[probes[ob_key]])
# -
# # Plot color activation
# +
# for tau_factor 0.05 show every third step, for other tau_factors show a multiple
# thereof
num_samples = sim.data[probes['Reference Blue Memory']].shape[0]
print('Number of samples:', num_samples)
if num_samples > 150:
stepsize = 5 * round(TAU_FACTOR / 0.05)
print("Number of samples:", num_samples, 'Stepsize:', stepsize)
time_points = np.arange(0, num_samples, stepsize)[-36:]
else:
time_points = np.arange(0, num_samples, 2)[-36:]
print("time_points: \n", time_points, len(time_points))
from cedar_modules import AbsSigmoid
sigmoid = AbsSigmoid()
# -
# ## Color and Relation fields 0-dimensional
plot_0d(sim, probes)
# ## Color
colour_data = sim.data[probes['Colour']]
plot_1d(colour_data, time_points, title='Colour', save=False)
# ## Spatial scene
spatial_scene = sim.data[probes['Indeterminent ']]
plot_2d(spatial_scene, time_points, colorbar=True, title='Spatial Scene', save=False)
# ## Object-centered
# Object-centered = relational field in the Plotting widget
object_centered_data = sim.data[probes['Object-centered ']]
plot_2d(object_centered_data, time_points, colorbar=True, title='Relational Field', save=False)
# ## Target
target = sim.data[probes['Target']]
plot_2d(target, time_points, colorbar=True, title='Target Field', save=False)
# ## Reference
reference_data = sim.data[probes['Reference']]
plot_2d(reference_data, time_points, colorbar=True, title='Reference Field', save=False)
# # 0-dimensional Group nodes
#
# ## Group Target Behavior
# +
if PROBE_ALL:
target_behavior_nodes = ['Target Behavior.intention node',
'Target Behavior.new StaticGain 6', 'Target Behavior.new Static Gain 4',
'Target Behavior.new Static Gain 12', 'Target Behavior.new Static Gain 15',
'Target Behavior.new Static Gain 25', 'Target Behavior.new Static Gain 26',
'Target Behavior.new Static Gain 27', 'Target Behavior.new StaticGain 2',
'Target Behavior.CoS node', 'Target Behavior.new Static Gain 5',
'Target Behavior.new Static Gain 18']
plt.figure(figsize=(15,12))
for i, name in enumerate(target_behavior_nodes):
plt.subplot(4,5,i+1)
plt.plot(x, sim.data[probes[name]])
name_split = name.rsplit('.',1)
if len(name_split) > 1:
plt.title(name_split[1])
else:
plt.title(name)
plt.tight_layout()
plt.show()
# -
# ## Group Reference Behavior
if PROBE_ALL:
ref_behavior_nodes = ['Reference Behavior.intention node', 'Reference Behavior.new Static Gain 10',
'Reference Behavior.new StaticGain 6', 'Reference Behavior.new Static Gain 19',
'Reference Behavior.new Static Gain 20', 'Reference Behavior.new Static Gain 31',
'Reference Behavior.new Static Gain 21', 'Reference Behavior.new StaticGain 2',
'Reference Behavior.CoS node', 'Reference Behavior.new Static Gain 5',
'Reference Behavior.new Static Gain 16']
plt.figure(figsize=(15,12))
for i, name in enumerate(ref_behavior_nodes):
plt.subplot(4,5,i+1)
plt.plot(x, sim.data[probes[name]])
name_split = name.rsplit('.',1)
if len(name_split) > 1:
plt.title(name_split[1])
else:
plt.title(name)
plt.tight_layout()
plt.show()
# ## Group Target Field & Target Production Nodes
if PROBE_ALL:
group_names = ['Target Field & Target Production Nodes.new StaticGain 6',
'Target Field & Target Production Nodes.new StaticGain 2',
'Target Field & Target Production Nodes.intention node',
'Target Field & Target Production Nodes.Static Gain 47',
'Target Field & Target Production Nodes.Projection 12',
'Target Field & Target Production Nodes.Static Gain 22',
'Target Field & Target Production Nodes.CoS node',
'Target Field & Target Production Nodes.Static Gain 40',
'Target Field & Target Production Nodes.Boost Target',
'Target Field & Target Production Nodes.Static Gain 39',
'Target Field & Target Production Nodes.Static Gain 46',
'Target Field & Target Production Nodes.new Static Gain 2']
plt.figure(figsize=(15,12))
for i, name in enumerate(group_names):
plt.subplot(4,5,i+1)
plt.plot(x, sim.data[probes[name]])
name_split = name.rsplit('.',1)
if len(name_split) > 1:
plt.title(name_split[1])
else:
plt.title(name)
plt.tight_layout()
plt.show()
# ## Group Reference Field & Reference Production Nodes
if PROBE_ALL:
names = ['Reference Field & Reference Production Nodes.new StaticGain 6',
'Reference Field & Reference Production Nodes.new StaticGain 2',
'Reference Field & Reference Production Nodes.intention node',
'Reference Field & Reference Production Nodes.Static Gain 47',
'Reference Field & Reference Production Nodes.Projection 12',
'Reference Field & Reference Production Nodes.Static Gain 22',
'Reference Field & Reference Production Nodes.CoS node',
'Reference Field & Reference Production Nodes.Static Gain 40',
'Reference Field & Reference Production Nodes.Boost Reference',
'Reference Field & Reference Production Nodes.Static Gain 39',
'Reference Field & Reference Production Nodes.Static Gain 46',
'Reference Field & Reference Production Nodes.new Static Gain 2']
plt.figure(figsize=(15,12))
for i, name in enumerate(names):
plt.subplot(4,5,i+1)
plt.plot(x, sim.data[probes[name]])
name_split = name.rsplit('.',1)
if len(name_split) > 1:
plt.title(name_split[1])
else:
plt.title(name)
plt.tight_layout()
plt.show()
# ## Group Relational Behavior
if PROBE_ALL:
names = ['Relational Behavior.new StaticGain 6',
'Relational Behavior.new Static Gain 3',
'Relational Behavior.new Static Gain 11',
'Relational Behavior.new Static Gain 22',
'Relational Behavior.new Static Gain 23',
'Relational Behavior.new Static Gain 24',
'Relational Behavior.new Static Gain 37',
'Relational Behavior.new StaticGain 2',
'Relational Behavior.intention node',
'Relational Behavior.CoS node',
'Relational Behavior.new Static Gain 5']
plt.figure(figsize=(15,12))
for i, name in enumerate(names):
plt.subplot(4,5,i+1)
plt.plot(x, sim.data[probes[name]])
name_split = name.rsplit('.',1)
if len(name_split) > 1:
plt.title(name_split[1])
else:
plt.title(name)
plt.tight_layout()
plt.show()
# ## Group OC Field and Spatial Production Nodes
if PROBE_ALL:
names = ['OC Field and Spatial Production Nodes .new StaticGain 6',
'OC Field and Spatial Production Nodes .new StaticGain 2',
'OC Field and Spatial Production Nodes .intention node',
'OC Field and Spatial Production Nodes .Static Gain 51',
'OC Field and Spatial Production Nodes .Projection 27',
'OC Field and Spatial Production Nodes .Static Gain 52',
'OC Field and Spatial Production Nodes .CoS node',
'OC Field and Spatial Production Nodes .new Static Gain 6',
'OC Field and Spatial Production Nodes .Static Gain 50',
'OC Field and Spatial Production Nodes .Static Gain 48',
'OC Field and Spatial Production Nodes .Boost OCF',
'OC Field and Spatial Production Nodes .Static Gain 49']
plt.figure(figsize=(15,12))
for i, name in enumerate(names):
plt.subplot(4,5,i+1)
plt.plot(x, sim.data[probes[name]])
name_split = name.rsplit('.',1)
if len(name_split) > 1:
plt.title(name_split[1])
else:
plt.title(name)
plt.tight_layout()
plt.show()
# ## Group Condition of Dissatisfaction
if PROBE_ALL:
names = ['Condition of Dissatisfaction .new StaticGain 6', 'Condition of Dissatisfaction .new StaticGain 2',
'Condition of Dissatisfaction .intention node', 'Condition of Dissatisfaction .Static Gain 40',
'Condition of Dissatisfaction .node', 'Condition of Dissatisfaction .Static Gain 37',
'Condition of Dissatisfaction .CoS node', 'Condition of Dissatisfaction .Static Gain 34']
plt.figure(figsize=(15,12))
for i, name in enumerate(names):
plt.subplot(4,5,i+1)
plt.plot(x, sim.data[probes[name]])
name_split = name.rsplit('.',1)
if len(name_split) > 1:
plt.title(name_split[1])
else:
plt.title(name)
plt.tight_layout()
plt.show()
# ## Group Spatial Memory Nodes
if PROBE_ALL:
names = ['Spatial Memory Nodes.new StaticGain 6', 'Spatial Memory Nodes.new StaticGain 2',
'Spatial Memory Nodes.intention node', 'Spatial Memory Nodes.Static Gain 47',
'Spatial Memory Nodes.CoS node', 'Spatial Memory Nodes.Static Gain 40']
plt.figure(figsize=(15,12))
for i, name in enumerate(names):
plt.subplot(4,5,i+1)
plt.plot(x, sim.data[probes[name]])
name_split = name.rsplit('.',1)
if len(name_split) > 1:
plt.title(name_split[1])
else:
plt.title(name)
plt.tight_layout()
plt.show()
# ## Group Reference Memory Nodes & Color Field
if PROBE_ALL:
names = ['Reference Memory Nodes & Color Field.new StaticGain 6',
'Reference Memory Nodes & Color Field.new StaticGain 2',
'Reference Memory Nodes & Color Field.intention node',
'Reference Memory Nodes & Color Field.Projection 15',
'Reference Memory Nodes & Color Field.Static Gain 60',
'Reference Memory Nodes & Color Field.CoS node',
'Reference Memory Nodes & Color Field.Static Gain 40',
'Reference Memory Nodes & Color Field.Static Gain 59',
'Reference Memory Nodes & Color Field.Boost Color Field',
'Reference Memory Nodes & Color Field.Static Gain 58']
plt.figure(figsize=(15,12))
for i, name in enumerate(names):
plt.subplot(4,5,i+1)
plt.plot(x, sim.data[probes[name]])
name_split = name.rsplit('.',1)
if len(name_split) > 1:
plt.title(name_split[1])
else:
plt.title(name)
plt.tight_layout()
plt.show()
# ## Group Reference Memory Nodes & Color Field 2
if PROBE_ALL:
names = ['Reference Memory Nodes & Color Field 2.new StaticGain 6',
'Reference Memory Nodes & Color Field 2.new StaticGain 2',
'Reference Memory Nodes & Color Field 2.intention node',
'Reference Memory Nodes & Color Field 2.Projection 15',
'Reference Memory Nodes & Color Field 2.Static Gain 60',
'Reference Memory Nodes & Color Field 2.CoS node',
'Reference Memory Nodes & Color Field 2.Static Gain 40',
'Reference Memory Nodes & Color Field 2.Static Gain 59',
'Reference Memory Nodes & Color Field 2.Boost Color Field',
'Reference Memory Nodes & Color Field 2.Static Gain 58']
plt.figure(figsize=(15,12))
for i, name in enumerate(names):
plt.subplot(4,5,i+1)
plt.plot(x, sim.data[probes[name]])
name_split = name.rsplit('.',1)
if len(name_split) > 1:
plt.title(name_split[1])
else:
plt.title(name)
plt.tight_layout()
plt.show()
# ## Group Match Field
if PROBE_ALL:
names = ['Match Field.new StaticGain 6', 'Match Field.new StaticGain 2',
'Match Field.intention node', 'Match Field.Static Gain 47', 'Match Field.Projection 12',
'Match Field.Static Gain 22', 'Match Field.CoS node', 'Match Field.Static Gain 40',
'Match Field.Boost Match Field', 'Match Field.Static Gain 39', 'Match Field.new Static Gain 2']
plt.figure(figsize=(15,12))
for i, name in enumerate(names):
plt.subplot(4,5,i+1)
plt.plot(x, sim.data[probes[name]])
name_split = name.rsplit('.',1)
if len(name_split) > 1:
plt.title(name_split[1])
else:
plt.title(name)
plt.tight_layout()
plt.show()
| 18,873 |
/Insurance - Model Training Notebook_VJ.ipynb | aa016661c5439b7a4d6be9b44ae696e8370be21d | [] | no_license | vinejain/insurance-bill-prediction-app | https://github.com/vinejain/insurance-bill-prediction-app | 1 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 262,369 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
pip install pycaret
from pycaret.datasets import get_data
data = get_data('insurance')
# # Experiment 1
from pycaret.regression import *
s = setup(data, target = 'charges', session_id = 123)
lr = create_model('lr')
plot_model(lr)
# # Experiment 2
s2 = setup(data, target = 'charges', session_id = 123,
normalize = True,
polynomial_features = True, trigonometry_features = True, feature_interaction=True,
bin_numeric_features= ['age', 'bmi'])
lr = create_model('lr')
plot_model(lr)
save_model(lr, 'deployment_lr_08012020')
deployment_lr_08012020 = load_model('deployment_lr_08012020')
deployment_lr_08012020
import requests
url = 'https://pycaret-insurance.herokuapp.com/predict_api'
pred = requests.post(url,json={'age':55, 'sex':'male', 'bmi':59, 'children':1, 'smoker':'male', 'region':'northwest'})
print(pred.json())
try = 3
# + slideshow={"slide_type": "fragment"}
list = [1, 2, 3] # Note the color of "list" - Python recognizes this but you are redefining it!
list((10, 20, 30)) # The in-built function will no longer work
# + [markdown] slideshow={"slide_type": "slide"}
# ## Best Practice
#
# * 📖 Use **`UPPERCASE_WITH_UNDERSCORES`** for constants, like passwords or secret keys
# * 📖 Use **`lowercase_with_underscore`** for variable names, functions, and methods
# * 📖 Use **`UpperCamelCase`** for classes (coming in Week 5!)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Resources
#
# In addition to the Python resources online, you can query any object to get help on what methods are available
# + slideshow={"slide_type": "-"}
dir(dict)
help(dict.popitem)
# + [markdown] slideshow={"slide_type": "slide"}
# # Strings
#
# * Ordered sequences of characters
# * Immutable
# + slideshow={"slide_type": "-"}
x = 'my string'
x = x.capitalize()
print(x)
print(x[3])
print(x[1:-1])
print(x[::2])
# + slideshow={"slide_type": "slide"}
# Exercise 1: Make three new strings from the first and last,
# second and second to last, and third and third to last letters
# in the string below. Print the three strings.
p = 'redder'
# Answer
print(p[0] + p[-1])
print(p[1] + p[-2])
print(p[2] + p[-3])
# + slideshow={"slide_type": "-"}
# Exercise 2: Make a new string that is the same as string1 but
# with the 8th and 22nd characters missing.
string1 = 'I cancelled my travelling plans.'
# Answers
#-----------------------------------------
string1[:7] + string1[8:21] + string1[22:]
# -
string2 = list(string1) # you can transform the string to a list
print(string2)
# + [markdown] slideshow={"slide_type": "slide"}
# ## String Methods
#
# * `S.upper()`
# * `S.lower()`
# * `S.capitalize()`
# * `S.find(S1)`
# * `S.replace(S1, S2)`
# * `S.strip(S1)`
# * `S.split(S1)`
# * `S.join(L)`
# + [markdown] slideshow={"slide_type": "slide"}
# ## Methods Can Be "Stringed"
#
# `sls = s.strip().replace(' ', ' ').upper().split()`
#
# However, be aware that this may reduce the clarity of your code.
#
# 📖 It is largely a question of code legibility.
#
# ⚡️ Except when you are working with large data — it is then also a question of memory.
# + slideshow={"slide_type": "slide"}
# Exercise 3: Remove the trailing white space in the string below,
# replace all double spaces with single space, and format to a sentence
# with proper punctuation. Print the resulting string.
string1 = ' this is a very badly. formatted string - I would like to make it cleaner\n'
# Answers
#-----------------------------------------
string2 = string1.strip().capitalize().replace('.','').replace(' -','.').replace(' ',' ').replace(' ',' ').replace(' i ',' I ')
print(string2 + '.')
s1_list = list(string2)
print(s1_list)
s1_list[0] = s1_list[0].upper()
print(''.join(s1_list))
# + slideshow={"slide_type": "slide"}
# Exercise 4: Convert the string below to a list
s = "['apple', 'orange', 'pear', 'cherry']"
# Answers
#-----------------------------------------
eval(s)
# + slideshow={"slide_type": "-"}
# Exercise 5: Reverse the strings below.
s1 = 'stressed'
s2 = 'drawer'
# Answers
#-----------------------------------------
print(s1[::-1])
print(s2[::-1])
# + [markdown] slideshow={"slide_type": "slide"}
# # Lists
#
# * Ordered sequence of values
# * Mutable
# + slideshow={"slide_type": "-"}
mylist = [1, 2, 3, 4]
mylist.append(5)
print(mylist)
# + [markdown] slideshow={"slide_type": "slide"}
# ## List Methods
#
# * `L.append(e)`
# * `L.extend(L1)`
# * `L.insert(i, e)`
# * `L.remove(e)`
# * `L.pop(i)`
# * `L.sort()`
# * `L.reverse()`
# + slideshow={"slide_type": "slide"}
# Exercise 6: Use a list operation to create a list of ten elements,
# each of which is '*'
# Answers
#-----------------------------------------
list2 = ['*']*10
print(list2)
list3 = list('*' * 10)
print(list3)
# + slideshow={"slide_type": "-"}
# Exercise 7: Assign each of the three elements in the list below
# to three variables a, b, c
ls = [['dogs', 'cows', 'rabbits', 'cats'], 'eat', {'meat', 'grass'}]
# Answers
#-----------------------------------------
a, b, c = ls
print(a)
print(b)
print(c)
# + slideshow={"slide_type": "-"}
# Exercise 8: Replace the last element in ls1 with ls2
ls1 = [0, 0, 0, 1]
ls2 = [1, 2, 3]
# Answers
#-----------------------------------------
ls1[-1] = ls2
print(ls1)
ls2.append('a') # changes in list2 are reflected in list1
print(ls1)
#-----------------------------------------
ls1 = [0, 0, 0, 1]
ls2 = [1, 2, 3]
ls1[-1] = ls2[::] # if you use [::] you make a copy, and chages to ls2 do not change ls1
ls2.append('a')
print(ls1)
# + slideshow={"slide_type": "slide"}
# Exercise 9: Create a new list that contains only unique elements from list x
x = [1, 5, 4, 5, 6, 2, 3, 2, 9, 9, 9, 0, 2, 5, 7]
# Answers
#-----------------------------------------
list(set(x))
# + slideshow={"slide_type": "-"}
# Exercise 10: Print the elements that occur both in list a and list b
a = ['red', 'orange', 'brown', 'blue', 'purple', 'green']
b = ['blue', 'cyan', 'green', 'pink', 'red', 'yellow']
# Answers
#-----------------------------------------
print(set(a) & set(b))
seta = set(a)
setb = set(b)
print(seta.intersection(setb))
# + slideshow={"slide_type": "-"}
# Exercise 11: Print the second smallest and the second largest numbers
# in this list of unique numbers
x = [2, 5, 0.7, 0.2, 0.1, 6, 7, 3, 1, 0, 0.3]
# Answers
#-----------------------------------------
x_sorted = sorted(x)
print(x_sorted)
print('second smallest=', x_sorted[1])
print('second largest=', x_sorted[-2])
# + slideshow={"slide_type": "-"}
# Exercise 12: Create a new list c that contains the elements of
# list a and b. Watch out for aliasing - you need to avoid it here.
a = [1, 2, 3, 4, 5]
b = ['a', 'b', 'c', 'd']
# Answers
#-----------------------------------------
c = a[::] + b[::]
print(c)
a.append(6)
print(a)
b.append('e')
print(b)
print(c)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Week 2 Assignment
#
# * Practice string and list manipulations
# * Practice working with data
| 7,250 |
/ice_cream_sales_Unsolved.ipynb | de50c7085de86f25636caca9f852c5e1e3cd60dc | [] | no_license | AhmadBouMerhi/Matplotlib | https://github.com/AhmadBouMerhi/Matplotlib | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 67,087 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# %matplotlib notebook
import matplotlib.pyplot as plt
import numpy as np
temp = [14.2, 16.4, 11.9, 15.2, 18.5, 22.1, 19.4, 25.1, 23.4, 18.1, 22.6, 17.2]
sales = [215, 325, 185, 332, 406, 522, 412, 614, 544, 421, 445, 408]
s = [10 * n for n in temp]
# Tell matplotlib to create a scatter plot based upon the above data
plt.scatter(temp, sales, marker="*", facecolors="red", edgecolors="black", s = s)
# Set the upper and lower limits of our y axis
plt.ylim(180,620)
# Set the upper and lower limits of our x axis
plt.xlim(11,26)
# Create a title, x label, and y label for our chart
plt.title("Ice Cream Sales v Temperature")
plt.xlabel("Temperature (Celsius)")
plt.ylabel("Sales (Dollars)")
# Save an image of the chart and print to screen
# NOTE: If your plot shrinks after saving an image,
# update matplotlib to 2.2 or higher,
# or simply run the above cells again.
plt.savefig("../Images/IceCreamSales.png")
plt.show()
| 1,206 |
/module_0/module_0.ipynb | 89889006e003069b7f48f886c416bad839efcdb2 | [] | no_license | Mormaethor1989/SF-DST-U0-GIT1 | https://github.com/Mormaethor1989/SF-DST-U0-GIT1 | 0 | 0 | null | null | null | null | Jupyter Notebook | false | false | .py | 2,469 | # ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="LF9lBSFFW_CF" executionInfo={"status": "ok", "timestamp": 1618242945965, "user_tz": -330, "elapsed": 1597, "user": {"displayName": "Prasad Pawar", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gjg3uqUXQkjb75lcNZlswi1lHdtRT7EUyDU7uIQWA=s64", "userId": "17658912636650039481"}}
import pandas as pd
import requests
df = pd.read_csv("DDD.csv")
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="pkg_16V4y8Ue" executionInfo={"status": "ok", "timestamp": 1618242951575, "user_tz": -330, "elapsed": 1622, "user": {"displayName": "Prasad Pawar", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gjg3uqUXQkjb75lcNZlswi1lHdtRT7EUyDU7uIQWA=s64", "userId": "17658912636650039481"}} outputId="4098833b-38a1-45b5-9ae6-0f3bcfe64686"
df
# + id="-OAyKnGL_wen" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1618246186716, "user_tz": -330, "elapsed": 245737, "user": {"displayName": "Prasad Pawar", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gjg3uqUXQkjb75lcNZlswi1lHdtRT7EUyDU7uIQWA=s64", "userId": "17658912636650039481"}} outputId="855777b1-4b9b-4e22-c198-de75423a28d0"
import pandas as pd
import requests
df = pd.read_csv("DDD.csv")
data=[]
for j in df['Code']:
print(j)
for i in range(13,31):
url='http://map.aviasales.ru/prices.json?origin_iata='+j+'&period=2021-04-'+str(i)+':season&direct=true&one_way=true&no_visa=true&schengen=true&need_visa=true&locale=ru&min_trip_duration_in_days=13&max_trip_duration_in_days=15'
response = requests.request("GET", url).json()
data.append(response)
# + colab={"base_uri": "https://localhost:8080/"} id="J6tQ3rqOJaMK" executionInfo={"status": "ok", "timestamp": 1618246220981, "user_tz": -330, "elapsed": 1601, "user": {"displayName": "Prasad Pawar", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gjg3uqUXQkjb75lcNZlswi1lHdtRT7EUyDU7uIQWA=s64", "userId": "17658912636650039481"}} outputId="fee1a5de-c8a1-43c8-cdd0-65e775b4945e"
len(data)
# + colab={"base_uri": "https://localhost:8080/"} id="vUnuPvB2zTb7" executionInfo={"status": "ok", "timestamp": 1618245677359, "user_tz": -330, "elapsed": 4994, "user": {"displayName": "Prasad Pawar", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gjg3uqUXQkjb75lcNZlswi1lHdtRT7EUyDU7uIQWA=s64", "userId": "17658912636650039481"}} outputId="0de509c8-c50d-435b-b02d-2d9e68e0b30b"
data
# + id="VksF2osm851r" executionInfo={"status": "ok", "timestamp": 1618246230893, "user_tz": -330, "elapsed": 1580, "user": {"displayName": "Prasad Pawar", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gjg3uqUXQkjb75lcNZlswi1lHdtRT7EUyDU7uIQWA=s64", "userId": "17658912636650039481"}}
price=[]
airline=[]
destination=[]
depart_date=[]
origin=[]
found_at=[]
via=[]
ttl=[]
created=[]
for i in data:
#if len(i)>50:
for j in i:
price.append(j["value"])
airline.append(j["airline"])
destination.append(j["destination"])
depart_date.append(j["depart_date"])
found_at.append(j["found_at"])
origin.append(j["origin"])
via.append(j["number_of_changes"])
# + id="k4BA-qIK21Ze" executionInfo={"status": "ok", "timestamp": 1618246234662, "user_tz": -330, "elapsed": 3634, "user": {"displayName": "Prasad Pawar", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gjg3uqUXQkjb75lcNZlswi1lHdtRT7EUyDU7uIQWA=s64", "userId": "17658912636650039481"}}
import pandas as pd
df=pd.DataFrame(price,columns=["Price"])
df["Airline"]=airline
df["Destination"]=destination
df["Depart_Date"]=depart_date
df["Time"]=found_at
df["Origin"]=origin
df["Via"]=via
# + id="odCl4pqlZkFO" executionInfo={"status": "ok", "timestamp": 1618246432030, "user_tz": -330, "elapsed": 1585, "user": {"displayName": "Prasad Pawar", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gjg3uqUXQkjb75lcNZlswi1lHdtRT7EUyDU7uIQWA=s64", "userId": "176589126366500394s[1], alpha=.5 * m_weights[1], color=color)
fig.cross(m_means[0][0], m_means[0][1], color=color, size=7, line_width=2)
fig.cross(m_means[1][0], m_means[1][1], color=color, size=7, line_width=2)
show(fig)
# -
# ## Hierarchical Generalized Subspace Model
#
# ### Creating the GSM
#
# The GSM is composed of a latent prior, an affine transformation, a generic subspace model which indicates how to transform the projections of the embedding into a concrete model and the instances of the generic subspace model (paired with latent posterior distributions, one for each subspace model instance).
#
# In the HGSM, the affine transformation of the GSM is itself generated by another GSM with its own parameters which is shared across (potentially) multiple child GSMs
# +
obs_dim = 2 # Dimension of the observations
lang_latent_dim = 2 # Dimension of the latent space of the child GSMs
latent_dim = 2 # Dimension of the latent space of the parent GSM
# Type of covariance for the Subspace GMMs.
cov_type = 'full' # full/diagonal/isotropic
# Prior over the latent space.
latent_prior = beer.Normal.create(
torch.zeros(latent_dim),
torch.ones(latent_dim),
prior_strength=1
).double()
language_priors = [beer.Normal.create(
torch.zeros(lang_latent_dim),
torch.ones(lang_latent_dim),
prior_strength=1e-3
).double() for _ in range(num_langs + 1)]
# Data model (SGMM).
modelsets = [beer.NormalSet.create(
mean=torch.zeros(obs_dim), cov=torch.ones(obs_dim),
size=2,
cov_type=cov_type
) for _ in range(num_langs + 1)]
sgmm_list = [beer.Mixture.create(modelsets[i]).double() for i in range(num_langs)]
# We specify which parameters will be handled by the
# subspace in the GMM.
for i, sgmm in enumerate(sgmm_list):
newparams = {
param: beer.SubspaceBayesianParameter.from_parameter(param, language_priors[i])
for param in sgmm.bayesian_parameters()
}
sgmm.replace_parameters(newparams)
# Create the Generalized Subspace Models
lang_gsms = [beer.GSM.create(sg, lang_latent_dim, lang_p, prior_strength=1e-3).double()
for sg, lang_p in zip(sgmm_list, language_priors)]
# Create the parent GSM
univ_affine_transform = AffineTransform.create(latent_dim, lang_gsms[0].transform.out_dim * (lang_gsms[0].transform.in_dim + 1),
prior_strength=1e-3)
# Create each child GSM's transform from the parent GSM
pseudo_transforms = [HierarchicalAffineTransform.create(latent_prior, lang_latent_dim,
lang_gsms[0].transform.out_dim,
univ_affine_transform, cov_type='diagonal').double()
for gsm in lang_gsms]
# Create the root GSM object which will be used to link all GSMs together in training
root_gsm = HierarchicalGSM(univ_affine_transform, latent_prior)
# Replace the child GSM transforms with the generated transforms
for pseudo_transform, lang_gsm in zip(pseudo_transforms, lang_gsms):
lang_gsm.transform = pseudo_transform
# Create the instance of SGMM for each dataset
lang_sgmms = [gsm.new_models(len(train_data_single), cov_type='diagonal')
for gsm, train_data_single in zip(lang_gsms, train_data)]
lang_latent_posts = [l[1] for l in lang_sgmms]
lang_sgmms = [l[0] for l in lang_sgmms]
print('Latent prior')
print('============')
print(latent_prior)
print()
print('Child GSM latent prior')
print('============')
print(language_priors[0])
print()
print('Subspace GMM (generic model)')
print('============================')
print(sgmm_list[0])
print()
print('Generalized Subspace Model')
print('==========================')
print(lang_gsms[0])
print()
print('Subspace GMMs (concrete instances)')
print('==================================')
print('(1) -', lang_sgmms[0][0])
print()
print('...')
print()
print(f'({len(datasets)}) -', lang_sgmms[0][-1])
print()
# -
# ### Pre-training
#
# Before starting the training, we need to inialize the subspace. To do so, we first train a Normal distribution for each dataset and we'll use its statistics as initial statistics for all the Normal distributions of the SGMMs.
# +
def create_normal(dataset, cov_type):
data_mean = dataset.mean(dim=0)
data_var = dataset.var(dim=0)
return beer.Normal.create(data_mean, data_var, cov_type=cov_type).double()
def fit_normal(normal, dataset, epochs=1):
optim = beer.VBConjugateOptimizer(normal.mean_field_factorization(), lrate=1.)
for epoch in range(epochs):
optim.init_step()
elbo = beer.evidence_lower_bound(normal, dataset)
elbo.backward()
optim.step()
lang_normals = []
for i in range(num_langs):
normals = [create_normal(dataset, cov_type=cov_type) for dataset in train_data[i]]
for normal, dataset in zip(normals, train_data[i]):
fit_normal(normal, dataset)
lang_normals.append(normals)
figs = []
ind = 0
for normals, train_data_single in zip(lang_normals, train_data):
ind += 1
fig = figure(width=400, height=400, title=f'Lang{ind}')
for normal, dataset, color in zip(normals, train_data_single, colors):
dataset = dataset.numpy()
mean = normal.mean.numpy()
cov = normal.cov.numpy()
plotting.plot_normal(fig, mean, cov, alpha=.5, color=color)
fig.circle(dataset[:, 0], dataset[:, 1], color=color, alpha=.1)
figs.append(fig)
fig = figure(width=400, height=400, title='All languages')
for normals, train_data_single in zip(lang_normals, train_data):
for normal, dataset, color in zip(normals, train_data_single, colors):
dataset = dataset.numpy()
mean = normal.mean.numpy()
cov = normal.cov.numpy()
plotting.plot_normal(fig, mean, cov, alpha=.5, color=color)
fig.circle(dataset[:, 0], dataset[:, 1], color=color, alpha=.1)
figs.append(fig)
figs_per_line = 2
figs = [figs[figs_per_line*i:figs_per_line*i+figs_per_line] for i in range(1 + len(figs)//figs_per_line)]
show(gridplot(figs))
# +
# Prepare the initial weights sufficient statistics.
for sgmms, train_data_single, normals in zip(lang_sgmms, train_data, lang_normals):
ncomp = len(sgmms[0].modelset)
weights_stats = torch.zeros(len(train_data_single), ncomp).double()
counts = torch.cat([torch.tensor(float(len(dataset))).view(1) for dataset in train_data_single]).double()
weights_stats[:] = counts[:, None] / ncomp
weights_stats[:, -1] = counts
weights_stats
# Prepare the initial sufficient statistics for the
# components of the GMM.
normals_stats = [normal.mean_precision.stats.repeat(ncomp, 1)
for normal in normals]
for i, gmm in enumerate(sgmms):
gmm.categorical.weights.stats = weights_stats[i]
gmm.modelset.means_precisions.stats = normals_stats[i]
# NOTE: we initialize the stats of all the parameters
# whether they are included in the subspace or not.
# For parameters that are not included in the subspace,
# this initialization will be discarded during
# the training ("optim.init_step()" clear the stats).
# +
epochs = 20_000
params = sum([list(gsm.conjugate_bayesian_parameters(keepgroups=True)) for gsm in lang_gsms], [])
cjg_optim = beer.VBConjugateOptimizer(params, lrate=1.)
params = sum([list(latent_posts.parameters()) + list(gsm.parameters())
for latent_posts, gsm in zip(lang_latent_posts, lang_gsms)], [])
std_optim = torch.optim.Adam(params, lr=5e-2)
optim = beer.VBOptimizer(cjg_optim, std_optim)
elbos = []
# -
for i in range(1, epochs + 1):
optim.init_step()
elbo = beer.evidence_lower_bound(root_gsm,
[(gsm, sgmm) for gsm, sgmm in zip(lang_gsms, lang_sgmms)],
univ_latent_nsamples=5,
latent_posts=lang_latent_posts,
latent_nsamples=5, params_nsamples=5)
elbo.backward()
optim.step()
elbos.append(float(elbo))
# +
figs_per_line = 2
figs = []
fig = figure(title='ELBO')
fig.line(range(len(elbos)), elbos)
figs.append(fig)
figs = [figs[figs_per_line*i:figs_per_line*i+figs_per_line] for i in range(1 + len(figs)//figs_per_line)]
show(gridplot(figs))
# +
fig1 = figure(title='True model', x_range=(-100, 100), y_range=(-10, 10))
for means, covs, weights, datasets in full_data:
for color, dataset, m_means, m_covs, m_weights in zip(colors, datasets, means, covs, weights):
dataset = dataset.numpy()
plotting.plot_normal(fig1, m_means[0], m_covs[0], alpha=.5 * m_weights[0], color=color)
plotting.plot_normal(fig1, m_means[1], m_covs[1], alpha=.5 * m_weights[1], color=color)
fig1.circle(dataset[:, 0], dataset[:, 1], alpha=.2, color=color)
fig2 = figure(title='Subspace GMM', x_range=fig1.x_range, y_range=fig1.y_range)
for sgmms, dataset in zip(lang_sgmms, train_data):
for gmm, dataset, color in zip(sgmms, datasets, colors):
dataset = dataset.numpy()
plotting.plot_gmm(fig2, gmm, alpha=.7, color=color)
fig2.circle(dataset[:, 0], dataset[:, 1], color=color, alpha=.5)
fig3 = figure(title='Unit latent space')
mean, cov = language_priors[0].mean.numpy(), language_priors[0].cov.numpy()
plotting.plot_normal(fig3, mean, cov, alpha=.5, color='pink')
for post, color in zip(lang_latent_posts, colors):
for mean, cov in zip(post.params.mean, post.params.diag_cov):
mean = mean.detach().numpy()
cov = (cov.diag().detach().numpy())
plotting.plot_normal(fig3, mean, cov, alpha=0.5, color=color)
fig4 = figure(title='Latent space')
mean, cov = pseudo_transform.latent_prior.mean.numpy(), pseudo_transform.latent_prior.cov.numpy()
plotting.plot_normal(fig4, mean, cov, alpha=.5, color='pink')
for gsm, color in zip(lang_gsms, colors):
mean, cov = gsm.transform.latent_posterior.params.mean, gsm.transform.latent_posterior.params.diag_cov
mean = mean.detach().numpy()
cov = (cov.squeeze().diag().detach().numpy())
plotting.plot_normal(fig4, mean, cov, alpha=0.5, color=color)
show(gridplot([[fig1, fig2], [fig3, fig4]]))
# -
# ### Training
#
# Now the HGSM is initialized so we start the "actual" training by updating the statistics of the parameters whenever the HGSM is updated
# +
epochs = 20_000
stats_update_rate = 100
# This function accumulate the statistics for the parameters
# of the subspace and update the parameters that are not
# part of the subspace.
def accumulate_stats(models, datasets, optims):
for model, X, optim in zip(models, datasets, optims):
optim.init_step()
elbo = beer.evidence_lower_bound(model, X)
elbo.backward(std_params=False)
optim.step()
# Prepare an optimzer for each SGMM. The optimizer
# will handle all parameters that are note included
# in the subspace.
all_sgmm_optims = []
for sgmms in lang_sgmms:
sgmms_optims = []
for gmm in sgmms:
pfilter = lambda param: not isinstance(param, beer.SubspaceBayesianParameter)
params = gmm.bayesian_parameters(
paramtype=beer.ConjugateBayesianParameter,
paramfilter=pfilter,
keepgroups=True
)
soptim = beer.VBConjugateOptimizer(params, lrate=1.)
sgmms_optims.append(soptim)
all_sgmm_optims.append(sgmms_optims)
elbos_f = []
# -
for epoch in range(1, epochs + 1):
if (epoch - 1) % stats_update_rate == 0:
for sgmms, train_data_single, sgmm_optims in zip(lang_sgmms, train_data, all_sgmm_optims):
accumulate_stats(sgmms, train_data_single, sgmms_optims)
optim.init_step()
elbo = beer.evidence_lower_bound(root_gsm,
[(gsm, sgmm) for gsm, sgmm in zip(lang_gsms, lang_sgmms)],
univ_latent_nsamples=5,
latent_posts=lang_latent_posts,
latent_nsamples=5, params_nsamples=5)
elbo.backward()
optim.step()
elbos_f.append(float(elbo))
# +
figs_per_line = 3
figs = []
fig = figure(title='Elbos')
fig.line(range(len(elbos_f)), elbos_f)
figs.append(fig)
figs = [figs[figs_per_line*i:figs_per_line*i+figs_per_line] for i in range(1 + len(figs)//figs_per_line)]
show(gridplot(figs))
# -
root_gsm.shared_transform.kl_div_posterior_prior()
# +
fig1 = figure(title='True model', x_range=(-100, 100), y_range=(-10, 10))
for color, (means, covs, weights, datasets) in zip(colors, full_data):
for dataset, m_means, m_covs, m_weights in zip(datasets, means, covs, weights):
dataset = dataset.numpy()
plotting.plot_normal(fig1, m_means[0], m_covs[0], alpha=.5 * m_weights[0], color=color)
plotting.plot_normal(fig1, m_means[1], m_covs[1], alpha=.5 * m_weights[1], color=color)
fig1.circle(dataset[:, 0], dataset[:, 1], alpha=.5, color=color)
fig2 = figure(title='Subspace GMM', x_range=fig1.x_range, y_range=fig1.y_range)
for color, sgmms, datasets in zip(colors, lang_sgmms, train_data):
for gmm, dataset in zip(sgmms, datasets):
dataset = dataset.numpy()
fig2.circle(dataset[:, 0], dataset[:, 1], color=color, alpha=.05)
plotting.plot_gmm(fig2, gmm, alpha=.5, color=color)
fig3 = figure(title='Unit latent space')#, y_range=(-1, 1))
mean, cov = language_priors[0].mean.numpy(), language_priors[0].cov.numpy()
plotting.plot_normal(fig3, mean, cov, alpha=.5, color='pink')
for post, color in zip(lang_latent_posts, colors):
for mean, cov in zip(post.params.mean, post.params.diag_cov):
mean = mean.detach().numpy()
cov = (cov.diag().detach().numpy())
plotting.plot_normal(fig3, mean, cov, alpha=0.5, color=color)
fig4 = figure(title='Language latent space', x_range=fig3.x_range, y_range=fig3.y_range)
mean, cov = pseudo_transform.latent_prior.mean.numpy(), pseudo_transform.latent_prior.cov.numpy()
plotting.plot_normal(fig4, mean, cov, alpha=.5, color='pink')
for gsm, color in zip(lang_gsms, colors):
mean, cov = gsm.transform.latent_posterior.params.mean, gsm.transform.latent_posterior.params.diag_cov
mean = mean.detach().numpy()
cov = (cov.squeeze().diag().detach().numpy())
plotting.plot_normal(fig4, mean, cov, alpha=0.5, color=color)
show(gridplot([[fig1, fig2], [fig3, fig4]]))
# -
lang_sgmms[0][2].categorical.weights.stats
lang_sgmms[0][2].modelset[0].mean_precision.stats
l0 = HierarchicalAffineTransform.new_latent_posteriors(univ_affine_transform, 1)
l0
root_gsm.shared_transform.bias.posterior
(root_gsm.shared_transform.weights.posterior)
entropies={'root_weight': gauss_entropy(root_gsm.shared_transform.weights.posterior.params.log_diag_cov),
'root_bias': gauss_entropy(root_gsm.shared_transform.bias.posterior.params.log_diag_cov),
'language': [gauss_entropy(gsm.transform.latent_posterior.params.log_diag_cov) for gsm in lang_gsms],
'units': [[gauss_entropy(_x) for _x in lat.params.log_diag_cov] for lat in lang_latent_posts]
}
entropies
| 19,150 |