norallm/normistral-7b-scratch
Text Generation
•
Updated
•
740
•
8
code
stringlengths 235
11.6M
| repo_path
stringlengths 3
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 09 Strain Gage
#
# This is one of the most commonly used sensor. It is used in many transducers. Its fundamental operating principle is fairly easy to understand and it will be the purpose of this lecture.
#
# A strain gage is essentially a thin wire that is wrapped on film of plastic.
# <img src="img/StrainGage.png" width="200">
# The strain gage is then mounted (glued) on the part for which the strain must be measured.
# <img src="img/Strain_gauge_2.jpg" width="200">
#
# ## Stress, Strain
# When a beam is under axial load, the axial stress, $\sigma_a$, is defined as:
# \begin{align*}
# \sigma_a = \frac{F}{A}
# \end{align*}
# with $F$ the axial load, and $A$ the cross sectional area of the beam under axial load.
#
# <img src="img/BeamUnderStrain.png" width="200">
#
# Under the load, the beam of length $L$ will extend by $dL$, giving rise to the definition of strain, $\epsilon_a$:
# \begin{align*}
# \epsilon_a = \frac{dL}{L}
# \end{align*}
# The beam will also contract laterally: the cross sectional area is reduced by $dA$. This results in a transverval strain $\epsilon_t$. The transversal and axial strains are related by the Poisson's ratio:
# \begin{align*}
# \nu = - \frac{\epsilon_t }{\epsilon_a}
# \end{align*}
# For a metal the Poission's ratio is typically $\nu = 0.3$, for an incompressible material, such as rubber (or water), $\nu = 0.5$.
#
# Within the elastic limit, the axial stress and axial strain are related through Hooke's law by the Young's modulus, $E$:
# \begin{align*}
# \sigma_a = E \epsilon_a
# \end{align*}
#
# <img src="img/ElasticRegime.png" width="200">
# ## Resistance of a wire
#
# The electrical resistance of a wire $R$ is related to its physical properties (the electrical resistiviy, $\rho$ in $\Omega$/m) and its geometry: length $L$ and cross sectional area $A$.
#
# \begin{align*}
# R = \frac{\rho L}{A}
# \end{align*}
#
# Mathematically, the change in wire dimension will result inchange in its electrical resistance. This can be derived from first principle:
# \begin{align}
# \frac{dR}{R} = \frac{d\rho}{\rho} + \frac{dL}{L} - \frac{dA}{A}
# \end{align}
# If the wire has a square cross section, then:
# \begin{align*}
# A & = L'^2 \\
# \frac{dA}{A} & = \frac{d(L'^2)}{L'^2} = \frac{2L'dL'}{L'^2} = 2 \frac{dL'}{L'}
# \end{align*}
# We have related the change in cross sectional area to the transversal strain.
# \begin{align*}
# \epsilon_t = \frac{dL'}{L'}
# \end{align*}
# Using the Poisson's ratio, we can relate then relate the change in cross-sectional area ($dA/A$) to axial strain $\epsilon_a = dL/L$.
# \begin{align*}
# \epsilon_t &= - \nu \epsilon_a \\
# \frac{dL'}{L'} &= - \nu \frac{dL}{L} \; \text{or}\\
# \frac{dA}{A} & = 2\frac{dL'}{L'} = -2 \nu \frac{dL}{L}
# \end{align*}
# Finally we can substitute express $dA/A$ in eq. for $dR/R$ and relate change in resistance to change of wire geometry, remembering that for a metal $\nu =0.3$:
# \begin{align}
# \frac{dR}{R} & = \frac{d\rho}{\rho} + \frac{dL}{L} - \frac{dA}{A} \\
# & = \frac{d\rho}{\rho} + \frac{dL}{L} - (-2\nu \frac{dL}{L}) \\
# & = \frac{d\rho}{\rho} + 1.6 \frac{dL}{L} = \frac{d\rho}{\rho} + 1.6 \epsilon_a
# \end{align}
# It also happens that for most metals, the resistivity increases with axial strain. In general, one can then related the change in resistance to axial strain by defining the strain gage factor:
# \begin{align}
# S = 1.6 + \frac{d\rho}{\rho}\cdot \frac{1}{\epsilon_a}
# \end{align}
# and finally, we have:
# \begin{align*}
# \frac{dR}{R} = S \epsilon_a
# \end{align*}
# $S$ is materials dependent and is typically equal to 2.0 for most commercially availabe strain gages. It is dimensionless.
#
# Strain gages are made of thin wire that is wraped in several loops, effectively increasing the length of the wire and therefore the sensitivity of the sensor.
#
# _Question:
#
# Explain why a longer wire is necessary to increase the sensitivity of the sensor_.
#
# Most commercially available strain gages have a nominal resistance (resistance under no load, $R_{ini}$) of 120 or 350 $\Omega$.
#
# Within the elastic regime, strain is typically within the range $10^{-6} - 10^{-3}$, in fact strain is expressed in unit of microstrain, with a 1 microstrain = $10^{-6}$. Therefore, changes in resistances will be of the same order. If one were to measure resistances, we will need a dynamic range of 120 dB, whih is typically very expensive. Instead, one uses the Wheatstone bridge to transform the change in resistance to a voltage, which is easier to measure and does not require such a large dynamic range.
# ## Wheatstone bridge:
# <img src="img/WheatstoneBridge.png" width="200">
#
# The output voltage is related to the difference in resistances in the bridge:
# \begin{align*}
# \frac{V_o}{V_s} = \frac{R_1R_3-R_2R_4}{(R_1+R_4)(R_2+R_3)}
# \end{align*}
#
# If the bridge is balanced, then $V_o = 0$, it implies: $R_1/R_2 = R_4/R_3$.
#
# In practice, finding a set of resistors that balances the bridge is challenging, and a potentiometer is used as one of the resistances to do minor adjustement to balance the bridge. If one did not do the adjustement (ie if we did not zero the bridge) then all the measurement will have an offset or bias that could be removed in a post-processing phase, as long as the bias stayed constant.
#
# If each resistance $R_i$ is made to vary slightly around its initial value, ie $R_i = R_{i,ini} + dR_i$. For simplicity, we will assume that the initial value of the four resistances are equal, ie $R_{1,ini} = R_{2,ini} = R_{3,ini} = R_{4,ini} = R_{ini}$. This implies that the bridge was initially balanced, then the output voltage would be:
#
# \begin{align*}
# \frac{V_o}{V_s} = \frac{1}{4} \left( \frac{dR_1}{R_{ini}} - \frac{dR_2}{R_{ini}} + \frac{dR_3}{R_{ini}} - \frac{dR_4}{R_{ini}} \right)
# \end{align*}
#
# Note here that the changes in $R_1$ and $R_3$ have a positive effect on $V_o$, while the changes in $R_2$ and $R_4$ have a negative effect on $V_o$. In practice, this means that is a beam is a in tension, then a strain gage mounted on the branch 1 or 3 of the Wheatstone bridge will produce a positive voltage, while a strain gage mounted on branch 2 or 4 will produce a negative voltage. One takes advantage of this to increase sensitivity to measure strain.
#
# ### Quarter bridge
# One uses only one quarter of the bridge, ie strain gages are only mounted on one branch of the bridge.
#
# \begin{align*}
# \frac{V_o}{V_s} = \pm \frac{1}{4} \epsilon_a S
# \end{align*}
# Sensitivity, $G$:
# \begin{align*}
# G = \frac{V_o}{\epsilon_a} = \pm \frac{1}{4}S V_s
# \end{align*}
#
#
# ### Half bridge
# One uses half of the bridge, ie strain gages are mounted on two branches of the bridge.
#
# \begin{align*}
# \frac{V_o}{V_s} = \pm \frac{1}{2} \epsilon_a S
# \end{align*}
#
# ### Full bridge
#
# One uses of the branches of the bridge, ie strain gages are mounted on each branch.
#
# \begin{align*}
# \frac{V_o}{V_s} = \pm \epsilon_a S
# \end{align*}
#
# Therefore, as we increase the order of bridge, the sensitivity of the instrument increases. However, one should be carefull how we mount the strain gages as to not cancel out their measurement.
# _Exercise_
#
# 1- Wheatstone bridge
#
# <img src="img/WheatstoneBridge.png" width="200">
#
# > How important is it to know \& match the resistances of the resistors you employ to create your bridge?
# > How would you do that practically?
# > Assume $R_1=120\,\Omega$, $R_2=120\,\Omega$, $R_3=120\,\Omega$, $R_4=110\,\Omega$, $V_s=5.00\,\text{V}$. What is $V_\circ$?
Vs = 5.00
Vo = (120**2-120*110)/(230*240) * Vs
print('Vo = ',Vo, ' V')
# typical range in strain a strain gauge can measure
# 1 -1000 micro-Strain
AxialStrain = 1000*10**(-6) # axial strain
StrainGageFactor = 2
R_ini = 120 # Ohm
R_1 = R_ini+R_ini*StrainGageFactor*AxialStrain
print(R_1)
Vo = (120**2-120*(R_1))/((120+R_1)*240) * Vs
print('Vo = ', Vo, ' V')
# > How important is it to know \& match the resistances of the resistors you employ to create your bridge?
# > How would you do that practically?
# > Assume $R_1= R_2 =R_3=120\,\Omega$, $R_4=120.01\,\Omega$, $V_s=5.00\,\text{V}$. What is $V_\circ$?
Vs = 5.00
Vo = (120**2-120*120.01)/(240.01*240) * Vs
print(Vo)
# 2- Strain gage 1:
#
# One measures the strain on a bridge steel beam. The modulus of elasticity is $E=190$ GPa. Only one strain gage is mounted on the bottom of the beam; the strain gage factor is $S=2.02$.
#
# > a) What kind of electronic circuit will you use? Draw a sketch of it.
#
# > b) Assume all your resistors including the unloaded strain gage are balanced and measure $120\,\Omega$, and that the strain gage is at location $R_2$. The supply voltage is $5.00\,\text{VDC}$. Will $V_\circ$ be positive or negative when a downward load is added?
# In practice, we cannot have all resistances = 120 $\Omega$. at zero load, the bridge will be unbalanced (show $V_o \neq 0$). How could we balance our bridge?
#
# Use a potentiometer to balance bridge, for the load cell, we ''zero'' the instrument.
#
# Other option to zero-out our instrument? Take data at zero-load, record the voltage, $V_{o,noload}$. Substract $V_{o,noload}$ to my data.
# > c) For a loading in which $V_\circ = -1.25\,\text{mV}$, calculate the strain $\epsilon_a$ in units of microstrain.
# \begin{align*}
# \frac{V_o}{V_s} & = - \frac{1}{4} \epsilon_a S\\
# \epsilon_a & = -\frac{4}{S} \frac{V_o}{V_s}
# \end{align*}
S = 2.02
Vo = -0.00125
Vs = 5
eps_a = -1*(4/S)*(Vo/Vs)
print(eps_a)
# > d) Calculate the axial stress (in MPa) in the beam under this load.
# > e) You now want more sensitivity in your measurement, you install a second strain gage on to
# p of the beam. Which resistor should you use for this second active strain gage?
#
# > f) With this new setup and the same applied load than previously, what should be the output voltage?
# 3- Strain Gage with Long Lead Wires
#
# <img src="img/StrainGageLongWires.png" width="360">
#
# A quarter bridge strain gage Wheatstone bridge circuit is constructed with $120\,\Omega$ resistors and a $120\,\Omega$ strain gage. For this practical application, the strain gage is located very far away form the DAQ station and the lead wires to the strain gage are $10\,\text{m}$ long and the lead wire have a resistance of $0.080\,\Omega/\text{m}$. The lead wire resistance can lead to problems since $R_{lead}$ changes with temperature.
#
# > Design a modified circuit that will cancel out the effect of the lead wires.
# ## Homework
#
| Lectures/09_StrainGage.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <table class="ee-notebook-buttons" align="left">
# <td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Algorithms/landsat_radiance.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
# <td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/landsat_radiance.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
# <td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/landsat_radiance.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
# </table>
# ## Install Earth Engine API and geemap
# Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://geemap.org). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
# The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
# +
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('Installing geemap ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# -
import ee
import geemap
# ## Create an interactive map
# The default basemap is `Google Maps`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/basemaps.py) can be added using the `Map.add_basemap()` function.
Map = geemap.Map(center=[40,-100], zoom=4)
Map
# ## Add Earth Engine Python script
# +
# Add Earth Engine dataset
# Load a raw Landsat scene and display it.
raw = ee.Image('LANDSAT/LC08/C01/T1/LC08_044034_20140318')
Map.centerObject(raw, 10)
Map.addLayer(raw, {'bands': ['B4', 'B3', 'B2'], 'min': 6000, 'max': 12000}, 'raw')
# Convert the raw data to radiance.
radiance = ee.Algorithms.Landsat.calibratedRadiance(raw)
Map.addLayer(radiance, {'bands': ['B4', 'B3', 'B2'], 'max': 90}, 'radiance')
# Convert the raw data to top-of-atmosphere reflectance.
toa = ee.Algorithms.Landsat.TOA(raw)
Map.addLayer(toa, {'bands': ['B4', 'B3', 'B2'], 'max': 0.2}, 'toa reflectance')
# -
# ## Display Earth Engine data layers
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
| Algorithms/landsat_radiance.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Copyright 2020 NVIDIA Corporation. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# ==============================================================================
# -
# <img src="http://developer.download.nvidia.com/compute/machine-learning/frameworks/nvidia_logo.png" style="width: 90px; float: right;">
#
# # Object Detection with TRTorch (SSD)
# ---
# ## Overview
#
#
# In PyTorch 1.0, TorchScript was introduced as a method to separate your PyTorch model from Python, make it portable and optimizable.
#
# TRTorch is a compiler that uses TensorRT (NVIDIA's Deep Learning Optimization SDK and Runtime) to optimize TorchScript code. It compiles standard TorchScript modules into ones that internally run with TensorRT optimizations.
#
# TensorRT can take models from any major framework and specifically tune them to perform better on specific target hardware in the NVIDIA family, and TRTorch enables us to continue to remain in the PyTorch ecosystem whilst doing so. This allows us to leverage the great features in PyTorch, including module composability, its flexible tensor implementation, data loaders and more. TRTorch is available to use with both PyTorch and LibTorch.
#
# To get more background information on this, we suggest the **lenet-getting-started** notebook as a primer for getting started with TRTorch.
# ### Learning objectives
#
# This notebook demonstrates the steps for compiling a TorchScript module with TRTorch on a pretrained SSD network, and running it to test the speedup obtained.
#
# ## Contents
# 1. [Requirements](#1)
# 2. [SSD Overview](#2)
# 3. [Creating TorchScript modules](#3)
# 4. [Compiling with TRTorch](#4)
# 5. [Running Inference](#5)
# 6. [Measuring Speedup](#6)
# 7. [Conclusion](#7)
# ---
# <a id="1"></a>
# ## 1. Requirements
#
# Follow the steps in `notebooks/README` to prepare a Docker container, within which you can run this demo notebook.
#
# In addition to that, run the following cell to obtain additional libraries specific to this demo.
# Known working versions
# !pip install numpy==1.21.2 scipy==1.5.2 Pillow==6.2.0 scikit-image==0.17.2 matplotlib==3.3.0
# ---
# <a id="2"></a>
# ## 2. SSD
#
# ### Single Shot MultiBox Detector model for object detection
#
# _ | _
# - | -
# 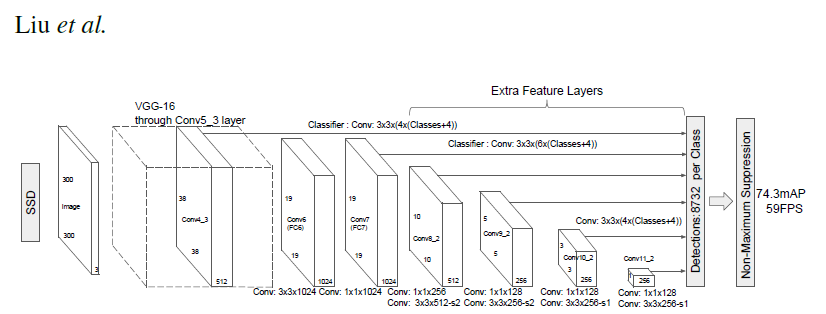 | 
# PyTorch has a model repository called the PyTorch Hub, which is a source for high quality implementations of common models. We can get our SSD model pretrained on [COCO](https://cocodataset.org/#home) from there.
#
# ### Model Description
#
# This SSD300 model is based on the
# [SSD: Single Shot MultiBox Detector](https://arxiv.org/abs/1512.02325) paper, which
# describes SSD as “a method for detecting objects in images using a single deep neural network".
# The input size is fixed to 300x300.
#
# The main difference between this model and the one described in the paper is in the backbone.
# Specifically, the VGG model is obsolete and is replaced by the ResNet-50 model.
#
# From the
# [Speed/accuracy trade-offs for modern convolutional object detectors](https://arxiv.org/abs/1611.10012)
# paper, the following enhancements were made to the backbone:
# * The conv5_x, avgpool, fc and softmax layers were removed from the original classification model.
# * All strides in conv4_x are set to 1x1.
#
# The backbone is followed by 5 additional convolutional layers.
# In addition to the convolutional layers, we attached 6 detection heads:
# * The first detection head is attached to the last conv4_x layer.
# * The other five detection heads are attached to the corresponding 5 additional layers.
#
# Detector heads are similar to the ones referenced in the paper, however,
# they are enhanced by additional BatchNorm layers after each convolution.
#
# More information about this SSD model is available at Nvidia's "DeepLearningExamples" Github [here](https://github.com/NVIDIA/DeepLearningExamples/tree/master/PyTorch/Detection/SSD).
import torch
torch.hub._validate_not_a_forked_repo=lambda a,b,c: True
# List of available models in PyTorch Hub from Nvidia/DeepLearningExamples
torch.hub.list('NVIDIA/DeepLearningExamples:torchhub')
# load SSD model pretrained on COCO from Torch Hub
precision = 'fp32'
ssd300 = torch.hub.load('NVIDIA/DeepLearningExamples:torchhub', 'nvidia_ssd', model_math=precision);
# Setting `precision="fp16"` will load a checkpoint trained with mixed precision
# into architecture enabling execution on Tensor Cores. Handling mixed precision data requires the Apex library.
# ### Sample Inference
# We can now run inference on the model. This is demonstrated below using sample images from the COCO 2017 Validation set.
# +
# Sample images from the COCO validation set
uris = [
'http://images.cocodataset.org/val2017/000000397133.jpg',
'http://images.cocodataset.org/val2017/000000037777.jpg',
'http://images.cocodataset.org/val2017/000000252219.jpg'
]
# For convenient and comprehensive formatting of input and output of the model, load a set of utility methods.
utils = torch.hub.load('NVIDIA/DeepLearningExamples:torchhub', 'nvidia_ssd_processing_utils')
# Format images to comply with the network input
inputs = [utils.prepare_input(uri) for uri in uris]
tensor = utils.prepare_tensor(inputs, False)
# The model was trained on COCO dataset, which we need to access in order to
# translate class IDs into object names.
classes_to_labels = utils.get_coco_object_dictionary()
# +
# Next, we run object detection
model = ssd300.eval().to("cuda")
detections_batch = model(tensor)
# By default, raw output from SSD network per input image contains 8732 boxes with
# localization and class probability distribution.
# Let’s filter this output to only get reasonable detections (confidence>40%) in a more comprehensive format.
results_per_input = utils.decode_results(detections_batch)
best_results_per_input = [utils.pick_best(results, 0.40) for results in results_per_input]
# -
# ### Visualize results
# +
from matplotlib import pyplot as plt
import matplotlib.patches as patches
# The utility plots the images and predicted bounding boxes (with confidence scores).
def plot_results(best_results):
for image_idx in range(len(best_results)):
fig, ax = plt.subplots(1)
# Show original, denormalized image...
image = inputs[image_idx] / 2 + 0.5
ax.imshow(image)
# ...with detections
bboxes, classes, confidences = best_results[image_idx]
for idx in range(len(bboxes)):
left, bot, right, top = bboxes[idx]
x, y, w, h = [val * 300 for val in [left, bot, right - left, top - bot]]
rect = patches.Rectangle((x, y), w, h, linewidth=1, edgecolor='r', facecolor='none')
ax.add_patch(rect)
ax.text(x, y, "{} {:.0f}%".format(classes_to_labels[classes[idx] - 1], confidences[idx]*100), bbox=dict(facecolor='white', alpha=0.5))
plt.show()
# -
# Visualize results without TRTorch/TensorRT
plot_results(best_results_per_input)
# ### Benchmark utility
# +
import time
import numpy as np
import torch.backends.cudnn as cudnn
cudnn.benchmark = True
# Helper function to benchmark the model
def benchmark(model, input_shape=(1024, 1, 32, 32), dtype='fp32', nwarmup=50, nruns=1000):
input_data = torch.randn(input_shape)
input_data = input_data.to("cuda")
if dtype=='fp16':
input_data = input_data.half()
print("Warm up ...")
with torch.no_grad():
for _ in range(nwarmup):
features = model(input_data)
torch.cuda.synchronize()
print("Start timing ...")
timings = []
with torch.no_grad():
for i in range(1, nruns+1):
start_time = time.time()
pred_loc, pred_label = model(input_data)
torch.cuda.synchronize()
end_time = time.time()
timings.append(end_time - start_time)
if i%10==0:
print('Iteration %d/%d, avg batch time %.2f ms'%(i, nruns, np.mean(timings)*1000))
print("Input shape:", input_data.size())
print("Output location prediction size:", pred_loc.size())
print("Output label prediction size:", pred_label.size())
print('Average batch time: %.2f ms'%(np.mean(timings)*1000))
# -
# We check how well the model performs **before** we use TRTorch/TensorRT
# Model benchmark without TRTorch/TensorRT
model = ssd300.eval().to("cuda")
benchmark(model, input_shape=(128, 3, 300, 300), nruns=100)
# ---
# <a id="3"></a>
# ## 3. Creating TorchScript modules
# To compile with TRTorch, the model must first be in **TorchScript**. TorchScript is a programming language included in PyTorch which removes the Python dependency normal PyTorch models have. This conversion is done via a JIT compiler which given a PyTorch Module will generate an equivalent TorchScript Module. There are two paths that can be used to generate TorchScript: **Tracing** and **Scripting**. <br>
# - Tracing follows execution of PyTorch generating ops in TorchScript corresponding to what it sees. <br>
# - Scripting does an analysis of the Python code and generates TorchScript, this allows the resulting graph to include control flow which tracing cannot do.
#
# Tracing however due to its simplicity is more likely to compile successfully with TRTorch (though both systems are supported).
model = ssd300.eval().to("cuda")
traced_model = torch.jit.trace(model, [torch.randn((1,3,300,300)).to("cuda")])
# If required, we can also save this model and use it independently of Python.
# This is just an example, and not required for the purposes of this demo
torch.jit.save(traced_model, "ssd_300_traced.jit.pt")
# Obtain the average time taken by a batch of input with Torchscript compiled modules
benchmark(traced_model, input_shape=(128, 3, 300, 300), nruns=100)
# ---
# <a id="4"></a>
# ## 4. Compiling with TRTorch
# TorchScript modules behave just like normal PyTorch modules and are intercompatible. From TorchScript we can now compile a TensorRT based module. This module will still be implemented in TorchScript but all the computation will be done in TensorRT.
# +
import trtorch
# The compiled module will have precision as specified by "op_precision".
# Here, it will have FP16 precision.
trt_model = trtorch.compile(traced_model, {
"inputs": [trtorch.Input((3, 3, 300, 300))],
"enabled_precisions": {torch.float, torch.half}, # Run with FP16
"workspace_size": 1 << 20
})
# -
# ---
# <a id="5"></a>
# ## 5. Running Inference
# Next, we run object detection
# +
# using a TRTorch module is exactly the same as how we usually do inference in PyTorch i.e. model(inputs)
detections_batch = trt_model(tensor.to(torch.half)) # convert the input to half precision
# By default, raw output from SSD network per input image contains 8732 boxes with
# localization and class probability distribution.
# Let’s filter this output to only get reasonable detections (confidence>40%) in a more comprehensive format.
results_per_input = utils.decode_results(detections_batch)
best_results_per_input_trt = [utils.pick_best(results, 0.40) for results in results_per_input]
# -
# Now, let's visualize our predictions!
#
# Visualize results with TRTorch/TensorRT
plot_results(best_results_per_input_trt)
# We get similar results as before!
# ---
# ## 6. Measuring Speedup
# We can run the benchmark function again to see the speedup gained! Compare this result with the same batch-size of input in the case without TRTorch/TensorRT above.
# +
batch_size = 128
# Recompiling with batch_size we use for evaluating performance
trt_model = trtorch.compile(traced_model, {
"inputs": [trtorch.Input((batch_size, 3, 300, 300))],
"enabled_precisions": {torch.float, torch.half}, # Run with FP16
"workspace_size": 1 << 20
})
benchmark(trt_model, input_shape=(batch_size, 3, 300, 300), nruns=100, dtype="fp16")
# -
# ---
# ## 7. Conclusion
#
# In this notebook, we have walked through the complete process of compiling a TorchScript SSD300 model with TRTorch, and tested the performance impact of the optimization. We find that using the TRTorch compiled model, we gain significant speedup in inference without any noticeable drop in performance!
# ### Details
# For detailed information on model input and output,
# training recipies, inference and performance visit:
# [github](https://github.com/NVIDIA/DeepLearningExamples/tree/master/PyTorch/Detection/SSD)
# and/or [NGC](https://ngc.nvidia.com/catalog/model-scripts/nvidia:ssd_for_pytorch)
#
# ### References
#
# - [SSD: Single Shot MultiBox Detector](https://arxiv.org/abs/1512.02325) paper
# - [Speed/accuracy trade-offs for modern convolutional object detectors](https://arxiv.org/abs/1611.10012) paper
# - [SSD on NGC](https://ngc.nvidia.com/catalog/model-scripts/nvidia:ssd_for_pytorch)
# - [SSD on github](https://github.com/NVIDIA/DeepLearningExamples/tree/master/PyTorch/Detection/SSD)
| notebooks/ssd-object-detection-demo.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **Run the following two cells before you begin.**
# %autosave 10
# ______________________________________________________________________
# **First, import your data set and define the sigmoid function.**
# <details>
# <summary>Hint:</summary>
# The definition of the sigmoid is $f(x) = \frac{1}{1 + e^{-X}}$.
# </details>
# +
# Import the data set
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import seaborn as sns
df = pd.read_csv('cleaned_data.csv')
# -
# Define the sigmoid function
def sigmoid(X):
Y = 1 / (1 + np.exp(-X))
return Y
# **Now, create a train/test split (80/20) with `PAY_1` and `LIMIT_BAL` as features and `default payment next month` as values. Use a random state of 24.**
# Create a train/test split
X_train, X_test, y_train, y_test = train_test_split(df[['PAY_1', 'LIMIT_BAL']].values, df['default payment next month'].values,test_size=0.2, random_state=24)
# ______________________________________________________________________
# **Next, import LogisticRegression, with the default options, but set the solver to `'liblinear'`.**
lr_model = LogisticRegression(solver='liblinear')
lr_model
# ______________________________________________________________________
# **Now, train on the training data and obtain predicted classes, as well as class probabilities, using the testing data.**
# Fit the logistic regression model on training data
lr_model.fit(X_train,y_train)
# Make predictions using `.predict()`
y_pred = lr_model.predict(X_test)
# Find class probabilities using `.predict_proba()`
y_pred_proba = lr_model.predict_proba(X_test)
# ______________________________________________________________________
# **Then, pull out the coefficients and intercept from the trained model and manually calculate predicted probabilities. You'll need to add a column of 1s to your features, to multiply by the intercept.**
# Add column of 1s to features
ones_and_features = np.hstack([np.ones((X_test.shape[0],1)), X_test])
print(ones_and_features)
np.ones((X_test.shape[0],1)).shape
# Get coefficients and intercepts from trained model
intercept_and_coefs = np.concatenate([lr_model.intercept_.reshape(1,1), lr_model.coef_], axis=1)
intercept_and_coefs
# Manually calculate predicted probabilities
X_lin_comb = np.dot(intercept_and_coefs, np.transpose(ones_and_features))
y_pred_proba_manual = sigmoid(X_lin_comb)
# ______________________________________________________________________
# **Next, using a threshold of `0.5`, manually calculate predicted classes. Compare this to the class predictions output by scikit-learn.**
# Manually calculate predicted classes
y_pred_manual = y_pred_proba_manual >= 0.5
y_pred_manual.shape
y_pred.shape
# Compare to scikit-learn's predicted classes
np.array_equal(y_pred.reshape(1,-1), y_pred_manual)
y_test.shape
y_pred_proba_manual.shape
# ______________________________________________________________________
# **Finally, calculate ROC AUC using both scikit-learn's predicted probabilities, and your manually predicted probabilities, and compare.**
# + eid="e7697"
# Use scikit-learn's predicted probabilities to calculate ROC AUC
from sklearn.metrics import roc_auc_score
roc_auc_score(y_test, y_pred_proba_manual.reshape(y_pred_proba_manual.shape[1],))
# -
# Use manually calculated predicted probabilities to calculate ROC AUC
roc_auc_score(y_test, y_pred_proba[:,1])
| Mini-Project-2/Project 4/Fitting_a_Logistic_Regression_Model.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# name: python2
# ---
# + [markdown] colab_type="text" id="1Pi_B2cvdBiW"
# ##### Copyright 2019 The TF-Agents Authors.
# + [markdown] colab_type="text" id="f5926O3VkG_p"
# ### Get Started
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/agents/blob/master/tf_agents/colabs/8_networks_tutorial.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/agents/blob/master/tf_agents/colabs/8_networks_tutorial.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# </table>
# + colab_type="code" id="xsLTHlVdiZP3" colab={}
# Note: If you haven't installed tf-agents yet, run:
# !pip install tf-nightly
# !pip install tfp-nightly
# !pip install tf-agents-nightly
# + [markdown] colab_type="text" id="lEgSa5qGdItD"
# ### Imports
# + colab_type="code" id="sdvop99JlYSM" colab={}
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import abc
import tensorflow as tf
import numpy as np
from tf_agents.environments import random_py_environment
from tf_agents.environments import tf_py_environment
from tf_agents.networks import encoding_network
from tf_agents.networks import network
from tf_agents.networks import utils
from tf_agents.specs import array_spec
from tf_agents.utils import common as common_utils
from tf_agents.utils import nest_utils
tf.compat.v1.enable_v2_behavior()
# + [markdown] colab_type="text" id="31uij8nIo5bG"
# # Introduction
#
# In this colab we will cover how to define custom networks for your agents. The networks help us define the model that is trained by agents. In TF-Agents you will find several different types of networks which are useful across agents:
#
# **Main Networks**
#
# * **QNetwork**: Used in Qlearning for environments with discrete actions, this network maps an observation to value estimates for each possible action.
# * **CriticNetworks**: Also referred to as `ValueNetworks` in literature, learns to estimate some version of a Value function mapping some state into an estimate for the expected return of a policy. These networks estimate how good the state the agent is currently in is.
# * **ActorNetworks**: Learn a mapping from observations to actions. These networks are usually used by our policies to generate actions.
# * **ActorDistributionNetworks**: Similar to `ActorNetworks` but these generate a distribution which a policy can then sample to generate actions.
#
# **Helper Networks**
# * **EncodingNetwork**: Allows users to easily define a mapping of pre-processing layers to apply to a network's input.
# * **DynamicUnrollLayer**: Automatically resets the network's state on episode boundaries as it is applied over a time sequence.
# * **ProjectionNetwork**: Networks like `CategoricalProjectionNetwork` or `NormalProjectionNetwork` take inputs and generate the required parameters to generate Categorical, or Normal distributions.
#
# All examples in TF-Agents come with pre-configured networks. However these networks are not setup to handle complex observations.
#
# If you have an environment which exposes more than one observation/action and you need to customize your networks then this tutorial is for you!
# + [markdown] id="ums84-YP_21F" colab_type="text"
# #Defining Networks
#
# ##Network API
#
# In TF-Agents we subclass from Keras [Networks](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/python/keras/engine/network.py). With it we can:
#
# * Simplify copy operations required when creating target networks.
# * Perform automatic variable creation when calling `network.variables()`.
# * Validate inputs based on network input_specs.
#
# ##EncodingNetwork
# As mentioned above the `EncodingNetwork` allows us to easily define a mapping of pre-processing layers to apply to a network's input to generate some encoding.
#
# The EncodingNetwork is composed of the following mostly optional layers:
#
# * Preprocessing layers
# * Preprocessing combiner
# * Conv2D
# * Flatten
# * Dense
#
# The special thing about encoding networks is that input preprocessing is applied. Input preprocessing is possible via `preprocessing_layers` and `preprocessing_combiner` layers. Each of these can be specified as a nested structure. If the `preprocessing_layers` nest is shallower than `input_tensor_spec`, then the layers will get the subnests. For example, if:
#
# ```
# input_tensor_spec = ([TensorSpec(3)] * 2, [TensorSpec(3)] * 5)
# preprocessing_layers = (Layer1(), Layer2())
# ```
#
# then preprocessing will call:
#
# ```
# preprocessed = [preprocessing_layers[0](observations[0]),
# preprocessing_layers[1](obsrevations[1])]
# ```
#
# However if
#
# ```
# preprocessing_layers = ([Layer1() for _ in range(2)],
# [Layer2() for _ in range(5)])
# ```
#
# then preprocessing will call:
#
# ```python
# preprocessed = [
# layer(obs) for layer, obs in zip(flatten(preprocessing_layers),
# flatten(observations))
# ]
# ```
#
# + [markdown] id="RP3H1bw0ykro" colab_type="text"
# ## Custom Networks
#
# To create your own networks you will only have to override the `__init__` and `__call__` methods. Let's create a custom network using what we learned about `EncodingNetworks` to create an ActorNetwork that takes observations which contain an image and a vector.
#
# + id="Zp0TjAJhYo4s" colab_type="code" colab={}
class ActorNetwork(network.Network):
def __init__(self,
observation_spec,
action_spec,
preprocessing_layers=None,
preprocessing_combiner=None,
conv_layer_params=None,
fc_layer_params=(75, 40),
dropout_layer_params=None,
activation_fn=tf.keras.activations.relu,
enable_last_layer_zero_initializer=False,
name='ActorNetwork'):
super(ActorNetwork, self).__init__(
input_tensor_spec=observation_spec, state_spec=(), name=name)
# For simplicity we will only support a single action float output.
self._action_spec = action_spec
flat_action_spec = tf.nest.flatten(action_spec)
if len(flat_action_spec) > 1:
raise ValueError('Only a single action is supported by this network')
self._single_action_spec = flat_action_spec[0]
if self._single_action_spec.dtype not in [tf.float32, tf.float64]:
raise ValueError('Only float actions are supported by this network.')
kernel_initializer = tf.keras.initializers.VarianceScaling(
scale=1. / 3., mode='fan_in', distribution='uniform')
self._encoder = encoding_network.EncodingNetwork(
observation_spec,
preprocessing_layers=preprocessing_layers,
preprocessing_combiner=preprocessing_combiner,
conv_layer_params=conv_layer_params,
fc_layer_params=fc_layer_params,
dropout_layer_params=dropout_layer_params,
activation_fn=activation_fn,
kernel_initializer=kernel_initializer,
batch_squash=False)
initializer = tf.keras.initializers.RandomUniform(
minval=-0.003, maxval=0.003)
self._action_projection_layer = tf.keras.layers.Dense(
flat_action_spec[0].shape.num_elements(),
activation=tf.keras.activations.tanh,
kernel_initializer=initializer,
name='action')
def call(self, observations, step_type=(), network_state=()):
outer_rank = nest_utils.get_outer_rank(observations, self.input_tensor_spec)
# We use batch_squash here in case the observations have a time sequence
# compoment.
batch_squash = utils.BatchSquash(outer_rank)
observations = tf.nest.map_structure(batch_squash.flatten, observations)
state, network_state = self._encoder(
observations, step_type=step_type, network_state=network_state)
actions = self._action_projection_layer(state)
actions = common_utils.scale_to_spec(actions, self._single_action_spec)
actions = batch_squash.unflatten(actions)
return tf.nest.pack_sequence_as(self._action_spec, [actions]), network_state
# + [markdown] id="Fm-MbMMLYiZj" colab_type="text"
# Let's create a `RandomPyEnvironment` to generate structured observations and validate our implementation.
# + id="E2XoNuuD66s5" colab_type="code" colab={}
action_spec = array_spec.BoundedArraySpec((3,), np.float32, minimum=0, maximum=10)
observation_spec = {
'image': array_spec.BoundedArraySpec((16, 16, 3), np.float32, minimum=0,
maximum=255),
'vector': array_spec.BoundedArraySpec((5,), np.float32, minimum=-100,
maximum=100)}
random_env = random_py_environment.RandomPyEnvironment(observation_spec, action_spec=action_spec)
# Convert the environment to a TFEnv to generate tensors.
tf_env = tf_py_environment.TFPyEnvironment(random_env)
# + [markdown] id="LM3uDTD7TNVx" colab_type="text"
# Since we've defined the observations to be a dict we need to create preprocessing layers to handle these.
# + id="r9U6JVevTAJw" colab_type="code" colab={}
preprocessing_layers = {
'image': tf.keras.models.Sequential([tf.keras.layers.Conv2D(8, 4),
tf.keras.layers.Flatten()]),
'vector': tf.keras.layers.Dense(5)
}
preprocessing_combiner = tf.keras.layers.Concatenate(axis=-1)
actor = ActorNetwork(tf_env.observation_spec(),
tf_env.action_spec(),
preprocessing_layers=preprocessing_layers,
preprocessing_combiner=preprocessing_combiner)
# + [markdown] id="mM9qedlwc41U" colab_type="text"
# Now that we have the actor network we can process observations from the environment.
# + id="JOkkeu7vXoei" colab_type="code" colab={}
time_step = tf_env.reset()
actor(time_step.observation, time_step.step_type)
# + [markdown] id="ALGxaQLWc9GI" colab_type="text"
# This same strategy can be used to customize any of the main networks used by the agents. You can define whatever preprocessing and connect it to the rest of the network. As you define your own custom make sure the output layer definitions of the network match.
| tf_agents/colabs/8_networks_tutorial.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Custom Types
#
# Often, the behavior for a field needs to be customized to support a particular shape or validation method that ParamTools does not support out of the box. In this case, you may use the `register_custom_type` function to add your new `type` to the ParamTools type registry. Each `type` has a corresponding `field` that is used for serialization and deserialization. ParamTools will then use this `field` any time it is handling a `value`, `label`, or `member` that is of this `type`.
#
# ParamTools is built on top of [`marshmallow`](https://github.com/marshmallow-code/marshmallow), a general purpose validation library. This means that you must implement a custom `marshmallow` field to go along with your new type. Please refer to the `marshmallow` [docs](https://marshmallow.readthedocs.io/en/stable/) if you have questions about the use of `marshmallow` in the examples below.
#
#
# ## 32 Bit Integer Example
#
# ParamTools's default integer field uses NumPy's `int64` type. This example shows you how to define an `int32` type and reference it in your `defaults`.
#
# First, let's define the Marshmallow class:
#
# +
import marshmallow as ma
import numpy as np
class Int32(ma.fields.Field):
"""
A custom type for np.int32.
https://numpy.org/devdocs/reference/arrays.dtypes.html
"""
# minor detail that makes this play nice with array_first
np_type = np.int32
def _serialize(self, value, *args, **kwargs):
"""Convert np.int32 to basic, serializable Python int."""
return value.tolist()
def _deserialize(self, value, *args, **kwargs):
"""Cast value from JSON to NumPy Int32."""
converted = np.int32(value)
return converted
# -
# Now, reference it in our defaults JSON/dict object:
#
# +
import paramtools as pt
# add int32 type to the paramtools type registry
pt.register_custom_type("int32", Int32())
class Params(pt.Parameters):
defaults = {
"small_int": {
"title": "Small integer",
"description": "Demonstrate how to define a custom type",
"type": "int32",
"value": 2
}
}
params = Params(array_first=True)
print(f"value: {params.small_int}, type: {type(params.small_int)}")
# -
# One problem with this is that we could run into some deserialization issues. Due to integer overflow, our deserialized result is not the number that we passed in--it's negative!
#
params.adjust(dict(
# this number wasn't chosen randomly.
small_int=2147483647 + 1
))
# ### Marshmallow Validator
#
# Fortunately, you can specify a custom validator with `marshmallow` or ParamTools. Making this works requires modifying the `_deserialize` method to check for overflow like this:
#
class Int32(ma.fields.Field):
"""
A custom type for np.int32.
https://numpy.org/devdocs/reference/arrays.dtypes.html
"""
# minor detail that makes this play nice with array_first
np_type = np.int32
def _serialize(self, value, *args, **kwargs):
"""Convert np.int32 to basic Python int."""
return value.tolist()
def _deserialize(self, value, *args, **kwargs):
"""Cast value from JSON to NumPy Int32."""
converted = np.int32(value)
# check for overflow and let range validator
# display the error message.
if converted != int(value):
return int(value)
return converted
# Now, let's see how to use `marshmallow` to fix this problem:
#
# +
import marshmallow as ma
import paramtools as pt
# get the minimum and maxium values for 32 bit integers.
min_int32 = -2147483648 # = np.iinfo(np.int32).min
max_int32 = 2147483647 # = np.iinfo(np.int32).max
# add int32 type to the paramtools type registry
pt.register_custom_type(
"int32",
Int32(validate=[
ma.validate.Range(min=min_int32, max=max_int32)
])
)
class Params(pt.Parameters):
defaults = {
"small_int": {
"title": "Small integer",
"description": "Demonstrate how to define a custom type",
"type": "int32",
"value": 2
}
}
params = Params(array_first=True)
params.adjust(dict(
small_int=np.int64(max_int32) + 1
))
# -
# ### ParamTools Validator
#
# Finally, we will use ParamTools to solve this problem. We need to modify how we create our custom `marshmallow` field so that it's wrapped by ParamTools's `PartialField`. This makes it clear that your field still needs to be initialized, and that your custom field is able to receive validation information from the `defaults` configuration:
#
# +
import paramtools as pt
# add int32 type to the paramtools type registry
pt.register_custom_type(
"int32",
pt.PartialField(Int32)
)
class Params(pt.Parameters):
defaults = {
"small_int": {
"title": "Small integer",
"description": "Demonstrate how to define a custom type",
"type": "int32",
"value": 2,
"validators": {
"range": {"min": -2147483648, "max": 2147483647}
}
}
}
params = Params(array_first=True)
params.adjust(dict(
small_int=2147483647 + 1
))
# -
| docs/api/custom-types.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:root] *
# language: python
# name: conda-root-py
# ---
# # Part 1: Data Ingestion
#
# This demo showcases financial fraud prevention and using the MLRun feature store to define complex features that help identify fraud. Fraud prevention specifically is a challenge as it requires processing raw transaction and events in real-time and being able to quickly respond and block transactions before they occur.
#
# To address this, we create a development pipeline and a production pipeline. Both pipelines share the same feature engineering and model code, but serve data very differently. Furthermore, we automate the data and model monitoring process, identify drift and trigger retraining in a CI/CD pipeline. This process is described in the diagram below:
#
# 
# The raw data is described as follows:
#
# | TRANSACTIONS || ║ |USER EVENTS ||
# |-----------------|----------------------------------------------------------------|----------|-----------------|----------------------------------------------------------------|
# | **age** | age group value 0-6. Some values are marked as U for unknown | ║ | **source** | The party/entity related to the event |
# | **gender** | A character to define the age | ║ | **event** | event, such as login or password change |
# | **zipcodeOri** | ZIP code of the person originating the transaction | ║ | **timestamp** | The date and time of the event |
# | **zipMerchant** | ZIP code of the merchant receiving the transaction | ║ | | |
# | **category** | category of the transaction (e.g., transportation, food, etc.) | ║ | | |
# | **amount** | the total amount of the transaction | ║ | | |
# | **fraud** | whether the transaction is fraudulent | ║ | | |
# | **timestamp** | the date and time in which the transaction took place | ║ | | |
# | **source** | the ID of the party/entity performing the transaction | ║ | | |
# | **target** | the ID of the party/entity receiving the transaction | ║ | | |
# | **device** | the device ID used to perform the transaction | ║ | | |
# This notebook introduces how to **Ingest** different data sources to the **Feature Store**.
#
# The following FeatureSets will be created:
# - **Transactions**: Monetary transactions between a source and a target.
# - **Events**: Account events such as account login or a password change.
# - **Label**: Fraud label for the data.
#
# By the end of this tutorial you’ll learn how to:
#
# - Create an ingestion pipeline for each data source.
# - Define preprocessing, aggregation and validation of the pipeline.
# - Run the pipeline locally within the notebook.
# - Launch a real-time function to ingest live data.
# - Schedule a cron to run the task when needed.
project_name = 'fraud-demo'
# +
import mlrun
# Initialize the MLRun project object
project = mlrun.get_or_create_project(project_name, context="./", user_project=True)
# -
# ## Step 1 - Fetch, Process and Ingest our datasets
# ## 1.1 - Transactions
# ### Transactions
# + tags=["hide-cell"]
# Helper functions to adjust the timestamps of our data
# while keeping the order of the selected events and
# the relative distance from one event to the other
def date_adjustment(sample, data_max, new_max, old_data_period, new_data_period):
'''
Adjust a specific sample's date according to the original and new time periods
'''
sample_dates_scale = ((data_max - sample) / old_data_period)
sample_delta = new_data_period * sample_dates_scale
new_sample_ts = new_max - sample_delta
return new_sample_ts
def adjust_data_timespan(dataframe, timestamp_col='timestamp', new_period='2d', new_max_date_str='now'):
'''
Adjust the dataframe timestamps to the new time period
'''
# Calculate old time period
data_min = dataframe.timestamp.min()
data_max = dataframe.timestamp.max()
old_data_period = data_max-data_min
# Set new time period
new_time_period = pd.Timedelta(new_period)
new_max = pd.Timestamp(new_max_date_str)
new_min = new_max-new_time_period
new_data_period = new_max-new_min
# Apply the timestamp change
df = dataframe.copy()
df[timestamp_col] = df[timestamp_col].apply(lambda x: date_adjustment(x, data_max, new_max, old_data_period, new_data_period))
return df
# +
import pandas as pd
# Fetch the transactions dataset from the server
transactions_data = pd.read_csv('https://s3.wasabisys.com/iguazio/data/fraud-demo-mlrun-fs-docs/data.csv', parse_dates=['timestamp'], nrows=500)
# Adjust the samples timestamp for the past 2 days
transactions_data = adjust_data_timespan(transactions_data, new_period='2d')
# Preview
transactions_data.head(3)
# -
# ### Transactions - Create a FeatureSet and Preprocessing Pipeline
# Create the FeatureSet (data pipeline) definition for the **credit transaction processing** which describes the offline/online data transformations and aggregations.<br>
# The feature store will automatically add an offline `parquet` target and an online `NoSQL` target by using `set_targets()`.
#
# The data pipeline consists of:
#
# * **Extracting** the data components (hour, day of week)
# * **Mapping** the age values
# * **One hot encoding** for the transaction category and the gender
# * **Aggregating** the amount (avg, sum, count, max over 2/12/24 hour time windows)
# * **Aggregating** the transactions per category (over 14 days time windows)
# * **Writing** the results to **offline** (Parquet) and **online** (NoSQL) targets
# Import MLRun's Feature Store
import mlrun.feature_store as fstore
from mlrun.feature_store.steps import OneHotEncoder, MapValues, DateExtractor
# Define the transactions FeatureSet
transaction_set = fstore.FeatureSet("transactions",
entities=[fstore.Entity("source")],
timestamp_key='timestamp',
description="transactions feature set")
# +
# Define and add value mapping
main_categories = ["es_transportation", "es_health", "es_otherservices",
"es_food", "es_hotelservices", "es_barsandrestaurants",
"es_tech", "es_sportsandtoys", "es_wellnessandbeauty",
"es_hyper", "es_fashion", "es_home", "es_contents",
"es_travel", "es_leisure"]
# One Hot Encode the newly defined mappings
one_hot_encoder_mapping = {'category': main_categories,
'gender': list(transactions_data.gender.unique())}
# Define the graph steps
transaction_set.graph\
.to(DateExtractor(parts = ['hour', 'day_of_week'], timestamp_col = 'timestamp'))\
.to(MapValues(mapping={'age': {'U': '0'}}, with_original_features=True))\
.to(OneHotEncoder(mapping=one_hot_encoder_mapping))
# Add aggregations for 2, 12, and 24 hour time windows
transaction_set.add_aggregation(name='amount',
column='amount',
operations=['avg','sum', 'count','max'],
windows=['2h', '12h', '24h'],
period='1h')
# Add the category aggregations over a 14 day window
for category in main_categories:
transaction_set.add_aggregation(name=category,column=f'category_{category}',
operations=['count'], windows=['14d'], period='1d')
# Add default (offline-parquet & online-nosql) targets
transaction_set.set_targets()
# Plot the pipeline so we can see the different steps
transaction_set.plot(rankdir="LR", with_targets=True)
# -
# ### Transactions - Ingestion
# +
# Ingest our transactions dataset through our defined pipeline
transactions_df = fstore.ingest(transaction_set, transactions_data,
infer_options=fstore.InferOptions.default())
transactions_df.head(3)
# -
# ## 1.2 - User Events
# ### User Events - Fetching
# +
# Fetch our user_events dataset from the server
user_events_data = pd.read_csv('https://s3.wasabisys.com/iguazio/data/fraud-demo-mlrun-fs-docs/events.csv',
index_col=0, quotechar="\'", parse_dates=['timestamp'], nrows=500)
# Adjust to the last 2 days to see the latest aggregations in our online feature vectors
user_events_data = adjust_data_timespan(user_events_data, new_period='2d')
# Preview
user_events_data.head(3)
# -
# ### User Events - Create a FeatureSet and Preprocessing Pipeline
#
# Now we will define the events feature set.
# This is a pretty straight forward pipeline in which we only one hot encode the event categories and save the data to the default targets.
user_events_set = fstore.FeatureSet("events",
entities=[fstore.Entity("source")],
timestamp_key='timestamp',
description="user events feature set")
# +
# Define and add value mapping
events_mapping = {'event': list(user_events_data.event.unique())}
# One Hot Encode
user_events_set.graph.to(OneHotEncoder(mapping=events_mapping))
# Add default (offline-parquet & online-nosql) targets
user_events_set.set_targets()
# Plot the pipeline so we can see the different steps
user_events_set.plot(rankdir="LR", with_targets=True)
# -
# ### User Events - Ingestion
# Ingestion of our newly created events feature set
events_df = fstore.ingest(user_events_set, user_events_data)
events_df.head(3)
# ## Step 2 - Create a labels dataset for model training
# ### Label Set - Create a FeatureSet
# This feature set contains the label for the fraud demo, it will be ingested directly to the default targets without any changes
def create_labels(df):
labels = df[['fraud','source','timestamp']].copy()
labels = labels.rename(columns={"fraud": "label"})
labels['timestamp'] = labels['timestamp'].astype("datetime64[ms]")
labels['label'] = labels['label'].astype(int)
labels.set_index('source', inplace=True)
return labels
# +
# Define the "labels" feature set
labels_set = fstore.FeatureSet("labels",
entities=[fstore.Entity("source")],
timestamp_key='timestamp',
description="training labels",
engine="pandas")
labels_set.graph.to(name="create_labels", handler=create_labels)
# specify only Parquet (offline) target since its not used for real-time
labels_set.set_targets(['parquet'], with_defaults=False)
labels_set.plot(with_targets=True)
# -
# ### Label Set - Ingestion
# Ingest the labels feature set
labels_df = fstore.ingest(labels_set, transactions_data)
labels_df.head(3)
# ## Step 3 - Deploy a real-time pipeline
#
# When dealing with real-time aggregation, it's important to be able to update these aggregations in real-time.
# For this purpose, we will create live serving functions that will update the online feature store of the `transactions` FeatureSet and `Events` FeatureSet.
#
# Using MLRun's `serving` runtime, craetes a nuclio function loaded with our feature set's computational graph definition
# and an `HttpSource` to define the HTTP trigger.
#
# Notice that the implementation below does not require any rewrite of the pipeline logic.
# ## 3.1 - Transactions
# ### Transactions - Deploy our FeatureSet live endpoint
# Create iguazio v3io stream and transactions push API endpoint
transaction_stream = f'v3io:///projects/{project.name}/streams/transaction'
transaction_pusher = mlrun.datastore.get_stream_pusher(transaction_stream)
# +
# Define the source stream trigger (use v3io streams)
# we will define the `key` and `time` fields (extracted from the Json message).
source = mlrun.datastore.sources.StreamSource(path=transaction_stream , key_field='source', time_field='timestamp')
# Deploy the transactions feature set's ingestion service over a real-time (Nuclio) serverless function
# you can use the run_config parameter to pass function/service specific configuration
transaction_set_endpoint = fstore.deploy_ingestion_service(featureset=transaction_set, source=source)
# -
# ### Transactions - Test the feature set HTTP endpoint
# By defining our `transactions` feature set we can now use MLRun and Storey to deploy it as a live endpoint, ready to ingest new data!
#
# Using MLRun's `serving` runtime, we will create a nuclio function loaded with our feature set's computational graph definition and an `HttpSource` to define the HTTP trigger.
# +
import requests
import json
# Select a sample from the dataset and serialize it to JSON
transaction_sample = json.loads(transactions_data.sample(1).to_json(orient='records'))[0]
transaction_sample['timestamp'] = str(pd.Timestamp.now())
transaction_sample
# -
# Post the sample to the ingestion endpoint
requests.post(transaction_set_endpoint, json=transaction_sample).text
# ## 3.2 - User Events
# ### User Events - Deploy our FeatureSet live endpoint
# Deploy the events feature set's ingestion service using the feature set and all the previously defined resources.
# Create iguazio v3io stream and transactions push API endpoint
events_stream = f'v3io:///projects/{project.name}/streams/events'
events_pusher = mlrun.datastore.get_stream_pusher(events_stream)
# +
# Define the source stream trigger (use v3io streams)
# we will define the `key` and `time` fields (extracted from the Json message).
source = mlrun.datastore.sources.StreamSource(path=events_stream , key_field='source', time_field='timestamp')
# Deploy the transactions feature set's ingestion service over a real-time (Nuclio) serverless function
# you can use the run_config parameter to pass function/service specific configuration
events_set_endpoint = fstore.deploy_ingestion_service(featureset=user_events_set, source=source)
# -
# ### User Events - Test the feature set HTTP endpoint
# Select a sample from the events dataset and serialize it to JSON
user_events_sample = json.loads(user_events_data.sample(1).to_json(orient='records'))[0]
user_events_sample['timestamp'] = str(pd.Timestamp.now())
user_events_sample
# Post the sample to the ingestion endpoint
requests.post(events_set_endpoint, json=user_events_sample).text
# ## Done!
#
# You've completed Part 1 of the data-ingestion with the feature store.
# Proceed to [Part 2](02-create-training-model.ipynb) to learn how to train an ML model using the feature store data.
| docs/feature-store/end-to-end-demo/01-ingest-datasources.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 
#
# <a href="https://hub.callysto.ca/jupyter/hub/user-redirect/git-pull?repo=https%3A%2F%2Fgithub.com%2Fcallysto%2Fcurriculum-notebooks&branch=master&subPath=Mathematics/Percentage/Percents.ipynb&depth=1" target="_parent"><img src="https://raw.githubusercontent.com/callysto/curriculum-notebooks/master/open-in-callysto-button.svg?sanitize=true" width="123" height="24" alt="Open in Callysto"/></a>
# **Run the cell below, this will add two buttons. Click on the "initialize" button before proceeding through the notebook**
# + tags=["hide-input"]
import uiButtons
# %uiButtons
# + tags=["hide-input"] language="html"
# <script src="https://d3js.org/d3.v3.min.js"></script>
# -
# # Percentages
# ## Introduction
# In this notebook we will discuss what percentages are and why this way of representing data is helpful in many different contexts. Common examples of percentages are sales tax or a mark for an assignment.
#
# The word percent comes from the Latin adverbial phrase *per centum* meaning “*by the hundred*”.
#
# For example, if the sales tax is $5\%$, this means that for every dollar you spend the tax adds $5$ cents to the total price of the purchase.
#
# A percentage simply represents a fraction (per hundred). For example, $90\%$ is the same as saying $\dfrac{90}{100}$. It is used to represent a ratio.
#
# What makes percentages so powerful is that they can represent any ratio.
#
# For example, getting $\dfrac{22}{25}$ on a math exam can be represented as $88\%$: $22$ is $88\%$ of $25$.
# ## How to Get a Percentage
# As mentioned in the introduction, a percentage is simply a fraction represented as a portion of 100.
#
# For this notebook we will only talk about percentages between 0% and 100%.
#
# This means the corresponding fraction will always be a value between $0$ and $1$.
#
# Let's look at our math exam mark example from above. The student correctly answered $22$ questions out of $25$, so the student received a grade of $\dfrac{22}{25}$.
#
# To represent this ratio as a percentage we first convert $\dfrac{22}{25}$ to its decimal representation (simply do the division in your calculator).
#
# $$
# \dfrac{22}{25} = 22 \div 25 = 0.88
# $$
#
# We are almost done: we now have the ratio represented as a value between 0 and 1. To finish getting the answer to our problem all we need to do is multiply this value by $100$ to get our percentage. $$0.88 \times 100 = 88\%$$
#
# Putting it all together we can say $22$ is $88\%$ of $25$.
#
# Think of a grade you recently received (as a fraction) and convert it to a percentage. Once you think you have an answer you can use the widget below to check your answer.
#
# Simply add the total marks of the test/assignment then move the slider until you get to your grade received.
# + tags=["hide-input"] language="html"
# <style>
# .main {
# font-family: 'Segoe UI', Tahoma, Geneva, Verdana, sans-serif;
# }
#
# .slider {
# width: 100px;
# }
#
# #maxVal {
# border:1px solid #cccccc;
# border-radius: 5px;
# width: 50px;
# }
# </style>
# <div class="main" style="border:2px solid black; width: 400px; padding: 20px;border-radius: 10px; margin: 0 auto; box-shadow: 3px 3px 12px #acacac">
# <div>
# <label for="maxValue">Enter the assignment/exam total marks</label>
# <input type="number" id="maxVal" value="100">
# </div>
# <div>
# <input type="range" min="0" max="100" value="0" class="slider" id="mySlider" style="width: 300px; margin-top: 20px;">
# </div>
# <h4 id="sliderVal">0</h3>
# </div>
#
# <script>
# var slider = document.getElementById('mySlider');
# var sliderVal = document.getElementById('sliderVal');
#
# slider.oninput = function () {
# var sliderMax = document.getElementById('maxVal').value;
# if(sliderMax < 0 || isNaN(sliderMax)) {
# sliderMax = 100;
# document.getElementById('maxVal').value = 100;
# }
# d3.select('#mySlider').attr('max', sliderMax);
# sliderVal.textContent = "If you answered " + this.value + "/" + sliderMax + " correct questions your grade will be " + ((
# this.value / sliderMax) * 100).toPrecision(3) + "%";
# }
# </script>
# -
# ## Solving Problems Using Percentages
#
# Now that we understand what percentages mean and how to get them from fractions, let's look at solving problems using percentages. Start by watching the video below to get a basic understanding.
# + tags=["hide-input"] language="html"
# <div align="middle">
# <iframe id="percentVid" width="640" height="360" src="https://www.youtube.com/embed/rR95Cbcjzus?end=368" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen style="box-shadow: 3px 3px 12px #ACACAC">
# </iframe>
# <p><a href="https://www.youtube.com/channel/UC4a-Gbdw7vOaccHmFo40b9g" target="_blank">Click here</a> for more videos by Math Antics</p>
# </div>
# <script>
# $(function() {
# var reachable = false;
# var myFrame = $('#percentVid');
# var videoSrc = myFrame.attr("src");
# myFrame.attr("src", videoSrc)
# .on('load', function(){reachable = true;});
# setTimeout(function() {
# if(!reachable) {
# var ifrm = myFrame[0];
# ifrm = (ifrm.contentWindow) ? ifrm.contentWindow : (ifrm.contentDocument.document) ? ifrm.contentDocument.document : ifrm.contentDocument;
# ifrm.document.open();
# ifrm.document.write('If the video does not start click <a href="' + videoSrc + '" target="_blank">here</a>');
# ifrm.document.close();
# }
# }, 2000)
# });
# </script>
# -
# As shown in the video, taking $25\%$ of 20 "things" is the same as saying $\dfrac{25}{100}\times\dfrac{20}{1}=\dfrac{500}{100}=\dfrac{5}{1}=5$.
#
# Let's do another example, assume a retail store is having a weekend sale. The sale is $30\%$ off everything in store.
#
# Sam thinks this is a great time to buy new shoes, and the shoes she is interested in are regular price $\$89.99$.<br>
# If Sam buys these shoes this weekend how much will they cost? If the sales tax is $5\%$, what will the total price be?
#
# <img src="https://orig00.deviantart.net/5c3e/f/2016/211/b/d/converse_shoes_free_vector_by_superawesomevectors-dabxj2k.jpg" width="300">
# <img src="https://www.publicdomainpictures.net/pictures/170000/nahled/30-korting.jpg" width="300">
#
# Let's start by figuring out the sale price of the shoes before calculating the tax. To figure out the new price we must first take $30\%$ off the original price.
#
# So the shoes are regular priced at $\$89.99$ and the sale is for $30\%$ off
#
# $$
# \$89.99\times 30\%=\$89.99\times\frac{30}{100}=\$26.997
# $$
#
# We can round $\$26.997$ to $\$27$.
#
# Ok we now know how much Sam will save on her new shoes, but let's not forget that the question is asking how much her new shoes will cost, not how much she will save. All we need to do now is take the total price minus the savings to get the new price:
#
# $$
# \$89.99- \$27=\$62.99
# $$
#
# Wow, what savings!
#
# Now for the second part of the question: what will the total price be if the tax is $5\%$?
#
# We must now figure out what $5\%$ of $\$62.99$ is
#
# $$
# \$62.99\times5\%=\$62.99\times\frac{5}{100}=\$3.15
# $$
#
# Now we know that Sam will need to pay $\$3.15$ of tax on her new shoes so the final price is
#
# $$
# \$62.99+\$3.15=\$66.14
# $$
#
# A shortcut for finding the total price including the sales tax is to add 1 to the tax ratio, let's see how this works:
#
# $$
# \$62.99\times\left(\frac{5}{100}+1\right)=\$62.99\times1.05=\$66.14
# $$
#
# You can use this trick to quickly figure out a price after tax.
# ## Multiplying Percentages together
# Multiplying two or more percentages together is probably not something you would encounter often but it is easy to do if you remember that percentages are really fractions.
#
# Since percentages is simply a different way to represent a fraction, the rules for multiplying them are the same. Recall that multiplying two fractions together is the same as saying a *a fraction of a fraction*. For example $\dfrac{1}{2}\times\dfrac{1}{2}$ is the same as saying $\dfrac{1}{2}$ of $\dfrac{1}{2}$.
#
# Therefore if we write $50\%\times 20\%$ we really mean $50\%$ of $20\%$.
#
# The simplest approach to doing this is to first convert each fraction into their decimal representation (divide them by 100), so
#
# $$
# 50\%\div 100=0.50$$ and $$20\%\div 100=0.20
# $$
#
# Now that we have each fraction shown as their decimal representation we simply multiply them together:
#
# $$
# 0.50\times0.20=0.10
# $$
#
# and again to get this decimal to a percent we multiply by 100
#
# $$
# 0.10\times100=10\%
# $$
#
# Putting this into words we get: *$50\%$ of $20\%$ is $10\%$ (One half of $20\%$ is $10\%$)*.
# ## Sports Example
#
# As we know, statistics play a huge part in sports. Keeping track of a team's wins/losses or how many points a player has are integral parts of today's professional sports. Some of these stats may require more interesting mathematical formulas to figure them out. One such example is a goalie’s save percentage in hockey.
#
# The save percentage is the ratio of how many shots the goalie saved over how many he/she has faced. If you are familiar with the NHL you will know this statistic for goalies as Sv\% and is represented as a number like 0.939. In this case the $0.939$ is the percentage we are interested in. You can multiply this number by $100$ to get it in the familiar form $93.9\%$. This means the Sv\% is $93.9\%$, so this particular goalie has saved $93.9\%$ of the shots he's/she's faced.
#
# You will see below a "sport" like game. The objective of the game is to score on your opponent and protect your own net. As you play the game you will see (in real time) below the game window your Sv% and your opponents Sv%. Play a round or two before we discuss how to get this value.
#
# _**How to play:** choose the winning score from the drop down box then click "Start". In game use your mouse to move your paddle up and down (inside the play area). Don't let the ball go in your net!_
# + tags=["hide-input"] language="html"
# <style>
# .mainBody {
# font-family: Arial, Helvetica, sans-serif;
# }
# #startBtn {
# background-color: cornflowerblue;
# border: none;
# border-radius: 3px;
# font-size: 14px;
# color: white;
# font-weight: bold;
# padding: 2px 8px;
# text-transform: uppercase;
# }
# </style>
# <div class="mainBody">
# <div style="padding-bottom: 10px;">
# <label for="winningScore">Winning Score: </label>
# <select name="Winning Score" id="winningScore">
# <option value="3">3</option>
# <option value="5">5</option>
# <option value="7">7</option>
# <option value="10">10</option>
# </select>
# <button type="button" id="startBtn">Start</button>
# </div>
# <canvas id="gameCanvas" width="600" height="350" style="border: solid 1px black"></canvas>
#
# <div>
# <ul>
# <li>Player's point save average: <output id="playerAvg"></output></li>
# <li>Computer's point save average: <output id="compAvg"></output></li>
# </ul>
# </div>
# </div>
# -
# If you look below the game screen you will see "Player's point save average" and "Computer's point save average". You might also have noticed these values changed every time a save was made (unless Sv% was 1) or a score happened, can you come up with a formula to get these values?
#
# The Sv% value is the ratio of how many saves was made over how many total shots the player faced so our formula is
#
# $$
# Sv\%=\frac{saved \ shots}{total \ shots}
# $$
#
# Let's assume the player faced $33$ shots and let in $2$, then the player's Sv% is
#
# $$
# Sv\%=\frac{(33-2)}{33}=0.939
# $$
#
# *Note: $(33-2)$ is how many shots where saved since the total was $33$ and the player let in $2$*
# ## Questions
# + tags=["hide-input"] language="html"
# <style>
# hr {
# width: 60%;
# margin-left: 20px;
# }
# </style>
# <main>
# <div class="questions">
# <ul style="list-style: none">
# <h4>Question #1</h4>
# <li>
# <label for="q1" class="question">A new goalie played his first game and got a shutout (did not let
# the other team score) and made 33 saves, what is his Sv%? </label>
# </li>
# <li>
# <input type="text" id="q1" class="questionInput">
# <button id="q1Btn" onclick="checkAnswer('q1')" class="ansBtn">Check Answer</button>
# </li>
# <li>
# <p class="q1Ans" id="q1True" style="display: none">✓ That's right! Until the goalie let's
# his/her
# first goal in he/she will have a Sv% of 1</p>
# </li>
# <li>
# <p class="q1Ans" id="q1False" style="display: none">Not quite, don't forget to take the total
# amount of shots minus how many went in the net</p>
# </li>
# </ul>
# </div>
# <hr>
# <div class="questions">
# <ul style="list-style: none">
# <h4>Question #2</h4>
# <li>
# <label for="q2" class="question">If a goalie has a Sv% of .990 can he/she ever get back to a Sv% of
# 1.00?</label>
# </li>
# <li>
# <select id="q2">
# <option value="Yes">Yes</option>
# <option value="No">No</option>
# </select>
# <button id="q2Btn" onclick="checkAnswer('q2')" class="ansBtn">Check Answer</button>
# </li>
# <li>
# <p class="q2Ans" id="q2True" style="display: none">✓ That's correct, the goalie could get back
# up to
# 0.999 but never 1.00</p>
# </li>
# <li>
# <p class="q2Ans" id="q2False" style="display: none">Not quite, the goalie could get back up to 0.999
# but never 1.00</p>
# </li>
# </ul>
# </div>
# <hr>
# <div class="questions">
# <ul style="list-style: none">
# <h4>Question #3</h4>
# <li>
# <label for="q3" class="question">A student received a mark of 47/50 on his unit exam, what
# percentage did he get?</label>
# </li>
# <li>
# <input type="text" id="q3" class="questionInput">
# <button id="q3tn" onclick="checkAnswer('q3')" class="ansBtn">Check Answer</button>
# </li>
# <li>
# <p class="q3Ans" id="q3True" style="display: none">✓ That's correct!</p>
# </li>
# <li>
# <p class="q3Ans" id="q3False" style="display: none">Not quite, try again</p>
# </li>
# </ul>
# </div>
# <hr>
# <div class="questions">
# <ul style="list-style: none">
# <h4>Question #4</h4>
# <li>
# <label for="q4" class="question">In a class of 24 students, 8 students own cats, 12 students own dogs
# and 6 students own both cats and dogs. What is the percentage of students who own both cats and
# dogs?</label>
# </li>
# <li>
# <input type="text" id="q4" class="questionInput">
# <button id="q4tn" onclick="checkAnswer('q4')" class="ansBtn">Check Answer</button>
# </li>
# <li>
# <p class="q4Ans" id="q4True" style="display: none">✓ That's correct!</p>
# </li>
# <li>
# <p class="q4Ans" id="q4False" style="display: none">Not quite, try again</p>
# </li>
# </ul>
# </div>
#
# </main>
# <script>
# checkAnswer = function(q) {
# var val = document.getElementById(q).value;
# var isCorrect = false;
# $("."+q+"Ans").css("display", "none");
# switch(q) {
# case 'q1' : Number(val) === 1 ? isCorrect = true : isCorrect = false; break;
# case 'q2' : val === 'No' ? isCorrect = true : isCorrect = false; break;
# case 'q3' : (val === '94%'|| val === '94.0%' || Number(val) === 94) ? isCorrect = true : isCorrect = false;break;
# case 'q4' : (Number(val) === 25 || val === '25%' || val === '25.0%') ? isCorrect = true : isCorrect = false; break;
# default : return false;
# }
#
# if(isCorrect) {
# $("#"+q+"True").css("display", "block");
# } else {
# $("#"+q+"False").css("display", "block");
# }
# }
# </script>
#
# -
# ## Conclusion
#
# As we saw in this notebook, percentages show up in many different ways and are very useful when describing a ratio. It allows for demonstrating any ratio on a familiar scale ($100$) to make data easier to understand. In this notebook we covered the following:
# - A percentage simply represents a fraction
# - To convert any fraction to a percent we turn it into it's decimal form and add $100$
# - A percentage of an amount is simply a fraction multiplication problem
# - To add or subtract a percentage of an amount we first find the percent value than add/subtract from the original value
# - When adding a percentage to an amount we an use the decimal form of percent and add $1$ to it (for example $\$12\times(0.05+1)=\$12.60$)
#
# Keep practising converting fractions to percentages and it will eventually become second nature!
# + tags=["hide-input"] language="html"
# <script>
# var canvas;
# var canvasContext;
# var isInitialized;
#
# var ballX = 50;
# var ballY = 50;
# var ballSpeedX = 5;
# var ballSpeedY = 3;
#
# var leftPaddleY = 250;
# var rightPaddleY = 250;
#
# var playerSaves = 0;
# var playerSOG = 0;
# var compSaves = 0;
# var compSOG = 0;
#
# var playerScore = 0;
# var compScore = 0;
# var winningScore = 3;
# var winScreen = false;
#
# var PADDLE_WIDTH = 10;
# var PADDLE_HEIGHT = 100;
# var BALL_RADIUS = 10;
# var COMP_SPEED = 4;
#
# document.getElementById('startBtn').onclick = function () {
# initGame();
# var selection = document.getElementById('winningScore');
# winningScore = Number(selection.options[selection.selectedIndex].value);
# canvas = document.getElementById('gameCanvas');
# canvasContext = canvas.getContext('2d');
# canvasContext.font = '50px Arial';
# ballReset();
#
# if (!isInitialized) {
# var framesPerSec = 60;
# setInterval(function () {
# moveAll();
# drawAll();
# }, 1000 / framesPerSec);
# isInitialized = true;
# }
#
# canvas.addEventListener('mousemove', function (event) {
# var mousePos = mouseYPos(event);
# leftPaddleY = mousePos.y - PADDLE_HEIGHT / 2;
# });
# }
#
# function updateSaveAvg() {
# var playerSaveAvgTxt = document.getElementById('playerAvg');
# var compSaveAvgTxt = document.getElementById('compAvg');
#
# var playerSaveAvg = playerSaves / playerSOG;
# var compSaveAvg = compSaves / compSOG;
#
# playerSaveAvgTxt.textContent = ((playerSaveAvg < 0 || isNaN(playerSaveAvg)) ? Number(0).toPrecision(3) + (' (0.0%)') :
# playerSaveAvg.toPrecision(3) + (' (' + (playerSaveAvg * 100).toPrecision(3) + '%)'));
# compSaveAvgTxt.textContent = ((compSaveAvg < 0 || isNaN(compSaveAvg)) ? Number(0).toPrecision(3) + (' (0.0%)') :
# compSaveAvg.toPrecision(
# 3) + (' (' + (compSaveAvg * 100).toPrecision(3) + '%)'));
#
# }
#
# function initGame() {
# playerScore = 0;
# compScore = 0;
# playerSaves = 0;
# playerSOG = 0;
# compSaves = 0;
# compSOG = 0;
# ballSpeedX = 5;
# ballSpeedY = 3;
# }
#
# function ballReset() {
# if (playerScore >= winningScore || compScore >= winningScore) {
# winScreen = true;
# }
# if (winScreen) {
# updateSaveAvg();
# if (confirm('Another game?')) {
# winScreen = false;
# initGame();
# } else {
# return;
# }
# }
# ballX = canvas.width / 2;
# ballY = canvas.height / 2;
# ballSpeedY = Math.floor(Math.random() * 4) + 1;
# var randomizer = Math.floor(Math.random() * 2) + 1;
# if (randomizer % 2 === 0) {
# ballSpeedY -= ballSpeedY;
# }
# flipSide();
# }
#
# function flipSide() {
# ballSpeedX = -ballSpeedX;
# }
#
# function moveAll() {
# if (winScreen) {
# return;
# }
# computerMove();
# ballX += ballSpeedX;
# if (ballX < (0 + BALL_RADIUS)) {
# if (ballY > leftPaddleY && ballY < leftPaddleY + PADDLE_HEIGHT) {
# playerSaves++;
# playerSOG++;
# flipSide();
# var deltaY = ballY - (leftPaddleY + PADDLE_HEIGHT / 2);
# ballSpeedY = deltaY * 0.35;
# } else {
# playerSOG++;
# compScore++;
# if (compScore === winningScore) {
# updateSaveAvg();
# drawAll();
# alert('Computer wins, final score: ' + playerScore + '-' + compScore);
# }
# ballReset();
# }
# }
# if (ballX >= canvas.width - BALL_RADIUS) {
# if (ballY > rightPaddleY && ballY < rightPaddleY + PADDLE_HEIGHT) {
# compSaves++;
# compSOG++;
# flipSide();
# var deltaY = ballY - (rightPaddleY + PADDLE_HEIGHT / 2);
# ballSpeedY = deltaY * 0.35;
# } else {
# compSOG++;
# playerScore++;
# if (playerScore === winningScore) {
# updateSaveAvg();
# drawAll();
# alert('You win, final score: ' + playerScore + '-' + compScore);
# }
# ballReset();
# }
# }
# ballY += ballSpeedY;
# if (ballY >= canvas.height - BALL_RADIUS || ballY < 0 + BALL_RADIUS) {
# ballSpeedY = -ballSpeedY;
# }
# updateSaveAvg();
# }
#
# function computerMove() {
# var rightPaddleYCenter = rightPaddleY + (PADDLE_HEIGHT / 2)
# if (rightPaddleYCenter < ballY - 20) {
# rightPaddleY += COMP_SPEED;
# } else if (rightPaddleYCenter > ballY + 20) {
# rightPaddleY -= COMP_SPEED;
# }
# }
#
# function mouseYPos(event) {
# var rect = canvas.getBoundingClientRect();
# var root = document.documentElement;
# var mouseX = event.clientX - rect.left - root.scrollLeft;
# var mouseY = event.clientY - rect.top - root.scrollTop;
# return {
# x: mouseX,
# y: mouseY
# };
# }
#
# function drawAll() {
#
# colorRect(0, 0, canvas.width, canvas.height, 'black');
# if (winScreen) {
# drawNet();
# drawScore();
# return;
# }
# //Left paddle
# colorRect(1, leftPaddleY, PADDLE_WIDTH, PADDLE_HEIGHT, 'white');
# //Right paddle
# colorRect(canvas.width - PADDLE_WIDTH - 1, rightPaddleY, PADDLE_WIDTH, PADDLE_HEIGHT, 'white');
# //Ball
# colorCircle(ballX, ballY, BALL_RADIUS, 'white');
#
# drawNet();
#
# drawScore();
#
# }
#
# function colorRect(x, y, width, height, drawColor) {
# canvasContext.fillStyle = drawColor;
# canvasContext.fillRect(x, y, width, height);
# }
#
# function colorCircle(centerX, centerY, radius, drawColor) {
# canvasContext.fillStyle = 'drawColor';
# canvasContext.beginPath();
# canvasContext.arc(centerX, centerY, radius, 0, Math.PI * 2, true);
# canvasContext.fill();
# }
#
# function drawScore() {
# canvasContext.fillText(playerScore, (canvas.width / 2) - (canvas.width / 4) - 25, 100);
# canvasContext.fillText(compScore, (canvas.width / 2) + (canvas.width / 4) - 25, 100);
# }
#
# function drawNet() {
# for (var i = 0; i < 60; i++) {
# if (i % 2 === 1) {
# colorRect(canvas.width / 2 - 3, i * 10, 6, 10, 'white')
# }
# }
# }
# </script>
# -
# [](https://github.com/callysto/curriculum-notebooks/blob/master/LICENSE.md)
| _build/html/_sources/curriculum-notebooks/Mathematics/Percentage/percentage.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <p align="center">
# <img src="https://github.com/GeostatsGuy/GeostatsPy/blob/master/TCG_color_logo.png?raw=true" width="220" height="240" />
#
# </p>
#
# ## Data Analytics
#
# ### Parametric Distributions in Python
#
#
# #### <NAME>, Associate Professor, University of Texas at Austin
#
# ##### [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1)
#
# ### Data Analytics: Parametric Distributions
#
# Here's a demonstration of making and general use of parametric distributions in Python. This demonstration is part of the resources that I include for my courses in Spatial / Subsurface Data Analytics at the Cockrell School of Engineering at the University of Texas at Austin.
#
# #### Parametric Distributions
#
# We will cover the following distributions:
#
# * Uniform
# * Triangular
# * Gaussian
# * Log Normal
#
# We will demonstrate:
#
# * distribution parameters
# * forward and inverse operators
# * summary statistics
#
# I have a lecture on these parametric distributions available on [YouTube](https://www.youtube.com/watch?v=U7fGsqCLPHU&t=1687s).
#
# #### Getting Started
#
# Here's the steps to get setup in Python with the GeostatsPy package:
#
# 1. Install Anaconda 3 on your machine (https://www.anaconda.com/download/).
# 2. From Anaconda Navigator (within Anaconda3 group), go to the environment tab, click on base (root) green arrow and open a terminal.
# 3. In the terminal type: pip install geostatspy.
# 4. Open Jupyter and in the top block get started by copy and pasting the code block below from this Jupyter Notebook to start using the geostatspy functionality.
#
# You will need to copy the data file to your working directory. They are available here:
#
# * Tabular data - unconv_MV_v4.csv at https://git.io/fhHLT.
#
# #### Importing Packages
#
# We will need some standard packages. These should have been installed with Anaconda 3.
import numpy as np # ndarrys for gridded data
import pandas as pd # DataFrames for tabular data
import os # set working directory, run executables
import matplotlib.pyplot as plt # for plotting
from scipy import stats # summary statistics
import math # trigonometry etc.
import scipy.signal as signal # kernel for moving window calculation
import random # for randon numbers
import seaborn as sns # for matrix scatter plots
from scipy import linalg # for linear regression
from sklearn import preprocessing
# #### Set the Working Directory
#
# I always like to do this so I don't lose files and to simplify subsequent read and writes (avoid including the full address each time).
os.chdir("c:/PGE383") # set the working directory
# ### Uniform Distribution
#
# Let's start with the most simple distribution.
#
# * by default a random number is uniform distributed
#
# * this ensures that enough random samples (Monte Carlo simulations) will reproduce the distribution
#
# \begin{equation}
# x_{\alpha}^{s} = F^{-1}_x(p_{\alpha}), \quad X^{s} \sim F_X
# \end{equation}
#
# #### Random Samples
#
# Let's demonstrate the use of the command:
#
# ```python
# uniform.rvs(size=n, loc = low, scale = interval, random_state = seed)
# ```
#
# Where:
#
# * size is the number of samples
#
# * loc is the minimum value
#
# * scale is the range, maximum value minus the minimum value
#
# * random_state is the random number seed
#
# We will observe the convergence of the samples to a uniform distribution as the number of samples becomes large.
#
# We will make a compact set of code by looping over all the cases of number of samples
#
# * we store the number of samples cases in the list called ns
#
# * we store the samples as a list of lists, called X_uniform
#
# +
from scipy.stats import uniform
low = 0.05; interval = 0.20; ns = [1e1,1e2,1e3,1e4,1e5,1e6]; X_uniform = []
index = 0
for n in ns:
X_uniform.append(uniform.rvs(size=int(ns[index]), loc = low, scale = interval).tolist())
plt.subplot(2,3,index+1)
GSLIB.hist_st(X_uniform[index],loc,loc+interval,log=False,cumul = False,bins=20,weights = None,xlabel='Values',title='Distribution, N = ' + str(int(ns[index])))
index = index + 1
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.3, top=1.6, wspace=0.2, hspace=0.3)
# -
# We can observe that by drawing more Monte Carlo simulations, we more closely approximate the original uniform parametric distribution.
#
# #### Forward Distribution
#
# Let's demonstrate the forward operator. We can take any value and calculate the associated:
#
# * density (probability density function)
# * cumulative probability
#
# The transform for the probability density function is:
#
# \begin{equation}
# p = f_x(x)
# \end{equation}
#
# where $f_x$ is the PDF and $p$ is the density for value, $x$.
#
# and for the cumulative distribution function is:
#
# \begin{equation}
# P = F_x(x)
# \end{equation}
#
# where $F_x$ is the CDF and $P$ is the cumulative probability for value, $x$.
# +
x_values = np.linspace(0.0,0.3,100)
p_values = uniform.pdf(x_values, loc = low, scale = interval)
P_values = uniform.cdf(x_values, loc = low, scale = interval)
plt.subplot(1,2,1)
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3, label='uniform PDF'); plt.title('Uniform PDF'); plt.xlabel('Values'); plt.ylabel('Density')
plt.subplot(1,2,2)
plt.plot(x_values, P_values,'r-', lw=5, alpha=0.3, label='uniform CDF'); plt.title('Uniform CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
plt.subplots_adjust(left=0.0, bottom=0.0, right=1.8, top=0.8, wspace=0.2, hspace=0.3)
# -
# #### Inverse Distribution
#
# Let's know demonstrate the reverse operator for the uniform distribution:
#
# \begin{equation}
# X = F^{-1}_X(P)
# \end{equation}
p_values = np.linspace(0.01,0.99,100)
x_values = uniform.ppf(p_values, loc = low, scale = interval)
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3, label='uniform pdf')
# #### Summary Statistics
#
# We also have a couple of convience member functions to return the statistics from the parametric distribution:
#
# * mean
# * median
# * mode
# * variance
# * standard deviation
#
# Let's demonstrate a few of these methods.
#
# ```python
# uniform.stats(loc = low, scale = interval, moments = 'mvsk')
# ```
#
# returns a tuple with the mean, variance, skew and kurtosis (centered 1st, 2nd, 3rd and 4th moments)
print('Stats: mean, variance, skew and kurtosis = ' + str(uniform.stats(loc = low, scale = interval, moments = 'mvsk')))
# We can confirm this by calculating the centered variance (regular variance) with this member function:
#
# ```python
# uniform.var(loc = low, scale = interval)
# ```
print('The variance is ' + str(round(uniform.var(loc = low, scale = interval),4)) + '.')
# We can also directly calculate the:
#
# * standard deviation - std
# * mean - mean
# * median - median
#
# We can also calculate order of a non-centered moment. The moment method allows us to calculate an non-centered moment of any order. Try this out.
m_order = 4
print('The ' + str(m_order) + 'th order non-centered moment is ' + str(uniform.moment(n = m_order, loc = low, scale = interval)))
# #### Symmetric Interval
#
# We can also get the symmetric interval (e.g. prediction or confidence intervals) for any alpha level.
#
# * Note the program mislabels the value as alpha, it is actually the significance level (1 - alpha)
level = 0.95
print('The interval at alpha level ' + str(round(1-level,3)) + ' is ' + str(uniform.interval(alpha = alpha,loc = low,scale = interval)))
# #### Triangular Distribution
#
# The great thing about parametric distributions is that the above member functions are the same!
#
# * we can plug and play other parametric distributions and repeat the above.
#
# This time we will make it much more compact!
#
# * we will import the triangular distribution as my_dist and call the same functions as before
# * we need a new parameter, the distribution mode (c parameter)
# +
from scipy.stats import triang as my_dist # import traingular dist as my_dist
dist_type = 'Triangular' # give the name of the distribution for labels
low = 0.05; mode = 0.20; c = 0.10 # given the distribution parameters
x_values = np.linspace(0.0,0.3,100) # get an array of x values
p_values = my_dist.pdf(x_values, loc = low, c = mode, scale = interval) # calculate density for each x value
P_values = my_dist.cdf(x_values, loc = low, c = mode, scale = interval) # calculate cumulative probablity for each x value
plt.subplot(1,3,1) # plot the resulting PDF
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3); plt.title('Sampling ' + str(dist_type) + ' PDF'); plt.xlabel('Values'); plt.ylabel('Density')
plt.subplot(1,3,2) # plot the resulting CDF
plt.plot(x_values, P_values,'r-', lw=5, alpha=0.3); plt.title('Sampling ' + str(dist_type) + ' CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
p_values = np.linspace(0.00001,0.99999,100) # get an array of p-values
x_values = my_dist.ppf(p_values, loc = low, c = mode, scale = interval) # apply inverse to get x values from p-values
plt.subplot(1,3,3)
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3, label='uniform pdf')
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.8, top=0.8, wspace=0.2, hspace=0.3); plt.title('Sampling Inverse ' + str(dist_type) + ' CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
print('The mean is ' + str(round(uniform.mean(loc = low, scale = interval),4)) + '.') # calculate stats and symmetric interval
print('The variance is ' + str(round(uniform.var(loc = low, scale = interval),4)) + '.')
print('The interval at alpha level ' + str(round(1-level,3)) + ' is ' + str(uniform.interval(alpha = alpha,loc = low,scale = interval)))
# -
# #### Gaussian Distribution
#
# Let's now use the Gaussian parametric distribution.
#
# * we will need the parameters mean and the variance
#
# We will apply the forward and reverse operations and calculate the summary statistics.
#
# +
from scipy.stats import norm as my_dist # import traingular dist as my_dist
dist_type = 'Gaussian' # give the name of the distribution for labels
mean = 0.15; stdev = 0.05 # given the distribution parameters
x_values = np.linspace(0.0,0.3,100) # get an array of x values
p_values = my_dist.pdf(x_values, loc = mean, scale = stdev) # calculate density for each x value
P_values = my_dist.cdf(x_values, loc = mean, scale = stdev) # calculate cumulative probablity for each x value
plt.subplot(1,3,1) # plot the resulting PDF
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3); plt.title('Sampling ' + str(dist_type) + ' PDF'); plt.xlabel('Values'); plt.ylabel('Density')
plt.subplot(1,3,2) # plot the resulting CDF
plt.plot(x_values, P_values,'r-', lw=5, alpha=0.3); plt.title('Sampling ' + str(dist_type) + ' CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
p_values = np.linspace(0.00001,0.99999,100) # get an array of p-values
x_values = my_dist.ppf(p_values, loc = mean, scale = stdev) # apply inverse to get x values from p-values
plt.subplot(1,3,3)
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3, label='uniform pdf')
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.8, top=0.8, wspace=0.2, hspace=0.3); plt.title('Sampling Inverse ' + str(dist_type) + ' CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
print('The mean is ' + str(round(my_dist.mean(loc = mean, scale = stdev),4)) + '.') # calculate stats and symmetric interval
print('The variance is ' + str(round(my_dist.var(loc = mean, scale = stdev),4)) + '.')
print('The interval at alpha level ' + str(round(1-level,3)) + ' is ' + str(my_dist.interval(alpha = alpha,loc = mean,scale = stdev)))
# -
# #### Log Normal Distribution
#
# Now let's check out the log normal distribution.
#
# * We need the parameters $\mu$ and $\sigma$
# +
from scipy.stats import lognorm as my_dist # import traingular dist as my_dist
dist_type = 'Log Normal' # give the name of the distribution for labels
mu = np.log(0.10); sigma = 0.2 # given the distribution parameters
x_values = np.linspace(0.0,0.3,100) # get an array of x values
p_values = my_dist.pdf(x_values, s = sigma, scale = np.exp(mu)) # calculate density for each x value
P_values = my_dist.cdf(x_values, s = sigma, scale = np.exp(mu)) # calculate cumulative probablity for each x value
plt.subplot(1,3,1) # plot the resulting PDF
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3); plt.title('Sampling ' + str(dist_type) + ' PDF'); plt.xlabel('Values'); plt.ylabel('Density')
plt.subplot(1,3,2) # plot the resulting CDF
plt.plot(x_values, P_values,'r-', lw=5, alpha=0.3); plt.title('Sampling ' + str(dist_type) + ' CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
p_values = np.linspace(0.00001,0.99999,100) # get an array of p-values
x_values = my_dist.ppf(p_values, s = sigma, scale = np.exp(mu)) # apply inverse to get x values from p-values
plt.subplot(1,3,3)
plt.plot(x_values, p_values,'r-', lw=5, alpha=0.3, label='uniform pdf')
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.8, top=0.8, wspace=0.2, hspace=0.3); plt.title('Sampling Inverse ' + str(dist_type) + ' CDF'); plt.xlabel('Values'); plt.ylabel('Cumulative Probability')
#print('The mean is ' + str(round(my_dist.mean(loc = mean, scale = stdev),4)) + '.') # calculate stats and symmetric interval
#print('The variance is ' + str(round(my_dist.var(loc = mean, scale = stdev),4)) + '.')
#print('The interval at alpha level ' + str(round(1-level,3)) + ' is ' + str(my_dist.interval(alpha = alpha,loc = mean,scale = stdev)))
# -
# There are many other parametric distributions that we could have included. Also we could have demonstrated the distribution fitting.
#
# #### Comments
#
# This was a basic demonstration of working with parametric distributions.
#
# I have other demonstrations on the basics of working with DataFrames, ndarrays, univariate statistics, plotting data, declustering, data transformations, trend modeling and many other workflows available at [Python Demos](https://github.com/GeostatsGuy/PythonNumericalDemos) and a Python package for data analytics and geostatistics at [GeostatsPy](https://github.com/GeostatsGuy/GeostatsPy).
#
# I hope this was helpful,
#
# *Michael*
#
# #### The Author:
#
# ### <NAME>, Associate Professor, University of Texas at Austin
# *Novel Data Analytics, Geostatistics and Machine Learning Subsurface Solutions*
#
# With over 17 years of experience in subsurface consulting, research and development, Michael has returned to academia driven by his passion for teaching and enthusiasm for enhancing engineers' and geoscientists' impact in subsurface resource development.
#
# For more about Michael check out these links:
#
# #### [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1)
#
# #### Want to Work Together?
#
# I hope this content is helpful to those that want to learn more about subsurface modeling, data analytics and machine learning. Students and working professionals are welcome to participate.
#
# * Want to invite me to visit your company for training, mentoring, project review, workflow design and / or consulting? I'd be happy to drop by and work with you!
#
# * Interested in partnering, supporting my graduate student research or my Subsurface Data Analytics and Machine Learning consortium (co-PIs including Profs. Foster, Torres-Verdin and van Oort)? My research combines data analytics, stochastic modeling and machine learning theory with practice to develop novel methods and workflows to add value. We are solving challenging subsurface problems!
#
# * I can be reached at <EMAIL>.
#
# I'm always happy to discuss,
#
# *Michael*
#
# <NAME>, Ph.D., P.Eng. Associate Professor The Hildebrand Department of Petroleum and Geosystems Engineering, Bureau of Economic Geology, The Jackson School of Geosciences, The University of Texas at Austin
#
# #### More Resources Available at: [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1)
#
| PythonDataBasics_ParametricDistributions.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
# %config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torchvision import datasets, transforms
import helper
# -
# The easiest way to load image data is with *datasets.ImageFolder* from *torchvision*. In generall we'll use *ImageFolder* like so:
#
# ```
# dataset = datasets.ImageFolder('path/to/data',
# transform=transform)
# ```
# ImageFolder expects the files and directories to be constructed like so:
#
# ```
# root/dog/xxx.png
# root/dog/xxy.ong
#
# root/cat/123.png
# root/cat/sad.png
# ```
# ## Transforms
#
# We can either resize them with *transforms.Resize()* or crop with *transforms.CenterCrop()*, *transforms.RandomResizedCrop()* . We'll also need to convert the images to PyTorch tensors with *transforms.ToTensor()*.
# ## Data Loaders
#
# With the *ImageFolder* loaded, we have to pass it to a *DataLoader*. It takes a dataset and returns batches of images and the corresponding labels. We can set various parameters.
#
# ```
# dataloader = torch.utils.data.DataLoader(
# dataset,
# batch_size=32,
# shuffle=True)
# ```
#
# Here dataloader is a *generator*. To get out of it, we need to loop through it or convert it to an iterator and call *next()*
#
# ```
# # looping thrpugh it, get batch on each loop
# for images, labels in dataloader:
# pass
#
# # Get one batch
# images, labels = next(iter(dataloader))
# ```
# **Exercise**
#
# Load images from the *Cat_Dog_data/train* folder, define a few transforms, then build the dataloader.
data_dir = 'Cat_Dog_data/train'
# compose transforms
transform = transforms.Compose([
transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()
])
# create the ImageFolder
dataset = datasets.ImageFolder(data_dir,
transform=transform)
# use the ImageFolder dataset to create the DataLoader
dataloader = torch.utils.data.DataLoader(dataset,
batch_size=32,
shuffle=True)
# Test the dataset
images, labels = next(iter(dataloader))
helper.imshow(images[0], normalize=False)
# ## Data Augmentation
#
# ```
# train_transforms = transforms.Compose([
# transforms.RandomRotation(30),
# transforms.RandomResizedCrop(224),
# transforms.RandomHorizontalFlip(),
# transforms.ToTensor(),
# transforms.Normalize([0.5, 0.5, 0.5],
# [0.5, 0.5, 0.5])
# ])
# ```
#
# We can pass a list of means and list of standard deviations, then the color channels are normalized like so
#
# ```
# input[channel] = (input[channel] - mean[channel]) / std[channel]
# ```
#
# Subtracting mean centers the data around zero and dividing by std squishes the values to be between -1 and 1. Normalizing helps keep the network work weights near zero which in turn makes backpropagation more stable. Without normalization, networks will tend to fail to learn.
#
# When we're testing however, we'll want to use images that aren't altered. So, for validation/test images, we'll typically just resize and crop.
#
# **Exercise**
#
# Define transforms for trainin data and testing data below. Leave off normalization for now.
# +
data_dir = 'Cat_Dog_data/'
# Define transforms the training data and
# testing data
train_transforms = transforms.Compose([
transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor()
#transforms.Normalize([0.5, 0.5, 0.5],
# [0.5, 0.5, 0.5])
])
test_transforms = transforms.Compose([
transforms.RandomResizedCrop(224),
transforms.ToTensor()
])
# Pass transforms in here, then turn the next
# cell to see how the transforms look
train_data = datasets.ImageFolder(data_dir + '/train',
transform=train_transforms)
test_data = datasets.ImageFolder(data_dir + '/test',
transform=test_transforms)
trainloader = torch.utils.data.DataLoader(train_data,
batch_size=32)
testloader = torch.utils.data.DataLoader(test_data,
batch_size=32)
# +
# change this to the trainloader or testloader
data_iter = iter(trainloader)
images, labels = next(data_iter)
fig, axes = plt.subplots(figsize=(10,4), ncols=4)
for ii in range(4):
ax = axes[ii]
helper.imshow(images[ii],
ax=ax,
normalize=False)
| Lesson 5: Introduction to PyTorch/07 - Loading Image Data.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# Probabilistic Programming and Bayesian Methods for Hackers
# ========
#
# Welcome to *Bayesian Methods for Hackers*. The full Github repository is available at [github/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers](https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers). The other chapters can be found on the project's [homepage](https://camdavidsonpilon.github.io/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers/). We hope you enjoy the book, and we encourage any contributions!
#
# #### Looking for a printed version of Bayesian Methods for Hackers?
#
# _Bayesian Methods for Hackers_ is now a published book by Addison-Wesley, available on [Amazon](http://www.amazon.com/Bayesian-Methods-Hackers-Probabilistic-Addison-Wesley/dp/0133902838)!
#
# 
# Chapter 1
# ======
# ***
# The Philosophy of Bayesian Inference
# ------
#
# > You are a skilled programmer, but bugs still slip into your code. After a particularly difficult implementation of an algorithm, you decide to test your code on a trivial example. It passes. You test the code on a harder problem. It passes once again. And it passes the next, *even more difficult*, test too! You are starting to believe that there may be no bugs in this code...
#
# If you think this way, then congratulations, you already are thinking Bayesian! Bayesian inference is simply updating your beliefs after considering new evidence. A Bayesian can rarely be certain about a result, but he or she can be very confident. Just like in the example above, we can never be 100% sure that our code is bug-free unless we test it on every possible problem; something rarely possible in practice. Instead, we can test it on a large number of problems, and if it succeeds we can feel more *confident* about our code, but still not certain. Bayesian inference works identically: we update our beliefs about an outcome; rarely can we be absolutely sure unless we rule out all other alternatives.
#
# ### The Bayesian state of mind
#
#
# Bayesian inference differs from more traditional statistical inference by preserving *uncertainty*. At first, this sounds like a bad statistical technique. Isn't statistics all about deriving *certainty* from randomness? To reconcile this, we need to start thinking like Bayesians.
#
# The Bayesian world-view interprets probability as measure of *believability in an event*, that is, how confident we are in an event occurring. In fact, we will see in a moment that this is the natural interpretation of probability.
#
# For this to be clearer, we consider an alternative interpretation of probability: *Frequentist*, known as the more *classical* version of statistics, assumes that probability is the long-run frequency of events (hence the bestowed title). For example, the *probability of plane accidents* under a frequentist philosophy is interpreted as the *long-term frequency of plane accidents*. This makes logical sense for many probabilities of events, but becomes more difficult to understand when events have no long-term frequency of occurrences. Consider: we often assign probabilities to outcomes of presidential elections, but the election itself only happens once! Frequentists get around this by invoking alternative realities and saying across all these realities, the frequency of occurrences defines the probability.
#
# Bayesians, on the other hand, have a more intuitive approach. Bayesians interpret a probability as measure of *belief*, or confidence, of an event occurring. Simply, a probability is a summary of an opinion. An individual who assigns a belief of 0 to an event has no confidence that the event will occur; conversely, assigning a belief of 1 implies that the individual is absolutely certain of an event occurring. Beliefs between 0 and 1 allow for weightings of other outcomes. This definition agrees with the probability of a plane accident example, for having observed the frequency of plane accidents, an individual's belief should be equal to that frequency, excluding any outside information. Similarly, under this definition of probability being equal to beliefs, it is meaningful to speak about probabilities (beliefs) of presidential election outcomes: how confident are you candidate *A* will win?
#
# Notice in the paragraph above, I assigned the belief (probability) measure to an *individual*, not to Nature. This is very interesting, as this definition leaves room for conflicting beliefs between individuals. Again, this is appropriate for what naturally occurs: different individuals have different beliefs of events occurring, because they possess different *information* about the world. The existence of different beliefs does not imply that anyone is wrong. Consider the following examples demonstrating the relationship between individual beliefs and probabilities:
#
# - I flip a coin, and we both guess the result. We would both agree, assuming the coin is fair, that the probability of Heads is 1/2. Assume, then, that I peek at the coin. Now I know for certain what the result is: I assign probability 1.0 to either Heads or Tails (whichever it is). Now what is *your* belief that the coin is Heads? My knowledge of the outcome has not changed the coin's results. Thus we assign different probabilities to the result.
#
# - Your code either has a bug in it or not, but we do not know for certain which is true, though we have a belief about the presence or absence of a bug.
#
# - A medical patient is exhibiting symptoms $x$, $y$ and $z$. There are a number of diseases that could be causing all of them, but only a single disease is present. A doctor has beliefs about which disease, but a second doctor may have slightly different beliefs.
#
#
# This philosophy of treating beliefs as probability is natural to humans. We employ it constantly as we interact with the world and only see partial truths, but gather evidence to form beliefs. Alternatively, you have to be *trained* to think like a frequentist.
#
# To align ourselves with traditional probability notation, we denote our belief about event $A$ as $P(A)$. We call this quantity the *prior probability*.
#
# <NAME>, a great economist and thinker, said "When the facts change, I change my mind. What do you do, sir?" This quote reflects the way a Bayesian updates his or her beliefs after seeing evidence. Even — especially — if the evidence is counter to what was initially believed, the evidence cannot be ignored. We denote our updated belief as $P(A |X )$, interpreted as the probability of $A$ given the evidence $X$. We call the updated belief the *posterior probability* so as to contrast it with the prior probability. For example, consider the posterior probabilities (read: posterior beliefs) of the above examples, after observing some evidence $X$:
#
# 1\. $P(A): \;\;$ the coin has a 50 percent chance of being Heads. $P(A | X):\;\;$ You look at the coin, observe a Heads has landed, denote this information $X$, and trivially assign probability 1.0 to Heads and 0.0 to Tails.
#
# 2\. $P(A): \;\;$ This big, complex code likely has a bug in it. $P(A | X): \;\;$ The code passed all $X$ tests; there still might be a bug, but its presence is less likely now.
#
# 3\. $P(A):\;\;$ The patient could have any number of diseases. $P(A | X):\;\;$ Performing a blood test generated evidence $X$, ruling out some of the possible diseases from consideration.
#
#
# It's clear that in each example we did not completely discard the prior belief after seeing new evidence $X$, but we *re-weighted the prior* to incorporate the new evidence (i.e. we put more weight, or confidence, on some beliefs versus others).
#
# By introducing prior uncertainty about events, we are already admitting that any guess we make is potentially very wrong. After observing data, evidence, or other information, we update our beliefs, and our guess becomes *less wrong*. This is the alternative side of the prediction coin, where typically we try to be *more right*.
#
#
# ### Bayesian Inference in Practice
#
# If frequentist and Bayesian inference were programming functions, with inputs being statistical problems, then the two would be different in what they return to the user. The frequentist inference function would return a number, representing an estimate (typically a summary statistic like the sample average etc.), whereas the Bayesian function would return *probabilities*.
#
# For example, in our debugging problem above, calling the frequentist function with the argument "My code passed all $X$ tests; is my code bug-free?" would return a *YES*. On the other hand, asking our Bayesian function "Often my code has bugs. My code passed all $X$ tests; is my code bug-free?" would return something very different: probabilities of *YES* and *NO*. The function might return:
#
#
# > *YES*, with probability 0.8; *NO*, with probability 0.2
#
#
#
# This is very different from the answer the frequentist function returned. Notice that the Bayesian function accepted an additional argument: *"Often my code has bugs"*. This parameter is the *prior*. By including the prior parameter, we are telling the Bayesian function to include our belief about the situation. Technically this parameter in the Bayesian function is optional, but we will see excluding it has its own consequences.
#
#
# #### Incorporating evidence
#
# As we acquire more and more instances of evidence, our prior belief is *washed out* by the new evidence. This is to be expected. For example, if your prior belief is something ridiculous, like "I expect the sun to explode today", and each day you are proved wrong, you would hope that any inference would correct you, or at least align your beliefs better. Bayesian inference will correct this belief.
#
#
# Denote $N$ as the number of instances of evidence we possess. As we gather an *infinite* amount of evidence, say as $N \rightarrow \infty$, our Bayesian results (often) align with frequentist results. Hence for large $N$, statistical inference is more or less objective. On the other hand, for small $N$, inference is much more *unstable*: frequentist estimates have more variance and larger confidence intervals. This is where Bayesian analysis excels. By introducing a prior, and returning probabilities (instead of a scalar estimate), we *preserve the uncertainty* that reflects the instability of statistical inference of a small $N$ dataset.
#
# One may think that for large $N$, one can be indifferent between the two techniques since they offer similar inference, and might lean towards the computationally-simpler, frequentist methods. An individual in this position should consider the following quote by <NAME> (2005)[1], before making such a decision:
#
# > Sample sizes are never large. If $N$ is too small to get a sufficiently-precise estimate, you need to get more data (or make more assumptions). But once $N$ is "large enough," you can start subdividing the data to learn more (for example, in a public opinion poll, once you have a good estimate for the entire country, you can estimate among men and women, northerners and southerners, different age groups, etc.). $N$ is never enough because if it were "enough" you'd already be on to the next problem for which you need more data.
#
# ### Are frequentist methods incorrect then?
#
# **No.**
#
# Frequentist methods are still useful or state-of-the-art in many areas. Tools such as least squares linear regression, LASSO regression, and expectation-maximization algorithms are all powerful and fast. Bayesian methods complement these techniques by solving problems that these approaches cannot, or by illuminating the underlying system with more flexible modeling.
#
#
# #### A note on *Big Data*
# Paradoxically, big data's predictive analytic problems are actually solved by relatively simple algorithms [2][4]. Thus we can argue that big data's prediction difficulty does not lie in the algorithm used, but instead on the computational difficulties of storage and execution on big data. (One should also consider Gelman's quote from above and ask "Do I really have big data?" )
#
# The much more difficult analytic problems involve *medium data* and, especially troublesome, *really small data*. Using a similar argument as Gelman's above, if big data problems are *big enough* to be readily solved, then we should be more interested in the *not-quite-big enough* datasets.
#
# ### Our Bayesian framework
#
# We are interested in beliefs, which can be interpreted as probabilities by thinking Bayesian. We have a *prior* belief in event $A$, beliefs formed by previous information, e.g., our prior belief about bugs being in our code before performing tests.
#
# Secondly, we observe our evidence. To continue our buggy-code example: if our code passes $X$ tests, we want to update our belief to incorporate this. We call this new belief the *posterior* probability. Updating our belief is done via the following equation, known as Bayes' Theorem, after its discoverer Thomas Bayes:
#
# \begin{align}
# P( A | X ) = & \frac{ P(X | A) P(A) } {P(X) } \\\\[5pt]
# & \propto P(X | A) P(A)\;\; (\propto \text{is proportional to } )
# \end{align}
#
# The above formula is not unique to Bayesian inference: it is a mathematical fact with uses outside Bayesian inference. Bayesian inference merely uses it to connect prior probabilities $P(A)$ with an updated posterior probabilities $P(A | X )$.
# ##### Example: Mandatory coin-flip example
#
# Every statistics text must contain a coin-flipping example, I'll use it here to get it out of the way. Suppose, naively, that you are unsure about the probability of heads in a coin flip (spoiler alert: it's 50%). You believe there is some true underlying ratio, call it $p$, but have no prior opinion on what $p$ might be.
#
# We begin to flip a coin, and record the observations: either $H$ or $T$. This is our observed data. An interesting question to ask is how our inference changes as we observe more and more data? More specifically, what do our posterior probabilities look like when we have little data, versus when we have lots of data.
#
# Below we plot a sequence of updating posterior probabilities as we observe increasing amounts of data (coin flips).
# + jupyter={"outputs_hidden": false}
"""
The book uses a custom matplotlibrc file, which provides the unique styles for
matplotlib plots. If executing this book, and you wish to use the book's
styling, provided are two options:
1. Overwrite your own matplotlibrc file with the rc-file provided in the
book's styles/ dir. See http://matplotlib.org/users/customizing.html
2. Also in the styles is bmh_matplotlibrc.json file. This can be used to
update the styles in only this notebook. Try running the following code:
import json, matplotlib
s = json.load( open("../styles/bmh_matplotlibrc.json") )
matplotlib.rcParams.update(s)
"""
# The code below can be passed over, as it is currently not important, plus it
# uses advanced topics we have not covered yet. LOOK AT PICTURE, MICHAEL!
# %matplotlib inline
from IPython.core.pylabtools import figsize
import numpy as np
from matplotlib import pyplot as plt
figsize(11, 9)
import scipy.stats as stats
dist = stats.beta
n_trials = [0, 1, 2, 3, 4, 5, 8, 15, 50, 500]
data = stats.bernoulli.rvs(0.5, size=n_trials[-1])
x = np.linspace(0, 1, 100)
# For the already prepared, I'm using Binomial's conj. prior.
for k, N in enumerate(n_trials):
sx = plt.subplot(len(n_trials) / 2, 2, k + 1)
plt.xlabel("$p$, probability of heads") \
if k in [0, len(n_trials) - 1] else None
plt.setp(sx.get_yticklabels(), visible=False)
heads = data[:N].sum()
y = dist.pdf(x, 1 + heads, 1 + N - heads)
plt.plot(x, y, label="observe %d tosses,\n %d heads" % (N, heads))
plt.fill_between(x, 0, y, color="#348ABD", alpha=0.4)
plt.vlines(0.5, 0, 4, color="k", linestyles="--", lw=1)
leg = plt.legend()
leg.get_frame().set_alpha(0.4)
plt.autoscale(tight=True)
plt.suptitle("Bayesian updating of posterior probabilities",
y=1.02,
fontsize=14)
plt.tight_layout()
# -
# The posterior probabilities are represented by the curves, and our uncertainty is proportional to the width of the curve. As the plot above shows, as we start to observe data our posterior probabilities start to shift and move around. Eventually, as we observe more and more data (coin-flips), our probabilities will tighten closer and closer around the true value of $p=0.5$ (marked by a dashed line).
#
# Notice that the plots are not always *peaked* at 0.5. There is no reason it should be: recall we assumed we did not have a prior opinion of what $p$ is. In fact, if we observe quite extreme data, say 8 flips and only 1 observed heads, our distribution would look very biased *away* from lumping around 0.5 (with no prior opinion, how confident would you feel betting on a fair coin after observing 8 tails and 1 head). As more data accumulates, we would see more and more probability being assigned at $p=0.5$, though never all of it.
#
# The next example is a simple demonstration of the mathematics of Bayesian inference.
# ##### Example: Bug, or just sweet, unintended feature?
#
#
# Let $A$ denote the event that our code has **no bugs** in it. Let $X$ denote the event that the code passes all debugging tests. For now, we will leave the prior probability of no bugs as a variable, i.e. $P(A) = p$.
#
# We are interested in $P(A|X)$, i.e. the probability of no bugs, given our debugging tests $X$ pass. To use the formula above, we need to compute some quantities.
#
# What is $P(X | A)$, i.e., the probability that the code passes $X$ tests *given* there are no bugs? Well, it is equal to 1, for code with no bugs will pass all tests.
#
# $P(X)$ is a little bit trickier: The event $X$ can be divided into two possibilities, event $X$ occurring even though our code *indeed has* bugs (denoted $\sim A\;$, spoken *not $A$*), or event $X$ without bugs ($A$). $P(X)$ can be represented as:
# \begin{align}
# P(X ) & = P(X \text{ and } A) + P(X \text{ and } \sim A) \\\\[5pt]
# & = P(X|A)P(A) + P(X | \sim A)P(\sim A)\\\\[5pt]
# & = P(X|A)p + P(X | \sim A)(1-p)
# \end{align}
# We have already computed $P(X|A)$ above. On the other hand, $P(X | \sim A)$ is subjective: our code can pass tests but still have a bug in it, though the probability there is a bug present is reduced. Note this is dependent on the number of tests performed, the degree of complication in the tests, etc. Let's be conservative and assign $P(X|\sim A) = 0.5$. Then
#
# \begin{align}
# P(A | X) & = \frac{1\cdot p}{ 1\cdot p +0.5 (1-p) } \\\\
# & = \frac{ 2 p}{1+p}
# \end{align}
# This is the posterior probability. What does it look like as a function of our prior, $p \in [0,1]$?
# + jupyter={"outputs_hidden": false}
figsize(12.5, 4)
p = np.linspace(0, 1, 50)
plt.plot(p, 2 * p / (1 + p), color="#348ABD", lw=3)
# plt.fill_between(p, 2*p/(1+p), alpha=.5, facecolor=["#A60628"])
plt.scatter(0.2, 2 * (0.2) / 1.2, s=140, c="#348ABD")
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.xlabel("Prior, $P(A) = p$")
plt.ylabel("Posterior, $P(A|X)$, with $P(A) = p$")
plt.title("Is my code bug-free?")
# -
# We can see the biggest gains if we observe the $X$ tests passed when the prior probability, $p$, is low. Let's settle on a specific value for the prior. I'm a strong programmer (I think), so I'm going to give myself a realistic prior of 0.20, that is, there is a 20% chance that I write code bug-free. To be more realistic, this prior should be a function of how complicated and large the code is, but let's pin it at 0.20. Then my updated belief that my code is bug-free is 0.33.
#
# Recall that the prior is a probability: $p$ is the prior probability that there *are no bugs*, so $1-p$ is the prior probability that there *are bugs*.
#
# Similarly, our posterior is also a probability, with $P(A | X)$ the probability there is no bug *given we saw all tests pass*, hence $1-P(A|X)$ is the probability there is a bug *given all tests passed*. What does our posterior probability look like? Below is a chart of both the prior and the posterior probabilities.
#
# + jupyter={"outputs_hidden": false}
figsize(12.5, 4)
colours = ["#348ABD", "#A60628"]
prior = [0.20, 0.80]
posterior = [1. / 3, 2. / 3]
plt.bar([0, .7], prior, alpha=0.70, width=0.25,
color=colours[0], label="prior distribution",
lw="3", edgecolor=colours[0])
plt.bar([0 + 0.25, .7 + 0.25], posterior, alpha=0.7,
width=0.25, color=colours[1],
label="posterior distribution",
lw="3", edgecolor=colours[1])
plt.ylim(0,1)
plt.xticks([0.20, .95], ["Bugs Absent", "Bugs Present"])
plt.title("Prior and Posterior probability of bugs present")
plt.ylabel("Probability")
plt.legend(loc="upper left");
# -
# Notice that after we observed $X$ occur, the probability of bugs being absent increased. By increasing the number of tests, we can approach confidence (probability 1) that there are no bugs present.
#
# This was a very simple example of Bayesian inference and Bayes rule. Unfortunately, the mathematics necessary to perform more complicated Bayesian inference only becomes more difficult, except for artificially constructed cases. We will later see that this type of mathematical analysis is actually unnecessary. First we must broaden our modeling tools. The next section deals with *probability distributions*. If you are already familiar, feel free to skip (or at least skim), but for the less familiar the next section is essential.
# _______
#
# ## Probability Distributions
#
#
# **Let's quickly recall what a probability distribution is:** Let $Z$ be some random variable. Then associated with $Z$ is a *probability distribution function* that assigns probabilities to the different outcomes $Z$ can take. Graphically, a probability distribution is a curve where the probability of an outcome is proportional to the height of the curve. You can see examples in the first figure of this chapter.
#
# We can divide random variables into three classifications:
#
# - **$Z$ is discrete**: Discrete random variables may only assume values on a specified list. Things like populations, movie ratings, and number of votes are all discrete random variables. Discrete random variables become more clear when we contrast them with...
#
# - **$Z$ is continuous**: Continuous random variable can take on arbitrarily exact values. For example, temperature, speed, time, color are all modeled as continuous variables because you can progressively make the values more and more precise.
#
# - **$Z$ is mixed**: Mixed random variables assign probabilities to both discrete and continuous random variables, i.e. it is a combination of the above two categories.
#
# #### Expected Value
# Expected value (EV) is one of the most important concepts in probability. The EV for a given probability distribution can be described as "the mean value in the long run for many repeated samples from that distribution." To borrow a metaphor from physics, a distribution's EV acts like its "center of mass." Imagine repeating the same experiment many times over, and taking the average over each outcome. The more you repeat the experiment, the closer this average will become to the distributions EV. (side note: as the number of repeated experiments goes to infinity, the difference between the average outcome and the EV becomes arbitrarily small.)
#
# ### Discrete Case
# If $Z$ is discrete, then its distribution is called a *probability mass function*, which measures the probability $Z$ takes on the value $k$, denoted $P(Z=k)$. Note that the probability mass function completely describes the random variable $Z$, that is, if we know the mass function, we know how $Z$ should behave. There are popular probability mass functions that consistently appear: we will introduce them as needed, but let's introduce the first very useful probability mass function. We say $Z$ is *Poisson*-distributed if:
#
# $$P(Z = k) =\frac{ \lambda^k e^{-\lambda} }{k!}, \; \; k=0,1,2, \dots, \; \; \lambda \in \mathbb{R}_{>0} $$
#
# $\lambda$ is called a parameter of the distribution, and it controls the distribution's shape. For the Poisson distribution, $\lambda$ can be any positive number. By increasing $\lambda$, we add more probability to larger values, and conversely by decreasing $\lambda$ we add more probability to smaller values. One can describe $\lambda$ as the *intensity* of the Poisson distribution.
#
# Unlike $\lambda$, which can be any positive number, the value $k$ in the above formula must be a non-negative integer, i.e., $k$ must take on values 0,1,2, and so on. This is very important, because if you wanted to model a population you could not make sense of populations with 4.25 or 5.612 members.
#
# If a random variable $Z$ has a Poisson mass distribution, we denote this by writing
#
# $$Z \sim \text{Poi}(\lambda) $$
#
# One useful property of the Poisson distribution is that its expected value is equal to its parameter, i.e.:
#
# $$E\large[ \;Z\; | \; \lambda \;\large] = \lambda $$
#
# We will use this property often, so it's useful to remember. Below, we plot the probability mass distribution for different $\lambda$ values. The first thing to notice is that by increasing $\lambda$, we add more probability of larger values occurring. Second, notice that although the graph ends at 15, the distributions do not. They assign positive probability to every non-negative integer.
# + jupyter={"outputs_hidden": false}
figsize(12.5, 4)
import scipy.stats as stats
a = np.arange(16)
poi = stats.poisson
lambda_ = [1.5, 4.25]
colours = ["#348ABD", "#A60628"]
plt.bar(a, poi.pmf(a, lambda_[0]), color=colours[0],
label="$\lambda = %.1f$" % lambda_[0], alpha=0.60,
edgecolor=colours[0], lw="3")
plt.bar(a, poi.pmf(a, lambda_[1]), color=colours[1],
label="$\lambda = %.1f$" % lambda_[1], alpha=0.60,
edgecolor=colours[1], lw="3")
plt.xticks(a + 0.4, a)
plt.legend()
plt.ylabel("probability of $k$")
plt.xlabel("$k$")
plt.title("Probability mass function of a Poisson random variable; differing \
$\lambda$ values")
# -
# ### Continuous Case
# Instead of a probability mass function, a continuous random variable has a *probability density function*. This might seem like unnecessary nomenclature, but the density function and the mass function are very different creatures. An example of continuous random variable is a random variable with *exponential density*. The density function for an exponential random variable looks like this:
#
# $$f_Z(z | \lambda) = \lambda e^{-\lambda z }, \;\; z\ge 0$$
#
# Like a Poisson random variable, an exponential random variable can take on only non-negative values. But unlike a Poisson variable, the exponential can take on *any* non-negative values, including non-integral values such as 4.25 or 5.612401. This property makes it a poor choice for count data, which must be an integer, but a great choice for time data, temperature data (measured in Kelvins, of course), or any other precise *and positive* variable. The graph below shows two probability density functions with different $\lambda$ values.
#
# When a random variable $Z$ has an exponential distribution with parameter $\lambda$, we say *$Z$ is exponential* and write
#
# $$Z \sim \text{Exp}(\lambda)$$
#
# Given a specific $\lambda$, the expected value of an exponential random variable is equal to the inverse of $\lambda$, that is:
#
# $$E[\; Z \;|\; \lambda \;] = \frac{1}{\lambda}$$
# + jupyter={"outputs_hidden": false}
a = np.linspace(0, 4, 100)
expo = stats.expon
lambda_ = [0.5, 1]
for l, c in zip(lambda_, colours):
plt.plot(a, expo.pdf(a, scale=1. / l), lw=3,
color=c, label="$\lambda = %.1f$" % l)
plt.fill_between(a, expo.pdf(a, scale=1. / l), color=c, alpha=.33)
plt.legend()
plt.ylabel("PDF at $z$")
plt.xlabel("$z$")
plt.ylim(0, 1.2)
plt.title("Probability density function of an Exponential random variable;\
differing $\lambda$");
# -
#
# ### But what is $\lambda \;$?
#
#
# **This question is what motivates statistics**. In the real world, $\lambda$ is hidden from us. We see only $Z$, and must go backwards to try and determine $\lambda$. The problem is difficult because there is no one-to-one mapping from $Z$ to $\lambda$. Many different methods have been created to solve the problem of estimating $\lambda$, but since $\lambda$ is never actually observed, no one can say for certain which method is best!
#
# Bayesian inference is concerned with *beliefs* about what $\lambda$ might be. Rather than try to guess $\lambda$ exactly, we can only talk about what $\lambda$ is likely to be by assigning a probability distribution to $\lambda$.
#
# This might seem odd at first. After all, $\lambda$ is fixed; it is not (necessarily) random! How can we assign probabilities to values of a non-random variable? Ah, we have fallen for our old, frequentist way of thinking. Recall that under Bayesian philosophy, we *can* assign probabilities if we interpret them as beliefs. And it is entirely acceptable to have *beliefs* about the parameter $\lambda$.
#
#
# ##### Example: Inferring behaviour from text-message data
#
# Let's try to model a more interesting example, one that concerns the rate at which a user sends and receives text messages:
#
# > You are given a series of daily text-message counts from a user of your system. The data, plotted over time, appears in the chart below. You are curious to know if the user's text-messaging habits have changed over time, either gradually or suddenly. How can you model this? (This is in fact my own text-message data. Judge my popularity as you wish.)
#
# + jupyter={"outputs_hidden": false}
figsize(12.5, 3.5)
count_data = np.loadtxt("data/txtdata.csv")
n_count_data = len(count_data)
plt.bar(np.arange(n_count_data), count_data, color="#348ABD")
plt.xlabel("Time (days)")
plt.ylabel("count of text-msgs received")
plt.title("Did the user's texting habits change over time?")
plt.xlim(0, n_count_data);
# -
# Before we start modeling, see what you can figure out just by looking at the chart above. Would you say there was a change in behaviour during this time period?
#
# How can we start to model this? Well, as we have conveniently already seen, a Poisson random variable is a very appropriate model for this type of *count* data. Denoting day $i$'s text-message count by $C_i$,
#
# $$ C_i \sim \text{Poisson}(\lambda) $$
#
# We are not sure what the value of the $\lambda$ parameter really is, however. Looking at the chart above, it appears that the rate might become higher late in the observation period, which is equivalent to saying that $\lambda$ increases at some point during the observations. (Recall that a higher value of $\lambda$ assigns more probability to larger outcomes. That is, there is a higher probability of many text messages having been sent on a given day.)
#
# How can we represent this observation mathematically? Let's assume that on some day during the observation period (call it $\tau$), the parameter $\lambda$ suddenly jumps to a higher value. So we really have two $\lambda$ parameters: one for the period before $\tau$, and one for the rest of the observation period. In the literature, a sudden transition like this would be called a *switchpoint*:
#
# $$
# \lambda =
# \begin{cases}
# \lambda_1 & \text{if } t \lt \tau \cr
# \lambda_2 & \text{if } t \ge \tau
# \end{cases}
# $$
#
#
# If, in reality, no sudden change occurred and indeed $\lambda_1 = \lambda_2$, then the $\lambda$s posterior distributions should look about equal.
#
# We are interested in inferring the unknown $\lambda$s. To use Bayesian inference, we need to assign prior probabilities to the different possible values of $\lambda$. What would be good prior probability distributions for $\lambda_1$ and $\lambda_2$? Recall that $\lambda$ can be any positive number. As we saw earlier, the *exponential* distribution provides a continuous density function for positive numbers, so it might be a good choice for modeling $\lambda_i$. But recall that the exponential distribution takes a parameter of its own, so we'll need to include that parameter in our model. Let's call that parameter $\alpha$.
#
# \begin{align}
# &\lambda_1 \sim \text{Exp}( \alpha ) \\\
# &\lambda_2 \sim \text{Exp}( \alpha )
# \end{align}
#
# $\alpha$ is called a *hyper-parameter* or *parent variable*. In literal terms, it is a parameter that influences other parameters. Our initial guess at $\alpha$ does not influence the model too strongly, so we have some flexibility in our choice. A good rule of thumb is to set the exponential parameter equal to the inverse of the average of the count data. Since we're modeling $\lambda$ using an exponential distribution, we can use the expected value identity shown earlier to get:
#
# $$\frac{1}{N}\sum_{i=0}^N \;C_i \approx E[\; \lambda \; |\; \alpha ] = \frac{1}{\alpha}$$
#
# An alternative, and something I encourage the reader to try, would be to have two priors: one for each $\lambda_i$. Creating two exponential distributions with different $\alpha$ values reflects our prior belief that the rate changed at some point during the observations.
#
# What about $\tau$? Because of the noisiness of the data, it's difficult to pick out a priori when $\tau$ might have occurred. Instead, we can assign a *uniform prior belief* to every possible day. This is equivalent to saying
#
# \begin{align}
# & \tau \sim \text{DiscreteUniform(1,70) }\\\\
# & \Rightarrow P( \tau = k ) = \frac{1}{70}
# \end{align}
#
# So after all this, what does our overall prior distribution for the unknown variables look like? Frankly, *it doesn't matter*. What we should understand is that it's an ugly, complicated mess involving symbols only a mathematician could love. And things will only get uglier the more complicated our models become. Regardless, all we really care about is the posterior distribution.
#
# We next turn to PyMC, a Python library for performing Bayesian analysis that is undaunted by the mathematical monster we have created.
#
#
# Introducing our first hammer: PyMC
# -----
#
# PyMC is a Python library for programming Bayesian analysis [3]. It is a fast, well-maintained library. The only unfortunate part is that its documentation is lacking in certain areas, especially those that bridge the gap between beginner and hacker. One of this book's main goals is to solve that problem, and also to demonstrate why PyMC is so cool.
#
# We will model the problem above using PyMC. This type of programming is called *probabilistic programming*, an unfortunate misnomer that invokes ideas of randomly-generated code and has likely confused and frightened users away from this field. The code is not random; it is probabilistic in the sense that we create probability models using programming variables as the model's components. Model components are first-class primitives within the PyMC framework.
#
# <NAME> [5] has a very motivating description of probabilistic programming:
#
# > Another way of thinking about this: unlike a traditional program, which only runs in the forward directions, a probabilistic program is run in both the forward and backward direction. It runs forward to compute the consequences of the assumptions it contains about the world (i.e., the model space it represents), but it also runs backward from the data to constrain the possible explanations. In practice, many probabilistic programming systems will cleverly interleave these forward and backward operations to efficiently home in on the best explanations.
#
# Because of the confusion engendered by the term *probabilistic programming*, I'll refrain from using it. Instead, I'll simply say *programming*, since that's what it really is.
#
# PyMC code is easy to read. The only novel thing should be the syntax, and I will interrupt the code to explain individual sections. Simply remember that we are representing the model's components ($\tau, \lambda_1, \lambda_2$ ) as variables:
# + jupyter={"outputs_hidden": false}
import pymc as pm
alpha = 1.0 / count_data.mean() # Recall count_data is the
# variable that holds our txt counts
with pm.Model() as model:
lambda_1 = pm.Exponential("lambda_1", alpha)
lambda_2 = pm.Exponential("lambda_2", alpha)
tau = pm.DiscreteUniform("tau", lower=0, upper=n_count_data)
# -
# In the code above, we create the PyMC variables corresponding to $\lambda_1$ and $\lambda_2$. We assign them to PyMC's *stochastic variables*, so-called because they are treated by the back end as random number generators. We can demonstrate this fact by calling their built-in `random()` methods.
# + jupyter={"outputs_hidden": false}
print("Random output:", tau.eval(), tau.eval(), tau.eval())
# + jupyter={"outputs_hidden": false}
# @pm.deterministic
def lambda_(tau=tau, lambda_1=lambda_1, lambda_2=lambda_2):
out = np.zeros(n_count_data)
out[:tau] = lambda_1 # lambda before tau is lambda1
out[tau:] = lambda_2 # lambda after (and including) tau is lambda2
return out
# -
# This code creates a new function `lambda_`, but really we can think of it as a random variable: the random variable $\lambda$ from above. Note that because `lambda_1`, `lambda_2` and `tau` are random, `lambda_` will be random. We are **not** fixing any variables yet.
#
# `@pm.deterministic` is a decorator that tells PyMC this is a deterministic function. That is, if the arguments were deterministic (which they are not), the output would be deterministic as well. Deterministic functions will be covered in Chapter 2.
# + jupyter={"outputs_hidden": false}
observation = pm.Poisson("obs", lambda_, value=count_data, observed=True)
model = pm.Model([observation, lambda_1, lambda_2, tau])
# -
# The variable `observation` combines our data, `count_data`, with our proposed data-generation scheme, given by the variable `lambda_`, through the `value` keyword. We also set `observed = True` to tell PyMC that this should stay fixed in our analysis. Finally, PyMC wants us to collect all the variables of interest and create a `Model` instance out of them. This makes our life easier when we retrieve the results.
#
# The code below will be explained in Chapter 3, but I show it here so you can see where our results come from. One can think of it as a *learning* step. The machinery being employed is called *Markov Chain Monte Carlo* (MCMC), which I also delay explaining until Chapter 3. This technique returns thousands of random variables from the posterior distributions of $\lambda_1, \lambda_2$ and $\tau$. We can plot a histogram of the random variables to see what the posterior distributions look like. Below, we collect the samples (called *traces* in the MCMC literature) into histograms.
# + jupyter={"outputs_hidden": false}
# Mysterious code to be explained in Chapter 3.
mcmc = pm.MCMC(model)
mcmc.sample(40000, 10000, 1)
# + jupyter={"outputs_hidden": false}
lambda_1_samples = mcmc.trace('lambda_1')[:]
lambda_2_samples = mcmc.trace('lambda_2')[:]
tau_samples = mcmc.trace('tau')[:]
# + jupyter={"outputs_hidden": false}
figsize(12.5, 10)
# histogram of the samples:
ax = plt.subplot(311)
ax.set_autoscaley_on(False)
plt.hist(lambda_1_samples, histtype='stepfilled', bins=30, alpha=0.85,
label="posterior of $\lambda_1$", color="#A60628", density=True)
plt.legend(loc="upper left")
plt.title(r"""Posterior distributions of the variables
$\lambda_1,\;\lambda_2,\;\tau$""")
plt.xlim([15, 30])
plt.xlabel("$\lambda_1$ value")
ax = plt.subplot(312)
ax.set_autoscaley_on(False)
plt.hist(lambda_2_samples, histtype='stepfilled', bins=30, alpha=0.85,
label="posterior of $\lambda_2$", color="#7A68A6", density=True)
plt.legend(loc="upper left")
plt.xlim([15, 30])
plt.xlabel("$\lambda_2$ value")
plt.subplot(313)
w = 1.0 / tau_samples.shape[0] * np.ones_like(tau_samples)
plt.hist(tau_samples, bins=n_count_data, alpha=1,
label=r"posterior of $\tau$",
color="#467821", weights=w, rwidth=2.)
plt.xticks(np.arange(n_count_data))
plt.legend(loc="upper left")
plt.ylim([0, .75])
plt.xlim([35, len(count_data) - 20])
plt.xlabel(r"$\tau$ (in days)")
plt.ylabel("probability");
# -
# ### Interpretation
#
# Recall that Bayesian methodology returns a *distribution*. Hence we now have distributions to describe the unknown $\lambda$s and $\tau$. What have we gained? Immediately, we can see the uncertainty in our estimates: the wider the distribution, the less certain our posterior belief should be. We can also see what the plausible values for the parameters are: $\lambda_1$ is around 18 and $\lambda_2$ is around 23. The posterior distributions of the two $\lambda$s are clearly distinct, indicating that it is indeed likely that there was a change in the user's text-message behaviour.
#
# What other observations can you make? If you look at the original data again, do these results seem reasonable?
#
# Notice also that the posterior distributions for the $\lambda$s do not look like exponential distributions, even though our priors for these variables were exponential. In fact, the posterior distributions are not really of any form that we recognize from the original model. But that's OK! This is one of the benefits of taking a computational point of view. If we had instead done this analysis using mathematical approaches, we would have been stuck with an analytically intractable (and messy) distribution. Our use of a computational approach makes us indifferent to mathematical tractability.
#
# Our analysis also returned a distribution for $\tau$. Its posterior distribution looks a little different from the other two because it is a discrete random variable, so it doesn't assign probabilities to intervals. We can see that near day 45, there was a 50% chance that the user's behaviour changed. Had no change occurred, or had the change been gradual over time, the posterior distribution of $\tau$ would have been more spread out, reflecting that many days were plausible candidates for $\tau$. By contrast, in the actual results we see that only three or four days make any sense as potential transition points.
# ### Why would I want samples from the posterior, anyways?
#
#
# We will deal with this question for the remainder of the book, and it is an understatement to say that it will lead us to some amazing results. For now, let's end this chapter with one more example.
#
# We'll use the posterior samples to answer the following question: what is the expected number of texts at day $t, \; 0 \le t \le 70$ ? Recall that the expected value of a Poisson variable is equal to its parameter $\lambda$. Therefore, the question is equivalent to *what is the expected value of $\lambda$ at time $t$*?
#
# In the code below, let $i$ index samples from the posterior distributions. Given a day $t$, we average over all possible $\lambda_i$ for that day $t$, using $\lambda_i = \lambda_{1,i}$ if $t \lt \tau_i$ (that is, if the behaviour change has not yet occurred), else we use $\lambda_i = \lambda_{2,i}$.
# + jupyter={"outputs_hidden": false}
figsize(12.5, 5)
# tau_samples, lambda_1_samples, lambda_2_samples contain
# N samples from the corresponding posterior distribution
N = tau_samples.shape[0]
expected_texts_per_day = np.zeros(n_count_data)
for day in range(0, n_count_data):
# ix is a bool index of all tau samples corresponding to
# the switchpoint occurring prior to value of 'day'
ix = day < tau_samples
# Each posterior sample corresponds to a value for tau.
# for each day, that value of tau indicates whether we're "before"
# (in the lambda1 "regime") or
# "after" (in the lambda2 "regime") the switchpoint.
# by taking the posterior sample of lambda1/2 accordingly, we can average
# over all samples to get an expected value for lambda on that day.
# As explained, the "message count" random variable is Poisson distributed,
# and therefore lambda (the poisson parameter) is the expected value of
# "message count".
expected_texts_per_day[day] = (lambda_1_samples[ix].sum()
+ lambda_2_samples[~ix].sum()) / N
plt.plot(range(n_count_data), expected_texts_per_day, lw=4, color="#E24A33",
label="expected number of text-messages received")
plt.xlim(0, n_count_data)
plt.xlabel("Day")
plt.ylabel("Expected # text-messages")
plt.title("Expected number of text-messages received")
plt.ylim(0, 60)
plt.bar(np.arange(len(count_data)), count_data, color="#348ABD", alpha=0.65,
label="observed texts per day")
plt.legend(loc="upper left");
# -
# Our analysis shows strong support for believing the user's behavior did change ($\lambda_1$ would have been close in value to $\lambda_2$ had this not been true), and that the change was sudden rather than gradual (as demonstrated by $\tau$'s strongly peaked posterior distribution). We can speculate what might have caused this: a cheaper text-message rate, a recent weather-to-text subscription, or perhaps a new relationship. (In fact, the 45th day corresponds to Christmas, and I moved away to Toronto the next month, leaving a girlfriend behind.)
#
# ##### Exercises
#
# 1\. Using `lambda_1_samples` and `lambda_2_samples`, what is the mean of the posterior distributions of $\lambda_1$ and $\lambda_2$?
# + jupyter={"outputs_hidden": false}
# type your code here.
# -
# 2\. What is the expected percentage increase in text-message rates? `hint:` compute the mean of `lambda_1_samples/lambda_2_samples`. Note that this quantity is very different from `lambda_1_samples.mean()/lambda_2_samples.mean()`.
# + jupyter={"outputs_hidden": false}
# type your code here.
# -
# 3\. What is the mean of $\lambda_1$ **given** that we know $\tau$ is less than 45. That is, suppose we have been given new information that the change in behaviour occurred prior to day 45. What is the expected value of $\lambda_1$ now? (You do not need to redo the PyMC part. Just consider all instances where `tau_samples < 45`.)
# + jupyter={"outputs_hidden": false}
# type your code here.
# -
# ### References
#
#
# - [1] Gelman, Andrew. N.p.. Web. 22 Jan 2013. [N is never large enough](http://andrewgelman.com/2005/07/31/n_is_never_larg/).
# - [2] <NAME>. 2009. [The Unreasonable Effectiveness of Data](http://static.googleusercontent.com/media/research.google.com/en//pubs/archive/35179.pdf).
# - [3] <NAME>., <NAME> and <NAME>. 2010.
# PyMC: Bayesian Stochastic Modelling in Python. Journal of Statistical
# Software, 35(4), pp. 1-81.
# - [4] <NAME> and <NAME>. Large-Scale Machine Learning at Twitter. Proceedings of the 2012 ACM SIGMOD International Conference on Management of Data (SIGMOD 2012), pages 793-804, May 2012, Scottsdale, Arizona.
# - [5] <NAME>. "Why Probabilistic Programming Matters." 24 Mar 2013. Google, Online Posting to Google . Web. 24 Mar. 2013. <https://plus.google.com/u/0/107971134877020469960/posts/KpeRdJKR6Z1>.
# + jupyter={"outputs_hidden": false}
from IPython.core.display import HTML
def css_styling():
styles = open("../styles/custom.css", "r").read()
return HTML(styles)
css_styling()
# + jupyter={"outputs_hidden": false}
| Chapter1_Introduction/Ch1_Introduction_PyMC2.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#Author: <NAME>
#Purpose: This is a program tailored to the M&M modeling project that uses a
# combination of the Bisection Method and Newton's Method in order to
# find the minimum of the least squares.
import matplotlib.pyplot as plt
from numpy import exp, array, linspace, sum
from numpy.random import random
#This will standardize all figure sizes.
plt.rcParams["figure.figsize"] = [10,6]
#Constant to determine how many bisections and recursive calls to perform.
RANGE = 20
#******************************************************************************
#0: Main.
def main():
#Fill data arrays and initialize values.
x = [a for a in range(15)]
y = [8, 13, 20, 27, 39, 46, 52, 53, 56, 59, 61, 61, 61, 61, 62]
#Carrying capacity, initial population size, initial guess for r-value.
K, p0, r = (62, 8, 1)
Plot(x,y,1)
#Set lower and upper value to r.
r_low = r_high = r
#If the derivative of the sum of squares function is already zero (i.e. we
#already have a minimum), then we are done.
if df(r, x, y, p0, K) == 0:
#Curve to fit.
Fxn = lambda t : K*p0/(p0+(K-p0)*exp(-r*t))
Plot(x,Fxn,0,1)
exit()
#Find appropriate values to use for bisection.
while df(r_low, x, y, p0, K) > 0:
r_low -= 0.5
while df(r_high, x, y, p0, K) < 0:
r_high += 0.5
#Use Bisection Method to find seed value for Newton's Method.
r = Bisect(r_low, r_high, x, y, p0, K)
#Use Newton's Method to find most accurate root value.
r = Newton(r, x, y, p0, K)
#Redifine our function with new r value.
Fxn = lambda t : K*p0/(p0+(K-p0)*exp(-r*t))
#Display values for user.
print("\nK : ", K, "\np0 : ", p0, "\nr : ", r)
print('*'*64)
Error(x, y, Fxn)
Plot(x,Fxn,0,1)
#******************************************************************************
#1: Plot data points and functions.
def Plot(x_vals, y_vals, scatter=0, show=0):
if scatter:
plt.plot(x_vals, y_vals,'ko')
else:
X = linspace(min(x_vals), max(x_vals), 300)
Y = array([y_vals(x) for x in X])
plt.plot(X, Y, 'purple')
if show:
plt.title("Logistic Model of Disease Spread")
plt.xlabel("Iteration number")
plt.ylabel("Number of Infecteds")
plt.show()
#*******************************************************************************
#2: Derivative of the sum of squares function. You are, assumedly, trying to
# locate a root of this function so as to locate the minimum of the sum of
# squares function. That being said, you will have to find the derivative
# of the sum of squares function. I tried to type it out in a way such that,
# if you would like to modify the equation, you need only mess with the lines
# between the octothorpes. AlSO BE MINDFUL OF THE LINE CONTINUATION
# CHARACTERS.
def df(r, t_val, y_val, p0, K):
return sum([\
# # # # # # # # # # # # # # TYPE YOUR FUNCTION HERE # # # # # # # # # # # # # #
-2*(y -K/(1 + exp(-r*t)*(K - p0)/p0))*K/(1 + exp(-r*t)*(K - p0)/p0)**2*t*exp( \
-r*t)*(K - p0)/p0 \
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
for t,y in zip(t_val, y_val)])
#*******************************************************************************
#3: Use the bisection method to get a nice seed value for Newton's Method.
def Bisect(lo, hi, t_val, y_val, p0, K):
for i in range(RANGE):
mid = (lo + hi) / 2.0
if df(lo, t_val, y_val, p0, K)*df(hi, t_val, y_val, p0, K) > 0:
lo = mid
else:
hi = mid
return mid
#*******************************************************************************
#4: Use Newton's Method to find accurate root value.
def Newton(r, t_val, y_val, p0, K):
for i in range(RANGE):
r -= df(r, t_val, y_val, p0, K)/ddf(r, t_val, y_val, p0, K)
return r
#******************************************************************************
#5: Calculate sum of squares error.
def Error(x, y, F):
y_p = array([F(x_i) for x_i in x])
error = 0.0
for i in range(len(y)):
error += (y[i]-y_p[i])**2
print('Error %0.10f' %error)
return error
#*******************************************************************************
#4.1: Second derivative of the sum of squares function. This is needed for
# Newton's Method. See notes above (in 2) about modifications.
def ddf(r, t_val, y_val, p0, K):
return sum([\
# # # # # # # # # # # # # # TYPE YOUR FUNCTION HERE # # # # # # # # # # # # # #
2*K**2/(1 + exp(-r*t)*(K - p0)/p0)**4*t**2*exp(-r*t)**2*(K - p0)**2/p0**2 - 4* \
(y - K/(1 + exp(-r*t)*(K - p0)/p0))*K/(1 + exp(-r*t)*(K - p0)/p0)**3*t**2* \
exp(-r*t)**2*(K-p0)**2/p0**2 + 2*(y - K/(1 + exp(-r*t)*(K - p0)/p0))*K/(1 + \
exp(-r*t)*(K-p0)/p0)**2*t**2*exp(-r*t)*(K - p0)/p0 \
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
for t,y in zip(t_val, y_val)])
#******************************************************************************
#Call main.
main()
# -
| BiNew_RF.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### This is Example 4.3. Gambler’s Problem from Sutton's book.
#
# A gambler has the opportunity to make bets on the outcomes of a sequence of coin flips.
# If the coin comes up heads, he wins as many dollars as he has staked on that flip;
# if it is tails, he loses his stake. The game ends when the gambler wins by reaching his goal of $100,
# or loses by running out of money.
#
# On each flip, the gambler must decide what portion of his capital to stake, in integer numbers of dollars.
# This problem can be formulated as an undiscounted, episodic, finite MDP.
#
# The state is the gambler’s capital, s ∈ {1, 2, . . . , 99}.
# The actions are stakes, a ∈ {0, 1, . . . , min(s, 100 − s)}.
# The reward is zero on all transitions except those on which the gambler reaches his goal, when it is +1.
#
# The state-value function then gives the probability of winning from each state. A policy is a mapping from levels of capital to stakes. The optimal policy maximizes the probability of reaching the goal. Let p_h denote the probability of the coin coming up heads. If p_h is known, then the entire problem is known and it can be solved, for instance, by value iteration.
#
import numpy as np
import sys
import matplotlib.pyplot as plt
if "../" not in sys.path:
sys.path.append("../")
#
# ### Exercise 4.9 (programming)
#
# Implement value iteration for the gambler’s problem and solve it for p_h = 0.25 and p_h = 0.55.
def value_iteration_for_gamblers(p_h, theta=0.0001, discount_factor=1.0):
"""
Args:
p_h: Probability of the coin coming up heads
"""
# The reward is zero on all transitions except those on which the gambler reaches his goal,
# when it is +1.
rewards = np.zeros(101)
rewards[100] = 1
# We introduce two dummy states corresponding to termination with capital of 0 and 100
V = np.zeros(101)
def one_step_lookahead(s, V, rewards):
"""
Helper function to calculate the value for all action in a given state.
Args:
s: The gambler’s capital. Integer.
V: The vector that contains values at each state.
rewards: The reward vector.
Returns:
A vector containing the expected value of each action.
Its length equals to the number of actions.
"""
A = np.zeros(101)
stakes = range(1, min(s, 100-s)+1) # Your minimum bet is 1, maximum bet is min(s, 100-s).
for a in stakes:
# rewards[s+a], rewards[s-a] are immediate rewards.
# V[s+a], V[s-a] are values of the next states.
# This is the core of the Bellman equation: The expected value of your action is
# the sum of immediate rewards and the value of the next state.
A[a] = p_h * (rewards[s+a] + V[s+a]*discount_factor) + (1-p_h) * (rewards[s-a] + V[s-a]*discount_factor)
return A
while True:
# Stopping condition
delta = 0
# Update each state...
for s in range(1, 100):
# Do a one-step lookahead to find the best action
A = one_step_lookahead(s, V, rewards)
# print(s,A,V) # if you want to debug.
best_action_value = np.max(A)
# Calculate delta across all states seen so far
delta = max(delta, np.abs(best_action_value - V[s]))
# Update the value function. Ref: Sutton book eq. 4.10.
V[s] = best_action_value
# Check if we can stop
if delta < theta:
break
# Create a deterministic policy using the optimal value function
policy = np.zeros(100)
for s in range(1, 100):
# One step lookahead to find the best action for this state
A = one_step_lookahead(s, V, rewards)
best_action = np.argmax(A)
# Always take the best action
policy[s] = best_action
return policy, V
# +
policy, v = value_iteration_for_gamblers(0.25)
print("Optimized Policy:")
print(policy)
print("")
print("Optimized Value Function:")
print(v)
print("")
# -
# ### Show your results graphically, as in Figure 4.3.
#
# +
# Plotting Final Policy (action stake) vs State (Capital)
# x axis values
x = range(100)
# corresponding y axis values
y = v[:100]
# plotting the points
plt.plot(x, y)
# naming the x axis
plt.xlabel('Capital')
# naming the y axis
plt.ylabel('Value Estimates')
# giving a title to the graph
plt.title('Final Policy (action stake) vs State (Capital)')
# function to show the plot
plt.show()
# +
# Plotting Capital vs Final Policy
# x axis values
x = range(100)
# corresponding y axis values
y = policy
# plotting the bars
plt.bar(x, y, align='center', alpha=0.5)
# naming the x axis
plt.xlabel('Capital')
# naming the y axis
plt.ylabel('Final policy (stake)')
# giving a title to the graph
plt.title('Capital vs Final Policy')
# function to show the plot
plt.show()
| DP/Gamblers Problem Solution.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## PyTorch Tutorial
#
# IFT6135 – Representation Learning
#
# A Deep Learning Course, January 2019
#
# By <NAME>
#
# (Adapted from <NAME>'s MILA welcome tutorial)
# ## 1. Introduction to the torch tensor library
# ### Torch's numpy equivalent with GPU support
import numpy as np
from __future__ import print_function
import torch
# ### Initialize a random tensor
torch.Tensor(5, 3)
# ### From a uniform distribution
# intialization
print(torch.Tensor(5, 3).uniform_(-1, 1))
# sampling
print(torch.rand(5,3)*2-1)
# ### Get it's shape
# +
x = torch.Tensor(5, 3).uniform_(-1, 1)
print(x.size())
# or your favorite np_array.shape
print(x.shape)
# dimensionality of the 0'th axis?
# print(???)
print(x.size(0))
print(x.shape[0])
# -
# ### Tensor Types
# source: http://pytorch.org/docs/master/tensors.html
# |Data type |Tensor|
# |----------|------|
# |32-bit floating point| torch.FloatTensor|
# |64-bit floating point| torch.DoubleTensor|
# |16-bit floating point| torch.HalfTensor|
# |8-bit integer (unsigned)|torch.ByteTensor|
# |8-bit integer (signed)|torch.CharTensor|
# |16-bit integer (signed)|torch.ShortTensor|
# |32-bit integer (signed)|torch.IntTensor|
# |64-bit integer (signed)|torch.LongTensor|
# ### Creation from lists & numpy
z = torch.LongTensor([[1, 3], [2, 9]])
print(z.type())
# Cast to numpy ndarray
print(z.numpy().dtype)
z_ = torch.LongTensor([[1, 3], [2, 9]])
z+z_
# Data type inferred from numpy
print(torch.from_numpy(np.random.rand(5, 3)).type())
print(torch.from_numpy(np.random.rand(5, 3).astype(np.float32)).type())
print(torch.from_numpy(np.random.rand(5, 3)).float().dtype)
# +
# examples of type error
a = torch.randn(1) # x ~ N(0,1)
b = torch.from_numpy(np.ones(1)).float()
x+b
# -
# ### Simple mathematical operations
y = x ** torch.randn(5, 3)
print(y)
# +
noise = torch.randn(5, 3)
y = x / torch.sqrt(noise ** 2)
# equal to torch.abs
y_ = x / torch.abs(noise)
print(y)
print(y_)
# -
# ### Broadcasting
print(x.size())
print(x)
#y = x + torch.arange(5).view(5,1)
y = x + torch.arange(3)
print(y)
# print(x + torch.arange(5))
# ### Reshape
y = torch.randn(5, 10, 15)
print(y.size())
print(y.view(-1, 15).size()) # Same as doing y.view(50, 15)
print(y.view(-1, 15).unsqueeze(1).size()) # Adds a dimension at index 1.
print(y.view(-1, 15).unsqueeze(1).unsqueeze(2).unsqueeze(3).squeeze().size())
# If input is of shape: (Ax1xBxCx1xD)(Ax1xBxCx1xD) then the out Tensor will be of shape: (AxBxCxD)(AxBxCxD)
print()
print(y.transpose(0, 1).size())
print(y.transpose(1, 2).size())
print(y.transpose(0, 1).transpose(1, 2).size())
print(y.permute(1, 2, 0).size())
# ### Repeat
print(y.view(-1, 15).unsqueeze(1).expand(50, 100, 15).size())
print(y.view(-1, 15).unsqueeze(1).expand_as(torch.randn(50, 100, 15)).size())
# don't confuse it with tensor.repeat ...
print(y.view(-1, 15).unsqueeze(1).repeat(50,100,1).size())
# ### Concatenate
# +
# 2 is the dimension over which the tensors are concatenated
print(torch.cat([y, y], 2).size())
# stack concatenates the sequence of tensors along a new dimension.
print(torch.stack([y, y], 0).size())
# Q: how to do tensor.stack using cat?
print(torch.cat([y[None], y[None]], 0).size())
# -
# ### Advanced Indexing
# +
y = torch.randn(2, 3, 4)
print(y[[1, 0, 1, 1]].size())
# PyTorch doesn't support negative strides yet so ::-1 does not work.
rev_idx = torch.arange(1, -1, -1).long()
print(rev_idx)
print(y[rev_idx].size())
# gather(input, dim, index)
v = torch.arange(12).view(3,4)
print(v.shape)
print(v)
# [0,1,2,3]
# [4,5,6,7]
# [8,9,10,11]
# want to return [1,6,8]
print(torch.gather(v, 1, torch.tensor([1,2,0]).long().unsqueeze(1)))
# -
# ### GPU support
x = torch.cuda.HalfTensor(5, 3).uniform_(-1, 1)
y = torch.cuda.HalfTensor(3, 5).uniform_(-1, 1)
torch.matmul(x, y)
# ### Move tensors on the CPU -> GPU
x = torch.FloatTensor(5, 3).uniform_(-1, 1)
print(x)
x = x.cuda(device=0)
print(x)
x = x.cpu()
print(x)
# ### Contiguity in memory
# +
x = torch.FloatTensor(5, 3).uniform_(-1, 1)
print(x)
#x = x.cuda(device=0)
print(x)
print('Contiguity : %s ' % (x.is_contiguous()))
x = x.unsqueeze(0).expand(30, 5, 3)
print('Contiguity : %s ' % (x.is_contiguous()))
x = x.contiguous()
print('Contiguity : %s ' % (x.is_contiguous()))
# -
| pytorch/1. The Torch Tensor Library and Basic Operations.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# <img src="joke.png"
# height=500
# width= 500
# alt="Example Visualization of a Snapshot (aggregated) Prediction Model"
# title="Snapshot Variable Prediction Model" />
# + [markdown] slideshow={"slide_type": "slide"}
# ### an important note before we start:
#
# <img src="model_comparison.png"
# height=500
# width= 500
# alt="Example Visualization of a Snapshot (aggregated) Prediction Model"
# title="Snapshot Variable Prediction Model" />
#
#
# sometimes a fancy algorithm can make a big impact, but often the difference between a well tuned simple and complex algorithm is not that high.
#
# Fancy algorithms don't magically make perfect predictions. The legwork done before and after model building is often the most important
#
# ------
# -
# + [markdown] slideshow={"slide_type": "slide"}
# # Now, lets learn about fancy algorithms: Random Forest and Gradient Boosted Trees
# * necessary background:
# * CART trees
# * bagging
# * ensembling
# * gradient boosting
# --------
# + [markdown] slideshow={"slide_type": "slide"}
# # Classification And Regression Trees (CART): glorified if/then statements
# ### example tree:
# <img src="Example_Decision_Tree.png"
# height=500
# width= 500
# alt="Example Visualization of a Snapshot (aggregated) Prediction Model"
# title="Snapshot Variable Prediction Model" />
#
# ### written as a rulebased classifier:
# 1. If Height > 180 cm Then Male
# 1. If Height <= 180 cm AND Weight > 80 kg Then Male
# 1. If Height <= 180 cm AND Weight <= 80 kg Then Female
# 1. Make Predictions With CART Models
# + [markdown] slideshow={"slide_type": "subslide"}
#
# * A final fitted CART model divides the predictor (x) space by successively splitting into rectangular regions and models the response (Y) as constant over each region
# * can be schematically represented as a "tree":
# * each interior node of the tree indicates on which predictor variable you split and where you split
# * each terminal node (aka leaf) represents one region and indicates the value of the predicted response in that region
#
# <br>
# + [markdown] slideshow={"slide_type": "slide"}
# ### CART Math: for those who want to take a simple idea and make it confusing
#
# we can write the equation of a regression tree as: $Y = g(X, \theta) + \epsilon$
#
# where: <br> $g(X;\theta)= \sum^M_{m=1}I(x \in R_m)$
#
#
# * $M$ = total number of regions (terminal nodes)
# * $R_m$ = $m$th region
# * $I(x \in R_m)$ = indicator function = $\{ \begin{array}{lr} 1:x \in R_m \\ 0:x \notin R_m \end{array} $
# * $c_m$ =constant predictor over Rm
# * $\theta$ = all parameters and structure (M, splits in Rm’s, cm’s, etc)
#
#
# #### illustration of tree for $M=6$ regions, $k=2$ predictors, and $n=21$ training observations
# <img src="CART3.png"
# height=500
# width= 500
# alt="Example Visualization of a Snapshot (aggregated) Prediction Model"
# title="Snapshot Variable Prediction Model" />
#
# + [markdown] slideshow={"slide_type": "subslide"}
# ### in more simple terms: a CART tree defines regions of the predictor space to correspond to a predicted outcome value
# * when fitting a CART tree, the model grows one tree node at a time
# * at each split, the tree defines boundaries in predictor space based on what REDUCES THE TRAINING ERROR THE MOST
# * stops making splits when the reduction in error falls below a threshold
# * branches can be pruned (ie nodes/boundaries removed)to reduce overfitting
# + [markdown] slideshow={"slide_type": "slide"}
# **example**: $GPA = g((HSrank, ACTscore), \theta) + \epsilon$
#
# <img src="CART2.png"
# height=800
# width= 800
# alt="Example Visualization of a Snapshot (aggregated) Prediction Model"
# title="Snapshot Variable Prediction Model" />
# + [markdown] slideshow={"slide_type": "slide"}
# # Why use a CART?
# * easy to interpret
# * handle categorical variables intuitively
# * computationally efficient
# * have reasonable predictive performance
# * not sensitive to MONOTONIC transformations (ie anything that preserves the order of a set, like log scaling).
# * form the basis for many commonly used algorithms
#
# + [markdown] slideshow={"slide_type": "slide"}
# --------
# # Next Background: Ensembling or Ensemble Learning
#
# * Ensemble: use multiple learning algorithms to obtain better predictive performance than could be obtained from any of the constituent learning algorithms alone.
# * A Machine Learning ensemble:
# * use multiple learning algorithms to obtain better predictive performance than a single learning algorithm alone.
# * concrete finite set of alternative models
# * but allows for much more flexible structure to exist among those
#
#
# + [markdown] slideshow={"slide_type": "slide"}
# --------
# # More Background: Ensembling, Bootstrapping & Bagging
#
# * **Ensemble** (in machine learning) :
# * use multiple learning algorithms to obtain better predictive performance than a single learning algorithm alone.
# * concrete finite set of alternative models
# * but allows for much more flexible structure to exist among those
#
#
# * **Bootstrapping**:
# * ~sampling WITH replacement
# + [markdown] slideshow={"slide_type": "slide"}
# * **Bagging**: (bootstrapping and aggregating)
# * a type of ensembling
# * designed to improve stability & accuracy of some ML algorithms
# * algorithm:
# 1. bootstrap many different sets from your training data
# 1. fit a model to each
# 1. average the predicted output (for regression) or voting (for classification) from bootstraped models across x values.
#
#
# **example**:
# * for $b= 1, 2, ..., B$: (aka: for i in range(1,B))
# * generate bootstrap sample of size n (ie sample B with replacement n times)
# * fit model (any kind) $g(x;\hat\theta^b)$
# * repeat for specified # of bootstraps
# * take y at each value of x as the average responce of each of the boostrapped models: $\hat y(x) = \frac{1}{B}\Sigma^B_{b=1}g(x;\hat\theta^b)$
#
# + [markdown] slideshow={"slide_type": "slide"}
# **Visualizations**:
# visualization for bagging ensemble (source: KDnuggets)
#
# <img src="bagged_ensemble.jpg"
# height=500
# width= 400
# alt="source KDNuggets"
# title="Snapshot Variable Prediction Model" />
#
#
# plotting boostrapped and bagged models: (source: Wikipedia)
#
# <img src="bagging_models.png"
# height=300
# width= 300
# alt="source: wikipedia"
# title="Snapshot Variable Prediction Model" />
#
# + [markdown] slideshow={"slide_type": "slide"}
# ### when is bagging useful:
# * For predictors where fitting is unstable (i.e., a small change in the data gives a very different fitted model) and/or the structure is such that the sum of multiple predictors no longer has the same structure
#
# ### when does bagging have no effect:
# * For predictors that are linear ($\hat y$ a linear function of training $y$)
#
#
#
# -
#
# + [markdown] slideshow={"slide_type": "slide"}
# -----
# # Random Forest: leveraging the wisdom of crowds
#
# * general idea: grow a bunch of different CART trees and let them all vote to get the prediction
#
# * Algorithm detail:
# 1. draw a bootstrap sample $Z^*$ of size $N$ from the training data
# 1. grow a CART tree $T_b$ to the bootstrapped data by recursively repeating the following steps for each terminal node until the minimum node size $n_min$ is reached:
# 1. randomly select $m$ predictor variables
# 1. pick the best variable/spit-point (aka boundary) for the $m$ predictor variables
# 1. split the node into two daughter nodes
# 1. output the ensemble of trees ${T_b}^B_1$.
#
# * make a prediction by taking majority vote (classification) or averaging prediction from each tree (regression)
#
# * in more simple terms: grow and train a lot of CART trees with a maximum size, each using randomly sampled observations (with replacement) and predictor variables (without replacement).
# + [markdown] slideshow={"slide_type": "slide"}
# Random forest simplified (source: towards data science blog)
#
# <img src="rf_vis.png"
# height=500
# width= 500
# alt="source: wikipedia"
# title="Snapshot Variable Prediction Model" />
# + [markdown] slideshow={"slide_type": "slide"}
# -----
# # Gradient boosting: leveraging the stupidity of crowds
#
# * **Boosting**:
# * a type of ensembling that turns a set of weak learners (ie predictors that are slightly better than chance) into a strong learner
# * many different types of algorithms that achieve boosting
#
# * **Gradient Boosting** :
# * Like other boosting methods, gradient boosting combines weak "learners" into a single strong learner in an iterative fashion.
# stated two different ways:
# * ensembles simple/weak CART trees in a stage-wise fashion and generalizes them by allowing optimization of an arbitrary differentiable loss function.
# * boosting sequentially fits simple/weak CART trees to the residuals from the previous iteration, taking the final model to be the sum of the individual models from each iteration
#
#
# explaining in the least-square regression setting:
# * goal: "teach" a model $F$ to predict values of the form $\hat y=F(x)$ by minimizing the mean squared error $\frac{1}{n}\sum_i (\hat y_i - y_i)^2$, where i indexes over some training set of size n.
# * at each iteration $m$, $1\leq m \leq M$, it may be assumed that there is some imperfect model $F_m$ (usually starts with just mean y).
# * in each iteration, the algorithm improves on $F_m$ by constructing a new model that adds an estimator $h$ to make it better: $F_{m+1}(x)= F_m(x) + h(x)$
# * a perfect $h$ implies that $F_{m+1}(x)= F_m(x) + h(x)=y$ or $ h(x) = y - F_m(x)$
# * thus, gradient boosting will fit $h$ to the **residual** $y-F_m(x)$.
# * in each iteration, $F_{m+1}$ attemps to correct the errors of it's predecessor $F_m$.
#
# to generalize this, we can observe that residuals $y- F(x)$ for a given model are the **negative gradients** (with respect to $F(x)$) of the squared error loss function $\frac{1}{2}(y-F(x))^2$
#
# + [markdown] slideshow={"slide_type": "slide"}
# for those of you who want the maths:
#
# <img src="gbm_algorithm.png"
# height=800
# width= 800
# alt="source: wikipedia"
# title="Snapshot Variable Prediction Model" />
#
# <br>
#
# for those of you who want pictures:
#
# <img src="gbm_vis.png"
# height=800
# width= 800
# alt="source: wikipedia"
# title="Snapshot Variable Prediction Model" />
#
# -
# + [markdown] slideshow={"slide_type": "slide"}
# -----
# # final thoughts about RandomForest and GBM
#
# * overfitting is definitely a thing with these models, so understanding some parameters is important.
#
#
# ### RF
# * tree size (depth) = big deal, larger trees = more likely to overfit
# * more trees = not that big of a deal. they make the out of bag error plot looks smoother
#
# ### GBM
# * tree size isn't that big of a deal, (smaller trees mean you can still capture error in next tree)
# * more trees = more likely to overfit. too many trees = the out of bag error look more U shaped.
#
# ### both algorithms:
# * neither alrogithm handles heavily imballanced classes very well (this can be an entire lecture on it's own)
# * both inherit all of the benefits of regular CART trees
# * both are better at regression than CART trees
# * both handle much more complex non-linear relationships between predictor and responce
# * both are capable of capturing **SOME** higher order predictor interactions, but these are often masked by marginal effects and cannot be differentiated from them. (ongoing research into this)
# -
import os
os.getcwd()
# +
import nbconvert
import nbformat
with open('hsip442/hsip442_algorithms_lecture.ipynb') as nb_file:
nb_contents = nb_file.read()
# Convert using the ordinary exporter
notebook = nbformat.reads(nb_contents, as_version=4)
exporter = nbconvert.HTMLExporter()
body, res = exporter.from_notebook_node(notebook)
# Create a dict mapping all image attachments to their base64 representations
images = {}
for cell in notebook['cells']:
if 'attachments' in cell:
attachments = cell['attachments']
for filename, attachment in attachments.items():
for mime, base64 in attachment.items():
images[f'attachment:{filename}'] = f'data:{mime};base64,{base64}'
# Fix up the HTML and write it to disk
for src, base64 in images.items():
body = body.replace(f'src="{src}"', f'src="{base64}"')
with open('my_notebook.html', 'w') as output_file:
output_file.write(body)
# -
# * **Stacking**: another type of ensembling
# 1. fit a number of different models to the entire training data ($g_m(x,\hat\theta^m)$)
# 2. take a linear combination (i.e. weighted average) of the models as the predictor($x$), using linear regression to determine the coefficients ($\theta$), with the consituent models ($g(x,\theta)$) as the basis function:
# * $\hat y(x) = \sum^M_{m=1}\hat \beta_m g_m(X,\hat\theta^m)$
# * linear regression: $\hat y(x)= \beta_0+ \sum^n_{i=1}\beta_i X$
| notebooks/hsip442/hsip442_algorithms_lecture-Copy1.ipynb |