|
--- |
|
base_model: Qwen/Qwen2.5-Math-1.5B-Instruct |
|
language: |
|
- en |
|
pipeline_tag: text-generation |
|
tags: |
|
- chat |
|
quantized_by: mukel |
|
license: apache-2.0 |
|
license_link: https://huggingface.co/Qwen/Qwen2.5-Math-1.5B-Instruct/blob/main/LICENSE |
|
--- |
|
|
|
> [!Warning] |
|
> <div align="center"> |
|
> <b> |
|
> 🚨 Qwen2.5-Math mainly supports solving English and Chinese math problems through CoT and TIR. We do not recommend using this series of models for other tasks. |
|
> </b> |
|
> </div> |
|
|
|
# GGUF models for qwen2.java |
|
Pure .gguf Q4_0 and Q8_0 quantizations of Qwen 2.5 models, ready to consume by `qwen2.java`. |
|
|
|
In the wild, Q8_0 quantizations are fine, but Q4_0 quantizations are rarely pure e.g. the token embeddings are quantized with Q6_K, instead of Q4_0. |
|
A pure Q4_0 quantization can be generated from a high precision (F32, F16, BFLOAT16) .gguf source with the llama-quantize utility from llama.cpp as follows: |
|
``` |
|
./llama-quantize --pure ./Qwen-2.5-7B-Instruct-BF16.gguf ./Qwen-2.5-7B-Instruct-Q4_0.gguf Q4_0 |
|
``` |
|
|
|
## Introduction |
|
|
|
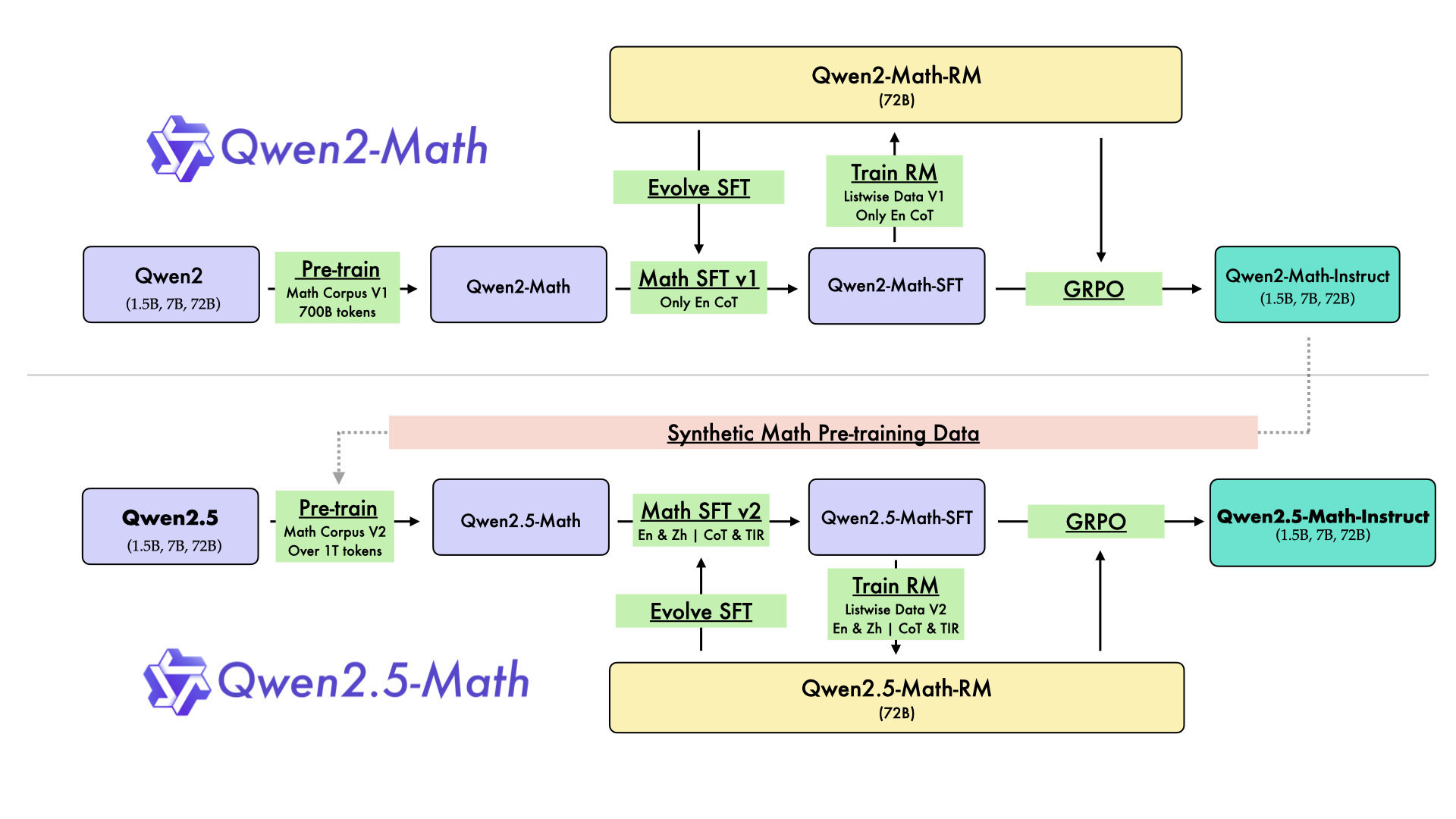
In August 2024, we released the first series of mathematical LLMs - [Qwen2-Math](https://qwenlm.github.io/blog/qwen2-math/) - of our Qwen family. A month later, we have upgraded it and open-sourced **Qwen2.5-Math** series, including base models **Qwen2.5-Math-1.5B/7B/72B**, instruction-tuned models **Qwen2.5-Math-1.5B/7B/72B-Instruct**, and mathematical reward model **Qwen2.5-Math-RM-72B**. |
|
|
|
Unlike Qwen2-Math series which only supports using Chain-of-Thught (CoT) to solve English math problems, Qwen2.5-Math series is expanded to support using both CoT and Tool-integrated Reasoning (TIR) to solve math problems in both Chinese and English. The Qwen2.5-Math series models have achieved significant performance improvements compared to the Qwen2-Math series models on the Chinese and English mathematics benchmarks with CoT. |
|
 |
|
|
|
While CoT plays a vital role in enhancing the reasoning capabilities of LLMs, it faces challenges in achieving computational accuracy and handling complex mathematical or algorithmic reasoning tasks, such as finding the roots of a quadratic equation or computing the eigenvalues of a matrix. TIR can further improve the model's proficiency in precise computation, symbolic manipulation, and algorithmic manipulation. Qwen2.5-Math-1.5B/7B/72B-Instruct achieve 79.7, 85.3, and 87.8 respectively on the MATH benchmark using TIR. |
|
|
|
## Model Details |
|
|
|
|
|
For more details, please refer to our [blog post](https://qwenlm.github.io/blog/qwen2.5-math/) and [GitHub repo](https://github.com/QwenLM/Qwen2.5-Math). |
|
|
|
|