nvidia/AceMath-1.5B-Instruct

Introduction

We introduce AceMath, a family of frontier models designed for mathematical reasoning. The models in AceMath family, including AceMath-1.5B/7B/72B-Instruct and AceMath-7B/72B-RM, are Improved using Qwen. The AceMath-1.5B/7B/72B-Instruct models excel at solving English mathematical problems using Chain-of-Thought (CoT) reasoning, while the AceMath-7B/72B-RM models, as outcome reward models, specialize in evaluating and scoring mathematical solutions.

The AceMath-1.5B/7B/72B-Instruct models are developed from the Qwen2.5-Math-1.5B/7B/72B-Base models, leveraging a multi-stage supervised fine-tuning (SFT) process: first with general-purpose SFT data, followed by math-specific SFT data. We are releasing all training data to support further research in this field.

We only recommend using the AceMath models for solving math problems. To support other tasks, we also release AceInstruct-1.5B/7B/72B, a series of general-purpose SFT models designed to handle code, math, and general knowledge tasks. These models are built upon the Qwen2.5-1.5B/7B/72B-Base.

For more information about AceMath, check our website and paper.

All Resources

AceMath Instruction Models

• AceMath-1.5B-Instruct, AceMath-7B-Instruct, AceMath-72B-Instruct

AceMath Reward Models

• AceMath-7B-RM, AceMath-72B-RM

Evaluation & Training Data

• AceMath-RewardBench, AceMath-Instruct Training Data, AceMath-RM Training Data

General Instruction Models

• AceInstruct-1.5B, AceInstruct-7B, AceInstruct-72B

Benchmark Results (AceMath-Instruct + AceMath-72B-RM)

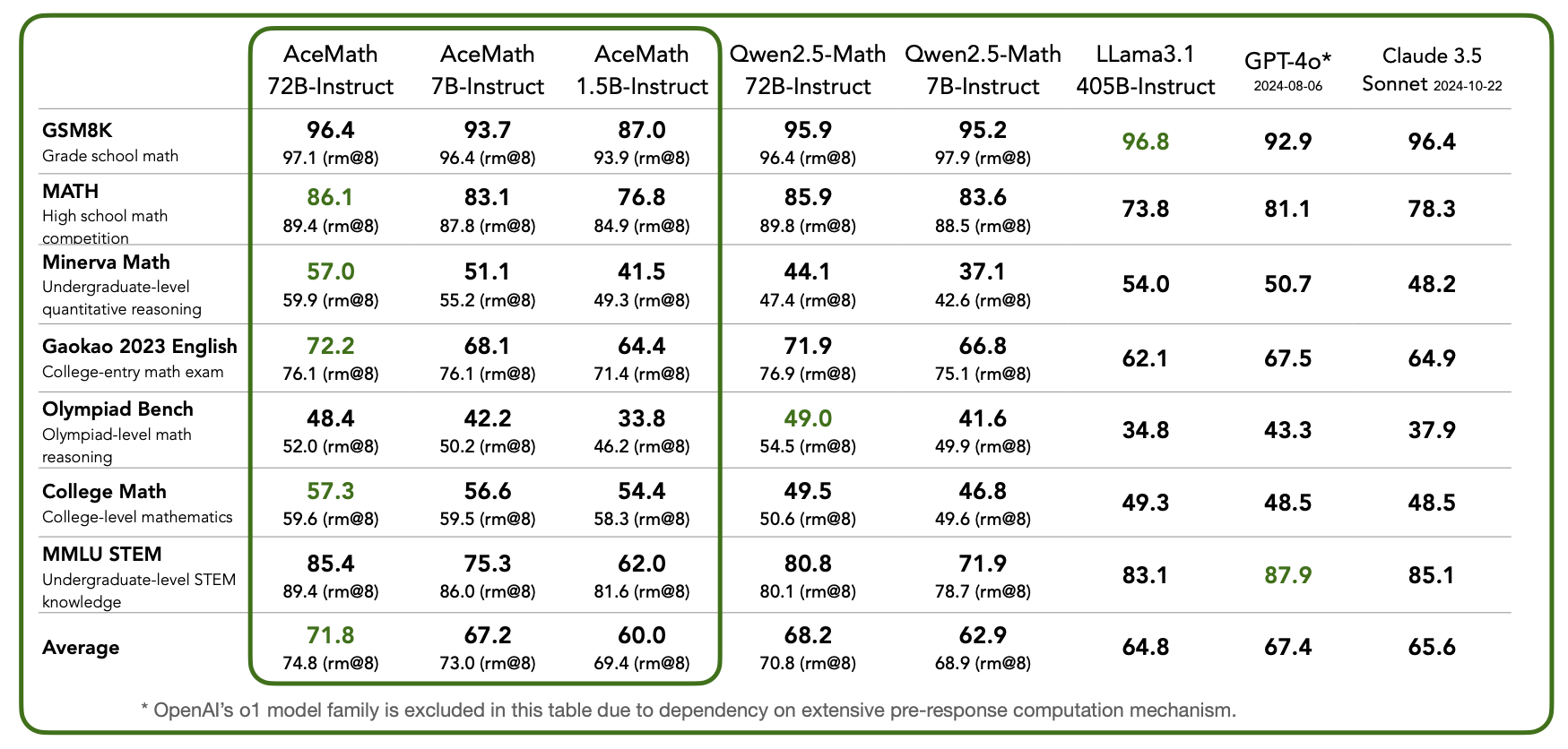
We compare AceMath to leading proprietary and open-access math models in above Table. Our AceMath-7B-Instruct, largely outperforms the previous best-in-class Qwen2.5-Math-7B-Instruct (Average pass@1: 67.2 vs. 62.9) on a variety of math reasoning benchmarks, while coming close to the performance of 10× larger Qwen2.5-Math-72B-Instruct (67.2 vs. 68.2). Notably, our AceMath-72B-Instruct outperforms the state-of-the-art Qwen2.5-Math-72B-Instruct (71.8 vs. 68.2), GPT-4o (67.4) and Claude 3.5 Sonnet (65.6) by a margin. We also report the rm@8 accuracy (best of 8) achieved by our reward model, AceMath-72B-RM, which sets a new record on these reasoning benchmarks. This excludes OpenAI’s o1 model, which relies on scaled inference computation.

How to use

from transformers import AutoModelForCausalLM, AutoTokenizer

model_name = "nvidia/AceMath-1.5B-Instruct"
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(model_name, torch_dtype="auto", device_map="auto")

prompt = "Jen enters a lottery by picking $4$ distinct numbers from $S=\\{1,2,3,\\cdots,9,10\\}.$ $4$ numbers are randomly chosen from $S.$ She wins a prize if at least two of her numbers were $2$ of the randomly chosen numbers, and wins the grand prize if all four of her numbers were the randomly chosen numbers. The probability of her winning the grand prize given that she won a prize is $\\tfrac{m}{n}$ where $m$ and $n$ are relatively prime positive integers. Find $m+n$."
messages = [{"role": "user", "content": prompt}]

text = tokenizer.apply_chat_template(
    messages,
    tokenize=False,
    add_generation_prompt=True
)
model_inputs = tokenizer([text], return_tensors="pt").to("cuda")

generated_ids = model.generate(
    **model_inputs,
    max_new_tokens=2048
)
generated_ids = [
    output_ids[len(input_ids):] for input_ids, output_ids in zip(model_inputs.input_ids, generated_ids)
]

response = tokenizer.batch_decode(generated_ids, skip_special_tokens=True)[0]

Correspondence to

Zihan Liu (zihanl@nvidia.com), Yang Chen (yachen@nvidia.com), Wei Ping (wping@nvidia.com)

Citation

If you find our work helpful, we’d appreciate it if you could cite us.

@article{acemath2024,
  title={AceMath: Advancing Frontier Math Reasoning with Post-Training and Reward Modeling},
  author={Liu, Zihan and Chen, Yang and Shoeybi, Mohammad and Catanzaro, Bryan and Ping, Wei},
  journal={arXiv preprint},
  year={2024}
}

License

All models in the AceMath family are for non-commercial use only, subject to Terms of Use of the data generated by OpenAI. We put the AceMath models under the license of Creative Commons Attribution: Non-Commercial 4.0 International.