uuid
stringlengths 36
36
| subject
stringclasses 6
values | has_image
bool 2
classes | image
stringclasses 160
values | problem_statement
stringlengths 32
784
| golden_answer
stringlengths 7
1.13k
|
|---|---|---|---|---|---|
00143e2e-2d9f-4fc3-a9c5-9d2e6aba5cba
|
multivariable_calculus
| false
| null |
Determine the coordinates, if any, for which $f(x,y) = 6 \cdot x^2 - 3 \cdot x^2 \cdot y + y^3 + 12$ has
1. a Relative Minimum(s)
2. a Relative Maximum(s)
3. a Saddle Point(s)
If a Relative Minimum or Maximum, find the Minimum or Maximum value. If none, enter None.
|
1. The function $f(x,y)$ has Relative Minimum(s) at None with the value(s) None
2. The function $f(x,y)$ has Relative Maximum(s) at None with the value(s) None
3. The function $f(x,y)$ has a Saddle Point(s) at $P(-2,2)$, $P(2,2)$
|
00282b7b-1bf6-415d-9f17-d04e9c9700e2
|
precalculus_review
| true
|
data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAdAAAAGoCAYAAAD2LLSsAAAYU2lDQ1BJQ0MgUHJvZmlsZQAAeJyVeQVUVF8X77mTzDAM3d0l3SAxdHeDwNAdQ4NKioSKIKCUCioIIliEiIUgooigAgYiYVAqqKAIyLuEfv/v/6313npn1rn3N/vss+PsU3sGAM5UcmRkKIIOgLDwGIqtkS6fs4srH/YdgAAO/ggBEbJPdCTJ2tocwOXP+7/L8jDMDZdnUpuy/rf9/1roff2ifQCArGHs7RvtEwbjawCgMn0iKTEAYFRhumB8TOQmdocxEwU2EMaRmzhgG2duYu9tfGKLx95WD8YNAFARyGRKAADENpjOF+cTAMshvoDbGMJ9g8Jh1nkYa/kEkn0B4NwF8+wKC4vYxM4wFvP+h5yA/5Lp/VcmmRzwF2/7slWo9IOiI0PJif+fw/H/LmGhsX90iMCVEEgxtt30GR63FyERZpuYAOP5cG9LKxgzwPhnkO8WP4wR+MBYY4dtfgSXT7QePGaABcayvmR9MxhzwdgwPNTSfIfu7R9kaAJjeIYgEoJiTOx3+mb7RRvY7cisoETYWv3B/hQ90k7fRjJlS+8mf1dsiANpR/6LQD+TP/K/JwXaO23bjMTHBTlawpgIY5boEDuzbR6kUFKgnuUfHkqs7ab9QjBW9ws30t2Wj/Twpxja7vBTwqL/+IvMDgwysdzBZTGB9sY7chp8yFv2s8G4zS+c5PBHjl+0s/kfX3z99A22fUcO+IU77PiLHI+M0bXd6fs1MtR6hx+F9ws12qQLwJgrOs5upy9KKwaekNvyUZaRMdb223aivIPJptbb9qASgDnQA/qAD8TC1RtEgGAQ1D/fOg9/224xBGRAAQHAD0jtUP70cNpqCYefdiAJfIKRH4j+2093q9UPxMH09b/U7acU8N9qjdvqEQI+wDgMmIFQ+HvsVq/wv9ocwTuYEvQ/2n1gW0Phutn2vzQSTDHfocT+kctH+4cTY4DRxxhjDDHiKA6UFkoDZQ4/deAqj1JFqf2x9j/86A/oQfQkegg9jn7pGZRO+Zc/fMACjMMaDHd89v6nzygRWKoSShelCcuHZaNYUBxACqUIayKhtGHdSjBVb8fyTe//Lfu/fPjHqO/w4WRxCBwrTgcn9u+eRAmi0l8pm2P6zxHattX777jq/W35t369f4y0L/w2+zcnMht5FdmDvIvsRXYgWwEf8jayDdmHvLmJ/86id1uz6I822y17QmA5Qf+jj7yjc3Mko2UvyM7Irm23xfglxGwuML2IyERKUEBgDB8J3vn9+EzCfaR38cnLyssCsHmObG9T32y3zgeI5cl/aH7TAOyG1wZu4D+04GMA1HcDwJr7H5qIGwDs8L58+alPLCVum4bafKABHtDCK4od8ABBIAb7Iw+UgQbQAQbAFFgBe+ACPOBRDoTnMwXEg70gDWSBPHAUFIMycAqcAefBRXAFtIIOcBfcB4/AABgCr+HZ8x7MgQWwDFYhCMJCNBAjxA7xQsKQJCQPqUJakAFkDtlCLpAXFACFQ7HQXigDyoMKoTKoCqqDLkPXobtQLzQIvYQmoBnoK/QLgUQQEEwIboQIQgahiiAhzBD2iD2IAEQUIgmRiTiCOIGoRjQgWhB3EY8QQ4hxxBxiCQmQ1EgWJD9SCqmK1ENaIV2R/kgKcj8yF1mCrEY2ItvhOD9DjiPnkSsoDIoRxYeSgmewMcoB5YOKQu1HHUKVoc6jWlBdqGeoCdQC6jeaBs2FlkSro03QzugAdDw6C12CrkE3o7vh1fQevYzBYFgwohgVeDW6YIIxyZhDmEpME+YOZhAzhVnCYrHsWEmsJtYKS8bGYLOwpdgG7G3sU+x77E8qaipeKnkqQypXqnCqdKoSqnqqW1RPqT5SreLocMI4dZwVzheXiMvHncW1457g3uNW8fR4Ubwm3h4fjE/Dn8A34rvxo/hv1NTUAtRq1DbUQdSp1CeoL1E/oJ6gXiEwECQIegR3QizhCKGWcIfwkvCNhoZGhEaHxpUmhuYITR3NPZoxmp9ERqI00YToS0whlhNbiE+Jn2lxtMK0JFoP2iTaEtqrtE9o5+lwdCJ0enRkuv105XTX6UbolugZ6eXorejD6A/R19P30k8zYBlEGAwYfBkyGc4w3GOYYkQyCjLqMfowZjCeZexmfM+EYRJlMmEKZspjusjUz7TAzMCsyOzInMBcznyTeZwFySLCYsISypLPcoVlmOUXKzcridWPNYe1kfUp6w82TjYdNj+2XLYmtiG2X+x87AbsIewF7K3sbzhQHBIcNhzxHCc5ujnmOZk4NTh9OHM5r3C+4kJwSXDZciVzneHq41ri5uE24o7kLuW+xz3Pw8KjwxPMU8Rzi2eGl5FXizeIt4j3Nu8sHzMfiS+U7wRfF98CPxe/MX8sfxV/P/+qgKiAg0C6QJPAG0G8oKqgv2CRYKfgghCvkIXQXqELQq+EccKqwoHCx4V7hH+IiIo4iRwUaRWZFmUTNRFNEr0gOipGI6YtFiVWLfZcHCOuKh4iXik+IIGQUJIIlCiXeCKJkFSWDJKslBzchd6ltit8V/WuESmCFEkqTuqC1IQ0i7S5dLp0q/RnGSEZV5kCmR6Z37JKsqGyZ2VfyzHImcqly7XLfZWXkPeRL5d/rkCjYKiQotCmsKgoqeineFLxhRKjkoXSQaVOpXVlFWWKcqPyjIqQipdKhcqIKpOqteoh1QdqaDVdtRS1DrUVdWX1GPUr6l80pDRCNOo1pneL7vbbfXb3lKaAJlmzSnNci0/LS+u01rg2vzZZu1p7UkdQx1enRucjSZwUTGogfdaV1aXoNuv+0FPX26d3Rx+pb6Sfq99vwGDgYFBmMGYoYBhgeMFwwUjJKNnojjHa2My4wHjEhNvEx6TOZMFUxXSfaZcZwczOrMxs0lzCnGLeboGwMLU4ZjFqKWwZbtlqBaxMrI5ZvbEWtY6yvmGDsbG2Kbf5YCtnu9e2x47RztOu3m7ZXtc+3/61g5hDrEOnI62ju2Od4w8nfadCp3FnGed9zo9cOFyCXNpcsa6OrjWuS24GbsVu792V3LPch/eI7knY0+vB4RHqcdOT1pPsedUL7eXkVe+1RrYiV5OXvE28K7wXfPR8jvvM+er4FvnO+Gn6Ffp99Nf0L/SfDtAMOBYwE6gdWBI4H6QXVBa0GGwcfCr4R4hVSG3IRqhTaFMYVZhX2PVwhvCQ8K4InoiEiMFIycisyPEo9ajiqAWKGaUmGoreE90WwwRf2PtixWIPxE7EacWVx/2Md4y/mkCfEJ7QlyiRmJP4Mckw6VwyKtknuXMv/960vRP7SPuq9kP7vfd3pgimZKa8TzVKPZ+GTwtJe5wum16Y/j3DKaM9kzszNXPqgNGBC1nELErWyEGNg6eyUdlB2f05CjmlOb9zfXMf5snmleStHfI59PCw3OEThzeO+B/pz1fOP3kUczT86HCBdsH5QvrCpMKpYxbHWor4inKLvhd7FveWKJacOo4/Hnt8/IT5ibZSodKjpWtlgWVD5brlTRVcFTkVPyp9K5+e1DnZeIr7VN6pX6eDTr+oMqpqqRapLjmDORN35sNZx7M951TP1dVw1OTVrNeG146ftz3fVadSV1fPVZ9/AXEh9sJMg3vDwEX9i22NUo1VTSxNeZfApdhLs5e9Lg9fMbvSeVX1auM14WsVzYzNuS1QS2LLQmtg63ibS9vgddPrne0a7c03pG/UdvB3lN9kvpl/C38r89bG7aTbS3ci78zfDbg71enZ+fqe873nXTZd/d1m3Q/uG96/10Pquf1A80FHr3rv9YeqD1sfKT9q6VPqa36s9Li5X7m/5YnKk7YBtYH2wd2Dt55qP737TP/Z/ecmzx8NWQ4NDjsMvxhxHxl/4fti+mXoy8VXca9WX6eOokdz39C9KRnjGqt+K/62aVx5/OaE/kTfpN3k6ymfqbl30e/W3md+oPlQ8pH3Y920/HTHjOHMwKzb7Pu5yLnV+axP9J8qPot9vvZF50vfgvPC+0XK4sbXQ9/Yv9V+V/zeuWS9NLYctrz6I/cn+8/zK6orPb+cfn1cjV/Drp1YF19v/232e3QjbGMjkkwhb10FkHBF+PsD8LUWABoXABgHAMC7bed5OwUJXz4Q8NsRMkCQkKooNjQeQ4WVpXLBZeBvEzA0ZGIrHZ4+lOEhkxJzBStgC2Hv51TmOso9x6vDl88/KIgXUhN2EQkRDRNzF9eV4JZYlLy/q1QqRFpThkbmrWyTXKq8jQK/wifF60oHlG1UuFTeqzaqJaiTNPAaz3ZXaPpq7dL6qt2qs5ekq0vQfat3S7/eoNKwwGi/MdlE25TNdNGsz7zRotKyyqrDesoWbcduz+FA54h0XHNadQGuODeiO80e1J4lj0nPAa875KveNT6lvrl+if4BAfaBukGKwRIh/KHsYbThyPDvEZORA1E3KGejj8SkxGbFNSegEv2S7uwF+0T2q6eYpLqlxaYfySjOTD6geGAqK/+gdbZwDnUuyEMcoj8sdkQr3/KoU4Froesx5yLHYvsSm+OWJ8xKjcp0y7Uq1CoVTkqdkjgtW2VWnXFm/JxJTUPtXB19vfAFuQaNi/qNFk1OlzwvB16JvBp/bX9zesuB1uy2vOv57cU3Kjpqbl671X175M743eHOpnv+XWxdD7pL7sf3+D/Y0+v00OaRWZ/RY+N++ydRA6cHXz6jfi4zpDdsMmLwQvWl8Cviq5XX06Mv3twdO/M2YzxgwmHScsrindV7qw+mH9WmWafHZ3JnFWfH587PJ30y/kz1ue6L0ZephTOLCV89vll9t1gKXu78efBX67r+xsZO/OWQKOQMahw9hVmgQuKU8YHUFYRxogRtPN19BnbGRKbnLPKs6WxvOJQ4s7gGeDh4nfkK+DsERgWXhJaFZ0Uei54Ro4hrSVBJPJc8tStYSknqt/R9mSOyTnK8ch/lGxXiFDWVIKVu5VwVK1VG1WG1UnU3DW6NUXgWuGuxa41oH9dxI4mQVnWH9C7rHzLwM9xtRG/0wbjDpNg0zszP3Nsi0DLCKsza28bKVsNOwp7TgeiIcFx2+ug87HLPtdGt3D13T5JHkKezlz5ZxpvNB/KZ9R3y6/JvDqgJLAnKDI4IcQnVCRMNp4FnwkTkWNT3aP4Yz9jSuLvxLxKmEueTVvZS7+PZL5bCl4pJfZvWnJ6fQcn0OOCQ5XwwKDsjpzL3Yl7zoZbD145czr94tK7gXOHpY+VFxcX5JTnH008klkaUBZQHVaRW3j4lfvp8teiZwrPPzq3UEs9z1AnWS8DzQOWiVqN+k8Ull8uhV7Kunrl2q3mwZax1uu1bO/IGa4fkTY1bOrdV7vDfRdyd7Oy519xV211+/2jPgQdJvZSHMY9y+jr6WZ7sG3jzlOOZ9nP7If/h1JFzL568/P6aYVTqjflY5Nvj4zcmnk6OTU2+m/uAhqOfNjM4Rz8v+0nps8gX2i8/Fz4sjnx9+O3696qllGXHH6I/ln92rCT90lglrOmvz+zEXxqaQ1QiPVDiaCx6ETODnaWaxC1S4wnCNCSiK20aXQP9IMMGkzCzAUsw6wG2U+zXOLo5H3Dd577BU8WbwKfL94v/rICZwJxgtpCoUKewh/CKSJGorOhDsQBxrHithLHER8msXWK7uqV8pIF0pcxumReysfDtpkneXH5aIUORR7FNyVZpXvmACq9KK3xrmVZLUWdRv6BB0ni622f3Z81kLaxWubai9rBOEomH1KZrpftSL1BvQ7/awNoQZ3jPaK+xovGsSbWpuxmb2bB5sYWdJa1lr1WGtYb1d5sm2xA7Ubt39lUOexzZHZ875TsbO2+4NLuGugm5vXEv2WO5Z9mjyFPY85oXyesVOcFbwPsFvI8E+hn5qwSoBZoEkYPDQsih2mF0YaPh5yLCIpUi16LuUXKjrWOYY17HnorzjReJ/5BwMtEgcTQpNJkp+dneG/tu7e9KuZd6Pa0uvSQjIzPigFuWwUGJbHT285zSXNc8obzVQ+OHHx+5nn/66P4Ct0L1YxzHVoqGi6+UHD9++ERhaVXZ1fL7FS8qZ0+unqap4qtWOGN81v1cRM3+2pzzh+pS68kXVBqIDV8vfmpcuUS4zHNF/qr1teTmay0/29SuR7aX3rjU0Xbzxq3e20t3jTqvd9l1L/WU9Co8fN53uN9rwOQp6bnucOhL4ujcZP/s0veVzfhv/963WTDKABxLgzPULAActAEo6ILzzCE478QDYE0DgL0aQIj4AwShD0DqE3/PDwg+bTCAGtADNsALRIEsUIezZCvgCvxBNJxd5oOToBHcAk/ABPgOZ45ckBxkBHlC8VAB1AA9gD4gMAgxhDkiGlEJ53kbcF4Xh7yO/I0yQh1DTaIV0Nnotxh1TClmFc6wHlKpUNXiOHEFeGp8DjWe+iiBg1BLo0jTQdQkttOq0t6gM6Z7TR/DQMdwkVGfcZDJnmmQ2Yr5KYsny0/WUjZNtjH2fRycHO2cHlw4rg7uOB5Fnm+8V/go/Er8awI9giVCgcK7RYgi46JXxbLFvSVIkiK7iLtWpT5Lv5MZkm2WS5aXkx9TyFZUUvyi1KZcqJKo6qtmri6rwbqbqCmtVa4jSTqs26v3xYDKkNmI3ZjLRMhU0czSPMrihGWX1VcbQVsnuyP2PY4oJ33nLJc+NxZ37z31Hu+8MGR6b4z3ks9731G/2QDaQLOg4uCPobvDisI/R5pG1UcTYqJiX8UbJrQlSSXX7OPbX57KklaQgc9MO7B0MDh7LjfvUNiR5gL6YxxFn0rqTniWsZQPVB4+ZXR6qTr/LNO57Jrl8yF1Xy8cvWjQRH9p8cqHa9Mtc20f26c6Fm+z3tW759Ht1WPXq/1I5rH4E+XB8Gc/R1CvcKOn3jJO3HpPnN47R/rU9GX1q/J3w2X8j8M/H65M/3q/+nLt2vrR394bslv7x2b8sYAAGAA74AcSQAFoAmNgD7xAGEgGOaAU1IHr4BF4AxYgNMQByW5FPxEqgi5B/dAnBC1CAeGKyEBcQbxH8iI9kWeR8yhlVCZqCC2OTkOPwrEvxwJsIHaIyoCqDSeDq8eL4xuoFalvE6wJUzQJRByxmJaf9hKcv76mj2dgYWhldGT8xLSPGc98gkWK5SFrBBsr2x32IA4mjjucEVxCXKPcpTzOvGy8L/kq+X0FZAWB4HOhC8KZIu6iinAuNyveJ3EVPsXypTKk98rEyPrI6cgT5PsVchXNlFiVFpVfqvSotqhVqx/SSNodp5mj1ab9g6Sg66uXp19j0GJ4w+iG8U2TXtMJc4SFhKWj1QHrVpt5OyF7T4dKxzFnAZdg1xZ37B4njzLPbq9Bcqd3nU+2b5Cfrb9xgEtgetCdEJpQ77COCI7IpKg30boxdXG08ZEJj5L4k+P2DuxXSjmbxplelIk/kJw1n03OmcxLOiybjzj6pvByUVyJ4vGvpZfLYyvVT/46XVMtf6by7Mca0drA85fqWS9UXNRs/HSp9Ira1f5mcstqW3W7TQe4WXfb/M5i56ku7/vqD/gfoh49fhz3BDOQ+5TwrHrIc8TiZejr2jcfx3knrd+lfbg1wzp39LPIwuNvRcuHVkxW5ddOrr/7vbgTfxTAATp49fMDSaAM9IA18IBjvw9e+VXgGngAxuB1T4BEIB1oD5QMlUM3oQkEDo46GVGMGEAyI/2QN1FcqFTULNoF/Rijh7mJ1cTepTKneoOLxtPiL1E7EpCEVpooohzxJ203XSl9LIMLowmTKbMNiymrCps4uxKHJ2ciVwy3N489ryWfBb+FgLmghZCtsKdItOhhsXrxBxIzu2ikVKT9Zcpkh+U5FHwVm5RWVaxVH6vn7HbRQmsf1VnTNdPLgCPYathhdMu432TVzMy8xVLaqsFG2rbFXs9h2CnMBe/a4O7oQe9F7e3p6+b3LkAjMC/oQ4htaF+4RcTTKDfKdExyHE/8WOL95Dv7KlMcUn+lV2U6ZvEeXMi5mXfosH++UQF74aMi/+Ll4xml9GXVFcqVj0/5V0HVFWdVzw3VxtZx1j9oSGk0uiRzxfBaSkt1W367SwfrzZHb5Xdd7mG7zt1X7LnRa/BwpC+hX2YAObjwbHpocKTgpeiryte/3xiM5b59NEE76TB1+t3MB7mPIdOnZx7Mzs6jP3F9lv2iv+C0SP7q+836u8D3paXDy1zL9T/UfpT9WPnp9LNlhWWFstKysvpL51fmr95V4qrd6vHVgTWqNZ21hLXLazPr/Osu64XrD9fXf8v99v19/Pej37835Db8Nk5s9G3GP9pfQX7r+IAIugCgxzY2vokAgC0EYL1gY2O1emNj/QycbIwCcCd0+z+krbOGDoCKhU30qO1X6r//y/k/jH7Z6+7fudwAAJvUSURBVHic7J13eBRV24fv9JBACCX0Ir0ogkpRpIoUCxaKoIiIvfAhKoIKoiAoAoICooJSpInSe++9hxZIIT0hvffdPd8fkx0DZCFld2fIe+7r4nKzO3Pm5+zsPHOe8xQHIYRAIpFIJBJJsXDUWoBEIpFIJPci0oBKJBKJRFICpAGVSCQSiaQESAMqkUgkEkkJkAZUIpFIJJISIA2oRCKRSCQlQBpQiUQikUhKgDSgEolEIpGUAGlAJRKJRCIpAdKASiQSiURSAqQBlUgkEomkBEgDKpFIJBJJCZAGVCKRSCSSEiANqEQikUgkJUAaUIlEIpFISoA0oBKJRCKRlABpQCUSiUQiKQHSgEokEolEUgKkAZVIJBKJpARIAyqRSCQSSQmQBlQikUgkkhIgDahEIpFIJCVAGlCJRCKRSEqANKASiUQikZQAaUAlEolEIikB0oBKJBKJRFICpAGVSCQSiaQESAMqkUgkEkkJkAZUIpFIJJISIA2oRCKRSCQlQBpQiUQikUhKgDSgEolEIpGUAGlAJRKJRCIpAdKASiQSiURSAqQBtUBubi5btmwhJyfnpvf9/f05fPiwRqokEolEohekAS2E7OxsnnzySZ599lk++uijmz578skn6dy5M1FRURqpk0gkEokekAa0EN577z3Cw8MB2L9//02feXl5AZCZmWlvWRKJRCLREdKA3kJubi65ubmcP38eV1dX/P39yc7OVj93dHSkUaNGNGrUSEOVEolEItEaaUBvwdXVlRUrVlCxYkUaN26MEEJ114aFhXH58mXGjh2Lg4ODxkolEolEoiXSgN6Bhg0bAhAdHQ3AtGnTaNWqFW+88YaWsiQSiUSiA5y1FqBn6tWrB0BMTAyBgYH8+eef7NmzBycnJ42VSSQSiURr5Az0DtSpUweAxMRERo4cybBhw+jYsaPGqiQSiUSiB+QM9A5Ur14dgDlz5pCYmMjff/+tsSKJRCKR6AVpQO+Aj48PABcuXGDr1q1qCotEIpFIJNKFewcqVKgAwLvvvstTTz2lsRqJRCKR6AkHIYTQWoQeEULw8ssv4+vry5kzZ/Dw8NBakkQikUh0hHThWuCLL75g3bp1nDhxQhpPiUQikdyGNKCF8OOPP/LDDz/w008/0aZNG63lSCQSiUSHSBduAXJzc/nggw/4888/GTJkCMuWLdNakkQikUh0ijSg+cTExNC/f3+OHDlC27ZtOXToEO7u7lrLkkgkEolOkVG4+ezdu5cGDRqwaNEiduzYIY2nRCKRSO6InIFKJBKJRFIC5AxUIpFIJJISIA3oHZCTc4lEIpFYQhrQO3D58mWtJUgkEolEp0gDegfWr1+vtQSJRCKR6BQZRGQBIQQtWrTAz88PBwcHreVIJBKJRGfIGagFQkJCuHbtGmFhYVpLkUgkEokOkQbUAkeOHAHg8OHDGiuRSCQSiR6RBtQCe/fuvem/EolEIpEURK6BFoIQgjp16hAVFUWdOnUICwuT66ASiUQiuQk5Ay2Es2fPEhUVBUBERATnz5/XVpBEIpFIdIc0oIWwevXqO/4tkUgkEol04d6CyWSiYcOGhIaGqu/dd999BAUF4egonzckEolEoiAtwi3s27fvJuMJSkrL/v37tREkkUgkEl0iDegt/P7778V6XyKRSCT/m0gXbgHCw8Np0KABRqPxts+cnZ0JCQmhdu3aGiiTSCQSid6QM9AC/Pzzz4UaTwCDwcDPP/9sZ0USiUQi0StyBppPQkIC9evXx9vbm+7du5Oens769esZM2YMUVFR7Nu3j9TUVEJCQqhcubLWciUSiUSiMXIGmk9mZia+vr6Eh4ezdOlSHnnkEQCeeeYZli5dSnh4OOfOnSMzM1NjpRKJRCLRA85aC9ALdevWvePnDg4ONGrUyE5qJBKJRKJ35AxUIpFIJJISIA2oBVJTUwGlLq5EIpFIJLciDagFfH19ASW1RSKRSCSSW5EG1ALmmaecgUokEomkMKQBlUgkEomkBEgDKpFIJBJJCZAGVCKRSCSSEiANqEQikUgkJUAaUIlEIpFISoA0oBKJRCKRlIAyV8ovKiqq0NQTR0dHatasqYEiiUQikZRFypQBzczMtNivs3Llyty4cQMXFxc7q5JIJBJJWaRMGdCwsDA8PT357LPPqF+/vvr+n3/+Sbdu3aTxlEgkEonVKFMG1GQy8cMPP/Dhhx+q76WlpTF+/HjWrFmjoTKJRCKRlDXKlAFt2bIlLVu2vOm92bNn07dvX6pVq6aRKonEduwLjeX3iyEEpWXjCLSuUp6+jWrwRN1qeLqWqZ+3RKI7yvQvLDU1lZ9++onjx49rLUUisSoxmdm8vv0s289ev+n9k8CCg1fAyZEBbRsx54kHqeFZThuREkkZp0ynscyePZvu3bvftRF2bGwsPXr0oHPnzuq/EydOADB58mQ6duyIj48PnTp1YsaMGbz00ktkZmYC8Oabb3Ljxg0ARo8ezdWrV9X9jh07BsC8efPYsmULACtXrmTZsmUA7Nixg9mzZwNw8uRJJk6cCIC/vz8ff/wxADdu3ODVV18FICMjg0GDBiGEwGQyMXDgQLKzswEYPnw4sbGxAHzyySf4+/sDMGnSJPX/Ze7cuWzfvh2AFStWsGLFCgC2bdvGL7/8AsCJEyf49ttvAbh27RqffvopANHR0bz22msApKenM3jwYABVR05ODgCvv/46cXFxAIwaNYqAgAAAJk6cyMmTJ9XvZceOHQAsW7aMv//+G4AtW7Ywb948AI4ePcqUKVMA8PPzY/To0QBERkYyfPhwhBCkpqby8ssvA2A0Ghk4cCC5ubkAvPbaayQkJAAwcuRIgoKCAPj66685c+YMAD/99BO7du0CYMmSJfzzzz8AbNq0id9++w2AI0eO8P333wNw+fJlxo4dC0BERATvvvsuubm5pKSk8MorrwBgMBgYOHAgeXl5AAwdOpSkpCQA/u///o/g4GAAvvrqK86ePQvAzJkz2bNnDwCLFy/m33//BWDDhg3Mnz8fgEOHDjF16lQA9p85R40py/8znkJAtYpQpbzyGsBoYvWJAGrO3MD4Q5d5ZcgQUlJSAPjggw8IDQ0FYNy4cZw/fx6AGTNmsG/fPgAWLlzI2rVrAVi3bh1//PEHAAcOHGD69OmA0rHoyy+/BCA0NJQPP/yQ3NxcEhMTGTp0KAC5ubkMHDgQo9EIwCuvvKK2Cnz//ffVbkdffPEFFy5cAGDatGkcOHAAgD/++IP169cDsHbtWhYuXAjAvn37+PHHHwE4f/4848aNAyA4OJgRI0aQm5tLQkKCes3m5OQwcOBATCYTAIMHDyY9PR2Ad999l4iICADGjh3LpUuXAJg6dSqHDh0CYP78+WzcuBGAf//9l8WLFwOwZ88eZs2aBcDZs2f56quvAAgKCmLkyJEYjUb1/11SBhFllJiYGFGxYkVx6tSpu25rNBrFkSNHxMGDB9V/LVu2FIAYN26cOHjwoFi2bJk4ePCgiI6OFlevXlX3Lfja399fGI1GIYQQ169fFzk5OUIIIcLDw0V6erqqKzExUQghRGJiooiJiRFCCJGWliYiIiKEEEJkZ2eL4OBg9XX58uULPV5RdeTm5qo6MjIyhBBC3LhxQyQlJak6YmNj76jDYDCI+vXrixs3bpRIR1BQkKojLCxM1REdHS2Sk5OFEEIkJCSoOlJTU0VkZKQQQoisrCwREhKi6njhhRfE9u3bi6zj2rVrwmQyqTry8vKEEEKEhoaKzMzM23TEx8eLuLi4O+rIy8sTU6dOFd98802JdAQGBhaqIyoqSqSkpNymIyUlRURFRYmsXIPgt62CcUsF45aKZkv2iMWbtou+ffsKIYQ4eeGSWHU1TDT9a6+6DeOWivt+3yTSc/LuqCMkJERkZWWpOlJTU4UQQsTFxYn4+HghhBDJyckiOjpaCCFEZmamCA0NFUIIkZubK4KCgkSrVq2EyWQS165dK9b5CAgIEAaDQdWRnZ0thBAiMjLyJh0JCQm36cjIyBBhYWE36Xj++edFQEBAkXWYKagjODhY1RERESHS0tKEEELExsaqOpKSktTfREZGhggPDxdCCJGTkyOuX78uJk2aJP755x8hKZs4CFE2+3W98847BAYGsnfv3hLt36tXL3bt2sVff/2lPk1rhclkwtFRe2eB1HEz5p+Og4OD3Y7Ze80Rdp5TZrG9HmrAjv6PA4Wfk83Xo+m76RTEKTM+6lQh8tXu1CrvbjN9evlupA6JPSiT3+z58+f5888/GTNmjNZSrIJefoBSx804ODjY1Xhuvh6tGk/vBtXZ9Pyj6meFnZNnG9Yk+d0+NGhSS3kjIoHai3aTkp1rM416+W6kDok9KJPf7qhRo3jggQfo06dPiccwr49ojcFgoH379lrLAOCpp54iJiZGaxl8/vnn6hqqlqxbt45JkybZ5Vi5BqMymwRwdebSS51wdXYCICQkhH79+hW6X0V3V/xf7cazbfPjAGKSeWjVYQxGk010PvTQQzYZt7gMGDCA69ev331DG/P999+ra9qSskeZc+GuW7eOfv36sWzZMoYMGVLicfTkwk1PT6d8+fKaatCTjoyMDDw8POw6+yuMvLw8TCYTbm5uNj/W+EOXmbLjHAATn36ECR1b3PT53b4bk0nQ9u+DnLuiBO30b9+E1c91sLpOvVwjetGRmZmJu7u7nImWUcrct9qxY0dCQ0PVqMiygB5uBKAfHZ6enpobTwAXFxe7GM/UnDym7FciQ6nuzZcdmt22zd2+G0dHBw4NeBxqVwFgzckAllwKtbpWvVwjetHh4eEhjWcZpsx9s9WrV6devXqlvsHqyYXbq1cvrWUAMGjQIDVFRUsmTZqkpltoyebNm9VUClsy+2wQ5ChpMat6tcbZ6eafbUhICMOHD7/rOJ6uzkS82g08FKP/+oYTRKZlWVVr9+7drTpeSRk+fLiaqqMls2bNUtNfJGWPMufCtRY9e/Zk9+7dunDhhoeHU7duXU01gJKDWatWLc1nf3FxcXh5edll9ncnMjMzyc7OpnLlyjY7htFkwvmnjZCYDlW9MH3Ut9DzHxERQZ06dYo05kq/cF5ZruRZtmhWmytDrWf09HKtRkVFUaNGDc1nf4mJibi7u+Ph4aGpDoltKHMzUGuhtZEoiB5uSAC1a9fWxXnx8fHR3HiC4p6zpfEEWHk1QjGewPTHm1s8/0U1ngAvt6hLr4caAOB3LZIFF4JLLzQfvVyrtWrV0tx4gtIFShrPsov2V5hOycjI0FoCoLhwzdV2tObdd99Vq/toyY8//qhWedKSXbt28fvvv9v0GEMPX1FelHPjgzYNC90mLCyMTz75pFjjrnqmHXgpJf7e2XmOzDxDqXSaGTBggFXGKS2jRo0iMjJSaxnMnz9frXYlKXtIA2qBcuX0UT/U2dlZLR+nNSNHjsTb21trGfTv3/+2pgFa0K5du1KlSt2Ng+FxEBYPwIePNsHDpfDS1XXq1CnSGmhBvN1dmfNkG+WP5EwmH7taGqkq48ePt8o4peXdd9/Fx8dHaxk89dRTPPLII1rLkNgIaUAtoAf3j5k2bdpoLQGA+++/HycnJ61lcN9991GxYkWtZeDt7X1T31lr88VRP+WFkyNfdmhucTtHR0datWpV7PE/aNMQalQC4PsDl4nJzC6RzoLo5Vpt0aIFrq6uWsugbt26NnfzS7RDP1ZCZ5iLxWuNwWBg5MiRWssAlILfycnJWstg/vz5nDt3TmsZHDp0SC3Ib21SsnM5ekUpcN6n9X13LL8XGRnJ5MmTi30MR0cHNvbOL3yQk8eovRdKpLUg77//fqnHsAbffPONLop+LF++nMOHD2stQ2IjpAG1gB6CVEBx4fbt21drGQA8/fTTunBtP/roo9SuXVtrGTRp0oQHH3zQJmP/4x8J+dWCPmzT4I7bVqtWjc6dO5foOH2b1FJL/f19MgC/hNQSjWPGUkUke9OrVy8qVKigtQwefvhhGjS48/cnuXeRaSwW0FMlIsn/Hg8tP8B5v3Ao50be5/1vy/20Jmdjknhk7hYQ0KlVfQ4NKpkxlkj+15AzUAuY+2xqjdFoVPtzas2MGTN0UWBi1apV+Pn5aS2D06dPs3nzZquPm5qTx/kAJYL0ufvr3NV4xsbGqn1US8LD1SvR+yElwvfwpTCCU0oegf7NN9+UeF9rMnv2bBITE7WWwaZNm9S+r5KyhzSgFnB2Ljzi0d44OjretSG4vWjUqJEugqtq166ti9y6ypUrU6VKFauP+69/JBgU9+0bD9w9SKl8+fLUrFmzVMec/Fh+bV0h+P7EtRKP06RJk1LpsBYNGzbURcBb9erVdeFKltgG6cK1gHThSrSi3cqDnL4cBu6u5H4xABcbum8LUv7PXWQEx0A5V9I/64enqz4eIiUSvaL9dEKn5OTkaC0BUBry2jpZv6gsWrRIF67tbdu2ERISorUMrly5woEDB6w6ZnpuHqevKe7bp+6vUyTjmZiYyKpVq0p97N8fy0+VycplwYWQEo3x66+/llqHNVi2bBlpaWlay2D//v1cvWqdHFuJ/pAG1AJ6KFlnJivLugW/S4rRaCQ313bNmIuKEEIXDzhCCKs/UKzxjwKDEYC37i9ajqmzs7NVjMXg5rXB2xOAj0tYWEEv16rJZNLFNWI0GnWhQ2IbpAvXAtKFK9GCjn8f5NilMHBzIeeLAWrTbHvx1eErTN6uBL1se+NJ+jSsYdfjSyT3EnIGaoG8vDytJQDKLGfdunVaywCUiEI9nJejR49y48YNrWUQHBxs1YIOGbkGjuW7b3u1rFNk45mWlma1eqsfP9IIXJTjfnGs+MFEa9eutYqO0rJ161ZdLDecOXNGF23VJLZBGlALGI1GrSUAiivq1KlTWssA4PLly7pYVwoNDdWFAY2PjycoKMhq460LjII85bp7uwjRt2Zyc3OtZsgrl3PjhfzCDeevhhOYVLy0pePHj1tFR2nx9/cnKSlJaxmEhYURFRWltQyJjZAuXAtIF67E3nT75xAHLoSCmwtZXwzA3c7uWzPnY5N5aLaS3zq8UwsW9pHF0CWSwpAzUAsYDNZp72QN9FJL8+jRo+jheevSpUu6qMkbExNDYGCgVcYymQQHAqIB6NqsVrGMZ3Z2NmfOnLGKDoA21byp3khZ+1x0OohcQ9G9MXq5Vo8fP66L37C/vz9xcXFay5DYCGlALaCHtT5QDPnixYu1lgHAunXriI+P11oGhw8f1kVqwLVr1zh06JBVxjoRnQhZSoTzwPzatEUlOTmZf//91yo6zPzQPr8gQnYuawOji7zfH3/8YVUdJWXr1q26cJ0eP36cixcvai1DYiOkC9cC0oUrsSdfHrzE9zvPAxDyWT/qV9S20lJmngHP71dDroHHHqjH0cFdNNUjkegROQO1gMlk0lqCih5mW6AfHWFhYbpoN5eSkkJ0dNFnZ3diYVB+UJSPV7GNp8FgsGowE4CHizN9HqgHwLGrEaRkFy3/Vy/XiL+/vy6WG6Kjo0lNLV2HG4l+kQbUAnpJCDcYDHz++edaywBg+vTpxMbGai2DVatWcfr0aa1lcPz4cVavXl3qcTLzDMSEKOd1cKPi513euHGD6dOnl1rHraht1AwmlvmFF2mf0aNHW11HSZgzZ44uqlWtW7dON+vCEutT5l24RqORM2fOIISgQ4cORd5PunAl9mJTUBTPLdoLwMpXuzG4eR2NFSkYTSacp6+FtGxqN6pBxPAntZYkkeiKMjsDjY2N5eOPP6ZmzZp8++23xc5f1NNzhR5mfaAfHUlJSboI8srNzSUlJaXU42w0u28dHOhzX7Vi7y+EsEmkp5OjI689eB8AkddvEJF2d6+MXq4RvehIS0vTRUEHiW0okwb03LlztGnThoMHD3Lo0CE2bdrEk08W7+k5I6PkPRGticFgYMCAAVrLAODdd98lJiZGaxnMnDmTgwcPai2Dbdu28dtvv5V6nD/MUa51q+Dt7lrs/cPCwhg5cmSpdRTGew/mu3EF/HEx5K7bP//88zbRUVw++eQTrl+/rrUMfv31V7Zv3661DImNKHMu3IiICO6//346dOjA5s2bcXUt/g0JpAtXYh9iMrOp8Z2yjjryiVb8/ERrjRXdjsPPGyEuFWpVRnzwtNZyJBLdUOZmoKNHjyY7O5slS5YUK5H6559/5tNPP1X/+fn5AbBixQpGjhzJ/fffzyeffMLUqVMZPny4GmT0f//3f+qsbPz48fj7+wMwY8YMTp48CSi5cTt27ABgzZo1auupPXv2qDOYM2fOMHXqVAACAwP54osvAMUV9dZbbwHKrHj48OEIITCZTLz++uuqe+jDDz9U3XhffvmlmuA/bdo0NeBmwYIF7N69G4B///1XzR3cvXs3CxYsAOD06dNMmzYNgICAAMaNGwcoRQPeeecdANLT03njjTcAVB3mjhPvv/++miv6xRdfqNGhU6dOVZP9f//9d/bs2QMoAUFr1qwBYOfOnWoe4cmTJ5kxYwag5FuOHz8eUKIa33vvPUwmE2lpabz55puAstY9bNgwtVvMe++9R2JiIgBjx44lODgYgO+++04tezdv3jz27dsHwMqVK9Waw9u3b2fhwoWAEig0c+ZMQIkwnTBhAgBRUVF89NFH5OTkkJqaqn5HBoOBYcOGqS7md955Ry368Nlnn6l1UadMmYKvry9br/83o+/bsAYrVqxg/fr1gJLLaM4BPnbsGLNmzQKUNmrffPMNoDwwfvLJJ2RnZ5OSksLbb78NKHnMw4YNU38Db7/9tupu/vTTTwkLCwPg22+/VfMU58yZo+a1Ll26lI0bNwLwTLn8CNyoRBbv2MfPP/8MKAUtJk6cCCiz4E8//ZTs7GySkpJ49913AcXNPWzYMLU05ltvvaUup3zyySdEREQAMHHiRC5fvgwov8UjR44A8Ndff7F5s1IVadOmTSxbtgyAQ4cOMWfOHAAuXrzIt99+CyhlHs33gMTERN577z1AaU84bNgwNbr+jTfeID1dKVM4atQoNWf066+/5sqVKwDMmjWLo0ePArB48WK2bt0KwPr161m+fDkABw4c4JdffgHA19eXKVOmAEqd5DFjxmAwGEjKlC7cMosoQ8TFxQlAVKlSRTz++OPC0dFR1KhRQ0yePPmu+y5fvlzMmDFD/VevXj0BiMGDB4sZM2aIUaNGiRkzZoilS5eKM2fOqPudO3dOmEwmIYQQFy5cEHl5eUIIIfz8/ERmZqYQQoigoCCRnJwshBAiPDxcxMTECCGEiI2NFeHh4UIIIZKTk0VgYKAQQojMzEzh5+cnhBAiKytLODk5qcc7e/Zsoa8t6bhy5YrIysoSQggRGBgoUlJSVB2xsbFCCCFiYmJERESEqiMoKOg2HXl5eaJatWrixo0btx3b0vnw9fW9q46wsDARFxd3m46kpCRx/fp1IYQQGRkZ4urVq0IIIXJzc0Xv3r3F9u3b76jj7NmzN+kwGAxCCCEuX74ssrOzhRBCBAQEiNTUVCGEEKGhoSI+Pl4IIcSNGzdEZGSkEEKIxMREERwcLIQQIj09XVy7dk3V8fXXX4uJEyfe8Xsp+LowHc+tOyoYt1TwzQqRazDepCM6OlpERUXdUUdOTo7YtGmT6Nu3rzCZTOLcuXMWz4eZ8+fPC6PRKIQQ4tKlSyInJ0cIIcS1a9dEWlqaEEKIkJAQkZCQIIQQ4tDVIEXjuKXijU3HREhIiBBCiLS0NOHv76/quHTpkmjVqpUwGo2l1pGeni6EECI4OFgkJiYKIYSIiooS0dHRQggh4uPjRWhoqBBCiNTUVFVHdna2uHz5snj++eeFv7+/OH/+fLF0XLx4UeTm5gohhLh69arIyMgQQghx/fp1VUdkZKT6O4iLi7tJR0BAgBBC+d1evnxZTJo0SXz4599CUjYpUy7cffv28cQTT/Dcc8/x4Ycf4uLiwscff4yvry9z5sxhxIgRRR5LTy5ck8mEo6P2zgKp42aEEKXuG+swYx0kZ9CiWW2uDO1e4nFsfU4c5m+HsHioUgHxseV1Tr18N3rREZSUztRT/izo9bDWUiQ2QPsrzIqY3a6DBg2iV69edO/enfnz5wPwzz//aCmtVOjhRgBSx62U1nheTUiDZCVY7eXGpeu7aetzMqlVfneYhDTOxyZrpqOo6EXH7tBYzicUr6ON5N5BH1eZlShfvjzwnyEFaNu2LVWrVi12UrV5fURrDAYD7dq101oGAL1799ZFFO7YsWPVNWUtWbduHZMmTSrx/puv/1fFqG+jmiUeJzg4mBdffLHE+xeFwc3rqq//vhphcbs2bdrYVEdR6devny6icN9bv4vTQWFay5DYCGetBViTBx98EEBd+AdllpCXl1dsI2Q2xlrj7OzM/v37tZYBKM2SPT09tZbB119/Tbly5bSWQd++fXnmmWdKvP9ac/5nBXfaVPMu8TgNGjRQg2tsRZNK5aG6N8Qk84NfBFO7PFDodubgH61ZunSp5teqwWgC50qQnUt6bh7lXV001SOxPmVqBtqmTRu6d+/O0aNH1Yi+I0eOkJKSopsSYyVB6xuBGb3o8PDwKLX71Bo4OzuXOE0K4Fiokuzf6b7qpdZij+/mgxb5FZLC4y0WVdDLNaIHHbtCYyG/hvCxqESN1UhsQZkyoKCkZ3Tq1IlOnTrx3HPP8dprr7FkyRKeeOKJYo2jJxdujx49tJYBwMCBA3VR4eWbb75R00+0ZNOmTSWuQeufmAZpSnrD0yWoPlSQkJAQhg0bVqoxisIrBUoM/nOtcDdu165dba6jKAwbNkzzWri/XQhWX+8Jkz1ByyJlKgq3IGFhYWRkZNCsWbMSBRT07NmT3bt36yIKNzIyktq1a2uqAZTcx5o1a2o++4uPj6dChQq4ublpqiMrK4vs7GwqVapU7H1/PX+dD1YrSw0nPnia9rUql0qLPa4RIQSO09dCapbFqGG9XKvR0dFUr15ds2Ci9Nw8Kny/GvLym5HXrox4XxahKGuUuRmomXr16tGiRYsS/4C0NhIF0cMNCaBWrVq6OC9Vq1bV3HgClCtXrkTGE2BHvvsWV2ceqeFdai32uEYcHBzonz8L9QuMJi3n9nrEerlWa9asqWkk7qJLYf8ZT4CoRFILOV+Se5sya0BLi55q4b700ktaywCUajYJCQlay2DGjBk3BYppxc6dO0tcC3dDfvuy+vV8cCrljT40NJRRo0aVaoyiMsS8Dmo0/VcEvwC2jgYuKiNHjlSrHNkbIQQjj93SF1XAhkDr9I6V6AdpQC2ghyhPUAJVzGXstObjjz/G29tbaxkMHDiQBx4oPArUnnTo0IGnny6+Wy4uK1upLQsMKOX6JyjeFnMpQVvzVIMa4KoE7//ld3t6hrm0n9Z88MEHVKtW+nNbErYE34DopNve/+1SiP3FSGyKNKAW0EsiNvyXnqM1LVu2xMnJSWsZ1K9fHy8vL61lULFiRerVq1fs/fYVCCjpUc+n1DocHBzs9kDh7uxEh6ZKzurOq1EY82vLmtHLtdq8efNSRUiXhqH7LhX6/lG/CJLzo3IlZQP9WAmdkZmZqbUEQHHhfvjhh1rLAGDMmDFqYXQt+f333zl79qzWMjh48GCJ8i93heYbUEcHOtepUmodkZGRpSroUFzeaJH/0JCVw95bokvNDQe0ZsKECdy4cbuL2dZsv36D5GALxUYMJpZclkUVyhLSgFpAD0EqoLhw+/Xrp7UMAJ577jk8PDy0lsHjjz9OnTp17r6hjWnatCkPP1z8Gqd/hOQbnVqVrZJcX61aNbp3L3kd3eLSv0ktyA8mW+F38zrjoEGD7KbjTjz99NN291KYTIKndp67/QPn/26zo04F2FGRxNZIA2oBPbgqzeglD7RTp06aucUK8sADD2i2vlWQGjVq0LJly2Ltk51nhEglEGuoFdy3AC4uLnTu3NkqYxWFKh5ueOev3S72C7/pM71cq48++qjdH/aCUjKY3KYBu9/uxekR/1WomvVse468/xT/170VGEwcjoi3qy6J7ZAG1ALmfp9aYzQadROYMW3aNF0UmFi5cqXas1FLTp06pfbMLCpHohLAqKwb9rJCABEovVrnzp1rlbGKyict8z0Aien4Figu/9VXX9lVhyV++uknu0eMN6lUnnGPNqdH/WqEpP4Xxe+WGE3H2lWY3aM1YsQzdKhZupxfiX6QBtQCLi76qFvp5OREs2bNtJYBUOKiFNamfv36uqhVXLVq1WLPhPeE/lfJ6Yl61jGgXl5edndpFywuv7JAcfnizshtRdOmTXF21q7U94X8KGuAh2pXvekzFyftf0MS61BmKxGVFj31A5WUHVou3Yfftci79tW8F3CYsxlikqFuVcS7fbSWoyueX3+MjaeDoJwbYtxAreVIbIR8FLJATk6O1hIApTHwvHnztJYBwJ9//qkL1/bWrVt10arq8uXLxarJK4TALz8Ct3d966x/AiQmJrJixQqrjVdUCisub29XsiX++usvUlNT776hjdhonoG6mXSx3CCxDdKAWkAPJevMGAwGrSUA/7WG0xo96SjOd+Mbl6J253iqvvWCoJydncnOzrbaeEWlsOLyerlWHR0dyc3VMOcyVjGgrT1ddHNOJNZHunAtIF24Emsz83QAn64/AcCFj/rSyqeixopKhxACx2lrIC2bNi3qcm6IPjqxaE1sRjbVv18NwISnHmbi4/pYF5ZYHzkDtYAeZjig3KRWr16ttQwA1q9fr4vzcvjwYaKjta8rev36dc6cOVPk7Xeaiw6Uc+WBqtbLUUxLS2P79u1WG6+oODg40KdJLQDOB0WTZzTx77//2l1HYWzevFmz5YbL8f+5jt2SYzRvqyaxHdKAWsBoNN59IztgMpk4f/681jIACAgI0EUaS2RkpC76kiYmJhbr5rgjXMn/a1K3qlWXCHJzc7l0qfDycbbmpab53VdyDewNj9VFhShQHm60qpp1sYABrZiRrElFJIl9kC5cC0gXrsSaJGXlUnnKPwCM6vEgs7rro2ZsaUnIzKHq96tBCN7u0pL5vYpfmams8eb2Myw87AdOjhi+HlzqbjsS/SK/WQvoaeH/4MGDWksA4NChQ5huKR6uBRcuXCAp6fZuF/YmOjoaf3//Im17JPq/pP4uVqh/W5CsrCxOnjxp1TGLShUPN6ir/P8s8I/mwIEDmui4laNHj2r2Gz5unoFW9SIwIICYGAu1cSX3PNKAWkAPa32gGPLly5drLQOALVu26KIf6PHjx4tsuGxJYGBgkfuSHgr/77w9Xsu6BjQ1NZX169dbdczi8En+Oig3kvhl2d+a6SjIzp07NVsnv5KfwtLBpwKnTp2SaSxlmDLpwo2MjLztPR8fn2LVcZUuXIk1eXD5fi76RZSJAgq3cjgins6/KUFMc/o9xoiHG2msSDuyDUbKTfwbhODD7g8wt0cbrSVJbEiZm4EmJCRQp06d2/4VN8hCD65KM3p5gtWLjpCQEF20m0tOTiYqKqpI214MUwKIulnZfQuKtyQgQLsuHx1rVYFySveiX874aaajIH5+fmgxN7iamAb5x23tU5HIyEhSUlLsrkNiH8qcAQ0JCaFly5YsWrRI/bdixYpit53SQ8UdUFy4einQPWvWLF1Ev65evZrTp09rLYOTJ0+ybt26u253PTkDMpRCB0/WrXqXrYtPbGwss2bNsvq4RcXR0YGuTWoAcPV6zG1NtrXgt99+IzQ01O7HvVQgAveBKl5s3LixyG5+yb2HdtWWbURISAjt27fn9ddfL9U4np6e1hFUSpydnVmzZo3WMgBYsGCB1hIAGD16tNYSAMXN36tXr7tudyjyv/ZVXWpb34DWrl1b83KPg5rW5sCFUHBy43BEAl2t1KqtpPz888+aHPf0jf+C2x6o6sVj77+viQ6JfSiTM9DGjRuTk5NTqlqYeloa1ksemV50JCYm6iLIKycnp0i5hgfy8z9xdKBdzUpW1yGE0Nwz8II5kAhYG1g0t7Yt0epa3ROVb0CrelHBzYWUlBRNyixK7EOZNKDz5s2jQoUKVKpUiXbt2pWoOkpGRsbdN7IDBoOBwYMHay0DgA8//FAXIfk///yzLlJ7duzYwfz58++63ZKI/AjcWpVxd7Z+o/awsDA+/vhjq49bHGp6ukMtpc/lbH/tDeiYMWM0aThwKToRgK61lAel+fPns2PHDrvrkNiHMheFe+TIEcqXL0+5cuU4dOgQY8aMITU1lQMHDtCxY8cij6OHKFyTSXAuNpmErFw8XJxoUrk81T3cNdEiKRkGowmXb1eBwcjgR5uy8tn2WkuyGR/sPs+v+5VgvRtfDvifu1ZvZGRR83tluWV8n4f5tpOsgVvWKXMz0Mcff5zWrVvTtGlT3nzzTT7++GMMBgNr1669436RkZEEBwer/9LS0gCIi4vj2rVrTJo0ieDgYFJSUpg7d65a6u+PP/5Qy9utWLFCdaVt2LCB4OBgAPbs2cPFixcBJYfx+PHjAFy6dIndu3cDEBwcrObyBYVH0v6n5ThNX0PbuVvo/ecuOv+2nRrfrcZh0hLe23WO09GJzJ07V40Wnj9/vhqZunz5cuLilLqr69evV8vN7d69m8uXLwNw7NgxTpxQCptfvHiRPXv2qDo2btwIQExMDH//reT1paSk8MsvvwCQnZ3Nb7/9BijRyr/88kuhOpYtW0Z8vOK+XLdunRrUsXPnTjWi9+jRo2oRgAsXLrB3717lHAQFsWnTJkApWGDWkZyczG+//YbJZLpJh9FoZO7cuarr/bffflNdZ3/99Zeav7pmzRrCw8MBZQbp56dEjR4+fFgNTDp//jz79+8HlFzPzZs3qzr++ecfVceiRYvIzs4mKyuL33//XdXxyy+/qDq++GUBGJRrxTH0mloAYvXq1UREKB1Mtm/fzrVr1wClWIW5vu65c+fUwgQBAQFs2bIFUK5Vs1clMTGRJUuWkJWVRWZmpjojNhgM6vcFMG/ePLU7yeLFi1XX87///qumfW3dulXNrz148KBalu/MmTMcOnQIgGvXrrFt2zYAIiIi1DrNCQkJeF6/qB7v4wUrLeowu98XLVqkRqj+888/akTzli1b1KjiAwcOqKUsT58+zeHDhwG4evWqWv83PDxcjRNISEhg6dKlZGVlkZGRoa7b5+Xl3aTjl19+UXUsXLhQXe5ZtWqVmj+6efNmAgMDAdi3bx++vr4AnDp1iiNHjgBKtK95hrn5wjV1/Oaejixbtoy8vDxdFWWRWJcyZ0BvpX///sCdo2qjo6Pp2rUrTzzxhPrPfPP4/vvv6d27N7Nnz6Z79+7Mnj0bV1dX1YC6uLio4zg5OeGYX7bLwcEBJ6f/3HXOzs7q++bXBd83j7UrJIbGfx/nVLyAtELWTnKd+P3AZdrN28qU9PKEJCvG29XVVTVid9Jhfn2rDvP/hxCiUH2Ojo6MGDGCmJgYnJ2d1Vqujo6OuLi43HQ+zMbDkg5L5+bW82l+7eDgoL52dHTk66+/Zvfu3TeN7+TkdJOOgufD2dlZ3c7R0bFE30th22/YsIFp06bdNL6TkxPOzs6qjiDx3yzsAQ/Hm86bY4ESb5a+F/NrIUShOhwdHQkPD2fw4ME4OTmp49+qw83NTX1dcPyC56Mk12xBHQ96OkKecs3uyLr5fJi/i4I6Cv7/3Kqj4DHudm4K0/rKK68QEhKinmNnZ2ecnJxu0lHw+ribjqJ8L2fi/1v2eaSqF87OzkydOlXTIhcS21LmXLi3snr1agYOHMiBAwfo0qVLkffTwoX785lARq07/t8b9Xz4+ZFGNK1UngyDgQPhCcwJjIaIeDB/ay5OzHi6LZ+2a2JzfUIIXfRJvZd0PLvuGFvOBIG7C6ZxL9lMt17OSdsVBzhzJRw83TF93l8zTVqcj8dXHeToxTDw9kSMflEzHRL7UaZmoFFRUTz66KOsXbuWnJwc4uLi+PHHHxk/fnyxjKcW7AyOYdQGxaWKixNT+7bD9HYvRj7SmN4NqtO/aR1m92iNeLcPfqOep+399ZRt84yM3nCCoVtP6SL/7n8JBweHu0Zrb8mPwK1fx7odWPTKq03zo3EzsjkelaitGDtzND8C96H8YCoo2jUiuXcpUwbU09OTnJwc+vfvj5eXF126dGHs2LF8++23xR7Lnm27ApLS6b3iIJgEODty4I0nGduhGQ4ODhgMBtq2bXvT9s2rVODUy13Y+VZP8CoHwLKj12i1/ADZebZrw9a7d29dROGOHTtWF5GNa9euZdKkSRY/T83Jgzhlje85GxRQMBMcHMwLL7xgs/GLw7wRw9XX6zRMZ+nXr59do3BTsnMhQYmbeKKAAZ0yZYpu+vlKrE+ZdOFGRkYihKBOnTolHsNeLtzUnDwqzt8BMckAzH/pcd5+sMFN22RmZuLh4VHo/qEpmdy3bB9EK0+/jz1Qj8MvdcbR0fqznTvpsCdZWVmUK1dOaxkYDIbb1iYLsv36DZ5aqASJrX6tG/2blvx6vBt6+W4yMzPx/GMPxKZAfR/E270102HP87ErJIZef+wC4N+h3RjQTPmus7OzcXNz+5/wPvwvUqZmoGZq165dKuNpT4ZsO60az7e7tLzNeAJ3vBHUr+hB6lu9qNSwOgDHLoXx5g7bNDXWww0a0IXxBCWQxJLxBDgY8V8FosdrW78GbkH08t14eHgw3OzGDYsnKStXMx325ET0fxWIOtT8bwbq7u4ujWcZpkwaUGtgDxfuyahENp8OAqBBk1r89uRDt21jMBjo3r37Hcep4ObC9Ve6QnVvABYf8WPaSeu3++rfv7/mFW8Avv76azXdRUs2bdrEtGnTLH6+01xAoZInNTxtZ/RDQkJ00zGoc+fO9DMbUCHYEqxNRaChQ4eq6Vv24FBU/nft6U5dr/+M948//iijcMswZdKFaw169uzJ7t27berCdf9jJzkhseDkyNWP+tKscoVCt4uOjqZmzZp3HS80JZP7ft8GqVng5MjZD57moXyjag1u3LhBjRo1rDZeSUlMTKR8+fLFak9nC7Kzs8nOzsbb27vQzx2mrYHULDo/WJ+DL3W2qZaiXiO2Jjo6mko+1Sg35R/IM/Jc20ZseOExu+uIiYnBx8fnplQhW+IwZzPEJNOwaS2CXntCfT85ORl3d3fc3f+3ikr8ryBnoBawtdtl2ZUwxXgCbzzWzKLxBIp8Y6xf0YODL3cFBwcwmnj43yNkG6wXVKQH4wlQuXJlzY0nKO45S8YzNCVTeZABnqxjuwAiM3ownqDocHd2okVD5VrZGKBNU+vq1avbzXhm5xnVYLFet9Q69vb2lsazDCMNqAVsWQs322Bk6Pb8dUoPN37s1sritgaDgQEDBhR57M51q/JR9weUP24kMWKPb2mk3sSbb76pVvTRkmnTpqmVYLRkx44dFrugHI787zx1sbEBDQ0NZeTIkTY9RlF5/nmlWfgwsxs3JZNz+Wv89mTEiBFqpSdbcyYmSYmgJ783agF+/fVXXUSMS2yDNKAWsGUQwtST/pCorLHO6NkGb3fLsylnZ2cmTpxYrPFndG0F+Y2b/zx8hdMFAhxKw2effWZxxmVPBg8ezIMPPqi1DB599FGee+65Qj/bH6GUUsTRgfY26MBSkHr16vHee+/Z9BhF5bvvvgNu7s6yLsD+6SwjR46kevXqdjnWiRsFA4hu/q6ff/55OnToYBcdEvsjDagFbOXCzTOamHhEqb9KtYqMeqTRXfe5//77i3UMZydHLg54HBwdQMAz286UROptNG/e/KZSb1pRr149KlSw7PK2FxUrVrQY7b0yPH8GWqMSHi62bbvr4OBAy5b6KFxuvlabVa4AVZTvaL4GBrRp06Z3jJC2JofNBSPcXGhSqfxNn9WqVUsXD50S2yANqAXMBdGtzV9XwiBFGXtu55Y43WWdxmAw8H4JmvI+UNWL1x5rBkDs9Rv8c7X07qzPPvusSP0vbc2vv/6qFlzXkgMHDrB06dLb3jeaTGTkR+AOqGvb9BVQirp/8803Nj9OUXjrrbfU10Py3bgxwTEkZ9s3neWrr76yW0/QdfmxDLXrVLntwXvp0qW6aL0nsQ3SgFrA/CRdrVo1q4771uH82aenO2+2uu+u2zs7OzNo0KASHWtWt1ZQTnEPD9p+hjxj6Ur99evXTxf5hl27dqVevXpay6BFixa3VYkC8I1LgTylA8cTdXxsrqNGjRr07NnT5scpCq+++qr6elDz2soLk2BDoH2Difr27UvFihVtfpzYjGylaAQw6L7b7xUdOnSgSRPb16mWaIM0oBYYMmQIoLgtrcWe0FjIDy759LFmRW6u3K1btxIdr3I5N6b0aK38EZ/GD6XMDX3sscd0Ef3asmVLfHxsb5juRrVq1WjRosVt7x+O+C+A6PE6tp+BOjs78/jjj9v8OEWh4LXau351cFXc10uvhttVR/v27e1ScGNPWJz6uleD2w1o06ZNdRMhLbE+0oBawBY1X8ea1z6dHfmsfdGeSo1GIxMmTCjxMce0awI+XgB8tecCCZk5JR5r6tSpap9ULVmxYoXa11RLTp48yYYNG257f5+5ApGbCw9U8bK5jpiYGGbPnm3z4xSFcePGqa9dnZ14LN+Nu+dqFIZSekCKw8yZM+0SMb49JP8+4eRI59q3R1uvX79e7TMrKXtIA2oBawepBCSlc8ZPeQp//qGGVPcoWm6Yk5MTrVpZTnO5G85Ojqx+6mHlj+xcvjrqV+KxHnjggZt6ImpFw4YN8fKyvWG6G9WrVy90drE+38tQrXYVm9QkvpWKFSvSoMHtJSC1oHXr1jf9/XqLusqL7Fz2hccVsodtaNmypV2CiP4Kyf9/qlOl0GCxunXrUqmSbaOwJdohDagFrL3WN/N0gNrDc1LH291+d2LgwIGlOnb/pnWgvuLy/PVEAJn563PF5dlnn9VFHdpHH32UunXrai2D+vXr0759+5vey8wzwI1kAJ6vU7mQvayPu7s7ffv2tcux7sZLL710098vNq2pFPYAVlohkK2o9OnTx+YPWak5eZAfgftuIeufAI888giNGt090l5ybyINqAWs6f4xmQS/+QYrf9T34UGfogc3mEwm5s6dW2oNSx/PN9pZOcz3DSnRGAsWLCArK6vUWkrL5s2b7dqqyhKXLl26rSbvqej/kuptXUDBTEJCAsuWLbPLse7Gzz//fNPfPuXccct/eFtkRwO6ePFiUlNTbXqMfeFxkF8JtbcFA7pnzx5dLDdIbIM0oBawpqtyR0gMJCupK7MeKv7TqDVyUl9uXgcqeQLwcQnduK6urhgMJZu9WhMXFxeMRtv1PS0qTk5OmG5pYn6oQAUiW3dgMePq6qqL8wEUWj5vbIv8XNn4NC7F29aomXF1dSUvL8+mx9iRn76CAzxRt/CgtsKuEUnZQRaTt8DBgwfp2rUrISEh1K9fv1Rj9Vl7lB1nr4OzI4ljB1CpnDaRrF8fucKkbUoJwY3Dn6Bvo1p32UNSXHr8e5i9viHg6Y74ouglGMsyV+JTuf+njQB81edhJnXSR9GH0uKwYAeExkGtyogPntZajkQD5AzUAikpKVYZJz03jx2XwgDo2KJOsY2nEIJ//vnHKlpGPdxYTSsYffRasfdft26dzZ/qi8KhQ4eIirJ/dZtbCQoKui3Ccm/+DPSBuvZx3wKkpqaybds2ux3vTqxateq291pW9YKqynrkFDu5cTdt2mTT5YbsPCPkpysNteC+BSVSOzg42GY6JNoiDagFrOWqXOEXAbnKWJ881LDY+5tMJqutoVQq58rghxUN/tcii+1Ou379ul36pN6N6Oho4uPj776hjUlOTiY8/L/8xsSsHIhX0nx62yH/04zBYMDPr+TR1dbk4sWLhb7/Rn5RBVNoHHFZ2TbXERoaarWH4MI4FBkP+Wk5ve+zXHM3JiaGuDj7RR9L7It04VrAWi7cuov3EBEYDZ7u5I3ph7OTts8sVxPSaDFLyV0c0KEJ//aVha6txebr0fRduAeAdcO680KT2hor0g+7Q2Lo+ccuAH4b0JF32xT/YVJPfLb/IjN2K52Obnw5oMhpaZKyRZmfgV69epXIyMhi72eNWrjRGdlEBCklzIa2vq/ExnP//v2l1mKmeZUKtMyfDaw+e12ZNRWRgwcP6iIgwtfXl8TERK1lEB0dzbVr/7nCD4XbtwKRmaysLE6cOGG3492Jffv2Ffp+93o+alnJJXZw4x4+fNimyw1/mwOIfLzuaDz9/PxsUpRFog/KtAGNjIykY8eObNmypdj7WiME/p+rEWru59tFqHtbGAaDodB1pdIw/bH88oR5RmadCSryftu3b9eF4Tp16hSBgYFayyAoKOgmw7XLHIFbuTw+5ew3I0lNTWXTpk12O96dWLFiRaHvOzk60rOZ8uB2zD+KXCs2ei+MvXv32qyYvMFoIiJUccu+2ODOLdPOnj2rG/e6xPqUWReuEILu3btz4MABfv/9d955551i7W8NF+79y/Zx5WokeJXD9Fk/m7VIKwkOczZDTDJU9UKMKrynpaR4OExbA6lZdH6wPgdf6qy1HN2x5HIor688BNzbUeCHI+Lp/Nt2ABa81Im3HrxPW0ESzSizM9BZs2aVKhAoN7d07ZfSc/O4kt+B4sXmdUplPC9dulQqLYUx0dyHND6Vo5FFKxphCx0lITg4mIyMDK1lkJycrC4PhKdmQqoS9fmEnQoomMnLy7vJlawld7pGXmhUE/KXMVb42daNe+XKFWw1N9hpdt8CPevfuVtTRESETYOZJNpSJg3ohQsX+PPPP/nuu+9KPEZsbOzdN7oDG4NugEFZLxzaovCmy0XBYDAwceLEUmkpjDdb3Qf5Nv1X36JV9ZkzZ06pz4s1WLduHWfPntVaBqdOnVKLyR+J+s+13amWfUr4mYmNjWXOnDl2PaYlxo8fb/Gziu6u1M93ef59tfhxCcVhwYIFhIaG2mTs9aH5v4FKntSveOeSn1u2bOHYsWM20SHRnjLnws3JyaF9+/bMmTMHT09P2rZtq4kLVy2e4OpM1pcDi9y6zJ4UjBA2jO131+beEst8uPs88/ZfAgcH0r56ifKuti9kfi/y/YlrfLnpFACnRzzDIzXurULrBqMJl+9XQ3YuvR5qwI7++mgjJ9GGMnfH/Pzzz+nSpQtdunQp1TilKY1mNJnY4ac8YXdoWrPUxtNWRQO+bJPfwSMjm83X7x5wER1t36bIloiPjy+1i90aZGdnk5SUBMBGcw/QahXtbjxNJpPNAmaKy92u1UHN/vPGLL0SZjMdtrpWd4fGQrZy7fVvfPc13OTkZF3Uj5bYhjJlQHft2sVff/3FW2+9RVBQkOrCiY2NJSgoqFgpGAUT5IvLntA4yE8PeaNFvRKPA4oL99VXXy3VGJYY0qIu5Bv3Oefv7sYdOXKkLkLy586dy+HDh7WWwc6dO/njjz8QQhCR3wP02br2S18xExERwejRo+1+3MIYPHjwHT9v6O0J+Sk+P1+wjYsV4IsvvrBJw4Fl+S0JcXRgQNO7G9A///yTXbt2WV2HRB+UKRfuyy+/zJEjR9S/c3NziYmJwcvLi4oVK3Lx4kUqVixaJ5TSuHCHbTvNX0eugqMD8Z8PoIqHW7H2tydd/jnEoQuh4OJM2hf9peuxBPglpNJyllLrdcbzHfi0XdGapf+vMumoH19vPQPAiQ+epr2d14xLg8OMdZCcQe1GNYgY/qTWciQaU6ZmoCtXriQsLEz9Z87/nD59OmFhYRaNZ2pqKpMmTWL8+PHqvwULFgAwY8YMxo8fz/Dhwxk/fjzbtm3j5MmT6r5nzpxRo30vXrxIVlYWf5kjDOtUpoqHGyEhIWrwTXR0tDq7TUxMVPMZMzIy1JJ9ubm5nD9/HlDccwcPHlSPV/DYBXMQz5w5o7qdL1y4oLqNrl27pkYBBgcHq2XFoqKiiIiI4COzGzfPwN9XI0lPT+fKlSuAsp7s66tUWzEajRZ1FHx9+vTpm3RkZytl265evarm1hamAxTXbFCQkpealpam5s/dquPIkSOYTCaEEBbPx+nTp1WPg6+vLzk5ikfAz8+PtDSl3N7169fVkoCRkZFqRG18fLw6e0lNTVV1ZGdnc+HCBVXHqVOnyM7O5nDEf1HMnWtXuUnTqVOn1GhQSzqCgoLU9nkRERGqGzQuLk6to5qamsrVq1dv02EwGDh79iyZmZkIITh16lSh56OgjvPnz6su8CtXrqjlGQMDA9U83/DwcNUNGhsbS0hICKDUiDZH/GZlZaml+4qq4+TJkwx/oL4awDbPV/m+L1++rEZW36rD7J6OiYlRvUrJycn4+/vfpiMvL8+iDkvX7Llz59SiC5cuXVJ1BAQEqC76sLAwtlwMgGTls1dqeN6mIzMzU41CzsvLU8fVQwcjiW0oUwb0VsLClDWWuxVFcHZ2xsXFBXd3d/Wf+Ybm5uaGk5MTFy9exM3NDVdXV/744w/VQP3111/qj2zVqlXs9rsOicoN6b0qysxz586d6k340KFDagTp6dOnVVfk5cuXVVdPSEiIGt0ZFRVF165dAeUHanYZmkwm/vjjD9VALVmyhOTkZFWH2dW6fv169aazc+dO9SZ86NAhzp07x3ONaoGzcjebdv46ly9fZvfu3YBi6DZuVGZWsbGxdO3alZiYGDIyMvjzzz8BxcAvWLBANQxLlixRDfbKlSvVB4d169ap38f27dvVm/CBAwfUh4VTp06pEYuXLl1izx6lLF5QUJBaKODGjRt06tSJ3bt3k56ezsKFCwHFoC1YsEA1DIsWLVK/9xUrVqg61q5dqz7AbN26Vb357d+/XzXSJ06c4Pjx44DyUGSurhMUFMTmzZsB5UFo8ODBTJ8+nV3B+ettTo60qlKe+fPnqzfkgjqWL1+uGuw1a9aoDw5bt24lICAAUCr5mI3j8ePHVR2+vr6qjoCAALZu3apeH9OmTeOVV14hNTWVRYsWAcoNfMGCBerNe+HCharBLqhj9erV6oPDli1b1Ae6vXv3qkbp2LFjqsE5f/68WhnL399fLWIfERHBmjVreOyxx0hOTmbJkiU36TA/VC1cuBBvByPe+fVjl1wIRQhxk46C/V737NmjGqVbdRw4cABQHhK3b9+u6li7di1Dhgzh9OnT/PXXX4DyEDZ//nz1oerPP/9UHxyWLl2qGux///1XfXDYtGmTqmP37t38evK/mtQNUxStZ8+e5dAhJbf16tWr7NixA1DuPevWrWPq1Knqb1lS9ihTLtyCjBw5kpUrVxIfH4+HhwfPP/+8xSophVFSF+6YAxeZvku5EQeOfpFG3p7F1n4rQgibFmEYvPkkq477g4MD0Z/3o4ZnOU10FBW96DDjMH8HhMVB3aqId/tookEv56SoOmaeDuDT9crMdPfbvehxl3xKW+koDg5zN8ONZKhdBfH+U5rpkOiHMjsDnT17NnFxcQghyMjIKJbxLA3TzfltNSpZxXjagw9a57txhWDhRdtFRpZF8gxGyM8BHWLH+rf3OkPvrwuOimGZfyFEWzFFwD8xTTGewGcti57X7eDgYLOCDhLtKbMGtLSUJIIvJTtX7RH4bjPrlCkzGAy0bdvWKmNZoktdH6hcHoBJlyxHRvbq1UsXUbhjx45VXWVasnbtWt6bPB3y67p2sXMFIjPBwcG88MILmhz7Vlq3bl2k7XzKudO0ifIb+ediKAajdZsU9OvXz6pRuCsKFMB/pUXdIu83efJkVq9ebTUdEn0hDagFGjYsfrul3WGxkP+0+cwdegQWB2dnZ7ukbLzRUrkp5ITGEZtReL/GjRs3Ur26df6/SsOkSZPo3bu31jJ4/vnnafnUi+rfnWprMwNt0KABf//9tybHvpXidIX51FxDNjOHbUXIQy4OK1asKNFv2BLfXslPX6lSgTbVvIu832effcaAAQOspkOiL6QBtSJbr+fPzhwd6F7fx2rjlitX+JqkNXm5eb5bSgjWBBSeDG8PHUXB3V0fvRednJw4dEMJIMPNhRZVKmimRS/fTXF0DG5eR81DnncxRDMddyMmMxtTfvm+N4pZltPNzU2ugZZhpAG1gDl9oDgsDM43oHWqWi2f0mAw0K1bN6uMdSeUfo1K1PBCC4W+X3zxRV3Uwp0wYYIaoaslGzduZMNZJeWnep0qmt0oQ0JCbFZso7g8/njRS9t5ubnwWH5v2u2Xw8nOs16Ls1dffVVNvSkt/1yNVNsSvloM9y0oaXDr16+3ig6J/pAG1AINGjQo1vZJWblqMMn7Da3n5nR2drZ6P9DCcHJ0pHcL5WZ22j+q0JvZ77//TrVq1o2WLAkff/xxqUs1WoPHuz8BJqVJ9IsaBhDdd999/Pjjj5odvyBr164t1vYjzAFsOXmsuma9Di0zZ84scRvCW5lvdt96utO1bvE8S2+99RZPPVW0iF3JvYc0oFZiV1iM+pT6tBUNKGC3dcfXzE/XeQa2Bt++JqUH4wlQqVIlXFy0r5h0MSlL/c47axRAZEYPa9NQfB39mtSC/EpdH57wt5qOatWqWcUjEJeVzaX8JY3nW9bB0bF4Y3p7e+Pmpt9KZJLSIQ2oBYrr/tliXv90cqR7HeutfxoMBvr162e18e7Ec41qqP0al129fTYwfPhwNQFfS3744Qdd1ML9ffd/GrQKIAIIDQ1lxIgRmh2/IH379i3W9u7OTrzbrjEAGcExnI9NtoqODz74oFT1rM3M9w2B/AjhD1sXzysFMG/ePLXIg6TsIQ2oBerWLd5ax19mA1qnCp6uzlbT4ezszOTJk6023p0o7+pCi8Y1AVh3NeK2/LUvvviCSpW0bz81ZMgQ2rRpo7UMwty9lRcV3Knndee+kLakXr16ujGgP/zwQ7H3+axdU7W03/dWmoV+8skn1KhRo9TjjD+tlBqkSgV6liCy/sUXX+TRRx8ttQ6JPpEG1AJOTkVvQZaQmQPRSjTm/zUs/Y/2Vlq2bGn1MS3xljnKMDWLo5EJN33WtGnTYp0XW1GnTh3Kly+vtQyOxigl+lpp7L51cHCgefPmmmowU5JrtZG3Jw/ktzn759x1JZ+6lDRu3LjUbv5jkQmQH2X9xSONSjRGzZo18fb2LpUOiX6RBtQCxXH/7Az9LzL1qQbWXYsyGAzFbgZeGgr2a1x5S1DHJ598otb91ZJ58+Zx+vRpTTUkZOZAglJbto/GFYgiIiKYMGGCphrMDB8+vET7fdshv4NNroHffIsfAX8rX375Zal7gs48q9QFxsGBDx4qmQFdsmSJWrNXUvaQBtQCxQmG2GJOAndypGtd685GnJ2d7ZqiULtCObVf4y9XbjagL730Ep6e2pcn7N69O/fdd5+mGo5GF+jAUktbA1qjRg369NGmBu+tlNSAPt+4FuTn0X5uBTduv379SjXzy8wzsPp8CAAtm9WiToWS5ZV27NiRpk2blliHRN9IA2oBV1fXIm+7PD//07OeDx4u1lv/NGPvlI3PzG7cmGQCk9LV9x999NFinRdb0aJFC6pW1dZteqhAC7OOGgYQgfKQ1bFjR001mCnpterg4MDXHfINTWwKO0JKV5mobdu2pSqmsOxKOOQoHXXGP9K4xOM0adKEmjVrlnh/ib6RBtQC5h6EdyM2I1stMv1WA+uneRgMBsaPH2/1ce/Ey83/C6D6u0A07pQpU9SWWFqybNkytcWVVuyKUHJ+cUfzhuk3btzgp59+0lSDmc8//7zE+/5fm4ZqZaKvj18rlY4ZM2aUKmL8k9P57ltPdwY0rV3icdauXXtT71FJ2UIaUAt4eXkVabuC659PN7B+AJGzszMPPfSQ1ce9Ew9V91aLy88pUJXooYcewtnZ+jPs4tKkSRPNAzPORyo356ZVtSvfZ8bb25vGjUs+S7ImpWl8UMXDjWda3wfAiSsRhKdmlnisBx98sMTekkPh8WTke5XeeqQhLk4lv002aNBAc2+JxHZIA2oBD4+ipSUUXP+0VTeO/v3722TcOzE0vzZubEgMiVlKs+ynn35aFzVXO3ToQJ06xatJak3CUjMhVWmo/mpr7de33N3defbZZ7WWAVDqwunjOzRTXpgEYw6W3MvQq1evIj8E38p7B5RG4jg58vVjLUqsAZSHTmsWtZfoC2lALZCQkHD3jYC/8/M/K9X3wd3F+ikeJpOJ2bNnW33cu/GKubi8SbA2QIlm/P3338nMLPmswFps3LiRoKAgzY5/pEB6j1tU6SNGS0tCQgJ//fWX1jIAmDVrVqn2f7RWZRo2Vdqc/X0ygGuJJVsyWLhwISkpKcXe73R0Elfye/oOaNuoxMFDZnbt2qX5coPEdkgDaoGi5JDFZGZDrPIjHW7l9BUzDg4OmpSte7J+NXBXXGCL/JQm2+XKlcNotF7B75Li7u6OyWTd/pHFYV94nPLCAe730j6oSg+BXWasoeWfXg8phRVMguE7z5VoDA8PDwwGQ7H3++hg/uzT0YGpnR8o0bELoqfvRmJ9HIRsl14oBw8epGvXroSEhFgsSr3GP4IBf+0HYNsbT9LHBkUUtKTHv4fZ6xsCbi7kfDEAV2ftiyjoAYcFOyA0DupUQbwnC4Xbgt5rjrDznDK7P/ReHzrZoVjFpfhUWv28EQT0ebgh2/rpI7JZol/kDNQCRXH/HAjPd+U5wGO1KttEhxCClStX2mTsu/FafpNtcvLYHRrL6tWryc0tfZWY0nLgwAEiIyM1OXa2wQj5KSzPVHTRRYRlamoqmzdv1loGoDSytga/PdlGrcvcZ0fxZ6Hr168v9nLD6IOXlOYADjCza+lnn6A0GL9+/bpVxpLoD2lALVAU98/G8PwweZ+KVHS3javGZDLh72+9LhXF4bmGNSG/o8XawGjCw8N1sQYaFxdHYmKiJsc+HpWoFhdvW8GFqKjCm4/bE4PBQGBgoNYyALh69apVxmlQ0ZM3OyrlCTOCY1hdzFZnUVFRpKamFnn7szFJ7DivzHg7PVCfFlVKFoB0K3FxcbpowCCxDdKFa4G7uXCFEDhO+Qey83jmkUZsfvExDVTaHtVdWcMbMUIfkZ5a8tXhK0zefhaA8LH9Sx1kIrFMYlYOVX7cANm5UK0ihhHP4ORo/Wd+o8mE8/wdimfB0YHzI56hdTVvqx9HUvaQM1AL3G2m5ZeQBtlKpZInrFy+71b27Nlj0/HvxKdNlIhIbiSzasduTYN3zJw7d67IUdLWZnNofgBRJU8c05Lw8/PTREdBMjMzOXbsmNYyAOteq5XLufFVt3xXamwKc84W3RV68OBB8vLyirTtt8evqW75D7rcb1XjeeXKlSIXZZHce0gDaoG7Vdw5FPGfW6ZLbdsZUIPBwNq1a202/t14ofF/Zch+O3xOM9dpQc6ePavZutL5/MIZPer7EBwcrHlRe4D09HS2bdumtQwA/vnnH6uO9+WjzcBbqb/88ZbTXIgrWmrKwYMHiYmJuet2AUnpTNx1XvnDx4sfu7UqqdRC8fX15dq10lVVkuiXMunCNRgM+Pr6kpGRQbt27UqU/H83F+7gzSdZddwfXJwwfDXIJq4lPWAyCZy+/xeycun8YH0OvtRZa0macSU+lft/2gjA9OfbM7qd9kUU/hfYFBDFc3/tVQJ8fLxIee8pvNysk9pVZ9FuIoOUGeLut3vRo771y3FKyi5l7q4fEhLCww8/TNu2benatSs1a9bkxIkTxR4nJyfnjp+vyo/AdatdxebG09fX16bj3wlHRwc65c9CD12NwGTS/nkrKCiI9PT0u29oZfaGxamvn6jnQ2JiYrHa3tmK3NxcXbiSwTbXat8mtfi0R2vlj7hUeq07etd9Ll26dNflhmkn/VXjOaBDE5sYz7CwMJKTk60+rkQflDkDOmzYMN58800SExP59ddfSUlJ4bvvviv2OHFxcRY/y84zQrTiyhxi416QBoOhRPqtyeD8yjDkGtlyWftoz40bN3L+/Hm7H3dHWH7dYzcX2vh4c/bsWV2kj8THxzNv3jytZQAwceJEm4w7vesDtGyuFHU/cSmcr49cueP2CxcuJCwszOLny6+EM3bTKeWPih780dM29aa3b99eogd4yb1BmXPh+vn50aKFUr/SZDJRoUIFevTowcaNG4s1zp1cuAfD4+j6+w4A/nq5C0Pvr2cd8TolPDWTetOUddjRT7ZmupXXie4VHH7eCHGpNGlaC//XntBazv8ciVk5VPl1GySmgwP8+HwHPmnbpNjjbA2K5pm/9inpSK7OHH7jSR63Q6EGSdmjzM1AzcYTYNOmTbi7u/PNN98Ue5w7law7WKAXZCcbz0ABIiKKlwNnbep6eUB1bwBmBGif9xgXF2f3gg6xGdkQp+QVvlDfB4CsrCxdBFWZTCZd5KOCba/VyuXcOPVyV3B1BgGfrj/B5xYKzlvSsS4gkmeWH1CMp5MjW4Z0tanxTEpK0kXutMQ2lDkDCnDhwgX69+/Piy++SJs2bYrcWaUgd7oR7DbXQq3gToOKniWVWSQMBgOvv/66TY9RFN5okh+NGxZPcra21Yh+/fVXDh8+bNdj7g//L+q6R74B3bNnDwsXLrSrjsKIiIgoVR9OazJkyBCbjt+2ZiWOvtkT8nuw/rDzPA8u38/15IybtpswYcJNkdrZBiMf7fWl35J9kGsABweWDerM041s2+x60aJF7N6926bHkGhHmXPhAqxevZqgoCAOHTrEtm3bqFKlCmfPni1WC6w7uXAdZq6HxHQealmXs690tbJ6fbL5ejR9Fyo5fsuHdOWVFnXvskfZ4u2dZ/nj4BVwdCB9/CA8XbXvi/q/zJX4VO5fvBuS82d3Lk680aEpr7WsR+c6VXF0VCpohaVmsupqhNIazbytqzPLBz7+P3cNS6xPmTSgBRk/fjxTpkxh7ty5fPjhh4Vuk5SUxNdff32TWzAqKopNmzbxyiuvUKFCBfLy8nBxceGhLt1474pS5u+LXm0Y37ahOsPNyspSU2ZycnJwcXHB0dGR3NxcnJyccHJywmAwIITAxcUFk8lEXl4ebm5ut+2fmZmpjhsbG0u1atVue9/S64LjZGdn4+bmhoODQ4l0mF9n5xkpN3kVGE282L4Jy3s+eNs2ttRRcNyEhAS8vb1xcnKy2/nwWHZQqchUqxLig2cAJf/S0dERDw8Pi8ez9LooOoxGIwaDATc3N4QQ5OTk4O7uXuj/q8lkonz58qU6HwWv2by8PBwcHHB2dsZoNGI0GnF1db1Nx63fkT11hCen8t7+y2w7c0tOsJsLeLopbtqUW9yn1b25+HIXGno4W/y+3N3drXY+nJyccHR01KSjksT2lEkXbkG6dOkC3LmtkIeHB61ataJNmzbqP/MF37JlS1q2bMnevXtp3bo1CRX/a1vWpU5VXnjhBbXSyPDhw7lyRYkO/OSTTzhy5AgA3333HRs2bACUnppmt9/q1auZPn06APv27VPdcBcvXuTtt98GIDQ0lOrVlWNmZGTQo0cPhBCYTCaeeOIJsrOzAXjuueeIjVWiRIcNG6bWJP344485elQJ+588ebIaNfrrr7+yZMkSQEl+nzlzJqC4Jb/88ktASUl45513AIiPiQZ/paj3umuR9OjRA1DW37p166am/fTt21eNYB46dKhax/ejjz7i+PHjgBKpuWXLFgDmzp2r9rJcuXKl2k9y586djB8/HlAqD73//vuAkhZQtWpV9uzZQ2pqKr169QKUNevu3burD0FPP/20Wq3olVdeUWvFjhgxglOnlOjLCRMmsH37dgB+/vlnli9fDsDy5cvVHqzbt2/ny6+/USvVOAVeAJR0qQoVKjBz5kxSUlLo3bs3oLjcu3XrplbB6dOnD0lJSQC8/PLLqlvxgw8+UIswfPXVV+zcuROAn376SW0esGzZMubOnQvAtm3b1LX8kydP8n//938AXL9+nccee4yhQ4eSlJREnz59AMjLy6N79+5qTefevXurDRIGDRpESEgIAO+99x7nzinf67hx41R348yZM1m1ahUAS5YsUaN8N2/ezLfffgvA8ePH+eijjwAIDAzk1VdfpVOnTiQkJPDMM8pDRm5uLt27d1djCnr16qUWKRk4cKAaKfvOO++oKTBffPEFe/fuBWDGjBn8+++/gOIO/e233wAlEnvBzBlsfbEjsx6rBXkpSgs0gJw8JdCooPH09sDrym5y3+/DA1W96Nmzp5oK1b9/f3XJ5u233+biRaWl2ZgxY9i/fz8AP/zwA2vWrAHgjz/+YP78+QCsW7eO77//HoBDhw7x6aefAkow4+uvv8706dOLHcAouXco8zPQr7/+mm+//Zbw8HBq165d5P0suXBH7fXl570XwQGSx71ksyLyemTysat8tUW56V8e9Rwtq1qn4Lbe2R8WR/f5/ztR1/cq0RnZrLkWyd6IeFJy8nB1cuRhn4o83aA6j9aqXGaLnUi0o0wt5ISEhDBgwAAmTJhA7969OXz4MEuXLuWXX34plvG8Eweik5UXVbzsZjxNJhOOOvjxP9ewBl/lv14fGK2ZAbX3+dhToIBC93o+mmqxhNQBNT3dGfFwI0Y83Eg358M8P3FwcLjLlpJ7Ee2vMCvi5uZGeno6zz//PB4eHowZM4a5c+eq7r/iYKnW6vn8Agoda3qXRmqRMRgMtG3b1i7HuhufvjoQKihrPcs0TGcZO3YsO3bssNvxChaQL9h9Zc2aNao7U0uCg4N54YUXtJYBQJs2bbSWAEC/fv100YdzypQprF69WmsZEhtRJl24wcHBuLu7U7NmyUPUC3PhJmblUGWKsh4ztlcbpnaxTtPdu5GTk6MGtGhJTk4Og7afY8OpQHBxImvcS7g7O2miw57nw+G7fyEzhx5t7mP3gE7q+0ajESEEzs7aO3L0dI1IHf+Rm5t7x/gLyb1NmZqBmmnQoEGpjKclTt9IVl+3r1HJ6uNbQg83AlB0DDC3N8szsi/McrlDW+uwF1fiUyFTCZB6qn71mz5zcnLShfEEfV0jekAvOqTxLNuUSQNqDYKDg29771RMkvq6rZ0MqMFgoHNnfXRAef7552lfwQny13PWaOTG/eqrr+yWnH5rAfmCbNy4UY3A1JLg4GBefvllrWUA8Nhj+mgs/8orrxT6G7Y306dPZ926dVrLkNiIMunCtQaFuXCfXXeMLWeCoJwbYtxAu2mJi4vDx8fn7hvamPj4eKpWrYrD/B0QFgc1vBEjnrW7juTkZMqXL2+X2Z/6nbu5YBz3kpqgD4qbMDc3lwoVKthcx93QyzWiFx3x8fFUqVJF8+Cd1NRU3N3d5Uy0jCJnoMVgS7QyA61ey37uW0AXNySAqlWVmqGfmMv63UgmIi3L7jq8vb3t5jrdkh9A1KS+z03GExQ3oR6MJ+jnGtGLjqpVq2puPAG8vLyk8SzDSANqAXOiuRmD0QQxyQA8Zcf1T4PBwPPPP2+3492JYcOGER8fzwuNa6nvbQqMtruOqVOncujQIZsfJyYzG+JvLiBfkG3btjFnzhyb67gboaGhfPDBB1rLAFALKGjNe++9p4terXPnzmXbtm1ay5DYCH1EQOiQevVuTpa/lJCqlAYDHq1pPwPq7OzMtGnT7Ha8O/HVV19RuXJlOgK4u0J2LqsCInn/oYZ21TF06FC8vb1tfpwDYbcXkC9Ip06ddJG2Ua9ePUaNGqW1DAC1opXWjBkzxiaBhMVlwIABJWpmIbk3kDNQC9yahH3qhv0DiMw0a9bMrsezROPGjXF0dMTJ0ZGOTWoAcCDgBiaTfZfRa9eujaenbbvgAOwyN9B2dKBTrdtbXlWoUEEXN2kHBweaNm2qtQxAP9dqw4YNdREhXaNGDby8/jcqdv0vIg2oBW51/5zIX//EyZEHfSraTYfBYODNN9+02/HuxKhRo/6r69okv7JTVg7Ho+3bE3Pu3LlqPVtb8kdIfgRurcqFdl/Zt28fixcvtrmOuxEeHq7WDdaaYcOGaS0BgM8//5zoaPsvL9zK4sWL1Xq6krKH9o9oOqVGjRo3/b3bbECrVcTFyX7PHc7Ozrzxxht2O96dGDJkCOXLlwfg+cY1+b/89//1j6Rjbds3FjfTs2dPNaDJVqRk50KE4sJ9475qhW7zwAMPWK1EZGmoVasWffv21VoGgNp8QGteeuklKlWyr6eoMDp37qz+ZiRlDzkDtcCt7YdC8w1obzuuf5p5/PHH7X7MwmjXrp16Xup6eUD+ufjpaqRddTRr1owqVWxrsHeExkC+a/q5xoW7aX18fHThOnVycqJDhw5aywD0c60+/PDDaosxLWnUqJHaTUlS9pAG1AIF3T+RaVmQobQNe9zOBtRgMPDFF1/Y9ZiW+Pbbb0lNTVX//rB5/uwrMkE5R3bir7/+UltO2YqNgUqLOpwcebJe4TPQ48ePqy2utOTGjRu6Cd757LPPtJYAwLRp09S2elqyZs0aTpw4obUMiY2QBtQCFSv+t855ukAFonbV7WtAnZ2dad++vV2PaYmCM1CAwc3qqK/X+NtvFtqiRQsqV65s02MsD1IMqHc9n0LXP0EJZrrvvvtsqqMoVKpUiRYtWmgtA4COHTtqLQHQ1wy0WrXCH8Ak9z6yEpEFClYimh+Wznc7lKbDseMG4FNO+x+mHhBC4Dh1DWRk81DLupx9pavWkqxCRFoWdX9QZpaf9WzNtK6tNFYkkUj0iJyBWiA+Ph5adyY0PYcj5ijTih52N55Go5FZs2bZ9ZiW+PXXX8nMzFT/dnBw4KnmSlGFcwHRZOcZ7aJjw4YNBAQE2Gz8rddvqK+fbVjD4nYXLlxg165dNtNRVOLj43URDQwwY8YMrSUA8Mcff5CcnKy1DHbu3Gnz5QaJdkgDagFXV1fw9qHrqlMcyF8Pa6lBAJGjo6Ndch6LgpeXFyaT6ab3Xm1eV3mRZ2B7yI1C9rI+np6eNi3TtjYof/3bzYXH7xBd7ObmpotcQ3d3d13oAHQTcVrYtaoF5cqV00Vjb4ltkC5cCxw8eJCu738GL/6f+l7tRjX4tVNLXJwccXNyxMXJER8PN5pV1kc9VC1Iy8nD67t/wWhi0KNN+ftZfazXlgaH6WshJZM2LepybkjZcEtLJBLrIx+NLJCcnAwJNydiRwbd4Lkle3lq4W6eWLCTzgt2Ep2ebVMdQgiWL19u02MUlX/++Yfc3Nyb3qvg5kL9BkqY/io7pbPs37+fiIgIm4x9MS4FUhQ39UuNLbtvAQICAnQRYZmSksKmTZu0lgHA0qVLtZYAwLp168jIyNBaBseOHSMoKEhrGRIbIQ2oBUwmEyTG3HGbxS89Trd6tu0+IYTQRV9DUFJ7Cq6BmnmneX40bnIGZwtELNuKxMREm61vbS7i+idARkYGMTF3vkbsgclk0s01cv36da0lABATE0N6errWMkhKSlKrd0nKHtKFawFzFC6TVkKO4bbP/697K2b3aK2BMv0RmJROkx/XAzC2VxumdnlAW0Gl4KHlBzjvFw5e5RBj+mstRyKR6Bg5A7WA6v7xdLvts/qNazKru/1SG/QQ6Qmwd+9ejMbbI20bVyoP1ZS82R/s4MY9e/YsCQkJVh/XaDJxPn8G2qvRnWefAJGRkVy5csXqOopLZmYmR44c0VoGoJ9r9cCBA7ctN2jB5cuXdVGTV2IbpAG1gGpA3W+JbvR059jAx3GyU2SdwWDQzfrW/v37Lbqj3jZXJQqPU/po2hBfX1+buCyPRiZCTh4A/RrdvctKaGgoZ8+etbqO4pKenq4bw7Vu3TqtJQBw5MgRYmNjtZbBxYsXbZpyJdGWMunCzcvLw9fXl5ycHNq1a1eijvBmF+59C7YQEvJft5HVr3Wjf9M6d9jzf5N9obE8sWAnAPMGdOT9NvbtEWoNxhy4yPRdvgCEj+1PnQrlNFYkkUj0TJmbgV64cIEWLVrQrl07OnXqRK1atTh9+nSxx8nJyQHAu0Dnld4PN9TEeJ4/f97uxyyMO+noUrcqlFPc3Uuv2iZC1kxgYKBNAkQWmOvfVqtYJOOZmJhIWFiY1XUUl9zcXF24kkE/1+qFCxd0kQcaGhoqg4jKMGXKgKalpTFw4ECGDRvG6dOn+eqrr0hISOC1114r9ljx8UorKydzwn45V/7q/bA15RYJg8HADz/8YPfjFsaCBQssusWcHB3p0Uxxex4LiCbPaLub15YtW/D19bXqmBm5BpLDlOLjQ4qw/glw7tw5tm7dalUdJSE+Pp7ff/9daxkATJkyRWsJgJJOc2tPXy3YtWuXXXrXSrShTLlwL168yIULFxgyZIj6XuvWrblw4QJxcXHF6iFpduG2WbiN80HxTH++PaPbad+6Ss8suhTKG38fAmDrG0/y1F3SQPTEP1cjGLRsPwD/Du3GgGbSTS+RSO5MmZqBtmrV6ibjCfDII4/g5eWFt7d3scYyGJTUlWSjCapVZNTDja0ls9jo4Uka7q7jhUY1wVGZsa+0oRs3NjZWdbFbi8V++a5YFyeeLqLhz8zMtEk0cHExmUxERtq3J6sl7pVr1V4kJiYWmjstKRuUKQNaGCdPnqRbt27FrhVqviGF5JpY3rMNzk7anCqDwcBbb72lybFvZcyYMXcsHFCpnCvV7lOqEi31s90N7Pfff+fo0aNWG89oMrHtivJ9P9KkFh4uRbtW9u7dy5IlS6ymo6REREQwbtw4rWUAMGzYMK0lADBx4kRdFJdYsmQJe/bs0VqGxEaUKRfuraxevZo33niD48eP07Jly2Lta3bhtl28nRNDe+HoaLvi5WWJH05c4/NNyprPwXf70Llu0d3mWrEj5AZ9/tgNwG8DOvLuPRhBLJFI7E+ZnYGGhYXx7rvvsnjx4iIZz9zcXLKystR/Zhfh0Hre5ORkq+8XVkjA1qSlpdn9mIVRFB2vPVAf8gOvFlwMsYmOzMxMq34Py67kz5YdHRjYrHaR9zOZTLpxz91L14g90IuOnJwc8vLytJYhsRFl0oBmZmYyaNAgxo4dS79+/e66fXJyMjVq1KBy5crqv6effhpwYPSzPahUqRKenp5UqlSJkSNH0rVrV/XG+eyzz6qVRoYNG8bly5cB+OSTTzhw4AAA3333HWvWKA2a58+fr0ZMrlu3To1aPHjwIB9//DGgVC8xu8JCQ0Px8vIClOIO3bp1QwiByWSiS5cuZGcrRQuefvppNUL21Vdf5erVqwCMGjWKw4cPAzB58mTWr18PwG+//cYff/wBwJo1a5g6dSqgVHD59NNPASUoa/jw4YDi0vby8lJrjHbv3h1A1WF+4HhjwIuUr1sZgKUHz+GXr2PkyJGq23XSpEls3LgRgHnz5rFw4UJAKVZvjjjeu3cvn332GaAUTnjjjTcA5cHI09OTvXv3kpqayhNPPAEofVM7d+6sVp/p1auXuj45ePBgAgMDAfjwww85fvw4AF9//TVbtmxh2ZX89Vp3I5XLufH333+rfS13797N559/DihRt2+//bb6vTg5OTFr1ixSUlJ48sknAcXl3rlzZ/Wm2bNnTzWN4aWXXlJrxb7//vucPHkSgK+++opt27YBMHv2bP766y8AVqxYwcyZMwGlr+SXX34JwJkzZ3jnnXcACA4Opm3btgwbNoykpCR69uwJKLnQnTt3Vtfye/ToQUpKCgADBgwgJCQEgHfffZczZ84AMG7cOHbs2AHArFmz1CYGS5cu5aeffgJg27ZtjB8/HoBTp07x/vvvAxAUFMSgQYPo2rUrCQkJ9O7dG1AeTDt37qw+8DzxxBOkpqYC0K9fPzUN6O233+bcOaVp/RdffKEWhvjxxx9ZuXIloLhD58yZA8DWrVuZMGECACdOnOCDDz4AlAL/gwcPZvjw4Zw4cYI+ffoAiiHr3LmzmtrSvXt3NRXqhRdeUJsTvPnmm2qE95gxY1T36/Tp01m1ahUAixYt4pdffgFg06ZNTJw4EVAKx//f/yndm65du8aQIUOYPn26bgqhSGyAKGPk5OSI3r17i3HjxqnvxcbGiqlTpxZrnAMHDghAhISECCGESEpKUj+z9Do5OVl9nZKSor5OS0sTBoNBCCFEZmamyMnJUbVmZmYKIYTIy8sT6enpQgghjEajSE1NLXTc4uoo+LqgjoyMDJGbmyuEECI7O1tkZWVZTcfPpwME45YKxi0VO4Nv3LZvamqqMBqNNtdxt3OTmpoqjoTHqVqnHLl8m47c3FyRkZFxmw6TyWTxPJdER2HnIysrS2RnZxeqIy0tTdVR8ForjY6UlBRhMpmEEEKkp6eLvLy8O+owGAxF0lHc10XRUfC3U1Qd1jofln7Dd9IhKZuUqTVQo9HISy+9xN69exk9ejSgPHlu3bqVdu3a8euvvxZ5LPMaaEhICPXr17eV5CJhNBpxcnLSVENxdCRk5lB16mowCQZ0aMK/fTtYVYfJZLJak+KRe3yZs+8iAKFj+lHPy6NY+99r343UYV/Mt1dbNoCXaEeZcuHOnDmTtWvXkpyczPjx4xk/fjzffvstZ86cUV1bRUUvbZkMBgPt2rXTWgYAffr0KVL7rioebrRoUguA1RfDMFi5qMLYsWNVV2NpmWNe/6xTpdjGc82aNUyePNkqOkpDSEgIL774otYyAGjTpo3WEgDo37+/Ln7DkydPZvXq1VrLkNiIMjUDtSZ6moHm5uaWqJ6vljrm+wbz7r9Kh5CNw5+gb6Namui4E1cT0mgxawNQsjZsJpMJIYQuZjr34jXyv6AjLy8PFxcXrWVIbESZmoGWVfRwI4Di6RjUrDY4K5fX7xdCNdNxJ5YXyFUd0qJusfd3dHTUhfGEe/MasSV60SGNZ9lGGlAL6MH9A4oLt1OnTlrLAOC5554rcouoiu6utM0vh7flchi5BuulnYwfP57du3eXepzJZvetjxetfCoWe/8NGzbw3XfflVpHaQkODmbw4MFaywCgQwfrrneXlJdfflkXhRSmTZvG2rVrtZYhsRHShWsBPblwExISqFKliqYaSqJjyeVQXl+p1MZdNbQrLzUr/iyvMFJSUvD09Cx2damCRKZlUecHJbXo3a7381vPh4o9hjnHr3z58iXWYS3u1WvEViQmJlK5cmWtZZCWloa7u7uciZZR5Az0HkAPNyQovo4BTWpDflm86WetNxuoWLFiqYwnwN8FavW+WgL3LYCbm5sujCfcu9eIrdCD8QSoUKGCNJ5lGGlALWBONNcag8HAc889p7UMAIYOHaq2eSsKnq7OPNtamb2fvhJOeKp1qvZ8//33HDp0qFRjTL+Uvy7rVY7Ha5fspr9t2zZmz55dKh3WICQkRC1ooDVPPfWU1hIApUCEHnq1zp07Vxct7yS2QbpwLbB//366d++uCxduQEAATZo00VQDKNVmGjRoUKwczJNRiXSYp9xARj7Rip+faF1qHVFRUXh7e+PhUby0EzMBSek0/XE9AK893pwlT7Ut0ThpaWlkZGRQo4a2bduEEAQFBdG4sXYdg8zo5VoNDg6mbt26pfZUlJaYmBg8PDyoUKGCpjoktkHOQC1grUR9a6CHGxJAo0aNin1e2teqDPkF5WefDrRKo+1atWqV2HgCzDoTqL7+tG3Jz22FChU0N56gJOnrwXiCfq7VBg0aaG48AapXry6NZxlGP1ZCZ+iln6DBYFDrwGrNRx99pNZ1LQ7zOuQ3Ik/NYsXV0p/XOXPmqHVki4vBaOJXswGt78ODJYi+NbN3714WLVpU4v2tRXh4uFonV2uGDh2qtQRAKbYRFRWltQwWLVrEvn37tJYhsRHSgFpADzMLAGdnZ7WAudYMHTq0REEzw++vD+XcABh13L/UOnr37l3iGdfqgChIUwrwz2tXutnSgw8+qIsUo1q1avHCCy9oLQNALequNYMHD9ZFIFHXrl2L3UpRcu8g10AtoKc0lrLAWzvO8uehKwD4ftS3VDO/0tBy6T78rkWCmwvpY/vj6aq9m08ikdybyBmoBcwtyrTGYDAwduxYrWUAMHHiRLUVVXEZ276p+vr7E9dKpWPJkiVcuHCh2PuFpmTi5x8JwKCHGpTaeB47dkwXdU6jo6PV9mtaY26FpzVTp04lLi5Oaxn8+++/avs8SdlDGlALeHt7ay0BUFy4HTt21FoGAI899liJS6Q1qVSeJk2Verh/nwsmLafkTYbvv/9+qlatWuz9Zp8NhHx/y+hHSh/sUqdOHRo2bFjqcUpL5cqVeeCB4tXxtRVdunTRWgIA7du3x93dXWsZNG3aVDfLQRLrI124FpAuXOuz+loEA5fuB+CH59ozpsCs1NaYTAKnmeshOQPqVEG8p498RYlEcu8iZ6AW0IP7B5S+hj/++KPWMgD45ZdfyMwseTGEfk1qQ2UlCGns/otk5BpKNM66desICAgo1j6r/SMV4wnMKkXqSkF8fX2t1latNMTHx7Nw4UKtZQBK7Vc9MH/+fJKTk7WWwfbt20u03CC5N5AG1AJ6cP+Ako/q5eWltQwAKlWqhMlU8jxOR0cHfu+RX0ghNYuJx/xKNI6Xl1ex81EHHbikvHB35c1W1vEolCtXThfXibu7uy50gH6WPipXrlyqa9ValC9fXhf5qBLbIF24FpAuXNtgMgmcftsKUUng6syN0S9Q3cO2N/+tQdE8s2gPAB890YqfrFANSSKRSOQM1AJ6cP+A0rR56dKlWssA4O+//yYnJ6dUYzg6OrCxd37nk1wDn+67WOwx9u7dW6xCF8MPXFZeuDrz1aPNi308S/j7+3Ps2DGrjVdSUlJSWL9+vdYyACVCWg+sXr2ajIwMrWVw9OhRAgMD776h5J5EGlAL6MH9Y0YvVZHi4uLIysoq9Th9G9WiTuOaACw/4Y9/Ylqx9k9JSSlyOs3B8Dhir98A4I32Taji4VY8sXcgMzOzWMX1bYUQgoiIiLtvaAf0UMAdlHZm6enpWssgJSWFlJQUrWVIbIR04VpAunBty6noRNr/ohSZ79SqPocGdbbJceou3kNEYDQ4ORIx+kVqVyhnk+NIJJL/PeQM1AJ6eHo1o4dIT4Bdu3ZhNBqtMla7mpXp0eY+AA5fDOVIRNFncqdPny7SzG+lX7hiPIGX2zexuvEMDw/n0qVLVh2zJGRkZJS6vZu12L59u9YSAMXNn5ubq7UMLl68SGRkpNYyJDZCGlALlCZdw5oYjUa2bdumtQwAjhw5YtW14d+ffAiclEuw0+ZT5BqKZpwvXbp0136tmXkGXtl6WvmjnBtzuj9YGqmFEhERoYsUhczMTN0ULN+8ebPWEgA4efKkLlLR/Pz8uH79utYyJDZCunAtIF249uGdnWdZcFCpkdu/fRNWP9fBKuN+uu8CM/coxu3HFzrwiZVyPyUSicSMnIFaoLTRptbkzJkzWksA4OzZs1Yf85cebaCeDwBrTgbwy7mgu+7j7+9PWprlwKOLcSnMNEfe1q7MqIdt0yszISGB0NBQm4xdHHJzc3XhSgb9XKvnz5/XRSBgSEgIiYmJWsuQ2AhpQC2QkJCgtQRAKSY/c+ZMrWUASm/D2NhYq47p4uRI+MtdwFPJBR2x4QQno+58w7lTdZfUnDweXHEADEZwgP3PtMPR0cGqms34+vrqYs0vPj6eP//8U2sZgH4qEa1YsUIX0et79uzh9OnTWsuQ2Igy78IVQnD+/HmaNWuGh4dHkfeTLlz7sjskhp4Ld4NJQCVPrr/ViwYVPYs9Tse/D3LskpJK8emTrZnRrZW1pUokEglQhmegcXFxvP3229SpU4eHH3642AEFBkPJ6rTagrsFzNgLW+p48r7qTHrqYeWPpAwazt+Bb2xyodveuHGjUBf7qL2+qvFs0aw207vatkNJRkaGLgJVjEajLmZboJ9rVQ+udVC8A3oo6CCxDWXWgHp4ePDyyy/TqFGjEu0fFRVlZUUlw2Aw8N5772ktA4Bx48YRExNjs/G/eqwFb3ZuqfyRkkmb+Tv559rthuHPP//k6NGj6t8Go4kXNhzn5735VY0ql+fwgI44ONjGdWtm//79LFu2zKbHKApRUVFMmDBBaxkAvPnmm1pLAGDy5MkEBwdrLYNly5axd+9erWVIbESZd+GOGzeO7777rtiuWOnC1Y4Jh6/w7fb/ApZaNq/Nqj6P8EDV24vqn45O4tntZ4gJUqoNUcmTi8N6FLqtRCKRWJMy3yagKF07cnNzWbZsGdnZ2ep75nZZf/31F1WqVFHfb9WqFZ0726ZqjiVSUlKoWLGiXY+ppY5JnVpSv6IHb204Cdm5XLkaSaurkeDjxRvNalO7nAs5ODA/8AbJwQVmxHWqEDW0OzU97dOZxGg0kp2djadn8ddqrc3/2jVyr+jIysrCycmpxI3oJfqmzLpwi4PBYOD8+fNcunRJ/Xfq1ClASZk4f/48v/76KxcvXiQsLIwRI0aoxnbs2LHqOth3331HUJCShjF37lw17WPZsmVqovumTZvUwt8HDx5Ui2/7+vry888/AxAcHMzkyZMBxT1nbhGVmZnJyJEjEUJgMpkYMWKEuhY4ZswYNXK4oPtq9uzZnD9/HlAeBg4cOADAhg0b2LhxIwAHDhxQC9afP3+eOXPmAHD9+nWmTJkCQGxsLN7e3sTExJCRkcFHH30EoOowV3357LPP1LD9SZMmqWtiP//8sxo5u3jxYrVyzvr169m0aRMA+/btU12iD+Ul8p1XHM+1LeCCj0tl4WE/vt11gWm7fP8zng4OPNnmPt66uJWqrk4AfPrpp2rRh4kTJ6o1WmfNmqWmfCxcuJAjR44AsHbtWrZs2QIokZMrVqwAlLSMX3/9FVAeqqZOnQoo67APPPAAP/30E2lpaYwaNQpQrqURI0aoa+iffPKJWrf366+/VmvWzpw5k8uXlVSbgi7p1atXq4Uzdu/ezcqVKwE4deoUv/32GwDXrl3jhx9+UK+PV199lTfeeIOUlBQ+/vhjAPLy8m7SMWrUKDX156uvvlKr48yYMQM/P6Wt3IIFCzh+/DgA//zzj1oBa+fOnaxatQqAEydOMH/+fEApEjB9+nQAIiMjmTBhAk888QTJycl8+umngPJwOmLECLWC1UcffaRW+Ro/fjzR0UqlqOnTp3Pt2jVA6eV58uRJAFatWsWuXbsAJfr633//BeD48eMsWLAAgCtXrjBjxgxAqQ719ddf89Zbb3H69GlGjx4NKGlpI0aMUFNbRo4cqa5Njhs3jhs3FA/GDz/8gL+/PwC//fabeh9YuXIlu3fvBmDr1q2sWbMGUIrFmyOgL126pEbMh4WFMXHiRGbOnKmb4hISGyDKOOPHjxeACAkJKdZ+e/bsuWm/AwcOqJ8dOHBAmEwmIYQQhw8fFgaDQQghxPHjx0VWVpYQQoizZ8+K1NRUIYQQV65cEbGxsUIIIYKCgkRYWJgQQojIyEgREBAghBAiPj5eXLx4UQghRFpamjh9+rQQQojc3Fxx9OjRm45d2OtbdWRnZ9+m4/LlyyIuLk4IIURgYKAIDw8XQggREREhAgMDVR2XLl1SdZw5c0YIIUROTk6RdBw6dEjVcezYMVXHmTNnRFpamhBCiEuXLon4+HghhBABAQEiIiJCCCFEeHi4qiMuLk5cvnxZGSc4Ugz9e6dg/nbBuKX//Zu8SvT6c4O4npxeqA6j0ajqyMnJEUIIcfr0aZGermx/8eJFkZCQIIQQwt/fX0RGRgohhAgLCxNBQUFCCCFiY2PFlStXhBBCpKSkiHPnzgkhhMjOzhbHjx8XQghhMpnEwYMHLZ4Ps46jR4+qOk6dOqXquHDhgkhMTFR1REVFCSGECA0NFdevXxdCCBETE6PqSE5OVnVkZWWJEydOCCGEMBqN4tChQ+qx9+/fr74+ePDgTTpyc3NVHRkZGUIIIXx9fVUd165dE9HR0UIIIUJCQkRwcLAQQogbN24IPz8/IYQQSUlJ4vz580IIITIzMy3qKHg+Dh48qP52Cuo4efKkyMzMVHUkJSUJIYS4evWquHHjhqrD/HuMjo4WV69eVXX4+vqqOk6ePCmEEMJgMIjDhw9bPB9mHUeOHBF5eXm36Th//rxITk4WQgjh5+en6ggODhahoaFCCCGioqLEtWvXhBBCJCYmigsXLgghhMjIyBCnTp0SkrJNmV8D/eqrr5g8efI9vQZqMBh00ZRXDzoMRhPJWTm4uzhT3s1FUy2gj3MidehXhxACIUSxG8BL7g3kt2oBvdSvNBgMtG/fXmsZAPTp08emUbhFwdnJkR8mTuDIfu0jG9esWaO6uLUkODiYfv36aS0DgIceekhrCQD0799fF7/hyZMnq+5eSdnjf2YGGhwczH333Vfk/fQ0A83Ly8PFRfvZltRxM+b1ND3MLvRyTqQOfeqQ2Abtf/k2xhzgo4fGxyVFLz9AqeNmHB0ddWE8QT/nROq4Gb3okNgGffz6bUBoaCiPP/64GqnXp0+fYhUk0IP7BxQXbseOHbWWAcCzzz6ruQsXlKhJc2SmlmzYsEE3LtyXXnpJaxkAtGvXTmsJAAwaNEgXv+EffvhBunDLMGXehVtS9OTCTUpKolKlSppq0JOO1NRUPD09cXJy0lRHbm4ueXl5usgD1ct3I3XcTHp6Ou7u7roIaJJYH/mt3gPo4UYA+tHh5aWPKkOurq66SZDXy3cjddxM+fLltZYgsSFl1oVbWvRSFNtgMPDMM89oLQOAIUOG6KJ4+pQpUzh48KDWMti6data/EJLQkJCeOedd7SWAUCvXr20lgDA22+/rRbP0JLZs2erBTokZQ/pwrXA/v376d69uy5cuEFBQSUuim9NgoODqV+/vuaBMzdu3MDLy6tY7elsQXp6OhkZGVSvXl1THaCs2Tds2FBrGbq5VkNDQ6ldu7bmrtPY2FjKlStHhQoVNNUhsQ3SgFpAT2ugEolEItEf0oVrAb30VzQYDAwbNkxrGQCMGDFCrXOrJT///DMnTpzQWgZ79uxR66BqSXh4OJ9//rnWMgB45ZVXtJYAKDWZ9dCS8M8//5TtzMowMojIAjVr1tRaAgDOzs588MEHWssAlF6Pegjgefrpp6latarWMmjTpk2xinPYilq1ajFw4ECtZQCoTQa05tVXX72pi5JWPPHEEzKQqAwjXbgWkC5ciUQikdwJ6cK1gLnNktYYDAa1JZPWfP3112prLi1ZtGgRvr6+Wsvg6NGj/PPPP1rLICoqimnTpmktA0Bt66Y13333HbGxsVrLYNWqVRw7dkxrGRIbIV24FtBLHpmzszPdunXTWgYAnTt31kXeY+vWralWrZrWMqhfv77mkcAAVapU0U0R9yeffFJrCQB07NhRF99Ny5YtdbHsIbEN0oVrAenClUgkEsmdkC5cC+ihYACA0WjUjXtu9uzZZGRkaC2DNWvW4O/vr7UMzp07x/bt27WWQVxcHH/88YfWMgD4/vvvtZYAwG+//UZSUpLWMti2bZsulhsktkEaUAu4u7trLQFQOn7oIeIUoHr16ujBYVG5cmXNE+RBKdOmBzehh4eHbiI99eBaB/3oqFixIm5ublrLkNgI6cK1gHThSiQSieROyBmoBZKTk7WWAChNmxcvXqy1DACWL19OTk6O1jLYvXu3LuqcXrt2jSNHjmgtg+TkZNauXau1DAAWLlyotQQA/vnnH9LT07WWweHDh3Wx3CCxDdKAWkBPE/MbN25oLQGAlJQUsrOztZZBRkaGLm6OOTk5unnQ0ss1ohcdqampZGZmai1DN9eqxDZIF64FpAtXIpFIJHdCzkAtkJaWprUEQJkJb926VWsZAOzYsQOj0ai1DE6ePKmLKOmwsDAuXryotQwyMjLYv3+/1jIAdNO6a/fu3bpYbvD19SUiIkJrGRIbIQ2oBbKysrSWAChroHv27NFaBgAnTpzQhcvy6tWrulgDjYqK4tKlS1rLIDMzk8OHD2stA4CdO3dqLQGAs2fPEh8fr7UM/P39ddNbWGJ9pAvXAtKFK5FIJJI7IWegFtBDsIyZU6dOaS0BgNOnT+siuOratWu6qMkbHx9PcHCw1jLIycnhwoULWssA9HOtnj17VhfLDdevXychIUFrGRIbIQ2oBfTQ9xKUYvJz5szRWgYAS5cu1cXa465du3ThOr148SK7d+/WWgaJiYksWbJEaxkAzJw5U2sJgJLGooe1x/3793P27FmtZUhshDSgFtBLP9DU1FRGjhyptQwAnn32WXx8fLSWQadOnWjcuLHWMrj//vtp166d1jKoXr06Tz31lNYyyMnJ4b333tNaBgD9+vXTRbWqp556igoVKmgt467s3bv3triPkJAQ1q5dS15enkaq9E+ZM6B5eXksXryY5cuXl2ocPbgIAY4cOcLnn3+utQwAXn/9dcLDw7WWwQ8//MC6deu0lsHWrVuZNGmS1jKIjY1l8ODBWsvg+vXrvPXWW1rLAODHH39k27ZtWstg06ZNTJ8+3SpjpaWl8eGHH1o1KCk7O5sePXrQo0cPhg4dqr6/bt06WrZsSf/+/Ut9Ly3LlBkDmpiYyPTp02nUqBHDhw+nbt26pRpPT/1A9ZAqAUrFGz30WAwICCAwMFBrGVy5ckUXEZbR0dG6KPIvhNDN78bX11cXyw1Hjhyxmo4KFSpw+PBhGjduzMsvv8zx48dLFZMghGD48OFkZWXh4eHBhg0biImJ4fjx4wwZMoRBgwbxyCOP6MLLolfuaQNqTvEYOnQotWvXZsyYMYSHh1OuXDk6dOhQqrHr1KljJZWlw8nJqdT/L9aiatWqunDhtm7dmubNm2stg4ceeohmzZppLYPatWvrxk1Yr149rSUAiptfD9fqU089Ra1ataw2Xrdu3TAajfz999889thjPPzww8yZM6dERjovL4+aNWuyb98+XnrpJQwGA/Pnz2fw4MF8//33LFq0iNOnT3P//fdbTX9Z454zoBkZGWzevJn33nuPWrVq8eSTT7Js2bKbomYfffTRMtUBQS9rECaTSWsJgHI+9BBhaTQa5XdzC3r4XgBdFFEARYc1z0m3bt1u+vv8+fOMHDmSmjVr0rNnT+bOnVvkmamrqyszZ87Ezc1NXQKYMGECXbp04aOPPrKa5rKMrvNAc3JyCAgI4OLFi5w5c4Zjx45x6tSpu960mjdvbnGG4uLiQo0aNe567C1btnD9+nWee+456tSpQ0BAAM2bN0cIwdWrV2nRogUODg74+/vTsGFDnJ2dCQoKolatWpQrV46wsDAqVapEhQoViIqKoly5clSqVIm4uDiEEFSrVo2kpCSysrKoVasWaWlpxMTEcPHiRfLy8sjJyaFcuXJERUUBUKtWLYQQqrvF/FRo1nHt2jUaNWqk6qhduzblypUjNDSUKlWqUL58eSIjI/Hw8KBSpUqqK7ZatWokJiaSnZ2t6khMTKR+/fpkZWURFRVFo0aNyM3NZd68ebz88sv4+Pjg7+9PixYtEELg5+en6rh69SqNGzfG2dmZwMBA6tSpg7u7OyEhIVStWpXy5csTERGBp6cnlStXJiYmBgcHh9t0pKamkpSUVKiO33//nVatWtGpUycCAgJUHVeuXFHPi5+fH02bNsXJyYmAgADq1auHm5sbwcHB+Pj4qDrKly+Pt7c3N27cwMnJCR8fHxISEsjJyaF27do36cjMzCQ6OlrVsWbNGnJzcxkyZIhFHVeuXKFZs2Y4OTnh7+9P/fr1cXNz4/r161SvXh1PT0/Cw8OpUKFCoTpyc3OpWbMmKSkppKSkUK9ePTIzM7lx4waNGjUiJyeH06dPc/LkSf7v//5P1WEymfDz81N1XL58mebNm+Pk5MS1a9do0KABrq6uBAUFUaNGDTw9PQkLC8PLywtvb2+io6NxcXGhatWqxMXFYTAYqFmzJsnJyaSmplKvXj0yMjKIiYmhYcOG5OTkcOnSJQ4ePMiIESMIDAy86Xw88MADAFy6dImWLVvi6OhoUUdoaCje3t5UrFiRqKgoXF1dVR1Go/E2Henp6cTGxtKwYUOys7MJCwtj37593H///VSpUkU9H4XpcHJyws/Pj0aNGuHq6kpgYCBXrlzBz8/vrvcIe/HWW2+p7dkyMzP56aef7rpPvXr16NSpE+3bt6dNmza0aNECHx8fHBwcCt0+Ly+PatWqkZycTHBwMPfdd58V/w/KLro2oAkJCfj5+XHp0iXOnDnD0aNH8fPzu+vTlaurK66urhY/a9CgwV2PfebMGUBxW9arV4+YmBiqV6+Og4MDMTEx6sUYFxdH5cqVcXJyIj4+nooVK+Li4kJiYiKenp64ubmRkpKCi4sLHh4epKWl4eDgQPny5cnMzCQvL4+KFSuSnZ1NcnKyajDvRuXKlSlXrhw+Pj44OjoSGxtLlSpVCtXh4eGh6nB1daVcuXK36TAYDHh5eZGdnU12djbe3t7k5uaSlpZGlSpVMBgMqjFwcXEhLi5O/VHHxsZStWpVHB0dbzofCQkJeHl54eLiQlJS0h11eHp6kpmZidFopEKFCrfpSE9Pp3LlyhgMBoKDg6lcuTKVKlUiPj6eatWqIYQgLi6u0O8lISGBihUr4uzsTFJSEp6enri6upKSkoKbmxvu7u6kpaXh6Oh4m46srCxycnKoWLEiubm5ZGRkUKlSJQwGA9HR0ZhMJurWrUtCQgI+Pj4IIYiPj6dq1aqqjipVquDo6KiejzvpSE9Px9HREQ8PDzIzMzGZTJQvX57s7Gxyc3Px8vK6SUdeXh5JSUnEx8fTrFkzEhMTqVq16m064uPjqVy5Mo6OjiQmJt6ko3z58ri4uJCSkoK7uztubm6kpaXh7OxMuXLl7qgjMzMTb29vDAYDCQkJpKam0qhRo9t0VKlSBQcHBxISEqhUqZKqo2LFijg5OZGcnIynpycuLi6kpqbi5uaGm5sb6enpODk5qTqEEHh6epKdnU1eXh4VKlQgNzeXrKwsKlasiMFgIC0tjczMTLWnb5UqVRBCkJCQoOooeD7M14dZR1F/g/akadOmgDLDDwoKuuv2lSpVomPHjrRv357WrVvTokUL9UG/MC5evEi7du3Iyclh/vz5vP3221bVX2YR9xixsbFi2bJlYvDgwaJChQoCuO3fk08+WerjbNmyRQAiJCTECqpLzoYNG0Tfvn011WCmXr16mp8PIYR44403xB9//KG1DLFixQoxePBgrWWImJgY4ePjo7UMcfnyZdGiRQutZQghhHjzzTfFggULtJYhVq5cKQYNGmS18TZu3FjoPQ8Qbdu2FWPHjhVHjx4VRqOxyGOmpaWJZs2aiUcffVQAomfPnlbTW9bRPlGqmPj4+DBkyBCGDBlCdnY2W7ZsYfHixWzbtk1dazh69Ch5eXm4uLhorFYikUisx61NAxo2bMjrr7/Oq6++WiTPWkGysrJwcXFh2LBhVKtWjY0bN1K9enX27NlDREQE169f5++//2bevHlW/D8oW9xzQUQFcXd3p3///mzatImQkBDGjRtH5cqVyczM1E1JMYlEIrEWZgP61FNPsX37dgICAvjqq6+KbTznzJlDpUqVaNq0KYcPH2b58uV4e3vTt29fTCYTXbt2pW/fvvTv398G/xdlh3vagBakTp06TJ48mbCwMGbNmsW1a9e0liSRSDTCwcHBYsDMvaojLS2NFi1acOHCBbZu3Urv3r1xdCzZLTwjI4OcnBwyMzPZtGmTmjc/evRoNcbhp59+okePHlbRXlbRdRCRlhw4cIBu3bpp3o0lMTGRs2fP8uSTT2qmwcz69et5+umnLQZo2YsTJ05Qo0YNzbvkxMTEcPXqVbp27aqpDiEEa9asYcCAAZrqyMvLY8uWLbzwwgua6gClkELVqlWpXbu2pjoSEhIICAjg0Ucf1VTHreTm5nL69GlatWp1Ww5xYGAgVatWxdvbWxtx9xDSgFpAtjOTSCQSyZ0oMy5ciUQikUjsiTSgEolEIpGUgHsujeV/CSEE58+fp1mzZnh4eGimIy8vD19fX3JycmjXrp1ma6AGgwFfX18yMjJo164d5cqV00SHmdzcXE6ePEmnTp000xAZGXnbez4+PpquUxuNRs6cOYMQwm51nNPT00lJSSn0s4oVK1K+fHm76BBCcPnyZWJjY2nfvr3djivRCO1SUPXNgQMHNCukEBsbK9566y1Rq1YtzYs5+Pr6ikaNGqnJ2lWqVBGnTp2yu47g4GDRqlUrVUfFihXF8ePH7a6jIJ999pmoWbOmZsePj48vNKH+zJkzmuiJiYkRo0aNEj4+PuLZZ58Vu3btstuxx4wZY7HAwIwZM+yiISEhQXTq1Ek8/PDD4uWXXxbly5e327El2iBnoDrEw8ODl19+mWvXrmlaViwtLY2BAwcybNgwnn76aTZs2MC3337La6+9xpUrV+yqZdiwYbz55pu89tprrFq1ivfff5/vvvuODRs22FWHmf379zN9+nRNG6+HhITQsmVLPvvsM/U9Nzc3Hn74YbtrOXfuHM888ww1a9bk0KFDdu9SExoaypNPPkm/fv1Uz0RaWhqjR4/mzTfftIuGL774gpCQEMLCwnBwcGDkyJGMHj2aV155RdPrRGJDtLbgekXLGaiZL7/8UlMNFy5cEMuWLbvpvQcffFAAIi4uzq5arly5or42Go3Cw8NDsxKHSUlJ4v777xetWrXSdAa6evVq8frrr2t2fDPh4eHCy8tL9OzZU+Tk5GiiYcKECbddk1OmTBGffPKJ3TS0aNFCNG3aVJhMJiGEUoYTEIcOHbKbBol9kUFEOqakSdLWolWrVgwZMuSm9x555BG1Y4c9adGihfp606ZNuLu7880339hVg5kPPviA//u//9M8vSkkJITGjRuTk5NDamqqZjpGjx5NdnY2S5YswWAwaKJh4sSJVK1aVf07NTWV2bNn8/HHH9tNQ/PmzfH391dL3506dQofHx/d5YBKrIc0oJJicfLkSbp162axq4MtuXDhAv379+fFF1+kTZs2mgRWLV++nNjYWN599127H/tWQkJCmDdvHhUqVKBSpUq0a9eOf//9164a4uPjWbVqFRUqVGDgwIFUqFCBmjVrMmXKFLvquJXZs2fTp08f6tSpY7djfvPNN3h7ezNixAg6duzIsmXL2L17tya/FYl9kAZUUmRWr15NWFgY33//vSbH9/f3p3379jz99NPs37+fLl26EBERYbfjh4WF8fnnn/Pnn3/a7Zh3YvDgwWzdupVLly4xf/58rl+/ziuvvMLRo0ftpuHixYsAPP7440yYMIHdu3dTvXp1xo8fz9y5c+2moyCpqanMmjXrprVhe/Dggw/y7rvv4urqyrFjx4iKiuLAgQN21SCxM1r7kPWKHtZAx48fr7kGM6GhoaJy5cpizZo1WksRQggxbtw4AYi5c+fa5XhGo1F06dJFjB49WgQGBorAwEDRpUsX4ePjIwIDA+2+JlwY3377rQDEp59+ardj/vLLLwIQy5cvV987ceKEAETnzp3tpqMgX3zxhXjmmWfsftwPPvhA1K9fX4SHh4tFixaJypUrC0Bs2bLF7lok9kHOQCV3JTMzk0GDBjF27Fj69euntRwAunTpAmC3fMczZ84QHBzMqlWr6N69O927d+fkyZPExcXRvXt3fv75Z7vouBPmzhlZWVl2O6Y5z9HPz099r23btlStWpWQkBC76TATHBzMzJkzGTNmjF2Pe+nSJebNm8c777xDnTp1eP3111m/fj2A3d3qEvshnfP3AELDcsW5ubn069ePHj16qDeluLg4Fi5cyNixYzXTdeTIERwcHHj66aftcrx27doRFhZ203t9+/blzJkzt72vFZcvXwZg0KBBdjvmgw8+CHCT29jBwYG8vDzatWtnNx1mRo8eTZs2bdQHLHuRlJQEgMlkUt/r0KEDLi4usi9xGUbOQPOJj4+/awRheno6aWlpdlKkGCpQtGmB0Wjk5Zdf5sSJE5QrV44pU6YwYcIEnnrqKbvOLkJCQmjbti0bN24kJyeHPXv2sHTpUn755RdNu22EhYWRkZFx003TXkRFRfHoo4+ydu1acnJyiIuL48cff2T8+PF2NR5t2rShe/fuHD16VDXgR44cISUlhdGjR9tNB8C+fftYu3atJg92HTp0wNvbmxUrVpCdnQ3Ali1bMBqNDB482O56JHZCax+yXjhx4oQoX7686NWrl/juu+/UtZ3FixeLsWPHig4dOogaNWqI9PR0m2sJCQkRHTt2FI6Ojmr1n3fffdfmx72VadOmWazuYs+10KioKNGsWTMBCEdHR/Hwww9ruq506tQp0bZtW/VctGzZUuzevduuGpKTk0WbNm0EIFxdXUXz5s3FunXr7KrBTHx8vHjyySeFt7e36Nu3r2jQoIFYsmSJ3XW0bt1aNG3aVBiNRrsfWwjlumjevLmoWrWq6Nmzp6hdu/ZtedSSsoVsZ1aAXr16sWvXLouff/vtt4wfP96OiiQFCQ4Oxt3dXVZ1KUBkZCRCCLuma1jCPCNv1qyZJjnMV65coX79+nh6etr92AWJjY0lMTGRxo0byxSWMo40oAXYuXMnvXv3LvQzT09PwsPDqVSpkp1VSSQSiUSPyDXQAvTq1eumijcFefXVV6XxlEgkEomKNKC38N577xXrfYlEIpH8byJduLeQmJhIzZo1yc3NVd97+OGHOXPmjIaqJBKJRKI35Az0FipXrkyfPv/f3r2FRNX1cRz/jZOW2Wk0jcgyspLMRC0lo4gKsZKgohPddMQI0Yiis910sKBzEVF0UUFRFkUXNdVFUEQRwdBFlnROwwi10A4ex/fCd/brPM5Irnqe8X3m+7nas/aatf9blB97u9fa073a/rqgOgAABKgPCxYs8Po8f/78AFUCAOiquIXrw5cvXxQdHa3m5malpKTI5XIFuiQAQBfDFagPDodDGRkZkqQZM2YEuBoAQFdEgPoxbdo0SdLUqVMDXAkAoCsiQP2YOHGi7Ha7MjMzA10KAKALIkD9SE9PV2JiYsCXBQMAdE0EqB+RkZHKyckJdBkAgC6KAO3AnDlzAl0CAKCLYhpLB9xud0DeKgEA6PoIUAAADHB5BQCAAQIUAAADBCgAAAYIUAAADBCgAAAYIEABADBAgAIAYIAABQDAAAEKAIABAhQAAAMEKAAABghQAAAMEKAAABggQAEAMECAAgBggAAFAMBAt0AXAPzd9u7dq2/fvvncFxERoU2bNun69es6e/as+vbtq9OnT//DFf4Zly5dUk1NjZYtWya73W61l5eX+/3OoEGDZLPZ/onygH8dW0tLS0ugiwD+Tg6HQ1+/fvW5Lzo6Wp8/f1ZRUZG2bNliff5/U1paqsTERLndbv348UPh4eGSpKqqKvXv39/v99r2BdA5XIEiaCQkJCg9Pd2rrXfv3pKkESNGKDs7W/369QtAZebevXunJ0+eaPPmzXK73e32f/r0SZJks9nUp08fr32hoaFeV6oAOocARdDIysrS0aNHfe6bN2+e5s2b53NfZWWlXr16pbFjxyo0NPSP1FJVVaWXL19q/PjxXu0fPnxQWVmZEhMT5XA4Ohzj+PHjysvL67CPJ0BHjhypFy9e/F7RALzwEBEgqaioSHa7XXFxcVZbfX29Zs6cqQEDBigzM1MxMTFavXq17Ha7kpOTJbUGod1ul91u17Vr16zvzp49W3a7XQsXLpQkFRQUyG63KzU1VYWFhRo4cKAWLVpk9X/8+LHi4+MVFxeniRMnKjIyUnPnzvX7v1vpf1fN2dnZGjFihM8+ngBte14A/gwCFPgvt9utnz9/Wp+3bt2qmzdvyu12KzExUTabTSdOnGjXz+12t7t96mnz9GtpaZHb7dazZ8+0a9cuNTY2Wn0rKiqUk5OjN2/eaNq0aZo7d65sNpuuXr2q7du3+603KytLTqdTTqdTy5Yt89mnbYBeuHBBeXl52rlzpx4+fNj5HxAAL9zCRdC4c+eOlixZ4tU2ZcoULV261Gf/8+fPS2q9vVtcXKyPHz8qISFB379/N66hsbFRM2bM0Jo1azR06FBJUnFxsSorKxUXFyen06lu3bpp7dq1OnTokM6dO6cDBw4YH88ToGfOnNGpU6es9sLCQh0+fFgFBQXGYwPBjgBF0CgtLVVpaalXW3h4uM8A/fDhgyoqKiRJM2fOlNQ65SMtLU337983riEsLEzFxcWKiIiw2m7fvi1JGj9+vLp1a/2TnDBhgg4dOqTKykp9+/ZNvXr1MjqeJ0AbGhq0cuVKJSUl6eDBg3r//r3WrVunRYsWKSYmxvh8gGBGgCJojBkzRrNmzfJqy8jI8Nm3qqrK2vZcKUrSkCFDfquGYcOGeYWnJCuo7969q9TUVElSbW2tVy2mATp58mT17t1bQ4cO1YYNGyRJ8fHxmjVrlpqamnTt2jXl5uYajQ0EOwIUQWPy5MnatWvXL/Wtq6uztnv27Glt/3UqSGd17969XZtnjmpNTY3XtJKBAwdK0m9NNVm5cmW7tnHjxlnb79+/Nx4bCHYEKOBD2/mg1dXV1nZHq/qY6tGjhyQpLy9P+/bt+6Nj//jxQ83NzerRo4c1BcfhcMhms6mlpUUNDQ1/9HhAMOEpXMCHtv8XLCsrs7Zfv37t1a/tMnjNzc3WdmceNIqOjpYkvX371mpzuVwaPXq0kpKSvJ747ayYmBj16dNHe/bssdpKSkrkWYCs7e1pAJ1DgAI+REVFKSUlRZJ0+PBhuVwu7d+/XyUlJV79+vXrZz3445kaUl5ernv37v3ysTyrI7lcLmt6y40bN1RSUqLq6urfWmrPM//zypUrqqmpkSRdvnzZ2p+ZmWk8NhDsCFDAj/z8fEmtV2xpaWlav369dbvVIyQkRAkJCZKkgwcPKi0tTSNHjlRTU9MvH6egoEDh4eF6+/atsrOzlZ+fr507d0qS3yk2v2rx4sWSpKdPnyo2NlYpKSnavXu3JCknJ0dpaWm/NT4QzAhQ/OuFhLT+mnf0MI6vN5IsX75cR44cUUZGhkaNGqWNGzdaS+e1XdJv9+7dCg8Pl9vtlsvlUkZGRrv5ph3VMHjwYJ08eVIOh0N3797VsWPHVFdXpxUrVqiwsLBT52qz2axjSdKGDRt0/PhxxcbGqra2Vk+fPlVISIgWL16sixcvdmpsAN54Gwvgh9PpVH19vVJSUqxbodOnT9etW7eUlZVlzd+UpM+fP6ukpETDhw9XbGys0fFqa2v1/PlzNTQ0aNSoUYqKivoj5yG1zgN99OiRwsLClJyc7PVkMQAzBCjgR3x8vN68eaNJkybpyJEjcrlcWrVqlRobG7Vjxw5t27Yt0CUCCCACFPDj9OnTys3NbbfO7ZgxY/TgwQPrVWgAghMBCnTg0aNHcjqdevnypSIjI5WcnKwlS5YoLCws0KUBCDACFAAAAzyFCwCAAQIUAAADBCgAAAYIUAAADBCgAAAYIEABADBAgAIAYIAABQDAAAEKAIABAhQAAAMEKAAABghQAAAMEKAAABggQAEAMECAAgBggAAFAMAAAQoAgAECFAAAAwQoAAAGCFAAAAwQoAAAGCBAAQAwQIACAGDgP4EktlO4QPdwAAAAAElFTkSuQmCC
|
Estimate the average rate of change from $x=2$ to $x=6$ for the following function $f(x)$ whose graph is given below:
Note that the average rate of change of a function from $x=a$ to $x=b$ is $\frac{ f(b)-f(a) }{ b-a }$.
|
The final answer: $0.5$
|
0075433c-0afb-41a9-a18a-986d8a81a653
|
multivariable_calculus
| false
| null |
Evaluate the integral by choosing the order of integration:
$$
\int_{0}^1 \int_{1}^2 \left(\frac{ y }{ x+y^2 }\right) \, dy \, dx
$$
|
$\int_{0}^1 \int_{1}^2 \left(\frac{ y }{ x+y^2 }\right) \, dy \, dx$ = $\ln\left(\frac{25\cdot\sqrt{5}}{32}\right)$
|
00f6affb-905a-4109-a78e-2dde7a0b83ac
|
integral_calc
| false
| null |
Solve the integral:
$$
\int \frac{ 1 }{ \sin(x)^7 \cdot \cos(x) } \, dx
$$
|
$\int \frac{ 1 }{ \sin(x)^7 \cdot \cos(x) } \, dx$ = $C+\ln\left(\left|\tan(x)\right|\right)-\frac{3}{2\cdot\left(\tan(x)\right)^2}-\frac{3}{4\cdot\left(\tan(x)\right)^4}-\frac{1}{6\cdot\left(\tan(x)\right)^6}$
|
0118dbbc-db0e-4ab9-a2ed-ddb2edd0eefc
|
sequences_series
| false
| null |
Find the Fourier series of the periodic function $f(x) = x^2$ in the interval $-2 \cdot \pi \leq x < 2 \cdot \pi$ if $f(x) = f(x + 4 \cdot \pi)$.
|
The Fourier series is: $\frac{4\cdot\pi^2}{3}+\sum_{n=1}^\infty\left(\frac{16\cdot(-1)^n}{n^2}\cdot\cos\left(\frac{n\cdot x}{2}\right)\right)$
|
0146d63a-d9e9-4910-9267-10f87812aff4
|
multivariable_calculus
| false
| null |
If $z = x \cdot y \cdot e^{\frac{ x }{ y }}$, $x = r \cdot \cos\left(\theta\right)$, $y = r \cdot \sin\left(\theta\right)$, find $\frac{ d z }{d r}$ and $\frac{ d z }{d \theta}$ when $r = 2$ and $\theta = \frac{ \pi }{ 6 }$.
|
The final answer:
$\frac{ d z }{d r}$: $\sqrt{3}\cdot e^{\left(\sqrt{3}\right)}$
$\frac{ d z }{d \theta}$: $2\cdot e^{\left(\sqrt{3}\right)}-4\cdot\sqrt{3}\cdot e^{\left(\sqrt{3}\right)}$
|
014e9af5-759a-4711-aa22-0f9c76acb502
|
sequences_series
| false
| null |
Consider the function $y = \left| \cos\left( \frac{ x }{ 8 } \right) \right|$.
1. Find the Fourier series of the function.
2. Using this decomposition, calculate the sum of the series $\sum_{n=1}^\infty \frac{ (-1)^n }{ 4 \cdot n^2 - 1 }$.
3. Using this decomposition, calculate the sum of the series $\sum_{n=1}^\infty \frac{ 1 }{ 4 \cdot n^2 - 1 }$.
|
1. The Fourier series is $\frac{2}{\pi}-\frac{4}{\pi}\cdot\sum_{n=1}^\infty\left(\frac{(-1)^n}{\left(4\cdot n^2-1\right)}\cdot\cos\left(\frac{n\cdot x}{4}\right)\right)$
2. The sum of the series $\sum_{n=1}^\infty \frac{ (-1)^n }{ 4 \cdot n^2 - 1 }$ is $\frac{(2-\pi)}{4}$
3. The sum of the series $\sum_{n=1}^\infty \frac{ 1 }{ 4 \cdot n^2 - 1 }$ is $\frac{1}{2}$
|
01683c2c-a5b7-4bff-8e4f-d8fdad3cac45
|
differential_calc
| false
| null |
For the function $r = \arctan\left(\frac{ m }{ \varphi }\right) + \arccot\left(m \cdot \cot(\varphi)\right)$, find the derivative $r'(0)$ and $r'(2 \cdot \pi)$. Submit as your final answer:
1. $r'(0)$
2. $r'(2 \cdot \pi)$
|
1. $0$
2. $\frac{1}{m}-\frac{m}{m^2+4\cdot\pi^2}$
|
01961276-06fd-4869-8e58-eb15a4eb4034
|
algebra
| false
| null |
Rewrite the quadratic expression $x^2 + \frac{ 2 }{ 3 } \cdot x - \frac{ 1 }{ 3 }$ by completing the square.
|
$x^2 + \frac{ 2 }{ 3 } \cdot x - \frac{ 1 }{ 3 }$ = $\left(x+\frac{1}{3}\right)^2-\frac{4}{9}$
|
01c011c6-2528-46de-aa90-9a86ace5747a
|
sequences_series
| false
| null |
Using the Taylor formula, decompose the function $f(x) = \ln(1+4 \cdot x)$ in powers of the variable $x$ on the segment $[0,1]$. Use the first nine terms.
Then estimate the accuracy obtained by dropping an additional term after the first nine terms.
|
1. $\ln(1+4 \cdot x)$ = $4\cdot x-\frac{(4\cdot x)^2}{2}+\frac{(4\cdot x)^3}{3}-\frac{(4\cdot x)^4}{4}+\frac{(4\cdot x)^5}{5}-\frac{(4\cdot x)^6}{6}+\frac{(4\cdot x)^7}{7}-\frac{(4\cdot x)^8}{8}+\frac{(4\cdot x)^9}{9}$
2. Accuracy is not more than $\frac{4^{10}}{10}$
|
01e4ed04-1ed3-4cda-af81-35686c0a16d0
|
differential_calc
| false
| null |
Compute the limit:
$$
\lim_{x \to 0}\left(\frac{ x-x \cdot \cos(x) }{ x-\sin(x) }\right)
$$
|
$\lim_{x \to 0}\left(\frac{ x-x \cdot \cos(x) }{ x-\sin(x) }\right)$ = $3$
|
023674a7-236e-4771-9662-77157e370160
|
differential_calc
| true
|
data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAASQAAAEYCAYAAAD1QYs6AABm4UlEQVR4nO39Z5AcV3anjT83s3x1ufbewXuCBAGCQ9AOSZAgh0Mzw1caiRppTcTGKnZjN2L1YT+8Efqwqw3F7sZfG1LEjEbi6F2NHw2HHA4tSNABhCU8YRvdQHtvqrury2Xd/4eszDLoBhpAo13lw2iiuyoz61bmzV+ee+455woppcTCwsJiEaAsdAMsFh/5z6jbfWYZ+1nPPIvZYgmShYkhHEKInNeFELckUtnHkVJedzwLi5mwBMnCxBCO6cQmW1SyRWY6ocredjoxs7CYCWH5kCwMbtWaudH2lmVkcTvYFroBFouHRCLB0NAQmqZRXl6Ow+Ew3+vt7SWZTOL3+/H5fAghcqwkKSUTExP4/X7g+uGaJVAWs8EaslmYjI2N8c///M/87d/+LV1dXaRSKQDC4TA//vGP+cEPfsClS5emHb7FYjE+/vhjksnktL4oS4wsZoMlSBYmiqLwu9/9jh//+Md8/fXXJJNJAD799FP+4R/+gQ8++ACPx5Ozj2EJhcNhfvrTn9LX13ed+FheAYvZYgmShUkgEMButzM8PExLSwvJZJKxsTF+/OMf09fXx6OPPsrKlStz9pFSkkqlaG9v58iRI5w6deq641rWkcVssQTJwsRms7Fq1SqcTifXrl0jmUyyd+9eDhw4wKZNm/izP/uzHL8S6GKTTCY5evQoIyMjHDhwIOd9yzqyuBUsQSpgphOLTZs24XQ6uXr1KoODg/zjP/4jqVSKP/mTP2H16tXTHiMej/Pxxx8TjUY5ePAg0WjUfN+yjixuBUuQLHLYsmULLpeL7u5uPvzwQ44cOcKuXbt47rnnUFXV3C5bzMLhMEeOHCGZTNLW1sbVq1ev28bCYjZYglSgzDQNv2bNGnw+H729vfzkJz+hqKiIP/3TP6WysjJnO2PfVCrF5cuX6e3tBWBiYoLjx4/nbGNhMVssQSpAbhRpXVJSQkVFBUNDQ5w6dYrnn3+ehx56CJvNlrO/QSKR4MCBA+aM3NTUFF9++eU8fAuL5YglSAXIjeKDhBB4vV7i8Ti1tbV873vfIxAIANfnqAEkk0k+/vhjc/9oNMpXX33F+Pj43f4aFssQS5AsAIhEIoyNjXHixAl6e3sJBAJ873vfY+PGjabvKFuIjN+Hh4c5ceKEKWyaptHV1cW5c+cW7LtYLF2s1BELAE6ePElraysff/wxfX19PPnkk3z3u9/F6/XmbJdtURn+IwC/38/4+Dh+vx+73c6pU6fYsWPHvH4Hi6WPJUgFwHQO7PzXjh8/zv79++nu7uahhx7i3/ybf0NTUxOKotxwv1Qqxcsvv0wkEuHtt9/mpZdewuVymTltFha3gpXtv4yZaSZtutfffPNNLl68SDAYZMuWLWzZsgW3233D40op6evrY2BggMHBQb73ve/xwQcfoCgKgUCA2trau/K9LJYvliAVINMlvw4ODhKNRnG5XBQXF19nGWXvO53I9fT08MADD3Dt2rW702iLgsAasi1TZhKOWCxGX18fdrud0tJS7HY7oE/3CyGIRqO0tLQwMjKCqqqUl5dTW1trCpRVTsTibmIJ0jJlOrEYGRnh2LFjHDp0iBUrVrB7926Ki4vN7aPRKB999BGHDh0ilUohpcTtdvPcc89xzz335NRAull5WkuwLG4Ha9q/ADB8Pe+//z779u3jzTff5ODBg0xOTuZsd/r0aV5//XWGh4epq6ujsrKSU6dO8cMf/pCxsTHzWNMdPx9LjCxuB0uQCgAhBO3t7XR0dLB27VpUVWV0dNSMrjb4zW9+w/DwMN/+9rf51re+xUsvvcTzzz/P+++/z4kTJ2asl22Jj8VcYQkSABKJBJavf9/v9/P444+ze/duSkpKzNcN62Z8fJzPP/+czZs3s3XrVmpqaqirq+Nb3/oWQgg+/vhjs4JkNre6IomFxY0oQB+SLj0CkZEfKUHActbn+vp6VFXFbrejqqrpDzKsm97eXoaGhli5cmXOdH9xcTF1dXV8/fXXOYIkpaStrY1IJIKUksHBQRKJBGfPnkVKiaIoBINBampq5v27WixdCk6QBkYmOdvag6oI1jdXUeLPLslqSNTyG4LkxxQZhfkNJiYm0DQNn8933ZS/3+8nHA7nvJZKpTh58iTd3d1mCdtoNMonn3yCEAKbzcbq1astQbK4JQpOkPq+PsfJ37zPaKCc4B99i1K/B4lYzlp0U4wytIBpPRmvg15rO3+4JoSgtLTU/Nvj8aCqqilANpuNYDA4D623WE4UnCCJzqvUXjnOWMUGYvEkUoBIi5E+lFv6zLQCbbYDOv89v9+PqqqMjY2haVqO9TQyMkJVVVXO9kIItm7dSiKRAKCvrw+Xy8Wjjz5qvp9f7tbC4mYUniAZ680Lw4dk+I+WgxTdnJmm6CsrKykrK+PSpUvEYjEzqba/v5+Ojg5279593VDO5/OZv8diMRRFMeOarNk3i9th+XpxZ0KmAKEP09Cd26SHbGKZTA5lO6sNRkZG6Onpoaenh2g0SiQSob+/n+7ubiYnJ/F4PDz44IOcPHmSkydPkkgkmJiY4I033kBKya5du2ZMJ8nHmmWzuF0KzkLSBUnmDdWE+f/laim9//77nD59GoCrV6/icrn4p3/6J4LBIC+88AJbt27lpZde4ty5c7z++uucPXuWaDTKxx9/zJ49e9iyZcstLfyYHaNkWUsWs6XwBCk9UEtlT/sDIJarFgG6s9ootLZnzx4URcHtdqMoiikWW7du5V//63/NkSNHuHjxIkIIHn74Yfbs2YPf75+1qFjiY3G7FJwgiZQEIZBCH6whBUKA1I2kZStKu3fvNh3O+fh8PtMB/fTTT7N9+3b6+/tRVZXq6moCgcCsh2vZzORAt7CYiYITpKmKBk6HVjPs9Os2UvpeWe5+bb/fP6uiaR6PB7fbTUVFBZAbBmBhcbcpPEGqrONk8Qocdltmli39r0RZzpo0a4zARguL+abgZtlcNgWnXWUymmAqngSpZ47kJZMUJNbsmMVCU3CC5Pe68XndjI1PMT4ZA4wpcuOncLlRbSMLi/mg4ATJ5bTjcthJaimSmrbQzbGwsMii4ARJCBAiK7G0sI2iacm3iCyntsV8UXCCJM0obZn1o78jLR8SYAmQxcJRcIJkv3aZtf0XKU5E0sFHhis7HZdUwKJkCZHFQlN4gtR2ntW95wimovr4LW0zSSnTlpN1U1pYLBQFJ0ginVybkkaRMsjMtBX6oM3CYmEpvOg3qVtE6RRbPW0knTIiLOvIwmJBKTgLyaGCalOYjCWIROP6i8s7r9bCYslQcILkcthxOuyEJ6OMR2JZdZCsWTYLi4Wm4ATJpghUVSWRkmgp3Z+Uk2BrYXGXkFKiaSlSKevBNxMF6ENK6dFHIpNIayyLlIlLsqTJ4na5vv8kkxpT8SThiSlGx6dwOmyEfB68bgdOuw2hzNTfCq8vFp4grdlCx+khxlo69b+FNNNqLae2xe2i9x/9gaYHmCqkpCQyFaO1c4ij5zu41N5PeGIKm91GdamPe9fWsXV1DaVBL6qqZo4hhV7RtACXwik8QVq7mba6XkZEP9kJtYVzyS3mnjzhEBItpTEwPMGBk618ePAC5672E4klCHhdTCXiTE3FOHaunad2rmP3A2upqwyhKiJr0VKQUiz7Ol35FJ4gAZm4I8iNzC6gK28xh4h0cK3+VyoFXf2jvPvlOX776Vl6B8fYtLKKb2xppqYswPhUlK++7uDQ1+3883vHSGmSl5/YQnlxEcZDUiCRQmZ1z8LomwUpSKoARehObS0l9SeTOcdmDdwsbgMpERJSQM9gmLc+/5pf7T1OPJniuV0beHbneu5ZU4PX4ySe0Lh/bQMVpWf4zSen+Jd9J6kuC/DUA6vxuOxImS6xLGW61HLh9MiCFCS3047LYSM8GSUSjeHzuLCGbha3j0yvpCUZCU/x8bFL/OqjEySSGi8+upnvPLGFpqoSVJuCROCw21jTUMF3n1AZm5jizc/O8NbnZ2iuLWFDcyWqkEgp0qlNhdUjC27aH6DI68brcTExGc0ER8rCu/gWc4VAojAxFefAqVZ+tfcEkWicbz2yiVef3MrK2jLTaW3kTiIkjVUhnntoIxuaqzh6rp39J1oJT+g5lnomk1g2awXOloIUJIddxWGzoaUkeUvWW1jcFolEkq+v9PKzD45ztXeYx+9fzXee2EpzdYm+gTC8QxmFUVSFLauqeXL7Gpw2hU++ukRr1yApmdIdCEJfP7CQKDxBOnuMyrbTOKWWXk5b6OYx0lxm28Iinxv1DC0lae8b4Y1PTnHqchf3rqvjO9+8hxU1JTmVkfWggOxyyYIij5PH7lvJ5lXVnLnSw/ELnUxOxTF8mgWmRwXoQzp5kIorl7CnyhHpGVZhzq0a5lKhdQOd3t5eRkdH0fJK+3o8HhoaGm5rbbZltWqtBJmOW0NmpkFGwhE+PnKZj45cpqEyyHcev4ctq2pQ1Vw3wEzO6cbqYrZvaODYhU6+PHOVXVtXsKahrOCm/KEQBSmlP3f0lWuzK0ZCoRf6f/fddzl8+DCBQMBc5RagoaGBP/uzPzMXk7wVlstS2kbxvkywiL7gaDSW4PTlLt76/AxCwPO7NrHrnhU408tIzcbKcdhtbN/YyN4jlzhxqZML1/pYUVOC3abeZM/lR+EN2aRuBWlCQUvns2WSapf2TXOnHD58mP379+NyuSgtLTV/AoGAKSxw81VI8rdb6mIEmMoiDaeOgFQqRUffCL/7/CytXUN8Y0sjux9cT8jn1hOR0qVuZsOahnI2rahkMhLn+IUuhsYm092xsNwIBWghpVBVgd2mMjkVZyqWSJvfxtCtcEkkEjQ1NfHqq6+aK9cC2Gw2bDbbddbOTJZP9hLay0aUcpZa17/T6PgU+45d4rOTV1hRW8q3H9lEY2XIfF9gnK+b20lFbif3ra3j42MtHD3XTsdD66go8RdcnyxAC0nidNrxFjkZn4wxNZXUZ0DMjlZYT6RsotEoVVVVJJNJhoeHGRoaIpVKmRYS5ArLbEVmyYsRmLNeRrRaPKFxtqWbtz47gxCC576xnu3rG9J+o3SUNbfwkJOweXUNK2pLudI5wJXOIWLxJIVmtRekhWS32XA6HSSSGkkthRGnXeihkQMDA8RiMfbu3YumaUSjUSoqKnjsscdYtWoViqKYVpGUkvPnzzM+Po4QgsHBQeLxOIcPHwZAVVWKi4tpampa4G81N2T3jZSU9AyO8fv9+lDtm9vX8PTOtRR5nObWGYf07PtTdWmAtQ1lfHmqla9be3nkvpVUOQNz+TUWPYUnSDKdkY1Aimzv0eIWoqSWIhLVh5hJLYWqKDgdKm6nA5djbi5jKBRicnKS4eFhAoEAyWSSvXv30trayn/+z/+ZysrKnOHa0aNH6ejoAGB8fJxoNMrevXsBsNvtbNiwgebm5jlp28KTcWdPTsU4cLKNj4+2UFsR5IWHN9JQWZyO1k4HM5oWd85Y74aHd9hVNq6ooqLEz+mWHvpHJqgq9d9832VE4QnSvd9gtKUbeXBY/9voPYsu6EOXylhCo294nI6+Ubr7RxkKR5iKJXDYbQS9TspKfFQW+yn2eygJeHE77dzel5F897vfYWJikrVr11JSUkI8Huedd97hhz/8Ibt27WLPnj2mlQSwbt06KisrARgeHsbhcHD//fcDuoVUVVU1R+diocn0kaSW4lJ7P29+dpapuMarO9awY2Mjqqp7P267C0mQQrC+qZLq0gBnr/TQMxhmY3NlzozncqfgBEne9w3G1Ctw6GNEdhjsohGj9OBRSsYno5xp7ePzE1c4c7mLsfEpFFWveKlpKVJaCqfTRnnIx6r6MjauqKK5ppTKEh9et1O3+kS+5k43o6hbjU899RSalsLv95s3QVFREf/9v/93zpw5w7PPPqvvKfRqCdu3bzeP0NPTg8vl4umnn56PkzTn5Ev4dZKulyliOBzh9198zdnWLu5d28Ceh9YTKHLnHkzk/3KTzpX1YTXlQeoqghw+e5XWrmEmpuIEijK5lsudghMkAShCAQRJTSOlaSw280ggGZuMse/YZX73xddcuNqH22GnusxPbXmAkM/LRCRK//AEQ2MRrnQOcrljgAOn21jbUMG2dXVsaK6iriKIy2WH9DDCcLCa/rKsKexYPM6FCxfxeDx4vV5TkFLp3Bqn03nT6f6lTGaaXhh/pDPt0+8KiMWTHD3XzntfnidQ5OLbj25kVX3FDY87uw/PlAd0OuysrC3B73Vx4VofI+NTaUEqDApOkEDP9nc77YyOTxKJxpGLyIMkEURjcQ5/fY3/750jdPSNsqGpksfuW8W65iqK/S7cDjuxRJKJqTgj4SlaOgc4d7WPtq4hDpxq5fTlbu5ZXc2urSu4Z3UNJcEibMIwkbJusvQnSiAWi/PGG79B01I8//zzVFdXk0gkePvttykuLua+++67rUjtpcSNZhBTqRSdfSP88qMTDIUjfOfxe3jsvlU4bHN1C2VEaU1DOaUhL+fbehkOR2isKp6jz1j8FKAgSXxeJz6vk67+YSKxxKIRIwApU1zrGeXXHx7nUns/j2xdxfeevpd1TZUE/V7SrgozmDOZlGxcWclDo820dg1x+MxVjl/s4pNjLVxuH+Sxbat4YFMjK+tK8br1SGtTfrNmgZxOBzU1tXzyySf8+te/pra2llgsxqlTp3jxxRfZsmXLspi+n4ns2cPro8v14fMHh85z6OtrrK6v4MVH76Ek4DUjuO/MwjYc3/p1XVlXRlmoiJMXO+kfCqNpKdNHtdwpOEGS6LMZdptCUpNo2uIahoQnYnx2vIWDZ66yqr6cP3jqXrZvaMBhVzGW/jYlRYLdJigLFlEW9FJfEWJtQwVb1nTx2VctnLncza8+PM65tj6euH8196+vpazYhz3PSaoPFZy89NJLBINBWltbicfjqKrKE088wWOPPZYTi7QcESI3pjr7u8aTKc5e6eWNT07idtj49iMb2LSyctZR2Dcje5EJAVSU+KktD3LozDVau4aYnIrhz/dTLVMKTpDMPGuZqRC5WEhqKVo6B/jd52dQVYVnHtzAfevqcDiMmTPjKUrG12GEmSPwuBw015ZQGvLSXFPKgROtHDjdwtFz12jrHuZK5wq+saWZdY3l+LyurOGbvn9NTQ3PPfccQ0NDJBIJVFUlEAhQVla27IdrYBiMudaRJiX9w2F+ve8017pHeGrnWnY/sA6X08Zc9iDdf6UfzGm30VxdTJHHyaWOAcYmo5YgLUsScTj7Fc5wLCdN8roi7XeVmWNTxiejfH6ylYsdAzywro4nd6zB69bFKDNDpqSPkuuYlmbzJX6vi00rKqks9rGuuZyPjlzi0Nlr/Orjk5y/2sej965g27p6GqtLcDhsOa0IhUKEQqHcFi9jZ3aGzPXIHrLF4kk+OnKBvUcvUFce4pUntlJdHsBMD5HGNObtY9hGksyM6IraUor9Hlq7hwlPxu7o+EuJwhOko5/hkA6gBtPiyJqBuuukP0zv8GDMx6eQdA2MsffQRYrcDp56YC31FQFTcIwKgqZhlOMHynZR68ezqQqVpT4CPhd1FSGaa0r47PgVzrb20NIxyNkrvTy6bRUbV1RSUezHpirXaaXxpxAyE/AH+l0j8z44x3ojT29zD5wrxTfwv8zj5GfmkWTYnwItleJcay+/3HuCRCLJC49u5v4NRhmWlPmN5iKs1ri8xldeXV9Bsd/DtZ4hRscjuT6t7NO/uCaI75jCEqT0FLaiKthUQTSWJJ7Qsp6Id78JMi8nzLiNI9EYxy92cKmjn/vX1vHIfSuxqYqhQWQp0Q0ODmaRp/QLbqedFbWlhPxu1jdX8smxyxw8fZWPj17iQns/Ozc1cN/aOtY1VlBR7ENNf2bGqyERUuSUd862xpASITLDufzYnenabAqWfiKy/+C6t+YJISGVdYolkv6RcX7y3lEutQ/w8L0rePGxLRS5naZFI8w2zoEqpPPkjBi0mvIA5SEfJy910Ds0Rjyh4XSkfX/mUHs+n6TzQ2EJUnro4XQ78bqdhCciTE7p5rDIchjfTTJakWXtCMlIeJIPD13A6bTx8L0rqCkLph2t2WJ5k/YJmX5iCuNPEBJF0R3ffq+bhspiNjRV8unxFr5u6+VXH5/k4Omr7NzUyLa1daysL6O6LIBNVTEGEvoKGGlxSocP6BnsqazgJl2xMmKSLTLiuqZncgev/16mDTWfI+mscyclJJIa7x08zweHLlBVGuSPn9lObUWQ7HXTrm/5HTUgc0QhcTps1FUGcdhstHYNMTEVw2l358yMznULFgOFJUhpC8nhsON2OZiKJYklknkb3eULbIwPjWEQEE+kuHRtgK/Od1BfFeKx+1ZhSxfnyn5qZqylmch7V2RmbozVLmrKg/g9LlY3lHPk63YOnrlKS8cAv9x7gkOnr3Lv2jruWVNDbUWIspCH4qAPl11Ni1F6OJM+rpQKQqR9TGnBzB+Qpb90vlmUFjZpxkZlxEyabb7+5rubpB9IUpCSGqcudfHz979CS6Z45YnN7NjQiCIEiBQpmVl4fRqtvQ2yzkvWkRori/F7XVxqH2R8MkZJwKNvaQ7fRJ6wL30KS5CkMWRTURW9amRqvquop5/AhrktpSQ8GeWTYy3EExr3rqmlubaUbL+Lfv9nHNo3Pn6+T0zvuNlC4fM6WdNQTlWJn/vX1XPsfDtfnrlKZ98I7xw8z6cnWlhRU0J9VTF1VcV4nbaMA90cauo3gtNmw1fkZnhoAM1dyefHWxBCHxIHi4p0K1CBIpcNt0tPBPa6XGbbZG7TM3d5jhjNh6mkL1+NhNbOIX701iFa2gd54v6VvPzYFrwuR7olImvIZLRtTjxIWcfSj99QEcLncdLaNch4JJa2lrPP2mIK6Z0bCkyQ0hfS6FDZ4+95Gh7k3G9AihS9Q2E+PX6FkN/DY/etxmlXs7fOsiJmcXxjtJPnEzO6rvE1bYpCsd9LoMhNTXmA+zfUc66th1MtvVy61kd73zAX2weYmIrr7ZWpdMMzgqRIcDsdlAR9JOJTxIs38P/7xWcIIXDYVCpKggCoqkLQ68RX5KTI7SDk15OA/V43Po+DkM9NyO/F53FO5xHnrl8U8yRJhsIRfvr+V3x07CIr6sp47bntVJUFMxZt2kydLv3mtj82/T9j+G4csLm2mIDPxcWrA0ykl+vSjevlNUzLpvAESQhQVNP0RcisHKZ5cVboHSr9WbG4xrm2Xjr6R3hgQyP3rKnJExPllvp89hAqU+Epy2EKWUGAElUVBP0e/F4X9RUhvrFlJS0d/VztHqZ3aJyOvhGSqbS/KC2MGWETJLUUU1MxosKBkEncLgfIFJNRjStdgwiZIqlJJqZiSCAWT5CSEp/HTWmwiJKAk4qQn6qyIDVlfipLfNSUBykNFOnBoOl2zv4M3C6SsfEpfrH3OG98egq/x82fPr+d+9cbs2rGemrGOc1qz536s9P/N4q6kY5JqiwLUB7yc/xCFwMj4yQSSRx2mzlXKfMs3+VAYQmS2wP3PQReH7ahXhRFEE8kSWop7OmF/O72pTVnzNN+iPFIjM9PtOJ02Ni5qTGdjpA/IMjUbbpxC7MmoXO+jCFH2b4KfXtjD1VR8HmdFHlclPg9bFlVQzypEYsnzSe4cajMd4CpeILB4TBDw6Mceuvv+fev/CWplMbIRIyJSBxkikRCo3d4nKSmMToRITwZJxrTmIrFaesa4UxLH9FYAo/LTlNNCavrK1hRW8rK2mJW1ZUR9HlmcWZne/Wm3240HOHnH5zg9d99iaZpvLZ7O3seWo/baTetTmT69s/y/+kG0532HGke35hEkIDdplJfGcLltHOlc4DJqeZMxL7hULy5Y3FJUWCC5IV7vwFIik6OUOR2MDYeJTIVJ+Bz5T717hYChNT9FSktRf/IBF+ebsNf5OYbW5pQ8yKijTbNrlU3emJP96LI1Sz06X2nw4ZzlkXfUilJY2WInl4nSnSQbevqkBKSqRSplExHBkjimgZSomkpovEkYxNRBkcn6ewfpW9knN7BMfqGxxkcmeRC2xkQsKaxjAc2NLBtbQNrG8vx+1x558KwKDK+JiND37ASM0sWGWcg7bsjY2WMhif52ftf8aO3DhFLJvneU/fxvWfuxV/kyrrhRdZQO9OGuewzRlya0X4hBLVlQTwuB1e6hpicihPyp8VZSHP4uJwoLEEyEfg8TopcdiLRGNF4En+6497tUZvxhBUIokmNr1v76B+Z4Bubm1nbWHl3P/w67vzLKorAodhw2FSE1HDY9S7lvME+Ukq0lCSppYgnNJKaxlQ0Tt9QmCtdQ5y/2seFq71cvtbP2cs9fNl4lR2b6tm8qpp1TZWUBot04c6KDsy4gw2bj7SYGO+JjH9GZjTm0rUB3t1/htffPUoinuSPnr2fP3t+BxUlPvOGFzKle+bnCTMIUkJdVYgij5OOvlEiMX0ByWxhXW4UoCDpHVQVCooQpKQkJWX+1NRdI+tZzuRUnE+PX8LjtPPgpka8nltf92wpIoTApgpsqmJaYkGfm/JQEWsaK3j0vpVc7R7iyNcdnLzczcVrfZz5XTeNlcU8sLmZLaurWddQTk15AIfdbh43x9MkjJAhkR5i6b8bw6+B4TCnLnfzzoFzvL//HIGQlxee2MqfvbCT8mBR2nmctq7E3Z5azz26IUYIyYq6UoJeN9e6h5mMxrMitvUxszSCVpcJBShImYnVTBkOeV22990jfUekJIOj43x5uo2g18VD9zQv62z6fIxkUrM6kxAIm4rNpuJxOQj6PKxprOKx/lEOnb3KobNXuXC1j1988BX7jl1k6+oaNq+sZnV9BbUVQcqCXux2m3kjG7OZxoPGMI66B8NcaOvlyNmrfHqylbauflbWVvDq0/fy7M51lAaLEIoANKRIx4JJZZ6GRlnWHBIpoarEj9/r4sSlDgaGx9E0qUfwG5bgMusyBShIxhVMmSkSkDWNm7PN3UEC8aTGxWt9DAxPsnNDA2uaypfdjMn1ZH0/kfm22eJkjMLsaXFaU19GQ1WQnZsa+epCBycutHOxvZ/3vjzPR0cus7a+ghV1JdRXhagIeakoDuK02wgFPDgdCkMjE8Q1GBwZp3sozOX2AY6fa+dyxyBlpX6+/ehmnti2jl1bm3A7bTkeKiPSfV6uSfpjMj49/TeX3UZZSE/p6ewfJRpPUuRR076x7Nil5UEBCpKOqqooiiAaT5BIamRPZt9NjNmZaDzBwbPtuJw2tq2vx+PUS80uZ3LC+PILogHkpJvoqRyqquBRHayuK6OpqphH7mni3NV+jp3v5FJ7P139o5xp7Sae1Cj1u6mpKMbtsFFR4sfpUOkbHCOWlHQPjHK1dxibqtBYFuSpnWvYsamJ3TvXEipyY7erekkaY9Ysq4rC3bdCZu53QkBDVQiv20lHf5ipWAKvx5E+k/PTZ+eTwhKksRFoPQ/BEnxFLoo8LsbGp5iMxECmp3LvdudLOzGmYjG+PH2VIredHRsb03W+lzfZpzZn4UnDyWyYCNn3WFoRVEWgOAQ15SEqS4Ps3NhER/8IF671cbVrhI6+EQZHJxifihOenKKlo5+kJnE5VYo8HkI+N6sb1lBXHmRTcxWb19RSHvLhtKu6jyl/xkoIcwB1t42Q6eKtzXQcKWiqKsbndtDaPcRkNE4ZRRina7k9xApLkEaH4NgX0LQGf2gDXpeDyWiSWELTs/DnIQJWCH1KvLN/lGvdw6yoLWHjisp5c6ovFnKW5M6KVsgeOktDrGT6dSFACOwK2LwK6xorWF1fTkpKRscm6RkaZ3h8ikgsrg/VkhKfx07A5yVU5KK2IkBJwItdVVEVJe0rSn922t8kzBgfmaWN8zMsyh4hZrqCpKYihMdlp7NvhGg8nuO9n2k586VKYQmSTKH3cAWBkg5Cy1qzdp4ubCyW5MtTbaRkirWNlZSFiow7guX2xJuJnIL62a9nOVKyDYD8pQmMpZiMsK3yEj9lxX7T2ZtdU04IY7ZtpmtsfIhy3QcL4wB3EePjcg2ezElorArh9bho7RwiGkuaRhvMT8mc+WT5jxOyMXqpoujRsELR0zhkVmzHPBCLJzlw+ipul4MdG+vNaelCEaO7gS5OesS5qijY1MyPqigoiliylkRFsY9iv5exiSn6RyZIaPqDNdvXtVwoLEFKpRNEFQWRrviXfnwChl7dXVGSCManYpxu6cHjsvPApibzHQuL6RACKkNenA4bHX2jROOJ9OykWG56VGCCJE1DF5ddxWlXGI/EmYom04GvxszF3UNLprjSOcjI2CSVpX4aK0vMNAYLi5loqC7B43LS0T9KNJYAMnWplhMFJkh6PSQUhaDPjc/rZDQcYSISS3sT7/7FjScSHDjVitNmZ/PKGhx2BaMOdmEU07e4VSSS5poyvG4HVzqHmIrFkUgzfms5UVhO7ZRRfkTB5XTgtNtJaBpaupLkfBBNJDlwsg23y8HOzfU5pWmXqo/D4m4jqCj24nSodPQOE4sl58XZvhAUloVUUq6XH6lfkY79EDkzG3fbQJFSMjQW4WJ7Px63gwc2NKB/vD7Pa1lIFtMhJDRUFeN1O+jqH2MqmsjMJi5w2+aaRSdIkUgETdPuzsFLK2Drg1DXjEwvFGnMst1oxn1ycnJO2pTUUpy70kskFqe+IkBlSUB/w/j4WT7xNE0jFouRTObXA7fIJh6PE4vFFpXQx2IxYrFbXGdNQHnIR6nfy/hklL7RifS1l3e6JBxSSmKxGPF4/M4ONEfMqSDd6YXXNI1f/vKXdHZ2zsnxZkIgUVVQFEk8mSKp6atnzDT1/8tf/pKOjo5ZtcfYJntT47WkluLIuWs4HXq6SE5y7y181d7eXvbv309bW9vsd5onFurmn+5zT506xf79+5mcnFyAFk3PwYMH2b9//y3tY3yzyhI/ToeN9t4RYvEUutfzzs731NQU+/fv58SJE7mfmXc+U6kU0WiU8fFxpqam7trDcE4FSdzhsEPTNH7+85+bN3/28eauo+vHCRS58bqdjExMmUshGSme+fzsZz+jvb19VhbMdGu8GfslkvpqFk67jfvW1eufaaSl34I7oLu7my+++ILW1tbZ7zRPLJQfbLrPPXnyJF988cWiEqQvv/ySL7744pb2Mb5ZTXkQt9NOe98o0UQqHex5Z+d7amqKL774whQk4z7LP24kEuHgwYO8/vrrvP/++5w9e5b+/n5ToOZqVHNHTm0p5ZwqZSKRMI9pHFdKyVtvvUV9fT333nsvAwMD7Nu3j8cee4zy8nKOHz9Oe3s73/72twF48803Z7Wtx2Gj78pJosM9TExG6e7unnFbo02JRGJ25wXdCjOWLxLplUZGwpNc6hjAZVNYXVtCIp5I19rJXU/+ZiSTSTRNu6U23W2MdhjXMDtxdqHQNA1N00gkEovmPGW3yeCdd96htraWLVu2MDQ0xKeffsojjzxCaWkpp06doqOjg+f27KGypAjb+FW+PmNj8rn7SUbCfPrZNNs+99ysj7tz585Z9aWxsTE+++wz/v7v/566ujqamppobm6mvr6e+vp6mpubKSsrw+Fw4HQ6sdls6Vrkt8YdCVIsFqOzs5OJiYlb2i8nyzvL8kkmk0xMTHD16lWCwaD5/g9+8AN27NiB0+mkpaWFv/mbv8HpdLJq1SrefPNNDh8+zKpVqwD4wQ9+wPbt22exreDc4Y+xyxJ6env58sveabddvXo1ExMTXLt2jeLi4ll8OwUpUulVOjIXREo43z3OaHiKxnI3w32djA/3IEQKKfXtxCwN8La2NgYGBmhvb+frr7+e/Ym/iwwNDZFIJK5rz51azbeLEIKenh4GBga4fPkyg4OD896G6RgYGCAej+ecp7/9279l+/bt2Gw2Wlpa+N//+39js9lYuXIlb7zxBoePHKapqZnY+CCJnlO0yUkuXLjIxFD39dsePkxTU9Psjnv4MMXFxQwMDCClNNs03f05MjJCd3c3vb299PT0cOTIEdxuN1VVVdTW1tLU1ERTUxOrVq1i3bp1NDc34/f7b/mBJOQd9JbBwUH27t1r+nxm/aFCkEqlUBSFVCplNlrTNF5//XW++c1v0tTUZG43NjaG0+nE5XKhaRrj4+P4fD5sNhuRSIR4PE4wGARgdHQUh8OBx+MhmUzeYFvB+yf6ONOj8c3NxWyqtDEeDuPz524bCoX44Q9/yJNPPmle6Jt8O93qyUvUTaXg0LU4B1un2FSl8uS6IoRQEEJLC5JAkJqVIHV2dnL+/Hnq6+tZs2bNLZ37u0U4HOZv//Zv+a//9b/mvL5QggRw5MgRxsbG2LlzJ0VFRQvShnz27dtHMpnkqaeeMl+7WZ+NJeKEAiHCsRS/OdRNDCev3Bsi6JKEJ8bx38G94HA42L9/Pz6fj507dwLTC9LExAQHDhzg448/zvk+iqLgdDpxOp2Ulpayfft2Hn/8cR555BGamppQVZVb4Y4sJIfDQU1NDS5z4b87I5FI4PF4qK2tZeXKlXNyzBtRPeDi9GAvoVAxq1ZXXFdg38Dj8VBTUzP7Nk0TQBuLa/zs6AkcDhuPbd/AqkpH1kZmfvus297X10d1dfW8nKfZMDIyYj59FwtXr15FVVUaGxvNm3ShOXXqFIlE4hbPU3ror9r5tBUudo3hDZawsj6Eqqh3FI40Pj7OuXPnCAaDN2zT2NgY586d09fcczhwu904nU78fj8NDQ00NzfT0NBAY2Mj9fX1t/0AuCNB8vv97Nq16479BIYax+Nx/uEf/oGHH36Yhx56KOe9uSNTEL5t8hO+uDBEw4o1PLX7QfxeF/neZSklf/d3f8euXbt4+OGHb/WjzMzskbEIf/nGZbxuyUvPPMraxvLMBrfI0aNHmZycZOfOnTz99NO3vP/doKenh7/8y7/kxRdfzHl9If1JQ0NDdHV18eyzz1JRUTGvnz0TFy5cIBaLXXeebkhWVMp7X0/Q2neO1Zu28dzD63E5HHd0XoeGhmhtbWWVx8GLO++HytpptxscHGRgYIDjx49TVVXFypUraWhooLa2lvr6ehoaGqipqcHn8912W2AOIrXnopNlH6OoqAibzWZ24LnvxJnpfb/XhdftIDwZJRJNpAUpVySEEGabZos0axulHdYpSVvXEEMjE6xvrqSuIpjZDr0IPelEydl8W5vNhsvlwm63z9uNHo/HGR0dNWesPB4PoVAIh2N2CxMshHPbbrfjdDpvy7l6t3A6nbd+LkTG6K4tD+F02OnqHyUe13A77+y8CiFwuVw09LfB8QPIZ7477QPE5XKxY8cOPB4PdXV11NfXU1NTQygUuqV742YsaOpI/tNTURQefPBBSkpK5qEDC9R0aYqctbemYefOnZSUlMz+yOm2p7LWCPvqYgeqqrK+uQqv25EXCGmI18xtyCYYDLJmzRrKysrm/DzlT/tKqedMnT59mi+//JKBgQEASktLefDBB7nvvvtueMPPpxDl96eGhgb8fj9O540WZZpfVq9efRsz0+lrIgWVZQFcDpsuSMk7T3lyOBysXbuWmoNXoOtabiXPLDweD9u3b2f79u1z5qKZjgUVpHwlVlWVF198kcrK3PXJ7sawDUjXRNJnt4TMLE6cz8svv3xdm276CVltTknJVxc6UW2CzStrAK4Xn1v4fhUVFTzwwAN4vd5batPNyKnimGWh9vb28nd/93dEo1EaGxsBPcDvxIkT/NVf/RVVVVVz2o7bJf9m2rhxo+mXXCzcf//9ObF1s+nXEpFeGw4aq4K4HCpXe4aJJe889sflcvHAAw/gv3rihtspinJXhchgUVhIBkIImpubp70p5hbdIrErAlUI4skkSU2bVoyAW3JAGgM+s3C9hFgiyZmWbmyKYGNzmb5dVnF78/+z7KAej+eu3GTZsyrZD4tPPvmEffv28T/+x//gG9/4BqAH+P3FX/wF+/bt43vf+96ct+VOkVJSWlq64LFQ+WT7smbbLgHmirw1pT6cdhtXO4eJxxPcaZVRm81GZWUl0uvJW3lnYVjQwfV0kdj5ApU9ZTzX08c+rxOPy87IeJTJ6My5PMaw5VY/X6A/1fqGx+nqH8HncbG2Sbe0zO+WVq1byWW7W+Q/AIw2vv3229TU1PD888+bgXDPP/88tbW1vP322wva5plYDIGZc4nhQ6ouC+JxuxgcmyASjc1ZQnj2OoU36+eRSISOjg66u7uJRCKAHkM4ODjI1atXGRoauu2A6QUTpOmexNmvT8fcdi5BkceFx+VgIhLTaxXPMO1u3KSzSh3J+t0QsUvXBojGk6yoLaMkkB5mGQXhhF75bzHkbU/3ABBCcPz4cTZu3Gj6YqSUOJ1ONm7cyPHjxxequdeR33eWghjd0kNOCgI+D6VBD3EtRf/wBJo2N6VzZPq/2dDd3c1vf/tb/vmf/5mzZ8+STCZpb2/nzTff5Oc//zlnz5697WTdBRuy5VtCmqYxNjZGPB5HURT8fj8ulytnu7l54mVif/RaywpSyGmd2pOTk2b1Aa/Xi9frvaUZGz2wE05f7kZRFDavrL5OsIyVNCB13efPRCqVIhaLmUFpc8V0Q2jQp3xLS0tzLCchBKWlpaaTezGQ31eMqghut3vBZ9qklExNTTE5OYmUErfbjcfjmWXgoLFEly4ZNaV+HA6VjoEx4kkNm+3Wgg+na1uirJpYNEqkrw+Hw0FRURH2rGXKs9E0jXPnzvHpp58Si8Xwer188MEHvP3226xYsYJdu3bdckCkwaIo0DY1NcW5c+c4d+4c8XicZDLJihUr2Lp1a87s1t1wbAPIVAqZMipGCpLJJF1dXZw9e9YM9S8vL2ft2rU0NzfPYqrb9CQhpeTYuXZdkFZUmjN65rI+t8jU1BTt7e20tbVRU1PDpk2bbvkYMzHdMGe6J3i2dXu7He9uMzo6yqVLl+jv7+eRRx7B7/cvWFvi8ThdXV1cvHiR3t5eNE2jpKSEtWvX0tDQgNvtnsVRpHltassDOO0q7T0jJO7Qsa1pGn19fbQlbHT3hQn//ve4XC7WrVvHunXrpm1bTU0N9957L++99x4fffQRY2NjHDlyBL/fz/PPP8+mTZtu+0G5KATp2LFjvP7663g8HgKBAKOjo+zbt49nn32WP/qjP5rjTp+52RwOG3a7ylQ0QSyeGfO2t7fz85//nLa2NjOn7siRIxw6dIjvf//7rFq16oZtMsOQgEg0zqnLXdhtKptWVZsfL0S+RXJzcQqHw5w6dYpPPvmEI0eOsHv37jkVJL1d4rq/i4qKcvIVjW0mJiYWTQR0Nh0dHRw5coQPPviAlpYW1q9fv6CC1N7ezm9+8xtaWlrM1I3h4WG++uorvvOd77Bp06abPpz0ten0barLAjhtNjp771yQwuEwb775JkePHqW4uBibrZ/+/n4OHTrEa6+9xv3333/dPkVFRTzwwAPcf//97Nu3j7a2Nurr63n11Vd59NFH7+hcz5kdeycO5/fee4/29naefPJJ9uzZw549e4hEIvzTP/0TY2Njd6E9+ng5VOTG53YxMhElEoubNtOpU6c4dOgQ9fX17N69m+eff55169axd+9eDhw4wNTU1A2PbSzLLaXkau8II+FJigNu6iuzk3PzO+DNBamtrY0PP/yQ1tZWLl26NC/1kKSUbNy4kQsXLuRkg0ejUc6dO8f69evvehtulX379nHs2DF6eno4duyY6XhdCDRN4+LFixw9epSysjJ2797Nnj17aGxs5IsvvuDAgQNEo9GbH0jojmcJ1FWEcDhstPeNEE/cviClUikGBgb45JNPKCoqYs+ePTz77LNs2bKFo0eP8t577027n5QSn89HRUUF4+PjDAwMsGHDBh555BECgcBttwfmyEK6U99OKBTitdde47nnnsNmsxGLxTh//jz/83/+T4aGhmaZZX99e2Zul/6ax+XA5VCJxpPEk5oZwW2323nkkUfYs2cPq1evNvOhfvKTn3Dx4kWi0eiMuTpGlLZAD2Q729KDosDq+jJcztzTfavnTNM0ysvLaWxspL29/Zb2vV2EEOzZs4e/+qu/4vjx46xduxYhBKdOneLSpUv8xV/8xby041ZIJBJs27YNt9vNkSNH5u1zp+tvmqbh8Xh46KGHeOSRR9i8eTOqquJ2u80ie5FI5CbDNqNn6o/M2rKAPvXfPbtYpJnuA+P1e++9l8cff5wdO3aY4RJ79+6dsZLEyMgI+/fv59y5c1RUVBCLxYhGo6Yj+0604LYFKftL3qlv56WXXiIUCpnlR4aGhhgfH6empiZnZmfWcRs3yTDPTe3I+HuMC79t2zY2b95MeXm5OTQbHx9HCJE2a2c+bUJkzZgJwZkrXQhFcO+aujuO8WhqaqKsrIzu7u55CVIzeOqpp/jVr37Fz3/+c7Zu3WoOYTds2JCTtb5YePzxxyktLWVoaGhefVzTPQQVRWHTpk2sWrWK4uJis8JFNBrFZrOZQ7gbY/js9L/KQz68Lgdt3SOMTUyRkhLlBvfGTPeNoihUVlbyh3/4h5SXlzMxMUE0qtcGs9lsOQGvxvcKh8N89tln/OIXv0DTNF555RVOnjzJsWPHzFHFnUy03LYgzfQl+/r6bloz2Ol0Ul5ebl7AFStWIKXk1KlTnD59mra2No4fP863v/1tysvLb/h5N2tfJBJhdHQ0Jy7CqOjY1TfK5FQELZkkZTq19eC17M/r7OzkjTfeoKKigu3bt98kKDEtSFIiheDkZV2Q7llZiyF4mqaZzvIb4Xa7KSsrM/8OhUKEQiF6e3vntaRHY2Mjf/7nf87Bgwc5efIkAF6vlz//8z+fZUmW+aW5uRlYmGn//M+02WyUlpYCmTCQzs5OvvjiC9xuN/fcc88sI+6N46Zwu52UBooQopeuvhHWN1bgsN/6rSyEwOfz4fP5GB8f54svvqCrq4uTJ0/icrl48sknc7Y1SpD87Gc/Y2hoiO985zvs3r2bX/ziF/zgBz/g448/Zvv27XdUEmfOndotLS03LYZVUlJCaWkpqqrmXMDu7m6OHz9OT0+PPptQW5vz9LidoaFRNiG3jKl+M49OxJkYDxOOxIjG4uZbxmdomsaVK1d49913OX/+PC+88AKbNm2acTo0F0FkKs6Fa/3YbSpr6svInsW7dOkSIyMjNzxCRUVFjiDlY3Twu33jqarK7t27WbNmjTnNX15ezsqVKxftLNtiJJFIcPXqVd5//30uX77MY489xv333z8LC+n661tdHsRhU+joHyOhpXDcpEvezI2R7Gij++hBTvQN0d3dTVVVlSmkBuPj47S2tqKqKs899xwvvfQSDQ0N7Nq1i8uXL2Oz2RgaGrrZabghcy5IRUVFNy0Xmv1EyD5B69atw+PxMDQ0xNGjR3nrrbd47LHHzPyp27nx7Hb7jGZxkQ9CviHGr4wyFU3kxCYaTtvf/va39Pb28thjj/HMM89QXFx8w/G4HngtQSi0dQ0SnohRV+GjssyPIUiKouDz+XIEZTqLZzZPzruRXDvTTNtcz+gVEhMTE1y4cIEPP/yQtrY2HnzwQXbv3m2OAG5OtmsBasoD2O0qnX2jJG+SZDudeyX/OnsvnuKbJW7qd36by5cv89VXX/HRRx+xZcsW0z1QVFTErl27uOeee6iurqahoQFFUdi2bRvFxcXE4/E7tpjnXJBWrlx507BxVVXNQLXJyUkuXbpklsBsbGwkEokQDAb5x3/8R44fP24K0u0QCARYv349qZzFIPWUDSkE75waJKm1o6VkOkRID9I8efIkv/vd7xgYGOCpp55i165dlJWVzWgRmBccfagGcPpyFwJY21iF02HDUDybzcaqVatuWhh9OhHNFq67YRlN12Fn+t1idiQSCc6cOcM777zD2NgYjz76KE888QTl5eW3F7ApJbUVAew2lY6+ERI36UfTZUMYwcjd3d2Ew2HWDXTR6LRR98QTNDU10drayueff86f/MmfUFur10jy+Xxs3rz5uuMXFxff8sTTTMy5IN1qBvrExAR/8zd/wzPPPMMrr7yCzWbD7Xbj9/tNJ/edYLfbZxxiScDhdKYXasxk+l+7do3f/va3RCIRXn75ZXbu3Dnr+sASfXYNAWeu9CJEim1r6tLvCTPx9nYr6t1KGsudMF3Edv7vS5X5FtVr167x7rvvMjw8zAsvvMC2bdtuqZyNEamNMRcjBA2VQRx2G+19o+lYpEwGgkw/cI1+TdbqJNkWeSKR4OTJk3z44Yf8vxV2yioqUVUVn8+HqqpMTU3N++IICx4Y6fP56O/v58c//jE+n4/S0lImJib48MMPqaurY926dea2c5k6ItPOZ5ddxWZTiEQTxBNJHHYbe/fuZe/evTz44INMTExw8OBBc2+/388999yD2+2eti3CrKYlOX6pC4TgntU1udGSt8H4+DgtLS309fVx6dIlBgYGcLvdvP/++7jdblauXElNTc1tH3+50N3dzeXLl5mamuLrr78mFotx4MABurq6CAQC3HvvvdfN3N5NgYrFYhw8eJAPPviATZs2MTExwZEjR8zPKy0tZeXKlTcPMNWfdHo3QlJTFsBpt9PZN0bCGLKZFUolipje8soeuhklRb766itOlyusWr+RroMHaWlp4ezZs6xfv37OLJ/ZsuCC5PV6ee2113jrrbd4++23KS4uZmRkhImJCf7gD/4gR5DmptNkTfdLfX02j8fJ8NgkE5EYxQEbIyMjhEIhxsbG+PTTT3M+t7a2llWrVpkzbTN15vGpGBeu9WG32VjdUE4mrO32vkM4HObYsWOcPn2ayclJiouL0TSNd955h1AohMvlsgQJfUZ03759DA8PmwF7x44d4+uvv6ahoYENGzbgSJd9nauwlRsRjUaJRCL4/X4ikQiffvppTurN2rVrKS0tvYkgidzIfikpDfnwuh1c6x1lfDKKlH4Exuo1ImfffIzPt9lsbNiwgd27dzPxya+5ePY0e5O/ZXBwkNraWl588cU7Lkl7qyy4IAE888wzNDc3m/WGjSL/69evn/MiZECWdStwO504bTai8aS+gi16HEv+1KVxEUOhkBnENrNvJcWVziEmIjHqK0KUl/jT/eL2BElKaTqV83P7pJR4PJ5FUyRtIZFSUllZyYMPPkgkErmuokRxcbEpRvM1bHM6nezcuZPy8vJpJzAqKipmGd2cvfiowOWwURbyItokfUNh1tSXotoUvdjgTY6U/b3Ly8t57bXX0MJXCY+NsnLlSjZu3Mi6detYu3btvCclL4oCbcFgkG3btrF69Wri8ThCCLP06F1xpmYdR1Wu98ds3rx5xpQIVVVxOp0zZsbrbYWzV7oQUrKhuQqHTU2P2G6v/Ua8yD333MPGjRuve19RlFnXtl7OCCGorq6mtLQ0bxJDx7h2xrbzgdPpZM2aNWZsVD42m22W105k+pAAZIraihBOm0JH3whJLYWadzfLdCXUmRRKCIHNZqOhoQFtxQrisRjVL7xw02z/u8mCCVL+00JVVUKh0HXvG9ydp5rEoSrYVYWpWMKcrZguCvqWPlsIzl7pBiHYtq42XfEv49S+aaumybifrxKiSx2bzZYT3zbddZuuGODdQghhrls2F8fKrkhaWxbCbrPR2jVMQkuR3zuyK0rcqP8KIbA1rMQGuLMClheCBa+HdKOTlM1ciZERJyTSAuEr0ou0DY9HmIzMHDk9nSDOmCMEnL3SiwQ2r6oxZ0fkLEds08UBWcyem80K3q0Qhrs1DDS7jcyu2yWoLvVhs6l09o+Z7gZzeznzeZjWmX/vN8ztFjK0Y1H4kG7GXJ4g/XpmHNtFHhcup51oLHHDUg4zBQxOt91ULEFL5xBCStY0VmBM2871JbZigu6MuT53d+9aZAdFGsG0UFnqx2ZTuNajD9nSdZDz9pnlaCNrPbaF7FOLZ8GqG3B3TpB+gRVFoCrpNIw5aIMQgva+EcITUUqCRZSHvPrS2mSyteeKuxGlnf1v/usWC4PZd9KBu8ajrbY8gMOm0jkwqpeyTU+ciLQwmfFIN7ASFxtLQpDmFpnz41Rt2FSVSCxOfA6WlQE439ZLUkq2rKrBrqoYT6rF2gkMsp+cdzsi3OJWEFn2tSE8gtqKIB6nnfD4OBNT8fQ1kzl7LTUKUJBE5kcKAj43XpeD4bEIk1M3rlIwW05d7EJKuGd1NaYrWzLH9tHcM5clZSzmDqPfSGn8pQdIOu0qpUE94r93aBwtJXP2uBtW+d2mAAUJTAtJgMdtx+m0EY1rmYjXO+RMiy5IG1dUs/hlKMNMPjGLhcW4KvrlUTACJZGChiq9Pte1nhG0VAophelHWoo+xiXh1J5z0ssOSSFRhDFUMZ5Ad0YiqdHWM4yQks0razKuxSXQL44cOcKlS5fQNC1HiMrLy3nqqafmdA13i9slLTak467KgyiqQmffKFpq5ti4m9Lbqf+b5dxeCAqwh+lZ/cYI22G3YVMVItEYidtc3C6bnuFxBseiBH0u6ir8WRW2F78m/cu//AsffPABa9euzYl5WrlyJd/85jcXsGUW2ZjhIxKqSn3YVJVrPcNoWur2raLjB/R/n311Lpt6yxSgIBk5ZfpVDRa5KXI7GA4bPqQ7k44zl7vRkhprVlejKkpWIL+EG0TNLgaGhoYoKiri+9//fk5huKKiIss6WmCM2CIE6Ouz6YpUnRakzt5BNC2VG2MF5hLcN6Xr2l1r+61QoL0sIxJetwOXw04soZHQ7tSOkZy50k1KamxqrgKjM5iJ/ovbTpJS0tTUxJYtW3IKhxmZ4RYLhd5vzBTMLLFpqgpht6l0DY+nfUikRcuwyxd3n8unQAUJjAJtwojtSDuRZn35zFIPmScXQEvHECkkm1ZU5+QSGSuPLhTTRefmm/ejo6NUV1dz5swZEokEqVSKlStXzlgjeSk6TZcmIscPKY36RlJSUxbEpuqF2jLLwafFSAoQs18ReTFQkIJkPm+kAKFbSU6HythEhGgsgds5i6RCkXVDisyL51u7IZViw4oqo1RWVhTJ/HWM0dFRs454dlxR9u92u51QKITNZkMIQVdXF729vUxOTiKEYHx8HK/Xy6uvvsqTTz6ZM2xLpVIcOHDArKE8MjJCJBLhzTffBPTcxNraWrZu3WoJ1xxhnMfs0Ayn00FxwEXXgKBvcIzKUj+KyLaMltZ5LzhByg4bMwqplfg9+NxOBkcnmZyKzU6QyJjFRhb2SHiSrsExPG4HTVXFYD7JmPd+0dLSwqVLl8x2Tjd9HwwGefDBB81aPA8++CB9fX1s3bqVxsZGxsfH+elPf8p/+2//jYaGBtatW5djXV24cMFcrHJycpJ4PM7Ro0cBXeySyaS5bJLFnTNdPpoQgprSIOda++jsH2XTqhoURUXKVLoUydI69wUnSAA51RuFwG5XUVUFTQpScvYXUO8UekF/KSXn23rRUtBQWYzHZQcp0mkj89cpjI7q9Xpzqv1NJ0p+v9+sES6l5D/+x/+IEIKqqirTGmpoaOC5557jk08+Yc2aNeb2iqKwe/ducxXfgYEBfv3rX/Mnf/In5vvzXdxruXKjPEopJfWVxdhsKh0DY6TS0dpCKFkuiKUjSgUnSAJpWitGiq2qKghFIRaLo81i6j/76STTGdhCCL5u6yOVSrG+sVLP7hfkDNvmA6Ojrlu3zqy2OZ3fKD9FRAhBfX09iUTCrIMjhOD+++9HVVW6u7uvSyepq6sz/zbq56xevdoaos0xNzqXQggaKgLYVYWWrkG0lIYwbmthuMJncS1qGuamsXdIwQmSQfZNE/Klp/7HIkxGb7x4I+SXdVAwIvrPXe1HapJ719enHdh5dXfmaeh2o+Jx+Y5t49/JyUl+85vfUFJSwsMPP4zH40FKyYkTJ9A0jaamphlLU9xI8KZrj8XcYJzXihIfqiLoHhgjlcpMzMj0SGBWZz5dfmShKUBBMm7EzAX1F7nxOB1MxhLEb5Y+Mk04kUiXFznf1ksqlWJDcxUIxbSK9JiQ+YtBuplwTCcOmqbx7rvvMjo6Sk9PDytXriQajfKTn/yEFStW8Oijj6IoyrTHzhe36awvS5TmHuN8NtWWYlNVugbCpDIDgPSwjdn1uwWO0DYoQEHKYFTgg3R1JClvmruV/65xvccjMTp6h5ECVtaVpS0kfZZDiFQ6uXb+RvPTWSc3EgS/38+/+3f/jtdff53f/e53VFRUkEgkmJiY4D/9p/9EQ0PDTY8zk1BZYjS35J/PymI/NlWlO12GJEeDlthpL0BBMsPLzFd8Hicuh42RcISp2PVDtpwOkB3iIUnHeSh09I8wFUtSVRYg6HXm9QOhm84LMNt2K0LwyCOPUFZWxtmzZxkfH8fhcLBmzRruu+++O1oy2xKjuSX/fJaFinA77fSMjDI2ESXo8+SUr11KFJwgGakcplmLpNjvpcjjpL1veNoSJNlDjvQzXz+OAEiBFFy82ktSg62ra1CFQBqFFPLFbJGzfv36GRc4sFi8VJf6udo3SEf/KHWVIbPooMiOqFwCFFw+wHShYnabPu0vU9dn/F8XUJhVJlQ3ePRyEKcudZLUNFbVlWXC9mX2IM0q42Fxd5BAXUUQm6JwtXsoa8UVI31k6VBwgsR1fiKB22XDaVcYj0SJxnOn/a+L3xGAUSYUME5hS/cIWiotSEp2HhHp8rhLo2PMxo9msciQkqoyPzZFob13OB2LZEzczNI66u3MlCBZQApPkISRW5a56UJFetXIkfEpIrHMWub5y+WYTnApMjFGEhKaRnvPCCDZvEofsmXbYUJMZ5ctTmaahbNYvAghaKgpRVWV9NS/biHd0mTC8QOZEiQLSMH5kK5H4nLacdhtJLUUyaRGSkqUGW7MzABMX7VECEFX/xgDQ+MEvE5qyvwZ4bpBbI6FxVxSU+pHVRTa+/RobSMYd9bzKIuk/EjhWUhpsuwXJAKHw45NFelCbdqNhy0ifbHT5vCZK93ENY0VNWUoihGVlCJ//G6JkcXdorY8gKIodA2MkUplMhKWWo8rSEESpmtbGvNlBH16cORIOMJUNHED8ZBm8SuRDols6xoiqSXZuKIaRVFNy8h8QqVLRSx2ZloGyWLxU1nix25T6RkaIxZPgFEbZ4n4Lg0KUpAyCITURcPvceBy2JicSprF/o3rmVn1QWYm2aRMxyJJrnQOkkyldP+RYsyrKelPMD5q8T+rrBVHli5et5OQ300iqdEzMIo0+60lSEuGbEvA5bBhs6lMRmPEcxJscxNKjYRcI3FRS0nOt/WhpWBtQwWqYt3MFvOPRFJbGkBRBNd6RzIlbG+hesVioKAFybQIgJDPg8flYCQ8SdSI1pbT5OnL3OHXcDhKz9A4boeNqtIiy7qwWAD0eLfa8gCqgK7BcdOxvRQs82ysWbb09fJ5XbicdiamEsQS+gq2ZnG1vO31RH49k7qta4i4ptFQVYy/yG0JksUCIakuD6EoCh09WRaSVX5kaeJ12XHaVcYmMsGRZhxS1gXNnk5Fwvm2HhIJjc2rarCpBW1wWiwgAqmv0aaodPWP6sGR4hbqIVnlRxYXAZ8Ht8vB4OgE0azgyEzGuhFTmf5F6kX7T7d0E09orGuoRFUt68hiIdBtofqKIKoiuNanO7Wz05xuyiIpP1Lwj3SZTvHwuh047TamokkS2UO29FbpjJHM3wK0VIoL1/pJJhOsrClFsRzaFguGoLGqBEWB7sFRPS9ziS2BBJYgmZcr4HXhdtoZCkeIxBLXT5aa2R/pPaReA6lvZAKHXaW5tgRVuf0SHRYWd4agLFSEx+lkaHSSyWg841pYQhS8ICH1iGu/14XHZWc8EmUqmkCmMqXbpr2oQnKtZ5SpaIyGqhKK/ZZD22IhkdhtChXFfhCCroHRpWYcAZYgAfp1U1WVIrcTh01lfDJKPJHIcmrnow/zzl7pIR5Psr6pCrtNXYrX32I5IaEunULS3jdqzrQtJQpckDIlQgCCPg8el52RiQjReJLclWavn///+kovsYRGc00xqjXDZrFgpH1FAmrKgyiKoLNvJCtaexZY5UcWH4EiJy6njbHJmBmLlI4uI9t3JBFoKWjpHCChaaxuKMemWKfSYmGRQG1FACGgs3ck/eIsJckqP7Iw6M+SvIuU1ppQkRuP087g6CRT0cR1+2bvMD45RffgGHabwtrGcisGyWIBSUcbybSFJNIWEnoZnVlhlR9ZGMzLI9N5PllT+yG/F7eZPjLNTFv6AAJo7RpifDJGdVmQkoDHmvK3WFAEelZTfVkQIQTt5pBtafXLghMkk2wtSvuSAj43boedkfAkU0YJhxmu59nWbqLxBKsbKvVlp3MDlSws5pHM5EtteQBVEXQOjJlW01KiQAUpu+5j5rWQz4XbaWNgdJKpWCIvYSSX81d7icaTrG0ow6Gq025jYTHfhAJeilwORieihCemFro5t0zB+ZCmw4hnDfrcuF0OhkYniUSN5ZDSRf5FxvekaZIrnUPEExrrmyqw21SmX89k8ZFIJBgcHMRmsxEKhXTrLotYLEZvby9jY2MoikJxcTGVlZUoeU57qxzvYiKdRitBVRSqSwP0joTp6BuhJOBd6MbdEgUpSJm1z8kZlQX9HrxuJ5PROOHJKEkthU1VsyJe9R2GwhF6BsfwOOysri/HblNYbGI0nWCEw2FOnz7N4cOHaWxs5PHHHycUCpnvx2Ix9u/fz+HDh4lGo4C+ou2zzz7L2rVrTVG6WY1wS6wWADNvLUVteYATLV109I1xz+rFkaM2Wwp0yAYgMsmyaevGabcRKnJjU1WGRiNE4wljUzKVkwSX2vuZmIzTVFNCsT/t0JaLe6GjoaEh9u3bx7vvvssvfvELvvjiCyYnJ3O2OX/+PD/60Y+4cuUKwWAQj8fD/v37+fu//3vGx8evW6NuJtHJXkLbYj7IqkEhJbUVIRShF2qbNdUN+s8CU5AWkiEe+at6CqCi2IfX7WBwbJJoLEmRS2Z5v/V/z7X1Eokleai5AqfDhpR6Z1iIpbJnIl8s2traOHv2LA0NDaRSKYaHh0kmc9ege+ONN+ju7ua//Jf/wubNm9E0jUAgwF//9V/zyiuv8OCDD95SmVvLSpofjL5sFGSrKPHpU/+9Q2TGAzfhvsVRfqQgLSSR/k/KTJ1sY56iPOTF63IwMKI7toE8f7Xk9OVuIrEYG5oqcKRn2PTOsPgsAsNK8Xg8PPbYYzz33HOUlZWZC0Ia709OTrJv3z42bdrEjh07qK+vp6mpiVdeeQVN0/joo49IpVLTWj3Zr1lW0fyT87iUgqpSP4rg1iykytpFUYKkMC0kIXNrxaSLHUkJJQFdkPqGxolMJZBCZDaXMBlNcLl9kKSmsaGpEoc9neEvBVKk8gveLjiGldLY2MiKFStwOBw5jmxj+NXb28vAwACrV6/G4/GY75WVlVFXV8fp06dJpVI5+4bDYRIJfYWW0dFRUqkUIyOZm8DpdOL1Li2n6lJEIvXFKgQIIaktD4EQdPaPsWhM9llSmIKEHkQGRsE1mXZwC0qCRXjcDroHRpmYihkbmYXZrvYMMxKOUOL3UlUewKYaZf/FvAShJRIJurq66OnpueF2wWCQ+vp6UxAMkZkOIQThcBhN0/D7/SiKkjPcCgaDjI6O5iyTJKXk8OHD9Pf3AzA2NkY0GuW9994DwG6309DQwI4dO+7o+1rMhmwbSVJXEUQgaO8dXnIVkQpUkESe5yhjSVSVBvF5HFzoGyVixiJlshRPX+5mIhpj04oqitzOzI0r5icmNpFI0NPTw5kzZ264XV1dHaWlpTe1UAzntDEcyxcjAEVRzOWZIWNVjYyMmII0Pj6Opmnm33a7nVAoZM24zQNCisy0sRCUBvU1BofHI4yEJyj2Fy10E2dNgQpSPpkbprLER0nAw+jkFCPhSZJJDdWmmF7Dk5e6mIzGuG9NLR6nI7P/PEVqO51O1q5dS23tjcf7LpeLQCAw4/v5zmmv14uqqkxMTJjiZLwXDocpKSlBURTzdSEEjz76KLFYDCkl/f39/PCHP+Tll1823/d4PNYS4vOByA61kNhsClWlPkbGp7jWPWwJ0lLGYVcoDfpQFUF77yiTU3H8PhcgmYzGuXitj2RCY8vqalwOW84khpwHD5KqqoRCoZz4oRtxo1ih7N+rq6spLi6mpaWFaDRqDvGGhobo6Ojg8ccfN4UGdCErLy8397fb7dhsNurq6nI+zxKj+UEIYZasFSjUloc439ZPz8gEW2dzAKP0yAI7tgtylu3GCKpLA3g9Ljr7R5mIxvWC/lLS2jXIwOgExQEvDdUleoS2yKxAshAFQ282q2VYKOFwmIGBAQYGBojH48RiMYaHhxkYGCAajeL1etm+fTunTp3iwoULaJrG1NQUv//974nH4zz44IPXRWvnf4bxe3a7rJik+SK9vLsEpKC2MgAC2ntHZ7f7Vwf0nwXGspCuQ9JcW0LI56Wjf5TJqSgCvSzoyYvdjE7EuHdtLYH8NdjS6SXzzWzjgT755BPOnz8PQEdHB4ODg/zqV78iFArx9NNPs2HDBl5++WXOnTvHP/3TP9Ha2ko0GuWNN97g8ccfZ9u2bTf8rGzrKdsqyh7iWdwlJMjs8yugtiKIENA126n/7sVRfsQSpGloqAwRKnJx8Wofo+MRpNDz146evcb4ZISdGxopctnJGa8t8htuZGSErq4uALZv344QgvHxcSKRCBMTE0gp2bFjB3/6p3/K/v372bt3L4qisHHjRl555RUCgcC0gpNNvlWU/7vFXUIYzoK0FSoFdRVBpBBc7Rla0KbdKpYgXYeguixASdDD8UudtPeOsWWVRu9wmPPXerGpgk0rq3A77RktAj10YNFFIelIKXnxxRfZvXv3tO/7/X7sdjuKovDtb3+bXbt20d3djc1mo76+nlAolDNcy3dUW8OxhcYYMkuE0Cce6ipCQIqO/lsIjlwEWIKUh5QSn9dFQ3UxLoeNU5e7eeieFXxx8gp9IxNsWV1LXWUoXUN71uuCzjvZgiGEIBAIEAgErrNushNlQZ9t83g8VFVVIYRAVdXrrBzLUb34yLVe9VgkBcHVntGsrfJ76+LrvZZTOw+BQBGCjc2VlAS8HDvfzsX2Pj4+eonxyRi7d64nFPCiz2kYJjK643tBW57LzRJf8//OH2YZs2bTHWemY1gsLBJhPlxK/UU4bAqTU3FGxzNJ1DJd+d+oXrHYbFtLkPIRujvovrX11FWGuHC1j5+8d4yT5zspC3m5d12d7j8Sij5ASzuzF9+ltShUhBAoiqCyNIgEOnqG0vmaueHAi3GZJEuQZqCpupiHtzTjdtr4/f5zjEfiPPfQBhrK/ahCL0NipoxIueid2haFg+HSa6gqRUpJ30jEeCfPEs66/Wsa9J8FxvIh5SHTyx4pCjz/8HqGw5Ocbe1jVV0J/8/T91ES8GWmWNNPGCNCVtclS5gs5hcztCL9t+HYri3zA9DRFyY7bDcz/ZLVV+9dHOVHLEHKw1gcUkporinl33/3Ybr6x6gu81Ea9KGoegqJbiRlX1SZ+8SxsJgnpkvPEULQVFWsr0DSO5IVtKsXJjQnM0j34EVQegQsQboeKZCkQOgh+GXFPspDRehPGAVJStchqYuRTCc1GgWyLPvIYiHImTkFkJKaMj9SStr7cqf+pUwhhJpTlnmxYD3SpyVTwE1BmpUl9XpHXLdEsRB55q+FxTySXRYG0kMyIagu1y2kjr5hI7Ek7e9UjB0XXeScJUh56EWuDBM4S3hMv1F6Gk4YqSKZ6NjFdWktCgXDh2mGcKRLmFaVeJFS0tE3Qm6ZHcPtsPh6rCVIeWQcg1kX1/y/kh7KZSoqmTK0+K6tRaEhswZgAhprSlAEDI9PEY9n6qcv5q5qCZKFxbLAeEBm6qSDpKrEB0B3/6j+ivFefrpPb2emBMkCYgmShcUyQGb/KzKJts11FQBc6xlEf2uGZPDjB/SfBcaaZbOwWOoYU/4iy62Z9n9Wl+gzbZ2D4+lN80vDoG/ctTjKj1gWkoXFUkfkzvrKtMgIYEVNMUjB1d7hXDEiN6l6sWAJkoXFUic9w2vWozIXGhSUBrwgJd0DY7oYpfUnk1S9EA2eGUuQLCyWOlnLeEE60Tu9mGBjdQkAPQOj18UrLUYsQbKwWOpIkWXpiJxQlNp05cjuofHr4pUWW5Q2WIJkYbH0yQuFM1YfkVJSV+5HEZLO/jESSS1jRcm8nRcJliBZWCwT8muaG4X2gkVOpITegXCm1G0659+kukH/WWAsQbKwWCbklyY2XqurDAFwrXc4Kw7JCKJM73DfN/SfBcYSJAuLJc50TursWKP68hKkhP7RSTJBSiJd8ja9Q2XtoihBYgmShcUS52br5dWVB9JlSEb1F42p/7vftFvGEiQLi2WKYTlVlfqQUtI1MGaEJ7FYq8BbqSMFRjgcZmRkBJfLRXFxMXa73XxvcHCQcDhMKpXK2cftdlNdXb0oy1VYzIxxvaorQkgp6e4f0Qds6YUpFuPVtASpQEgkEgwPD/PVV1/x2WefsXr1al544QVKS0vNbT788EOOHTtGUVERqqqar9fV1fHHf/zHOeJlsXjJL2fbUFUCEvqGxjMr3JohSIsrFskashUIfX197N27l88//5xf//rXfPrpp4yPj+c4RD/77DPeffddIpHIDY50PflO1cUcCVwI5FuyNaV6gm3P0DhadixS9kaLpPyIZSEVCL29vXR3d7Np0yY++eSTnFgV44maTCZpbm7mtddeo7y83NzX4XBgs+V2lewVb62FIxc3QZ8bl9PGxFSU4XCEsuIiY2G2TDKbUXrk2VcXrJ1gWUhLntlaI6FQiKeeeornn3+esrKynLwmQ0BisRhVVVWoqko0GmVqagqHw0EoFJrVircWixMhBLVlAVJIugbH9Iqn+YtEdl1bFCVILAtpiZFKpUgkEiSTyWnfN4TGZrPhcDhQFP2Z09DQgKIo5t/TCcrAwADBYJB9+/ahaRrRaJTq6mp27dpl7p/9OT09PUSjUaSUDAwMkEwmaW1tRUqJqqp4vV7KysruynmwuDXqK4vpGAjTPzyR9erie5hYgrTE0DSN3t5e+vr6gOvTBQyLJxAIUFtbi9frBbhuyJW9j4Hb7WZkZIRr167h9/sJh8McO3aM1tZW/vzP/zzHAS6l5MiRI/T29iKlZGxsjGg0ygcffACA3W5n5cqVPProo3N+DixuDQnUVoRInW6ld1BfNBJhrNS2uFYesQRpiaFpGmNjY3R0dOS8ni1IoM+qlZeXm4KUj5TyumHbyy+/TDgcZuPGjZSWlhKLxXjrrbf42c9+xs6dO3nyySdRFMXcz+12m8dPJpMoikJRURGgC6DT6Zz7E2BxywghqC0PkkKmBSl3gdPFZClZgrTEsNlsVFZW4nA4zNfyLR0pJUVFRbjd7mmdzvkY7z///POkUikCgYA57R8IBPg//+f/cOLECb75zW/mbP/AAw+QSCQAfRbvr//6r3nmmWfMbSxBWhwIoLLEh0zpWf+YqbWLbz1BS5CWGDabjfLy8pxZsLkgkUjQ0dGB0+nE5/OZgmQIX7ZlBJjDwuz9FUXJGdZZLBIE1FUESaWgo38EzDz/xWUdgSVIy5Z8y6irq4twOAzAxMQEiqLQ0tLC1NQUVVVVKIrCL37xC2w2G3v27KGqqopEIsE777yDz+dj69atOU5ti6WEpLYihExl0kfMAElDlGoWvvQIWIK0bMkfph0+fJizZ88CujUzMTHBhx9+iM/n45lnnmHNmjUEg0G++OILwuEwjY2NRKNRDh48yLPPPsvWrVutKf4likBQGijCYVMZGZ8iEkviddrSg7a01XvvwpceAUuQliXT+Y2cTicejweAp556CiEEbrcbIQQ2mw2Xy8Wrr76K3++nra2NgYEBhBB84xvf4KmnnqK4uNgSpCWKEAKbqlAWKiI8FaVvMExTTTE5sdqLoPQIWIK0LJkugnr79u1s2LBh2u2Li4ux2WzU19fz8ssvMzAwQDweR1VViouLqaystIZrSxgjILuqNMDYtQjdA6M01ZSYBdoW03PGEqRlSr41U1ZWNqsgxdLS0uvijWZKEbFYIgiJEJLK0gDnrvbQ3T+aXpREpNdMWjxYjz0LYOYUFEuMlj4C/TrWl4dISUnv0IQuRIvwklqCZAHcvOqgxRJGinRwpJ9UStI9rM+2XpfPtgiwBMnCYrkj9IdKdVmAlCbp6h8100ZMFkn5EUuQLCwKACGgoiRdyrZ/FBBIkRWpffxApgTJAmI5tS0sljn6KtuChsoQmpQMjU2SSqZQbVn2yCIoPQKWhWRhsexJL3iEx+0g4HURSyQZDk+m37Vm2SwsLBYAIQQNFcUkJfQMjqfX015cbm1LkCwsCgAJKEJQFvIiNY2+kcmsmkiLB0uQLCwKAZmui1QRQtM02nuH9NcWul15WIJkYbHs0ZfMVtLpI8mUoH94XF9Re5HZSNYsm4VFgaDPtAVIScm13pHcVUes8iMWFhbziRCC8pAPLQVDYxE9x80YtFnlRywsLOYTRRFUlwXRtBTdfSO55f0XSfkRy4dkYVEASClRhKA44MHlsDE+FSc8GV1sYUiWIFlYFAJGgrRNFVSX+YlrKbr6hhe4VddjCZKFRQEgpQQJqqJQWxZAk5K+4clFN+9vCZKFxTInU89KIhSF2vIAyWSCrr7RxTZiswTJwmK5Y4gRQl/OqrG6BE1L0dE3ltmotxN6O2Y8xnxhCdIyZKbqj7e6jcXyIGs1PWyKYGVNKYlkkpMtXelSthJ5fL9efkRm7yXn3eltTfsvQ2ZTdna6bWbaxyphu7QRWf9XFWioLkYogqu9w0xGY3jdduhqT5cpAaTM/D7Pl92ykJYZhuVjCMh0llD+a9n7SCnNH+M943WLpY8QCjXlQSqKg0xEolzu7EeimIaQhPSiAAvzALIEaZmR35Gy/06lUiQSCRKJBPF4nFQqlWP9GKKjaVrONtMd12LpYVxru6pyz4pKYjGNr853Qrq2duYKi7x/5w9ryFYgJBIJOjo6uHr1KhMTEzgcDmpra2lsbMTr9ZqCMzw8zMWLFxkaGkJVVaqqqli7di1ut3uBv4HFnWJYug6bwvYNjXx49DKHv+7g+89tRzU2khIpRHp1JKMcwPwJkyVIyxjjiahpGkePHuX3v/893d3d5ms+n49vfetb7Nq1C4/Hw+joKL/85S85dOgQqqqSSqVQFIVXXnmFp556CrvdvtBfyeI2MfqCEGC3Kdy7vh5FkZy+3E1H7xiN6e1yDGFjdm4esYZsy5hsq+enP/0phw8fZuPGjbzyyis8/vjjnD17lh/96Ef09vYC8MUXX/CjH/2IkpISXnzxRfbs2cPIyAh//dd/bW5jsQRJF4bUh+QSVVVpri1mU3MFgyOTvP35WZLltemMf5G2kjAcSvPaVMtCWsYYT8VwOExJSQn/6l/9K5599lmCwSAAHR0d/N//+38ZGRkhlUrxs5/9jOrqav7Df/gPNDY26uUqGhp45plnOHDgAN/97netJbWXIsIYeYl0xRGB1+Xg1Se38d9+vJfffXGWXd+9l3tW1yLRV7k1hEjmpuDedazetYwxLKTKykq+//3v89xzz5lilEgkUBQFr9eLoiiMjo5y+vRp7r//foqLi819d+zYQUVFBR999BGapuUcP5lM5vwYrxmO8/ztLRYGiQQpDEMJicTtsPPUA+t4/P6VjE1Osb8vAVU15sraQoIUEjHPs6uWhbTEkFISi8WIxWI33MZut+NyuVBVFa/XS3Nzs/l+PB7nwoULnDhxgp07d1JaWkp3dzeJRIKamprrfEV1dXV0dnbmTP1LKens7GRqagqAgYEBEokEly9f1jPLFYVAIEBVVZW5vTVTt7AY/mmBBKFQFvTy77/zMO9/eZ4tq2vI2ENCH7JBnlPp7mMJ0hIjFovR0tJCS0vLDberqKhg3bp1pkVkMDU1xblz5/iXf/kXnE4nr776KuXl5fT395NKpXA4HDlBk1JKXC4X4XA45zhSSo4ePUp3dzdSSsLhMNFolA8++ECfyXE4WLt2rSlIlhgtHAKRlhr0/6cLRaqqwvqmShoqi3E6dCkwr72x0TxjCdISI5VKEY1GrxOIfHw+X86QSUrJxMQER44c4f3332doaIg//MM/ZNu2bTidTmw2G0IIkslkjjUjhCCRSEw7w+b3+4lGo6ZFpCgKxcXFANhsNjwezxx+c4vbJqtUbUZo0rltQuDzuvTNIB2PJPQx27x7kCxBWnJ4PB62bdvGtm3bpn1/pqFRJBJh3759vPPOO7hcLv74j/+YHTt2mPFFxcXFuFwuBgYGTH8Q6MO7gYEBtmzZknNcRVF4+umnzb+7u7v5X//rf/Haa69Z0d2LDaFbR0hdaNJx+bo4ZXuWTEVKLy0pmXdLyXJqLzOmE6NkMsmRI0f46U9/itvt5nvf+x733XcfqqoSj8fRNI2KigoaGxs5e/YsQ0NDSCnRNI0LFy7Q09PDjh07pp1hmy5VJdu6slh4pMxYRPoLxjsiPZDTf88OgjSc3/M97W8JUgHQ19fHL37xC3p7e9mwYQOJRIKzZ89y/Phxjh8/zsDAAKqq8uSTT3Lt2jU+/fRTWltbuXjxIj//+c8pLy9n586dOYKUL0QGN8qhs1gYzGuCLk4iS24yb6StofSfpmEkrFk2izmmq6uLvr4+XC4Xp06d4uLFi0Cmo7744ouEQiGef/55zp07x0cffURHRweJRIKvv/6aP/iDP2DNmjU54nMz6yf/fWuWbaERmVgkQBjTaCI9kjOjJzGNovn2H4ElSAVBaWkpr776KkNDQ9O+7/f7URSF5uZm/u2//bccOnSIrq4ubDYb3/3ud3niiSfuOG3EEqOFJi91VmT+yi5Pkj1yW4grJqRlW1vkEY/HGR4eRlVVSkpKZhWd3dPTwwMPPMC1a9fmoYUWyxXLQlqGzGZ4dKNt7HY7lZWVd6NpFhY3xHJqL0Nm41i+WTVJC4uFwBKkZcpc1tW2RvUW84UlSMuUO7WSsve1LCaL+cISpGXMnQqJJUQW840lSMscS1QslhKWIFlYWCwaLEGysLBYNFiCZGFhsWiwBMnCwmLRYAmShYXFosESJAsLi0WDJUgWc4Lb7eaFF15Y6GZYLHGsbH8LC4tFg2UhWVhYLBosQbKwsFg0WIJkYWGxaLAEycLCYtFgCZKFhcWiwRIkCwuLRYMlSBYWFosGS5AsLCwWDZYgWVhYLBosQbKwsFg0WIJkYWGxaPj/A2DzOpcQ1GMhAAAAAElFTkSuQmCC
|
Determine where the local and absolute maxima and minima occur on the graph given. Assume domains are closed intervals unless otherwise specified.
|
Absolute minimum at: $x=3$
Absolute maximum at: $x=-2.4$
Local minimum at: $x=-2$, $x=1$
Local maximum at: $-1, 2$
|
0296afc7-857a-46e2-8497-63653d268ac8
|
differential_calc
| false
| null |
Compute the derivative of the function $y = \sqrt{\frac{ x^5 \cdot \left(2 \cdot x^6+3\right) }{ \sqrt[3]{1-2 \cdot x} }}$ by taking the natural log of both sides of the equation.
|
Derivative: $y'=\frac{-128\cdot x^7+66\cdot x^6-84\cdot x+45}{-24\cdot x^8+12\cdot x^7-36\cdot x^2+18\cdot x}\cdot\sqrt{\frac{x^5\cdot\left(2\cdot x^6+3\right)}{\sqrt[3]{1-2\cdot x}}}$
|
029deb6d-6866-4e2d-9d92-3a555ec4de2c
|
algebra
| false
| null |
1. On a map, the scale is 1/2 inch : 25 miles. What is the actual distance between two cities that are 3 inches apart?
2. What are the dimensions of a 15 foot by 10 foot room on a blueprint with a scale of 1.5 inches : 2 feet?
3. The distance between Newark, NJ and San Francisco, CA is 2,888 miles. How far would that measure on a map with a scale of 3 cm to 1,000 miles?
4. If the scale for a model train is 1 inch for every 10 feet of a real train, how big is the model for an 83-foot train?
|
1. $150$ miles
2. $11.25$ feet by $7.5$ feet
3. $8.664$ cm
4. $8.3$ inches
|
02a70481-c574-417a-bf03-50e5080f4d19
|
differential_calc
| true
|
data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAT0AAAFlCAIAAAAWJKhQAABqgklEQVR4nO39Z5Acx5nnAWeWr+qu9nZmeryF956gAyk6iKKk5VFakZI2dlfa29uL996Ni/twEaeI/XBfLmIvbmMvNvb2vePuSjxJJ1KURNFDoAFJEADhzQCYwXjT3tvqqsr3Q3bX9BgYAgNO90z+JA56aqqrq6rzX8+TTz75JEQIAUJjghCCEN5i45I7EFYBkOiWQGg4mJU+AcJtQAiVy2VVVSmK4jiOoigAgKZppVIJAMBxHE3TtUZV13Vd1xdsJKwyiG7rnUKhMDQ0dP36davVumfPHovFomlaKBT6/PPPVVXduXNnIBBgmLnvMZvNhsNhv98vSRKR7mqF6LbeKRaLp0+f/j//5/94vd7Ozk5ZlvP5/NGjR//X//pfFoultbW1paWldv/h4eHPP//86aefDgQCRLerFWqlT4BwGziOM5vNMzMzV65cicfjqqrOzMy89tprw8PDAwMDbW1tLMviPRFCCKFTp0699957sViMRC5WMUS39Y4gCM3NzSaTSVXVcDicTCY///zzS5cudXZ2Pvfccy6Xy9gTQogQOnny5KlTp0KhkKZpK3jahPsK0W29wzCM3W73eDwIoampqeHh4d/+9re6rj///PMDAwOGscUkk8mhoaFQKHT9+vVsNost8EqdOeH+QXTbAEiS1NXVRdP0jRs3Pvzww8uXLw8MDBw6dMhqtdbuhhC6cOFCJBLRdf306dPYVSZd3FUJ0W0DYDKZenp6aJq+fv36m2++ybLsCy+8EAgE8JiQga7rn3/+eTKZBACcOnWKdHFXMSSe3ACIotja2qpp2unTp0ul0tNPP33w4EFZlhfshhA6f/58Op1GCI2Njc3OziqKIggCMbmrD2JvGwBBEFpaWiCEoVDI7/e/8MILHo9nwT4IoVAoNDQ0lM/nAQClUunq1avpdHolzpdw3yG6bQAQQrquI4RkWf7a1762adMmQRAW7KBp2okTJxKJhLHl7Nmz8XicuMqrEqLbuqZcLkej0atXr7733nvFYnH79u3f+ta33G73gt3wCNC5c+dqDeypU6ei0aiu61/tKRO+Ckj/tq4Jh8Ovv/76xYsXP/zwQ6/X++KLL/b39y8Y+8EghKanpyVJkmVZ13VBEIrFYiKRKJfLtVmQhNUB+UbrF4RQNBo9duzY5OTkunXrHn300ccff3zB2I8BRVF79uxpamo6d+5cKpXatGmT1Wp1Op3YwSahqVUGmcdXv+i6PjMzg+cP9PT0dHZ2Wq1WY+xngRoRQrlcTlXVV155ZWpq6oUXXmhtbZUkiWXZBcNFhFUAsbf1C0VRPp/vySefBABwHIfdXUVRstksAMBisdQ6wBBCs9mMEBJFked5WZZtNhsxs6sVotu6hmEYLE5sTm/cuHH9+vWZmRkAQGdn58DAQGtrK8dxC961wA4T9a4+iG4bg0KhcPr06V/+8pfBYBBHno4ePbpx48Yf/OAHHR0dNE3f7I1EtKsSotvGIJVKffTRR5OTk08//fS+ffsURXnnnXfefPPN3t5er9e7IHeqNmZB7O2qhOi2MaBp2ufzPfXUU08++WRLS4umaQihN95449q1a/l8fnHOI6iql4h2VUJ02xjY7fZnn32Woii73U7TtK7r5XKZoiir1XqL4dlGFy0C4OYXcMs/rnaIbhsDlmW9Xi9+rWna5OTkkSNHXC7X1q1bTSZTsViMRqOKogAAIpFIMpmcnJzEHrLD4ZBl+RYd4HplniznaxQBABEAACBY2Yz7BbBmh1rgvM1w7hcEAASwun3uzwghVdMoiqIoCtblA4LotsEol8s3btx45513rly58vjjj2/cuJFl2XA4/MknnySTSYTQ5cuXE4nEsWPHnE4nhHDXrl39/f2iKDaU7a0ID0sqlSlmCyUIodUsiAIHIYAAQQAQgACgYqmczhcZmjJLAkvTEEAAIIAIAQhqRKqoaiZX0hGSTTzPMvhmQAAAQBX1Aog/V9dRMpO/Oh7iWbqn1SNLQh3eOaLbhgEhVCgUrl279vvf/35kZGTfvn1PPfWUy+WCEOISrTzPI4RYlqVpmud5nuchhAzDNJRiAQKoRlMgGE9/dn50JpqxmcVd61tbfPZgLK2UVa9dtpgFXdcHR0NDU5FWn31dh4+VDLeiRrQAAQBKinptMjwdTva0uPva3QLPz4kWghqLjlRNuzEd++lbp1ka/sUfHehvnzeFo04gum0YSqXShQsXfv/734fD4UOHDh04cKCpqYlhGISQ3W7ft2+fqqoIoUQiMTMzs3//flzP0Wq1YgGv9OnfORAghA2mpukffDH81mdXLGZxY4df11E2X3zr0yvZgvK13X397Z7pcOr9E9fyRaXZZaMhhd9dPQoAAGsWAgBYloEAXroxOzYdZ1mmp9XNMjTEmp3vV2uaHkvlhqdissQpZa0+bxzRbWNQLpeHhoZ+97vfZTKZJ5988sCBA06nEycwQgg5jvP5fAAArOFMJuPz+fCU3ZU+8S8NNrYIIQBQMls4eXmiqJQf39C/c6C12W0NJzJXx0KyJFAUTOeKH5+9cX0yvHNda6vfLvAsgAAZSgVGzxQBADiWbvc7Ah7b8YtjdovkspncdnPl/iBY7dwChICq6Yl0QVVVm2zlWBrM97jrBJK52hgkEom33377888/9/v9brc7FAoNDg5euXJlbGwML1ywiqh0OCeCic8ujA5PxRiaoQCUBE7g2USmUCipHrvstJhGZmInL49bzMKm3ma33awhfTqcGp6MxJI5VdMBQBrSI8ns4Fh4bDZRKpVdNmljT5MkcGevTY7PxlVVA1jmc7KEEEJNR8lsQdU1uyzwLAPq8tlH7G1jkMvlLl++nM/np6am3n33XWxpaZpubW195plneJ5f6RNcTnCA6PTVqTeOXR6diflclk8ujPhcssMi6jpqdlva/XaWpa+OhqLJ3INd3W1eB8fS2YJy6srExeGZrX0tB7Z0WU1CLJU7dm7k8khwXbv34LZOl83U5nf0tXuPnb1xZSTY3eJyWKS5cHLlw5Gm6alMQdV0uywKLFNvlhZDdNsYSJK0ffv2trY2QRCMQR0cf1p1030gHpxpcslARzQFBzq8G7t8HoeZoSmfQz60s7fJbc0VSkOTUYFn23wOWRIoCHmWZmnqxlRMQ6An4EG6/sWVyU/Pj5oFzueUJZ6DgHJYpL5Wz0dnhq+MBh/c3u2wSnM94CqarsfTubKq2y0mnl9iqnM9QHTbGNjt9m984xt4hNYAQigIgtlsXqmzuq+s7/C5bCafUz6wueOBLZ1Oi8SxtNdpcdhMLEOfvTY1HUnaLZLPKbMsDQDgWWZ9l//MtanpcOri8IxZ5D69MMIx9EPbuzd1N5lEDkLAMYzHbpZFfjaaTmbyOrJRkJpvT5GqafF0TlE1q1ngWLo+EzyIbhsDjuNaW1tX+iy+IvBQkKajXLHsdVmaPVan1cSzDACA5yge0AiAWDIbT+VbPHabLDJ0RVd+l3VrX8tUOHXk5DWTyAk8c2BLx+aeJnPNGKwksi6baWw2EU8XlLLOcxQ00jcAQACUNT2ZLei65rCaBI6tQ9ECEpci1B84kwmFk7lUruhzyHazREGIKv3QSuA3V1QLJVXkWUnkaKoSR+Y5pqPZZTELZ65NT0dS2/oCO9e12mSJgjitAiIAWIY2iRxCKJdXVBUBABGcGwjSdZQrKsVSmaNpi0lgmTrNMyO6JdQbFfs2GUomMnmXzWQx8TQ1L6oLAdB1pCPE0JClKWO4S1HUdLaoqrqqaZCCTptZNglUjSMMAYCAoigIAFKRBgCqDgBVpKvqejKTVzVklUWuItp6LAhDdEuoOyBAEMCpYDxfKLptJrO4OG8EMjRFU0DVdFXV8bTFsqqNzsROXBrTdX1zTxNC6PpEKJnJ46Hg6v+BjnRVQwhApvowgPhPCCCENFVPZYu6jhwWM88x1TfVHUS3hHpER2gmmuI51mUz8fxcqiZClWxEi4mXJT6TL6WyBU3TNR1Nh5MfnhkaD8Y3dTcdfmCD22a+ODw7PBktldXaGQqlsprKFmiaspoFhqGq8eRKcoWq6vFUTtV0p1USuDoNJgOiW0JdAgulcjCedVgkq1mkYKV6IQLIyEv0OGSnzZTMFKKpfFFRg7H0sbOjl28E25sc+7d27t/Usbm7KZHJn78+E0sVdMMZRiiTK8ZTOYln7bLEMhQAAAFopESpmh5L5cua6rBIAscACOoz74LollBvIARALl/mOban1e20mmhqfu8WQAiA1yk3uSzpXDGcyGbypaGpyNBEJOCxH9za3e53uB3mLb3NrR5bKpNPZfKapuO+bVHRwvFMvlT2uywWkwAhRNVZBTgpWtVxkqPuqG97S8aBCPUGhADwHPPE3n5J5JrcVpqijEl2xj5Oi6mv1Ts4Gh4Pxjd2+a1maf/mjhavrbPFKXAMRLA74H72wU0lpWyTRViZVAtiqdz1iQhL0xs6/VazaMzkg9UZBqqmxVJ5TdOdFonn6lcd9XtmhLWM1Sw8sqNnwUZoTJgHkGPpjV1Np65Mjs3EZ6LpnesCW3qbqrtBAIHNIu3e2F6bDqWo6sh09Np4xO+ybOjyyRKHcyqqxhwCADRNS2ZyZQ1ZTAJbSboAdTiES/xkQuNQcWkrhrej2bl3Y1tJKZ+/Ph2MpsuqDgCsTaKYUx2Cqoamo+mz16dUXd+xrrXFa2NoqmplK5PmEUKlspbIFhBCdouEMz3qE6JbQsOAqjEkLEezxO/f3LGh0xdOpEdmYvmiAvR5gzbQmH0PQLFUHp6MzMbSm3ub9mxqr3GSjWMDVdPTuZKqIbPIyRJP01T1L3U3FlS/TxQCYT4QzomoEgBu9ti+trf/2kTEbpEoChewMSbm1RSjBQgA4JClA5u7elrczU4LTUEAIKoRLQ4mx1M5XVMdVomfF5SqOz+Z6JbQSBjpTUZNuL42b1+b19i8UGEIQQAQhGaJ3zEQQAhAABGe4osQBBBBVDkWgqqmJ9MFTdOdFhPPMbBue7dEt4QGA9YUtECGeCFE2NIucGgRgNWUCvw2WDO9B4Kq+iuVMcqqFk3lyhqyW0SBoyufVoeqJbolNBCoRkgV6c0FnlC1LE1tfxTOrzBTeWfNmNK8knCqpicyeU0DTouZZ1lcdqMuZUviUoTGAQI8alNTJ7k68DoXFkZU9VXNxgWuLqopw1pTpkZVtXgqp2uaw2riORZngNQnxN4SGo8FNRsXbVvSRsL5L5fYR9X0RKag6prDKvIcbUS/7v2Elx2iWwIBAAAQAqWyGk3lVAQcFklg6XrUaxWiWwIBAAA0TU9mCoWSKnKMbBKYyuTbOhUv6d8SCAAAoKhaJJHTVM1hEXmWAcjoFddjJ5folkAAAABV0zK5PAK6w2riOQbhqQh1KVpA/GQCAaOoWiiZK6vIYTHxHDM327cuPWWi23rhtstMo6VGJRpxJZH6RNP0TK6IAHLbzQLPGsHkeqzCSnRbJ2QymVAoRNN0c3Mzx3GLd9A0LZFIBIPBcrlsbGQYpqurS5Kkr/BMVy1KWQ3H06qmuWxmkWNh7ehu/UF0u8Louh4KhT7++OOPP/64tbX1hz/8ocfjWbxbLpf75JNP3nrrLYSQscC82Wz+q7/6q7VTV3m5QLVmtJosqWl6Jl9COrLLPMfSi2bq1xckLrXCjI+Pv/rqq7/4xS/efvvtU6dO5XK5xfvglW/PnTv36aefCoLQVMXv97PsErVUIITQKPFAWMT8ojd46i3Il9RgLKOqutsmi5XJQDgLsh7vIbG3K8zIyMjk5OSWLVtomhaEyhLJCKHajit+TVFUS0vLn//5nw8MDBh/MtYKItwDSNX0VLaoakgSeZHnaBrgelOwouu6g+j2q8bQJDaG69ata25uTqfTMzMzhUIB71MrWrw/QoimaZ/Px3FcJpPRdd1kMi1YkNqwrqjKqlvy636AAEAlRQnHU5qmOW0mgWcBoKrzF/BCm3UnXaLbrxpYrSqKJef1er1e7+DgIKgKb0ljq6pqMplMpVJHjx4tFovlcrm1tXXr1q0dHR1GHMs4MuHOwUa1rOnxdF7XKzNvjdl79RlMBkS3K0KtLI014w0jXPvC+KlpWjabDQaDb731lsViURTl3Xff3bx58w9+8IOBgQGWZZdU+4KNhDmqU3Lx7L+yqsfSBR3AJrdVErhKXVZYu8vKnu5CiG7rCEO9tVuw9sxm8/79+9va2jZv3rxhw4Zisfjmm2/+4he/cLlcXq+XYZjz589ns1kAwLlz56LR6JEjRzweD4RwYGAgEAgs8KgJABhhZQAAKqt6IpPXdd0uCzxL43wLiNBcsmOdQXRbd2ChzlUHhRAAYLPZvvGNb2iaxvM8z/O6rn/jG9/4+OOPz507l06nAQAffPDB7OwsAOD69eu5XE7TNFmWAQAMw3g8nlW2IP3yAI0p9FApq9FEVtOQy2YSOGONeQgRIrol3BGLg1IAAFVVE4kEwzCSJEEIaZrGcalSqQQAaGtr+3f/7t+pqgoA+OUvfzk9Pf1Hf/RHgUAAQijLsslkIsZ2PrV1oyBAQClrkWRO1XSbLPIsg4PJYEFtjHqC6HZlwIJUVbVUKimKkkqlisViqVRKpVKJRILjOFEUc7nc9PS0xWLxeDypVOrtt98uFouPPfZYd3e3pmnDw8MzMzObNm0SRZHjOCNbw2azpdNpj8fT1NRE5HpbEACarmcKxUKxxLOUw2riOAYYndp6TVAmul0ZcMc1mUyeP39+ZGRkfHx8eHhYUZTf/va3zc3N3d3dO3bsmJiY+OlPf7ply5Ynn3wSQpjP548cORIKhXbs2FEulz/88EOWZQ8ePGiz2QAJJn85sBWtGNWSooZjGaWsWWVR4jkKwMpfcOyqLmN7RLcrBpbi2NjY2bNn0+m0y+XSdX14eDgcDrMsu3nzZoqiGIahaRpCaLVaH3744Wg0euPGjeHhYQCAJEn/5t/8m/379xv5yUS6XwYIqoM9ZVWLZwoIAZfNLHDsfBtL+reERXg8nieffPLAgQO6rhsbaZq2WCyyLAuC8Od//ucmk8lkMlEU1d/f/2d/9mczMzPxeBxC2Nra6vf7bTYbSa64W3BpdKSUy5F4RtN1t80scMyCQR+SL0WYB0IIJxvfbAeGYYw5AwghnudbW1ubmprwlCCe5w3F1qcv1wBAABAslbVYqqBX1uCj52db1OldJbpdMb6U0oyBXJZlGaZ2/fXbzNol3AYIFFWPpXI6AD6XVRT46kSDeg1JAQDIfKD6x+iyLhjRNV4b2ZFf/bmtDpRyOZrM6DqqrDFfs/RmfQ4CAaLb+ue2thRCeCe7EZZE0/VsQckWSixDO6147czaGfN1eleJbglrFgQAKClqJJFVyprVLJhEnqKqyRj1DdEtYQ1SyZdCAJTKajyVQwg4rRLPNUy4h+iWsAaZ84SVshZN5RECXrtF5JYoHlKfEN0S1jRKWY0lcwghtwOXcWwMiG4JaxGjalRJ0aLJjI6Qx24RiW4JhPoHIVAoKaFYRtN1l62R+rcNc6IEwvKB8IR5Tdcy+VImr7A0bZMFjmkYM9YwJ0ogLB+V6lElRY0lsxrSHRbJLPINlOlN7C1h7VFNQC6W1FA8g3TdbTc1UFAKEHtLWItUykrBUlmLp/MQQK9TJrolEBqDolIOxbM6AD6nRSK6JRDqmWp5eFAslYPxtKYjp1Xi2UZa+YHolrDmwFEpHaF8SUlmizRNuW2kf0sg1DsQ116Np3KFkmIWOYfVzDLE3hIIdU9RUcOJHNKR0yrWTt9rCIhuCWuUUlmNp/IUpPxOqygssVZ4PUN022CQuhbLAgIgXywHYymAUJPLKvFEt4TlplarpK7F8oBAUSmHE1mEdIdF4rhG6twCotuGYLFWF1hdYoS/LAigfLEcS+UBgNU1gRoJott6p1aTi2vE4fWpScXzLwkqq1oyk0tl8xxLO6wmjmEa6/Y12GNmDbJgJVtVVQuFAl5v3ijISuonfxkQAKBYKocTWU1HDqvJJHIUxGuLNMw9JLptALAsdV0vFApTU1MnTpzI5/PPPfccXuGWiPZLAgFARUWNJnMMTQW8DpPAAVh/S1PfEqLbBgDLslAonDlz5oMPPvj973+fSCT27Nnj9XoBiVTdDTBfVILRNASwyW0RBa6xRAtI/7YhwH3XVCp15MiRiYkJr9eL16Em0am7plAqhxNZHSGHBddMbjCIbhsAbFEZhunt7f3hD3+4c+dOURTBIktLDO+dUyyp8VSeoiiPw5jB10hPPaLbhsHlcn3729/u6+tj2S+RAU+M8GKUshpLZeOZvMizXodZYGmAAEKN9NQjum0YKIqqXYOvFoSQVgWPDOm6jn8FRLqLyOZLU5G0pml2C89Vpu+hxnJWGs+zJyzwhxFCuVxucnKyWCwCACYnJ0Oh0NWrV9PpNISwqanJ4XB8KRO96imWtUQ6z1CUz2EROA7Bykq4DRSdIrptPBaHo+Lx+NGjRyORCIQQr14vCILdbgcAPProo1u2bKldepNQKCmReJqhqVaf0yzyDSZZAADRbcMBIVysQEmSenp68LBQOByORqN9fX1utxtC6HK5iGgXkM0VJ0JxHek+u1nkabzuXmMN4BLdNjYIIYqiXC7X448/jn9Np9MTExNf+9rX2tvbKYoiWRkLQAjlCkokmQeQctpNlRkFCDaSaoluG4VyuTw7Ozs7OxuLxUZHRzOZzNmzZ3O5nMVi6e7uxsNCS7K2RbuEEVXKWjJbVFTdKUsum5lnOQBwDlUjGVyi2wYAIZTP50+ePPn+++/H4/FoNCpJ0m9+8xuLxdLb2/unf/qnS+p2bSvWACEAao1ptlCajqRoAFs8VkngjDU1G8tTJrptACCEHMf19vYihEqlkjEHiKZpj8djMplW+gTrF7To13S2ODmb0JDuspl4bq48TSPNKiC6bQgQQoIgrFu3rq+vz9iCzSmEkIzx3Bw8zWceuaISTGQoivK5rJUF+BCoDgU1jHKJbusdY3otwzAMw9RuXNkTaxTm3yZUUJRYOscyVIvHatQ6hwCBhhrCJflS9Y5hVxdvxAO5xnAuyYu6DQipqpbIFBLpvMizfpdF4NkaucJGES0gum1EaqteGIaXWOCbUFUjAgDCTL40FUqomm6XJYFnIYQ1QatGuntEtw1GrT5rXxPR3gYIAADZfGk2moEQ+JxmgWMbagrQPEj/tsFYUrSEW4Iq/wGYLSihWIah6Ca3TeTZhhu2NSD2tlEhor0DEKqYVITd5WyhFIxlOIZq9dlNIlcRLWo8u0t0S1jFQIjwVB8IEFBVLZkpxFJ5jmO9TovAsYalhY2mXKJbwqoGAlANPmXypelIStE0h8VkNQk0TVUcaIgHgRpJukS3hFVMrSBhJl+aiaQoCLxOs8Qzho1FoMGKXQCiW8KqBoKKcBECIFMohmJphobNeOQWAYgQgABWx8hX+my/BES3hNVNZXQbIpTLKcFYhmPoFq9NEvj50w0aSbSA6JawBoAAQlXTE9lCLJXjOcbntIgcA+bZ2Ebq3AKiW8KqpppYBmC2UJqNphRVd1pNNlmkaapmH1S7c0NA8i4Iq5bazJRUrjgVTjIM3eyxmUW+ZvS7wTxkDNEtYZWCDEUiAEAqU5gKJxkaNrur0/caGeInE1YpNXZU11EyWwhG0yxNNTktRLcEQh1TGQaCJUWNJrLJTEEWeb/bKnBEtwRCXQMBAJlCaTaWQTrwOS32eUGpRqXhL4BAuC2pbHE6nGRZutljFQW2sULHS0J0S1jdIABAMlOYjqQ4hmrx2ESeW+lTWgaIbgmrGAQA0HQ9ns4HY2mOZ/142m1jjv3UQnRLWN3AXF6ZjaRyBcUui26biWNWw9gn0S1hFQMBAPF0bjKUYBi6xWuzmHiq4W0tACTvYsVBCJXL5UKhUCqVKIoSRVEQBJqml9ytWCzWVm+kKEqSJGZVGJD7RzJbmI6kBI5t9TskcTV0bgHR7YqTz+dHR0evX78ejUZZlm1paenv7/f7/ViNRhEpRVHGxsauXbumqqqRo8fz/L59+2w22wqef52j6yiezs9E0wLHtLhtIs811LIEN4XodiVRVXVwcPDNN9+cmppiGEbXdQjh9u3bDx8+7PF4KIoyKq3m8/njx4+/8cYbLpdLkiT8drPZvGnTJkO3pH7yYgqlcjCaSWTy7T6HzyEL7Cpp8KvkMhqUWCz28ccfnzt3bvfu3Zs3b85msx988MGRI0fa29sPHDiAV+sy7O34+PjY2NjevXsDgQB+uyAIZHGgm4MAAIlMfjKcBAD4XRaHZTVkXGCIbr9qaiuVj46OXrp0qb29/Zvf/GZXV5eqqqIovvzyy1988cWWLVsWrLJH03RLS8tTTz3V09ODlx2hKGrBYYnJrQECgGLp3HgoLnBMm98h8nyDVl1dDNHtV01tpfJgMBiPx9evX+9wOGiaxsq02Wyjo6P5fL72Xbqua5omy3Iqlbp69aqu63a73el0iqKI1btAtKRKKwAAIRBL5qZCSVHgWn12SWj4tGQDotuVJJfLlctls9lsxIRFURRFMRqNqqpau6eqqolEIhqNvvPOO+VyWVVVh8OxY8eO7du322w2Yw0hYm9rKSrlUCwTT+Xbm5zNHpvAs6vD2AKi25VF0zTs8RrmkaIomqbx9gU7cxxHUdT4+LjP51NV9bPPPrt06RIAYN++fRzHZbNZTdMAALlcrlAoJBIJWZYhhJIk8Txf61GvHeLpwmQoCQDwO2WHRWLohl2eYBFEtyuJETGuHZXFA7MLHF2r1fr4449v3bp13bp1vb29pVLp/fff/9u//dt33313YGCApumPPvoomUwihL744ot4PP722287nU4I4a5du/r6+kRRXIOeczSZmwglRJ5p89lXR3qjAdHtSiIIAsMw+Xxe13W8pVQqKYoiyzJN01jMWNhms/mBBx6gKAp71KIoPvTQQ6+++urw8HA2m+V5fmJiIhKJIITC4XA6nR4fH08mkxDCnp4ebIfXGgihSCIzEUqaBL59dXVuAdHtyuJyuUwmUzAYzOVyNptN07RwOJxMJvv7+wVB0HVdVVWs1UKhMDw8TFFUe3u72WxGCCmKous6x3E0Tbe3t//H//gfAQAIoZdffnliYuKll15qb29fm+4xJl8sz0TS8VSuu8Xd7LGJHLNqnGRAdPvVU7uOXiAQaGtrGxsbu3jxIsuymUzmzJkzpVKpr69PkqREInH58mWv19vR0ZHJZN5///1oNPrUU0+tX79e07Qvvvhidnb2wQcfNJvNCw6LWePr4kaT2bGZGIQw4LO57GaGoVeNaAHR7VdPrYpaWlr2798/Pj7+6quvDg4OptPpwcHB9evX79y5U5KkkZGRV155Zffu3V6vl+M4WZbff//9WCy2efNmVVWPHz/u9XoPHTqE86UWB5OxYtemaAEAoUR2PBiXeLbVa18FBaUWQHS7kvA8v3v3bkVRPvzww88++4xl2a1btz755JOBQICmabPZ3N/f39TUxLKsJEmHDx/WNO3UqVN/+MMfIIRtbW1PPvnkrl27BEEAi/Iu1vgyuZqmz0aTY7Mxuyx2NNklgTNWnUdwNZhdMuJXF2QymXA4zPO81+tl2ZsaB03TkslkIpGAELa0tPA8v2AH3L+dnJzE/VuwxhIwKgvZIpDJFX/+3un/88bJrX0t/5/vPNQbcFMUwJJdHX1cYm/rAlmWZVm+7W40TTudTqfTeevdjIGltSFarFUIYHWJaghD8czoTILn2BaPTZZ4ioIAAAQRAACuCoO7duONhNUCrP7ATymIEJyNpUdmY2aJ62hyGCNAcHVM4QMAEN0SGh5sRKu/QQDKqjoTTQejaadV6m5xSgJnFHBEq8NLJn4yYVUwb9npaDI7Nh1TVa3FbfW7rHx1zi2av3JmQ0N0S2hsUEW0sBKVgmAqnBqeisiS0NnslnhuXiRqlciW+MmEBqd2YT0IgKrpU+Hk6ExcNvFtfrtYU1BqtWgWAKJbQsODYLV/iwBEqWxhbDaRyZWaXLY2v0PgWQSNFW5xB3c1QHS7XCzVINDtdljTLL4hd3uLsGoRAAjMhFNjMzGLWexpddllYWHV1dVic4lua0HVHwjVNiKEQM2vaMG/C1/jXxFCoPo/UF3UfLVJ9zZJO/i2Va5/wZruCCz8vbofQrVW8c5uXOUtOkIz0eRYMG4xCe1+h8jzEEAI4Orr4BLd1oCMkUAAEQIAIdxmIEAIwUozRRDgloVbAKr6XrBG9RABCCBCECKAKn9YLS2mlkV5HcbdqNwhVIngoupAzUL9wOrjDQF804xjVh6fEA/I3kK41S8NApjNKzemYrPRtNtuavc7Vl9asgGJJy9krr0AiBNsSqqmKOWyqhdKZU3XWIbiOZaGFMfSHMtUp7gjHCHB/1W1Ws0Zhvjvq1C6oJICbZhEOKe2uUuel2CIqg8547EIsDhxLhPCsSaEAILQ2PvmWU7V24sgmI6kbkxFRY7pbHY6rSZmtVRvXAzR7Rw4fRUiCACFEEhns7FMKZ7ORxK5RDKTzivhWLZYVmUTb7dIPENbTILDItlkUTaLVjNvkQSOpbALU2mveMQQzpnxVQnEzzdk2NCK2mruAUAIFRW1rOoI6VhmAECIEMvSHMtSNKjqu4LxLmg8DW/+8dhdR7o+HozfmI46beb+Np8sCffncusCots5sFFEAIVimVA8c/76+Nmh4IWhYCqTZWiKoimWZiAAiqbpOgIAFMtliIDfae0KeHoDrt42d7PH4rVbbLLIMjTEU+sAwC0L/7ui13c/wV5x1cDqCJQUNZsv5YtKrlguFIsFRYsms9m8ouuoak0BgkA28W6bxSYLdll0WCSeZylouCwIQljxfG75yfjv2XxxeDI8E0lt729tb3IIwmpu26v52r4sOtKz+dLITPzd41c/vTA6E0kIHCtwXJvX4XPbzCbO65QFlo4msplcSdXBTDSVyuYVrXzu+sSJS6M0Tbf5bbvXt23rD3Q1u9x2E8/SVeMDAFhN5RbmqMzyBQAgoCOQLZTi6Vw0mZuNpsdm4pOhxFQ4NRtNZgslmqapimmkAEAQUQjoiqZxDBvwWtZ3+TZ1t3Q2OwNem2zi6Wr3Axpu9U1uneFKj87Gr4yFOYbpaHK4bRKzqmt9EN1W0HR9MpT8/NLorz+4NDQZ4limq9m1b1PH5t6WJqdFFDiGpliWpiAoq5qm6QgApayls4XZWOb6ePj6RHh0Nj4ZTA5NRt4/cW3vxo59m9r72z1um8yxNLqts9ew4A58USnHUvlQPDM8FTt3dWpwdDaSzEEIWZZiKMiyjFfk/C6bwOGSihBAABFESI+mcolMMZrIvPNZ6vfHBntbXQ/v6N0+EOjwO8wib9THu9UcHgggApoOhqdiQxNRj0Pu7/CaJX61RhMwRLcAAFRS1OsTkdc/vHjkxGBe0XoC7ke29+zf3OV3yWZJ4Fkawtq2g+PMEACoaXpPq7pjoDVfVCZDifNDM8cvjY1OR37z0YXPL44e2Np5cGtXf5vHJkuLl9hbBeg6yhWVUCx9Yyp84vLkuaHpSCIHEBI42u+ytPkdXS2ugNfqc1pliRd4lqIWWs5yWUukCxOzsTPXZ88PTw9NRq6NRzZ0+Z/cO7BnY5vXaeEYGtx2QiIEyUx+dCqayuTXdXq7A25JWDgzeZWxJnWLqrM1IUAI5YvKhaHpl39/6ovBCbPAP/fg+if3D7R5rVbZxFBwLhd9ruXMBZoYmmJoThI4AExep9zb5n1gS8fJy+Mfnxsdmoy89sH5i8Mzj+3u37epI+C1i9XO27xTmX/o+qF2hg2Y5+MjAKCuo1yxNBNNX7ox++nZGxdvzGQLisBzbT77+k7fpp6mVp/NahIlgRN5lmcZmqbhfM0iACACCKCyX+9r9+ze2D4WTH52/saxcyPnh6bHZ+PjwfjX9vZ1Nbslga0MzEFUNb6Vd1e/CDQ6E7s2HpJErifgcdlMNF2Pt3QZWZO6hag6MoFyReX4xYlfvHPq1OBEk9v6na/teGhbZ7PHRtPULcsjLLGNY2iXzWSXxSa3bcdA22cXxz46MzQyHfvXN08NT0Qf2927vsvvsEgMTRvzyVC14dVfK0MQAB1ACKoz8AG+aIQQKpTKwVjmwvD0R2eGLgzNpHMli0ncua5194b2DZ1+t91kkUWJYykIAJzXyYSLXkMAWJriJF4WObfd3NXs2LEu8NYng59dHPt/758LxTLfeGjjpu4mWRIANTdCXn3qVn4pq9r1icjwdMzrkHsDLrPA1eMdXVbWpG4rDVAvlMpnr03//37z2fXxUG+764VDOw5u63ZZRYqi5tIlqgOztz8ohAghmqacFpPNLPjd1o3d/iMnr312YfTIqesTwfijO3v3b+4M+OwCx1RNdjVno/6Ye2BV9AEAAGVViybzl0eDx86NnL4yHklmzCK/b3PngU2dG7p8PpdFNgk0jlPdPjcMgardBAAhCFmW9jllq1lodtlavPa3Prl89IvrmXzp+ce27hgIyBIPKVidsVfttEAIAAjF0tfHQ9l8aff6tq4W1ypOtzBYm7oFEIGiop27PvOzt05dvjG7sbfpTw7v3DHQbjUJeJUshIeE7njoZl7xRIhoGrrtJosp4HdZegOe905cGxwPTkfSY7Pxx/f0DXT4bGaRgrAuLS0Ac+47Agji/AddR5l8cWQq9umF0WPnbkyGUhLP7NvYsXdTx4aupma31SxVVjOBRnbnLaNx2O/FHgeshowRQgLPdgdcz5s222Xhtx9d/OLKOAKApqjt/c1mPCQL0TyvHaGhyejV8bDNLPS1ue0WkYKrOZKMWaO6LWva8GT0lbe/OHFpvKPJ+cdf27FnQ6dZ4quJNxXfFd3MTQYAVLW6uNxpJdsCIIFjOvwOuyy1NTne/uzKJ+dG3jl+dSKU/NregX0b271OmWPp+hzVhUa5JogggEVFDcbSpy6P/+HU9cHRoKbrA+3eB7f1bOtvCXhtsshTNASG71odcUWoZtsSnwEB0rG0K/e80n2BkII+l+Wp/QN2i/Szt05+MThuEliRZzZ0+yWeq3EFIAAgW1AujwTHZ+Pru/z97T5J4FdFAanbsBZ1q+n6TCT1xscXj18ac9ul7zyxbe+mdrPAVaPFEOEgyJ25sYZ057bghogggICioMMibe9vcdtM7T77eyeuXR4JRZO56XDiwW09XS1Oq0mAdTjSWImfI1XTU7ni9fHwh2dufHp+dDaaanJZDm7t2r+5o7fVa7OIDM7bBxAhnBc656VUMx5v+gkAQiPshbMnYDXPFALgtJkPbuvO5kv/993Tn5wfk02iWeK7Ay6OpRGcS88anY5fGQ0DCHtbPa1eG8+u9pAUAGBt6jaVLXx09sY7J65xLP3MA+sf2t5lM4uQqmbnVfYy/r15y1vK2FbfjACci6PwHNPd4rLJQovX/t6Ja2cGJ9746OLodPyRnT0717V6HTLLMvXW2hBAhWJ5Opw8fmnsozPD18fDkKL2bmx/ZEfPtv6AzylzLENBY06QUSbRsHbo1sOuFWdmrrtarTWDH4IIQICsJuHRXX25YvkX7539w6nrfpdskwWf00JRFA4wq6p+eWTm+kSo2W1d3+mzmsVK3/pLdHEakjWn26JSvjwy+7uPL6ZzxSf29j+5b73HJlfqdFbEOpcAD7EVufnRFhtb4y/4z3OvKOixywe2dPpdlg6//YPTw19cnZiKJMdm4g9s7epsdlrN4jLmwd9j1oGiqrFkbnAs9OGZG59fHEum8x1Njge2du3b1NHV4pIlAVbu2FxGyfzPwxODbnUSFYcEzVneeWde7bF47Oav7e4Px9O/+ejieyeuBry2B7YIsknA0g7GMldGg6lsYftAoKvFJXAMqtr41azaldXtfS+lXzPAh3/XdDQVTr316ZXrE+FN3U3PPbSp3e8w1AJrvvDbW1tg7HHnlwDNIr++0+eymVr9jj+cun7++vTrH128NhF5cGvX1v6WZrfVLFaK/S6VFblwy9wNnP+XpabXzTuNBcdEAECg4+26jjL50uhM7NMLY59dGB2djvEsfXBb9yM7ejb3NHudZoam5oWYAYTze7agZvut7kXtP/OEbxysomq/2/Lkvr7x2fjJKxMfnh5u8dgG2r08x+i6PjgWGhwN2y2m9R1+t91M0zTEg8Kr2tiCldXtV5CJVhl+rKxwBZLZwqcXRo6dG7FbpGcOrF/f6eNYI41pXrRj/ou7+uSlQQwFm1zWh7cLAY/t4+YbH50ePn99ajIUvzgyu39j+/ouv9tmEgWeomoTHpaex7Zo5a65MHDl/7e8gupjrWL1NB3lCko4njl7bfLjszcuj4byBaW71f3Qtq7d69s6mlwmgYUUnK+4eeq7g8v/cvvgy6Jpqq/d//jegclI8vNLYz0Bt9chex1yKpO/MDQ1GUpsHwis6/SZRd6YkrDKVbuyui2VSizL3se1HiHCM2BxE1VUbWgi/NanV3IF5ZkHNuzb1FEZ6Lufy0+Uy2UIIU3TlcluAAAAEACyxG/qbvI45J6A+5PzI6evTH70xdDV0eCmbv+u9e0DHV6n1WwSOYamjJmo1ZkxCxKZaiea4+l0eqV2BKw1ifO6AXNvRgAAoOp6vlgOJzKXR4KnLo2fH5oJJdJ+l+XQzt69mzrWd/qcFhNd6f8vAV7vk2GYZfoqa0+28rvIc/u3dF4dD73+wfnPLoz2tbpFjr50Y+bc9WmOpdZ3els8No6hK5dWHRRe3q9UURSapm+Wr3pr53HZXctl0O1dn9P58+f7+/tlWb5/Kz7iGdy46UeT2WNnb1wbC3e2uJ7Y0+91ylRlHN+IZS4/ExMTLMv6/X686g+sPEggBIBhqBaP1WmVOpqdA22+z86PXhmbfefzqxduzG7o9G/pbelv97psJklgRZ7FDiAAVTVWi0kYXXEAQHViK6w8sRCYV11pfsANL0VSKquZvBJJZK6Oh08PTlweCc5GUzZZfGRH376N7Zt6mv1uC8cwOGB8s1GdZDIZDodbWlrwip7Lw/zeMQTAa5cP7ei9Nhq+Oh4+8vnlYi55/MrU0ESov8O3vstvMeGJBMiY1re8otU07erVq36/3+12L3WySNd1COHNnlzL3rDvXrdzc5rv9px+9rOf/eVf/qXJZMLPsPvgNmP7ggCEJUW5PBr68IthkecO7ewdaPfixzOs5lcs90dX+PTTT2VZfvTRR1mWhdVJuKjSKiEASOS5/lavz2EZaPeeG5o+dWXi2njoD6eunx+aDXhtvQF3d6ur3e9wWCSR5wSO4TkGzj1t5l2sEUi9+ekghICm6UpZKyhqJl+YDiUvjYYGR4Jjs7FwPMfzzPaBwN5NHTsHWlu9DkFgKFh9TuDPWOrgExMTx44dO3z48DLqdkFjwI1tQ5d/z8a24anI+5+dv3z54mxKLUNpY1dzZ7OL51hkdIoRWvavs1wu//a3v33sscdqdVsrgenpaUVRTCaTJEmCINxfR/JedHvvMjtx4sT3vve9+7ogYGU8AaFQPHPs7I3xYGJrX/PBrZ2yma8YrsqY4f3qag8PDzudTkVRAACG91fjrgIAAKSAwyJaB1q6Wl3b+loGR4MXbswMjoZPD04MjgbtFsnrlNt9jlafvcVj87usksAwNMUyNMPQNE1TALAsDhbN2RoAKr6iqumahjRdVzVdKatKWU1mCjOR9GQ4OTwVngwmZ6PpbKHksJoe2N69qcs/0OHtaHJYJIEygtuVSjtL3CHccOPx+NWrVx9++OH7cwsBqDY2SeR3r28/dWXi6PHg8ESSZsV92wIbOv0Oi0RT80tQLfejWFXV8+fPb9myZfFZYd55552LFy/6/f7Ozs62tjaPxyPLsiiKgiAwDFNH9lbX9VKpVG2Rd4OmadlsNpVKMQxzH9aPM7LtgKLqF4dnPj13Q1cLASs0MXoukwWg4kFDCHUA7tOiT6VSqVAopNNphpl3q+d7uZVzpQDsapKbHEJPs/VGp2doMjI0GRmaDJ2/NmLieZdd9jrtHqfFYzNZZdFpNVtlwSyJPI2cdjNXPX4ir2ZKIBjPMFISQpjKFXKFcjZfyuSLuI5HKJ4ORlPhWCqSSDEM093s2tnf1tvmWdfhb/FYJY4FmpLJKMaJ4vPDr2tjUcYDN5vNlkqlTCaTSqWW676hmt48nNuAvDauwyfbrHKhDHmO6W62uS1sKZ/TSgVjjgYyytAt01eKEMrlcuVyOZfL3ewajx8//tvf/laW5ebmZr/f39LS0tHR0dHR0d7e7nQ6sREWBGG5jPDd67ZYLI6Ojk5OTmqadndHyGQy58+fz2az92duajVIgVCqiD4bSo9OBtlSJDaunDohmCSp6lfeP1sLAAATExPJZPLEiRMWi6WSCgRqBTAXPkFzXVYAADTrepdVYYuaoIBxpMxGo8MRNMSaGV60mc2yLNlkSeQZUeBpCCwmnqYpACAC6OrVeDarZt85L1tGIAD5kqKU9ZJSLpTUWDITTWRyuXy5mOVB0WXhA057jwd1Wcs2PREeT0cmFliq6jpYRuh5KVf50qVLs7OzZ8+ejcfjy3HPjGAHAAsH1RECQE3NSozGsoxNBLAQuXHtQnCcq3Vlbp1eeRcghIrFYjQaHRwcvNlyp8FgMJ/PJxKJiYkJAIDJZPL5fIFAoL29vbu7u7e3t7+/v6urS5KkZTmlu9dtuVwOh8NDQ0PlcvnujlAsFsfHxzVNo2kad+trV0y/d3CObaGkDoUKZ2cApZetIB2dTQ8NyaIo1k4EW3a3yuj5xGKxYrF448aNyheGbl4vqRpuAmBuBwGBPg/XbLZF3ExWQYiVKM7MMCLkTTqkU5l8OlsslrVUJqeoOkAQQD2Xz2uaHrwwydAUhXTZLEoCL0uCLPGy19LmYJEi6ArLg5LDzNtkiWNLyehMMnLrOzCX8Ll4r6mpqWQyOTo6WiwW7/qO1VBr4udOwHjMMYrultmCxrbbAatlJkYLFFX7BFz+SDIAoFQqZbPZ6enpa9eugaViqKlUymi6EEKsjlQqNTU1FY/HaZr2+Xx3beEWc/e65Xm+o6NDkiRd1+/uCP/7f//vjRs39vX11drbZZYuQOPB5PnQoIJyPa1OPyp6HeadO3fJ8vJFPm/JpUuXrFbrjh07bDbbPVwXBECvvKBYiuUpTtIhk87ki4paLGupTL6s6QhBAPSTp04mEomdOzbYHQ4KIItJFAXOLHKySaBQGZQLuloEqNqAluNOcxwXCoW2bNnS2dm5DIe7DQgAKFwKXplKbOlwbmp3SDxzHwMkVfL5/Pvvv9/f3793794ldzh27BjP8xzHcRwniqLf729tbQ0EAi0tLe3t7W1tbS0tLYKwbCUm7163giC0t7e3t7ff9RHMZvPGjRu3bduGhzfv+ji3oKiUM2duJNVRt4N+YEtAjyOf27lr106bzXY/Pm4xb7/9ttPp3LFjh8vl+vLvnm86EMLZ+6Da76spUFzZVweITw1NTqb++NCGtvZ2WMm9QjXOZyUx896tkmFzCoXC4ODg5s2bN2zYcA/Hu+3nAQBwVwDktLNILWzqad61db1ZEu/jh1bJZrMOh6Ovr+9muu3p6ZmZmXG73S0tLYZWA4GAx+MRRbGO4lL3jizLWLE3z/K9V2Kp/Nlr0+FEdnt/YOf6tmvngzzPfZUVw3BEkaKou7pAw+szlumAEABV04rFoqqWAYAcx1WiHfO8SwpUV9cwZjbh0NtcxHk5Ovb4ohiGkaSvpIBW9XxFSjWhLKMXIbpLX+9LfzKEJpMJD8IvySOPPLJhw4ampqbW1tampiZJku72S78j7km393hahw4dcjgc90+0ZVUbnYmdujJuloS9Gzt62psopV/gOe7md3/Z2bBhg8lk4ri7flhUkkaqAW+klJTp6Zlr164mEgmapr1e77p161wulzFnHYLqTKS5G4sQwiUUq4fE/ZF769YbV+TxeLZt22a1Wu/6UHdCJasNAQCh22nr6+7wul0M8xVV22MYZt++fU1NTTfb4Yknnliw5b6m3y9D3sVdn9/3v/99rNv7lC+VzhUu3ZgZmYn1tbp3rmv1u50O604KQn75uhm35cCBAzRNi+K9+HKVYpIAIFXVJicnX//165cHB1mWBQghpD/00ENPPfWU3W6vmNgam1qddVBZpKcaEza2Lg9tbW1ut/tmgdblAxkefqCt1evz8hzHsdzt37cccBz33HPP3UliCR4chRDyPI8HOEulUrlcZhimLsaBasV2d5Lz+/3G62UXLUJoOpz8YnCSpZnNvS0Bn10QOOErL89pt9uX4zCVW5PPZT/66MN33nlr5649e/buLRTy77z99iuvvNLZ2blj587qEC5VWQcLp4NVOsELYzfLeL9FUby3B9OdgQyPAYmCIAqCMUr1FQAh9Hg8d7Ln6Ojo4OAgwzAbNmxobm7OZDKXLl0KhUKtra3r169frqfbvdrbe0x1NFh2j6KolIcmY5dHgh67tHdju0lgjZGWr653u1zgWhIIxePxDz74IBBo/ZMf/rC7p1vTtOampr/+678+derUwMAAa7cvXJe5si7gfJEa6Zb3ex7lsoK9DpwlXR3dvQ+zB+6ZycnJX/ziF7FY7Pvf//4DDzxw9uzZ1157rVQqPfPMM93d3cul27u32vf+ld/HDEcEQvHM+aHpQlHpDrh7W90sy1R7f42EMSAIANA0LRKJTkxMDQysdzqdFEWxLLtp0yaPx3PmzJlUKjUXWcbmFuK4M4K1c5EAQLBarHL5RHtfk1UrH7Eg4wP32CFa7ErcrxO4s2vs6+tzuVyDg4NHjx594403/vVf/3V4eHjz5s27du1axhDAfYwn13aAVVVFCLEsO68OU81rVVUXjEpTFEXT9O37A8gYLakUOAIIaJo+Oh0/c3XKbpF2rW+zmATszKvlMoKIZdhl98lVVcX5JzRN3yynXNM0TdNqv36KovBl3uzI1dAvMobyEdI9XjfHc8YRPB5PNBotlUo1JzSXwTFXPmL+Me/iGjVNU1VV13WKohiGqUxOrHG78KXhfeY+DkJ8jcbI/N3dfCMhBSGg6zo+DWMhkmVB13VN0/C8y8XniX/FV7fgS6zNQG5tbT148ODp06c///zzEydOQAifffbZb37zm93d3bcIR39Z7pduDdFqmpbJZMbGxmia7uvr47iFgQS8540bNxKJRO12h8PR1NRkMplu88VUyxoBI6segnS+eG0iMhVJru/wberyCxyra1o6nZ6anAQQ9vb28vwydHSNvn06nR4bGwuFQqqq2my2jo4Ol8uFv6RaXzQSieBZI8YWSZL8fr/D4bj1IAreX9d1nA1eG52GEHIchx+L935Ft7jSQqEwOzs7NTWVy+VEUWxubm5ubhZFsfYJBSHM5XKjo6PZbNa4cJqmPR6P3+83Tvse/XNVVUOhUDgcdrlcPp9vcYu6wyua13VAqFwux2KxcDhssVj8fv+SORIIodHR0VgsZjyAEEIOh6O5udloqAihnTt3DgwM/OY3vykUCl//+tefeOKJjo6OZRQtWHbd1s5swk/oYDD4+eefv/vuuw6H4z/9p//kcDgWvAXv/+qrrw4NDUmSZOTfb9q06fHHH8ct41Yzkud6OXP7BKOpSzdmWIbe0Olr9tgA0maDoc9PfP7B0aNms/zXf/3XdxhjuDX4rHK53Icffvjhhx/ir5PjuN27dz/22GOBQKDWIgEAvvjiizfffLNcLuOLQgg1Nzc/9NBDeBz7zj+xVqIILey93g8URbly5cp77703NDSkqipN052dnYcOHdq8ebPJZKo9mWAw+LOf/SwYDBrTMyVJ2rt3r9VqNQR2L2dbLBZHRkaOHj16+vTpQ4cOPfXUU3en2wVRVZxs/8knn5w/f37r1q2HDx9eUreapv3mN785f/68LMuVCdUQbtiw4fHHH5ckCR+zVCqFQqFCoUDTNMdx3d3dgUDg7k7yFiyzbhfcjlgs9tprr506der48eNNTU3zfLkqeOePP/44lUrt37/f7XbjgzidTny1t/6aKymzRjcHgrKqjgXjV8dCXod5x/o2QWBD4fDv3/z9hx98eO7cObfb/Rd/8RfLeMmXL1/+53/+Z4ZhHnzwQYvFcuzYsddee00Uxaefftput9eK6tq1a6dPn+7r62tra8OX5vF4jO/7tjAMYzabIYSZTEZVVbxR1/VsNmu1Wpf3cb7AoZ2ZmXnjjTe++OKLLVu29Pb2joyMnDx5MpfLud3urq6u2vBkPB7/7LPPeJ7fvXs3jsEIgmCxWGiaru03gbtSL0Lo0qVLb7/99meffXbhwoXW1tZHH330Xi7TUNq1a9fee++948ePX7lyheO4Q4cO3ewEPv3007GxsUcffdR49BsNFQCgquq1a9defvnlwcHB5ubmSCRy4cKFa9eueTye2gfcvXNf/GQsWl3Xp6enL168+NRTT2Wz2UwmU7vPAsuMENq1a9ePf/zj9vZ2bHK/3PdaU6s3mSlcHQ0FY+l9mzq6m10cQ4eCwWtXr23dslXgxZnZmeW7UIAQeuedd4rF4l/8xV888sgjJpNp586dP/nJT86dO7dt2zZZlhdM3+vo6Hj++ecffvhhLNcvdY0syzY3N5vN5pGREaxVXdcjkcjMzMwDDzywnLUm5t98rJarV6/u3bv3pZdeCgQCoVDoX//1X0+dOnX16lXcl6l9r9VqPXjw4EsvvYQfwYuv8a7tLYTwwoULmqbt3bs3n8/fY2fHaIH5fP7atWulUumpp57K5XK3fcvOnTt//OMf1z6wMLquj46OvvLKKydPnty2bdvevXvfe++9c+fOnThxYmBgQBCEZUwpu49T8iGEXq/3v/yX/7Kk17EgKIUQ8vl8CKFoNBoOh/P5/B1PV6j2bHGYFKGpcOrSSMhqljZ2NTksEk1R7e2dP/rRj5577psOp2N5XcpcLnfp0qVAINDa2srzPIRwYGCgq6trbGxsYmJCVVUjGIODUhaLRRTFdDodDofT6XS5XMbPrDv5LIqi7HZ7f3//0NDQ1atXs9lsNBo9evRosVjcsGHD8uoWnxL+qSgKnrbV1dVls9nw17phwwZVVQcHB7PZbO27VFVlWdZut5dKpXA4HIvFSqXSsvS98UEefvjhH/3oR3v37r33ARXjqxEEYefOnX/5l3954MCBW8+zw0Epj8cDIYxEIkZDxceZmZn5xS9+ceTIkc7Ozu9973svvPDCnj17KIr64osv8HPhHk+4lruxt9iW3uyvOH6IfzY3NwMACoXCzY6DVRSPx8vl8uzs7HvvvYd37uzs3LFjR1NT0y3cP1Sldg6XqqHRmdjg6KzHbt7S0yQILALI7rA57Pbx8fEvNf/l1rOucDwmFArlcrne3l6z2Wzko7pcrkuXLmUyGXwEfI3ZbDaXyyUSiVOnTl26dKlcLrvd7s2bN/f09Ny5B2W1Wh977LG///u/f+WVVyYmJnK53DvvvLNhw4bdu3cvrxtWOyyfSqXi8bgoik6n03CFTCaTKIqpVEpRFON7VBQllUrlcrmhoaFCoVAoFERRHBgY2LJlS21i3L2cUnt7O4Tw6tWr93iBtWFwSZI6OzsRQpFIBFTb1ZJvSSQSuPv6/vvv53I5hFBtQ52amioUCvv27Tt8+PCuXbvMZvPBgwfT6XQ0GlUUZRkn8YG7020ymbzZtFtsE7q6uu6ku2V8i9FolOf5s2fPXr9+XRTFXC6XTqcPHz783e9+t62t7WbeRSaTmZqaSqVSuq5XBIlAvgxOnJ+OxJNdPtljlxi6pj4SvPnc10Xoun7hwoV8Pr/kXyVJ6urqkmW5VCqpqooz2owr4nkelzg0vn6EEJbx7OzskSNHRFHUdT2dTvf19b344ou7d+++w3wjSZL279+fSCTefPPNn/3sZyzLDgwM/PEf/7Hf778fCWeVwTNVLZfLOMpiRI/xOBC2P8bnKoqCa1989tlnZrOZYZhsNsuy7He/+92vf/3ri0OSd8FyXSNclORXG6Jf8lNw3gvLshcvXpyamuJ5vlAopFKpp59++o//+I/b29v37NmzZ8+e2rfs2rVr165dy3LCC7gb3UYiEfy8WfwnlmV7e3sDgcCSur3ZY8zhcDz77LOaph08eLC3tzccDv+P//E/XnvtNVzjw2KxLHkf4/H46dOnh4dvqOVypSINgrNZ9ewsYineZ2WhrgAEcF8A249K2cM7QNf1Y8eOBYPBJf/q8/nsdvuCUOotLhNCaDab9+zZ4/F4+vv7t27dCiH83e9+97Of/ez1119vbW1tb2+/w8xVi8Xyne985/Dhw8FgkGGYpqYmnufvR0i51uRilrwuYwc8Pt/V1fWtb33Lbrfv27fP4/FcuHDh7/7u7/75n/+5p6dnz549X8WcoTug1tjeORBCp9P5zDPPFIvFgwcPDgwMRCIR3FBxQSkcNbxP57yAu9Ftb2/vf/7P/xksNQi25APsFlvwW/x+/7/9t//W2Nja2vpHf/RHZ8+enZiYSKfTNyvUiqc41iTfQlXT3zh26eq/ftDuMD/7+IG2QEttGBMsanlLNndUnZv2V3/1Vzf7Gow34sp9xWKx1rriutA8zxtSRAjZbLZnnnmm9hMffvjhwcHB2dnZYDDY0tJy50MFEEJZlo0OnmEYl7HR1B6T4zie51VVLZVKRv+oXC7rul4ba4EQ8jy/devWrVu3guqt3rhx4+HDh//xH/9xdHR08+bNZrP5/o1a3fmRb72b4ScvPmBTU9OPfvQj49dAIIAb6tjYWCqVun2uwfJx93GpxVcF76BUxYId8BFwYkYmk8FdfNwCcPGa2s7G4uNDCI3OLUIonSuOBxOZfKHFY+lodrLMwqyXxU+ZJW3IkgMVS36dTU1NLpdreno6kUjgNp3P56empux2u8fjqW3TxWJxdnY2EongDiGoZlbdeVzqZrdx2UUL5htbq9Xq8/mKxWIwGMTBFUVRIpFIqVRqamqq9fA1TYvH41NTU7h/gWMc+PmFM5zu5Txve5e+1JHv5J4vftxns1ksUWMLx3FGQ73zT793lrkO64KweKFQUBSlWCwqilIul5PJpCAIPM8LgoBHuj0ej91un5qaevnll3fs2HHgwAGPx1MsFs+cOZPNZr1eb63vseS3bqwDByEMxtIj0xGnTVrf7bdIAi72oOs6PoF0Oo27o+l0OplMsixrpPvUDi3ezINa0uYLgrBhw4YPPvjg+vXrXV1dZrP59OnTY2Nj69at83g8uq6Pj49TFOV0OnGntFAoPPTQQz09PTRNj4yMjI+Py7J823ypO7z5yw6+WJZlW1tbBUEYGhoKhUKSJE1MTFy4cIFl2ba2NpZlI5FIOp3GKdNnzpz59NNP9+7du3PnTrPZjAcw8WDBPVZpgRCWy2X8DWaz2XK5XCwWU6mUKIq4QMyXmiJX+21qmpbP53HDwB+BW4goigzDJBKJaDTq9/vNZvPk5ORPf/rTgYEBXEi5WCyePXs2nU77fL6v0kkGyzV+u6SiyuXyhx9+ODY2VigUxsfHM5nMa6+9ZrFYNm7cuGvXromJib/5m795/vnnDx065Ha7w+HwP/7jP46Nja1fvz4Sibz22mstLS0DAwM4Trv4IxZ/oo70yWDi2njEYZX62rw8V0kzTKfT586du3r1ajAYvHLlSjAYfO2117xeb0dHx8GDB3EftTYmcdvrWsBjjz125syZN954o1gsOhyOd999F49Ft7S0JBKJn/70p4IgfP3rX/d6vaqqvv3228PDw/v376dpGqdYHThwwOv13kXHr/bc7lOLMQ47MDCwbt26kydP/vKXv9ywYcO1a9cuXry4ffv29evXI4SOHTt2/Pjxp59+etu2baIoXrp06cKFC6Ojo83NzVeuXPnkk082bdqEs3PvxTVACM3Ozp45c2ZmZmZwcHB6evrs2bMcxzU1NW3ZsgUPkC75bL3tBSYSiaNHjwaDwXA4PDk5mcvlfv3rXzc3N+/evbutre2TTz759a9//eMf/3jv3r1OpzMWi/3TP/3T9PT05s2bw+Hwa6+91tTUhMfhGky3C4yVsb1cLp89e/bUqVPlctlut9tstk8//RQnYW/ZsoWiKKMQhMPh+LM/+7Of//zn77333htvvEHTdGtr60svvbR582YjvrWkTw7hXBGHfKE8Mh2bCaf2bWoPeB0MU+nZ5vP5K1euHD16NJfL4UDOyZMnRVHEsT6TyXSzr3lxv3HJPTdu3Pjiiy++/vrrP//5z1VVdbvdzz333M6dO/EkaVw1l6Zpk8n02GOP5fP5Tz755B/+4R8AAC6X69lnnz18+PDdTRP5sm30Xmhubn7mmWfK5fLJkyePHj1qNpt37dp1+PBht9utKAquhMYwDI5vP//882+88cbPf/5zXddFUdy+ffuLL74YCARqfe+7OG0IYTQaPXXq1JUrVwqFgs/nK5VKn376qdvtxkMYoijeecCp9gTS6fSJEycGBwd1XXe73RRFnTx50maz+f3+5uZmlmVNJhOeOeB0On/wgx/83//7f997770333yTYZhAIPC9731v69atCxJs7jf3Wjxx8RdgdA4RQrlcbnHKO/aT8V+xhwMhVFW1UCiMjIxkMhmLxeL1eu12+4L5Q0s+IIy1MoenIv/4+vGPTg9/66FNf/bNfQ5LZQDd8JMX9Amxn7wgIvplv3IMHrecnp4ul8s+n8/pdGLR4p4CRVG4F6RpWqlUws91hmHcbrfL5VqQmn+PIIRefvnliYmJl156qaOjYxklrapqLpeLRCLJZNJsNmPPELsJiqLgdAv8kMV3Y2JiQlEUh8Ph9XpxnmPtSd7diWEndsEAJO5Cfyk/ecET2fCTa/eBEIqiyLIs/lD8YMK+Ou7ipVIpq9W6ZEP9CrjXh8QtLBKE0EjiWVJyRqAYAMAwjCzL2O/C87PAzW3svFBTdTx2MpQcmgi57aa+do/AzbUSiqIkSVqQB7Nk5OnOnasFLY/jOJfLhUtbGCePX9eOFdE0LUlSe3s7Nj61e9Y/DMNYLBZZlo0FrIw7wPN87VgUz/Nut9vhcBhf5U19pS8Jy7K1M+buWv8LToCmaVmWb3Y0w7QY58Cy7Lp16/D+968U6a1ZBuN+s4DtkvvceufbOhtLHR8BAMqaPhlKjM8mNvU0dQfcHMuAWxY9u8d7vUR4DMI79JTuXK63bpdfjYdcC35i3smSc7e9G3d95nfS2L7scW57tLtoqPebhnne35pEOj8dTuq63uSyeBzYf1uBp+C9s8CZX7yx9q+oJh/rKzg3Qv2wCnQLAQCz0czYbNJhlbta3CLHfGW1S5YdeJMh5QVbav38r97wElachtctAgAhMBFMDE9GnBaxs9nFsSvsw9wJNzOVi4e7lnz7YneRmNw1RcPrFiKQLyoTwUQonvE65Y4mJ8sw9e8k32zodYG9vbWrbGwnJnet0QCm6TZAFElkJkNxgWcDXrvVLOA0jfqXroGmablcDo8Ymc1mPI/X+KuhyQUZwqA6VrGgGg5hLdD4ugVwNpaZDCUcstjqtfEsjkihRpFuLpcbGxu7fPny9PQ0z/Pd3d0DAwN+v9+IWGI1lsvl8fFxnHJgvFcQhAcffHBBNRzCWqDhdavr+kwkNRVONbtt7f7KXII6V6wRVVJV9cKFC7/61a9mZmZMJlO5XD527NiuXbuef/55v99fuzBUJpM5cuTIq6++KsuykehrsVg2b95st9u/1KgGYRXQQLpdYD8r6Y2ZfGliNpFI5XcMtLb67V/ZQk/3giGqcDj8ySefTE1NPfzww9u2bctms+++++6JEyf6+/vtdrtRMg4hpKpqOBzO5XJ/8id/gpeZRQixLLtkYcp7z0wg1DkNpFswX7qVF6F4ZiKUEAWuxWM3S3xlPUlUWYBuZU7zltRqCXvIgUDg0KFDnZ2duAf78ssvnz59evv27UaOF96fYRifz7d9+/b+/v4l871qPwJzX5dyJKwgjaVbAGpqSeHfZqKpyXDKZTO1+mwsQ9Ws7LzC3EwwtRvD4XAymdywYYPdbqdpmqbppqYmWZYnJiYWFOXCpfQlSQqHw/jguOATnqt9iw8iol2VNJBucfub5y3rOpqNpKcjqZ4WZ5vPWunc1sHSXYqiFAoFXK5x8V85jsMV3vG8i9pyraIoSpIUjUYXpLmXSqXZ2dnZ2dnXX39dURScsv/AAw/s3bt3yf4tuD91MAh1QuPoFlWXcQUIVpbnQvliaTaazuQKHofsd9tYmjbMzEqeKgCJRGJoaCgWiy1Z+NLv9/f29tpsNk3TdF2vzZXHVnfBMkJ4O54gTlFUV1dXsVi8cuXKv/zLv0AIH3zwQbxGBpb67OxsLBYbGRkplUoQQrfbbbVaVzyflrC8NNTXiYz19PBSkCiaygdjGYnnmj1Wszg37LniQ0C4+iHP87WlWI1OqTHtC8+Vqa1ygl8vnmXidDq/+93vxuNxr9fr8XhUVT1z5szf/u3fHj16dMOGDVNTU0ePHk2n0wghXAK2VCrhenpPPPEErglKrO5qoqF0awSaIMDaDEYzM9Gky24KeO0sU7PA1Mqc3xxWq7Wvr+9mfjLP83jqL57Vmc1mjeK6xWKxWCwutpCCIGzcuBEAgBf7QwgxDOP1esfGxorFos/n27FjB+4SF4vFSCSydetWXJ67paVleZcgIdQDjaNbWPsPQgAiBGaiyelwMuC1Bzx2hl5wLStpdFmWvZMqFm63W5blUCiUyWTsdrumaaFQKJVKrVu3ThAEVVXz+TzLsoIgFAqF69evI4R6enrwrGZcsguXbu7q6urq6gIAIISSyeTExMQTTzyBS4Tf90slrASNo1sA5pbuAhAgUCqXpyKpaCq3pbfF65BpmsJrkddHOPmm1AaKAoFAZ2fnjRs3Tp8+ret6JpM5efKkrusDAwOSJMVisdOnTzc1NfX392ez2Q8//HBqauqpp57q6enRNO3kyZPxePzhhx9e3hVGCA1B4+gWGe4xAAACiGLJ7Gw4RVO0x2mRzQJFzc3eQ6BOB28xhnR9Pt/u3btnZmbeeeedixcv5vN5XHBs27ZtuGziRx99tHXr1o6ODo7jbDbb0aNHk8lkV1eXqqrDw8N4QTqbzbbkR3zVV0X4Cmkc3QJQm0sBAQjFMsF4xmk1tXisHGukSdW3tZ0/oCqK4s6dOwEAFy5ciEajDMMcPHhw7969eO1cWZYHBgbw2jM8zx86dIhhmEuXLsXjcQDAunXrtm/fvnXr1mVZg5vQWDSSbmu6uAgAMBPNzEazTqvU5JIZ2lhMBLPiEeU7xePxPPbYY5s3b47FYizL+nw+q9WKq6j5fL7Dhw/jMnoURbW0tHzrW9/at29fOp2GEOICdCTmtDZpHN1C4wcAAGgamomkgrFUR1O7z2ll5tUfbgAXsbaXy3FcS0tLS0vLgn04jnM6nbVbRFHE8SfjIPf7PAn1SSPNm8dJF1iWmUIxFEuXlLLbbnbZZLpxCiNibl3wbcnXi/MZSbh4zdJQzR3NJV4Eo5lgIiubRJ9TFnmGmheGgo3iJN+C2jLUK30uhLqjcfxkMC/kFIylQ/G0y2byO624c7tqWDAf4M6NKlH42qGBWjwCqLKmCEIglMxEk1mXzeRzWRiaboQu7f3CkCtxm9cODaRbLFsEECqrWiiWiWcKXofc5LIyNNX4fvHdQ+S6BmkgPxlW4lIQpLLF2WgG6brXIVvlynqZBMLaoYF0CwCoeISzsXQ4nnFYTG6baZV1bgmEO6GBdIsAABBBXOMinMi4rCavw8I02ggQgXDvNFqjhwBAGIlnY8mc2yb7nBaa2FvC2qOB7C3EA7iqqkeSmVSu6LSKTpvUQEtREgjLRSM1epyJkMzkQ7EMBaDHIVtNAjG3hDVIA7V6nCqFpsOpUDzrcWAnuVHXyyQQ7oUG0m0lX2o2lo4lsk6LyWkzk84tYW3SQO2+knUcjKYiyYzDKrqsEk1GbglrkgbSLQAA6JoezxQzBcVpFV02iWRcENYmDabbdL4YSWURQG6HbDEJxN4S1iaNo1sEAECz0VQ0kXPZLW67hSFBKcJapXF0CxAAYCqUCsczVhNnM/EUyacnrFUaR7cQAACC8Uw0lXNapWoweQ3P3yOsYRpGt7jQeSSRSWbybrvstptpejXUtSAQ7oKG0S1EoFRWE5mCqmpNTqvbZqIoiphbDKl0sdZoGN0CACaD8VA8a7eY7VaJwkNAa8Pc3kyWeDtZKXMN0ji6hSAYyybSOZuJs0o8XV3hbu0YmsV1Ho1KVGvpNhAAaKD5QAiAUCKTTOd9TtlVcZIhxJVrVrXZNcwp1qeiKMFgUFGUQCAgCALeh9jbtUbD6BYCFEvmU9nSlt4Wj8NC0/W8ANByYmhS1/VkMnnu3LnXXnstkUj8zd/8TXd3NyB+8pqkYXRbVvXpcCKRyVvMgsXEV6fdrqH2mk6n33rrrTfeeOPq1auKouRyObydiHYN0jD920giG0sXOIZxWc0mcW0lXeDuayqVunDhwp49ex566CFJkkifdi3TMPY2ls5n8yWnzeywSjQNAQIAGsvhrnKwRXW5XC+99BLP8//v//2/BVU+lnSVif+8iqlT3SKEIAQIwKpAUSiWSWTybrvktJooil4Dal2IKIp9fX3pdHpxaR6iz7VG3ekWWwkI8YuKzYAABqPpeDo/0OG1yxJNwWoQuSHba60lzOfziUSiWCwu6fcKguDxeDiOQwhRFLV4aS98tEKhkM1mdV1HCKVSqWw2G41GRVGEEJrNZkkiVbhWG3WnWwghQqAqXQArzjAIJdLJTMFhEW0yT0EIAWhcN7D2vEOh0CeffDI1NaVp2uI9m5ubv/71rzudTmg8w2rAW3RdHxkZOXPmTDabRQidOXMmkUi8++67DocDQrhnz57+/n6s4ft+YYSvirrTLQCgamyxOBGEQClrsVS+qJS9DovDaqrkSkFQnVfQwC3S6/U+8sgjN7O3PM/Lslz1QRZeprEFIVSbiUFY9dSjbsHcyvE6hBAAGIpl4qmcwLNWs8CxzGpqm5IkSZJ0L0egKKqzs9PtdmM/uVgsTk9PHzp0KBAIQAgtFgvP80TPq4x61O3cKrfV1hZJ5NLZosMsWCSBmrM8aO2ETHVdLxaLhUIhFovlcrlyuRyPxyORCMuysiybTCaTyQQAQAjZbLZ0Ou31epubm2E1G3SlT5+wzNSfbhGoRpFB1QFG0VQuky/5XVaXzURTlWm3qLJTA+v2Dp872IpeunTp4sWL8Xh8cHAwn88fOXLk6tWrfr//oYcestlsNzvO2nm0rSnqT7cA1KQcV17MRBLxdL6tucXo3AIAGlqxmDtUFIRQ07RoNHrjxo10Om02mzdt2hSPx/P5vKqqiqIsGbX6Uh9BaCzqU7e1kkQAoEgyl86VHLJoNRmrZuJc+9U/rwAjCMKWLVuamppUVTU24mEeq9UKiD7XGPWnW1jbGYMAIEXV4+mcoihOqySbBQriwdu11WdjWbapqampqWmlT4RQF9TpcDyqyhIBGIln46m8JHEOq4lnmWpUCgFSXYqwVqlD3cJ5sSaEwvFMKleyW0wWk0BDWJE0wha3seNSBMLdUX9+MgA1UkQQgGg6n82XXDaTzSRSFAQAIkTESljT1KG9BTX+LwIQzURSiUzeYzPbLJU8WwhRA2cnEwj3TB3qFs37B8BQPJ3KFhxWqSaYjP+Cl8QlnVzCmqMOdQtAVYsIQFXT4+l8saw6rWbZJFAQAqAbOxCDS1ib1GH/FuKgE1ZmLJmLp3IixzqtJpFnYTWJCs7tTCCsOepQt6AqXYBXqU5lizazaBY5CEn0mEAAoC79ZDwlrSLRWCqXLSguq9liEtdUTSkC4RbUo27x/FvsJ89G06ls0eMw22SRrFJNIGDqULe4+4rnBIHZSDKVKdhkQZZYYm8JBEwd9m/nxKnrejxdKChlj0O2miVibwkETB3a27kZPpl8KZkp0hTltstmiRRtIBAq1KVuK/MGYDCWSedLNrNoFlkiWgLBoA51iyNSCAAUTmSy+aLLIsqSQDq3BIJBHeoWAFyAFcCZSCqZK7jsZoskEHtLIBjUoW5hdaU9FElkswXFaTNbzAIJShEIBnWoW1x/ECGEYulCvqh6XRYrGbwlEGqoR91CCACCRUUNRpOFfNFukUwiCSYTCHPUoW51XIk1lspni2VJ5C0iz9I0US2BYFCHuoW4ulQkkckVlGaP3W4xkWAygVBLXeoWQojQbDSTyRVsZs4ksGQ1OQKhlroThLFAZiSRzRVKTqsJz+Bb9VUtjLW5br2DXgNZQGTNUnf5yRAggCCCIBhLZ/KK2yFbzCK1Whzlmy0MXy6X8/k8AECWZZqml3xjsVjEi9yC6pI/NE3bbDaWZe//iRPqi7rTLQAQF46Kp3L5UtlllWSJbTjVLrlWLVhqVQFd13O53PXr1y9evGi1Wh9++GGbzbb4gHh9oJMnTxYKBWOjJEnf+ta3vF7v8l8Aob6pQ90ChEChqMTSeV1DLpu5EQeBjIXwjDO/2SUkEonjx4//+te/fu+993bs2LFlyxabzbZY9ul0+s033/yXf/mXpqYmWZbxRqvV+thjjxHdrkHqT7cIQKhPhBLpbMEhC5LILbFgcyNQqz38uvansduFCxd+97vflcvlnp4eURTxxiWvmKKojo6Ov/u7v9uwYcPijyCsKepPtxAAAFK5UqGsuhyyReIpWF0MqKGaaK3Jxa8XiBa/9ng83/72t3mef+WVV4rFIri5GlmWdbvdtb1ZIto1S/3pFgAA4HQklcmVulrcNtmEa50D2JDr7mGtgqrGaheSxq/Xr1+/fv36K1euUNXBrsU+NgBA07RSqcRx3MTERDqdRgiZzeampiaLxUKRUbK1R93pFgEAAYwnc4VSWZZYgaMAAA3nDpZKpUwmoyjKkkM1giDIssyyt5pUvMCvLhaLw8PDV65c+e///b+Hw+Fisej3+59//vlnnnnG6/US6a416k63uCGHEtlsvuR1WiwmqREHgUKh0OnTp2dmZlRVrTW5+EVnZ+eOHTs8Hs+SQz4GtX41x3GBQCCZTO7bt2/nzp2FQuF3v/vd//yf/5NhmG9+85s0TY+NjeFQ8+joaCgUunjxYjQahRC2tLS4XC4yVrTKqDvdAoA0HUwE4+lcyW6WTAJHNeDi1FardWBgoKWlZUl7a7PZzGbzbY1kravc1NT0k5/8RNM0hmFomtZ1va+v79//+3//hz/84eDBg/l8/r/9t/82MTEBAAgGg8Vi8cKFC4IgAAD+9E//9Mknn3Q4HI3mshBuRR3qFmbzxaKicizlsEgCzwJINVzc1GKxmM1mnCMBlurlUhR120taEMfSdZ2maZZlseAdDofX602n05qmDQwM/P3f/z3OoPrZz342PT39wgsvtLa2QghFUeQ4rsFuH+F21KFu0Uwklc2Xmt02m0WiKdiIcVMIIU3TdyLOxRhaVRQlm81yHCdJUiaTOXXqFIRw69atdrsdIZROp6PRqMPhYFmWYRiLxYLfazKZBEGwWCw2m80IZRNWGXWoWxhNZvMlxWISRI6ptLoGc5OXGLxdcrdCoRCNRlOp1NDQUDweLxQKg4ODuVzOZrN5vd6ZmZl33323u7t79+7dmUzm/fffv3Llyne+850tW7aoqvqHP/whkUg8+eSTVqv1ZslYRLSrlTrULQjHs7lCqTvgNUkChNXRWwQbSLpLDtguZmZm5le/+tWxY8dSqVQmk0EI/df/+l/tdvvDDz/84osvJpPJM2fOsCy7fft2h8PxyCOPXL9+/R/+4R9aWlpUVU0kEnv37sW6XfARhpkliRmrlTrULRqfjWWyJacsmHD5VbxcUKM1v9qMi8V/wi/cbvcTTzyxefPmcrls/JVlWZzM2Nra+v3vf9/tdkuSxLLs/v37/X7/hQsXotEoRVG9vb0bNmzw+Xw0TS+pT6LYVUwd6hbGM8WCojjtJrPAQWPVkVWEoSiz2bxu3bq+vr4FO+D4E8dx27dvp2mapmkIoclkWrduXUdHBxa5KIo8z+MYVW06R+0LIt3VSt3pVtO0cDydK5bddotJwrqt1GVtLO5EMxRFcRx3iyPwPF/7K03TxqSCJfdfLF3CqmTF8mxqm1VNI0OJTD5bKDOQskg8xzAUgABABAFphoDYT0KVFdNtJU5sJBJVN0cSuXxJafLYbLJI0xBAgCCAqOG6twTCfWQl81oRqsSIEUKganKDsXS+UHA7TDgopQMIECKiJRBqWUndwurKBDjuim1vNJUvKJrLajLxPAUgBAjHXIijTCAYrFz/FqEFP7F0J4PxdK7ksVlMEg8prGz8gwiXQKiwcv3bmhKNtcVcgvFsvqA4LILEM5X1NAFAWL0EAgEAsMJ+8oKhCwAUTYulcoqq+VxWWRIgBQFACCBiawmEWlZQt3O5ARVvGYB4MpPOFliGspoFlmVw9xcCRJxkAqGWlRy/RdVwE8QreQEQSxaKiuq2mSWBhRCQWBSBsCQrOH6LO7VzxhYCMBNJ5QuK2yFLIgdxlxbhf0jnlkCYY4XrEtVMroUAgFA8kyuVnVaTxHNGqIqIlkBYwAqPA9X8DgACoXguXyr7HGazyFMUcZQJhKWpg3GgmoGeYDxdKCpep2wSSWkVAuGm1EH9TghwL1bV9Vgqo5bLXrssCRwEFO7gEqtLICygDnQLANZuIp1PZYsCy9hlkatUqEF4+UgiXQKhlhWbf4sQqo7+4OATiCQyxZLmsMkCz1HGfANAKpsRCAtZ0f7t/FV/gtFMvlT2OCwmsTJdvqbMC7G3BMIcK5kvBSFENTHj6WgqX1DcNkniKwtwIADRXP+WSHcepLTFWmaF8xxrPeBIMldSFI9DloSqvcU/qgmRX/UJ1jFGIThSsXFtUg9xqYouZ6OpXEnxuywmCS9UjarFVyGZOQ/m29XaGVTE3q5BVjDvAlZixRACAHQdxZI5pazZZVHgGAggQjUNEpK2ubBoo/GaSHcNsnL2FkeTcZtDKJ0rJNN5hqacNjPPMaCmeDdYfYVYvzxLllYlrvKaZSXrsGJbCwEEEE2Fk7lS2WU1iTwDKwND1ba45tuksRCuqqqKomiaBgBgGIbjOFxaeaVPkPBVs5K6rTQ4BACEs7FMsVT2OmQRB5NRpYwjES2oesK5XO7GjRsjIyOpVAoA4HK5+vv7A4EAz/PE5K41Vky3xiQ+nKg8HU4WCqXegEcSeAiJZBdSLBbPnz//6quvjo6OIoQ0TWNZdsuWLd/97nc7Oztvvf41YfWxgvYWIWCEjUEkkSuWVZfNLPJsZU0sQJQLQNVJTiQSb7755rlz55599tkHHnhAUZQ333zz17/+dXt7u8/nM5vNJDq1pli5PEcs3Mr/9GAsVSipAZ9Vljhqzbh8d+LfGkv7OZ3O55577oUXXvB4PJqmWa3WP/zhD1evXs3n87IsG33gu/gIQsOxkv1bCgAAdQAoXQfBaKaglK1mkWPZtWNn71BRCCG/3/8f/sN/KJfLLMsCADRNy+fzFEXJsoyd5Jsdioh2VbJy/VsEccU3gEAmX8oUywxNeR2yyDNrqqXpVZb8K0VRRsTYWARMVdXZ2dm33npLluU9e/ZgY6vrOkIIv9B1XdM0VVUhhBRF4TX7CKuJlbO3EKdDUQiCsdlkUSl77dVg8loik8lMT09ns9klpWs2m7u6ugRBMG5LuVyenJw8cuTIyZMnn3jiiU2bNnEcVywWZ2dnFUVBCIVCoXg8Pj4+rqoqAMDj8VitVoapu4UXCffCCvZvYcXgQl3gmP42N9Dddllaa7qNRCKffvrpxMQEHpVdQCAQ8Hq9oijiX0ul0vDw8BtvvPH5558/+OCD3/3ud10ul67r0Wj0nXfeiUajAICzZ8+mUimWZW02G4TwkUce2bJli8lkWms3dnWzguNACP8DAOhtdf9/v/uwriOf00KvAaeuNlbU3d3d3d19J+8qlUqDg4O/+tWvLl269K1vfevZZ5+1Wq2gukxuIBCwWCwIocnJSQhhIBBwu90AAJvNRkaJVh8rO3iAsLsMEUCAhD1vhaqq169f/6d/+qfp6ekXX3zx4YcfliQJzM8GBQAghF5++eWJiYmXXnqpo6OD3NLVysp2e6DxH1wzMeS7ACGUSCR+//vfHz9+/Ic//GFPT08sFotGoxBCQRAcDgfLsmS8Z01BwhUNAIQwHo9//PHH5XL5iy++uHbtGh6qpWm6o6Pj29/+ttvtJqJdUxDdNgAIIbPZvHPnztnZWQhhPp8HAOAxnmKxSCztGoTotgGAEDY3N//kJz9Z6RMh1AurP3jb6NxJ4JBkJq81iG7rnZuVuVhQtoZId01BdNsA1M4ZMF4vGP4hXdw1BdFtA1Ar1NqftTuszJkRVgii28aAKJNQC9EtgdB4EN0SCI0H0S2B0HgQ3RIIjQfRLYHQeBDdEgiNB9EtgdB4EN0SCI0H0S2B0HiQeXyrDYfDoSgKz/MrfSKE+wiZR0IgNB7ETyYQGg+iWwKh8SC6JRAaj/8/4ldZH+Phb+4AAAAASUVORK5CYII=
|
List all intervals where $f$ is increasing or decreasing and the minima and maxima are located.
|
The function is increasing at: $(-1,0)\cup(0,1)\cup(1,\infty)$
The function is decreasing at: $(-\infty,-1)$
The minimum is at: $x=-1$
The maximum is at: None
|
02c57487-7f56-412a-8aeb-b1abc78ac85b
|
sequences_series
| false
| null |
Find the radius of convergence $R$ and interval of convergence for the power series $\sum_{n=0}^\infty a_{n} \cdot x^n$:
$$
\sum_{n=1}^\infty (-1)^n \cdot \frac{ x^n }{ \ln(2 \cdot n) }
$$
|
* $R$ = $1$
* $I$ = $(-1,1]$
|
02d22949-d7a2-46ca-8af8-4bda85bc8e0e
|
differential_calc
| false
| null |
Sketch the curve:
$$
y = 16 \cdot x^2 \cdot e^{\frac{ 1 }{ 4 \cdot x }}
$$
Submit as your final answer:
1. The domain (in interval notation)
2. Vertical asymptotes
3. Horizontal asymptotes
4. Slant asymptotes
5. Intervals where the function is increasing
6. Intervals where the function is decreasing
7. Intervals where the function is concave up
8. Intervals where the function is concave down
9. Points of inflection
|
1. The domain (in interval notation): $(-\infty,0)\cup(0,\infty)$
2. Vertical asymptotes: $x=0$
3. Horizontal asymptotes: None
4. Slant asymptotes: None
5. Intervals where the function is increasing: $\left(\frac{1}{8},\infty\right)$
6. Intervals where the function is decreasing: $\left(0,\frac{1}{8}\right)$, $(-\infty,0)$
7. Intervals where the function is concave up: $(0,\infty)$, $(-\infty,0)$
8. Intervals where the function is concave down: None
9. Points of inflection: None
|
02d80ab4-c222-493c-a91d-448fba115380
|
multivariable_calculus
| false
| null |
Evaluate $L=\lim_{P(x,y) \to P\left(1,\frac{ 1 }{ 2 }\right)}\left(f(x,y)\right)$ given $f(x,y) = \frac{ x^2 - 2 \cdot x^3 \cdot y - 2 \cdot x \cdot y^3 + y^2 }{ 1 + x + y - 2 \cdot x \cdot y - 2 \cdot x^2 \cdot y - 2 \cdot x \cdot y^2 }$.
|
The final answer: $L=\frac{1}{2}$
|
032cf885-c1e2-49f9-8584-c99b0161c08c
|
precalculus_review
| false
| null |
Form the compositions $f\left(g(x)\right)$ and $g\left(f(x)\right)$ if $f(x) = \sin(3 \cdot x)$ and $g(x) = \frac{ 1 }{ \sqrt{2-x^2} }$.
1. Find $f\left(g(x)\right)$ and $g\left(f(x)\right)$.
2. Find the domain and range of $f\left(g(x)\right)$ and $g\left(f(x)\right)$.
|
1. $f\left(g(x)\right)$ = $\sin\left(\frac{3}{\sqrt{2-x^2}}\right)$
$g\left(f(x)\right)$ = $\frac{1}{\sqrt{2-\sin(3\cdot x)^2}}$
2. Domain of $f\left(g(x)\right)$ is $\left(-\sqrt{2},\sqrt{2}\right)$
Range of $f\left(g(x)\right)$ is $[-1,1]$
Domain of $g\left(f(x)\right)$ is $(-\infty,\infty)$
Range of $g\left(f(x)\right)$ is $\left[\frac{1}{\sqrt{2}},1\right]$
|
03b87419-fe7c-481a-9396-1d0723fc2b15
|
differential_calc
| false
| null |
Sketch the curve:
$y = 5 \cdot x \cdot \sqrt{4-x^2}$.
Submit as your final answer:
1. The domain (in interval notation)
2. Vertical asymptotes
3. Horizontal asymptotes
4. Slant asymptotes
5. Intervals where the function is increasing
6. Intervals where the function is decreasing
7. Intervals where the function is concave up
8. Intervals where the function is concave down
9. Points of inflection
|
1. The domain (in interval notation): $[-2,2]$
2. Vertical asymptotes: None
3. Horizontal asymptotes: None
4. Slant asymptotes: None
5. Intervals where the function is increasing: $\left(-\sqrt{2},\sqrt{2}\right)$
6. Intervals where the function is decreasing: $\left(-2,-\sqrt{2}\right)$, $\left(\sqrt{2},2\right)$
7. Intervals where the function is concave up: $(-2,0)$
8. Intervals where the function is concave down: $(0,2)$
9. Points of inflection: $P(0,0)$
|
03c28ad4-cfe4-430f-ab38-cb3e56091616
|
precalculus_review
| false
| null |
Solve the following equation:
$$
x^2 - x + 1 = \frac{ 1 }{ 2 } + \sqrt{x - \frac{ 3 }{ 4 }}
$$
|
The final answer: $x=1$
|
040dbb94-2747-4799-89f8-dd544c248a9c
|
integral_calc
| false
| null |
Consider the function $f(x) = x^2$ on $[-1,1]$ and the partition $\left\{-1, -\frac{ 1 }{ 2 }, \frac{ 1 }{ 4 }, 1\right\}$. Find the upper and lower sums.
|
The upper sum is: $\frac{23}{16}$
The lower sum is: $\frac{11}{64}$
|
0429a27b-d694-4e42-a60c-d446ae515ed2
|
differential_calc
| true
|
data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAyAAAAMgCAYAAADbcAZoAABQIUlEQVR4nO3dfXDd1Zkf8EfBJhDDVYDFWbNXIQnZNZEEnkY7IRIQ0m5YIDNJs0PG7kxCPBCc7dIkDfVOt2leIKbTNjQE6CTsECekeduModl0mUljN25jCEhmi7drVsIlG0KEtLCGBqKLzZth3T88UpB/R7Ze7r2/l/v5zDADx7L0HF1J/L46zzmn6+DBgwejhL7yla9ERMRHPvKRnCtprV27dkVExMDAQM6VtFanzvO0007LvM1jjz3W1ppaoeqv5w033BA33HBDRERs3LgxNm7cmHNFrVH113FaVed5+M+XAwcOxNatWys3z2lVfR0P5/mnWqo+z7nm96o8igEAADqTAAI5qtfrmbGJiYkcKgEAaA8BBHLU09OTGRNAAIAqE0AAAIC2EUAAAIC2EUAAAIC2EUAgR7VaLTNmDwiwVKmfIytXrsyhEoAsAQRy1N/fnxmbnJzMoRKgSlIB5HWve10OlQBkCSAAAEDbCCAAAEDbCCAAAEDbCCCQI5vQAYBOI4BAjvr6+jJjAggAUGUCCAAA0DYCCABUTKPRyIydcMIJOVQCkCWAAEDFjI2NZcbOOOOMHCoByBJAIEfd3d2ZMRcRAgBVJoBAjmxCBwA6jQACAAC0jQACAAC0jQACAAC0jQACOUvdhp46QhMAoAoEEMhZaiP66OhoDpUAVTE1NZUZW7FiRQ6VAGQJIABQMe4BAYpMAAEAANpGAAEAANpGAIGc9fT0ZMZcRggAVJUAAjlLBZDJyckcKgEAaD0BBAAAaBsBBAAAaBsBBAAAaBsBBHI2ODiYGRseHs6hEqAqRkZGMmNnn312DpUAZAkgAABA2wggAABA2wggAABA2wggkLPUPSBjY2M5VAIA0HoCCOQsFUAajUYOlQAAtJ4AAgAAtI0AAgAAtI0AAgWlDQtYjNQ9Qqn7hgDyIoBAAaQeDkZHR3OoBACgtQQQAACgbQQQAACgbQQQoNJuvfXW6OrqOuo/3/nOd/IuFQA6ggACBeAywtZ48cUX46GHHsq7DADgFZblXQDgMsJWee6552JiYiIiIjZt2hTnn3/+nG/7xje+sV1lAUBHE0CAynryySfjkUceiVWrVsW73/3uGBgYyLskAOh4WrCAynrsscdi165dsXr16li1alXe5UBbpNo3+/r6cqgEIE0AgYKamprKu4TS27NnT0RE9Pb2xsknn5xzNdAeqfbN7u7uHCoBSBNAoABSFxHahL40r9yA3tPTEzt27Ii1a9fGKaecEl1dXfHOd74zvvSlL8Uvf/nLnCsFgM5iDwhQSfv374+f/vSnERHxyU9+MvPnd911V9x1113x1a9+Nf70T/80GQIBgOazAgJU0hNPPBGTk5MREbF69eq47bbb4qmnnoqDBw/Gvn374s4774w1a9bE7t274+qrr55p1wIAWksAASpp3759ceqpp8ZZZ50Vt956a1x++eVx0kknRUTEihUr4j3veU9897vfjXPOOSfuu++++NrXvhYvvPBCzlUDQPUJIFAALiJsvoGBgfjRj34UDzzwQFxwwQXJtznzzDNj/fr1ERGxffv2+MUvftHGCgGgMwkgUAAuIsxHV1dXvO1tb4tVq1bF7t27Y+/evXmXBACVt+wrX/lK3jUsyt133513CW0xPj4eERG7du3KuZLWMs+IZ599NjNW1u/PPF7PgYGBWLNmTSxbNvfZGk888UTs3Lkzzj777Dj99NOjq6srTjjhhFi5cmU8/vjjM7emHzx4MB599NG45557Yv/+/Zn3s3PnzpnXa+fOnaV9nY7G92U5/ff//t8zP08eeuiheOqppyKiOvM8XNVex7l4/qmWqs9zrvlZAQEq4YUXXoiXX3551ti+fftiamoqDh48GBERxxxzzMz49NgrrVy5MiIOrYy86lV+PFJOTz/9dGZsev8TQBEs+8hHPpJ3DUtS9vqPZjoxDgwM5FxJa5lnxLXXXpsZ+2f/7J9FrVZrdVlNl/fr+fzzz8fGjRvjlltuicsuuyy+/OUvx4knnhinnHJKvPe97531tnv37o3du3fHqlWrZl1W2NPTEx/4wAeS7/+ZZ56Je++9NyIi3v72t1f251Der2O7VG2e27Zti7//+7+fNfZP/+k/jVe/+tURUZ15Hq5qr+PRVPXnzrROeT2rPs+55udXfFAQqXsoRkdHc6ik/I477rg4++yzIyLi/vvvj0cffTT5di+//HJs3749Ig4FiTe96U1tqxEAOpUAAlTSeeedF295y1tiz5498f3vfz9eeumlzNvcc8898c1vfjMiIi699FJtKgDQBgIIUElnnnlmXH755RERcf3118enP/3pePzxxyPi0C3p3/72t2P9+vUxPj4eV111Vbzvfe/LsVoA6BxzHxcDUGLHHHNMfPSjH40XXnghrr/++vj85z8fn//85zNvd8UVV8S1114bK1asyKFKAOg8VkCgIFxG2HzHH398fOpTn4qf/OQn8fGPfzxWr14dERGnn356rF+/Pn784x/HrbfeGqeeemrOlQJA57ACAgXhMsLW6OrqijVr1sTNN9+cdynQFpOTk5mxnp6eeOKJJ3KoBiDLCggAVMj0hZqvlPoFB0BeBBAAAKBtBBAosKmpqbxLAABoKgEECiJ1EaFN6ABA1QggAABA2wggAABA2wggAABA2wggUBAuIgSWKnV3UK1Wy6ESgLkJIFAQLiIElmp0dDQz1tfXl0MlAHMTQAAAgLYRQAAAgLYRQKDgtGEBAFUigECBpC4jTPV0AwCUlQACAAC0jQACAAC0jQACABXhHhCgDAQQKBCXEQJLkfp50d/fn0MlAHMTQKBAXEYIAFSdAAIAALSNAAIAALSNAAIFNzU1lXcJAABNI4BAgaQuIrQJHQCoEgEEAABoGwEEAABoGwEEACpieHg4M5Zq7QTIkwACBTI0NJQZGxkZyaESAIDWEEAAAIC2EUAAAIC2EUAAAIC2EUCgYFIbRlMbSwEAykgAAQAA2kYAAQAA2kYAAYCKSB3bnTreGyBPAggUjLtAAIAqE0AAAIC2EUAAAIC2EUCgBKampvIuAQCgKQQQKJjUPSBjY2M5VAIA0HwCCAAA0DYCCAAA0DYCCJRAo9HIuwSg4FKtmr29vTlUAnBkAggUTOoeEHtAgKNJHVbR3d2dQyUARyaAAAAAbSOAAAAAbSOAQEnYBwIAVIEAAgWUugtkdHQ0h0oAAJpLAAEAANpGAAEAANpGAIGSsAcEOJKJiYnMWE9PTw6VABzZsl27duVdw6KMj49HRERZ65+vPXv25F1CW5jnbK9//evj7rvvnjW2bdu2OPXUU1tRVtNV/fWcnJyMAwcOzPx7VX8OVf11nFaVee7cuXPm63JaV1fXzNdnVeY5l6rPb5rnn2qp+jznmp8VEAAAoG2WDQwM5F3Dokwn/7LWv1DmWS1Hm+eOHTti+fLls8bq9XrpPj9lq3e+Xvn6lPF1Waiqz29a2ec5358bZZ/n0VR9fp5/qqnq8zx8flZAoCSmpqbyLgEAYMkEECig1D0gY2NjOVQCANBcAggAANA2AggAANA2AgiUhHtAgCMZHR3NjNXr9RwqATgyAQQKaGhoKDNmDwhwJKlfUriIECgiAQQAAGgbAQQAAGgbAQQKqlarZcbsAwEAyk4AgYLq6+vLjKU2mQIAlIkAAgAAtI0AAgAVkGrR7O7uzqESgCMTQKCg7AEBFiJ1VHeqlRMgbwIIFFR/f39mzF0gAEDZCSAAAEDbCCAAAEDbCCBQUKk9IFNTUzlUAgDQPAIIFFRq86g9IABA2QkgAABA2wggAFByw8PDmbHBwcEcKgE4OgEECip1gZh7QACAshNAoKDsAQEAqkgAAQAA2kYAAQAA2kYAgQJL3QUyMTGRQyUAAM0hgECBpfaBCCAAQJkJIABQcqlfTPT09ORQCcDRCSAAUHKTk5OZMQEEKCoBBAos1YI1MjKSQyUAAM0hgECBpS4jBAAoMwEEAABoGwEECswxvABA1QggUGCO4QUAqkYAAYCSm5qayoylVlABikAAAYCSGxsby4ylVlABikAAgQLr7+/PjDmGFwAoMwEECkwLBQBQNQIIAADQNgIIFJyjeAGAKhFAoOAcxQsAVIkAAgAAtI0AAgAllzodb2hoKIdKAI5OAIGCS7VgOYoXACgrAQQKrru7O+8SAACaRgABAADaRgCBgnMMLwBQJQIIFJxjeAGAKhFAAACAthFAAKDEUiui9Xo9h0oA5kcAgYLr7+/PjDmGF5iWCiA9PT05VAIwPwIIFFxqEzoAQFkJIAAAQNsIIFACjuIFAKpi2a5du/KuYVHGx8cjIqKs9c/Xnj178i6hLczzyE477bT45S9/OWts+/btcfbZZzejrKar+us5OTkZBw4cmPn3qv4cqvrrOK3s83zooYdmvh6nPf3005mvy7LP82iqPr9pnn+qperznGt+VkAAAIC2WTYwMJB3DYsynfzLWv9CmWe1LHSeJ510UixfvnzW2OrVqwv/+Sp6fYu1Y8eOmdejXq9Xdp7Tqj6/aWWd55NPPpn5+XD66afPOZ+yznO+qj4/zz/VVPV5Hj4/KyBQAqnb0B3FC0REjI2NZcZSx3cDFIUAAiXQ3d2ddwkAAE0hgAAAAG0jgEAJOIYXAKgKAQRKILUHRAABAMpIAAEAANpGAAEAANpGAIESSB2pmTp6E+g8w8PDmbHBwcEcKgGYHwEESiC1Cb3RaORQCQDA0gggAABA2wggUBJWQQCAKhBAoCRSR/GOjo7mUAkAwOIJIAAAQNsIIAAAQNsIIFASqRYsR/ECk5OTmbGenp4cKgGYHwEESqK7uzszZhM6MDExkRkTQIAiE0AAAIC2EUCgJOr1embMKVgAQNkIIFASqZYKLVgAQNkIIAAAQNsIIFASqRUQp2ABAGUjgEBJaMECDpf6GVCr1XKoBGD+BBAAKKnUQRSpO4MAikQAgRJJ/WYzdQcAAEBRCSBQIqnfbAogAECZCCAAAEDbCCBQIlqwAICyE0CgRPr7+zNjk5OTOVQCALA4AggAANA2AgiUiBYs4JVGRkYyY47hBYpOAIEScQoWcDTd3d15lwBwRAIIAADQNgIIlFyj0ci7BACAeRNAoESGhoYyY2NjYzlUAgCwOAIIAADQNgIIVIA2LACgLAQQKJnBwcHM2OjoaA6VAHlLnYJXr9dzqARg/gQQACipVADp6enJoRKA+RNAoAK0YAEAZSGAQMk4CQsAKDMBBAAAaBsBBAAAaBsBBEqmr68vMzY8PJxDJQAACyeAQMnUarW8SwAKInUARXd3dw6VAMyfAAIAJZU6gCK1SgpQJAIIlEx/f39mbGRkJIdKAAAWTgCBktGCBQCUmQACAAC0jQACJdTb25sZcxIWAFAGAgiUkFNuAICyEkAAAIC2EUCghHp6ejJjqeM4gepKtV0ODg7mUAnAwgggUEKpAJK6kAwAoGgEEAAAoG0EECih1E3Ho6OjOVQCALAwy3bt2pV3DYsyPj4eERFlrX++9uzZk3cJbWGeC/P444/HgQMHZo2Nj48X5vuh6q/n5OTkzOd/cnKyMJ/3Zqv66zitrPN86KGHMj8Hnn766Tm/Hss6z/mq+vymef6plqrPc675WQGBinj22WfzLgEA4KiWDQwM5F3Dokwn/7LWv1DmWS1LnefAwEB86lOfmjX26KOPFu7zV7R6mmXHjh2xfPnyiIio1+uVnee0qs9vWtnm+bOf/Wzm63Da2WeffdR5lG2eC1X1+Xn+qaaqz/Pw+VkBAYASmpyczIylTsgDKBoBBEqqVqtlxiYmJnKoBABg/gQQKKnUSVgCCABQdAIIAADQNgIIlFSq13tsbCyHSgAA5k8AgZJKBZBGo5FDJQAA8yeAAEAJDQ8PZ8ZSe8MAikYAgZJKPWikHkiAzpE6HQ+gaAQQKCkPGgBAGQkgUFLd3d2ZMXtAAICiE0CgpFItWE7BAgCKTgABAADaRgCBEqvX65kxqyDQGVItl6nWTICiEUCgxFJ3gUxNTeVQCdBuqV82OIYXKAMBBAAAaBsBBEos9dvOkZGRHCoBAJgfAQRKTL83AFA2AghUjD0gAECRCSBQYoODg5kxp2ABAEUmgABAyaR+0dDb25tDJQALJ4BAiaX2gExOTuZQCdBOqVZLe8KAshBAoMRSp2BNTEzkUAkAwPwIIAAAQNsIIFBy9Xo9M2YjOgBQVAIIlFxPT09mzFG8AEBRCSAAUDKNRiPvEgAWTQCBkhsaGsqMjYyM5FAJ0C6pNsvUzwKAIhJAAACAthFAoORqtVpmzFG8AEBRCSBQcu4CAQDKRAABAADaRgCBkuvv78+M2YQOABSVAAIll9oDAlRbqs0ydSkpQBEJIFABbkOHzpIKIKlLSQGKSACBCnAbOgBQFgIIVJSbkgGAIhJAoAJSNyBrwQIAikgAAQAA2kYAgQpIXUY4PDycQyUAAEcmgEAFOIoXOkvqrp9UKyZAEQkgUAGpU7DsAQEAikgAgQpIBRCnYAEARSSAQIUJIQBA0QggUBGDg4OZsdHR0RwqAQCYmwACAAC0jQACFZE6ijd1Ug5QbhMTE5mxer2eQyUAiyOAQEV0d3fnXQLQBqkAkjqIAqCoBBCoiNRdIKkHFQCAPAkgUBGpFiwBBAAoGgEEKswxvABA0QggUBFDQ0OZMbehAwBFI4AAAABtI4BAhaSO4rQKAtWS+p5O7QEDKCoBBCokdRTn1NRUDpUArZLa2+UYbqBMBBCoEEfxAgBFt2zXrl1517Ao4+PjERFR1vrna8+ePXmX0Bbm2Ryvfe1r48CBA7PGdu7cGW9+85tb+nEPV/XXc3JycubzPDk5WdmfQ1V/HaeVbZ6v/Pp75djRvg7LNs+Fqvr8pnn+qZaqz3Ou+VkBgYrbt29f3iUAAMxYNjAwkHcNizKd/Mta/0KZZ7W0ap4vvPBCbNmyZdbYU089ldvntaqv544dO2L58uURcWjjf1XnOa3q85tWlnm+8utv2kK+Dssyz8Wq+vw8/1RT1ed5+PysgEDFuYwQqiV1sERq/xdAUQkgUCEuI4TqcwwvUHYCCAAA0DYCCFRMb29vZmx4eDiHSgAAsgQQqBgXkgEARSaAQMWkesFHRkZyqAQAIEsAgYqxAgIAFJkAAhWTWgGxBwSqI3UKVn9/fw6VACyOAAIV4z4AqLbU3T6+74EyEUCgYlK/CbUHBAAoCgEEKsZvQgGAIhNAoILcBQIAFJUAAhXkJCwAoKgEEKignp6ezJh9IFB+qQ3oAGUjgEAFpQIIUH6jo6OZscHBwRwqAVg8AQQqqF6vZ8ZSDy4AAO0mgEAFpVZAtG4AAEUggEAFpQJI6vZkAIB2E0CggqyAAABFJYBARaX2gVgFAQDyJoBARaVWQaampnKoBGiWiYmJzJhT74CyEUCgouwDgeqZnJzMjAkgQNkIIFBR9oEAAEUkgEBFuQsEACgiAQQqygoIAFBEAghUVH9/f2ZsZGQkh0oAAH5NAIGKqtVqyXGrIABAngQQqLDBwcHMmH0gUF7Dw8OZsdT3OUCRCSBQYalVkNQ9AgAA7SKAQIWl9oGk7hEAAGgXAQQqzFG8AEDRCCBQYY7iBQCKRgCBCnMUL1RL6hcI3d3dOVQCsHgCCFSYo3ihWsbGxjJjfX19OVQCsHgCCFSco3gBgCIRQKDiHMULABSJAAIV5yheAKBIBBCoOEfxAgBFsizvAoDWchRv842Pj8eLL74YERHPP/98ztXQKVLft3MdNAFQZAIIVFwqgDiKd2HGxsbi9ttvj61bt8bExETs378/9u3bFxER119/fXzrW9+KSy65JK688konEtEyqZVLX29AGWnBgopLBZAIqyDzMTExEe9///vjwgsvjM2bN8+5eb/RaMSWLVviwgsvjPe///3Jo1IBgEMEEOgAvb29mTH7QObWaDTimmuuiXPOOSeGh4cX9HeHh4fjwgsvjBtuuKFF1QFAuQkg0AFSqyCO4k2bmJiISy+9NDZv3ryk93PDDTfEhRdeaKUJAA4jgEAHcBTv/IyNjcWFF1541Baq173udXHsscfG8uXLj/r+Lr30UiEEAF5BAIEOkNqoutDWoqqb3sMxV1io1+tx4403xv/9v/83/vAP/zBOOumkOPnkk+Nf/+t/HTfeeGOyzS1CCKF5UquWc+3xAigyAQQ6QOohxQrIr23dujWuvvrq5J/VarXYuHFj/OVf/mWsW7cuc+zpcccdF+vWrYvt27fHxo0bk+9jOoTAUqS+ZwUQoIwEEOgAqRUQe0AOGRsbi0984hPJP6vX6/G9731vzmBxuI0bN8Z//a//NXk3w9jY2JwhBwA6iQACHSLVItTpbVhHao/q7e2N7du3L/iehaGhofje976XDCFbtmxZ8uZ2ACg7AQQ6hJOwZps+7SoVPgYHB2P79u2LvmW6r68vvve97yX/7JprrnFPCAAdTQCBDuEkrNmuvvrqOVc+vv71ry/5/ff19cWNN96Y/LO5Wr4AoBMIINAh6vV6ZqxTW7BuuOGG5Nx7e3vjz//8zxe98nG4devWxZVXXpkZHxsbc1EhC5ZasUx9XwMUnQACHcJJWIcMDw8nH/5rtVpTw8e0TZs2JfffbN68uaNb4Fg4x/ACVSGAQIcYGhrKjHXaA3Cj0Ygrrrgi+We33XZb08PHtJtvvjlZi1OxAOhEXV/4whcO5l3EYuzcuTMiIt7+9rfnXElrTf+GuurL7ObZHjfffHNMTU3NGvvQhz4Ub3jDG5r6cfKe51y+8Y1vxPj4eGb8ggsuiAsuuGDe7+euu+6Ku+66a0F/d9u2bXHfffdlxlvx+W+Wor6OzVaWeaa+fhfy9VOWeS5W1ec3zfNPtVR9nnPNr2vVqlWlDCDPPvtsRES85jWvybmS1jpw4EBERCxfvjznSlrLPNvj6aefjhdffHHWWHd3dxx33HFN/Th5zzPl2WefjWeeeSYzfuyxx8ZJJ520oPe1f//+2LdvX0REnHDCCbFixYqj/p2DBw/GL3/5y3j55ZdnjR9zzDHxG7/xGwv6+O1SxNexFcoyz9T370knnRTHHnvsvP5+Wea5WFWf3zTPP9VS9XnONT8tWNBBUg8qhz8QV9HLL78c+/fvz4y/6lWvite+9rVtqaGrqyvZ4vXyyy/H888/35YaAKAIls33ht+isQRZLebZHn/9138dd95556yx008/PdavX9/Uj5P3PA+3ZcuW5EP+YtufFtOCNS3VRnPiiSfGxz/+8QXX0WpFex1bpSzzvP766zNfx3/0R3807xBdlnkuVtXnN83zT7VUfZ5zza+0AeQrX/lKRER85CMfybmS1tq1a1dERAwMDORcSWuZZ3sMDw/H//yf/3PW2PHHHx/N/jmQ9zxfaevWrTE5OZlpk7ryyitj06ZNi36/999/f0QcCiAL+fwNDg7G+9///lljBw4ciHq9HuvWrVt0Pa1QpNexlcoyzxtuuCHzdXzdddfN+++XZZ6LVfX5TfP8Uy1Vn+dc89OCBR1krpOwUhfyVUGj0YhrrrkmM16r1eKP//iPc6jo0GswODiYGf/iF7+YQzUA0H4CCHSY1J0Uo6OjOVTSel/4wheSRw3fdNNNLTtydz5SKyYTExOxZcuWHKoBgPYSQKDD9Pf3Z8bGxsZyqKS1xsbG4qtf/WpmfHBwMC6++OIcKvq1oaGhWLt2bWY8VS8AVI0AAh0mdXNyFQPIXK1XN910U/uLSUgFkLGxsRgeHs6hGgBoHwEEOkxq/0HVAsiWLVuSD/IbNmxIBrA8zLUXZPPmzTlUQ9GlvkdT7ZQAZSCAQIepegtWo9FIbuju7e1t+mlfS5VaBdm2bVty3wqdbWpqKjPW3d2dQyUAS1faAPLBD34wPvjBD+ZdBpROrVZLnjdeldafzZs3Jx/gF3JcabusW7cu+VpYBQHm4vmHKihtAHnNa14Tr3nNa/IuA0qpr68vM1aFVZBGo5F8eF+7dm2y3akIUnd/3H777ZU9GhlYGs8/VEFpAwiweFVtw/rsZz+bfHAvWuvVK23YsCFzJHCj0Ygf/vCHOVUEAK1VqgBy6623RldX11H/+c53vpN3qVBoVdyIPjExEbfffntm/Morr4yDBw/Gv/t3/y7e+ta3RldXV5xyyinxoQ99KO666674h3/4hxyq/bVarZY8FtiRvEBExGOPPRb/+B//46M++1x88cXxy1/+Mu9yYV5KE0BefPHFeOihh/IuAyqhiisgcx27Ozg4GL//+78fn/nMZ+L//J//ExERTz31VHzrW9+Kd77znXHdddfFc8891+5yZ9mwYUNmbGxszGZ0ZoyMjGTGUq2UVM/jjz/u+YfKWZZ3AfP13HPPzfzPeNOmTXH++efP+bZvfOMb21UWlNL0RvTJyclZ42NjY6V8qBkeHo6tW7dmxt/73vfG5z73uXjooYfiqquuin/7b/9tnHbaafHMM8/En/3Zn8WnPvWpuPbaa+O0006LK6+8Mrq6unKo/tCDZG9vbzz44IOzxjdv3hybNm3KpSaKzylYneHv/u7v4vHHH4/zzz8//uRP/iRWrFiRfLvjjjsuTjjhhDZXB4tTmgDy5JNPxiOPPBKrVq2Kd7/73TEwMJB3SVBqPT09mQAyOjpaygCSOnb3t37rt6Krqyvuu++++NCHPhT/4T/8h5m9FrVaLf7wD/8warVa/PN//s/ja1/7WrzrXe/K9ZcX69aty6zibNu2TQCBDje9Ov27v/u7ceGFF8axxx6bc0WwdKVpwXrsscdi165dsXr16li1alXe5UDpDQ0NZcZSbR5Ft3Xr1uQRwuvXr4+77rorIg4dW3n4Ru+urq645JJL4l3velfcd9998b/+1/9qS71zSZ2GNTExkVzZATrDs88+Gz//+c8jImL16tXCB5VRmgCyZ8+eiDh0mdjJJ5+cczVQflXZiJ7a+1Gv1+P1r3993HfffTE0NBS/8zu/k/y7r33ta+Pss8+OiIi/+qu/iueff76ltR5JrVaLiy66KDMugEDn+tWvfhU/+9nP4sQTT4w1a9bkXQ40TSkCyCs3oPf09MSOHTti7dq1ccopp0RXV1e8853vjC996UtOf4AFmGsjepnun9iyZUtyo/ZNN90UDz/8cEREnHHGGXP+0qKrqyt++7d/OyIiHn744di/f3/rip0Hd4IArzS9Af2ss86KF198cdZpfm94wxviyiuvjJGRkdxP84OFKkUA2b9/f/z0pz+NiIhPfvKTcckll8Qdd9wRTz31VERE3HXXXfGxj30sfu/3fq+ULSSQh1qtFr29vZnxstyI3mg0kqsfg4ODcc4558STTz4ZEYcu7Vq2bO7tbj09PRER8fd///fx//7f/2tNsfN08cUXZ1rFIsKdICS/L4t6uSbN87Of/Swef/zxGB4ejgsuuGDWaX7j4+Pxta99LYaGhuIzn/lM7r9AgYUoRQB54oknZjbLrl69Om677bZ46qmn4uDBg7Fv37648847Y82aNbF79+64+uqrZ9q1gCNL7QMpSxvW5s2b57x08MUXX5z5BcVv/dZvxfHHHz/n+znmmGNaVuNirF27NjOmDQs60/QvXyMiPvShD8UDDzwQBw4ciJdffjkefvjhuPrqqyMi4t//+38fX/rSl+Kll17Kq1RYkFIEkH379sWpp54aZ511Vtx6661x+eWXx0knnRQREStWrIj3vOc98d3vfjfOOeecuO++++JrX/tavPDCCzlXDcWXOvGqDCsgjUYjNm/enBlfu3ZtMlSVSaoNa9u2bdqwoMM8//zz8eKLL8bb3/72uOqqq+KWW26Js846K5YtWxavetWr4k1velNcf/318R//43+MiIg//dM/jb/+67/Ot2iYp1IEkIGBgfjRj34UDzzwQFxwwQXJtznzzDNj/fr1ERGxffv2+MUvftHGCqGcynoS1mc/+9k5Vz/Krq+vL+r1emZcGxZ0luOOOy6uu+66GBkZiS9/+cvJ+z+WLVsWH/jAB+L888+P8fHx2Lp1axw8eDCHamFhShFA5qOrqyve9ra3xapVq2L37t2xd+/evEuCwuvp6Uk+7BZ5FWRiYiJuv/32zPiVV145s5+j7C6++OLMmDYsIGXlypXxu7/7uxFxaF/Ic889l3NFcHS5BpB77703urq65vzn3nvvnfPvPvHEE3HnnXfOGjvhhBNi5cqVERHJk3GArFQbVpFXQW644YbMWK1Wm7X6cdxxx8Vv/uZvRsShW4SP9D/kl19+OSIO/SaxKPtBtGFxOK890+6///64++67Z/772GOPnWlLn5iYEEAohdKsgOzbty+mpqZmlhaP9qAwHUSAI0u1YY2OjuZQydENDw8nVz82bNgQ3d3dM//d1dU189/PPvvsETdmTv+y4jd+4zdm/ieeN21YHC51OETZ9ztxdC+99FI8/fTT8eKLL86MLVu2bM5AunLlSpcVUgq5BpBzzz03Dh48OOc/5557bjz//PPxL/7Fv4gTTzwxPvaxj8W+ffsi4tBvOE888cRZ72/v3r2xe/fuWLVqlcsKYZ7KtA/ki1/8YmasXq/Hhg0bMuPT95xMTEzEM888k3x/Bw8ejL/927+NiEP3haR6rPOiDQs6286dO+Pkk0+Ok08+Oe66666Z8RNOOCFe+9rXzvz3s88+G48++mhEHPpFyqtf/ep2lwoLVvgVkOOOO27mpuL7779/5ptsxYoVce6558683csvvxzbt2+PiIi3v/3t8aY3van9xUIJpVqwGo1G4Y7jHR4eTu5N2bhxY/LujDe/+c1xzjnnxK5du+Y8mvtXv/pVPPDAAxER8da3vjWOO+645ha9BKkAog0LOsfrX//6GBgYiIiIn/zkJzPtom984xvjnHPOmXm7Rx55ZKZl/bzzzrMCQikUPoBEHPqGestb3hJ79uyJ73//+zPtFK/8Jrvnnnvim9/8ZkREXHrppYVppYAyuOiiizJjRduInrp0sF6vJ/dLREScdtppcd5558UzzzwT3/jGN+JXv/rVrD8/ePBg/OAHP4jvf//7cc4558Q/+Sf/pBVlL9rQ0JBLCaGDve51r4vzzz8/IiLuvPPOmTtBjjnmmFi+fHlEHLqo+ZZbbok9e/bEe9/73jjvvPNyqxcWohQB5Mwzz4zLL788IiKuv/76+PSnPx2PP/54RBz65vv2t78d69evj/Hx8bjqqqvife97X47VQvmk2rCK1O6zZcuW5IrMpk2b5vw7r371q+PDH/5wnHPOOfGtb30rrrrqqvj5z38eBw8ejEajEbfeemv8y3/5LyMi4sMf/nC84Q1vaFX5i6YNCzrXMcccE5dddlmcc845sXv37li/fn386Ec/ipdeein+4R/+If72b/82NmzYELfcckucfvrp8a/+1b+y/5XSKEUAOeaYY+KjH/1oXHfddRER8fnPfz5OO+206OrqihNOOCEuu+yyGB8fjyuuuCKuvfbaQvVxQxmkHnRHRkYK0+6T2vsxODiYrPuV3vKWt8T1118fq1evju9+97txxhlnxKte9aro7u6OP/qjP4qnnnoqrr322vjgBz8YXV1drSp/0eZ6Xegsqe/D1OoY1fPbv/3bccstt8S5554b//t//+/4/d///Vi+fHkcc8wx8Tu/8zvx3e9+N1avXh033nhjvOMd78i7XJi3UgSQiIjjjz8+PvWpT8VPfvKT+PjHPx6rV6+OiIjTTz891q9fHz/+8Y/j1ltvjVNPPTXnSqF8inwfyObNm5PHas/30sF3vOMd8T/+x/+I6667Lv7RP/pHERFx8sknx2WXXRY7duyIz3zmM3H88cc3teZmufjiizMPmo1GoxCvC+2TOpUutXeLanrrW98a27Zti69+9atx8cUXzxzAc8EFF8QXvvCF+PGPfxx/8Ad/UMhfosBcluVdwEJ0dXXFmjVr4uabb867FKicoaGhzBG3w8PDR11laKVGo5G892NwcHBBR5C+/vWvj09/+tPx6U9/upnltcXg4GBs27Zt1tjWrVsdwQodZMWKFfHhD384PvzhD+ddCjRFaVZAgNaa69SlPG3evDnZfnLTTTe1v5icaMMCoGoEECAi0hvRJyYmku1P7dBoNGLz5s2Z8bVr10ZPT08OFeXjkksuyYyNjY3l9roAwFKVNoA88MADM+f3A0tXq9VicHAwM57XqUuf/exnk6sf8937URW1Wi16e3sz4/aBQGfy/EMVlDaA7Ny5M3bu3Jl3GVApqXafw/eFtMPY2Fjy427cuLGjVj+mpVZBHMfbOVKrXU7B6lyef6iC0gYQoPlSASSPdp/UpYO1Wi02bNjQ1jqKooj7c2ifycnJzFh/f38OlQA0hwACzOjp6Um2+7Tzt+1bt25Nthdt2LChY3/r29fXl5y7VRAAykgAAWZZt25dZqxdbViNRiO5+lGv1ztu78fhUqsg9oEAUEYCCDBLnm1Yc1062EnH7s4ldUCANiwAykgAAWaZqw2r1asgExMTyUsHL7roIpfuRXojep7HJAPAYgkgQEYebVhXX311cnzTpk0t/bhlMddxvPaBVF8qZNbr9RwqAWgOAQTISLVhTUxMxJYtW1ry8ebaeN6px+7OJbUKYh9I9aUCiO8LoMwEECCjp6cnLrroosz4HXfc0fSP1Wg04hOf+ERmvF6vd+yxu3NJ7QMZGRnJoRIAWDwBBEhKPfwPDw83fc/BJz7xieSN55s2berYY3fnMjQ0lPmcNBqNGBsby6kiAFg4AQRIGhoaSvaZpzaKL9bmzZuTexguuuiiZBsY6VUQbVgAlIkAAswpdffG7bff3pRVkLlOvarVanHzzTcv+f1XVepEMAEEgDIRQIA5XXLJJck2qGasglx99dXJ1qubbrpJ69URpAKIfSDVlmqxswkdKDMBBJhTrVZL7gW5/fbbl/Rb96uvvjr596+88kqtV0fR19eX3AdiFaS6UkFdAAHKTAABjmjDhg3JFYkvfvGLi3p/mzdvTh7nW6/X44//+I8X9T47jdOwACgzAQQ4olqtFp/73Ocy48PDwwtuxdq6dWtcc801yT/TejV/9oEAUGYCCHBU69atm/NErPk++G7ZsiWuuOKK5J/deOONyYdq0uwDAaDMBBBgXm666abk+BVXXHHUeyi2bNkSV199dfLP1q5dG+vWrVtqeR2lr68vGQitglRPav+HlUKg7AQQYF6GhoaSx/I2Go249NJLkw+/ExMTccUVV8wZPi666KI5gw1HZhWkM4yOjmbG+vr6cqgEoHmW5V0AUB4bN26M4eHhzINuo9GI97///TE0NBSDg4MxOTkZe/fujR07dsz5vnp7e933sQSDg4Nx++23zxrbunVrMiQCQJEIIMCCfP3rX4+3ve1tydaQ4eHhGB4ejgMHDkRExPLly5PvY+3atbFp0yatJEuQWgE5WiscABSBFixgQWq1WvzlX/5l9Pb2Lurvr1271olXTdDT02MfCACltGzXrl1517Ao4+PjERFR1vrna8+ePXmX0BbmWT6f+cxn4nOf+1z8zd/8TebPXnrppczYihUrYuPGjTE0NFT679vJycmZVZ7Jycnc5vPmN785HnnkkVljd9xxR7z61a9uyvuv0tfrkRR5nrt27Zr5Wpv29NNPL+prrsjzbIaqz2+a559qqfo855qfFRBgUU444YT4T//pP8XGjRtj5cqVc77dihUr4oMf/GB84xvfcNRuk73pTW/KjO3evTuHSmiVn//855mxNWvW5FAJQPMsGxgYyLuGRZlO/mWtf6HMs1qqNM+BgYH4N//m38Tw8HCMjY3F2NhYdHV1RcShU64uvvjinCtsvh07dszsb6nX67m9nscdd1zcdttts8Yee+yxptdTpa/XIyniPF/5tTZtqV9zRZxnM1V9fp5/qqnq8zx8fjahA00xNDQ0s8LRaf+DzEtfX1/UarVZBwI0Go0YGxtzVCsAhaUFC6DEUkHDRnQAikwAASix1L4aAQSAIhNAAEpscHAwM/bggw/mUAmtkAqT2uuAshNAAEostQIyMTERExMTOVRDO7hDByg7AQSg5FKrINqwACgqAQSg5FItOWNjYzlUAgBHJ4AAlFyqDWtkZCSHSgDg6AQQgJJLBZCxsbFZ94NQTqmVrJ6enhwqAWgeAQSg5Gq1WtTr9cz46OhoDtXQTKkQKYAAZSeAAFSANiwAykIAAagAJ2EBUBYCCEAFWAEBoCwEEIAK6OnpSV5Q5zje8kpdJukSQqAKBBCAitCGVS2pAJK68wWgbAQQgIro7+/PjFkBAaBoBBCAikitgAggABSNAAJQEXOtgLiQEIAiEUAAKsKFhNUiOAJVJYAAVIjjeKsj1T6Xen0BykYAAaiQ1ClJVkAAKBIBBKBCUgHkwQcfzKESAEgTQAAqJNWiMzExkbxTAgDyIIAAVIzjeAEoMgEEoGJSbVgCSPmkbrF3EzpQBQIIQMWkHlJTD7OUT61Wy7sEgCUTQAAqJnUhoaN4ASgKAQSgYvr6+pK/KdeGBUARCCAAFeQ+EACKSgABqKDUcbxWQMol9Xr19PTkUAlAcwkgABWUWgGxD6RcGo1GZkwAAapAAAGoIEfxAlBUAghABfX09ES9Xs+MO44XgLwJIAAVZRUEgCISQAAqKnUfiABSDhMTE5kxlxACVSGAAFTU4OBgZkwAKYdUAEmtaAGUkQACUFFWQAAoIgEEoKJqtZqN6AAUjgACUGGptp1Uew8AtIsAAlBh2rDKKXUJIUBVCCAAFeYo3nJKvUZDQ0M5VALQfAIIQIWlAsjIyEgOlQDAIQIIQIX19PQk74+wCgJAXgQQgIpLrYKMjo7mUAkACCAAlZfaO2AFBIC8CCAAFWcjevmk7mpxEzpQFQIIQMXZiF4Nqb08AGUkgABUXE9PT3LchYQA5EEAAegAg4ODmTFtWADkQQAB6AD2gQBQFAIIQAdIBZDURmeKIRUO52qlAygbAQSgA/T392fGrIAUV6PRyIwJIEBVCCAAHSC1AtJoNGxEB6Dtlu3atSvvGhZlfHw8IiLKWv987dmzJ+8S2sI8q6Xq85ycnIwDBw7M/HtZfg6deeaZ8Td/8zezxv7bf/tvyYsKI6r/Ok4r4jynv75eaalfZ0WcZzNVfX7TPP9US9XnOdf8rIAAdIgzzjgjM/bzn/88h0oA6GTLBgYG8q5hUaaTf1nrXyjzrBbzLLcdO3bE8uXLIyKiXq+XZp7vete74gc/+MGssV/96ldHrb8s81uqosxzYmJi5utrWjO/zooyz1ap+vw8/1RT1ed5+PysgAB0iNQm5gcffDCHSjiS1L4cG9CBKhFAADpEaq/HxMRE8sQlAGgVAQSgg/T29mbGRkdHc6gEgE4lgAB0kNR9ICMjIzlUAkCnEkAAOkhqL4G7QIrFLehA1QkgAB1kcHAwM+ZG9GJxCzpQdQIIQAdJtWAJIAC0kwAC0EFqtVrUarXMuBACQLsIIAAdpq+vLzNmHwgA7SKAAHSY1H0gVkCKY3h4ODOWCo0AZSWAAHSYer2eGUs99FIcqbY5gLISQAA6TGoj+uTkZA6VANCJBBCADjPXHpDU8a8A0GwCCEAH6u3tzYyNjo7mUAmHS61GdXd351AJQGsIIAAdKHWxnY3oxZA6kcwmdKBKBBCADuRCQgDyIoAAdKDBwcHMmLtAAGgHAQSgA6VasEZGRnKoBIBOI4AAdKCenp7k3RJWQfKVaoNL3dsCUGYCCECHSm1stg8kX1NTU5mx1GoVQJkJIAAdSgABIA8CCECHSgUQd4EA0GoCCECHSrX2PPjggzlUAkAnEUAAOtTQ0FBmzCb0fKVOIku9TgBlJoAAdLDUCUvDw8M5VAJApxBAADqYjegAtJsAAtDB+vv7M2PasABoJQEEoINZASmWVPhLXRgJUGYCCEAHE0CKJRVAUq8RQJkJIAAdLHUUb6PR0IYFQMsIIAAdbnBwMDMmgADQKgIIQIdLtfik7qMAgGYQQAA6XKoNa3R0NIdKSO2/SZ1UBlBmAghAh0utgExOTuZQCY1GIzPmFCygagQQgA6X+g27k7AAaBUBBKDD1Wq15G/ZH3744RyqAaDqBBAAkm1Ye/fuzaGSzpVqvwKoIgEEgGQA+fnPf55DJZ0rtfE/dUQyQNkJIAAkT8LSggVAKwggACRXQJ544okcKgGg6gQQAJInYVkBAaAVBBAAnIRVABMTE5kxd4AAVSSAABARTsLKW+ryR7egA1UkgAAQERFDQ0OZMSdhAdBsAggAERFRr9czY1qwAGg2AQSAiEgfxeskLACaTQABICLSLVhWQNpneHg4M5balwNQdgIIADNSbVhjY2M5VEKEU7CAahJAAJiRasNKHQ8LAIslgAAwI9WGZQUEgGYSQACYkWrBGh0dzaGSztNoNPIuAaAtBBAAZqRasFIX5NF8qZWm1IoUQNkJIADM0IIFQKsJIADM4iQsAFpJAAFgFidhAdBKy3bt2pV3DYsyPj4eERFlrX++9uzZk3cJbWGe1VL1eU5OTsaBAwdm/r1qP4de//rXx9133x0vvfTSzNi2bdvi1FNPzbGq1inC1+vevXtnvqamrVy5sqlfW0WYZytVfX7TPP9US9XnOdf8rIAAMMvrXve6zNju3btzqKRz7N27NzOWeh0AqmDZwMBA3jUsynTyL2v9C2We1WKe5bZjx45Yvnx5RBzaL1G1eb7wwgvxn//zf5757+XLl8f+/fsrN8/D5Tm/F154YeZratpJJ53Ukpq8juXm+aeaqj7Pw+dnBQSAWVInYdkDAkCzCCAAZKROwhoeHs6hEgCqRgABIMNJWO01MjKSGevr68uhEoDWE0AAyEi1YbkRvb26u7vzLgGgJQQQADK0YAHQKgIIABmpFiwrIAA0gwACQIaTsNprdHQ0M2YPCFBVAggASStXrsyMacNqjUajkRmr1Wo5VALQegIIAEmpm7itggCwVAIIAElr1qzJjNkHAsBSCSAAJKVWQLRgtcbY2FhmLHUQAEAVCCAAJKUCiBWQ1kjtARFAgKoSQABIOvvsszNj9oAAsFQCCABzchIWAM0mgAAwJydhtV7q85m6iR6gKgQQAObkJKzWSwUQ+z+AKhNAAJiTk7AAaDYBBIA5pQJI6sQmAJgvAQSAOaVOwkrdWcHipVqwarVaDpUAtIcAAsARpR6GhZDmSe2p6e/vz6ESgPYQQAA4or6+vsyYk7AAWCwBBIAjSgUQKyAALJYAAsARpY6EtQLSPFNTU5kxe0CAKhNAADgiLVitlVpNSn3OAapCAAHgiFIbokdGRnKoBIAqEEAAOKK52oGsggCwGAIIAEc1ODiYGRNAmsPFjkCnEUAAOKrURnRtWM2R2gMyNDSUQyUA7SGAAHBUqQCSOr0JAI5GAAHgqFItWO4CAWAxBBAAjiq1AiKALJ39H0AnEkAAOKpUAGk0Gh6gl2h0dDQzllptAqgSAQSAeent7c2MpR6gAeBIBBAA5kUbFgDNIIAAMC+pG9G1YAGwUAIIAPPS19eXGRseHs6hkupI3aWS+jwDVIkAAsC81Gq1zNjk5GQOlVRbd3d33iUAtJQAAsC8pG7nnpiYyKESAMpMAAFg3ur1emZMGxYACyGAADBvqZOwrIIsXiq82QMCVJ0AAsC8pdqw7ANprtReG4AqEUAAmLdUC5bLCAFYCAEEgHlLtWBZAQFgIQQQAOYtdRmh29AXL/W5S32OAapEAAFg3mq1WnKPghCyOKmb5O0BAapOAAFgQVKnNDkJC4D5EkAAWJBUALECAsB8CSAALIi7QJojFdpSp4wBVI0AAsCCaMFqjqmpqcxYKtwBVI0AAsCCpB6SR0ZGcqgEgDISQABYkLl+S28VBID5EEAAWLDBwcHMmACyMKk9IFqwgE4ggACwYNqwli51B4gAAnQCAQSABUs9KKc2VQPA4QQQABYs1YLlLhAA5mPZrl278q5hUcbHxyMioqz1z9eePXvyLqEtzLNaqj7PycnJOHDgwMy/V/Xn0JFex1d+Dqb91V/9VSk/F3l9vf7gBz/IfA5PPvnkln0Oq/59WfX5TfP8Uy1Vn+dc87MCAsCCnXHGGZmxffv2xb59+3KoBoAyWTYwMJB3DYsynfzLWv9CmWe1mGe57dixI5YvXx4Rh26uruo8p801vzVr1sSDDz44a2z58uWl/Xy0u+6TTjpp5uto2urVq1teR1lfn/mq+vw8/1RT1ed5+PysgACwKKmN6I7inb/JycnMWHd3dw6VALSXAALAovT392fGUg/VpKXCWl9fXw6VALSXAALAoqQeloeHh3OoBIAyEUAAWJRarZYZswICwNEIIAAsytDQUGbMHpD5Sd2Z0tvbm0MlAO0ngACwaPV6PTOmDevoUrfG24AOdAoBBIBFS52E1Wg0cqgEgLIQQABYtFQbVqq9iNmENKCTCSAALFqqBWt0dDSHSsolFdJSYQ6gigQQABYt1YLlJCwAjkQAAWDRUpcRasEC4EgEEAAWrVarJe8DEUKOLHVccaqdDaCKBBAAliR1I3rqmFl+LRVAUu1sAFUkgACwJKkAMjIykkMlAJSBAALAkqR+c+9GdADmIoAAsCSpFRAB5MhSK0SpDf0AVSSAALAkqRUQLVgLl9rMD1BFAggASzLX5mmrIACkCCAALNng4GBmTABJazQaeZcAkCsBBIAlS62CuAskbXR0NDOWCnAAVSWAALBkTsICYL4EEACWLPUbfCsgAKQIIAAsWXd3d2ZMAElLfV7cgg50EgEEgCVL3QXSaDRsuE5IfU4EEKCTCCAANEVvb29mLLXhGoDOJoAA0BROwgJgPgQQAJqiv78/M6YFK2t4eDgzlmphA6gqAQSApkg9RKcetsmq1Wp5lwDQNgIIAE2RasGanJzMoRIAikwAAaApUisgLiPMSoWy1DHGAFUlgADQNPV6PTOmDWu2VCizBwToJAIIAE2TasOyCgLAKwkgADTN0NBQZsw+EABeSQABoGlSLVguI/y11L0oqc8ZQJUJIAA0jZOwjmxqaiozlvqcAVSZAAJA06RasNyGDsArCSAANFXqUj0h5JDUhnyXEAKdRgABoKncBzK3VDtaf39/DpUA5EcAAaCpUgHECggA0wQQAJrKXSBzS21CB+g0AggATaUFa26plaDBwcEcKgHIjwACQFOl9jSMjIzkUAkARSSAANBUc53qZBUEgAgBBKi4W2+9Nbq6uo76z3e+8528S62UVFuRAJJeCXIKFtBpBBCgsl588cV46KGH8i6jI6U2omvDSnMPCNBpluVdAECrPPfcczO/dd+0aVOcf/75c77tG9/4xnaV1RFSAcQJUABECCBAhT355JPxyCOPxKpVq+Ld7353DAwM5F1Sx0i1YHX6XSCp+dfr9RwqAciXFiygsh577LHYtWtXrF69OlatWpV3OR0ltQLS6QEktQKU+jwBVJ0AAlTWnj17IiKit7c3Tj755Jyr6SypB+tGoxGNRiOHagAoEgEEqKRXbkDv6emJHTt2xNq1a+OUU06Jrq6ueOc73xlf+tKX4pe//GXOlVZXb29vZmx0dDSHSoohdQqYDehAJxJAgErav39//PSnP42IiE9+8pNxySWXxB133BFPPfVURETcdddd8bGPfSx+7/d+z+lMLaINa7bJycnMmCN4gU4kgACV9MQTT8w88K1evTpuu+22eOqpp+LgwYOxb9++uPPOO2PNmjWxe/fuuPrqq2fatWie1MO1u0AAEECAStq3b1+ceuqpcdZZZ8Wtt94al19+eZx00kkREbFixYp4z3veE9/97nfjnHPOifvuuy++9rWvxQsvvJBz1dXS19eXGevkFRAtWACHCCBAJQ0MDMSPfvSjeOCBB+KCCy5Ivs2ZZ54Z69evj4iI7du3xy9+8Ys2Vlh9qRasVBtSp0gFkFRIA6g6AQToWF1dXfG2t70tVq1aFbt37469e/fmXVKlpB6utWABsOwrX/lK3jUsyt133513CW0xPj4eERG7du3KuZLWMs9qaeY8jz/++DjvvPPiDW94Q3R1dcW9994b55133pxvf88998S5556b/LMnnngidu7cGWeffXacfvrp0dXVFSeccEKsXLkyHn/88ZmH44MHD8ajjz4a99xzT+zfvz/zfnbu3BnPPvvszL+X9efo0TTjdezu7o7HH3981tif/MmfxBlnnLGk2pqpXd+Xe/bsmfm6mfYXf/EXbTsZrOo/f6o+v2mef6ql6vOca35WQIDK2rdvX0xNTcXBgwcjIuKYY46ZGZ8ee6WVK1dGxKGVkVe9yo/HZjj++OMzY08//XQOleTvsccey4wVKYgBtMuyj3zkI3nXsCRlr/9ophPjwMBAzpW0lnlWSyvnee655ybDwys9//zzsXHjxrjlllvisssuiy9/+ctx4oknximnnBLvfe97Z73t3r17Y/fu3bFq1apZlxX29PTEBz7wgeT7f+aZZ+Lee++NiIi3v/3tlf051IzX8Zlnnokbbrhh1tjq1asL9Tlr1/fltddemxlr5+eh6j9/qj6/wxXpe6gVOuX1rPo855qfX/EBlXPcccfF2WefHRER999/fzz66KPJt3v55Zdj+/btEXEoSLzpTW9qW42dol6vZ8aGh4dzqASAohBAgEo677zz4i1veUvs2bMnvv/978dLL72UeZt77rknvvnNb0ZExKWXXjpzTC/NkzoJq9Fo5FBJvlKhK3VTPEAnEECASjrzzDPj8ssvj4iI66+/Pj796U/PbIbev39/fPvb347169fH+Ph4XHXVVfG+970vx2qra2hoKDPWyXeBvFJ3d3feJQDkQgABKumYY46Jj370o3HddddFRMTnP//5OO2002ZOvrrssstifHw8rrjiirj22mtjxYoVOVdcXak2LCEEoHMJIEBlHX/88fGpT30qfvKTn8THP/7xWL16dUREnH766bF+/fr48Y9/HLfeemuceuqpOVdabak2rE67DyQVuFKfF4BOsCzvAgBaqaurK9asWRM333xz3qV0rL6+vhgZGZk1NjY2FhdffHFOFbVfat+LAAJ0KisgALRU6kG7XZfvAVA8AggALdXX15cZ67STsFItZ6m9MQCdQAABoKX6+/szY4e3ZFVdKoBowQI6lQACQEvVarWo1WqZ8U7biA7AIQIIAC2XasPqpAAyOTmZGXMPCNCpBBAAWi7VbtRJbVipsJUKZQCdQAABoOXcBQLANAEEgJYbHBzMjHVKAEnNM7UnBqBTCCAAtFwnt2BpvwKYTQABoOXmOnK20+4DAUAAAaBNUm1YnXAj+tjYWGbMHSBAJxNAAGiL1EN36uG8alKrPAII0MkEEADawklYAEQIIAC0SWrjdSesgAwPD2fGbEIHOpkAAkBbdGoLVopjeIFOJoAA0Bap3/o7BQug8wggALRNb29vZizVolQlqftOhoaGcqgEoBgEEADaxkZ0AAQQANqmv78/MzY5OZlDJe2hxQwgSwABoG3q9XpmrMotWKmLFlMXMgJ0EgEEgLZJtWBVeQUEgCwBBIC2SW2+rvIekNTcHMELdDoBBIC2SrVhVfU+kNTqTmofDEAnEUAAaCsnYQF0NgEEgLZKtWFVdQUktQk9tQIE0EkEEADaKvUAnnpQr4LUMbypFSCATiKAANBWTsIC6GwCCABt1UktWCMjI5kxm9CBTieAANB2nXYh4Ss5hhfodAIIAG3XCSdhpfZ/ACCAAJCDVBtW1faBpDbWDw4O5lAJQLEIIAC0XSe3YAF0OgEEgLZLbcSu2gpIqgXL/g8AAQSAHPT19WXGJiYmKrVvInWylxOwAAQQAHLS29ubGavqhYQA/JoAAkAuUidhVek+kNSpXlqwAAQQAHKSakeq0lG8qbmkWs8AOo0AAkAuUg/jVVoBASBNAAEgF1UPICMjI5kxm9ABBBAAcpLaA9JoNCp1Etbh7AEBEEAAyFHqZvAqnISVWslJXb4I0IkEEAByk1oFSbUulc3U1FRmLDVXgE4kgACQm9RDeRVOwqpyGxnAUgkgAOQm1YJVhQCSasEaGhrKoRKA4hFAAMhNVVuwAJibAAJAbnp6epInQ5V9FSS1kd4mdIBDBBAAcpW6D6TsASS1B8QmdIBDlu3atSvvGhZlfHw8IiLKWv987dmzJ+8S2sI8q6Xq85ycnIwDBw7M/HtVfw6163U8+eSTZz6f0+6444549atf3ZaP34p5/t3f/V1mTnl/rVT9+7Lq85vm+adaqj7PueZnBQSAXL3uda/LjD388MM5VNI8qfrPOOOMHCoBKJ5lAwMDedewKNPJv6z1L5R5Vot5ltuOHTti+fLlEXGor7+q85zW6vm98MILcdttt80ae+6559r+eW3mx5v++mjV+1+KotTRKlWfn+efaqr6PA+fnxUQAHLV39+fGUsdY1sWw8PDmbHe3t4cKgEoJgEEgFzVarXkSVhlDiGH6+7uzrsEgMIQQADIXZVOwkrVnQpYAJ1KAAEgd6lbwsu6AjI5OZkZS7WZAXQqAQSA3KUu6UvtpQCg/AQQAHKXuqQvtZJQBqnglGoxA+hUAggAuUu1YJV1D0iKPSAAvyaAAFAIVWnDSu1dSa3wAHQqAQSAQkg9pJdxFaTRaGTGBBCAXxNAACiEKpyElQofAMwmgABQCKmN2mULIKOjo5mxwcHBHCoBKC4BBIBCSAWQkZGRHCoBoJUEEAAKoaenJ3laVJn2gaQCkyN4AWYTQAAojCq0YR2uu7s77xIACkUAAaAwyh5AXEIIcHQCCACFkXpYL+NdIK/kEkKA2QQQAAqjv78/M1amFRCXEAIcnQACQGGkVkAajUZp7tdwCSHA0QkgABRKb29vZix1v0bRpFY/6vV6DpUAFJsAAkChpNqwynAfyNTUVGbM6gdAlgACQKGk2rDKugIigABkCSAAFEoqgExOTuZQycLY/wEwPwIIAIUyNDSUGSvDSVipG9sdwQuQJYAAUDipzdtFvw8kFUBcQgiQJYAAUDhlvBE91SbW3d2dQyUAxSaAAFA4ZbyQ0AoIwPwIIAAUzuDgYGYs9YBfFPZ/AMyfAAJA4aROjyryXSBWPwDmTwABoHB6enqSKwhFbcNKHcELQJoAAkAhlelCwlQwSh0nDIAAAkBBpR7gi3oh4dTUVN4lAJSGAAJAIaVWQIp6F0hqBSS1kR4AAQSAgkptRLcHBKD8BBAACim1AtJoNAp5HK89IADzJ4AAUFipNqairYK4AwRgYQQQAAqrDPtA3AECsDACCACFlWpjKtoKSKqe1P4VAA4RQAAorNRKQtFuRE9tQBdAAOYmgABQWGW4ET3VEqYFC2BuAggAhVb0G9FTKyA2oQPMTQABoNBS+0CK1IaVWo3p7+/PoRKAchBAACi0Ih/FO9edJFZAAOYmgABQaKnVhCIHkFRgAuDXBBAACq1Wq0W9Xs+MF+E+kFQQsvoBcGQCCACFl9qIXoRVkNQGdPs/AI5MAAGg8FIb0YuwApI6jSu1WgPArwkgABReagXkwQcfzKGS2VxCCLBwAggAhZdaAZmYmEgGgHZKHQesBQvgyAQQAEqht7c3M5ZnG9Zc4ccmdIAjE0AAKIWiHceb2v/hCF6AoxNAACiF1MN9nisgqfBj/wfA0QkgAJRC0VZAUpcQCiAARyeAAFAKqZOwGo1GbiEk9XG1YAEcnQACQGkUqQ1LCxbA4gggAJRG6jjePFZAGo2GO0AAFmnZrl278q5hUcbHxyMioqz1z9eePXvyLqEtzLNaqj7PycnJOHDgwMy/V/XnUBFfx5NPPnnmcz9t+/btS3oNFjPPBx54IFPHWWedVeivhSK+ns1U9flN8/xTLVWf51zzswICQGmcffbZmbG9e/fG3r1721rHww8/nBn7zd/8zbbWAFBWywYGBvKuYVGmk39Z618o86wW8yy3HTt2xPLlyyMiol6vV3ae04o2v3e84x2ZG8ifeeaZePe7372k97uQef7FX/zFzNfAK/9+0T5XKWWocSmqPj/PP9VU9XkePj8rIACUSmofyOGBpNWcgAWweAIIAKWSOo63CAHEBnSA+RFAACiV1ArIxMRE8lSqVnACFsDSCCAAlEqtVove3t7MeLvuAxkdHc2MpeoBIE0AAaB0Uqsg7QogqXav/v7+tnxsgCoQQAAonTw3oqdWQFL7UgBIE0AAKJ3UA//Y2Fhb9oFMTk7Oqx4A0gQQAEqnp6cn6vV6ZrwdbVipE7BSKzIApAkgAJRSHvtAUu/fBnSAhRFAACiliy++ODO2bdu2ln5M938ALJ0AAkApzXUfyMTERMs+ZiqAOAELYGEEEABKKY/7QFIBZHBwsGUfD6CKBBAASuuSSy7JjG3durVlH88KCMDSCSAAlFZq9aFV94GkVlbq9XrUarWWfDyAqhJAACitoaGhTABoNBrJlYqlSr1P938ALJwAAkCppVZBWtGGlVoBcf8HwMIJIACUWuo43lYEkFRrlxUQgIUTQAAotdQqxNjYWDQajaZ9jLnenxUQgIUTQAAotZ6enqjX65nxH/7wh037GKOjo5kxx+8CLI4AAkDptboNK9V+ZfUDYHEEEABKb926dZmxbdu2Na0NKxVArIAALI4AAkDp9fX1tawNa2JiIiYmJjLjVkAAFkcAAaASWtWGlTp+1+oHwOIJIABUQqvasFIhxvG7AIsngABQCX19fZlb0SOW3oaV2v+RWm0BYH4EEAAqo9ltWMPDw5kVlFqtZv8HwBIIIABURiqALKUNKxVerH4ALI0AAkBlXHzxxck2rC1btizq/W3bti0zZgM6wNIIIABUytq1azNjX/3qVxf8fuY6fveSSy5ZVF0AHCKAAFApGzZsyIxNTEwkj9M9ks2bN2fGent7kyssAMyfAAJApfT09CTbpG6//fYFvZ9U+1XqqF8AFkYAAaByUm1Yt99+e7KlKmXr1q3JtxVAAJZOAAGgctatWxf1ej0zfsMNN8zr76dOv7rooou0XwE0gQACQCWlVivmswoyMTGRbNey+gHQHAIIAJW0YcOG5IrF0VZBUn9eq9Xc/wHQJAIIAJVUq9WSJ2LdfvvtMTY2lvw7c61+pN4PAIsjgABQWXOtgnziE59I3o5+zTXXZMbmCjIALI4AAkBlzRUexsbGMmFjy5Ytyc3nc4UYABZnWd4FAEArbdy4MX74wx/Ggw8+OGt8y5YtERHxvve9L0ZGRuK//Jf/kvm7Vj8Amk8AAaDybr755rj00kszbVdbtmyJb3/72xERsXz58szf+9znPmf1A6DJtGABUHl9fX2xcePGBf2dtWvXOnoXoAUEEAA6woYNG+YdQnp7e2PTpk0trgigMwkgAHSMjRs3xo033njEt7noooviz//8z7VeAbSIAAJAR1m3bl3cd999sXbt2lkhY3BwMG688cb4+te/LnwAtJBN6AB0nJ6enrjpppsiImLXrl0RETEwMJBjRQCdwwoIAADQNgIIAADQNgIIAADQNgIIAADQNgIIAADQNgIIAADQNv8frcq5wuYIzTwAAAAASUVORK5CYII=
|
The graph of $g'$ is given.
Let $g$ be a differentiable function with $g(1)=-4$. The graph of $g'(x)$, the derivative of $g$, is shown. Write an equation for the line tangent to the graph of $g$ at $x=1$.
|
The equation for the tangent line is $y+4=-3\cdot(x-1)$
|
04960c86-a731-4641-a3a8-fd0529de5a51
|
multivariable_calculus
| false
| null |
Evaluate $\int\int\int_{E}{(x+2 \cdot y \cdot z) \, dV}$, where $E = \left\{(x,y,z) | 0 \le x \le 1, 0 \le y \le x, 0 \le z \le 5-x-y \right\}$.
|
$I$ = $\frac{439}{120}$
|
U-MATH is a comprehensive benchmark of 1,100 unpublished university-level problems sourced from real teaching materials.
It is designed to evaluate the mathematical reasoning capabilities of Large Language Models (LLMs).
The dataset is balanced across six core mathematical topics and includes 20% of multimodal problems (involving visual elements such as graphs and diagrams).
For fine-grained performance evaluation results and detailed discussion, check out our paper.
- 📊 U-MATH benchmark at Huggingface
- 🔎 μ-MATH benchmark at Huggingface
- 🗞️ Paper
- 👾 Evaluation Code at GitHub
Key Features
- Topics Covered: Precalculus, Algebra, Differential Calculus, Integral Calculus, Multivariable Calculus, Sequences & Series.
- Problem Format: Free-form answer with LLM judgement
- Evaluation Metrics: Accuracy; splits by subject and text-only vs multimodal problem type.
- Curation: Original problems composed by math professors and used in university curricula, samples validated by math experts at Toloka AI, Gradarius
Use it
from datasets import load_dataset
ds = load_dataset('toloka/u-math', split='test')
Dataset Fields
uuid: problem id has_image: a boolean flag on whether the problem is multimodal or not image: binary data encoding the accompanying image, empty for text-only problems subject: subject tag marking the topic that the problem belongs to problem_statement: problem formulation, written in natural language golden_answer: a correct solution for the problem, written in natural language \
For meta-evaluation (evaluating the quality of LLM judges), refer to the µ-MATH dataset.
Evaluation Results
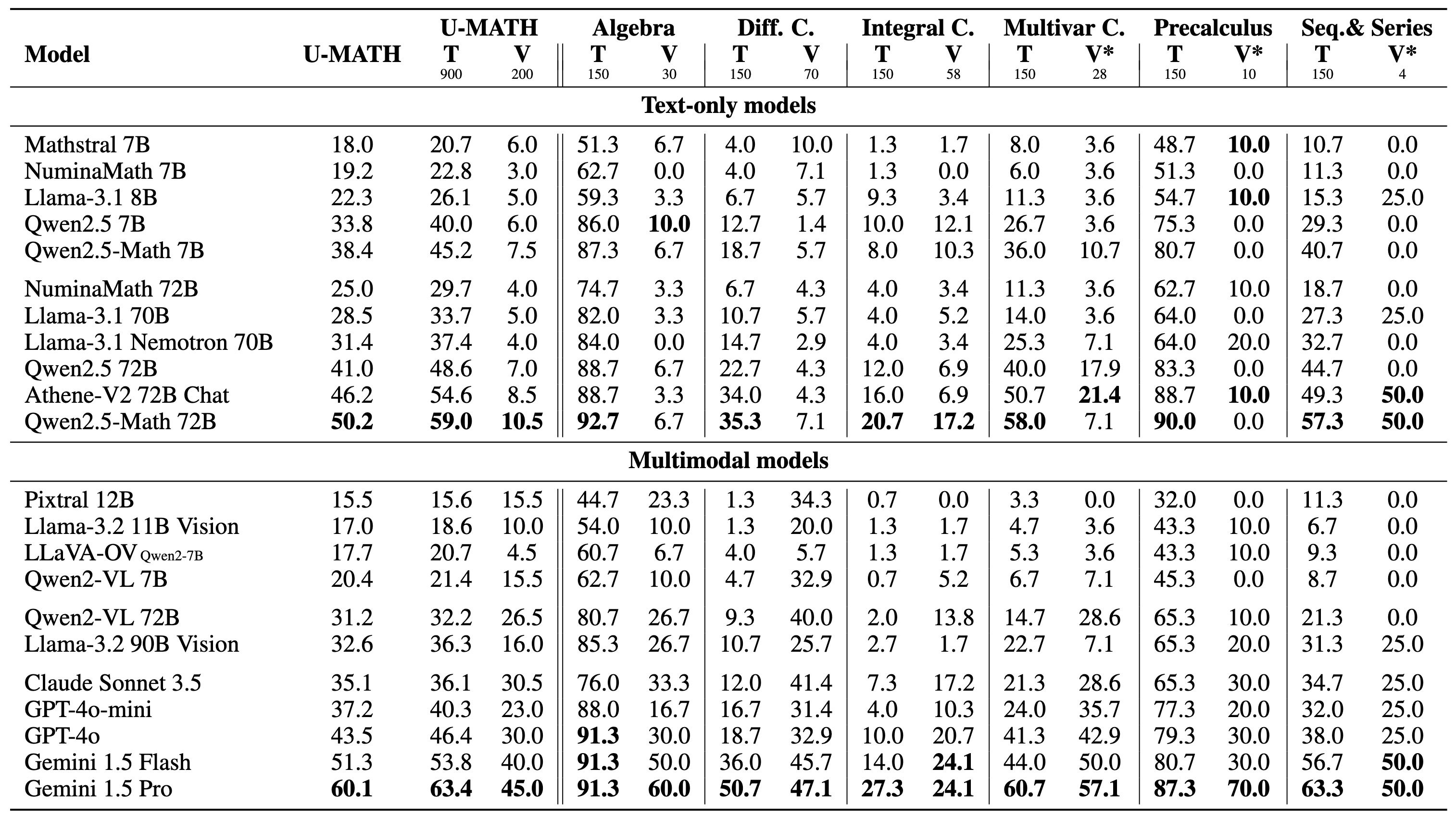
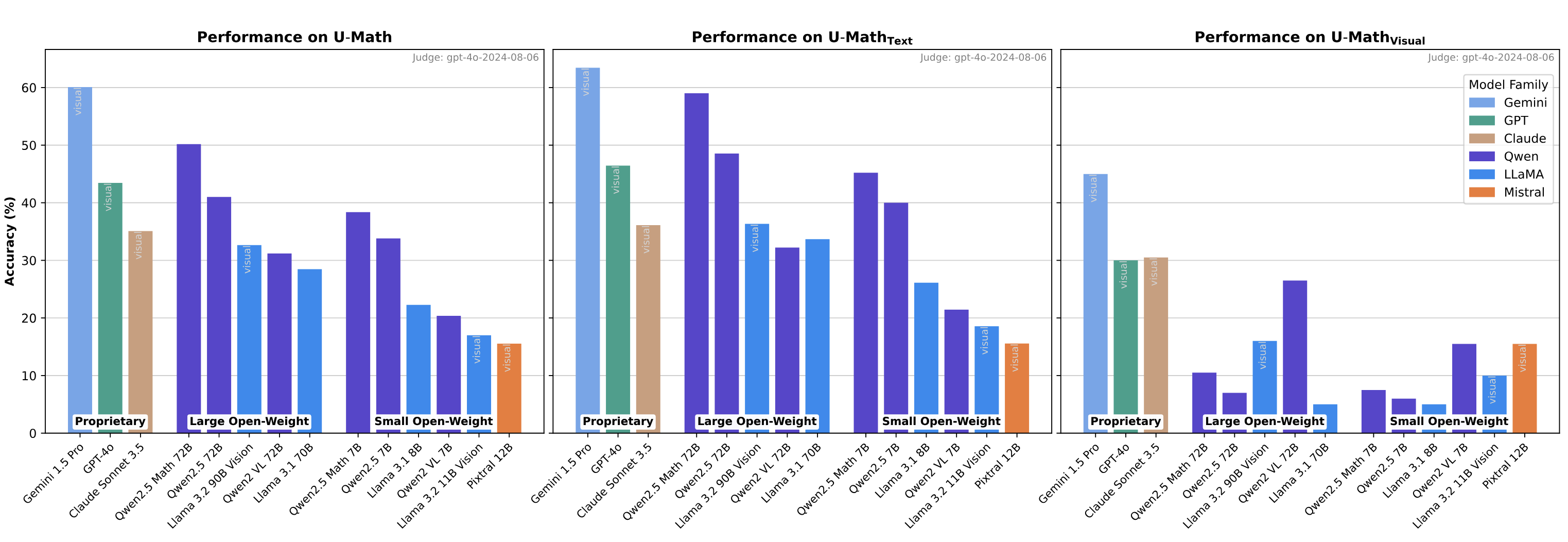
The prompt used for inference:
{problem_statement}
Please reason step by step, and put your final answer within \boxed{}
Licensing Information
All the dataset contents are available under the MIT license.
Citation
If you use U-MATH or μ-MATH in your research, please cite the paper:
@inproceedings{umath2024,
title={U-MATH: A University-Level Benchmark for Evaluating Mathematical Skills in LLMs},
author={Konstantin Chernyshev, Vitaliy Polshkov, Ekaterina Artemova, Alex Myasnikov, Vlad Stepanov, Alexei Miasnikov and Sergei Tilga},
year={2024}
}
Contact
For inquiries, please contact kchernyshev@toloka.ai
- Downloads last month
- 270